Short-Term Prediction of Ship Heave Motion Using a PSO-Optimized CNN-LSTM Model
Abstract
1. Introduction
- (1)
- A hybrid PSO-CNN-LSTM prediction model is proposed to improve the prediction accuracy of nonlinear and unsteady ship heave motion, laying the foundation for developing an active wave compensation control system;
- (2)
- The wave model based on the P–M spectrum and the ship model based on slice theory are constructed, and the ship heave motion simulation under different sea conditions is carried out. The simulation signal is used as the input data of the PSO-CNN-LSTM prediction model;
- (3)
- The PSO algorithm optimizes the parameters of the CNN, and a hybrid PSO-CNN-LSTM neural network is constructed. The prediction accuracy and stability of the hybrid neural network model are verified by simulation.
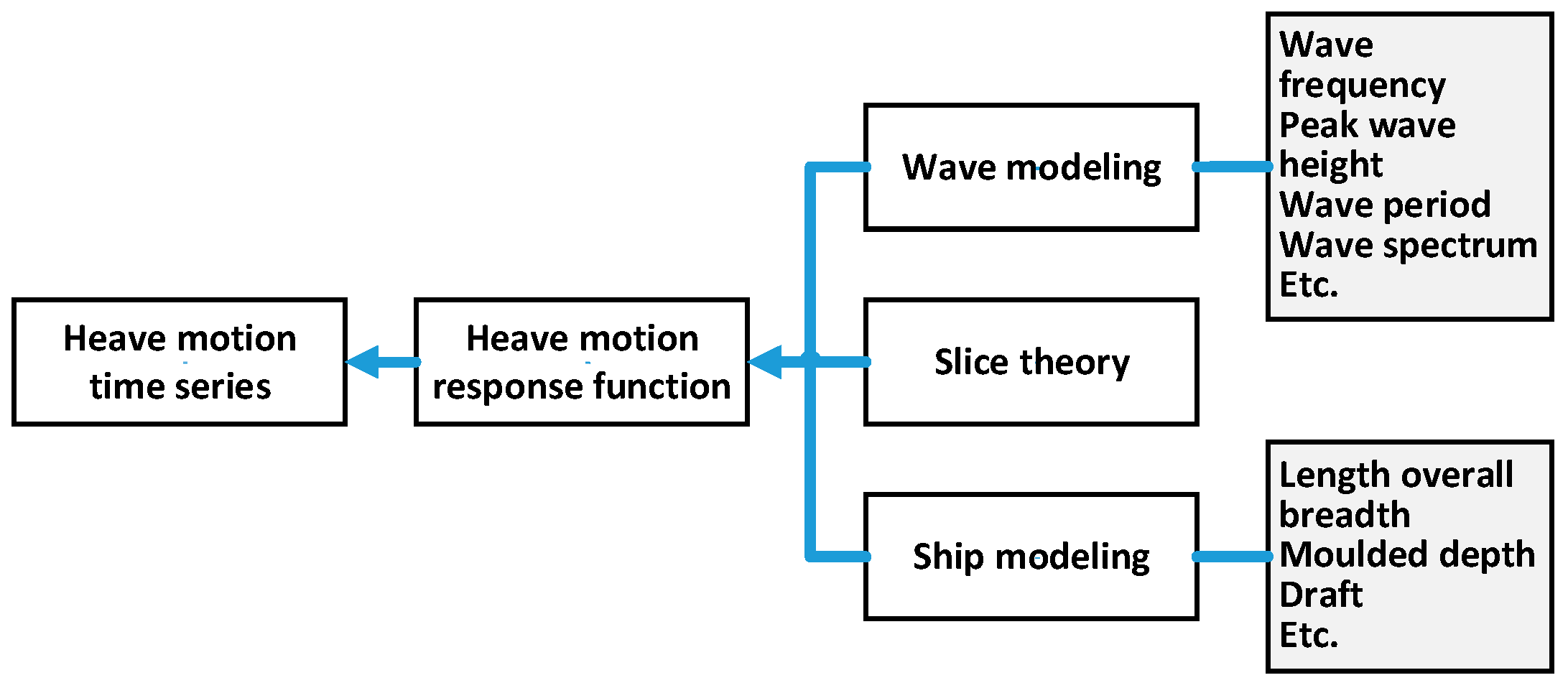
2. Data Generation
2.1. Modeling of Ship Heave Motion
- (1)
- Wave Modeling
- (2)
- Ship Motion Modeling
- (1)
- It is assumed that the ship is constrained in the direction of longitudinal displacement and pitch angle (pitch); that is, the ship does not produce fore-and-aft displacement and pitch angle motion;
- (2)
- It is assumed that the ship is constrained in the direction of lateral displacement and roll angle (roll); that is, the ship does not produce left–right displacement and roll motion;
- (3)
- It is assumed that the rotation (yaw) of the ship about the axis perpendicular to the water surface is constrained; that is, the ship does not rotate around the vertical axis.
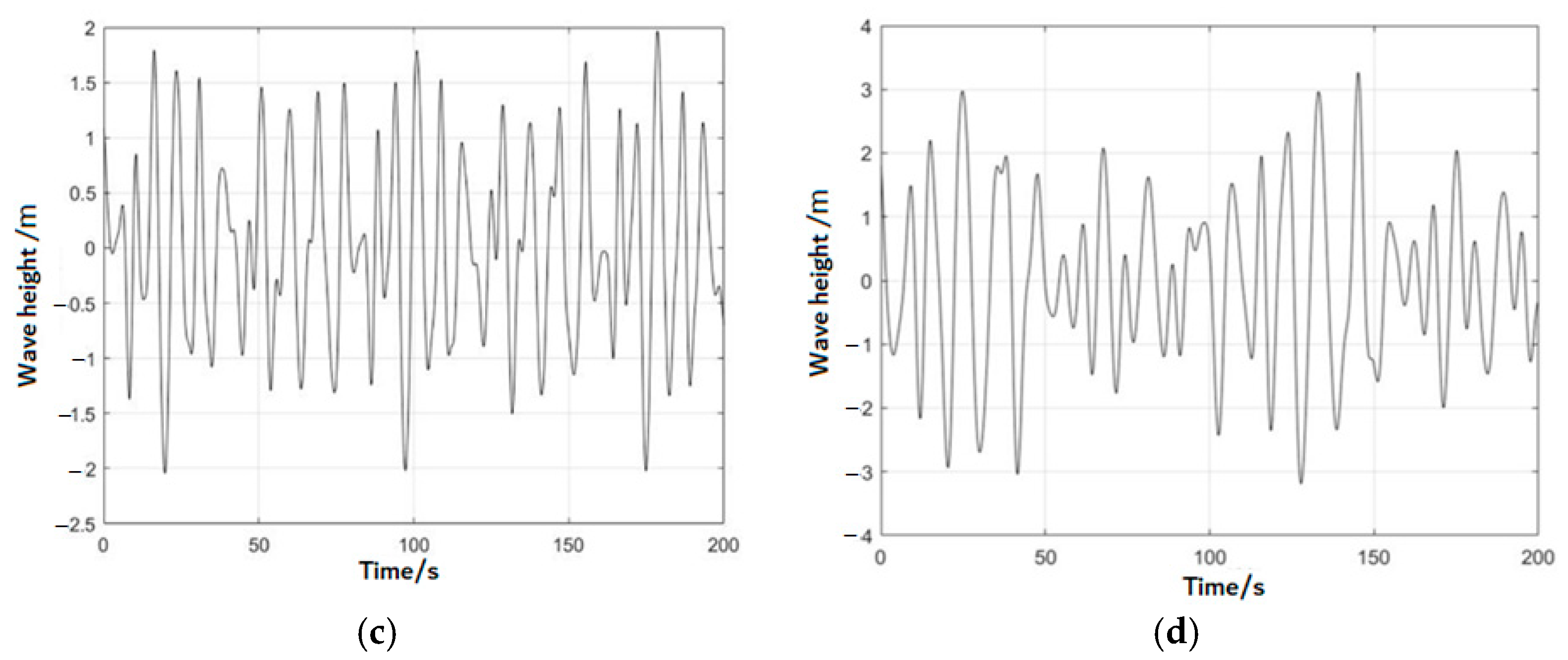
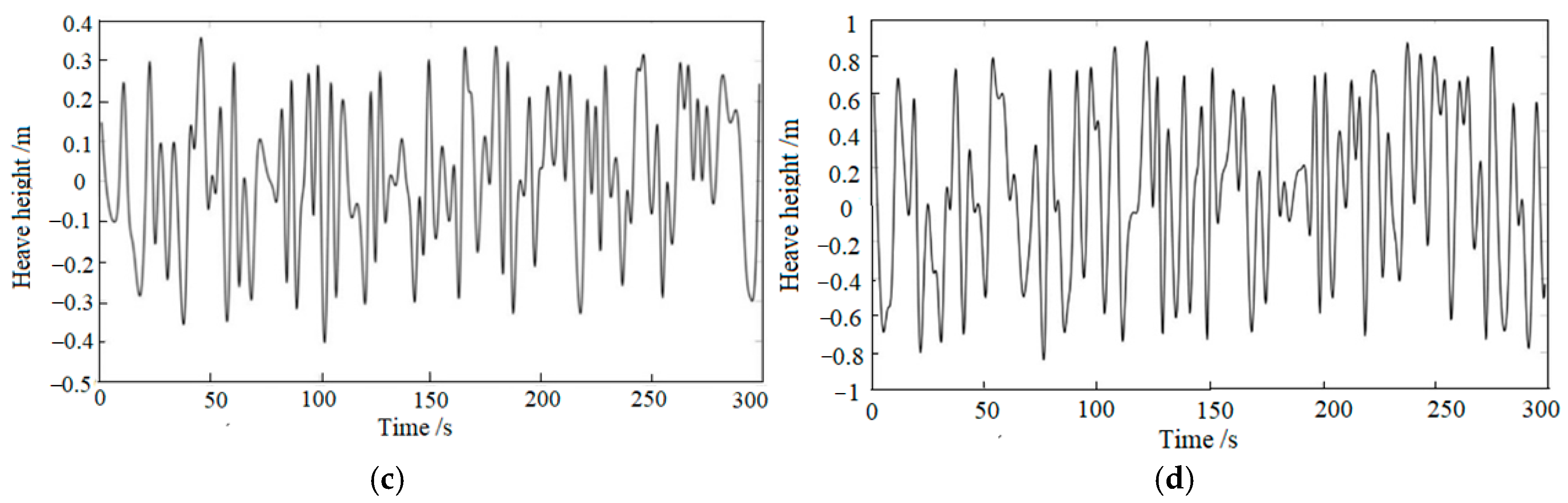
2.2. Simulation of Ship Heave Motion
3. The Proposed Methodology
3.1. CNN-LSTM Modeling and Simulation
3.2. PSO-CNN-LSTM Hybrid Model Modeling
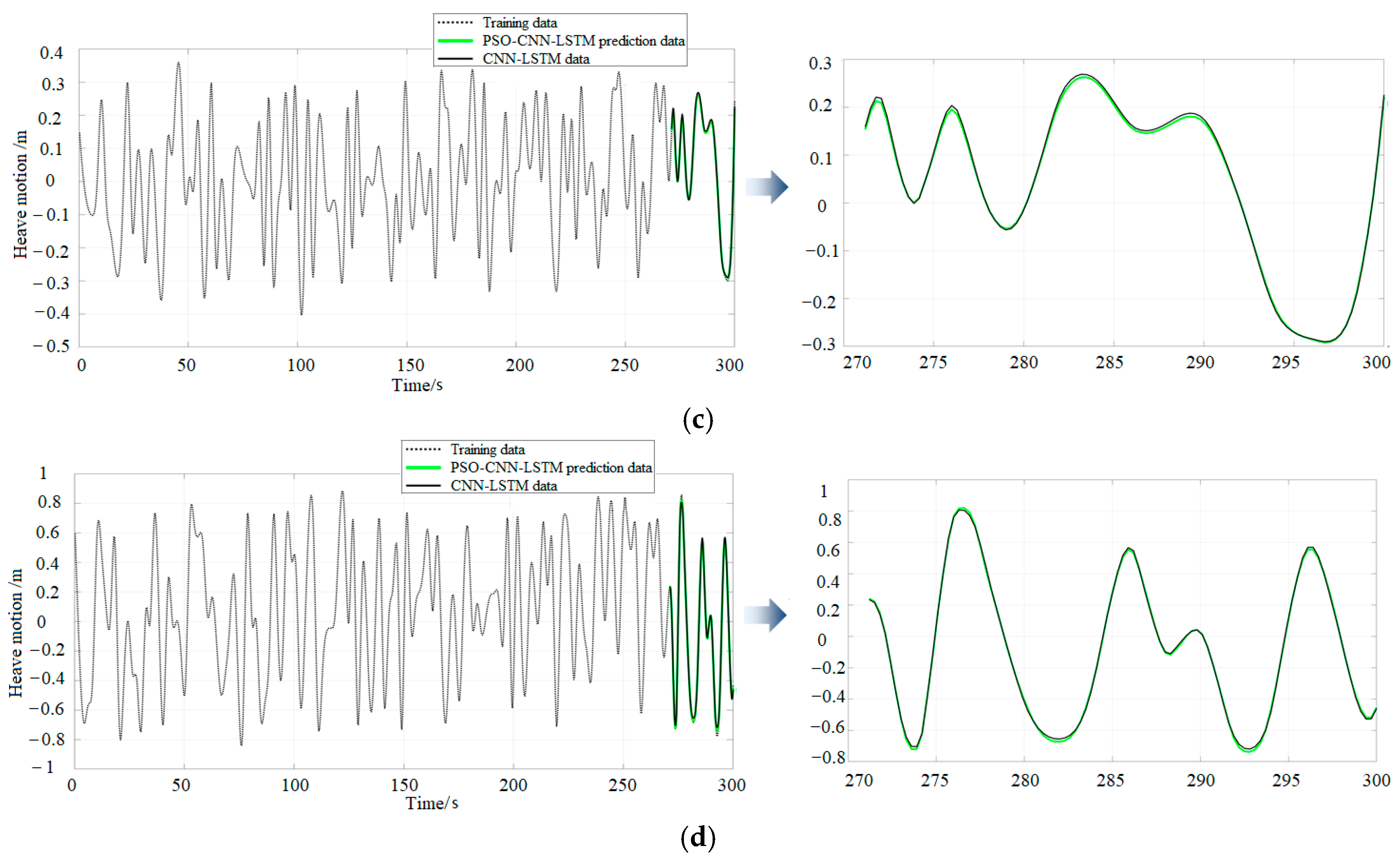
3.3. Performance Analysis of the PSO-CNN-LSTM Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Chen, S. Overview of research on marine resources and economic development. Mar. Econ. Manag. 2022, 5, 69–83. [Google Scholar] [CrossRef]
- Pan, Z.; Guo, X.; Li, X. Research on Short-Term Prediction of Offshore Platforms Based on Multi-Platform Training. Ocean Eng. 2024, 42, 68–79. [Google Scholar] [CrossRef]
- Kim, D.; Song, S.; Jeong, B.; Tezdogan, T. Numerical evaluation of a ship’s manoeuvrability and course keeping control under various wave conditions using CFD. Ocean Eng. 2021, 237, 109615. [Google Scholar] [CrossRef]
- Woodacre, J.K.; Bauer, R.J.; Irani, R.A. A review of vertical motion heave compensation systems. Ocean Eng. 2015, 104, 140–154. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Benbouzid, M.; Charpentier, J.-F.; Aϊt-Ahmed, N.; Han, J. Improved Fractional-Order PID Controller of a PMSM-Based Wave Compensation System for Offshore Ship Cranes. J. Mar. Sci. Eng. 2022, 10, 1238. [Google Scholar] [CrossRef]
- Yi, Z.; Jiamin, G.; Huanghua, P. Simulation of Offshore Wind Turbine Blade Docking Based on the Stewart Platform; College of Ocean Science and Engineering, Shanghai Maritime University: Shanghai, China, 2023; Volume 120, pp. 70–78. [Google Scholar]
- Ibrahim, M.M. Active Heave Compensation Aids Research from Vessels. Sea Technol. 2019, 60, 165–178. [Google Scholar]
- Wu, H.M.; Yang, W.; Ong, M.C.; Fan, T.; Yin, G.; Zeng, W.; Situa, W.; Wang, Y. A Control Algorithm of Active Wave Compensation System Based on the Stewart Platform. J. Phys. Conf. Ser. 2023, 2458, 012040. [Google Scholar] [CrossRef]
- Tang, G.; Lu, P.; Hu, X.; Men, S. Control system research in wave compensation based on particle swarm optimization. Sci. Rep. 2021, 11, 15316. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Kujala, P.; Musharraf, M.; Zhang, J.; Hirdaris, S. A machine learning method for the prediction of ship motion trajectories in real operational conditions. Ocean Eng. 2023, 283, 114905. [Google Scholar] [CrossRef]
- Chen, Z.; Che, X.; Wang, L.; Zhang, L. Machine learning for ship heave motion prediction: Online adaptive cycle reservoir with regular jumps. Ocean Eng. 2024, 294, 116767. [Google Scholar] [CrossRef]
- Huang, L.; Deng, X.; Bo, Y.; Zhang, Y.; Wang, P. Evolutionary optimization assisted delayed deep cycle reservoir modeling method with its application to ship heave motion prediction. ISA Trans. 2022, 126, 638–648. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Chen, Z.; Zhao, C.; Chen, X.; He, J.; Zhang, C. A time-varying ensemble model for ship motion prediction based on feature selection and clustering methods. Ocean Eng. 2023, 270, 113659. [Google Scholar] [CrossRef]
- D’Agostino, D.; Serani, A.; Stern, F.; Diez, M. Time-series forecasting for ships maneuvering in waves via recurrent-type neural networks. J. Ocean Eng. Mar. Energy 2022, 8, 479–487. [Google Scholar] [CrossRef]
- Li, D.; Wang, S.; Song, X.; Zheng, Z.; Tao, W.; Che, J. A BP-Neural-Network-Based PID Control Algorithm of Shipborne Stewart Platform for Wave Compensation. J. Mar. Sci. Eng. 2024, 12, 2160. [Google Scholar] [CrossRef]
- Sun, Q.; Tang, Z.; Gao, J.P.; Zhang, G.C. Short-term ship motion attitude prediction based on LSTM and GPR. Appl. Ocean Res. 2022, 118, 102927. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, W.; Li, S.; Liu, H.; Hu, Q. YOLO-Ships: Lightweight ship object detection based on feature enhancement. J. Vis. Commun. Image Represent. 2024, 101, 104170. [Google Scholar] [CrossRef]
- Yang, W.; Liang, Y.; Li, M. The Autocorrelation Function Obtained from the Pierson-Moskowitz Spectrum. In Proceedings of the Global Oceans 2020: Singapore-U.S. Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Katopodes, N.D. Chapter 2—Air-Water Interface. In Free-Surface Flow; Butterworth-Heinemann: Oxford, UK, 2019; pp. 44–121. ISBN 9780128154878. [Google Scholar] [CrossRef]
- Bandyk, P.J. A Body-Exact Strip Theory Approach to Ship Motion Computations. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2009. [Google Scholar]
- Li, C.; Zhu, R.; Wang, Z.; Xu, D.; Wang, H. A hybrid harmonic polynomial cell and STF strip theory method for marine hydrodynamics and ship motion analysis. Ships Offshore Struct. 2025, 1–19. [Google Scholar] [CrossRef]
- Duan, W.; Ma, X.; Huang, L.; Liu, Y.; Duan, S. Phase-resolved wave prediction model for long-crest waves based on machine learning. Comput. Methods Appl. Mech. Eng. 2020, 372, 113350. [Google Scholar] [CrossRef]
- Mu, D.; Lang, Z.; Fan, Y.; Wang, G. Simulation and Control Applications Based on PM Wave Spectra. In Proceedings of the 2022 7th International Conference on Automation, Control and Robotics Engineering (CACRE), Xi’an, China, 14–16 July 2022; pp. 109–114. [Google Scholar] [CrossRef]
- Hao, W.; Huang, L.-m.; Wang, C.-y.; Jing, Y.; Ma, X.-w. Comparative Analysis and Research on Forecasting Methods of Significant Wave Height in Ocean Waves. In Proceedings of the 16th National Conference on Hydrodynamics and the 32nd National Symposium on Hydrodynamics, Wuxi, China, 29 October–1 November 2021; pp. 1671–1677. [Google Scholar]
- Wen, X.; Li, J.; Wang, H.; Zhu, H. Research on ship heave estimation method based on simplified Sage-Husa adaptive filtering. Ship Sci. Technol. 2023, 45, 45–49. [Google Scholar] [CrossRef]
- Carlisle, A.J.Z. Applying the Particle Swarm Optimizer to Non-Stationary Environments. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2002. [Google Scholar]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]











| Sea States | Significant Wave Height (h1/3/m) | Sea-Breeze Speed (m/s) | Wave Period (T/s) | Main Range of Wave Period (s) |
|---|---|---|---|---|
| Force three | 1.01 | 6.9 | 3.6 | 1.4~7.6 |
| Force four | 2.01 | 9.8 | 5.1 | 2.8~10.6 |
| Force five | 3.33 | 12.6 | 6.6 | 3.8~13.6 |
| Force six | 5.15 | 15.7 | 8.2 | 4.8~17 |
| Significant Wave Height (ℎ1/3/m) | Sea-Breeze Speed (m/s) | Simulation Frequency (rad/s) | Simulation Frequency Increment (rad/s) |
|---|---|---|---|
| 1.01~2.50 | <10.00 | 0.30~3.00 | 0.10 |
| 2.50~5.00 | 10.00~12.75 | 0.25~2.40 | 0.08 |
| >5.00 | >12.75 | 1.00~1.7 | 0.06 |
| Parameters | Symbols | Unit | Value |
|---|---|---|---|
| Length overall | L | m | 189.9 |
| Breadth | B | m | 32.26 |
| Moulded depth | D | m | 15.7 |
| Draft | d | m | 10.3 |
| Full load displacement | V | t | 48,000 |
| Added mass of heave | Izz | kg | 4,897,959 |
| Heave natural circular frequency | w | rad/s | 6.28 |
| Non-dimensional damping coefficient | / | / | 7.048 |
| Correction factor | / | / | 0.8 |
| Sea States | Hybrid Model | R2 | RMSE | MAE | MSE |
|---|---|---|---|---|---|
| Force three | PSO-CNN-LSTM CNN-LSTM | 0.98824 0.98238 | 0.01549 0.01603 | 0.01501 0.01446 | 0.00021 0.00023 |
| Force four | PSO-CNN-LSTM CNN-LSTM | 0.99029 0.98916 | 0.01342 0.01381 | 0.01284 0.01271 | 0.00018 0.00018 |
| Force five | PSO-CNN-LSTM CNN-LSTM | 0.99257 0.99068 | 0.01168 0.01185 | 0.01014 0.01069 | 0.00012 0.00014 |
| Force six | PSO-CNN-LSTM CNN-LSTM | 0.99818 0.99314 | 0.00837 0.01049 | 0.00781 0.00983 | 0.00007 0.00011 |
| Sea States | Hybrid Model | R2 | RMSE | MAE | MSE |
|---|---|---|---|---|---|
| Force three | PSO-CNN-LSTM CNN-LSTM | 0.98351 0.97338 | 0.01673 0.01975 | 0.01621 0.01833 | 0.00028 0.00039 |
| Force four | PSO-CNN-LSTM CNN-LSTM | 0.98836 0.98025 | 0.01549 0.01871 | 0.01476 0.01798 | 0.00024 0.00035 |
| Force five | PSO-CNN-LSTM CNN-LSTM | 0.99062 0.98471 | 0.01265 0.01673 | 0.01197 0.01595 | 0.00016 0.00028 |
| Force six | PSO-CNN-LSTM CNN-LSTM | 0.99531 0.99053 | 0.01140 0.01479 | 0.01093 0.01330 | 0.00013 0.00024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Tang, G.; Zhang, J.; Sun, Q.; Liu, X. Short-Term Prediction of Ship Heave Motion Using a PSO-Optimized CNN-LSTM Model. J. Mar. Sci. Eng. 2025, 13, 1008. https://doi.org/10.3390/jmse13061008
Li G, Tang G, Zhang J, Sun Q, Liu X. Short-Term Prediction of Ship Heave Motion Using a PSO-Optimized CNN-LSTM Model. Journal of Marine Science and Engineering. 2025; 13(6):1008. https://doi.org/10.3390/jmse13061008
Chicago/Turabian StyleLi, Guowei, Gang Tang, Jingyu Zhang, Qun Sun, and Xiangjun Liu. 2025. "Short-Term Prediction of Ship Heave Motion Using a PSO-Optimized CNN-LSTM Model" Journal of Marine Science and Engineering 13, no. 6: 1008. https://doi.org/10.3390/jmse13061008
APA StyleLi, G., Tang, G., Zhang, J., Sun, Q., & Liu, X. (2025). Short-Term Prediction of Ship Heave Motion Using a PSO-Optimized CNN-LSTM Model. Journal of Marine Science and Engineering, 13(6), 1008. https://doi.org/10.3390/jmse13061008






