Dynamic Modeling and Experimental Validation of Shock Isolation Performance for Shipborne Stewart-Platform-Based Bumper
Abstract
1. Introduction
- (1)
- A dynamic model of a Stewart-platform-based bumper under impact is derived;
- (2)
- An experimental/analytical simulation of impact is established;
- (3)
- Dynamic analyses of the bumper considering the dynamic properties and impact condition are conducted.
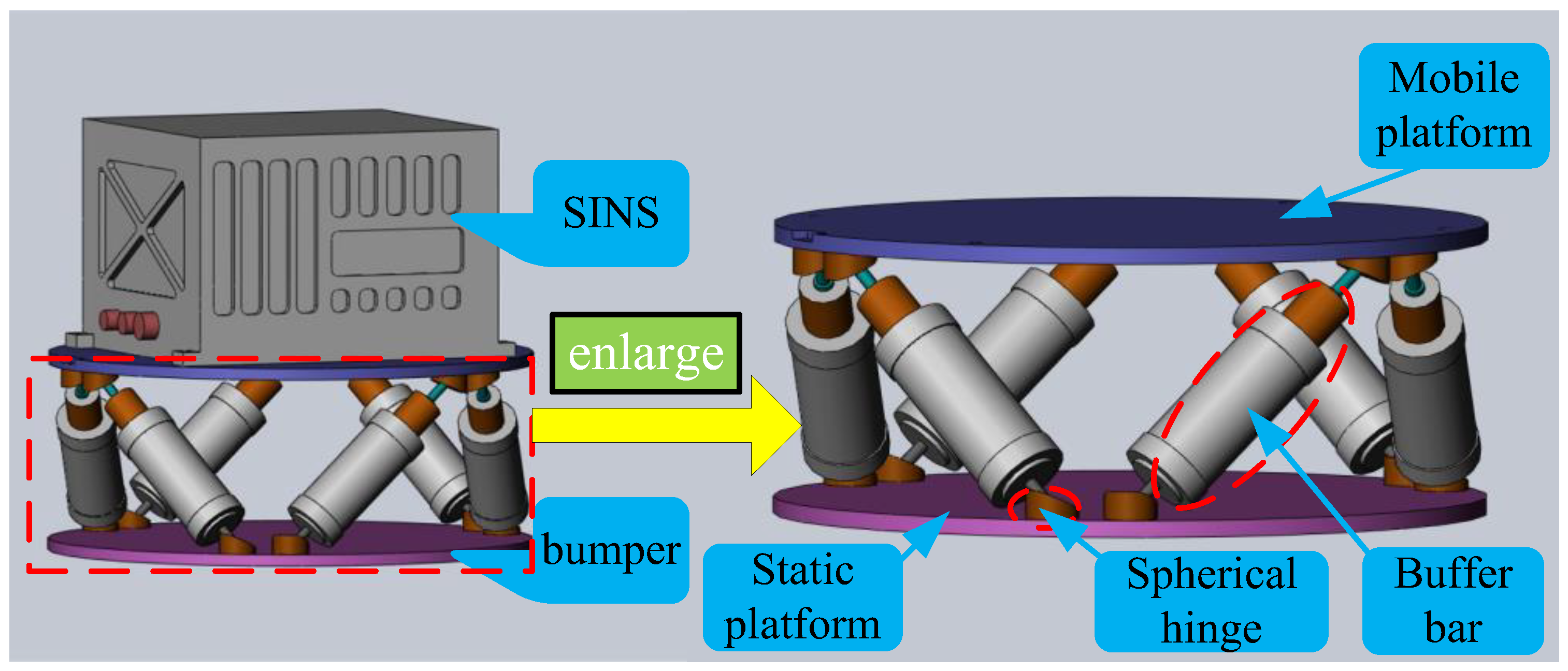
2. Stewart-Platform-Based Bumper
2.1. Anti-Shock Principle
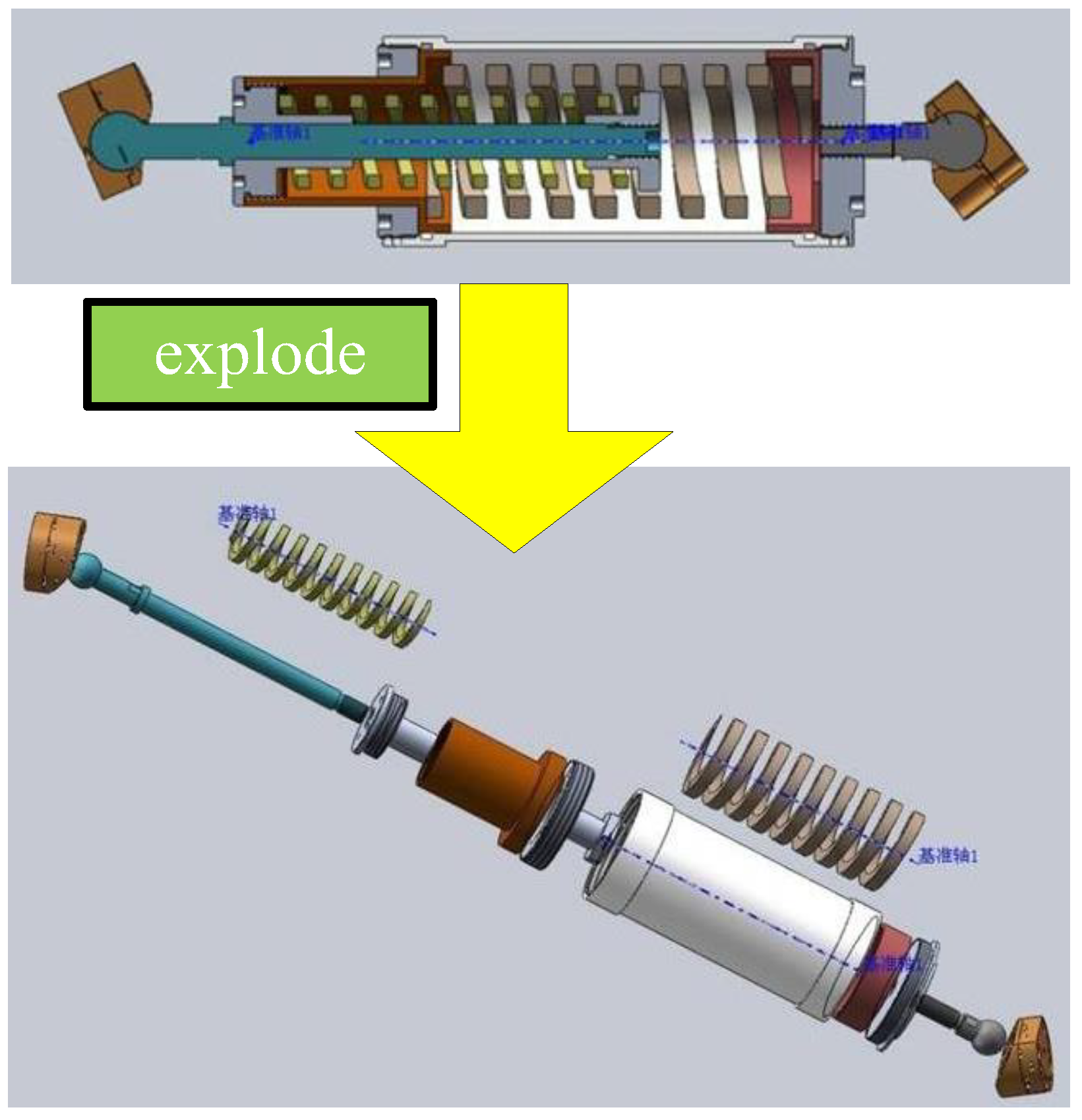
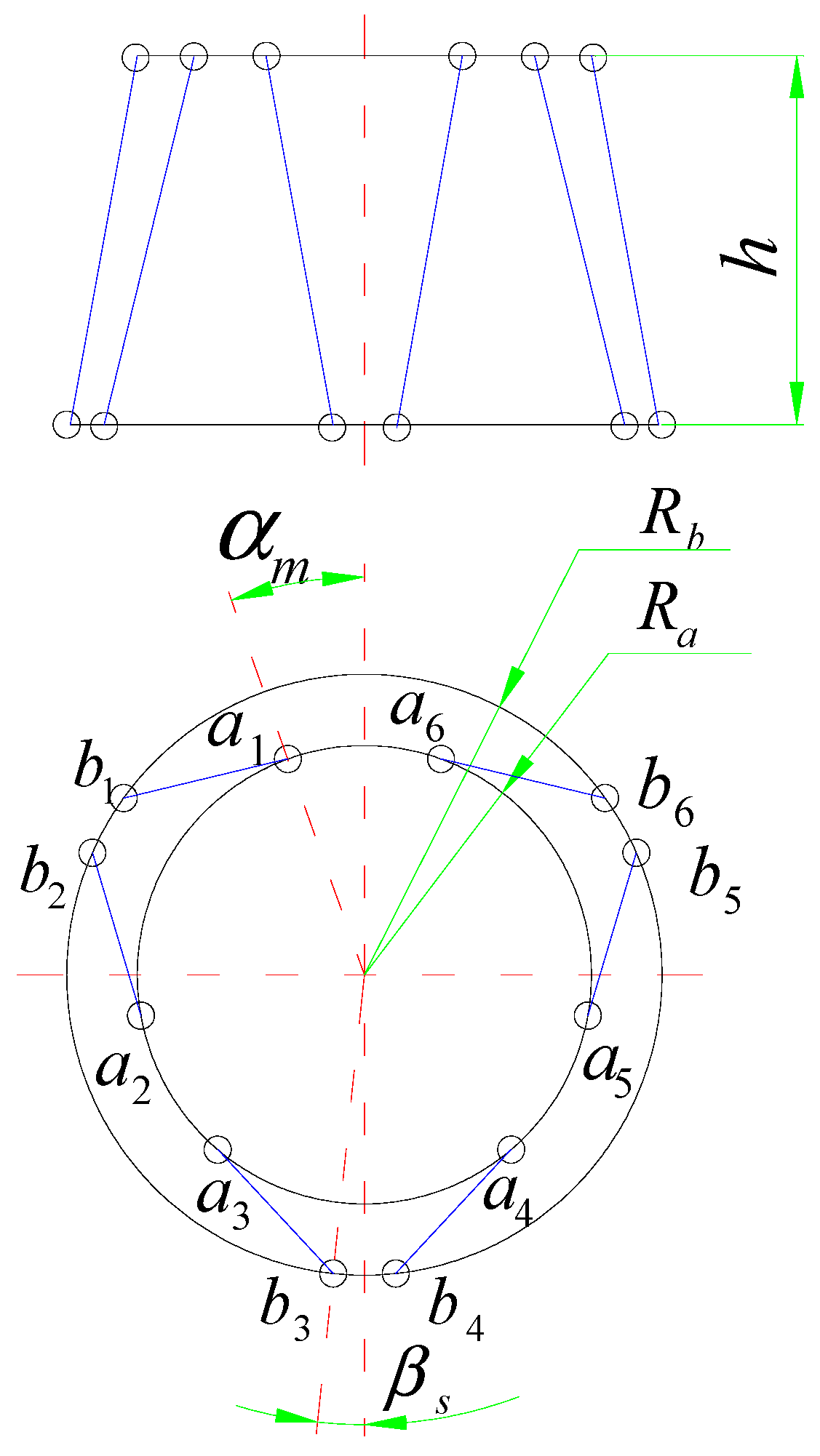
2.2. Mechanical Configuration
3. Dynamic Modeling
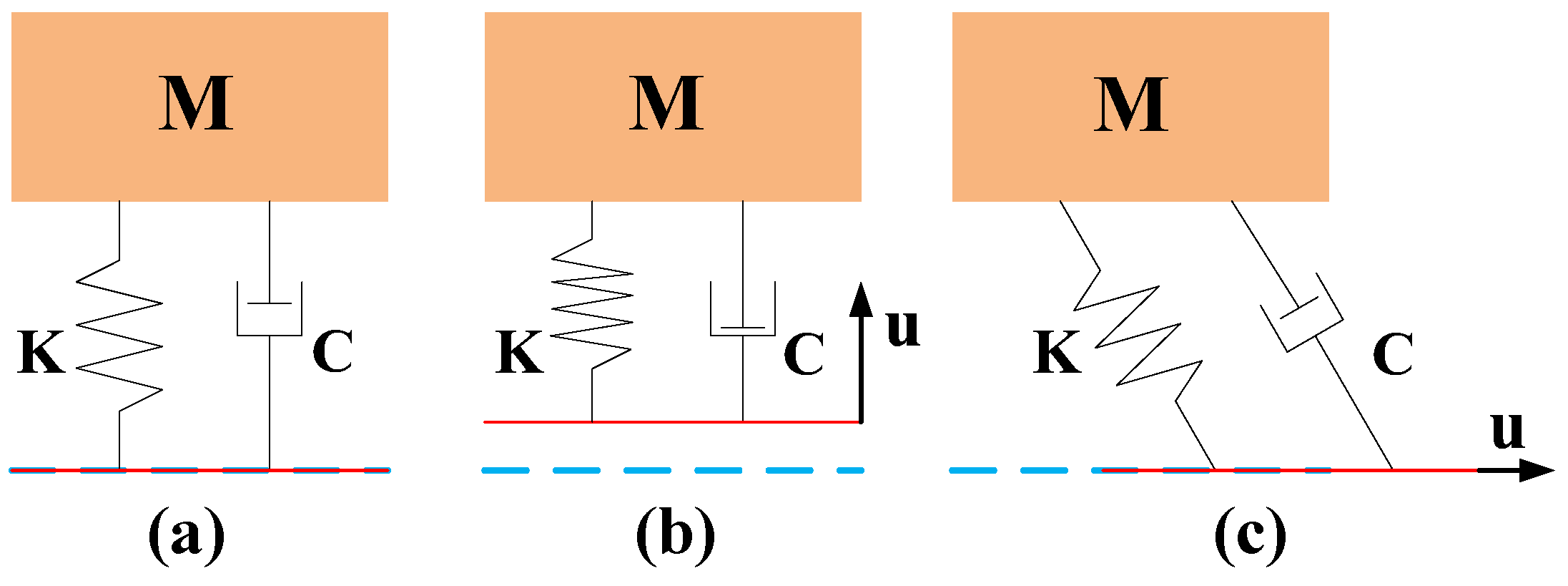
3.1. Dynamic Model of Bumper
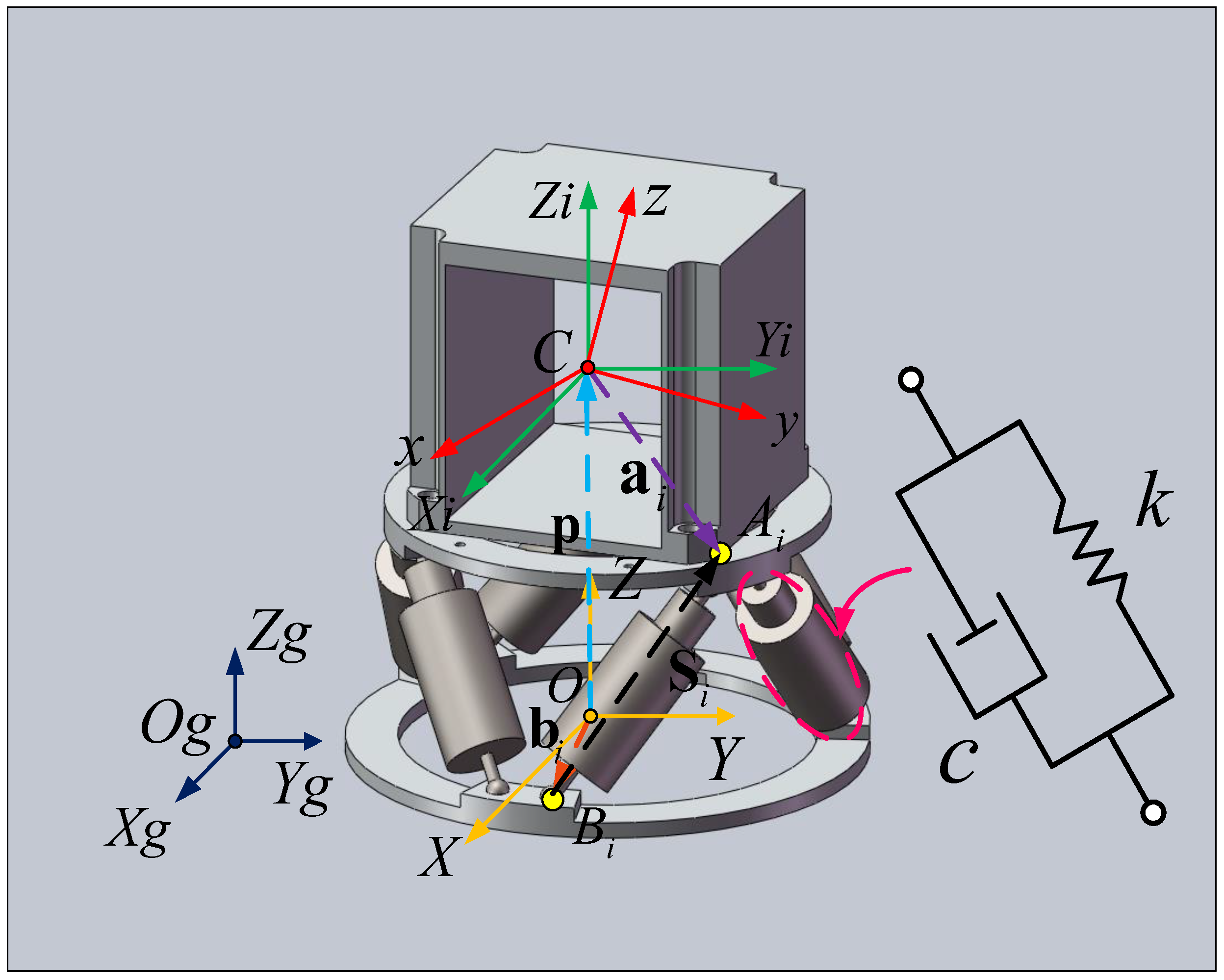
3.1.1. Coordinate Definition
3.1.2. Jacobian Matrix
3.1.3. Stiffness Matrix and Damping Matrix
3.1.4. Mass Matrix
3.2. Dynamic Model of Impact
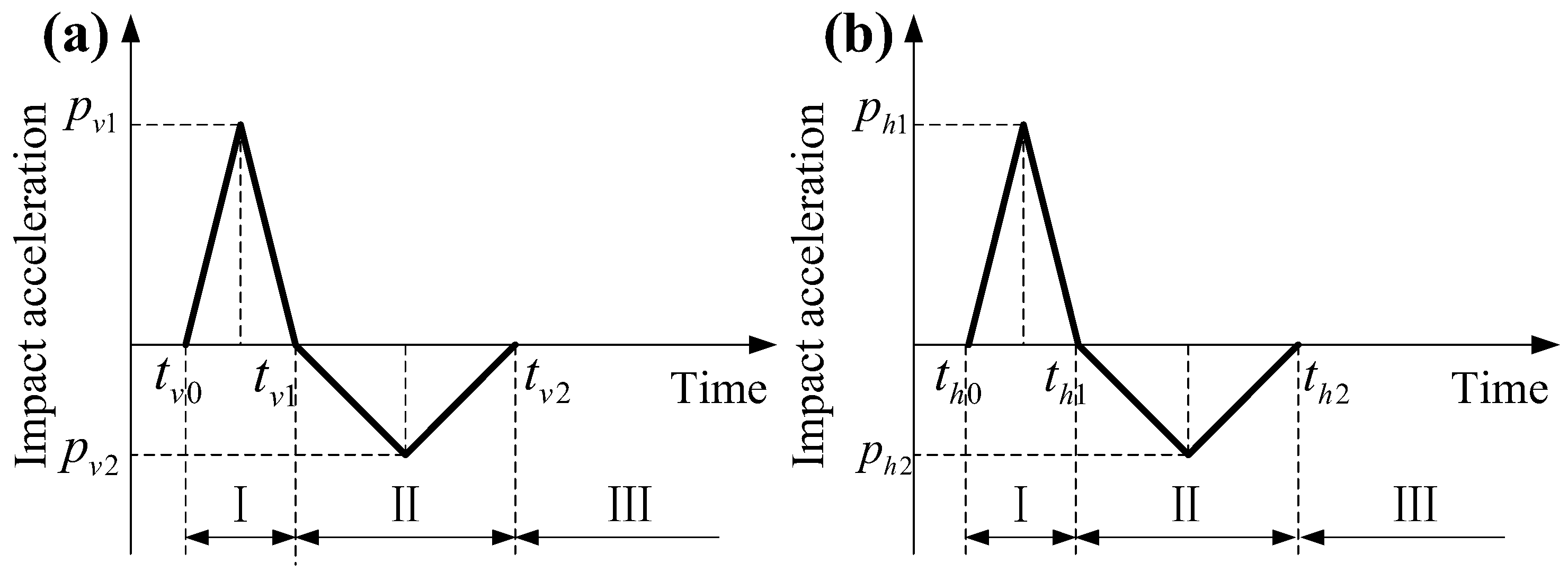
3.2.1. Simulation of Impact
3.2.2. Impact Force
3.3. Dynamic Equations of Bumper Under Impact
3.3.1. Dynamic Equations in Stage I and Stage II
3.3.2. Dynamic Equations in Stage III
4. Shock Isolation Performance
4.1. Evaluation of Shock Isolation Performance
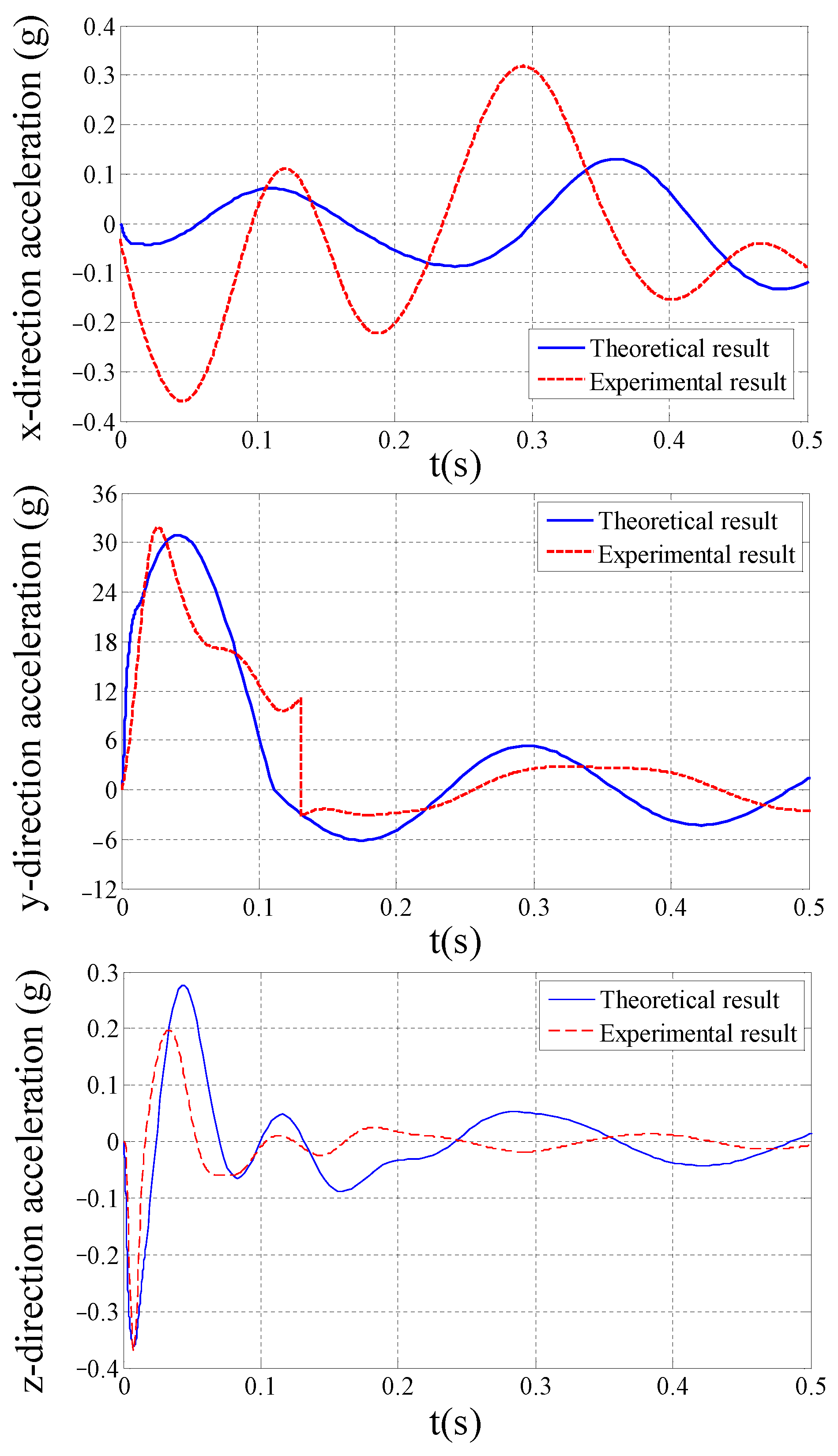
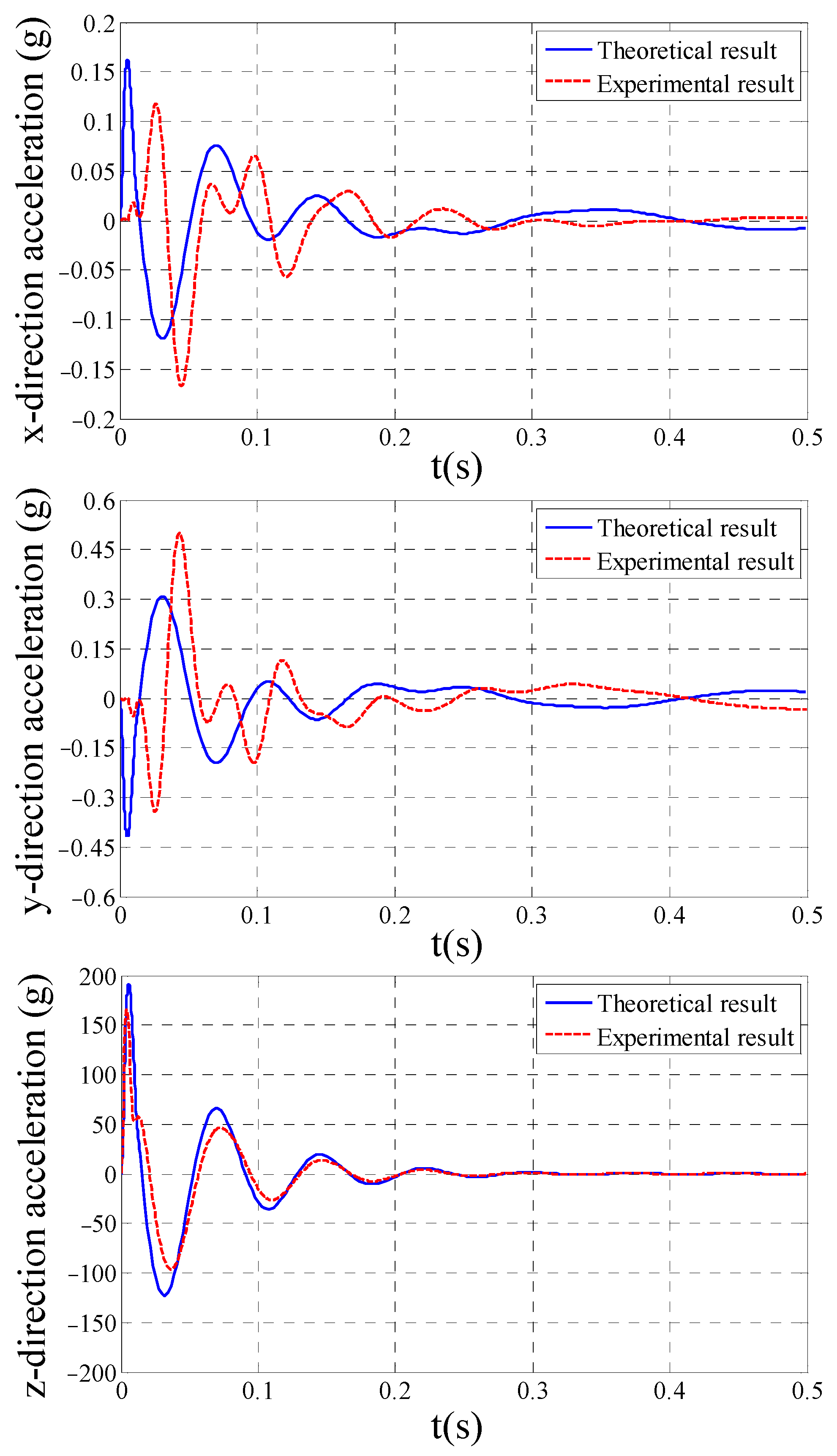
4.2. Theoretical Results
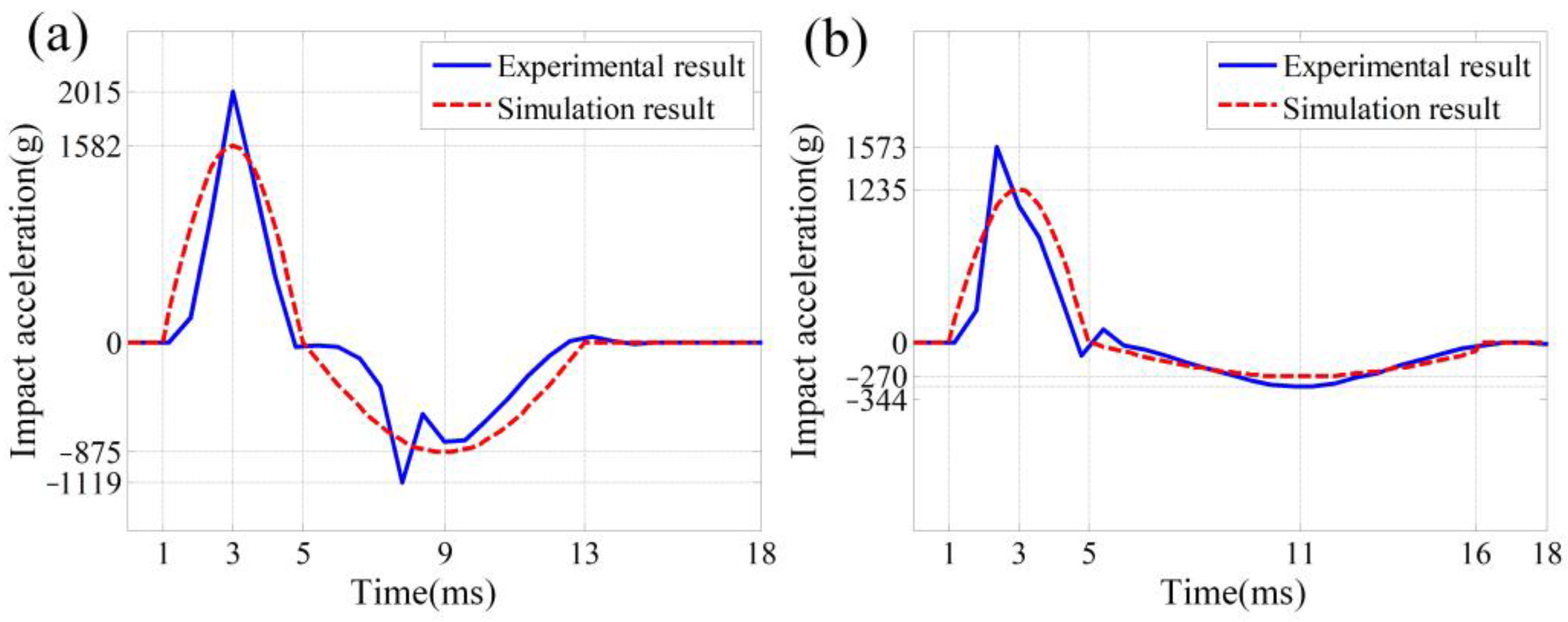
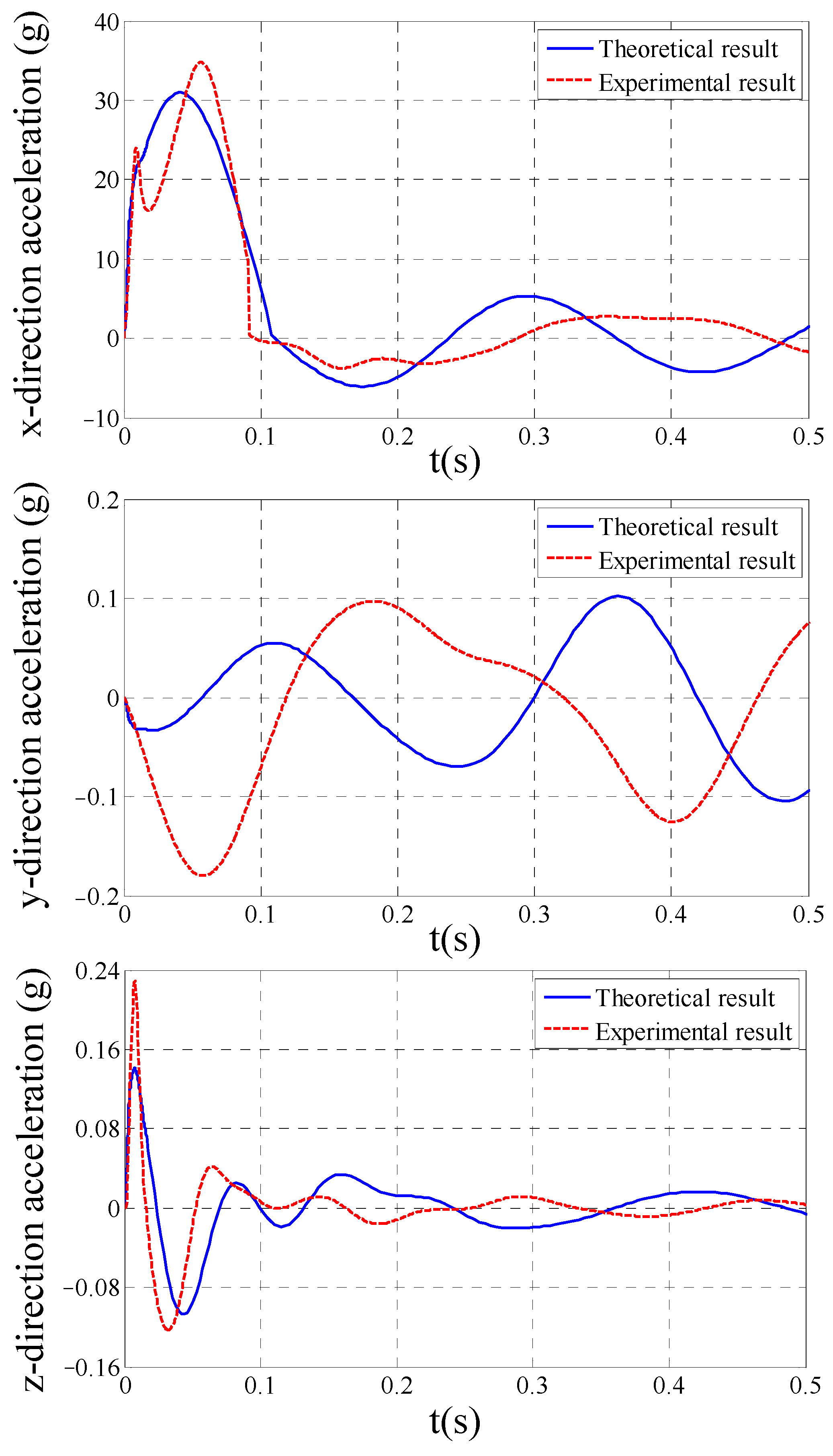
4.3. Experiment Results and Discussions
5. Conclusions
- (1)
- The theoretical x-, y- and z-direction-impact SARs are 1.96%, 1.96% and 9.51%, respectively;
- (2)
- The experimental x-, y- and z-direction-impact SARs are 2.21%, 2.21% and 8.23%, respectively;
- (3)
- The theoretical time domain responses of the load agree with the experiment results, with the theoretical predictions deviating less than 1.28% from the empirical data, verifying the proposed method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SINS | Strap-down inertial navigation system |
| DOF | Degree-of-freedom |
| GPS | Global positioning system |
| Height of the bumper | |
| Radius of the static platform | |
| Radius of the mobile platform | |
| Half-flare angle of the adjoining spherical hinge on the static platform | |
| Half-flare angle of the adjoining spherical hinge on the mobile platform | |
| Center of mass of the static platform | |
| Static platform frame | |
| Center of mass of the load (SINS and mobile platform) | |
| Load frame | |
| Intermediate frame of the load | |
| Ground frame | |
| Position vector of C in | |
| Upper spherical hinge centers | |
| Lower spherical hinge centers | |
| Generalized coordinate of the mobile platform | |
| Rotation matrix of the platform | |
| Rotation angular velocity vector of the mobile platform | |
| Length scalars of the buffer bars | |
| Stiffness of the buffer bar | |
| Damping of the buffer bar | |
| Mass of the load | |
| Gravitational acceleration | |
| Inertial tensor with respect to point C in | |
| Simulation function for vertical impact | |
| Simulation function for horizontal impact |
References
- Liu, Y.; Sun, Y.; Li, B.; Wang, X.; Yang, L. Experimental Analysis of Deep-Sea AUV Based on Multi-Sensor Integrated Navigation and Positioning. Remote Sens. 2024, 16, 199. [Google Scholar] [CrossRef]
- Tang, J.; Bian, H. Ship SINS/CNS Integrated Navigation Aided by LSTM Attitude Forecast. J. Mar. Sci. Eng. 2024, 12, 387. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, R.; Wei, T.; Guo, Z.; Ben, Y. A Method for Predicting Inertial Navigation System Positioning Errors Using a Back Propagation Neural Network Based on a Particle Swarm Optimization Algorithm. Sensors 2024, 24, 3722. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Huang, S.; Nikolay, T.; Li, M. Vibration damping of naval ships based on ship shock trials. Appl. Acoust. 2018, 133, 52–57. [Google Scholar] [CrossRef]
- Li, Y.; He, L.; Shuai, C.-g.; Wang, C.-y. Improved hybrid isolator with maglev actuator integrated in air spring for active-passive isolation of ship machinery vibration. J. Sound Vib. 2017, 407, 226–239. [Google Scholar] [CrossRef]
- Tao, Y.; Rui, X.; Yang, F.; Hao, B. Development of a MRE isolation system for strapdown inertial measurement unit. Mech. Syst. Signal Process. 2019, 117, 553–568. [Google Scholar] [CrossRef]
- Chen, W.; Wang, S.; Li, J.; Lin, C.; Yang, Y.; Ren, A.; Li, W.; Zhao, X.; Zhang, W.; Guo, W.; et al. An ADRC-based triple-loop control strategy of ship-mounted Stewart platform for six-DOF wave compensation. Mech. Mach. Theory 2023, 184, 105289. [Google Scholar] [CrossRef]
- Chen, N.; Huang, D.; Tu, Y.; Wei, D.; Lin, X. A novel inertial parameter identification method for the ship-mounted Stewart platform based on a wave compensation platform. Measurement 2025, 242, 116010. [Google Scholar] [CrossRef]
- Li, Z.; Du, H.; Si, J.; Wang, Z.; Xiong, W. Rigid-flexible coupling dynamic modeling and validation of a helicopter rescue simulator based on an inverted Stewart platform. Ocean Eng. 2025, 319, 120164. [Google Scholar] [CrossRef]
- Marneffe, B.D.; Avraam, M.; Deraemaeker, A.; Horodinca, M.; Preumont, A. Vibration Isolation of Precision Payloads: A Six-Axis Electromagnetic Relaxation Isolator. J. Guid. Control Dyn. 2009, 32, 395–401. [Google Scholar] [CrossRef]
- Luo, Q.; Li, D.; Jiang, J. Coupled dynamic analysis of a single gimbal control moment gyro cluster integrated with an isolation system. J. Sound Vib. 2014, 333, 345–363. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, K.; Jiao, J.; Cao, D.; Chi, W.; Tang, J. Dynamic isotropy design and analysis of a six-DOF active micro-vibration isolation manipulator on satellites. Robot. Comput.-Integr. Manuf. 2018, 49, 408–425. [Google Scholar] [CrossRef]
- Yang, X.; Wu, H.; Chen, B.; Kang, S.; Cheng, S. Dynamic modeling and decoupled control of a flexible Stewart platform for vibration isolation. J. Sound Vib. 2019, 439, 398–412. [Google Scholar] [CrossRef]
- Tu, Y.; Yang, G.; Cai, Q.; Wang, L.; Zhou, X. Optimal design of SINS’s Stewart platform bumper for restoration accuracy based on genetic algorithm. Mech. Mach. Theory 2018, 124, 42–54. [Google Scholar] [CrossRef]
- Yang, J.; Xu, Z.; Wu, Q.; Zhu, M.; He, S.; Qin, C. Dynamic modeling and control of a 6-DOF micro-vibration simulator. Mech. Mach. Theory 2016, 104, 350–369. [Google Scholar] [CrossRef]
- Chen, G.; Yu, W.; Li, Q.; Wang, H. Dynamic modeling and performance analysis of the 3-PRRU 1T2R parallel manipulator without parasitic motion. Nonlinear Dyn. 2017, 90, 339–353. [Google Scholar] [CrossRef]
- Chen, G.; Rui, X.; Abbas, L.K.; Wang, G.; Yang, F.; Zhu, W. A novel method for the dynamic modeling of Stewart parallel mechanism. Mech. Mach. Theory 2018, 126, 397–412. [Google Scholar] [CrossRef]
- Bernal, J.; Campa, R.; Soto, I. Kinematics and dynamics modeling of the 6-3-PUS-type Hexapod parallel mechanism. J. Mech. Sci. Technol. 2018, 32, 4555–4570. [Google Scholar] [CrossRef]
- Shao, P.; Wang, Z.; Yang, S.; Liu, Z. Dynamic modeling of a two-DoF rotational parallel robot with changeable rotational axes. Mech. Mach. Theory 2019, 131, 318–335. [Google Scholar] [CrossRef]
- Luo, G.W.; Lv, X.H.; Zhu, X.F.; Shi, Y.Q.; Du, S.S. Diversity and transition characteristics of sticking and non-sticking periodic impact motions of periodically forced impact systems with large dissipation. Nonlinear Dyn. 2018, 94, 1047–1079. [Google Scholar] [CrossRef]
- Shen, Y.; Xiang, D.; Wang, X.; Jiang, L.; Wei, Y. A contact force model considering constant external forces for impact analysis in multibody dynamics. Multibody Syst. Dyn. 2018, 44, 397–419. [Google Scholar] [CrossRef]
- Shu, D.-W.; Shi, B.-J.; Meng, H.; Yap, F.F.; Jiang, D.-Z.; Ng, Q.; Zambri, R.; Lau, J.H.T.; Cheng, C.-S. Shock analysis of a head actuator assembly subjected to half-sine acceleration pulses. Int. J. Impact Eng. 2007, 34, 253–263. [Google Scholar] [CrossRef]
- Harmoko, H.; Yap, F.F.; Vahdati, N.; Li, C. Design and Analysis of Shock and Random Vibration Isolation of Operating Hard Disk Drive in Harsh Environment. Shock Vib. 2009, 16, 143–154. [Google Scholar] [CrossRef]
- Wang, X.; Yang, B.; Yu, H.; Gao, Y. Transient vibration analytical modeling and suppressing for vibration absorber system under impulse excitation. J. Sound Vib. 2017, 394, 90–108. [Google Scholar] [CrossRef]
- Yan, L.; Xuan, S.; Gong, X. Shock isolation performance of a geometric anti-spring isolator. J. Sound Vib. 2018, 413, 120–143. [Google Scholar] [CrossRef]
- He, Q.; Zeng, C.; Gao, Z.; Wu, Z. Analysis and Design of the Stewart Platform-Based Parallel Support Bumper for Inertially Stabilized Platforms. IEEE Trans. Ind. Electron. 2020, 67, 4203–4215. [Google Scholar] [CrossRef]
- Wu, P.; Xiong, H.; Kong, J. Dynamic analysis of 6-SPS parallel mechanism. Int. J. Mech. Mater. Des. 2012, 8, 121–128. [Google Scholar] [CrossRef]
- Wohlhart, K. Mobile 6-SPS Parallel Manipulators. J. Robot. Syst. 2003, 20, 509–516. [Google Scholar] [CrossRef]
- Hassan, A.; Abomoharam, M. Modeling and design optimization of a robot gripper mechanism. Robot. Comput.-Integr. Manuf. 2017, 46, 94–103. [Google Scholar] [CrossRef]
- Gosselin, C.; Schreiber, L. Kinematically Redundant Spatial Parallel Mechanisms for Singularity Avoidance and Large Orientational Workspace. IEEE Trans. Robot. 2016, 32, 286–300. [Google Scholar] [CrossRef]
- Jiang, H.-Z.; He, J.-F.; Tong, Z.-Z. Characteristics analysis of joint space inverse mass matrix for the optimal design of a 6-DOF parallel manipulator. Mech. Mach. Theory 2010, 45, 722–739. [Google Scholar] [CrossRef]
- Su, Y.; Gu, Y.; Keogh, P.S.; Yu, S.; Ren, G. Nonlinear dynamic simulation and parametric analysis of a rotor-AMB-TDB system experiencing strong base shock excitations. Mech. Mach. Theory 2021, 155, 104071. [Google Scholar] [CrossRef]
- Wang, X.; Yang, B. Transient vibration control using nonlinear convergence active vibration absorber for impulse excitation. Mech. Syst. Signal Process. 2019, 117, 425–436. [Google Scholar] [CrossRef]

| /mm | /mm | /mm | /° | /° |
|---|---|---|---|---|
| 174.02 | 250.00 | 250.00 | 14.58 | 14.58 |
| Dynamic Parameters | Values |
|---|---|
| mm | |
| 44,000 N/m | |
| 200 N·s/m | |
| 30.78 kg | |
| kg·m2 |
| /g | /g | /ms | /ms | /ms |
| 2015 | −1119 | 1 | 5 | 13 |
| /g | /g | /ms | /ms | /ms |
| 1573 | −344 | 1 | 5 | 16 |
| Impact Direction | Theoretical Results | Experimental Results | ||||
|---|---|---|---|---|---|---|
| /g | /g | /g | /g | |||
| x-direction | 30.85 | 1573 | 1.96% | 34.78 | 1573 | 2.21% |
| y-direction | 30.90 | 1573 | 1.96% | 31.84 | 1573 | 2.21% |
| z-direction | 191.7 | 2015 | 9.51% | 166.0 | 2015 | 8.23% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, Y.; Zhang, H.; Li, Y.; Wang, W.; Lu, G.; Lin, H.; Chen, X.; Huang, Y.; Fan, J. Dynamic Modeling and Experimental Validation of Shock Isolation Performance for Shipborne Stewart-Platform-Based Bumper. J. Mar. Sci. Eng. 2025, 13, 1007. https://doi.org/10.3390/jmse13061007
Tu Y, Zhang H, Li Y, Wang W, Lu G, Lin H, Chen X, Huang Y, Fan J. Dynamic Modeling and Experimental Validation of Shock Isolation Performance for Shipborne Stewart-Platform-Based Bumper. Journal of Marine Science and Engineering. 2025; 13(6):1007. https://doi.org/10.3390/jmse13061007
Chicago/Turabian StyleTu, Yongqiang, Haoran Zhang, Yintao Li, Wei Wang, Gang Lu, Hongwei Lin, Xinkai Chen, Yan Huang, and Jianyu Fan. 2025. "Dynamic Modeling and Experimental Validation of Shock Isolation Performance for Shipborne Stewart-Platform-Based Bumper" Journal of Marine Science and Engineering 13, no. 6: 1007. https://doi.org/10.3390/jmse13061007
APA StyleTu, Y., Zhang, H., Li, Y., Wang, W., Lu, G., Lin, H., Chen, X., Huang, Y., & Fan, J. (2025). Dynamic Modeling and Experimental Validation of Shock Isolation Performance for Shipborne Stewart-Platform-Based Bumper. Journal of Marine Science and Engineering, 13(6), 1007. https://doi.org/10.3390/jmse13061007






