Three-Dimensional Spatio-Temporal Slim Weighted Generative Adversarial Imputation Network: Spatio-Temporal Silm Weighted Generative Adversarial Imputation Net to Repair Missing Ocean Current Data
Abstract
1. Introduction
- (1)
- Unsupervised-GAIN: This is a data-driven approach that employs an iterative training mechanism of a generator and a critic, capable of accurately filling in missing flow field data.
- (2)
- Three-dimensional Feature Space: Innovatively extending the network’s input from two-dimensional to three-dimensional, it not only encompasses multiple potentially discontinuous temporal three-dimensional spatial features but also includes flow velocity information at different depths and positions, breaking through the limitation of traditional filling methods that usually can only handle two-dimensional planar data.
- (3)
- Spatio-temporal Attention Module: This model integrates a spatio-temporal attention mechanism, aiming to effectively capture the complex spatio-temporal characteristics of ocean data, thereby enhancing the accuracy of the filling results.
2. Preliminary Knowledge
2.1. Imputation Methods for Marine Data Based on Traditional Interpolation Algorithms
2.2. Imputation Methods for Marine Data Based on Traditional Machine Learning
2.3. GAN and SGAIN
| Algorithm 1 Slim-GAIN Algorithm Flow |
| 1: Input: Dataset X with missing values; mask matrix M; random noise distribution N; |
| 2: Parameter: Small-batch samples mb; Generator loss hyperparameters a: Number of iterations ; |
| 3: Output: The interpolated dataset |
| 4: Initialize the initial state M ← mask(X): Set each missing value to 0, and 1 otherwise. |
| 5: For ← 1, do |
| 6: Draw mb samples from X: |
| 7: Draw mb samples from m: |
| 8: Draw mb independent and identically distributed samples from N and add random noise: |
| 9: For j = 1, mb do |
| 10: |
| 11: End for |
| 12: Generator optimization, using Adam or RMSprop or SGD to update D |
| 13: . |
| 14: Discriminator optimization, update G using Adam or RMSprop or SGD. |
| 15: . |
| 16: End for |
| 17: |
| 18: Save the generated data that is closest to the real distribution and output it: |
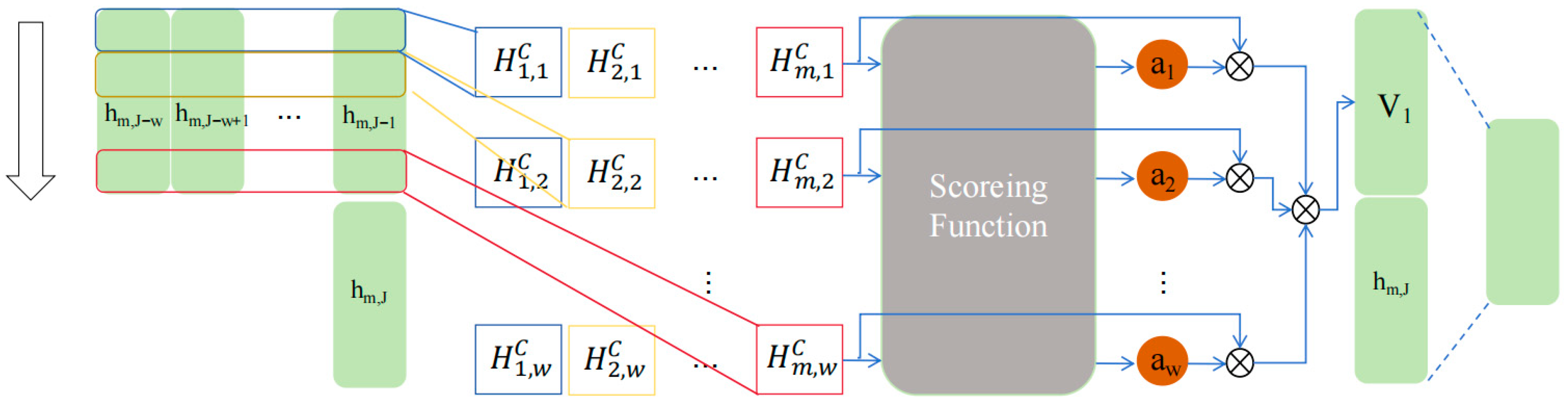
2.4. Attention Mechanism
3. Proposed Method
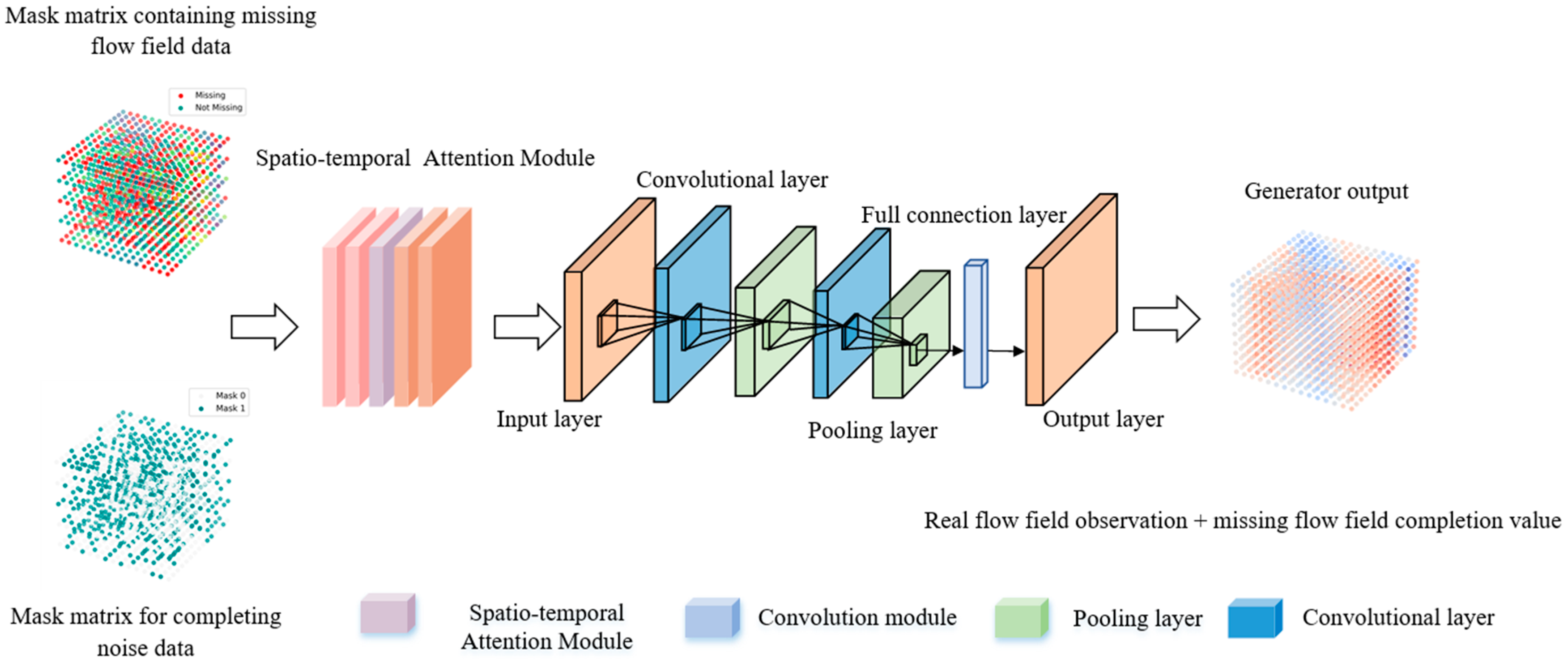
3.1. Framework
3.2. Core Modules
3.2.1. The Main Model of 3D-STA-SWGAIN
- (1)
- Generator: The generator in 3D-STA-SWGAIN is composed of a convolutional neural network based on the spatio-temporal attention mechanism, which can capture the spatial and temporal dependencies of ocean flow field data. It takes incomplete ocean current field data as input, with the goal of generating missing values through adversarial learning that are consistent with the distribution of real ocean current field data. The interpolation process of the generator can be expressed by Equations (4) and (5).
- (2)
- Critic: As shown in Figure 2, the Critic in 3D-STA-SWGAIN adopts a convolutional neural network architecture enhanced by a spatio-temporal attention mechanism. The key difference from the generator lies in the input form: the critic receives a combination of the data output by the generator and the mask matrix. Its core objective is to learn the global features and spatio-temporal relationships of multiple sets of 3D ocean current field data, thereby accurately distinguishing real data from the data generated by the generator.
3.2.2. Spatio-Temporal Attention Mechanism Module
3.2.3. Gradient Penalty Module
3.2.4. Loss Function
3.3. Implementation Procedures
4. Experiments
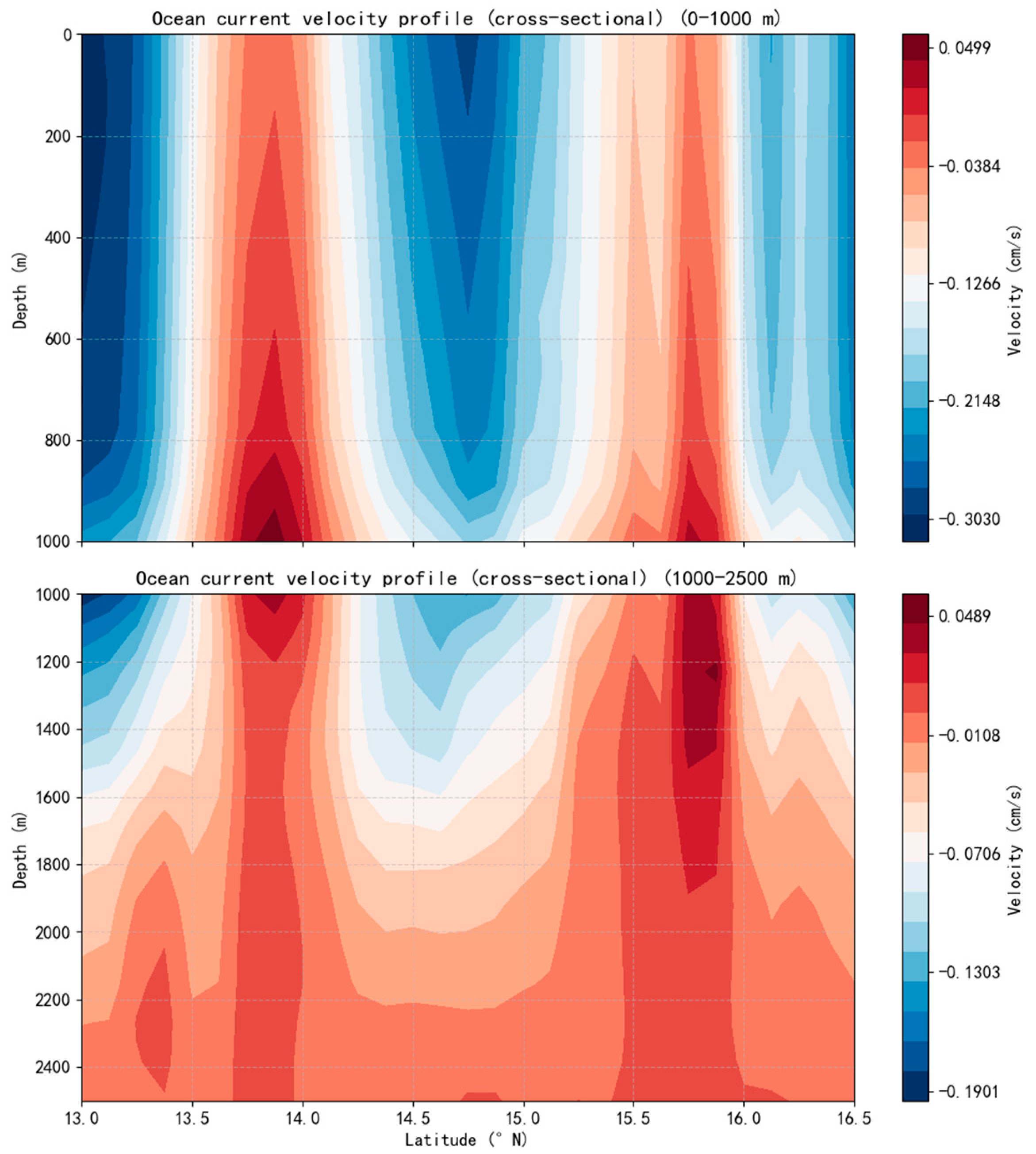
4.1. Datasets and Settings
4.2. Baseline Models for Interpolation of Ocean Current Field Data
- (1)
- Cubic Spline Interpolation: It is a commonly used interpolation method for constructing smooth curves between known data points. By fitting cubic polynomials between adjacent data points, it ensures that the entire interpolation curve has continuous first and second derivatives at these points, thereby guaranteeing the smoothness of the curve.
- (2)
- Deep Matrix Factorization (DMF): This is a novel imputation technique that improves upon traditional matrix factorization methods. Its key feature is the ability to handle data with nonlinear structures. By leveraging deep learning techniques, this method can more accurately learn the features and structures of the data, thereby achieving more effective imputation of missing values.
- (3)
- Transformer deep learning network: A deep learning model based on the self-attention mechanism, its core advantage lies in the parallel processing of long sequence data and the capture of global dependencies, which has completely transformed the traditional RNN/LSTM model’s approach to sequence modeling.
- (4)
- 3D-SGAIN: This is a method based on GAN for imputing missing data. It estimates the missing values by training a generator and a discriminator.
4.3. Evaluation Indicators for Interpolation of Ocean Current Field Data
5. Discussion
5.1. Experimental Analysis of Ocean Current Field Data Completion Under Different Modes
5.1.1. Pattern (a) Random Missing Pattern of 3D-STA-SWGAIN
5.1.2. Pattern (b) the 2D Ocean Current Layer Missing Pattern Caused by Cloud Cover in Satellite Data of 3D-STA-SWGAIN
5.1.3. Pattern (c) Block-Shaped Missing Patterns Caused by Sensor Array Faults of 3D-STA-SWGAIN
5.2. Ablation Experiments and Evaluation
- (1)
- A comparative experiment on the impact of data completion results under models with and without spatio-temporal attention mechanism.
- (2)
- A comparative experiment on the impact of different loss function models on data completion results.
- (1)
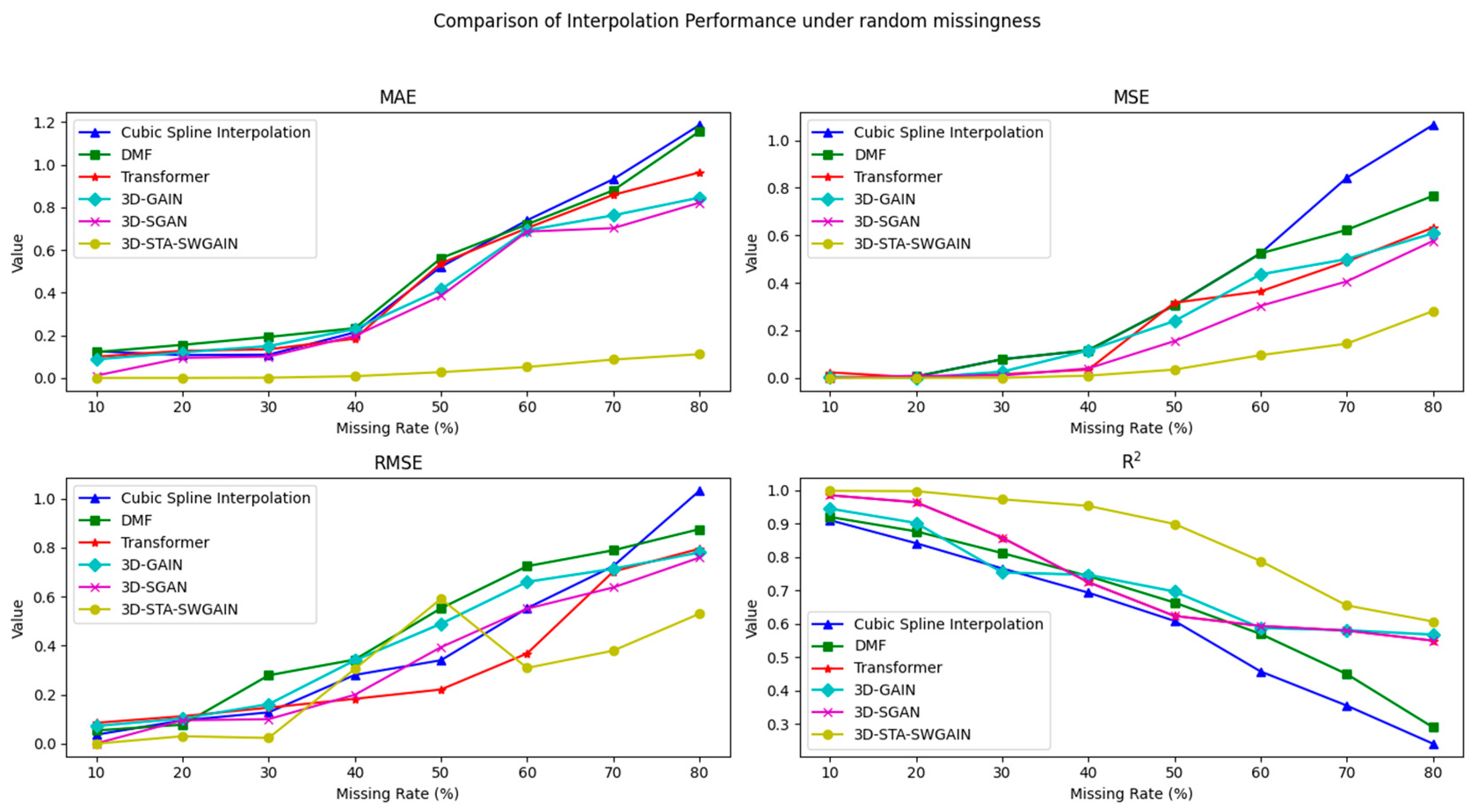
- The advantage of spatio-temporal feature fusion. The algorithm proposed in this paper, through the input and output design of the ocean current field (time × depth × latitude × longitude), enables the neural network to more effectively extract the three-dimensional global features of the complex ocean current field. This design not only considers the spatial dimension but also combines the information about the temporal dimension, thereby comprehensively capturing the dynamic changes in the ocean current field. Compared with traditional methods that only rely on spatial features, the spatio-temporal feature fusion can better reflect the spatio-temporal correlation of the ocean current field and significantly improve the accuracy of data completion. By introducing the spatio-temporal attention mechanism, the model can dynamically adjust the importance of different positions and time points in the ocean current field. This makes the model more flexible and robust when dealing with different missing patterns and missing rates. For example, in cases where there are large areas of missing data in certain depth layers or nodes, the attention mechanism can more accurately estimate the missing values by learning the spatial and temporal relationships.
- (2)
- The adaptive learning ability of the model. The algorithm proposed in this paper adopts an unsupervised machine learning model, which can fully utilize the observed ocean current data for adaptive learning. Compared with traditional interpolation methods and regression algorithms, this adaptive learning ability enables the model to better cope with the layer and block missing patterns of ocean currents and changes in the missing rate. No matter in what extreme ocean current field observation scenarios, the model can maintain excellent data completion performance by learning the spatio-temporal features of the ocean current field.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, H.; Wu, G.; Wang, X.; Zhang, T.; Zhang, P.; Chen, W.; Zhu, Q. Research on a Measurement Method for the Ocean Wave Field Based on Stereo Vision. Appl. Sci. 2022, 12, 7447. [Google Scholar] [CrossRef]
- Yang, S.; Cheng, D.; Chen, G.; Luo, C.; Niu, W.; Ma, W.; Fa, S. Review on the application of underwater gliders for observing typical ocean phenomena. J. Trop. Oceanogr. 2022, 41, 54–74. [Google Scholar]
- Greenberg, O.; Ben-Moshe, B. Real-Time Stereo-Based Ocean Surface Mapping for Robotic Floating Platforms: Concept and Methodology. J. Sens. 2023, 23, 3857. [Google Scholar] [CrossRef] [PubMed]
- Alvera-Azcárate, A.; Barth, A.; Sirjacobs, D.; Lenartz, F.; Beckers, J.M. Data Interpolating Empirical Orthogonal Functions (DINEOF): A tool for geophysical data analyses. Med. Mar. Sci. 2011, 5–11. [Google Scholar]
- Lou, R.; Lv, Z.; Dang, S.; Su, T.; Li, X. Application of machine learning in ocean data. Multimed. Syst. 2023, 29, 1815–1824. [Google Scholar] [CrossRef]
- Desbruyères, D.; Chafik, L.; Maze, G. A shift in the ocean circulation has warmed the subpolar North Atlantic Ocean since 2016. Commun. Earth Environ. 2021, 2, 48. [Google Scholar] [CrossRef]
- Kopte, R.; Becker, M.; Fischer, T.; Brandt, P.; Krahmann, G.; Betz, M.; Faber, C.; Winter, C.; Karstensen, J.; Wiemer, G. FAIR ADCP data with OSADCP: A workflow to process ocean current data from vessel-mounted ADCPs. Front. Mar. Sci. 2024, 11, 1425086. [Google Scholar] [CrossRef]
- Lin, M.; Yang, C. Ocean observation technologies: A review. Chin. J. Mech. Eng. 2020, 33, 18. [Google Scholar] [CrossRef]
- Dong, S.; Goni, G.; Domingues, R.; Bringas, F.; Goes, M.; Christophersen, J.; Baringer, M. Synergy of in situ and satellite ocean observations in determining meridional heat transport in the Atlantic Ocean. J. Geophys. Res. Ocean. 2021, 126, e2020JC017073. [Google Scholar] [CrossRef]
- Yang, L.; Ding, S.; Liu, J.W.; Zhang, S.P. Effects of radiative cooling on advection fog over the northwest Pacific Ocean: Observations and large-eddy simulations. Atmos. Chem. Phys. 2024, 24, 6809–6824. [Google Scholar] [CrossRef]
- Khan, M.; Almazah, M.M.; EIlahi, A.; Niaz, R.; Al-Rezami, A.Y.; Zaman, B. Spatial interpolation of water quality index based on Ordinary kriging and Universal kriging. Geomat. Nat. Hazards Risk 2023, 14, 2190853. [Google Scholar] [CrossRef]
- Deng, X.; Han, R.; Yang, C.; Zhao, H.; Zheng, H.; Yang, S. Assimilation of Scattered Ocean Observations Using the Localized Equivalent-Weights Particle Filter with Statistical Observations. J. Atmos. Ocean. Technol. 2024, 41, 1181–1195. [Google Scholar] [CrossRef]
- Hua, X.; Zhang, C.; Zhang, C.; Cheng, L.; Zhang, T.; Li, J. Enhancing the robustness of ocean sound speed profile representation via interpretable deep matrix decomposition. J. Acoust. Soc. Am. 2023, 154, 3868–3882. [Google Scholar] [CrossRef]
- Yue, W.; Xu, Y.; Xiang, L.; Zhu, S.; Huang, C.; Zhang, Q.; Zhang, L.; Zhan, X. Prediction of 3-D ocean temperature based on self-attention and predictive RNN. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Neves, D.T.; Naik, M.G.; Proença, A. SGAIN, WSGAIN-CP and WSGAIN-GP: Novel GAN methods for missing data imputation. In International Conference on Computational Science; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Reynolds, R.W.; Zhang, H.M.; Smith, T.M.; Gentemann, C.L.; Wentz, F. Impacts of in situ and additional satellite data on the accuracy of a sea-surface temperature analysis for climate. Int. J. Climatol. 2005, 25, 857–864. [Google Scholar] [CrossRef]
- Mehmet, B.; Pinar, E.; Tahir, D. Global monthly sea surface temperature forecasting using the SARIMA, LSTM, and GRU models. Earth Sci. Inform. 2025, 18. [Google Scholar]
- Sugiura, N.; Kouketsu, S.; Osafune, S. Ocean data assimilation focusing on integral quantities characterizing observation profiles. Front. Mar. Sci. 2024, 11, 1398901. [Google Scholar] [CrossRef]
- Li, Z.; Fei, J.; Zhang, R.; Jiang, X.; Ma, W.; Cheng, X.; Liu, L.; Wang, G.; Chen, C. Numerical prediction of oceanic mesoscale circulation and satellite altimetry data assimilation in the Western Pacific. Sci. China Earth Sci. 2025, 68, 909–927. [Google Scholar] [CrossRef]
- Feng, H.; Luo, L.; Wang, Y.; Ye, M. Multi-objective data collecting strategies for wireless sensor network based on the time variable multi-salesman problem and genetic algorithm. J. Commun. 2017, 38, 112–123. [Google Scholar]
- Zheng, Q.; Han, G.; Li, W.; Cao, L.; Zhou, G.; Wu, H.; Shao, Q.; Wang, R.; Wu, X.; Cui, X.; et al. Generating Unseen Nonlinear Evolution in Sea Surface Temperature Using a Deep Learning-Based Latent Space Data Assimilation Framework. arXiv 2024, arXiv:2412.13477. [Google Scholar]
- Pan, Y.C.; Dai, Z.; Ma, H.; Zheng, J.; Leng, J.; Xie, C.; Yuan, Y.; Yang, W.; Yalikun, Y.; Song, X.; et al. Self-powered and speed-adjustable sensor for abyssal ocean current measurements based on triboelectric nanogenerators. Nat. Commun. 2024, 15, 6133. [Google Scholar] [CrossRef] [PubMed]
- Diouf, S.; Deme, A.; El Hadji Deme, P.F.; Diouf, I. An evaluation of the performance of imputation methods for missing meteorological data in Burkina Faso and Senegal. Afr. J. Environ. Sci. Technol. 2023, 17, 252–274. [Google Scholar]
- Hao, R.; Zhao, Y.; Zhang, S.; Deng, X. Deep Learning for Ocean Forecasting: A Comprehensive Review of Methods, Applications, and Datasets. IEEE Trans. Cybern. 2025. [Google Scholar] [CrossRef] [PubMed]
- Zi, N.; Li, X.M.; Gade, M.; Fu, H.; Min, S. Ocean eddy detection based on YOLO deep learning algorithm by synthetic aperture radar data. Remote Sens. Environ. 2024, 307, 114139. [Google Scholar] [CrossRef]
- Cao, C.; Bao, L.; Gao, G.; Liu, G.; Zhang, X. A novel method for ocean wave spectra retrieval using deep learning from sentinel-1 wave mode data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar] [CrossRef]
- Zhao, Z.; Guo, J.; Xiao, R.; Zheng, W.; Wang, Y.; Lv, X.; Shi, H. A Three-Dimensional Spatial Interpolation Method and Its Application to the Analysis of Oxygen Deficit in the Bohai Sea in Summer. J. Mar. Sci. Eng. 2024, 12, 426. [Google Scholar] [CrossRef]
- Li, A.; Shao, T.; Zhang, Z.; Fang, W.; Li, W.; Xu, J.; Jiang, Y.; Shu, C. Improvement in Spatiotemporal Chl-a Data in the South China Sea Using the Random-Forest-Based Geo-Imputation Method and Ocean Dynamics Data. J. Mar. Sci. Eng. 2023, 12, 13. [Google Scholar] [CrossRef]
- Chi, J.; Bae, J.; Kwon, Y.-J. Two-stream convolutional long-and short-term memory model using perceptual loss for sequence-to-sequence Arctic sea ice prediction. Remote. Sens. 2021, 13, 3413. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, F.; Lou, W.; Wang, X.; Yang, J. A comprehensive review of advances in physics-informed neural networks and their applications in complex fluid dynamics. Phys. Fluids 2024, 36, 10. [Google Scholar] [CrossRef]
- Qin, M. Spatiotemporal Prediction Method of Marine Environment Based on Deep Learning. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2021. [Google Scholar]
- Han, B.; Qu, T.; Jiang, J. GN-GCN: Grid neighborhood-based graph convolutional network for spatio-temporal knowledge graph reasoning. ISPRS J. Photogramm. Remote Sens. 2025, 220, 728–739. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Jiang, F.; Zhou, Y.; Li, X. Reconstructing three-dimensional thermohaline structures for mesoscale eddies using satellite observations and deep learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–16. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, J.; Yuan, F.; Qiu, Y.; Wang, P.; Cheng, F.; Gu, Y. Enhancement Methods of Hydropower Unit Monitoring Data Quality Based on the Hierarchical Density-Based Spatial Clustering of Applications with a Noise–Wasserstein Slim Generative Adversarial Imputation Network with a Gradient Penalty. Sensors 2023, 24, 118. [Google Scholar] [CrossRef]
- Yingtao, L.; Liu, Q.; Liu, Z. Stan: Spatio-temporal attention network for next location recommendation. Proc. Web Conf. 2021, 2021, 2177–2185. [Google Scholar]
- Manucharyan, G.E.; Siegelman, L.; Klein, P. A deep learning approach to spatiotemporal sea surface height interpolation and estimation of deep currents in geostrophic ocean turbulence. J. Adv. Model. Earth Syst. 2021, 13, e1029/2019MS001965. [Google Scholar] [CrossRef]
- Prants, S.V. Marine life at Lagrangian fronts. Prog. Oceanogr. 2022, 204, 102790. [Google Scholar] [CrossRef]
- Du, J.; Li, X.; Dong, S.; Liu, Z.; Chen, G. A novel attention enhanced deep neural network for hypersonic spatiotemporal turbulence prediction. Phys. Fluids 2024, 36, 5. [Google Scholar] [CrossRef]
- Kolstad, E.W.; Lee, S.H.; Butler, A.H. Diverse surface signatures of stratospheric polar vortex anomalies. J. Geophys. Res. Atmos. 2022, 127, E2022JD037422. [Google Scholar] [CrossRef]
- Hauser, D.; Tourain, C.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; et al. New observations from the SWIM radar on-board CFOSAT: Instrument validation and ocean wave measurement assessment. IEEE Trans. Geosci. Remote. Sens. 2020, 59, 5–26. [Google Scholar] [CrossRef]
- Uchiyama, Y.; Kanki, R.; Takano, A.; Yamazaki, H.; Miyazawa, Y. Mesoscale reproducibility in regional ocean modelling with a three-dimensional stratification estimate based on aviso-argo data. Atmosphere-Ocean 2017, 56, 212–229. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.N.; Ardizzone, J.; Leidner, S.M.; Jusem, J.C.; Smith, D.K.; Gombos, D. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]


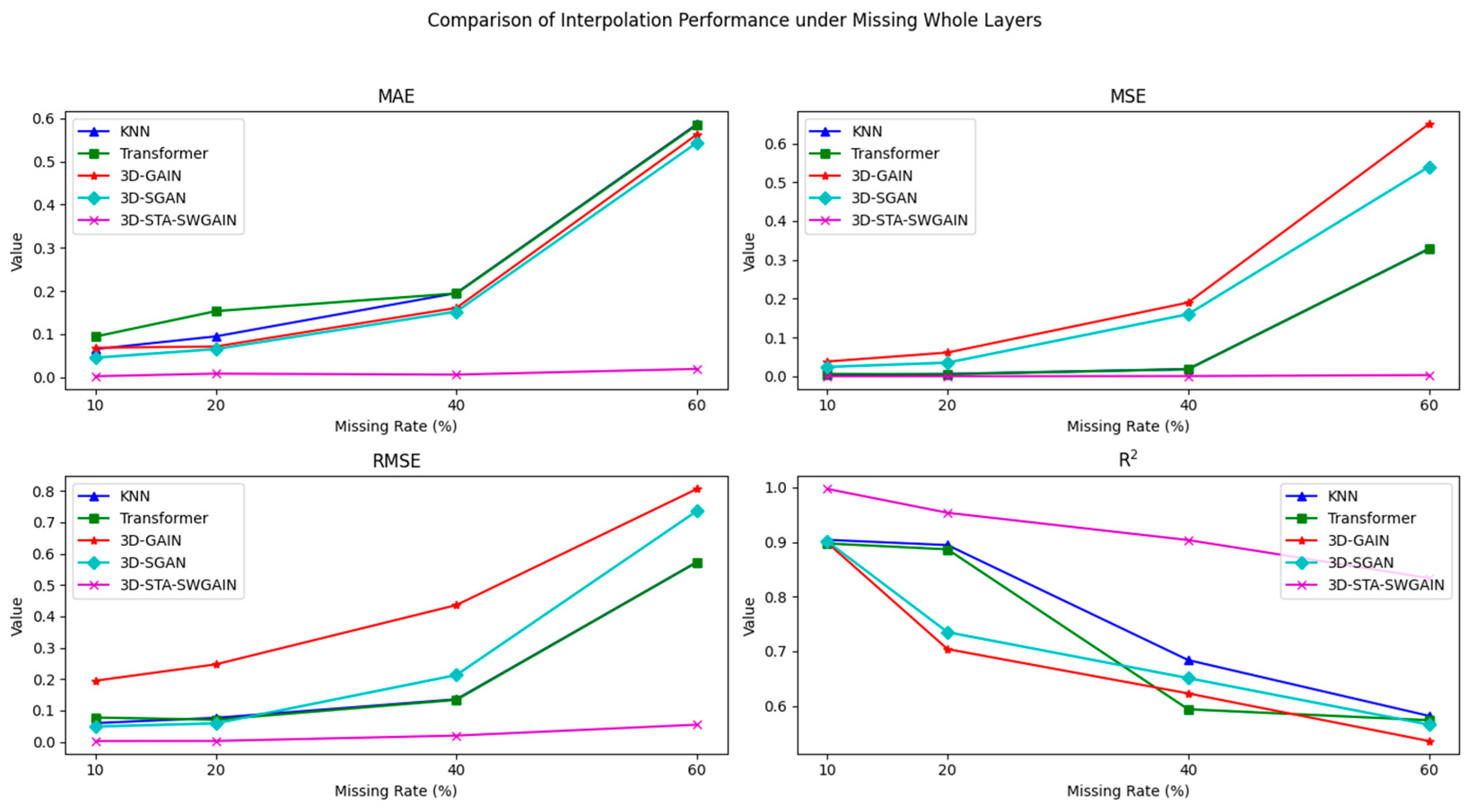
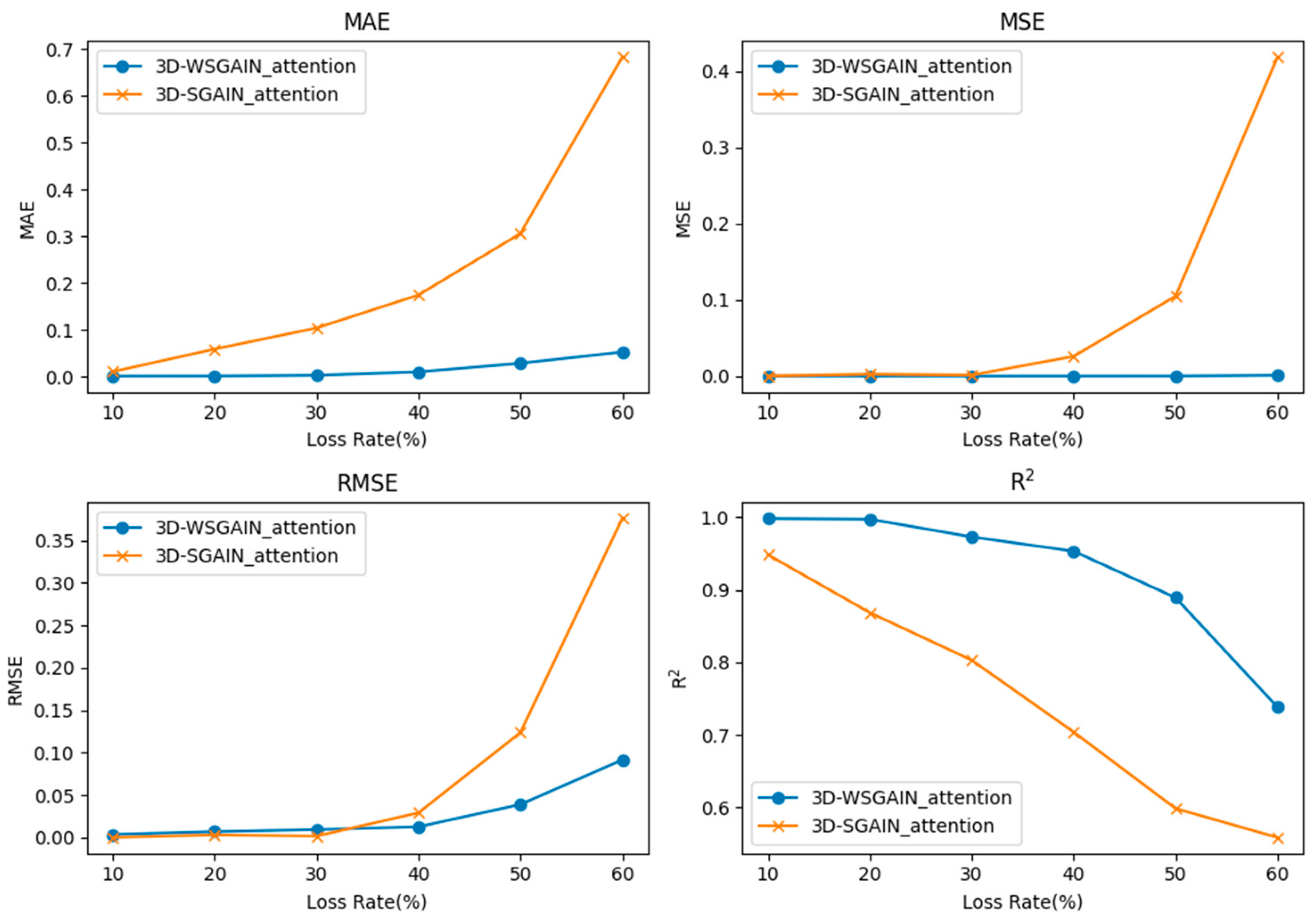
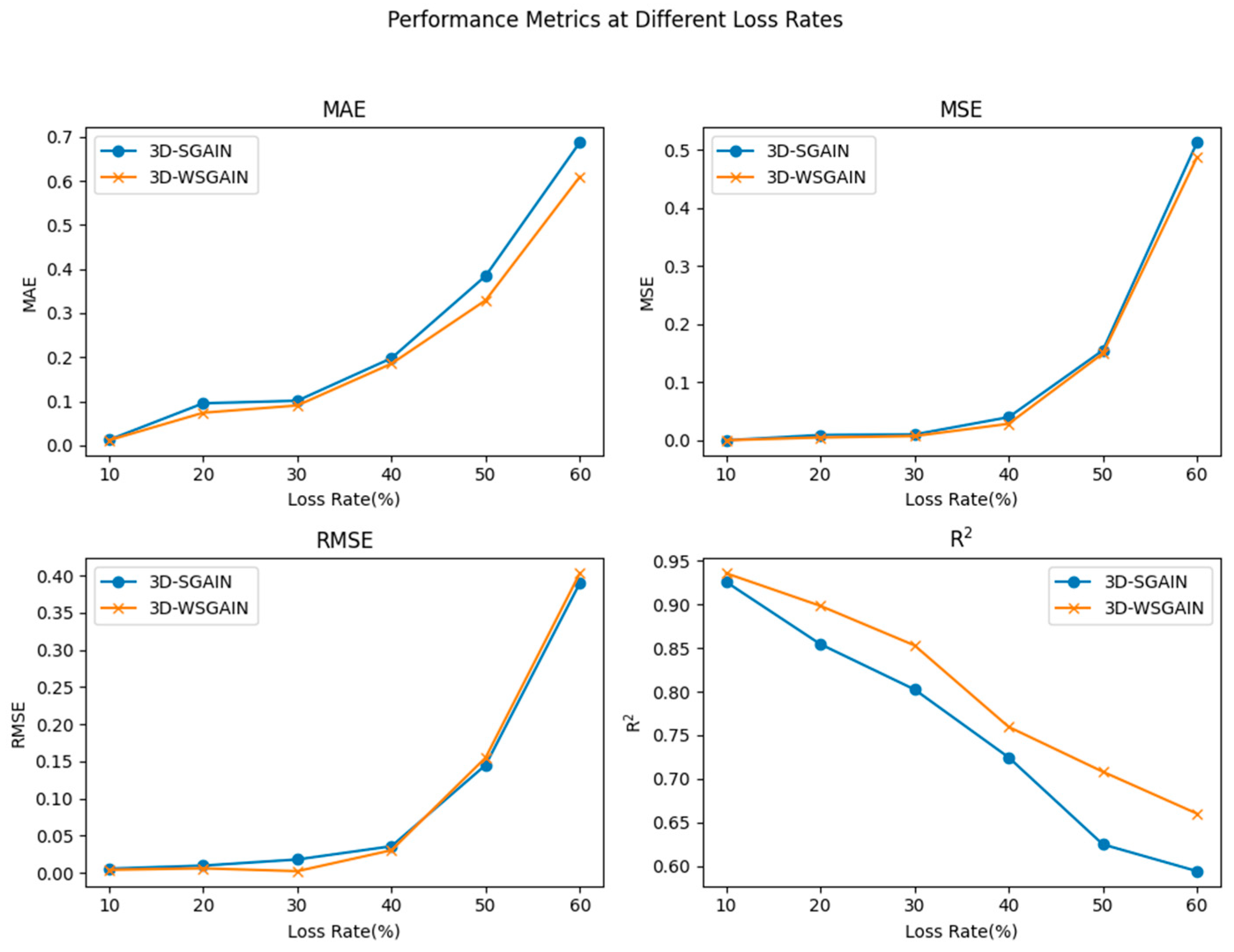
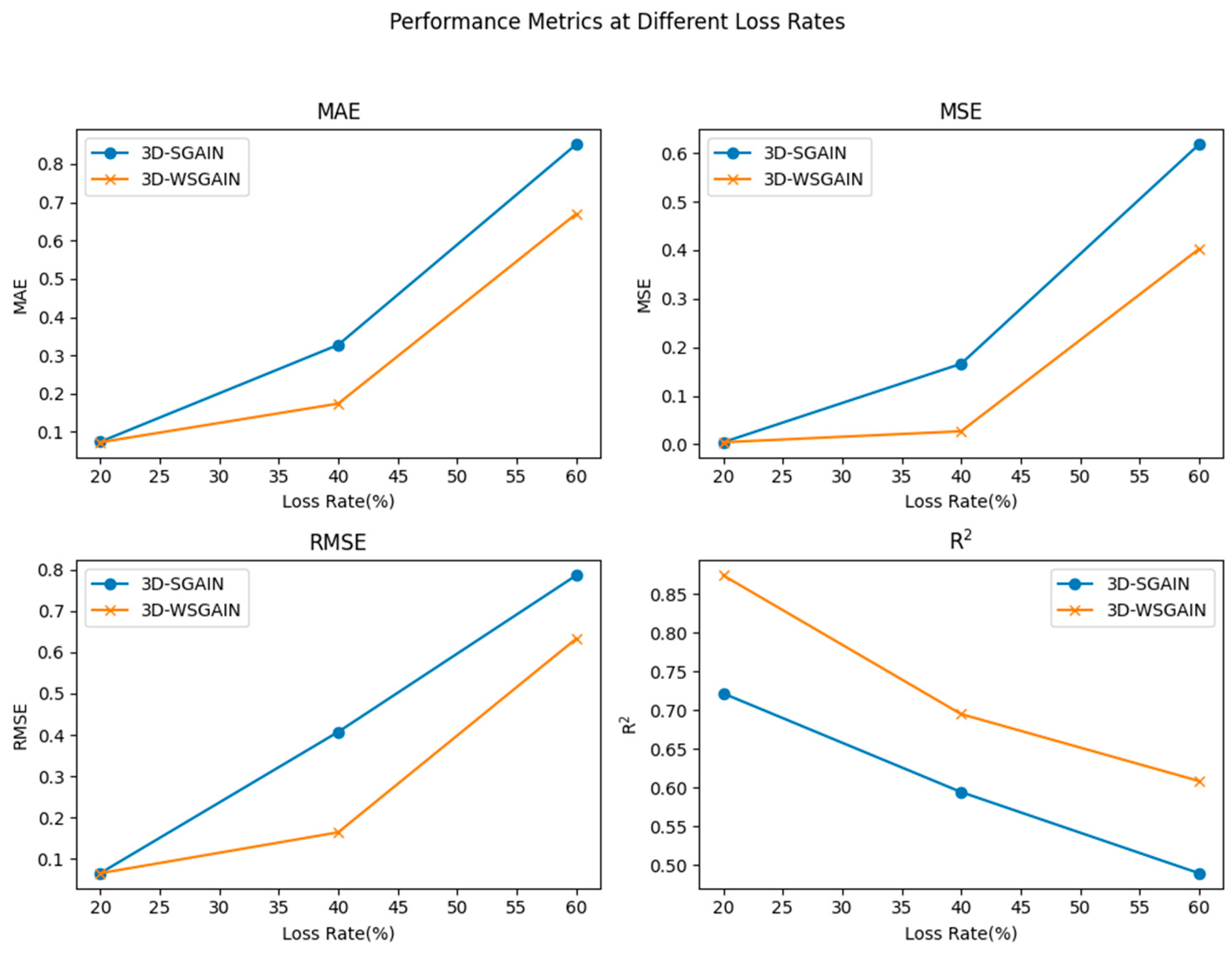
| Model | Evaluation Indicators | Missing Rate (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | ||
| Cubic Spline Interpolation | MAE | 0.126 | 0.1078 | 0.1099 | 0.2143 | 0.5218 | 0.7399 | 0.9324 | 1.186 |
| MSE | 0.0013 | 0.0065 | 0.07865 | 0.1158 | 0.3055 | 0.5245 | 0.842 | 1.064 | |
| RMSE | 0.0368 | 0.095 | 0.1278 | 0.2804 | 0.3403 | 0.5527 | 0.7242 | 1.0315 | |
| 0.9104 | 0.8415 | 0.766 | 0.6935 | 0.6091 | 0.4578 | 0.3557 | 0.2418 | ||
| DMF | MAE | 0.122 | 0.156 | 0.193 | 0.234 | 0.562 | 0.721 | 0.880 | 1.156 |
| MSE | 0.003 | 0.006 | 0.078 | 0.117 | 0.305 | 0.524 | 0.623 | 0.766 | |
| RMSE | 0.054 | 0.0775 | 0.279 | 0.343 | 0.5523 | 0.724 | 0.789 | 0.875 | |
| 0.92 | 0.877 | 0.812 | 0.743 | 0.664 | 0.570 | 0.450 | 0.291 | ||
| Transformer | MAE | 0.10 | 0.128 | 0.135 | 0.185 | 0.538 | 0.703 | 0.859 | 0.964 |
| MSE | 0.0232 | 0.002 | 0.0154 | 0.0345 | 0.3164 | 0.3641 | 0.49 | 0.632 | |
| RMSE | 0.085 | 0.112 | 0.147 | 0.183 | 0.221 | 0.368 | 0.702 | 0.795 | |
| 0.920 | 0.884 | 0.761 | 0.738 | 0.653 | 0.568 | 0.565 | 0.48 | ||
| 3D-GAIN | MAE | 0.088 | 0.121 | 0.150 | 0.230 | 0.415 | 0.693 | 0.763 | 0.846 |
| MSE | 0.005 | 0.0001 | 0.0259 | 0.1156 | 0.2392 | 0.4358 | 0.50 | 0.6084 | |
| RMSE | 0.0722 | 0.103 | 0.161 | 0.340 | 0.4891 | 0.6602 | 0.7134 | 0.780 | |
| 0.945 | 0.902 | 0.754 | 0.747 | 0.697 | 0.588 | 0.581 | 0.568 | ||
| 3D-SGAIN | MAE | 0.012 | 0.095 | 0.101 | 0.198 | 0.385 | 0.687 | 0.703 | 0.822 |
| MSE | 0.0001 | 0.0091 | 0.010 | 0.0398 | 0.1549 | 0.3032 | 0.406 | 0.576 | |
| RMSE | 0.001 | 0.0955 | 0.10 | 0.1995 | 0.3936 | 0.5507 | 0.6372 | 0.7590 | |
| 0.985 | 0.964 | 0.858 | 0.7245 | 0.624 | 0.594 | 0.58 | 0.55 | ||
| 3D-STA-SWGAIN | MAE | 0.001 | 0.001 | 0.002 | 0.009 | 0.028 | 0.052 | 0.087 | 0.112 |
| MSE | 5.62 × 10−8 | 9.21 × 10−8 | 5.42 × 10−6 | 9.33 × 10−6 | 3.49 × 10−5 | 9.56 × 10−4 | 0.144 | 0.281 | |
| RMSE | 2.371 × 10−4 | 3.04 × 10−4 | 2.33 × 10−3 | 3.05 × 10−3 | 5.91 × 10−3 | 3.09 × 10−2 | 0.3795 | 0.53 | |
| 0.9982 | 0.9973 | 0.9729 | 0.9532 | 0.8991 | 0.7882 | 0.6554 | 0.6073 | ||
| Model | Evaluation Indicators | Missing Rate (%) | |||
|---|---|---|---|---|---|
| 10 | 20 | 40 | 60 | ||
| KNN | MAE | 0.06483 | 0.094385 | 0.194853 | 0.5868 |
| MSE | 0.003583 | 0.0058593 | 0.018385 | 0.32853 | |
| RMSE | 0.05986 | 0.07655 | 0.13561 | 0.573 | |
| 0.90385 | 0.8943 | 0.684 | 0.582 | ||
| Transformer | MAE | 0.094 | 0.153 | 0.1941 | 0.585 |
| MSE | 0.006 | 0.005 | 0.018 | 0.328 | |
| RMSE | 0.0775 | 0.0707 | 0.134 | 0.573 | |
| 0.8973 | 0.8865 | 0.594 | 0.574 | ||
| 3D-GAIN | MAE | 0.068 | 0.071 | 0.1605 | 0.563 |
| MSE | 0.038 | 0.061 | 0.19 | 0.65 | |
| RMSE | 0.1949 | 0.2470 | 0.4359 | 0.8062 | |
| 0.8988 | 0.704 | 0.623 | 0.536 | ||
| 3D-SGAIN | MAE | 0.045 | 0.065 | 0.1520 | 0.544 |
| MSE | 0.024 | 0.035 | 0.160 | 0.54 | |
| RMSE | 0.049 | 0.059 | 0.213 | 0.736 | |
| 0.901 | 0.735 | 0.651 | 0.566 | ||
| 3D-STA-SWGAIN | MAE | 0.002 | 0.008 | 0.0057 | 0.019 |
| MSE | 7.95 × 10−6 | 9.03 × 10−6 | 0.0004 | 0.003 | |
| RMSE | 0.0028 | 0.00301 | 0.02 | 0.0548 | |
| 0.9971 | 0.9534 | 0.9035 | 0.83391 | ||
| Model/MAE | 10/% | 20/% | 30/% | 40/% | 50/% | 60/% |
|---|---|---|---|---|---|---|
| KNN | 0.004 | 0.011 | 0.039 | 0.068 | 0.105 | 0.486 |
| Cubic Spline | 0.18 | 0.28 | 0.38 | 0.53 | 0.68 | 0.92 |
| Transformer | 0.12 | 0.15 | 0.22 | 0.38 | 0.65 | 0.88 |
| 3D-GAIN | 0.08 | 0.12 | 0.18 | 0.36 | 0.628 | 0.866 |
| 3D-SGAIN | 0.05 | 0.07 | 0.114 | 0.327 | 0.617 | 0.8513 |
| 3D-STA-SWGAIN | 0.0007 | 0.0009 | 0.0028 | 0.0075 | 0.0184 | 0.0386 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Y.; Li, J.; Zhang, Y.; Ji, M.; Zhang, J.; Ma, R. Three-Dimensional Spatio-Temporal Slim Weighted Generative Adversarial Imputation Network: Spatio-Temporal Silm Weighted Generative Adversarial Imputation Net to Repair Missing Ocean Current Data. J. Mar. Sci. Eng. 2025, 13, 911. https://doi.org/10.3390/jmse13050911
Yue Y, Li J, Zhang Y, Ji M, Zhang J, Ma R. Three-Dimensional Spatio-Temporal Slim Weighted Generative Adversarial Imputation Network: Spatio-Temporal Silm Weighted Generative Adversarial Imputation Net to Repair Missing Ocean Current Data. Journal of Marine Science and Engineering. 2025; 13(5):911. https://doi.org/10.3390/jmse13050911
Chicago/Turabian StyleYue, Yiwan, Juan Li, Yu Zhang, Meiqi Ji, Jingyao Zhang, and Rui Ma. 2025. "Three-Dimensional Spatio-Temporal Slim Weighted Generative Adversarial Imputation Network: Spatio-Temporal Silm Weighted Generative Adversarial Imputation Net to Repair Missing Ocean Current Data" Journal of Marine Science and Engineering 13, no. 5: 911. https://doi.org/10.3390/jmse13050911
APA StyleYue, Y., Li, J., Zhang, Y., Ji, M., Zhang, J., & Ma, R. (2025). Three-Dimensional Spatio-Temporal Slim Weighted Generative Adversarial Imputation Network: Spatio-Temporal Silm Weighted Generative Adversarial Imputation Net to Repair Missing Ocean Current Data. Journal of Marine Science and Engineering, 13(5), 911. https://doi.org/10.3390/jmse13050911





