Risk Assessment Method for Flooding Incident Emergency Operating Procedure Considering Mutual Dependence Between Human Error and Available Time
Abstract
1. Introduction
2. Background of Research Methods
2.1. DBN
2.2. SPAR-H
3. Methodology
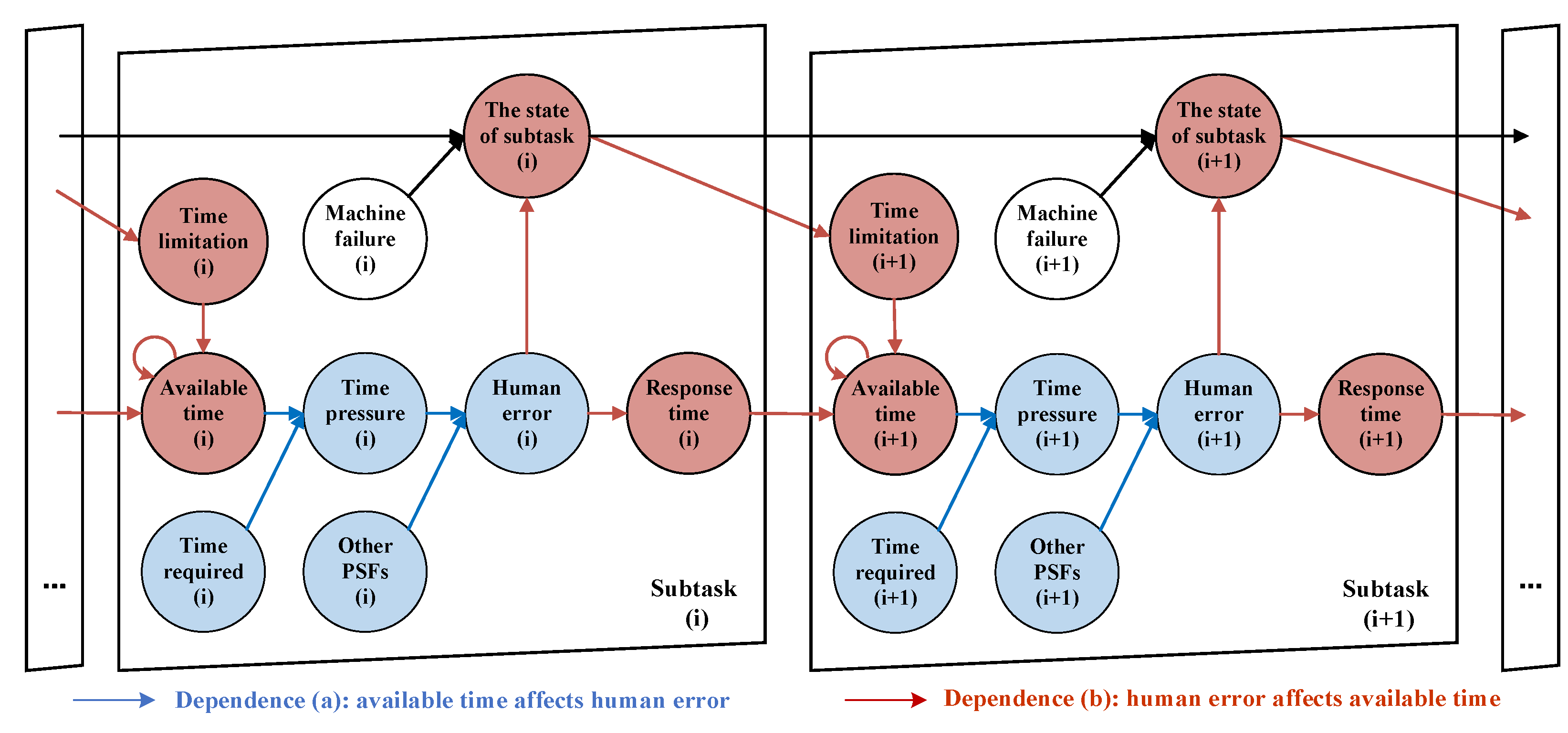
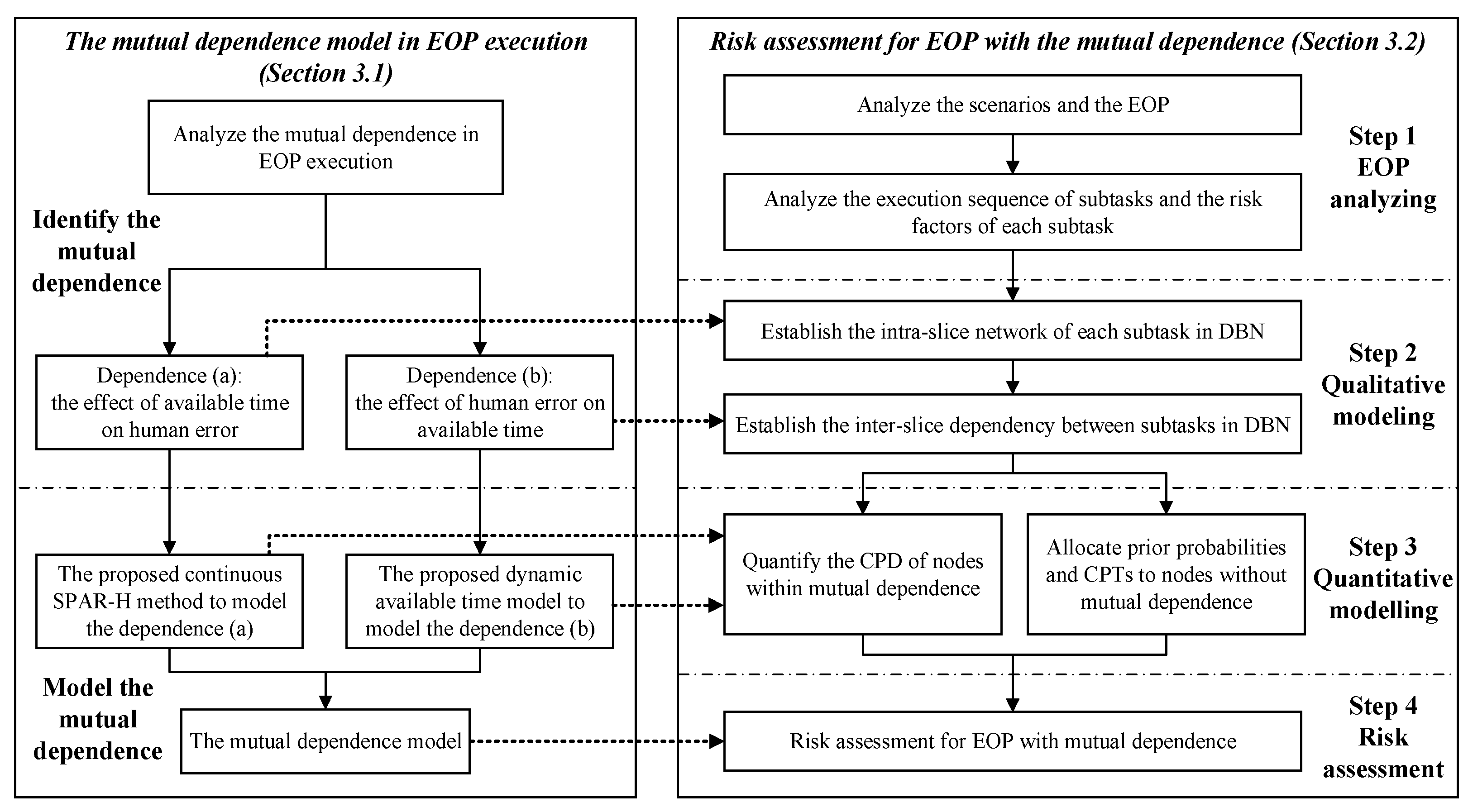
3.1. Modeling the Mutual Dependence in the Execution of EOP
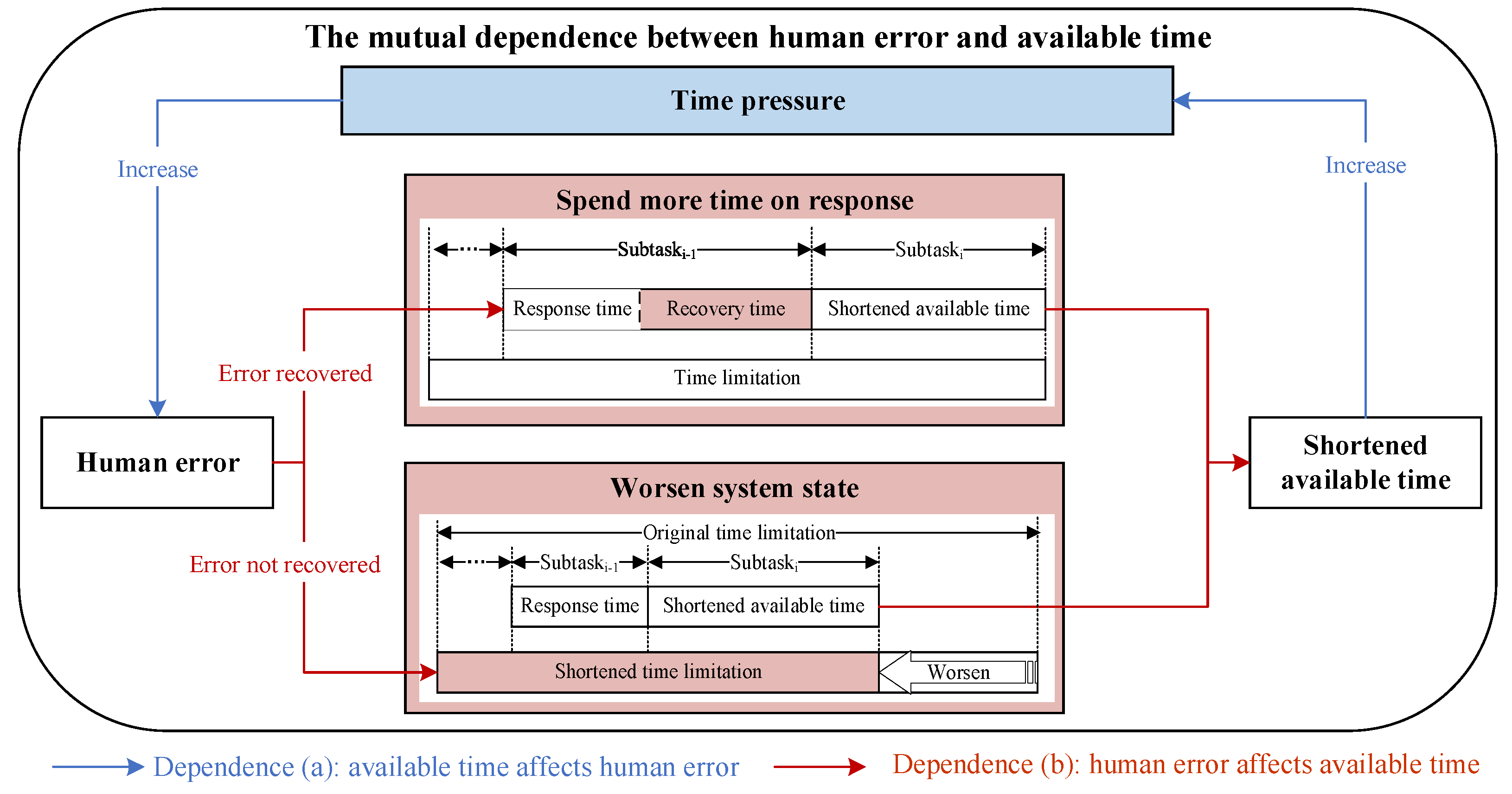
3.1.1. The Mutual Dependence Between Human Error and Available Time
- (1)
- Dependence (a): Available time affects human error. During the execution of the EOP, the available time for a task can be defined as the difference between the time limitation of all tasks in the EOP and the response time spent on preceding tasks. Shorter available time can induce emotions such as tension and anxiety, serving as factors triggering time pressure [40]. Time pressure is a significant factor influencing human error [41] and is incorporated as one of the PSFs in many HRA methods to adjust the HEP. It will become higher as the available time decreases. Higher time pressure can have a negative impact on personnel’s psychological state, triggering emotions such as anxiety and stress, which in turn weaken cognitive functions and operational performance [42]. HRA methods, such as SPAR-H, categorize time pressure into several levels to evaluate its effect on human error. At the highest level of time pressure, it is assumed that operators have no time to carry out the required actions, making human error nearly unavoidable. Conversely, at the lowest level, it is assumed that the operator has sufficient time to complete the task and that the time pressure has no effect on the task execution [38].
- (2)
- Dependence (b): Human error affects available time. Human error can dynamically affect available time in two ways, depending on whether the error is recovered. On the one hand, when human error occurs, personnel may discover and recover the error [43]. This requires personnel to respond again and spend more time on the task. For example, in the EOP of the flooding incident, if a crew member opens the wrong valve when opening the emergency bilge pump and notices the error, the crew needs to spend additional time closing the wrong valve and opening the correct one. The longer the response time for the current task, the shorter the available time for subsequent tasks. On the other hand, if the personnel fail to detect the error, the required emergency function will not be activated effectively. This will worsen the system state and shorten the time limitation for EOP execution, which in turn will shorten the available time for subsequent tasks. For example, according to SOLAS regulations, when adjacent compartments or multiple compartments are flooded simultaneously, a roll angle of 12° can be tolerated, while a single compartment flooding allows a roll angle of 15° [44]. Failure to close the watertight door will reduce the maximum tolerable heeling angle of the ship and accelerate the capsizing of the ship, thus shortening the time limitation and the time available for personnel to execute subsequent emergency tasks.
3.1.2. Modeling Dependence (a)
3.1.3. Modeling Dependence (b)
3.1.4. Modeling Mutual Dependence Based on DBN
3.2. The Framework of the Risk Assessment Method for EOP with the Mutual Dependence
4. Case Study
4.1. The Flooding Scenario
4.2. Application of Proposed Method
4.2.1. EOP Analysis
- (i)
- detect the alarm;
- (ii)
- close watertight doors remotely;
- (iii)
- close watertight doors on site if (ii) fails;
- (iv)
- open the emergency bilge pump;
- (v)
- plug the leak.
4.2.2. Qualitative Modeling
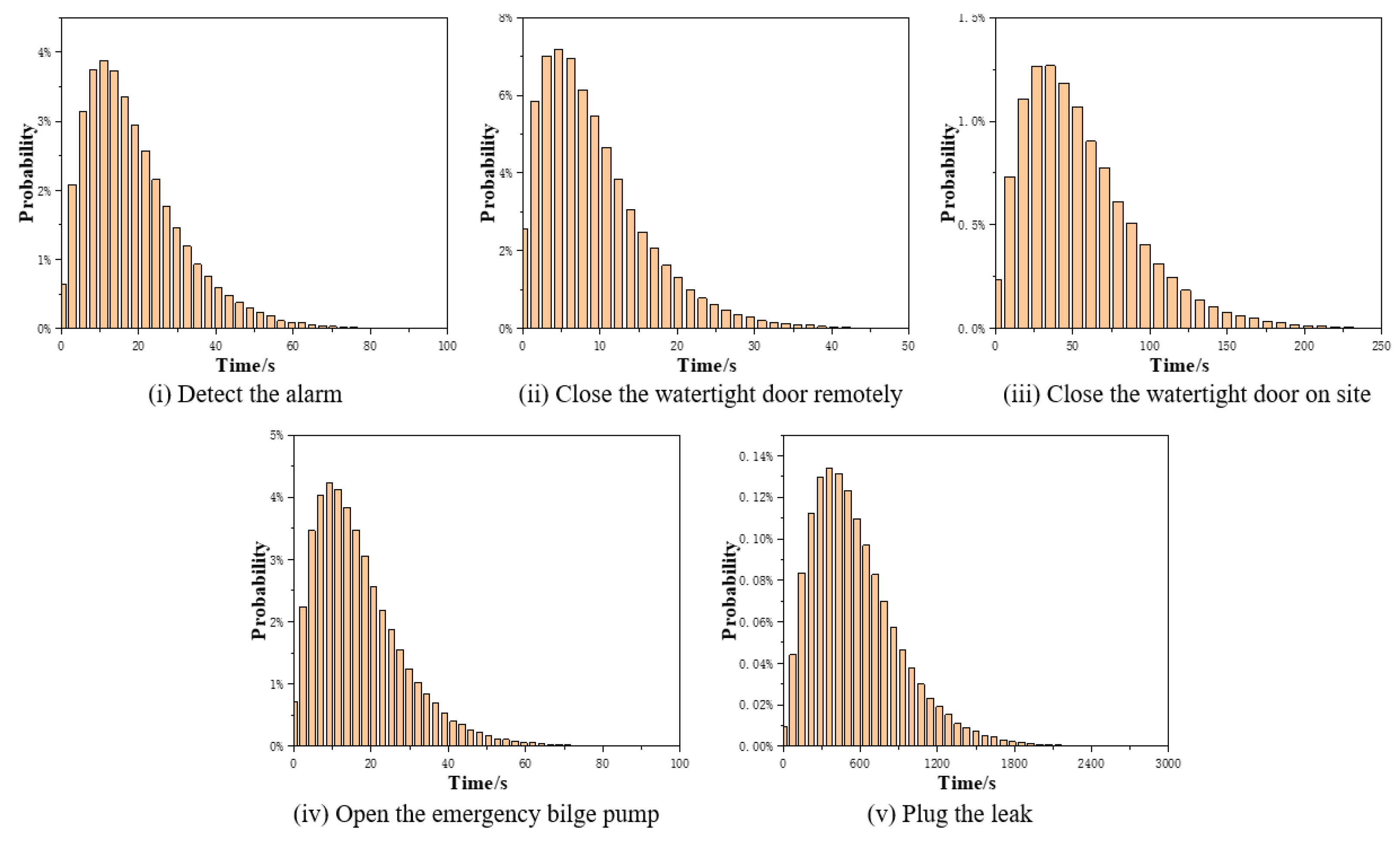
4.2.3. Quantitative Modeling
- (a)
- Quantify dependence (a) with the continuous SPAR-H method
- (b)
- Quantify dependence (b) with the dynamic available time model
4.3. Result Analysis and Discussion
4.3.1. The Result of the Assessment
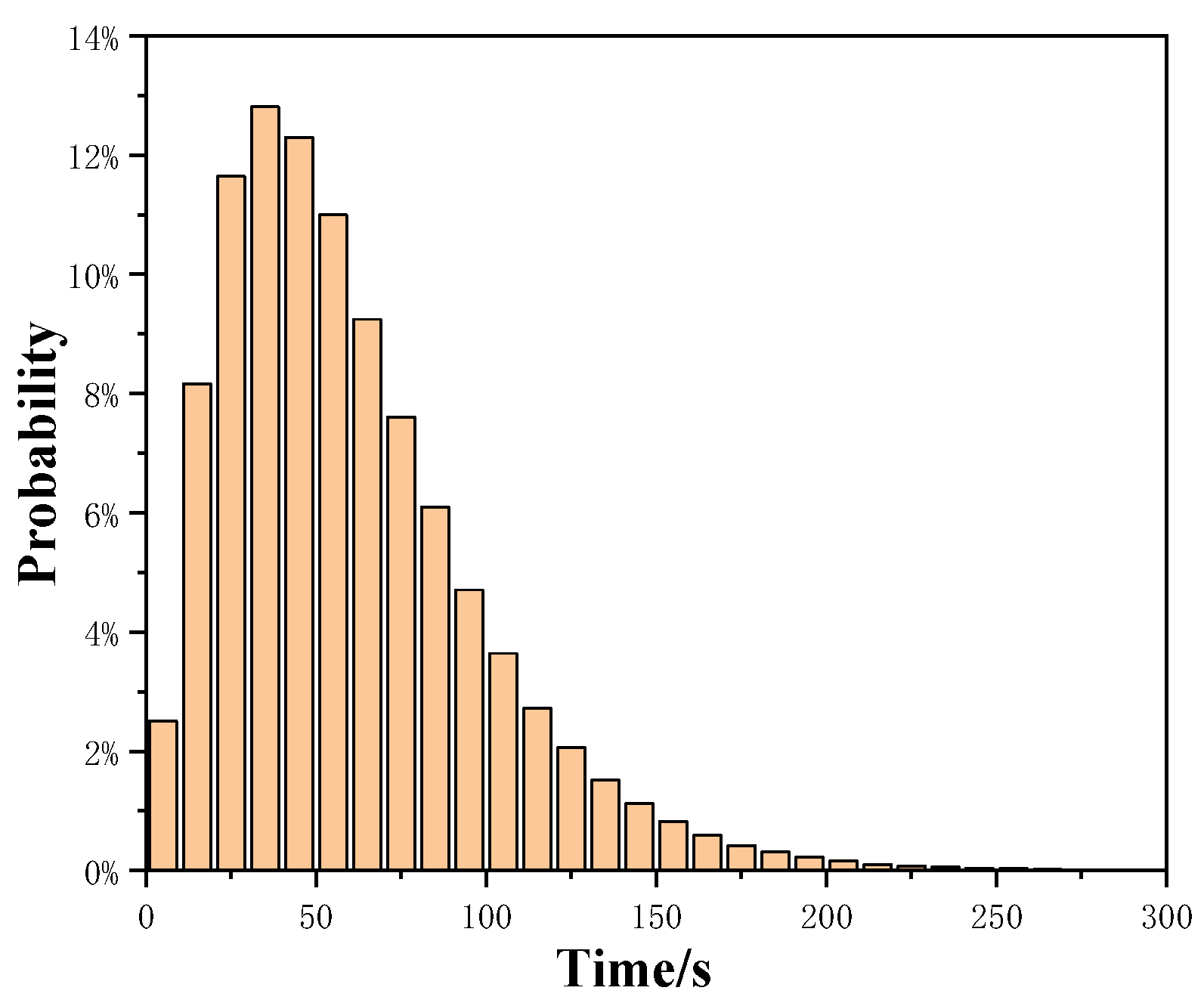
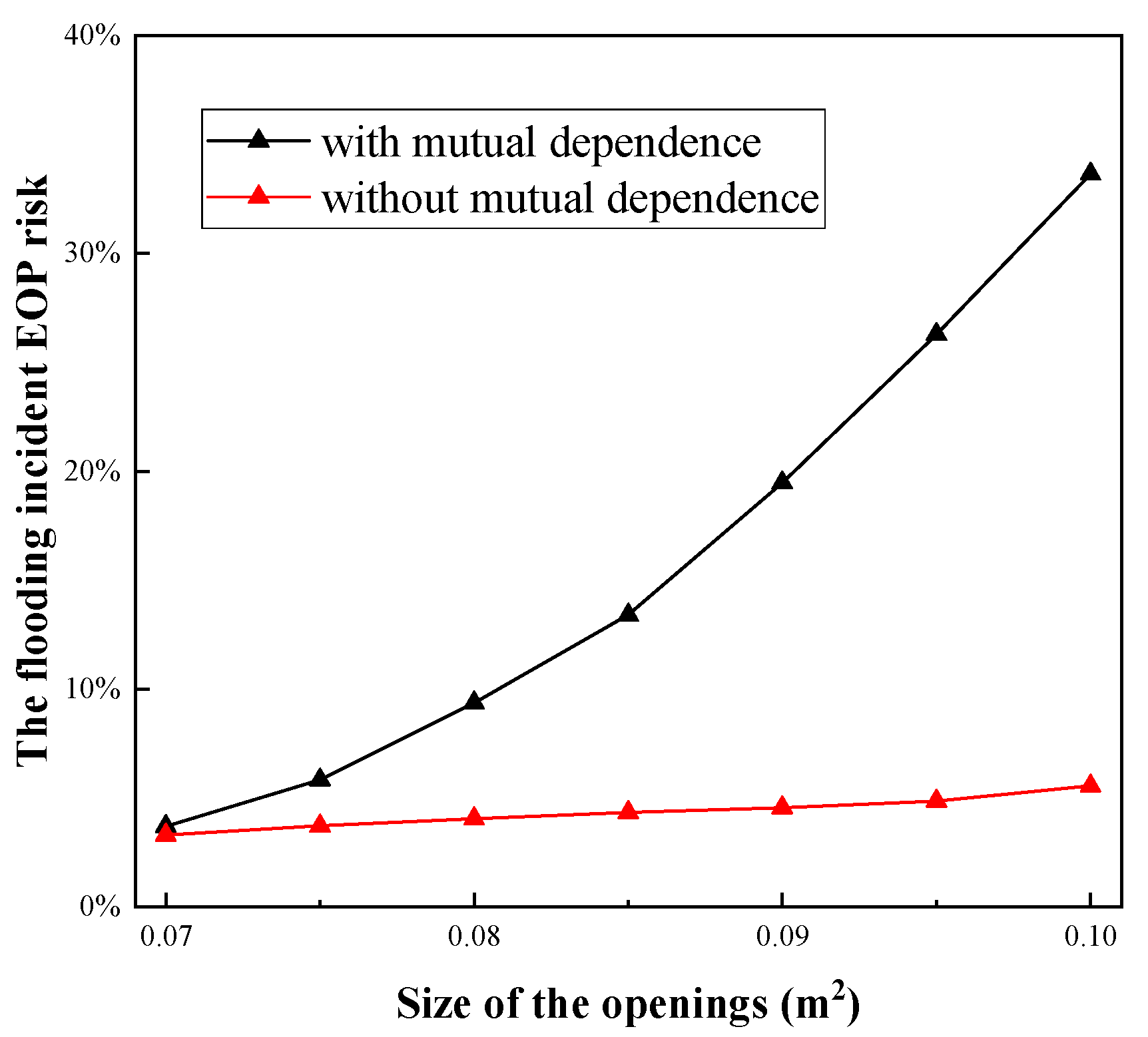
4.3.2. Sensitivity Analysis
- (1)
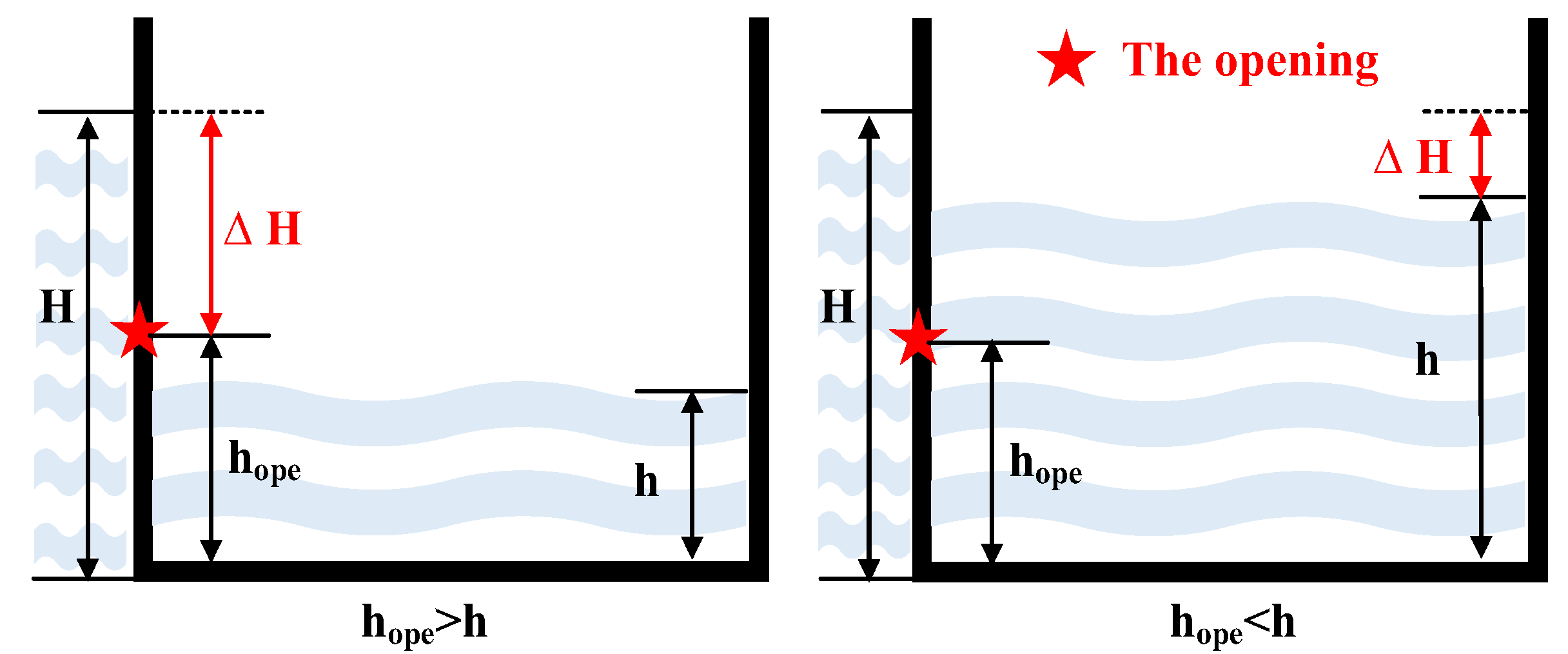
- Effect of the opening size
- (2)
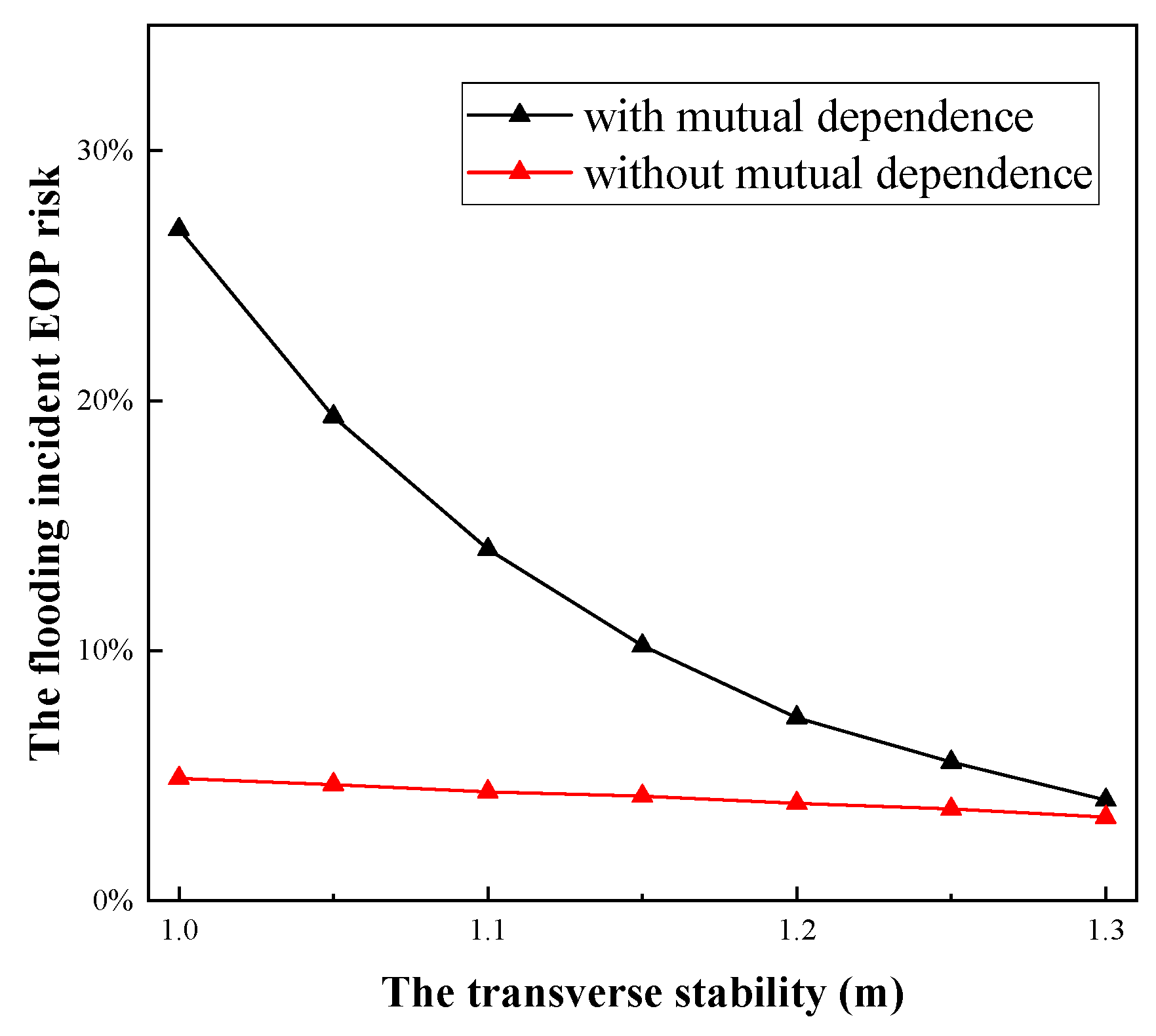
- Effect of the transverse stability
- (3)
- Effect of the compartment type
- (4)
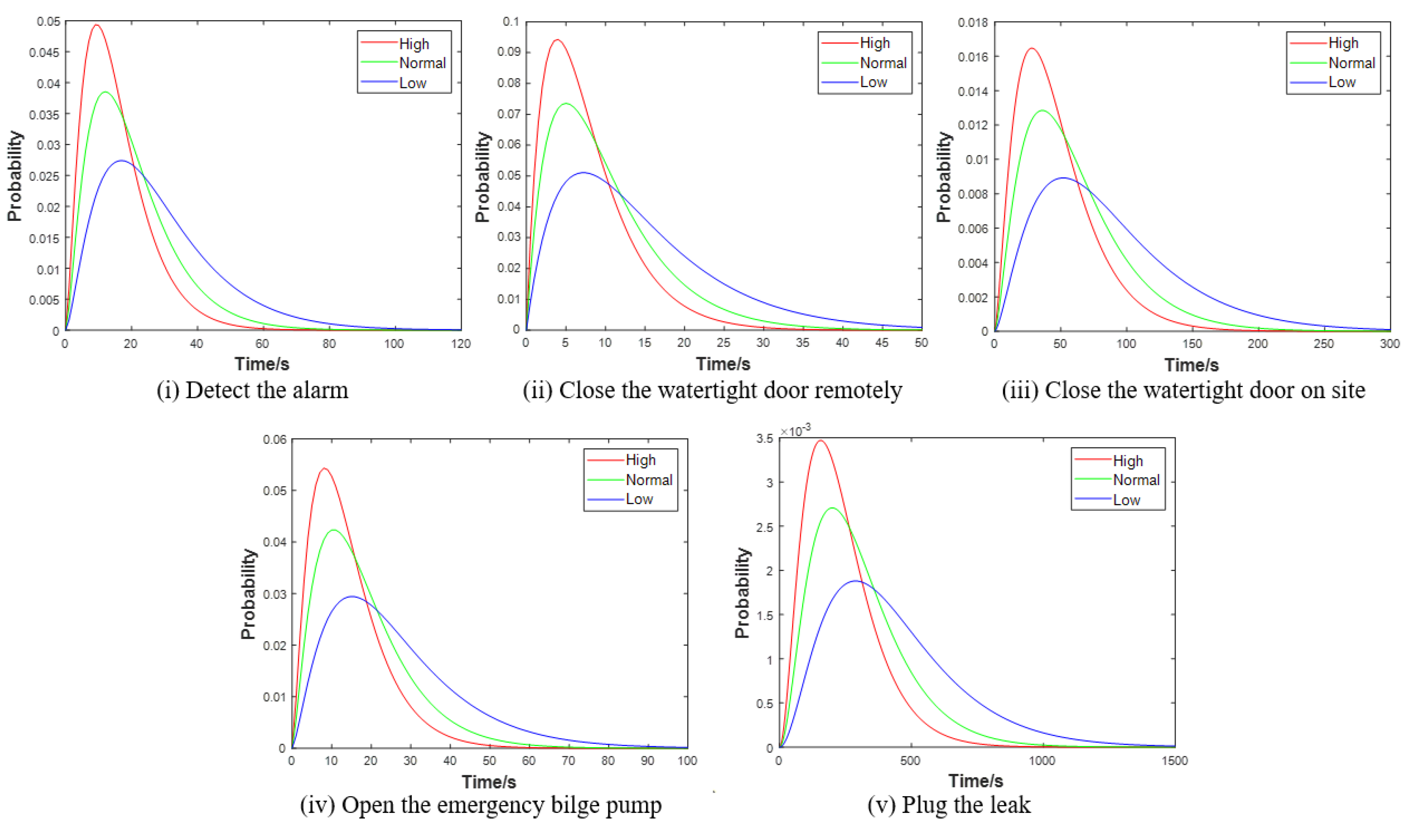
- Effect of the crew’s experience level
4.3.3. Findings and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Kujala, P.; Goerlandt, F.; Way, B.; Smith, D.; Yang, M.; Khan, F.; Veitch, B. Review of Risk-Based Design for Ice-Class Ships. Mar. Struct. 2019, 63, 181–195. [Google Scholar] [CrossRef]
- Sepehri, A.; Vandchali, H.R.; Siddiqui, A.W.; Montewka, J. The Impact of Shipping 4.0 on Controlling Shipping Accidents: A Systematic Literature Review. Ocean Eng. 2022, 243, 110162. [Google Scholar] [CrossRef]
- Zhou, J.; Reniers, G.; Khakzad, N. Application of Event Sequence Diagram to Evaluate Emergency Response Actions during Fire-Induced Domino Effects. Reliab. Eng. Syst. Saf. 2016, 150, 202–209. [Google Scholar] [CrossRef]
- Spanos, D.; Papanikolaou, A. On the Time for the Abandonment of Flooded Passenger Ships Due to Collision Damages. J. Mar. Sci. Technol. 2014, 19, 327–337. [Google Scholar] [CrossRef]
- Wu, B.; Yip, T.L.; Yan, X.; Guedes Soares, C. Review of Techniques and Challenges of Human and Organizational Factors Analysis in Maritime Transportation. Reliab. Eng. Syst. Saf. 2022, 219, 108249. [Google Scholar] [CrossRef]
- Kim, T.; Nazir, S.; Øvergård, K.I. A STAMP-Based Causal Analysis of the Korean Sewol Ferry Accident. Saf. Sci. 2016, 83, 93–101. [Google Scholar] [CrossRef]
- Kaptan, M. Analysis of Accidents during Vehicle Stowage on RO-RO Vessels by Using Fuzzy Bayesian Networks. Ocean Eng. 2022, 260, 111997. [Google Scholar] [CrossRef]
- Maternová, A.; Materna, M.; Dávid, A.; Török, A.; Švábová, L. Human Error Analysis and Fatality Prediction in Maritime Accidents. J. Mar. Sci. Eng. 2023, 11, 2287. [Google Scholar] [CrossRef]
- Zeng, S.; You, Q.; Guo, J.; Che, H. Situation Awareness-Based Safety Assessment Method for Human–Autonomy Interaction Process Considering Anchoring and Omission Biases. J. Mar. Sci. Eng. 2025, 13, 158. [Google Scholar] [CrossRef]
- Ahn, S.I.; Kurt, R.E. Application of a CREAM Based Framework to Assess Human Reliability in Emergency Response to Engine Room Fires on Ships. Ocean Eng. 2020, 216, 108078. [Google Scholar] [CrossRef]
- Hollnagel, E. Cognitive Reliability and Error Analysis Method: CREAM, 1st ed.; Elsevier: Oxford, UK; New York, NY, USA, 1998; ISBN 978-0-08-042848-2. [Google Scholar]
- Fan, H.; Enshaei, H.; Jayasinghe, S.G. Human Error Probability Assessment for LNG Bunkering Based on Fuzzy Bayesian Network-CREAM Model. J. Mar. Sci. Eng. 2022, 10, 333. [Google Scholar] [CrossRef]
- Li, K.; Guo, J.; Zeng, S.; Che, H. Reliability Assessment of Man-machine Systems Subject to Probabilistic Common Cause Errors. Qual. Reliab. Eng. Int. 2024, 40, 2399–2422. [Google Scholar] [CrossRef]
- Bye, A.; Laumann, K.; Taylor, C.; Rasmussen, M.; Øie, S.; van de Merwe, K.; Øien, K.; Boring, R.; Paltrinieri, N.; Wærø, I.; et al. The Petro-HRA Guideline; Institutt for Energiteknikk: Kjeller, Norway, 2017; ISBN 978-82-7017-901-5. [Google Scholar]
- Xi, Y.T.; Yang, Z.L.; Fang, Q.G.; Chen, W.J.; Wang, J. A New Hybrid Approach to Human Error Probability Quantification–Applications in Maritime Operations. Ocean Eng. 2017, 138, 45–54. [Google Scholar] [CrossRef]
- Ruan, F.; Chen, C.-H.; Cheng, Y.; Wang, J.-Y.; Chen, L.-W. Study on Evaluation Method for Nuclear Emergency Rescue Measures at Containment Vessel. Ann. Nucl. Energy 2021, 151, 107942. [Google Scholar] [CrossRef]
- Zou, Y.; Zhao, F.; Xu, S.; Zou, S. Evaluation of Emergency Response Measures for the LOCA of A Marine Reactor. Sustainability 2022, 14, 13873. [Google Scholar] [CrossRef]
- Ceylan, B.O.; Akyuz, E.; Arslan, O. Systems-Theoretic Accident Model and Processes (STAMP) Approach to Analyse Socio-Technical Systems of Ship Allision in Narrow Waters. Ocean Eng. 2021, 239, 109804. [Google Scholar] [CrossRef]
- Peng, C.; Zhen, X.; Huang, Y. A Multi-Layer FRAM Based Approach to Short-Term Human-Automation Resilience Assessment: A Case Study on Dynamic Positioning System in Offshore Tandem Offloading Process. Ocean Eng. 2022, 266, 112728. [Google Scholar] [CrossRef]
- Chen, C.; Reniers, G.; Khakzad, N. A Thorough Classification and Discussion of Approaches for Modeling and Managing Domino Effects in the Process Industries. Saf. Sci. 2020, 125, 104618. [Google Scholar] [CrossRef]
- Ricci, F.; Yang, M.; Reniers, G.; Cozzani, V. Emergency Response in Cascading Scenarios Triggered by Natural Events. Reliab. Eng. Syst. Saf. 2024, 243, 109820. [Google Scholar] [CrossRef]
- Zhou, C.; Qin, S.; Jiahao, Z.; Du, L.; Zhang, F. Modeling and Analysis of External Emergency Response to Ship Fire Using HTCPN and Markov Chain. Ocean Eng. 2024, 297, 117089. [Google Scholar] [CrossRef]
- Zhou, J.; Reniers, G.; Cozzani, V. A Petri-Net Approach for Firefighting Force Allocation Analysis of Fire Emergency Response with Backups. Reliab. Eng. Syst. Saf. 2023, 229, 108847. [Google Scholar] [CrossRef]
- Zhou, J.; Reniers, G. Petri Net Simulation of Multi-Department Emergency Response to Avert Domino Effects in Chemical Industry Accidents. Process Saf. Environ. Prot. 2021, 146, 916–926. [Google Scholar] [CrossRef]
- Liu, Q.; Guo, K.; Wu, X.; Xiao, Z.; Zhang, L. Simulation-Based Rescue Plan Modeling and Performance Assessment towards Resilient Metro Systems under Emergency. Reliab. Eng. Syst. Saf. 2024, 241, 109642. [Google Scholar] [CrossRef]
- Liu, Q.; He, R.; Zhang, L. Simulation-Based Multi-Objective Optimization for Enhanced Safety of Fire Emergency Response in Metro Stations. Reliab. Eng. Syst. Saf. 2022, 228, 108820. [Google Scholar] [CrossRef]
- Groth, K.; Wang, C.; Mosleh, A. Hybrid Causal Methodology and Software Platform for Probabilistic Risk Assessment and Safety Monitoring of Socio-Technical Systems. Reliab. Eng. Syst. Saf. 2010, 95, 1276–1285. [Google Scholar] [CrossRef]
- Jiang, C.; He, Z.; Li, F.; Xie, F.; Zheng, L.; Yang, J.; Yang, M. A Hybrid Computing Framework for Risk-Oriented Reliability Analysis in Dynamic PSA Context: A Case Study. Qual. Reliab. Eng. Int. 2022, 39, 3445–3471. [Google Scholar] [CrossRef]
- Mosleh, A.; Dias, A.; Eghbali, G.; Fazen, K. An Integrated Framework for Identification, Classification, and Assessment of Aviation Systems Hazards. In Probabilistic Safety Assessment and Management; Spitzer, C., Schmocker, U., Dang, V.N., Eds.; Springer: London, UK, 2004; pp. 2384–2390. ISBN 978-1-4471-1057-6. [Google Scholar]
- Wang, T.; Wu, Q.; Diaconeasa, M.A.; Yan, X.; Mosleh, A. On the Use of the Hybrid Causal Logic Methodology in Ship Collision Risk Assessment. J. Mar. Sci. Eng. 2020, 8, 485. [Google Scholar] [CrossRef]
- Zhang, D.; Han, Z.; Zhang, K.; Zhang, J.; Zhang, M.; Zhang, F. Use of Hybrid Causal Logic Method for Preliminary Hazard Analysis of Maritime Autonomous Surface Ships. J. Mar. Sci. Eng. 2022, 10, 725. [Google Scholar] [CrossRef]
- Meng, H.; An, X. Dynamic Risk Analysis of Emergency Operations in Deepwater Blowout Accidents. Ocean Eng. 2021, 240, 109928. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Lian, X.; Luo, J.; Liang, C.; Ma, H. Dynamic Risk Assessment of Plugging and Abandonment Operation Process of Offshore Wells Based on Dynamic Bayesian Network. Ocean Eng. 2023, 270, 113625. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, Q.; Cai, B.; Liu, Y.; Zheng, C. Risk Assessment on Deepwater Drilling Well Control Based on Dynamic Bayesian Network. Process Saf. Environ. Prot. 2021, 149, 643–654. [Google Scholar] [CrossRef]
- An, X.; Yin, Z.; Tong, Q.; Fang, Y.; Yang, M.; Yang, Q.; Meng, H. An Integrated Resilience Assessment Methodology for Emergency Response Systems Based on Multi-Stage STAMP and Dynamic Bayesian Networks. Reliab. Eng. Syst. Saf. 2023, 238, 109445. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C.; Yin, Z.; An, X.; Meng, H. Risk-Informed Multi-Objective Decision-Making of Emergency Schemes Optimization. Reliab. Eng. Syst. Saf. 2024, 245, 109979. [Google Scholar] [CrossRef]
- Guo, Y.; Jin, Y.; Hu, S.; Yang, Z.; Xi, Y.; Han, B. Risk Evolution Analysis of Ship Pilotage Operation by an Integrated Model of FRAM and DBN. Reliab. Eng. Syst. Saf. 2023, 229, 108850. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, S. Framework for Process Analysis of Maritime Accidents Caused by the Unsafe Acts of Seafarers: A Case Study of Ship Collision. J. Mar. Sci. Eng. 2022, 10, 1793. [Google Scholar] [CrossRef]
- Xi, Y.; Zhang, X.; Han, B.; Zhu, Y.; Fan, C.; Kim, E. Advanced Human Reliability Analysis Approach for Ship Convoy Operations via a Model of IDAC and DBN: A Case from Ice-Covered Waters. J. Mar. Sci. Eng. 2024, 12, 1536. [Google Scholar] [CrossRef]
- Qian, S.S.; Miltner, R.J. A Continuous Variable Bayesian Networks Model for Water Quality Modeling: A Case Study of Setting Nitrogen Criterion for Small Rivers and Streams in Ohio, USA. Environ. Model. Softw. 2015, 69, 14–22. [Google Scholar] [CrossRef]
- Ahn, S.I.; Kurt, R.E.; Akyuz, E. Application of a SPAR-H Based Framework to Assess Human Reliability during Emergency Response Drill for Man Overboard on Ships. Ocean Eng. 2022, 251, 111089. [Google Scholar] [CrossRef]
- Parhizkar, T.; Utne, I.B.; Vinnem, J.E.; Mosleh, A. Dynamic Probabilistic Risk Assessment of Decision-Making in Emergencies for Complex Systems, Case Study: Dynamic Positioning Drilling Unit. Ocean Eng. 2021, 237, 109653. [Google Scholar] [CrossRef]
- IMO. Guidelines for a Structure of an Integrated System of Contingency Planning for Shipboard Emergencies; International Maritime Organization: Lambeth, London, 1997. [Google Scholar]
- Kim, Y.; Kim, J.; Park, J.; Choi, S.Y.; Kim, S.; Jung, W.; Kim, H.E.; Shin, S.K. An Algorithm for Evaluating Time-Related Human Reliability Using Instrumentation Cues and Procedure Cues. Nucl. Eng. Technol. 2021, 53, 368–375. [Google Scholar] [CrossRef]
- Siegel, A.I. Man-Machine Simulation Models: Psychosocial and Performance Interaction; Wiley-Interscience: Hoboken, NJ, USA, 1969. [Google Scholar]
- Hu, L.; Pan, X.; Kang, R.; Chu, J.; Gao, Y.; Xue, Z.; Baoyin, H. Dynamic Risk Assessment of Uncertain Random System Considering Operator’s Simple Emergency-Stop Action in Short Time Window. Reliab. Eng. Syst. Saf. 2024, 252, 110479. [Google Scholar] [CrossRef]
- Palmer, E.M.; Horowitz, T.S.; Torralba, A.; Wolfe, J.M. What Are the Shapes of Response Time Distributions in Visual Search? J. Exp. Psychol. Hum. Percept. Perform. 2011, 37, 58–71. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, S.; Guo, J.; Che, H. A Bayesian Network for Reliability Assessment of Man-Machine Phased-Mission System Considering the Phase Dependencies of Human Cognitive Error. Reliab. Eng. Syst. Saf. 2021, 207, 107385. [Google Scholar] [CrossRef]
- Endrina, N.; Rasero, J.C.; Konovessis, D. Risk Analysis for RoPax Vessels: A Case of Study for the Strait of Gibraltar. Ocean Eng. 2018, 151, 141–151. [Google Scholar] [CrossRef]
- Papanikolaou, A. (Ed.) Risk-Based Ship Design; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-89041-6. [Google Scholar]
- IMO. SOLAS Consolidated Edition 2020; International Maritime Organization: London, UK, 2020; p. 576. [Google Scholar]
- Ruponen, P. Progressive Flooding of a Damaged Passenger Ship; Helsinki University of Technology: Espoo, Finland, 2007; p. 130. [Google Scholar]
- Ignjatović, L.; Stojković, M.; Ivetić, D.; Milašinović, M.; Milivojević, N. Quantifying Multi-Parameter Dynamic Resilience for Complex Reservoir Systems Using Failure Simulations: Case Study of the Pirot Reservoir System. Water 2021, 13, 3157. [Google Scholar] [CrossRef]
- Stojkovic, M.; Simonovic, S.P. System Dynamics Approach for Assessing the Behaviour of the Lim Reservoir System (Serbia) under Changing Climate Conditions. Water 2019, 11, 1620. [Google Scholar] [CrossRef]
- Stojković, M.; Mijić, A.; Dobson, B.; Marjanović, D.; Majkić-Dursun, B. Novel Perspectives on Environmental Dynamic Resilience: Adapting Urban Water Systems to a Changing Climate. Water Resour. Manag. 2024, 38, 4455–4472. [Google Scholar] [CrossRef]
- Lee, G.J.; Lee, D.; Choi, J.; Kang, H.J. A Concept Study on Design Alternatives for Minimizing Accident Consequences in Maritime Autonomous Surface Ships. J. Mar. Sci. Eng. 2023, 11, 907. [Google Scholar] [CrossRef]
- Guidelines for Damage Control Plans and Information to the Master 2010. International Maritime Organization (IMO), London, United Kingdom. Available online: https://imorules.com/MSCCIRC_1245.html (accessed on 20 March 2024).
- Ruponen, P.; Montewka, J.; Tompuri, M.; Manderbacka, T.; Hirdaris, S. A Framework for Onboard Assessment and Monitoring of Flooding Risk Due to Open Watertight Doors for Passenger Ships. Reliab. Eng. Syst. Saf. 2022, 226, 108666. [Google Scholar] [CrossRef]
- Minette, R.S.; SilvaNeto, S.F.; Vaz, L.A.; Monteiro, U.A. Experimental Modal Analysis of Electrical Submersible Pumps. Ocean Eng. 2016, 124, 168–179. [Google Scholar] [CrossRef]
- Xin, G.; Cheng, Z.; Gao, C. Design of Marine Automatic Leakage Stoppage System Based on Artificial Eddy Current. IOP Conf. Ser. Mater. Sci. Eng. 2019, 563, 042030. [Google Scholar] [CrossRef]
- Parhizkar, T.; Hogenboom, S.; Vinnem, J.E.; Utne, I.B. Data Driven Approach to Risk Management and Decision Support for Dynamic Positioning Systems. Reliab. Eng. Syst. Saf. 2020, 201, 106964. [Google Scholar] [CrossRef]
- Fan, X.; Zuo, M.J. Fault Diagnosis of Machines Based on D–S Evidence Theory. Part 1: D–S Evidence Theory and Its Improvement. Pattern Recognit. Lett. 2006, 27, 366–376. [Google Scholar] [CrossRef]
- Jalonen, R.; Ruponen, P.; Weryk, M.; Naar, H.; Vaher, S. A Study on Leakage and Collapse of Non-Watertight Ship Doors under Floodwater Pressure. Mar. Struct. 2017, 51, 188–201. [Google Scholar] [CrossRef]
- Final Report Research Study on the Sinking Sequence of MV Estonia 2008. Swedish National Maritime and Transport Engineering Research Institute (SSPA), Gothenburg, Sweden. Available online: https://estonia1994.ee/en/news/sspa-consortium-final-report (accessed on 20 March 2024).
- Jasionowski, A. Decision Support for Ship Flooding Crisis Management. Ocean Eng. 2011, 38, 1568–1581. [Google Scholar] [CrossRef]
- Lee, K.W.; Han, G.Y.; Kim, M.E. Proposed Design Criteria for a Bilge Pumping System for Large Container Ships. Int. J. Marit. Eng. 2021, 163, A71–A79. [Google Scholar] [CrossRef]
- You, Q.; Guo, J.; Zeng, S.; Che, H. A Dynamic Bayesian Network Based Reliability Assessment Method for Short-Term Multi-Round Situation Awareness Considering Round Dependencies. Reliab. Eng. Syst. Saf. 2024, 243, 109838. [Google Scholar] [CrossRef]
- Groth, K.M.; Swiler, L.P. Bridging the Gap between HRA Research and HRA Practice: A Bayesian Network Version of SPAR-H. Reliab. Eng. Syst. Saf. 2013, 115, 33–42. [Google Scholar] [CrossRef]
- Ramezani, A.; Nazari, T.; Rabiee, A.; Hadad, K.; Faridafshin, M. Human Error Probability Quantification for NPP Post-Accident Analysis Using Cognitive-Based THERP Method. Prog. Nucl. Energy 2020, 123, 103281. [Google Scholar] [CrossRef]
- Stojković, M.; Marjanović, D.; Rakić, D.; Ivetić, D.; Simić, V.; Milivojević, N.; Trajković, S. Assessment of Water Resources System Resilience under Hazardous Events Using System Dynamic Approach and Artificial Neural Networks. J. Hydroinform. 2023, 25, 208–225. [Google Scholar] [CrossRef]
- Simic, V.; Stojkovic, M.; Milivojevic, N.; Bacanin, N. Assessing Water Resources Systems’ Dynamic Resilience under Hazardous Events via a Genetic Fuzzy Rule-Based System. J. Hydroinform. 2023, 25, 318–331. [Google Scholar] [CrossRef]
- Milivojević, V.; Ćirović, V.; Stojković, M.; Mirković, U.; Kuzmanović, V.; Milivojević, N.; Stojanović, B. Machine Learning-Based Interactive Dynamic Resilience Assessment for Complex Hydropower Systems. J. Big Data 2025, 12, 44. [Google Scholar] [CrossRef]
- Sheng, Z. Principles of Naval Architecture, 2nd ed.; Shanghai Jiao Tong University Press: Shanghai, China, 2017; ISBN 978-7-313-17996-8. [Google Scholar]
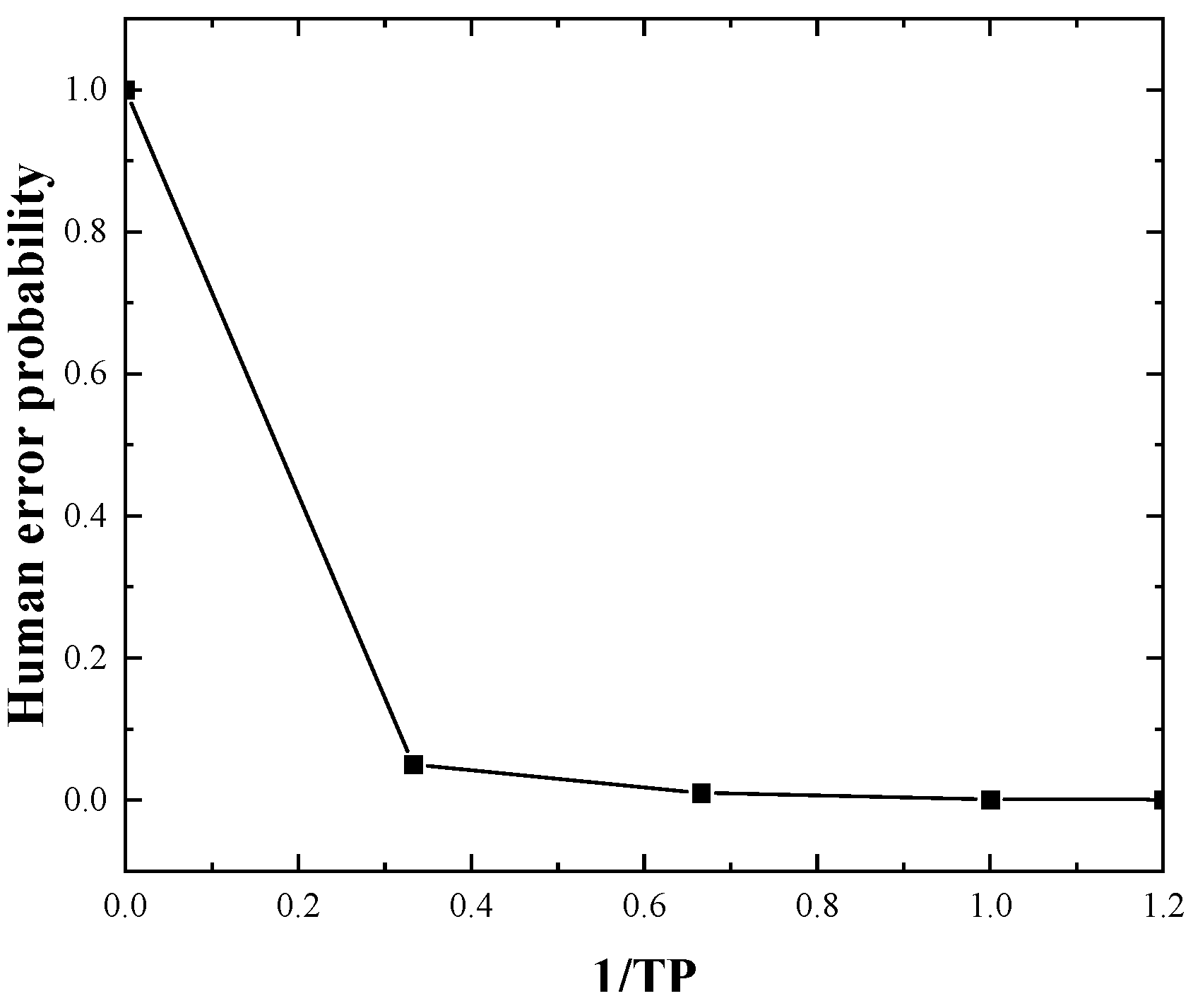



| SPAR-H Levels | Multipliers |
|---|---|
| Inadequate time | - |
| Barely adequate time: 1/3 the average time | 50 |
| Barely adequate time: 2/3 the average time | 10 |
| Nominal time | 1 |
| Operating Procedure | Machine Failure | Probability | Sources |
|---|---|---|---|
| Detect the alarm | Sensor failure | 1.22 × 10−7 | [61] |
| Hardware component failure | 1.22 × 10−7 | [61] | |
| Close the watertight door remotely | Controller failure | 1.22 × 10−7 | [61] |
| Switch failure | 1.22 × 10−7 | [61] | |
| Close the watertight door on site | Bulkhead deformation | 2.44 × 10−7 | Assumed |
| Deck deformation | 2.44 × 10−7 | Assumed | |
| Open the emergency bilge pump | Hardware component failure | 1.22 × 10−7 | [61] |
| Blocked pipe | 1.22 × 10−7 | [61] | |
| Controller failure | 1.22 × 10−7 | [61] | |
| Switch failure | 1.22 × 10−7 | [61] | |
| Plug the leak | Lack of equipment | 2.44 × 10−7 | Assumed |
| Leak plugging equipment breakdown | 2.44 × 10−7 | Assumed |
| Operating Procedure | Experts | ||
|---|---|---|---|
| P1 | P2 | P3 | |
| Detect the alarm | [17, 21] | [18, 22] | [19, 23] |
| Close the watertight door remotely | [10, 12] | [9, 13] | [8, 11] |
| Close the watertight door on site | [56, 61] | [58, 64] | [59, 65] |
| Open the emergency bilge pump | [15, 18] | [16, 19] | [18, 21] |
| Plug the leak | [287, 302] | [292, 312] | [300, 307] |
| Operating Procedure | Mean Value | |
|---|---|---|
| Detect the alarm | 20 | 2.5 |
| Close the watertight door remotely | 10 | 2 |
| Close the watertight door on site | 60 | 2.5 |
| Open the emergency bilge pump | 18 | 2.4 |
| Plug the leak | 300 | 3 |
| Dimension | Value | Sources |
|---|---|---|
| 0.85 | [51] | |
| 1.17 m | [64,65] | |
| 137.4 m | [64,65] | |
| 24.2 m | [64,65] | |
| 5.4 m | [64,65] | |
| 6 m | Assumed | |
| 5 m | Assumed | |
| 0.08 m2 | Assumed | |
| Flow rate of the emergency bilge pump | 0.15 m3/s | [66] |
| (flooding in single compartment) | 15° | [51] |
| (flooding in adjacent compartments) | 12° | [51] |
| Scenario | The EOP Risk |
|---|---|
| With mutual dependence | 9.4% |
| Without mutual dependence | 4.1% |
| Compartment Type | Permeability |
|---|---|
| Appropriated to stores | 0.6 |
| Occupied by machinery | 0.85 |
| Occupied by accommodation | 0.95 |
| Void spaces | 0.95 |
| Compartment Type | With Mutual Dependence | Without Mutual Dependence |
|---|---|---|
| Appropriated to stores | 4.5% | 3.5% |
| Occupied by machinery | 9.4% | 4.1% |
| Occupied by accommodation | 10.6% | 4.2% |
| Void spaces | 10.6% | 4.2% |
| Operating Procedure | High | Normal | Low |
|---|---|---|---|
| Detect the alarm | 15.6 | 20 | 28.8 |
| Close the watertight door remotely | 7.8 | 10 | 14.4 |
| Close the watertight door on site | 46.8 | 60 | 86.4 |
| Open the emergency bilge pump | 14.04 | 18 | 25.92 |
| Plug the leak | 234 | 300 | 432 |
| Scenario | High | Normal | Low |
|---|---|---|---|
| With mutual dependence | 1.3% | 9.4% | 55.7% |
| Without mutual dependence | 1.1% | 4.1% | 25.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Zeng, S.; Guo, J.; Che, H. Risk Assessment Method for Flooding Incident Emergency Operating Procedure Considering Mutual Dependence Between Human Error and Available Time. J. Mar. Sci. Eng. 2025, 13, 853. https://doi.org/10.3390/jmse13050853
Li K, Zeng S, Guo J, Che H. Risk Assessment Method for Flooding Incident Emergency Operating Procedure Considering Mutual Dependence Between Human Error and Available Time. Journal of Marine Science and Engineering. 2025; 13(5):853. https://doi.org/10.3390/jmse13050853
Chicago/Turabian StyleLi, Kehui, Shengkui Zeng, Jianbin Guo, and Haiyang Che. 2025. "Risk Assessment Method for Flooding Incident Emergency Operating Procedure Considering Mutual Dependence Between Human Error and Available Time" Journal of Marine Science and Engineering 13, no. 5: 853. https://doi.org/10.3390/jmse13050853
APA StyleLi, K., Zeng, S., Guo, J., & Che, H. (2025). Risk Assessment Method for Flooding Incident Emergency Operating Procedure Considering Mutual Dependence Between Human Error and Available Time. Journal of Marine Science and Engineering, 13(5), 853. https://doi.org/10.3390/jmse13050853






