Research on the Wetland Vegetation Classification Method Based on Cross-Satellite Hyperspectral Images
Abstract
1. Introduction
2. Method and Data
2.1. Method
2.1.1. Generator
2.1.2. Double Branch Discriminator
2.2. Data
2.2.1. Public Dataset
2.2.2. Hyperspectral Satellite Data of Yellow River Estuary Wetland
2.3. Other
3. Experimental Results and Analysis
3.1. Unsupervised Cross-Domain Hyperspectral Object Classification Experiment
3.2. Supervised Cross-Domain Hyperspectral Object Classification Experiment
3.3. Semi Supervised Classification Test
3.4. Ablation Test
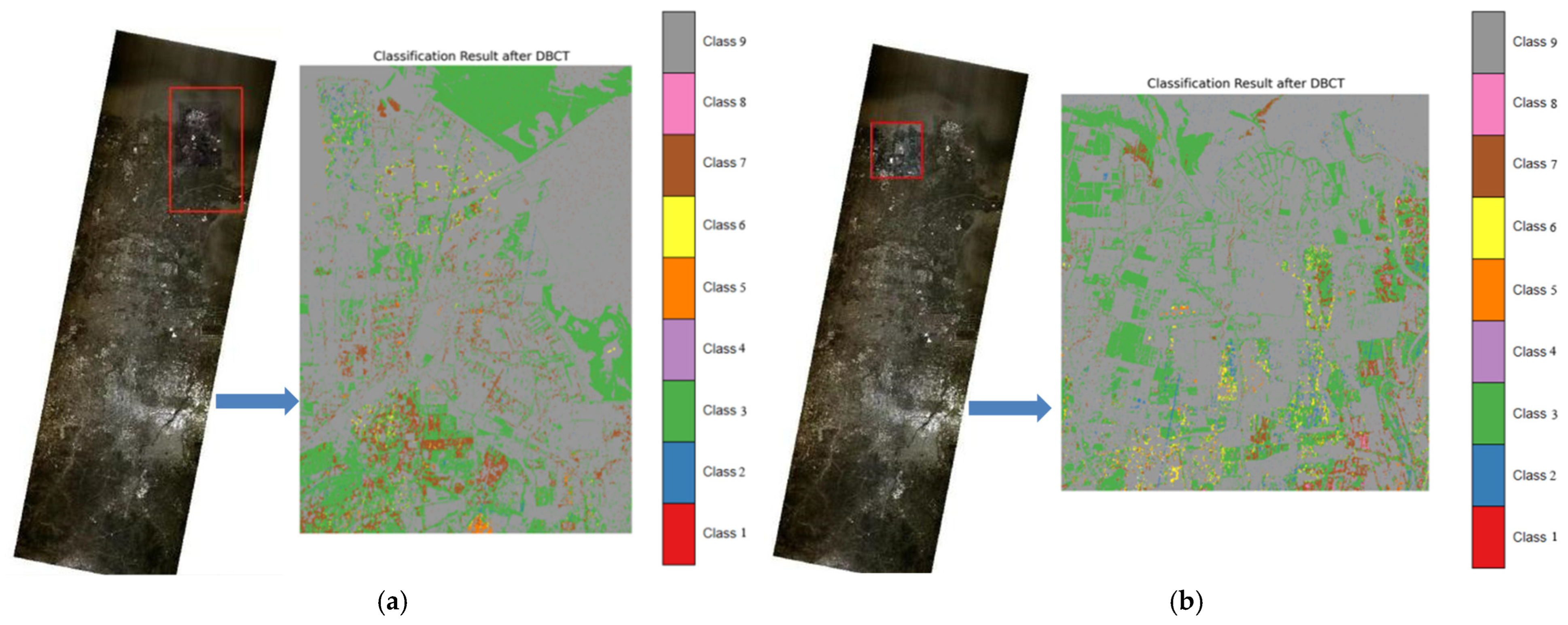
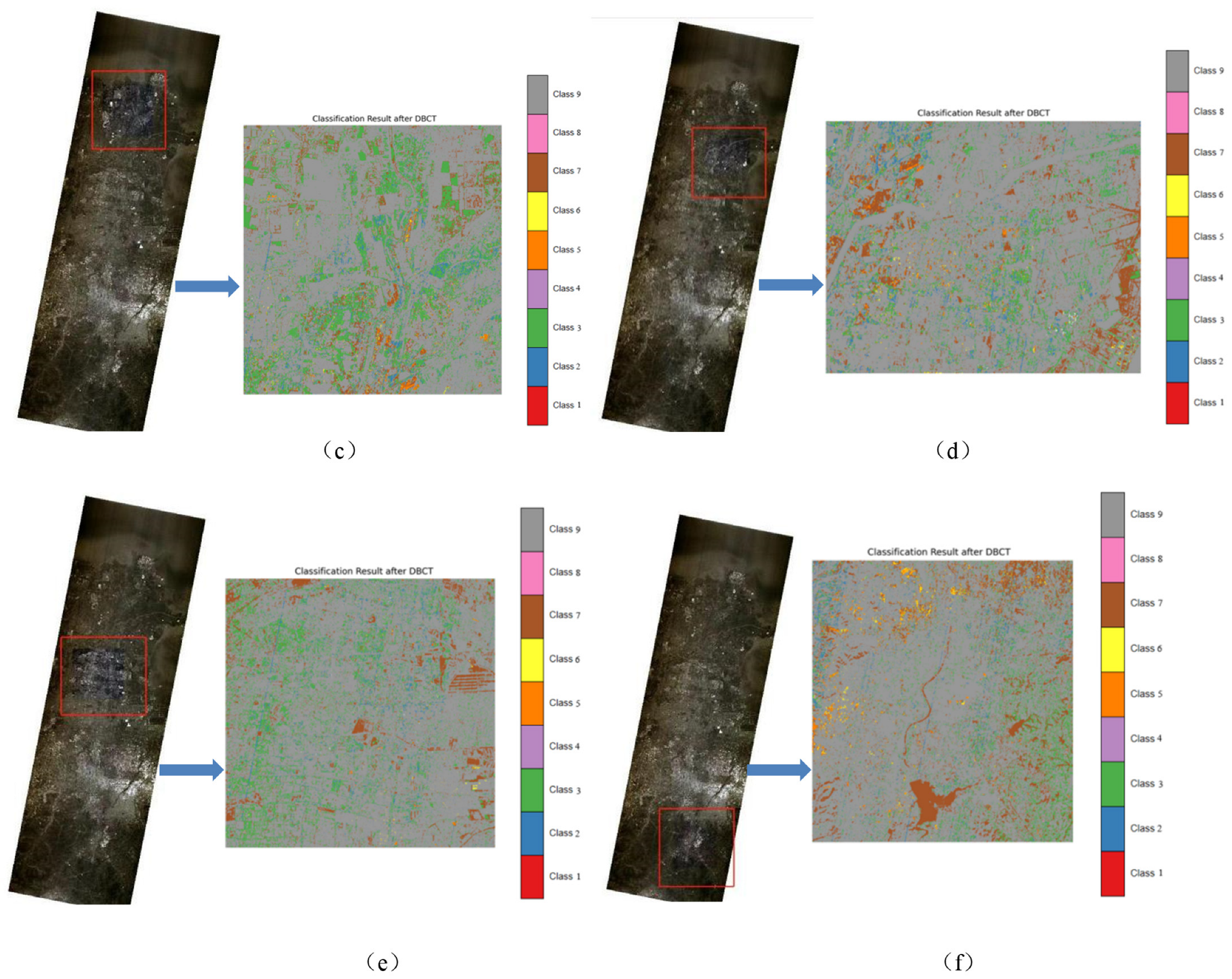
3.5. Vegetation Distribution in Yellow River Estuary Reserve
4. Summary and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, W.W.; Liu, W.W.; Wang, Y.M.; Zhao, R.; Huang, M.Z.; Wang, Y.; Yang, G.; Meng, X.C. Research progress and prospects of hyperspectral remote sensing for global wetland from 2010 to 2022. Natl. Remote Sens. Bull. 2023, 27, 1281–1299. [Google Scholar]
- Chen, P.S.; Tong, Q.X.; Guo, H.D. Research on Remote Sensing Information Mechanism; Science Press: Beijing, China, 1998; pp. 1–2. [Google Scholar]
- Zhao, Y.Q.; Yang, J.X. Hyperspectral image denoising via sparse representation and low-rank constraint. IEEE Trans. Geosci. Remote Sens. 2014, 53, 296–308. [Google Scholar] [CrossRef]
- Tuia, D.; Persello, C.; Bruzzone, L. Domain adaptation for the classification of remote sensing data: An overview of recent advances. IEEE Geosci. Remote Sens. Mag. 2016, 4, 41–57. [Google Scholar] [CrossRef]
- Torralba, A.; Efros, A.A. Unbiased look at dataset bias. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1521–1528. [Google Scholar]
- Mateo-Garcia, G.; Laparra, V.; Lopez-Puigdollers, D.; Gomez-Chova, L. Cross-sensor adversarial domain adaptation of Landsat-8 and Proba-V images for cloud detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 747–761. [Google Scholar] [CrossRef]
- Tuia, D.; Pasolli, E.; Emery, W.J. Using active learning to adapt remote sensing image classifiers. Remote Sens. Environ. 2011, 115, 2232–2242. [Google Scholar] [CrossRef]
- Chen, Y.S.; Lin, Z.H.; Zhao, X.; Wang, G.; Gu, Y.F. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Li, Z.W.; Guo, F.M.; Ren, G.B.; Ma, Y.; Xin, Z.L.; Huang, W.H.; Sui, H.; Meng, Q. Hyperspectral remote sensing in the Yellow River Delta wetland. Mar. Sci. 2023, 47, 161–175. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.C.; Bengio, Y.Q. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Zhong, Z.L.; Li, J.; Luo, Z.M.; Chapman, M. Spectral-spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 2096–3030. [Google Scholar]
- Long, M.S.; Cao, Z.J.; Wang, J.M.; Joedan, M.I. Conditional adversarial domain adaptation. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Tzeng, E.; Hoffman, J.; Saenko, K.; Darrell, T. Adversarial discriminative domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7167–7176. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Zhang, Y.H.; Wu, J.Q.; Zhang, Q.; Hu, X.G. Multi-view feature learning for the over-penalty in adversarial domain adaptation. Data Intell. 2024, 1, 183–198. [Google Scholar] [CrossRef]
- Yi, Z.L.; Zhang, H.; Tan, P.; Gong, M.L. Dual GAN: Unsupervised dual learning for image-to-image translation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Li, X.; Ma, J.; Wu, J.D.; Li, Z.R.; Tan, Z.Z. Transformer-based conditional generative transfer learning network for cross domain fault diagnosis under limited data. Sci. Rep. 2025, 15, 6836. [Google Scholar] [CrossRef]
- Li, W.C.; He, P.S.; Li, H.L.; Wang, H.X.; Zhang, R.M. Detection of GAN-Generated Images by Estimating Artifact Similarity Source. IEEE Signal Process. Lett. 2022, 29, 862–866. [Google Scholar] [CrossRef]
- Ma, X.P.; Zhang, X.K.; Wang, Z.G.; Pun, M.O. Unsupervised Domain Adaptation Augmented by Mutually Boosted Attention for Semantic. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5400515. [Google Scholar]
- Xu, Y.H.; He, F.X.; Du, B.; Tao, D.C.; Zhang, L.P. Self-Ensembling GAN for Cross-Domain Semantic Segmentation. IEEE Trans. Multimed. 2023, 25, 7837–7850. [Google Scholar] [CrossRef]
- Zheng, X.T.; Xiao, X.L.; Chen, X.M.; Lu, W.X.; Liu, X.Y.; Lu, X.Q. Advancements in cross-domain remote sensing scene interpretation. J. Image Graph. 2024, 29, 1730–1746. [Google Scholar] [CrossRef]
- Yu, C.Y.; Liu, C.Y.; Song, M.P.; Chang, C.I. Unsupervised domain adaptation with content-wise alignment for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2021, 19, 5511705. [Google Scholar] [CrossRef]
- Ma, X.R.; Mou, X.R.; Wang, J.; Liu, X.K.; Geng, J.; Wang, H.Y. Cross-dataset hyperspectral image classification based on adversarial domain adaptation. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4179–4190. [Google Scholar] [CrossRef]
- Wang, X.Z.; Liu, J.H.; Ni, Y.; Chi, W.J.; Fu, Y.Y. Two-stage domain alignment single-source domain generalization network for cross-scene hyperspectral images classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5527314. [Google Scholar] [CrossRef]
- Bejiga, M.B.; Melgani, F. An adversarial approach to cross-sensor hyperspectral data classification. In Proceedings of the IGARSS 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3575–3578. [Google Scholar]
- Kalita, I.; Kumar, R.N.S.; Roy, M. Deep learning-based cross-sensor domain adaptation under active learning for land cover classification. IEEE Trans. Geosci. Remote Sens. 2021, 19, 6005005. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Ahmadyfard, A. A GAN-based method for cross-scene classification of hyperspectral scenes captured by different sensors. Multimed. Tools Appl. 2024. [Google Scholar] [CrossRef]
- Wang, J.Y.; Wang, Y.M.; Li, C.L. Noise model of hyperspectral imaging system and influence on radiation sensitivity. J. Remote Sens. 2010, 14, 607–620. [Google Scholar]
- Sun, H.Z. Research on Hyperspectral Remote Sensing Image Denoising Method and Its Application in Target Detection. Ph.D. Thesis, Harbin Institute of Technology, Harbin, Chian, 2022. [Google Scholar]
- Zhou, Q.Z.; Guo, Q.; Wang, H.R.; Li, A. Two discriminators deep residual GAN hyperspectral image pan-sharpening. J. Image Graph. 2024, 29, 2046–2062. [Google Scholar] [CrossRef]
- Hu, Y.B.; Ren, G.B.; Ma, Y.; Yang, J.F.; Wang, J.B.; An, J.B.; Liang, J.; Ma, Y.Q.; Song, X.K. Coastal wetland hyperspectral classification under the collaborative of subspace partition and infinite probabilistic latent graph ranking. Sci. China (Technol. Sci.) 2022, 65, 759–777. [Google Scholar] [CrossRef]
- Cover description. Hyperspectral pseudo color image of lakes on the Gongzhucuo Plateau in Tibet obtained by Xiamen Science and Technology No.1 satellite. Natl. Remote Sens. Bull. 2024, 28, 321. [Google Scholar]
- Xu, R.; Dong, X.M.; Li, W.; Peng, J.T.; Sun, W.W.; Xu, Y. DBCT Net: Double branch convolution-transformer network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5509915. [Google Scholar]
- Chen, Y.L.; Teng, W.T.; Li, Z.; Zhu, Q.Q.; Guan, Q.F. Cross-domain scene classification based on a spatial generalized neural architecture search for high spatial resolution remote sensing images. Remote Sens. 2021, 13, 3460. [Google Scholar] [CrossRef]
- Zhu, S.; Pan, X.; Li, X. Effect of Spartina spp. invasion on saltmarsh community of the Yellow River Delta. Shandong Agric. Sci. 2012, 44, 73–75, 83. [Google Scholar]
- Zhang, Y.X.; Li, W.; Sun, W.D.; Tao, R. Single-source domain expansion network for cross-scene hyperspectral image classification. IEEE Trans. Image Process. 2023, 32, 1498–1512. [Google Scholar] [CrossRef]
- Zhao, H.Q.; Zhang, J.W.; Lin, L.L.; Wang, J.K.; Gao, S.; Zhang, Z.W. Locally linear unbiased randomization network for cross-scene hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5526512. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cunningham, P.; Delany, S.J. k-Nearest neighbour classifiers—A tutorial. ACM Comput. Surv. (CSUR) 2021, 54, 128. [Google Scholar] [CrossRef]
- Wang, D.; Du, B.; Zhang, L.; Xu, Y. Adaptive spectral–spatial multiscale contextual feature extraction for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2461–2477. [Google Scholar] [CrossRef]
- An, L.S.; Zhou, B.H.; Zhao, Q.S.; Wang, L. Spatial distribution of vegetation and environmental interpretation in the Yellow River Delta. Acta Ecol. Sin. 2017, 37, 6809–6817. [Google Scholar]
- Chen, J.N.; Lu, Y.Y.; Yu, Q.H.; Luo, X.D.; Adeli, E.; Wang, Y.; Lu, L.; Alan, L.Y.; Zhou, Y.Y. TransUNet: Transformers Make Strong Encoders for Medical Image Segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.Y.; Chen, J.; Jiang, D.S.; Zhang, X.P.; Tian, Q.; Wang, M.N. Swin-Unet: Unet-like Pure Transformer for Medical Image Segmentation. In Proceedings of the Computer Vision—ECCV 2022 Workshops, Tel Aviv, Israel, 23–27 October 2022; pp. 205–218. [Google Scholar]
- Kamal, M.; Phinn, S. Hyperspectral Data for Mangrove Species Mapping: A Comparison of Pixel-Based and Object-Based Approach. Remote Sens. 2011, 3, 2222–2242. [Google Scholar] [CrossRef]
- Guo, F.M.; Li, Z.W.; Ren, J.B.; Wang, L.Q.; Zhang, J.; Wang, J.B.; Hu, Y.B.; Yang, M. Instance-Wise Domain Generalization for Cross-Scene Wetland Classiffcation with Hyperspectral and LiDAR Data. IEEE Trans. Geosci. Remote Sens. 2024, 63, 5501212. [Google Scholar]

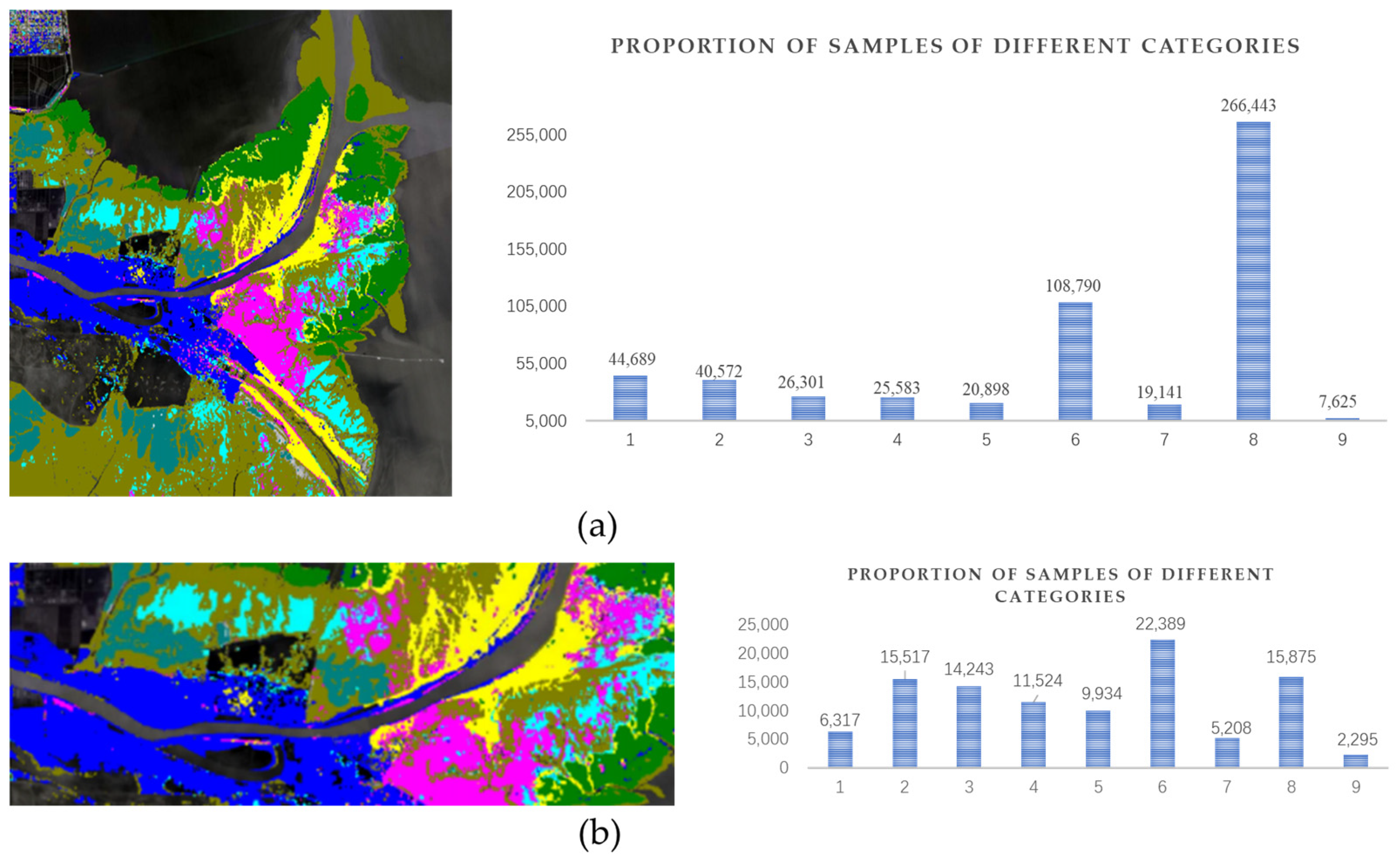
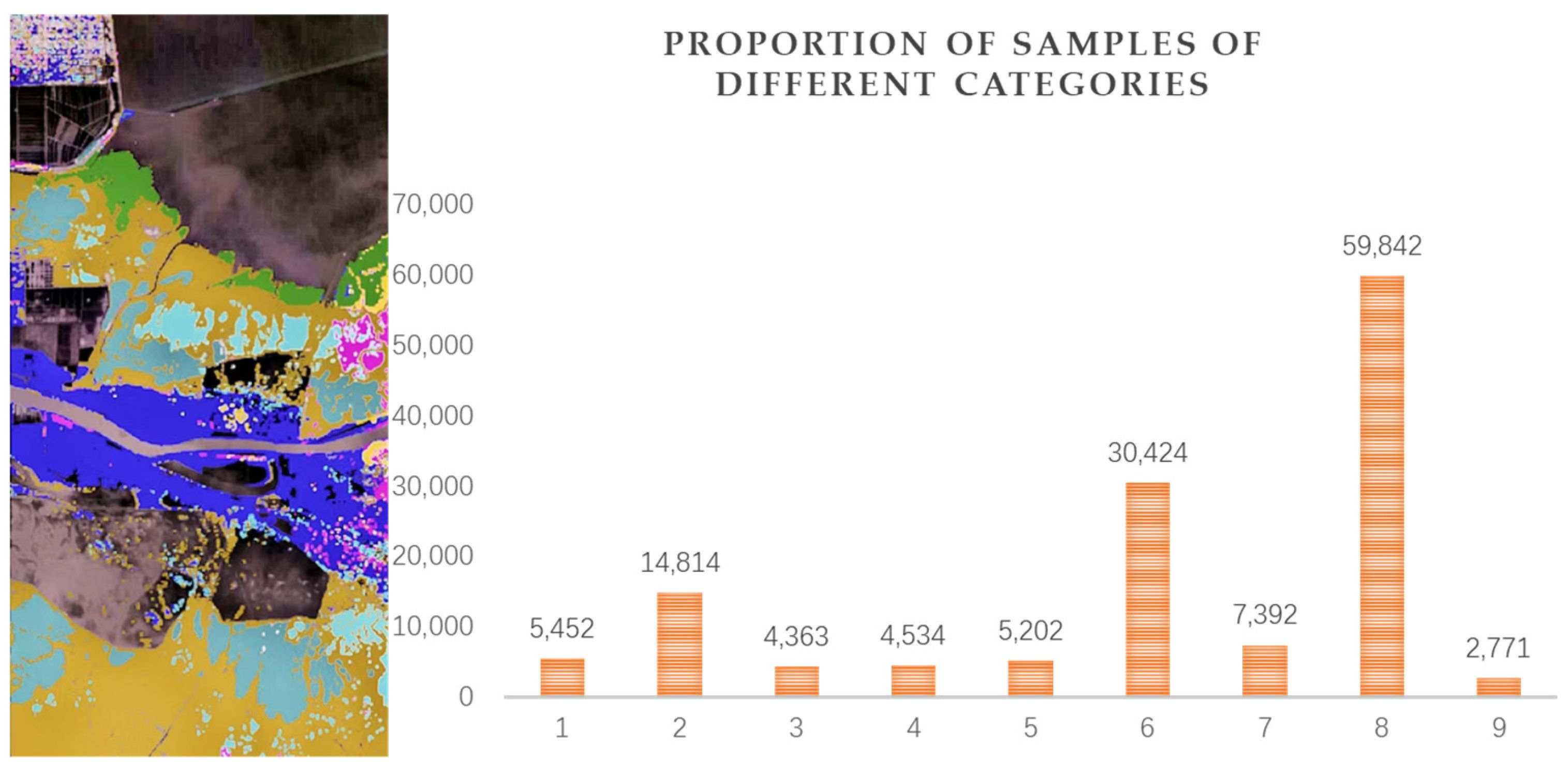
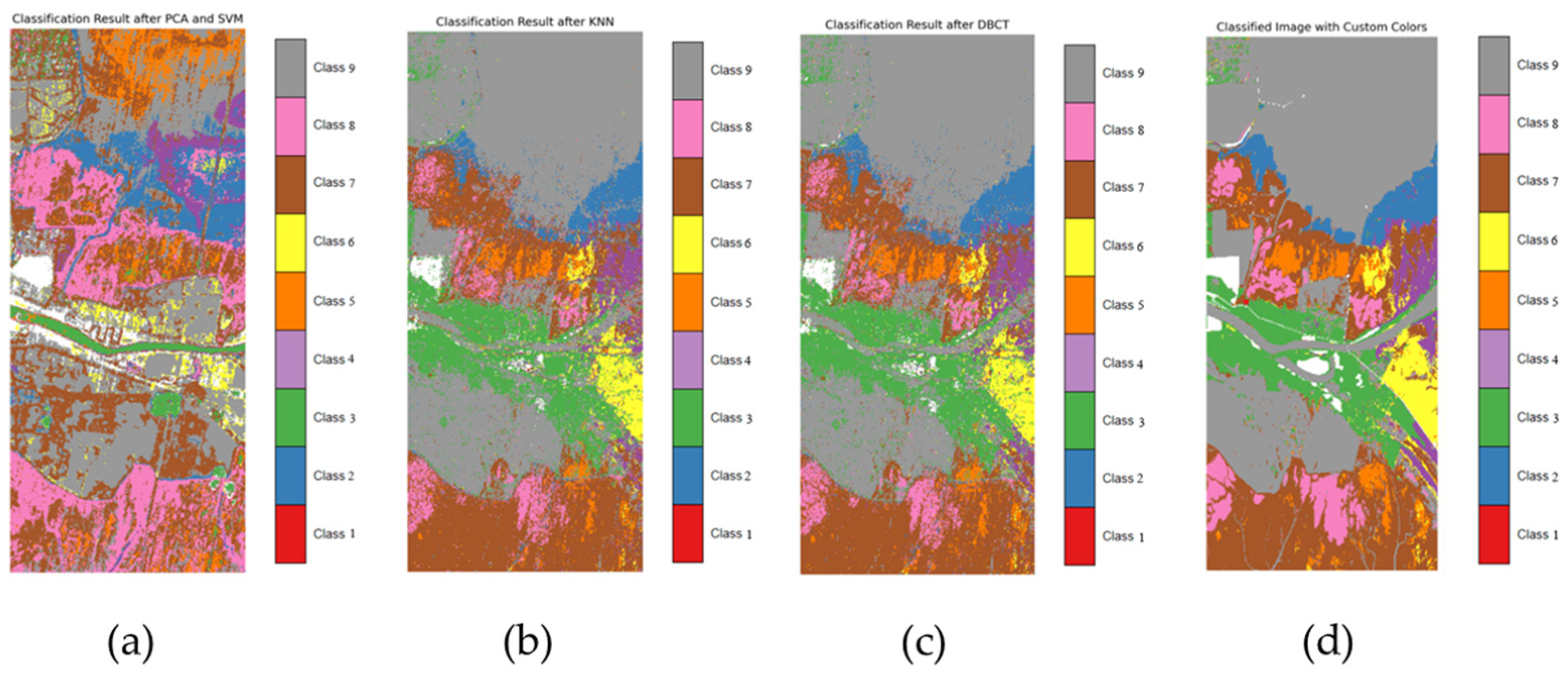

| Class | Number of Samples | ||
|---|---|---|---|
| No. | Name | Pavia U (Source) | Pavia C (Target) |
| 1 | Tree | 3064 | 7598 |
| 2 | Asphalt | 6631 | 9248 |
| 3 | Bricks | 3682 | 2685 |
| 4 | Bitumen | 1330 | 7287 |
| 5 | Shadows | 947 | 2863 |
| 6 | Meadows | 18,649 | 3090 |
| 7 | Bare soil | 5029 | 6584 |
| Total | 39,332 | 39,355 | |
| Class | Number of Samples | ||
|---|---|---|---|
| No. | Name | Shanghai (Source) | Hangzhou (Target) |
| 1 | Water | 18,043 | 123,123 |
| 2 | Land/Building | 77,450 | 161,689 |
| 3 | Plant | 40,207 | 83,188 |
| Total | 135,700 | 368,000 | |
| Satellite | Track Height (km) | Width (km) | Spatial Resolution (m) | Number of Spectral Channels (Number) | Spectral Range (nm) | Spectral Resolution (nm) | Time |
|---|---|---|---|---|---|---|---|
| GF-5 | 705 | 60 | 30 | 330 | 400–2500 | VNIR: 5 nm SWIR: 10 nm | 1 November 2018 |
| XG-003 | 530 | 80 | 40 | 150 | 430–850 | 3 nm | 28 September 2024 |
| Class | Number of Samples | ||
|---|---|---|---|
| No. | Name | GF-5 (Source) | XG-003 (Target) |
| 1 | Spartina alterniflora | 6317 | 5452 |
| 2 | Phragmites australis | 15,517 | 14,814 |
| 3 | Tamarix chinensis Lour | 14,243 | 4363 |
| 4 | Suaeda glauca Bunge | 11,524 | 4534 |
| 5 | Phragmites australis on the Tidal Flats | 9934 | 5202 |
| 6 | Naked Tide Beach | 22,389 | 30,424 |
| 7 | Salt Marsh | 5208 | 7392 |
| 8 | Water Body | 15,875 | 59,842 |
| 9 | Others | 2295 | 2271 |
| Total | 103,302 | 134,294 | |
| Ground Objects | Spartina alterniflora | Phragmites australis | Tamarix chinensis Lour | Suaeda glauca Bunge | Phragmites australis on the Tidal Flats | Naked Tide Beach | Salt Marsh | Water Body | Others |
|---|---|---|---|---|---|---|---|---|---|
| Category | class1 | class 2 | class 3 | class 4 | class 5 | class 6 | class 7 | class 8 | class 9 |
| Legend |
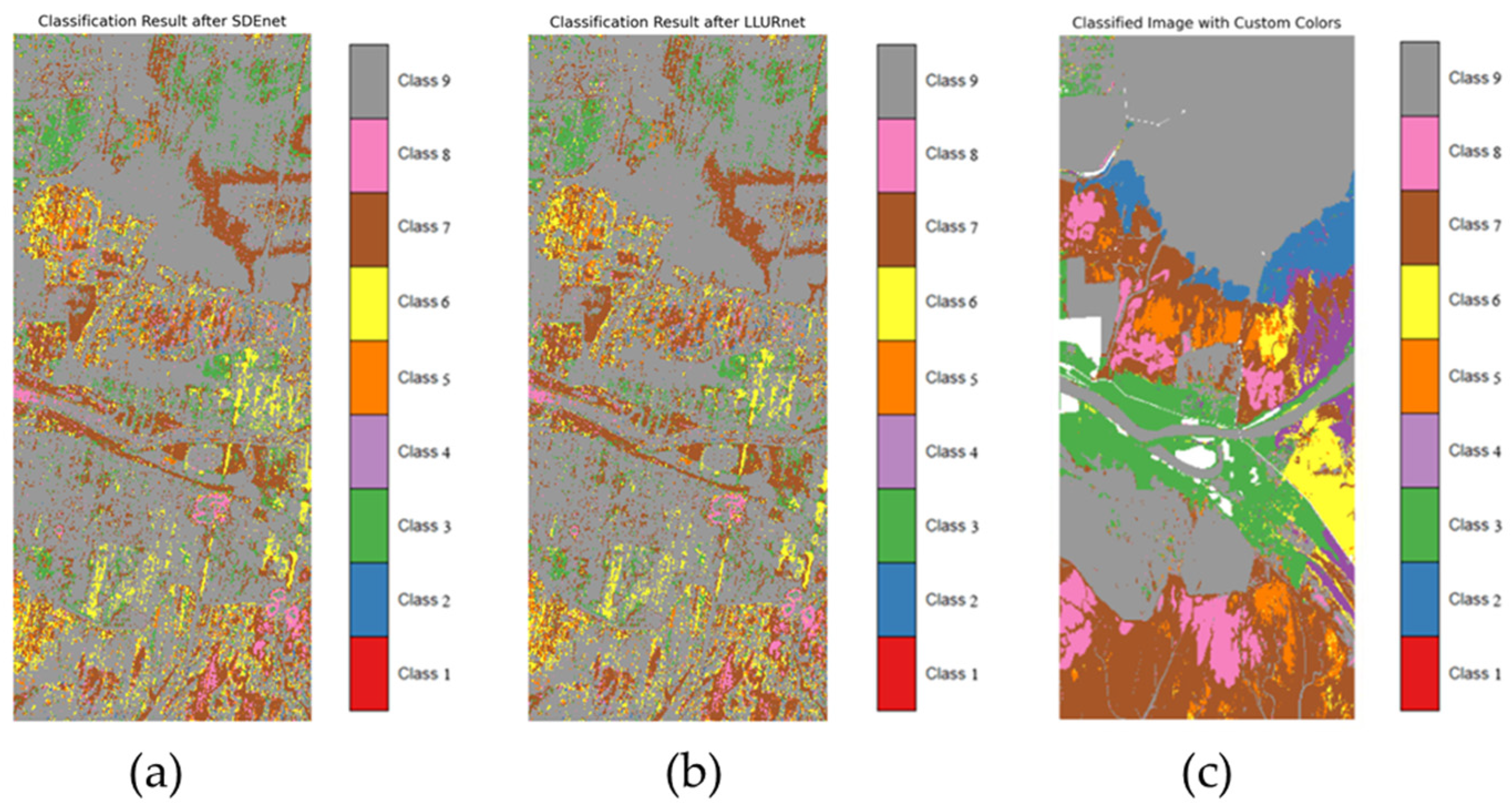
| Method | OA (%) | AA (%) |
|---|---|---|
| SDE net [38] | 0.43 | 0.11 |
| LLU net [39] | 0.45 | 0.16 |
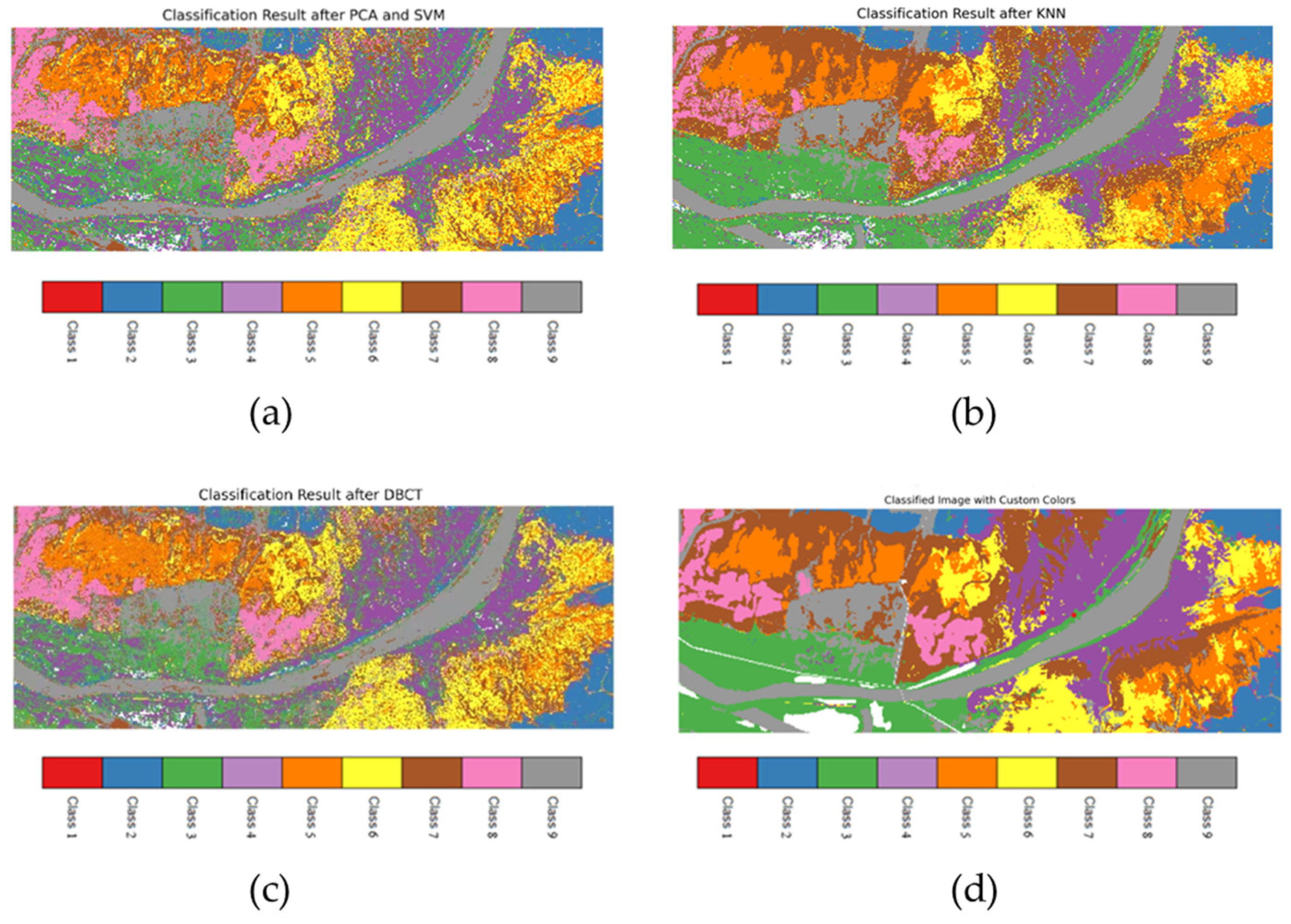
| Method | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | OA (%) | AA (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM [40] | 0.71 | 0.54 | 0.53 | 0.51 | 0.4 | 0.54 | 0.64 | 0.66 | 0.46 | 0.56 | 0.56 |
| K-NN [41] | 0.87 | 0.74 | 0.76 | 0.74 | 0.66 | 0.76 | 0.84 | 0.93 | 0.81 | 0.78 | 0.79 |
| Ours | 0.91 | 0.82 | 0.85 | 0.75 | 0.71 | 0.78 | 0.88 | 0.84 | 0.72 | 0.81 | 0.81 |
| Method | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | OA (%) | AA (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM [40] | 0.21 | 0.38 | 0.03 | 0.09 | 0.14 | 0.48 | 0.28 | 0.61 | 0.37 | 0.43 | 0.29 |
| K-NN [41] | 0.76 | 0.79 | 0.62 | 0.54 | 0.66 | 0.83 | 0.65 | 0.89 | 0.45 | 0.81 | 0.76 |
| Ours | 0.94 | 0.88 | 0.83 | 0.76 | 0.82 | 0.81 | 0.88 | 0.91 | 0.84 | 0.87 | 0.85 |
| Method | 1 | 2 | 3 | 4 | 5 | 6 | 7 | OA (%) | AA (%) |
|---|---|---|---|---|---|---|---|---|---|
| SVM [40] | 0.92 | 0.80 | 0.84 | 0.85 | 0.90 | 0.78 | 0.79 | 0.94 | 0.84 |
| K-NN [41] | 0.80 | 0.78 | 0.78 | 0.90 | 0.81 | 0.82 | 0.83 | 0.96 | 0.84 |
| ASSMN [42] | 0.99 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 | 1.00 | 0.99 | 0.99 |
| Ours | 0.99 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 | 1.00 | 0.99 | 0.99 |
| Method | 1 | 2 | 3 | OA (%) | AA (%) |
|---|---|---|---|---|---|
| SVM [40] | 0.99 | 1.00 | 1.00 | 1.00 | 0.99 |
| K-NN [41] | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 |
| ASSMN [42] | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Ours | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Method | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | OA (%) | AA (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM [42] | 0.02 | 0.05 | 0.04 | 0.01 | 0.01 | 0.07 | 0.06 | 0.5 | 0.04 | 0.18 | 0.09 |
| K-NN [43] | 0.03 | 0.11 | 0.04 | 0.1 | 0.05 | 0.26 | 0.04 | 0.5 | 0.00 | 0.38 | 0.13 |
| ASSMN [44] | 0.89 | 0.84 | 0.84 | 0.86 | 0.63 | 0.89 | 0.85 | 0.81 | 0.68 | 0.81 | 0.81 |
| Ours | 0.91 | 0.82 | 0.85 | 0.75 | 0.71 | 0.78 | 0.88 | 0.84 | 0.72 | 0.87 | 0.86 |
| Experimental Setup | OA (%) | AA (%) |
|---|---|---|
| Original settings | 0.99 | 0.99 |
| Single-branch CNN | 0.97 | 0.98 |
| Single-branch Transformer | 0.99 | 0.98 |
| Experimental Setup | OA (%) | AA (%) |
|---|---|---|
| Original settings | 1.00 | 1.00 |
| Single-branch CNN | 1.00 | 0.99 |
| Single-branch Transformer | 0.99 | 0.99 |
| Experimental Setup | OA (%) | AA (%) |
|---|---|---|
| Original settings | 0.87 | 0.86 |
| Single-branch CNN | 0.78 | 0.70 |
| Single-branch Transformer | 0.79 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Qin, J.; Wang, X.; Gu, Y. Research on the Wetland Vegetation Classification Method Based on Cross-Satellite Hyperspectral Images. J. Mar. Sci. Eng. 2025, 13, 801. https://doi.org/10.3390/jmse13040801
Yang M, Qin J, Wang X, Gu Y. Research on the Wetland Vegetation Classification Method Based on Cross-Satellite Hyperspectral Images. Journal of Marine Science and Engineering. 2025; 13(4):801. https://doi.org/10.3390/jmse13040801
Chicago/Turabian StyleYang, Min, Jing Qin, Xiaodan Wang, and Yanfeng Gu. 2025. "Research on the Wetland Vegetation Classification Method Based on Cross-Satellite Hyperspectral Images" Journal of Marine Science and Engineering 13, no. 4: 801. https://doi.org/10.3390/jmse13040801
APA StyleYang, M., Qin, J., Wang, X., & Gu, Y. (2025). Research on the Wetland Vegetation Classification Method Based on Cross-Satellite Hyperspectral Images. Journal of Marine Science and Engineering, 13(4), 801. https://doi.org/10.3390/jmse13040801






