Risk–Failure Interactive Propagation and Recovery of Sea–Rail Intermodal Transportation Network Considering Recovery Propagation
Abstract
1. Introduction
- (1)
- In view of the problem that the network risk–failure interactive propagation problem has not been considered in previous studies, a risk regression and failure propagation mechanism with an interactive propagation mechanism is proposed.
- (2)
- The proposed resilience recovery model refines the station risk–failure dynamics by introducing a risk recovery mechanism, a load-balancing strategy, and a repair mechanism. In addition, it establishes resiliency metrics based on the severity of station failure.
- (3)
- To study the effectiveness of the model, an empirical study is conducted on the multimodal transport network of the Belt and Road Initiative. Through multi-scenario simulation experiments, the resilience changes of the sea–rail multimodal transport network under the hybrid attack mode are systematically analyzed.
2. Related Works
- (1)
- To address the incomplete assessment of network risk–failure interaction causing recovery delays, this research breaks through the limitations of traditional single risk or failure propagation models. We propose a risk backward and failure forward propagation mechanism with interactive propagation mechanisms to quantify risk–failure interaction propagation and recovery dynamics in networks.
- (2)
- The proposed resilience recovery model focuses on refining the extent of station risk–failure, introducing a risk recovery mechanism, load-balancing strategy, and repair mechanism. Additionally, a resilience metric based on station failure severity is established to accurately represent the evolutionary process of network resilience during propagation and recovery.
- (3)
- This paper conducts empirical research on the Belt and Road multimodal transportation network. Characterized by cross-regional and multimodal features, this network provides an ideal scenario for validating risk–failure interactive propagation and recovery mechanisms. Through multi-scenario simulation experiments, we systematically analyze resilience variation in the sea–rail intermodal transportation network under hybrid attack modes, focusing on three dimensions: repair capacity adjustment, risk management, and hub station allocation equalization. Simulation results offer scientific evidence for enhancing transportation network safety.
3. Method
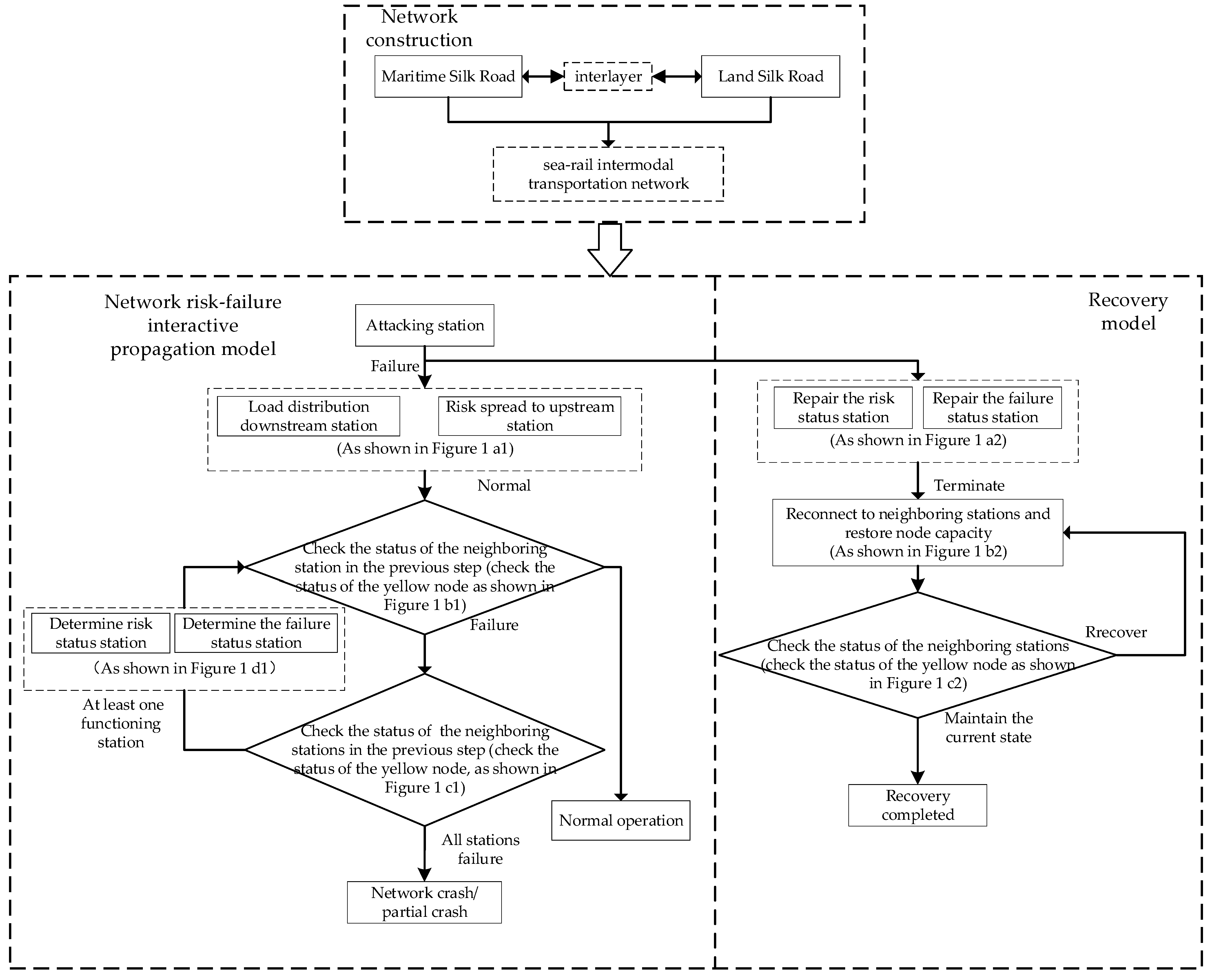
3.1. Risk–Failure Interactive Propagation and Recovery
3.2. Model Assumptions
3.3. Risk–Failure Interactive Propagation and Recovery Model
3.3.1. Attack Mode
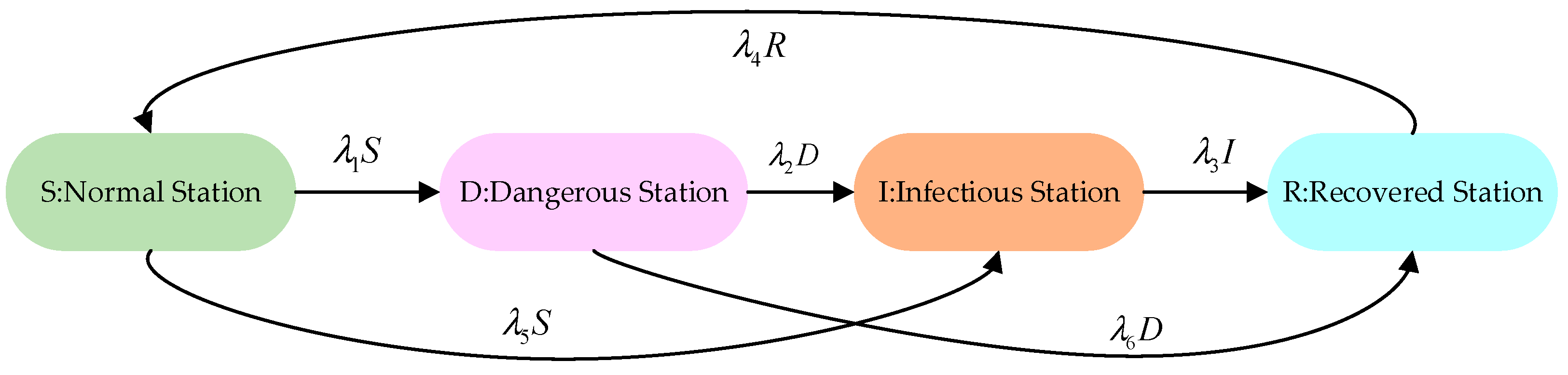
3.3.2. Propagation Mechanism
- (1)
- Risk backward propagation
- (2)
- Failure forward propagation
- (3)
- Interactive propagation
3.3.3. Repair Mechanism
- (i)
- Transportation route fine-tuning during restoration
- (ii)
- Restoration termination
3.4. Resilience Metric
4. Simulation Validation
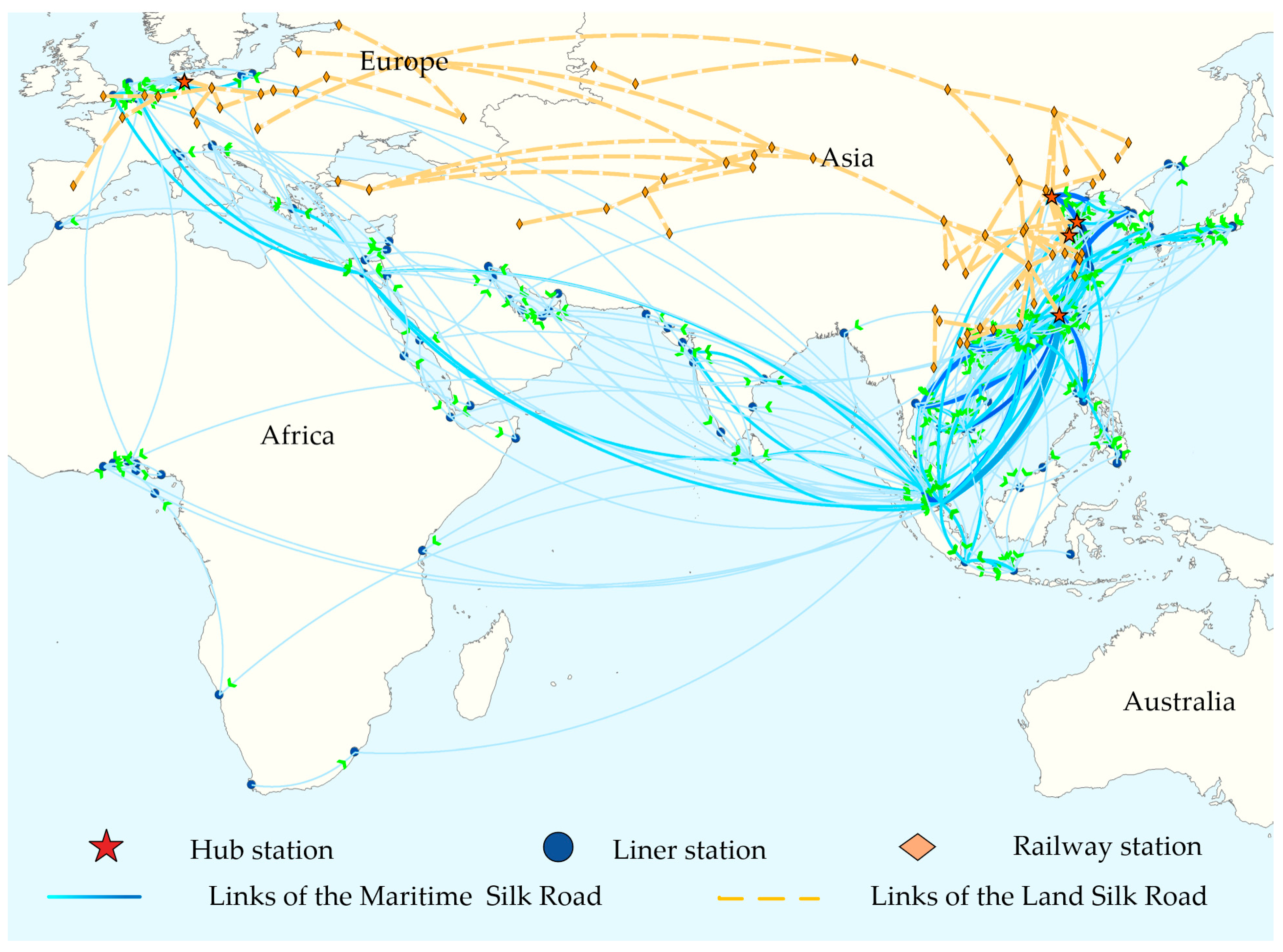
4.1. Transportation Network Design
4.2. Validation of Model Effectiveness
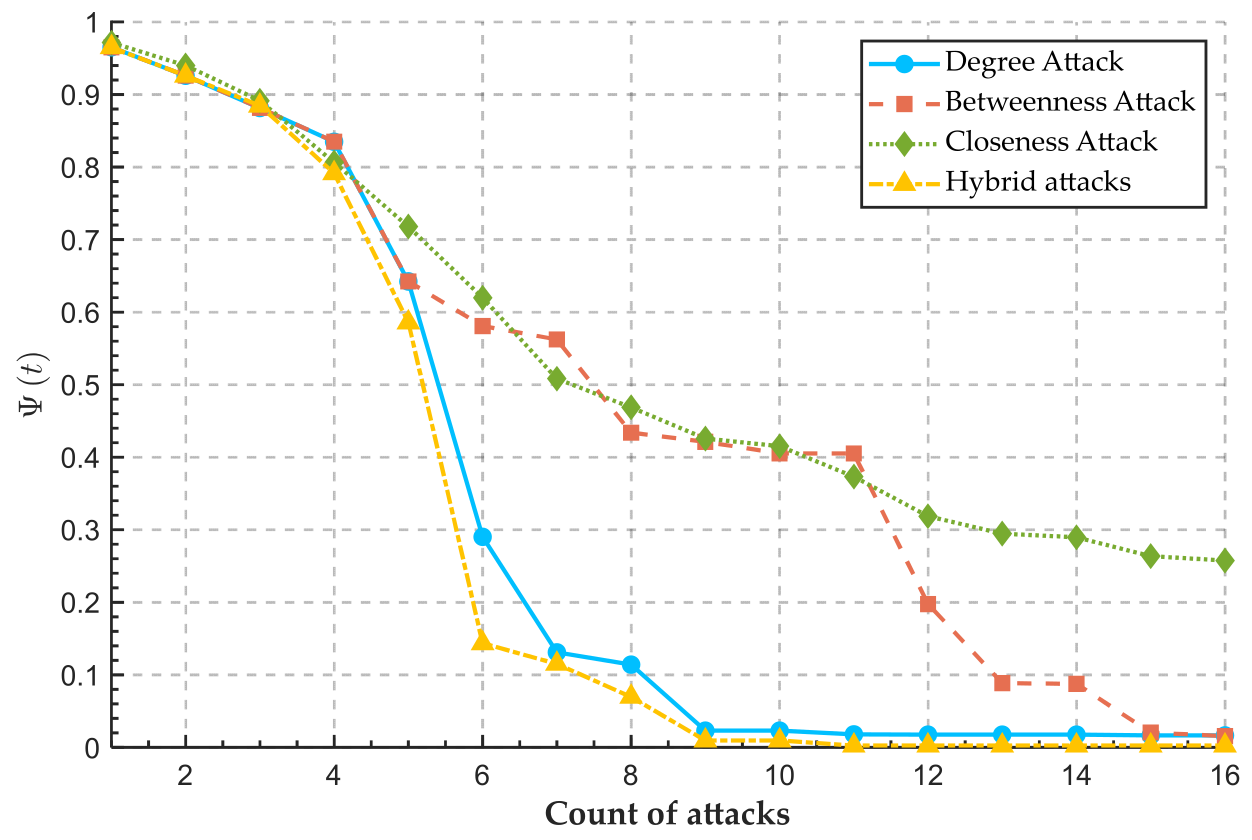
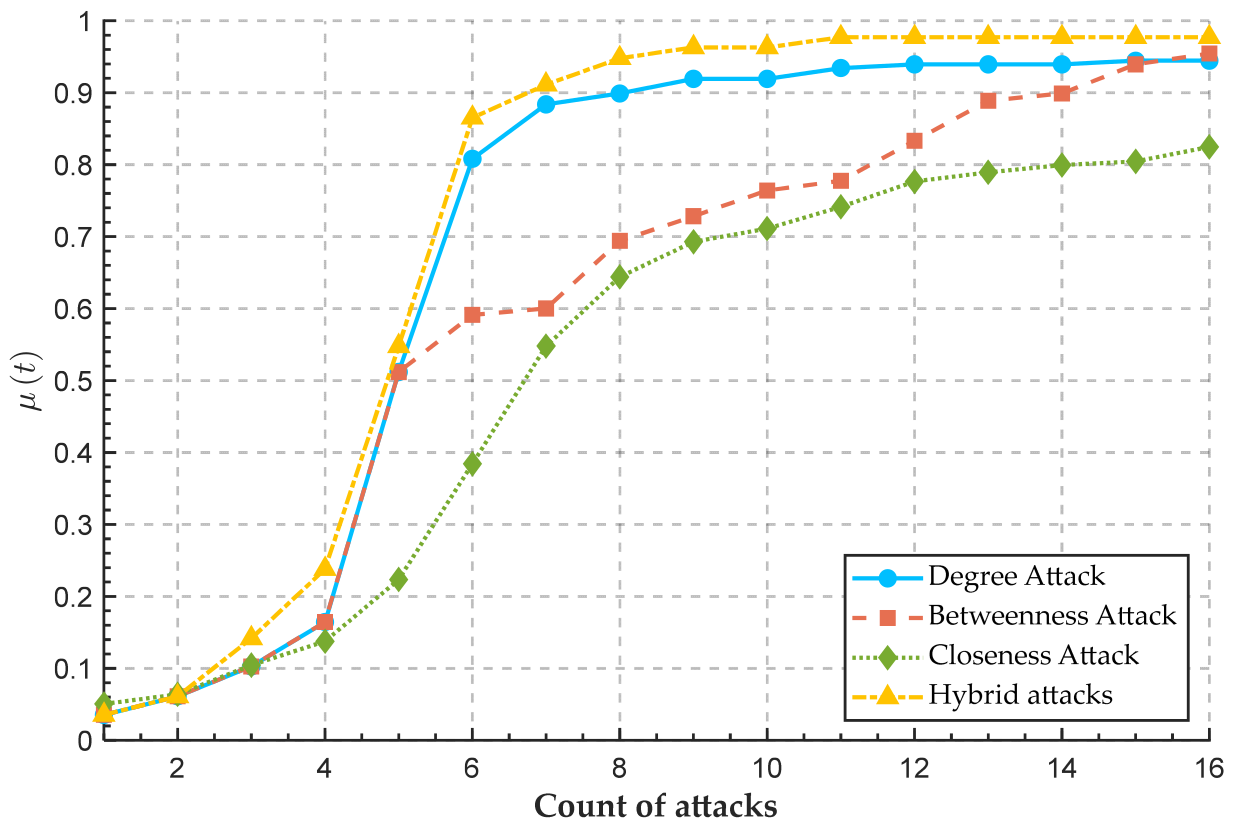
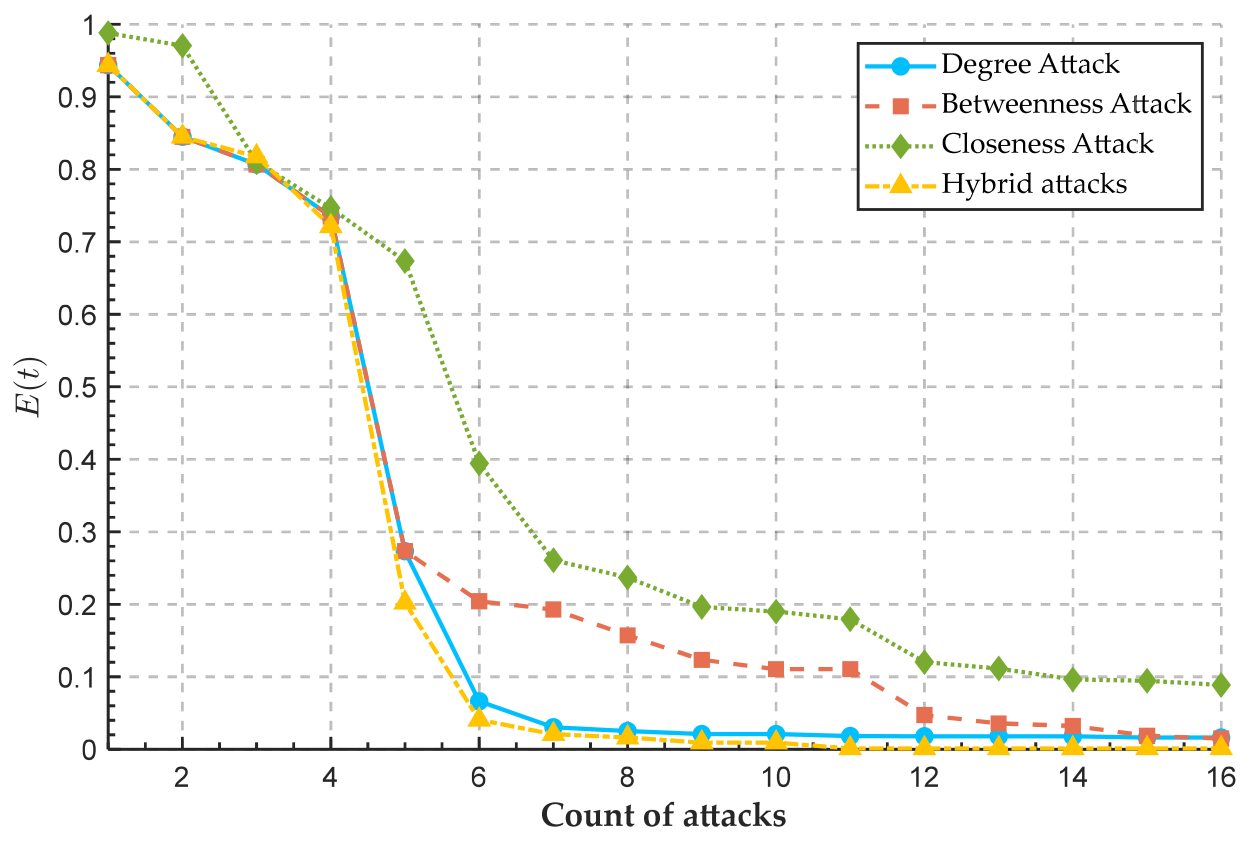
4.2.1. Different Attack Modes
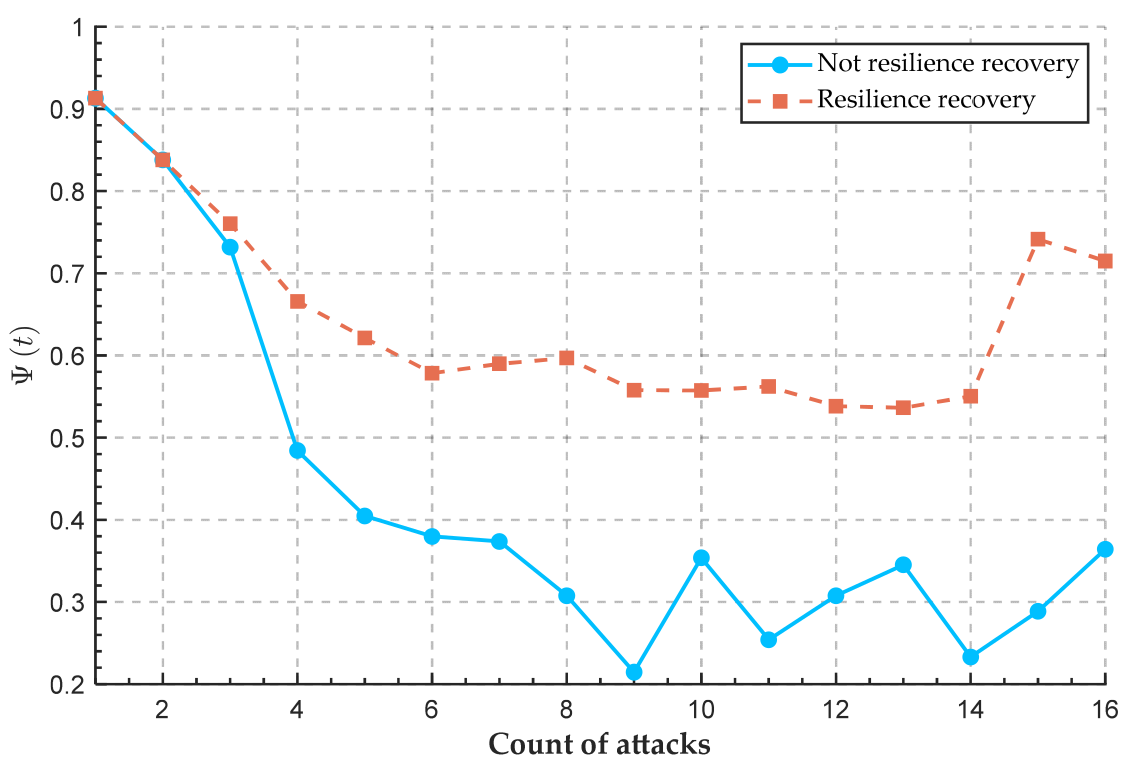
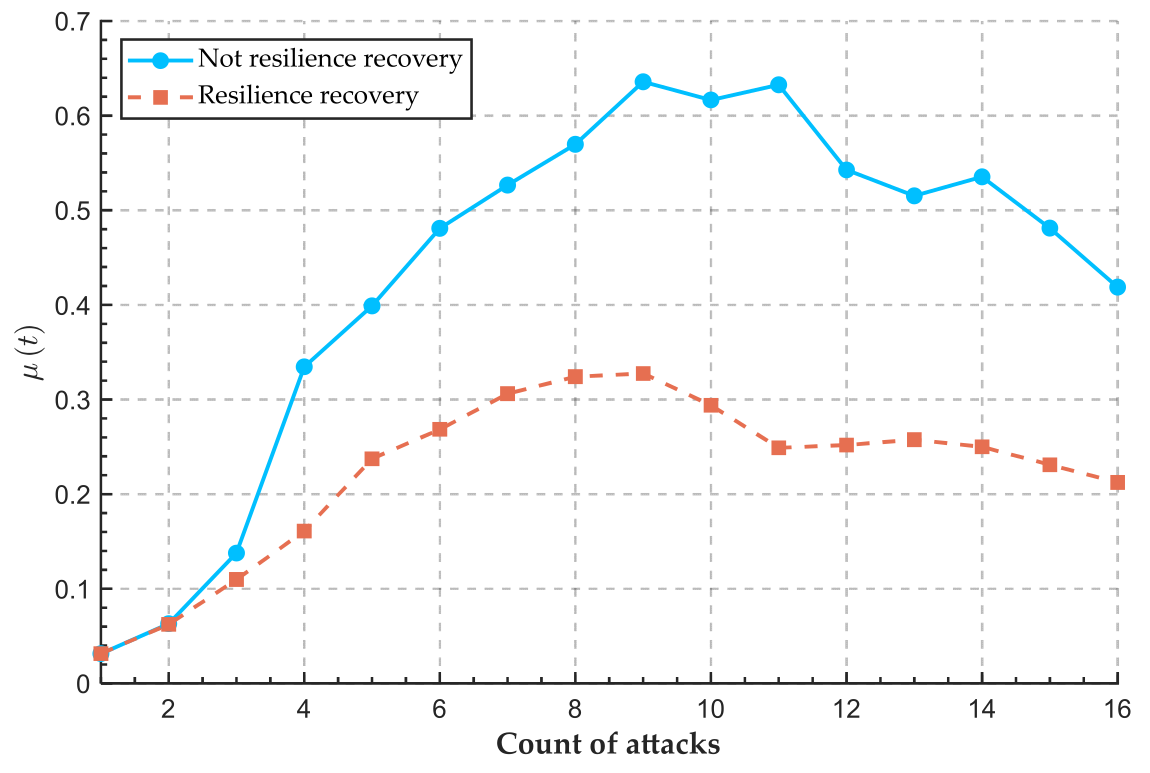
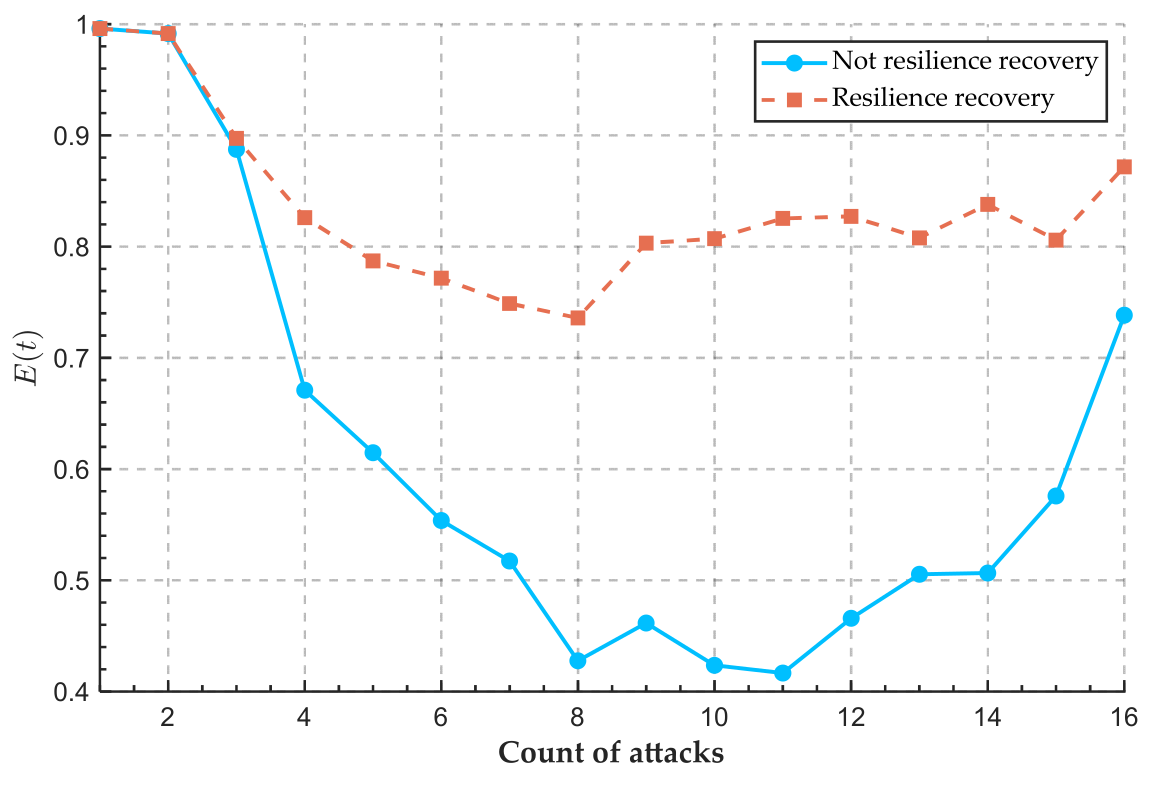
4.2.2. Resilience Recovery
5. Case Study
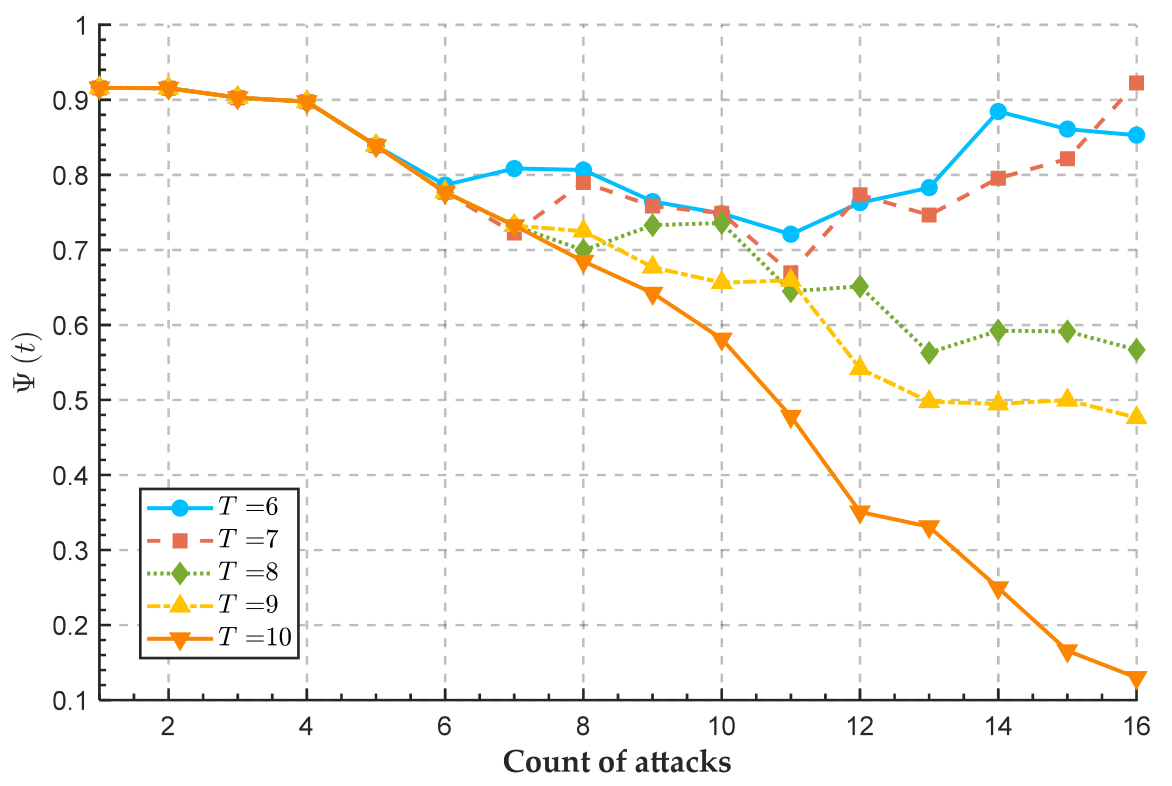
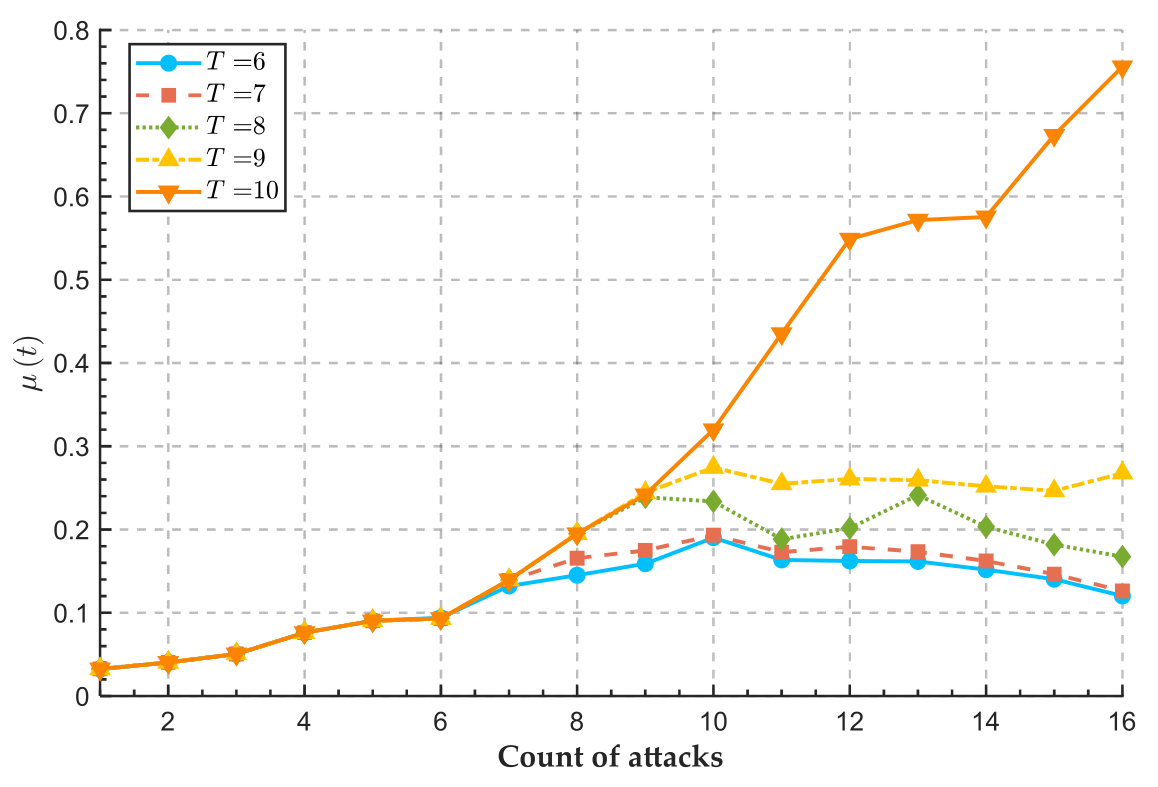
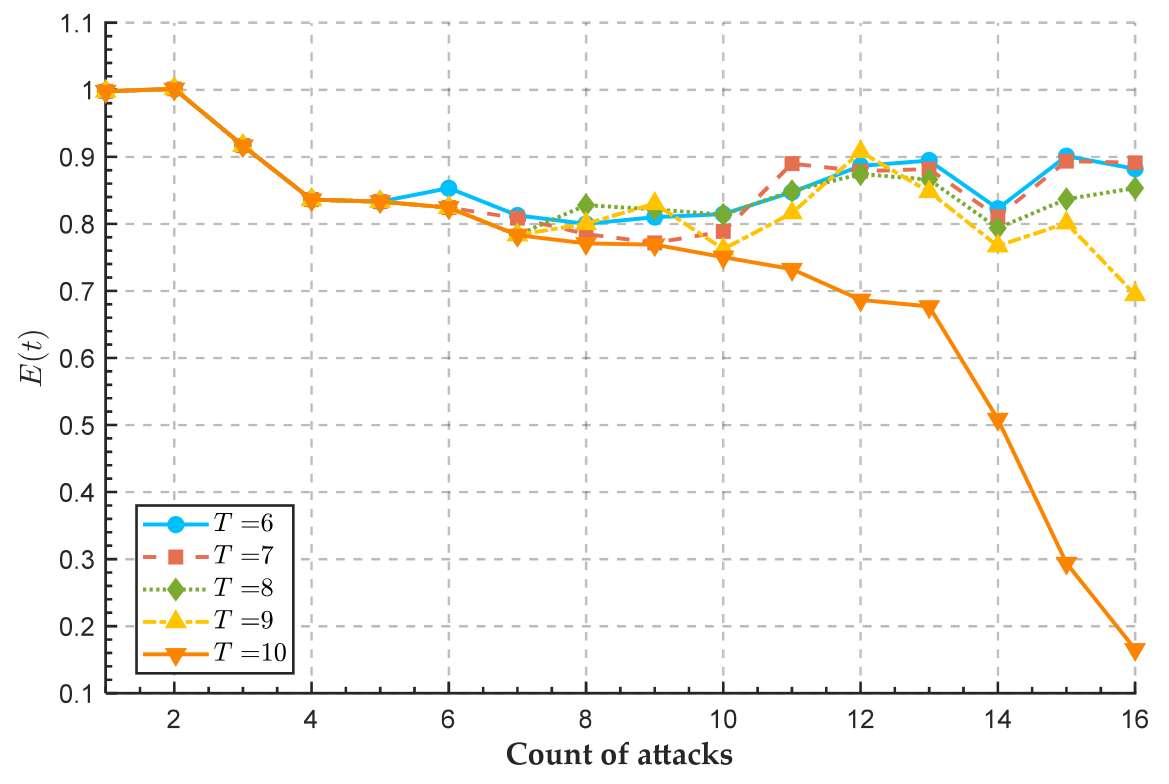
5.1. Repair Capacity Adjustment
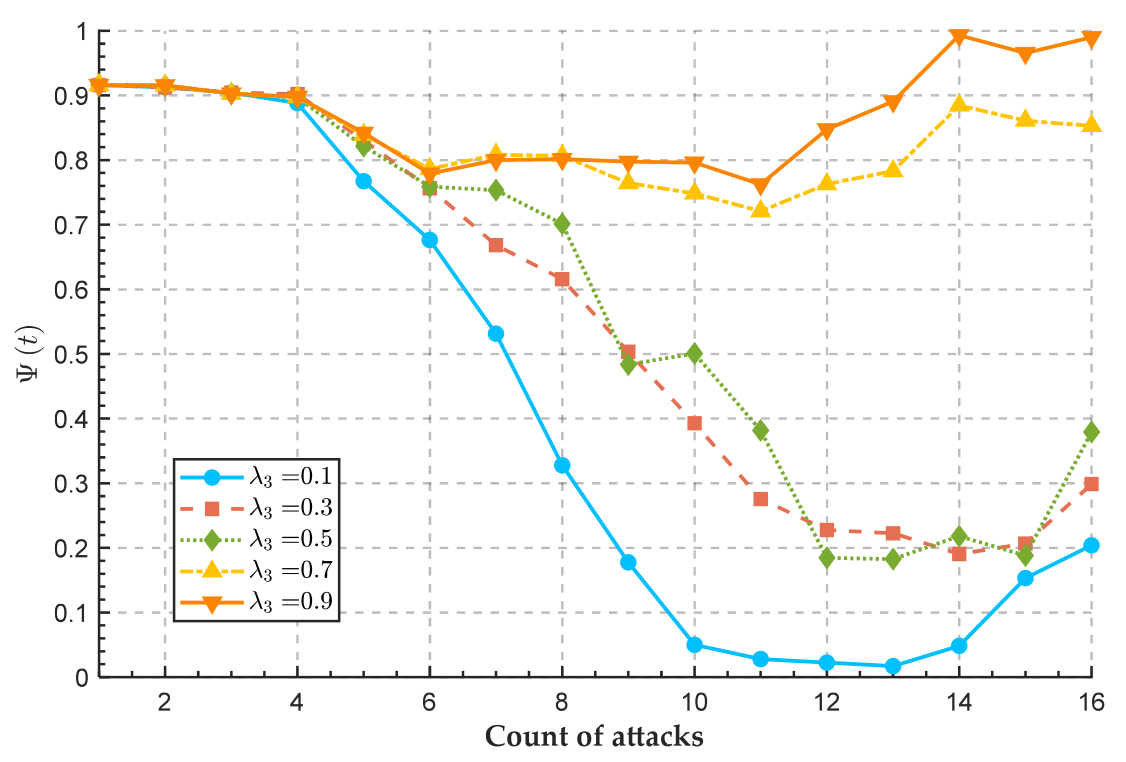
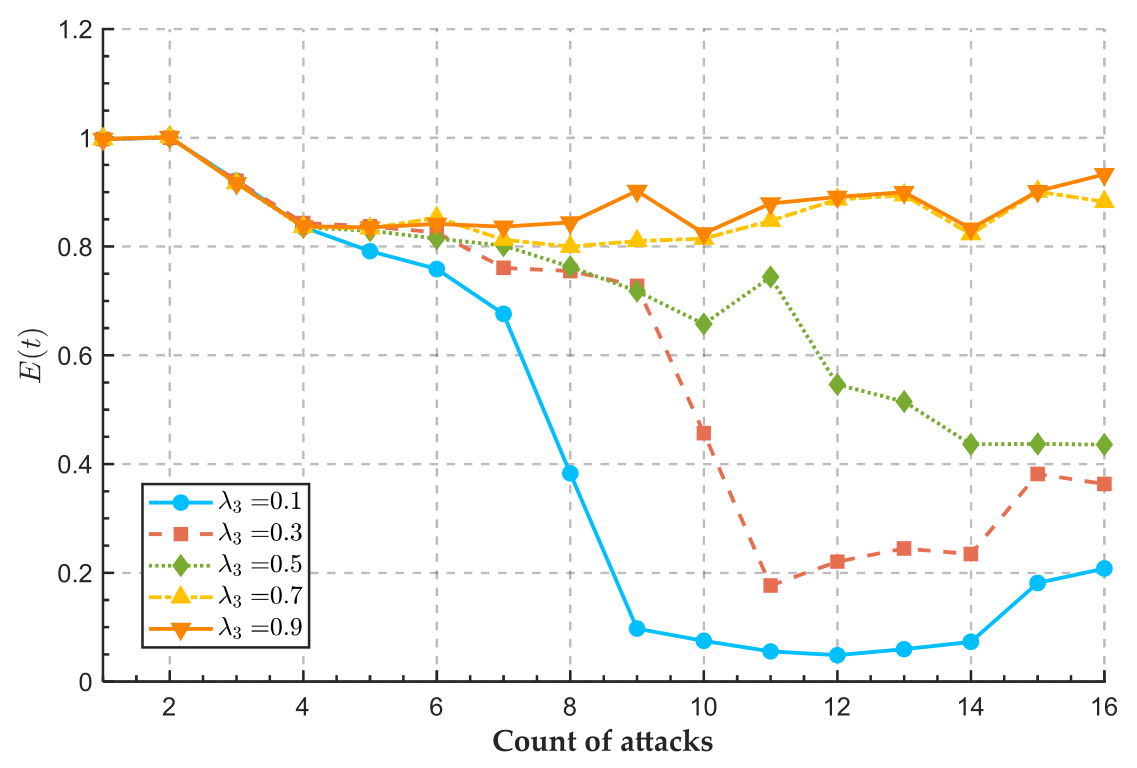
5.2. Risk Management
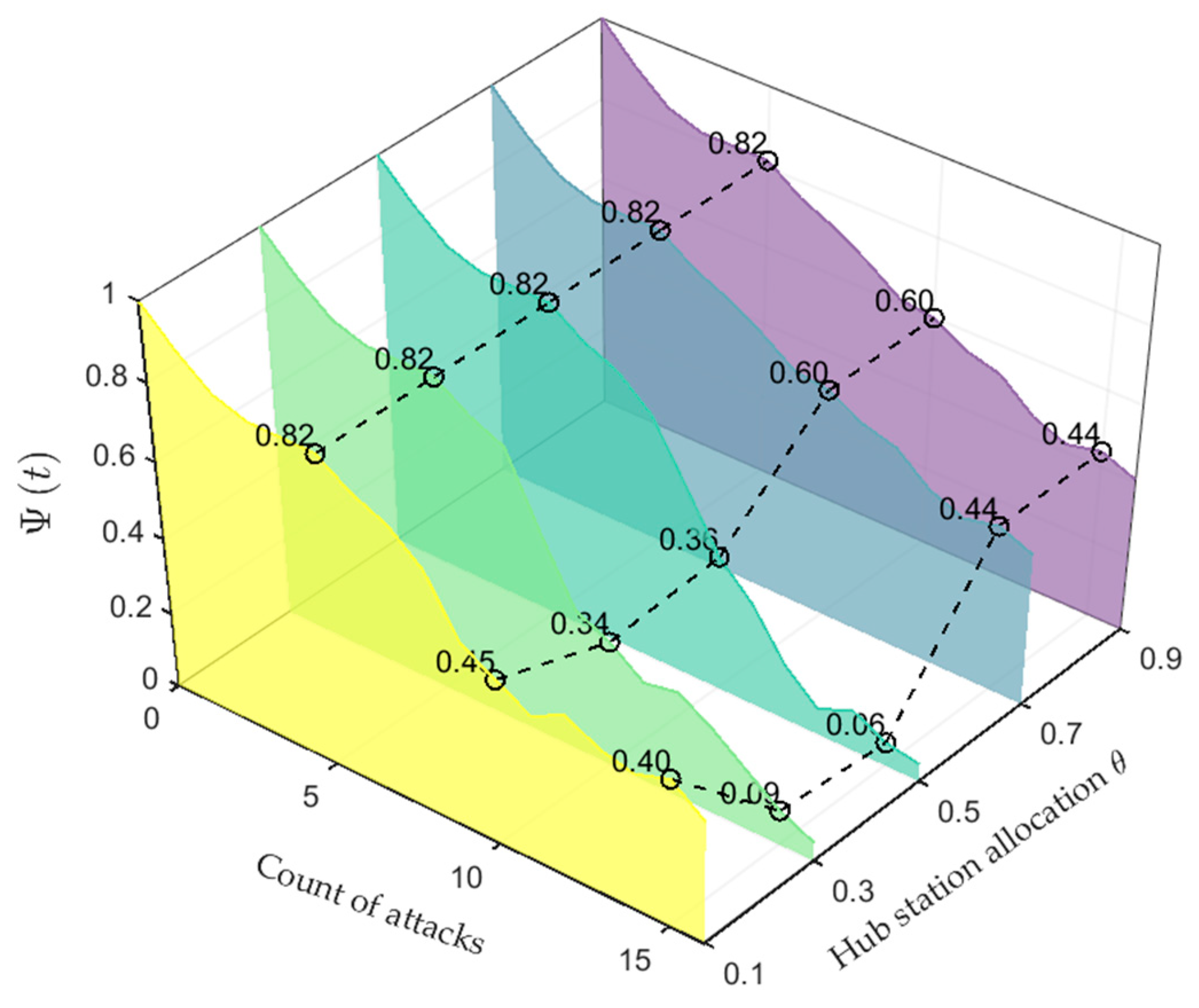
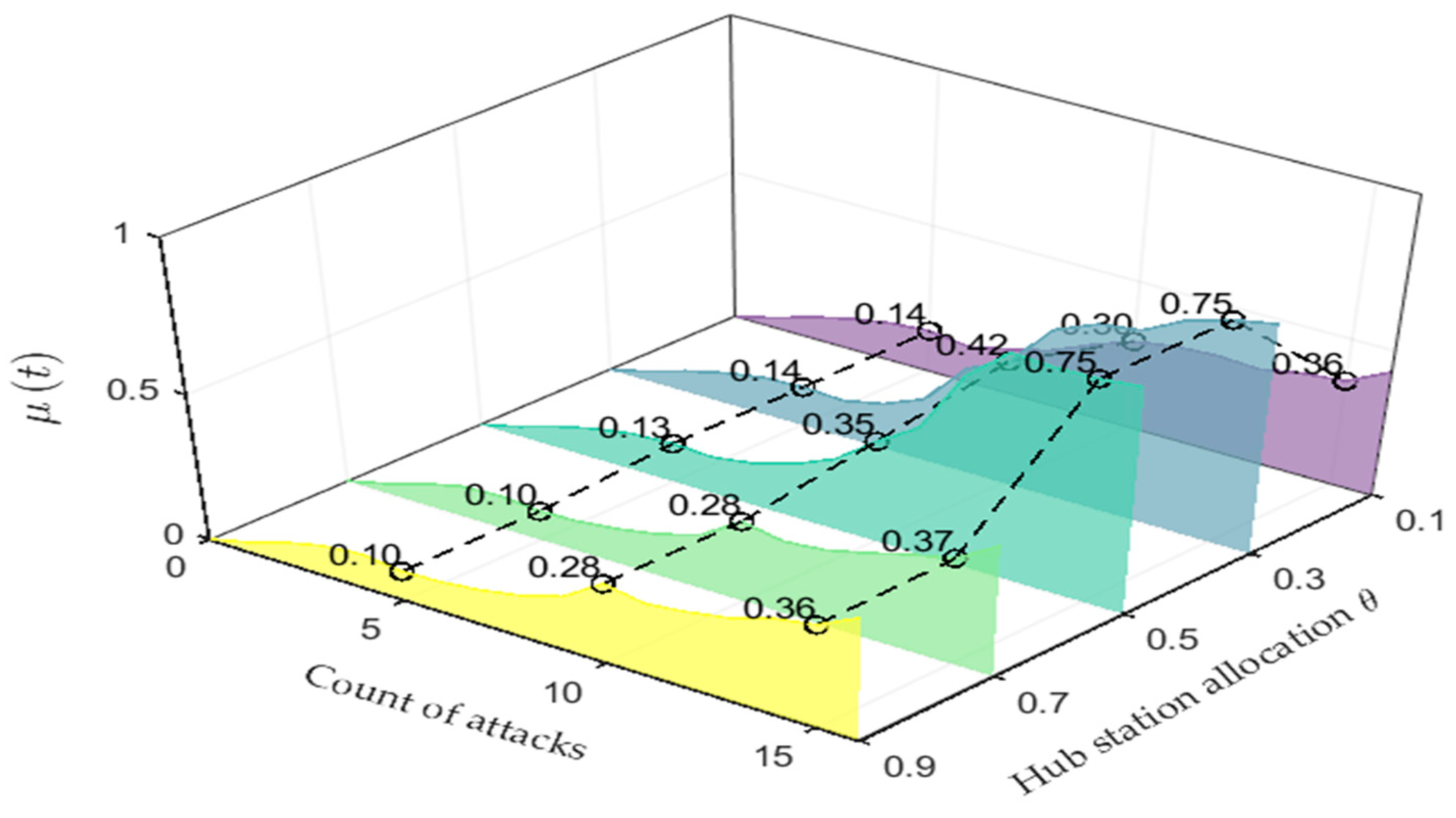
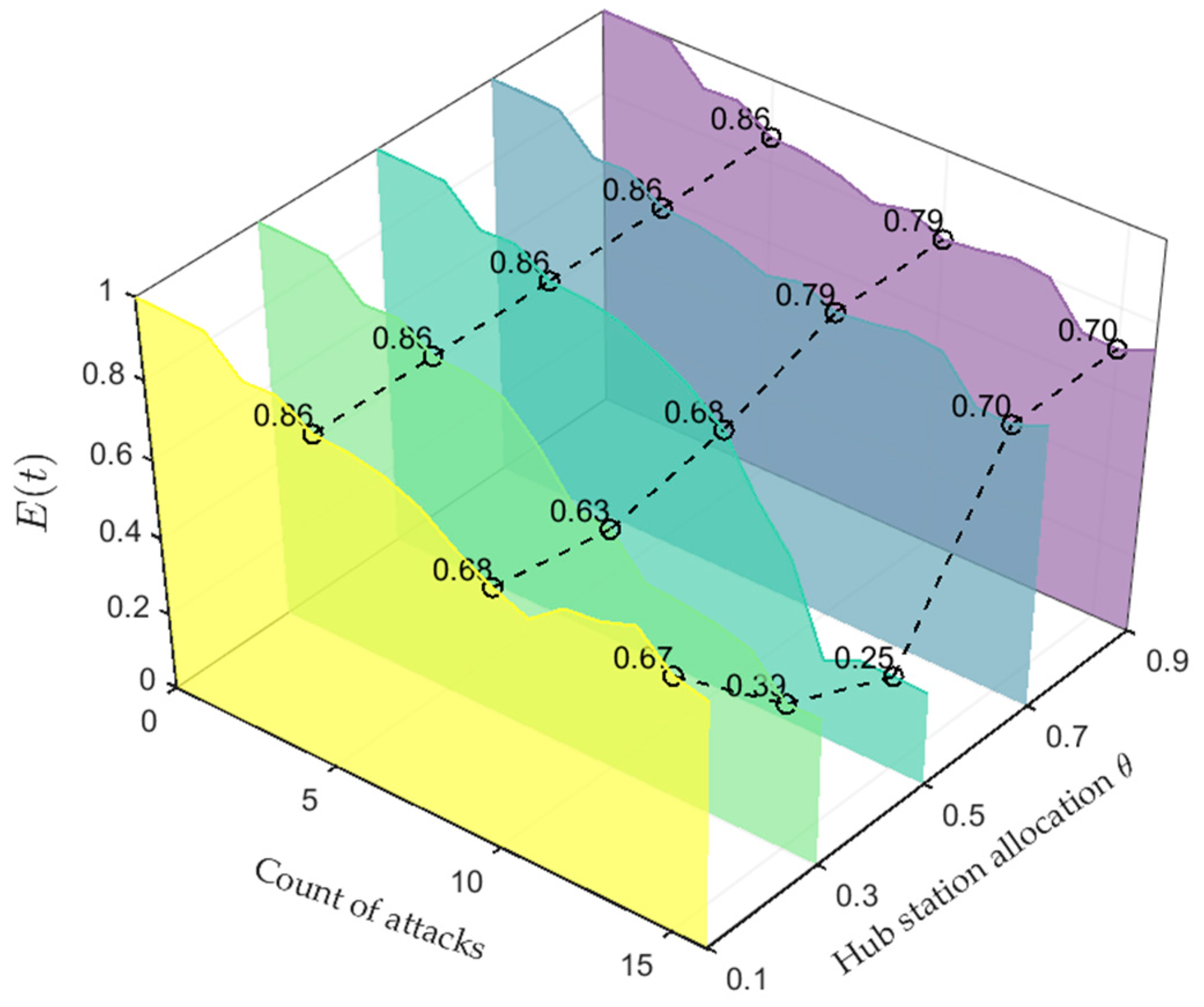
5.3. Hub Station Allocation Equalization
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, T.; Wang, H. Evaluating the Service Capacity of Port-Centric Intermodal Transshipment Hub. J. Mar. Sci. Eng. 2023, 11, 1403. [Google Scholar] [CrossRef]
- Macedo, F.C.; Alminhana, F.; Miguel, L.F.F.; Beck, A.T. Performance-Based Reliability Assessment of Transmission Lines under Tornado Actions. Reliab. Eng. Syst. Saf. 2024, 252, 110475. [Google Scholar] [CrossRef]
- Li, S.; Wu, J.; Jiang, Y.; Yang, X. Impacts of the Sea-Rail Intermodal Transport Policy on Carbon Emission Reduction: The China Case Study. Transp. Policy 2024, 158, 211–223. [Google Scholar] [CrossRef]
- Derpich, I.; Duran, C.; Carrasco, R.; Moreno, F.; Fernandez-Campusano, C.; Espinosa-Leal, L. Pursuing Optimization Using Multimodal Transportation System: A Strategic Approach to Minimizing Costs and CO2 Emissions. J. Mar. Sci. Eng. 2024, 12, 976. [Google Scholar] [CrossRef]
- Li, H.; Zhou, K.; Zhang, C.; Bashir, M.; Yang, Z. Dynamic Evolution of Maritime Accidents: Comparative Analysis through Data-Driven Bayesian Networks. Ocean Eng. 2024, 303, 117736. [Google Scholar] [CrossRef]
- Ma, L.; Ma, X.; Wang, T.; Chen, L.; Lan, H. On the Development and Measurement of Human Factors Complex Network for Maritime Accidents: A Case of Ship Groundings. Ocean Coast. Manag. 2024, 248, 106954. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, C.-Y. Risk Analysis of Weather-Related Railroad Accidents in the United States. Reliab. Eng. Syst. Saf. 2025, 255, 110647. [Google Scholar] [CrossRef]
- Abu-Aisha, T.; Audy, J.-F.; Ouhimmou, M. Toward an Efficient Sea-Rail Intermodal Transportation System: A Systematic Literature Review. J. Shipp. Trade 2024, 9, 23. [Google Scholar] [CrossRef]
- Wan, C.; Tao, J.; Yang, Z.; Zhang, D. Evaluating Recovery Strategies for the Disruptions in Liner Shipping Networks: A Resilience Approach. Int. J. Logist. Manag. 2022, 33, 389–409. [Google Scholar] [CrossRef]
- Dui, H.; Zheng, X.; Wu, S. Resilience Analysis of Maritime Transportation Systems Based on Importance Measures. Reliab. Eng. Syst. Saf. 2021, 209, 107461. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Bian, Z.; Dai, L.; Hu, H. Subsidy Policy Optimization of Multimodal Transport on Emission Reduction Considering Carrier Pricing Game and Shipping Resilience: A Case Study of Shanghai Port. Ocean Coast. Manag. 2023, 243, 106760. [Google Scholar] [CrossRef]
- Piccirillo, V. Nonlinear Control of Infection Spread Based on a Deterministic SEIR Model. Chaos Solitons Fractals 2021, 149, 111051. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Du, Y.; Li, Z.; Hu, J.; Hu, R.; Lv, B.; Jia, P. HK–SEIR Model of Public Opinion Evolution Based on Communication Factors. Eng. Appl. Artif. Intell. 2021, 100, 104192. [Google Scholar] [CrossRef]
- Qiu, Z.; Sun, Y.; He, X.; Wei, J.; Zhou, R.; Bai, J.; Du, S. Application of Genetic Algorithm Combined with Improved SEIR Model in Predicting the Epidemic Trend of COVID-19, China. Sci. Rep. 2022, 12, 8910. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. An Initial Model for Complex Dynamics in Electric Power System Blackouts. In Proceedings of the 34th Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 6 January 2001. [Google Scholar]
- Motter, A.E.; Lai, Y.-C. Cascade-Based Attacks on Complex Networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef]
- Covello, V.T.; Slovic, P.; Von Winterfeldt, D. Risk Communication: A Review of the Literature. Risk Absract 1986, 3, 171–182. [Google Scholar]
- Hampel, J. Different Concepts of Risk—A Challenge for Risk Communication. Int. J. Med. Microbiol. 2006, 296, 5–10. [Google Scholar] [CrossRef]
- Liang, D.; Bhamra, R.; Liu, Z.; Pan, Y. Risk Propagation and Supply Chain Health Control Based on the SIR Epidemic Model. Mathematics 2022, 10, 3008. [Google Scholar] [CrossRef]
- He, Z.; Guo, J.-N.; Xu, J.-X. Cascade Failure Model in Multimodal Transport Network Risk Propagation. Math. Probl. Eng. 2019, 2019, 3615903. [Google Scholar] [CrossRef]
- Lyu, M.; Shuai, B.; Zhang, Q.; Li, L. Ripple Effect in China–Europe Railway Transport Network: Ripple Failure Risk Propagation and Influence. Phys. A Stat. Mech. Its Appl. 2023, 620, 128739. [Google Scholar] [CrossRef]
- Shi, J.; Liu, Z.; Feng, Y.; Wang, X.; Zhu, H.; Yang, Z.; Wang, J.; Wang, H. Evolutionary Model and Risk Analysis of Ship Collision Accidents Based on Complex Networks and DEMATEL. Ocean Eng. 2024, 305, 117965. [Google Scholar] [CrossRef]
- Feng, J.R.; Zhao, M.; Lu, S. Accident Spread and Risk Propagation Mechanism in Complex Industrial System Network. Reliab. Eng. Syst. Saf. 2024, 244, 109940. [Google Scholar] [CrossRef]
- Li, J.; Zhang, S.; Xu, B. Containership Delay Propagation Risk Analysis Based on Effective Multivariate Transfer Entropy. Ocean Eng. 2024, 298, 117077. [Google Scholar] [CrossRef]
- Diakakis, M.; Lekkas, E.; Stamos, I.; Mitsakis, E. Vulnerability of Transport Infrastructure to Extreme Weather Events in Small Rural Catchments. Eur. J. Transp. Infrastruct. Res. 2016, 16, 114–127. [Google Scholar] [CrossRef]
- Başpınar, B.; Gopalakrishnan, K.; Koyuncu, E.; Balakrishnan, H. An Empirical Study of the Resilience of the US and European Air Transportation Networks. J. Air Transp. Manag. 2023, 106, 102303. [Google Scholar] [CrossRef]
- Nie, Y.; Li, J.; Liu, G.; Zhou, P. Cascading Failure-Based Reliability Assessment for Post-Seismic Performance of Highway Bridge Network. Reliab. Eng. Syst. Saf. 2023, 238, 109457. [Google Scholar] [CrossRef]
- Zhang, Y.; Ng, S.T. Robustness of Urban Railway Networks against the Cascading Failures Induced by the Fluctuation of Passenger Flow. Reliab. Eng. Syst. Saf. 2022, 219, 108227. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, Y.; Xu, M.; Deng, W.; Zuo, Y. Vulnerability Analysis of the Global Liner Shipping Network: From Static Structure to Cascading Failure Dynamics. Ocean Coast. Manag. 2022, 229, 106325. [Google Scholar] [CrossRef]
- Lu, Q.C.; Zhang, L.; Xu, P.C.; Cui, X.; Li, J. Modeling Network Vulnerability of Urban Rail Transit under Cascading Failures: A Coupled Map Lattices Approach. Reliab. Eng. Syst. Saf. 2022, 221, 108320. [Google Scholar] [CrossRef]
- Duan, J.; Li, D.; Huang, H.-J. Reliability of the Traffic Network against Cascading Failures with Individuals Acting Independently or Collectively. Transp. Res. Part C Emerg. Technol. 2023, 147, 104017. [Google Scholar] [CrossRef]
- Jing, K.; Du, X.; Shen, L.; Tang, L. Robustness of Complex Networks: Cascading Failure Mechanism by Considering the Characteristics of Time Delay and Recovery Strategy. Phys. A Stat. Mech. Its Appl. 2019, 534, 122061. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, P.; Han, X. Agri-Food Supply Chain Network Disruption Propagation and Recovery Based on Cascading Failure. Phys. A Stat. Mech. Its Appl. 2022, 589, 126611. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Zhong, J.; Sun, Y.; Guo, Z.; Chen, Z.; Fu, C. Network Resilience Assessment and Reinforcement Strategy against Cascading Failure. Chaos Solitons Fractals 2022, 160, 112271. [Google Scholar] [CrossRef]
- Lu, Q.-C.; Li, J.; Xu, P.-C.; Zhang, L.; Cui, X. Modeling Cascading Failures of Urban Rail Transit Network Based on Passenger Spatiotemporal Heterogeneity. Reliab. Eng. Syst. Saf. 2024, 242, 109726. [Google Scholar] [CrossRef]
- Guo, X.; Du, Q.; Li, Y.; Zhou, Y.; Wang, Y.; Huang, Y.; Martinez-Pastor, B. Cascading Failure and Recovery of Metro–Bus Double-Layer Network Considering Recovery Propagation. Transp. Res. Part D Transp. Environ. 2023, 122, 103861. [Google Scholar] [CrossRef]
- Kong, L.; Mu, X.; Hu, G.; Zhang, Z. The Application of Resilience Theory in Urban Development: A Literature Review. Environmental Science and Pollution Research 2022, 29, 49651–49671. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and Stability of Ecological Systems; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Fan, D.; Sun, B.; Dui, H.; Zhong, J.; Wang, Z.; Ren, Y.; Wang, Z. A Modified Connectivity Link Addition Strategy to Improve the Resilience of Multiplex Networks against Attacks. Reliab. Eng. Syst. Saf. 2022, 221, 108294. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Y.; Ng, A.K.Y.; Jiang, C. An Analysis on the Resilience of the European Port Network. Transp. Res. Part A Policy Pract. 2023, 175, 103778. [Google Scholar] [CrossRef]
- Cao, Y.; Xin, X.; Jarumaneeroj, P.; Li, H.; Feng, Y.; Wang, J.; Wang, X.; Pyne, R.; Yang, Z. Data-Driven Resilience Analysis of the Global Container Shipping Network against Two Cascading Failures. Transp. Res. Part E Logist. Transp. Rev. 2025, 193, 103857. [Google Scholar] [CrossRef]
- Dong, S.; Gao, X.; Mostafavi, A.; Gao, J.; Gangwal, U. Characterizing Resilience of Flood-Disrupted Dynamic Transportation Network through the Lens of Link Reliability and Stability. Reliab. Eng. Syst. Saf. 2023, 232, 109071. [Google Scholar] [CrossRef]
- Yin, K.; Wu, J.; Wang, W.; Lee, D.-H.; Wei, Y. An Integrated Resilience Assessment Model of Urban Transportation Network: A Case Study of 40 Cities in China. Transp. Res. Part A: Policy Pract. 2023, 173, 103687. [Google Scholar] [CrossRef]
- Bai, X.; Ma, Z.; Zhou, Y. Data-Driven Static and Dynamic Resilience Assessment of the Global Liner Shipping Network. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 103016. [Google Scholar] [CrossRef]
- Chen, X.; Ma, S.; Chen, L.; Yang, L. Resilience Measurement and Analysis of Intercity Public Transportation Network. Transp. Res. Part D Transp. Environ. 2024, 131, 104202. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, J.; Fu, H.; Ge, F.; Wu, J.; Lev, B. Resilience Analysis of the Integrated China-Europe Freight Transportation Network under Heterogeneous Demands. Transp. Res. Part A Policy Pract. 2024, 186, 104130. [Google Scholar] [CrossRef]
- China Economic Information Service China-Europe Railway Express: Summary of Routes. Available online: https://www.imsilkroad.com/news/silubanlie (accessed on 19 February 2025).
- Fujian Silk Road Maritime Shipping Operation Co., Ltd. Silk Road Maritime. Available online: https://www.cnsrma.com/silk-road/index (accessed on 19 February 2025).



| Symbol | Type | Description | Symbol | Type | Description |
|---|---|---|---|---|---|
| State | Node is in a susceptible state | Parameter | The station additional load capacity | ||
| State | Node is in a dangerous state | Parameter | Hybrid attack | ||
| State | Node is in an infectious state | Parameter | The failure propagation rate | ||
| State | Node is in a recovered state | Parameter | The propagation interaction coefficient | ||
| Parameter | Degree attack | Parameter | The in-degree value of a station in the network | ||
| Parameter | Betweenness attack | Parameter | Network failure intensity rate based on the node failure state | ||
| Parameter | Closeness attack | Parameter | Network maximum connectivity rate based on the node failure state | ||
| Parameter | Node state conversion rate | Parameter | Network efficiency | ||
| Parameter | The total number of shortest paths from the station to the station | Parameter | Load of partial failure node at time | ||
| Parameter | The length of the shortest path from the station to the station | Parameter | The out-degree scale factor | ||
| Intermediate variables | The load increment distributed from the hub station to its neighboring stations at the time | Function | The functional relationship between the station failure state function | ||
| Function | The functional station set of the neighboring stations of the hub station | Set | Set of normal nodes | ||
| Intermediate Variables | The load increment distributed from the non-hub station to its neighboring stations at time | Set | Set of partial failure nodes | ||
| Parameter | Backward risk propagation rate | Set | Set of complete failure nodes | ||
| Decision variables | The station repair time | Set | Set of nodes | ||
| Decision variables | The station risk state recovery rate | Decision variables | The load redistribution parameter based on residual capacity | ||
| Set | The set of neighboring stations for the risk recovered status station | Decision variables | A load redistribution parameter based on the intermediary strength |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Q.; Xu, B.; Li, J. Risk–Failure Interactive Propagation and Recovery of Sea–Rail Intermodal Transportation Network Considering Recovery Propagation. J. Mar. Sci. Eng. 2025, 13, 781. https://doi.org/10.3390/jmse13040781
Xiong Q, Xu B, Li J. Risk–Failure Interactive Propagation and Recovery of Sea–Rail Intermodal Transportation Network Considering Recovery Propagation. Journal of Marine Science and Engineering. 2025; 13(4):781. https://doi.org/10.3390/jmse13040781
Chicago/Turabian StyleXiong, Qiuju, Bowei Xu, and Junjun Li. 2025. "Risk–Failure Interactive Propagation and Recovery of Sea–Rail Intermodal Transportation Network Considering Recovery Propagation" Journal of Marine Science and Engineering 13, no. 4: 781. https://doi.org/10.3390/jmse13040781
APA StyleXiong, Q., Xu, B., & Li, J. (2025). Risk–Failure Interactive Propagation and Recovery of Sea–Rail Intermodal Transportation Network Considering Recovery Propagation. Journal of Marine Science and Engineering, 13(4), 781. https://doi.org/10.3390/jmse13040781





