Co-Optimization of the Hardware Configuration and Energy Management Parameters of Ship Hybrid Power Systems Based on the Hybrid Ivy-SA Algorithm
Abstract
1. Introduction
1.1. Hardware Configuration of Ship Hybrid Power Systems
1.2. Energy Management Strategies for Hybrid Ships
1.3. Optimization Algorithms for Hybrid Ships
1.4. Summary
1.5. The Main Research Content of This Paper
- The main engine model and hybrid ship model are established on the basis of the hardware configuration, and the accuracy of the models is validated.
- To meet the real-time response requirements of the system, an ECMS-based energy management strategy is formulated, and energy management parameters are set.
- A sensitivity analysis is conducted based on the hardware configuration and energy management parameters to determine the optimization parameters.
- The Ivy-SA algorithm is developed and tested with the CEC2017 benchmark functions, concurrently optimizing the hardware configuration and the energy management parameters of the hybrid power system.
2. Hybrid Power System Modeling
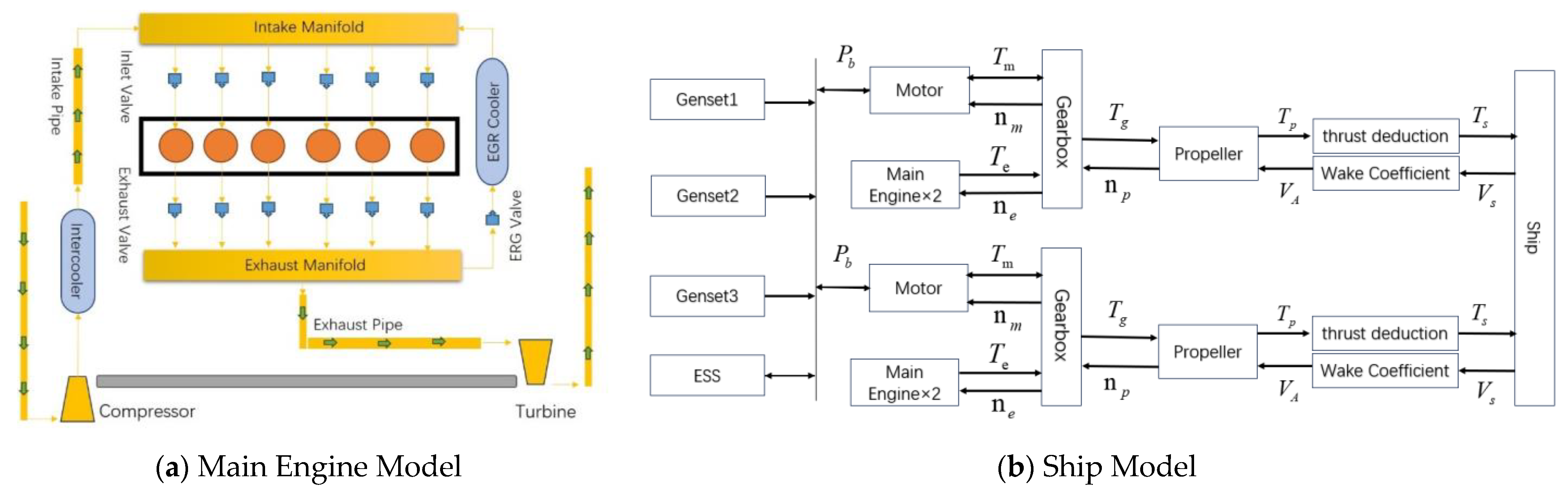
2.1. Diesel Engine Model
- (1)
- In-Cylinder Thermodynamic Calculation
- (2)
- Intake and Exhaust Mass Flow Rate
- (3)
- Turbocharger
2.2. Ship Power System Model
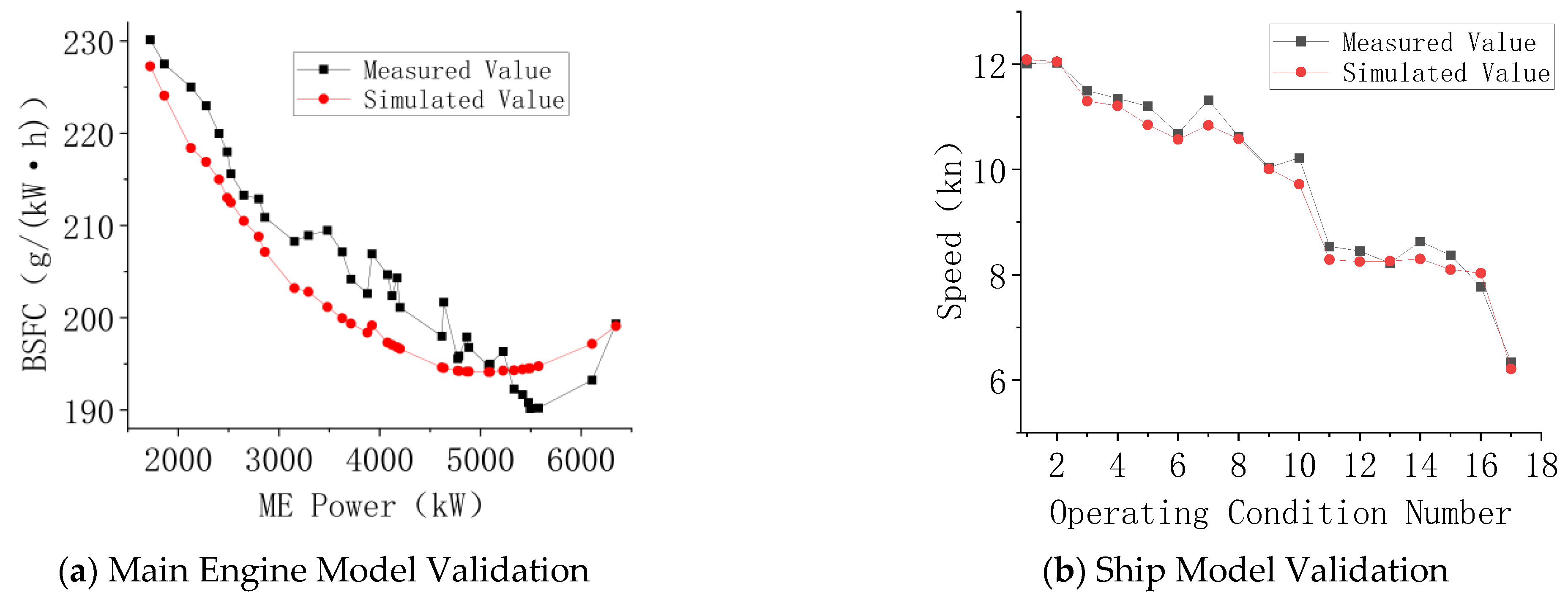
2.3. Model Validation
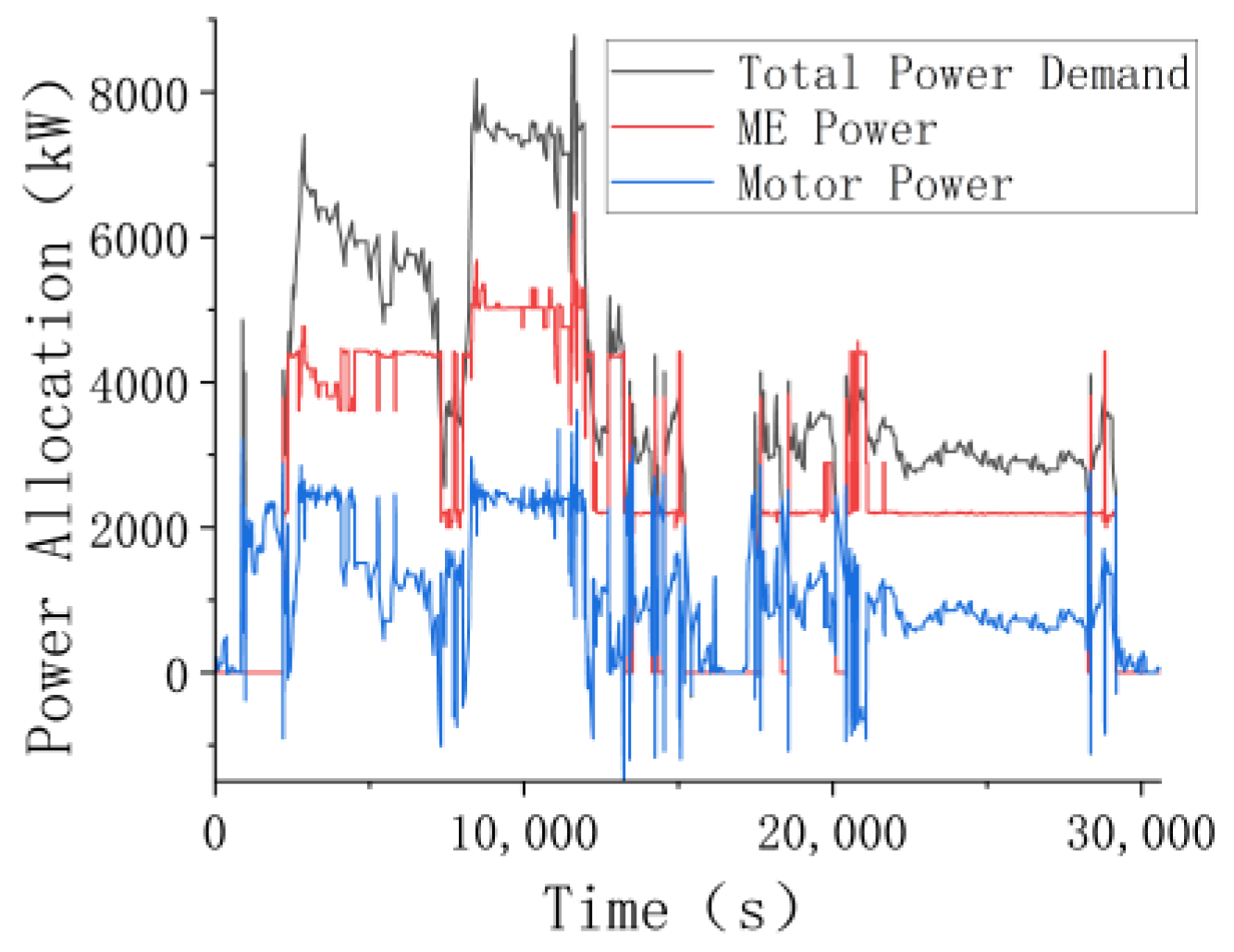
3. Energy Management Strategy
4. Optimization of the Power System
4.1. Parameter Sensitivity Analysis
4.2. System Optimization Problem
5. Ivy-SA Algorithm for Hybrid Power Systems
5.1. Ivy Algorithm
5.2. Simulated Annealing Algorithm
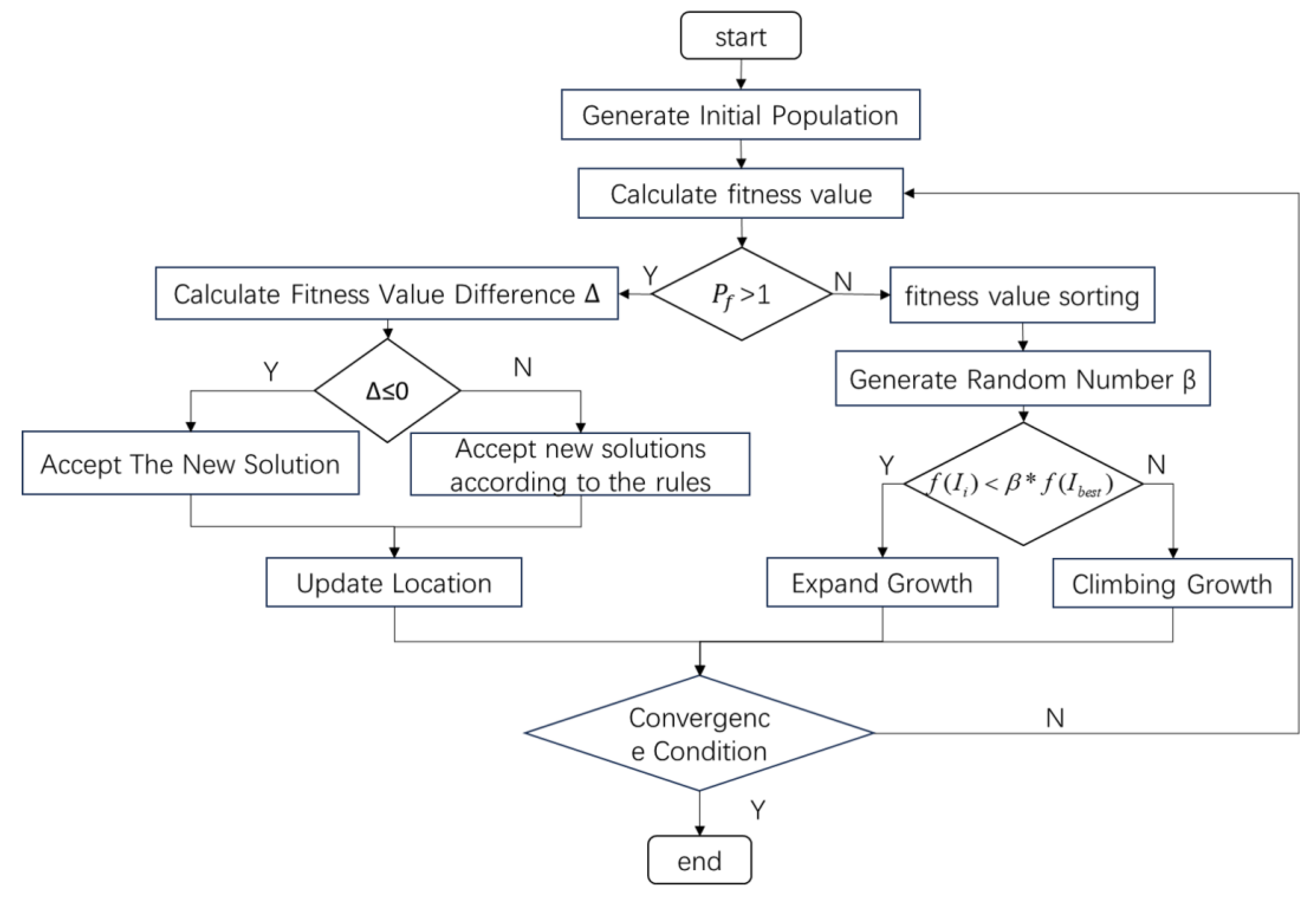
5.3. Ivy-SA Algorithm
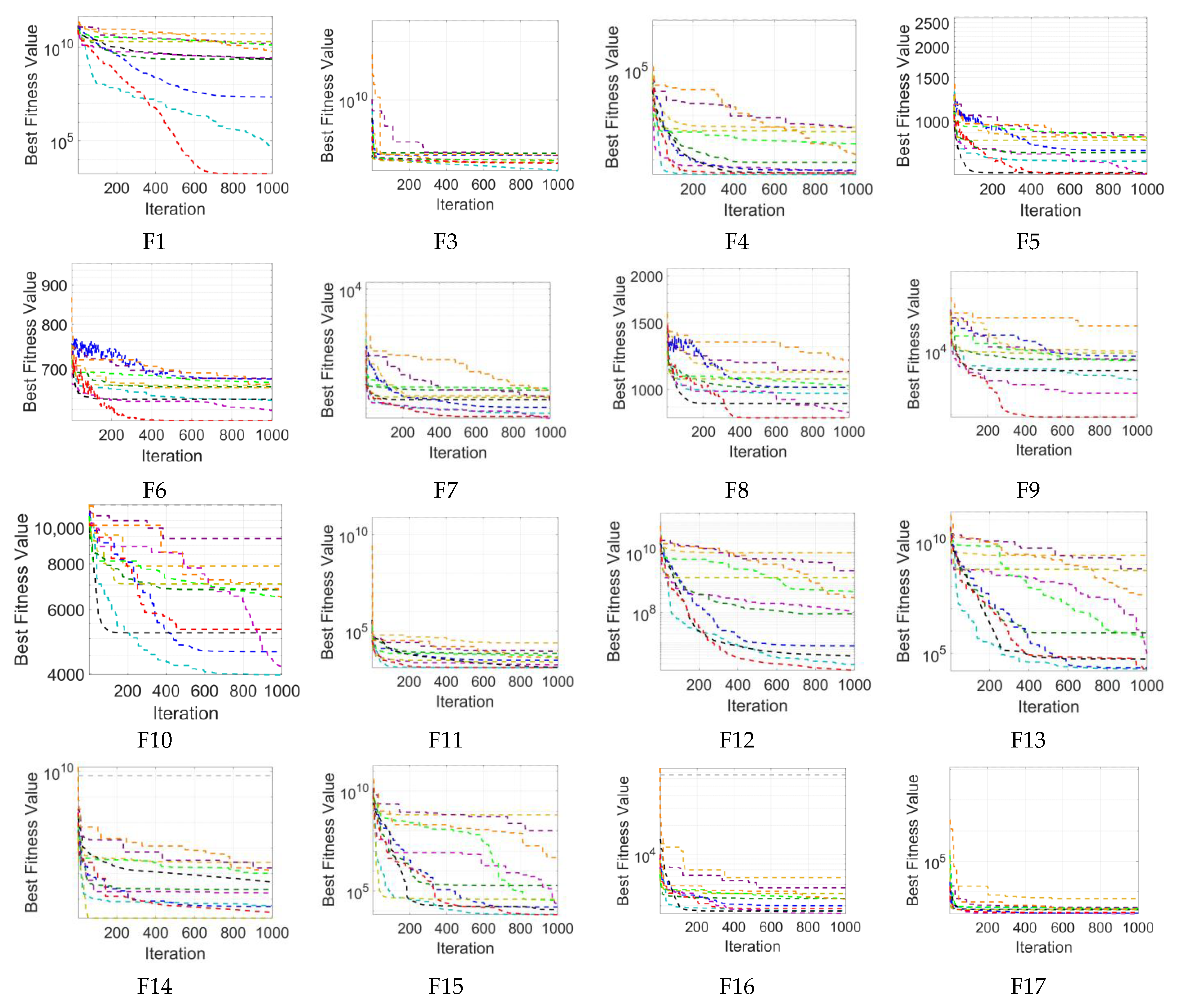
5.4. Ivy-SA Algorithm Testing
5.5. Co-Optimization of Hybrid Power Systems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Inal, O.B.; Charpentier, J.-F.; Deniz, C. Hybrid power and propulsion systems for ships: Current status and future challenges. Renew. Sustain. Energy Rev. 2022, 156, 111965. [Google Scholar]
- Wu, P.; Bucknall, R. Hybrid fuel cell and battery propulsion system modelling and multi-objective optimisation for a coastal ferry. Int. J. Hydrog. Energy 2020, 45, 3193–3208. [Google Scholar]
- Wang, Y.; Iris, Ç. Transition to near-zero emission shipping fleet powered by alternative fuels under uncertainty. Transp. Res. Part D Transp. Environ. 2025, 142, 104689. [Google Scholar]
- Zhang, C. The research of power allocation in diesel-electric hybrid propulsion system. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 3664–3668. [Google Scholar]
- Zaccone, R.; Campora, U.; Martelli, M. Optimisation of a diesel-electric ship propulsion and power generation system using a genetic algorithm. J. Mar. Sci. Eng. 2021, 9, 587. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Soares, C.G. Optimization procedure to minimize fuel consumption of a four-stroke marine turbocharged diesel engine. Energy 2019, 168, 897–908. [Google Scholar]
- Liu, L.; Wang, X.; Liu, D.; Mao, W.; Xiong, F. Research on combustion process optimization of marine diesel engines based on dual-injector system. J. Phys. Conf. Ser. 2024, 2683, 012019. [Google Scholar]
- Chen, X.; Liu, L.; Du, J.; Liu, D.; Huang, L.; Li, X. Intelligent optimization based on a virtual marine diesel engine using GA-ICSO hybrid algorithm. Machines 2022, 10, 227. [Google Scholar] [CrossRef]
- Li, X.; Pan, L.; Zhang, J.; Jin, Z.; Jiang, W.; Wang, Y.; Liu, L.; Tang, R.; Lai, J.; Yang, X. A novel capacity allocation method for hybrid energy storage system for electric ship considering life cycle cost. J. Energy Storage 2025, 116, 116070. [Google Scholar]
- Barrera-Cardenas, R.; Mo, O.; Guidi, G. Optimal sizing of battery energy storage systems for hybrid marine power systems. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019; pp. 293–302. [Google Scholar]
- Balci, G.; Phan, T.T.N.; Surucu-Balci, E.; Iris, Ç. A roadmap to alternative fuels for decarbonising shipping: The case of green ammonia. Res. Transp. Bus. Manag. 2024, 53, 101100. [Google Scholar]
- Antonopoulos, S.; Visser, K.; Kalikatzarakis, M.; Reppa, V. MPC framework for the energy management of hybrid ships with an energy storage system. J. Mar. Sci. Eng. 2021, 9, 993. [Google Scholar] [CrossRef]
- Liu, B.; Gao, D.; Yang, P.; Hu, Y. An energy efficiency optimization strategy of hybrid electric ship based on working condition prediction. J. Mar. Sci. Eng. 2022, 10, 1746. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, Y.; Tong, L.; Yuan, C.; Shen, B.; Long, T. Energy Management Strategy for Diesel–Electric Hybrid Ship Considering Sailing Route Division Based on DDPG. IEEE Trans. Transp. Electrif. 2023, 10, 187–202. [Google Scholar] [CrossRef]
- Gao, D.; Wang, X.; Wang, T.; Wang, Y.; Xu, X. An energy optimization strategy for hybrid power ships under load uncertainty based on load power prediction and improved NSGA-II algorithm. Energies 2018, 11, 1699. [Google Scholar] [CrossRef]
- Tjandra, R.; Wen, S.; Zhou, D.; Tang, Y. Optimal sizing of BESS for hybrid electric ship using multi-objective particle swarm optimization. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019-ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 1460–1466. [Google Scholar]
- Xiang, Y.; Yang, X. An ECMS for multi-objective energy management strategy of parallel diesel electric hybrid ship based on ant colony optimization algorithm. Energies 2021, 14, 810. [Google Scholar] [CrossRef]
- Chen, L.; Gao, D.; Xue, Q. Energy Management Strategy of Hybrid Ships Using Nonlinear Model Predictive Control via a Chaotic Grey Wolf Optimization Algorithm. J. Mar. Sci. Eng. 2023, 11, 1834. [Google Scholar] [CrossRef]
- Shang, Q.; Sun, Y.; Zhou, Y.; Yan, L.; Wei, C.; Hu, W. Exploring the optimization of energy management strategy for hybrid ships based on the Grey Wolf optimization algorithm. In Proceedings of the 2023 7th International Conference on Transportation Information and Safety (ICTIS), Xi’an, China, 4–6 August 2023; pp. 298–305. [Google Scholar]
- Liu, Z.; Munnannur, A. Design and development of heavy duty diesel engines. In Future Diesel Engines; Springer: Singapore, 2019; pp. 887–914. [Google Scholar]
- Reitz, R.; Rutland, C. Development and testing of diesel engine CFD models. Prog. Energy Combust. Sci. 1995, 21, 173–196. [Google Scholar] [CrossRef]
- Kim, K.-H.; Kong, K.-J. One-dimensional gas flow analysis of the intake and exhaust system of a single cylinder diesel engine. J. Mar. Sci. Eng. 2020, 8, 1036. [Google Scholar] [CrossRef]
- Molland, A.F.; Turnock, S.R.; Hudson, D.A. Ship Resistance and Propulsion; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Zahedi, B.; Norum, L.E. Modeling and simulation of all-electric ships with low-voltage DC hybrid power systems. IEEE Trans. Power Electron. 2012, 28, 4525–4537. [Google Scholar] [CrossRef]
- Paganelli, G.; Delprat, S.; Guerra, T.-M.; Rimaux, J.; Santin, J.-J. Equivalent consumption minimization strategy for parallel hybrid powertrains. In Proceedings of the Vehicular Technology Conference, IEEE 55th Vehicular Technology Conference, VTC Spring 2002 (Cat. No. 02CH37367), Birmingham, AL, USA, 6–9 May 2002; pp. 2076–2081. [Google Scholar]
- Onori, S.; Serrao, L.; Rizzoni, G.; Onori, S.; Serrao, L.; Rizzoni, G. Pontryagin’s minimum principle. In Hybrid Electric Vehicles: Energy Management Strategies; Springer: London, UK, 2016; pp. 51–63. [Google Scholar]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Serrao, L.; Onori, S.; Rizzoni, G. ECMS as a realization of Pontryagin’s minimum principle for HEV control. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3964–3969. [Google Scholar]
- Nejatzadegan, F.; Sobhani, V.; Pahlavan, M.; Dehghan, A. Effect of exhaust manifold geometry design on the performance of an internal combustion engine. Int. Commun. Heat Mass Transf. 2025, 162, 108593. [Google Scholar]
- Sawant, P.; Warstler, M.; Bari, S. Exhaust tuning of an internal combustion engine by the combined effects of variable exhaust pipe diameter and an exhaust valve timing system. Energies 2018, 11, 1545. [Google Scholar] [CrossRef]
- Balmelli, M.; Zsiga, N.; Merotto, L.; Soltic, P. Effect of the intake valve lift and closing angle on part load efficiency of a spark ignition engine. Energies 2020, 13, 1682. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Yoon, S.; Sa, S.; Kim, W. Effect of valve timing and lift on flow and mixing characteristics of a CAI engine. Int. J. Automot. Technol. 2007, 8, 687–696. [Google Scholar]
- Alrwashdeh, S.S.; Almajali, M.R.; Alsaraireh, F.M.; Ala’M, A.-F. Green performance enhancement of marine engines via turbocharger compression ratio optimization. Results Eng. 2024, 24, 102989. [Google Scholar] [CrossRef]
- Xin, R.; Zhai, J.; Liao, C.; Wang, Z.; Zhang, J.; Bazari, Z.; Ji, Y. Simulation Study on the Performance and Emission Parameters of a Marine Diesel Engine. J. Mar. Sci. Eng. 2022, 10, 985. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, H.; Jia, B.; Zuo, Z.; Smallbone, A.; Roskilly, A.P. Effect of the stroke-to-bore ratio on the performance of a dual-piston free piston engine generator. Appl. Therm. Eng. 2021, 185, 116456. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Zhao, Y.; He, T.; Zeng, H. Optimization design of hybrid energy storage capacity configuration for electric ship. Energy Rep. 2024, 11, 887–894. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li (NiMnCo) O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Ghasemi, M.; Zare, M.; Trojovský, P.; Rao, R.V.; Trojovská, E.; Kandasamy, V. Optimization based on the smart behavior of plants with its engineering applications: Ivy algorithm. Knowl.-Based Syst. 2024, 295, 111850. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [PubMed]


| Certain Type of 4-Stroke Diesel Engine | Parameter |
|---|---|
| Cylinder number | 6 |
| Cylinder arrangement | Inline |
| Engine type | 4-stroke |
| Piston displacement | 96.4 L/cyl |
| Engine speed | 600 rpm |
| Engine output | 7200 kW |
| Bore | 460 mm |
| Stroke | 580 mm |
| Mean piston speed | 11.6 m/s |
| Title | Parameter | Unit | Value |
|---|---|---|---|
| Main engine | Number | - | 4 |
| Rated power | kW | 7200 | |
| Rated speed | r/min | 600 | |
| GenSet | Number | - | 3 |
| Rated power | kW | 2610 | |
| Motor | Number | - | 2 |
| Rated power | kW | 2500 | |
| Rated speed | r/min | 675 | |
| Propeller | Type | - | CPP |
| Diameter | m | 5.4 | |
| Gearbox | ME reduction gear ratio | - | 4.6 |
| Motor reduction gear ratio | - | 2 | |
| Battery | Type | - | Ternary lithium battery |
| Energy | kWh | 4972 |
| Algorithm | Parameters |
|---|---|
| PSO | Learning factors c1 = 2, c2 = 2; the inertia factor wMax = 0.9; wMin = 0.6; |
| GA | Crossover probability pc = 0.8; mutation probability pm = 0.05; |
| WOA | Constant a = 2 − t × ((2)/Max_iter); |
| SA | Initial temperature T0 = 100; cooling coefficient alpha = 0.95; |
| CPO | Convergence rate alpha = 0.2; percentage of tradeoff Tf = 0.8; |
| HEOA | Warning value A = 0.6; leaders LN = 0.4; explorers EN = 0.4; followers FN = 0.1; |
| NRBO | Deciding factor DF = 0.6; |
| Ivy-SA | Balance factor Bf = 2 |
| Function | PSO | GA | GWO | WOA | CDO | SA | IVY | CPO | HEOA | LEA | NRBO | Ivy-SA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 7.81 × 104 | 3.02 × 1010 | 2.69 × 109 | 1.73 × 109 | 5.24 × 1010 | 5.58 × 107 | 1.23 × 109 | 2.21 × 1010 | 1.23 × 1010 | 7.11 × 109 | 1.64 × 1010 | * 1.79 × 104 |
| STD | 1.14 × 105 | 1.45 × 1010 | 1.40 × 109 | 8.30 × 108 | 2.20 × 108 | 5.33 × 107 | 2.56 × 109 | 3.38 × 109 | 4.00 × 109 | 3.74 × 109 | 4.28 × 109 | 5.15 × 104 | |
| F3 | Mean | 1.63 × 104 | 2.90 × 105 | 4.66 × 104 | 2.52 × 105 | 8.69 × 104 | 1.55 × 105 | 5.86 × 104 | 1.48 × 105 | 6.54 × 104 | 2.22 × 105 | 4.88 × 104 | 3.92 × 104 |
| STD | 6.46E+03 | 7.02 × 104 | 1.12 × 104 | 7.66 × 104 | 4.43 × 103 | 2.03 × 104 | 4.93 × 103 | 4.23 × 104 | 8.43 × 103 | 5.84 × 104 | 7.21 × 103 | 4.93 × 103 | |
| F4 | Mean | 4.79 × 102 | 5.76 × 103 | 5.99 × 102 | 8.42 × 102 | 5.43 × 103 | 5.86 × 102 | 6.47 × 102 | 4.31 × 103 | 1.59 × 103 | 1.05 × 103 | 1.95 × 103 | 5.03 × 102 |
| STD | 1.64 × 101 | 3.38 × 103 | 7.18 × 101 | 1.42 × 102 | 1.09 × 102 | 2.98 × 101 | 5.20 × 102 | 1.30 × 103 | 6.86 × 102 | 2.90 × 102 | 9.14 × 102 | 1.67 × 101 | |
| F5 | Mean | 6.92 × 102 | 9.79 × 102 | 6.19 × 102 | 8.31 × 102 | 8.51 × 102 | 7.42 × 102 | 7.01 × 102 | 8.48 × 102 | 8.42 × 102 | 8.30 × 102 | 8.33 × 102 | 5.67 × 102 |
| STD | 3.82 × 101 | 7.76 × 101 | 2.42 × 101 | 6.12 × 101 | 1.64 × 101 | 3.68 × 101 | 4.41 × 101 | 2.51 × 101 | 3.58 × 101 | 5.51 × 101 | 4.10 × 101 | 3.61 × 101 | |
| F6 | Mean | 6.47 × 102 | 7.17 × 102 | 6.11 × 102 | 6.77 × 102 | 6.70 × 102 | 6.80 × 102 | 6.21 × 102 | 6.67 × 102 | 6.75 × 102 | 6.79 × 102 | 6.71 × 102 | 6.00 × 102 |
| STD | 7.45 × 100 | 1.50 × 101 | 4.43 × 100 | 1.18 × 101 | 4.89 × 100 | 5.75 × 100 | 1.90 × 101 | 8.41 × 100 | 6.85 × 100 | 1.34 × 101 | 8.62 × 100 | 1.49 × 10− | |
| F7 | Mean | 9.27 × 102 | 1.84 × 103 | 8.97 × 102 | 1.30 × 103 | 1.31 × 103 | 1.08 × 103 | 1.15 × 103 | 1.25 × 103 | 1.34 × 103 | 1.41 × 103 | 1.22 × 103 | 8.05 × 102 |
| STD | 6.21 × 101 | 2.20 × 102 | 5.41 × 101 | 7.81 × 101 | 2.16 × 101 | 4.76 × 101 | 1.12 × 102 | 5.51 × 101 | 6.96 × 101 | 1.51 × 102 | 7.79 × 101 | 4.68 × 101 | |
| F8 | Mean | 9.31 × 102 | 1.22 × 103 | 8.97 × 102 | 1.04 × 103 | 1.09 × 103 | 1.02 × 103 | 9.40 × 102 | 1.11 × 103 | 1.08 × 103 | 1.13 × 103 | 1.08 × 103 | 8.58 × 102 |
| STD | 3.13 × 101 | 6.31 × 101 | 2.15 × 101 | 4.97 × 101 | 1.88 × 101 | 3.16 × 101 | 3.07 × 101 | 1.71 × 101 | 2.54 × 101 | 5.21 × 101 | 3.38 × 101 | 3.15 × 101 | |
| F9 | Mean | 4.90 × 103 | 8.57 × 103 | 2.30 × 103 | 1.17 × 104 | 9.56 × 103 | 7.75 × 103 | 5.10 × 103 | 1.00 × 104 | 8.00 × 103 | 1.80 × 104 | 6.82 × 103 | 9.85 × 102 |
| STD | 1.14 × 103 | 1.83 × 103 | 9.14 × 102 | 4.47 × 103 | 1.07 × 103 | 1.68 × 103 | 4.52 × 102 | 1.91 × 103 | 9.51 × 102 | 4.59 × 103 | 1.32 × 103 | 1.03 × 102 | |
| F10 | Mean | 4.84 × 103 | 7.92 × 103 | 4.87 × 103 | 7.40 × 103 | 9.00 × 103 | 4.38 × 103 | 5.27 × 103 | 9.35 × 103 | 7.09 × 103 | 7.71 × 103 | 7.81 × 103 | 5.02 × 103 |
| STD | 6.83 × 102 | 8.64 × 102 | 1.48 × 103 | 7.53 × 102 | 2.93 × 102 | 3.15 × 102 | 6.57 × 102 | 2.97 × 102 | 5.89 × 102 | 6.82 × 102 | 5.94 × 102 | 6.32 × 102 | |
| F11 | Mean | 1.22 × 103 | 1.99 × 104 | 2.89 × 103 | 6.31 × 103 | 2.04 × 104 | 3.13 × 103 | 1.28 × 103 | 7.92 × 103 | 4.04 × 103 | 7.85 × 103 | 2.53 × 103 | 1.20 × 103 |
| STD | 3.82 × 101 | 1.16 × 104 | 1.34 × 103 | 2.90 × 103 | 6.92 × 103 | 7.46 × 102 | 1.93 × 102 | 2.11 × 103 | 1.55 × 103 | 2.52 × 103 | 6.75 × 102 | 4.44 × 101 | |
| F12 | Mean | 1.61 × 106 | 2.85 × 109 | 1.07 × 108 | 2.46 × 108 | 9.77 × 109 | 6.34 × 106 | 4.48 × 107 | 2.70 × 109 | 4.86 × 108 | 3.10 × 108 | 1.20 × 109 | 1.58 × 106 |
| STD | 1.07 × 106 | 2.95 × 109 | 1.05 × 108 | 1.54 × 108 | 8.34 × 107 | 4.33 × 106 | 2.26 × 108 | 1.03 × 109 | 3.89 × 108 | 1.31 × 108 | 5.41 × 108 | 1.19 × 106 | |
| F13 | Mean | 1.53 × 104 | 1.98 × 109 | 1.46 × 107 | 1.92 × 106 | 2.40 × 109 | 2.65 × 104 | 4.23 × 104 | 7.92 × 108 | 2.19 × 106 | 5.15 × 107 | 2.41 × 108 | 4.28 × 104 |
| STD | 1.33 × 104 | 2.39 × 109 | 3.64 × 107 | 1.72 × 106 | 1.20 × 108 | 9.43 × 103 | 1.86 × 104 | 3.83 × 108 | 2.27 × 106 | 4.03 × 107 | 1.71 × 108 | 2.21 × 104 | |
| F14 | Mean | 2.78 × 104 | 1.26 × 107 | 4.83 × 105 | 1.46 × 106 | 2.68 × 106 | 4.03 × 104 | 8.34 × 105 | 1.69 × 106 | 1.34 × 106 | 1.66 × 106 | 2.32 × 105 | 6.80 × 104 |
| STD | 2.55 × 104 | 1.36 × 107 | 4.79 × 105 | 1.65 × 106 | 1.09 × 105 | 3.11 × 104 | 7.10 × 105 | 1.03 × 106 | 7.20 × 105 | 1.50 × 106 | 4.05 × 105 | 5.18 × 104 | |
| F15 | Mean | 5.02 × 103 | 7.26 × 107 | 1.32 × 106 | 1.20 × 106 | 6.52 × 108 | 1.54 × 104 | 2.00 × 106 | 7.24 × 107 | 1.11 × 106 | 6.33 × 106 | 2.39 × 106 | 1.18 × 104 |
| STD | 3.36 × 103 | 1.63 × 108 | 3.15 × 106 | 2.07 × 106 | 2.02 × 105 | 5.95 × 103 | 1.05 × 107 | 4.24 × 107 | 1.28 × 106 | 9.28 × 106 | 5.77 × 106 | 6.22 × 103 | |
| F16 | Mean | 2.72 × 103 | 4.12 × 103 | 2.57 × 103 | 4.16 × 103 | 7.98 × 103 | 2.73 × 103 | 2.94 × 103 | 4.59 × 103 | 3.76 × 103 | 3.61 × 103 | 3.87 × 103 | 2.36 × 103 |
| STD | 2.82 × 102 | 5.50 × 102 | 2.72 × 102 | 4.80 × 102 | 1.73 × 103 | 2.20 × 102 | 3.61 × 102 | 2.21 × 102 | 4.89 × 102 | 3.98 × 102 | 4.60 × 102 | 2.52 × 102 | |
| F17 | Mean | 2.40 × 103 | 3.04 × 103 | 2.10 × 103 | 2.75 × 103 | 1.59 × 104 | 2.09 × 103 | 2.57 × 103 | 3.01 × 103 | 2.55 × 103 | 2.77 × 103 | 2.61 × 103 | 1.92 × 103 |
| STD | 3.23 × 102 | 3.09 × 102 | 2.05 × 102 | 3.17 × 102 | 1.40 × 104 | 9.51 × 101 | 3.19 × 102 | 1.61 × 102 | 2.40 × 102 | 2.86 × 102 | 2.23 × 102 | 1.78 × 102 | |
| F18 | Mean | 5.29 × 105 | 1.49 × 107 | 2.31 × 106 | 9.96 × 106 | 9.02 × 106 | 5.02 × 105 | 7.34 × 105 | 2.32 × 107 | 6.62 × 106 | 1.36 × 107 | 1.89 × 106 | 4.09 × 105 |
| STD | 4.78 × 105 | 1.56 × 107 | 4.13 × 106 | 1.30 × 107 | 1.08 × 106 | 3.13 × 105 | 6.15 × 105 | 2.07 × 107 | 5.46 × 106 | 1.44 × 107 | 2.91 × 106 | 2.58 × 105 | |
| F19 | Mean | 9.47 × 103 | 3.31 × 107 | 8.34 × 105 | 1.11 × 107 | 1.37 × 108 | 4.49 × 105 | 1.35 × 106 | 9.98 × 107 | 5.83 × 106 | 2.55 × 107 | 1.82 × 107 | 1.55 × 104 |
| STD | 9.79 × 103 | 4.97 × 107 | 8.99 × 105 | 9.23 × 106 | 5.45 × 106 | 6.05 × 105 | 5.12 × 106 | 7.66 × 107 | 3.43 × 106 | 1.97 × 107 | 1.77 × 107 | 1.43 × 104 | |
| F20 | Mean | 2.63 × 103 | 3.22 × 103 | 2.49 × 103 | 2.91 × 103 | 2.99 × 103 | 2.54 × 103 | 2.71 × 103 | 3.24 × 103 | 2.71 × 103 | 2.93 × 103 | 2.81 × 103 | 2.40 × 103 |
| STD | 1.87 × 102 | 2.80 × 102 | 1.49 × 102 | 2.48 × 102 | 1.34 × 102 | 8.81 × 101 | 2.51 × 102 | 1.52 × 102 | 1.61 × 102 | 2.38 × 102 | 1.66 × 102 | 1.46 × 102 | |
| F21 | Mean | 2.48 × 103 | 2.84 × 103 | 2.41 × 103 | 2.60 × 103 | 2.63 × 103 | 2.52 × 103 | 2.40 × 103 | 2.63 × 103 | 2.60 × 103 | 2.60 × 103 | 2.59 × 103 | 2.36 × 103 |
| STD | 2.74 × 101 | 6.79 × 101 | 3.48 × 101 | 4.46 × 101 | 1.71 × 101 | 4.10 × 101 | 3.92 × 101 | 2.58 × 101 | 4.70 × 101 | 3.90 × 101 | 5.11 × 101 | 2.83 × 101 | |
| F22 | Mean | 5.15 × 103 | 9.90 × 103 | 5.61 × 103 | 7.74 × 103 | 1.00 × 104 | 3.67 × 103 | 4.29 × 103 | 6.41 × 103 | 6.65 × 103 | 6.21 × 103 | 6.07 × 103 | 2.68 × 103 |
| STD | 2.30 × 103 | 9.88 × 102 | 1.68 × 103 | 1.74 × 103 | 9.78 × 102 | 1.62 × 103 | 2.39 × 103 | 1.75 × 103 | 1.81 × 103 | 2.71 × 103 | 2.25 × 103 | 1.17 × 103 | |
| F23 | Mean | 3.24 × 103 | 3.49 × 103 | 2.76 × 103 | 3.09 × 103 | 3.69 × 103 | 2.94 × 103 | 2.80 × 103 | 3.19 × 103 | 3.12 × 103 | 2.97 × 103 | 3.07 × 103 | 2.70 × 103 |
| STD | 1.33 × 102 | 1.76 × 102 | 3.17 × 101 | 9.63 × 101 | 7.10 × 101 | 5.94 × 101 | 5.53 × 101 | 6.20 × 101 | 1.23 × 102 | 5.45 × 101 | 5.71 × 101 | 2.72 × 101 | |
| F24 | Mean | 3.23 × 103 | 3.74 × 103 | 2.96 × 103 | 3.23 × 103 | 3.82 × 103 | 3.04 × 103 | 2.96 × 103 | 3.37 × 103 | 3.18 × 103 | 3.11 × 103 | 3.19 × 103 | 2.90 × 103 |
| STD | 9.49 × 101 | 1.70 × 102 | 6.18 × 101 | 1.09 × 102 | 5.54 × 101 | 1.16 × 102 | 6.36 × 101 | 7.46 × 101 | 9.84 × 101 | 6.24 × 101 | 6.18 × 101 | 2.38 × 101 | |
| F25 | Mean | 2.88 × 103 | 5.32 × 103 | 3.01 × 103 | 3.11 × 103 | 3.58 × 103 | 3.03 × 103 | 2.93 × 103 | 3.81 × 103 | 3.20 × 103 | 3.54 × 103 | 3.41 × 103 | 2.90 × 103 |
| STD | 9.86 × 100 | 9.69 × 102 | 4.13 × 101 | 5.07 × 101 | 2.38 × 101 | 2.70 × 101 | 3.74 × 101 | 2.02 × 102 | 1.17 × 102 | 2.21 × 102 | 2.62 × 102 | 1.44 × 101 | |
| F26 | Mean | 6.40 × 103 | 9.50 × 103 | 4.68 × 103 | 8.16 × 103 | 8.64 × 103 | 3.86 × 103 | 7.08 × 103 | 8.35 × 103 | 8.26 × 103 | 7.28 × 103 | 7.55 × 103 | 3.46 × 103 |
| STD | 2.05 × 103 | 9.64 × 102 | 4.92 × 102 | 1.22 × 103 | 2.28 × 102 | 3.59 × 102 | 1.22 × 103 | 7.36 × 102 | 1.45 × 103 | 5.28 × 102 | 1.11 × 103 | 7.31 × 102 | |
| F27 | Mean | 3.49 × 103 | 4.23 × 103 | 3.26 × 103 | 3.45 × 103 | 3.63 × 103 | 3.34 × 103 | 3.32 × 103 | 3.85 × 103 | 3.41 × 103 | 3.36 × 103 | 3.42 × 103 | 3.22 × 103 |
| STD | 2.90 × 102 | 2.81 × 102 | 2.95 × 101 | 1.27 × 102 | 3.73 × 101 | 2.37 × 101 | 9.79 × 101 | 1.09 × 102 | 1.10 × 102 | 6.83 × 101 | 7.04 × 101 | 1.01 × 101 | |
| F28 | Mean | 3.23 × 103 | 6.61 × 103 | 3.52 × 103 | 3.57 × 103 | 5.01 × 103 | 3.39 × 103 | 3.27 × 103 | 5.04 × 103 | 4.10 × 103 | 3.95 × 103 | 4.11 × 103 | 3.21 × 103 |
| STD | 2.21 × 101 | 1.46 × 103 | 1.67 × 102 | 1.08 × 102 | 2.15 × 101 | 4.06 × 101 | 3.39 × 101 | 3.64 × 102 | 3.22 × 102 | 3.26 × 102 | 5.43 × 102 | 1.57 × 101 | |
| F29 | Mean | 4.17 × 103 | 5.89 × 103 | 3.88 × 103 | 5.24 × 103 | 6.21 × 103 | 4.22 × 103 | 4.25 × 103 | 5.52 × 103 | 5.33 × 103 | 5.09 × 103 | 4.97 × 103 | 3.67 × 103 |
| STD | 3.02 × 102 | 9.15 × 102 | 1.92 × 102 | 4.24 × 102 | 3.09 × 102 | 1.72 × 102 | 3.06 × 102 | 2.82 × 102 | 4.76 × 102 | 4.86 × 102 | 4.41 × 102 | 1.78 × 102 | |
| F30 | Mean | 2.94 × 104 | 3.82 × 107 | 1.48 × 107 | 5.15 × 107 | 2.86 × 109 | 2.06 × 106 | 1.55 × 105 | 1.30 × 108 | 5.68 × 107 | 4.12 × 107 | 6.51 × 107 | 1.19 × 105 |
| STD | 1.15 × 104 | 4.20 × 107 | 1.40 × 107 | 2.77 × 107 | 8.15 × 108 | 1.67 × 106 | 1.53 × 105 | 6.33 × 107 | 3.75 × 107 | 3.04 × 107 | 4.80 × 107 | 9.17 × 104 |
| Function | PSO | GA | GWO | WOA | CDO | SA | IVY | CPO | HEOA | LEA | NRBO | Ivy-SA |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 3 | 12 | 2 | 8 | 9 | 4 | 5 | 7 | 10 | 11 | 6 | 1 |
| F3 | 3 | 12 | 2 | 6 | 9 | 5 | 4 | 10 | 7 | 11 | 8 | 1 |
| F4 | 3 | 8 | 2 | 9 | 10 | 6 | 4 | 11 | 7 | 12 | 5 | 1 |
| F5 | 3 | 10 | 2 | 7 | 11 | 1 | 5 | 12 | 6 | 8 | 9 | 4 |
| F6 | 2 | 11 | 5 | 8 | 12 | 6 | 3 | 9 | 7 | 10 | 4 | 1 |
| F7 | 2 | 10 | 5 | 6 | 12 | 4 | 3 | 11 | 8 | 7 | 9 | 1 |
| F8 | 1 | 11 | 5 | 6 | 12 | 2 | 3 | 10 | 7 | 8 | 9 | 4 |
| F9 | 1 | 12 | 5 | 7 | 11 | 2 | 6 | 10 | 8 | 9 | 4 | 3 |
| F10 | 1 | 10 | 5 | 7 | 12 | 3 | 4 | 11 | 8 | 9 | 6 | 2 |
| F11 | 3 | 9 | 2 | 10 | 12 | 4 | 5 | 11 | 7 | 6 | 8 | 1 |
| F12 | 4 | 10 | 3 | 8 | 12 | 2 | 6 | 11 | 5 | 9 | 7 | 1 |
| F13 | 3 | 10 | 6 | 7 | 11 | 2 | 4 | 12 | 8 | 9 | 5 | 1 |
| F14 | 1 | 10 | 5 | 7 | 12 | 4 | 3 | 11 | 6 | 9 | 8 | 2 |
| F15 | 4 | 11 | 2 | 8 | 10 | 3 | 5 | 12 | 6 | 9 | 7 | 1 |
| F16 | 4 | 12 | 3 | 8 | 11 | 5 | 2 | 10 | 7 | 9 | 6 | 1 |
| F17 | 4 | 11 | 5 | 10 | 12 | 2 | 3 | 8 | 9 | 6 | 7 | 1 |
| F18 | 10 | 11 | 2 | 8 | 12 | 4 | 3 | 9 | 7 | 5 | 6 | 1 |
| F19 | 9 | 11 | 2 | 8 | 12 | 4 | 3 | 10 | 6 | 5 | 7 | 1 |
| F20 | 1 | 12 | 4 | 6 | 10 | 5 | 3 | 11 | 7 | 9 | 8 | 2 |
| F21 | 4 | 12 | 3 | 8 | 11 | 2 | 6 | 10 | 9 | 5 | 7 | 1 |
| F22 | 6 | 12 | 2 | 9 | 10 | 4 | 3 | 11 | 7 | 5 | 8 | 1 |
| F23 | 2 | 12 | 5 | 6 | 10 | 4 | 3 | 11 | 9 | 7 | 8 | 1 |
| F24 | 3 | 11 | 2 | 8 | 12 | 4 | 5 | 10 | 9 | 7 | 6 | 1 |
| F25 | 1 | 6 | 5 | 8 | 12 | 4 | 3 | 11 | 9 | 7 | 10 | 2 |
| F26 | 3 | 12 | 2 | 8 | 9 | 4 | 5 | 7 | 10 | 11 | 6 | 1 |
| F27 | 3 | 12 | 2 | 6 | 9 | 5 | 4 | 10 | 7 | 11 | 8 | 1 |
| F28 | 3 | 8 | 2 | 9 | 10 | 6 | 4 | 11 | 7 | 12 | 5 | 1 |
| F29 | 3 | 10 | 2 | 7 | 11 | 1 | 5 | 12 | 6 | 8 | 9 | 4 |
| F30 | 2 | 11 | 5 | 8 | 12 | 6 | 3 | 9 | 7 | 10 | 4 | 1 |
| MFr | 3.07 | 10.83 | 3.52 | 7.59 | 10.86 | 4.03 | 3.90 | 10.10 | 7.52 | 8.03 | 7.07 | 1.48 |
| Final rank | 2 | 11 | 3 | 8 | 12 | 5 | 4 | 10 | 7 | 9 | 6 | 1 |
| Parameter | Initial Value | PSO | GWO | IVYA | SA | Ivy-SA |
|---|---|---|---|---|---|---|
| Exhaust Manifold | 200 | 180 | 180 | 180 | 180 | 180 |
| Exhaust Pipe | 160 | 162 | 168 | 158 | 155 | 165 |
| Intake Valve Lift Ratio | 3.055 | 3.345 | 3.345 | 3.345 | 3.345 | 3.345 |
| Exhaust Valve Lift Ratio | 3.055 | 3.194 | 3.194 | 3.194 | 3.194 | 3.194 |
| Compressor Pressure Ratio | 6.3 | 6.1 | 9.1 | 5.98 | 7.4 | 6.3 |
| Compressor Mass Flow Rate | 14.2 | 11.8 | 15.2 | 14.5 | 13.3 | 14.2 |
| Bore | 460 | 442 | 448 | 448 | 467 | 455 |
| Stroke | 580 | 603 | 595 | 595 | 571 | 586 |
| Motor Rated Power | 2550 | 2983 | 1925 | 2078 | 2031 | 2813 |
| Number of Parallel Batteries | 88 | 121 | 62 | 78 | 72 | 113 |
| Depth of Discharge | 80 | 88 | 74 | 84 | 78 | 84 |
| Charge Efficiency Factor | 1.7 | 1.63 | 1.78 | 1.62 | 1.82 | 1.66 |
| Discharge Efficiency Factor | 2.3 | 1.95 | 2.06 | 1.93 | 2.18 | 1.97 |
| CO₂ Emissions (ton) | 41.86 | 35.80 | 40.53 | 37.52 | 40.53 | 34.50 |
| Battery Energy Consumption (kWh) | 2875.46 | 2983.34 | 1268.08 | 1682.45 | 2134.92 | 2402.33 |
| Fuel Consumption (ton) | 12.85 | 10.98 | 12.44 | 11.51 | 12.44 | 11.03 |
| LCC ($) | 1.28 × 108 | 1.11 × 108 | 1.21 × 108 | 1.13 × 108 | 1.22 × 108 | 1.09 × 108 |
| Cost Savings | - | 13.19% | 5.30% | 11.43% | 4.13% | 14.49% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Fu, Z.; Zhang, X. Co-Optimization of the Hardware Configuration and Energy Management Parameters of Ship Hybrid Power Systems Based on the Hybrid Ivy-SA Algorithm. J. Mar. Sci. Eng. 2025, 13, 731. https://doi.org/10.3390/jmse13040731
Guo Q, Fu Z, Zhang X. Co-Optimization of the Hardware Configuration and Energy Management Parameters of Ship Hybrid Power Systems Based on the Hybrid Ivy-SA Algorithm. Journal of Marine Science and Engineering. 2025; 13(4):731. https://doi.org/10.3390/jmse13040731
Chicago/Turabian StyleGuo, Qian, Zhihang Fu, and Xingming Zhang. 2025. "Co-Optimization of the Hardware Configuration and Energy Management Parameters of Ship Hybrid Power Systems Based on the Hybrid Ivy-SA Algorithm" Journal of Marine Science and Engineering 13, no. 4: 731. https://doi.org/10.3390/jmse13040731
APA StyleGuo, Q., Fu, Z., & Zhang, X. (2025). Co-Optimization of the Hardware Configuration and Energy Management Parameters of Ship Hybrid Power Systems Based on the Hybrid Ivy-SA Algorithm. Journal of Marine Science and Engineering, 13(4), 731. https://doi.org/10.3390/jmse13040731







