Research on Energy Dissipation Mechanism of Hump Characteristics Based on Entropy Generation and Coupling Excitation Mechanism of Internal Vortex Structure of Waterjet Pump at Hump Region
Abstract
1. Introduction
2. Hydraulic Performance Testing and Numerical Simulation Methods
2.1. Pump Design Parameters
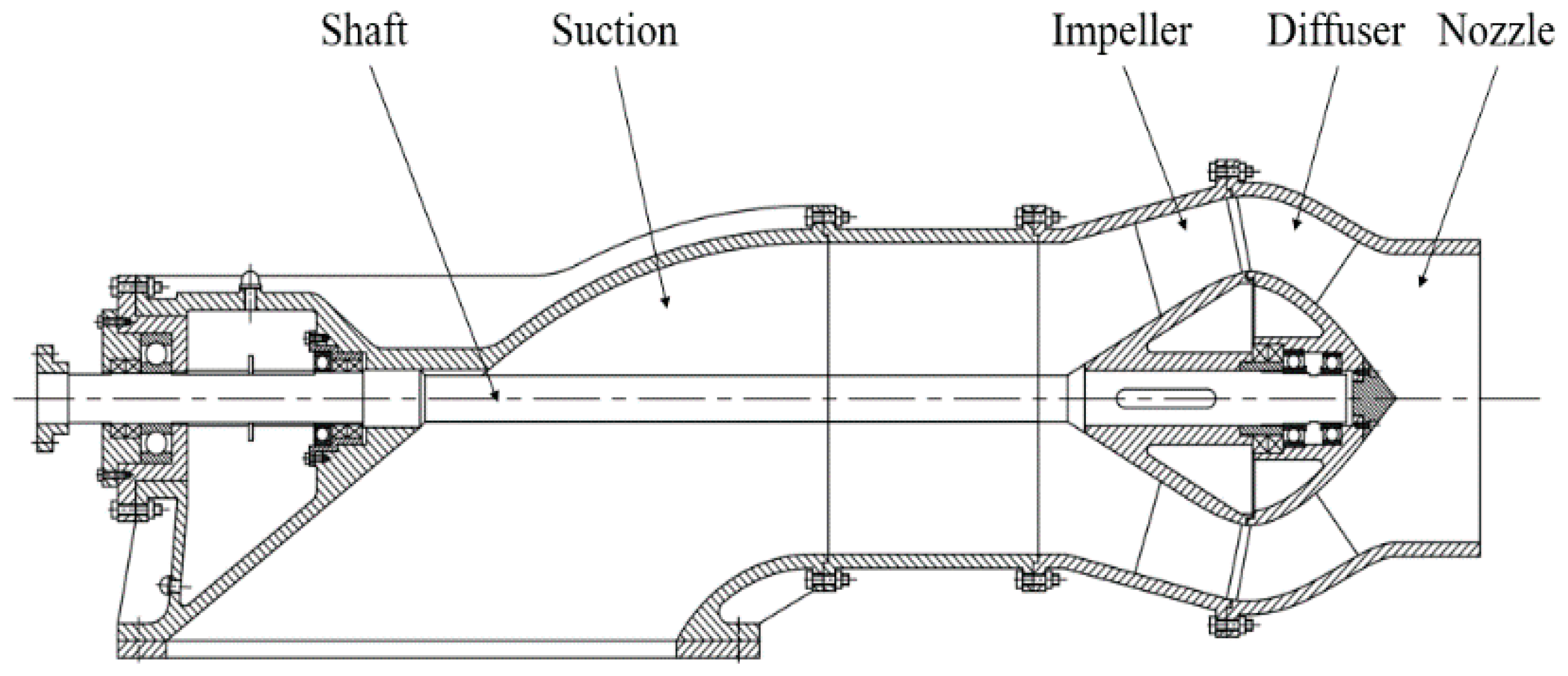
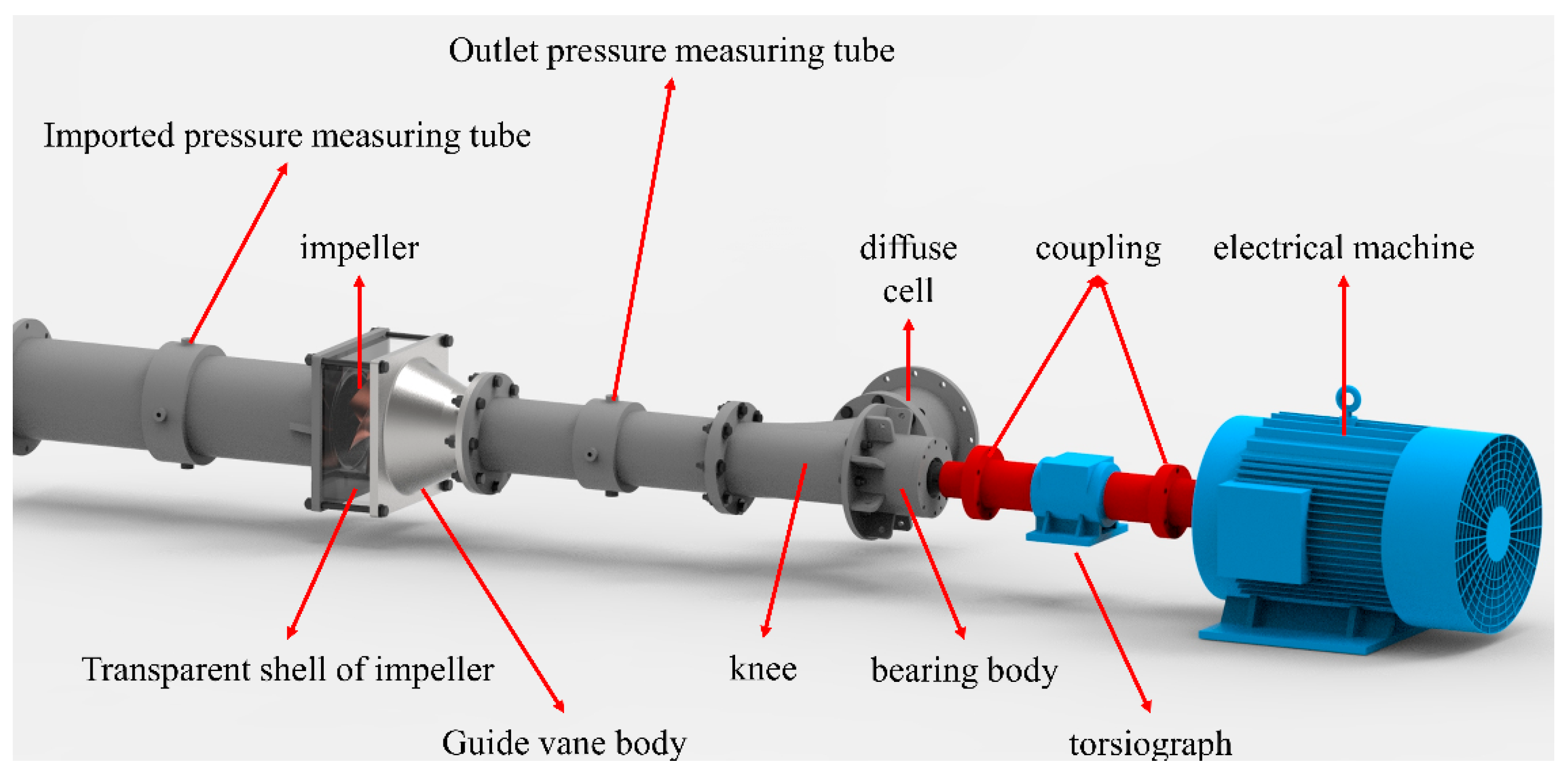
2.2. Structure and Parameters of the Test Pump
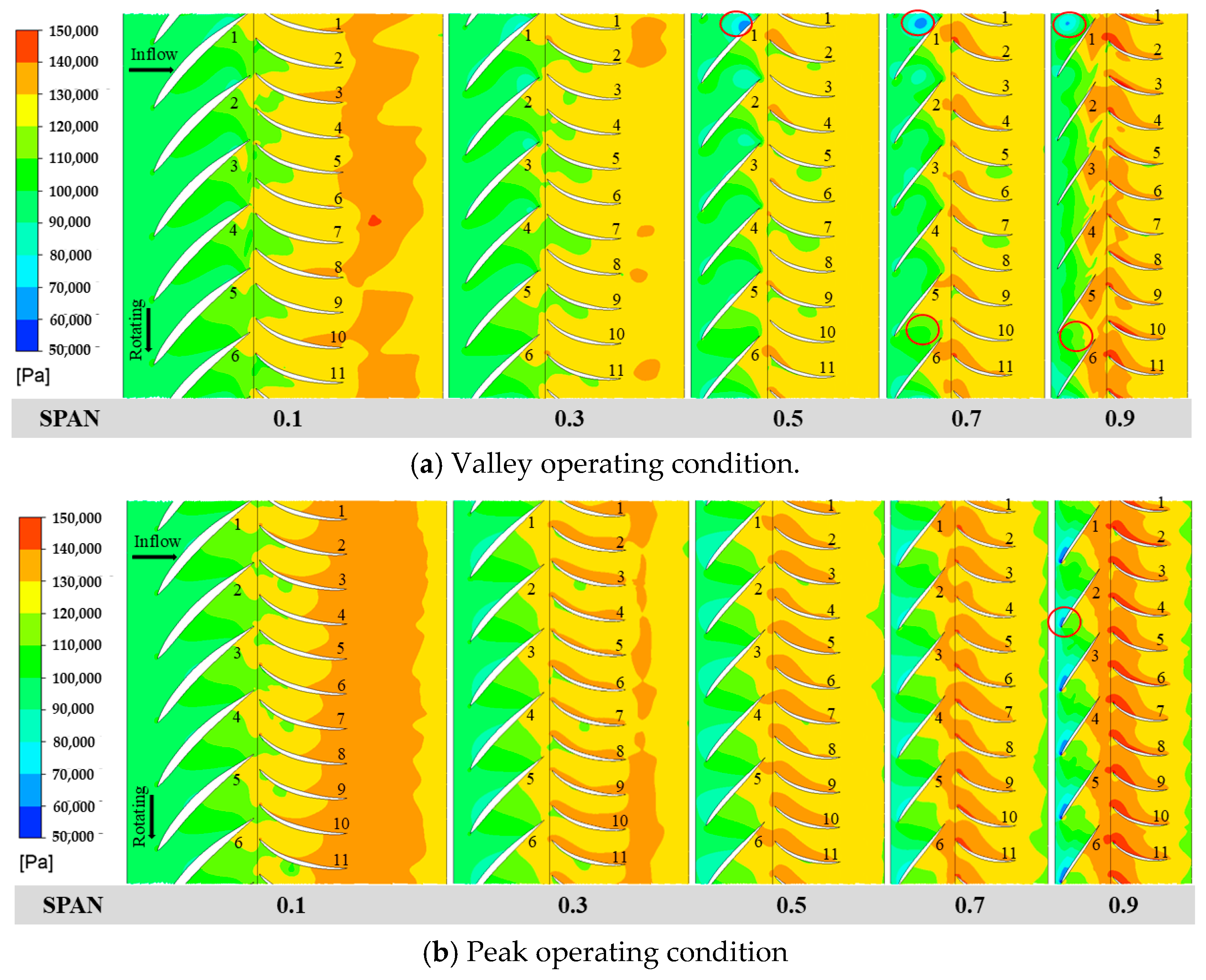
2.2.1. The Pressure Distribution Inside the Pump
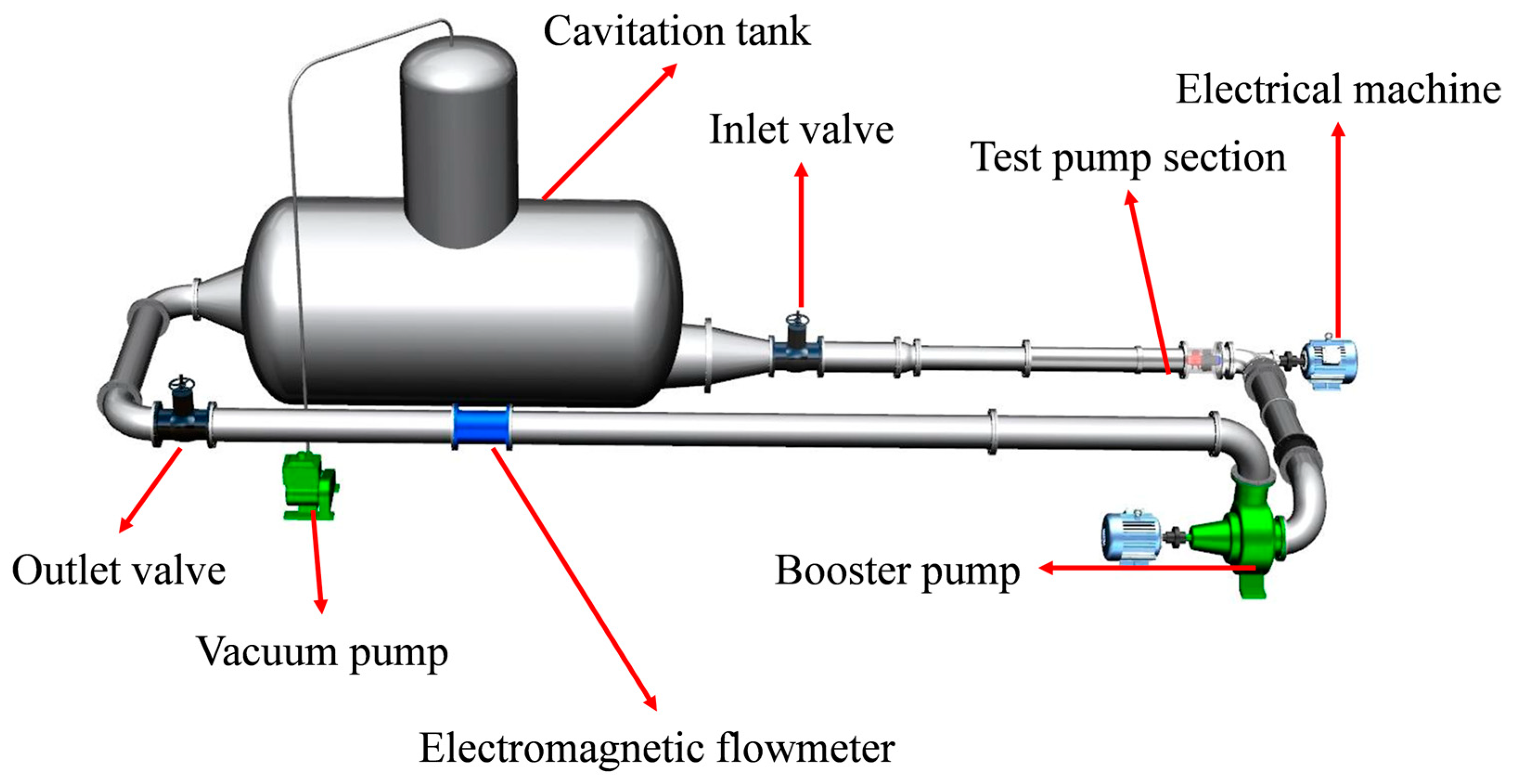
2.2.2. Test Principle and Method
2.3. Experimental Study on Hydraulic Performance
2.4. Numerical Simulation Method of Hump Characteristics
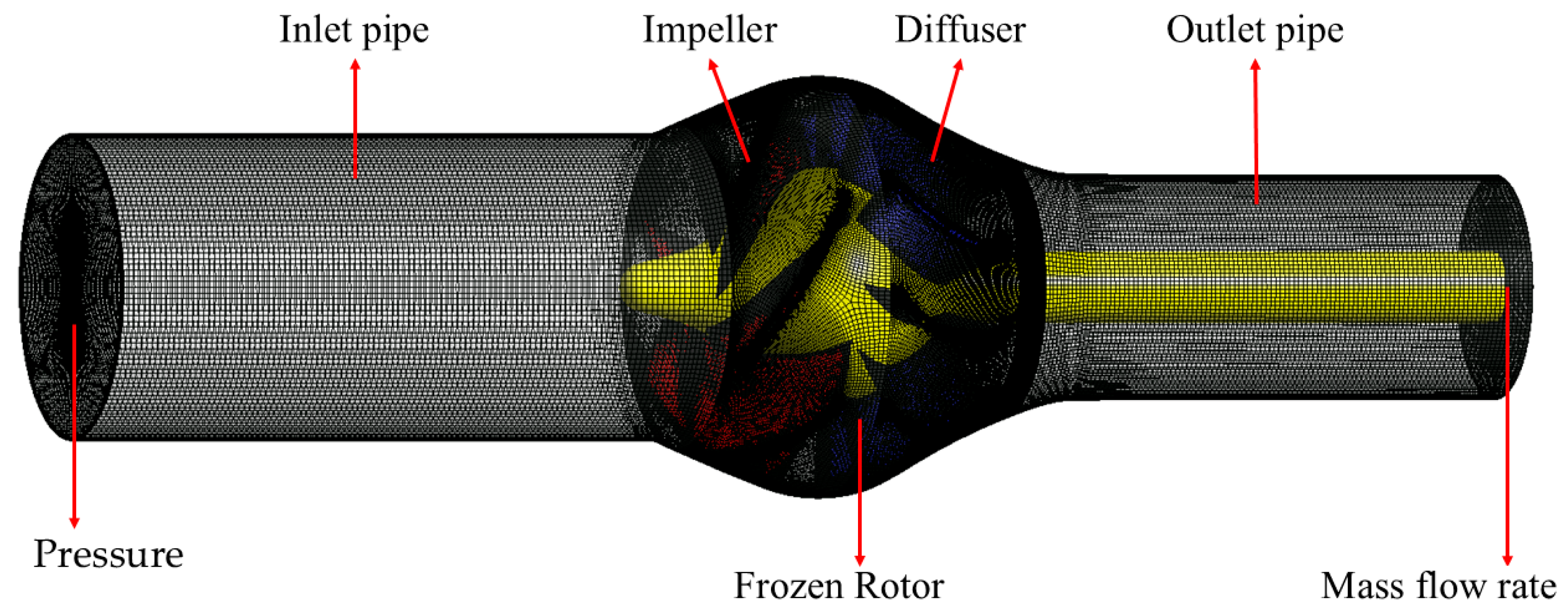
2.4.1. Computational Fluid Domain
2.4.2. Mesh Subdivision
2.4.3. Boundary Conditions
2.4.4. Grid Independence Verification
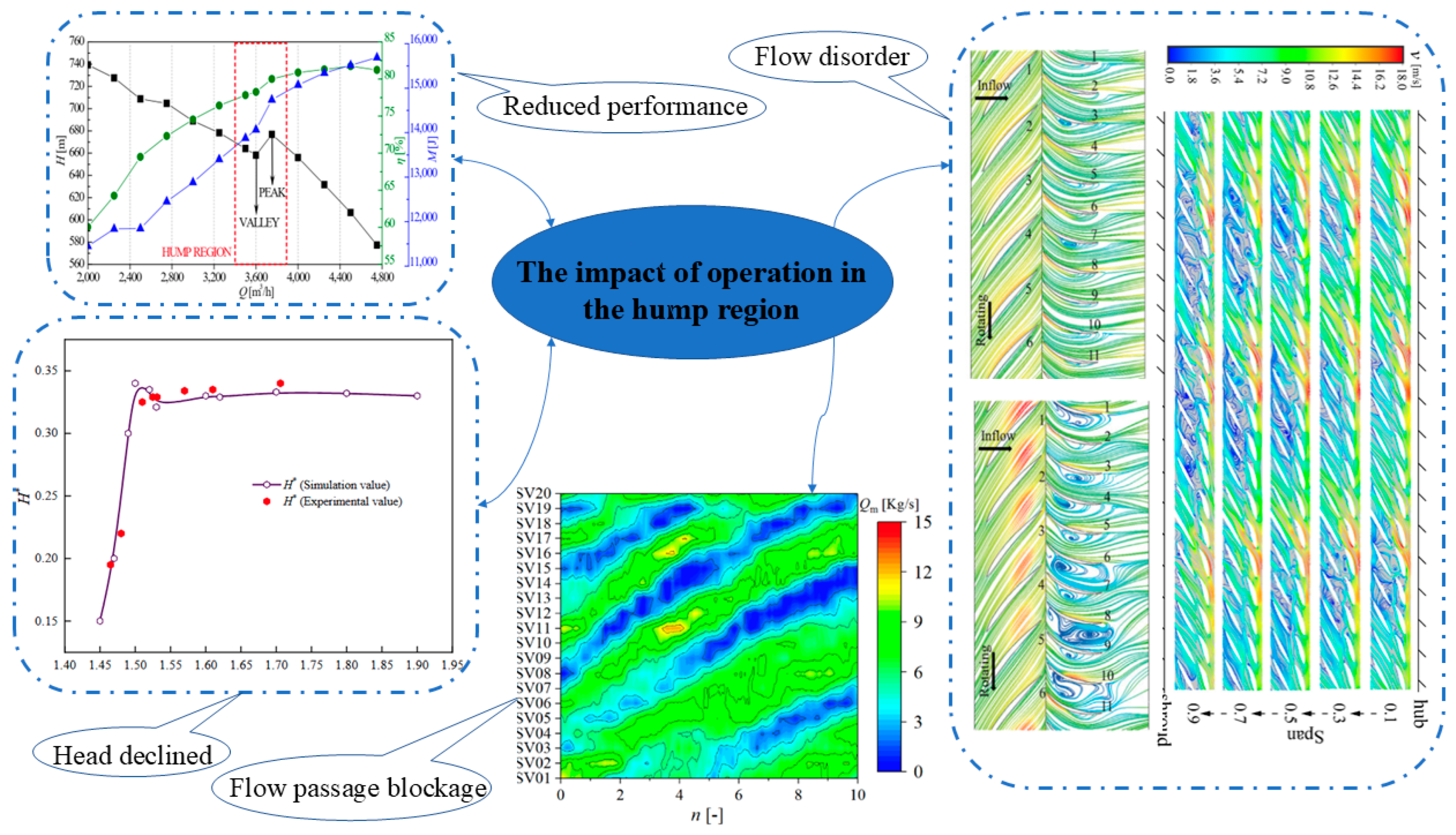
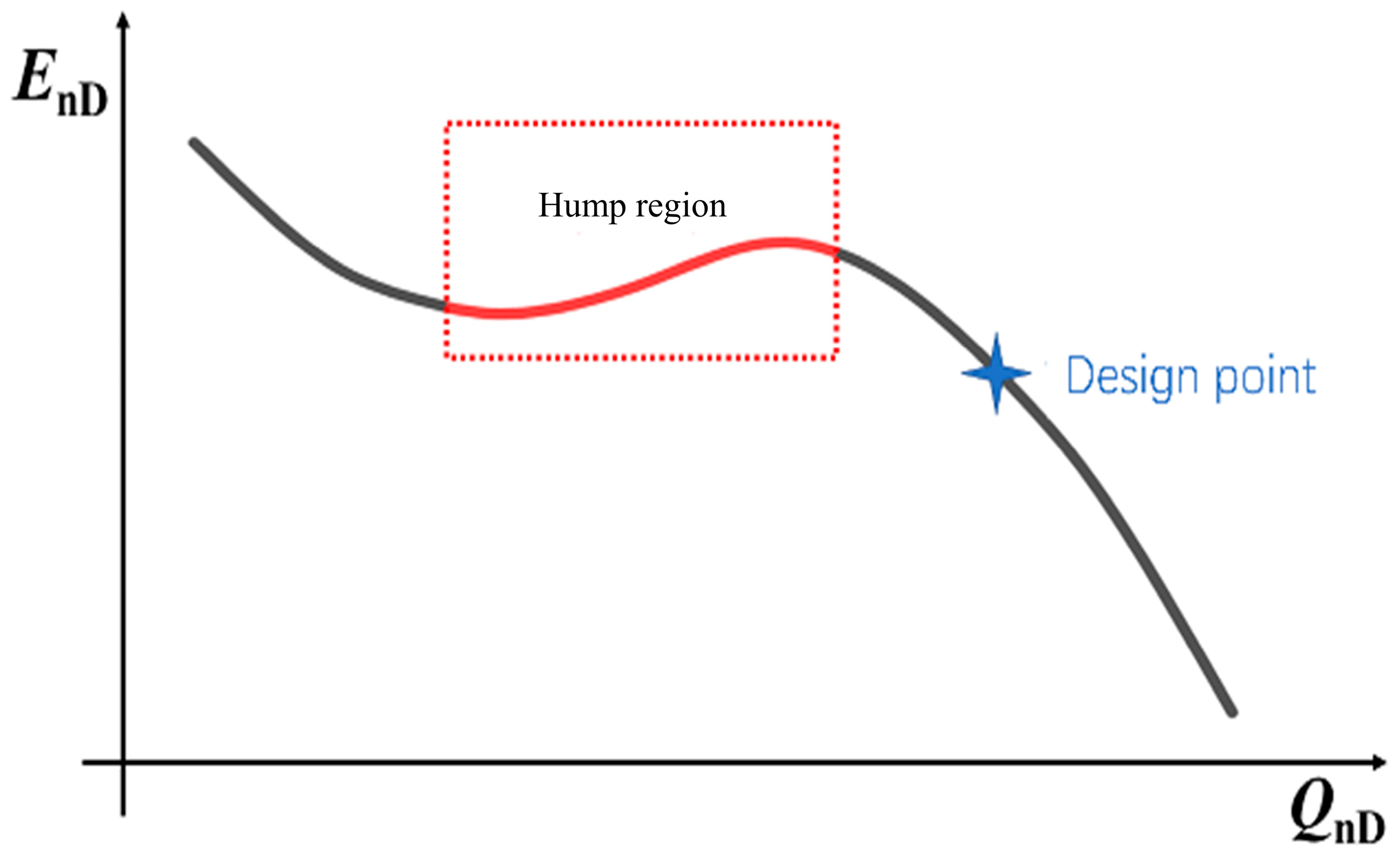
3. Hump Characteristics Analysis
3.1. Hump Characteristics Analysis Method
3.1.1. Energy Characteristic Curve Analysis Method
3.1.2. Entropy Generation Analysis Method
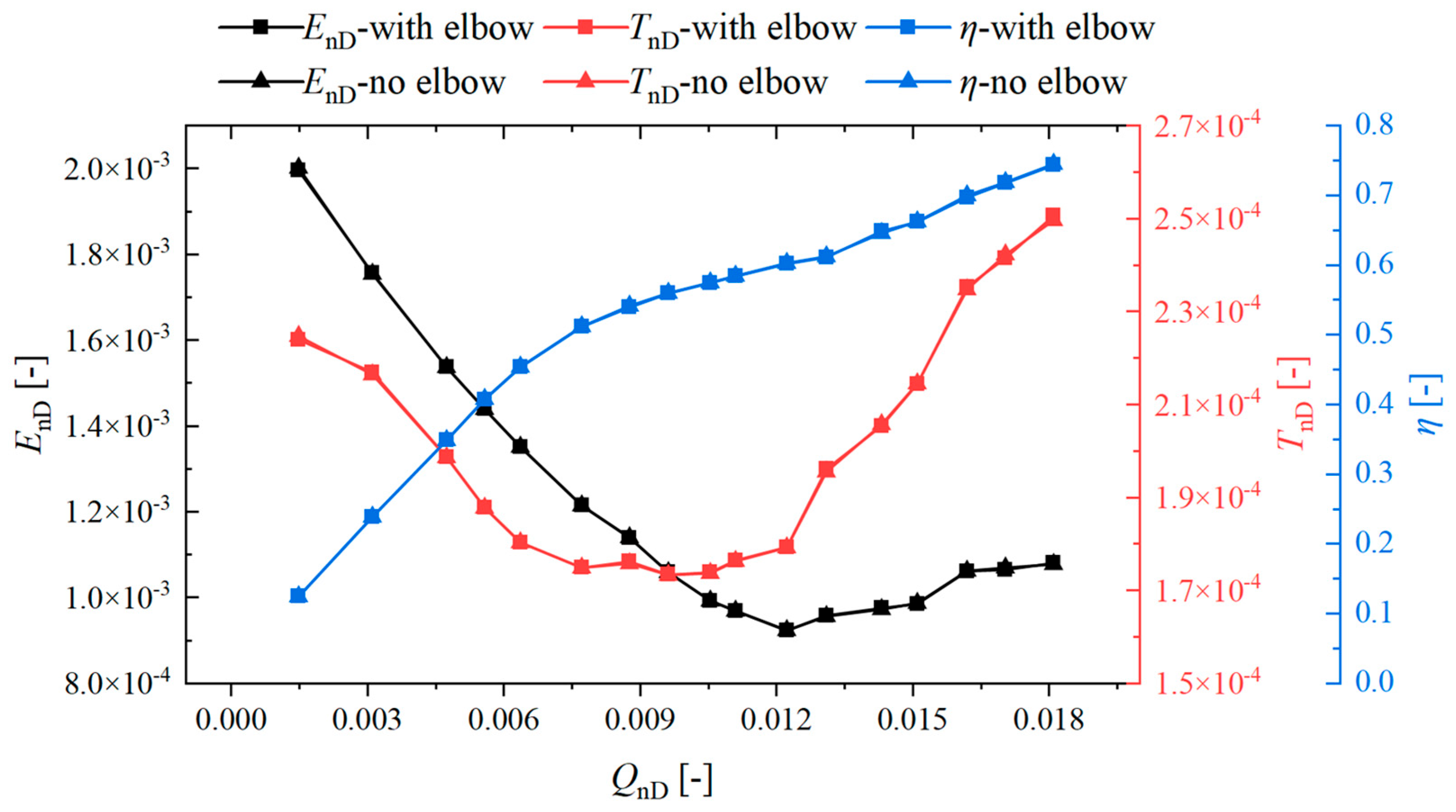
3.2. Energy Characteristic Curve Analysis
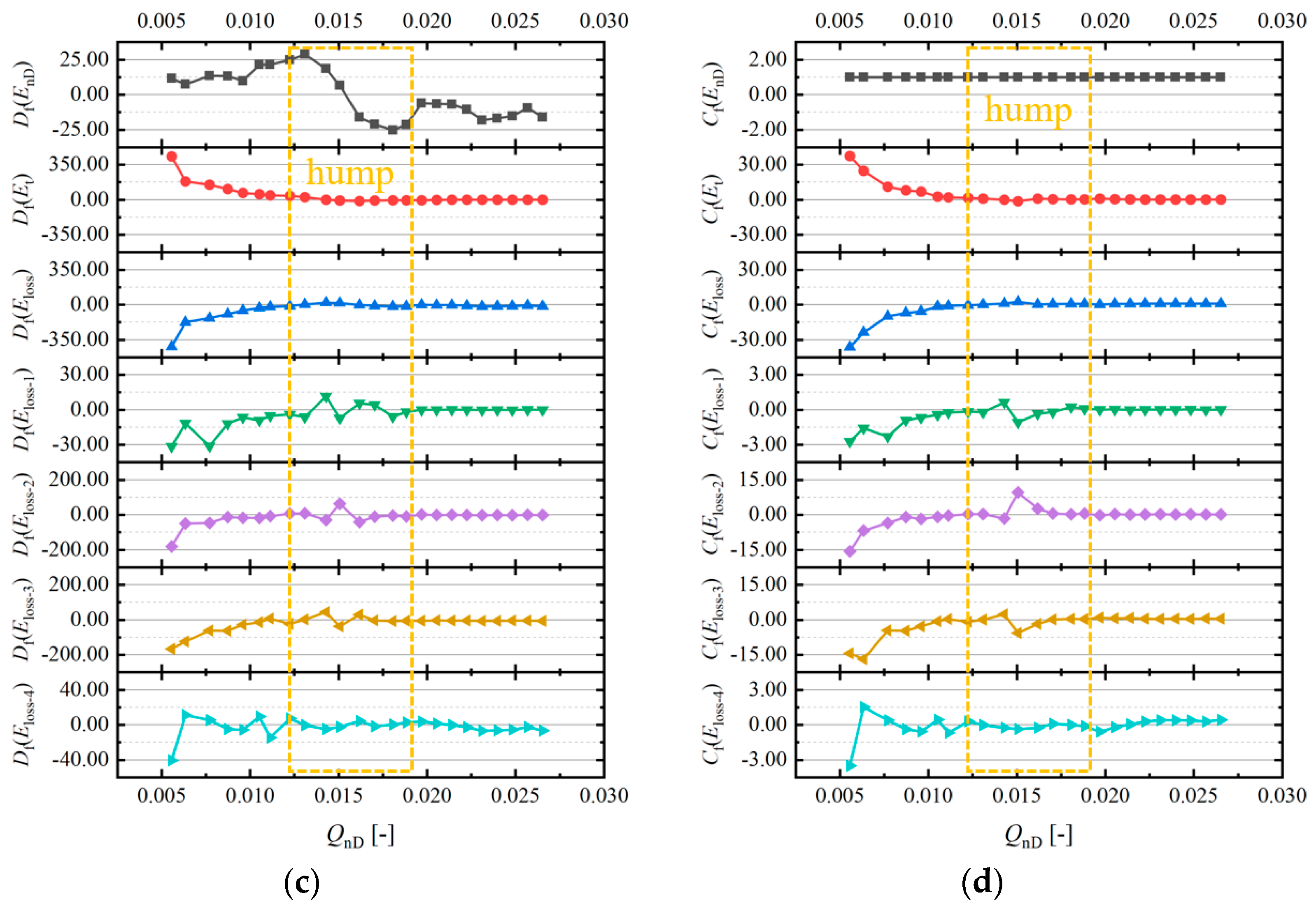
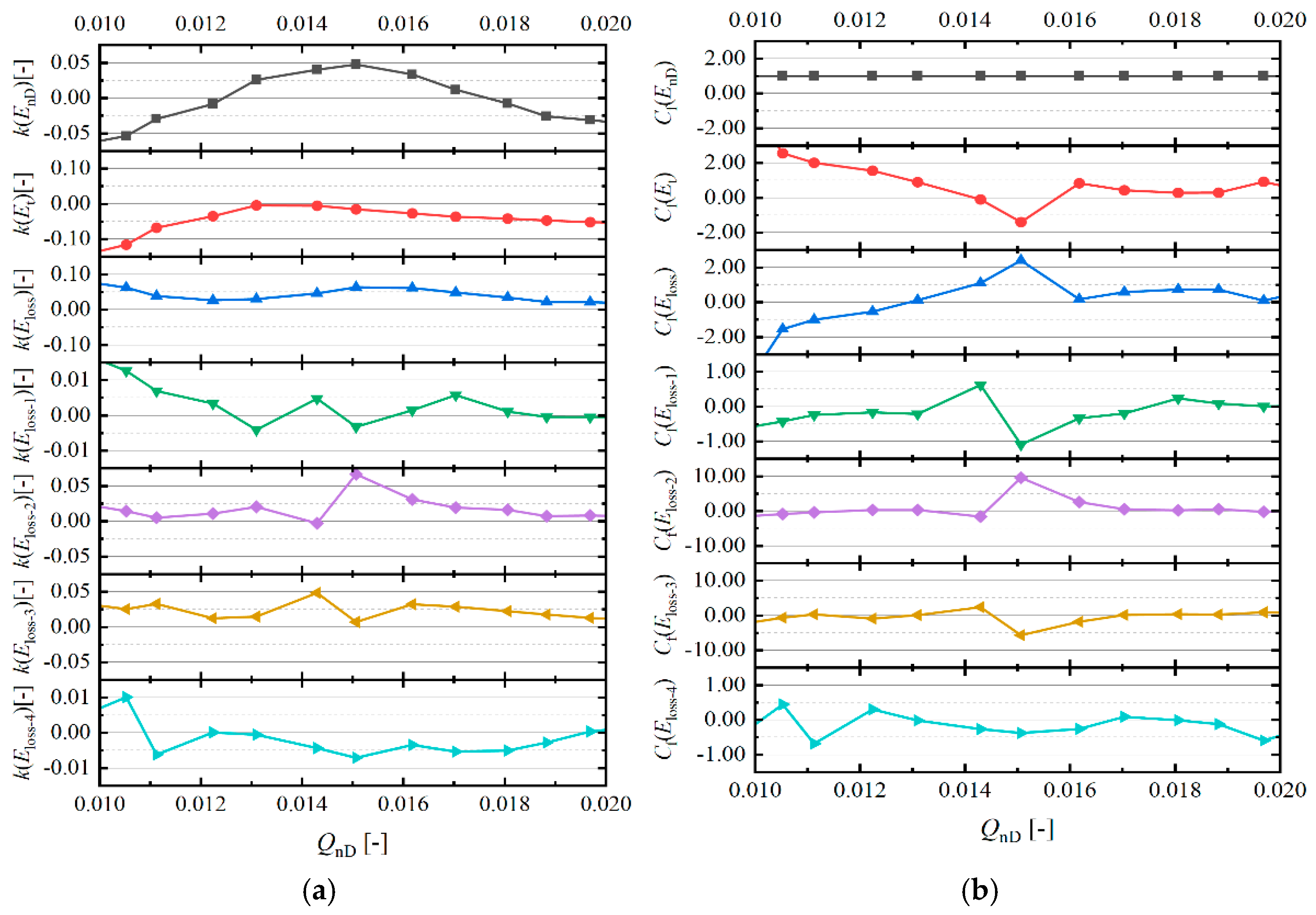
3.3. Analysis of Entropy Generation in Pump
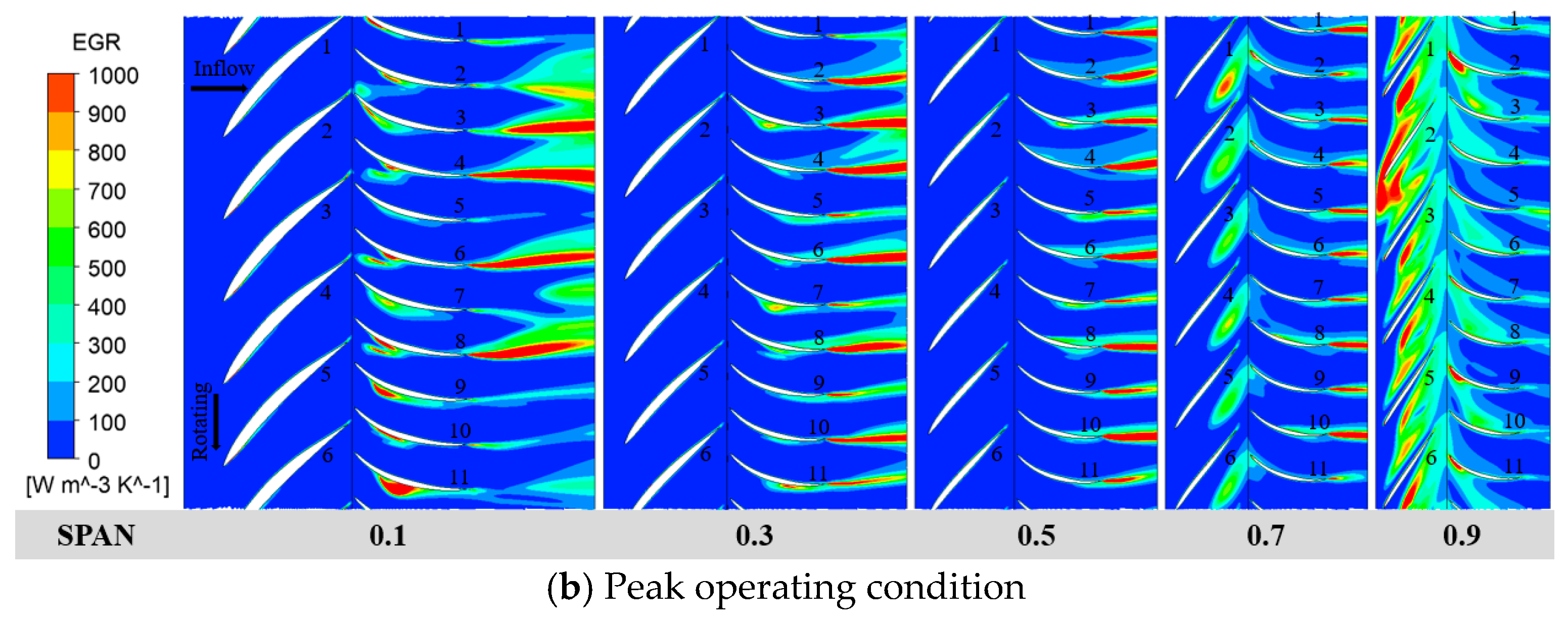
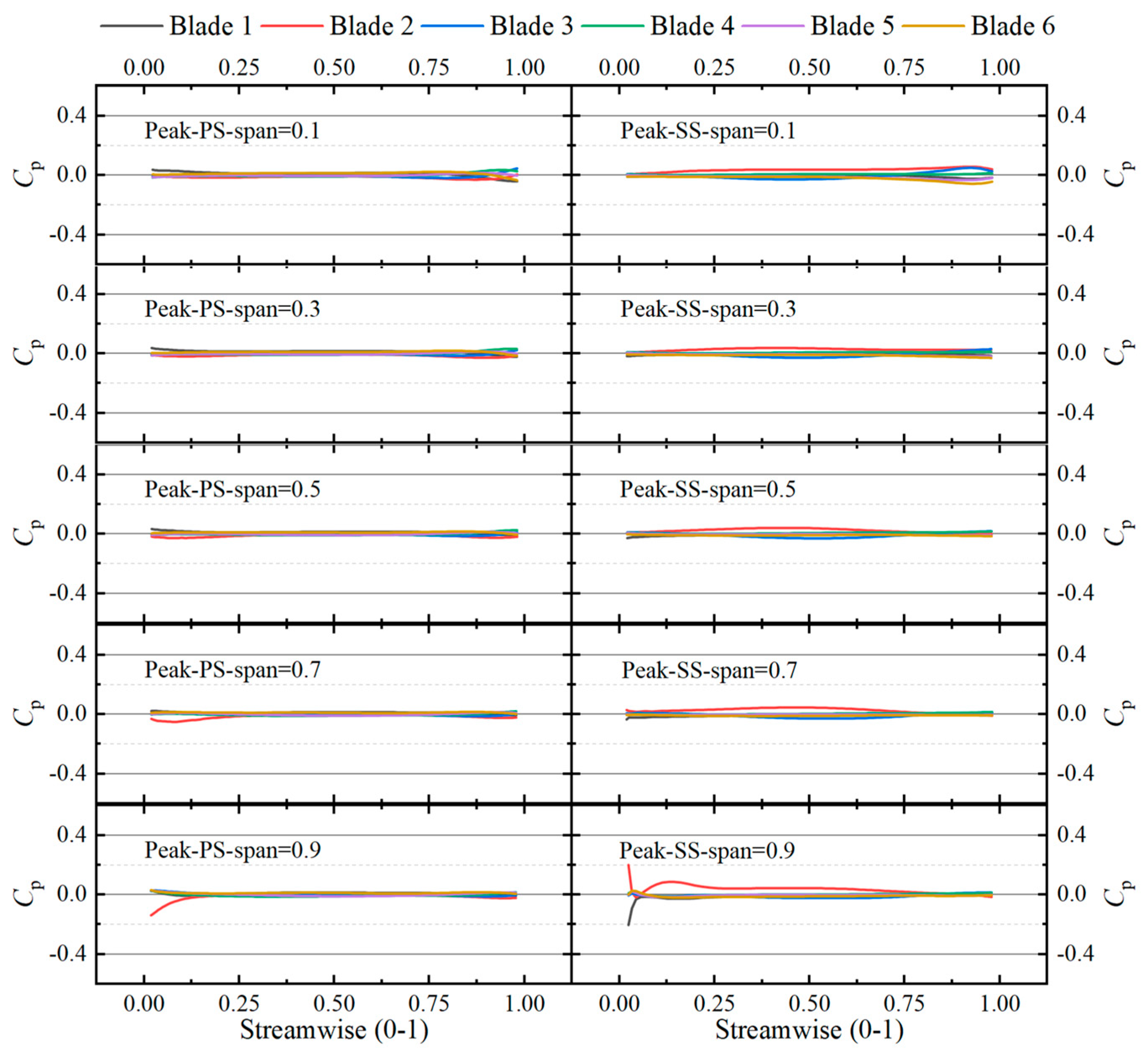
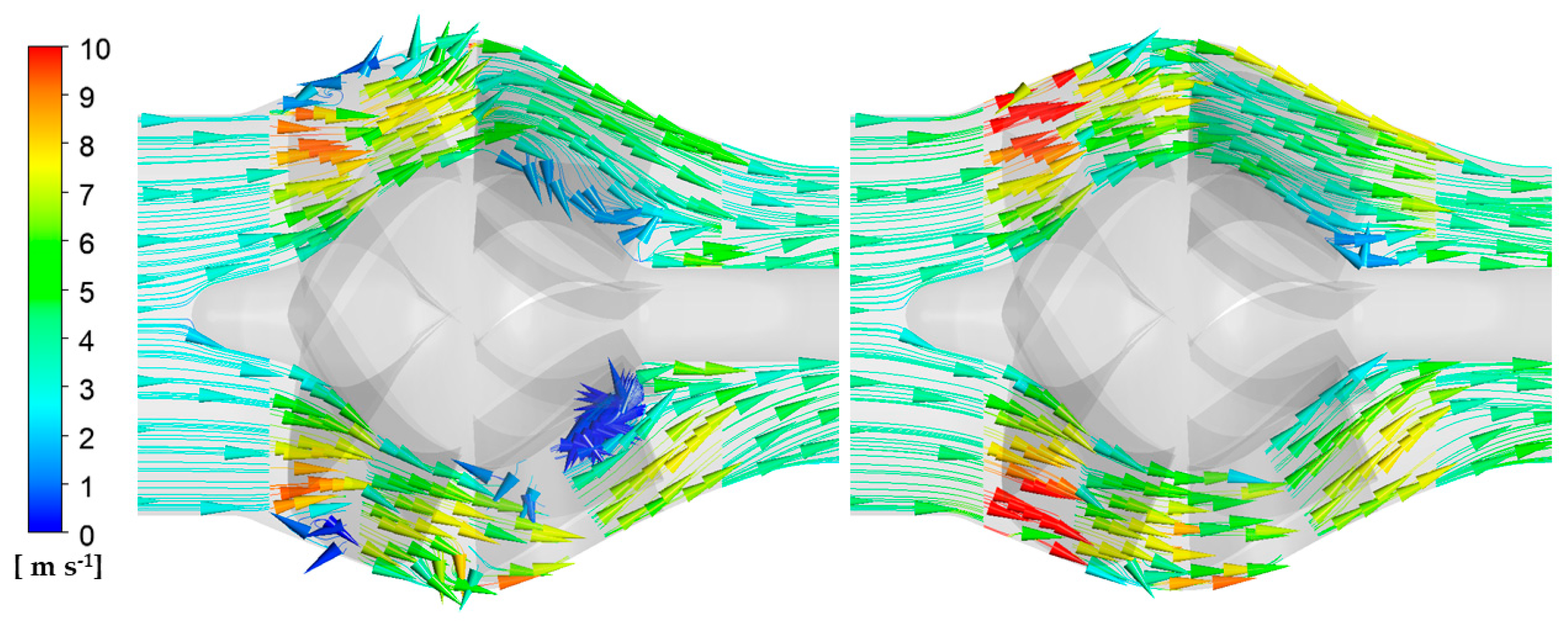
3.4. Analysis of Flow Characteristics in Pump
3.5. The Evolution Process of the Internal Rotating Stall of the Impeller in the Hump Region
4. Experimental Study on Cavitation Structure in Hump Region
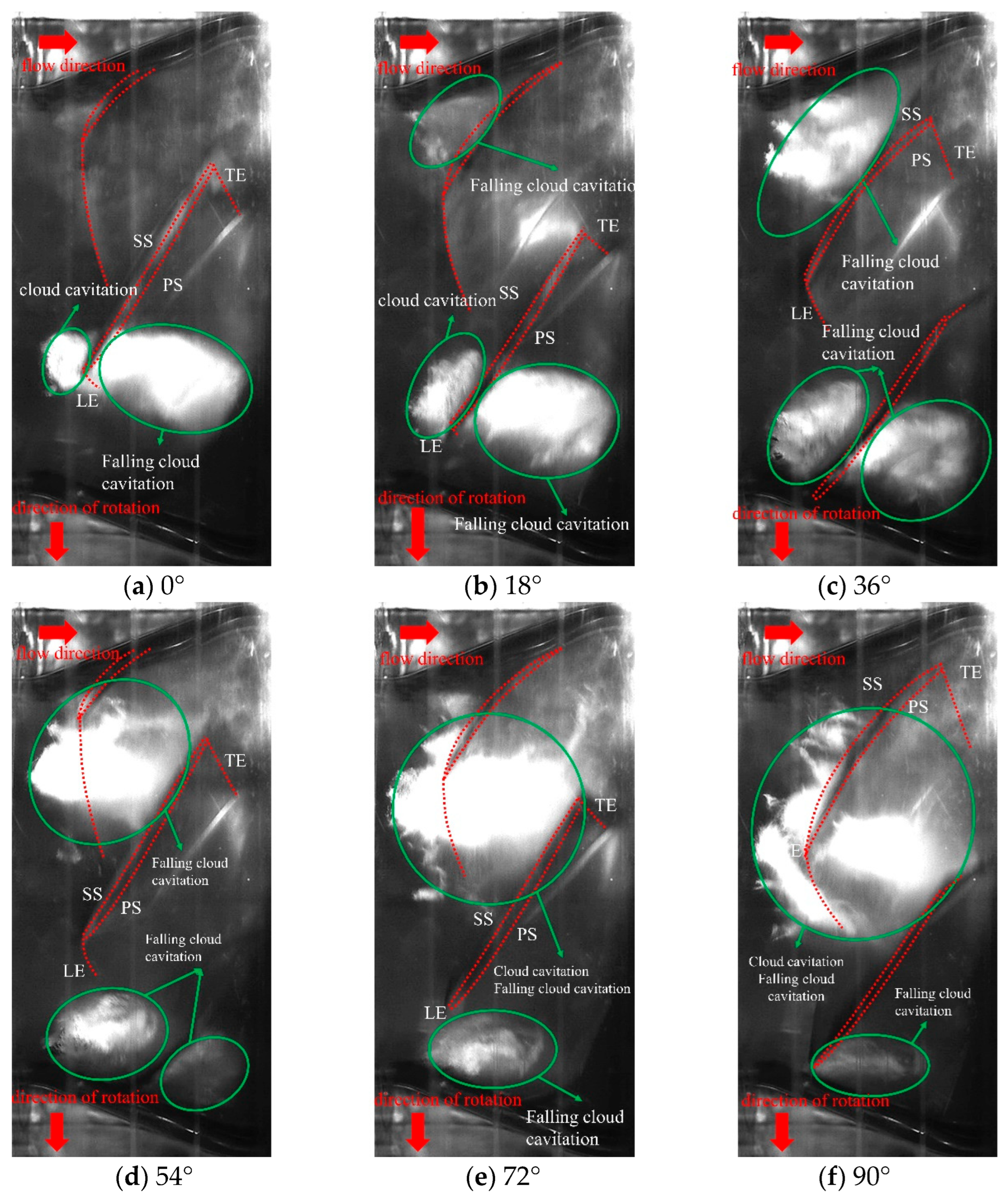
4.1. The Critical Cavitation Stage of the Near Valley Condition
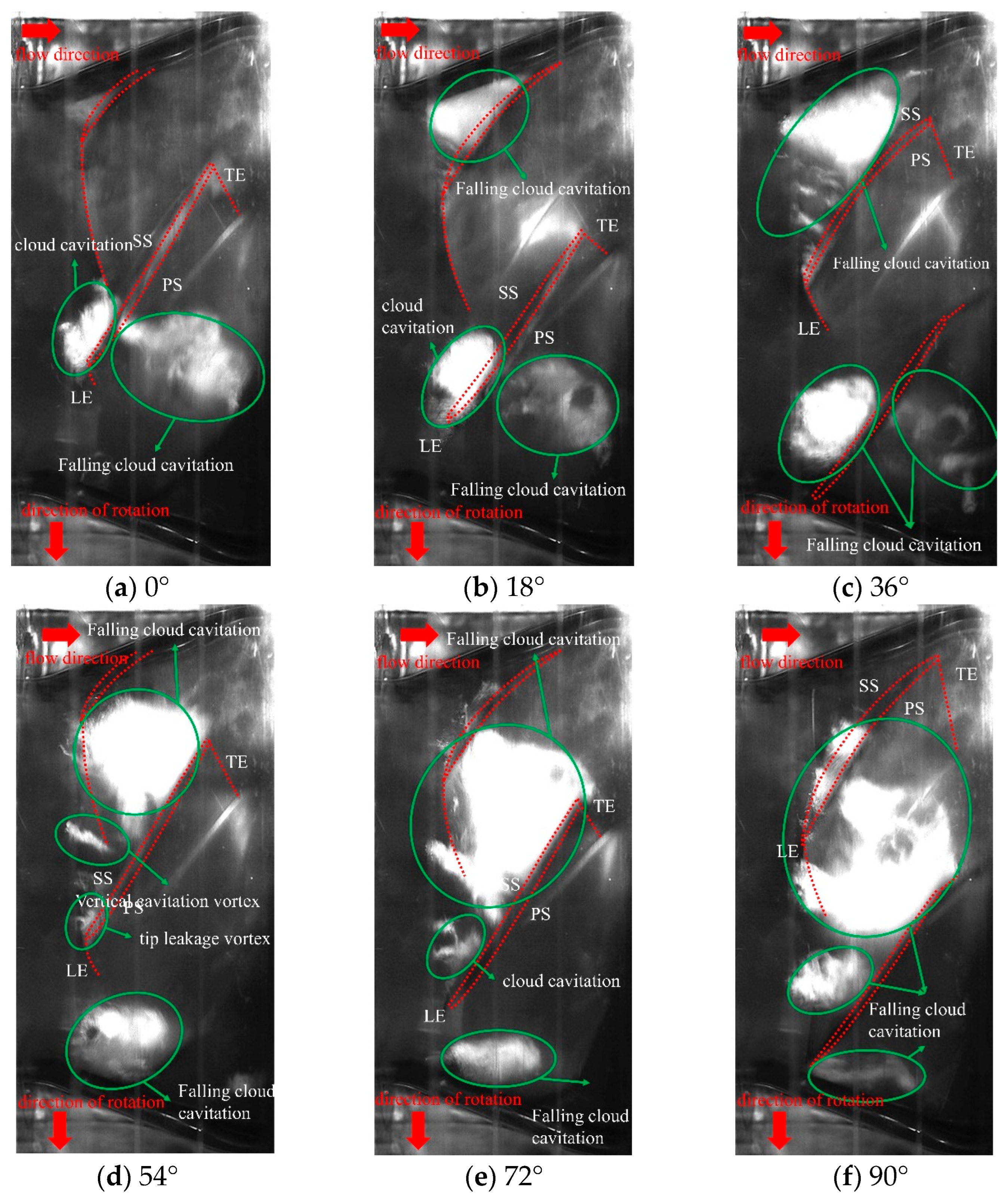
4.2. The Critical Cavitation Stage of the Near Peak Condition
5. Conclusions
- Utilizing a standard axial- or mixed-flow pump test bench and precise testing, this study compared impeller work on unit fluid and internal flow losses during hump formation through model pump energy characteristic curve analysis. The results indicate that at the onset of the hump, the decrease in work performed by the impeller on unit fluid diminishes, while internal fluid loss reduction increases. These factors collectively result in a counter-intuitive increase in the energy characteristic curve, contributing to hump formation.
- Compared to the valley condition, the impeller blades’ pressure surfaces at peak conditions exhibit higher and more uniform pressures, resulting in enhanced work performance. At the valley condition, flow losses primarily arise from the impeller, guide vanes, and draft tube, with guide vanes being the most significant contributors. At peak conditions, the loss distribution changes, showing reduced losses in the impeller and guide vanes, but increased losses in the draft tube. Turbulent dissipation is the main source of flow losses under both conditions. Particularly at the valley condition, substantial backflow vortices and flow separations near the impeller rim and guide vane hub increase flow losses, resulting in reduced head in the waterjet propulsion pump.
- Under valley operating conditions, pressure and velocity distributions show significant variation across impeller channels, accompanied by prominent low-pressure areas that rotate with the impeller. These areas propagate circumferentially slower than the impeller’s rotation, leading to rotational stall, particularly in higher spanwise areas where vortices and flow separations occur. At peak conditions, pressure distribution is more uniform, and streamlines are smoother, with flow separation limited to high-span regions and minimal differences between channels. Overall, valley conditions reveal more intense vortex cores in the impeller and guide vanes, with large-scale vortex cores periodically growing and dissipating, alongside persistent vortices in the guide vane area.
- This study compares the evolution of cavitation flow structures during critical stages under near valley (QnD = 0.014) and peak (QnD = 0.016) operating conditions. The analysis highlights differences in cavitation flows within the pump, with forms like vortex cavitation, cloud cavitation, and vertical cavitation vortices noted at valley operating conditions. At peak conditions, cavitation forms are similar to those at valley conditions, but larger blade tip leakage vortices occur, attributed to increased pressure differences between the impeller blades’ pressure and suction sides.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Zhou, L.; Shi, W.-D.; Ji, L.; Yang, Y.; Zhao, X. PIV experiment of the unsteady flow field in mixed-flow pump under part loading condition. Exp. Therm. Fluid Sci. 2017, 83, 191–199. [Google Scholar] [CrossRef]
- van Esch, B.P.M.; Kruyt, N.P. Hydraulic performance of a mixed-flow pump: Unsteady inviscid computations and loss models. J. Fluids Eng.-Trans. ASME 2001, 123, 256–264. [Google Scholar] [CrossRef]
- Heo, M.-W.; Kim, K.-Y.; Kim, J.-H.; Choi, Y.S. High-efficiency design of a mixed-flow pump using a surrogate model. J. Mech. Sci. Technol. 2016, 30, 541–547. [Google Scholar] [CrossRef]
- Suh, J.-W.; Yang, H.-M.; Kim, Y.-I.; Lee, K.-Y.; Kim, J.-H.; Joo, W.-G.; Choi, Y.-S. Multi-objective optimization of a high efficiency and suction performance for mixed-flow pump impeller. Eng. Appl. Comput. Fluid Mech. 2019, 13, 744–762. [Google Scholar] [CrossRef]
- Yun, L. Study on the Hydraulic Optimization Design Method and Cavitation of Waterjet Pump. Ph.D. Dissertation, Shanghai Jiao Tong University, Shanghai, China, 2018. [Google Scholar]
- Yun, L.; Chao, F.; Luyi, W.; Dezhong, W.; Youlin, C.; Rongsheng, Z. Experiment on cavitation flow in critical cavitation condition of water-jet propulsion pump. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 1512–1518. [Google Scholar]
- Long, Y.; An, C.; Zhu, R.; Chen, J. Research on hydrodynamics of high velocity regions in a water-jet pump based on experimental and numerical calculations at different cavitation conditions. Phys. Fluids 2021, 33, 045124. [Google Scholar] [CrossRef]
- Niazi, S.; Stein, A.; Sankar, L. Numerical studies of stall and surge alleviation in a high-speed transonic fan rotor. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000; p. 225. [Google Scholar]
- Shahriyari, M.J.; Khaleghi, H.; Heinrich, M. A Model for Stall and Surge in Low-Speed Contra-Rotating Fans. J. Eng. Gas Turbines Power-Trans. Asme 2019, 141, 081009. [Google Scholar] [CrossRef]
- Ye, W.; Ikuta, A.; Chen, Y.; Miyagawa, K.; Luo, X. Numerical simulation on role of the rotating stall on the hump characteristic in a mixed fl ow pump using modi fi ed partially averaged Navier-Stokes model. Renew. Energy 2020, 166, 91–107. [Google Scholar] [CrossRef]
- Yang, J.; Yuan, S.; Pavesi, G.; Chun, L.; Zhou, Y. Study of hump instability phenomena in pump turbine at large partial flow conditions on pump mode. Jixie Goneheng Xuebao 2016, 52, 170–178. [Google Scholar] [CrossRef]
- Pavesi, G.; Yang, J.; Cavazzini, G.; Ardizzon, G. Experimental analysis of instability phenomena in a high-head reversible pump-turbine at large partial flow condition. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Madrid, Spain, 23–26 March 2015. [Google Scholar]
- Pavesi, G.; Cavazzini, G.; Ardizzon, G. Numerical Analysis of the Transient Behaviour of a Variable Speed Pump-Turbine during a Pumping Power Reduction Scenario. Energies 2016, 9, 534. [Google Scholar] [CrossRef]
- Jese, U.; Fortes-Patella, R.; Dular, M. Numerical study of pump-turbine instabilities under pumping mode off-design conditions. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference (AJK-FED), Seoul, Republic of Korea, 26–31 July 2015. [Google Scholar]
- Braun, O.; Kueny, J.L.; Avellan, F. Numerical analysis of flow phenomena related to the unstable energy-discharge characteristic of a pump-turbine in pump mode. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Houston, TX, USA, 19–23 June 2005; pp. 1075–1080. [Google Scholar]
- Li, D.; Zhu, Y.; Lin, S.; Gong, R.; Wang, H.; Luo, X. Cavitation effects on pressure fluctuation in pump-turbine hump region. J. Energy Storage 2022, 47, 103936. [Google Scholar] [CrossRef]
- Long, Y.; Tian, C.; Li, Y.; Zhong, J. Internal Flow Mechanism of the Water jet Pump at Crest and Trough Conditions in the Hump Region. Ship Boat 2023, 34, 56. [Google Scholar]
- Yang, J.; Feng, X.; Liu, X.; Peng, T.; Chen, Z.; Wang, Z. The suppression of hump instability inside a pump turbine in pump mode using water injection control. Processes 2023, 11, 1647. [Google Scholar] [CrossRef]
- Zhu, R.; Shi, W.; Gan, G.; Li, H.; Yang, D.; Duan, Y.; Fu, Q. Transient Hydrodynamic Characteristics of a High-Speed Axial Flow Water-Jet Pump during Variable Speed Process. J. Mar. Sci. Eng. 2023, 11, 1965. [Google Scholar] [CrossRef]
- Han, H.; Long, Y.; Zhong, J. Research on the internal flow difference between peak and valley conditions of water jet propulsion pump during working at hump region. J. Mar. Sci. Eng. 2024, 12, 258. [Google Scholar] [CrossRef]
- Long, Y.; Zheng, Y.; Han, H.; Zhong, J.; Zhu, R. Research on hydraulic optimization design method of water-jet propulsion pump considering hump index. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 377. [Google Scholar] [CrossRef]
- Long, Y.; Zhou, Z.; Zhong, J.; Han, H. Experimental Study on Evolution of Cavitation Flow Structure in Hump Region of Waterjet Pump. J. Appl. Fluid Mech. 2024, 17, 2734–2744. [Google Scholar]
- Kock, F.; Herwig, H.J.I.J.O.H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]










| Parameter | Numerical Value |
|---|---|
| Impeller inlet diameter | 250 mm |
| Number of impeller blades | 6 |
| Number of guide vanes | 11 |
| Exit diameter | 183 mm |
| Maximum design speed | 1500 r/min |
| Design point flow at the highest design speed | 1660 m3/h |
| Design point head at the highest design speed | ≥17 m |
| Tip clearance | 1 mm |
| Unit | Wall Shear | Wall Minimum | Wall Maximum | Wall Average | Component Average |
|---|---|---|---|---|---|
| Inlet pipe | Pipe wall | 1.083 | 15.882 | 4.110 | 4.151 |
| Propeller cap | 1.168 | 17.727 | 6.549 | ||
| Impeller | Hub | 0.038 | 4.739 | 2.004 | 3.504 |
| Blade | 0.051 | 15.673 | 4.212 | ||
| Wheel rim | 0.131 | 10.202 | 3.198 | ||
| Diffuser | Hub | 0.049 | 7.150 | 2.075 | 3.714 |
| Blade | 0.041 | 10.330 | 4.035 | ||
| Wheel rim | 0.131 | 10.202 | 3.937 | ||
| Outlet pipe | Axis | 5.495 | 12.737 | 8.000 | 7.518 |
| Pipe wall | 5.323 | 9.857 | 7.368 |
| Settings Item | Parameters |
|---|---|
| Inlet boundary condition | Pressure |
| Outlet boundary condition | Mass flow rate |
| Wall boundary condition | No-slip wall |
| Turbulence model | SST k-ω |
| Interface between static and dynamic | Frozen rotor |
| Convergent residuals (math.) | 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Long, Y.; Yin, H.; Tian, C.; Zhong, J. Research on Energy Dissipation Mechanism of Hump Characteristics Based on Entropy Generation and Coupling Excitation Mechanism of Internal Vortex Structure of Waterjet Pump at Hump Region. J. Mar. Sci. Eng. 2025, 13, 442. https://doi.org/10.3390/jmse13030442
Liu M, Long Y, Yin H, Tian C, Zhong J. Research on Energy Dissipation Mechanism of Hump Characteristics Based on Entropy Generation and Coupling Excitation Mechanism of Internal Vortex Structure of Waterjet Pump at Hump Region. Journal of Marine Science and Engineering. 2025; 13(3):442. https://doi.org/10.3390/jmse13030442
Chicago/Turabian StyleLiu, Min, Yun Long, Hong Yin, Chenbiao Tian, and Jinqing Zhong. 2025. "Research on Energy Dissipation Mechanism of Hump Characteristics Based on Entropy Generation and Coupling Excitation Mechanism of Internal Vortex Structure of Waterjet Pump at Hump Region" Journal of Marine Science and Engineering 13, no. 3: 442. https://doi.org/10.3390/jmse13030442
APA StyleLiu, M., Long, Y., Yin, H., Tian, C., & Zhong, J. (2025). Research on Energy Dissipation Mechanism of Hump Characteristics Based on Entropy Generation and Coupling Excitation Mechanism of Internal Vortex Structure of Waterjet Pump at Hump Region. Journal of Marine Science and Engineering, 13(3), 442. https://doi.org/10.3390/jmse13030442