Three-Dimensional In Situ Stress Distribution in a Fault Fracture Reservoir, Linnan Sag, Bohai Bay Basin
Abstract
1. Introduction
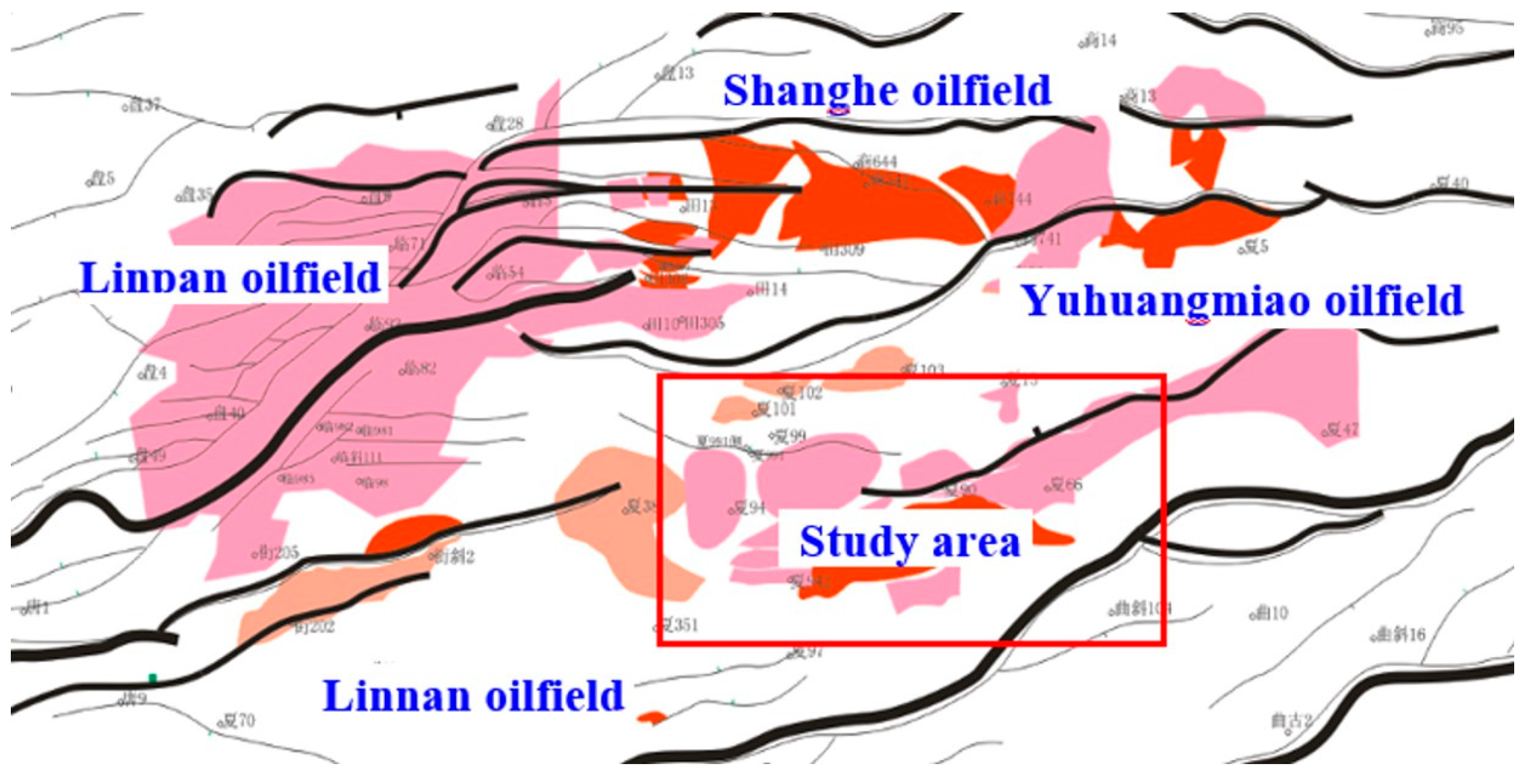
2. Geological Profile of the Study Area
2.1. Structural Characteristics of the Study Area
2.2. Sedimentary Characteristics of the Study Area
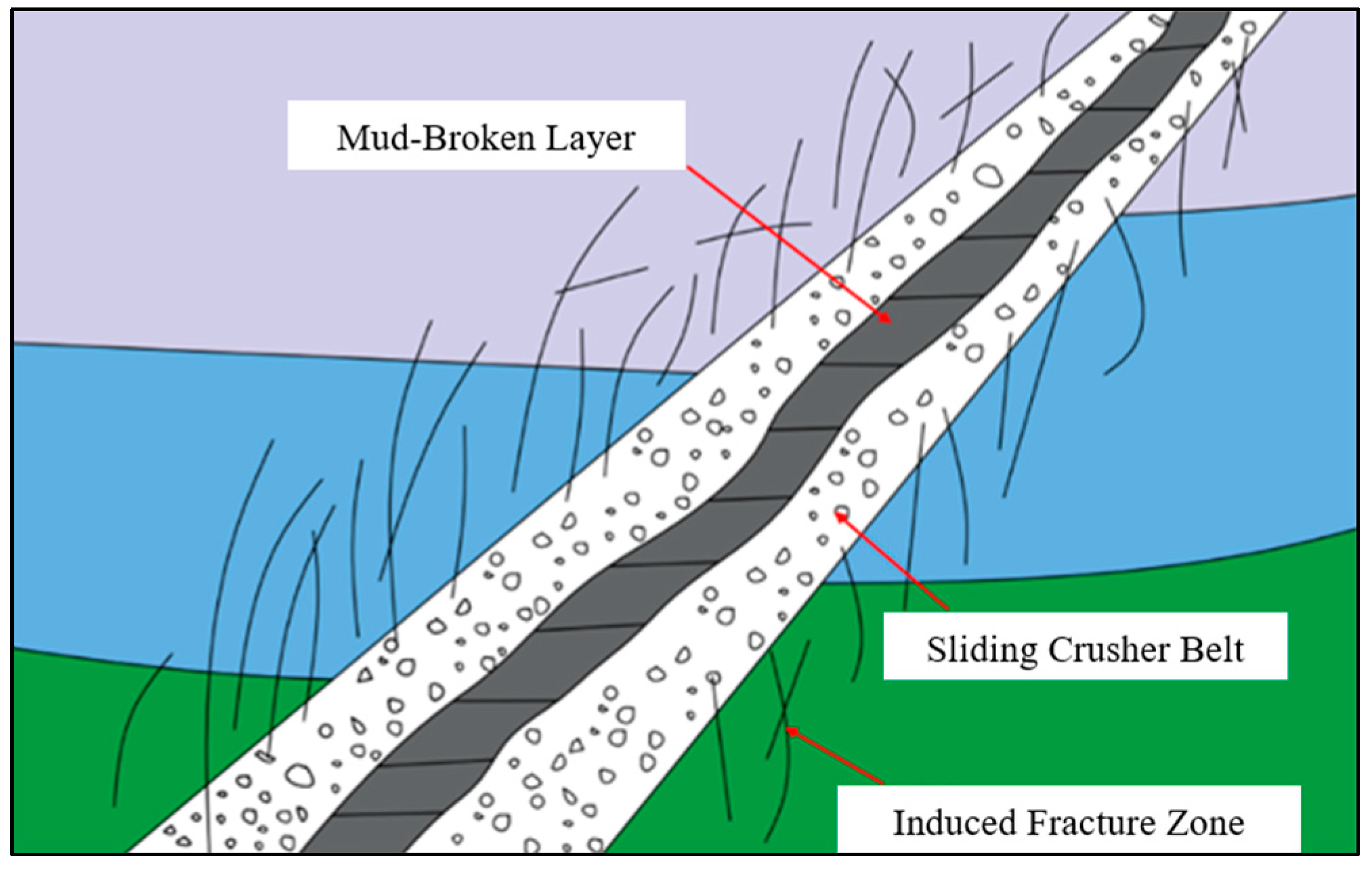
2.3. Characteristics of Reservoir Space in the Study Area
3. Geomechanical Modeling of Fault Fracture Body Reservoirs
3.1. Skeleton Modeling of the Fault Fracture Body
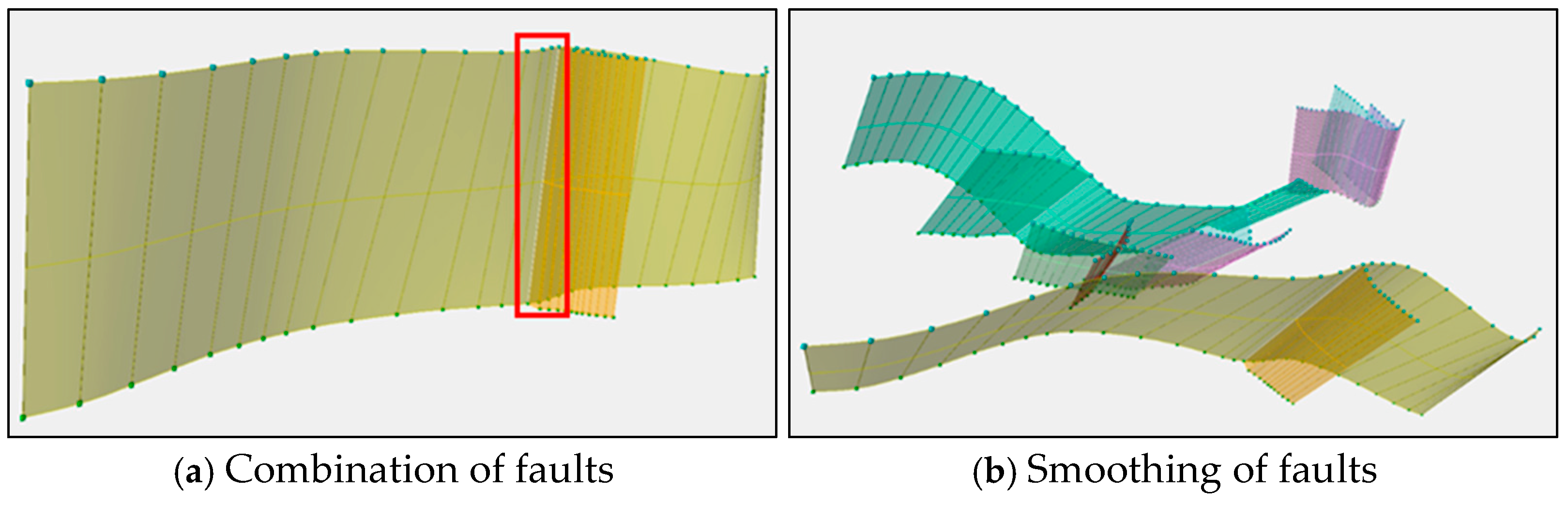
3.2. Principles of Fault Model Optimization
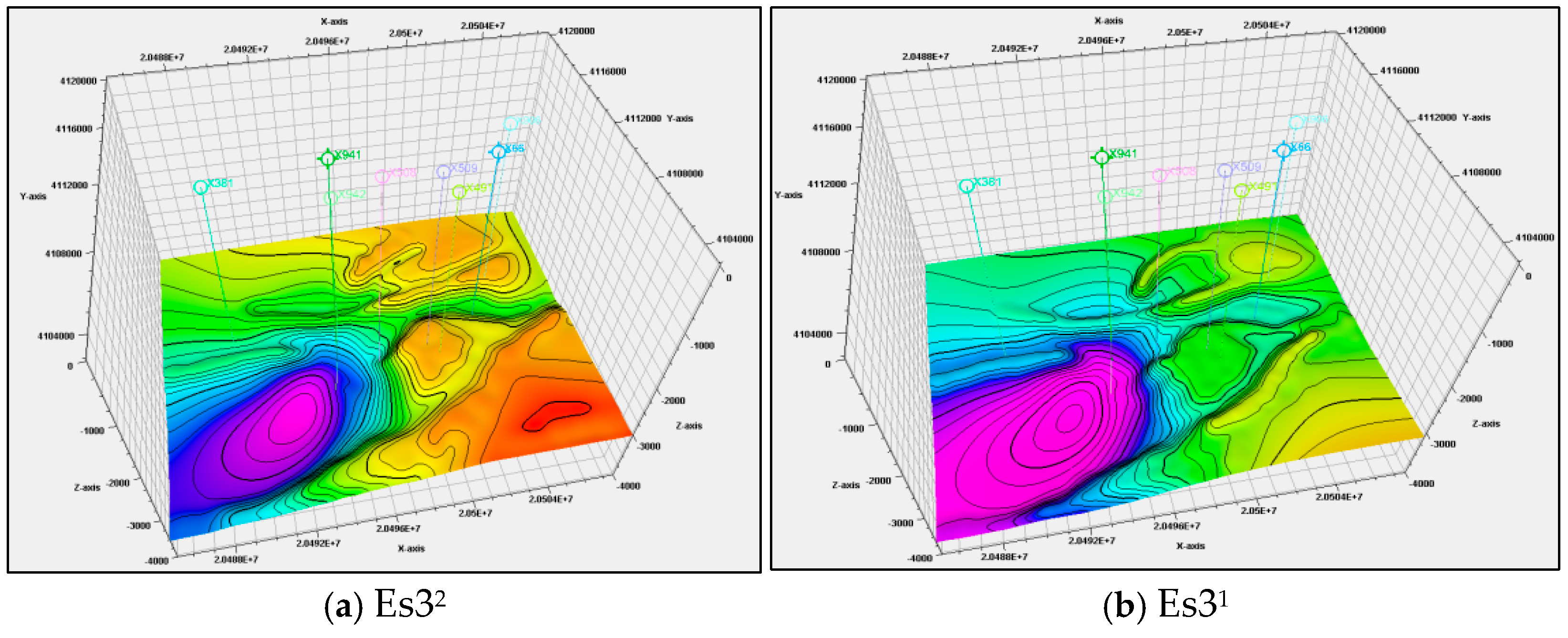
3.3. Inverse Reconstruction of Fault Fracture Body Reservoir Models
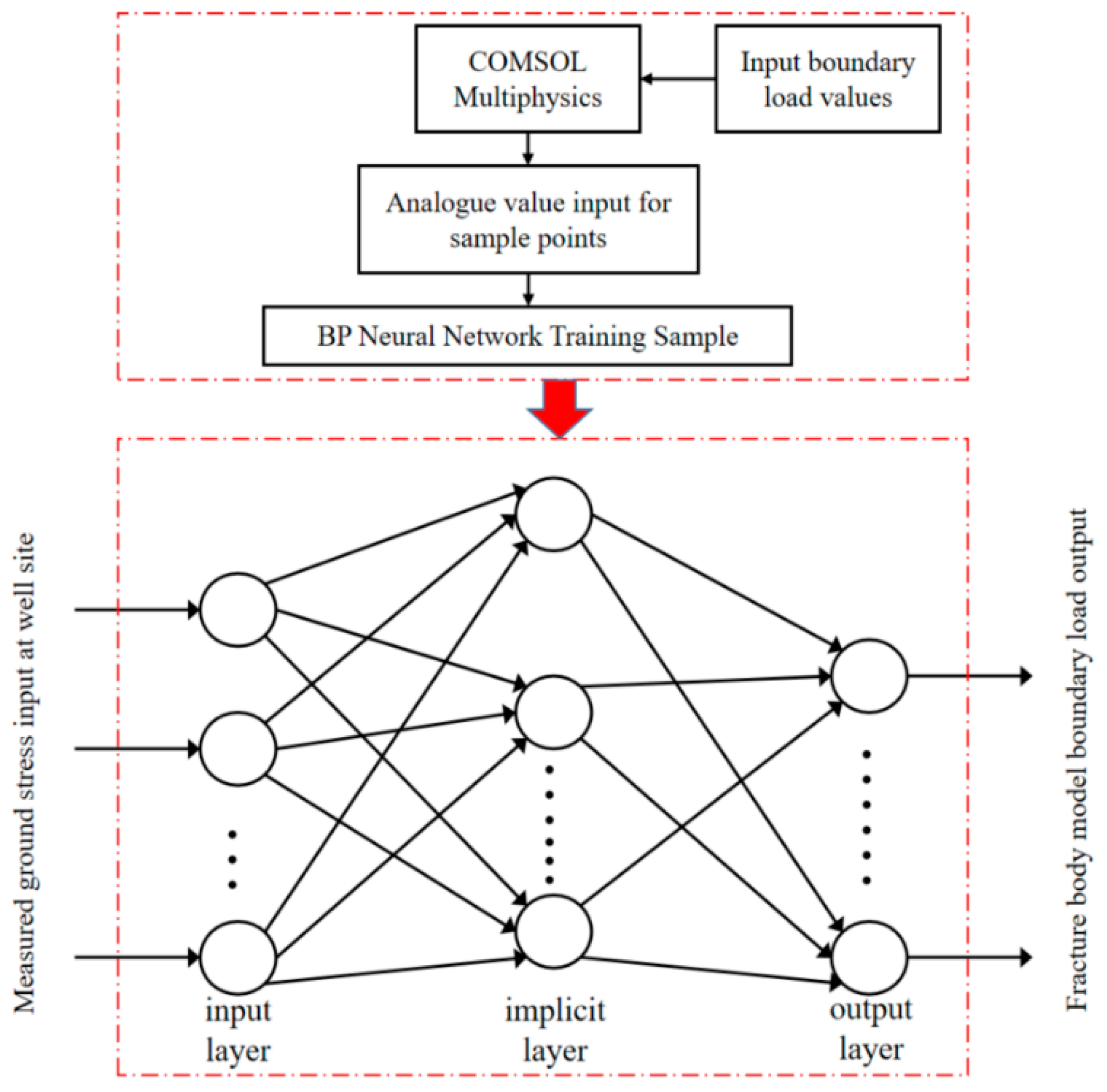
4. Machine Learning-Based Inversion of Boundary Conditions in the Study Area
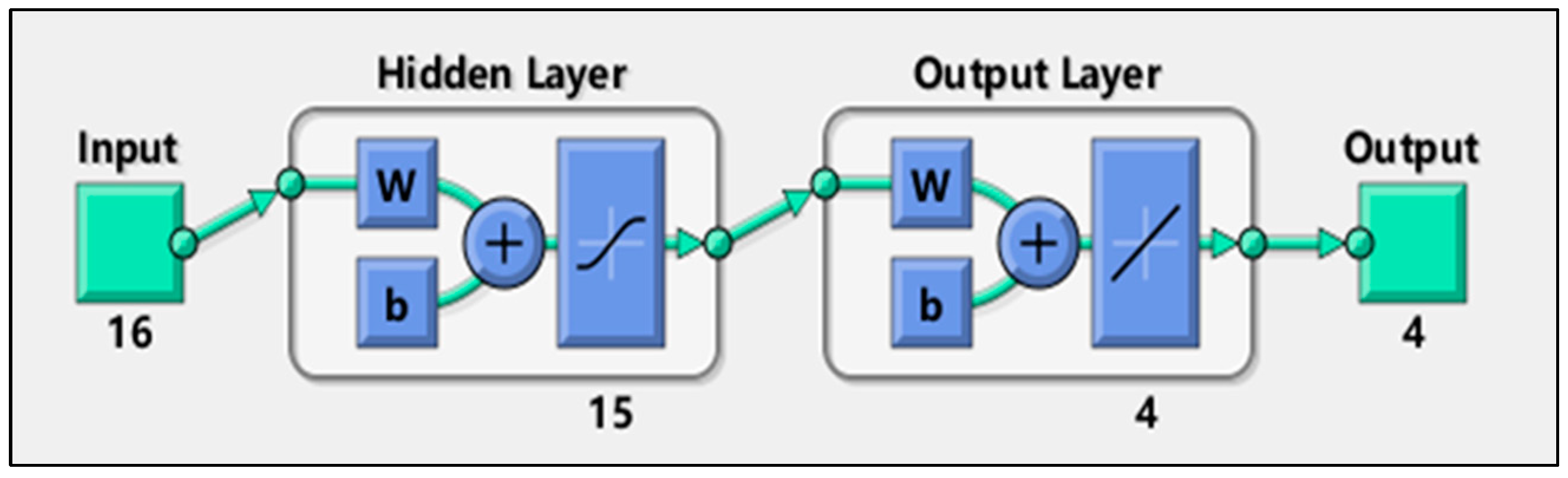
4.1. Principles of Machine Learning Model Prediction
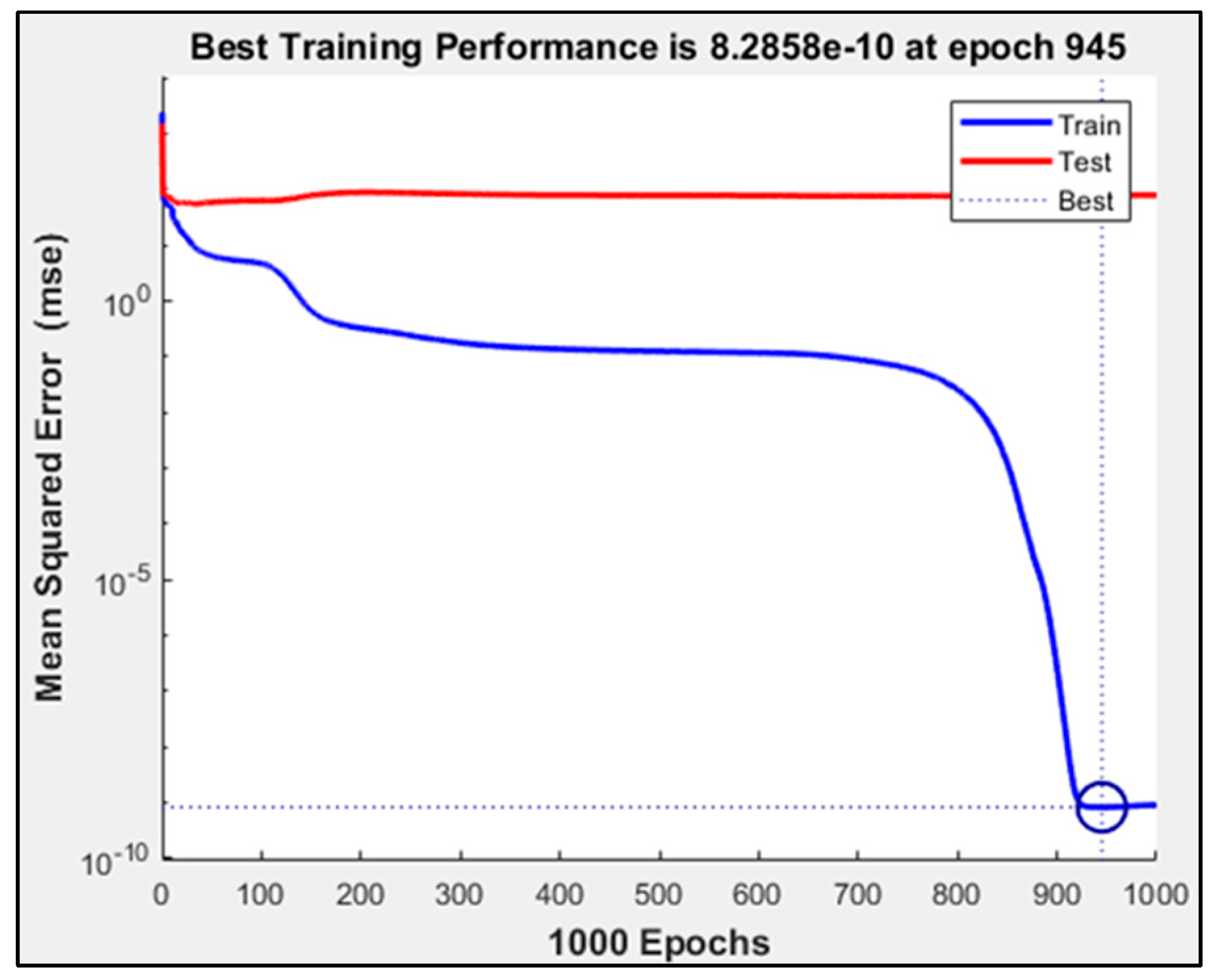
4.2. Inversion of Boundary Conditions
5. Three-Dimensional In Situ Stress Field Distribution of Fracture Reservoirs
5.1. Coupled Flow–Solid Control Equations
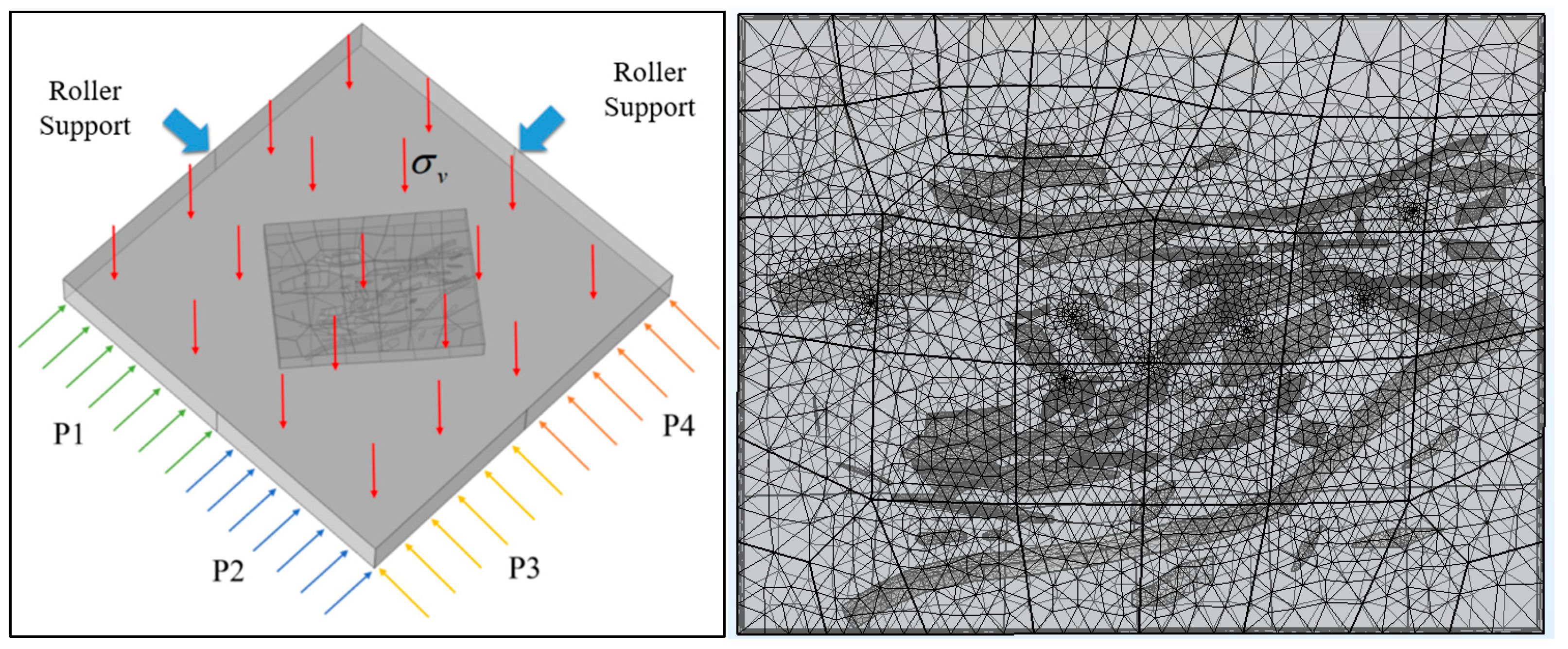
5.2. Model Parameter Setting
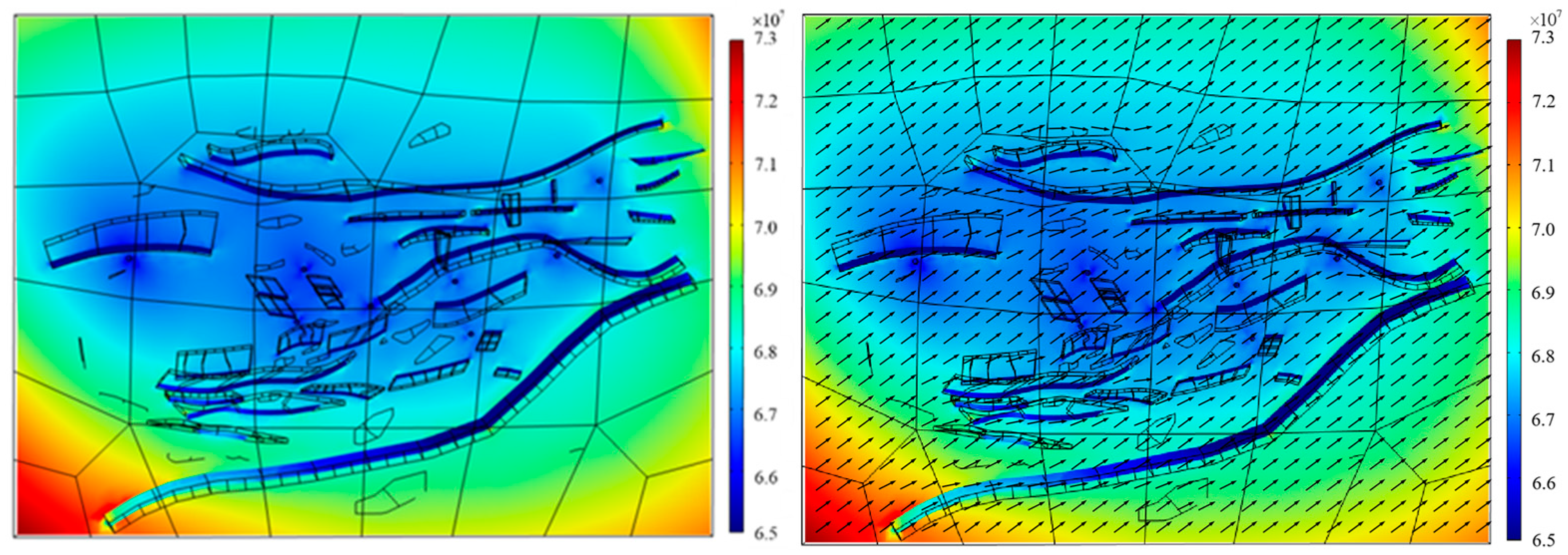
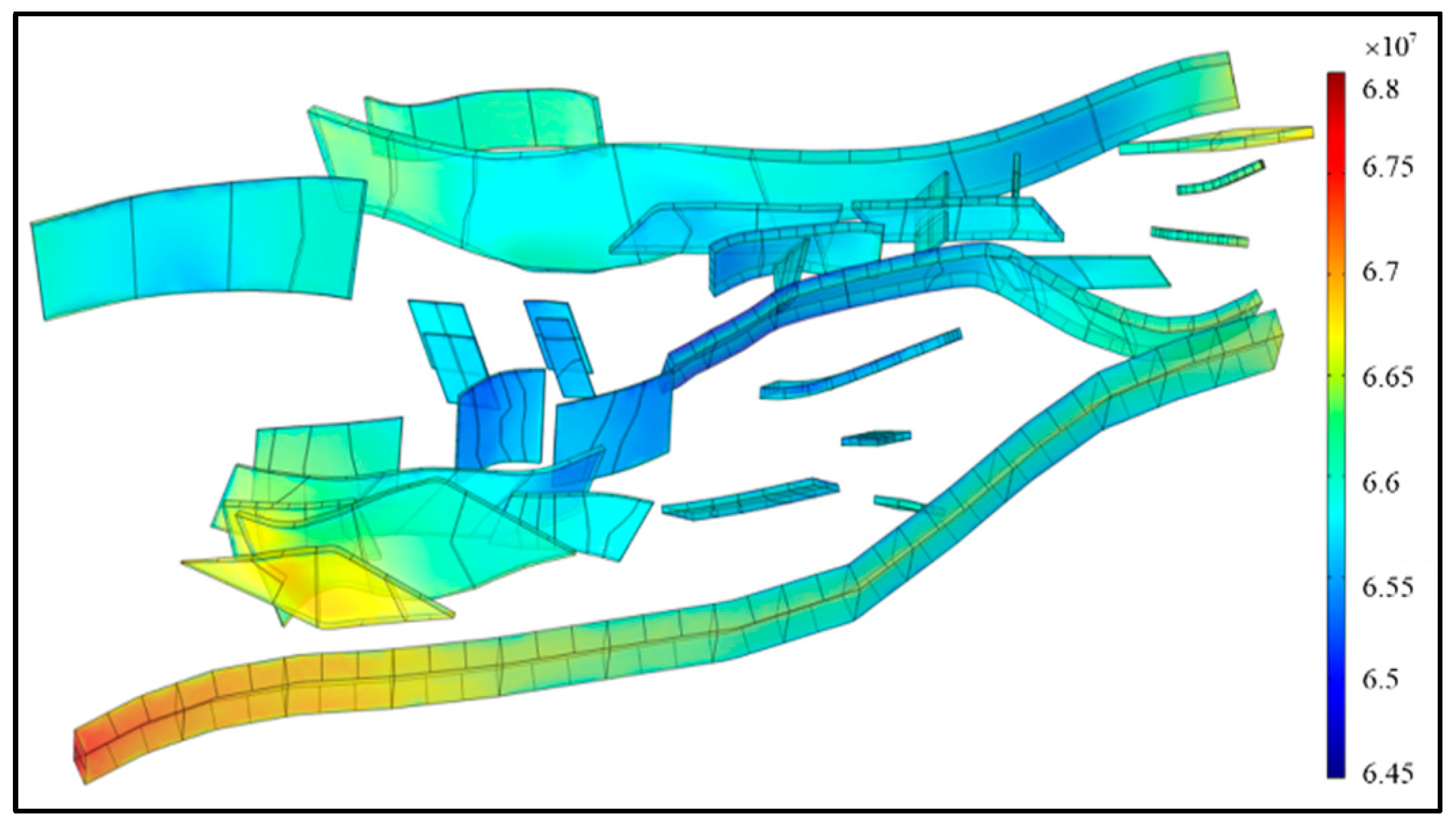
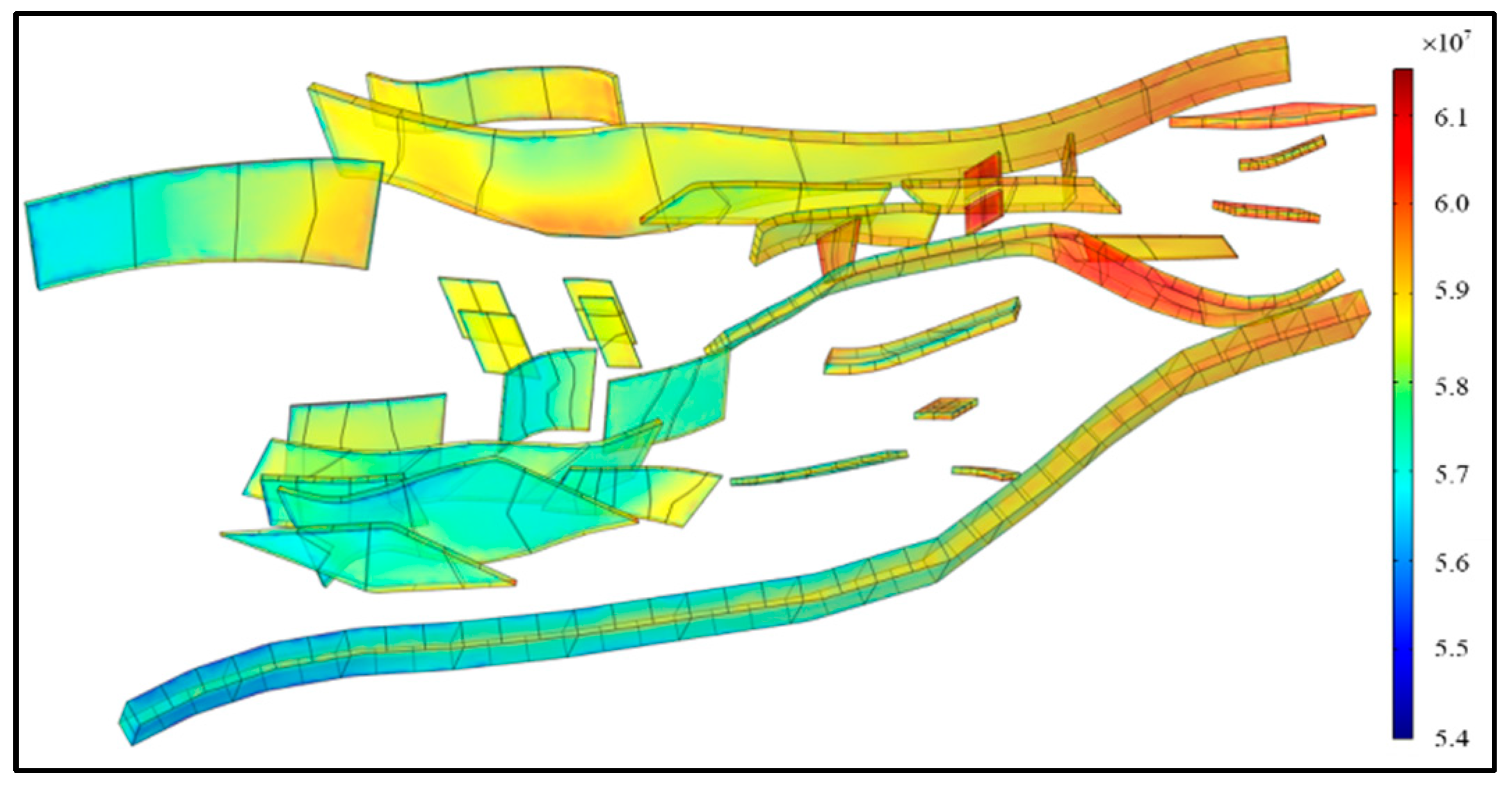
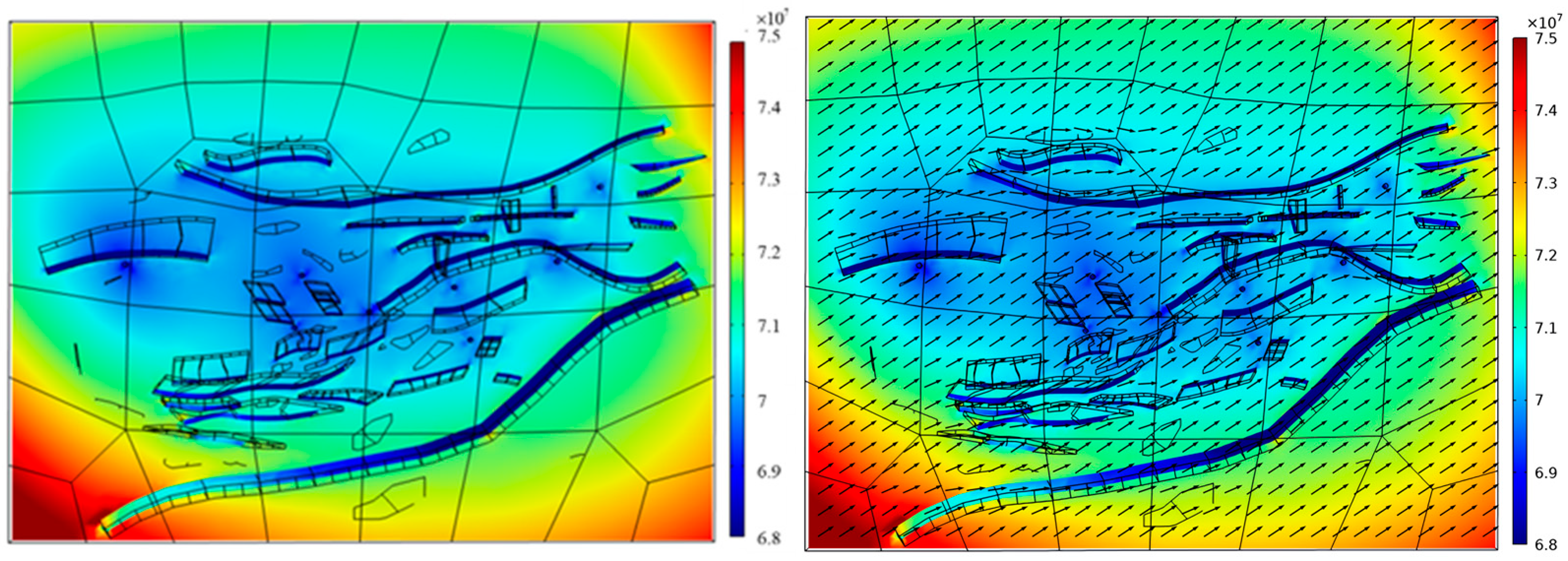
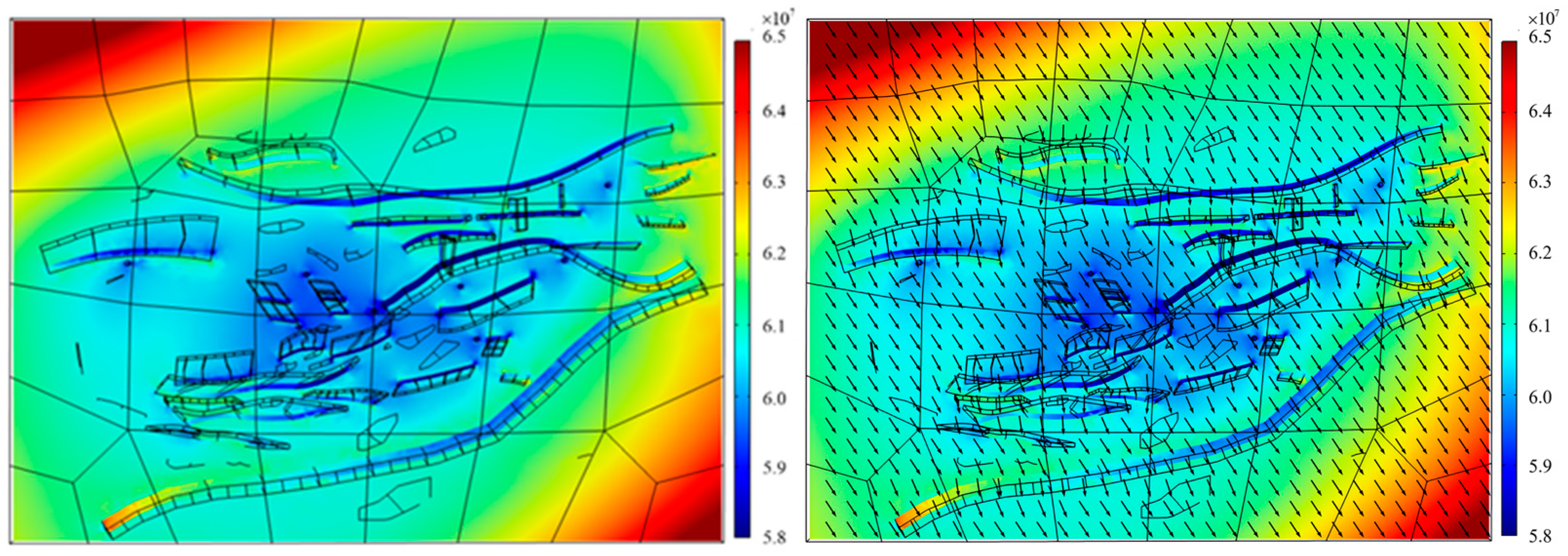
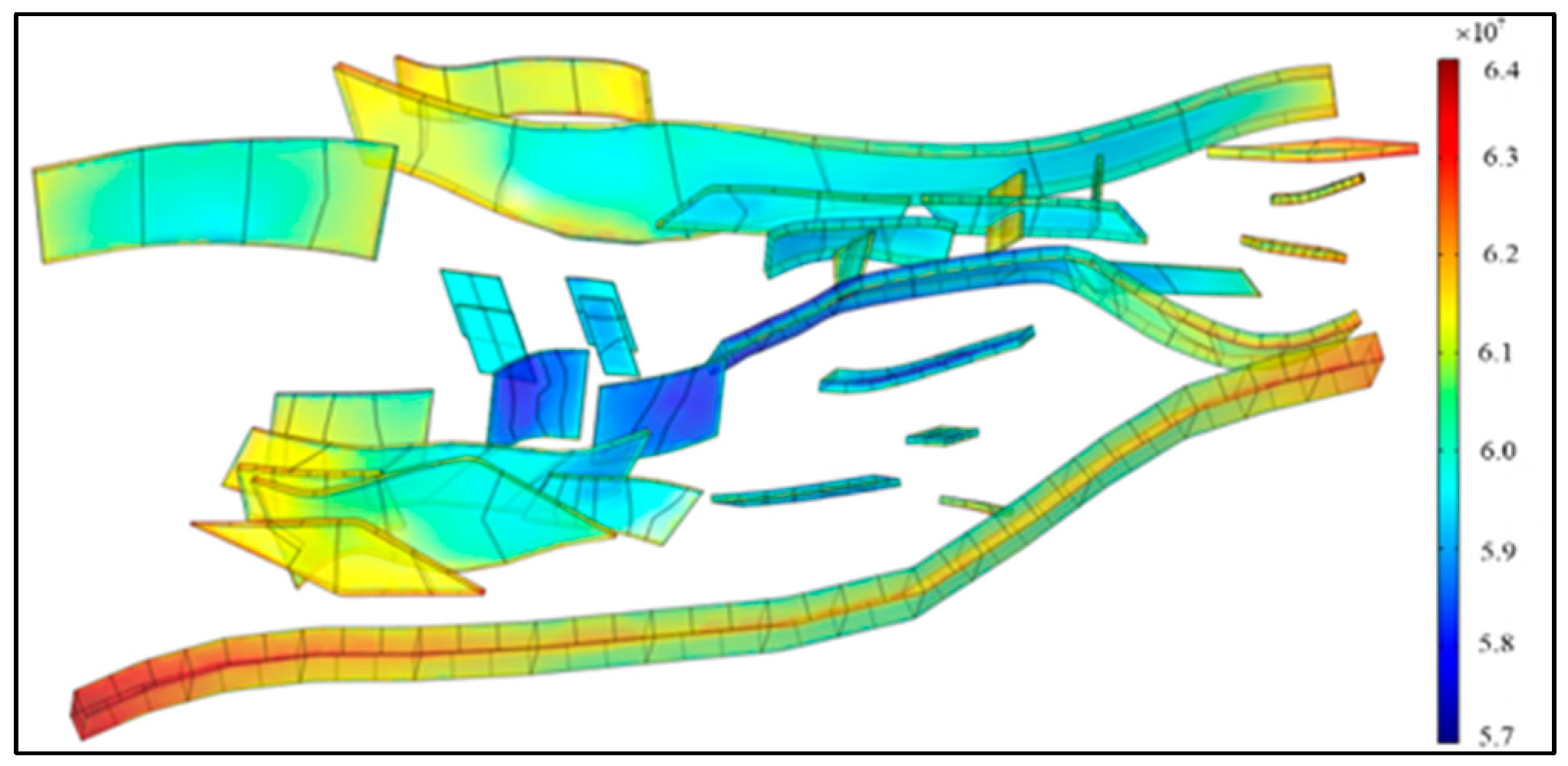
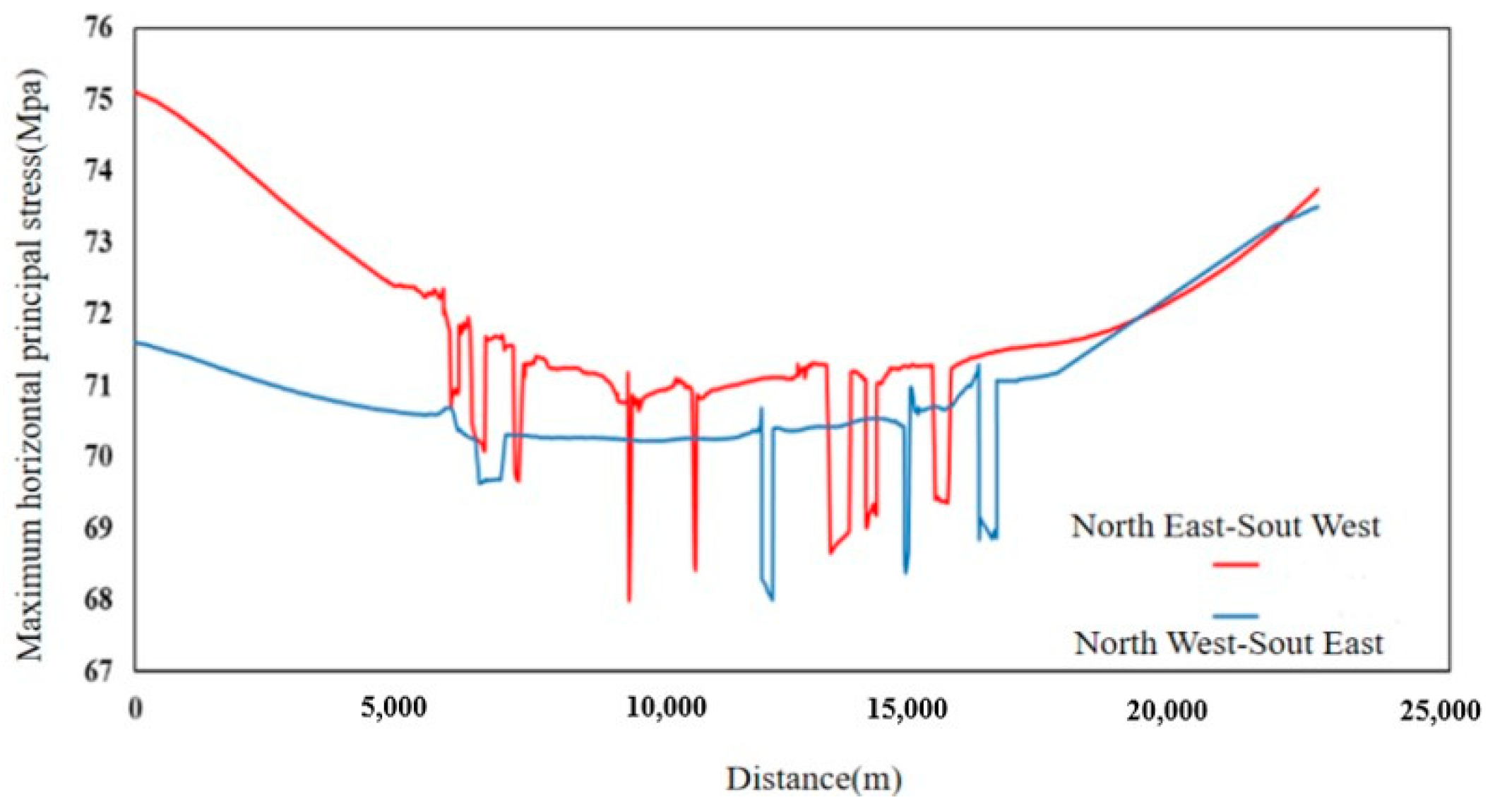
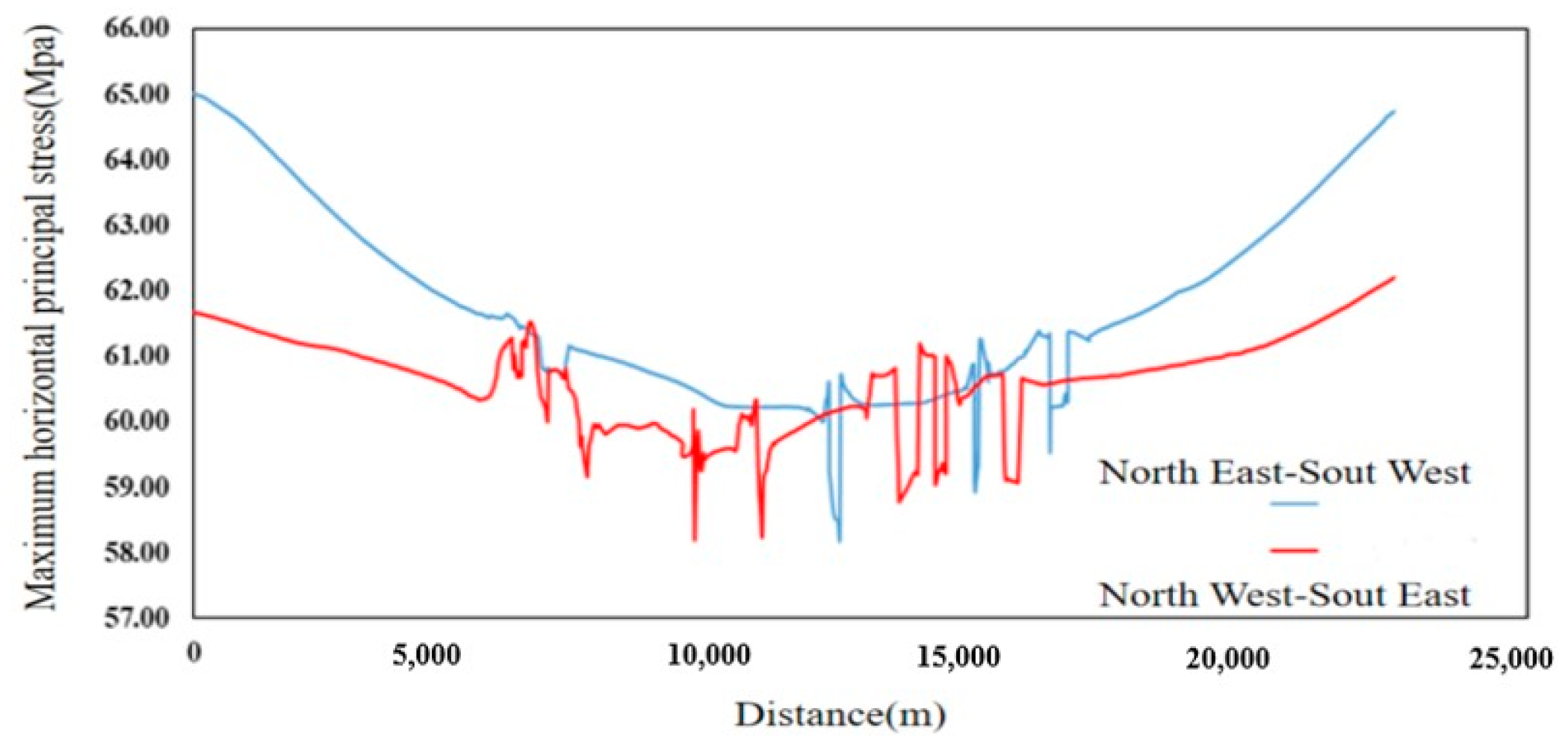
5.3. Study of Stress Field Distribution in the Area Without Considering Fluid Flow Coupling Effects
5.4. Analysis of In Situ Stress Field Characteristics in the Fault Fracture Body Reservoir Under Fluid–Solid Coupling Effects
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vincenzo, G.; Stefano, M.; Alessandro, I.; Stefano, V.; Armando, C.; Christoph, S. A permeability model for naturally fractured carbonate reservoirs. Mar. Pet. Geol. 2013, 40, 115–134. [Google Scholar]
- Xu, Y.F.; Sheng, G.L.; Zhao, H.; Hui, Y.N.; Ma, J.L.; Rao, X.; Zhang, X.; Gong, J. A New Approach for Gas-Water Flow Simulation in Multi-Fractured Horizontal wells of Shale Gas Reservoirs. J. Pet. Sci. Eng. 2021, 199, 108292. [Google Scholar] [CrossRef]
- Tomassi, A.; Trippetta, F.; de Franco, R.; Ruggieri, R. How petrophysical properties influence the seismic signature of carbonate fault damage zone: Insights from forward-seismic modelling. J. Struct. Geol. 2023, 167, 104802. [Google Scholar] [CrossRef]
- Li, D.J.; Zhao, Z.F.; Wang, B.; Yang, H.T.; Cui, W.H.; Ruan, J.Y.; Zhang, Y.X.; Wang, F. Study on Production Optimization Method of Fractured Reservoir Based on Connectivity Model. Front. Earth Sci. 2021, 9, 767738. [Google Scholar] [CrossRef]
- Han, P.; Ding, W.; Ma, H.; Yang, D.; Lv, J.; Li, Y.; Liu, T. The method and application of numerical simulation of high-precision stress field and quantitative prediction of multiperiod fracture in carbonate reservoir. Tectonophysics 2024, 885, 230421. [Google Scholar] [CrossRef]
- Zhang, S.L.; Yan, J.P.; Cai, J.G.; Zhu, X.J.; Hu, Q.H.; Wang, M.; Geng, B.; Zhong, G.H. Fracture characteristics and logging identification of lacustrine shale in the Jiyang Depression Bohai Bay Basin, Eastern China. Mar. Pet. Geol. 2023, 132, 105192. [Google Scholar] [CrossRef]
- Tuong, L.; Stephen, A.; Pierre, V.; Gioacchino, V. Fracture mechanisms in soft rock: Identification and quantification of evolving displacement discontinuities by extended digital image correlation. Tectonophysics 2011, 503, 117–128. [Google Scholar]
- Adrià, R.; Jesús, G.; Antonio, P.; Conxi, A.; Félix, R.; Carlos, P.; Jose, F.M. Salt control on the kinematic evolution of the Southern Basque-Cantabrian Basin and its underground storage systems (Northern Spain). Tectonophysics 2022, 822, 229178. [Google Scholar]
- Lyu, W.Y.; Zeng, L.B.; Liu, Z.Q.; Liu, G.P.; Zu, K.W. Fracture responses of conventional logs in tight-oil sandstones: A case study of the Upper Triassic Yanchang Formation in southwest Ordos Basin, China. AAPG Bull. 2016, 100, 1399–1417. [Google Scholar] [CrossRef]
- Zhang, T.T.; Li, Z.P.; Adenutsi, D.; Lai, F.P. A new model for calculating permeability of natural fractures in dual-porosity reservoir. Adv. Geo-Energy Res. 2017, 1, 86–92. [Google Scholar] [CrossRef]
- Laubach, S. A method to detect natural fracture strike in sandstones. AAPG Bull. 1997, 81, 604–623. [Google Scholar]
- Velázquez, S.; Vicente, G.; Elorza, F. Intraplate stress state from finite element modeling: The southern border of the Spanish Central System. Tectonophysics 2009, 473, 417–427. [Google Scholar] [CrossRef]
- Jarosinski, M.; Beekman, F.; Matenco, L.; Cloetingh, S. Mechanics of basin inversion: Finite element modeling of the Pannonian Basin system. Tectonophysics 2011, 502, 121–145. [Google Scholar] [CrossRef]
- Sollberger, D.; Igel, H.; Schmelzbach, C.; Edme, P.; Van, M.D.; Bernauer, F.; Yuan, S.; Wassermann, J.; Schreiber, U.; Robertsson, J. Seismological processing of six degree-of-freedom ground-motion data. Sensors 2020, 20, 6904. [Google Scholar] [CrossRef]
- Brossier, R.; Operto, S.; Virieux, J. Velocity model building from seismic reflection data by full-waveform inversion. Geophys. Prospect. 2015, 63, 354–367. [Google Scholar] [CrossRef]
- Miao, S.J.; Li, Y.; Tan, W.H.; Ren, F.H. Relation between the in-situ stress field and geological tectonics of a gold mine area in Jiaodong Peninsula, China. Int. J. Rock Mech. Min. Sci. 2012, 51, 1365–1609. [Google Scholar] [CrossRef]
- Moinfar, A.; Sepehrnoori, K.; Johns, R.T.; Abdoljalil, V. Coupled Geomechanics and Flow Simulation for an Embedded Discrete Fracture Model. In Proceedings of the SPE Reservoir Simulation Conference, The Woodlands, TX, USA, 18–20 February 2013. [Google Scholar]
- Liu, R.; Liu, J.Z.; Zhu, W.L.; Hao, F.; Xie, Y.H.; Wang, Z.F.; Wang, L.F. In situ stress analysis in the Yinggehai Basin, northwestern South China Sea: Implication for the pore pressure-stress coupling process. Mar. Pet. Geol. 2016, 77, 341–352. [Google Scholar] [CrossRef]
- Papanastasiou, P.; Kyriacou, A.; Sarris, E. Constraining the in-situ stresses in a tectonically active offshore basin in Eastern Mediterranean. J. Pet. Sci. Eng. 2017, 149, 208–217. [Google Scholar] [CrossRef]
- Fanchi, J. Chapter 2—Geological Modeling. In Principles of Applied Reservoir Simulation; Gulf Professional Publishing: Houston, TX, USA, 2018; pp. 9–33. [Google Scholar]
- Li, J.; Xie, Y.T.; Liu, H.M.; Zhang, X.C.; Li, C.H.; Zhang, L.S. Combining macro and micro experiments to reveal the real-time evolution of permeability of shale. Energy 2023, 262, 125509. [Google Scholar] [CrossRef]
- Randen, T.; Pedersen, S.; Sonneland, L. Automatic Extraction of Fault Surfaces from Three-Dimensional Seismic Data. In Proceedings of the SEG International Exposition and Annual Meeting, San Antonio, TX, USA, 9–14 September 2001; pp. 551–554. [Google Scholar]
- Silva, C.; Marcolino, C.; Lima, F. Automatic Fault Extraction Using Ant Tracking Algorithm in the Marlim South Field, Campos Basin. In Proceedings of the SEG International Exposition and Annual Meeting, Houston, TX, USA, 6–11 November 2005; pp. 857–860. [Google Scholar]
- Pepper, R.; Bejarano, G. PSAdvances in Seismic Fault Interpretation Automation. In Proceedings of the AAPG Annual Convention, Calgary, AB, Canada, 19–22 June 2005. [Google Scholar]
- Titus, Z.; Heaney, C.; Jacquemyn, C.; Salinas, P.; Jackson, M.; Pain, C. Conditioning surface-based geological models to well data using artificial neural networks. Comput. Geosci. 2022, 26, 779–802. [Google Scholar] [CrossRef]
- Pradeep, T.; Bardhan, A.; Burman, A.; Samui, P. Rock Strain Prediction Using Deep Neural Network and Hybrid Models of ANFIS and Meta-Heuristic Optimization Algorithms. Infrastructures 2021, 6, 129. [Google Scholar] [CrossRef]
- Liu, H.; Xu, Y.; Wang, C.Y.; Ding, F.; Xiao, H.S. Study on the linkages between microstructure and permeability of porous media using pore network and BP neural network. Mater. Res. Express 2022, 9, 025504. [Google Scholar] [CrossRef]
- Jolfaei, S.; Lakirouhani, A. Sensitivity analysis of effective parameters in borehole failure, using neural network. Adv. Civ. Eng. 2022, 2022, 4958004. [Google Scholar] [CrossRef]
- Gao, Y.F.; Chen, M.; Jiang, H.L. Influence of unconnected pores on effective stress in porous geomaterials: Theory and case study in unconventional oil and gas reservoirs. J. Nat. Gas Sci. Eng. 2021, 88, 1875–5100. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, X.D.; Wang, X.T.; Xiong, F.; Tao, Z.G.; Lin, Y.; Chen, J. Experimental Investigation on Nonlinear Flow Anisotropy Behavior in Fracture Media. Geofluids 2019, 2019, 5874849. [Google Scholar] [CrossRef]
- Wang, X.; Jia, Z. Porous Media Model of Reservoir considering Seepage Stress Coupling and Seepage Field Analysis. Geofluids 2023, 2023, 3759667. [Google Scholar] [CrossRef]
- Yin, D.Y.; Li, C.G.; Song, S.; Liu, K. Nonlinear Seepage Mathematical Model of Fractured Tight Stress Sensitive Reservoir and Its Application. Front. Energy Res. 2022, 10, 819430. [Google Scholar] [CrossRef]
- Liu, K.; Yin, D.Y.; Sun, Y.H. The mathematical model of stress sensitivities on tight reservoirs of different sedimentary rocks and its application. J. Pet. Sci. Eng. 2020, 193, 107372. [Google Scholar]
- Li, J.; Wang, H.S.; Wu, Z.P.; Zhong, A.H.; Yang, F.; Meng, X.Y.; Liu, Y.S. Mesoscale migration of oil in tight sandstone reservoirs by multi-field coupled two-phase flow. Mar. Pet. Geol. 2024, 161, 106684. [Google Scholar] [CrossRef]
- Zhang, D.X.; Zhang, L.H.; Tang, H.Y.; Zhao, Y.L. Fully coupled fluid-solid productivity numerical simulation of multistage fractured horizontal well in tight oil reservoirs. Pet. Explor. Dev. 2022, 9, 2–393. [Google Scholar] [CrossRef]
- Lakirouhani, A.; Jolfaei, S. Hydraulic fracturing breakdown pressure and prediction of maximum horizontal in situ stress. Adv. Civ. Eng. 2023, 1, 8180702. [Google Scholar] [CrossRef]




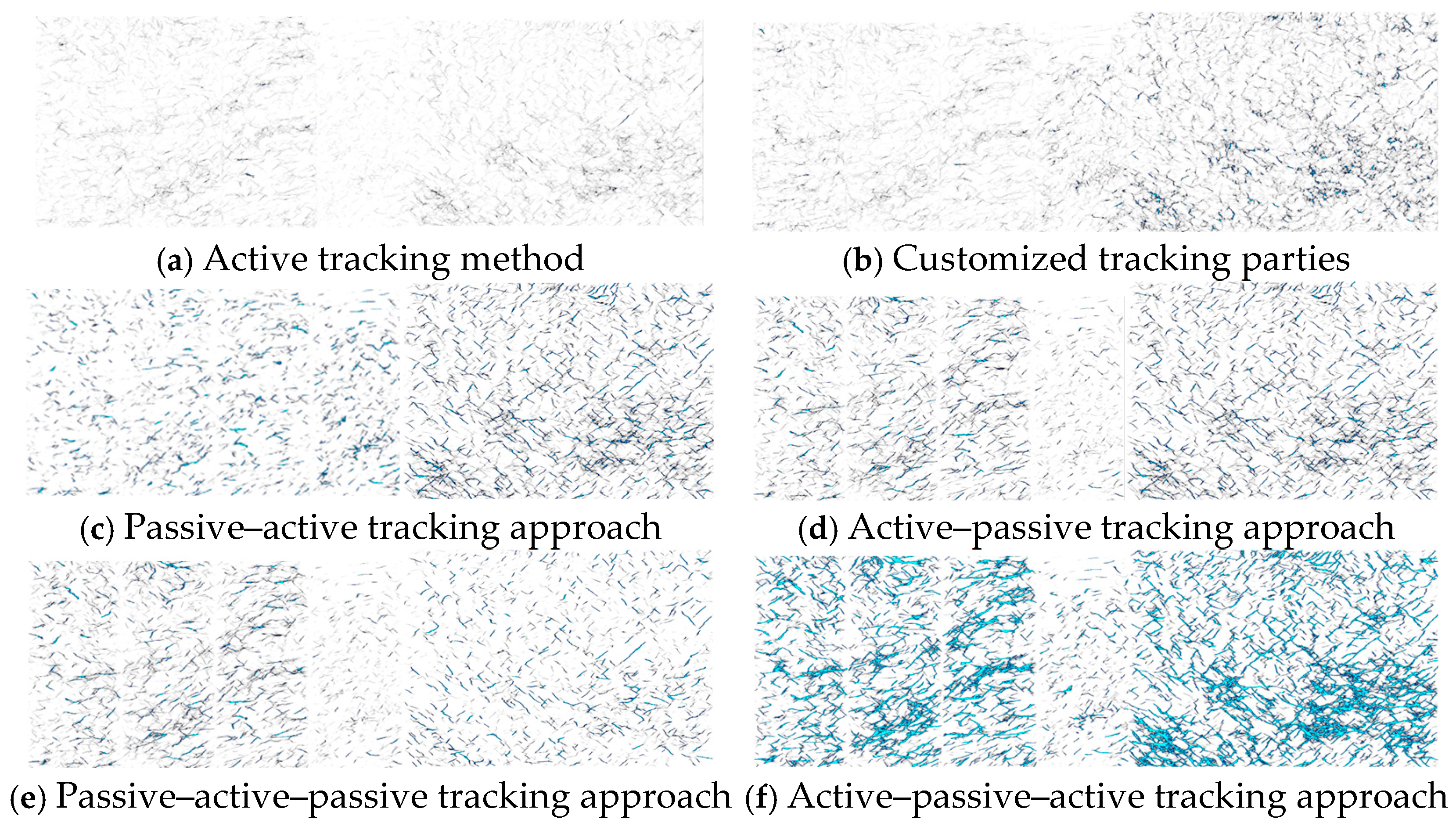





| Initial Boundary | Ant-Tracking Deviation | Ant’s Pacemaker | Allowable Illegal Steps | Legal Steps Required | Stopping Criteria | |
|---|---|---|---|---|---|---|
| Passive tracking method | 7 | 2 | 3 | 1 | 3 | 5 |
| Active tracking method | 5 | 2 | 3 | 2 | 2 | 10 |
| Customized tracking methods | 3 | 2 | 2 | 3 | 3 | 10 |
| Boundary Load | P1 | P2 | P3 | P4 |
|---|---|---|---|---|
| Pedicted value (MPa) | 62.69 | 78.02 | 78.47 | 64.18 |
| Reservoir Matrix | Fractured Seam Entity | |
|---|---|---|
| Coefficient of restitution | 18.00 | 14.40 |
| Poisson ratio | 0.220 | 0.310 |
| Density | 2.48 | 2.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, Y.; Li, J.; Meng, X.; Teng, J.; Wang, Z.; Li, M.; Zhu, R. Three-Dimensional In Situ Stress Distribution in a Fault Fracture Reservoir, Linnan Sag, Bohai Bay Basin. J. Mar. Sci. Eng. 2025, 13, 436. https://doi.org/10.3390/jmse13030436
Liu J, Wang Y, Li J, Meng X, Teng J, Wang Z, Li M, Zhu R. Three-Dimensional In Situ Stress Distribution in a Fault Fracture Reservoir, Linnan Sag, Bohai Bay Basin. Journal of Marine Science and Engineering. 2025; 13(3):436. https://doi.org/10.3390/jmse13030436
Chicago/Turabian StyleLiu, Jiageng, Yanzhong Wang, Jing Li, Xiaoyu Meng, Jiayi Teng, Zhicheng Wang, Mingzhi Li, and Rui Zhu. 2025. "Three-Dimensional In Situ Stress Distribution in a Fault Fracture Reservoir, Linnan Sag, Bohai Bay Basin" Journal of Marine Science and Engineering 13, no. 3: 436. https://doi.org/10.3390/jmse13030436
APA StyleLiu, J., Wang, Y., Li, J., Meng, X., Teng, J., Wang, Z., Li, M., & Zhu, R. (2025). Three-Dimensional In Situ Stress Distribution in a Fault Fracture Reservoir, Linnan Sag, Bohai Bay Basin. Journal of Marine Science and Engineering, 13(3), 436. https://doi.org/10.3390/jmse13030436






