Research on the Response Characteristics of Excavation and Support in Circular Sand Soil Foundation Pit Based on Parameter Verification
Abstract
1. Introduction
2. Material and Methods
2.1. Study Area
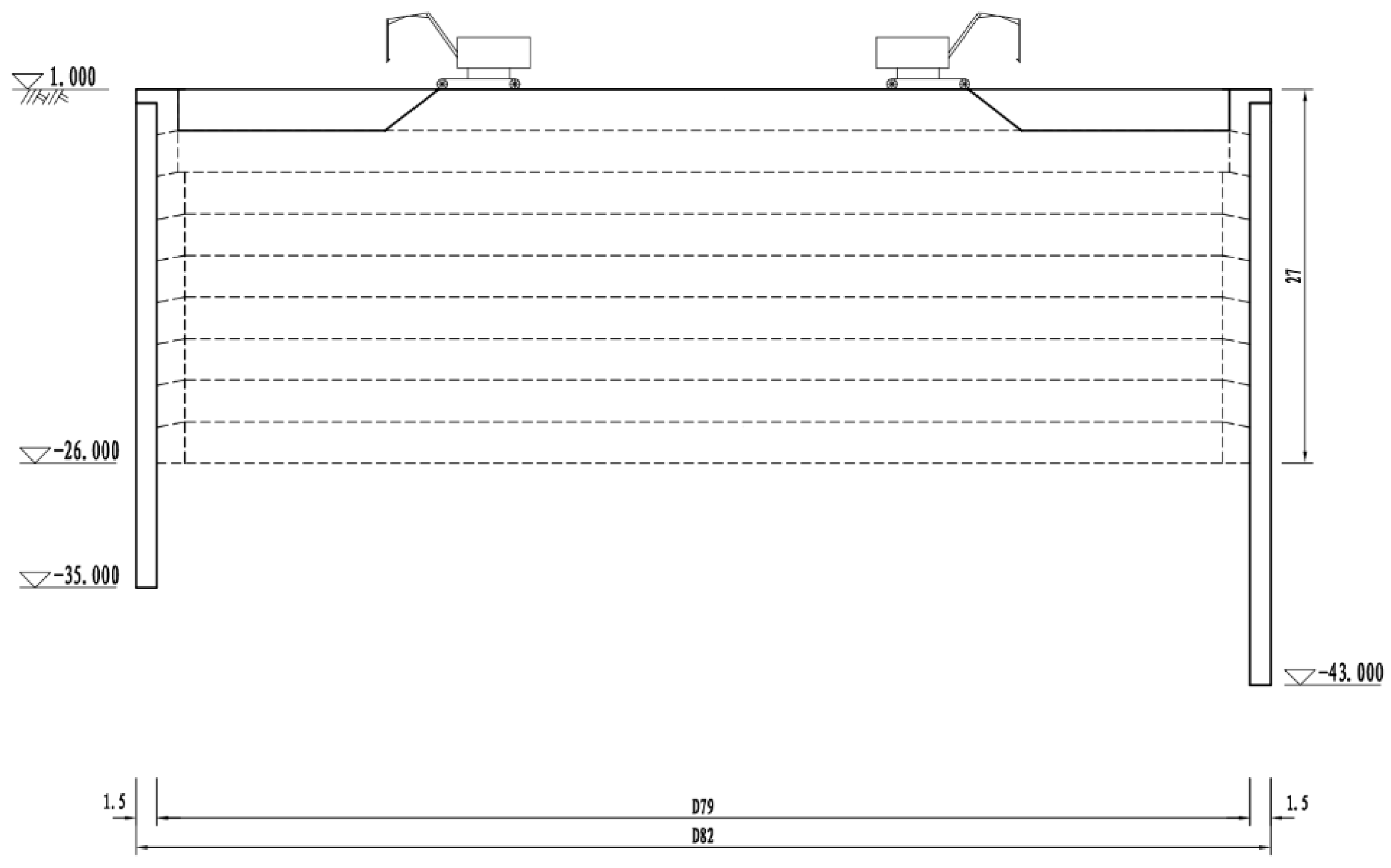
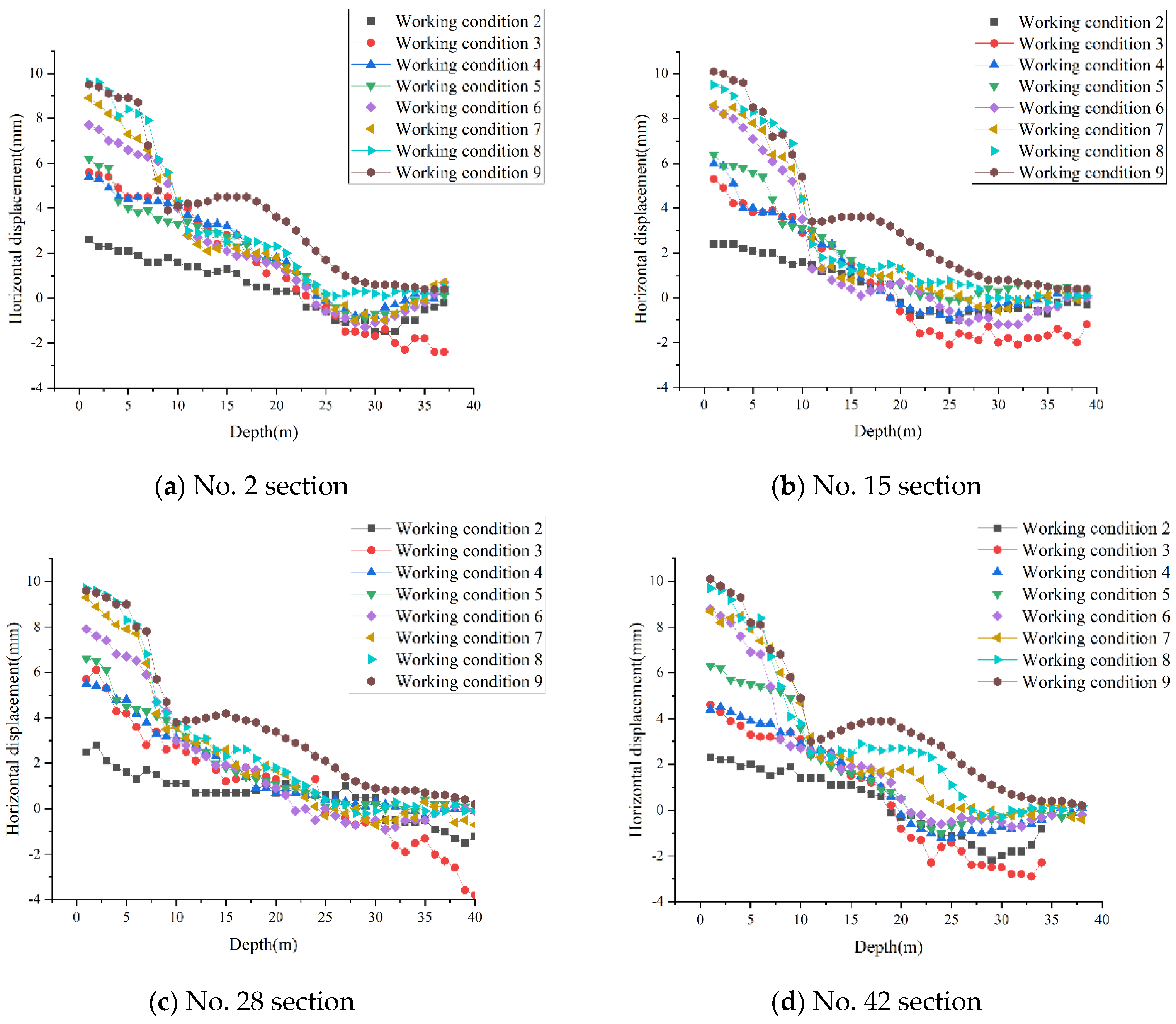
2.2. Monitoring the Horizontal Displacement of the Diaphragm Wall
2.3. Model Design and Establishment
2.3.1. Simulation Assumptions and Regions
| Depth (m) | Soil Layer Category |
|---|---|
| 0–3 | silt |
| 3–6 | silty clay |
| 6–12 | silty sand |
| 12–18 | medium sand |
| 18–24 | coarse sand |
| 24–40 | strong weathered mudstone |
| 40–70 | middle weathered mudstone |
| 70–100 | micro-weathered mudstone |
2.3.2. Model Boundary Conditions
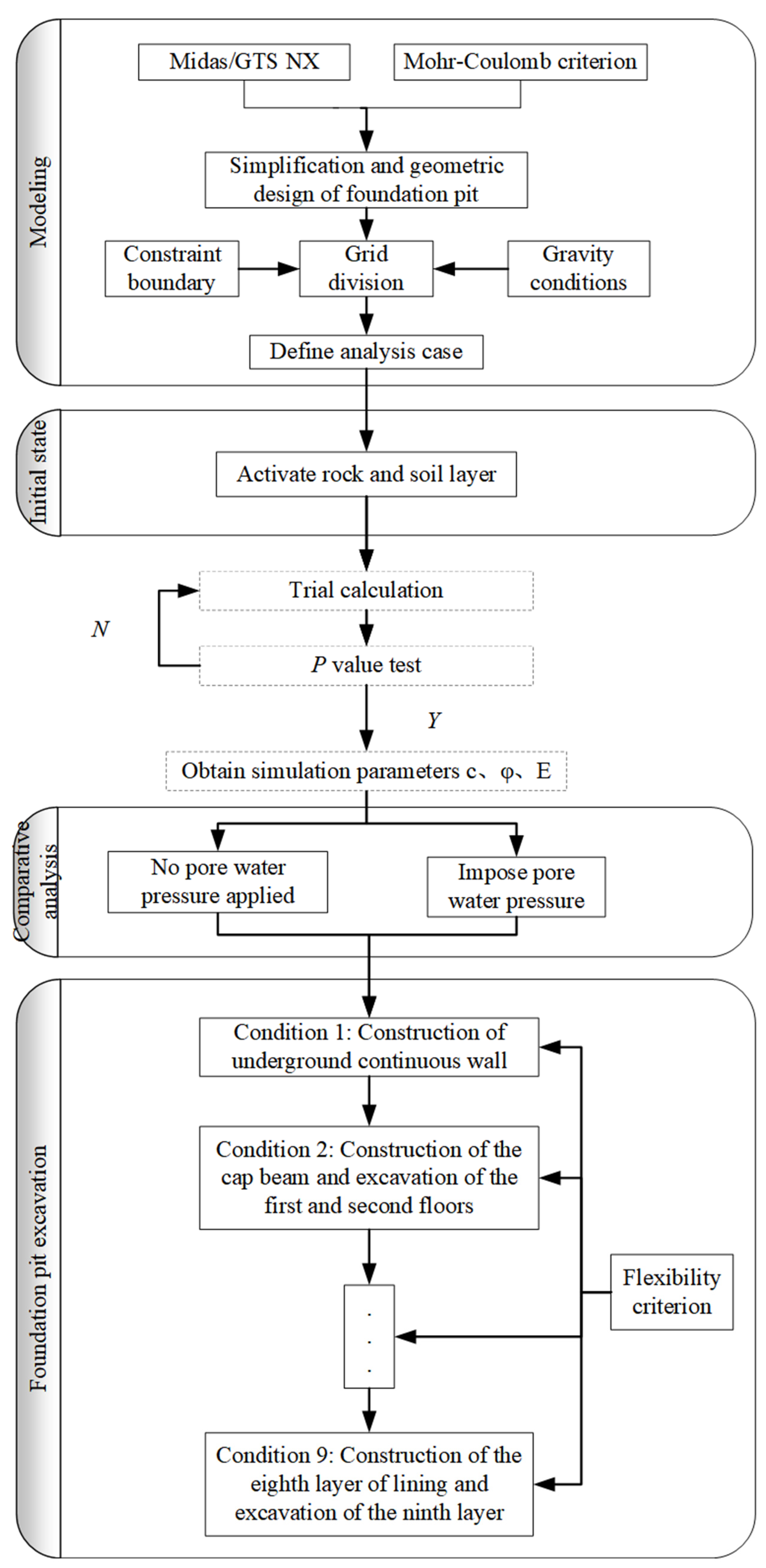
2.3.3. Seepage-Stress Coupling and Process Analysis
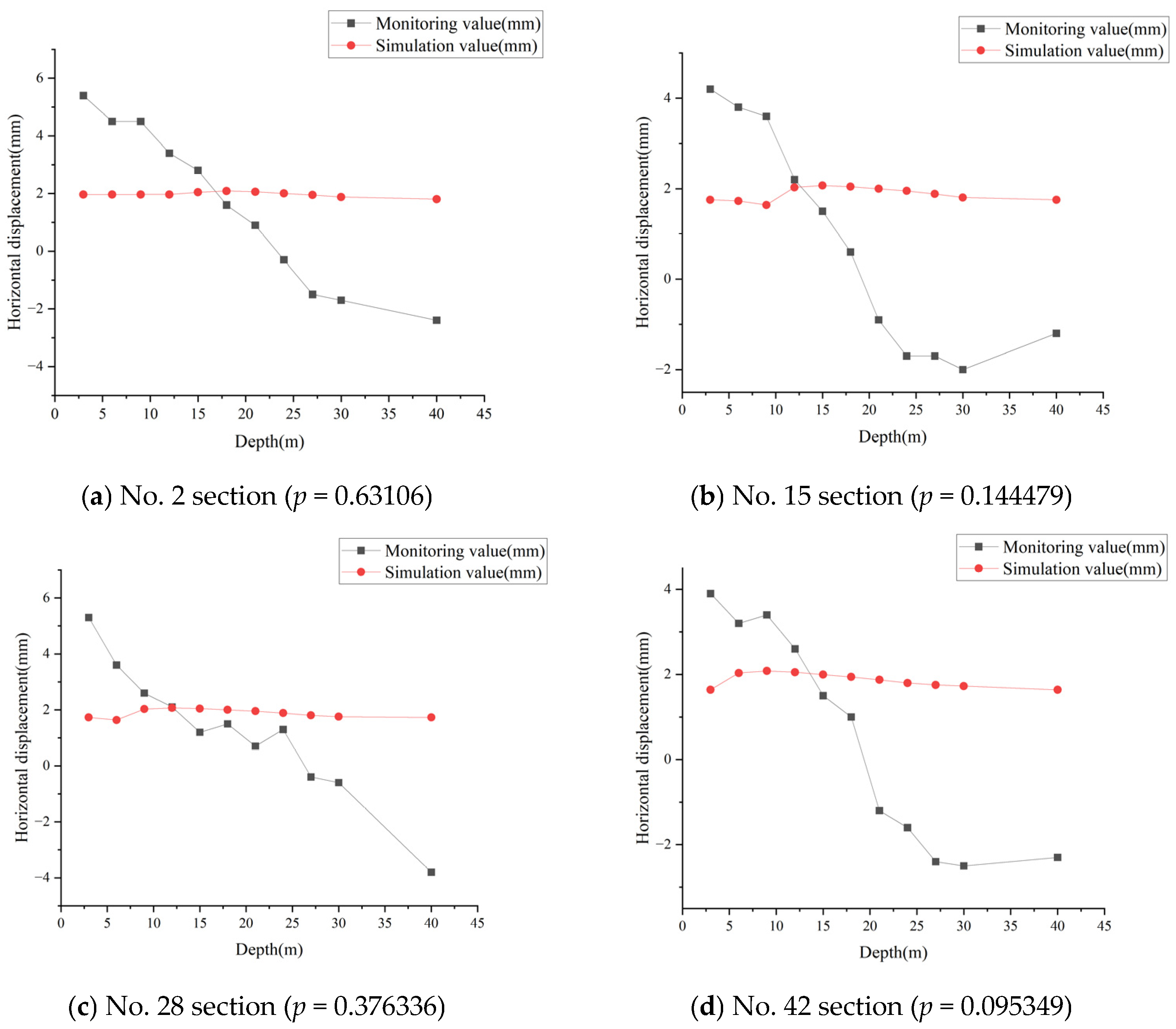
2.3.4. Model Parameter Validation
3. Results and Discussion
3.1. Simulation Parameter Selection
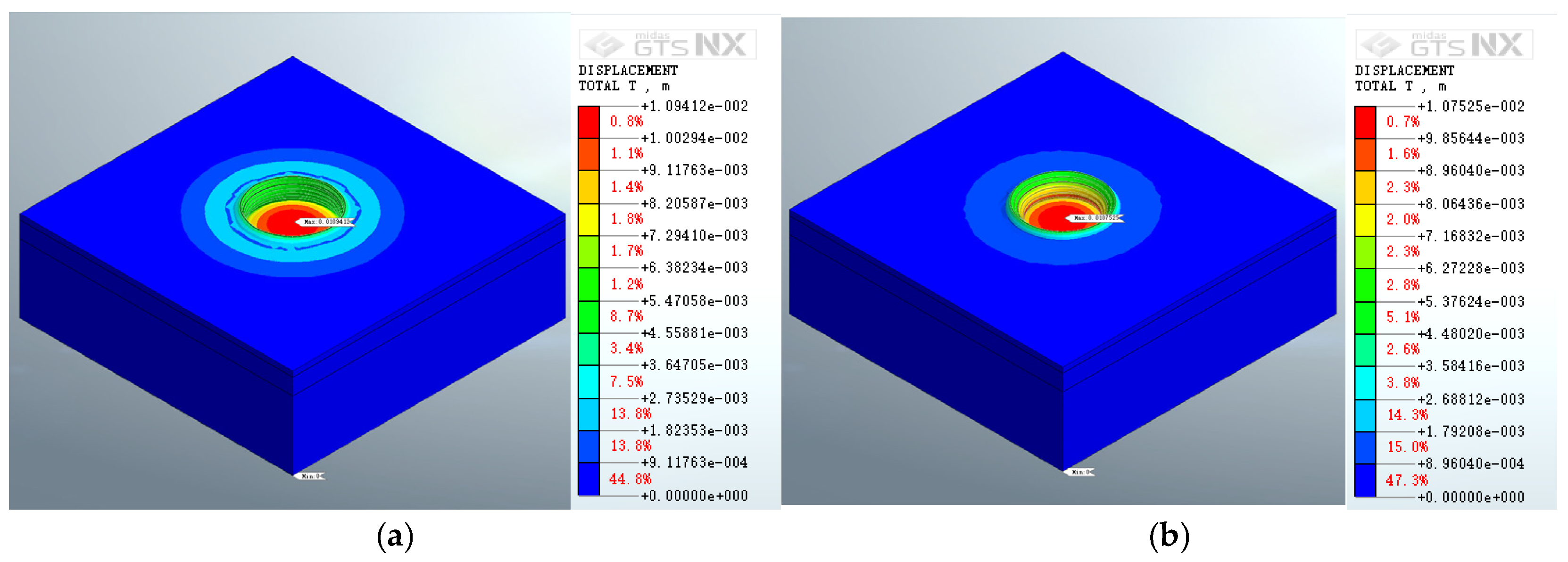
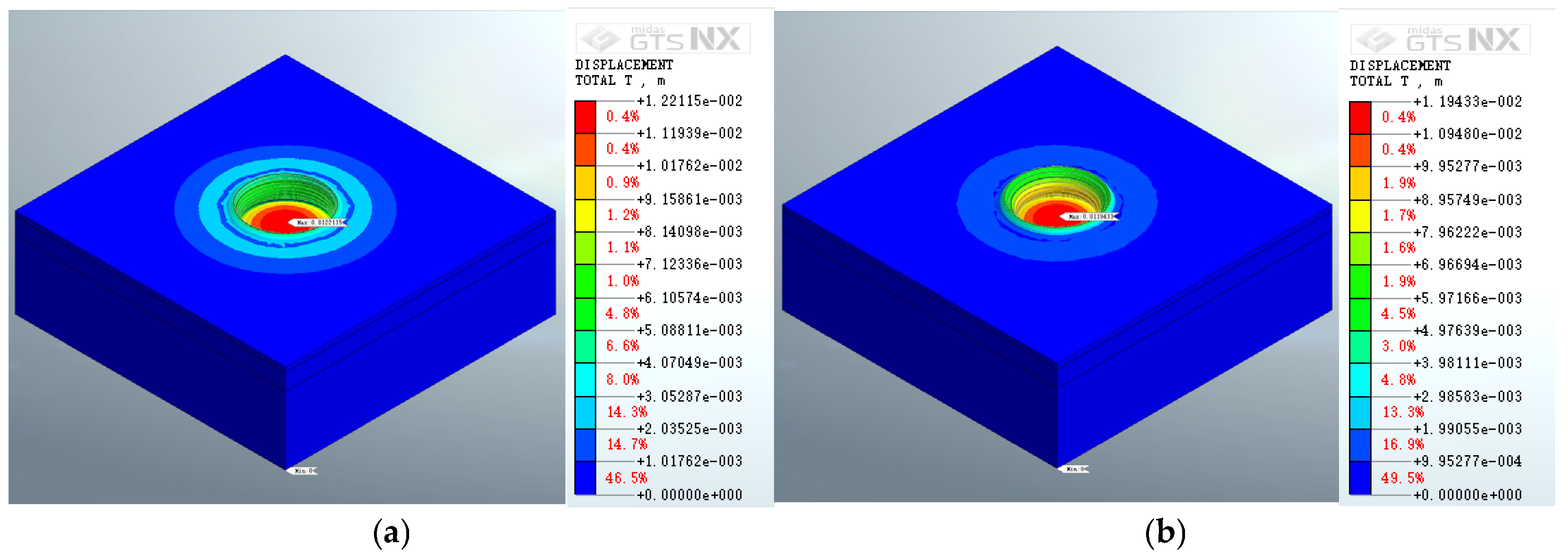
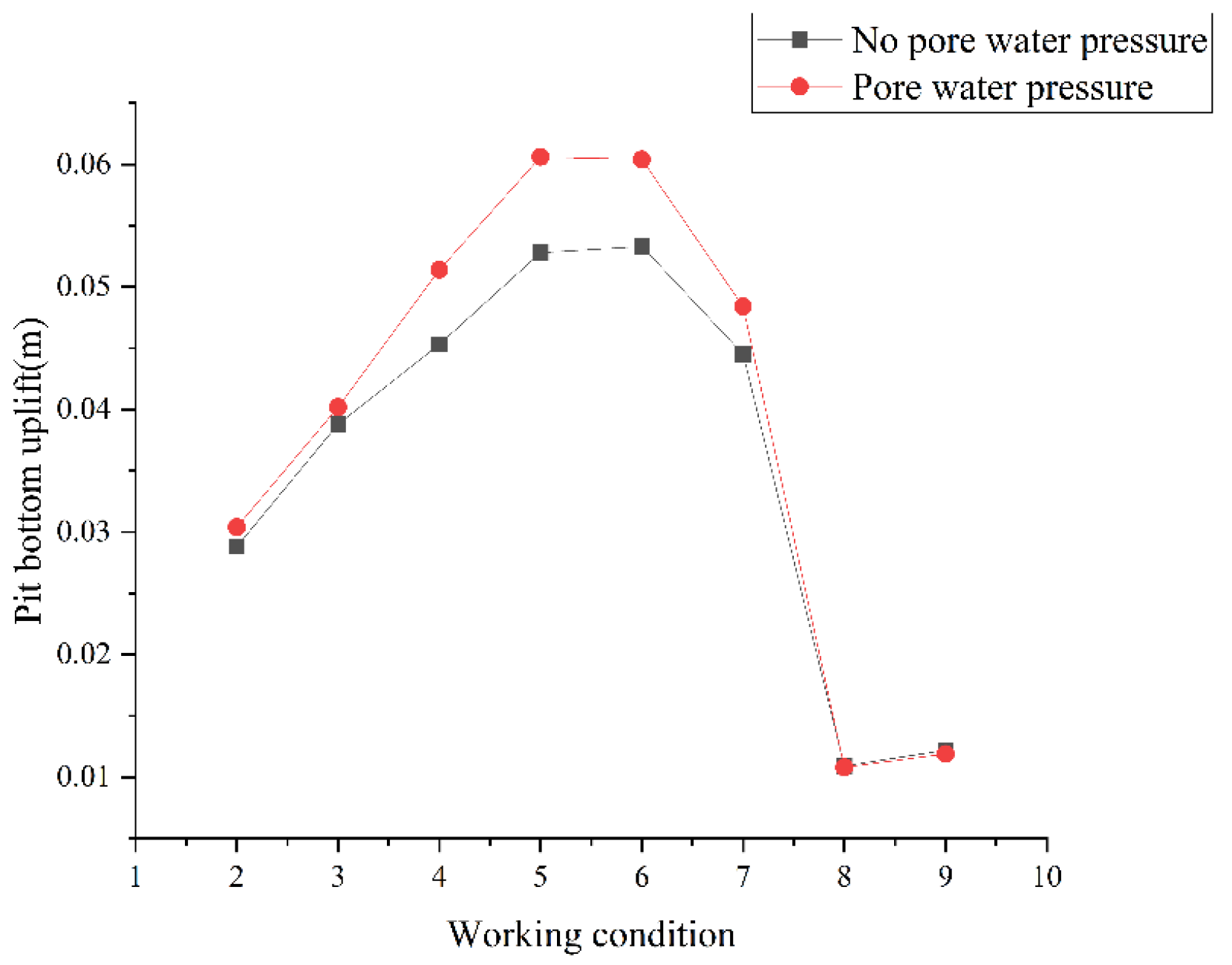
3.2. Analysis of Pit Bottom Uplift
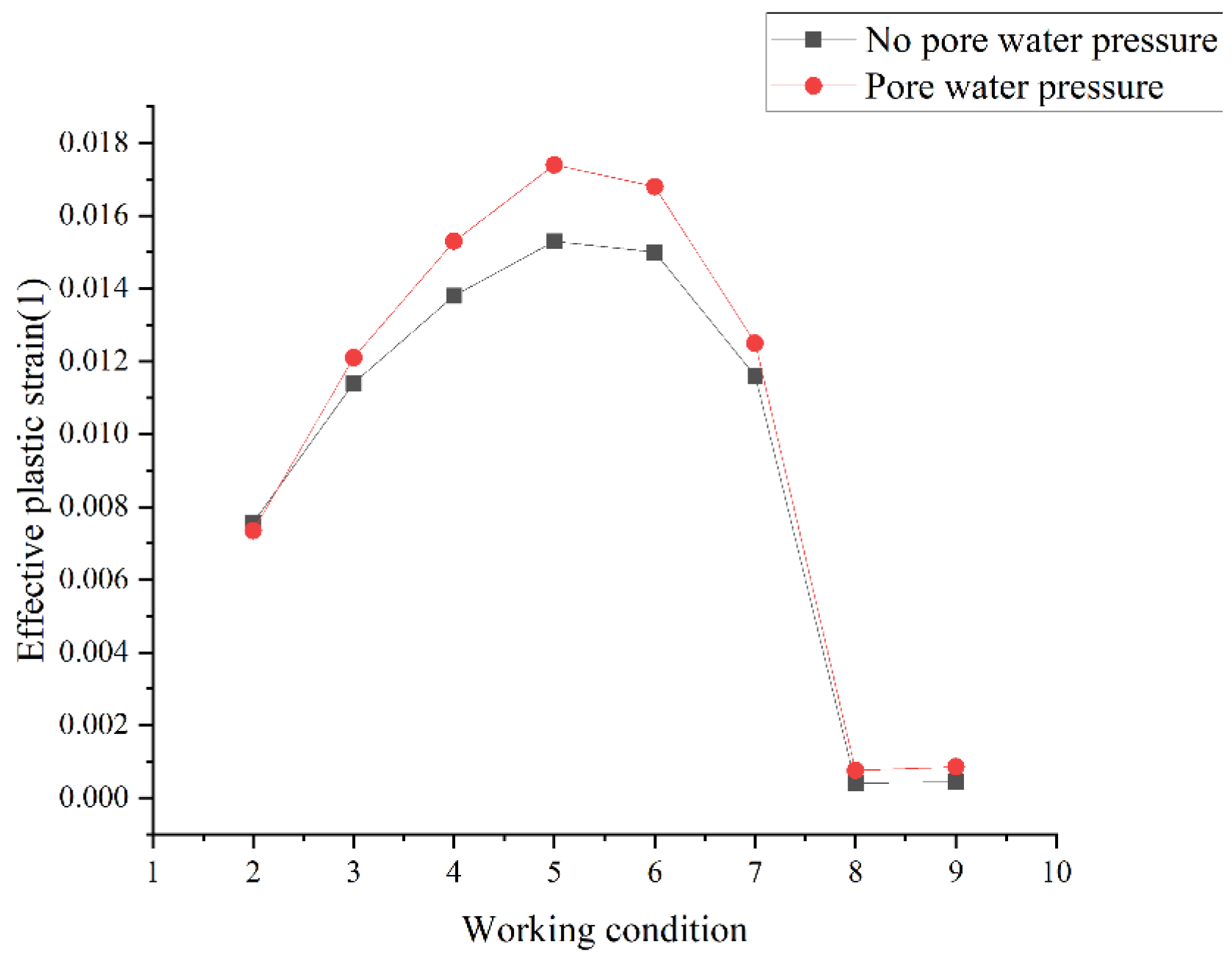
3.3. Effective Plastic Strain Analysis
3.4. Analysis of Relationship Between Pit Bottom Uplift and Effective Plastic Strain
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tan, Y.; Wang, D.L. Characteristics of a large-scale deep foundation pit excavated by the central-island technique in shanghai soft clay. I: Bottom-up construction of the central cylindrical shaft. J. Geotech. Geoenviron. Eng. 2013, 139, 1875–1893. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, D.L. Structural behaviors of large underground earth-retaining systems in shanghai. I: Unpropped circular diaphragm wall. J. Perform. Constr. Facil. 2015, 29, 04014058. [Google Scholar]
- Tan, Y.; Wang, D.L. Structural behaviors of large underground earth-retaining systems in shanghai. II: Multipropped Rectangular Diaphragm Wall. J. Perform. Constr. Facil. 2015, 29, 04014059. [Google Scholar] [CrossRef]
- Maddah, A.; Soroush, A. A Comprehensive Numerical Study on Building-Excavation Interaction. Civ. Eng. J. 2020, 6, 326–343. [Google Scholar] [CrossRef]
- Olia, A.S.R.; Oliaei, M.; Heidarzadeh, H. Performance of Ground Anchored Walls Subjected to Dynamic and Pseudo-Static Loading. Civ. Eng. J. 2021, 7, 974–987. [Google Scholar] [CrossRef]
- Xu, C.J.; Chen, Q.Z.; Wang, Y.L.; Hu, W.T.; Fang, T. Dynamic deformation control of retaining structures of a deep excavation. J. Perform. Constr. Facil. 2016, 30, 04015071. [Google Scholar] [CrossRef]
- Tan, Y.; Lu, Y. Responses of shallowly buried pipelines to adjacent deep excavations in Shanghai soft ground. J. Pipeline Syst. Eng. Pract. 2018, 9, 05018002. [Google Scholar] [CrossRef]
- Chen, R.P.; Meng, F.Y.; Li, Z.C.; Ye, Y.H.; Ye, J.N. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils. Tunn. Undergr. Space Technol. 2016, 58, 224–235. [Google Scholar] [CrossRef]
- Guo, P.P.; Gong, X.N.; Wang, Y.X. Displacement and force analyses of braced structure of deep excavation considering unsymmetrical surcharge effect. Comput. Geotech. 2019, 113, 103102. [Google Scholar] [CrossRef]
- Simpson, B. Retaining structures-displacement and design. Thirty-second Rankine Lecture. Geotechnique 1992, 42, 541–576. [Google Scholar] [CrossRef]
- Farrell, R.; Mair, R.; Sciotti, A.; Pigorini, A. Building response to tunnelling. Soils Found. 2014, 54, 269–279. [Google Scholar] [CrossRef]
- Zhao, C.Y.; Lavasan, A.A.; Barciaga, T.; Zarev, V.; Datcheva, M.; Schanz, T. Model validation and calibration via back analysis for mechanized tunnel simulations-the western scheldt tunnel case. Comput. Geotech. 2015, 69, 601–614. [Google Scholar] [CrossRef]
- Schwamb, T.; Elshafie, M.; Soga, K.; Mair, R.J. Considerations for monitoring of deep circular excavations. Proc. Inst. Civ. Eng. Geotech. Eng. 2016, 169, 477–493. [Google Scholar] [CrossRef]
- Jin, Y.F.; Yin, Z.Y.; Zhou, W.H.; Liu, X. Intelligent model selection with updating parameters during staged excavation using optimization method. Acta Geotech. 2020, 15, 2473–2491. [Google Scholar] [CrossRef]
- Zhou, H.Z.; Zheng, G.; He, X.P.; Wang, E.Y.; Guo, Z.Y.; Nie, D.Q.; Ma, S.K. Numerical modelling of retaining structure displacements in multi-bench retained excavations. Acta Geotech. 2020, 15, 2691–2703. [Google Scholar] [CrossRef]
- Gao, X.; Tian, W.P.; Zhang, Z. Analysis of Deformation Characteristics of Foundation-Pit Excavation and Circular Wall. Sustainability 2020, 12, 3164. [Google Scholar] [CrossRef]
- Gao, X.; Tian, W.P.; Li, J.; Qi, H.; Li, S.; Zhang, Z. Research on the Stress and Deformation Characteristics of Circular Foundation Pit during Excavation in Sand Soil. Adv. Mater. Sci. Eng. 2023, 2023, 3008695. [Google Scholar] [CrossRef]
- Bagherzadeh, P.; Goshtasbi, K.; Kazemzadeh, E.; Mojtaba Kashef, M.; Bakhtiari, H.A. Stress-dependence of the permeability, porosity, and compressibility in fractured porous media regarding fracturing condition. Bull. Eng. Geol. Environ. 2021, 80, 5091–5110. [Google Scholar] [CrossRef]
- Wang, L.Y.; Zhang, Y.J. Interpreting correlations in stress-dependent permeability, porosity, and compressibility of rocks: A viewpoint from finite strain theory. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 2000–2019. [Google Scholar] [CrossRef]
- Liu, B.; Lin, H.; Chen, Y.; Liu, J.; Guo, C. Deformation Stability Response of Adjacent Subway Tunnels considering Excavation and Support of Foundation Pit. Lithosphere 2022, 10, 7227330. [Google Scholar] [CrossRef]
- Li, Z. Displacement Monitoring during the Excavation and Support of Deep Foundation Pit in Complex Environment. Adv. Civ. Eng. 2021, 2021, 5715306. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Shlash, K.T.; Salim, N.M. Effect of reduced K0 Zone on time dependent analysis of tunnels. Adv. Civ. Eng. 2011, 2011, 963502. [Google Scholar]
- Fattah, M.Y.; Shlash, K.T.; Al-Soud, M.M. Boundary element analysis of a lined tunnel problem. Int. J. Eng. Trans. B Appl. 2012, 25, 87–94. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Shlash, K.T.; Salim, N.M. Prediction of settlement trough induced by tunneling in cohesive ground. Acta Geotech. 2013, 8, 167–179. [Google Scholar] [CrossRef]
- Luo, J.Y.; Zhang, L.L.; Zhang, H.Q.; Wei, X.; Liu, D.S.; Xu, J.B. Probabilistic model calibration of spatial variability for a physically-based landslide susceptibility model. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 1988986. [Google Scholar] [CrossRef]
- Yang, H.Q.; Zhang, L.L.; Pan, Q.J.; Phoon, K.K.; Shen, Z.C. Bayesian estimation of spatially varying soil parameters with spatiotemporal monitoring data. Acta Geotech. 2021, 16, 263–278. [Google Scholar] [CrossRef]
- Kim, K.Y.; Lee, D.S.; Cho, J.; Jeong, S.S.; Lee, S. The effect of arching pressure on a vertical circular shaft. Tunn. Undergr. Space Technol. 2013, 37, 10–21. [Google Scholar] [CrossRef]
- Schwamb, T.; Soga, K.; Mair, R.J.; Elshafie, M.Z.E.B.; Sutherden, R.; Boquet, C.; Greenwood, J. Fibre optic monitoring of a deep circular excavation. Proc. Inst. Civ. Eng. Geotech. Eng. 2014, 167, 144–154. [Google Scholar] [CrossRef]
- Faustin, N.E.; Elshafie, M.Z.E.B.; Mair, R.J. Case studies of circular shaft construction in London. Proc. Inst. Civ. Eng. Geotech. Eng. 2018, 171, 391–404. [Google Scholar] [CrossRef]
- Le, B.T.; Goodey, R.J.; Divall, S. Subsurface ground movements due to circular shaft construction. Soils Found. 2019, 59, 1160–1171. [Google Scholar] [CrossRef]
- Borges, J.L.; Guerra, G.T. Cylindrical excavations in clayey soils retained by jet grout walls: Numerical analysis and parametric study considering the influence of consolidation. Comput. Geotech. 2014, 55, 42–56. [Google Scholar] [CrossRef]
- Cho, J.; Lim, H.; Jeong, S.; Kim, K. Analysis of lateral earth pressure on a vertical circular shaft considering the 3D arching effect. Tunn. Undergr. Space Technol. 2015, 48, 11–19. [Google Scholar] [CrossRef]
- Chehadeh, A.; Turan, A.; Abed, F. Numerical investigation of spatial aspects of soil structure interaction for secant pile wall circular shafts. Comput. Geotech. 2015, 69, 452–461. [Google Scholar] [CrossRef]
- Schwamb, T.; Soga, K. Numerical modelling of a deep circular excavation at Abbey Mills in London. Géotechnique 2015, 65, 604–619. [Google Scholar] [CrossRef]
- Chehadeh, A.; Turan, A.; Abed, F.; Yamin, M. 2019. Lateral earth pressures acting on circular shafts considering soil-structure interaction. Int. J. Geotech. Eng. 2019, 13, 139–151. [Google Scholar] [CrossRef]



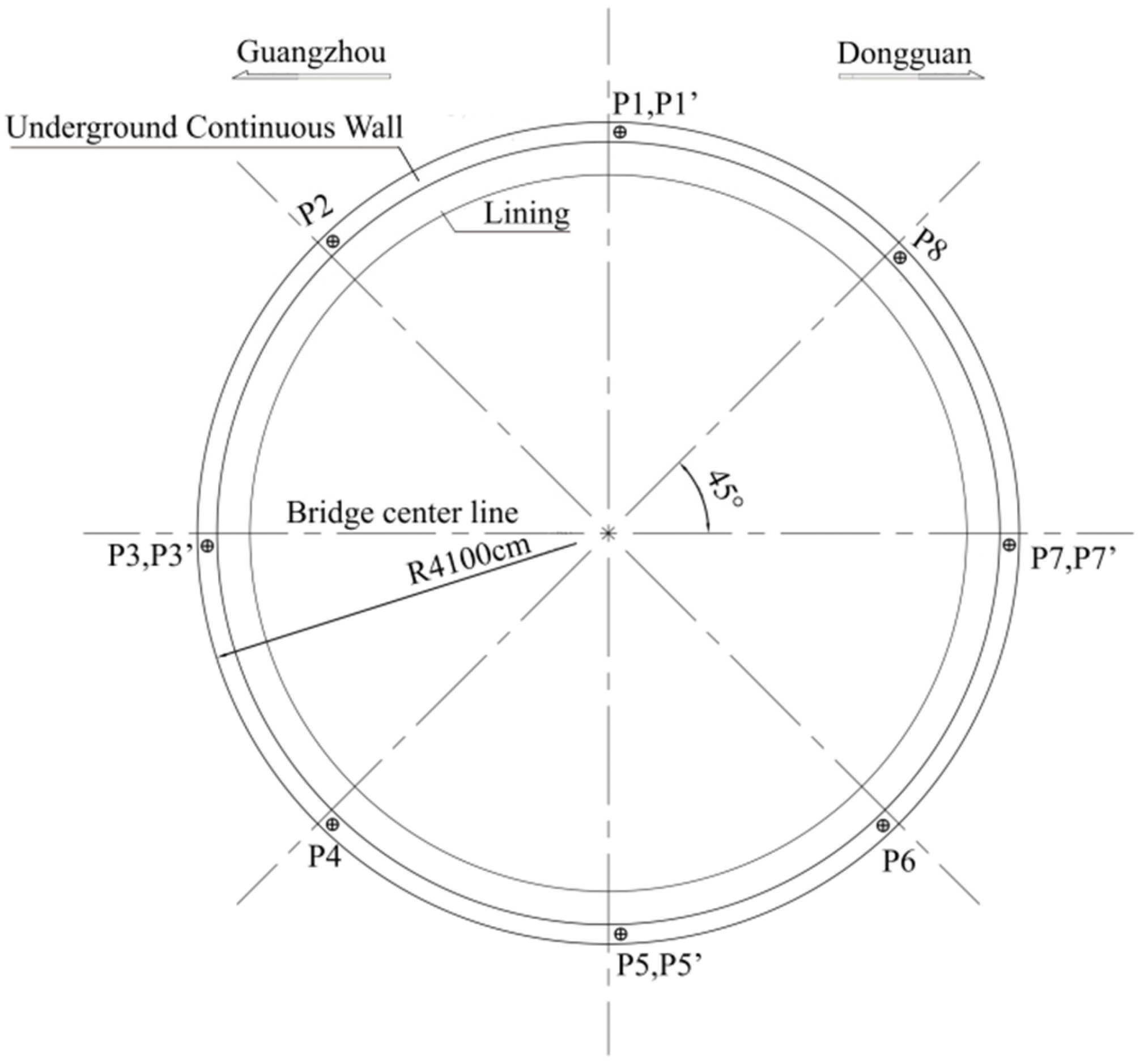
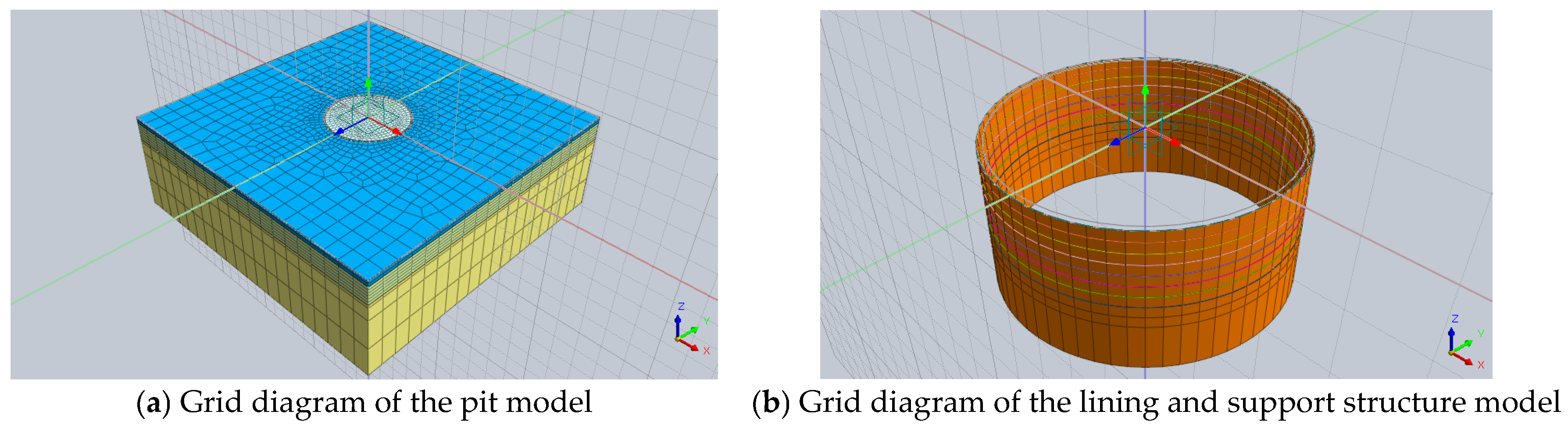








| Working Condition | Construction Steps |
|---|---|
| 0 | Initial state |
| 1 | Construction of diaphragm wall |
| 2 | Construction of the cap beam and excavation of the first and second layers |
| 3 | Construction of the second layer of lining and excavation of the third layer |
| 4 | Construction of the third layer of lining and excavation of the fourth layer |
| 5 | Construction of the fourth layer of lining and excavation of the fifth layer |
| 6 | Construction of the fifth layer of lining and excavation of the sixth layer |
| 7 | Construction of the sixth layer of lining and excavation of the seventh layer |
| 8 | Construction of the seventh layer of lining and excavation of the eighth layer |
| 9 | Construction of the eighth layer of lining and excavation of the ninth layer |
| Working Condition | Construction Steps | Location of Groundwater Head |
|---|---|---|
| 1 | Completion of diaphragm wall construction | The water head inside and outside the foundation pit is the same and level with the ground |
| 2 | Completion of the excavation of the second layer | the water head outside the foundation pit is level with the ground, and the water head inside the foundation pit is at the bottom of the second layer of excavation |
| 3 | Completion of the excavation of the third layer | the water head outside the foundation pit remains unchanged, while the water head inside the foundation pit is at the bottom of the third layer of excavation |
| 4 | Completion of the excavation of the fourth layer | the water head outside the foundation pit remains unchanged, while the water head inside the foundation pit is at the bottom of the fourth layer of excavation |
| 5 | Completion of the excavation of the fifth layer | the water head outside the foundation pit remains unchanged, while the water head inside the foundation pit is at the bottom of the fifth layer of excavation |
| 6 | Completion of the excavation of the sixth layer | the water head outside the foundation pit remains unchanged, while the water head inside the foundation pit is at the bottom of the sixth layer of excavation |
| 7 | Completion of the excavation of the seventh layer | the water head outside the foundation pit remains unchanged, while the water head inside the foundation pit is at the bottom of the seventh layer of excavation |
| 8 | Completion of the excavation of the eighth layer | the water head outside the foundation pit remains unchanged, while the water head inside the foundation pit is at the bottom of the eighth layer of excavation |
| 9 | Completion of the excavation of the ninth layer | the water head outside the foundation pit remains unchanged, while the water head inside the foundation pit is at the bottom of the ninth layer of excavation |
| Soil Layer | Elastic Modulus (kN/m2) | Poisson’s Ratio | Friction Angle (°) | Cohesion (kN/m2) | Unit Weight (kN/m3) | Permeability Coefficient (cm/s) |
|---|---|---|---|---|---|---|
| Silt | 10,000 | 0.3 | 5 | 10 | 15.4 | 1.15 × 10−6 |
| Muddy soil | 30,000 | 0.27 | 5 | 10 | 16.5 | 1.18 × 10−6 |
| Fine sand | 60,000 | 0.23 | 25 | 0 | 19 | 5.01 × 10−3 |
| Medium sand | 100,000 | 0.24 | 25 | 0 | 19.5 | 1.21 × 10−2 |
| Coarse sand | 300,000 | 0.22 | 25 | 0 | 18.8 | 3.12 × 10−2 |
| Strong weathered mudstone | 1,100,000 | 0.19 | 30 | 450 | 19.99 | 1.02 × 10−4 |
| Middle weathered mudstone | 1,100,000 | 0.17 | 35 | 450 | 20.5 | 1.14 × 10−5 |
| Micro-weathered mudstone | 1,100,000 | 0.15 | 35 | 450 | 20.7 | 9.71 × 10−7 |
| Soil Layer | Elastic Modulus (kN/m2) | Poisson’s ratio | Friction Angle (°) | Cohesion (kN/m2) | Unit Weight (kN/m3) | Permeability Coefficient (cm/s) |
|---|---|---|---|---|---|---|
| Silt | 3000 | 0.3 | 3 | 5 | 15.4 | 1.15 × 10−6 |
| Muddy soil | 50,000 | 0.27 | 5 | 8 | 16.5 | 1.18 × 10−6 |
| Fine sand | 80,000 | 0.23 | 18 | 0 | 19 | 5.01 × 10−3 |
| Medium sand | 120,000 | 0.24 | 25 | 0 | 19.5 | 1.21 × 10−2 |
| Coarse sand | 200,000 | 0.22 | 28 | 0 | 18.8 | 3.12 × 10−2 |
| Strong weathered mudstone | 500,000 | 0.19 | 20 | 50 | 19.99 | 1.02 × 10−4 |
| Middle weathered mudstone | 1,000,000 | 0.17 | 30 | 450 | 20.5 | 1.14 × 10−5 |
| Micro-weathered mudstone | 1,400,000 | 0.15 | 35 | 600 | 20.7 | 9.71 × 10−7 |
| Structure | Elastic Modulus (kN/m2) | Weight Measurement (kN/m3) | Poisson’s Ratio |
|---|---|---|---|
| Diaphragm wall | 3.0 × 107 | 25 | 0.2 |
| Lining | 3.0 × 107 | 25 | 0.2 |
| Working Condition | No Pore Water Pressure Applied | Pore Water Pressure Applied | Regional Morphology | ||
|---|---|---|---|---|---|
| Maximum Value (1) | Position | Maximum Value (1) | Position | ||
| 2 | 7.56959 × 10−3 | Bottom edge of foundation pit | 7.33992 × 10−3 | Bottom edge of foundation pit | Circular distribution |
| 3 | 1.13526 × 10−2 | Bottom edge of foundation pit | 1.20842 × 10−2 | Bottom edge of foundation pit | Circular distribution |
| 4 | 1.37693 × 10−2 | Bottom edge of foundation pit | 1.53166 × 10−2 | Bottom edge of foundation pit | Circular distribution |
| 5 | 1.53290 × 10−2 | Bottom edge of foundation pit | 1.73822 × 10−2 | Bottom edge of foundation pit | Circular distribution |
| 6 | 1.50441 × 10−2 | Bottom edge of foundation pit | 1.67615 × 10−2 | Bottom edge of foundation pit | Circular distribution |
| 7 | 1.15651 × 10−2 | Bottom edge of foundation pit | 1.25059 × 10−2 | Bottom edge of foundation pit | Circular distribution |
| 8 | 4.10912 × 10−4 | The junction of the fourth and fifth lining. | 7.58077 × 10−4 | The middle of the fifth lining. | Circular distribution |
| 9 | 4.47740 × 10−4 | The junction of the fifth and sixth lining. | 8.58466 × 10−4 | The middle of the fifth lining. | Circular distribution |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Bi, Y.; Dong, Y.; Wang, J.; Liu, X.; Li, J. Research on the Response Characteristics of Excavation and Support in Circular Sand Soil Foundation Pit Based on Parameter Verification. J. Mar. Sci. Eng. 2025, 13, 349. https://doi.org/10.3390/jmse13020349
Gao X, Bi Y, Dong Y, Wang J, Liu X, Li J. Research on the Response Characteristics of Excavation and Support in Circular Sand Soil Foundation Pit Based on Parameter Verification. Journal of Marine Science and Engineering. 2025; 13(2):349. https://doi.org/10.3390/jmse13020349
Chicago/Turabian StyleGao, Xuhe, Yanqiu Bi, Yi Dong, Jiading Wang, Xiaoling Liu, and Jiachun Li. 2025. "Research on the Response Characteristics of Excavation and Support in Circular Sand Soil Foundation Pit Based on Parameter Verification" Journal of Marine Science and Engineering 13, no. 2: 349. https://doi.org/10.3390/jmse13020349
APA StyleGao, X., Bi, Y., Dong, Y., Wang, J., Liu, X., & Li, J. (2025). Research on the Response Characteristics of Excavation and Support in Circular Sand Soil Foundation Pit Based on Parameter Verification. Journal of Marine Science and Engineering, 13(2), 349. https://doi.org/10.3390/jmse13020349








