Innovations in Wave Energy: A Case Study of TALOS-WEC’s Multi-Axis Technology

Abstract

The technologically advanced learning ocean system—wave energy converter (TALOS-WEC) project addresses the urgent need for sustainable and efficient energy solutions by leveraging the vast potential of wave energy. This project presents a pioneering approach to wave energy capture through its unique multi-axis and omnidirectional point absorber design. Featuring a fully enclosed power take-off (PTO) system, the TALOS-WEC harnesses energy across six degrees of freedom (DoFs) using an innovative internal reaction mass (IRM) mechanism. This configuration enables efficient energy extraction from the relative motion between the IRM and the hull, aiming for energy conversion efficiencies ranging between 75–80% under optimal conditions, while ensuring enhanced durability in harsh marine environments. The system’s adaptability is reflected in its versatile geometric configurations, including triangular, octagonal, and circular designs, customised for diverse marine conditions. Developed at Lancaster University, UK, and supported by international collaborations, the TALOS-WEC project emphasises cutting-edge advancements in hydrodynamic modelling, geometric optimisation, and control systems. Computational methodologies leverage hybrid frequency-time domain models and advanced panel codes (WAMIT, HAMS, and NEMOH) to address non-linearities in the PTO system, ensuring precise simulations and optimal performance. Structured work packages (WPs) guide the project, addressing critical aspects such as energy capture optimisation, reliability enhancement, and cost-effectiveness through innovative monitoring and control strategies. This paper provides a comprehensive overview of the TALOS-WEC, detailing its conceptual design, development, and validation. Findings demonstrate TALOS’s potential to achieve scalable, efficient, and robust wave energy conversion, contributing to the broader advancement of renewable energy technologies. The results underscore the TALOS-WEC’s role as a cutting-edge solution for harnessing oceanic energy resources, offering perspectives into its commercial viability and future scalability.

1. Introduction

The global energy demand is projected to rise by 20–30% by 2040, underscoring the urgent need to transition from fossil fuels, which currently account for 78.5% of global energy consumption, to renewable energy sources (RES), which contribute only 12.6% [1,2,3,4,5,6]. Ocean energy is a promising type of RES due to its abundance, predictability, and environmental benefits. Systems harnessing power from waves, tides, currents, and thermal gradients can enhance energy security and sustainability [7,8,9,10,11].

Wave energy, in particular, stands out for its high energy density, 24/7 availability, and greater predictability compared to wind [12,13,14]. With a global potential of 32,000 TWh/year and approximately 2 TW of extractable power, wave energy has the capacity to meet a substantial share of global energy demand [15]. In Europe, wave energy resources, such as those off the coasts of Ireland and Scotland (70 kW/m), could generate 50 TWh/year, covering 16% of the UK’s annual electricity consumption [16,17].

Wave energy converters (WECs) are essential for extracting this energy and come in various designs, such as point absorbers, oscillating water columns, and overtopping devices, deployed across onshore, nearshore, and offshore locations [18,19]. The development of commercial systems like the Islay LIMPET, the first grid-connected wave energy device in the UK, highlights progress in this field [20,21].

Despite their potential, WECs face significant challenges, including high costs, low conversion efficiency, and vulnerability to extreme weather [22,23]. To address these issues, innovative designs are essential to enhance efficiency, reliability, and survivability. Over 100 WEC designs have been proposed, with some achieving grid connection and proving feasibility after extensive testing. Research efforts focus on areas such as hydrodynamic performance [24], power take-off (PTO) optimisation [25,26,27,28], and advancements in control strategies [29,30]. The point absorber WEC, characterised by its small size relative to the wavelength, has been widely studied. Examples include Lancaster University’s PS Frog [31], Oregon Limited’s multi-resonant chamber [32], and prototypes from Carnegie Wave Energy Limited. Other notable designs include attenuators, oscillating wave surge converters, oscillating water columns, and terminators. However, most of these are single-axis systems, extracting energy from one direction of motion [33,34]. This inherently limits their energy capture efficiency, as wave motion spans six degrees of freedom (DoFs), including heave, pitch, surge, roll, sway, and yaw.

In response, multi-axis WECs have garnered interest for their ability to utilise multiple motion modes, such as surge, heave, and pitch, to enhance energy extraction efficiency [35,36]. Despite their promise, research and development on multi-axis WECs remain limited compared to single-axis designs due to the complexities of modelling, control, and integration [33,37]. A notable example of a multi-axis WEC is Pelamis, featuring a snake-like structure with interconnected tubes linked by hydraulic rams [35]. The device aligns with wave propagation, and the relative motion between its segments drives the hydraulic rams to generate electricity. Deployed off the coasts of Scotland and Portugal, Pelamis successfully supplied electricity to national grids. However, financial and operational challenges ultimately halted its development when the company became insolvent in 2015.

To the best knowledge of the authors at the time of authorship, the TALOS-WEC is the only existing multi-axis and omnidirectional WEC. It builds on earlier work conducted at Lancaster University, such as the PS Frog, a device designed to capture energy through pitching and surging motions, and subsequent developments like the GAIA multi-axis concept. Elements of the PS Frog were later adopted by École Centrale de Nantes (ECN) in their SeaREV device, which focused solely on pitching motion [32,38,39]. The TALOS-WEC, however, advances the field by incorporating a multi-axis PTO system capable of harnessing energy across all six degrees of freedom. This system consists of a heavy mass ball housed within the hull, connected via springs and hydraulic cylinders (see Figure 1). As waves induce motion in the hull, significant relative movement occurs between the ball and the hull, driving the hydraulic cylinders to pump fluid through a hydraulic circuit to generate electricity. This fully enclosed design not only maximises energy absorption but also enhances durability in harsh marine environments, a feature shared by other advanced enclosed WECs like the Lancaster University PS Frog and SeaREV.

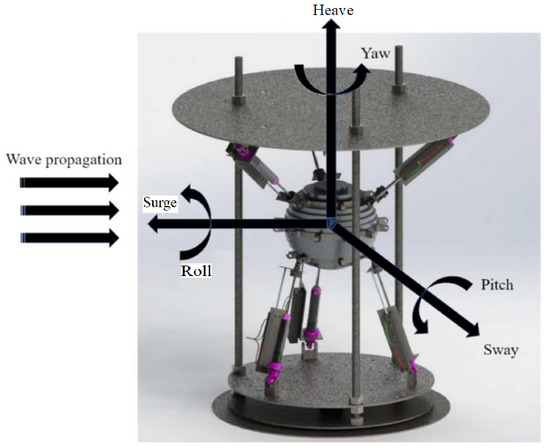
Figure 1. TALOS six DoFs mechanism (Reproduced with permission from [40]. 2024, Wu, Y., et al.).

The TALOS-WEC leverages a multi-axis design and a fully enclosed PTO system to maximise energy absorption across six degrees of freedom, ensuring durability in harsh marine environments. Developed at Lancaster University, UK, it adopts a novel point absorber-style design. Its PTO system is centred around a heavy internal reaction mass (IRM), strategically housed within the hull and supported by spring dampers. This configuration enables TALOS to capture energy from the relative motion between the IRM and the hull, which remains stable under wave excitations. This versatility allows TALOS to extract energy from multiple motion modes, such as surge, heave, and pitch, significantly enhancing overall efficiency. The fully enclosed PTO system protects moving parts from the corrosive marine environment, making TALOS a robust solution for long-term deployment.

The TALOS project, also known as NHP-WEC, was selected by UK Research and Innovation (UKRI) as part of efforts to advance wave energy technologies and harness oceanic energy resources. The project emphasises refining the TALOS design and PTO system while driving innovations in control systems, monitoring, and resource forecasting. A collaboration in 2023 between Lancaster University and the National Renewable Energy Laboratory (NREL), under the U.S. Department of Energy’s TEAMER programme, further supported the development of numerical models to enhance the system’s reliability and performance. Figure 2 illustrates the various configurations of the TALOS-WEC, highlighting its structural adaptability. The models include triangular, octagonal, and circular configurations, showcasing the system’s versatility in accommodating diverse marine environments.

Figure 2. Various TALOS models.

One of the primary challenges of the TALOS-WEC is modelling the flexible connections between the hull and the IRM, which introduce significant non-linearities in the PTO system. Advanced computational techniques, including an in-house hybrid frequency-time domain modelling approach, are employed to address these complexities. Hydrodynamic parameters are calculated using panel codes such as WAMIT, HAMS, and NEMOH, with results transformed into Cummins’ time-domain equations for precise simulations [41,42]. This approach ensures optimal performance across diverse wave conditions, reinforcing TALOS’s role as a cutting-edge wave energy solution.

The TALOS-WEC project tackles critical challenges through structured work packages (WPs). WP1 focuses on concept development, covering hydrodynamic studies, geometric optimisation, and PTO design to enhance energy capture and structural integrity [43,44,45,46,47,48]. WP2 emphasises reliability and control, integrating smart sensors, artificial intelligence (AI)-based predictive maintenance, and adaptive control systems to optimise performance under variable sea states [40,49,50,51,52,53]. WP3 addresses resource evaluation, including mapping wave energy potential, testing efficiency, and optimising array layouts for maximum energy capture [40,54]. Lastly, WP4 involves validation and cost analysis, ensuring commercial viability through real-world testing, scalability studies, and levelised cost of energy (LCOE) assessments [55,56].

The main purpose of this paper is to provide a comprehensive overview of the TALOS-WEC project, highlighting its innovative design, advanced hydrodynamic modelling, and multi-axis energy extraction capabilities. Specifically, the paper aims to detail the development and validation of the system, address the challenges of wave energy conversion, and present the outcomes of its structured WPs. These efforts underline the system’s potential as a scalable and efficient solution for renewable energy production, contributing to advancements in sustainable ocean energy technologies.

The remainder of this paper is organised as follows: Section 2 explores WPs detailing the TALOS-WEC’s conceptual design, validation, and optimisation. The details of the four WPs are presented in Section 3, Section 4, Section 5 and Section 6. Key findings and results are presented in Section 7. Finally, Section 8 and Section 9 discuss the broader implications of the TALOS-WEC within the renewable energy sector, main challenges faced, and future directions.

2. Work Packages (WPs)

The TALOS-WEC project adopts a pioneering approach to wave energy conversion, addressing critical challenges in efficiency, survivability, and economic viability. Its structured WPs encompass the entire development process, from conceptual design to deployment and validation, ensuring a comprehensive strategy for advancing wave energy technology. Each WP targets specific objectives, integrating advanced engineering solutions and complementary technologies to achieve project goals.

WP1 focuses on concept development, combining experimental and numerical hydrodynamic studies, geometric optimisation, and PTO system design. These efforts define hydrodynamic parameters critical for energy capture, balance efficiency with structural integrity, and create a robust PTO capable of delivering reliable power output [43,44,45,46,47,48].

WP2 addresses survivability, reliability, and control to ensure operational efficiency in harsh marine environments. Key tasks include integrating smart sensors for real-time health monitoring, deploying AI algorithms for predictive maintenance, and implementing adaptive control systems to optimise energy capture under variable wave conditions. Collectively, these measures enhance system reliability, minimise downtime, and extend the device’s operational lifespan [40,49,50,51,52,53].

WP3 centres on sea state forecasting and resource evaluation, crucial for identifying high-energy deployment zones and assessing WEC performance in controlled environments. This includes resource characterisation to map wave energy potential, efficiency testing in wave tanks to establish performance benchmarks, and studying array effects to optimise layouts for multiple WECs [40,54].

Finally, WP4 emphasises validation and cost analysis, involving real-world performance testing, scalability studies for WEC arrays, and a comprehensive levelised cost of energy (LCOE) assessment. These efforts aim to ensure the commercial viability and competitiveness of the TALOS-WEC system [55,56].

Table 1 provides a detailed breakdown of the WPs, their objectives, and expected outcomes.

Table 1. Overview of TALOS-WEC work packages (WPs), objectives, and outcomes.

WP & Objective	Sub-Package	Refs.	Description	Outcome
WP1: Concept Development Establish the foundational design and concept of the WEC.	WP1.1—Experimental and Numerical Hydrodynamics	[43,45,46,47,48]	Study WEC interaction with wave dynamics through wave tank testing and CFD modelling.	Define hydrodynamic parameters for optimal energy capture.
	WP1.2—Geometric Optimisation	[44]	Refine the WEC’s geometry using simulation and testing.	Achieve a balance between energy efficiency and structural integrity.
	WP1.3—PTO Design and Optimisation	[44]	Design an efficient PTO system.	A robust PTO design ensuring reliable power output.
WP2: Survivability, Reliability, and Control Ensure operational reliability in harsh marine environments.	WP2.1—Smart Sensors	N/A	Integrate sensors for real-time monitoring.	Comprehensive data on health and environmental performance.
	WP2.2—Condition Monitoring	[40,51]	Use AI algorithms to assess system health and predict maintenance needs.	Minimised downtime and extended lifespan.
	WP2.3—Predictive Maintenance	[40,51]	Develop models to anticipate failures.	Improved reliability and reduced costs.
	WP2.4—Optimised Control	[49,50,52,53]	Implement adaptive controls for varying sea conditions.	Enhanced energy capture and safe operation.
WP3: Sea State Forecasting and Resource Evaluation Analyse and predict wave resources for optimised deployment.	WP3.1—Resource Characterisation	[40,54]	Map wave energy potential in deployment areas.	Identify high-energy zones for WEC operation.
	WP3.2—Efficiency Testing	[54]	Test WEC performance in wave tanks.	Establish performance benchmarks for marine conditions.
	WP3.3—Array Effects	N/A	Study the interactions between multiple WECs in arrays.	Optimise array layout to maximise energy capture.
WP4: Validation and Cost Analysis Validate performance and assess economic feasibility of the WEC.	WP4.1—Validation and Demonstration	N/A	Conduct real-world testing to validate performance.	Verified data for commercialisation.
	WP4.2—Array Deployment	N/A	Test scalability of WEC arrays.	Awarenesses into large-scale deployment challenges.
	WP4.3—LCOE Assessment	[55,56]	Calculate the LCOE.	Cost analysis to ensure commercial competitiveness.

3. WP1: Concept Development

WP1 establishes the foundational design and concept of the TALOS-WEC by addressing critical aspects of system performance and design through three sub-packages. WP1.1 focuses on validating hydrodynamic models and studying wave–structure interactions via laboratory experiments and numerical simulations. WP1.2 emphasizes geometric optimisation to enhance energy capture and hydrodynamic stability across varying wave conditions. WP1.3 develops efficient PTO systems, ensuring alignment with the WEC’s hydrodynamic and geometric configurations.

3.1. WP1.1—Experimental and Numerical Hydrodynamics

WP1.1 develops a comprehensive hydrodynamic framework for evaluating and optimising the TALOS-WEC. It establishes the theoretical basis of hydrodynamic modelling, including key equations, force components, and numerical approaches, and provides detailed analyses of hydrodynamic coefficients critical to performance. Validation studies using CFD results benchmark numerical tools, while additional intutions explore mooring effects and power absorption trends.

3.1.1. Hydrodynamic Modelling Framework

The TALOS-WEC faces challenges from dynamic wave–structure interactions, requiring optimisation of energy absorption, stability, and structural integrity in harsh marine environments [43,45]. Accurate hydrodynamic modelling is crucial for predicting system responses to varying sea conditions, supporting the optimised design and operational strategies.

• Governing equations

The TALOS-WEC adopts a multibody configuration comprising a primary floater (hull) and an internal reaction mass (sphere, also referred to as the ball) connected via a PTO system. These components are dynamically coupled through the PTO system and the restoring spring force, enabling energy extraction from their relative motion. The dynamics of each component are governed by distinct yet interdependent equations, as described below.

Dynamics of the Hull: The hull’s motion is influenced by wave-induced forces, hydrodynamic effects, and the PTO system. Its dynamic response is governed by the Cummins time-domain equation [43,45]:

$$\begin{array}{cc}\hfill (M_{\mathrm{hull}}+m_{\infty ,\mathrm{hull}}){\ddot{x}}_{\mathrm{hull}}\left(t\right)+{\int }_0^{t}B(t-\tau ){\dot{x}}_{\mathrm{hull}}\left(\tau \right)d\tau & +C{x}_{\mathrm{hull}}\left(t\right)+K{x}_{\mathrm{hull}}\left(t\right)\hfill \\ \hfill & =F_{\mathrm{exc}}\left(t\right)+F_{\mathrm{PTO},\mathrm{res}}\left(t\right),\hfill \end{array}$$

(1)

where $M_{\mathrm{hull}}$ represents the structural mass of the hull (in kg), $m_{\infty ,hull}$ accounts for the added mass due to hydrodynamic effects at infinite frequency, and $B(t-\tau )$ is the radiation damping kernel that captures energy dissipation through radiated waves. ${\mathbf{x}}_{\mathrm{hull}}\left(\mathbf{t}\right)$, ${\dot{\mathbf{x}}}_{\mathrm{hull}}\left(\mathbf{t}\right)$, and ${\ddot{\mathbf{x}}}_{\mathrm{hull}}\left(\mathbf{t}\right)$ represent the displacement (location), velocity, and acceleration of the hull as functions of time t, respectively. The coefficient C describes the hydrostatic restoring forces acting on the hull, while K is the mooring stiffness coefficient providing stability. The terms $F_{\mathrm{exc}}\left(t\right)$ and $F_{{\mathrm{PTO}}_{\mathrm{res}}}\left(t\right)$ represent the wave excitation force caused by incident waves and resistive force generated by the PTO system, respectively. $F_{\mathrm{exc}}\left(t\right)$ is expressed as follows:

$$F_{\mathrm{exc}}\left(t\right)={\int }_0^t{K}_{\mathrm{exc}}(t-\tau )\eta \left(\tau \right)d\tau ,$$

(2)

where $K_{\mathrm{exc}}\left(t\right)$ is the excitation impulse response function (IRF), and $\eta \left(\tau \right)$ represents wave elevation. For the k-th degree of freedom (e.g., surge, heave, or pitch), the wave excitation force, $F_{\mathrm{exc},k}\left(t\right)$, can be further expressed in terms of the response amplitude operators (RAOs) as follows:

$$F_{\mathrm{exc},k}\left(t\right)=RA{O}_k·A_w·F_{\mathrm{wave},k}\left(t\right),$$

(3)

where $RA{O}_k$ is the RAO for the k-th mode, $A_w$ is the wave amplitude, and $F_{\mathrm{wave},k}\left(t\right)$ represents the wave-induced force specific to that degree of freedom. RAOs provide a critical link between wave-induced forces and the dynamic response of the TALOS-WEC, enabling a deeper understanding of system performance. RAOs are defined as the ratio of the displacement amplitude of a specific motion mode ${\xi }_k$ to the wave amplitude $A_w$:

$$RA{O}_k={\displaystyle \frac{{\xi }_k}{A_w}}.$$

(4)

The resistive force generated by the PTO system, $F_{{\mathrm{PTO}}_{\mathrm{res}}}\left(t\right)$, extracts energy from the relative motion between the hull and the internal reaction mass and is given by [57]:

$$F_{{\mathrm{PTO}}_{\mathrm{res}}}\left(t\right)=-B_{\mathrm{PTO}}·({\dot{x}}_{\mathrm{ball}}\left(t\right)-{\dot{x}}_{\mathrm{hull}}\left(t\right))=-B_{\mathrm{PTO}}·V_{\mathrm{rel}},$$

(5)

where $B_{\mathrm{PTO}}$ is the PTO damping coefficient, and $V_{\mathrm{rel}}$ represents the relative velocity between the floater and the internal reaction mass. The variables $x_{\mathrm{ball}}$ denotes the position of the ball.

Under realistic conditions, the hull’s dynamics are influenced by additional forces arising from buoyancy, drag, friction, viscous damping, mooring forces, nonlinear hydrodynamics, and the restoring spring force. The extended governing equation for the hull’s motion is given by [49]:

$$\begin{array}{cc}\hfill m_{\mathrm{hull}}{\ddot{x}}_{\mathrm{hull}}\left(t\right)=& F_{\mathrm{exc}}\left(t\right)+F_{\mathrm{hs}}\left(t\right)-F_{\mathrm{rad}}\left(t\right)-F_{\mathrm{buoy}}\left(t\right)-F_{\mathrm{drag}}\left(t\right)-F_{\mathrm{fric}}\left(t\right)-F_{\mathrm{v}}\left(t\right)-F_{\mathrm{m}}\left(t\right)+\hfill \\ \hfill & F_{\mathrm{nh}}\left(t\right)+F_{\mathrm{rest}}\left(t\right)-F_{{\mathrm{PTO}}_{\mathrm{res}}}\left(t\right),\hfill \end{array}$$

(6)

where $F_{\mathrm{v}}$, $F_{\mathrm{m}}$, and $F_{\mathrm{nh}}$ are viscous damping force, mooring force, and nonlinear hydrodynamic force, respectively. $F_{\mathrm{hs}}\left(t\right)$ represents the hydrostatic restoring force, expressed as follows:

$$F_{\mathrm{hs}}=K_{\mathrm{h}}\Delta q,$$

(7)

where $K_{\mathrm{h}}$ is the hydrostatic stiffness matrix, and $\Delta q$ is the displacement. The radiation force $F_{\mathrm{rad}}\left(t\right)$ accounts for energy radiated through outgoing waves and is given by [58]:

$$F_{\mathrm{rad}}\left(t\right)={\int }_0^t{K}_{\mathrm{rad}}(t-\tau )\dot{x}\left(\tau \right)d\tau ,$$

(8)

where $K_{\mathrm{rad}}\left(t\right)$ is the radiation IRF, and $\dot{x}\left(\tau \right)$ is the velocity of the structure. Additional forces include $F_{\mathrm{v}}$, the viscous damping force, $F_{\mathrm{m}}$, the mooring force, and $F_{\mathrm{nh}}$, which represents the nonlinear hydrodynamic force acting on the system. $F_{\mathrm{buoy}}\left(t\right)$ represents buoyancy force acting on the hull, expressed as [49]:

$$F_{\mathrm{buoy}}=\pi \rho g{R}_b^2\left(1-{\displaystyle \frac{|x_{\mathrm{hull}}|x_{\mathrm{hull}}}{3R_b^2}}\right)x_{\mathrm{hull}},$$

(9)

where $\rho$ is the fluid density (approximately 1025 kg/m³), g is the gravitational acceleration, and $R_b$ represents the characteristic radius of the hull.

$F_{\mathrm{drag}}\left(t\right)$ is the drag force due to relative motion with the fluid, given by

$$F_{\mathrm{drag}}=0.5\rho A_w{C}_d|{\dot{x}}_{\mathrm{hull}}-v_f|({\dot{x}}_{\mathrm{hull}}-v_f),$$

(10)

where $A_w$ is the wetted area, $C_d$ is the drag coefficient, and $v_f$ is the fluid velocity.

$F_{\mathrm{rest}}\left(t\right)$ represents the restoring Spring Force and is given by

$$F_{\mathrm{rest}}\left(t\right)=K_{\mathrm{PTO}}·(x_{\mathrm{ball}}\left(t\right)-x_{\mathrm{hull}}\left(t\right)),$$

(11)

where $K_{\mathrm{PTO}}$ is the spring stiffness coefficient between the ball and the hull. $F_{{\mathrm{PTO}}_{\mathrm{mech}}}\left(t\right)$ refers to the mechanical-hydraulic PTO force acting on the ball, given by

Lastly, $f_{\mathrm{fric}}\left(t\right)$ represents the friction force, expressed as follows:

$$F_{\mathrm{fric}}=F_n{\mu }_{d}tanh\left(\alpha {\dot{x}}_{\mathrm{hull}}\right)+{\mu }_s{\dot{x}}_{\mathrm{hull}}+F_n({\mu }_s-{\mu }_d)e^{-\left(\right|{\dot{x}}_{\mathrm{hull}}{|/v_s)}^2}tanh\left(\alpha {\dot{x}}_{\mathrm{hull}}\right),$$

(12)

where $F_n$ is the normal force, ${\mu }_d$ and ${\mu }_s$ are the dynamic and static friction coefficients, respectively, $\alpha$ is a scaling parameter, and $v_s$ is a velocity threshold.

Dynamics of the Ball: The internal reaction mass (ball) is connected to the hull via a spring and the PTO system. Its motion is influenced by the relative displacement and velocity between the ball and the hull. The equation governing the ball’s dynamics is

$$M_{\mathrm{ball}}{\ddot{x}}_{\mathrm{ball}}\left(t\right)=-F_{\mathrm{rest}}\left(t\right)-F_{{\mathrm{PTO}}_{\mathrm{res}}}\left(t\right)-F_{{\mathrm{PTO}}_{\mathrm{mech}}}\left(t\right),$$

(13)

where $M_{\mathrm{ball}}$ is the mass of the internal reaction mass (ball).

$$F_{{\mathrm{PTO}}_{\mathrm{mech}}}\left(t\right)=|P_A-P_B|·A_{\mathrm{cyl}}·\mathrm{sign}({\dot{x}}_{\mathrm{ball}}\left(t\right)-{\dot{x}}_{\mathrm{hull}}\left(t\right)),$$

(14)

where $P_A$ and $P_B$ are the pressures in the hydraulic cylinder chambers, $A_{\mathrm{cyl}}$ is the piston area, and the sign function ensures the force direction depends on the relative velocity.

The interactions between $F_{{\mathrm{PTO}}_{\mathrm{res}}}$, $F_{{\mathrm{PTO}}_{\mathrm{mech}}}$, and $F_{\mathrm{rest}}$ allow efficient harvesting of energy from the relative motion.

The governing equations include boundary conditions to enhance simulation realism, applying dynamic and kinematic constraints at the free surface, linking velocity potential to structural motion for fluid–structure interactions, and enforcing a no-flow condition at the seabed to reflect real-world environments [44].

• Hydrodynamic coefficients

Hydrodynamic coefficients are crucial in defining the interaction between the WEC and the surrounding fluid, governing added mass, damping, and excitation forces. Added mass ($A_{ij}$) quantifies increased inertia from water movement, with TALOS showing the highest values in heave ($4.2·{10}^6\mathrm{N}/\mathrm{m}$) due to strong vertical interaction. Radiation Damping ($B_{ij}$) capture energy dissipation, also highest in heave ($7.8·{10}^4\mathrm{N}/\mathrm{m}$), emphasising the importance of radiation effects. Wave excitation forces ($F_{\mathrm{exc}}$) drive structural motion, with heave experiencing the largest forces ($8.6·{10}^5\mathrm{N}/\mathrm{m}$), highlighting TALOS’s efficiency in vertical energy capture [59].

Derived from potential flow theory, the velocity potential $\varphi$ satisfies Laplace’s equation ${\nabla }^2\varphi =0$, decomposed into components for incident (${\varphi }_I$), diffraction (${\varphi }_D$), and radiation (${\varphi }_R$) interactions. The TALOS-WEC’s hydrodynamic behaviour was analysed across six degrees of freedom (surge, sway, heave, roll, pitch, yaw), with specific motions influenced by geometry, mooring systems, and PTO configuration [60].

Table 2 summarises the hydrodynamic coefficients across all six degrees of freedom (shown in Figure 1). Notable findings include higher added mass in sway compared to surge due to lateral wave interactions, significant radiation damping in roll stabilising rotational motion, and sensitivity of sway, roll, and yaw to oblique wave angles, emphasising dynamic coupling in multi-directional sea states.

Table 2. Hydrodynamic coefficients for TALOS-WEC across six degrees of freedom [43,45,46].

Coefficient	Surge (kg)	Sway (kg)	Heave (kg)	Roll (kg·m2)	Pitch (kg·m2)	Yaw (kg·m2)
Added Mass $A_{ij}$	$2.5·{10}^6$	$3.0·{10}^6$	$4.2·{10}^6$	$1.7·{10}^6$	$1.3·{10}^6$	$8.5·{10}^5$
Coefficient	Surge (Ns/m)	Sway (Ns/m)	Heave (Ns/m)	Roll (Nms/rad)	Pitch (Nms/rad)	Yaw (Nms/rad)
Damping $B_{ij}$	$5.3·{10}^4$	$6.1·{10}^4$	$7.8·{10}^4$	$5.6·{10}^3$	$4.1·{10}^3$	$3.0·{10}^3$
Coefficient	Surge (N)	Sway (N)	Heave (N)	Roll (Nm)	Pitch (Nm)	Yaw (Nm)
Wave Excitation Force $F_{exc}$	$1.1·{10}^5$	$1.3·{10}^5$	$8.6·{10}^5$	$4.0·{10}^4$	$3.7·{10}^4$	$2.8·{10}^4$

• Frequency-domain and time-domain analyses

The frequency-dependent hydrodynamic coefficients and exciting forces for the TALOS-WEC demonstrate distinct behaviours across surge, heave, and pitch motions. Added mass in surge is higher at low frequencies due to larger fluid volumes engaged, while heave exhibits a sharper decrease as oscillation frequency increases, reflecting reduced fluid coupling. Radiation damping shows moderate values for surge and pronounced resonance peaks for heave at intermediate frequencies, highlighting its sensitivity to oscillatory behaviour. Excitation forces are most significant in surge and heave at low frequencies, while pitch forces display more complex trends due to rotational dynamics.

The time-domain impulse response functions (IRFs) provide intuitions into transient behaviours. Surge IRFs emphasize radiation damping and decay, heave IRFs highlight vertical responses, and pitch IRFs capture rotational dynamics. Coupled interactions, such as between surge and pitch, illustrate energy transfer across motion modes. These analyses employ complementary computational methods to ensure robustness and consistency, reflecting the system’s multi-modal interactions and dynamic responses [61,62].

3.1.2. Numerical Tools for Hydrodynamic Analysis

Hydrodynamic modelling of the TALOS-WEC utilises numerical tools to predict key parameters, such as added mass, radiation damping, and wave excitation forces. This study evaluates three boundary element method (BEM)-based tools: WAMIT, NEMOH, and HAMS [63,64,65]. Each tool was chosen for its unique strengths in addressing specific modelling challenges, such as handling thin structures, overlapping panels, and multi-body dynamics.

These tools solve the velocity potential $\varphi$ which satisfies Laplace’s equation (${\nabla }^2\varphi =0$) subject to boundary conditions defined by free surface interactions, seabed constraints, and structure geometry.

Table 3 summarises the functionalities of WAMIT, HAMS, and NEMOH, highlighting their suitability for TALOS-WEC applications. While WAMIT excels in accuracy and advanced capabilities, it is computationally intensive and costly. HAMS offers a balance between precision and runtime efficiency, making it suitable for most TALOS applications. NEMOH, as an open-source tool, is a cost-effective choice for initial studies but struggles with complex configurations, such as overlapping panels and thin structures.

Table 3. Comparison of WAMIT, HAMS, and NEMOH functionalities [45,63,64,65].

Feature/Capability	WAMIT	HAMS	NEMOH
Runtime (125 frequencies)	1395 s	1076 s	5620 s
Multi-core support	Yes	Yes	No
Thin structures handling	Effective	Effective	Limited
Overlapping panels	Effective	Effective	Limited
Impulse response functions	Yes	Yes	Yes
Irregular frequency removal	Yes	Yes	No
RAO computation	Yes	Yes	Limited
Accuracy (based on validation)	High	High	Moderate
Mesh sensitivity	Low	Low	High
Cost (Licensing/Usage)	High	Moderate	Open-source
User interface	Moderate (command-line)	Moderate (command-line)	Moderate (command-line with MATLAB wrapper)
Applications for TALOS	Excellent	Excellent	Adequate

• Validation and Accuracy of Numerical Tools

The numerical tools (i.e., WAMIT, HAMS, and NEMOH) were validated by comparing key hydrodynamic parameters, such as added mass, radiation damping, and wave excitation forces, for surge motion across various frequencies (Figure 3). WAMIT and HAMS demonstrated consistent accuracy across all frequencies, effectively handling complex geometries, while NEMOH showed reliability only at lower frequencies, with deviations at higher frequencies due to its limitations in modelling overlapping panels and thin structures [45].

Figure 3. Hydrodynamic coefficients for surge motion of the TALOS device across various frequencies using different numerical tools (i.e., WAMIT, HAMS, and NEMOH) (Reproduced with permission from [45]. 2022, Sheng, W., et al.).

For sway motion, WAMIT and HAMS maintained robust accuracy, but NEMOH’s reliability diminished at higher frequencies. Heave motion, critical for vertical energy absorption, showed strong agreement between WAMIT and HAMS, whereas NEMOH exhibited increasing deviations. Similarly, WAMIT and HAMS accurately predicted pitch motion, while NEMOH struggled with the complex rotational dynamics at higher frequencies. For roll motion, WAMIT and HAMS effectively modelled dynamics across frequencies, whereas NEMOH faced challenges due to its sensitivity to coupled interactions and geometric intricacies.

3.1.3. Numerical Modelling

Numerical modelling is essential for assessing the dynamic behaviour of the TALOS-WEC under varying wave excitations and PTO configurations. Numerical simulations utilise WEC-Sim, which is an open-source tool developed in the MATLAB/Simulink environment. WEC-Sim enables coupling between the hydrodynamic response of the TALOS-WEC and the hydraulic PTO system for comprehensive system performance evaluation. Hydrodynamic coefficients (i.e., added mass, radiation damping, and excitation forces) were pre-computed using linear potential flow solvers like WAMIT [47].

• Hydraulic PTO System Modelling

The hydraulic PTO comprises several key components: the hydraulic cylinder, which serves as the core energy conversion device, transforms mechanical motion into hydraulic power. Check valves ensure unidirectional fluid flow by rectifying hydraulic movement for consistent operation. Hydraulic accumulators store pressurised fluid energy, stabilize system dynamics, and regulate stiffness. The hydraulic motor converts pressurised fluid into rotational mechanical energy, which the electric generator then transforms into electrical power [66,67].

The hydraulic PTO system for the TALOS-WEC is designed with six symmetrically distributed PTOs to balance forces and enhance energy transfer. The system has a total power capacity of 2.4 MW, with each PTO unit capable of delivering 400 kW. It operates at a maximum hydraulic pressure of 5000 psi and supports a maximum flow rate of 700 litres per minute, ensuring efficient energy conversion and robust system performance [47]. Table 4 specifies the attachment locations for these PTOs.

Table 4. PTO attachment locations in the TALOS-WEC (relative to center of mass (CoM)).

PTO	Hull (m)			Sphere (m)
	x	y	z	x	y	z
PTO1	5.00	0	8.66	2.50	0	4.33
PTO2	−2.50	4.33	8.66	−1.25	2.16	4.33
PTO3	−2.50	−4.33	8.66	−1.25	−2.16	4.33
PTO4	5.00	0	−8.66	2.50	0	−4.33
PTO5	−2.50	4.33	−8.66	−1.25	2.16	−4.33
PTO6	−2.50	−4.33	−8.66	−1.25	−2.16	−4.33

3.1.4. Validation of TALOS-WEC Numerical Models Using CFD

Accurate modelling of wave–structure interactions is critical for the performance and reliability of WECs. To validate the HydroChrono numerical model for TALOS-WEC applications, high-fidelity computational fluid dynamics (CFD) simulations were conducted. These simulations provide a benchmark for assessing HydroChrono’s accuracy and highlight its utility for advanced hydrodynamic analysis [43,68].

The CFD simulations of the TALOS buoy were performed using ANSYS^® Fluent, Release 2021R2, as an unsteady Reynolds-averaged Navier–Stokes (URANS) simulation. Figure 4a illustrates the computational domain and overset mesh configuration used for the CFD simulation setup. The rectangular domain spans dimensions of 1 km × 1 km × 200 m, where the horizontal axes (X and Y) and vertical axis (Z) are shown in metres. The green fill represents the initial location of the air–water interface, which is set as a constant baseline in the simulation. The grey surface at the bottom indicates the stationary wall boundary condition, while symmetry boundary conditions are applied to the sides, and fixed pressure is maintained at the top boundary. The spherical overset zone, highlighted in the magnified insert, demonstrates mesh refinement near the TALOS buoy and the expected location of the free surface. Table 5 summarises the CFD setup parameters, including time-stepping and boundary conditions.

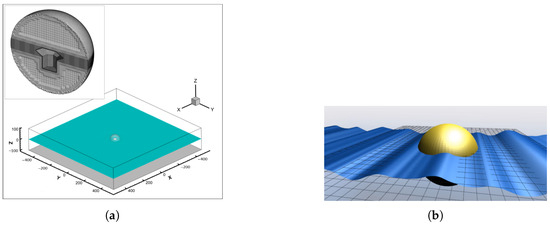
Figure 4. CFD validation setup and HydroChrono simulation results for TALOS-WEC: the X-axis represents the horizontal distance, the Y-axis represents the width, and the Z-axis represents the vertical dimension. (a) CFD domain and overset mesh used for TALOS-WEC simulations. (b) HydroChrono simulation of a floating body in irregular waves. (Reproduced with permission from [43]. 2023, Ogden, D., et al.).

Table 5. CFD setup parameters for TALOS-WEC validation (Adopted with permission from [43]. 2023, Ogden, D., et al.).

Parameter	Value	Description
Domain Size	$1000\times 1000\times 200\mathrm{m}$	Defines the computational domain dimensions, ensuring sufficient space to capture wave–structure interactions and minimise boundary effects.
Mesh Type	Overset Mesh	Refined overlapping grids near the TALOS structure allow for detailed resolution while enabling flexible simulation of large wave domains.
Boundary Conditions	Pressure outlet, symmetry walls	Configures flow behaviour at domain boundaries, ensuring waves and fluid exit the domain without reflections.
Time Step	$0.05\mathrm{s}$	Specifies the temporal resolution for accurately capturing dynamic responses while maintaining numerical stability.

The CFD validation process compared the dynamic behaviour of TALOS-WEC under regular and irregular wave conditions against HydroChrono predictions. The results showed strong agreement, affirming HydroChrono’s reliability in predicting hydrodynamic forces, motion responses, and energy capture efficiency. This validation established a solid foundation for using HydroChrono in further design iterations of TALOS.

It is important to note that the CFD modelling presented in this study focuses exclusively on decay tests and does not include wave conditions. These decay tests were conducted to evaluate the natural oscillatory behaviour of the TALOS-WEC following initial perturbations, serving as robust benchmarks for validating HydroChrono against CFD results. Figure 5a and Figure 5b present the outcomes for heave and pitch decay tests, respectively. The results demonstrate that HydroChrono accurately replicates CFD observations, particularly in capturing buoyancy-driven stabilisation dynamics in heave and rotational inertia effects in pitch. This agreement further reinforces HydroChrono’s capability to model the complex nonlinear interactions critical to TALOS-WEC’s performance.

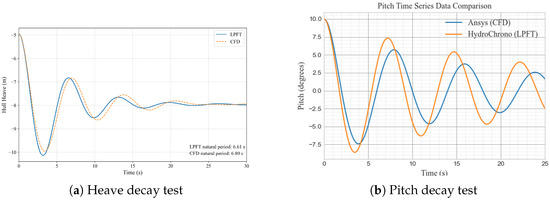
Figure 5. HydroChrono (LPFT) vs CFD test results (Reproduced with permission from [43]. 2023, Ogden, D., et al.).

It must be mentioned that the vertical domain of 200 m (in simulations as outlined in Table 5) was chosen to represent a realistic water depth that might be encountered in real sea conditions. This depth is generally regarded as deep water for most wave energy converters, providing a valid and practical testing environment for the TALOS buoy. Although the fluctuations shown in Figure 5 appear to be −5 to 10 m, the additional vertical space ensures numerical stability, prevents boundary effects, and supports high-fidelity modelling of wave–structure interactions. It should also be noted that the domain shown in Figure 5 represents a smaller section of the computational domain for improved visual clarity, while the full dimensions are outlined in Table 5.

3.1.5. Mooring System Effects on Hydrodynamics

The mooring system plays a critical role in the hydrodynamic performance of the TALOS-WEC, affecting motion responses, energy absorption, and overall stability [69,70]. This subsection examines the system’s behaviour under two mooring configurations: slack (MLC1) and moderately slack (MLC2). Figure 6 illustrates the four-leg mooring system’s geometry and layout, emphasising the spatial arrangement and interaction of the mooring lines with the TALOS-WEC under wave conditions.

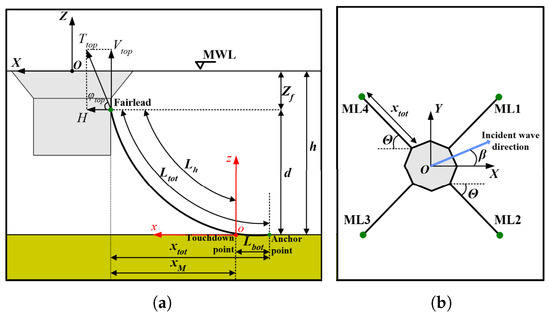
Figure 6. Mooring system for TALOS-WEC. (a) Mooring line in the vertical plane. (b) Four-leg mooring system for TALOS-WEC. (Reproduced with permission from [48]. 2024, Loukogeorgaki, E., et al.).

Table 6 presents the key characteristics of the mooring lines, comparing the configurations for MLC1 and MLC2. In this context, $L_h$ represents the hanging length of the mooring line, $L_{\mathrm{bot}}$ is the length of the mooring line on the seabed, $T_{\mathrm{top}}$ denotes the pretension at the fairlead, and $Z_f$ indicates the vertical position of the fairlead relative to the mean water level (MWL).

Table 6. Characteristics of the examined mooring lines (Adopted with permission from [48]. 2024, Loukogeorgaki, E., et al.).

Parameter	MLC1 (Slack)	MLC2 (Moderately Slack)
Hanging length, $L_h$ (m)	134	199
Submerged weight, w (N/m)	1230	1230
Pretension, $T_{top}^{wet}$ (kN)	174.1	314.9

Notably, MLC1 features a shorter hanging length and lower pretension, enabling greater freedom of motion, while MLC2 employs a longer hanging length and higher pretension to enhance stability. These configurations underscore the trade-offs between energy absorption, motion control, and structural stability, which will be explored in greater detail in subsequent sections.

Figure 7 shows the motion responses of the TALOS-WEC floater under regular wave conditions for different mooring configurations. MLC1 exhibit larger surge displacements due to lower restoring forces, while MLC2 reduce displacements, enhancing stability and horizontal motion control. Heave and pitch motions remain consistent across configurations, highlighting the significant influence of mooring setups on dynamic stability and overall system performance. These results underscore the trade-off between motion freedom and restoring forces in determining the TALOS-WEC’s stability and efficiency.

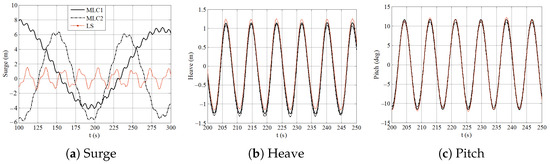
Figure 7. Floater’s motion responses under regular wave conditions (Reproduced with permission from [48]. 2024, Loukogeorgaki, E., et al.).

• Power Absorption Analysis for Single-Mode and Multi-Mode PTOs

The analysis of power absorption under slack (MLC1) and moderately slack (MLC2) mooring configurations was performed for single-mode and multi-mode PTO systems, with a focus on their effectiveness under varying wave conditions. The single-mode PTO system primarily accounts for power absorbed in the heave mode, while the multi-mode system considers power absorption contributions from both heave and surge motions. The power absorption equations are defined as follows:

For the single-mode PTO system, the absorbed power is calculated as [48]:

$$\mathrm{Power}=B_{\mathrm{PTO},\mathrm{heave}}{({\dot{x}}_{\mathrm{hull},\mathrm{heave}}-{\dot{x}}_{\mathrm{ball},\mathrm{heave}})}^2,$$

(15)

where $B_{\mathrm{PTO},\mathrm{heave}}$ represents the PTO damping coefficient in the heave mode, and ${\dot{x}}_{\mathrm{hull},\mathrm{heave}}$ and ${\dot{x}}_{\mathrm{ball},\mathrm{heave}}$ denote the heave velocities of the hull and the ball, respectively.

For the multi-mode PTO system, the absorbed power is given by [48]:

$$\mathrm{Power}=B_{\mathrm{PTO},\mathrm{surge}}{({\dot{x}}_{\mathrm{hull},\mathrm{surge}}-{\dot{x}}_{\mathrm{ball},\mathrm{surge}})}^2+B_{\mathrm{PTO},\mathrm{heave}}{({\dot{x}}_{\mathrm{hull},\mathrm{heave}}-{\dot{x}}_{\mathrm{ball},\mathrm{heave}})}^2,$$

(16)

where $B_{\mathrm{PTO},\mathrm{surge}}$ is the PTO damping coefficient for the surge mode, while ${\dot{x}}_{\mathrm{hull},\mathrm{surge}}$ and ${\dot{x}}_{\mathrm{ball},\mathrm{surge}}$ are the surge velocities of the hull and ball.

Table 7 summarises the mean power and power standard deviation for regular wave conditions for both mooring configurations. The results highlight that MLC1 achieves slightly higher mean power due to greater motion freedom but exhibits higher standard deviations, signifying more variability and less consistent performance. MLC2, while slightly less efficient in mean power absorption, ensures more stable operation with reduced standard deviations, emphasising the trade-off between energy capture and structural stability.

Table 7. Power absorption for MLC1 and MLC2 under regular waves (with incident wave angle $\beta =0^{\circ }$) (Adopted with permission from [48]. 2024, Loukogeorgaki, E., et al.).

Configuration	Wave Period (s)	Mean Power (kW)	Power Std. Dev. (kW)
MLC1 (Slack)	7.0	15.3	1.2
MLC2 (Moderately Slack)	7.0	14.8	0.9
MLC1 (Slack)	8.5	16.8	1.5
MLC2 (Moderately Slack)	8.5	15.2	1.0
MLC1 (Slack)	10.0	15.0	1.1
MLC2 (Moderately Slack)	10.0	14.9	0.8

3.2. WP1.2: Geometric Optimisation

Building on the hydrodynamic modelling perspectives from WP1.1, sub-package WP1.2 focuses on optimising the geometry of the TALOS-WEC to enhance energy absorption and stability across different wave conditions. This phase explores design modifications aimed at improving hydrodynamic performance while balancing efficiency and structural integrity. By analysing configurations ranging from simplified axisymmetric to refined multi-axis designs, WP1.2 seeks to identify geometries that maximise energy capture, improve stability, and ensure practicality for real-world deployment.

3.2.1. Baseline Geometry Studies for Optimisation

Hydrodynamic modelling is essential for optimising WECs to maximise energy absorption and stability, with geometry playing a critical role in hydrodynamic parameters and wave–structure interactions. This study evaluated four baseline geometries for optimisation [46]:

• A truncated cylinder, an axisymmetric design with well-documented hydrodynamic properties, serves as a baseline for validation and numerical tool testing.
• A truncated cylinder with a heave plate, which enhances vertical stability by increasing added mass and radiation damping.
• The original TALOS-WEC, a multi-axis point absorber optimised for energy absorption but characterised by its complex thin structures and overlapping panels.
• A simplified circular version of TALOS, designed to address numerical modelling challenges while retaining critical hydrodynamic features and improving computational efficiency.

Geometric modifications, including the shortened TALOS, tailless TALOS, and a truncated hemisphere, were introduced to refine performance further. These modifications aim to optimise energy capture, improve stability, and address structural and computational constraints.

Figure 8 illustrates the studied geometries, facilitating an in-depth comparison of the original and circular TALOS configurations and highlighting trade-offs between performance and computational efficiency.

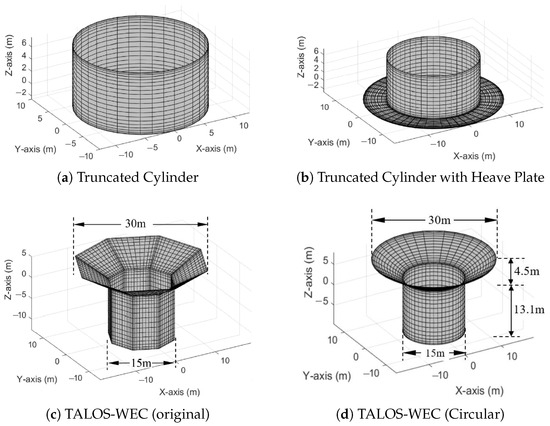
Figure 8. Studied geometries for hydrodynamic modelling (Reproduced with permission from [46]. 2022, Sheng, W., et al.).

Key hydrodynamic parameters, including added mass, radiation damping, wave excitation forces, and RAOs, were analysed using numerical tools (WAMIT, HAMS, and NEMOH) to explore the influence of geometry on energy capture and stability. The circular TALOS configuration, due to its axisymmetric design, demonstrated higher added mass at low frequencies, enhancing inertia, but both geometries converged in added mass at higher frequencies (Figure 9a). Radiation damping trends showed smoother variations for the circular design, reflecting its simplified geometry, while the original TALOS displayed sharper changes, indicative of its complex structure (Figure 9b). Wave excitation forces were generally higher for the circular TALOS, especially near resonance frequencies, due to its symmetric interaction with waves (Figure 9c). The RAOs for surge motions revealed broader resonance peaks for the original TALOS, indicating a distributed response, while the circular TALOS exhibited narrower peaks, emphasising its concentrated resonance behaviour (Figure 9d).

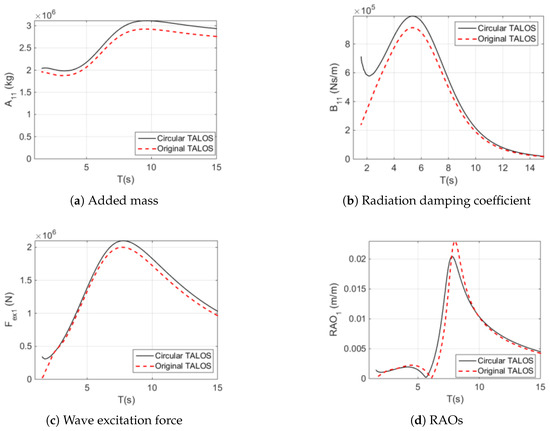
Figure 9. Comparison of hydrodynamic parameters and responses for surge motions (original vs. circular TALOS) (Reproduced with permission from [46]. 2022, Sheng, W., et al.).

Heave and pitch motions further highlighted the differences in geometry. For heave, the original TALOS had higher resonance peaks in RAOs, capturing energy across a broader spectrum due to its intricate wave–structure interactions. The circular TALOS, while achieving narrower peaks and higher excitation forces, offered more concentrated performance around resonance frequencies. In pitch, the original TALOS demonstrated greater variability in added mass and radiation damping, reflecting its non-axisymmetric geometry and complex wave interactions. By contrast, the circular TALOS exhibited smoother radiation damping trends and a more predictable pitch response, particularly at low frequencies. However, the circular design was less effective at capturing higher-frequency interactions, where the original TALOS excelled [46].

3.2.2. Geometric Modifications

Figure 10 illustrates the geometric modifications made to the TALOS-WEC to optimise its performance and displacement. Three configurations are shown. In Figure 10a, the tail-shortened TALOS reduces the length of the lower cylindrical section, leading to a lower draft and a displacement of 2387 m³. Figure 10b presents the tailless TALOS, which eliminates the lower cylindrical section entirely, achieving a displacement of 2969 m³ with a more streamlined geometry. Finally, Figure 10c showcases the truncated hemisphere configuration, characterised by a modified hemispherical structure that provides enhanced stability with a displacement of 3046 m³ [44].

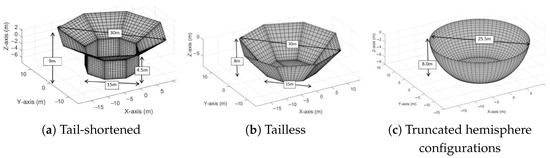
Figure 10. Geometric modifications of the TALOS-WEC (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

The displacement values and percentage reduction from the original TALOS configuration are summarised in Table 8.

Table 8. Displacement comparison between different TALOS geometries.

Configuration	Displacement (m3)	Reduction from Original (%)
Original TALOS	3755	—
Tail-Shortened TALOS	2387	36.4
Tailless TALOS	2969	20.9
Truncated Hemisphere TALOS	3046	18.9

Figure 11 illustrates the power curves for various TALOS geometries, including the original, shortened, tailless, and hemispherical designs. The average power absorbed, $P_{\mathrm{avg}}$, is shown as a function of the energy period, $T_e$, which represents the characteristic period of ocean waves. The power absorption is defined by the equation $P\left(t\right)=B_{\mathrm{PTO}}·V_{rel}{\left(t\right)}^2$. This equation quantifies the resistance of the PTO system to motion and its role in energy absorption. To isolate the effect of geometry on performance, the comparison was conducted under fixed PTO parameters. The spring stiffness was set to $K_{\mathrm{PTO}}=500\mathrm{kN}/\mathrm{m}$, and the damping coefficient was set to $B_{\mathrm{PTO}}=200\mathrm{kNs}/\mathrm{m}$. Additionally, the ball mass was fixed at 800 tonnes, and the overall centre of gravity (CoG) was positioned at $Z_g=0.0\mathrm{m}$, corresponding to the water surface.

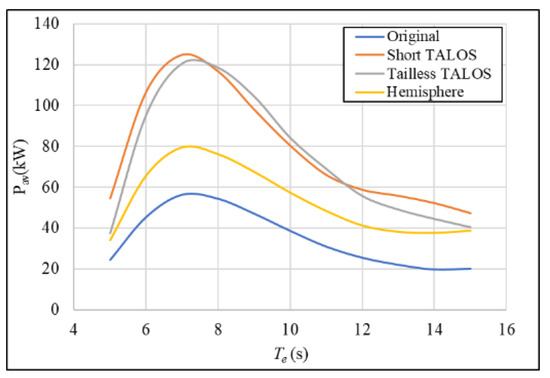
Figure 11. Power curves comparing the optimised TALOS geometries with the original configuration (under fixed PTO parameters with spring stiffness $K_{\mathrm{PTO}}=500\mathrm{kN}/\mathrm{m}$ and damping coefficient $B_{\mathrm{PTO}}=200\mathrm{kNs}/\mathrm{m}$) (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

As can be seen in Figure 11, the shortened TALOS achieves the highest power output, with peak values exceeding $120\mathrm{kW}$ for moderate energy periods ($T_e\approx 8–9\mathrm{s}$). Similarly, the tailless TALOS configuration performs comparably well, demonstrating robust absorption characteristics. The hemispherical design, while slightly less effective in peak power absorption, still outperforms the original TALOS over the entire range of $T_e$, showing its potential as a viable alternative. The original TALOS configuration, indicated by the blue curve, demonstrates significantly lower energy absorption, highlighting the need for geometric optimisation.

3.2.3. Geometric Optimisation Strategies

To further enhance performance, the TALOS-WEC was optimised by varying the centre-of-gravity (CoG) and panel configurations.

• CoG Adjustments

Adjusting the CoG influences how the system interacts with incident waves, which directly impacts wave energy conversion efficiency [71,72]. Lowering the CoG below the water surface enhances the stability of the system by reducing pitch and roll motions, leading to improved energy absorption under operational conditions. However, practical constraints, such as construction feasibility and buoyancy stability, must also be considered when selecting the optimal CoG position.

Figure 12a,b illustrate the energy absorption trends for short TALOS and tailless TALOS configurations with varying CoG positions ($Z_g=0.0\mathrm{m}$, $-1.25\mathrm{m}$, and $-2.5\mathrm{m}$). The results demonstrate that lowering the CoG significantly enhances energy absorption, particularly for moderate wave energy periods $T_e=8–9\mathrm{s}$. It can be observed that a CoG position of $Z_g=-1.25\mathrm{m}$ achieves wave energy conversion performance comparable to $Z_g=-2.5\mathrm{m}$, indicating diminishing returns for further lowering the CoG. For practical purposes, positioning the CoG at $Z_g=-1.25\mathrm{m}$ is ideal, as it balances hydrodynamic performance with construction feasibility and operational stability. By placing the CoG near the water surface, the TALOS-WEC maintains sufficient stability without incurring unnecessary design complexities.

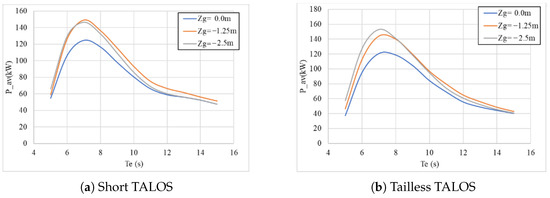
Figure 12. Wave energy absorption for different CoG configurations ($K=500\mathrm{kN}/\mathrm{m}$, $B_{\mathrm{PTO}}=200\mathrm{kNs}/\mathrm{m}$) with ball mass of 800 tonnes (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

• Panel Configurations: Panel Gaps and Overlaps

Here, the effects of panel configurations, specifically panel gaps and overlaps, on the hydrodynamic performance of the TALOS-WEC are evaluated. Panel gaps and overlapping panels significantly affect hydrodynamic coefficients, influencing the added mass, radiation damping, and excitation forces. The results provide visions into optimising the panel designs for energy absorption and structural stability.

Figure 13 illustrates the two panel configurations: Figure 13a shows incomplete (gapped) panels (x-direction) and Figure 13b demonstrates overlapping panels (10° overlap). These configurations form the basis for hydrodynamic comparison, emphasising the effects of design adjustments on performance.

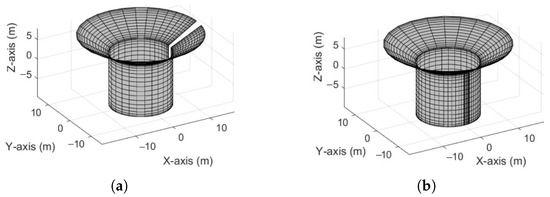
Figure 13. Panel configurations for circular TALOS. (a) Incomplete (gapped) panels by 10°. (b) Overlapping panels by 10°. (Reproduced with permission from [46]. 2023, Sheng, W., et al.).

A comparative analysis of TALOS-WEC configurations with 10° panel gaps and overlapping panels highlights the detrimental effects of gaps and the advantages of overlapping panels. Gaps reduce displacement volume by up to $3.15\%$ and roll restoring coefficients by $5.73\%$, negatively impacting stability and energy capture efficiency. In contrast, overlapping panels enhance hydrodynamic performance, with the 10° overlap configuration increasing displacement volume by $2.30\%$, heave restoring coefficients by $2.40\%$, and roll restoring coefficients by $4.55\%$, significantly improving stability and energy capture. However, a slight decrease in pitch restoring coefficients is observed for both configurations, though the reduction is minimal [46].

Figure 14 and Figure 15 compare hydrodynamic coefficients and RAOs for surge motion in gapped and overlapping panel configurations. The 10° gapped configuration exhibits reduced added mass $A_{11}$ and radiation damping $B_{11}$, indicating lower energy absorption and stability. Additionally, increased RAO amplitudes at resonant wave periods highlight a compromise in surge motion stability. Conversely, the overlapping panel configuration demonstrates improved hydrodynamic coefficients, enhancing performance and stability.

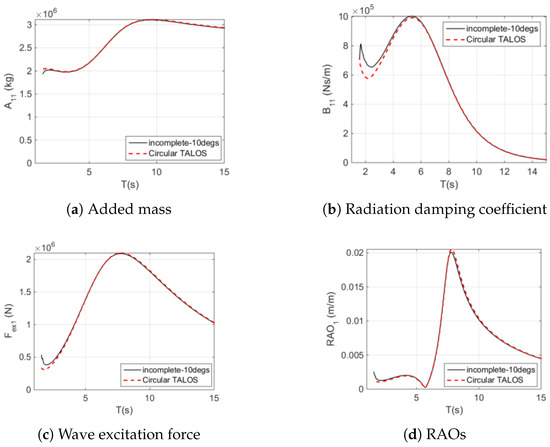
Figure 14. Comparison of hydrodynamic parameters and the response of surge: incomplete TALOS (10 degrees) vs. circular TALOS (Reproduced with permission from [46]. 2023, Sheng, W., et al.).

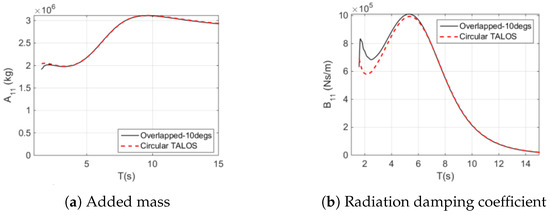
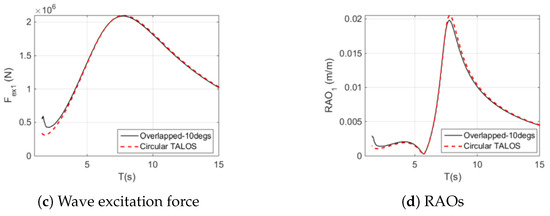
Figure 15. Comparison of hydrodynamic parameters and response of surge: overlapped TALOS (10 degrees) vs. circular TALOS (Reproduced with permission from [46]. 2023, Sheng, W., et al.).

Figure 15 illustrates the overlapping panel configuration (10°), which exhibits enhanced hydrodynamic coefficients. The added mass and radiation damping values are more aligned with the circular TALOS baseline, suggesting better energy capture and motion control. The RAOs for the overlapping configuration show dampened response amplitudes, highlighting improved stability under surge excitation.

3.3. PTO Design and Optimisation for TALOS-WEC

The PTO system of the TALOS-WEC integrates damping and spring elements specifically optimised to enhance energy conversion and ensure operational stability. The TALOS-WEC is modelled as a two-body system in terms of numerical analysis. The first body is the hull (floater), which moves in six DoFs, as shown in Figure 1, as a rigid body under wave excitation. The second body is the mass ball (sphere), located inside the hull, which is linked to the hull through springs and PTO dampers. The interplay between these components governs the energy absorption characteristics of the system. Figure 16 illustrates this two-body system.

Figure 16. The two-body system for the TALOS multi-axis wave energy converter (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

Optimisation of the PTO System

The performance trends observed in the power curves shown in Figure 11 highlight the critical interplay between geometry and PTO design. Geometries like the shortened and tailless TALOS offered higher energy absorption potential, which can be further amplified by tuning the PTO system’s damping coefficients $B_{\mathrm{PTO}}$ and spring stiffness $K_{\mathrm{PTO}}$ to align with the dominant wave energy periods [73,74].

• Role of PTO Damping Coefficients

Damping coefficients play a critical role in controlling the relative motion between the floater and submerged sphere, influencing energy absorption and system stability. Softer damping coefficients allow freer oscillations with wave motion, enhancing energy capture, but excessively low damping can risk mechanical instability. For both the short TALOS and tailless TALOS configurations (with constant spring stiffness of $K=250\mathrm{kN}/\mathrm{m}$), the optimal PTO damping coefficient range lies between $100\mathrm{kNs}/\mathrm{m}$ and $150\mathrm{kNs}/\mathrm{m}$, where energy absorption is maximised without compromising system performance (see Figure 17). While softer damping improves energy efficiency, care must be taken to avoid durability issues or instability due to excessive oscillations, necessitating a balance between energy capture and structural integrity.

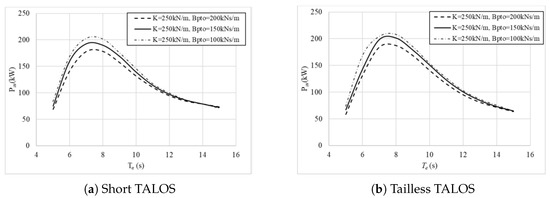
Figure 17. Energy absorption for varying damping coefficients with $K_{\mathrm{PTO}}=250\mathrm{kN}/\mathrm{m}$ (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

• Influence of PTO spring stiffness

Spring stiffness significantly influences the resonance characteristics of the TALOS-WEC by determining its natural frequency. Figure 18 compares energy absorption for the short TALOS and tailless TALOS configurations with three spring stiffness values, $K_{\mathrm{PTO}}=500\mathrm{kN}/\mathrm{m}$ (hard spring), $K_{\mathrm{PTO}}=350\mathrm{kN}/\mathrm{m}$ (moderate spring), and $K_{\mathrm{PTO}}=250\mathrm{kN}/\mathrm{m}$ (soft spring), keeping the PTO damping coefficient constant at $B_{\mathrm{PTO}}=200\mathrm{kNs}/\mathrm{m}$.

Figure 18. Energy absorption for varying spring stiffness coefficients (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

Figure 18a,b reveal that energy absorption peaks are higher for softer ($K_{\mathrm{PTO}}=250\mathrm{kN}/\mathrm{m}$) and moderate ($K_{\mathrm{PTO}}=350\mathrm{kN}/\mathrm{m}$) springs, particularly for wave energy periods $T_e$ between $7\mathrm{s}$ and $10\mathrm{s}$. The softest spring achieves the highest energy absorption, demonstrating that optimising spring stiffness to moderate or soft values significantly enhances performance within the operational wave period range of $T_e\approx 7–10\mathrm{s}$.

A key component of this evaluation is the wave power spectrum, which describes the distribution of wave energy across different frequencies. For this analysis, the Bretschneider spectrum was employed [44], which is a well-established model commonly used for describing energy in wind-driven sea states. The Bretschneider spectrum is defined as follows:

$$S\left(\omega \right)={\displaystyle \frac{5{\omega }_p^4}{16{\omega }^5}}{H}_s^{2}exp\left(-{\displaystyle \frac{5{\omega }_p^4}{4{\omega }^4}}\right),$$

(17)

where $S\left(\omega \right)$ is the spectral density of the wave energy as a function of circular frequency, $\omega$ is the circular frequency, ${\omega }_p$ is the frequency at the peak of the spectrum, $H_s$ is the significant wave height, representing the average height of the highest one-third of the waves, and $T_p={\displaystyle \frac{2\pi }{{\omega }_p}}$ is the spectral peak period, corresponding to the peak frequency ${\omega }_p$.

The power matrices presented in Figure 19 compare the energy extraction capabilities of three TALOS geometries (original, short, and tailless) under both hard and soft PTO systems. In these matrices, $T_e$, the energy period of irregular waves, represents an average measure of wave energy distributed across all frequencies in the spectrum. In contrast, $T_p$, the spectral peak period, focuses specifically on the energy at the peak frequency. The relationship between $T_e$ and $T_p$ depends on the wave spectrum shape and conditions. For the Bretschneider spectrum, $T_e$ is generally close to $T_p$, although the exact ratio may vary. Both parameters are widely used in wave energy analyses, with $T_e$ offering a broader perspective on overall energy distribution, while $T_p$ focuses on peak energy characteristics.

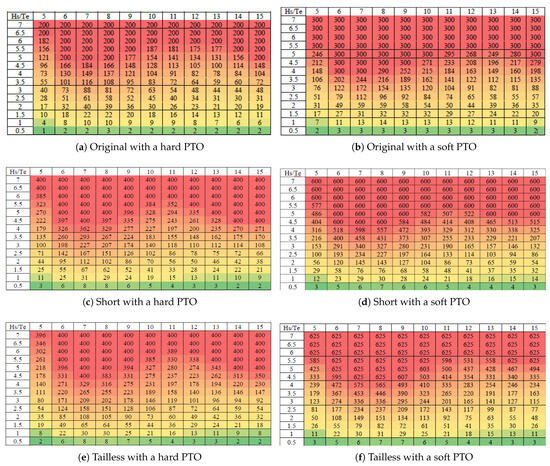
Figure 19. Power matrix for different TALOS geometries. The color coding (red, yellow, and green) highlights regions of higher and lower power extraction (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

The original TALOS demonstrates limited energy conversion capacity, with the soft PTO (see Figure 19b) improving the annual energy production (AEP) to 612 MWh compared to 345 MWh for the hard PTO (see Figure 19a). In contrast, the short TALOS exhibits significantly enhanced performance, achieving an AEP of 865 MWh with the hard PTO (see Figure 19c) and 1.274 GWh with the soft PTO (see Figure 19d), representing a 47% improvement. Similarly, the tailless TALOS shows comparable performance to the short TALOS, achieving 846 MWh under the hard PTO (see Figure 19e) and a slightly higher 1.311 GWh under the soft PTO (see Figure 19f), marking a 3% improvement over the short TALOS. The color coding in Figure 19 (e.g., red, yellow, and green regions) visually highlights the regions of higher and lower power extraction.

The AEP values presented in this study were calculated based on probabilistic weighting of wave conditions derived from the European Marine Energy Centre (EMEC) wave scatter diagram, shown in Figure 20 [44]. This diagram represents the statistical distribution of significant wave heights $H_s$ and energy periods $T_e$ observed at the EMEC site. The power matrices in Figure 19 were integrated across the range of wave states in this diagram, providing a realistic estimate of AEP that accounts for high-probability wave conditions. This methodology ensures that the results are representative of typical operational scenarios, rather than being based solely on extreme or maximum conditions.

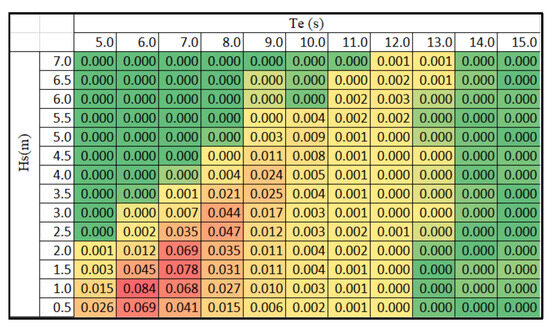
Figure 20. Wave scatter diagram for the EMEC site, showing the distribution of significant wave heights $H_s$ and energy periods $T_e$. The color coding (red, yellow, and green) highlights regions of higher and lower power extraction (Reproduced with permission from [44]. 2024, Sheng, W., et al.).

4. WP2: Survivability, Reliability, and Control

WP2 focuses on enhancing the survivability, reliability, and operational efficiency of the TALOS-WEC in extreme marine environments. This WP is divided into four sub-packages: WP2.1 integrates smart sensors for real-time monitoring of system health and environmental conditions. WP2.2 employs AI algorithms for condition monitoring and predictive health assessment. WP2.3 develops predictive maintenance models to forecast component failures and enhance reliability. Finally, WP2.4 implements adaptive control strategies to optimise energy capture and ensure safe operation under varying and extreme conditions.

4.1. WP2.1—Smart Sensors

This sub-package integrates smart sensors across the TALOS-WEC to monitor critical parameters such as structural integrity, motion, and environmental conditions (e.g., wave height, pressure, and temperature). Using technologies like strain gauges, accelerometers, wave probes, ultrasonic level sensors, and the Internet of things (IoT) sensors, it ensures continuous monitoring of structural, hydraulic, electrical, and mooring components, as detailed in Table 9 [75,76].

Table 9. Sensor types and detection targets for the TALOS-WEC subsystems [9,75,76].

Subsystem	Detection Targets	Types of Sensors
Structural	Humidity	Relative humidity (RH) sensors, dew point sensors
	Water leak detection	Pressure sensors, radar sensors, acoustic emission sensors
	Applied force	Fibre optic strain gauge
	Incoming waves	Wave probes
	Acceleration	Accelerometers
Hydraulic	Oil leakage	Pressure transducers, ultrasonic level sensors
	Contamination	Inline contamination monitor
	Position	Linear position sensors
Electrical	Electrical parameters	Voltage transducers, current transducers, power transducers
	Generator speed	Absolute encoders
	Generator torque	Torque transducers
	Temperature	Thermocouples, infrared, and resistance temperature sensors
Mooring	Position	Global Positioning System (GPS)
	Entanglement	Load shackles
	Inertial	Inertial measurement unit
Instrumentation	Data collection and processing	Remote diagnostic sensors

The framework illustrated in Figure 21 enables the collection and real-time processing of data, which are essential for monitoring the WEC’s health and analysing its performance under varying wave conditions.

Figure 21. Workflow for sensor integration: from selection to optimised placement and deployment.

4.2. WP2.2—Intelligent Condition Monitoring

Condition monitoring is crucial for the TALOS-WEC to mitigate mechanical, hydrodynamic, and environmental stresses encountered in its challenging operating environment. By continuously monitoring system conditions, it ensures early detection of anomalies, prevents catastrophic failures, and minimises unplanned downtime, thereby maintaining the efficient operation of interconnected subsystems such as structural, hydraulic, electrical, and mooring components. The monitoring framework integrates advanced ML algorithms and strategically deployed smart sensors to collect real-time data on key parameters like forces, accelerations, pressures, temperatures, and wave conditions.

Advanced dual-model frameworks, namely ANN-LSTM and KPCA-LSTM, have been developed to predict system performance and detect anomalies, leveraging the strengths of machine learning techniques such as long short-term memory (LSTM) [77,78] and artificial neural networks (ANNs) [79,80]. The ANN-LSTM framework combines the sequential modelling capabilities of LSTM, which excels at capturing long-term trends in time-series data, with an ANN, which refines predictions by addressing residual errors. This integrated approach directly operates on time-series data, achieving high accuracy by effectively capturing both macro-level trends and short-term fluctuations.

In contrast, the KPCA-LSTM framework enhances prediction performance through kernel principal component analysis (KPCA), which performs feature extraction and dimensionality reduction [81,82]. By preprocessing input data, KPCA reduces redundancy and retains nonlinear relationships, improving computational efficiency and enabling LSTM to focus on modelling dynamic dependencies. Like the ANN-LSTM framework, KPCA-LSTM incorporates ANNs for residual adjustments, ensuring refined and reliable predictions. The key distinction lies in the use of KPCA in the KPCA-LSTM framework, making it particularly advantageous for complex, high-dimensional datasets. In comparison, ANN-LSTM offers a simpler implementation suitable for systems with fewer preprocessing requirements [40,51].

4.2.1. ANN-LSTM Framework

The combined ANN-LSTM framework, depicted in Figure 22, integrates real-time data preprocessing, feature extraction via KPCA, long-term trend prediction by LSTM, and residual adjustment by ANNs. This dual-model framework leverages LSTM networks to capture long-term dependencies and model overall power trends while employing ANNs to adjust residual errors, addressing short-term variations and anomalies for enhanced prediction accuracy [40].

Figure 22. Dual-model power generation prediction framework: LSTM for force prediction and ANN for residual adjustment.

The TALOS-WEC operates through a 6-DOF PTO system (shown in Figure 1), where wave forces induce relative motions between a central ball and the external hull connected by PTO dampers. The theoretical mechanical power output based on forces in the PTO system $P_{PTO}$ is calculated using $P_{\mathrm{PTO}}={\displaystyle \frac{F^2}{\lambda }}$, where $\lambda$ is an empirically determined power coefficient, set at $\lambda =250,000$. This equation establishes a theoretical benchmark linking the mechanical forces generated by the PTO system to the overall output power $P_{\mathrm{PTO}}$, which provides a foundation for evaluating the predictive accuracy of ML models.

Accurate predictions require comprehensive preprocessing of high-resolution time-series data (sampled at 0.05 s intervals). Feature selection focuses on variables such as water elevation, PTO forces, hull motions (heave, pitch, roll), and velocities. KPCA is employed to reduce dimensionality, extracting dominant features while retaining nonlinear relationships to enhance computational efficiency [40,51].

• LSTM for Primary Power Prediction

LSTM networks, a type of recurrent neural network (RNN), handle long-term dependencies effectively by using memory cells regulated by forget, input, and output gates. For the TALOS-WEC, LSTM predicts PTO forces and power trends over a five-wave horizon, suitable for real-time condition monitoring. The equations governing LSTM operation are [40]:

$$\left\{\begin{array}{cc}\hfill f_t& =\sigma \left(W_f[h_{t-1},X_t]+b_f\right),\hfill \\ \hfill i_t& =\sigma \left(W_i[h_{t-1},X_t]+b_i\right),\hfill \\ \hfill C_t& =f_t·C_{t-1}+i_t·tanh\left(W_c\left[h_{t-1}{X}_t\right]+b_c\right),\hfill \\ \hfill h_t& =O_t·tanh\left(C_t\right).\hfill \end{array}\right.$$

(18)

Here, the forget gate $f_t$, input gate $i_t$, and cell state $C_t$ collaboratively manage the flow and retention of information within the memory cells. The hidden state $h_t$ represents the output of the LSTM at each time step, while the input at time t, denoted as $X_t$, feeds the network with time-series data. The computations rely on the weight matrices $W_f, W_i, W_c$ and corresponding bias terms $b_f, b_i, b_c$, which are learned during training. The sigmoid activation function $\sigma$ is utilised to scale values between 0 and 1, enabling effective gating operations within the LSTM [40].

• ANN for Residual Adjustment

The ANN component refines the predictions from the LSTM model by addressing residual errors, thereby enhancing overall accuracy through its ability to model fine-scale variations. The ANN architecture consists of an input layer that accepts features reduced through KPCA. Its hidden layers comprise two fully connected layers, each containing 64 neurons, employing the rectified linear unit (ReLU) activation function, defined as $\mathrm{ReLU}\left(z\right)=max(0,z)$, to introduce nonlinearity and effectively model complex patterns [83]. The output layer includes a single neuron with a linear activation function, specifically designed to compute and apply the residual corrections to the LSTM predictions [40].

The total corrected power output is calculated as ${\widehat{y}}_{\mathrm{total}}={\widehat{y}}_{\mathrm{LSTM}}+{\widehat{y}}_{\mathrm{ANN}}$, where ${\widehat{y}}_{\mathrm{LSTM}}$ represents the power output predicted by the LSTM model, and ${\widehat{y}}_{\mathrm{ANN}}$ denotes the residual correction provided by the ANN [43].

4.2.2. KPCA-LSTM Framework

The hybrid KPCA-LSTM framework is a powerful machine learning approach for predicting PTO forces and power outputs, combining efficiency and accuracy. KPCA reduces data complexity by extracting dominant features while retaining critical nonlinear relationships, enhancing computational efficiency. LSTM effectively models long-term dependencies and sequential patterns, enabling accurate predictions of PTO forces and power trends. Additionally, an ANN corrects residual errors, refining short-term variations and improving prediction accuracy. This integrated framework offers robust feature extraction, reliable sequential modelling, and efficient computational performance, making it well-suited for condition monitoring and power prediction in the TALOS-WEC system [51].

• KPCA for feature extraction

KPCA is employed to preprocess and reduce the dimensionality of the input dataset while preserving nonlinear relationships. The process involves standardising the data, calculating the covariance matrix, and performing singular value decomposition (SVD) to extract dominant principal components. Only components that account for at least $85\%$ of the variance are retained, significantly reducing computational load while maintaining critical features for prediction. The standardised data $Z_{ij}$ is obtained as $Z_{ij}={\displaystyle \frac{x_{ij}-{\overline{x}}_j}{{\sigma }_{x_j}}}$, where $x_{ij}$ is the raw input data, ${\overline{x}}_j$ is the mean, and ${\sigma }_{x_j}$ is the standard deviation. The covariance matrix $\sigma$ and its eigen decomposition provide the principal components, which are used as inputs to the LSTM model.

The implementation of the KPCA-LSTM framework begins with reducing the dimensionality of the input features using KPCA, which ensures computational efficiency while retaining the most significant nonlinear relationships in the data. The reduced feature set is then fed into the LSTM model, which predicts PTO forces and captures the primary trends over a defined time horizon. To enhance the accuracy of these predictions, an ANN is employed to adjust the residual errors, refining the LSTM outputs by accounting for short-term variations and anomalies. Finally, the predicted PTO forces are used to compute the power output.

4.2.3. Evaluation Metrics and Model Comparison

The performance of the KPCA-LSTM framework is evaluated using standard metrics, root mean square error (RMSE), coefficient of determination $R^2$, and mean absolute error (MAE), which collectively assess predictive accuracy and reliability.

RMSE measures the square root of the average squared differences between the actual $y_i$ and the predicted values ${\widehat{y}}_i$, penalising large deviations more heavily. It is defined as [84]:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{{\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2}{N}}},$$

(19)

where N is the number of observations. The coefficient of determination $R^2$ evaluates how well the model’s predictions fit the actual data by comparing the residual sum of squares ${\mathrm{SS}}_{\mathrm{res}}$ to the total sum of squares ${\mathrm{SS}}_{\mathrm{tot}}$. It is given by

$$R^2=1-{\displaystyle \frac{{\mathrm{SS}}_{\mathrm{res}}}{{\mathrm{SS}}_{\mathrm{tot}}}},$$

(20)

where ${\mathrm{SS}}_{\mathrm{res}}={\sum }_{i=1}^N{(y_i-{\widehat{y}}_i)}^2$ and ${\mathrm{SS}}_{\mathrm{tot}}={\sum }_{i=1}^N{(y_i-\overline{y})}^2$, with $\overline{y}$ representing the mean of the actual values. MAE calculates the average magnitude of the absolute differences between the actual and predicted values without considering the direction of the errors:

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N|y_i-{\widehat{y}}_i|.$$

(21)

Table 10 presents a comparative analysis of KPCA-LSTM, LSTM, regression tree (RT) [85,86], support vector regression (SVR) [87,88], and ANN across six PTO systems. The table demonstrates that KPCA-LSTM consistently achieves the highest $R^2$ values and the lowest RMSE and MAE scores across all PTO systems, highlighting its ability to balance long-term trend prediction with computational efficiency and short-term residual refinement.

Table 10. Prediction accuracy metrics for different algorithms across PTO systems (Adopted with permission from [40]. 2024, Wu, Y., et al.).

PTO	Metric	KPCA-LSTM	LSTM	RT	SVR	ANN
	$R^2$	0.87	0.67	0.44	0.78	0.56
1st	RMSE	0.12	0.13	0.17	0.13	0.16
	MAE	0.09	0.10	0.13	0.11	0.12
	$R^2$	0.93	0.49	0.56	0.67	0.45
2nd	RMSE	0.08	0.15	0.16	0.14	0.17
	MAE	0.07	0.12	0.13	0.10	0.15
	$R^2$	0.92	0.83	0.75	0.74	0.78
3rd	RMSE	0.09	0.11	0.14	0.13	0.13
	MAE	0.08	0.09	0.11	0.10	0.10
	$R^2$	0.89	0.93	0.74	0.74	0.77
4th	RMSE	0.11	0.08	0.13	0.13	0.13
	MAE	0.10	0.06	0.11	0.10	0.09
	$R^2$	0.85	0.92	0.52	0.81	0.83
5th	RMSE	0.12	0.09	0.13	0.12	0.12
	MAE	0.11	0.08	0.10	0.09	0.10
	$R^2$	0.92	0.92	0.79	0.89	0.80
6th	RMSE	0.09	0.09	0.13	0.11	0.12
	MAE	0.08	0.07	0.09	0.09	0.10

4.2.4. PTO Power Output Prediction Comparison

Both frameworks exhibit high performance in power output prediction. As shown in Figure 23, the integration of ANN compensation results in precise power output predictions, outperforming direct prediction methods. This framework’s ability to adjust for short-term deviations makes it highly effective for accurate power prediction under varying wave conditions.

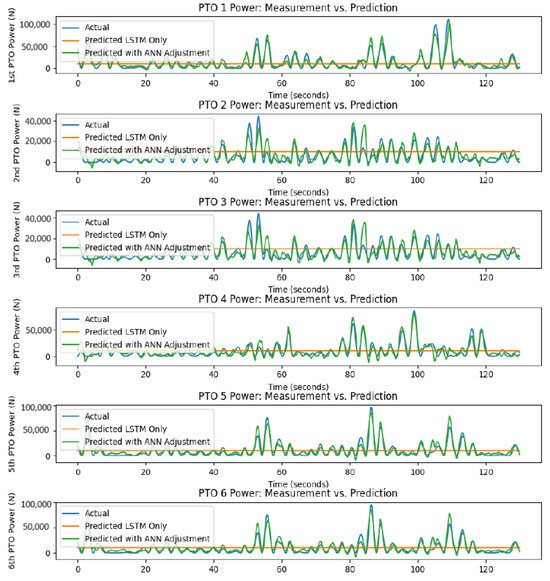
Figure 23. Comparison of direct power predictions with measured power (ANN-LSTM framework) (Reproduced with permission from [40]. 2024, Wu, Y., et al.).

The KPCA-LSTM framework, on the other hand, utilizes KPCA to preprocess input data, ensuring that the LSTM model focuses on the most relevant features. Figure 24 demonstrates the framework’s consistent performance across different PTO systems, with minimal variability in prediction error.

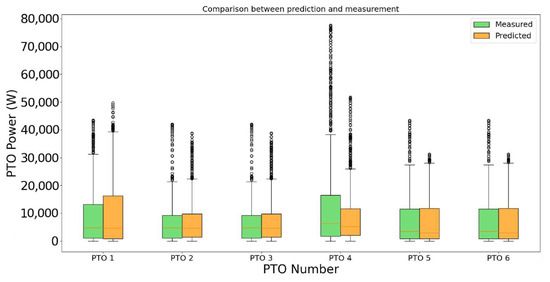
Figure 24. Comparison of direct power predictions with measured power (KPCA-LSTM framework) (Reproduced with permission from [51]. 2024, Wu, Y., et al.).

4.3. WP2.3—Predictive Maintenance

The TALOS-WEC project leverages advanced predictive maintenance strategies to address the challenges posed by its complex multi-axis design and harsh offshore operating environments. These strategies are essential for ensuring reliability, minimising downtime, and maintaining system efficiency over time. The hydraulic PTO system, coupled with a heavy internal mass, operates across six DoFs and is subject to wear and degradation, especially in components like hydraulic cylinders, accumulators, and valves [40]. The demanding ocean conditions exacerbate mechanical stresses, increasing the risk of performance degradation and failures that can significantly reduce energy capture efficiency. Predictive maintenance aims to preemptively detect and mitigate issues, such as hydraulic system degradation or accumulator failure, aligning with TALOS’s broader goals of integrating advanced control, optimisation, and survivability systems.

The PTO system operates within motion, force, and power constraints that, if violated due to wear or degradation, can compromise energy output and system longevity. Offshore maintenance costs are substantially higher than onshore systems, further highlighting the importance of predictive strategies. Using sensor data from components monitoring parameters like pressure, temperature, flow rates, and structural stresses, ML frameworks, such as ANN-LSTM and KPCA-LSTM, play a pivotal role in identifying patterns indicative of component wear [40,51]. Key indicators include accumulator pressure drops, hydraulic fluid leaks, and changes in PTO damping or stiffness, which serve as inputs for predictive models to forecast maintenance needs.

Simulation tools like WEC-Sim, discussed in Section 3.1.3, further enhance these predictive capabilities by modelling failure scenarios and stress conditions to refine the algorithms. By integrating condition monitoring systems, predictive maintenance frameworks ensure TALOS-WEC operates reliably, safely, and efficiently, minimising unplanned interventions and optimising maintenance schedules to reduce overall costs while extending the system’s operational lifespan [40,51].

4.4. WP2.4—Optimised Control

Optimising energy capture in the TALOS-WEC system presents significant challenges due to the irregular dynamics of wave energy and the complexity of its multi-axis design. To tackle these issues, the TALOS project leverages model predictive control (MPC), a sophisticated optimisation framework renowned for its real-time decision-making under constraints [89,90]. MPC facilitates adaptive control strategies that enhance energy capture, ensure system safety during extreme events, and adapt to varying sea conditions [14,20]. This section delves into linear and nonlinear MPC models, ML-driven wave predictions, and multi-DOF hydraulic PTO systems, showcasing innovative approaches to WEC control. Table 11 summarizes these methodologies, outlining their novelties, advantages, and limitations.

Table 11. Summary of MPC-based control strategies for TALOS-WEC.

Ref.	Methodology	Novelty	Advantages	Limitations
[49]	Compared MPC with hydrodynamics-only and PTO-integrated models; analysed prediction horizons.	Integrated PTO dynamics; prediction horizon analysis.	23% increase in power, better constrained performance.	High computational cost, limited nonlinear interaction analysis.
[50]	Incorporated constraints (position, force, power) in MPC with nonlinear PTO models.	Detailed study of realistic constraints.	Improved reliability and control accuracy.	Increased computational burden, reduced max output power.
[52]	Compared linear and nonlinear MPC under constraints.	First comparison of linear vs. nonlinear MPC for TALOS.	Nonlinear improves power by 10%; linear is computationally efficient.	Nonlinear is computationally heavy; sensitive to wave prediction errors.
[53]	Developed six-DOF WEC-Sim model; evaluated PTO actuation strategies.	Selective actuation for multi-axis PTOs.	More energy capture, scalable, lower computation demand.	Coupling effects complicate control; real-time optimisation is prohibitive.

The analyses underscore MPC’s potential in optimising TALOS-WEC performance. Nonlinear MPC achieves the highest energy capture efficiency but is computationally intensive, making linear MPC a practical alternative for simpler scenarios [52]. The inclusion of realistic constraints ensures a balance between energy optimisation and system reliability, albeit with reductions in theoretical maximum outputs [50]. Multi-axis systems, leveraging selective PTO actuation, enhance power output and computational efficiency but face challenges in coupling effects and real-time implementation [53]. Bridging theoretical advancements and practical implementation, the study in [49] provides a comprehensive comparison of hydrodynamics-only MPC models with those incorporating PTO dynamics. It further examines the effects of prediction horizons and operational constraints, offering valuable perspectives into achieving scalable and efficient WEC control.

4.4.1. System Dynamics and State-Space Representation

Figure 25 provides a schematic of the two-DoF point absorber system with a hydraulic PTO. The TALOS-WEC system harnesses wave energy through the coupled dynamics of the primary floater and an internal reaction mass ball. These components are connected via a hydraulic PTO system that converts their relative motion into usable energy. The PTO system includes critical components such as an accumulator, check valves, and a hydraulic generator, which together optimise energy capture and maintain system stability.

Figure 25. Two-DoF point absorber WEC system with hydraulic PTO (Reproduced with permission from [49]. 2024, Hall, C., et al.).

The system dynamics are driven by the interplay of hydrodynamic forces, mechanical constraints, and PTO operations. Hydrodynamic effects include wave excitation, radiation, and buoyancy forces, while mechanical interactions are governed by the relative motion between the sphere and hull, mediated by a spring-damping mechanism. The PTO system regulates energy extraction through resistive and hydraulic forces.

These dynamics are modelled using a comprehensive ten-state representation, capturing the physical and hydrodynamic phenomena that govern energy extraction and motion. The system’s behaviour under varying sea conditions is expressed in the state-space form as $\dot{\mathbf{x}}=f(\mathbf{x},\mathbf{u})$, where the state vector is defined as follows:

$$\mathbf{x}={[x_{\mathrm{sphere}},{\dot{x}}_{\mathrm{sphere}},q_1,q_2,q_3,q_4,V,L,x_{\mathrm{hull}},{\dot{x}}_{\mathrm{hull}}]}^T.$$

(22)

This vector encapsulates the position $x_1$ and velocity $x_2$ of the reaction mass (sphere), auxiliary states ($x_3$ to $x_6$) representing hydrodynamic radiation forces, and accumulator dynamics $x_7$ related to volume changes. Additionally, $x_8$ models the hydraulic generator shaft’s angular momentum, while $x_9$ and $x_{10}$ describe the position and velocity of the primary floater (hull). The control input vector $\mathbf{u}=\left[F_{{\mathrm{PTO}}_{\mathrm{mech}}}\right]$ represents the PTO forces applied to the system.

The ten-state model is governed by the following equations:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2,\hfill \\ \hfill {\dot{x}}_2& ={\displaystyle \frac{1}{M_{\mathrm{ball}}}}\left(-S_{\mathrm{rs}}(x_1-x_9)-F_{{\mathrm{PTO}}_{\mathrm{mech}}}\right),\hfill \\ \hfill {\dot{x}}_3& =A_{r1}·x_3+A_{r2}·x_4+A_{r3}·x_5+A_{r4}·x_6+x_{10},\hfill \\ \hfill {\dot{x}}_4& =x_3,{\dot{x}}_5=x_4,{\dot{x}}_6=x_5,\hfill \\ \hfill {\dot{x}}_7& =-k_{l}h\left(x_7\right)-{\displaystyle \frac{D}{J}}{x}_8+S(x_2-x_{10}),\hfill \\ \hfill {\dot{x}}_8& =D{\eta }_{m}h\left(x_7\right)-{\displaystyle \frac{B}{J}}{x}_8-T_G,\hfill \\ \hfill {\dot{x}}_9& =x_{10},\hfill \\ \hfill {\dot{x}}_{10}& ={\displaystyle \frac{1}{M_{\mathrm{hull}}+m_{\infty ,\mathrm{hull}}}}(-C_{r1}{x}_3-C_{r2}{x}_4-C_{r3}{x}_5-C_{r4}{x}_6\hfill \\ \hfill & +K_{\mathrm{PTO}}(x_1-x_{10})-\pi \rho g{R}_b^2\left(1-{\displaystyle \frac{|x_9|x_9}{3R_b^2}}\right)x_9\hfill \\ \hfill & -0.5\rho A_w{C}_d|x_{10}-v_f|(x_{10}-v_f)-F_n{\mu }_{d}tanh\left(\alpha x_{10}\right)-{\mu }_s{x}_{10}\hfill \\ \hfill & -F_n({\mu }_s-{\mu }_d)e^{-{(x_{10}/v_s)}^2}tanh\left(\alpha x_{10}\right)+F_{\mathrm{exc}}+F_{{\mathrm{PTO}}_{\mathrm{mech}}}).\hfill \end{array}\right.$$

(23)

The model incorporates parameters such as the restoring spring stiffness $S_{\mathrm{rs}}$, radiation damping coefficients ($A_{r1}$ to $A_{r4}$), and hydrodynamic restoring coefficients ($C_{r1}$ to $C_{r4}$). These elements govern the interactions between the hydrodynamic and mechanical subsystems. The hydraulic PTO system is modelled using the piston cross-sectional area S, motor leakage coefficient $k_l$, motor dynamics ($D, J, B$), and motor efficiency ${\eta }_m$. Nonlinear dynamics of the hydraulic accumulator are represented by $h\left(x_7\right)$, while generator torque $T_G$ reflects mechanical-to-electrical energy conversion. Together, these parameters enable an accurate representation of the TALOS-WEC’s hydrodynamic, mechanical, and hydraulic interactions. This state-space model forms the foundation for advanced control strategies, such as MPC.

4.4.2. MPC Control Framework

The TALOS-WEC employs a structured control framework to optimise energy extraction from wave motion while ensuring system stability and adherence to physical constraints. The three strategies summarised in Table 12 focus on regulating the PTO system and hydrodynamic interactions under varying sea states.

Table 12. Summary of control approaches for TALOS-WEC.

Control Approach	Description	Advantages	Limitations
Baseline Proportional Control (Figure 26a)	Simple control where PTO force is proportional to velocity. optimised for average wave conditions and includes position constraints for stability.	Computationally efficient; ensures system stability.	Limited adaptability to varying sea states and nonlinear dynamics.
Reduced-State Linear MPC (Figure 26b)	Focuses on hydrodynamic states using a simplified linear model. Solves quadratic programming to optimise energy capture and enforce position/velocity constraints.	Balances computational efficiency and adaptability to wave states.	Excludes PTO dynamics; may yield suboptimal results.
Full-State Linear MPC (Figure 26c)	Incorporates hydrodynamic, mechanical, and PTO dynamics for comprehensive control. Solves an optimisation problem with physical constraints over a prediction horizon.	Achieves superior energy output and ensures compliance with constraints.	High computational cost due to complexity.

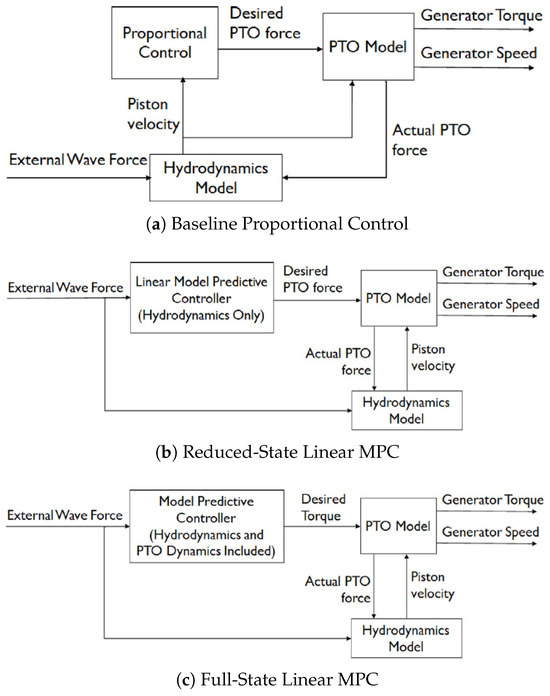
Figure 26. Control frameworks for the TALOS-WEC system (Reproduced with permission from [49]. 2024, Hall, C., et al.).

Table 12. Summary of control approaches for TALOS-WEC.

Control Approach	Description	Advantages	Limitations
Baseline Proportional Control (Figure 26a)	Simple control where PTO force is proportional to velocity. optimised for average wave conditions and includes position constraints for stability.	Computationally efficient; ensures system stability.	Limited adaptability to varying sea states and nonlinear dynamics.
Reduced-State Linear MPC (Figure 26b)	Focuses on hydrodynamic states using a simplified linear model. Solves quadratic programming to optimise energy capture and enforce position/velocity constraints.	Balances computational efficiency and adaptability to wave states.	Excludes PTO dynamics; may yield suboptimal results.
Full-State Linear MPC (Figure 26c)	Incorporates hydrodynamic, mechanical, and PTO dynamics for comprehensive control. Solves an optimisation problem with physical constraints over a prediction horizon.	Achieves superior energy output and ensures compliance with constraints.	High computational cost due to complexity.

• System Constraints

The TALOS-WEC system operates under critical constraints to ensure both safety and efficiency, with particular focus on the PTO system and the relative motion between the sphere and hull. These constraints include PTO force limits to prevent overpressure and ensure proper hydraulic system operation, as well as relative position constraints to maintain safe clearance and avoid collisions. These parameters are embedded within the MPC framework, ensuring compliance with physical and operational limits. However, achieving all constraints simultaneously, especially during extreme wave conditions, poses significant challenges [49].

• Wave Prediction

Advances in wave prediction methods have significantly enhanced accuracy over time. Traditional approaches, such as Fourier analysis and time-domain models, historically provided reliable estimates of wave height and period. However, modern techniques, including ML methods like LSTM networks, have introduced substantial improvements in prediction accuracy. These advanced methods are particularly valuable for control optimisation, enabling more precise forecasts of wave characteristics to support efficient and adaptive system responses.

Wave data from the deployment site were collected over a year at hourly intervals. Seasonal variations were represented by selecting February and July as test cases, corresponding to rough and calm sea states, respectively. Simulated wave forces based on observed conditions were used as inputs for evaluating control strategies.

4.4.3. Results and Discussion

This section presents key results from the evaluation of control strategies for the TALOS-WEC, focusing on the impact of constraints, the performance of full-state MPC, and the influence of prediction horizons on energy capture.

• Impact of Constraints on Reduced-State MPC

Figure 27 illustrates PTO force and power output for reduced-state MPC under February wave conditions with different constraints. The inclusion of position constraints (e.g., 0 m and 0.1 m limits) ensures safe operation by preventing excessive motion of the sphere relative to the hull. Without constraints, the system exhibits large relative displacements, leading to potential collisions and instability.

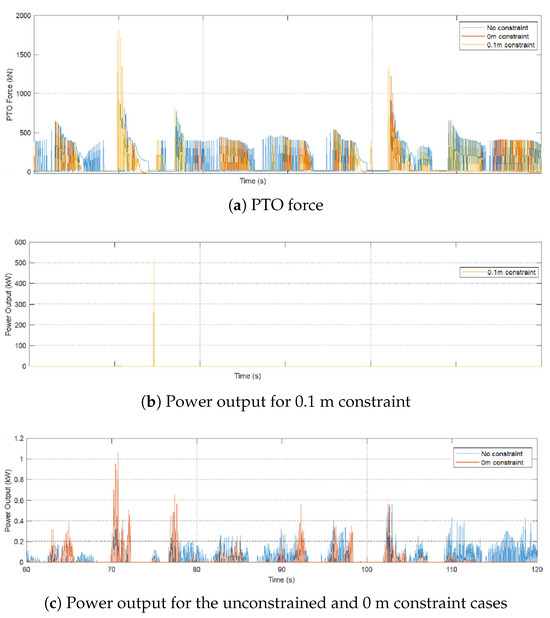
Figure 27. Results for reduced-state MPC under February wave conditions (Reproduced with permission from [49]. 2024, Hall, C., et al.).

The constrained cases (0.1 m limit) demonstrate improved power output compared to the unconstrained scenario, balancing safety and energy capture, which highlights the importance of integrating realistic constraints into the control framework, particularly in rough sea conditions.

• Performance of Full-State MPC

Figure 28 presents the results for full-state MPC under February wave conditions. The advanced control strategy significantly outperforms reduced-state MPC by incorporating all ten system states, including PTO dynamics, into the optimisation process. As can be seen, the full-state MPC achieves smoother and more stable PTO force profiles, minimising reactive oscillations and enhancing energy extraction. The ability to handle complex system dynamics ensures robust performance, even under extreme wave conditions, achieving higher power outputs compared to reduced-state MPC.

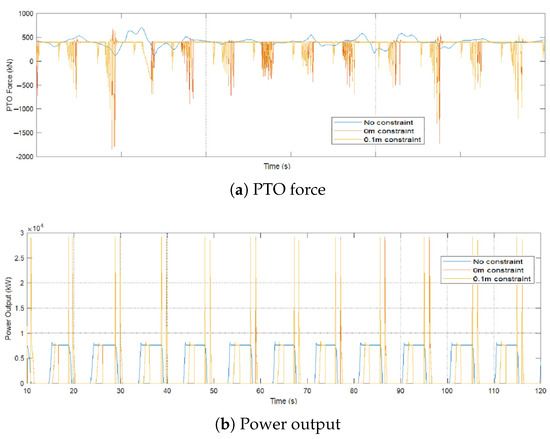
Figure 28. Results for full-state MPC under February wave conditions (Reproduced with permission from [49]. 2024, Hall, C., et al.).

The comparison of average power outputs across baseline, reduced-state MPC, and full-state MPC strategies under rough (February) and calm (July) sea conditions highlights the superiority of advanced control methods. Full-state MPC consistently achieves the highest power output, delivering approximately 3.7 MW in February and 3.5 MW in July. Reduced-state MPC shows moderate performance, reaching 3 MW in February and 2.5 MW in July. The baseline approach, however, performs significantly worse, generating less than 1 MW in both scenarios, underscoring the effectiveness of MPC strategies in optimising energy capture under varying sea states.

5. WP3: Sea State Forecasting and Resource Evaluation

This WP focuses on analysing and predicting wave energy resources to optimise the deployment of WECs. This work package encompasses three key tasks: resource characterisation, efficiency testing, and array effects. WP3.1 involves mapping wave energy potential in deployment areas to identify high-energy zones suitable for WEC operation. WP3.2 emphasizes testing WEC performance in controlled wave tanks to establish performance benchmarks under various marine conditions. Finally, WP3.3 investigates the interactions within WEC arrays to optimise their layout for maximising energy capture.

5.1. WP3.1—Resource Characterisation

This sub-package aims to map the wave energy potential in targeted deployment areas, providing a comprehensive understanding of resource availability. This task focuses on identifying high-energy zones where WECs can operate most effectively, ensuring optimal energy capture and efficient deployment. By characterising wave resources, this subtask lays the foundation for strategic planning and decision-making in the deployment of wave energy technologies [91].

5.1.1. Wave Energy Resource Dynamics in the North-West European Shelf

The rising demand for renewable energy has spurred interest in marine resources, with wave energy emerging as a promising option. Effective deployment of WECs requires a detailed assessment of wave energy potential. This analysis examines wave energy dynamics in the north-west European shelf using a 42-year (1980–2021) hindcast dataset from the Copernicus Marine Environment Monitoring Service (CMEMS). The study evaluates key variables such as significant wave height $H_s$ and energy period $T_e$ to assess wave energy flux using the WAVEWATCH III (v.6.07) model with high spatial ($0.{017}^{\circ }\times 0.{017}^{\circ }$) and temporal (3 h) resolution [92].

• Wave Power Calculation

Wave energy flux, $P_{\mathrm{wave}}$, quantifies the transport of energy by waves per unit crest length and is a critical parameter in assessing wave energy resources. For deep-water conditions, where the water depth is significantly greater than the wavelength, $P_{\mathrm{wave}}$ is calculated using the simplified equation [47]:

$$P_{\mathrm{wave}}={\displaystyle \frac{\rho g^2}{64\pi }}{H}_s^2{T}_e\approx 0.49H_s^2{T}_e\left(\mathrm{kW}/\mathrm{m}\right).$$

(24)

This formulation is widely used for initial assessments of wave power in deep-water scenarios due to its simplicity and reliance on readily available parameters. However, for shallow and intermediate water depths, wave energy flux is influenced by additional factors, such as bathymetry and the complex interaction between wave characteristics and seabed properties. To account for these effects, the general wave energy assessment equation (GWEAE) provides an improved and more accurate formulation [56]:

$$P_{\mathrm{GWEAE}}={\displaystyle \frac{\pi \rho gd{H}_s^2}{16T_e}}\left[{\displaystyle \frac{1}{\mu }}+{\displaystyle \frac{2}{sinh\left(2\mu \right)}}\right],$$

(25)

where d is the water depth, and $\mu$ is a dimensionless parameter describing the wave’s interaction with the seabed [46].

For the data obtained from the Copernicus Marine Service (which includes numerical and in-situ buoy data), specific formulas are necessary to derive energy metrics. While the service provides variables such as significant wave height $H_s$ and energy period $T_e$, it does not directly output energy flux per unit wave crest length. Equations (24) and (25) serve as approximations to estimate the required energy metrics for calculations and are widely used for initial assessments of wave power in deep-water scenarios due to their simplicity and reliance on readily available parameters.

• Variability Metrics

Temporal variability is a key factor in evaluating the stability and reliability of WEC deployments. Stable wave energy resources are essential for ensuring consistent power generation and reducing the risk of system failures caused by extreme variability. Several metrics were used to quantify and analyse wave energy variability across different time scales, including coefficient of variation (COV), seasonal variability (SV), and monthly variability (MV) [93,94]. COV is a statistical measure used to assess the relative variability of wave power over time. It is defined as follows:

$$COV={\displaystyle \frac{{\sigma }_P}{{\mu }_P}},$$

(26)

where ${\sigma }_P$ is the standard deviation of the wave power and ${\mu }_P$ is its mean. The COV provides a normalised measure of variability, allowing comparisons across regions with differing wave power magnitudes. A low COV indicates stable wave power with minimal fluctuations, which is desirable for reliable WEC operation. Conversely, a high COV highlights significant variability, which may pose challenges for energy production consistency. SV quantifies the differences in wave power across the most and least energetic seasons within a year. It is calculated using the following equation:

$$SV={\displaystyle \frac{P_{S\max }-P_{S\min }}{P_{{\mathrm{wave}}_{\mathrm{year}}}}},$$

(27)

where $P_{S\max }$ and $P_{S\min }$ represent the seasonal maxima and minima of mean wave power, respectively, and $P_{{\mathrm{wave}}_{\mathrm{year}}}$ is the annual mean wave power. This metric helps identify seasonal patterns, such as high wave power during winter and reduced levels during summer, which are critical for scheduling maintenance and ensuring optimal device performance during peak energy periods. MV measures the fluctuations in wave power between the most and least energetic months within a year. It is expressed as follows:

$$MV={\displaystyle \frac{P_{M\max }-P_{M\min }}{P_{{\mathrm{wave}}_{\mathrm{year}}}}},$$

(28)

where $P_{M\max }$ and $P_{M\min }$ are the monthly maxima and minima of mean wave power, respectively. MV offers a finer temporal resolution compared to SV, providing perspectives into intra-annual variability. This is particularly useful for regions with significant monthly fluctuations, enabling better planning for energy capture and device operation.

• Results

Temporal Variability: Understanding temporal variability is crucial for evaluating the consistency and reliability of wave energy resources over different time scales. The three key metrics, namely COV, SV, and MV, were used to quantify wave power fluctuations and identify stable regions suitable for WEC deployment. COV analysis shown in Figure 29a highlights regions with significant variability over the entire 42-year dataset. The North Sea demonstrates higher variability compared to the more energetic western regions, where wave power is more consistent. SV and MV analysis shown in Figure 29b,c provide perspectives into shorter-term fluctuations. Coastal areas, including the Irish Sea and the English Channel, exhibit reduced variability in both seasonal and monthly metrics, indicating more stable wave power conditions. These areas may be favourable for consistent energy generation, despite their lower overall energy potential compared to the Atlantic-facing regions.

Figure 29. Wave power temporal variability indexes (scaled to maximum) (Reproduced with permission from [91]. 2023, Rizaev, I. G., et al.).

Multifractal Spectra Analysis: For the first time, multifractal spectra of the COV were Analysed to understand wave power variability across annual $CO{V}_Y$, seasonal $CO{V}_S$, and monthly $CO{V}_M$ scales. The analysis revealed that annual variability $CO{V}_Y$ peaked in 2007, while the lowest variability occurred in 1986 (see Figure 30a). Seasonal variability $CO{V}_S$ was highest in winter and summer, with spring and autumn showing moderate levels (see Figure 30b). Monthly variability $CO{V}_M$ highlighted significant differences between months, with May being the least variable and April showing the greatest variation (see Figure 30c).

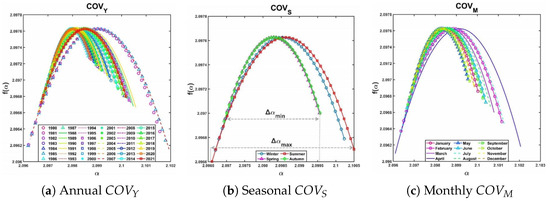
Figure 30. Multifractal spectra of COV for different time periods(Reproduced with permission from [91]. 2023, Rizaev, I. G., et al.).

5.1.2. Site-Specific Assessments and Optimisation

The site-specific wave climates were analysed for four locations: Isle of Islay, SW Irish Coast, Cantabrian Sea, and West of Sardinia. These locations represent diverse marine environments with varying wave conditions critical for the optimisation of the TALOS-WEC. Figure 31 provides joint probability distributions of significant wave height $H_s$ and energy period $T_e$ at each site, offering a comprehensive overview of the most probable sea states. The wave climate at Isle of Islay is characterised by relatively high energy conditions, with $H_s$ frequently exceeding 2.5 m and $T_e$ centred around 7.5 s, making this location ideal for TALOS-WEC deployment due to its consistent wave energy availability. Similarly, the SW Irish Coast exhibits high energy conditions, with $H_s$ ranging from 2.0 to 3.0 m and $T_e$ also peaking near 7.5 s, ensuring efficient energy capture and stable energy resources. In contrast, the Cantabrian Sea demonstrates slightly longer energy periods averaging 8.5 s and $H_s$ between 1.5 and 2.5 m, requiring adjustments to the device’s dimensions, such as increasing its width to 47 m, to optimise energy extraction. Finally, the West of Sardinia features distinct wave conditions with shorter energy periods (3.5–4.5 s) and $H_s$ generally below 1.5 m, posing challenges for large-scale deployment. However, reducing the TALOS-WEC’s width to 10 m can align its resonance frequency with the local wave climate, enabling some energy capture despite the limited energy potential.

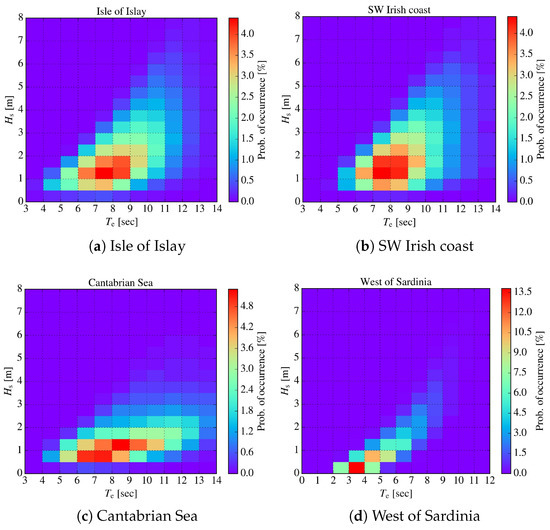
Figure 31. Probability of occurrence of a sea state for four wave climates (Reproduced with permission from [54]. 2023, Oikonomou, C., et al.).

5.1.3. Uncertainty Mitigation and Reliability Improvement in Wave Energy Resource Assessments

This subsection highlights efforts to quantify and reduce uncertainties in wave energy resource assessments, addressing issues such as wind speed errors, modelling assumptions, and inaccuracies in extreme wave conditions. Advanced statistical metrics and bias correction techniques were applied to improve the reliability of energy predictions and optimise site selection, ensuring more effective deployment of WECs.

• Wave Energy Flux and Uncertainty Metrics

Wave energy flux per unit crest length $P_{\mathrm{wave}}$ in (24) is a critical parameter in assessing wave energy resources. It quantifies the transport of energy by waves. Accurate estimation of $H_s$ and $T_e$ is essential for reliable wave energy assessments, as any error in them propagates directly to errors in $P_{\mathrm{wave}}$.

To quantify the uncertainties in the modelled data, several statistical metrics were employed, including (1) bias, (2) root-mean-squared difference (RMSD), and (3) Pearson correlation coefficient r.

Bias measures the systematic error between modelled $M_i$ and observed $O_i$ values. It is calculated as follows:

$$\mathrm{Bias}={\displaystyle \frac{1}{n}}\sum _{i=1}^n(M_i-O_i),$$

(29)

where n is the total number of data points. A positive bias indicates an overestimation, while a negative bias signals underestimation. RMSD evaluates the magnitude of deviations between modelled and observed values, providing an aggregated measure of accuracy:

$$\mathrm{RMSD}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(M_i-O_i)}^2}.$$

(30)

Unlike bias, RMSD captures both systematic and random errors, offering perspectives into overall model performance. Pearson’s r assesses the linear relationship between modelled and observed datasets:

$$r={\displaystyle \frac{{\sum }_{i=1}^n(M_i-\overline{M})(O_i-\overline{O})}{\sqrt{{\sum }_{i=1}^n{(M_i-\overline{M})}^2{\sum }_{i=1}^n{(O_i-\overline{O})}^2}}},$$

(31)

where $\overline{M}$ and $\overline{O}$ are the mean modelled and observed values, respectively. A high r value (close to 1) indicates strong agreement between the datasets, while a low r suggests discrepancies.

• Bias Correction Techniques

Two primary bias correction (BC) techniques were employed to improve model accuracy, including (1) the delta-change (DC) method and (2) empirical quantile mapping (EQM) [95,96]. The DC method applies a constant adjustment $\Delta$ to the modelled data:

$$C_i=M_i+\Delta ,$$

(32)

where $C_i$ is the corrected value and $\Delta =O_i-M_i$. The EQM method adjusts modelled data to align their statistical distribution with observed data:

$$\Delta \left(q_j\right)=CD{F}_M^{-1}\left(q_j\right)-CD{F}_O^{-1}\left(q_j\right),$$

(33)

where $CD{F}^{-1}$ represents the inverse cumulative distribution function. Corrected values are computed as $C\left(q_j\right)=M\left(q_j\right)+f(\Delta \left(q_j\right),n_q)$.

To provide a comprehensive framework for addressing uncertainties in wave energy resource assessments, the study integrated uncertainty exploration, evaluation techniques, and mitigation measures into a structured process. This approach ensures systematic identification and correction of errors in modelled data, particularly for critical parameters such as significant wave height $H_s$ and energy period $T_e$.

• Comparison of Metrics and BC Efficiency

A summary of the performance of the modelled dataset against in situ observations for significant wave height $H_s$ and mean wave period $T_m$ is presented here. Additionally, the efficiency of bias correction methods, BC-DC and BC-EQM, is evaluated. Table 13 combines the key metrics for the original model and the bias-corrected datasets, allowing for a streamlined comparison.

Table 13. Comparison of observed, original model, and bias-corrected datasets for $H_s$ and $T_m$.

Metric	Observed	Model (Original)	Model (BC-DC)	Model (BC-EQM)
${\mathit{H}}_{\mathit{s}}$ (m)
Mean	$1.08$	$1.03$	$1.08$	$1.08$
Bias	−	$-0.04$	$0.00$	$0.00$
RMSD	−	$0.23$	$0.22$	$0.22$
50th Percentile	$0.83$	$0.80$	$0.84$	$0.84$
95th Percentile	$2.69$	$2.56$	$2.60$	$2.69$
Pearson r	−	$0.96$	$0.96$	$0.96$
${\mathit{T}}_{\mathit{m}}$ (s)
Mean	$4.07$	$3.83$	$4.07$	$4.06$
Bias	−	$-0.24$	$0.00$	$0.00$
RMSD	−	$0.55$	$0.49$	$0.43$
50th Percentile	$3.91$	$3.65$	$3.89$	$3.91$
95th Percentile	$5.83$	$5.86$	$6.10$	$5.83$
Pearson r	−	$0.89$	$0.89$	$0.89$

The table highlights that both DC and EQM effectively eliminate bias for both $H_s$ and $T_m$, with EQM demonstrating slightly superior performance in reducing RMSD for $T_m$ ($0.43\mathrm{s}$). Pearson correlation coefficients r remain consistent across all methods, indicating a robust agreement between modelled and observed datasets. For $H_s$, EQM preserves the observed 95th percentile values more accurately than delta-change, making it a preferable method for assessing extreme wave conditions. Similarly, for $T_m$, EQM achieves the lowest RMSD and aligns closely with observed median and 95th percentile values.

5.2. WP3.2—Efficiency Testing

Efficiency testing is critical for assessing the TALOS-WEC’s performance under both controlled and marine environments. This phase involves numerical modelling, experimental validation, and performance metrics to optimise energy capture and hydrodynamic efficiency.

The energy conversion efficiency is evaluated using the following equation:

$$\eta ={\displaystyle \frac{P_{\mathrm{converted}}}{P_{\mathrm{wave}}}}={\displaystyle \frac{{\int }_0^{T_e}{F}_{\mathrm{PTO}}\left(t\right)·v_{\mathrm{rel}}\left(t\right)dt}{0.5\rho g{H}_s^2{C}_g{A}_w}},$$

(34)

This equation highlights the proportional relationship between wave-induced motion and energy conversion efficiency.

A comparison of numerical predictions and experimental results (wave tank testing) underscored the dominance of surge and heave modes in energy capture. Laboratory experimental results for RAOs closely matched numerical predictions, validating the hydrodynamic model’s reliability for performance evaluations. Pitch modes, however, remained less effective due to their narrow resonance bandwidths [54].

5.3. WP3.3—Array Effects

WP3.3 focuses on understanding and optimising the interactions between multiple WECs in arrays to maximise energy capture. This involves mitigating destructive interference, enhancing constructive wave interactions, and optimising device spacing and alignment to ensure efficient deployment and scalability of WEC technologies like the TALOS-WEC.

TALOS-WEC project provides foundational perspectives into spatial and temporal wave dynamics and validates the impact of alignment, spacing, and resonance tuning on wave interference. The work in [54] offers the primary contribution to WP3.3, using advanced frequency-domain simulations to analyse hydrodynamic interactions, including radiation forces, added mass, and wave scattering. Key findings from [54] quantify the power enhancement coefficient (PEC) and identify optimal array layouts customised to various wave climates.

WP3.3 establishes guidelines for WEC farm designs. For example, inter-device spacing of 1.5–2 wavelengths minimises destructive interference and wave shadowing, while alignment with dominant wave directions enhances power capture [54]. These strategies are crucial for achieving energy efficiency and economic viability in real-world marine environments.

6. WP4: Validation and Cost Analysis

WP4 aims to validate the performance and evaluate the economic feasibility of WECs to ensure their commercial viability and scalability. It comprises three interconnected tasks: WP4.1—Validation and Demonstration, which focuses on real-world testing to verify performance against industry standards and benchmarks; WP4.2—Array Deployment, addressing challenges in scaling up to multiple WEC arrays and understanding inter-device interactions; and WP4.3—LCOE Assessment, developing robust techno-economic models to calculate the LCOE and optimise cost structures, with detailed analyses in [55,56]. These tasks collectively advance the commercialisation potential of WECs.

6.1. WP4.1—Validation and Demonstration

This sub-package focuses on validating the performance of the TALOS-WEC system as it transitions from controlled experiments to real-world operational environments. The primary objectives include rigorous evaluation of energy conversion efficiency, grid integration capabilities, and scalability, ensuring the system’s readiness for commercialisation. Building on laboratory tests from WP3.2, which established benchmarks for hydrodynamic efficiency and power conversion mechanisms, the dominance of surge and heave modes in energy capture was demonstrated, along with the ability to replicate dynamic wave profiles and generate consistent PTO forces.

To address commercialisation challenges, WP4.1 emphasises key aspects critical to the TALOS-WEC’s success. These include modular PTO designs that ensure system scalability and efficient energy extraction across diverse marine environments, integration of battery energy storage systems (BESS) to smooth power fluctuations and enhance grid compatibility, and the demonstration of consistent power output under dynamic wave conditions for seamless grid integration. Additionally, the system’s robust and adaptable design supports long-term deployment, ensuring longevity, cost-effectiveness, and operational reliability [97].

6.2. WP4.2—Array Deployment

This sub-package addresses the scalability of the TALOS-WEC in array configurations, focusing on the challenges and perspectives related to large-scale deployments. By extending the performance of individual units, WP4.2 aims to optimise array layouts, evaluate resource sharing, and address operational challenges unique to array-based energy capture systems.

6.2.1. Scalability of TALOS-WEC Arrays

The modular design of the TALOS-WEC, established through laboratory validations and numerical simulations, supports scalability for deployment in arrays. Key principles enabling scalability include:

• Distributed energy extraction: Arrays of TALOS-WECs exploit constructive wave interactions, enhancing energy capture while mitigating destructive interference effects.
• Adaptive spacing and alignment: Optimal spacing ensures maximum energy absorption while minimising wake-induced losses. Alignment with dominant wave directions improves array performance under varying marine conditions.
• Modular design flexibility: Each TALOS-WEC unit operates independently, allowing scalable configurations customised to site-specific wave climates and energy demands.

6.2.2. Array Performance and Interference Effects

Numerical modelling and experimental analyses of TALOS-WEC arrays highlight the importance of managing inter-device interactions, as spacing, alignment, and environmental factors influence constructive and destructive interference. Optimising layouts mitigates shadowing effects while ensuring high energy capture efficiency.

6.2.3. Challenges for Large-Scale Deployment

Deploying TALOS-WEC arrays at scale introduces several technical challenges:

• Wake effects and hydrodynamic loads: Arrays face complex wake interactions, which can reduce energy capture efficiency for downstream units. Advanced simulations are necessary to model these effects and optimise array configurations.
• Grid integration and power management: Scaling up arrays requires efficient power conditioning and smoothing. Integration with BESS ensures grid compatibility by addressing variability in wave energy output.
• Structural and mooring system durability: Large arrays impose significant loads on mooring and structural systems, especially under extreme marine conditions.

6.3. WP4.3—LCOE Assessment

The LCOE is a pivotal metric for evaluating the economic feasibility of WECs, such as the TALOS-WEC. This subsection focuses on developing robust techno-economic models that encompass capital expenditure (CAPEX), operational expenditure (OPEX), pre-installation cost or pre-operating cost (PC), and decommissioning costs (DC) to calculate the LCOE and ensure the cost competitiveness of wave energy [55].

6.3.1. Levelised Cost of Wave Energy

The levelised cost of energy (LOCE) represents the average minimum price at which electricity must be sold to break even over a project’s operational lifespan.

$$LCO{E}_{\mathrm{base}}={\displaystyle \frac{CAPEX+{\sum }_{y=1}^u{\displaystyle \frac{OPE{X}_y}{{(1+dr)}^y}}}{{\sum }_{y=1}^u{\displaystyle \frac{AE{P}_y}{{(1+dr)}^y}}}},$$

(35)

where the discount rate $dr$ reflects the time value of money, accounting for the cost of capital and financial risks associated with the project. The variable u denotes the project’s operational lifespan in years, encompassing the duration over which the system is expected to produce energy and incur associated costs. $AE{P}_y$ represents the AEP at year y. AEP is a pivotal metric in determining the economic viability of wave energy projects, as it directly impacts the LCOE. AEP quantifies the total energy output of the system over a year and is calculated using the following equation:

$$AEP={\eta }_{conv}\times P_{\mathrm{wave}}\times \mathrm{availability}\mathrm{factor},$$

(36)

where ${\eta }_{conv}$ represents the energy conversion efficiency of the system, a crucial parameter influenced by the design and operation of the PTO mechanisms. The availability factor accounts for system downtime caused by maintenance activities, environmental conditions, or operational inefficiencies, impacting the overall energy output and reliability of the system.

Optimising AEP is critical for reducing the LCOE and enhancing the economic competitiveness of wave energy technologies. The TALOS-WEC system can achieve higher AEP through several targeted strategies. PTO Optimisation (as described in Section Optimisation of the PTO System) involves fine-tuning the force damping and stiffness of the PTO mechanisms to align with the dynamic characteristics of site-specific wave climates, thereby maximising energy capture. Site-Specific Tuning (as described in Section 5.1.2) focuses on customising key device parameters, such as resonance frequency and mooring configurations, to fully exploit the energy potential of high-energy wave environments. Additionally, Minimising Downtime is achieved by implementing predictive maintenance strategies and incorporating robust design features to enhance the availability factor, ensuring consistent energy output and long-term system reliability.

6.3.2. Cost Breakdown

CAPEX, OPEX, PC, and sometimes decommissioning costs, can be incorporated to provide a comprehensive framework for comparing wave energy projects with other renewable and non-renewable energy sources (see Figure 32). As such, LCOE serves as a key indicator of the commercial viability of wave energy technologies.

Figure 32. Distribution of CAPEX, OPEX, PC, and DC across the project lifecycle (Reproduced with permission from [55]. Licensed under CC-BY 4.0, MDPI, 2023.).

• Capital Expenditure (CAPEX)

CAPEX constitutes 50–70% of the levelised cost of energy (LCOE) for wave energy projects. Key components include device costs (e.g., TALOS-WEC construction and PTO systems), installation (e.g., mooring systems and vessel mobilisation), and grid connection (e.g., subsea cables and substations), as depicted in Figure 33. Modular PTO designs and lightweight structural components enable phased installations and lower material costs, enhancing economic feasibility.

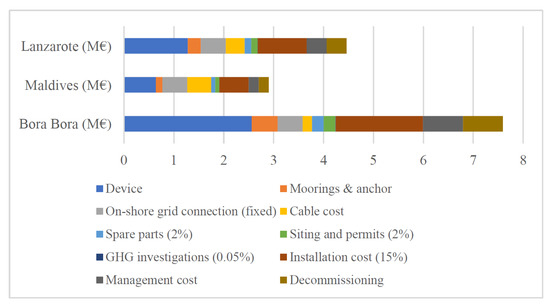
Figure 33. Breakdown of CAPEX costs across device, installation, and grid connection categories (Reproduced with permission from [55]. Licensed under CC-BY 4.0, MDPI, 2023.).

Geographical factors also influence CAPEX and LCOE. High-energy locations like Bora Bora achieve favourable LCOE values (£0.282/kWh for two WECs with $3406.32\mathrm{MWh}$ AEP and 98% availability), driven by strong wave energy potential and reduced infrastructure costs. Conversely, harsher climates or less developed regions experience higher CAPEX and OPEX, underscoring the importance of site-specific planning.

Key CAPEX components for wave energy systems include device costs for essential elements like gravity foundations (EUR 2125), buoys (EUR 8400), translators (EUR 21,120), stators (EUR 8100), casings (EUR 5300), labour (EUR 25,000), and materials (EUR 10,000). Electrical system costs cover intra-array cables (EUR 46/m), transmission cables (EUR 72.5/m), communication cables (EUR 2/m), and substations (EUR 168/km). Installation costs involve deploying WECs (EUR 4100), substations (EUR 10,000), and cables (EUR 500/km). Decommissioning costs include dismantling and recycling these components, ensuring proper waste management [55].

CAPEX distribution shows structure costs at 38.2%, foundation and mooring at 19.1%, installation at 10.2%, PTO components at 24.2%, and grid connection at 8.3%. Specific development costs are EUR 250/kW for site development, EUR 1340/kW for WECs, EUR 1600/kW for balance of plant, EUR 590/kW for installation, and EUR 420/kW for decommissioning. Large-scale deployments include WEC and installation costs (EUR 2.5–6.0 million/MW), mooring systems (EUR 0.265/day), and electrical substations (EUR 1.2 million).

A phased investment approach, starting with smaller-scale installations, can reduce upfront CAPEX, validate performance, and address operational challenges. This strategy enables optimised resource allocation and risk reduction, improving economic feasibility for large-scale TALOS-WEC deployments.

• Operational Expenditure (OPEX)

OPEX is vital for the long-term sustainability of wave energy projects, covering regular and corrective maintenance of the WEC structure and PTO systems, insurance costs to mitigate environmental and operational risks, and administrative costs for monitoring and regulatory compliance. IoT-based predictive maintenance systems can reduce downtime and costs by enabling real-time monitoring and proactive interventions. Insurance premiums can also be lowered through validated system reliability, as highlighted in WP4.1, improving the economic feasibility of TALOS-WEC over its lifespan.

Figure 34 shows that CAPEX consistently dominates total costs, underscoring the importance of modular PTO designs and efficient installations in the TALOS-WEC project to minimise upfront capital expenditures.

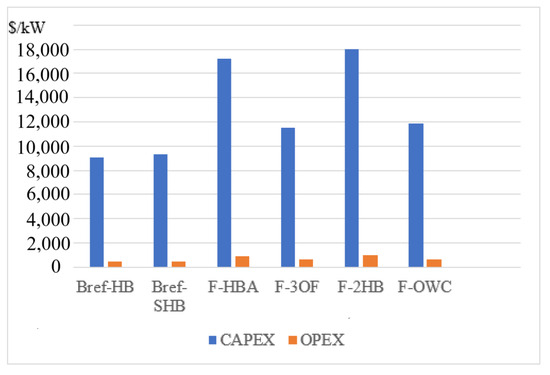
Figure 34. CAPEX per unit of case study simulated in the sea area of the USA (Reproduced with permission from [55]. Licensed under CC-BY 4.0, MDPI, 2023.).

Key OPEX components for wave energy projects include repair and maintenance of critical systems, such as buoys (EUR 723/year) and generators (EUR 10,000/year), along with site lease and insurance costs (EUR 5000/year). Annual operational and maintenance (O&M) expenses account for 29% of OPEX, with overhauls at 15% and replacements at 45%. Insurance represents 11% of OPEX, with additional costs equal to 1% of CAPEX, emphasising risk mitigation’s role. OPEX typically ranges from 5–15% of CAPEX, reflecting its economic significance. Maintenance activities require four vessel-days and sixteen person-days, with mooring tension adjustments performed periodically (e.g., after 1, 5, and 10 years). Replacements contribute 1.5% of CAPEX, underscoring the need for effective lifecycle planning [55].

• Decommissioning costs (DC)

Decommissioning costs, while representing a smaller portion of total costs, include dismantling and recycling components at the end of the project lifespan.

• Pre-installation Costs (PC)

PC encompasses early-stage expenses in wave energy projects, such as site selection, environmental assessments, permitting, farm design, and consenting procedures. These costs are critical for ensuring well-prepared deployment strategies that align with regulatory and site-specific requirements.

Including PC in the total cost significantly affects LCOE calculations by shifting the project timeline earlier, necessitating the compounding of PC to reflect its future value at the project’s formal start. The revised LCOE calculation is shown in Equation (37):

$$LCO{E}_{\mathrm{revised}}={\displaystyle \frac{{\sum }_{y=i-3}^u{\displaystyle \frac{P{C}_y+CAPE{X}_y+OPE{X}_y+D{C}_y}{{(1+dr)}^y}}}{{\sum }_{y=i-3}^u{\displaystyle \frac{AE{P}_y}{{(1+dr)}^y}}}},$$

(37)

Efficient PC management through strategies such as phased investments and modular CAPEX structures minimises financial risks and improves economic feasibility. By addressing pre-installation inefficiencies like permitting delays, projects can further enhance LCOE and operational viability.

6.3.3. Seasonal and Geographic Variability

Beyond costs, seasonal and geographic variability significantly influence the performance and economic viability of wave energy systems like TALOS-WEC. The monthly energy production (MEP) can be modelled as [56]:

$$MEP=P_{\mathrm{wave}}\times W_{\mathrm{absorber}}\times {\eta }_{\mathrm{wave}-\mathrm{to}-\mathrm{wire}}\times \mathrm{availability}\mathrm{factor}\times \mathrm{hours}\mathrm{per}\mathrm{month}\times n_{\mathrm{WEC}\mathrm{devices}},$$

(38)

where $W_{\mathrm{absorber}}$ is the absorber width, which is specified as 30 m, ${\eta }_{\mathrm{wave}-\mathrm{to}-\mathrm{wire}}$ denotes the wave-to-wire efficiency, calculated at 20%, and $n_{\mathrm{WEC}\mathrm{devices}}$ refers to the number of wave energy converter devices deployed in the system.

Wave power varies significantly with seasons. Winter months typically exhibit higher wave power due to stronger winds and ocean dynamics, while summer months see reduced wave activity. For example, at Location A, wave power in winter reaches 109.63 kW/m compared to just 17.79 kW/m in summer. This seasonal variation directly affects energy capture, necessitating robust designs and energy storage solutions to ensure consistent supply.

Geographic location also plays a critical role in determining wave energy potential. Locations with higher $H_s$ and $T_e$ (see (24)), such as Location A in Figure 35, exhibit significantly greater energy potential compared to less dynamic wave environments. This figure highlights annual mean wave power variations across locations, emphasising the importance of site selection for TALOS-WEC deployments.

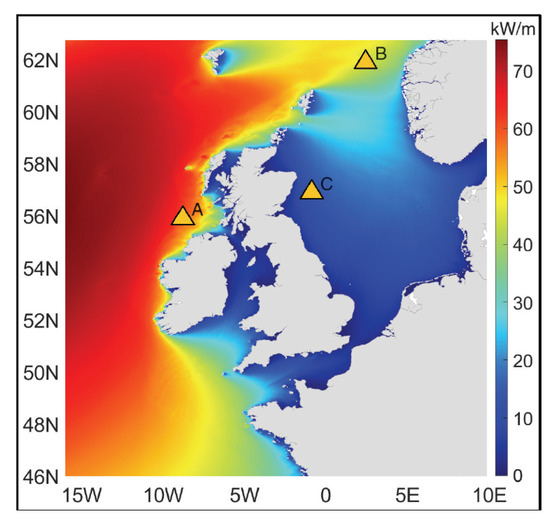
Figure 35. Annual mean wave power at different locations around the British Isles, displaying wave power density in kW/m. The color scale represents wave energy flux, with red indicating higher energy levels and blue indicating lower values. The marked locations correspond to key study sites: (A) off the west coast of Scotland, (B) in the North Sea near Norway, and (C) in the Irish Sea. (Reproduced with permission from [56]. 2024, DiLellio, J.A., et al.).

6.3.4. Advanced Financial Metrics

Having established the importance of costs and seasonal variability, this section delves into financial models that incorporate these dynamics to assess project viability. The financial feasibility of TALOS-WEC is assessed by integrating LCOE with NPV and stochastic models for electricity price forecasting. These advanced metrics provide a comprehensive evaluation of project profitability and long-term viability [55,56].

NPV complements LCOE by incorporating revenue generation, market value, and electricity price trends. The NPV formula is given by

$$NPV=\sum _{y=1}^u{\displaystyle \frac{R_y-C_y}{{(1+dr)}^y}}-\mathrm{CAPEX},$$

(39)

where $R_y$ is revenue and $C_y$ represents costs at year y. Positive NPV values indicate economic viability, especially when supported by favourable electricity prices and policy incentives. The inclusion of NPV enhances the traditional LCOE analysis, accounting for market uncertainties and policy-driven incentives.

6.3.5. LCOE Sensitivity to Discount Rate and Discount Factor

The LCOE is highly sensitive to the discount rate ($dr$), which represents the time value of money and financing costs. Higher discount rates significantly increase the LCOE, potentially reducing the economic competitiveness of wave energy. For example

• At $dr=11\%$, the LCOE exceeds $160/MWh, limiting cost competitiveness.
• Lowering $dr$ to 6% reduces the LCOE to approximately $102/MWh, demonstrating the importance of favourable financing conditions.

The discount factor ($D{F}_y$), defined as follows:

$$D{F}_y={\displaystyle \frac{1}{{(1+dr)}^y}},$$

(40)

adjusts future costs and revenues to their present value, enabling accurate economic assessments. Break-even analysis equates the present value of revenues ($RE{V}_y$) and total costs ($T{C}_y$) over the project lifespan, as expressed by

$$\sum _{y=1}^i{\displaystyle \frac{RE{V}_y}{{(1+dr)}^y}}=\sum _{y=1}^i{\displaystyle \frac{T{C}_y}{{(1+dr)}^y}}.$$

(41)

7. Results and Key Findings

Table 14 summarizes the results and key findings of the study, providing information on the performance, design, and optimisation of the TALOS-WEC system in various aspects.

Table 14. Summary of results and key findings.

Aspect	Key Findings
Hydrodynamic Modelling	Heave motion plays a dominant role in energy absorption, exhibiting the highest added mass ($4.2\times {10}^6\mathrm{kg}$) and damping coefficient ($7.8\times {10}^4\mathrm{Ns}/\mathrm{m}$). Coupled surge–pitch dynamics are critical for multi-modal energy transfers, highlighting the importance of addressing transient dynamics in design.
Numerical Tools	WAMIT excels in validating complex configurations, HAMS offers computational efficiency for iterative designs, and NEMOH is suitable for cost-effective preliminary studies.
Numerical Modelling	The hydraulic PTO system ensures stable energy harvesting with synchronised heave oscillations. Asymmetric PTO placements, such as PTO2 and PTO3, highlight the need for optimised spatial design.
Mooring System Effects	Slack mooring (MLC1) enhances energy absorption but increases variability and structural instability. Moderately slack mooring (MLC2) balances energy efficiency and stability.
Geometric optimisation	Shortened and Tailless TALOS configurations excel in energy absorption (8–9 s wave periods). Lowering the centre of gravity and adding overlapping panels enhance stability and performance.
PTO optimisation	Soft springs ($K_{\mathrm{PTO}}=250\mathrm{kN}/\mathrm{m}$) and damping coefficients ($B_{\mathrm{PTO}}=150\mathrm{kNs}/\mathrm{m}$) maximise energy absorption. Low damping improves efficiency but risks instability.
Condition Monitoring	KPCA-LSTM provides computational efficiency for long-term trends, while ANN-LSTM is effective for real-time monitoring. Combined approaches enhance reliability and reduce downtime.
Control Strategies	Full-state MPC delivers the highest power output (3.7 MW) but requires significant computational resources. Reduced-state MPC balances performance (3 MW) with efficiency.
Wave Energy Resource Dynamics	The highest wave energy potential (>70 kW/m) is west of the UK and Ireland, with peaks in winter (>140 kW/m). Coastal areas offer moderate but stable energy levels (35 kW/m).
Site-Specific Assessments	High-energy sites (Isle of Islay, SW Irish Coast) require minimal optimisation for deployment. Moderate-energy sites (Cantabrian Sea) need customised adjustments, while low-energy sites (West of Sardinia) necessitate significant design modifications.
Uncertainty Mitigation	Bias correction techniques (e.g., BC-QM) improve data reliability, achieving high correlation ($r=0.96$ for $H_s$), particularly under extreme conditions.
Validation and Demonstration	Laboratory experiments validated numerical predictions, aligning strongly with real-world performance. Modular, scalable designs ensure efficient array deployment and energy extraction.
LCOE optimisation	Competitive LCOE (0.2–0.35 €/kWh) achieved through modular designs, predictive maintenance, and targeted high-wave-energy deployments. Reactive control improves efficiency and scalability.

8. Discussions and Conclusions

The TALOS-WEC project underscored several valuable lessons for future renewable energy developments. A key factor was the use of a structured approach to project management, dividing tasks into distinct WPs to effectively handle the complexity of integrating multiple technical fields. For instance, WP1 concentrated on the foundational design and optimisation of the WEC, including hydrodynamic interactions (WP1.1), geometric refinement (WP1.2), and PTO system development (WP1.3). WP2, on the other hand, tackled reliability and survivability by integrating smart sensors (WP2.1), employing AI-based condition monitoring (WP2.2), developing predictive maintenance strategies (WP2.3), and implementing adaptive control systems for variable sea states (WP2.4). This division allowed for parallel advancements in different areas, a method that can be broadly applied in multidisciplinary endeavours.

The findings from the hydrodynamic and numerical modelling of the TALOS-WEC provide a comprehensive understanding of the system’s energy absorption mechanisms, dynamic behaviour, and optimisation potential. The dominance of heave motion in vertical energy capture underscores the importance of designing systems that maximise its efficiency, particularly by tuning frequency-dependent parameters to leverage resonance effects. The coupled interactions between surge and pitch reveal critical perspectives into multi-modal energy transfers, necessitating a holistic approach to optimising rotational-translational dynamics.

Numerical tools such as WAMIT, HAMS, and NEMOH demonstrate complementary strengths, making them invaluable for different phases of the design process. While WAMIT provides high accuracy for validating advanced configurations, HAMS offers computational efficiency for iterative design iterations, and NEMOH is suitable for cost-effective preliminary studies. These tools, combined with hydrodynamic modelling, support a robust and efficient design pipeline.

The optimisation of mooring configurations, PTO parameters, and geometric features like the centre of gravity and overlapping panels significantly enhances energy capture and system stability. However, trade-offs between energy absorption and structural integrity remain, particularly in slack mooring systems and low damping configurations. Intelligent condition monitoring frameworks, integrating KPCA-LSTM and ANN-LSTM models, offer reliable solutions for real-time and long-term system health assessments, ensuring operational safety and efficiency.

Control strategies further refine energy performance, with full-state MPC achieving superior energy output but at higher computational costs. Reduced-state MPC balances computational demand and performance, making it an effective alternative for moderate conditions. These findings highlight the importance of tailoring control strategies to the specific operational context and energy capture objectives.

Wave energy resource assessments emphasize the need for strategic site selection, balancing high-energy potential with temporal stability. Locations such as the Isle of Islay and SW Irish Coast offer prime conditions for large-scale deployment with minimal optimisation. Conversely, low-energy sites like Sardinia require significant design modifications to achieve operational feasibility.

The validation and demonstration phases confirm the reliability of the TALOS-WEC’s numerical models, with laboratory experiments aligning closely with real-world performance metrics. Modular and scalable designs enhance array deployment potential, ensuring efficient energy extraction even in large-scale applications. Furthermore, the optimisation strategies for reducing the levelised cost of energy (LCOE) demonstrate the system’s economic viability, supported by advanced PTO designs, predictive maintenance, and strategic geographic deployments.

The development and optimisation of the TALOS-WEC highlight its potential as a reliable and efficient wave energy converter, capable of addressing the challenges associated with dynamic marine environments. By leveraging advanced hydrodynamic modelling, numerical tools, and intelligent monitoring frameworks, the system achieves significant improvements in energy capture, operational stability, and cost-effectiveness.

Key advancements in PTO design, geometric optimisation, and control strategies enhance the TALOS-WEC’s adaptability across diverse wave climates. The system’s modular and scalable design supports large-scale deployments, while its competitive LCOE positions it as a viable solution in the renewable energy market. Site-specific assessments and resource evaluations further refine its deployment strategy, aligning performance with local wave conditions to maximise energy yield.

The knowledge gained from this project can contribute to improving the effectiveness and dependability of other renewable energy technologies, such as wind turbines and tidal energy converters.

9. Challenges and Future Work

The development of TALOS-WEC faced several challenges that provided valuable learning opportunities for future advancements. One significant issue was accurately modelling the flexible connections between the hull and the internal reaction mass, which introduced considerable non-linearities into the system. To address this, bespoke numerical models, such as the hybrid frequency-time domain approach, were developed. While these efforts ultimately enhanced system understanding, they also caused delays. Another challenge was integrating smart sensors for real-time monitoring. Ensuring reliable data transmission in harsh marine environments required iterative hardware testing and recalibration. In hindsight, more extensive prototype testing in controlled settings could have mitigated some of these delays. Building on these experiences, future work will focus on real-world validation through large-scale marine trials, grid integration solutions, and adaptive biomimetic designs. These efforts aim to ensure the scalability and commercialisation of the TALOS-WEC, contributing to global renewable energy goals and advancing the transition to sustainable energy solutions.