Deep Reinforcement Learning Based Optimal Operation of Low-Carbon Island Microgrid with High Renewables and Hybrid Hydrogen–Energy Storage System
Abstract
1. Introduction
2. Problem Statement
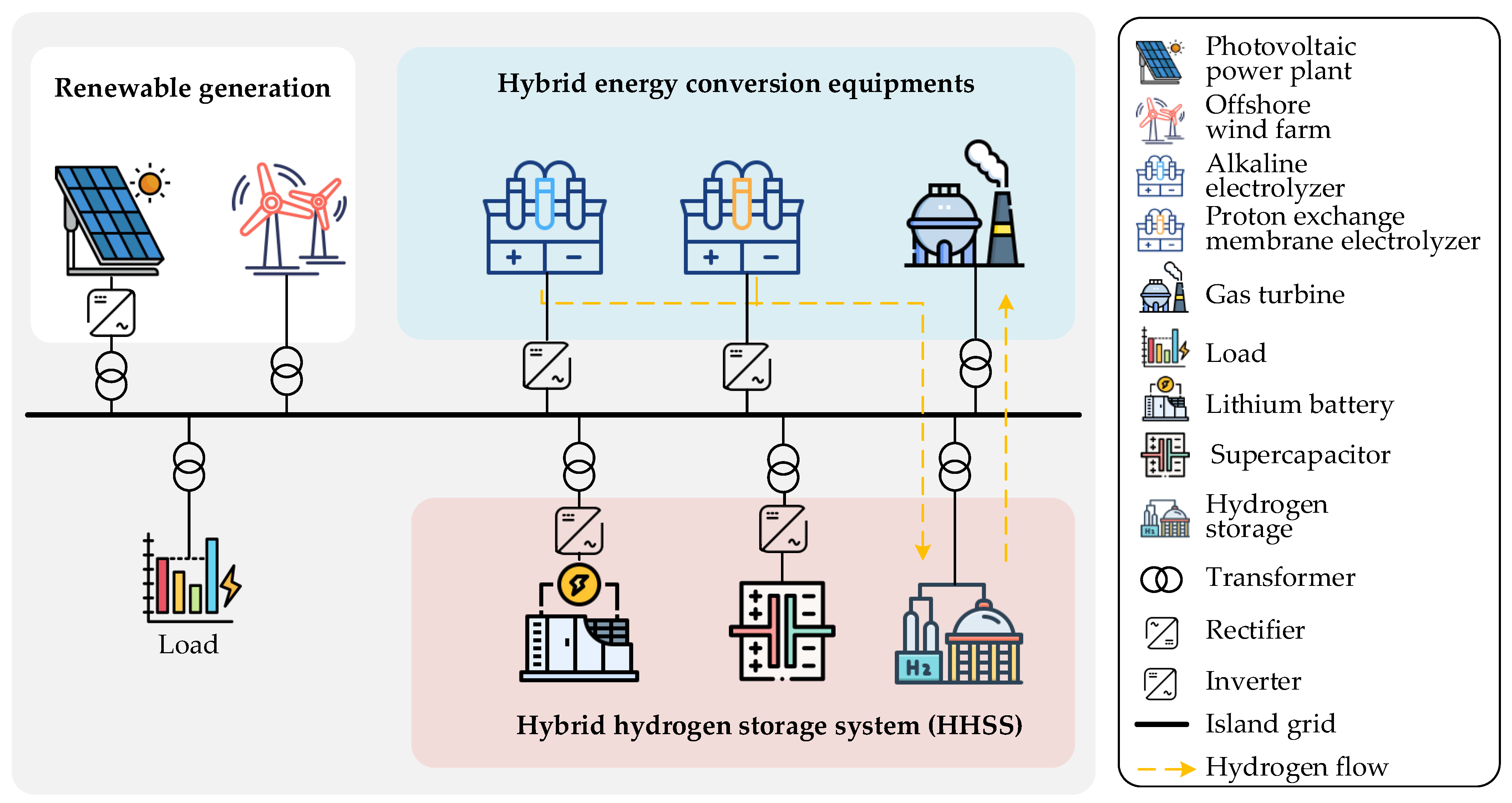
2.1. Hybrid Hydrogen–Energy Storage-Based Island Microgrid
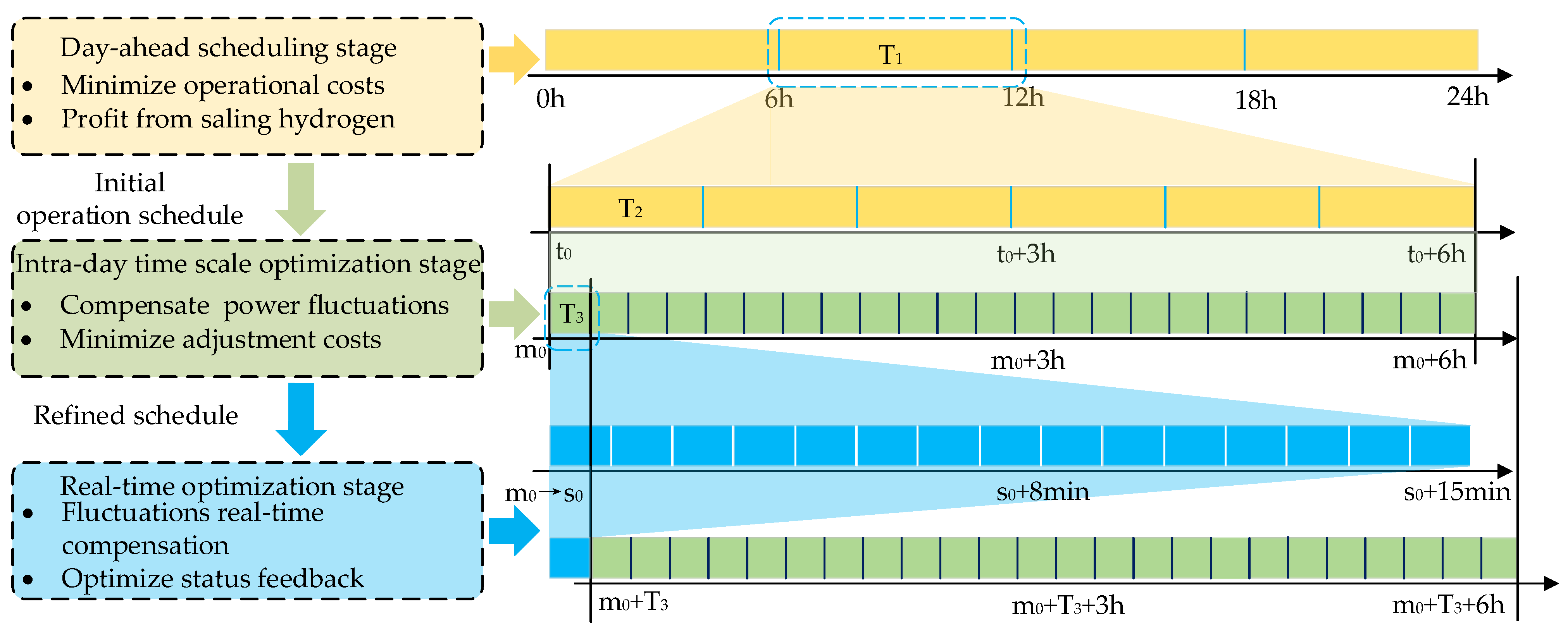
2.2. Multi-Stage Optimization Framework
3. Mathematical Formulation
3.1. Day-Ahead Scheduling Model
3.1.1. Objective Function of Day-Ahead Scheduling Model
3.1.2. Constraints
- Power balance:
- Constraints for gas turbines:
- Constraints for alkaline electrolyzers (ALKs) and proton exchange membrane electrolyzers (PEMs):
- Constraints for hydrogen storage:
3.2. Intra-Day Two-Stage Optimal Operation Model
3.2.1. First-Stage Intraday Optimal Operation Model
- Objective function
- Constraints
3.2.2. Intraday Real-Time Optimal Operation Model
- Objective function
- Constraints
4. Solution Method
4.1. Discrete Wavelet Transform-Based Power Imbalance Decomposition
- Decomposition for first-stage intraday optimization
- Decomposition for intraday real-time optimization
4.2. Reinforcement Learning Method
4.2.1. Markov Decision Process
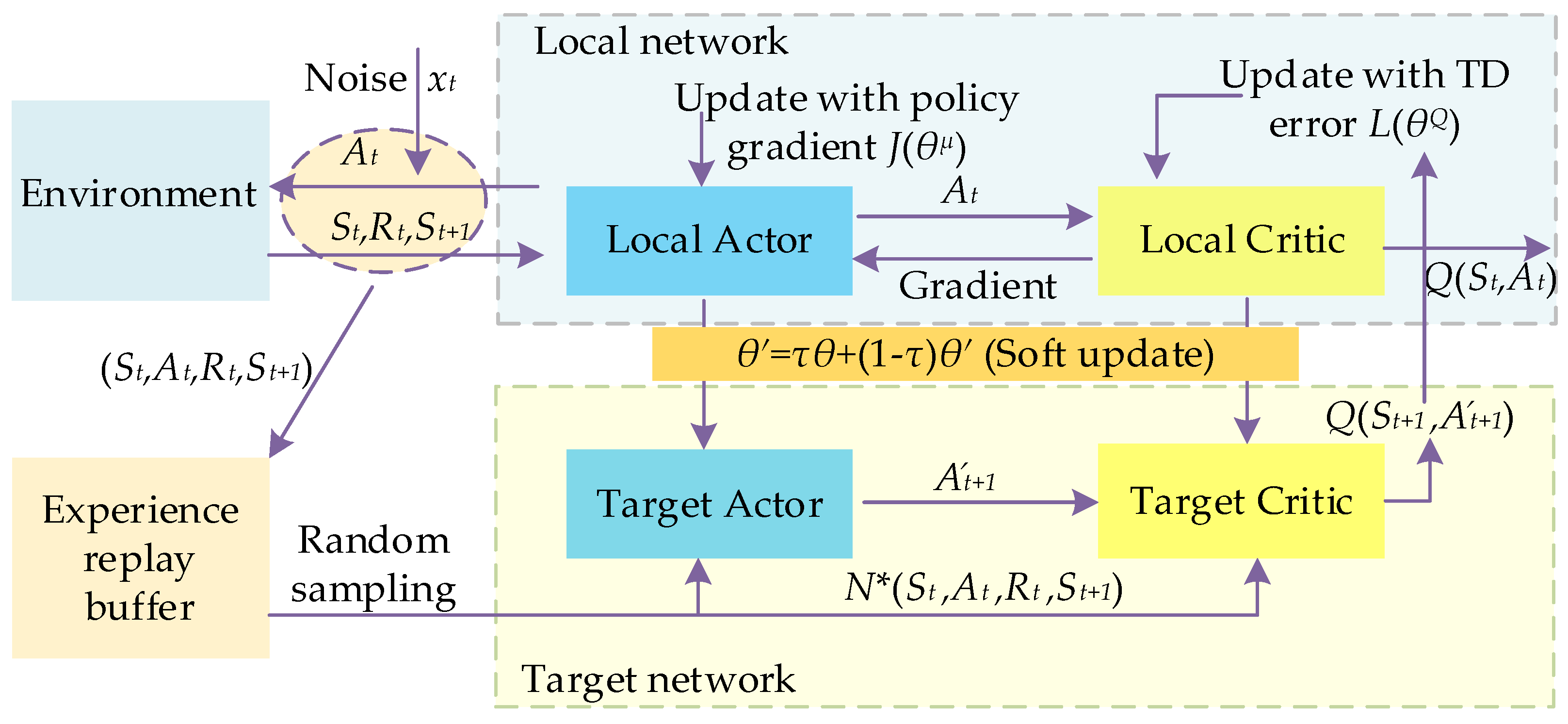
4.2.2. Deep Deterministic Policy Gradient
4.3. Frequency-Decomposed Reinforcement Learning Method
- Initialization
- 2.
- First-layer optimization
- 3.
- Second-layer optimization
- 4.
- Feedback loop
- 5.
- Iteration
| Algorithm 1 Multi-stage optimization framework with frequency decomposition |
| 1: Initialize the network parameters ,,, experience replay buffer E, model of PEM, LB, SC, day-ahead dispatch plan for next 6 h as state (0) 2: for m = 0 to M do 3: Receive power fluctuation data for the current 15 min period 4: Apply DWT to decompose power fluctuation signal into frequency components, and assign to PEM and LB, minimize cost for hydrogen production and battery operation 5: Pass , to the second layer for real-time optimization 6: for s = m to m+1 do 7: Receive real-time power fluctuation data for the current 1 min period 8: Apply DWT to decompose real-time power fluctuation signal, minimize short-term fluctuation with real-time response from battery and supercapacitor 9: Store the 1 min power adjustment plan 10: Update state 11: end for 12: Feedback results of real-time optimization to the first layer 13: Update state and proceed to the next 15 min window 14: end for |
5. Case Study
5.1. Data Set
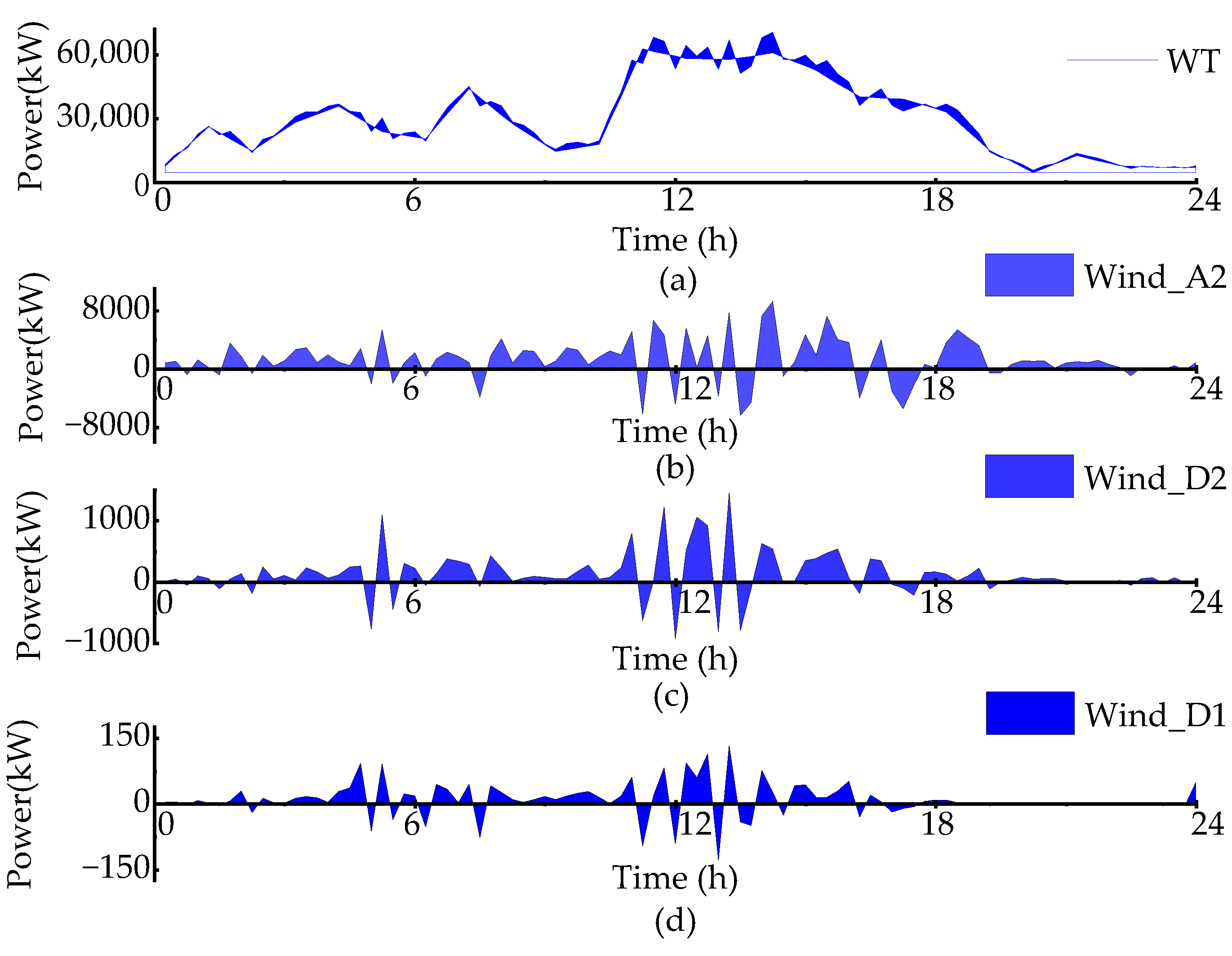
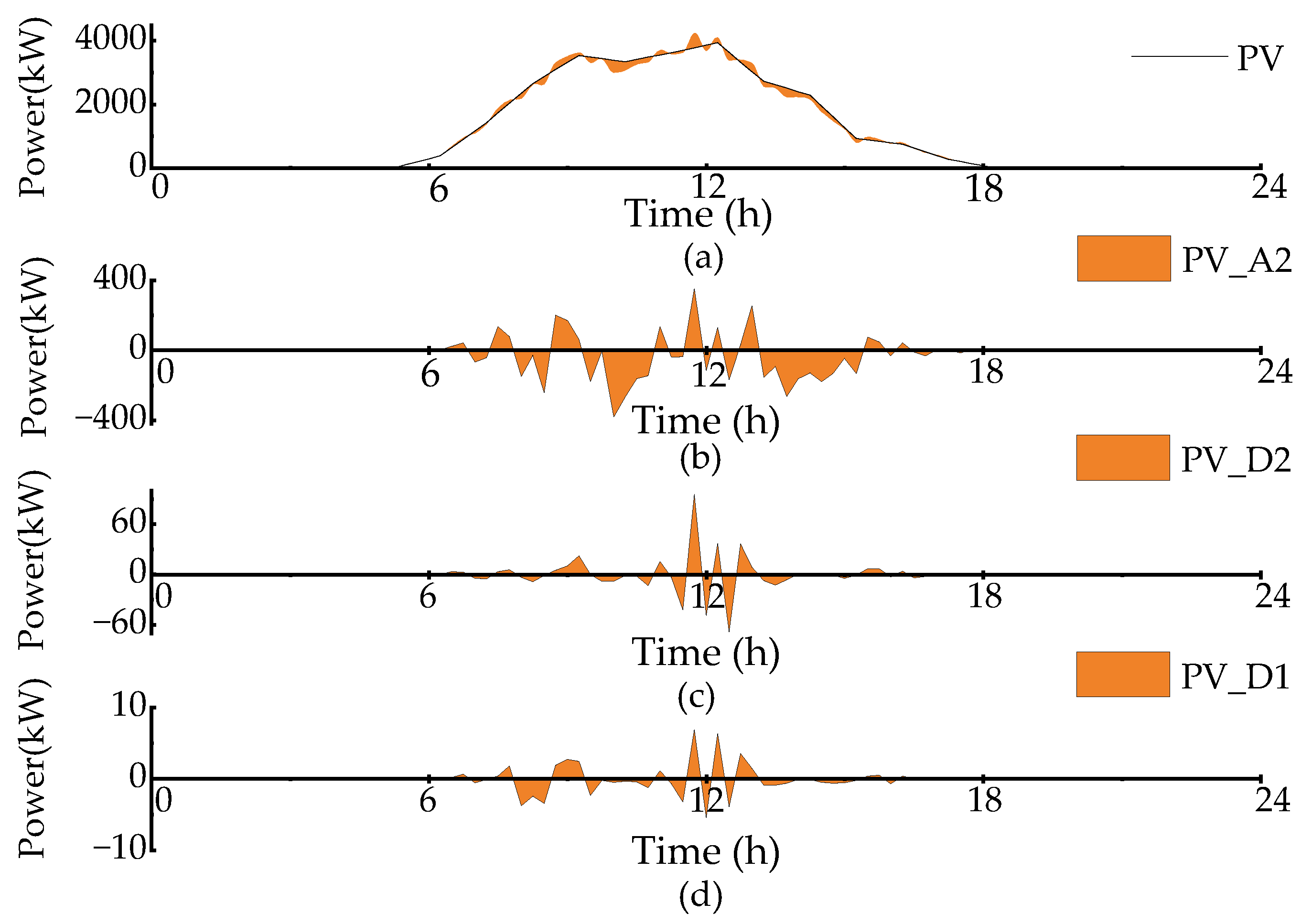
5.2. Fluctuation Power Decomposition Analysis
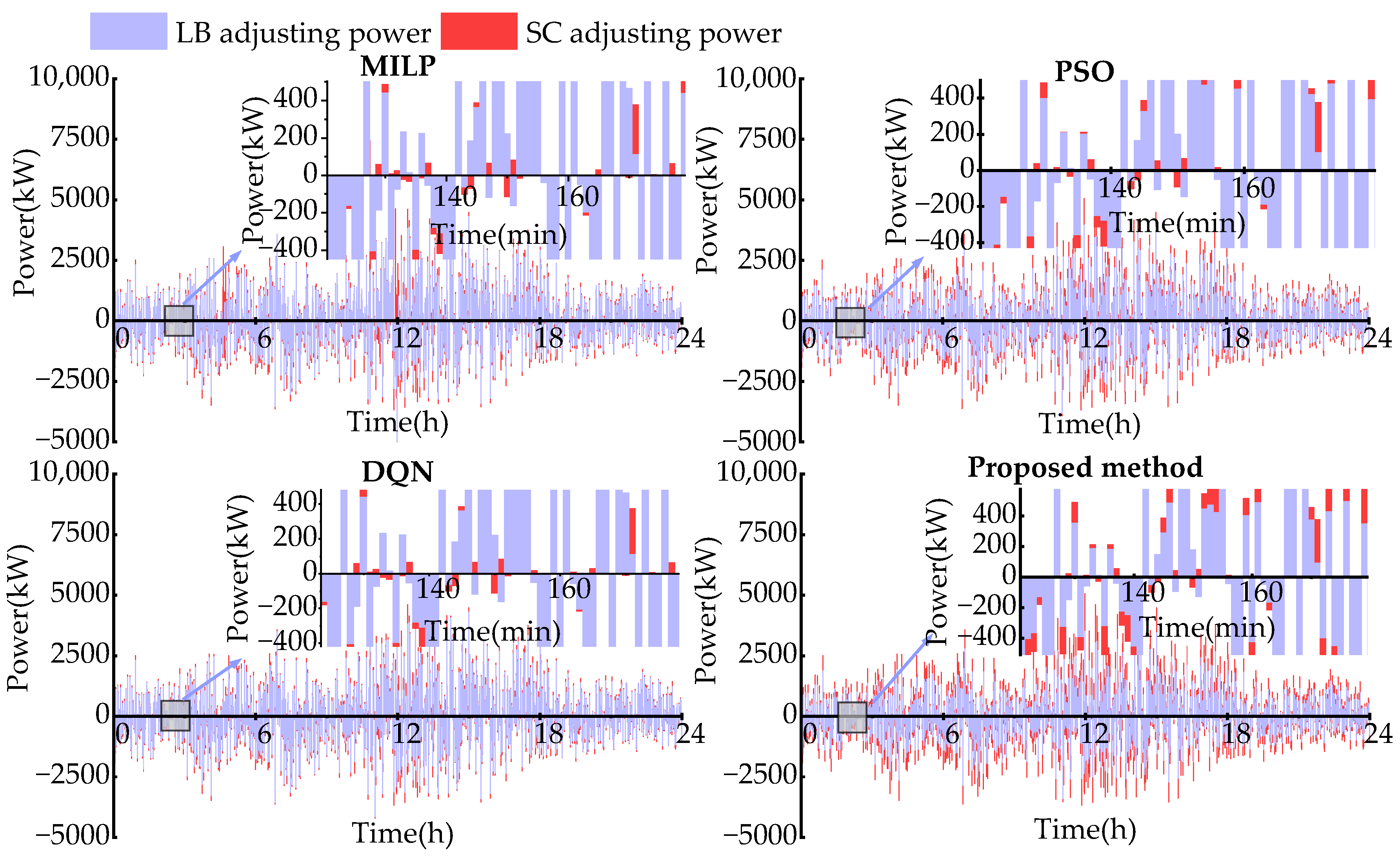
5.3. Economic Analysis
5.4. Carbon Analysis
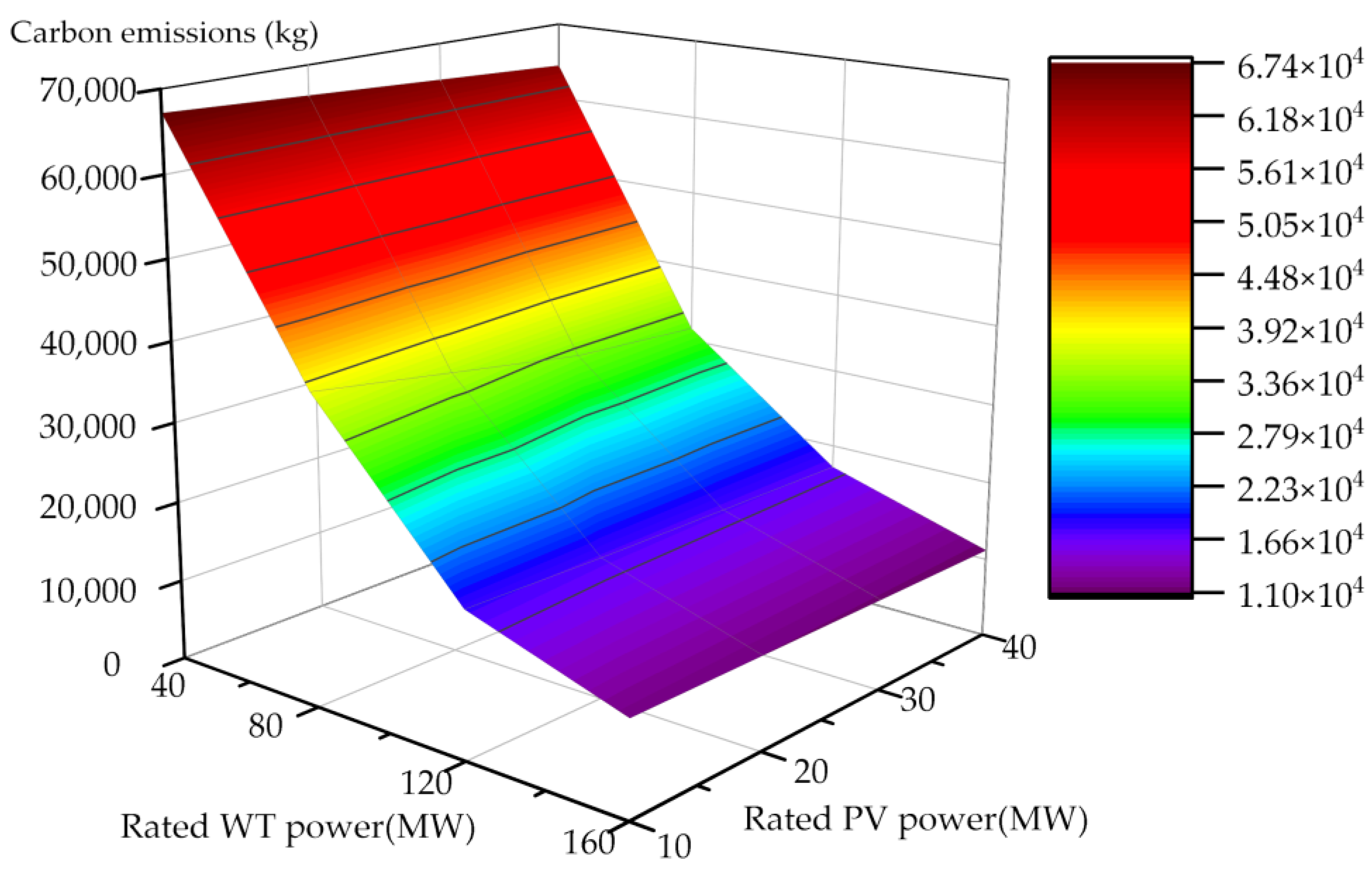
5.5. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices: | |
| Indices of time periods | |
| Index of devices, | |
| Index of energy storage devices, | |
| Indices of the input signal/output coefficients | |
| Parameters: | |
| Various scheduling time scales | |
| Gas constant and temperature of hydrogen before compression | |
| Real-time/cut-in/rated/cut-out wind speeds at time t | |
| Proportion/lower heating values of hydrogen/natural gas | |
| Efficiencies of the gas turbine/ALK/PEM | |
| Charging and discharging efficiencies of lithium batteries/supercapacitors/hydrogen loss rate | |
| Electricity required per unit of hydrogen produced by the ALK/PEM | |
| Pressures before and after compression | |
| Rated power/ramp rates of the gas turbine/ALK/PEM | |
| Scale factor of the gas turbine/ALK/PEM | |
| Maximum load demand of the island microgrid | |
| Rated power of the photovoltaic/wind power generation | |
| Maximum proportion of hydrogen | |
| Maximum charging/discharging flows of the hydrogen storage tank | |
| Maximum charging/discharging of a supercapacitor/lithium battery | |
| Maximum capacities of the supercapacitor/lithium battery/hydrogen storage tank | |
| Fixed cost/start–stop cost coefficients of the ALK/PEM | |
| Cost factors of the wind turbine/photovoltaic generation/gas turbine/supercapacitor/hydrogen storage tank | |
| Low-pass/high-pass filter coefficients | |
| Discount factor | |
| Learning rate | |
| Parameters of the local/target critic networks | |
| Parameters of the local/target actor networks | |
| Parameters of the local/target networks | |
| Variables: | |
| Power of photovoltaic generation/wind turbine/gas turbine/supercapacitor/lithium battery at time t | |
| Power of the gas turbine/supercapacitor/lithium battery at time t | |
| Curtailed costs of wind turbine/photovoltaic generation at time t | |
| Response frequencies of the PEM/lithium battery/supercapacitor at time t | |
| Actual solar radiation intensity/temperature of photovoltaic generation at time t | |
| Total/hydrogen/natural gas fuel volume flow rates at time t | |
| Energy stored in the supercapacitor/lithium battery/hydrogen storage tank at time t/t − 1 | |
| Binary states of the ALK/PEM/supercapacitor/lithium battery/hydrogen storage tank at time t | |
| Input/output flow of HS at time t | |
| Hydrogen volume produced by the ALK/PEM at time t | |
| Cutoff frequencies of high-pass/low-pass filters under time scale m/s | |
| Costs of three stages | |
| Curtailment cost of renewable energy | |
| Operating costs of hydrogen production/storage/gas turbines/lithium batteries/supercapacitors | |
| Power adjustment costs of the PEM/lithium battery | |
| Proceeds/adjustment in proceeds from hydrogen sales | |
References
- Matthew, G., Jr.; Nuttall, W.J.; Mestel, B.; Dooley, L.S. Low Carbon Futures: Confronting Electricity Challenges on Island Systems. Technol. Forecast. Soc. Change 2019, 147, 36–50. [Google Scholar] [CrossRef]
- Ioannidis, A.; Chalvatzis, K.J.; Li, X.; Notton, G.; Stephanides, P. The Case for Islands’ Energy Vulnerability: Electricity Supply Diversity in 44 Global Islands. Renew. Energy 2019, 143, 440–452. [Google Scholar] [CrossRef]
- Psarros, G.N.; Dratsas, P.A.; Papathanassiou, S.A. A Comprehensive Review of Electricity Storage Applications in Island Systems. J. Energy Storage 2024, 83, 110658. [Google Scholar] [CrossRef]
- Psarros, G.N.; Karamanou, E.G.; Papathanassiou, S.A. Feasibility Analysis of Centralized Storage Facilities in Isolated Grids. IEEE Trans. Sustain. Energy 2018, 9, 1822–1832. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, B.; Sun, Q.; Wennersten, R. Application of Energy Storage in Integrated Energy Systems—A Solution to Fluctuation and Uncertainty of Renewable Energy. J. Energy Storage 2022, 52, 104812. [Google Scholar] [CrossRef]
- Barrera-Santana, J.; Sioshansi, R. An Optimization Framework for Capacity Planning of Island Electricity Systems. Renew. Sustain. Energy Rev. 2023, 171, 112955. [Google Scholar] [CrossRef]
- Sihvonen, V.; Riikonen, J.; Price, A.; Nordlund, E.; Honkapuro, S.; Ylönen, M.; Kivioja, V.; Hedman, Å.; Tullberg, R. Combined Utilization of Electricity and Thermal Storages in a Highly Renewable Energy System within an Island Society. J. Energy Storage 2024, 89, 111864. [Google Scholar] [CrossRef]
- Keiner, D.; Salcedo-Puerto, O.; Immonen, E.; Van Sark, W.G.J.H.M.; Nizam, Y.; Shadiya, F.; Duval, J.; Delahaye, T.; Gulagi, A.; Breyer, C. Powering an Island Energy System by Offshore Floating Technologies towards 100% Renewables: A Case for the Maldives. Appl. Energy 2022, 308, 118360. [Google Scholar] [CrossRef]
- Frković, L.; Ćosić, B.; Pukšec, T.; Vladimir, N. The Synergy between the Photovoltaic Power Systems and Battery-Powered Electric Ferries in the Isolated Energy System of an Island. Energy 2022, 259, 124862. [Google Scholar] [CrossRef]
- Groppi, D.; Astiaso Garcia, D.; Lo Basso, G.; Cumo, F.; De Santoli, L. Analysing Economic and Environmental Sustainability Related to the Use of Battery and Hydrogen Energy Storages for Increasing the Energy Independence of Small Islands. Energy Convers. Manag. 2018, 177, 64–76. [Google Scholar] [CrossRef]
- Sadeghi, S.; Ahmadian, A.; Diabat, A.; Elkamel, A. Modeling Energy Management of an Energy Hub with Hybrid Energy Storage Systems for a Smart Island Considering Water–Electricity Nexus. Int. J. Hydrog. Energy 2024, 71, 600–616. [Google Scholar] [CrossRef]
- Ma, Z.; Han, J.; Chen, H.; Houari, A.; Saim, A. Research on Power Allocation Strategy and Capacity Configuration of Hybrid Energy Storage System Based on Double-Layer Variational Modal Decomposition and Energy Entropy. J. Energy Storage 2024, 95, 112492. [Google Scholar] [CrossRef]
- Ramu, S.K.; Vairavasundaram, I.; Palaniyappan, B.; Bragadeshwaran, A.; Aljafari, B. Enhanced Energy Management of DC Microgrid: Artificial Neural Networks-Driven Hybrid Energy Storage System with Integration of Bidirectional DC-DC Converter. J. Energy Storage 2024, 88, 111562. [Google Scholar] [CrossRef]
- Robayo, M.; Mueller, M.; Sharkh, S.; Abusara, M. Assessment of Supercapacitor Performance in a Hybrid Energy Storage System with an EMS Based on the Discrete Wavelet Transform. J. Energy Storage 2023, 57, 106200. [Google Scholar] [CrossRef]
- Kim, J.; Sin, S.; Kim, J. Early Remaining-Useful-Life Prediction Applying Discrete Wavelet Transform Combined with Improved Semi-Empirical Model for High-Fidelity in Battery Energy Storage System. Energy 2024, 297, 131285. [Google Scholar] [CrossRef]
- Peng, B.; Li, Y.; Liu, H.; Kang, P.; Bai, Y.; Zhao, J.; Nian, H. Design of Energy Management Strategy for Integrated Energy System Including Multi-Component Electric–Thermal–Hydrogen Energy Storage. Energies 2024, 17, 6184. [Google Scholar] [CrossRef]
- Ji, J.; Zhou, M.; Guo, R.; Tang, J.; Su, J.; Huang, H.; Sun, N.; Nazir, M.S.; Wang, Y. A Electric Power Optimal Scheduling Study of Hybrid Energy Storage System Integrated Load Prediction Technology Considering Ageing Mechanism. Renew. Energy 2023, 215, 118985. [Google Scholar] [CrossRef]
- Ding, Y.; Xu, Q.; Hao, L.; Xia, Y.; Li, D.; Chen, J. Day-Ahead Robust Dispatch of Interconnected Multi-Microgrids Considering Two-Stage Model of Hybrid Energy Storage. J. Energy Storage 2024, 92, 112120. [Google Scholar] [CrossRef]
- Emrani, A.; Achour, Y.; Sanjari, M.J.; Berrada, A. Adaptive Energy Management Strategy for Optimal Integration of Wind/PV System with Hybrid Gravity/Battery Energy Storage Using Forecast Models. J. Energy Storage 2024, 96, 112613. [Google Scholar] [CrossRef]
- Fatih Guven, A.; Abdelaziz, A.Y.; Mahmoud Samy, M.; Barakat, S. Optimizing Energy Dynamics: A Comprehensive Analysis of Hybrid Energy Storage Systems Integrating Battery Banks and Supercapacitors. Energy Convers. Manag. 2024, 312, 118560. [Google Scholar] [CrossRef]
- Li, C.; Yang, H.; Shahidehpour, M.; Xu, Z.; Zhou, B.; Cao, Y.; Zeng, L. Optimal Planning of Islanded Integrated Energy System With Solar-Biogas Energy Supply. IEEE Trans. Sustain. Energy 2020, 11, 2437–2448. [Google Scholar] [CrossRef]
- Kong, X.; Lu, W.; Wu, J.; Wang, C.; Zhao, X.; Hu, W.; Shen, Y. Real-Time Pricing Method for VPP Demand Response Based on PER-DDPG Algorithm. Energy 2023, 271, 127036. [Google Scholar] [CrossRef]
- Da Silva André, J.; Stai, E.; Stanojev, O.; Hug, G. Battery Control with Lookahead Constraints in Distribution Grids Using Reinforcement Learning. Electr. Power Syst. Res. 2022, 211, 108551. [Google Scholar] [CrossRef]
- Pompodakis, E.E.; Kryonidis, G.C.; Karapidakis, E.S. Volt/Var Control and Energy Management in Non-Interconnected Insular Networks with Multiple Hybrid Power Plants. Appl. Energy 2023, 331, 120427. [Google Scholar] [CrossRef]
- Maïzi, N.; Mazauric, V.; Assoumou, E.; Bouckaert, S.; Krakowski, V.; Li, X.; Wang, P. Maximizing Intermittency in 100% Renewable and Reliable Power Systems: A Holistic Approach Applied to Reunion Island in 2030. Appl. Energy 2018, 227, 332–341. [Google Scholar] [CrossRef]
- Kafetzis, A.; Ziogou, C.; Panopoulos, K.D.; Papadopoulou, S.; Seferlis, P.; Voutetakis, S. Energy Management Strategies Based on Hybrid Automata for Islanded Microgrids with Renewable Sources, Batteries and Hydrogen. Renew. Sustain. Energy Rev. 2020, 134, 110118. [Google Scholar] [CrossRef]
- Cabrera, P.; Carta, J.A.; Matos, C.; Rosales-Asensio, E.; Lund, H. Reduced Desalination Carbon Footprint on Islands with Weak Electricity Grids. The Case of Gran Canaria. Appl. Energy 2024, 358, 122564. [Google Scholar] [CrossRef]
- Wang, B.; Wang, X.; Wei, F.; Shao, C.; Zhou, J.; Lin, J. Multi-Stage Stochastic Planning for a Long-Term Low-Carbon Transition of Island Power System Considering Carbon Price Uncertainty and Offshore Wind Power. Energy 2023, 282, 128349. [Google Scholar] [CrossRef]
- Shahid, Z.; Santarelli, M.; Marocco, P.; Ferrero, D.; Zahid, U. Techno-Economic Feasibility Analysis of Renewable-Fed Power-to-Power (P2P) Systems for Small French Islands. Energy Convers. Manag. 2022, 255, 115368. [Google Scholar] [CrossRef]
- Abomazid, A.M.; El-Taweel, N.A.; Farag, H.E.Z. Optimal Energy Management of Hydrogen Energy Facility Using Integrated Battery Energy Storage and Solar Photovoltaic Systems. IEEE Trans. Sustain. Energy 2022, 13, 1457–1468. [Google Scholar] [CrossRef]
- Basher, B.G.; Ghanem, A.; Abulanwar, S.; Hassan, M.K.; Rizk, M.E.M. Fault Classification and Localization in Microgrids: Leveraging Discrete Wavelet Transform and Multi-Machine Learning Techniques Considering Single Point Measurements. Electr. Power Syst. Res. 2024, 231, 110362. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, Z.; Liu, X. Short-Term Offshore Wind Power Forecasting-A Hybrid Model Based on Discrete Wavelet Transform (DWT), Seasonal Autoregressive Integrated Moving Average (SARIMA), and Deep-Learning-Based Long Short-Term Memory (LSTM). Renew. Energy 2022, 185, 611–628. [Google Scholar] [CrossRef]
- Ahmed, M.H.; AboHussien, A.; El-Shafei, A.; Darwish, A.M.; Abdel-Gawad, A.H. Active Control of Flexible Rotors Using Deep Reinforcement Learning with Application of Multi-Actor-Critic Deep Deterministic Policy Gradient. Eng. Appl. Artif. Intell. 2023, 124, 106593. [Google Scholar] [CrossRef]
- Benhmidouch, Z.; Moufid, S.; Ait-Omar, A.; Abbou, A.; Laabassi, H.; Kang, M.; Chatri, C.; Hammou Ou Ali, I.; Bouzekri, H.; Baek, J. A Novel Reinforcement Learning Policy Optimization Based Adaptive VSG Control Technique for Improved Frequency Stabilization in AC Microgrids. Electr. Power Syst. Res. 2024, 230, 110269. [Google Scholar] [CrossRef]
- Ye, J.; Wang, X.; Hua, Q.; Sun, L. Deep Reinforcement Learning Based Energy Management of a Hybrid Electricity-Heat-Hydrogen Energy System with Demand Response. Energy 2024, 305, 131874. [Google Scholar] [CrossRef]
- Arenas-López, J.P.; Badaoui, M. The Ornstein-Uhlenbeck Process for Estimating Wind Power under a Memoryless Transformation. Energy 2020, 213, 118842. [Google Scholar] [CrossRef]
- Yu, X.; Gao, Z.; Xiong, Z.; Zhao, C.; Yang, Y. DDPG-AdaptConfig: A Deep Reinforcement Learning Framework for Adaptive Device Selection and Training Configuration in Heterogeneity Federated Learning. Future Gener. Comput. Syst. 2025, 163, 107528. [Google Scholar] [CrossRef]
- World’s First Dynamic Green Ammonia Plant Officially Opened. Available online: https://nelhydrogen.com/articles/in-depth/worlds-first-dynamic-green-ammonia-plant-officially-opened/ (accessed on 11 January 2025).
- PEM Electrolyser-PSM Series. Available online: https://nelhydrogen.com/product/psm-series-electrolyser/ (accessed on 11 January 2025).
- SGT-700 Industrial Gas Turbine. Available online: https://www.siemens-energy.com/global/en/home/products-services/product/sgt-700.html (accessed on 11 January 2025).
- Wu, X.; Huang, B.; Wang, Q.; Wang, Y. Thermally Chargeable Supercapacitor Using a Conjugated Conducting Polymer: Insight into the Mechanism of Charge-Discharge Cycle. Chem. Eng. J. 2019, 373, 493–500. [Google Scholar] [CrossRef]
- Zhao, T.; Qiu, J.; Wen, S.; Zhu, M. Efficient Onboard Energy Storage System Sizing for All-Electric Ship Microgrids Via Optimized Navigation Routing Under Onshore Uncertainties. IEEE Trans. Ind. Appl. 2022, 58, 1664–1674. [Google Scholar] [CrossRef]




| Literature | Hybrid Energy | Hydrogen System | Muti-Stage | Full Renewable Utilization |
|---|---|---|---|---|
| [12,13,16,17,19,20,21,27] | √ | - | - | - |
| [18,26,29] | √ | √ | - | - |
| [25] | √ | - | - | √ |
| [28] | √ | √ | √ | - |
| This paper | √ | √ | √ | √ |
| Component | Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|---|
| Load | 35 | MW | / | / | / | |
| PV | 40 | MW | 0.034 | $/kWh | ||
| WT | 160 | MW | 0.014 | $/kWh | ||
| Gas turbine | 35 | MW | 0.018 | $/kWh | ||
| 0.55 [40] | / | |||||
| SC | 0.5 | MWh | 0.014 | $/kWh | ||
| 10 | MW | |||||
| 0.95 [41] | / | |||||
| LB | 10 | MWh | 0.0348 | $/kWh | ||
| 10 | MW | |||||
| 0.95 [42] | / | |||||
| PEM | 1.25 × 16 | MW | 0.09 | $/kWh | ||
| 0.77 [39] | / | |||||
| ALK | 2.5 × 8 | MW | 0.052 | $/kWh | ||
| 0.75 [39] | / |
| Stage | Method | MILP | PSO | DQN | Proposed |
|---|---|---|---|---|---|
| Day-ahead scheduling stage | Power for ALK and PEM (kWh) | 228,693.82 | 255,942.06 | 235,794.75 | 235,874.82 |
| Gas turbine output (kWh) | 79,081.83 | 78,869.63 | 78,313.07 | 78,095.0 | |
| Operation cost (USD) | 16,273.05 | 16,262.37 | 16,572.62 | 16,229.33 | |
| Hydrogen revenue (USD) | 16,603.17 | 16,599.81 | 16,971.92 | 17,378.33 | |
| Intra-day two stage | Power fluctuation smoothing by PEM (kWh) | 17,147.14 | 16,959.60 | 17,765.41 | 17,947.11 |
| Power fluctuation smoothing by LB (kWh) | 5946.03 | 5268.70 | 5143.43 | 3627.75 | |
| Power fluctuation smoothing by SC (kWh) | 3719.10 | 4583.97 | 3903.43 | 5237.41 | |
| Operation cost (USD) | 16,763.50 | 16,923.23 | 17,007.31 | 16,890.19 | |
| Hydrogen revenue (USD) | 18,990.54 | 19,816.65 | 20,027.96 | 20,588.17 |
| Method | Carbon Emissions (kg) | Computation Time (s) |
|---|---|---|
| MILP | 11,403.60 | 30.16 |
| PSO | 11,373.67 | 13.14 |
| DQN | 11,292.76 | 7.07 |
| Proposed | 11,258.33 | 6.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Wen, S.; Zhao, Q.; Zhang, B.; Huang, Y.; Zhu, M. Deep Reinforcement Learning Based Optimal Operation of Low-Carbon Island Microgrid with High Renewables and Hybrid Hydrogen–Energy Storage System. J. Mar. Sci. Eng. 2025, 13, 225. https://doi.org/10.3390/jmse13020225
Zhu W, Wen S, Zhao Q, Zhang B, Huang Y, Zhu M. Deep Reinforcement Learning Based Optimal Operation of Low-Carbon Island Microgrid with High Renewables and Hybrid Hydrogen–Energy Storage System. Journal of Marine Science and Engineering. 2025; 13(2):225. https://doi.org/10.3390/jmse13020225
Chicago/Turabian StyleZhu, Wangwang, Shuli Wen, Qiang Zhao, Bing Zhang, Yuqing Huang, and Miao Zhu. 2025. "Deep Reinforcement Learning Based Optimal Operation of Low-Carbon Island Microgrid with High Renewables and Hybrid Hydrogen–Energy Storage System" Journal of Marine Science and Engineering 13, no. 2: 225. https://doi.org/10.3390/jmse13020225
APA StyleZhu, W., Wen, S., Zhao, Q., Zhang, B., Huang, Y., & Zhu, M. (2025). Deep Reinforcement Learning Based Optimal Operation of Low-Carbon Island Microgrid with High Renewables and Hybrid Hydrogen–Energy Storage System. Journal of Marine Science and Engineering, 13(2), 225. https://doi.org/10.3390/jmse13020225











