Finite-Time Fault-Tolerant Tracking Control for an Air Cushion Vehicle Subject to Actuator Faults

Abstract

This paper proposes a finite-time fault-tolerant tracking controller for an air cushion vehicle (ACV) based on the backstepping method. A four-degree-of-freedom ACV with model uncertainties is considered, where the unknown nonlinearities can be approximated by radial basis function neural networks. By combining the command filter with the backstepping method, the calculation of virtual control derivatives is avoided. The proposed adaptive finite-time fault-tolerant controller can estimate the unknown boundaries of actuator fault parameters so that an unbounded number of actuator faults can be processed. The proposed theory ensures that the stability of the system and its tracking performance can be guaranteed in a finite time. This paper focuses on simulation-based work. Simulation results confirm the capability of the proposed trajectory tracking control scheme.

1. Introduction

With the development of the global economy, land resources have been unable to meet the needs of economic development, and countries have begun to compete for marine resources. As an important means of transportation in the fields of marine transportation, marine resource exploration, and offshore defense, the demand for high-performance ships with higher speeds and larger load capacities has become stronger and stronger [1,2,3,4]. As a kind of amphibious high-performance ship that can be detached from the sailing surface by the air cushion apron system, the air cushion vehicle (ACV) as shown in Figure 1. can fulfill the tasks in a variety of complex sea environments, so it has been emphasized by various countries [5]. In control systems, actuators may experience total loss of effectiveness (TLOE) or partial loss of effectiveness (PLOE) faults during operation. If these faults are not handled properly, they may cause instability and ultimately lead to the failure of tasks. Dealing with such faults is very important for ensuring the safety of the system. Currently, there are many typical examples of highly successful fault-tolerant control approaches. The authors in [6] proposed an active fault-tolerant control method for linear constant time-delay systems subject to actuator faults. The authors in [7] proposed an integral backstepping sliding mode fault-tolerant control strategy based on an adaptive observer for the problem of actuator faults in quadrotor aircraft. Due to its unique skirt cushion lifting system, the hovercraft can complete special operation tasks in various complex terrain environments such as at sea, on land, in shoals, in swamps, and on ice and snow. To counteract the impacts of the changing marine environment and increasing complexity, the actuator outputs change in response to control commands, making actuator faults unavoidable. If the ACV operates under these conditions, it will directly cause the ship’s position to drift, which, in turn, will affect normal operations and pose a threat to the safety of the people on the ACV [8]. Fault-tolerant control can enable the system to continue to work normally when a fault occurs or operate safely at the cost of some performance loss [9]. Therefore, it is necessary to design an effective fault-tolerant control scheme for the ACV system.

In the extant literature on ACVs, mathematical models with three degrees of freedom (DOFs) have been the predominant choice of model [10,11,12,13]. Nevertheless, the turning radius of the ACV is strongly influenced by the roll angle and serves as a crucial safety indicator. During the course of actual navigation, it is imperative that the roll angle is maintained in a specified scope, as exceeding this range could result in the submergence of the ship’s deck, which in turn could lead to capsizing. Some studies have developed four-DOF models, incorporating sway, surge, yaw, and roll [14,15]. The backstepping method has been extensively explored in control theory for addressing control challenges in complex nonlinear systems. When using the backstepping method to design the controller for the ACV, it is required that the ship model does not contain uncertainties. However, due to the strong coupling and model uncertainties of the ACV, this is impractical. To address the influence of uncertainties, the authors in [16] used a finite-time output feedback control method to deal with system uncertainties. The authors in [17] introduced a class of robust adaptive functions to offset the influence of model uncertainties. The authors in [18,19,20] proposed a method of combining the backstepping method with intelligent control to estimate uncertainties. The authors in [21,22,23] proposed a nonlinear disturbance observer method to estimate uncertainties to facilitate the controller design for ships. For the “differential explosion” problem of the backstepping occurring in the design of the controller, the authors in [24] proposed a second-order filter to resolve it instead of directly analyzing the differential. The author in [25] proposed a smooth inversion controller without fractional power terms.

Motivated by these observations, this article investigates the finite-time fault-tolerant trajectory tracking control issue for an ACV subject to actuator faults. This paper makes the following contributions to the field: (1) Designing a controller for a four-DOF ACV model, where radial basis function neural networks (RBFNNs) are employed to provide an estimation of model uncertainties. Combining the backstepping method with the command filter avoids the complex calculation of the virtual control derivative. (2) Introducing an intermediate variable into the backstepping method, where an adaptive finite-time control system is designed to account for actuator failures, and the constructed controller is free from the need for prior information of inconclusive system parameters and actuator failures. (3) Rather than estimating the parameters directly, their boundaries are estimated. Therefore, the controller designed in this paper can deal with a boundless number of actuator failures. (4) The final results demonstrate that the proposed control method is capable of precisely tracking the specified trajectory and ensuring that all the closed-loop signals in the control system converge to a small vicinity around zero within a finite time frame. The final results validate the performance of the suggested trajectory tracking control method.

2. Preliminaries and Problem Formulation

2.1. Preliminaries

Definition 1. 

The equilibrium $\varsigma =0$ of a nonlinear system $\dot{\varsigma }=f(\varsigma ,I)$, where I is the control input, is practically finite-time stable, if for any initial condition $\varsigma \left(0\right)\in {\varsigma }_0$, there exists a constant ε > 0 and a settling time $T(\epsilon ,{\varsigma }_0)<\infty$ such that

$$\parallel \varsigma \parallel <\epsilon ,\forall t>T.$$

(1)

Lemma 1 

([26]). If there exist some design constants $\beta >0$, $\alpha >0$, $0<b<\infty$, and $0<a<1$ such that

$$\dot{V}\left(\varsigma \right)\le -\alpha V\left(\varsigma \right)-\beta V^a\left(\varsigma \right)+b,$$

(2)

the path of the system $\dot{\varsigma }=f(\varsigma ,I)$ is practically stable within a limited time frame, where V is the Lyapunov function, ς is the system state, and I is the control input.

Lemma 2 

([27]). For any unknown continuously nonlinear function $f\left(X\right):R^M\to R$, the RBFNN is utilized to estimate it within a closed and bounded set $\Omega \in R^M$ as below:

$$f\left(X\right)=W^{⁎T}H\left(X\right)+\delta \left(X\right)$$

(3)

where $X\in R^M$ is the input vector, $H\left(X\right)={[h_1\left(X\right),\dots ,h_m\left(X\right)]}^T$ is the radial basis function, and $h_j=exp(-{\displaystyle \frac{{\parallel X-c_j\parallel }^2}{{2b_j}^2}})$. $c={\left[c_{ij}\right]}_{n\ast m}$ is the center, and $b_j$ is the width of the neural cell of the hidden layer. $\delta \left(X\right)$ denotes the approximate error satisfying $\delta \left(X\right)\le \overline{\delta }\left(X\right)$, and $\overline{\delta }\left(X\right)$ is any small positive constant. The RBFNN optimal weight vector is $W^{⁎T}={[W_1^{⁎},W_2^{⁎},W_3^{⁎}\dots ,W_n^{⁎}]}^T$. The weight vector of $W^{⁎}$ is calculated by

$$W^{⁎}=arg\underset{\widehat{W}}{min}\{\underset{X\in \Omega }{sup}|f\left(X\right)-{\widehat{W}}^{T}H\left(X\right)|\}$$

(4)

where $\widehat{W}$ is the estimate of $W^{⁎}$, which is calculated by an adaptive update law.

Lemma 3 

([28]). For ${\chi }_j\in R(j=1,\dots ,n)$, $0<c\le 1$, the subsequent inequality is valid:

$$(\sum _{j=1}^n|{\chi }_j{|)}^c\le \sum _{j=1}^n|{\chi }_j{|}^c\le n^{1-c}\sum _{j=1}^n|{\chi }_j|.$$

(5)

Lemma 4 

([29]). If there exist the positive constants $m_1,m_2$, and $m_3$, the following inequality is satisfied:

$$|x_1{|}^{m_1}|x_2{|}^{m_2}\le {\displaystyle \frac{m_2{m_3}^{-\frac{m_1}{m_2}}}{m_1+m_2}}|x_2{|}^{m_1+m_2}+{\displaystyle \frac{m_1{m}_3}{m_1+m_2}}{|x_1|}^{m_1+m_2}$$

(6)

where $x_1$ and $x_2$ are real variables.

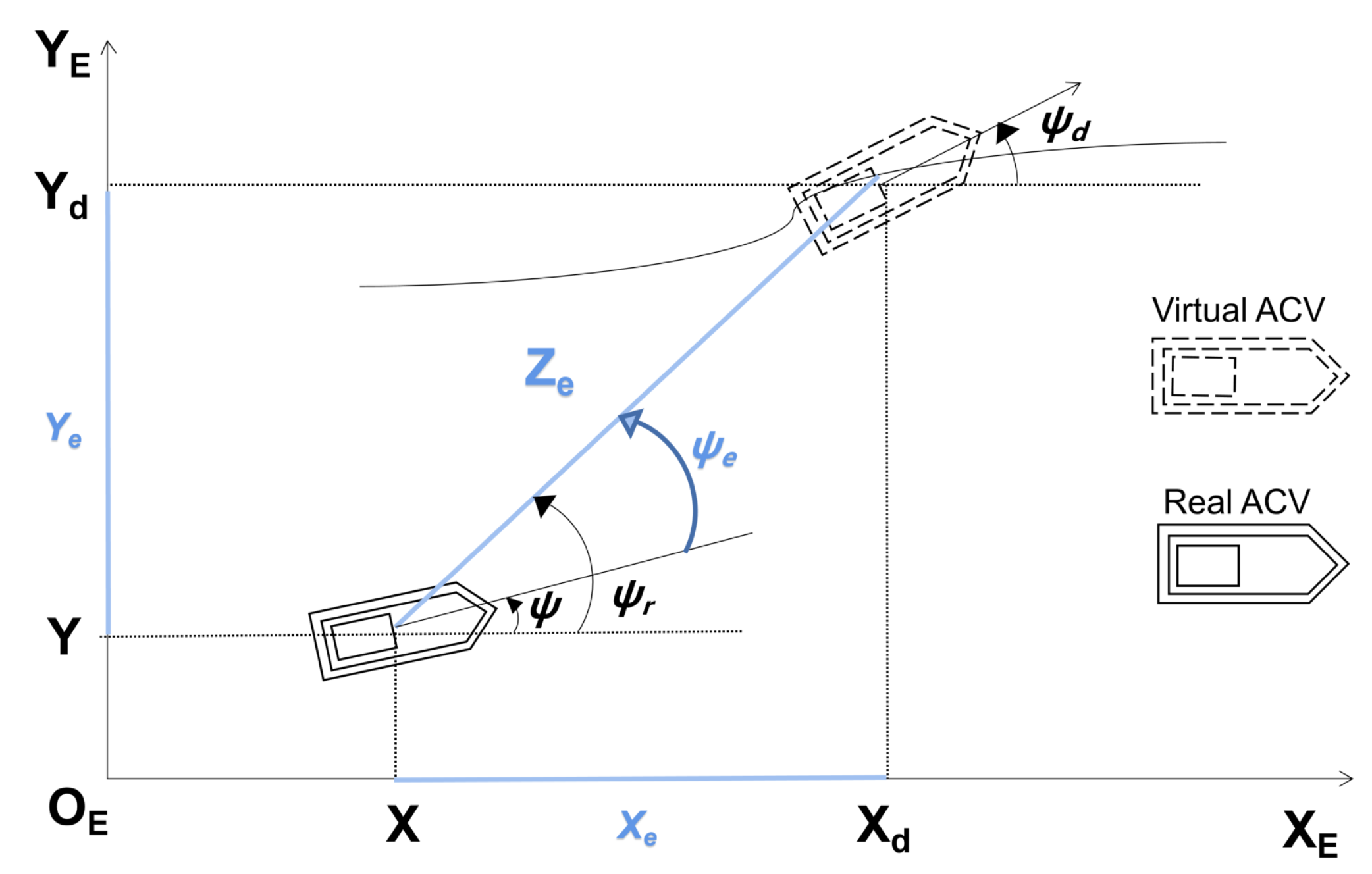
2.2. Problem Formulation

A four-DOF model of the ACV in the presense of unknown system uncertainties is described as follows [30]:

$$\begin{array}{cc}\hfill \dot{x}& =u\cos \psi -v\sin \psi \cos \phi \hfill \\ \hfill \dot{y}& =u\sin \psi +v\cos \psi \sin \phi \hfill \\ \hfill \dot{\psi }& =r\cos \phi \hfill \\ \hfill \dot{\phi }& =P\hfill \\ \hfill \dot{u}& =vr+f_u+{\tau }_{ua}\hfill \\ \hfill \dot{v}& =-ur+f_v\hfill \\ \hfill \dot{r}& =f_r+{\tau }_{ra}\hfill \\ \hfill \dot{P}& =f_P\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill f_u& =-(d_{11}u+d_{12}v)/m\hfill \\ \hfill f_v& =-(d_{21}u+d_{22}v+d_{24}r)/m\hfill \\ \hfill f_P& =-(d_{31}u+d_{32}v+d_{34}r)/J_x\hfill \\ \hfill f_r& =-(d_{41}u+d_{42}v+d_{44}r)/J_z\hfill \end{array}$$

(8)

where x, y, $\psi$, and $\phi$ refer to the positions and stances of the ACV in the earth-fixed frame. The speeds and angular velocities are denoted by $u,v,r$, and P. The mass and moment of inertia are represented by $m, J_x$, and $J_z$, respectively. ${\tau }_{ua}={\tau }_u/m$ and ${\tau }_{ra}={\tau }_r/J_z$ represent the control inputs. $d_{mn}(m=1,2,3,4, n=1,2,3,4)$ denotes the skew-symmetric Coriolis and the resistance matrix [30,31]. The model uncertainties are represented by $f_u$, $f_v$, $f_P$, and $f_r$.

In [32], the actuator faults comprise total loss of control effectiveness and partial loss of effectiveness fault described by

$$\begin{array}{cc}\hfill {\tau }_{ia,j}\left(t\right)& ={\rho }_{i,jh}{\tau }_{i,j}\left(t\right)+{\psi }_{i,j,h},t\in [t_{i,jh,k},t_{i,jh,e})\hfill \\ \hfill {\rho }_{i,jh}{\psi }_{i,j,h}& =0,h=1,2,3\dots ,i=u,r\hfill \end{array}$$

(9)

where ${\tau }_{i,j}\left(t\right)$ is the commanded control signal, serving as the actuator inputs; ${\rho }_{i,jh}\in [0,1]$ denotes the multiplicative fault, for example, the partial loss of effectiveness; and ${\psi }_{i,j,h}$ characterizes the additive faults, for example, bias. In the case of ${\rho }_{i,jh}=1$ and ${\psi }_{i,j,h}=0$, the ACV is free from actuator faults.

Assumption 1. 

There is an undetermined parameter denoted by ${\overline{\psi }}_{i,j,h}$, which satisfies $|{\psi }_{i,j,h}|\le {\overline{\psi }}_{i,j,h}$.

Assumption 2. 

The parameters $g_{u,j}=1/m$, $g_{r,j}=1/J_z$, i.e., $sign\left(g_{i,j}\right)$, for $j=1,\dots ,m$, $i=u,r$, are given.

Assumption 3. 

At most $m-1$ actuators can experience TLOE simultaneously.

The main objective of this work is to design control signals ${\tau }_{u,a}$ and ${\tau }_{r,a}$ for system (7), such that the system output signal $[x,y,\psi ]$ tracks the specified reference signal $[x_d,y_d,{\psi }_r]$ in a finite time, where $[x_d,y_d,{\psi }_r]$ and its first derivative are known and bounded. At the same time, all signals in the resulting system are required to be practically finite-time bounded regardless of the infinite number of actuator faults.

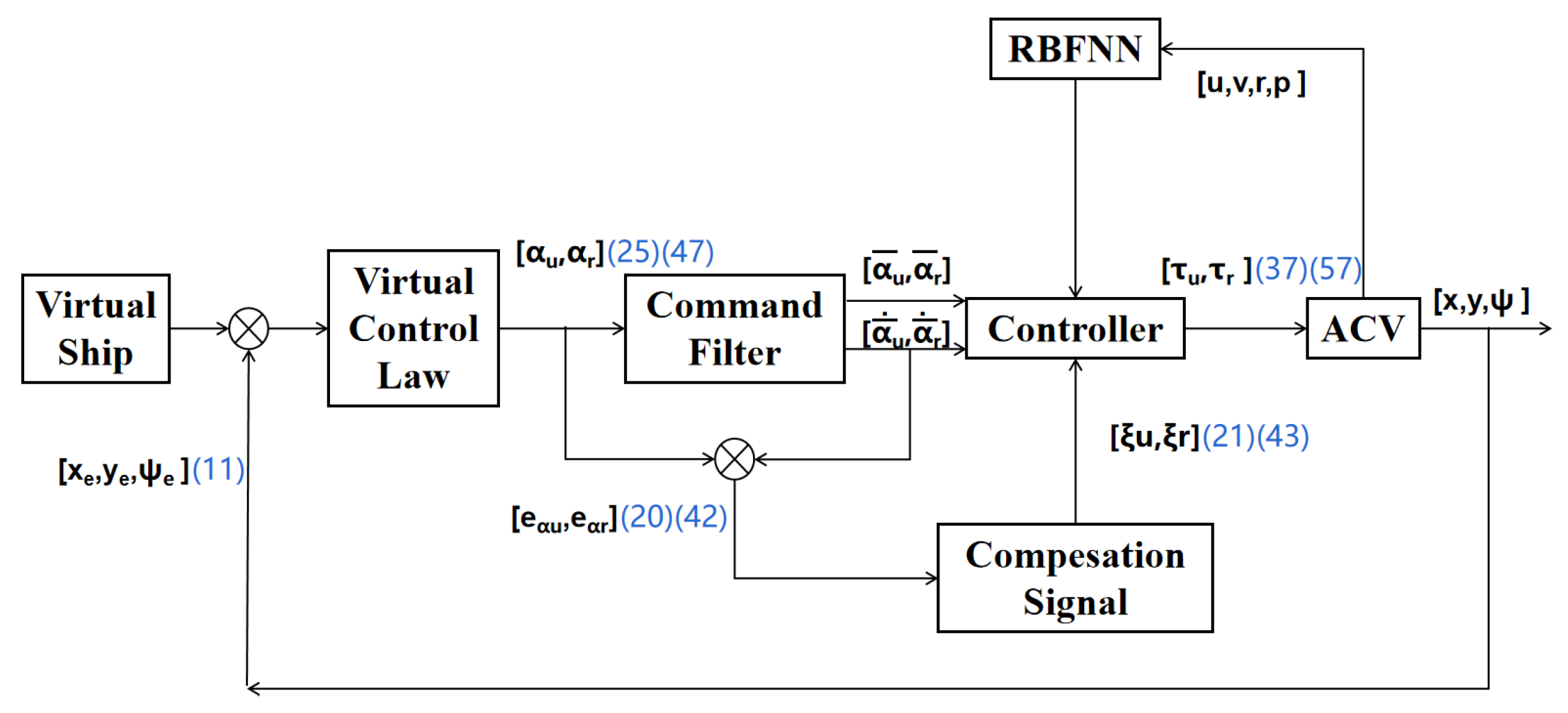
3. Finite-Time Controller Design

A schematic diagram of the control system of the ACV is shown in Figure 2.

3.1. Position Controller Design

Our control objective is to track the desired trajectory in a finite time. We define the desired trajectory based on a virtual ship model, which is described by the following equations:

$$\begin{array}{cc}\hfill {\dot{x}}_d& =u_d\cos {\psi }_d\hfill \\ \hfill {\dot{y}}_d& =u_d\sin {\psi }_d\hfill \\ \hfill \dot{{\psi }_r}& =r_d\hfill \end{array}$$

(10)

where ${[x_d,y_d,{\psi }_r]}^T$ are the ideal state variables describing the input signal. We define the tracking errors $x_e,y_e$, and ${\psi }_e$ as follows:

$$\begin{array}{cc}\hfill x_e& =x_d-x\hfill \\ \hfill y_e& =y_d-y\hfill \\ \hfill {\psi }_e& ={\psi }_r-\psi \hfill \end{array}$$

(11)

The target direction is illustrated in Figure 3 as

$$\begin{array}{c}\hfill {\psi }_r=\left\{\begin{array}{cc}{\displaystyle \frac{1}{2}}\left(\left[sign\left(x_e\right)\right]sign\left(y_e\right)\pi \right)+\arctan (y_e/z_e),\hfill & z_e\ne 0\hfill \\ {\psi }_d,\hfill & z_e=0\hfill \end{array}\right.\end{array}$$

(12)

The symbolic function $sign\left(t\right)$ is defined as

$$\begin{array}{c}\hfill sign\left(t\right)=\left\{\begin{array}{cc}-1,\hfill & t<0\hfill \\ 0,\hfill & t=0\hfill \\ 1,\hfill & t>0.\hfill \end{array}\right.\end{array}$$

(13)

The position error is defined as follows:

$$\begin{array}{cc}\hfill z_e& =\sqrt{{x_e}^2+{y_e}^2}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\psi }_e& ={\psi }_r-\psi .\hfill \end{array}$$

(15)

From Equations (14) and (15), the time derivatives, $z_e$ and ${\psi }_e$, are given as follows:

$$\begin{array}{cc}\hfill \dot{z_e}& =-u\cos {\psi }_e+{\rho }_1\left(t\right)\hfill \\ \hfill & =-(u_e+{\overline{\alpha }}_u+{\alpha }_u-{\alpha }_u)\cos {\psi }_e+{\rho }_1\left(t\right)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \dot{{\psi }_e}& =\dot{{\psi }_r}-\dot{\psi }\hfill \\ \hfill & =\dot{{\psi }_r}-r\cos \psi \hfill \\ \hfill & =-r\cos \psi +{\rho }_2\left(t\right)\hfill \end{array}$$

(17)

where the functions ${\rho }_1\left(t\right)=v\sin {\psi }_e\cos \phi +\dot{x_d}\cos {\psi }_r+\dot{y_d}\sin {\psi }_r$ and ${\rho }_2\left(t\right)=\dot{{\psi }_r}$ are bounded.

3.2. Surge Controller Design

Surge velocity tracking error is defined as

$$u_e=u-{\overline{\alpha }}_u$$

(18)

In this context, let ${\alpha }_u$ pass through the first-order command filter with time constant ${\epsilon }_u$ to obtain ${\overline{\alpha }}_u$ as follows:

$${\epsilon }_u{\dot{\overline{\alpha }}}_u+{\overline{\alpha }}_u={\alpha }_u,{\overline{\alpha }}_u\left(0\right)={\alpha }_u\left(0\right)$$

(19)

where ${\epsilon }_u$ is the positive constant to be designed.

In order to address the impact of the identified error $({\overline{\alpha }}_u-{\alpha }_u)$, we propose the introduction of a compensating signal, designated as ${\xi }_1$.

$$\dot{{\xi }_1}=-k_1{\xi }_1-({\overline{\alpha }}_u-{\alpha }_u)\cos {\psi }_e-l_{1}sign\left({\xi }_1\right)-{\xi }_2\cos {\psi }_e,{\xi }_1\left(0\right)=0$$

(20)

where $k_1>0$ and $l_1>0$ are given constants.

Define the compensation tracking error

$${\chi }_1=z_e-{\xi }_1.$$

(21)

Define a Lyapunov function as

$$V_1={\displaystyle \frac{1}{2}}{\chi }_1^2.$$

(22)

Based on (16) and (20), the differentiation of $V_1$ is

$$\begin{array}{cc}\hfill \dot{V_1}& ={\chi }_1(\dot{z_e}-\dot{{\xi }_1})\hfill \\ \hfill & ={\chi }_1[-(u_e+{\overline{\alpha }}_u+{\alpha }_u-{\alpha }_u)\cos {\psi }_e+{\rho }_1\left(t\right)+k_1{\xi }_1+({\overline{\alpha }}_u+{\alpha }_u)\cos {\psi }_e+l_{1}sign\left({\xi }_1\right)+{\xi }_2\cos {\psi }_e]\hfill \\ \hfill & ={\chi }_1[-{\chi }_2\cos {\psi }_e-{\alpha }_u\cos {\psi }_e+k_1{\xi }_1+l_{1}sign\left({\xi }_1\right)+{\rho }_1\left(t\right)].\hfill \end{array}$$

(23)

From (23), the virtual control law ${\alpha }_u$ can be defined as

$${\alpha }_u=(-k_1{z}_e+C_1{\chi }_1^{2p-1}+{\rho }_1\left(t\right))/\cos {\psi }_e$$

(24)

where $C_1>0$ is a design constant.

Using Young’s inequality, we have

$${\chi }_1{l}_{1}sign\left({\xi }_1\right)\le {\displaystyle \frac{1}{2}}{\chi }_1^2+{\displaystyle \frac{1}{2}}{l}_1^2.$$

(25)

Substituting (24) and (25) into (23), we can obtain

$$\dot{V_1}\le -{\chi }_1{\chi }_2\cos {\psi }_e-(k_1-{\displaystyle \frac{1}{2}}){\chi }_1^2-C_1{\chi }_1^{2p}+{\displaystyle \frac{1}{2}}{l}_1^2.$$

(26)

According to Assumptions 2 and 3, it can be reasonably deduced that ${\sum }_{j=1}^m|g_{i,j}|{\rho }_{i,jh}\ge min\{|g_{i,1}|{\underline{\rho }}_{i,1h},\dots ,|g_{i,m}|{\underline{\rho }}_{i,mh}\}$$>0$, $i=u,r$. Therefore, we have $in{f}_{t\ge 0}{\sum }_{j=1}^m|{\tau }_{ia,j}|{\rho }_{i,jh}\ge min\{|g_{i,1}|{\underline{\rho }}_{i,1h},\dots ,|g_{i,m}|{\underline{\rho }}_{i,mh}\}$$>0$. Then, we can obtain

$$\begin{array}{cc}\hfill s& =\underset{t\ge 0}{inf}\sum _{j=1}^m|g_{i,j}|{\rho }_{i,jh},\vartheta ={\displaystyle \frac{1}{s}}\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \zeta & =\underset{t\ge 0}{sup}(\sum _{j=1}^m{g}_{i,j}{\psi }_{i,j,h}),\hfill \end{array}$$

(28)

We will be able to estimate the unknown parameters $\vartheta$ and $\zeta$ through the design of adaptive laws.

Define compensation tracking error

$${\chi }_2=u_e-{\xi }_2.$$

(29)

Define the compensating signal ${\xi }_2$

$$\dot{{\xi }_2}=-k_2{\xi }_2-l_{2}sign\left({\xi }_2\right)+{\xi }_1\cos {\psi }_e,{\xi }_2\left(0\right)=0$$

(30)

where $k_2>0$ and $l_2>0$ are known constants.

Construct the following Lyapunov function:

$$V_2=V_1+{\displaystyle \frac{1}{2}}{\chi }_2^2+{\displaystyle \frac{1}{2r_1}}{\tilde{W}}_u^2+{\displaystyle \frac{s}{2r_2}}{\tilde{\vartheta }}_u^2+{\displaystyle \frac{1}{2r_3}}{\tilde{\zeta }}_u^2$$

(31)

where $r_1$, $r_2$, $r_3>0$. ${\tilde{W}}_u=W_u-{\widehat{W}}_u$, ${\tilde{\vartheta }}_u={\vartheta }_u-{\widehat{\vartheta }}_u$, and ${\tilde{\zeta }}_u={\zeta }_u-{\widehat{\zeta }}_u$, and the estimation errors are denoted by ${\tilde{W}}_u$, ${\tilde{\vartheta }}_u$, and ${\tilde{\zeta }}_u$. ${\widehat{W}}_u$, ${\widehat{\vartheta }}_u$, and ${\widehat{\zeta }}_u$ represent the estimates of the parameters $W_u$, ${\vartheta }_u$, and ${\zeta }_u$, respectively.

The differentiation of (31) with respect to time is as follows:

$$\begin{array}{cc}\hfill \dot{V_2}& =\dot{V_1}+{\chi }_2(\dot{u_e}-{\dot{\xi }}_2)+{\displaystyle \frac{1}{r_1}}{\tilde{W}}_u{\dot{\tilde{W}}}_u+{\displaystyle \frac{s}{r_2}}{\tilde{\vartheta }}_u{\dot{\tilde{\vartheta }}}_u+{\displaystyle \frac{1}{r_3}}{\tilde{\zeta }}_u{\dot{\tilde{\zeta }}}_u\hfill \\ \hfill & =\dot{V_1}+{\chi }_2(vr+f_u+(\sum _{j=1}^m{g}_{u,j}({\rho }_{u,jh}{\tau }_{u,j}+{\psi }_{u,j,h}))+k-k-{\dot{\overline{\alpha }}}_u-{\dot{\xi }}_2)\hfill \\ & +{\displaystyle \frac{1}{r_1}}{\tilde{W}}_u{\dot{\tilde{W}}}_u+{\displaystyle \frac{s}{r_2}}{\tilde{\vartheta }}_u{\dot{\tilde{\vartheta }}}_u+{\displaystyle \frac{1}{r_3}}{\tilde{\zeta }}_u{\dot{\tilde{\zeta }}}_u\hfill \end{array}$$

(32)

where k as an intermediate control law will be designed.

Similar to (25), using Young’s inequality, we can obtain

$${\chi }_2{l}_{2}sign\left({\xi }_2\right)\le {\displaystyle \frac{1}{2}}{\chi }_2^2+{\displaystyle \frac{1}{2}}{l}_2^2.$$

(33)

From (33), we design the intermediate control law k as

$$k=-z_e\cos {\psi }_e+k_2{u}_e+C_2{\chi }_2^{2p-1}+{\widehat{\zeta }}_u\tanh ({\displaystyle \frac{{\chi }_2}{ϵ}})-{\dot{\overline{\alpha }}}_u+vr+{\widehat{W}}_u{H}_u\left(x\right).$$

(34)

where $C_2>0$ and $ϵ>0$ are given constants.

Substituting (30), (33) and (34) into (32) we can obtain ${\dot{V}}_2$, which has the following structure:

$$\begin{array}{cc}\hfill \dot{V_2}\le & -(k_1-{\displaystyle \frac{1}{2}}){\chi }_1^2-(k_2-{\displaystyle \frac{1}{2}}){\chi }_2^2-C_1{\chi }_1^2-C_2{\chi }_2^2+k{\chi }_2+{\chi }_2\sum _{j=1}^m{g}_{u,j}{\rho }_{u,jh}{\tau }_{u,j}\hfill \\ \hfill & -{\displaystyle \frac{{\tilde{W}}_u}{r_1}}({\dot{\widehat{W}}}_u-H_u\left(x\right)r_1{\chi }_2)+{\displaystyle \frac{s}{r_2}}{\tilde{\vartheta }}_u{\dot{\tilde{\vartheta }}}_u+{\displaystyle \frac{1}{2}}{l}_1^2+{\displaystyle \frac{1}{2}}{l}_2^2+{\zeta }_u(|{\chi }_2|-{\chi }_2{\widehat{\zeta }}_u\tanh ({\displaystyle \frac{{\chi }_2}{ϵ}}))\hfill \\ \hfill & -{\displaystyle \frac{1}{r_3}}{\tilde{\zeta }}_u({\dot{\widehat{\zeta }}}_u-r_3\tanh ({\displaystyle \frac{{\chi }_2}{ϵ}}){\chi }_2).\hfill \end{array}$$

(35)

With (35), the actual control input ${\tau }_{u,j}$ can be designed as

$${\tau }_{u,j}=sign(g_{u,j})(-{\displaystyle \frac{{\chi }_2{\widehat{\vartheta }}_u^2{k}^2}{\sqrt{{\chi }_2^2{\widehat{\vartheta }}_u^2{k}^2+{\sigma }^2}}})$$

(36)

where $\sigma >0$ is a designed parameter.

The adaptive laws are specified as

$$\begin{array}{cc}\hfill {\dot{\widehat{W}}}_u& =r_1{\chi }_2{H}_u\left(x\right)-{\sigma }_1{\widehat{W}}_u\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill {\dot{\widehat{\zeta }}}_u& =r_3{\chi }_2\tanh ({\displaystyle \frac{{\chi }_2}{ϵ}})-{\sigma }_3{\widehat{\zeta }}_u\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {\dot{\widehat{\vartheta }}}_u& =r_2{\chi }_{2}k-{\sigma }_2{\widehat{\vartheta }}_u\hfill \end{array}$$

(39)

where ${\sigma }_1>0$, ${\sigma }_2>0$, and ${\sigma }_3>0$ are known quantities.

3.3. Yaw Controller Design

Yaw velocity tracking error is defined as

$$r_e=r-{\overline{\alpha }}_r$$

(40)

In this context, let ${\alpha }_r$ pass through the first-order command filter with time constant ${\epsilon }_r$ to obtain ${\overline{\alpha }}_r$ as follows:

$${\epsilon }_r{\dot{\overline{\alpha }}}_r+{\overline{\alpha }}_r={\alpha }_r,{\overline{\alpha }}_r\left(0\right)={\alpha }_r\left(0\right)$$

(41)

where the positive constant ${\epsilon }_r$ is to be designed.

To handle the impact of the error $(\overline{{\alpha }_r}-{\alpha }_r)$, we define the compensating signal ${\xi }_3$.

$$\dot{{\xi }_3}=-k_3{\xi }_3-({\overline{\alpha }}_r-{\alpha }_r)\cos \phi -l_{3}sign\left({\xi }_3\right)-{\xi }_4\cos \phi ,{\xi }_3\left(0\right)=0$$

(42)

where $k_3>0$ and $l_3>0$ are known constants.

Design the Lyapunov function

$${\chi }_3={\psi }_e-{\xi }_3.$$

(43)

The Lyapunov function is designed as

$$V_3={\displaystyle \frac{1}{2}}{\chi }_3^2.$$

(44)

Based on (17) and (42), the time differentiation of $V_3$ is

$$\begin{array}{cc}\hfill {\dot{V}}_3& ={\chi }_3({\dot{\psi }}_e-{\dot{\xi }}_3)\hfill \\ \hfill & ={\chi }_3[-(r_e+{\overline{\alpha }}_r+{\alpha }_r-{\alpha }_r)\cos \phi +{\rho }_2\left(t\right)+k_3{\xi }_3+({\overline{\alpha }}_r+{\alpha }_r)\cos \phi +l_{3}sign\left({\xi }_3\right){\xi }_4\cos \phi \hfill \\ \hfill & ={\chi }_3[-{\chi }_4\cos \phi -{\alpha }_r\cos \phi +k_3{\xi }_3+l_{3}sign\left({\xi }_3\right)+{\rho }_2\left(t\right)].\hfill \end{array}$$

(45)

Thus, the virtual control law for ${\alpha }_r$ is formulated as

$${\alpha }_r=(-k_3{\psi }_e+C_3{\chi }_3^{2p-1}+{\rho }_2\left(t\right))/\cos \phi ,$$

(46)

where $C_3>0$ is a known constant.

Similarly to (33), we can obtain

$${\chi }_3{l}_{3}sign\left({\xi }_3\right)\le {\displaystyle \frac{1}{2}}{\chi }_3^2+{\displaystyle \frac{1}{2}}{l}_3^2.$$

(47)

Substituting (46) and (47) into (45), we can obtain ${\dot{V}}_3$ with the following structure:

$$\dot{V_3}\le -{\chi }_3{\chi }_4\cos \phi -(k_3-{\displaystyle \frac{1}{2}}){\chi }_3^2-C_3{\chi }_3^{2p}+{\displaystyle \frac{1}{2}}{l}_3^2.$$

(48)

Define the compensating signal ${\xi }_4$

$$\dot{{\xi }_4}=-k_4{\xi }_4-l_{4}sign\left({\xi }_4\right)+{\xi }_4\cos \phi ,{\xi }_4\left(0\right)=0$$

(49)

where $k_4>0$ and $l_4>0$ are given constants.

Define compensation tracking error

$${\chi }_4=r_e-{\xi }_4$$

(50)

Construct the following Lyapunov function:

$$V_4=V_3+{\displaystyle \frac{1}{2}}{\chi }_4^2+{\displaystyle \frac{1}{2r_4}}{\tilde{W}}_r^2+{\displaystyle \frac{s}{2r_5}}{\tilde{\vartheta }}_r^2+{\displaystyle \frac{1}{2r_6}}{\tilde{\zeta }}_r^2$$

(51)

where $r_4$, $r_5$, $r_6>0$ are design constants. ${\tilde{W}}_r=W_r-{\widehat{W}}_r$, ${\tilde{\vartheta }}_r={\vartheta }_r-{\widehat{\vartheta }}_r$, and ${\tilde{\zeta }}_r={\zeta }_r-{\widehat{\zeta }}_r$, and the estimation errors are denoted by ${\tilde{W}}_r$, ${\tilde{\vartheta }}_r$, and ${\tilde{\zeta }}_r$. ${\widehat{W}}_r$, ${\widehat{\vartheta }}_r$, and ${\widehat{\zeta }}_r$ represent the estimates of the parameters $W_r$, ${\vartheta }_r$, and ${\zeta }_r$, respectively.

The time of differentiation of (51) gives

$$\begin{array}{cc}\hfill \dot{V_4}=& \dot{V_3}+{\chi }_4(f_r+(\sum _{j=1}^m{g}_{r,j}({\rho }_{r,jh}{\tau }_{r,j}+{\psi }_{r,j,h})\hfill \\ & + \iota -\iota -{\dot{\overline{\alpha }}}_r-{\dot{\xi }}_4)+{\displaystyle \frac{1}{r_4}}{\tilde{W}}_r{\dot{\tilde{W}}}_r+{\displaystyle \frac{s}{r_5}}{\tilde{\vartheta }}_r{\dot{\tilde{\vartheta }}}_r+{\displaystyle \frac{1}{r_6}}{\tilde{\zeta }}_r{\dot{\tilde{\zeta }}}_r\hfill \end{array}$$

(52)

Similar to (47), (31), and (47), we can obtain

$${\chi }_4{l}_{4}sign\left({\xi }_4\right)\le {\displaystyle \frac{1}{2}}{\chi }_4^2+{\displaystyle \frac{1}{2}}{l}_4^2.$$

(53)

We designed the intermediate control law $\iota$ as

$$\iota =-{\psi }_e\cos \phi +k_4{r}_e+C_4{\chi }_4^{2p-1}+\widehat{{\zeta }_r}\tanh ({\displaystyle \frac{{\chi }_4}{ϵ}})-{\dot{\overline{\alpha }}}_r+{\widehat{W}}_r{H}_r\left(x\right)$$

(54)

where $C_4>0$ is a known constant.

Substituting (53) and (54) into (52), we can obtain ${\dot{V}}_4$ as follows:

$$\begin{array}{cc}\hfill \dot{V_4}\le & -(k_3-{\displaystyle \frac{1}{2}}){\chi }_3^2-(k_4-{\displaystyle \frac{1}{2}}){\chi }_4^2-C_3{\chi }_3^2-C_4{\chi }_4^2+\iota {\chi }_4+{\chi }_4\sum _{j=1}^m{g}_{r,j}{\rho }_{r,jh}{\tau }_{r,j}\hfill \\ \hfill & - {\displaystyle \frac{{\tilde{W}}_r}{r_3}}({\dot{\widehat{W}}}_r-H_r\left(x\right)r_3{\chi }_4)+{\displaystyle \frac{s}{r_5}}{\tilde{\vartheta }}_r{\dot{\tilde{\vartheta }}}_r+{\displaystyle \frac{1}{2}}{l}_3^2+{\displaystyle \frac{1}{2}}{l}_4^2+{\zeta }_r(|{\chi }_4|-{\chi }_4\widehat{{\zeta }_r}\tanh ({\displaystyle \frac{{\chi }_4}{ϵ}}))\hfill \\ \hfill & - {\displaystyle \frac{1}{r_6}}{\tilde{\zeta }}_r({\dot{\widehat{\zeta }}}_r-r_6\tanh ({\displaystyle \frac{{\chi }_4}{ϵ}}){\chi }_4).\hfill \end{array}$$

(55)

From (55), the actual control input ${\tau }_{ra}$ was defined as

$${\tau }_{r,j}=sign\left(g_{r,j}\right)(-{\displaystyle \frac{{\chi }_4{\widehat{\vartheta }}_r^2{\iota }^2}{\sqrt{{\chi }_4^2{\widehat{\vartheta }}_r^2{\iota }^2+{\sigma }^2}}}).$$

(56)

The adaptive laws are specified as

$$\begin{array}{cc}\hfill {\dot{\widehat{W}}}_r& =r_4{\chi }_4{H}_r\left(x\right)-{\sigma }_4{\widehat{W}}_r\hfill \end{array}$$

(57)

$$\begin{array}{cc}\hfill {\dot{\widehat{\zeta }}}_r& =r_6{\chi }_4\tanh ({\displaystyle \frac{{\chi }_4}{ϵ}})-{\sigma }_6{\widehat{\zeta }}_r\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill {\dot{\widehat{\vartheta }}}_r& =r_5{\chi }_{4}p-{\sigma }_5{\widehat{\vartheta }}_r\hfill \end{array}$$

(59)

where ${\sigma }_4>0$, ${\sigma }_5>0$, and ${\sigma }_6>0$ are given constants.

4. Stability Analysis

Theorem 1: Consider the ACV system (7), the surge speed control low (24) and yaw rate control law (46), the surge force (36) and moment (56), and the adaptive updating laws (37)–(39); and (57)–(59). In accordance with the Assumptions 1–3, all the closed-loop signals in the system are limited in magnitude, and the tracking errors converge to a residual set within a finite time. It is possible to reduce the size of the residual set by modifying the design parameters.

Proof. 

From (36) and (56), we can obtain

$$\begin{array}{cc}\hfill {\chi }_2\sum _{j=1}^m{g}_{u,j}{\rho }_{u,jh}{\tau }_{u,j}& \le -\sum _{j=1}^m{g}_{u,j}{\rho }_{u,jh}{\displaystyle \frac{{\chi }_2^2{\widehat{\vartheta }}_u^2{k}^2}{\sqrt{{\chi }_2^2{\widehat{\vartheta }}_u^2{k}^2+{\sigma }^2}}}\hfill \\ \hfill & \le -{\displaystyle \frac{s{\chi }_2^2{\widehat{\vartheta }}_u^2{k}^2}{\sqrt{{\chi }_2^2{\widehat{\vartheta }}_u^2{k}^2+{\sigma }^2}}}\hfill \\ \hfill & \le s\sigma -s{\chi }_2{\widehat{\vartheta }}_{u}k\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill {\chi }_4\sum _{j=1}^m{g}_{r,j}{\rho }_{r,jh}{\tau }_{r,j}& \le -\sum _{j=1}^m{g}_{r,j}{\rho }_{r,jh}{\displaystyle \frac{{\chi }_4^2{\widehat{\vartheta }}_r^2{\iota }^2}{\sqrt{{\chi }_4^2{\widehat{\vartheta }}_r^2{\iota }^2+{\sigma }^2}}}\hfill \\ \hfill & \le -{\displaystyle \frac{s{\chi }_4^2{\widehat{\vartheta }}_r^2{\iota }^2}{\sqrt{{\chi }_4^2{\widehat{\vartheta }}_r^2{\iota }^2+{\sigma }^2}}}\hfill \\ \hfill & \le s\sigma -s{\chi }_4{\widehat{\vartheta }}_r\iota .\hfill \end{array}$$

(61)

□

According to the inequality $0\le |\varrho |-\varrho \tanh \left({\displaystyle \frac{\varrho }{ϵ}}\right)\le \kappa ϵ$, where $\varrho \in R$ and ${\kappa }_1={\kappa }_2=0.2785$, one has

$${\zeta }_u(|{\chi }_2|-{\chi }_2{\widehat{\zeta }}_u\tanh ({\displaystyle \frac{{\chi }_2}{ϵ}}))\le {\kappa }_1{\zeta }_uϵ$$

(62)

$${\zeta }_r(|{\chi }_4|-{\chi }_4{\widehat{\zeta }}_r\tanh ({\displaystyle \frac{{\chi }_4}{ϵ}}))\le {\kappa }_2{\zeta }_rϵ.$$

(63)

Substituting (37)–(39) and (57)–(59) into (35) and (55), and after a simple calculation, the following is obtained:

$$\begin{array}{cc}\hfill \dot{V}\le & -{\chi }_1^2(k_1-{\displaystyle \frac{1}{2}})-{\chi }_2^2(k_2-{\displaystyle \frac{1}{2}})-{\chi }_3^2(k_3-{\displaystyle \frac{1}{3}})-{\chi }_4^2(k_4-{\displaystyle \frac{1}{2}})\hfill \\ \hfill & -C_1{\chi }_1^{2p}-C_2{\chi }_2^{2p}-C_3{\chi }_3^{2p}-C_4{\chi }_4^{2p}\hfill \\ \hfill & -{\displaystyle \frac{{\sigma }_1}{2r_1}}{\tilde{W}}_u^2-{\displaystyle \frac{s{\sigma }_2}{2r_2}}{\tilde{\vartheta }}_u^2-{\displaystyle \frac{{\sigma }_3}{2r_3}}{\tilde{\zeta }}_u^2-{\displaystyle \frac{{\sigma }_4}{2r_4}}{\tilde{W}}_r^2-{\displaystyle \frac{s{\sigma }_5}{2r_5}}{\tilde{\vartheta }}_r^2-{\displaystyle \frac{{\sigma }_6}{2r_6}}{\tilde{\zeta }}_r^2\hfill \\ \hfill & +{\displaystyle \frac{{\sigma }_1}{2r_1}}{W_u}^2+{\displaystyle \frac{s{\sigma }_2}{2r_2}}{{\vartheta }_u}^2+{\displaystyle \frac{{\sigma }_3}{2r_3}}{{\zeta }_u}^2+{\displaystyle \frac{{\sigma }_4}{2r_4}}{W_r}^2+{\displaystyle \frac{s{\sigma }_5}{2r_5}}{{\vartheta }_r}^2+{\displaystyle \frac{{\sigma }_6}{2r_6}}{{\zeta }_r}^2\hfill \\ \hfill & +s_u{\sigma }_u+{\kappa }_1{\zeta }_uϵ+s_r{\sigma }_r+{\kappa }_2{\zeta }_rϵ+{\displaystyle \frac{1}{2}}{l}_1^2+{\displaystyle \frac{1}{2}}{l}_2^2+{\displaystyle \frac{1}{2}}{l}_3^2+{\displaystyle \frac{1}{2}}{l}_4^2.\hfill \end{array}$$

(64)

Recalling the definitions of ${\tilde{W}}_i$, ${\tilde{\vartheta }}_i$, and ${\tilde{\vartheta }}_i$$(i=u,r)$, we can obtain the following inequalities:

$${\displaystyle \frac{\sigma }{r}}{\tilde{W}}_i{\widehat{W}}_i\le -{\displaystyle \frac{\sigma }{2r}}{\tilde{W}}_i^2+{\displaystyle \frac{\sigma }{2r}}{W}_i^2$$

(65)

$${\displaystyle \frac{\sigma }{r}}{\tilde{\zeta }}_i{\widehat{\zeta }}_i\le -{\displaystyle \frac{\sigma }{2r}}{\tilde{\zeta }}_i^2+{\displaystyle \frac{\sigma }{2r}}{\zeta }_i^2$$

(66)

$${\displaystyle \frac{\sigma }{r}}{\tilde{\vartheta }}_i{\widehat{\vartheta }}_i\le -{\displaystyle \frac{\sigma }{2r}}{\tilde{\vartheta }}_i^2+{\displaystyle \frac{\sigma }{2r}}{\vartheta }_i^2.$$

(67)

Substituting (65)–(67) into (64) yields

$$\begin{array}{cc}\hfill \dot{V}\le & -{\chi }_1^2(k_1-{\displaystyle \frac{1}{2}})-{\chi }_2^2(k_2-{\displaystyle \frac{1}{2}})-{\chi }_3^2(k_3-{\displaystyle \frac{1}{3}})-{\chi }_4^2(k_4-{\displaystyle \frac{1}{2}})\hfill \\ \hfill & -C_1{\chi }_1^{2p}-C_2{\chi }_2^{2p}-C_3{\chi }_3^{2p}-C_4{\chi }_4^{2p}\hfill \\ \hfill & +{\displaystyle \frac{{\sigma }_1}{r_1}}{\tilde{W}}_u{\widehat{W}}_u+{\displaystyle \frac{s{\sigma }_2}{r_2}}{\tilde{\vartheta }}_u{\widehat{\vartheta }}_u+{\displaystyle \frac{{\sigma }_3}{r_3}}{\tilde{\zeta }}_u{\widehat{\zeta }}_u+{\displaystyle \frac{{\sigma }_4}{r_4}}{\tilde{W}}_r{\widehat{W}}_r+{\displaystyle \frac{s{\sigma }_5}{r_5}}{\tilde{\vartheta }}_r{\widehat{\vartheta }}_r+{\displaystyle \frac{{\sigma }_6}{r_6}}{\tilde{\zeta }}_r{\widehat{\zeta }}_r\hfill \\ \hfill & +s_u{\sigma }_u+{\kappa }_1{\zeta }_uϵ+s_r{\sigma }_r+{\kappa }_2{\zeta }_rϵ+{\displaystyle \frac{1}{2}}{l}_1^2+{\displaystyle \frac{1}{2}}{l}_2^2+{\displaystyle \frac{1}{2}}{l}_3^2+{\displaystyle \frac{1}{2}}{l}_4^2\hfill \\ \hfill =& -{\chi }_1^2(k_1-{\displaystyle \frac{1}{2}})-{\chi }_2^2(k_2-{\displaystyle \frac{1}{2}})-{\chi }_3^2(k_3-{\displaystyle \frac{1}{2}})-{\chi }_4^2(k_4-{\displaystyle \frac{1}{2}})\hfill \\ \hfill & -C_1{\chi }_1^{2p}-C_2{\chi }_2^{2p}-C_3{\chi }_3^{2p}-C_4{\chi }_4^{2p}\hfill \\ \hfill & -{\sigma }_1{({\displaystyle \frac{{\widetilde{W_u}}^2}{4r_1}})}^p+{\sigma }_1{({\displaystyle \frac{{\widetilde{W_u}}^2}{4r_1}})}^p-s{\sigma }_2{({\displaystyle \frac{{\widetilde{{\vartheta }_u}}^2}{4r_2}})}^p+s{\sigma }_2{({\displaystyle \frac{{\widetilde{{\vartheta }_u}}^2}{4r_2}})}^p-{\sigma }_3{({\displaystyle \frac{{\widetilde{{\zeta }_u}}^2}{4r_3}})}^p+{\sigma }_3{({\displaystyle \frac{{\widetilde{{\zeta }_u}}^2}{4r_3}})}^p\hfill \\ \hfill & -{\sigma }_4{({\displaystyle \frac{{\widetilde{W_r}}^2}{4r_4}})}^p+{\sigma }_4{({\displaystyle \frac{{\widetilde{W_r}}^2}{4r_4}})}^p-s{\sigma }_5{({\displaystyle \frac{{\widetilde{{\vartheta }_r}}^2}{4r_5}})}^p+s{\sigma }_5{({\displaystyle \frac{{\widetilde{{\vartheta }_r}}^2}{4r_5}})}^p-{\sigma }_6{({\displaystyle \frac{{\widetilde{{\zeta }_r}}^2}{4r_6}})}^p+{\sigma }_6{({\displaystyle \frac{{\widetilde{{\zeta }_r}}^2}{4r_6}})}^p\hfill \\ \hfill & +{\displaystyle \frac{{\sigma }_1}{r_1}}{\tilde{W}}_u{\widehat{W}}_u+{\displaystyle \frac{s{\sigma }_2}{r_2}}{\tilde{\vartheta }}_u{\widehat{\vartheta }}_u+{\displaystyle \frac{{\sigma }_3}{r_3}}{\tilde{\zeta }}_u{\widehat{\zeta }}_u+{\displaystyle \frac{{\sigma }_4}{r_4}}{\tilde{W}}_r{\widehat{W}}_r+{\displaystyle \frac{s{\sigma }_5}{r_5}}{\tilde{\vartheta }}_r{\widehat{\vartheta }}_r+{\displaystyle \frac{{\sigma }_6}{r_6}}{\tilde{\zeta }}_r{\widehat{\zeta }}_r\hfill \\ \hfill & +s_u{\sigma }_u+{\kappa }_1{\zeta }_uϵ+s_r{\sigma }_r+{\kappa }_2{\zeta }_rϵ+{\displaystyle \frac{1}{2}}{l}_1^2+{\displaystyle \frac{1}{2}}{l}_2^2+{\displaystyle \frac{1}{2}}{l}_3^2+{\displaystyle \frac{1}{2}}{l}_4^2.\hfill \end{array}$$

(68)

Applying Lemma 4 to the terms ${\sigma }_o{({\displaystyle \frac{{\tilde{W}}_i^2}{4r}})}^p$, ${\sigma }_o{({\displaystyle \frac{{\tilde{\zeta }}_i^2}{4r}})}^p$, and ${\sigma }_o{({\displaystyle \frac{{\tilde{\vartheta }}_i^2}{4r}})}^p$$(o=1,\dots 6;i=u,r)$, where $r={[r_1,r_2,r_3,r_4,r_5,r_6]}^T$, we can obtain

$${\sigma }_o{({\displaystyle \frac{{\tilde{W}}_i^2}{4r}})}^p\le {\displaystyle \frac{{\sigma }_o}{4r}}{\tilde{W}}_i^2+{\sigma }_o(1-p)p^{{\displaystyle \frac{1-p}{p}}}$$

(69)

$${\sigma }_o{({\displaystyle \frac{{\tilde{\zeta }}_i^2}{4r}})}^p\le {\displaystyle \frac{{\sigma }_o}{4r}}{\tilde{\zeta }}_i^2+{\sigma }_o(1-p)p^{{\displaystyle \frac{1-p}{p}}}$$

(70)

$$s{\sigma }_o{({\displaystyle \frac{{\tilde{\vartheta }}_i^2}{4r}})}^p\le {\displaystyle \frac{s{\sigma }_o}{4r}}{\tilde{\vartheta }}_i^2+s{\sigma }_o(1-p)p^{{\displaystyle \frac{1-p}{p}}}.$$

(71)

Substituting (69)–(71) into (68), and after a simple calculation, the following is obtained:

$$\begin{array}{cc}\hfill \dot{V}\le & -{\chi }_1^2(k_1-{\displaystyle \frac{1}{2}})-{\chi }_2^2(k_2-{\displaystyle \frac{1}{2}})-{\chi }_3^2(k_3-{\displaystyle \frac{1}{3}})-{\chi }_4^2(k_4-{\displaystyle \frac{1}{2}})\hfill \\ \hfill & -C_1{\chi }_1^{2p}-C_2{\chi }_2^{2p}-C_3{\chi }_3^{2p}-C_4{\chi }_4^{2p}\hfill \\ \hfill & -{\sigma }_1{({\displaystyle \frac{{\widetilde{W_u}}^2}{4r_1}})}^p-s{\sigma }_2{({\displaystyle \frac{{\widetilde{{\vartheta }_u}}^2}{4r_2}})}^p-{\sigma }_3{({\displaystyle \frac{{\widetilde{{\zeta }_u}}^2}{4r_3}})}^p-{\sigma }_4{({\displaystyle \frac{{\widetilde{W_r}}^2}{4r_4}})}^p-s{\sigma }_5{({\displaystyle \frac{{\widetilde{{\vartheta }_r}}^2}{4r_5}})}^p-{\sigma }_6{({\displaystyle \frac{{\widetilde{{\zeta }_r}}^2}{4r_6}})}^p\hfill \\ \hfill & -{\displaystyle \frac{{\sigma }_1}{4r_1}}{\widetilde{W_u}}^2-{\displaystyle \frac{s{\sigma }_2}{4r_2}}{\widetilde{{\vartheta }_u}}^2-{\displaystyle \frac{{\sigma }_3}{4r_3}}{\widetilde{{\zeta }_u}}^2-{\displaystyle \frac{{\sigma }_4}{4r_4}}{\widetilde{W_r}}^2-{\displaystyle \frac{s{\sigma }_5}{4r_5}}{\widetilde{{\vartheta }_r}}^2-{\displaystyle \frac{{\sigma }_6}{4r_6}}{\widetilde{{\zeta }_r}}^2\hfill \\ \hfill & +({\sigma }_1+s{\sigma }_2+{\sigma }_3+{\sigma }_4+s{\sigma }_5+{\sigma }_6)(1-p){\displaystyle \frac{1-p}{p}}\hfill \\ \hfill & +{\displaystyle \frac{{\sigma }_1}{r_1}}{\tilde{W}}_u{\widehat{W}}_u+{\displaystyle \frac{s{\sigma }_2}{r_2}}{\tilde{\vartheta }}_u{\widehat{\vartheta }}_u+{\displaystyle \frac{{\sigma }_3}{r_3}}{\tilde{\zeta }}_u{\widehat{\zeta }}_u+{\displaystyle \frac{{\sigma }_4}{r_4}}{\tilde{W}}_r{\widehat{W}}_r+{\displaystyle \frac{s{\sigma }_5}{r_5}}{\tilde{\vartheta }}_r{\widehat{\vartheta }}_r+{\displaystyle \frac{{\sigma }_6}{r_6}}{\tilde{\zeta }}_r{\widehat{\zeta }}_r\hfill \\ \hfill & +s_u{\sigma }_u+{\kappa }_1{\zeta }_uϵ+s_r{\sigma }_r+{\kappa }_2{\zeta }_rϵ+{\displaystyle \frac{1}{2}}{l}_1^2+{\displaystyle \frac{1}{2}}{l}_2^2+{\displaystyle \frac{1}{2}}{l}_3^2+{\displaystyle \frac{1}{2}}{l}_4^2.\hfill \end{array}$$

(72)

Applying Lemma 3 gives

$$\begin{array}{cc}\hfill \dot{V}\le & -\alpha \sum _{m=1}^4{\chi }_m^2-\alpha \sum _{i=u,r}({\widetilde{W_i}}^2+{\widetilde{{\zeta }_i}}^2+{\widetilde{{\vartheta }_i}}^2)-\beta \sum _{m=1}^4{({\displaystyle \frac{{\chi }_m^2}{4}})}^2\hfill \\ \hfill & -\beta {({\displaystyle \frac{{\widetilde{W_u}}^2}{4r_1}})}^p-\beta {({\displaystyle \frac{{\widetilde{{\zeta }_u}}^2}{4r_1}})}^p-\beta {({\displaystyle \frac{{\widetilde{{\vartheta }_u}}^2}{4r_3}})}^p-\beta {({\displaystyle \frac{{\widetilde{W_r}}^2}{4r_4}})}^p-\beta {({\displaystyle \frac{{\widetilde{{\zeta }_r}}^2}{4r_5}})}^p-\beta {({\displaystyle \frac{{\widetilde{{\vartheta }_r}}^2}{4r_6}})}^p+Q\hfill \\ \hfill \le & -\alpha V-\beta V^2+Q.\hfill \end{array}$$

(73)

where $\alpha =min\left\{(k_1-{\displaystyle \frac{1}{2}}),(k_2-{\displaystyle \frac{1}{2}}),(k_3-{\displaystyle \frac{1}{2}}),(k_4-{\displaystyle \frac{1}{2}}),{\displaystyle \frac{{\sigma }_1}{4r_1}},{\displaystyle \frac{s{\sigma }_2}{4r_2}},{\displaystyle \frac{{\sigma }_3}{4r_3}},{\displaystyle \frac{{\sigma }_4}{4r_4}},{\displaystyle \frac{s{\sigma }_5}{4r_5}},{\displaystyle \frac{{\sigma }_6}{4r_6}}\right\}>0$, $\beta =min\left\{4^p{C}_i,{\sigma }_1,s{\sigma }_2,{\sigma }_3,{\sigma }_4,s{\sigma }_5,{\sigma }_6,i=1,2,3,4\right\}>0$, and $Q=({\sigma }_1+s{\sigma }_2+{\sigma }_3+{\sigma }_4+s{\sigma }_5+{\sigma }_6){(1-p)}^{{\displaystyle \frac{1-p}{p}}}{\displaystyle \frac{{\sigma }_1}{r_1}}{\tilde{W}}_u{\widehat{W}}_u+{\displaystyle \frac{s{\sigma }_2}{r_2}}{\tilde{\vartheta }}_u{\widehat{\vartheta }}_u+{\displaystyle \frac{{\sigma }_3}{r_3}}{\tilde{\zeta }}_u{\widehat{\zeta }}_u+{\displaystyle \frac{{\sigma }_4}{r_4}}{\tilde{W}}_r{\widehat{W}}_r+{\displaystyle \frac{s{\sigma }_5}{r_5}}{\tilde{\vartheta }}_r{\widehat{\vartheta }}_r+{\displaystyle \frac{{\sigma }_6}{r_6}}{\tilde{\zeta }}_r{\widehat{\zeta }}_r+s_u{\sigma }_u+{\kappa }_1{\zeta }_uϵ+s_r{\sigma }_r+{\kappa }_2{\zeta }_rϵ+{\sum }_{i=1}^4{l}_i^2$.

In accordance with the tenets set forth in Lemma 1. The reduction in V over a finite period of time results in the closed-loop system being driven towards $V^p\left(\chi \right)<Q/(1-\lambda )\beta$, and $0<\lambda <1$ is a constant, which means that the closed-loop system’s trajectory is limited within a finite time frame.

$$\parallel {\chi }_m\parallel \le \sqrt{2{({\displaystyle \frac{Q}{(1-\lambda )\beta }})}^{{\displaystyle \frac{1}{2}}}}$$

(74)

Then, we can obtain

$$T_1\le {\displaystyle \frac{1}{\alpha (1-p)}}\ln {\displaystyle \frac{\alpha V^{1-p}\left({\chi }_0\right)+\lambda \beta }{\lambda \beta }}.$$

(75)

It can be seen from the definition ${\chi }_m=\Gamma -{\xi }_m\left(m=1,2,3,4;\Gamma =z_e,u_e,{\psi }_e,r_e\right)$ that, if it is ensured that ${\xi }_m$ converges in finite time, it can be demonstrated that the tracking errors $\Gamma$ are also practically finitely settled. The following section will present evidence that the ${\xi }_m$ are within finite time.

We define the following Lyapunov:

$$V_t=\sum _{m=1}^4{\displaystyle \frac{1}{2}}{\xi }_m^2$$

(76)

The time derivative of $V_t$ gives

$${\dot{V}}_t=-k_1{\xi }_1^2-k_2{\xi }_2^2-k_3{\xi }_3^2-k_4{\xi }_4^2+{\xi }_1({\overline{\alpha }}_u-{\alpha }_u)\cos {\psi }_e+{\xi }_3({\overline{\alpha }}_r-{\alpha }_r)\cos \phi -\sum _{m=1}^4{l}_m{\xi }_m.$$

(77)

According to the Lemma in [33], $\parallel {\overline{\alpha }}_u-{\alpha }_u\parallel \cos {\psi }_e\le {\eta }_u$ and $\parallel {\overline{\alpha }}_r-{\alpha }_r\parallel \cos \phi \le {\eta }_r$ can be accomplished in a finite time $T_2$. ${\eta }_{u,r}$ is the known quantity. Accordingly, the subsequent inequality is satisfied when an appropriate parameter that satisfies a specific condition is selected:

$$\begin{array}{cc}\hfill {\dot{V}}_t& \le -k_w\sum _{i=1}^4{\xi }_i^2+({\xi }_1+{\xi }_3){\eta }_i+\sum _{i=m}^4{l}_m{\xi }_m\hfill \\ \hfill & \le -k_w{V}_t-d{V}_t^{{\displaystyle \frac{1}{2}}}.\hfill \end{array}$$

(78)

where $k_w=2min\left\{-k_1,-k_2,-k_3,-k_4\right\}$ and $d=\sqrt{2}min\left\{{\eta }_{u,r},l_m,m=1,2,3,4\right\}$. According to Lemma 1 it can be demonstrated that the variable ${\xi }_m$ will reach the origin within a finite time $T_3$. As $\Gamma ={\chi }_m+{\xi }_m,$ the tracking errors $\Gamma$ are observed to be practically finite and stable within the specified time frame $T=T_1+T_2+T_3.$ This completes the proof.

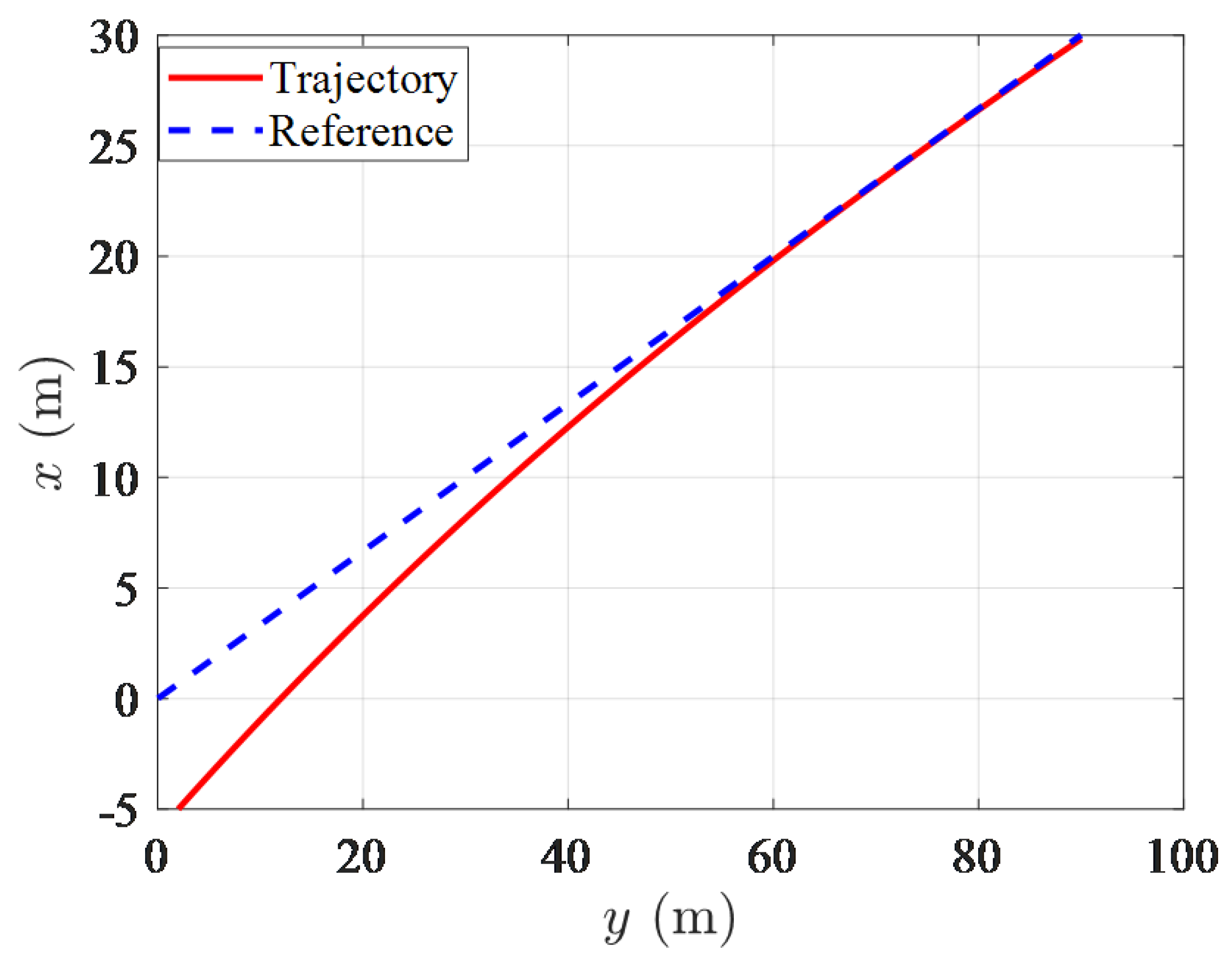
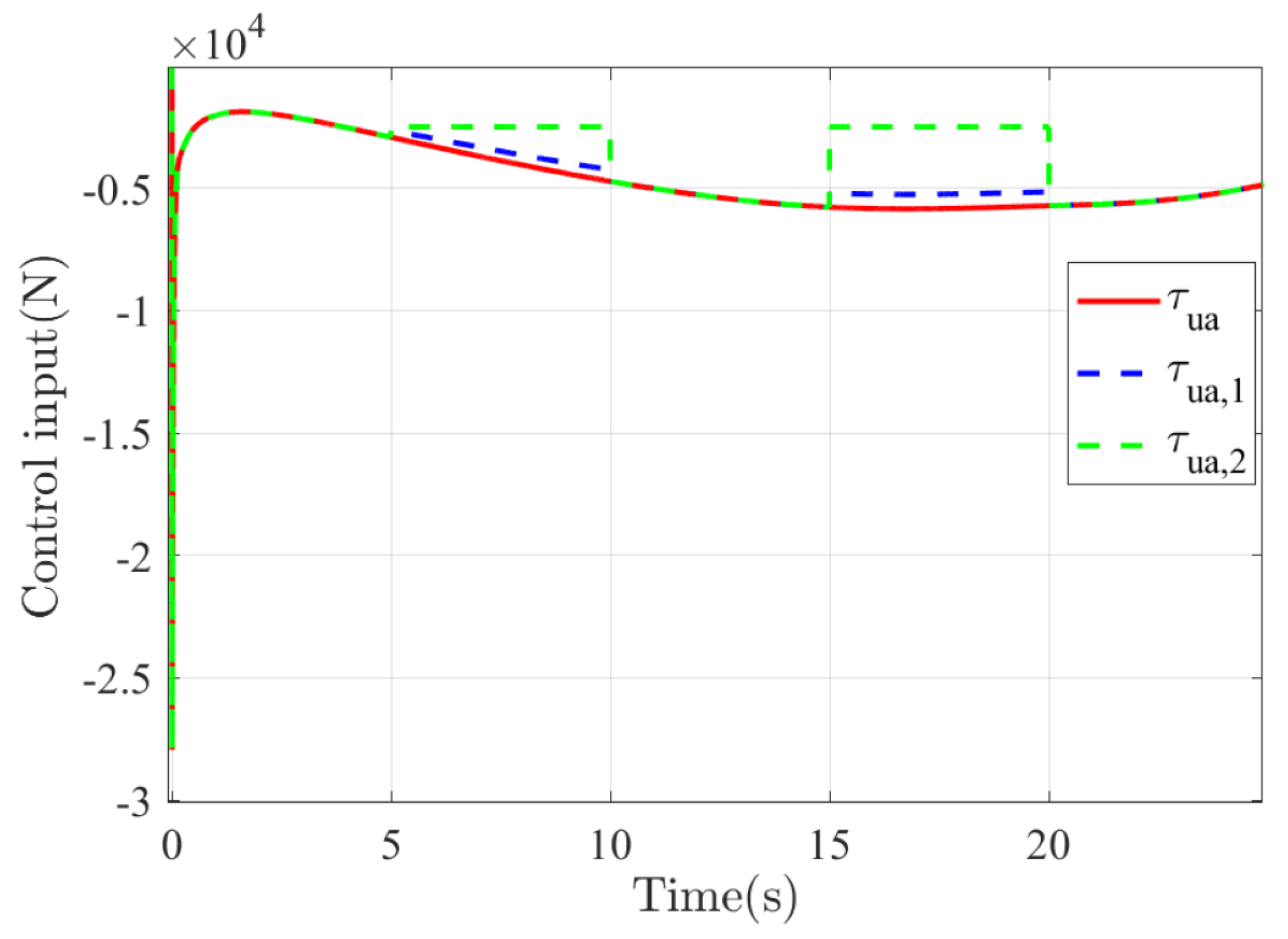
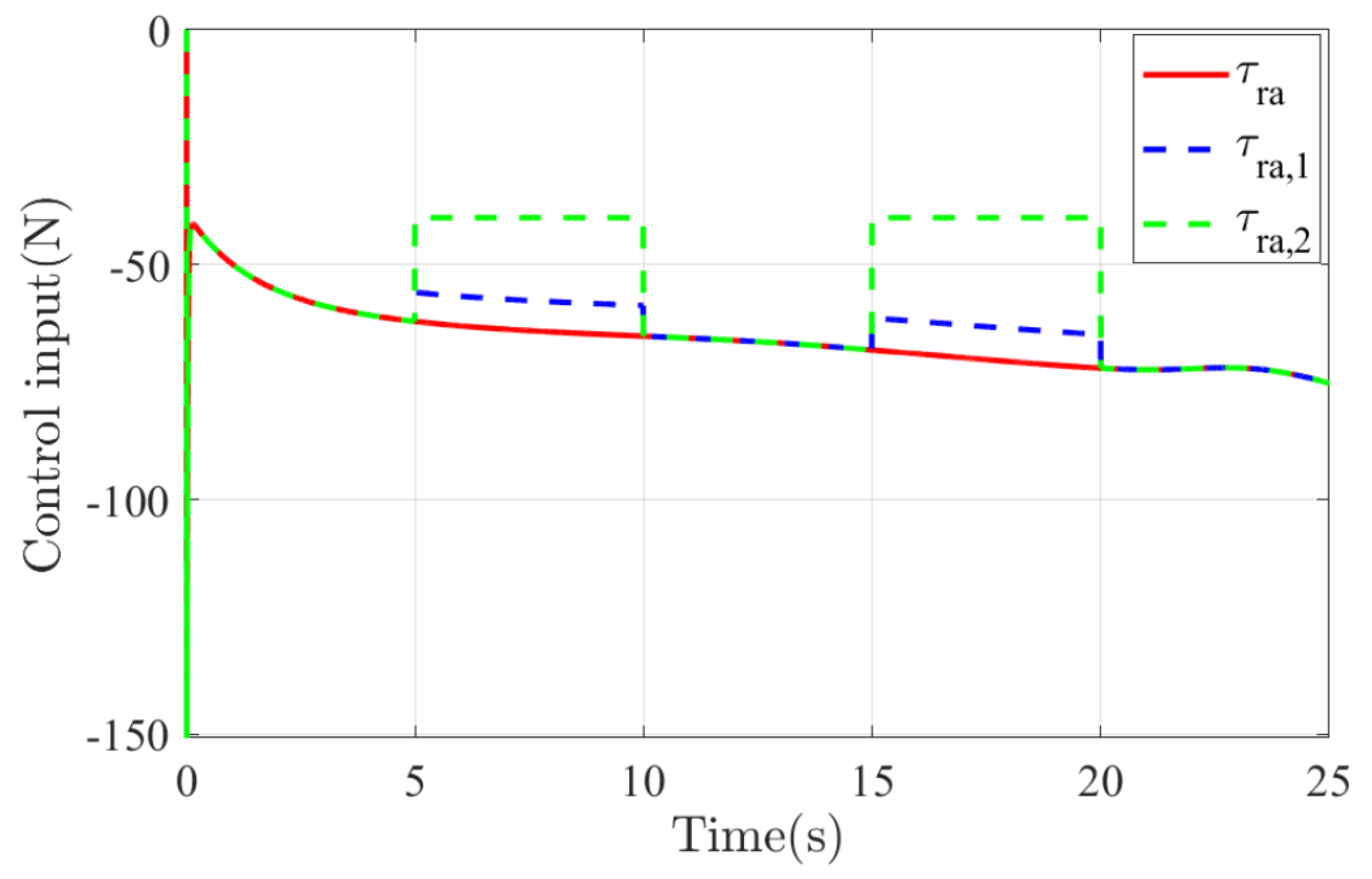
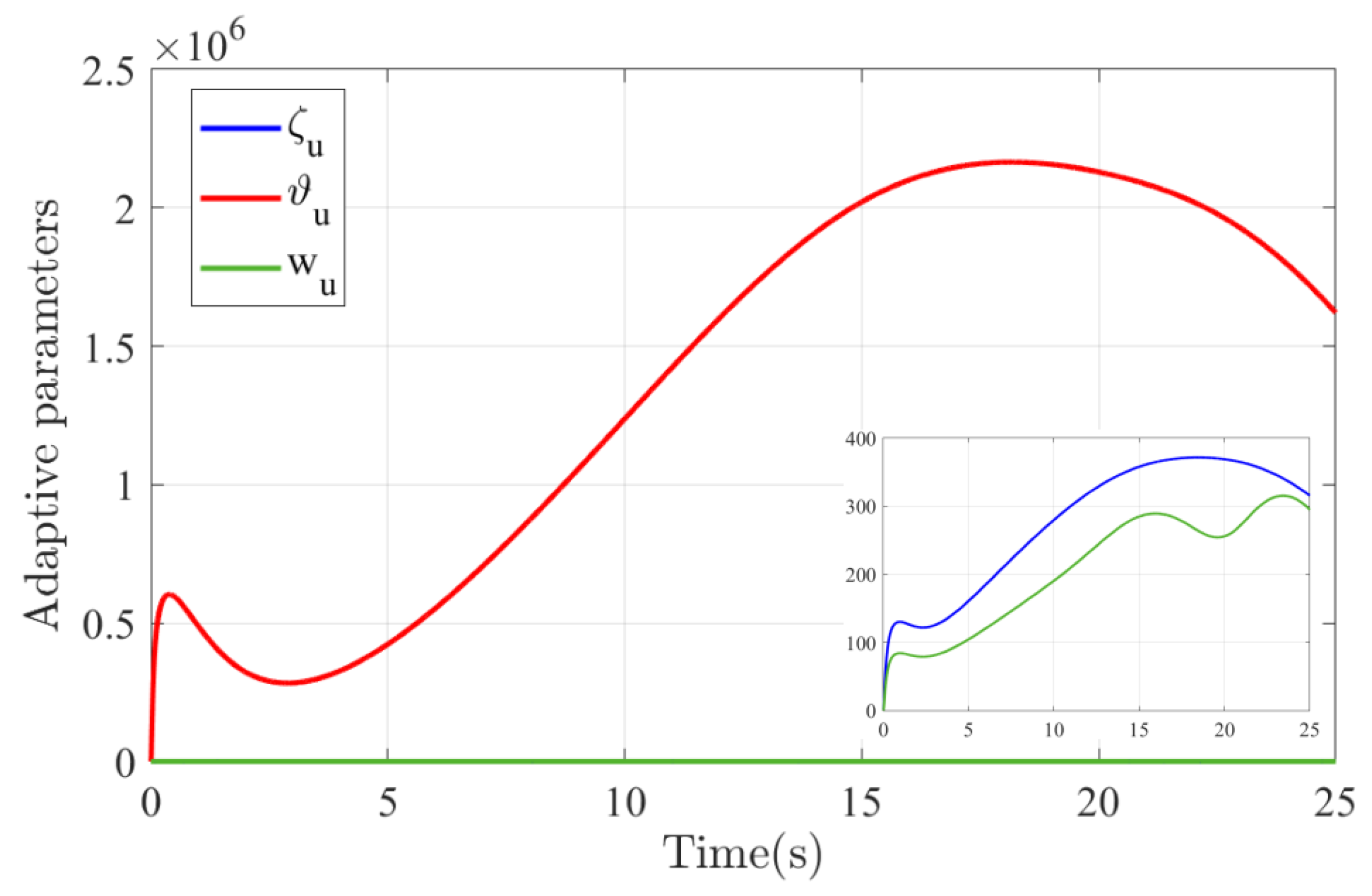
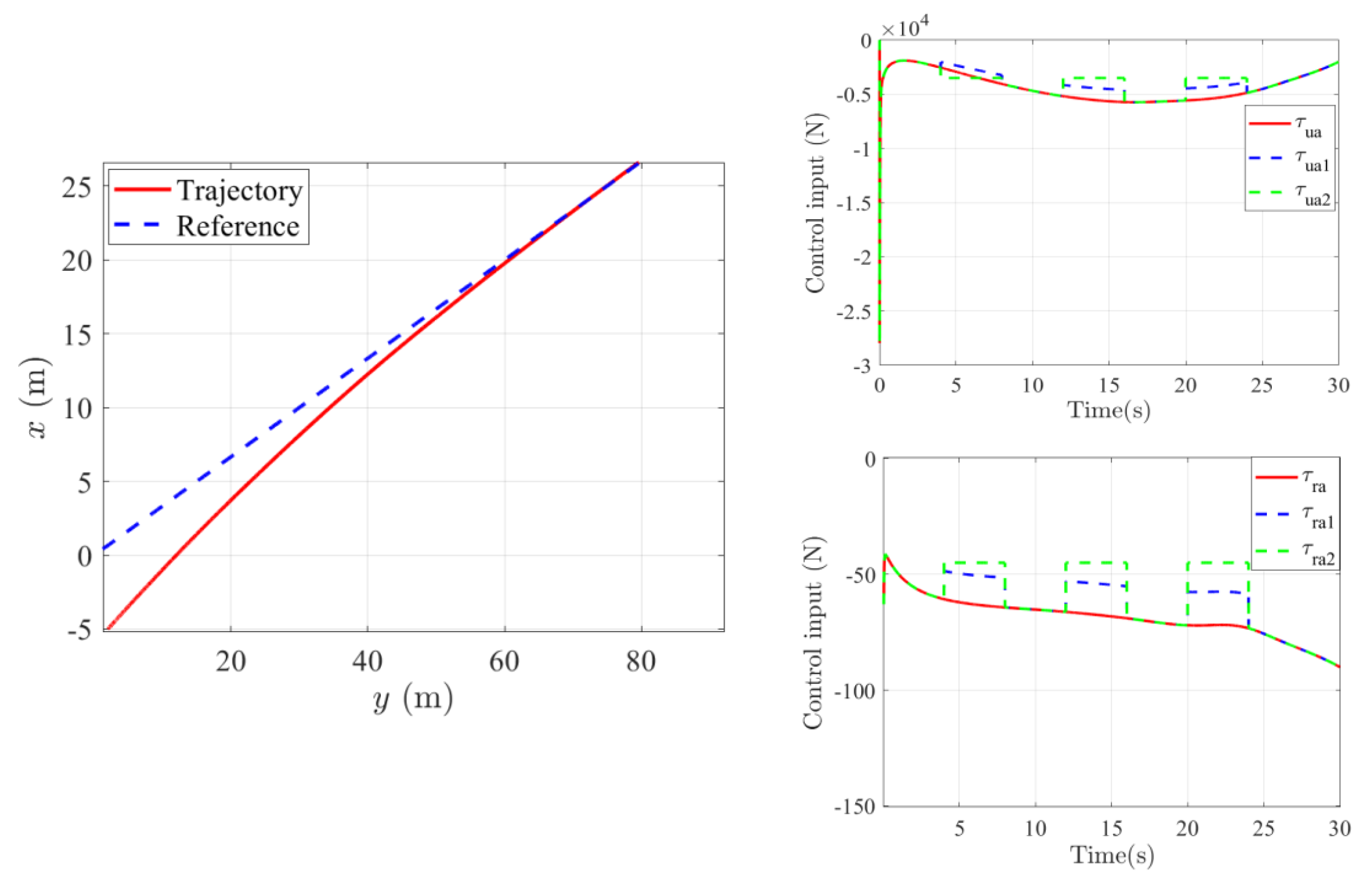
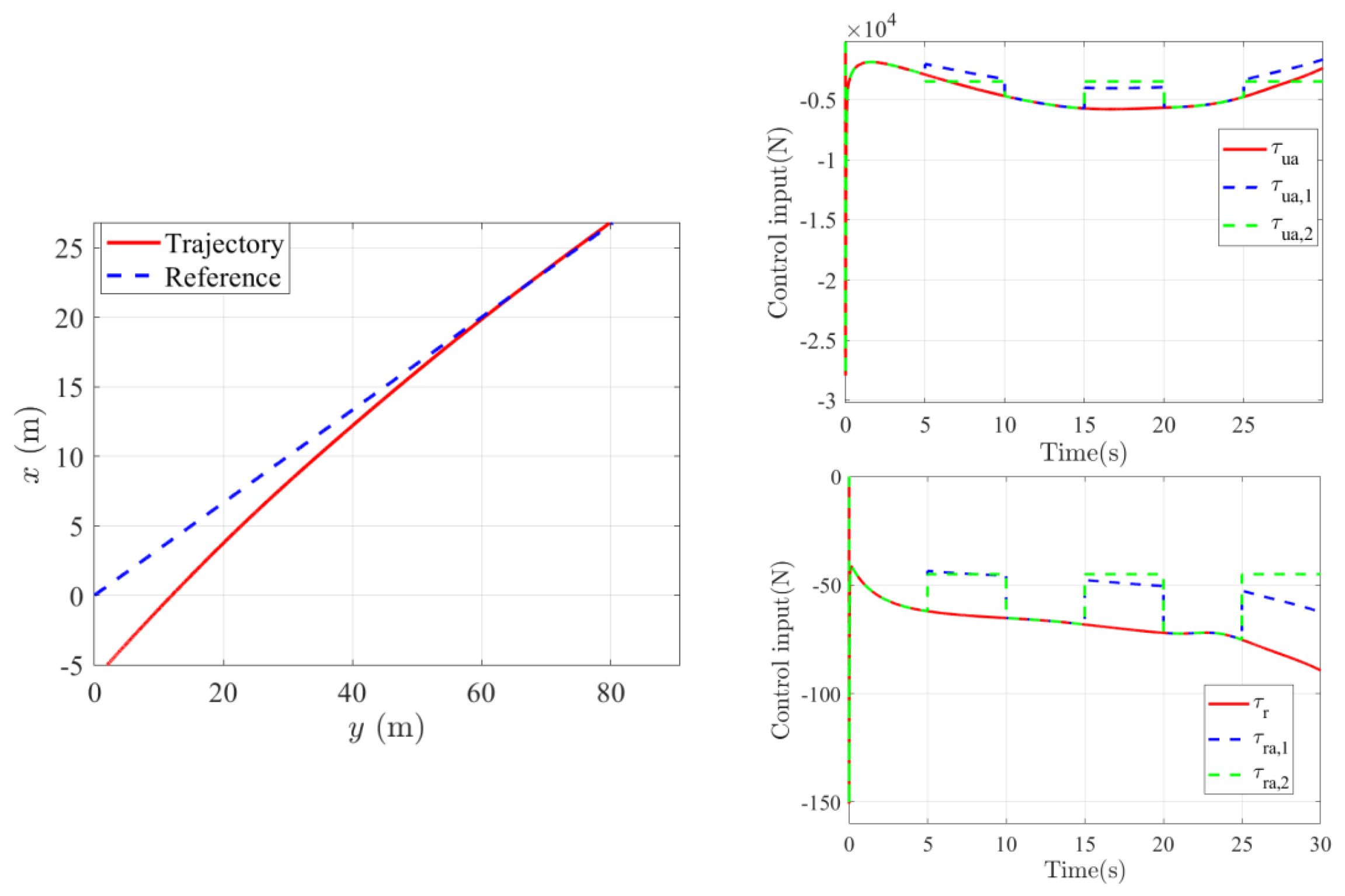
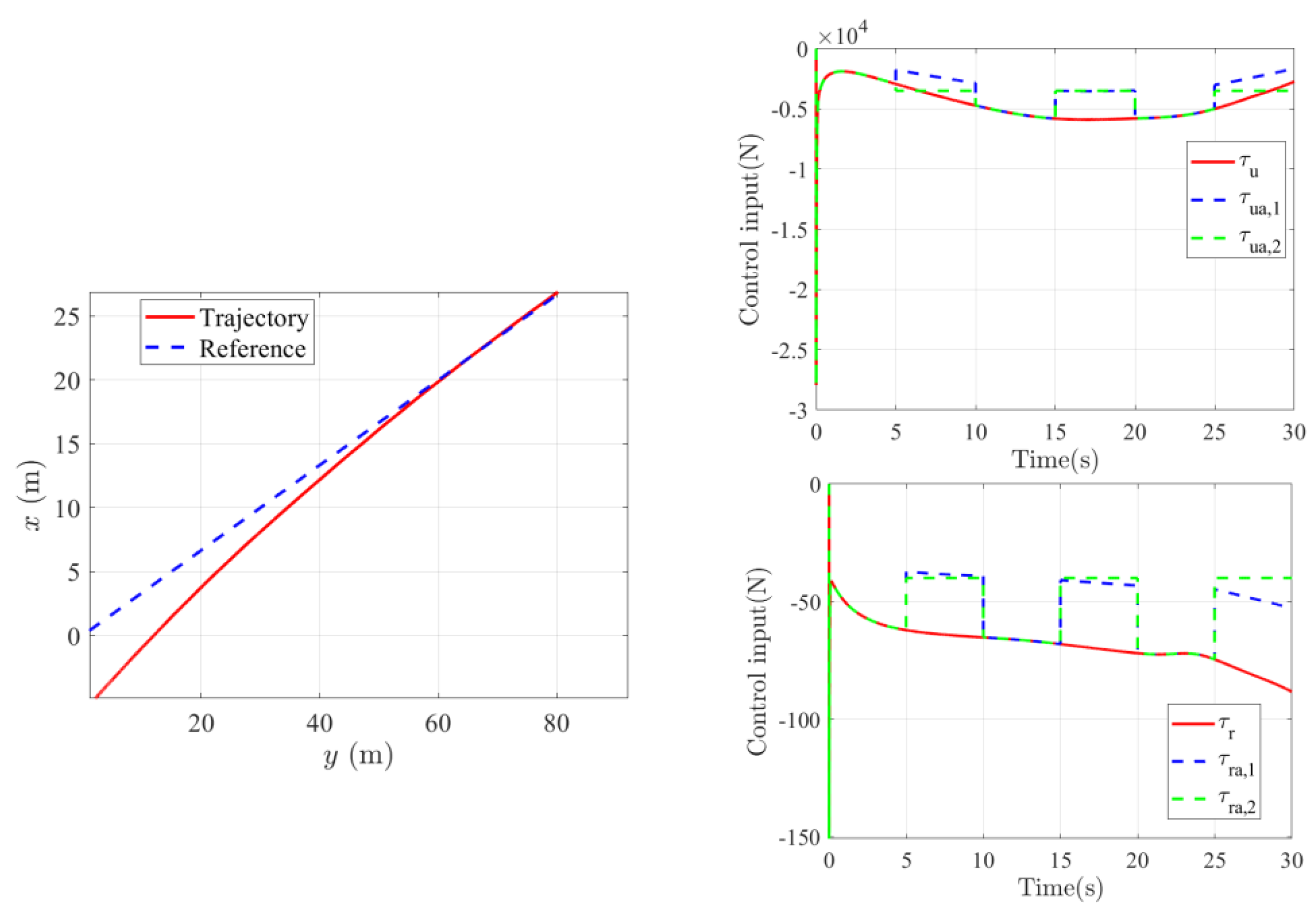
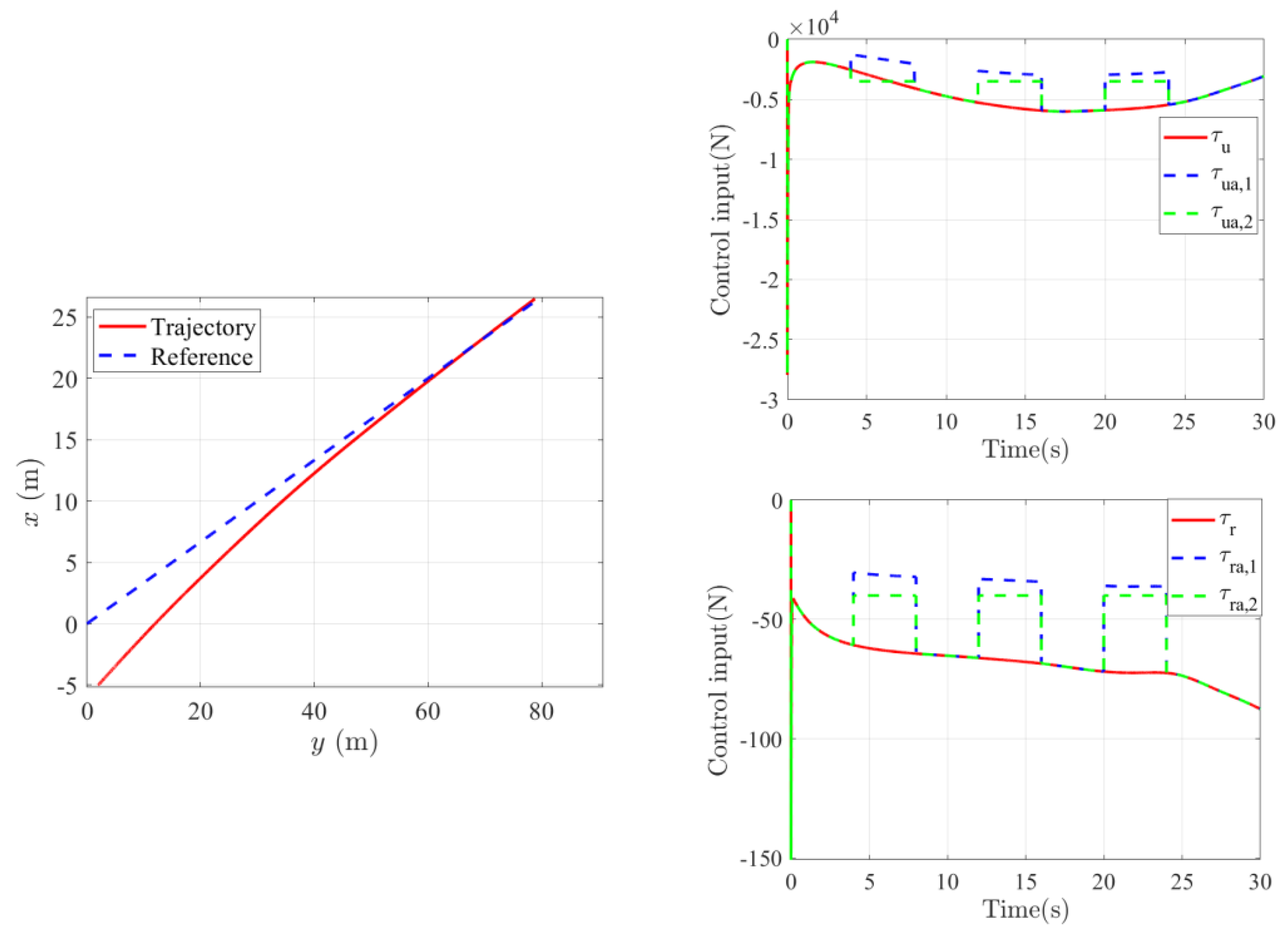
5. Simulation

Within this segment, the findings from the simulation analysis of an ACV are presented, and the parameters used are shown in

Table 1. Main parameters of the ACV.

Variable	Value	Variable	Value
m (kg)	$4\times {10}^4$	$J_z$ (kg)	$1.8\times {10}^6$
$J_x$ (kg)	$2.5\times {10}^5$	$S_a$ (${\mathrm{m}}^2$)	260
$L_a$ (m)	23.6	$(x_a,y_a,z_a)$	(2.8, 0, 0.3)
${\rho }_a$ (kg/${\mathrm{m}}^3)$	1.29	${\rho }_h$ (kg/${\mathrm{m}}^3)$	1025
$C_{ya}$	1	$C_{mxa}$	0.9
$C_{mza}$	1.02	$C_{xa}$	1.05

^Note More information about the coefficients can be found in [34].

and

Table 2. Design parameters used in the simulation.

Parameter	Value	Parameter	Value
$C_1$	10	$C_2$	$16.5$
$C_3$	$0.3$	$C_4$	9
$k_1$	3	$k_2$	1.5
$k_3$	1.5	$k_4$	1.5
$r_i$$(i=1,2,3,4,5,6)$	1	$l_i$$(i=1,2,3,4,5,6)$	1
${\sigma }_i$$(i=1,2,3,4,5,6)$	1	${\epsilon }_u$	0.02
${\epsilon }_r$	0.02	$\epsilon$	0.2
p	99/101

.

Remark 1. 

Theoretically speaking, we can increase the constant parameters $k_j,C_j,r_i$, and ${\sigma }_i$, and reduce $l_i$ and λ to achieve exceptional system performance from (74). However, from (25), (47), (37), and (57) increasing $k_j,C_j,r_i$, and ${\sigma }_i$ may increase the amplitude of control signals. As a result, a tradeoff should be made between the system performance and the control effort.

In the emulation, we selected the model as below:

$$\begin{array}{cc}\hfill {\tau }_{ua,1}\left(t\right)& ={\rho }_{u,1h}{\tau }_{u,1}\left(t\right),t\in [5h,5(h+1)]\hfill \\ \hfill {\tau }_{ua,2}\left(t\right)& ={\psi }_{u,2,h},t\in [5h,5(h+1)],h=1,3\hfill \\ \hfill {\tau }_{ra,1}\left(t\right)& ={\rho }_{r,1h}{\tau }_{r,1}\left(t\right),t\in [5h,5(h+1)]\hfill \\ \hfill {\tau }_{ra,2}\left(t\right)& ={\psi }_{r,2,h},t\in [5h,5(h+1)],h=1,3.\hfill \end{array}$$

(79)

The parameters for these actuator faults are selected as ${\psi }_{i,j,h}=-2.5\times {10}^3, {\rho }_{i,j,h}=0.9$, $i=u,r$, and $j=1,2$, and the initial conditions are chosen as ${[x_0,y_0,{\psi }_0]}^T=[-5,2,-2.05],{\widehat{\vartheta }}_u\left(0\right)={\widehat{\vartheta }}_r\left(0\right)=1,{\widehat{\zeta }}_u\left(0\right)={\widehat{\zeta }}_r\left(0\right)=1$, and ${\widehat{W}}_u\left(0\right)={\widehat{W}}_r\left(0\right)=0.05$. The desired trajectory and heading are chosen as $x_d=t,y_d=3t,{\psi }_d=arctan(y_e,x_e).$

The result of the simulation are depicted in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. The performance of tracking is illustrated in Figure 4. It can be observed that the tracking performance can be maintained even in the presence of actuator faults. Figure 5 and Figure 6 show the control input, and Figure 7 and Figure 8 show the parameter adaptive laws. Figure 9 shows the comparison experiment. Figure 10, Figure 11, Figure 12 and Figure 13 show the four different cases of actuator failure. As can be seen from Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, all of them are bounded.

To show the effectiveness of our proposed scheme, we make a comparison on convergence results between the proposed scheme and the method in [30] in Figure 9. The two control schemes are applied to the same ACV model with the same initial conditions and the same design parameters, so that a fair comparison can be made.

It is shown in Figure 9 that the method proposed in this paper converges at 30 s, while the method in [30] did not. Please refer to the detailed data in

Table 3. Comparison of convergence accuracy and convergence time.

	Convergence Accuracy	Convergence Time
The method in this paper	3.24 m	30 s
The method in [30]	7.95 m	35 s

.

Four cases of actuator faults have been considered, as shown in

Table 4. Different fault cases.

	Control Effectiveness Rate ${\mathit{\rho }}_{\mathit{i},\mathbf{jh}}$	Parameter T
case1	0.8	4
case2	0.7	5
case3	0.6	5
case4	0.5	4

. From Figure 10 and Figure 13, it can be observed that the intermittent actuator fault model results in partial loss of effectiveness every 4 s, and then works normally for the next 4 s. It can also be seen from Figure 11 and Figure 12 that the intermittent actuator fault model results in partial loss of effectiveness every 5 s, and then works normally for the next 5 s. Based on the above fault-tolerant tests, the effectiveness of the designed fault-tolerant controller can be verified.

6. Conclusions

A innovative finite-time fault-tolerant method is suggested for the ACV, integrating command filter techniques with backstepping control, with the objective of addressing model uncertainties. The proposed adaptive finite-time fault-tolerant controller can estimate the unknown boundaries of actuator fault parameters so that an infinite number of actuator faults can be handled. Utilizing the stability criterion within a limited time, it can be demonstrated that both control performance and system stability can be maintained within a finite time. The results of the simulations, when considered alongside one another, serve to validate the efficiency of the proposed control approach. Further effort is required to deal with the security control problem for the ACV, in the context of cyber attacks and privacy preservation [35,36].