Mechanism and Regularity of Wet Modes in a Highly Integrated Marine Magnetic Levitation Pump Rotor Under Confined Water Conditions
Abstract
1. Introduction
2. Theoretical Foundations
2.1. Theoretical Analysis of Rotor Wet Mode via an Added Mass-Based Analytical Method
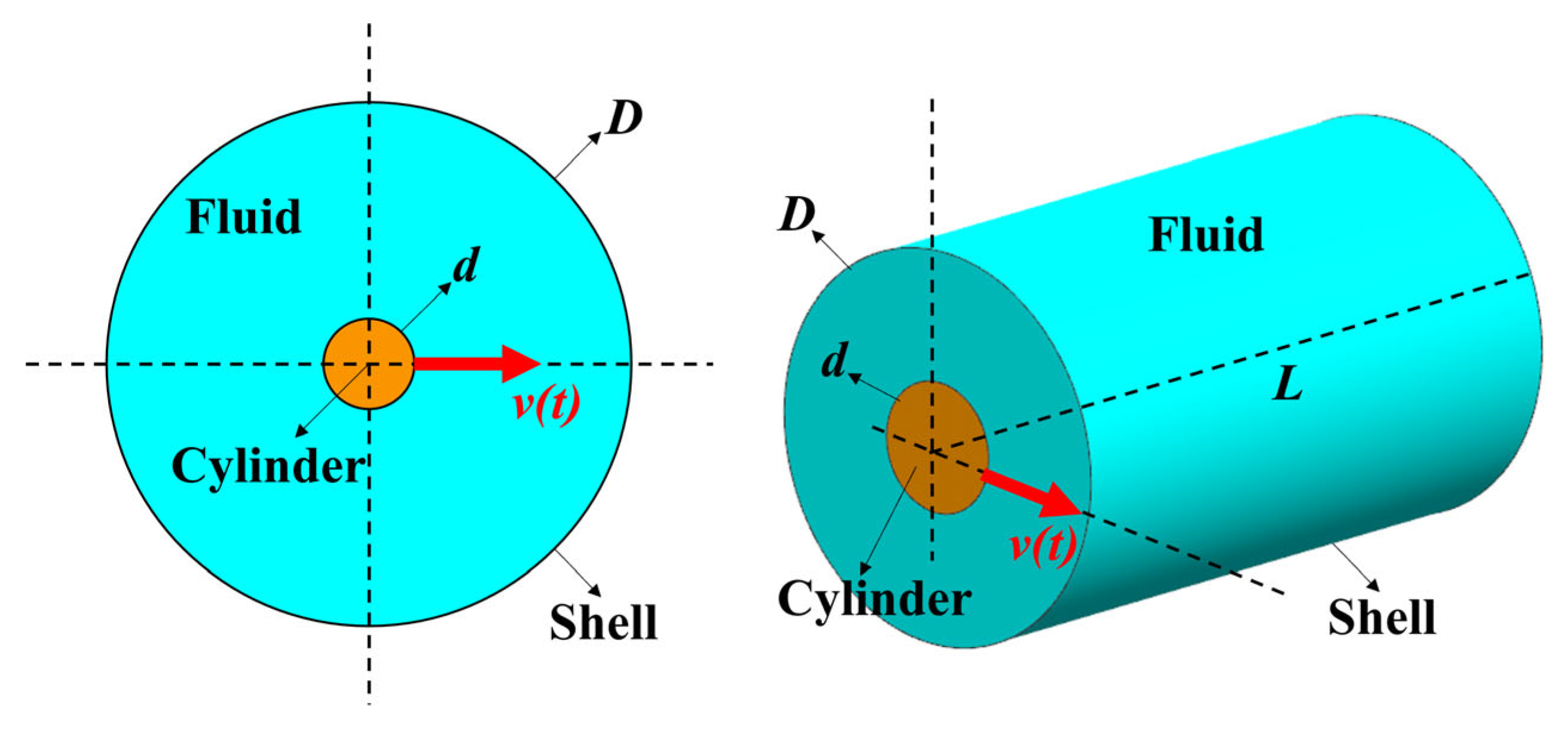
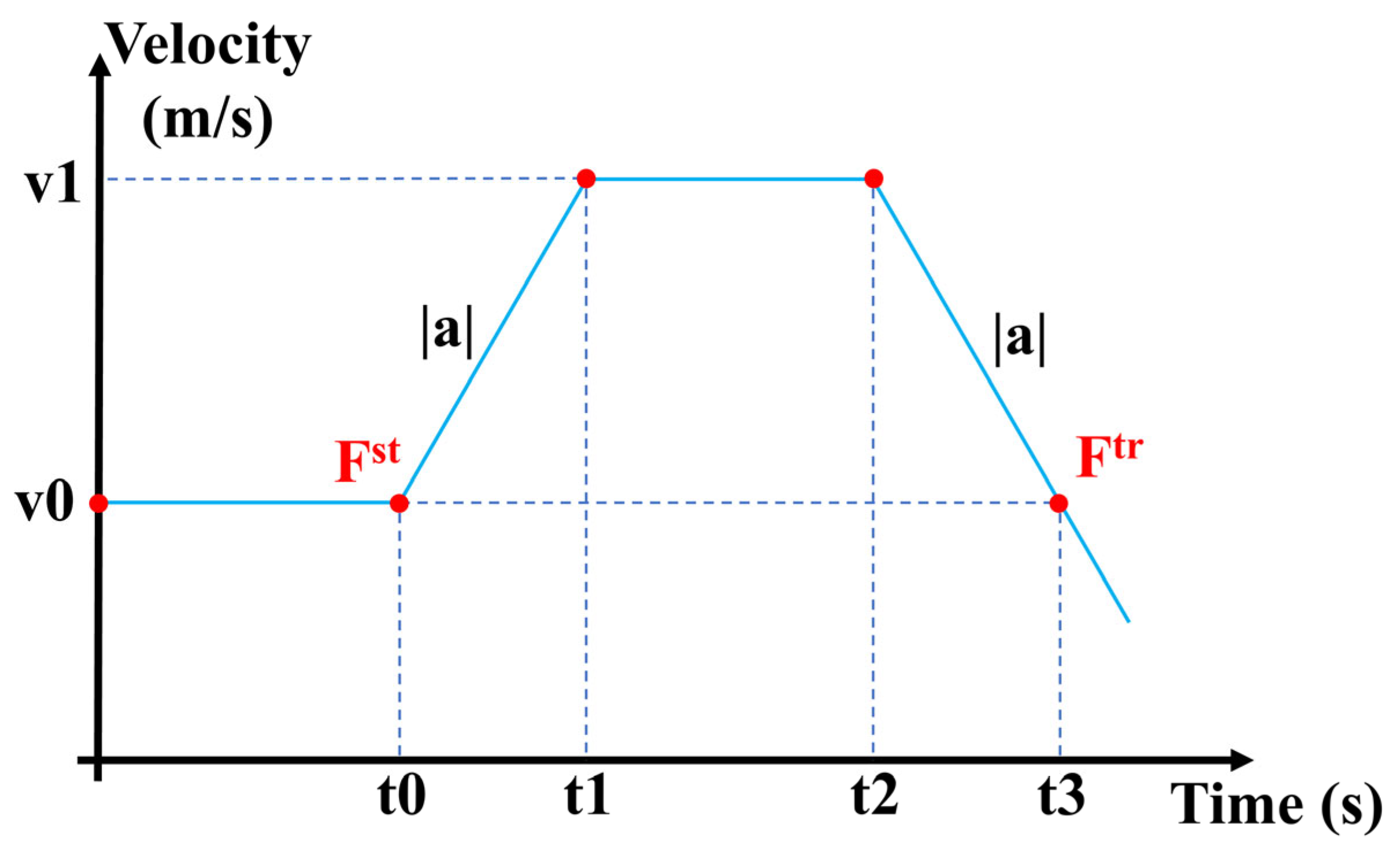
2.1.1. Analysis of Added Mass Effects
2.1.2. Analysis of the Wet Modal Analytical Method
2.2. Theoretical Analysis of Rotor Wet Mode via the AFSI Method
3. Computational Model and Method Validation
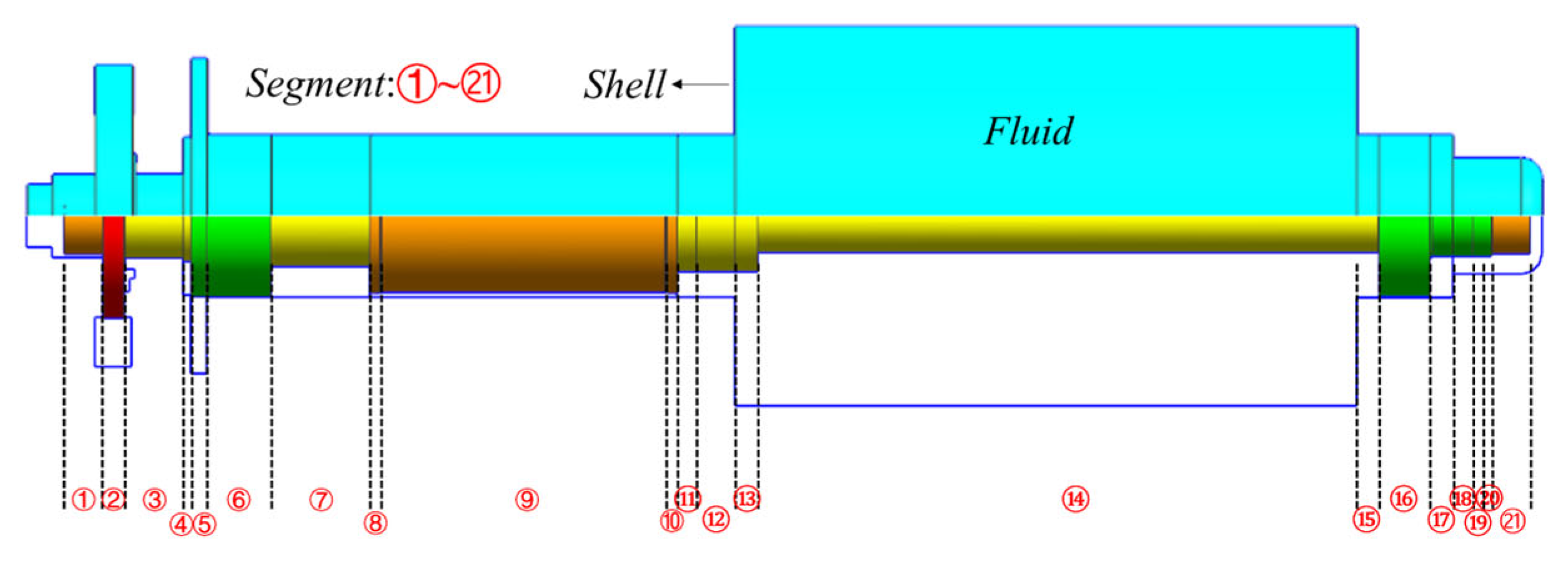
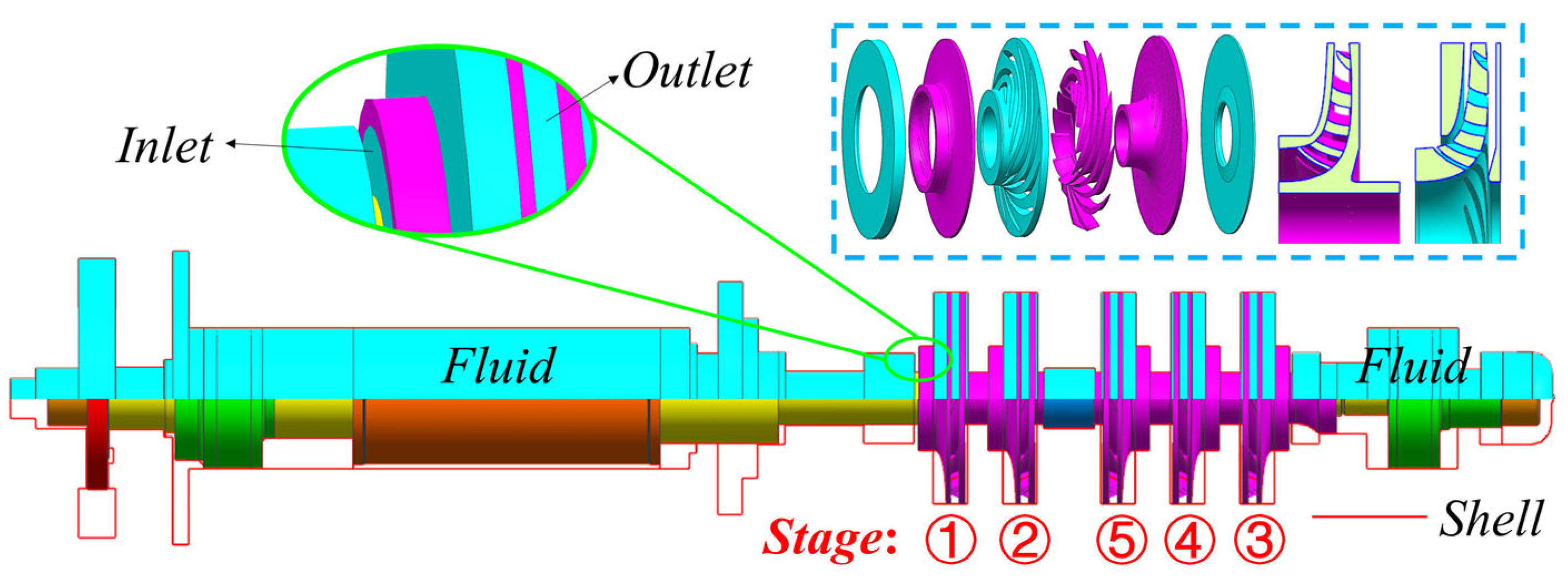
3.1. Model Description and Material Properties
- Permanent magnets: density = 8400 kg/m3, Young’s modulus = 120 GPa, Poisson’s ratio = 0.27;
- Retention sleeve: density = 8900 kg/m3, Young’s modulus = 210 GPa, Poisson’s ratio = 0.28;
- Potting compound: density = 2400 kg/m3, Young’s modulus = 0.5 GPa, Poisson’s ratio = 0.36.
3.2. Validation of the Added Mass Calculation Method
- Model I: cross-sectional radius = 5 mm, length = 500 mm, aspect ratio = 50;
- Model II: cross-sectional radius = 30 mm, length = 14 mm, aspect ratio = 0.233.
- Model III: cylinder radius = 5 mm, fluid annulus = 1 mm, initial length = 200 mm;
- Model IV: cylinder radius = 5 mm, fluid annulus = 5 mm, initial length = 200 mm.
- Model V: cylinder radius = 10 mm, fluid annulus = 10 mm, initial length = 400 mm.
3.3. Validation of the Added Mass-Based Analytical Method for Wet Mode
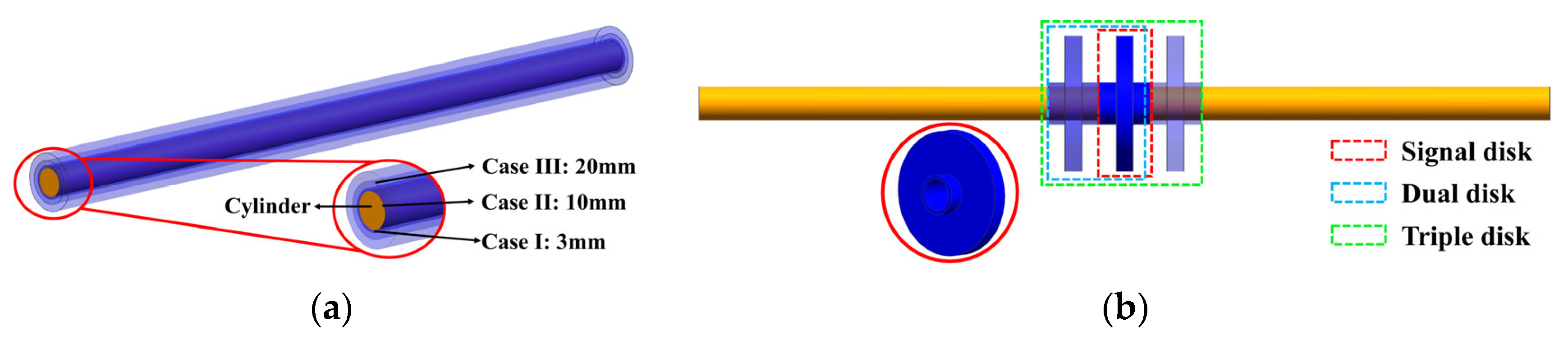
- Model VI: A cylindrical shaft segment with a radius of 20 mm and a length of 1000 mm, assembled with three disk components of different thicknesses (3 mm, 10 mm, and 20 mm), each extending the full length of the shaft;
- Model VII: A cylindrical shaft segment with a radius of 20 mm and a length of 1000 mm, equipped with varying numbers of impeller-like disk components (single, dual, and triple disks).
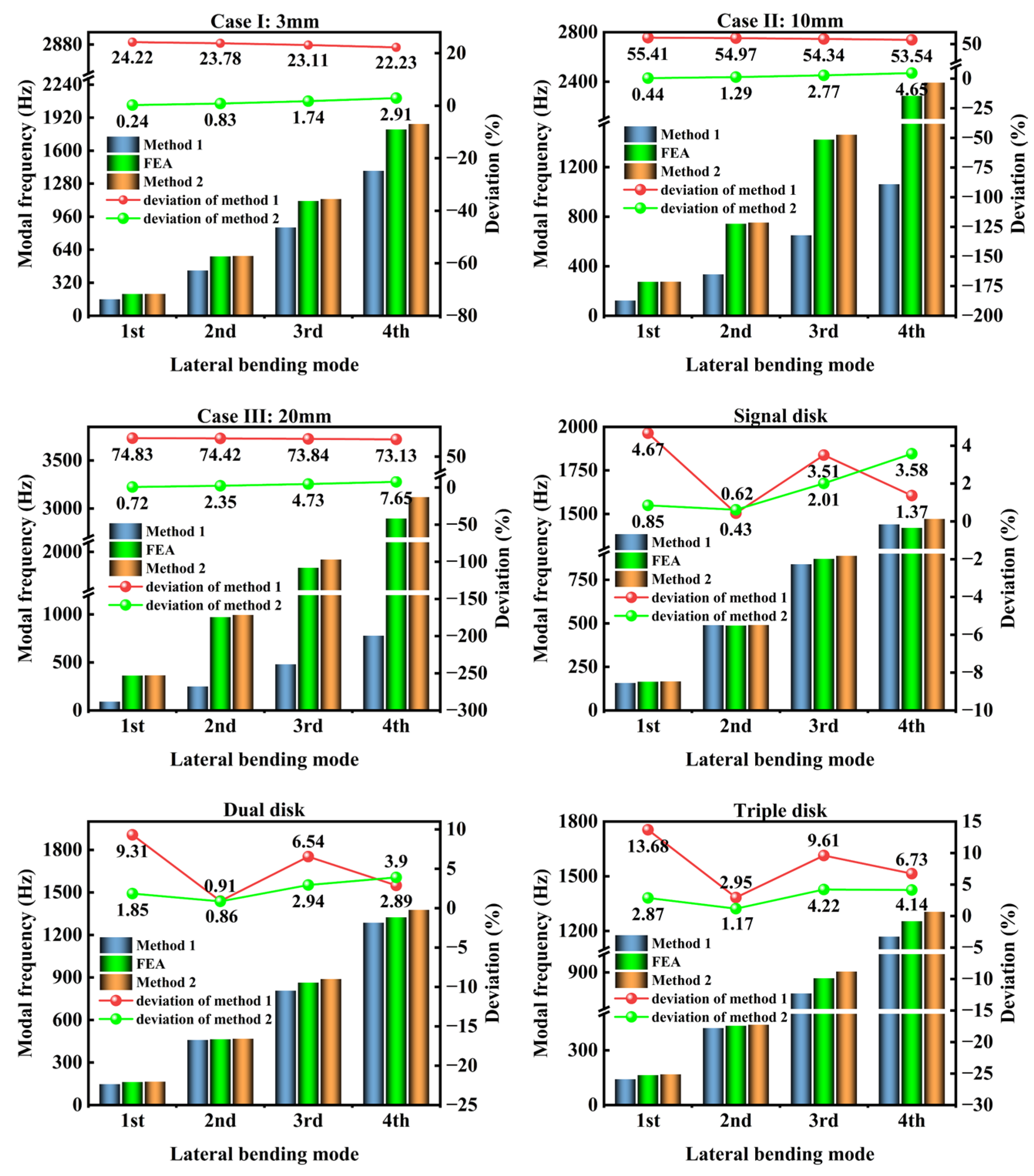
- Method 1: Conventional lumped mass and inertia representation;
- Method 2: Treatment as a locally thickened segment of the corresponding shaft section.
4. Results and Discussion
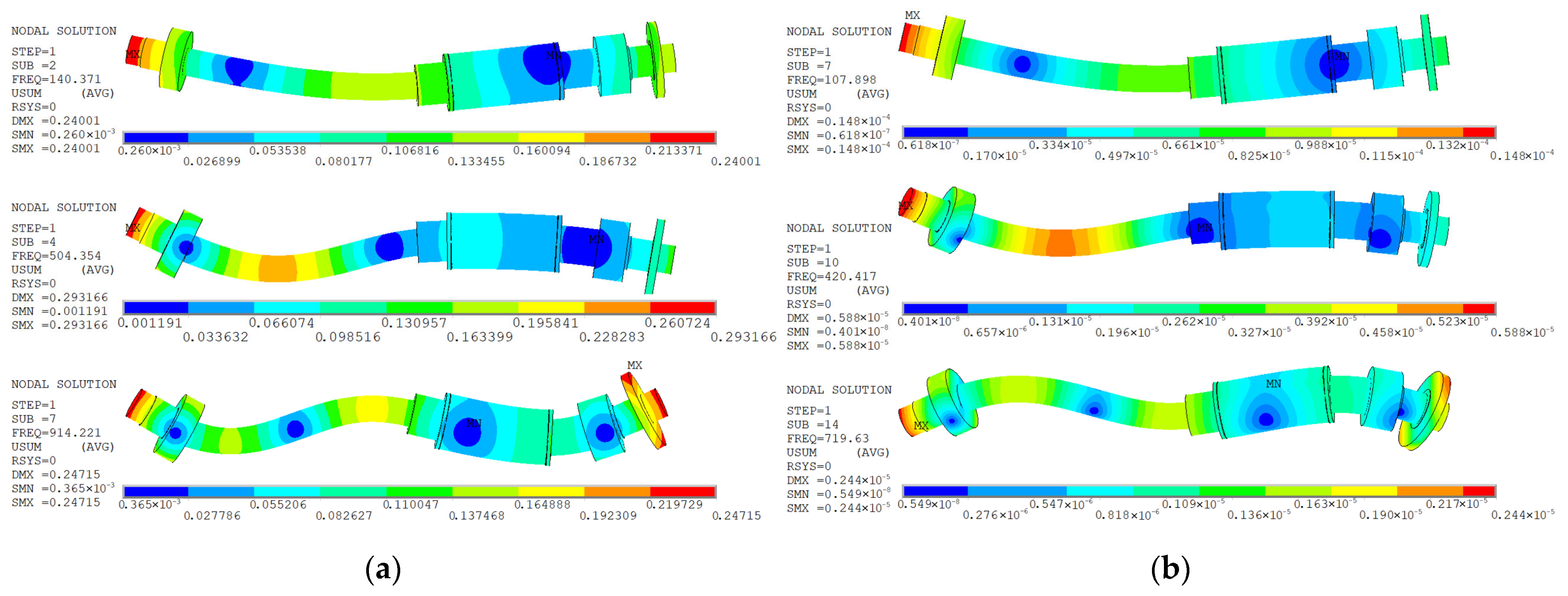
4.1. Wet Modal Analysis of a Magnetic Levitation Pump Rotor (Without Impeller)
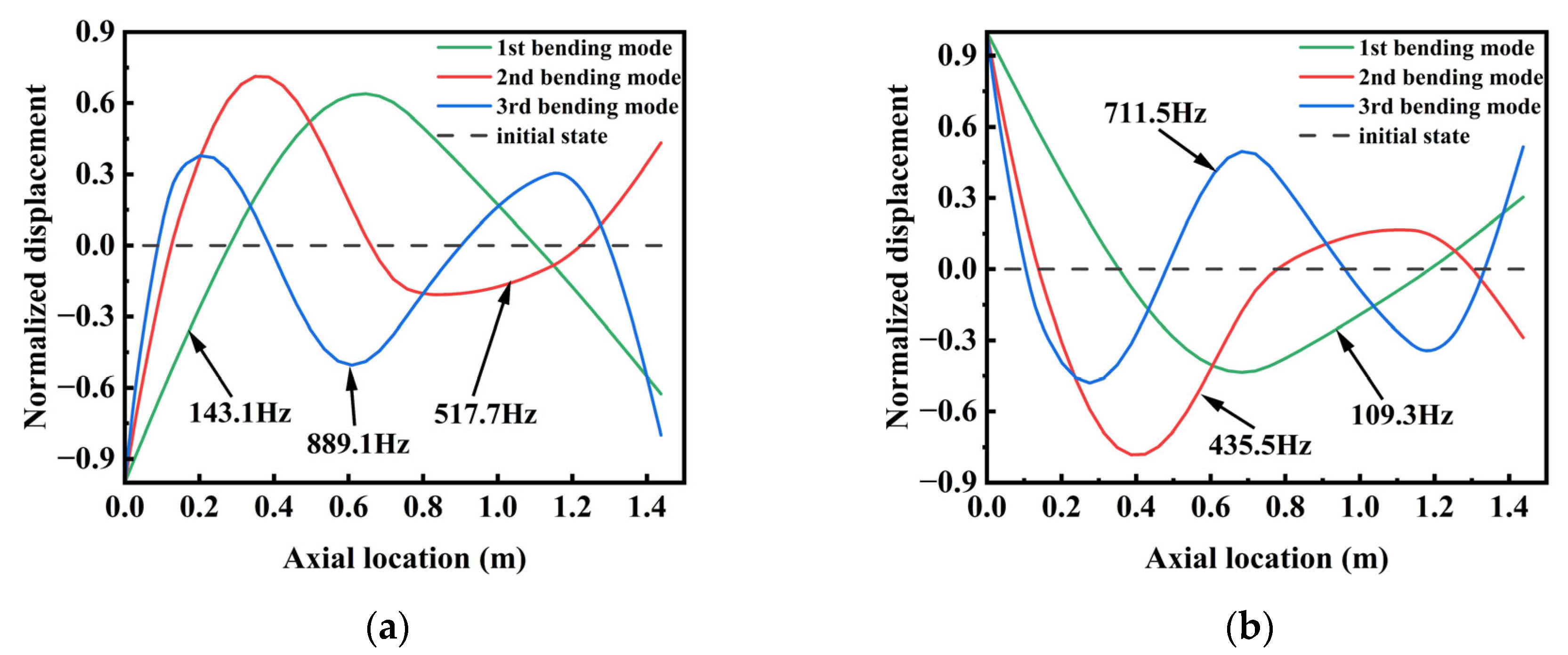
- Dry mode: 1st bending = 143.1 Hz; 2nd bending = 517.7 Hz; 3rd bending = 889.1 Hz;
- Wet mode: 1st bending = 109.3 Hz; 2nd bending = 435.5 Hz; 3rd bending = 711.5 Hz.
- Dry mode: 1st bending = 140.4 Hz; 2nd bending = 504.4 Hz; 3rd bending = 914.2 Hz;
- Wet mode: 1st bending = 107.9 Hz; 2nd bending = 420.4 Hz; 3rd bending = 719.6 Hz.
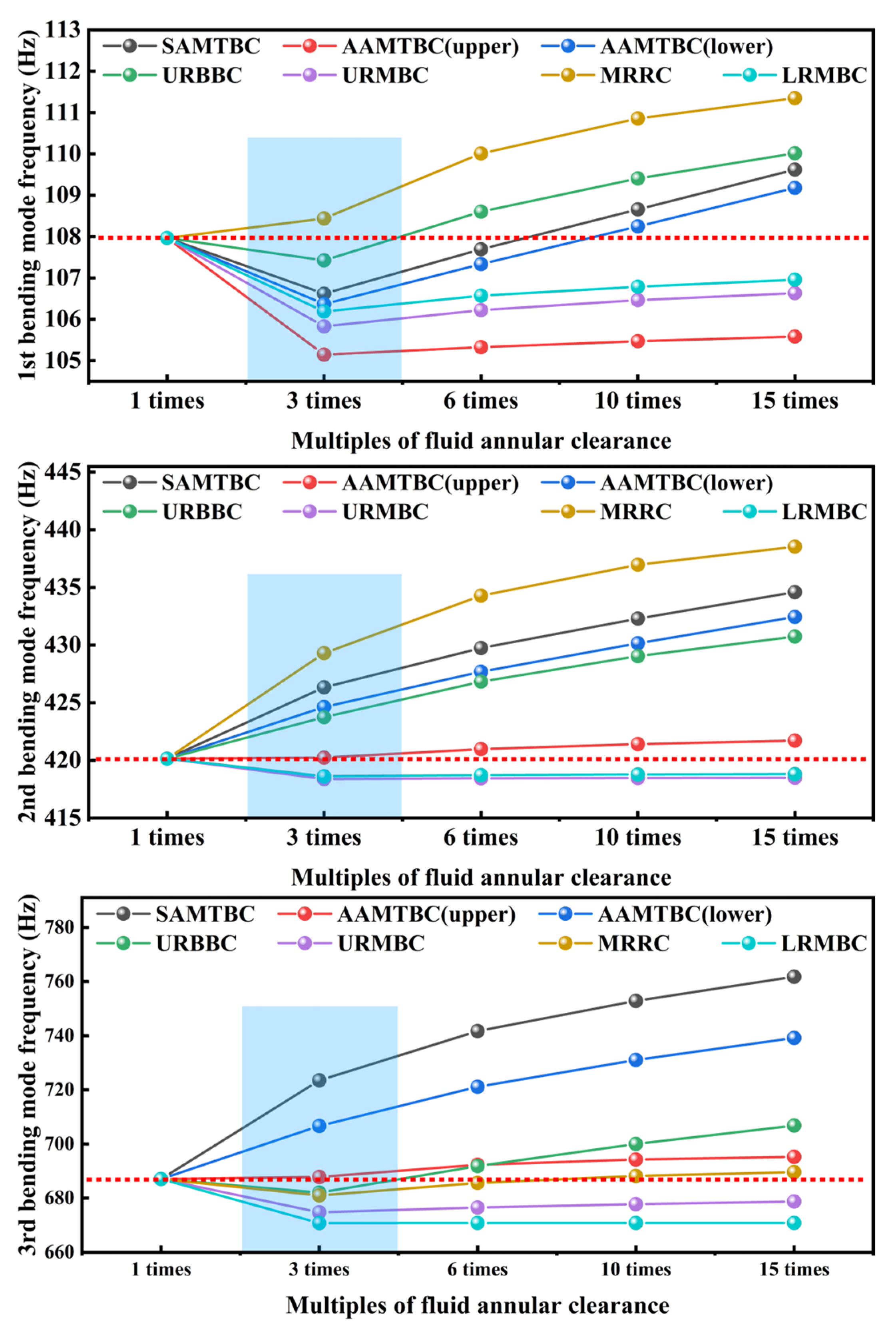
4.2. Regularity Analysis of Rotor Wet Mode in Confined Water
- Simplified fluid domain: 1st bending = 107.97 Hz; 2nd bending = 420.15 Hz; 3rd bending = 687.05 Hz.
- In general, the first three bending modes exhibit an overall increasing trend with the enlargement of the various fluid clearance. However, the 3 times clearance size serves as a transition point. For certain fluid clearance, a decrease in modal frequency is observed when transitioning from the 1× to the 3× size. Moreover, larger clearance sizes do not invariably yield modal frequencies higher than the initial values.
- The influence of different fluid clearance on modal behavior exhibits modal dependency, spatial specificity, and size difference. This result stems from two factors: differential changes in added mass due to clearance size variation, and the distinct sensitivity of each mode to fluid clearance, governed by mode shape. Therefore, a fluid clearance near a region of minimal modal deformation has negligible effect. For example, modifying the motor rotor radial clearance (MRRC) significantly impacts global added mass, strongly influencing the first and second bending modes, while minimally affecting the third bending mode due to negligible deformation near the MRRC.
- Both symmetric and asymmetric changes in bilateral axial fluid clearance affect all modal orders. Thus, the axial added mass effect should be considered in the analysis of practical submerged rotor systems.
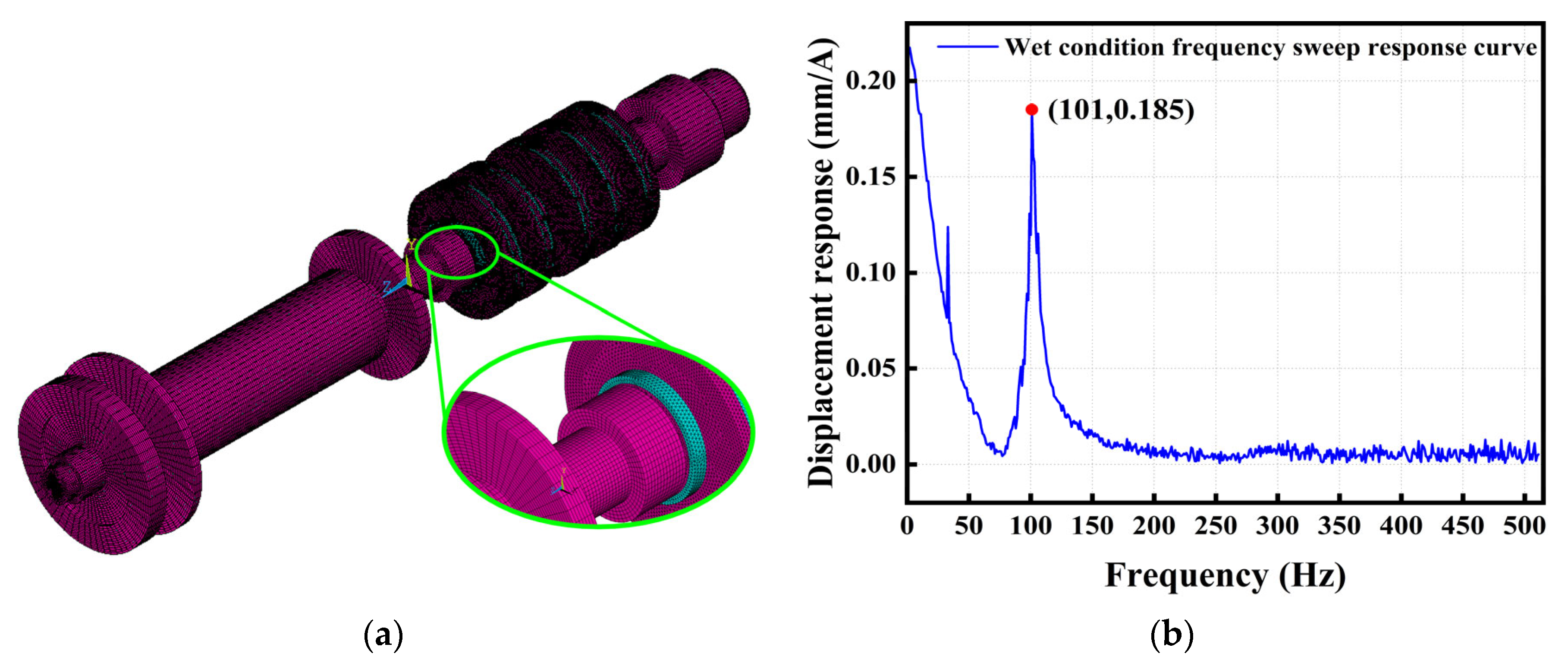
4.3. Wet Modal Analysis of a Magnetic Levitation Pump Rotor (With Impeller)
5. Conclusions
- (1)
- When accounting for actual fluid viscosity, the analytical formula produces significant overestimation errors in the added mass for confined annular fluid domains featuring narrow clearances or for cylindrical structures with low aspect ratios. Under these conditions, correction through a CFD-based approach becomes necessary. Nevertheless, for large fluid clearance, the analytical formula remains applicable provided that the aspect ratio satisfies L/d ≥ 5.
- (2)
- Following validation of the thickening treatment for elongated disk components and the disk equivalent density (DED) method, the proposed improved analytical method for wet modal analysis—based on added mass effects—was successfully verified. Wet modal analysis was conducted on two types of magnetic levitation pump rotors using both analytical and the AFSI method. The results, compared against experimental data from swept-frequency modal tests, demonstrate good agreement with measured values. For the first bending mode—the primary mode of interest—the maximum observed error was 4.1%, thereby validating the accuracy of both computational methods in predicting the wet modal behavior of the rotor.
- (3)
- Relative to infinite or extensive open water domains, confined water markedly amplifies its influence on the wet mode of the rotor.
- (4)
- The modal frequencies generally exhibit an increasing trend with the enlargement of the fluid clearance. A fluid clearance size of three times the original serves as a transition point. However, increasing the fluid clearance size does not invariably result in modal frequencies higher than their initial values. And the sensitivity to such variations differs across modal orders, depending chiefly on the mode shape and the location of fluid clearance. Additionally, changes in the axial fluid clearance also exert a discernible influence on all modal orders.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| added mass | |
| E | elastic modulus |
| inner and outer diameters of the confined water | |
| r | radius |
| drag force acting on the object when moving at the initial velocity v0 | |
| mass per unit length of the shaft segment | |
| mean fluid density | |
| dynamic viscosity | |
| density of fluid medium | |
| inner to outer diameter ratio | |
| rotational angular velocity | |
| a | acceleration |
| total force exerted on the object during uniform deceleration to velocity v0 | |
| c | speed of sound in the fluid medium |
| K | fluid bulk modulus |
| l | length of the shaft segment element |
| I | cross-sectional moment of inertia |
| AFSI | Acoustic Fluid–Structure Interaction |
| SSED | shaft segment equivalent density method |
| DED | disk equivalent density method |
| SAMTBC | symmetric axial magnetic thrust bearing clearances |
| MRRC | motor rotor radial clearance |
| URBBC | upper radial backup bearing clearance |
| URMBC | upper radial magnetic bearing clearance |
| LRMBC | lower radial magnetic bearing clearance |
| AAMTBC | asymmetric axial magnetic thrust bearing clearances |
References
- Wu, Y.; Wu, D.; Fei, M.; Sørensen, H.; Ren, Y.; Mou, J. Application of GA-BPNN on Estimating the Flow Rate of a Centrifugal Pump. Eng. Appl. Artif. Intell. 2023, 119, 105738. [Google Scholar] [CrossRef]
- Zhao, J.; Pei, J.; Wang, W.; Gan, X. Blade Redesign Based on Inverse Design Method for Energy Performance Improvement and Hydro-Induced Vibration Suppression of a Multi-Stage Centrifugal Pump. Energy 2024, 308, 132862. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, J.; Liu, S.; Han, Z.; Ni, X. Hydraulic Optimization Design of Centrifugal Pumps Aiming at Low Vibration Noise. AIP Adv. 2022, 12, 95026. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, K.; Liu, H.; Cheng, Z. Influence of Shaft Combined Misalignment on Vibration and Noise Characteristics in a Marine Centrifugal Pump. J. Low Freq. Noise Vibr. Act. Control 2022, 41, 1286–1306. [Google Scholar] [CrossRef]
- Lu, J.; Liu, X.; Zeng, Y.; Zhu, B.; Hu, B.; Hua, H. Investigation of the Noise Induced by Unstable Flow in a Centrifugal Pump. Energies 2020, 13, 589. [Google Scholar] [CrossRef]
- Soltani Dehkharqani, A.; Cervantes, M.J.; Aidanpää, J.-O. Numerical Analysis of Fluid-Added Parameters for the Torsional Vibration of a Kaplan Turbine Model Runner. Adv. Mech. Eng. 2017, 9, 168781401773289. [Google Scholar] [CrossRef]
- Sigrist, J.-F.; Broc, D.; Lainé, C. Dynamic Analysis of a Nuclear Reactor with Fluid–Structure Interaction. Nucl. Eng. Des. 2006, 236, 2431–2443. [Google Scholar] [CrossRef]
- Münch, C.; Ausoni, P.; Braun, O.; Farhat, M.; Avellan, F. Fluid–Structure Coupling for an Oscillating Hydrofoil. J. Fluids Struct. 2010, 26, 1018–1033. [Google Scholar] [CrossRef]
- Rodriguez, C.G.; Egusquiza, E.; Escaler, X.; Liang, Q.W.; Avellan, F. Experimental Investigation of Added Mass Effects on a Francis Turbine Runner in Still Water. J. Fluids Struct. 2006, 22, 699–712. [Google Scholar] [CrossRef]
- Du Buat, P.L.G. Principes D’hydraulique: Vérifiés Par Un Grand Nombre d’expériences Faites Par Ordre Du Gouvernement; Ouvrage Dans Lequel on Traite Du Mouvement Uniforme & Varié de l’eau Dans Les Rivières, Les Canaux, & Les Tayaux de Conduite; Imprimerie de Monsieur: Paris, France, 1786; Volume 1. [Google Scholar]
- Sarpkaya, T.; Garrison, C.J. Vortex Formation and Resistance in Unsteady Flow. J. Appl. Mech. 1963, 30, 16–24. [Google Scholar] [CrossRef]
- Sarpkaya, T. Lift, Drag, and Added-Mass Coefficients for a Circular Cylinder Immersed in a Time-Dependent Flow. J. Appl. Mech. 1963, 30, 13–15. [Google Scholar] [CrossRef]
- Chen, S.S.; Wambsganss, M.W.; Jendrzejczyk, J.A. Added Mass and Damping of a Vibrating Rod in Confined Viscous Fluids. Am. Soc. Mech. Eng. 1976, 43, 325–329. [Google Scholar] [CrossRef]
- Villaggio, P. The Added Mass of a Deformable Cylinder Moving in a Liquid. Contin. Mech. Thermodyn. 1996, 8, 115–120. [Google Scholar] [CrossRef]
- Kaneko, S.; Nakamura, T.; Inada, F.; Kato, M.; Ishihara, K.; Nishihara, T.; Mureithi, N.W.; Langthje, M.A. Flow-Induced Vibrations: Classifications and Lessons from Practical Experiences, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Lagrange, R.; Puscas, M.A.; Piteau, P.; Delaune, X.; Antunes, J. Modal Added-Mass Matrix of an Elongated Flexible Cylinder Immersed in a Narrow Annular Fluid, Considering Various Boundary Conditions. New Theoretical Results and Numerical Validation. J. Fluids Struct. 2022, 114, 103754. [Google Scholar] [CrossRef]
- Fackrell, S. Study of the Added Mass of Cylinders and Spheres; University of Windsor: Windsor, ON, Canada, 2011. [Google Scholar]
- Javanmard, E.; Mansoorzadeh, S.; Mehr, J.A. A New CFD Method for Determination of Translational Added Mass Coefficients of an Underwater Vehicle. Ocean Eng. 2020, 215, 107857. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, S.; Wang, X.; Qi, D. Numerical Simulation and Analysis of Added Mass for the Underwater Variable Speed Motion of Small Objects. J. Mar. Sci. Eng. 2024, 12, 686. [Google Scholar] [CrossRef]
- Hannoura, A.A. Numerical and Experimental Modelling of Unsteady Flow in Rockfill Embankments. Ph.D. Thesis, University of Windsor, Windsor, ON, Canada, 1972. [Google Scholar]
- Hannoura, A.A.; McCorquodale, J.A. Rubble Mounds: Hydraulic Conductivity Equation. J. Waterw. Port Coastal Ocean Eng. 1985, 111, 783–799. [Google Scholar] [CrossRef]
- Noca, F. On the Evaluation of Time-Dependent Fluid-Dynamic Forces on Bluff Bodies; California Institute of Technology: Pasadena, CA, USA, 2005. [Google Scholar]
- Noca, F.; Shiels, D.; Jeon, D. Measuring Instantaneous Fluid Dynamic Forces on Bodies, Using Only Velocity Fields and Their Derivatives. J. Fluids Struct. 1997, 11, 345–350. [Google Scholar] [CrossRef]
- Zhang, Y. Dynamics Modeling and Modal Analysis for the Rotor in Water Medium. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2013. [Google Scholar]
- Zhang, M.; Chen, Q. Numerical Investigation of the Added Mass Effect of Submerged Blade Disk Structures: From Simplified Models to Francis Turbine Runners. Alexandria Eng. J. 2022, 61, 3013–3020. [Google Scholar] [CrossRef]
- Peng, G.; Zhang, Z.; Bai, L. Wet Modal Analyses of Various Length Coaxial Sump Pump Rotors with Acoustic-solid Coupling. Shock Vib. 2021, 2021, 8823150. [Google Scholar] [CrossRef]
- Hu, D.; Wang, W.; Wang, S.; Wang, Z. Study on the Influence of Gap Water Body on the Modal Characteristics of Pump Turbine Runner. In Proceedings of the 2021 3rd International Conference on Artificial Intelligence and Advanced Manufacture (AIAM), Manchester, UK, 23–25 October 2021; pp. 43–46. [Google Scholar]
- Wang, L.; Yu, S.; Wang, Z. Modal Characteristics Analysis of a Variable-Speed Pump-Turbine Rotor System: A Perspective of Resonance. J. Phys. Conf. Ser. 2024, 2854, 12084. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Presas, A.; Ahn, S.-H.; Wang, Z.; Huang, X.; Liu, Y. Influence of Rotation on the Modal Characteristics of a Bulb Turbine Unit Rotor. Renew. Energy 2022, 187, 887–895. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Liu, X.; Presas, A.; Deng, L.; Zhao, W.; Xia, M.; Wang, Z. Numerical Theory and Method on the Modal Behavior of a Pump-Turbine Rotor System Considering Gyro-Effect and Added Mass Effect. J. Energy Storage 2024, 85, 111064. [Google Scholar] [CrossRef]
- Cao, J.; Luo, Y.; Shi, Y.; Liu, X.; Xu, D.; Wang, Y.; Zhai, L.; Wang, Z. A Review of Hydro-Turbine Unit Rotor System Dynamic Behavior: Multi-Field Coupling of a Three-Dimensional Model. Phys. Fluids 2024, 36, 121304. [Google Scholar] [CrossRef]
- Zhang, Y. Rotor Dynamics; Tsinghua University Press: Beijing, China, 1987. [Google Scholar]
- Gamarra, J. Effect of Component Interference Fit and Fluid Density on the Lateral and Torsional Natural Frequencies of Turbomachinery Rotor Systems. In Proceedings of the Twenty-Ninth Pump Symposium, Houston, TX, USA, 30 September–3 October 2013. [Google Scholar] [CrossRef]


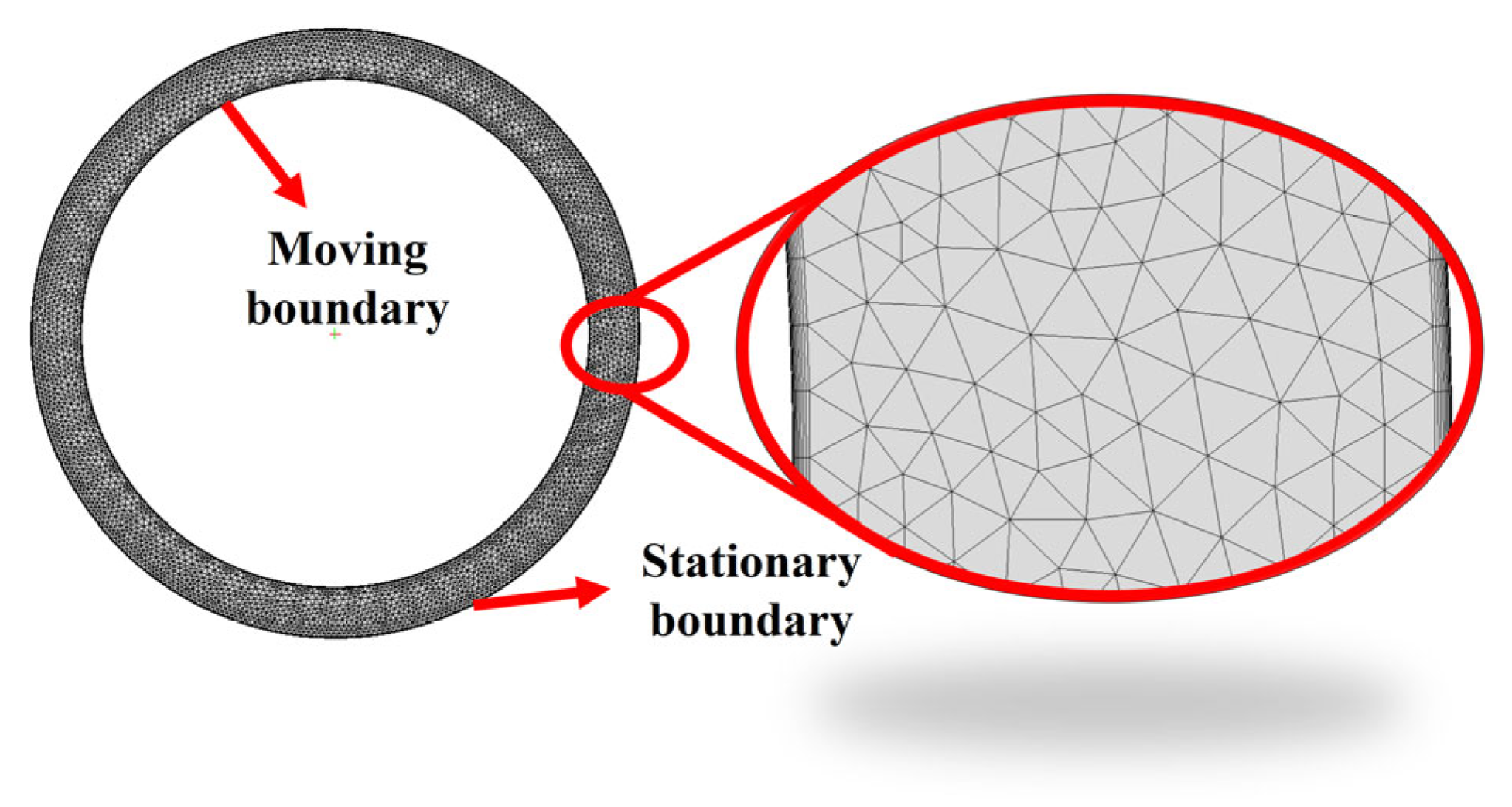





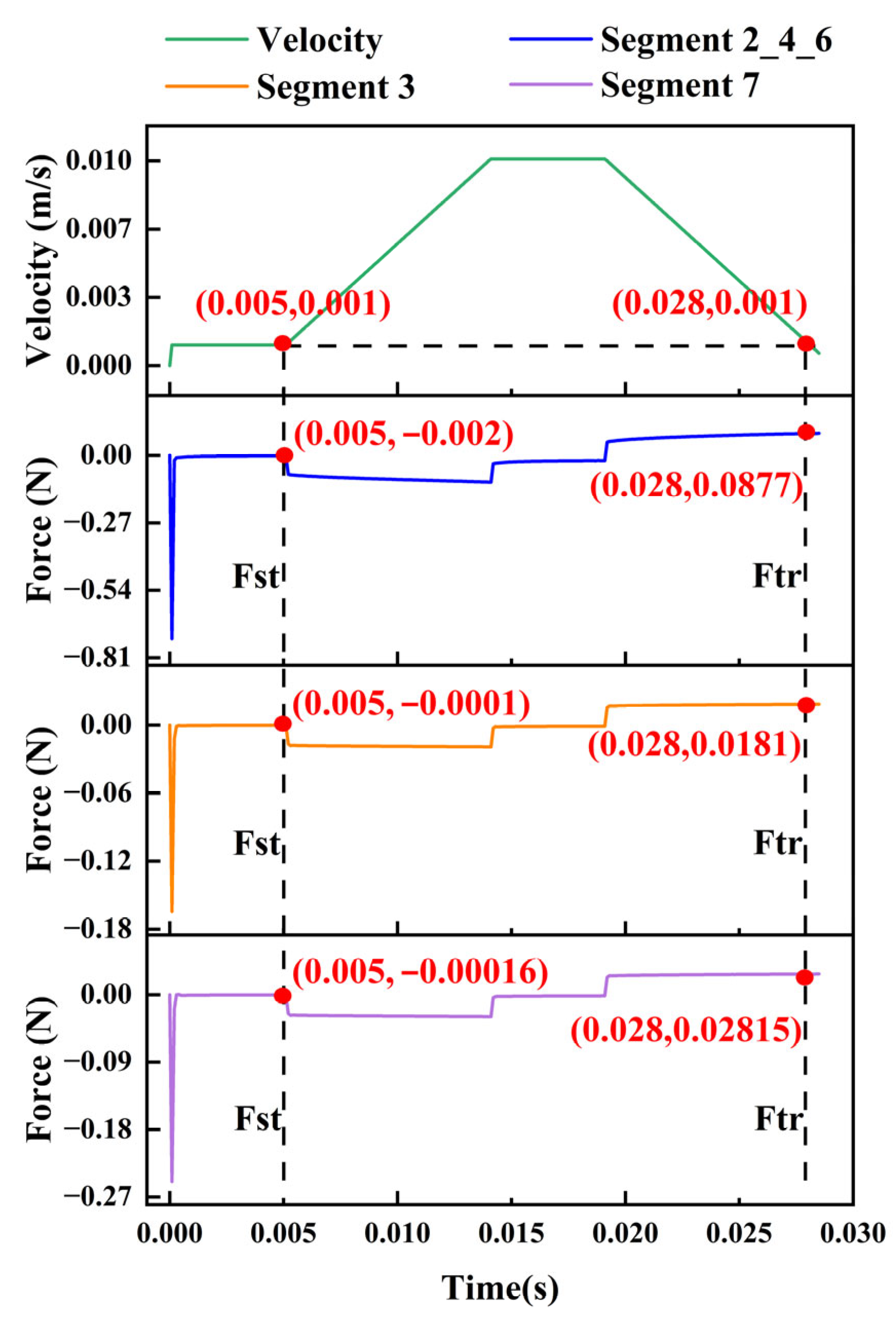
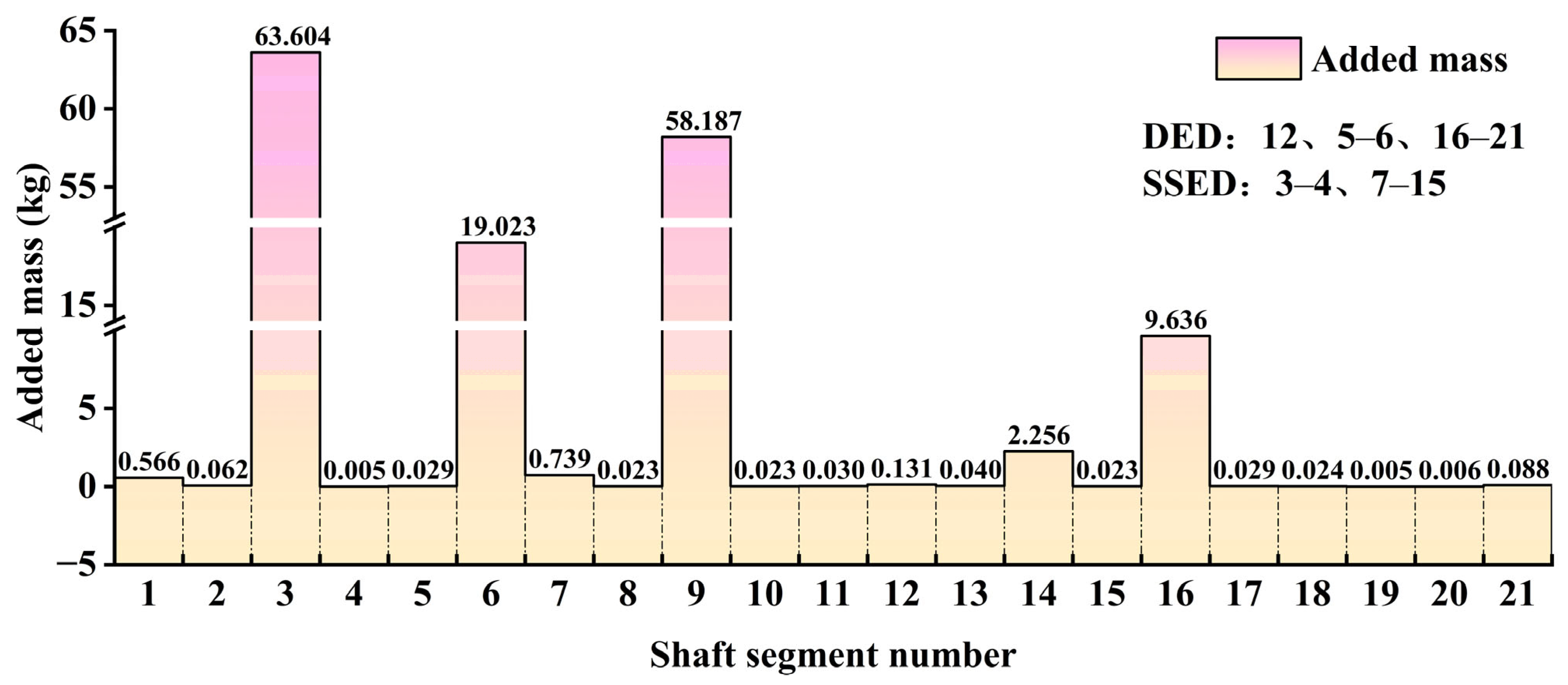


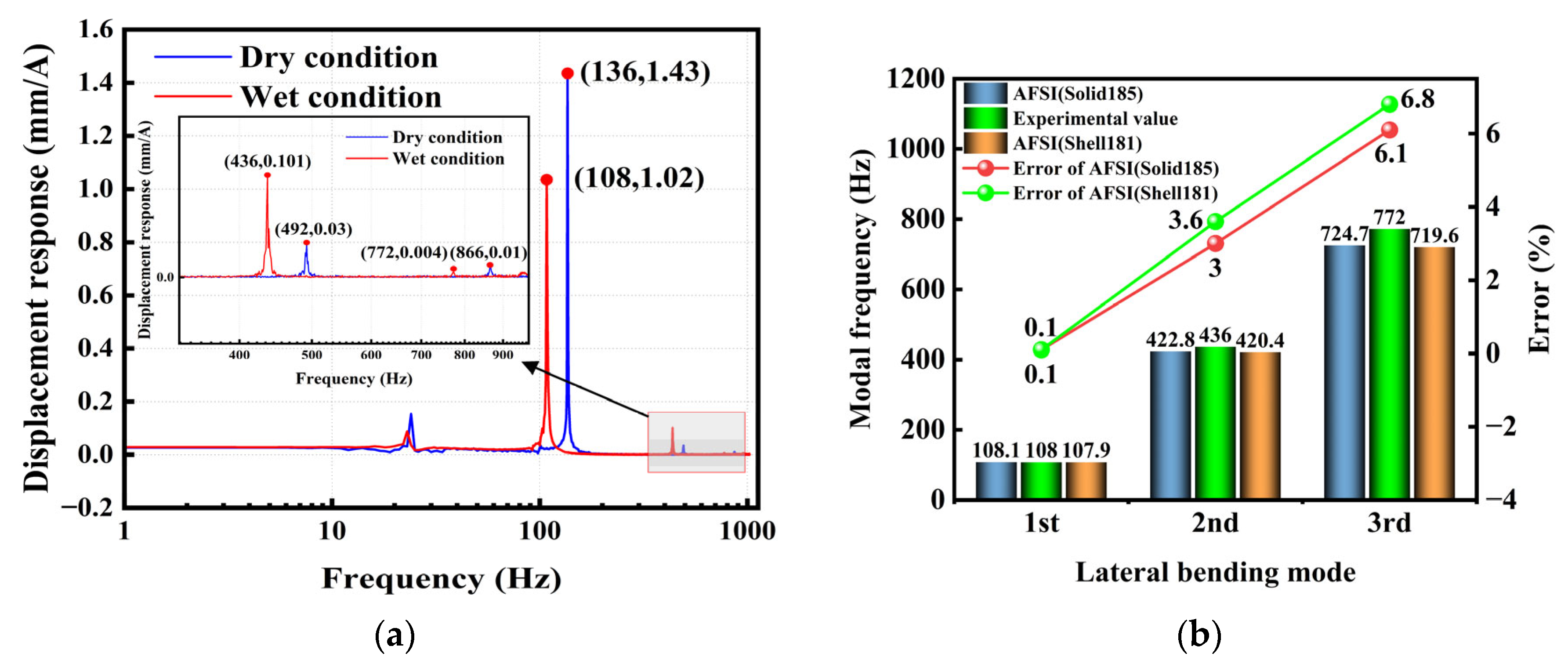
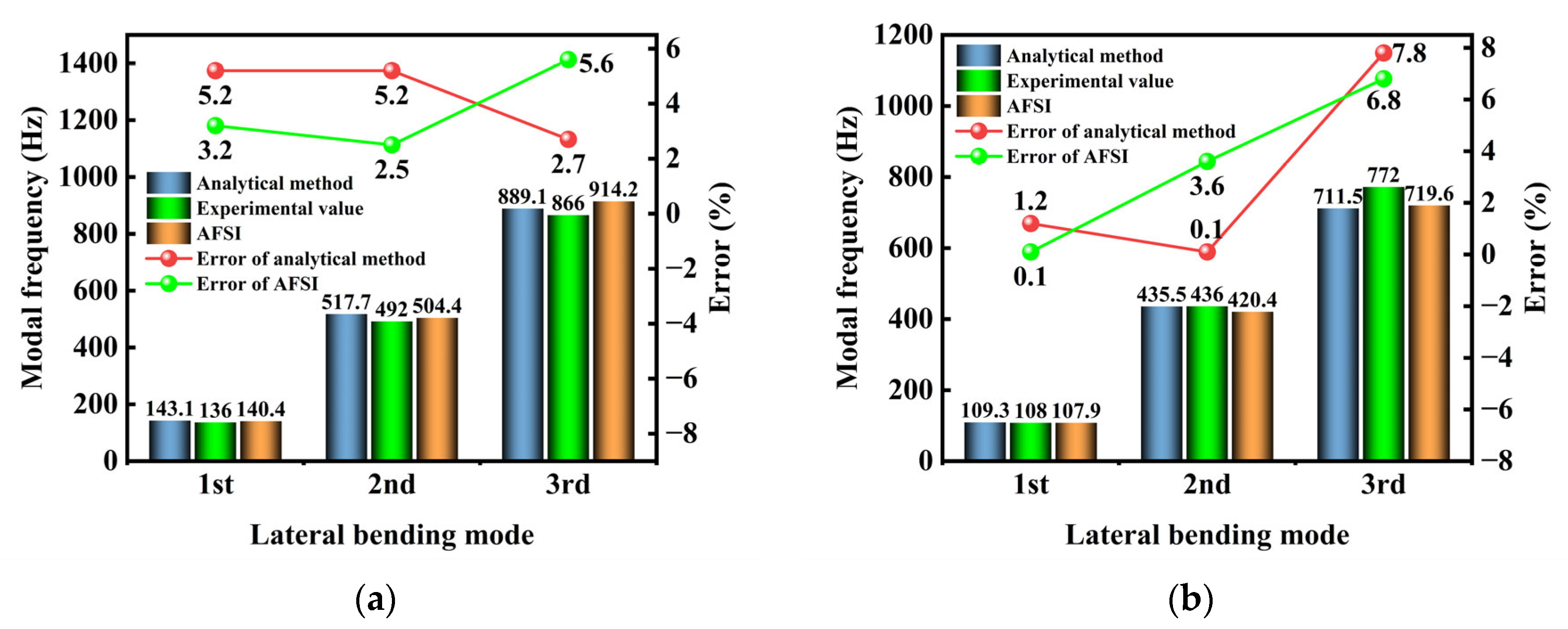
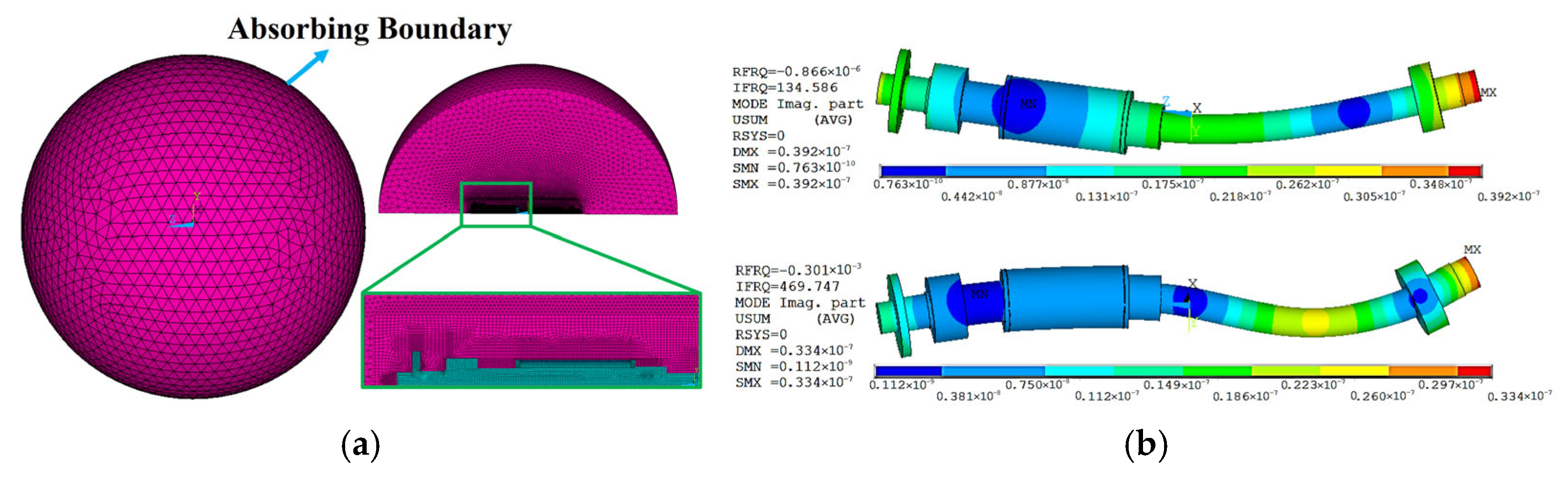
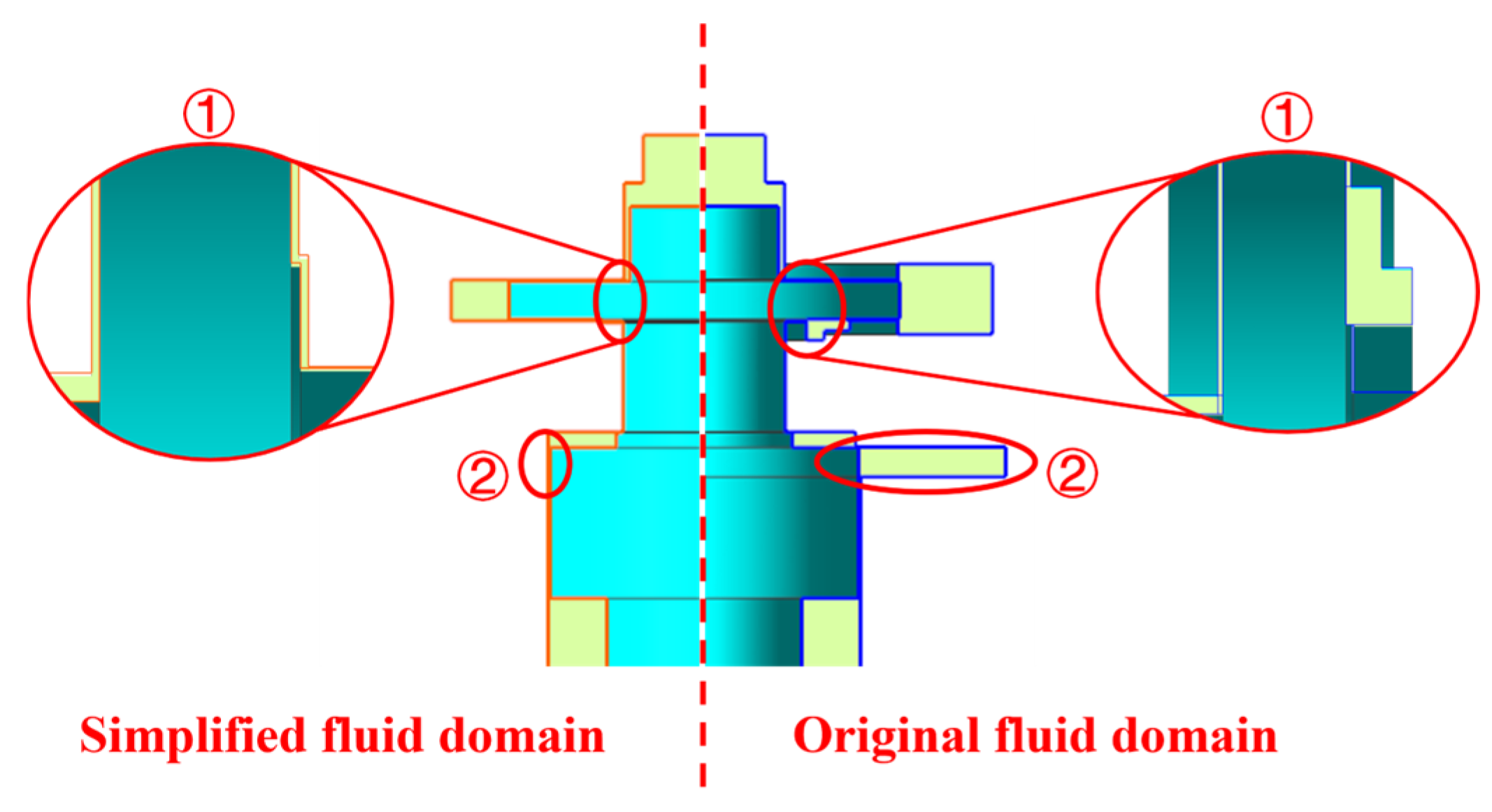
| Modal Shapes | Modal Frequencies (Hz) | Deviation (%) | |
|---|---|---|---|
| AFSI Method | Analytical Method | ||
| 1st bending mode | 143.5 | 140.9 | 1.79 |
| 2nd bending mode | 395.1 | 388.1 | 1.77 |
| 3rd bending mode | 773.5 | 760.1 | 1.74 |
| Type | Inner Diameter d (mm) | Length L (mm) | Aspect Ratio L/d | Fluid Clearance (mm) |
|---|---|---|---|---|
| Segment 1 | 20 | 168 | 8.4 | 21 |
| Segment 2_4_6 | 60 | 14 | 0.233 | 1 |
| Segment 3 | 20 | 61 | 3.05 | 21 |
| Segment 5 | 20 | 141 | 7.05 | 21 |
| Segment 7 | 20 | 88 | 4.4 | 21 |
| Modal Shapes | Modal Frequencies (Hz) | ||
|---|---|---|---|
| Dry Mode | Wet Mode (Confined Domain) | Wet Mode (Infinite Domain) | |
| 1st bending mode | 140.4 | 107.9 | 134.6 |
| 2nd bending mode | 504.4 | 420.4 | 469.7 |
| 3rd bending mode | 914.2 | 719.6 | / |
| Type | Fluid Volume Within the Impeller Cavity (m3) | Swept Volume of the Impeller (m3) | Total Added Mass |
|---|---|---|---|
| Stage 1 Impeller | 4.0123 × 10−4 | 5.5083 × 10−4 | 0.95206 |
| Stage 2 Impeller | 4.0383 × 10−4 | 5.5083 × 10−4 | 0.95466 |
| Stage 3 Impeller | 4.0019 × 10−4 | 5.5083 × 10−4 | 0.95102 |
| Stage 4 Impeller | 4.0138 × 10−4 | 5.5083 × 10−4 | 0.95221 |
| Stage 5 Impeller | 4.0029 × 10−4 | 5.5083 × 10−4 | 0.95112 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, S.; Wei, Y.; Cheng, G.; Liu, Q.; Wu, X. Mechanism and Regularity of Wet Modes in a Highly Integrated Marine Magnetic Levitation Pump Rotor Under Confined Water Conditions. J. Mar. Sci. Eng. 2025, 13, 2400. https://doi.org/10.3390/jmse13122400
Fang S, Wei Y, Cheng G, Liu Q, Wu X. Mechanism and Regularity of Wet Modes in a Highly Integrated Marine Magnetic Levitation Pump Rotor Under Confined Water Conditions. Journal of Marine Science and Engineering. 2025; 13(12):2400. https://doi.org/10.3390/jmse13122400
Chicago/Turabian StyleFang, Shiyu, Yingsan Wei, Gong Cheng, Qi Liu, and Xingyu Wu. 2025. "Mechanism and Regularity of Wet Modes in a Highly Integrated Marine Magnetic Levitation Pump Rotor Under Confined Water Conditions" Journal of Marine Science and Engineering 13, no. 12: 2400. https://doi.org/10.3390/jmse13122400
APA StyleFang, S., Wei, Y., Cheng, G., Liu, Q., & Wu, X. (2025). Mechanism and Regularity of Wet Modes in a Highly Integrated Marine Magnetic Levitation Pump Rotor Under Confined Water Conditions. Journal of Marine Science and Engineering, 13(12), 2400. https://doi.org/10.3390/jmse13122400






