Robust Daytime In Situ Target Strength Estimation of Pacific Hake (Merluccius productus) over a Wide Size Range
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
2.2. Data Analysis
- Fish tracks were selected throughout the depth range of aggregations but primarily from the outskirts of fish aggregations away from regions of highest densities (generally the center of aggregations) to minimize potential biases from multiple targets.
- Each fish track had to contain at least five contiguous echoes.
- Following track selection, only targets that were within 2° of the acoustic beam axis were retained for further analyses.
- Sample TS values greater than −30 dB were excluded to eliminate larger, non-hake targets or potential multiple targets.
| Single-Target Detection | |
|---|---|
| General Parameter | Parameter Value |
| TS threshold (dB) | −60 |
| Pulse length determination level (dB) | 6.0 |
| Minimum normalized pulse length | 0.2 |
| Maximum normalized pulse length | 1.8 |
| Beam compensation | |
| Beam compensation model | Simrad LOBE |
| Maximum beam compensation (dB) | 12.0 |
| Exclusion | |
| Maximum standard deviation of | |
| Minor-axis angles (deg) | 2.0 |
| Major-axis angles (deg) | 2.0 |
| Direction on a 3D Orthogonal Frame | Major Axis | Minor Axis | Depth |
|---|---|---|---|
| A | 0.7 | 0.7 | 0.7 |
| B | 0.5 | 0.5 | 0.5 |
| Exclusion distance (m) | 4.0 | 4.0 | 0.4 |
| Weights | 30 | 30 | 40 |
| Minimum number of single targets | 3 | ||
| Minimum number of pings | 3 | ||
| Maximum gap (pings) | 1 | ||
2.3. Estimation of
2.4. Statistical Analysis
- Resampling: All TS data were randomly resampled with non-replacement, using 95%, 90%, and down to 5% of the original data, with 1000 realizations for each percentage bracket. This addresses the sensitivity of the data to marginally high or low TS samples (or specific to trawl hauls) by assessing significant divergence in slope estimates as the TS sample size is gradually reduced down to a small fraction of all available data. This resampling approach also helps in identifying potential bias due to outliers, or disproportionate weight to sample values that are at the tail end of the distribution (e.g., hauls with the smallest and largest mean fork lengths).
- Jackknife: The jackknife cross-validation technique, a leave-one-out resampling method with replacement, was used for bias and variance estimation [28].
3. Results and Discussion
3.1. Target Strength (TS) Data Processing and Acceptance
3.2. TS Distribution and Depth Analysis
3.3. Spatial Variability and Fork Length Association
3.4. TS-Length Regression
3.5. Statistical Robustness of
- Partial sampling: For the partial sampling, we resampled the whole data population with 95% down to 5% in 5% increments, and at each percentage value, we performed the resampling with replacement 1000 times or realizations. The results are tabulated in Table 4, and their graphic representation is shown in Figure 9. All distributions from the resampling can be well described by Gaussian or normal distributions. A representative example at 90% resampling is illustrated in Figure 10, where a Gaussian Probability Density Function (PDF) with a mean of −67.9 dB and standard deviation of 0.03 dB is superimposed onto the plot of the raw resampled values. Note that even with a substantially low number of selected TS samples at 5% of the original data, the estimated mean value of the in situ TS was only 0.003 dB lower than −67.9 dB.
- Bootstrapping: Bootstrapping yielded a mean of −67.9 dB with a 95% confidence interval of [−68.09, −67.72]
- Jackknife analysis also resulted in a mean of −67.9 dB with a standard deviation of 0.002 dB.
3.6. Comparison with Previous Studies
- Data Collection Conditions: Previous studies on Pacific hake used TS data collected at night, while all of the data presented in this paper were collected during the daytime, i.e., consistent with the hake survey time from sunrise to sunset [38]. Hake TS measurements during daylight are more representative for biomass estimation as hake aggregate at depth during the day, but tend to scatter at night when there are fewer visual cues. As hake scatter and spread out through the water column at night, they could present increased tilt angles, resulting in reduced TS values.
- Length Range and Regression Consistency: Henderson and Horne’s ex situ TS data spanned a narrow fork length range (44–53 cm), with TS values spread over an 8 dB range [16], potentially reducing regression reliability and robustness.
- Backscatter Model Discrepancies: The Kirchhoff Ray-Mode (KRM) [30] backscatter model used by Henderson and Horne, with X-ray images of fish bodies and the swimbladders of live fish captured at sea, showed predictions 4–6 dB higher than their ex situ TS measurements [16], indicating inconsistencies between model predictions and the ex situ measurements, but consistent with the findings from this study. It has been shown that when the fish body and swimbladder morphology are known, the KRM model is appropriate and suitable for single fish [39].
3.7. Limitations of the Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Year | Haul Number | Latitude (Deg North) | Longitude (Deg West) | Mean Fork Length (cm) | Standard Deviation of Fork Length (cm) | CV (%) | # of Length Samples | Total Catch (kg) | % of Hake by Weight |
|---|---|---|---|---|---|---|---|---|---|
| Shimada | |||||||||
| 2009 | 8 | 37.0401 | 122.6764 | 40 | 3.76 | 9.4 | 324 | 321 | 95 |
| 2009 | 22 | 39.0280 | 123.9685 | 40 | 2.58 | 6.5 | 347 | 1426 | 100 |
| 2009 | 39 | 42.7018 | 124.7260 | 38 | 2.34 | 6.2 | 437 | 4590 | 100 |
| 2009 | 56 | 44.2032 | 124.9930 | 42 | 2.12 | 5.0 | 301 | 1100 | 99 |
| 2009 | 57 | 44.3706 | 124.8315 | 41 | 2.5 | 6.1 | 288 | 446 | 100 |
| 2009 | 62 | 44.8783 | 124.4680 | 19 | 1.64 | 8.6 | 336 | 1749 | 100 |
| 2009 | 64 | 44.8796 | 124.8209 | 43 | 2.52 | 5.9 | 248 | 128 | 99 |
| 2009 | 66 | 45.3749 | 124.4020 | 41 | 2.48 | 6.0 | 339 | 268 | 100 |
| 2011 | 2 | 35.3790 | 121.0993 | 22 | 1.25 | 5.7 | 242 | 82 | 99 |
| 2011 | 4 | 35.7137 | 121.4605 | 23 | 1.13 | 4.9 | 280 | 941 | 100 |
| 2011 | 9 | 37.3658 | 122.9050 | 24 | 1.88 | 7.8 | 208 | 18 | 100 |
| 2011 | 18 | 39.3728 | 123.9755 | 35 | 2.00 | 5.7 | 276 | 116 | 100 |
| 2011 | 27 | 44.3747 | 124.8392 | 39 | 2.96 | 7.6 | 307 | 216 | 99 |
| 2011 | 40 | 46.8773 | 124.9192 | 37 | 1.83 | 5.0 | 264 | 259 | 100 |
| 2011 | 44 | 47.3707 | 124.8633 | 38 | 1.93 | 5.1 | 325 | 140 | 100 |
| 2013 | 5 | 35.4248 | 121.3085 | 35 | 1.00 | 2.9 | 118 | 33 | 99 |
| 2013 | 10 | 35.9212 | 121.5310 | 26 | 1.42 | 5.5 | 317 | 463 | 100 |
| 2013 | 13 | 36.5982 | 122.6653 | 37 | 1.56 | 4.2 | 308 | 181 | 100 |
| 2013 | 16 | 37.2632 | 123.0873 | 37 | 1.72 | 4.7 | 536 | 177 | 99 |
| 2013 | 18 | 37.4207 | 122.9600 | 37 | 1.54 | 4.2 | 333 | 495 | 100 |
| 2013 | 33 | 40.5868 | 124.6773 | 38 | 2.24 | 5.9 | 556 | 198 | 98 |
| 2013 | 38 | 41.5960 | 124.5763 | 37 | 1.56 | 4.2 | 414 | 369 | 100 |
| 2013 | 42 | 43.0928 | 124.8732 | 37 | 1.94 | 5.2 | 397 | 259 | 98 |
| 2013 | 45 | 43.9313 | 124.9667 | 38 | 2.15 | 5.7 | 345 | 446 | 100 |
| 2013 | 48 | 44.2608 | 124.9428 | 39 | 2.69 | 6.9 | 230 | 86 | 100 |
| 2013 | 56 | 46.2453 | 124.2052 | 40 | 2.97 | 7.4 | 353 | 318 | 97 |
| 2013 | 76 | 50.0928 | 128.0172 | 51 | 3.62 | 7.1 | 537 | 522 | 89 |
| 2014 | 15 | 43.8840 | 124.7910 | 43 | 3.16 | 7.3 | 237 | 642 | 100 |
| 2014 | 16 | 43.8858 | 124.7343 | 44 | 3.35 | 7.6 | 200 | 192 | 100 |
| 2015 | 9 | 36.4460 | 122.1363 | 23 | 2.22 | 9.7 | 373 | 49 | 98 |
| 2015 | 13 | 37.4495 | 122.9712 | 22 | 1.46 | 6.6 | 285 | 431 | 88 |
| 2015 | 15 | 38.1177 | 123.6143 | 24 | 1.06 | 4.4 | 375 | 69 | 94 |
| 2015 | 21 | 39.7728 | 124.0748 | 35 | 3.40 | 9.7 | 418 | 166 | 100 |
| 2015 | 39 | 43.4477 | 124.7072 | 24 | 1.36 | 5.7 | 323 | 1316 | 100 |
| 2015 | 42 | 43.7828 | 124.9052 | 42 | 1.56 | 3.7 | 62 | 34 | 96 |
| 2015 | 46 | 44.7827 | 124.6060 | 21 | 1.23 | 5.9 | 481 | 290 | 100 |
| 2015 | 60 | 47.3663 | 124.8485 | 23 | 2.02 | 8.8 | 237 | 314 | 99 |
| 2015 | 73 | 49.1188 | 126.8678 | 44 | 2.37 | 5.4 | 288 | 156 | 100 |
| 2016 Winter | 2 | 42.1750 | 124.6632 | 29 | 2.74 | 9.4 | 235 | 35 | 92 |
| 2016 Winter | 4 | 41.3485 | 124.4978 | 27 | 1.58 | 5.9 | 474 | 440 | 93 |
| 2016 Winter | 7 | 41.4722 | 125.0988 | 44 | 2.72 | 6.2 | 195 | 234 | 96 |
| 2016 Winter | 8 | 40.4218 | 125.0995 | 44 | 3.04 | 6.9 | 221 | 460 | 100 |
| 2016 Winter | 9 | 39.8428 | 125.0960 | 44 | 3.02 | 6.9 | 123 | 61 | 97 |
| 2016 Winter | 10 | 39.1192 | 125.2397 | 43 | 2.55 | 5.9 | 256 | 141 | 85 |
| 2016 Winter | 11 | 39.1202 | 125.2287 | 43 | 2.59 | 6.0 | 256 | 118 | 99 |
| 2016 Winter | 13 | 37.9578 | 123.5278 | 28 | 1.67 | 6.0 | 210 | 125 | 96 |
| 2016 Winter | 18 | 37.2152 | 124.0930 | 42 | 3.01 | 7.2 | 211 | 237 | 100 |
| 2016 Winter | 21 | 35.9870 | 123.8852 | 43 | 2.43 | 5.7 | 235 | 139 | 92 |
| 2016 Winter | 29 | 37.1723 | 124.0630 | 42 | 2.99 | 7.1 | 231 | 332 | 98 |
| 2016 Winter | 30 | 39.0515 | 125.1992 | 42 | 3.00 | 7.1 | 200 | 225 | 99 |
| 2016 Winter | 32 | 42.5568 | 125.8293 | 44 | 2.75 | 6.3 | 287 | 143 | 97 |
| 2017 Summer | 1 | 34.9915 | 121.0798 | 26 | 2.14 | 8.2 | 331 | 37 | 98 |
| 2017 Summer | 4 | 36.4908 | 122.1897 | 28 | 2.15 | 7.7 | 415 | 1163 | 98 |
| 2017 Summer | 10 | 38.3297 | 123.6627 | 37 | 2.39 | 6.5 | 395 | 531 | 98 |
| 2017 Summer | 14 | 39.1445 | 124.0088 | 38 | 2.30 | 6.1 | 403 | 351 | 95 |
| 2017 Summer | 16 | 40.8132 | 124.5613 | 40 | 2.90 | 7.3 | 419 | 316 | 91 |
| 2017 Summer | 19 | 41.6540 | 124.4612 | 27 | 1.91 | 7.1 | 250 | 90 | 99 |
| 2017 Summer | 20 | 41.8235 | 124.4860 | 28 | 1.87 | 6.7 | 242 | 586 | 100 |
| 2017 Summer | 25 | 42.9898 | 125.1188 | 41 | 2.92 | 7.1 | 226 | 119 | 95 |
| 2017 Summer | 31 | 44.1580 | 124.9715 | 39 | 2.76 | 7.1 | 396 | 202 | 98 |
| 2017 Winter | 3 | 42.1720 | 124.5940 | 19 | 1.28 | 6.7 | 156 | 51 | 96 |
| 2017 Winter | 4 | 37.2585 | 123.3062 | 35 | 2.22 | 6.3 | 201 | 123 | 93 |
| 2017 Winter | 6 | 35.4527 | 123.5482 | 43 | 3.21 | 7.5 | 191 | 99 | 100 |
| 2017 Winter | 7 | 34.4397 | 120.7680 | 21 | 1.07 | 5.1 | 401 | 100 | 100 |
| 2017 Winter | 12 | 38.9510 | 124.0153 | 34 | 1.67 | 4.9 | 301 | 1080 | 100 |
| 2018 | 18 | 44.5778 | 124.6725 | 41 | 2.81 | 6.9 | 245 | 378 | 100 |
| 2018 | 19 | 44.5685 | 124.6752 | 43 | 2.67 | 6.2 | 236 | 156 | 97 |
| 2019 | 7 | 35.3937 | 121.1582 | 22 | 1.26 | 5.7 | 212 | 52 | 100 |
| 2019 | 8 | 35.5583 | 121.4342 | 23 | 1.69 | 7.3 | 212 | 104 | 99 |
| 2019 | 12 | 36.0648 | 121.7403 | 24 | 2.44 | 10.2 | 220 | 87 | 97 |
| 2019 | 19 | 37.5640 | 123.0483 | 32 | 2.32 | 7.3 | 356 | 178 | 100 |
| 2019 | 22 | 38.0565 | 123.5303 | 42 | 3.70 | 8.8 | 349 | 525 | 99 |
| 2019 | 24 | 38.5600 | 123.7883 | 38 | 3.01 | 7.9 | 322 | 121 | 94 |
| 2019 | 25 | 38.7320 | 123.8278 | 39 | 3.17 | 8.1 | 334 | 141 | 100 |
| 2019 | 29 | 39.4012 | 123.9842 | 40 | 2.25 | 5.6 | 326 | 182 | 92 |
| 2019 | 30 | 39.7312 | 124.2135 | 41 | 2.22 | 5.4 | 441 | 210 | 98 |
| 2019 | 33 | 40.3948 | 124.7948 | 41 | 2.07 | 5.0 | 403 | 413 | 100 |
| 2019 | 35 | 40.5643 | 124.7252 | 41 | 2.68 | 6.5 | 438 | 612 | 99 |
| 2019 | 36 | 40.7295 | 124.8352 | 41 | 2.57 | 6.3 | 468 | 648 | 100 |
| 2019 | 38 | 41.0465 | 124.4185 | 42 | 2.83 | 6.7 | 373 | 393 | 100 |
| 2019 | 45 | 42.7263 | 124.7283 | 42 | 3.23 | 7.7 | 381 | 1567 | 100 |
| 2019 | 46 | 42.8943 | 124.9795 | 42 | 2.99 | 7.1 | 366 | 576 | 100 |
| 2019 | 47 | 43.0708 | 125.0855 | 42 | 2.54 | 6.0 | 235 | 115 | 97 |
| 2019 | 48 | 43.2257 | 124.7650 | 42 | 2.47 | 5.9 | 343 | 313 | 100 |
| 2019 | 50 | 43.7210 | 125.0668 | 43 | 2.44 | 5.7 | 215 | 111 | 100 |
| 2019 | 54 | 44.0552 | 124.9563 | 41 | 2.73 | 6.7 | 381 | 701 | 99 |
| 2019 | 56 | 45.0540 | 124.7597 | 44 | 1.97 | 4.5 | 83 | 46 | 97 |
| 2019 | 57 | 45.2223 | 124.6620 | 43 | 2.02 | 4.7 | 276 | 148 | 97 |
| 2019 | 59 | 45.5570 | 124.5612 | 45 | 2.12 | 4.7 | 184 | 107 | 97 |
| DAISY | |||||||||
| 9/7/2014 | 36 | 41.6582 | 124.5003 | 29 | 1.25 | 4.3 | 101 | 259 | 80 |
| 9/12/2014 | 41 | 48.9242 | 126.5505 | 48 | 3.41 | 7.1 | 174 | 161 | 82 |
| 3/23/2016 | 30 | 50.0170 | 123.9078 | 33 | 4.70 | 14.2 | 150 | 29 | 99 |
| Mean | 41.0717 | 124.1269 | 36.2 | 2.34 | 6.5 | 299 | 379 | 98 |
References
- Longo, G.C.; Head, M.; Parker-Stetter, S.; Taylor, I.; Tuttle, V.; Billings, A.; Gauthier, S.; McClure, M.; Nichols, K.M. Population genomics of coastal Pacific Hake (Merluccius productus). N. Am. J. Fish. Manag. 2024, 44, 222–234. [Google Scholar] [CrossRef]
- Grandin, C.J.; Johnson, K.F.; Edwards, A.M.; Berger, A.M. Status of the Pacific Hake (Whiting) Stock in U.S. and Canadian Waters in 2024; Joint Technical Committee of the U.S. and Canada Pacific Hake/Whiting Agreement: Seattle, WA, USA; National Marine Fisheries Service: Silver Spring, MD, USA; Fisheries and Oceans Canada: Vancouver, BC, Canada, 2024; 246p. [Google Scholar]
- Sherman, K. The Large Marine Ecosystem Concept: Research and Management Strategy for Living Marine Resources. Ecol. Appl. 1991, 1, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Fleischer, G.W.; Cooke, K.D.; Ressler, P.H.; Thomas, R.E.; de Blois, S.K.; Hufnagle, L.C.; Kronlund, A.R.; Holmes, J.A.; Wilson, C.D. The 2003 Integrated Acoustic and Trawl Survey of Pacific Hake, Merluccius Productus, in U.S. and Canadian Waters off the Pacific Coast; U.S. Department of Commerce: Washington, WA, USA, 2005; NOAA Technical Memorandum NMFS-NWFSC-65. [Google Scholar]
- Simmonds, J.; MacLennan, D.N. Fisheries Acoustics: Theory and Practice, 2nd ed.; Blackwell Publishing: London, UK, 2005; ISBN 978-0-632-05994-2. [Google Scholar]
- Koslow, J.A. The role of acoustics in ecosystem-based fishery management. ICES J. Mar. Sci. 2009, 66, 966–973. [Google Scholar] [CrossRef]
- Jech, J.M.; Zydlewski, G.B.; Lebourges-Dhaussy, A.; Stevens, J. Ushering in a new era in fisheries and plankton acoustics. ICES J. Mar. Sci. 2024, 81, 1325–1329. [Google Scholar] [CrossRef]
- Scherbino, M.; Truskanov, M.D. Determination of fish concentration by means of acoustic apparatus. ICES CM 1966, 3, 6. [Google Scholar]
- Medwin, H.; Clay, C.S. Fundamentals of Acoustic Oceanography; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar] [CrossRef]
- Ona, E. (Ed.) Methodology for Target Strength Measurements (With Special Reference to in Situ Techniques for Fish and Mikro-Nekton); ICES Cooperative Research Report No. 235; ICES: Copenhagen, Denmark, 1999; 55p. [Google Scholar]
- Gauthier, S.; Rose, G.A. In situ target strength studies on Atlantic redfish (Sebastes spp.). ICES J. Mar. Sci. 2001, 59, 805–815. [Google Scholar] [CrossRef]
- Peña, H. In situ target-strength measurements of Chilean jack mackerel (Trachurus symmetricus murphyi) collected with a scientific echosounder installed on a fishing vessel. ICES J. Mar. Sci. 1996, 65, 594–604. [Google Scholar] [CrossRef]
- Kloser, R.J.; Ryan, T.E.; Macaulay, G.J.; and Lewis, M.E. In situ measurements of target strength with optical and model verification: A case study for blue grenadier, Macruronus novaezelandiae. ICES J. Mar. Sci. 2008, 68, 1986–1995. [Google Scholar] [CrossRef]
- Madirolas, A.; Membiela, F.A.; Gonzalez, J.D.; Cabreira, A.G.; dell’Erba, M.; Prario, I.S.; Blanc, S. Acoustic target strength (TS) of argentine anchovy (Engraulis anchoita): The nighttime scattering layer. ICES J. Mar. Sci. 2017, 74, 1408–1420. [Google Scholar] [CrossRef]
- Kang, D.; Hwang, D.J. Ex situ target strength of rockfish (Sebastes schlegeli) and red sea bream (Pagrus major) in the Northwest Pacific. ICES J. Mar. Sci. 2003, 60, 538–543. [Google Scholar] [CrossRef]
- Henderson, M.J.; Horne, J.K. Comparison of in situ, ex situ, and backscatter model estimates of Pacific hake (Merluccius productus) target strength. Can. J. Fish. Aquat. Sci. 2007, 64, 1781–1794. [Google Scholar] [CrossRef]
- Boswell, K.M.; Wislon, C.A. Side-aspect target-strength measurements of bay anchovy (Anchoa mitchilli) and Gulf menhaden (Brevoortia patronus) derived from ex situ experiments. ICES J. Mar. Sci. 2008, 65, 1012–1020. [Google Scholar] [CrossRef]
- Love, R.H. Resonant acoustic scattering by swimbladder-bearing fish. J. Acoust. Soc. Am. 1978, 64, 571–580. [Google Scholar] [CrossRef]
- Foote, K.G. Rather-high-frequency sound scattering by swimbladdered fish. J. Acoust. Soc. Am. 1985, 78, 688–700. [Google Scholar] [CrossRef]
- Jech, J.M.; Horne, J.K.; Chu, D.; Demer, D.A.; Francis, D.T.I.; Gorska, N.; Jones, B.; Lavery, A.C.; Stanton, T.K.; Macaulay, G.J.; et al. Comparisons among ten models of acoustic backscattering used in aquatic ecosystem research. J. Acoust. Soc. Am. 2015, 138, 3742–3764. [Google Scholar] [CrossRef]
- Chu, D. Development and Application of Advanced Science and Technology in Fisheries Acoustics. J. Marine Acoust. Soc. Jpn. 2024, 51, 117–149. [Google Scholar]
- Traynor, J.J. Target-strength measurements of walleye pollock (Theragra chalcogramma) and Pacific whiting (Merluccius productus). ICES J. Mar. Sci. 1996, 53, 253–258. [Google Scholar] [CrossRef]
- Demer, D.A.; Berger, L.; Bernasconi, M.; Bethke, E.; Boswell, K.; Chu, D.; Domokos, R.; Dunford, A.; Fassler, S.; Gauthier, S.; et al. Calibration of Acoustic Instruments; ICES Cooperative Research Reports No. 326; ICES: Copenhagen, Denmark, 2015; 130p. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple-Target Tracking with Radar Applications; Artech House: Norwood, MA, USA, 1986. [Google Scholar]
- Demer, D.A.; Andersen, L.N.; Bassett, C.; Berger, L.; Chu, D.; Condiotty, J.; Cutter, G.R.; Hutton, B.; Korneliussen, R.; Macaulay, G.; et al. 2016 USA–Norway EK80 Workshop Report: Evaluation of a Wideband Echosounder for Fisheries and Marine Ecosystem Science; ICES Cooperative Research Report No. 336; ICES: Copenhagen, Denmark, 2017; 69p. [Google Scholar] [CrossRef]
- Horowitz, J.L. Bootstrap methods in econometrics. Ann. Rev. Ecol. 2009, 11, 193–224. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman & Hall/CRC: Boca Raton, FL, USA, 1993. [Google Scholar]
- Jones, H.L. Jackknife estimation of functions of stratum mean. Biometrika 1974, 61, 343–348. [Google Scholar] [CrossRef]
- Berenbrick, M. Historical reconstructions of evolving physiological complexity: O2 secretion in the eye and swimbladder of fishes. J. Exp. Biol. 2007, 210, 1641–1652. [Google Scholar] [CrossRef]
- Clay, C.S.; Horne, J.K. Acoustic models of fish: The Atlantic cod (Gadus morhua). J. Acoust. Soc. Am. 1994, 96, 1661–1668. [Google Scholar] [CrossRef]
- Nero, R.W.; Thompson, C.H.; Love, R.H. Low-frequency acoustic measurements of Pacific hake, Merluccius productus, off the west coast of the United States. Fish. Bull. 1998, 96, 329–343. [Google Scholar]
- Lauffenburger, N.; De Robertis, A.; Williams, K. Mining previous acoustic surveys to improve walleye pollock (Gadus chalcogrammus) target strength estimates. ICES J. Mar. Sci. 2023, 80, 1683–1696. [Google Scholar] [CrossRef]
- Morse, P.H.; Ingard, U. Theoretical Acoustics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Stanton, T.K. Sound scattering by cylinders of finite length. I. Fluid cylinders. J. Acoust. Soc. Am. 1988, 83, 55–63. [Google Scholar] [CrossRef]
- Stanton, T.K. Sound scattering by cylinders of finite length. III. Deformed cylinders. J. Acoust. Soc. Am. 1989, 86, 691–705. [Google Scholar] [CrossRef]
- McClatchie, S.; Alsop, J.; and Coombs, R.F. A re-evaluation of relationships between fish size, acoustic frequency and target strength. ICES J. Mar. Sci. 1996, 53, 780–791. [Google Scholar] [CrossRef]
- McClatchie, S.; Macaulay, G.J.; Coombs, R.F. A requiem for the use of 20 log (10) length for acoustic target strength with special reference to deep-sea fishes. ICES J. Mar. Sci. 2003, 60, 419–428. [Google Scholar] [CrossRef]
- Clemons, J.E.; Gauthier, S.; de Blois, S.K.; Billings, A.A.; Phillips, E.M.; Pohl, J.E.; Stanley, C.P.; Thomas, R.E.; Beyer, E.M. The 2023 Joint U.S.—Canada Integrated Ecosystem and Pacific Hake Acoustic Trawl Survey: Cruise Report SH-23-06; U.S. Department of Commerce: Washington, WA, USA, 2024; NOAA Processed Report NMFS-NWFSC-PR-2024-01. [Google Scholar]
- Li, C.; Chu, D.; Horne, J.; Li, H. Comparison of Coherent to Incoherent Kirchhoff-Ray-Mode (KRM) Models in Predicting Backscatter by Swim-Bladder-Bearing Fish. J. Mar. Sci. Eng. 2023, 11, 473. [Google Scholar] [CrossRef]
- Rose, G.A.; Porter, D.R. Target-strength studies on Atlantic cod (Gadus morhua) in Newfoundland waters. ICES J. Mar. Sci. 1996, 53, 259–265. [Google Scholar] [CrossRef]
- Pedersen, G.; Godø, O.R.; Ona, E.; Macaulay, G.J. A revised target strength–length estimate for blue whiting (Micromesistius poutassou): Implications for biomass estimates. ICES J. Mar. Sci. 2011, 68, 2222–2228. [Google Scholar] [CrossRef]
- Dunning, J.; Jansen, T.; Fenwick, A.J.; Fernades, P.G. A new in-situ method to estimate fish target strength reveals high variability in broadband measurements. Fish. Res. 2023, 261, 106611. [Google Scholar] [CrossRef]
- Foote, K.G. Fish target strengths for use in echo integrator surveys. J. Acoust. Soc. Am. 1987, 82, 981–987. [Google Scholar] [CrossRef]
- Sawada, K.; Furusawa, M.; Williamson, N.J. Conditions for the precise measurement of fish target strength in situ. Fish. Sci. 1993, 20, 15–21. [Google Scholar] [CrossRef]
- Gauthier, S.; Rose, G.A. Diagnostic tools for unbiased in situ target strength estimation. Can. J. Fish. Aqua. Sci. 2001, 58, 2149–2155. [Google Scholar] [CrossRef]
- Winger, P.D.; Eayrs, S.; Glass, C.W. Fish Behavior near Bottom Trawls. In Behavior of Marine Fishes; He, P., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
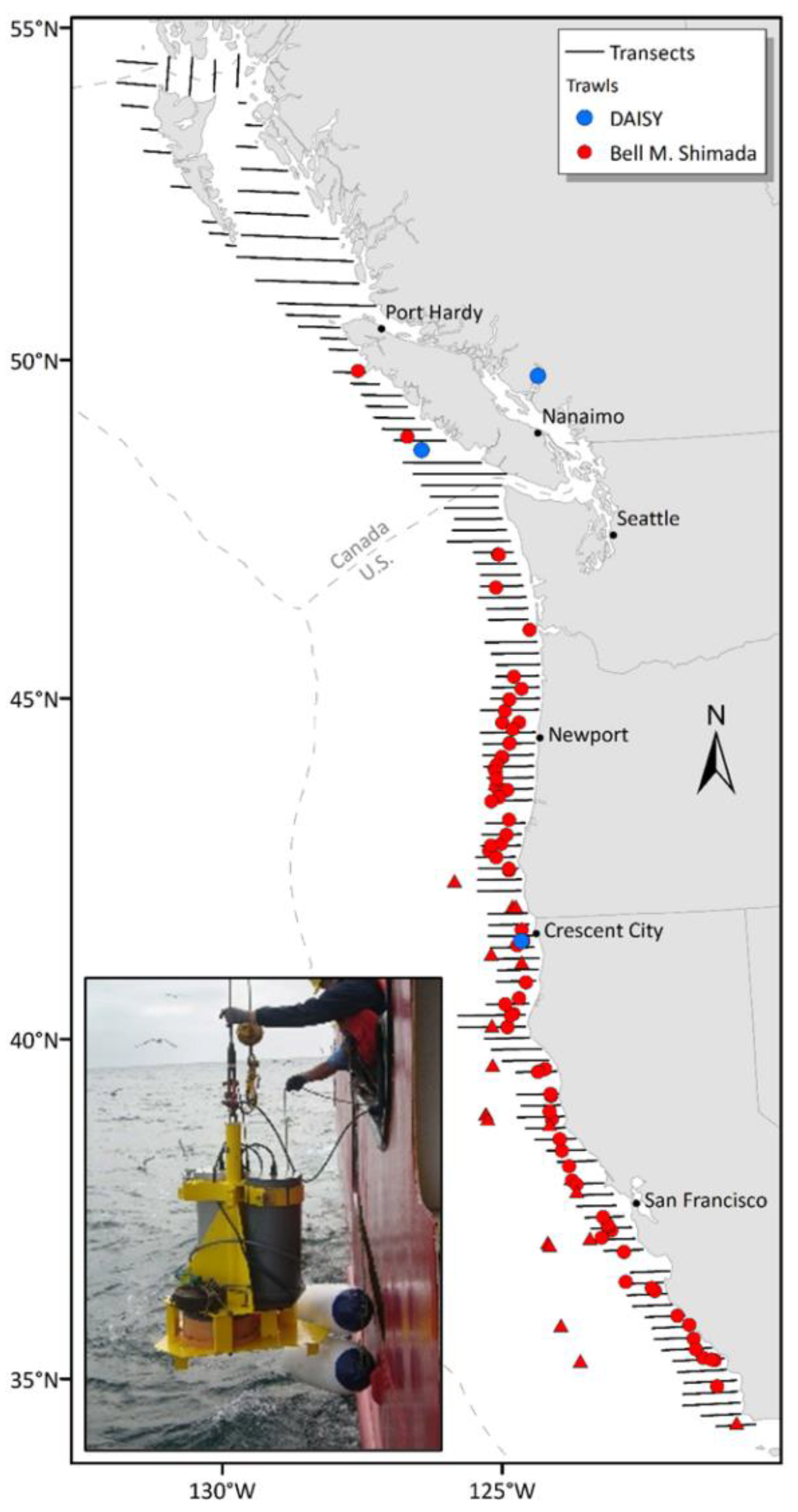

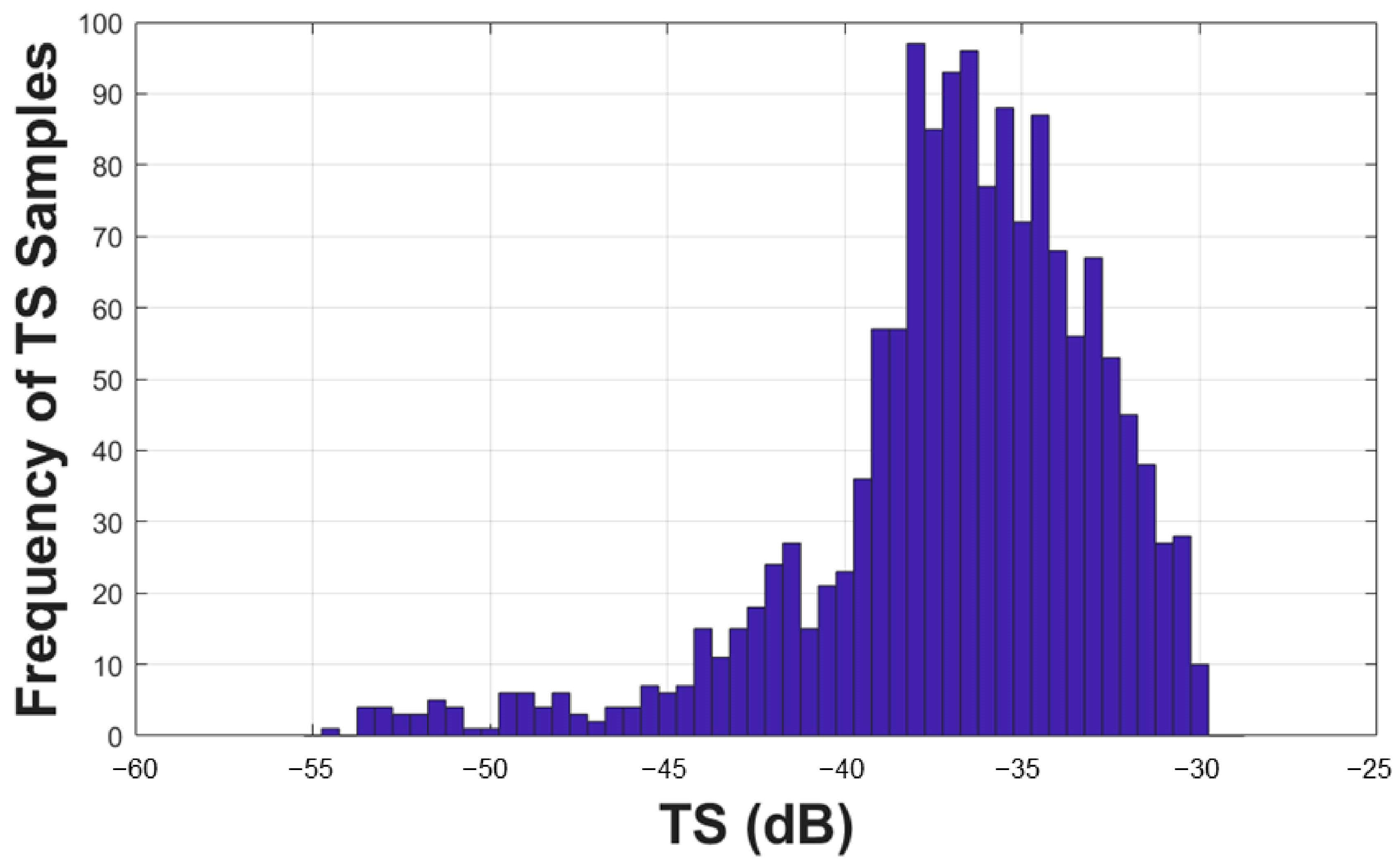



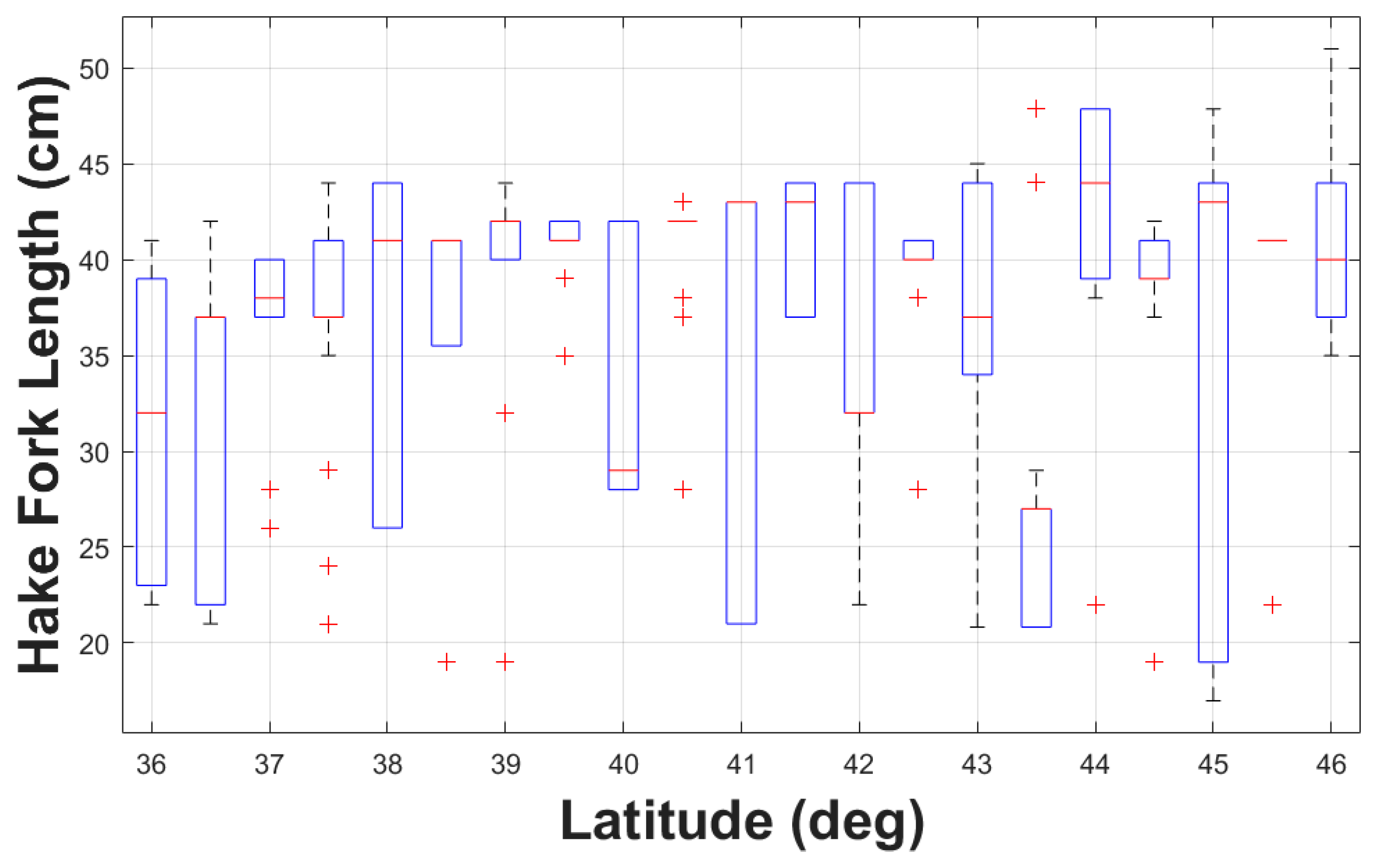
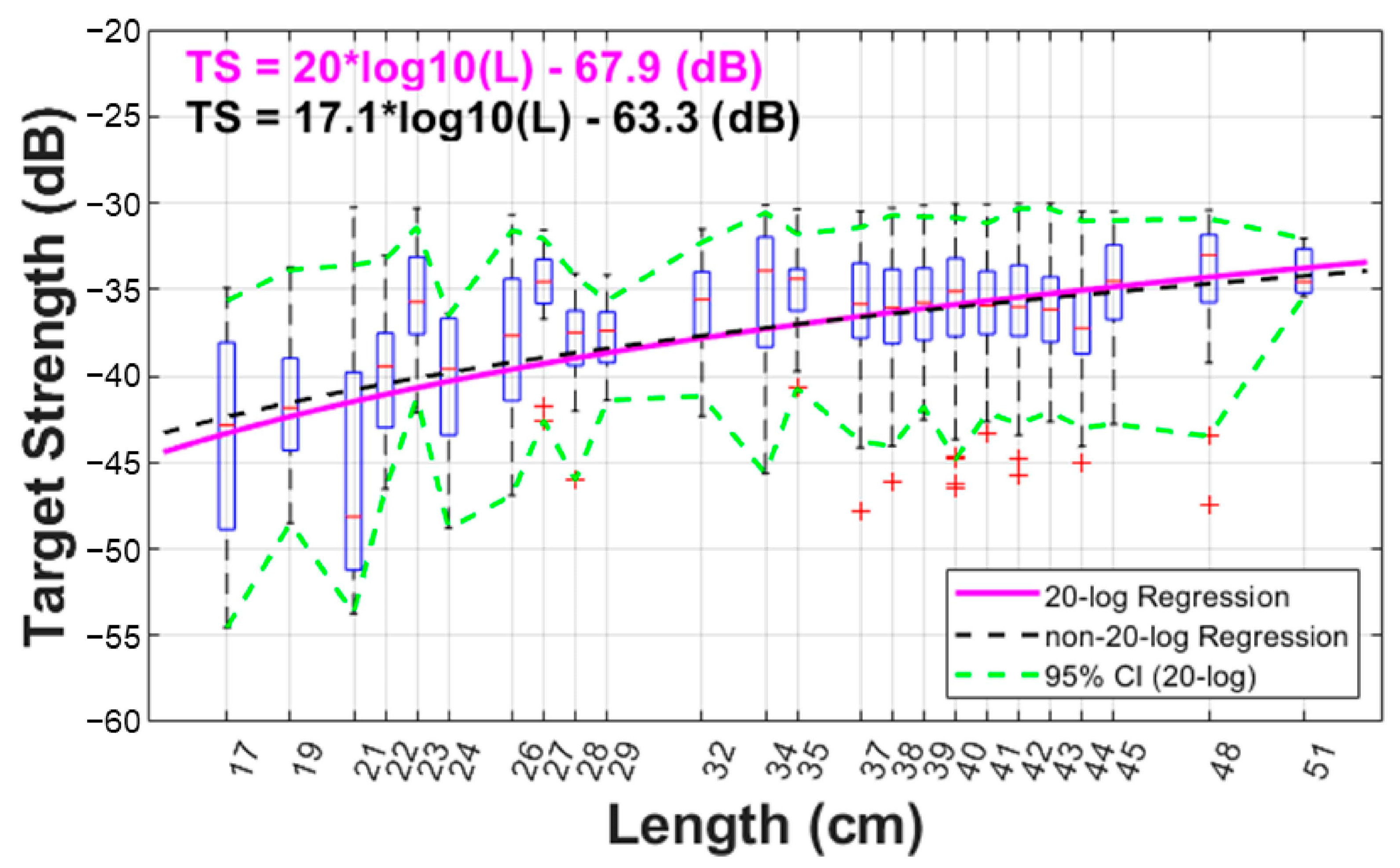


| Dataset | No. of Hauls | TS Samples (Original) | TS Samples (Pulse-Energy Filtered’) |
|---|---|---|---|
| 2009 | 8 | 6891 | 150 |
| 2011 | 7 | 4875 | 98 |
| 2013 | 12 | 14,103 | 241 |
| 2014 | 2 | 1898 | 6 |
| 2015 | 9 | 1915 | 48 |
| 2016 Winter | 13 | 9922 | 218 |
| 2017 Winter | 9 | 4158 | 92 |
| 2017 Summer | 5 | 3365 | 61 |
| 2018 | 2 | 216 | 5 |
| 2019 | 22 | 16,829 | 481 |
| DAISY 7 September 2014 | 1 | 3722 | 40 |
| DAISY 12 September 2014 | 1 | 3788 | 47 |
| DAISY 23 March 2016 | 1 | 5372 | 23 |
| Sum | 92 | 77,054 | 1510 |
| Resample Percentage | Mean (dB) | Standard Deviation (dB) |
|---|---|---|
| 5% | −67.9 | 0.42 |
| 10% | −67.9 | 0.29 |
| 20% | −67.9 | 0.19 |
| 30% | −67.9 | 0.15 |
| 40% | −67.9 | 0.12 |
| 50% | −67.9 | 0.10 |
| 60% | −67.9 | 0.08 |
| 70% | −67.9 | 0.06 |
| 80% | −67.9 | 0.05 |
| 85% | −67.9 | 0.04 |
| 90% | −67.9 | 0.03 |
| 95% | −67.9 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, D.; Gauthier, S.; de Blois, S.; Clemons, J.; Thomas, R. Robust Daytime In Situ Target Strength Estimation of Pacific Hake (Merluccius productus) over a Wide Size Range. J. Mar. Sci. Eng. 2025, 13, 2255. https://doi.org/10.3390/jmse13122255
Chu D, Gauthier S, de Blois S, Clemons J, Thomas R. Robust Daytime In Situ Target Strength Estimation of Pacific Hake (Merluccius productus) over a Wide Size Range. Journal of Marine Science and Engineering. 2025; 13(12):2255. https://doi.org/10.3390/jmse13122255
Chicago/Turabian StyleChu, Dezhang, Stéphane Gauthier, Stephen de Blois, Julia Clemons, and Rebecca Thomas. 2025. "Robust Daytime In Situ Target Strength Estimation of Pacific Hake (Merluccius productus) over a Wide Size Range" Journal of Marine Science and Engineering 13, no. 12: 2255. https://doi.org/10.3390/jmse13122255
APA StyleChu, D., Gauthier, S., de Blois, S., Clemons, J., & Thomas, R. (2025). Robust Daytime In Situ Target Strength Estimation of Pacific Hake (Merluccius productus) over a Wide Size Range. Journal of Marine Science and Engineering, 13(12), 2255. https://doi.org/10.3390/jmse13122255






