Abstract
Simulating wave propagation is crucial for forecasting processes offshore and near the coast. Many operational wave models consider only atmospheric and wave forcing as boundary conditions. However, waves and currents are interdependent, and simulating their interaction is crucial for accurately representing wave propagation. This study examines the influences of the current velocity and water levels on waves on the southern coast of the Iberian Peninsula. These forcing elements were simulated by a 3D hydrodynamic model (MOHID) and included in the Simulating WAves Nearshore (SWAN) model. The standalone SWAN model was calibrated and validated by comparing results of significant wave height, mean wave direction, and peak period with in situ observations. Then, the effects of water levels and current velocities on wave propagation were assessed by forcing the SWAN model with water levels as well as current velocities extracted from different depths: the surface layer and depth-averaged velocities from the surface down to 10 m, 20 m, and the full water column. The results revealed that incorporating the current velocity and water levels from MOHID into the SWAN model reduced the root mean square error (RMSE) between 1.6% and 27.6%. The most accurate results were achieved with model runs that included both the current velocity from the surface layer and water levels. Opposing currents resulted in increases in wave height, whereas following currents resulted in decreases in wave height. This work presents novel results on the effects of hydrodynamics on wave propagation along the southern coast of the Iberian Peninsula, a region of key importance for the blue economy.
1. Introduction
The simulation of wave propagation is strongly determined by a variety of forcing conditions, including wind, waves, bottom friction, bathymetry, sea surface height, and current velocity. Numerical models are powerful tools that can simulate and predict the interactions among these factors dynamically at fine spatial scales and accurately portray wave propagation. This is crucial for coastal engineering, forecasting storm events, analyzing sediment transport, and gaining a deeper understanding of shallow water processes. Accurate representations of the dynamics of wave propagation are essential for coastal protection assessments [1] and wave energy conversion models [2] and to evaluate wave and hydrodynamic loading on coastal and offshore structures [3,4,5]. The interaction between waves and currents directly impacts the bed shear stress, which further affects sediment transport rates. These processes further influence the evolution of coastal morphology and can cause scouring to marine structures [1,5], making the accurate representation of wave propagation crucial for coastal management and in the design of offshore and coastal structures.
For forecasting purposes, besides the lateral boundary conditions, many operational wave models include only atmospheric input in their predictions of wave propagation, as modeling both hydrodynamics and wave propagation can be computationally expensive [6,7]. However, the integration of wave and hydrodynamic models has been shown to improve model performance by reducing the bias and error of simulated wave results [8,9]. Consequently, the study of wave–current interactions has been of recent interest, and many wave models are commencing now to incorporate hydrodynamic forcing, such as the current velocity and water levels.
The wave spectrum consists of various components that respond differently to currents, and, thus, there is no simple relationship between these two processes [10]. Currents are influenced by multiple variables, including wind stress, tides, and density gradients. At the same time, wind stress can be affected by the sea state, as surface waves modify the air–sea momentum transfer [9,11]. The sea state, in turn, depends on wind stress and currents, creating complex feedback mechanisms between waves and hydrodynamics [11]. The integration between wave and hydrodynamic models allows for the computation of wave–current interaction processes, which include wave radiation stress and enhanced orbital velocities, which further influence water circulation and sediment transport [5,12]. Hydrodynamics directly impact the wave field by causing the Doppler effect to occur as well as refraction induced by currents [9]. This amount of refraction depends on the current velocity, the incident wave direction compared to that of the current, and the wave period [8]. On one hand, the Doppler effect can be seen when waves travel with a current (following current), and the observed frequency decreases. On the other hand, when a wave meets a current from the opposite direction (opposing current), the observed frequency increases, and the waves appear to be moving faster [13,14]. Longuet-Higgins and Stewart [13] were some of the first researchers to discover changes in wave amplitude due to nonlinear interactions between waves and currents. More recently, several studies have found that an opposing current directly impacts the wave by increasing the wave height due to the compression of the wave energy into steeper waves, while a following current increases the mean wavelength, which, in turn, leads to a decrease in wave height [8,15,16]. This, furthermore, impacts the vertical structure of the mean current due to the wave-induced Reynolds stress [5]. Negative wave-induced stress causes a decrease in velocity near the surface when a wave and a current propagate in the same direction and an increase in velocity near the surface when a wave propagates against a current [5]. These wave–current interaction effects have been validated in several laboratory and numerical studies [7,8,15,16,17,18,19,20,21].
Changes in the spatial distribution of the wave action have been observed by Barnes and Rautenbach [8] when implementing the SWAN model in the strong Agulhas Current System off the coast of South Africa. These authors found increases in significant wave heights of 20–40% with an opposing current and decreases of approximately 20% in the case of a following current. Similarly, Saruwatari et al. [22] observed changes in wave energy of up to ±60% when implementing SWAN around the Orkney Islands in Scotland, where tidal currents exceed 3 m/s. In a weaker current system off the south coast of Ireland, Calvino et al. [7] also found redistribution of the wave action when implementing WAVEWATCH III forced with surface currents. These authors stated that these significant changes in the wave field would not have been captured without hydrodynamic forcing, highlighting the need to include these parameters in wave models for an accurate representation of the wave field.
Several studies have found improvements in wave model results when adding current velocity as a forcing condition of the wave model [7,8,9,10,16]. The magnitude of improvement showed to be dependent on how accurate the modeled current fields are as well as the location of the wave/current regime. For example, Barnes and Rautenbach [8] found only minor improvements of 0.01 to 0.02 m in significant wave height accuracy when forcing their SWAN wave model with a surface current field obtained from the Operational Mercator global ocean model. In another study in the North Atlantic Ocean off the coast of Ireland, the highest change in the significant wave height was approximately 10 cm when comparing results from a WAVEWATCH III simulation forced with surface currents and the same simulation without current velocity forcing [7]. Marechal and Ardhuin [10] found that forcing their WAVEWATCH III model with a well-resolved surface current field could accurately capture significant wave height gradients in the Agulhas Current System when comparing their results with satellite altimetry data. In a fully integrated wave–hydrodynamic model (NEMO and WAVEWATCH III) for the Black Sea, Causio et al. [9] found improvements in both the wave field and hydrodynamics when they considered the wave–current interaction in their model. A fully two-way coupled model between an unstructured 2D ocean circulation model Advanced CIRCulation (ADCIRC) and SWAN used depth-averaged currents for the 2D current field and was able to accurately simulate wave propagation in deep and shallow waters in the Gulf of Mexico and Louisiana during four hurricanes [23]. Recently, Fragkou et al. [18] developed a wave–current modeling framework with Python version 3.10 that resolves all wave–current interactions online between SWAN and the 2D ocean circulation model Thetis for the coastal waters of Duck, North Carolina in the United States.
The majority of previous numerical studies have considered only surface currents or the full depth-averaged current velocity field, but none of these aforementioned studies have deeply investigated the depth at which current velocity impacts the wave field. This is especially true for the south coast of Portugal, where very few modeled studies on the wave regime exist. Silva et al. [24] implemented the WAVEWATCH III and SWAN models to simulate waves off the Iberian Peninsula and further assess the spatial distribution of wave energy. These authors used the default SWAN settings to run a three-year hindcast and did not consider the effects of currents in their wave model [24]. Rusu et al. [25] also developed a wave-forecasting system based on SWAN for western Iberia but did not force their model with currents. In a nearshore wave–hydrodynamic study in the western margin of the south coast of Portugal, Horta et al. [26] implemented the Steady-State Spectral WAVE (STWAVE) model along with field observations to understand how the orientation of the coast impacts nearshore water circulation under different wave conditions. These authors found that the angle at which the waves approach the coastline strongly determines whether the water circulation will be dominated by longshore currents or rip currents [26]. While their study highlights the significance of the effects of waves on water circulation at a specific site along the south coast, the effects of currents on wave propagation along the entire coast have yet to be investigated. To the best of our knowledge, the present study is the first comprehensive study quantifying the effects of currents and water levels on wave propagation modeling in this region. This work, furthermore, represents an innovative approach that assesses changes in wave propagation due to current velocity fields obtained from different depths in the water column. The spatial variability of the effects of currents associated with the different circulation patterns in the region is also analyzed, which will contribute to the regional significance of this study. Furthermore, the experiments implementing different hydrodynamic forcings in the wave model can be generalized to other regions. This study consists of novel results on how current velocity and water levels impact wave propagation on the south coast of Portugal and sets the stage for future work on how wave propagation influences water circulation by coupling both processes in a fully operational modeling system.
2. Materials and Methods
2.1. Study Area
The study area covers the southern coast of the Iberian Peninsula (southwestern Europe), located in the North Atlantic Ocean (Figure 1). Ocean circulation patterns in this region are complex, as the Azores Current separates the oceanic gyre circulation into the Portugal Current in the north and the Canary Current in the south [27]. Furthermore, the entrance to the Mediterranean Sea allows the exchange between two different water masses, which further impacts the regional circulation [28]. The Portugal Current flows southward year round along the west coast of Iberia [29]. In summer, predominantly northeasterly winds transport water southward along the west coast of Portugal. In autumn and winter, the wind direction shifts to southwesterly, reversing the surface circulation and forming the Portugal Coastal Counter Current that flows northward for all layers in the water column from the surface to a depth of ~1500 m [27]. Mesoscale activity is the dominant factor influencing the meteo-oceanographic variability in the region, with variations in coastal alongshore wind stress occurring on a timescale of several tens of days [30].
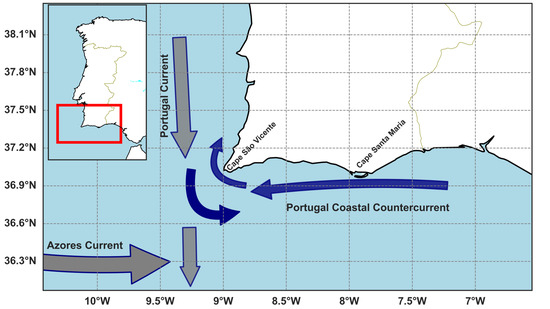
Figure 1.
Map of the study area within the Iberian Peninsula (upper left) highlighting the general circulation patterns relative to the study. The year-round Portugal Current and Azores Current are highlighted in gray. The southward Portugal Current, which occasionally turns eastward at Cape São Vicente, and the Portugal Coastal Countercurrent, which propagates northward in winter, are shown in dark blue.
The region is, furthermore, a part of the Canary Current Upwelling System (CCUS), which extends from 43° N to 10° N along the west coast of Iberia to the northwest coast of Africa. Upwelling off the west coast of Portugal occurs in spring and summer, when surface water along the coastline is transported offshore due to the combined effects of the northeasterly winds and the Coriolis force [29]. Off the southern coast of Portugal, the Portugal Coastal Countercurrent transports warm surface water westward in winter [31]. Once these waters reach the furthest western point along the south coast of Portugal at Cape São Vicente, they occasionally rotate clockwise and are further transported northward along the west coast [31]. The northward transportation of surface water along the west coast produces downwelling events [30].
The wave regime in the region is characterized by dominant more energetic waves coming from W-SW and less energetic E-SE waves [32]. On the south coast of the Algarve, the average significant wave height offshore is 0.9 m. Storm wave events are marked by waves reaching a significant wave height of more than 3 m and an associated peak period of 10–12 s [33]. The two different types of storms that occur are from W-SW or E-SE, the former being more frequent and energetic [32,34]. A study based on measured data off the south coast of Portugal for a 14-year period found that 70% of storm occurrences in this region are from the southwest, while the other 30% are from the southeast [34]. Waves are much more energetic off the west coast, with average significant wave heights ranging between 2 and 3 m and peak periods between 9 and 11 s [35].
The coastline along the south coast of Portugal is highly variable, as Cape Santa Maria at 36.97° N, 7.90° W splits the south coast into western and eastern margins. The western margin extends from Cape São Vicente to Cape Santa Maria, and the eastern margin extends from Cape Santa Maria to the Guadiana River at the border between Portugal and Spain [36] (Figure 1). The western margin consists of a cliff-dominated, rocky coastline with pocket beaches and is fully exposed to W-SW wave conditions [26]. The eastern margin consists of mainly sandy beaches in front of the Ria Formosa barrier system and lagoon and is fully exposed to E-SE waves [36].
2.2. Model Descriptions
2.2.1. Wave Model: SWAN
The Simulating WAves Nearshore (SWAN) model, developed at Delft University of Technology, is a third-generation wave model that simulates waves in coastal and inland waters. In addition to studies on wave–current interactions, SWAN has been applied globally for a range of applications, including assessments of wave energy potential [22,37,38], as well as to evaluate the influences of different wind datasets and boundary conditions on the wave field [37,38,39]. SWAN solves the full spectral balance equation, incorporating source and sink terms. Since SWAN is a third-generation model, the wave spectrum can propagate freely without any constraints on its evolution. All processes of wave generation, dissipation, and wave–wave interactions are represented [40]. The spectral balance equation is shown below [40].
The terms on the left describe (1) the action density rate of change ) at a single point in space over time , which is further equivalent to E/, where E is the energy density, and is the relative frequency; (2) the propagation of wave energy in two-dimensional geographical -space, where is the group velocity, and is the ambient current velocity vector; (3) shifts in frequency due to currents and changes in depth; and (4) depth- and current-induced refraction. The term on the right represents the sources and sinks of wave energy, which include the total wave growth by wind, the redistribution of energy from nonlinear interactions between different wave components, and wave decay caused by bottom friction, whitecapping, and depth-induced wave breaking [41]. In deep water, the most influential processes impacting wind–wave growth are the atmospheric input from wind to waves, wave dissipation, and the nonlinear energy transfer between wave components [42]. Processes such as bottom friction and triad interactions become more important in shallow waters with finite depth (up to a few hundred meters) [42].
2.2.2. Hydrodynamic Model: SOMA
The current velocity and water level used to force the wave model are produced by the Algarve Operational Modeling and Monitoring System (SOMA) [43] (https://soma.ualg.pt/ (accessed on 10 January 2025)), which is based on the hydrodynamic model MOHID [44]. The MOHID water-modeling system [45] is a three-dimensional water-modeling system programmed in ANSI FORTRAN 95 that simulates physical processes in an object-oriented approach. The design of SOMA consists of two nested grids of increasing resolution. The coarser level 1 grid covers the SW Iberian region, with a horizontal resolution of 2 km, with the finer level 2 grid nested with a resolution of 1 km, allowing a finer resolution of processes near the coast. The model bathymetry was created with data from the European Marine Observation and Data Network (EMODNET). The discretization of the water depth consists of 50 unevenly spaced layers of Cartesian coordinates. Eddy viscosity is computed by the General Ocean Turbulence Model (GOTM), which is coupled to MOHID and provides vertical turbulent diffusion coefficients [46]. Refer to [46] for a complete description on how the eddy viscosity and turbulent diffusions are computed. SOMA has been previously calibrated and validated with data from tide gauges, mooring buoys, and vertical profiles [43]. This model has been fully operational since July 2019, producing four-day forecasts of current velocity, water levels, temperature, and salinity for both level 1 and level 2 grids [47]. For a complete description on the setup and validation of SOMA, please refer to Janeiro et al. [43].
2.3. Standalone SWAN Model
2.3.1. Model Setup
The standalone SWAN model shared the same spatial domain and resolution as the level 1 SOMA grid, with 195 cells in the x-direction and 115 cells in the y-direction, spanning from 38.35° N to 36.07° N and from −10.45° E to −6.55° E (Figure 2). The model uses the same bathymetric dataset from EMODNET. SWAN Cycle III version 41.31 A, with MPI (Message-Passing Interface) parallel computing over 8 cores, was used for all the wave simulations. Although there is a newer version of SWAN available (version 41.51 AB), this version was selected due to its compatibility with MPI for Windows. Simulations were run in the two-dimensional (2D) nonstationary mode with spherical coordinates. The Nautical convention was used for wind and wave directions. The wave spectra are computed over the entire 360° directional range, using 72 bins with a resolution of 5° each. The grid resolution in the frequency space was set at 35, ranging from a minimum frequency of 0.0345 Hz to a maximum frequency of 1 Hz. Since wave observations in the breaking zone are very limited and insufficient, the authors opted to use the default values for depth-induced wave breaking, which consist of a proportionality coefficient of the rate of dissipation set at 1 and the ratio of the maximum individual wave height over the depth (breaker index) set at 0.73, in agreement with previous studies [25]. Bottom friction, triads, and quadruplets were also activated. All the simulations were run with a time step of 10 min, producing output every hour.
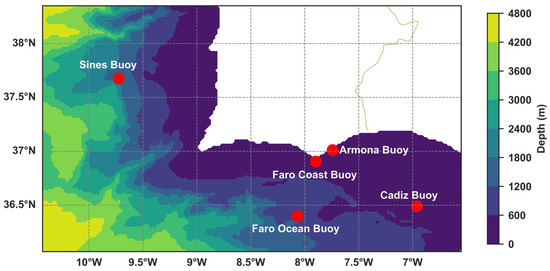
Figure 2.
Bathymetry of the computational grid. Buoy locations used for the model calibration and validation are shown in red.
2.3.2. Wind Input
The SWAN and MOHID models are forced with wind input from the SKIRON Atmospheric Modeling and Forecasting Group in Athens [48]. The wind data from SKIRON consist of wind velocities in the x- and y-directions at a height of 10 m at hourly intervals. The wind output covers well over the entire spatial domain of the present study and has a resolution of 0.05° (approximately 5 km).
2.3.3. Wave Conditions at the Boundary
Wave conditions at the boundary are provided from the Atlantic–Iberian Biscay Irish-Ocean Wave Analysis and Forecast product from the Copernicus Marine Iberia–Biscay–Ireland Monitoring and Forecasting Center (IBI-MFC). The Copernicus Marine IBI-MFC assimilates data from satellite altimeters to include near-real-time wave observation data in their models [49]. The dataset consists of a high-resolution wave analysis and forecast product on a 0.0278° × 0.0278° spatial grid covering the Iberia–Biscay–Ireland area from 26° N to 56° N and from −19° E to 5° E [50]. Hourly instances of significant wave height, peak period, and mean wave direction from this dataset were imposed along the boundary. Since the spatial resolution does not match perfectly the spatial resolution in this work, segments were set up along the boundary with the same spatial resolution from the IBI-MFC dataset. Each segment represents one grid point from the IBI-MFC dataset. Hourly instances of directional spreading values were also imposed along the boundary. The value of directional spreading measures how the wave energy is distributed around the mean wave direction entering the domain [51]. As this value was not provided by the CMEMS product, the sensitivity of the model to directional spreading () was tested by running the model with different coefficients of directional spreading at the boundary and assessing whether to measure this parameter in degrees or as a power of . A summary of these sensitivity tests is provided in Appendix A (Table A3). The SWAN manual recommends using default values of 30 when measuring in degrees or 2 when measuring in powers. As the southern and western boundaries are exposed to more open swell and the eastern boundary is more sheltered, the sensitivity analysis included modifying the coefficients based on the boundary side. The conclusion of this sensitivity test was that model configurations that used a directional spreading power of set at 2 around the lateral boundaries yielded overall results most similar to observations, particularly near the coast. The results of this sensitivity analysis are shown in Appendix A (Table A3, Table A4, Table A5, Table A6 and Table A7).
2.4. Buoy Data
The five buoys within the computational grid of Figure 2 were used to compare model results with in situ observations. These buoys are equipped with high-precision sensors that accurately represent wave parameters, such as the significant wave height, mean wave direction, and peak period. Wave data at the Faro Ocean Buoy, Cadiz Buoy, and Sines Buoy were obtained from the CMEMS In Situ Thematic Assembly Center (In Situ TAC) product Global Ocean In Situ Near-Real-Time Observations [52]. Wave data provided by CMEMS In Situ TAC is quality controlled, and only good data are made publicly available. Therefore, only quality controlled data have been used to validate the model results. For a complete description of the validation and quality control of these data, refer to the CMEMS In Situ TAC Quality Control document for waves [53]. Measurements from the Faro Ocean Buoy and Sines Buoy are provided by Instituto Hidrográfico (IH), whereas measurements from the Cadiz Buoy are provided by Puertos del Estado. Data from the two buoys closer to shore (the Faro Coast and Armona Buoys) only contain data for the year 2023. The 2023 dataset at the Faro Coast Buoy was purchased from IH, and the Armona Buoy dataset was provided by CIMA at the University of Algarve. The buoy locations and their depths are described in Table 1.

Table 1.
Names of buoys and their locations and depths for model calibration and validation.
2.5. Experimental Design
2.5.1. Selection of Simulation Timeframes
The buoy data described in Section 2.4 were used to identify specific timeframes to run the SWAN simulations to ensure model robustness across distinct wave conditions. The first simulation was run during the month of February 2024 for model calibration. Wave data at the Faro Ocean, Faro Coast, Cadiz, and Sines buoys showed that the model was representative of the full range of wave variability that is typical of the study region, including southwesterly and southeasterly waves, as well as storm and calm conditions. As buoy data were then later acquired closer to the shore at the Faro Coast Buoy, but only for the year 2023, it was decided to validate the model for the month of November 2023. This time period further covered a strong southwesterly storm, which is indicative of the most frequent storm occurrence in the region [32,34]. Calm conditions were also observed for this timeframe. For the purpose of analyzing the effects of hydrodynamic forcing on the wave model, two other timeframes were chosen that represent the two typical storm conditions in the region: (1) October/November 2023, which consisted of two consecutive storms from the southwest, and (2) February 2023, which consisted of a storm coming from the southeast. An additional timeframe was selected that included wave measurements close to the coast (Armona Buoy), located very close to the shore, east of Cape Santa Maria. This period represents low wave conditions in April 2023. All five of these simulation scenarios are summarized in Table 2.

Table 2.
Simulation timeframes used for SWAN calibration, validation, and to test hydrodynamic forcing under different wave conditions.
2.5.2. Standalone SWAN Calibration and Validation
The standalone SWAN model was calibrated by testing the model with a set of formulae that represent the physical parameters influencing wave propagation. Several source-term packages are available in SWAN, each implementing different formulae for wind growth and whitecapping. The newest source-term package is called ST6, which consists of new formulae for wind and whitecapping and considers the influences of swell dissipation, wind scaling, and other processes [54]. This ST6 package has been recommended by Edwards et al. [55] to use in regions exposed to swells generated in the Atlantic, Pacific, Indian, and Southern Oceans, and, thus, it was chosen to calibrate the model with different formulae and coefficients within this package. The SWAN manual provides several ST6 physics settings to use for model calibration [54]. The various calibration settings of the ST6 physics formulae consist of the modification of the dissipation coefficients ( and ) and power coefficients ( and ), normalization of the wind drag formula with the commands UP or DOWN , selection of a formula for wind drag (HWANG, FAN, or ECMWF), implementation of a vector (VECTAU) or a scalar (SCATAU) to calculate stress, and selection of the true value for the wind (TRUE10) or a scaling factor (U10PROXY) [42]. The term AGROW activates the wave growth term from Cavaleri and Malanotte [56]. The model cases used for calibration are shown in Table 3, which correspond to the recommended settings from the SWAN user manual [54]. The terms for the swell were also modified with the options Ardhuin, which refers to the nonbreaking dissipation from Ardhuin et al. [57], which uses a coefficient related to the laminar atmospheric boundary layer, and Zieger [58], which uses a nondimensional proportionality coefficient.

Table 3.
Model cases incorporating the various ST6 physics formulae.
Calibration was achieved by obtaining hourly measurements of significant wave height (Hs), mean wave directions (Dir), and peak periods (Tp) from the three mooring buoys that were available during the calibration period (Faro Ocean, Cadiz, and Sines) and comparing them with results from the various simulations of altered physics formulae.
2.5.3. Hydrodynamic Forcing on Wave Propagation
The coupling between hydrodynamic and wave models can be implemented in two ways: offline coupling, in which the output of one model serves as input for another, and online coupling, where both models exchange information dynamically during the simulation. Online two-way coupling allows for a complete exchange of all the complex processes and interactions between wave and ocean circulation models throughout a simulation but is computationally expensive [6,8,21,23] and requires extensively modifying the source code of both models [18,59]. While online coupling provides a more complete interaction between wave and hydrodynamic processes, it requires significantly higher computational resources and an external mechanism to facilitate communication between models [9,18,59]. In contrast, offline coupling is computationally more efficient and allows for a controlled analysis of how one process influences the other. In an offline coupling approach, a one-way coupling system is achieved by running one model and using the results of that model as boundary conditions for the other model. This controlled analysis to analyze the specific effects of hydrodynamic forcing on the wave model was chosen for the present study, as it is (1) more computationally efficient and (2) allows for a controlled evaluation of where in the vertical water column of the SOMA hydrodynamic model the current velocity has the most influence on wave propagation. This is crucial, since many coupled wave–hydrodynamic models assume a depth-uniform current, but in reality, currents are sheared vertically [5].
To complete this assessment, various outputs from SOMA were used to test the model sensitivity to hydrodynamic forcing. The calibrated and validated standalone SWAN setup without any current velocity or water level forcing from SOMA was used as the control run (Run 1). To test the hydrodynamic influence on wave propagation in the region, several simulations were run with different forcing outputs from SOMA, as indicated in Table 4. The rationale for forcing the wave model with the current velocity from the surface (Run 3), upper 10 m (Run 4), and upper 20 m (Run 5) of the water column is that wave-induced velocities, i.e., orbital velocities, are more significant near the surface and decay exponentially with depth [60]. Therefore, to properly simulate wave propagation, it is important to have an appropriate characterization of the ambient currents at the surface or near the surface. In contrast, the depth-averaged velocity for the entire water column (Run 6), which is used in many wave model applications, is expected to have the least influence on wave propagation, so including this current field in the hydrodynamic forcing experiments allows for a complete assessment of how currents from different depths affect wave propagation. All the outputs from SOMA that were used as initial conditions for the wave model during these experiments were time and space varying, covering the same spatial grid and timeframe of each simulation.

Table 4.
Model runs with various hydrodynamic forcings from SOMA.
The surface current field consists of northward and eastward velocity components of the uppermost layer of the vertical coordinate in SOMA’s grid. The base value of this first layer is 0.494 m to hydrographic zero. Therefore, the depth of this first layer varies according to the variation in the tides such that it will be 0.494 m + the sea surface height (SSH). Since SWAN only takes two-dimensional inputs, the current velocities referring to various depths needed to be weight-averaged.
To compute the depth-averaged velocity for the first 10 m, first 20 m, and the entire water column, the depth-integrated velocities of both the eastward and northward velocity components were computed. As SOMA consists of 50 vertical Cartesian coordinate layers with varying thicknesses for each layer, with cell thickness increasing toward the bottom, it was imperative to compute depth-weighted velocities as opposed to a simple mean. The depth of each layer corresponds to the depth of the bottom of each cell, and the cell thickness corresponds to the distance (m) between the top and bottom of that cell. In this configuration, layer 6 corresponds to a depth of approximately 10 m. To obtain the depth-averaged velocity of these 6 upper layers, the values for both the eastward and northward velocity components were selected and then multiplied by the cell thickness. This result was then summed and divided by the total thickness of these vertical layers, resulting in a 2D array for each eastward () and northward () velocity component. The same method was applied to compute depth-averaged velocity up to 20 m, except in this case, it was applied up to layer 11 in the SOMA grid. To compute the depth-averaged velocity for the entire water column, all 50 vertical Cartesian coordinate layers of the SOMA grid were included.
For a depth of , the depth-averaged average horizontal (eastward) and (northward) velocity components are represented as follows:
For a more discrete representation with to vertical layers, the equations are as follows:
where is the eastward component of the velocity, is the northward velocity component, and is the cell thickness (the distance from the bottom to the top of one cell).
2.5.4. Model Performance Assessment
To visually assess how the model performance varied across simulations in different storm scenarios, timeseries of relative error along with boxplots of absolute error according to Hs class (low, medium, and high wave conditions) were computed.
To quantify the model performance, several metrics were computed: root mean square error (), , Pearson’s Correlation Coefficient (R), and model skill score (). measures the magnitude of the error between model predictions and observations and is expressed as follows:
where and represent modeled data and observed data from the mooring buoys, respectively, and is the number of observations [61]. Similarly, BIAS represents an absolute measure of how much model results differ from observations and is used to determine whether the model tends to overestimate (positive value) or underestimate (negative value) observations. It is expressed as follows:
To quantify the correlation between predicted values and observations, Pearson’s Correlation Coefficient was used. It is expressed with the following formula:
Pearson’s Correlation Coefficient measures the linearity between observed and predicted values, ranging from −1 (perfect negative correlation) to 1 (perfect positive correlation), with 0 indicating no correlation. It should be noted that this statistics measure can be influenced by outliers and may not reflect the magnitude of the agreement between observations and predictions [61], and, thus, it should be interpreted alongside other statistics metrics.
Willmott’s model skill score (MSS) provides a more quantitative measurement of model accuracy by measuring the degree to which model predictions are free from errors relative to the observed data [62]. It overcomes the sensitivity of simple correlation statistics by normalizing errors relative to the variability in the observations [61]. It is represented by the following formula:
An MSS with a value of 1 represents perfect agreement between modeled data and observed data, whereas a value of 0 indicates no agreement between the two.
In addition to the standard statistics metrics of RMSE, BIAS, R, and MSS, a Diebold–Mariano test [63] was used to asses if each of the model runs implementing the various hydrodynamic inputs from SOMA was statistically different from the run without hydrodynamic forcing. The DM test is used to compare model accuracies over a given timeframe by comparing the differences in the forecasting error between two models. It further evaluates whether this difference is statistically significant by computing a -value under the null hypothesis that the two models have the same forecasting accuracy. It is represented by the following equation:
where is the loss differential based on the mean-squared error between the two models at all the timesteps, and is the estimated variance of this loss. For > 1.96, the null hypothesis that the difference between the two models is not statistically significant is rejected, so it can be concluded that the two models are statistically different. It further implies that at the 5% significance level, the average difference in the error is not zero [64]. More specifically, a DM statistic of higher than 1.96 implies that model 2 is better than model 1, whereas a negative value lower than −1.96 implies that model 1 is better than model 2. In this case, model 1 is the run without hydrodynamic forcing, which was compared to each hydrodynamically forced run (Runs 2–6 in Table 4). The DM test was applied only to the experiments implementing hydrodynamic forcing to assess if forcing the calibrated wave model with hydrodynamic input leads to a statistically significant improvement in results compared to the baseline run with no hydrodynamic input.
2.5.5. Wave–Current Interaction Analysis
The effects of wave–current interactions were analyzed by computing the differences in the angle between the mean wave direction and mean current velocity direction for each storm, using the average values over the simulation period. A wave–current angle absolute difference of 30° or less implies a following current, whereas a wave–current angle difference of 150–180° implies an opposing current. The current velocity magnitude was binned into 1 m/s bins, and the differences between current and wave angles were binned into 3-degree bins over the entire spatial domain. This was performed for each storm as well as for the runs incorporating current velocities from different depths in the water column.
3. Results and Discussion
3.1. Standalone SWAN Calibration
To assess the model performance between the runs that altered the different physics formulae during the calibration period, the time series of Hs for the Faro Ocean Buoy, Cadiz Buoy, and Sines Buoy are shown in Figure 3, highlighting the observed Hs of each buoy on the left axis and the relative error between modeled results and observations (the envelope of seven runs) on the right axis. Time series showing predicted values and observations at each buoy location are shown in Appendix A (Figure A1, Figure A2 and Figure A3).
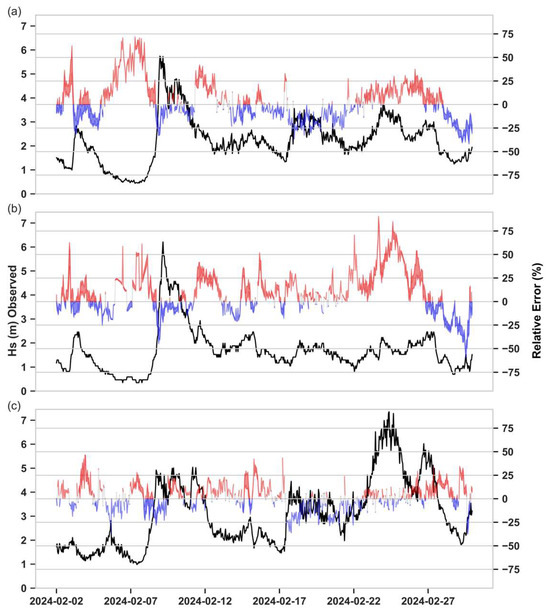
Figure 3.
Time series of Hs at the (a) Faro Ocean, (b) Cadiz, and (c) Sines buoys to assess differences in error during the model calibration period. Black lines show buoy observations (left axis), and shaded areas indicate the range of the relative error across the seven model runs (Table 4), with overpredictions in red and underpredictions in blue.
Overall, Figure 3 demonstrates that the modeled Hs only slightly varied across the different ST6 physics calibration settings, demonstrating that the model was not sensitive to changes made in the formulae for the wind input, quadruplet interactions, and whitecapping dissipation. The largest difference between modeled results occurred at the Cadiz Buoy (Figure 3b) on 9 February 2024, directly after the highest peak of the significant wave height, with differences in relative error ranging from −40% to −20%. Another large difference between modeled results can be seen at the Faro Ocean Buoy (Figure 3a) in the beginning of the simulation on 3 February 2024, when some modeled results underpredicted Hs right after the peak of the first storm, whereas other modeled results overpredicted Hs. At the Faro Ocean Buoy, the highest peak of Hs occurred on 8 February 2024 at 23:00, with a value of 5.74 m. The highest peak of Hs for the Cadiz Buoy occurred on 9 February 2024 at 4:00, with a value of 6.21 m. For both of these peaks that occurred at the beginning of the simulation, all the models underpredicted Hs but then tended to overpredict Hs for the remainder of the simulation. At the Sines Buoy, the highest peak of Hs occurred on 24 February 2024 at 9:00, when the observed Hs reached 7.35 m and the modeled results only slightly underpredicted this value. The modeled results at the Sines Buoy achieved Hs values most similar to observations compared to the results at the other buoy stations.
For a more quantitative analysis of each model’s agreement with buoy observations, error metrics computed at each buoy site are shown in Table 5. The values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases at each site. The physics formulae implemented for each case are referenced in Table 3. The metrics for the mean wave direction and peak period at each site are in Appendix A.

Table 5.
Error metrics of the significant wave height, comparing the model results of each calibration setting with buoy observations. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
Small differences in the error metrics at each of the buoy locations were found when comparing the results from the various physics settings. In general, the values of RMSE and BIAS were quite low, with the values of RMSE varying between 0.361 and 0.409 and the BIAS varying between −0.001 and 0.172. Case 6 was selected as the best setting for the model, as it had the highest MSS (0.963) and Pearson’s Correlation Coefficient (0.928) and the lowest RMSE (0.366) and BIAS (−0.001) at the Faro Ocean Buoy. This case also resulted in the highest value in MSS and Pearson’s Correlation Coefficient at the Cadiz buoy. The RMSE at this location was slightly higher compared to other simulations, but this can be influenced by the initial conditions at the boundary, since the Cadiz Buoy is located very close to the boundary. The error metrics at the Sines Buoy did not vary much between simulations. Case 6 was chosen, as the results at the Faro Ocean Buoy exceeded all the other simulations, and this location is a strong indicator of how the model propagates wave energy further in the domain. The BIAS value of nearly 0 and high MSS of 0.963 indicate the model’s adequacy for simulating wave propagation well into the computational domain. The calibrated set of parameters is thus the ST6 formula, with dissipation coefficients of 4.7 × 10−7 and 6.6 × 10−6 and power coefficients of 4.0 and 4.0, normalization with the command UP, a wind drag formula of HWANG, vector calculation for the stress calculation with the command VECTAU, windscaling equal to 28 with the command U10PROXY 28.0, and linear growth with the command AGROW. Furthermore, the swell is activated with the command ZIEGER and set at the nondimensional proportionality coefficient 0.00025, which is the default in SWAN [54]. The wind drag formula of HWANG was also found to be the best formula within the ST6 package in a recent study that used SWAN to assess wave energy off the Iberian Peninsula [65]. Another recent study that implemented the SWAN model for the South China Sea also used the wind drag formula of HWANG along with windscaling set at 28 [39].
The results of the model calibration demonstrated that the modeled wave height was not very sensitive to the selected physics parameters, and the maximum differences in RMSE at each of the three buoys were approximately 0.13 m. This behavior was also observed by Zhang et al. [66] and Aydoğan and Ayat [67], who found improvements to the SWAN model when calibrating with ST6 parameters but small differences between the various ST6 calibration settings.
3.2. Standalone SWAN Validation
For model validation of the previously calibrated model configuration, Figure 4 presents scatter plots showing the correlation between buoy observations and model results during the simulation period of November 2023.
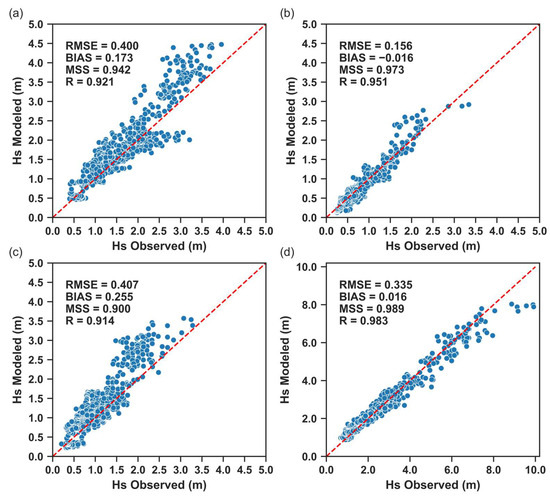
Figure 4.
Scatter plots showing the RMSE, BIAS, MSS, and R (Pearson’s Correlation Coefficient) values between observations and modeled Hs at the (a) Faro Ocean Buoy, (b) Faro Coast Buoy, (c) Cadiz Buoy, and (d) Sines Buoy during the validation period of November 2023.
Figure 4 demonstrates a very strong correlation between observations and modeled results at all four buoy sites. The strongest correlation is at the Faro Coast Buoy, which is located very close to the shore. The results at the Faro Ocean Buoy and Cadiz are slightly more spread out. The SWAN model tended to overestimate Hs at these two sites, which are located in the southern part of the domain, offshore. At the Sines Buoy, the highest values of Hs were observed, with values reaching close to 10 m. The SWAN model underpredicted Hs at this high peak. For a more precise quantitative analysis of how the model results differ from buoy observations, Table 6 summarizes the error metrics of the significant wave height, mean wave direction, and peak period.

Table 6.
Error metrics of Hs, mdir, and Tp between modeled results and observations during the validation period. Data not available are marked with “N/A” (not applicable).
The results of the modeled Hs showed strong agreement with observational data across all four buoy locations for the validation period of November 2023. This agreement is reflected in the low values of RMSE and BIAS, as well as the high values of MSS and R, demonstrating the model’s ability to capture both the temporal variability and magnitude of these wave parameters. Among the four buoy locations, the Faro Coast Buoy, which is located closer to the shore, exhibited the best agreement, with an MSS of 0.973 and an RMSE of 0.156 m for Hs, demonstrating the model’s ability in accurately capturing wave propagation far into the computational domain. The Faro Coast Buoy did not have data available for the mean wave direction, so this parameter could not be compared with the model results. The modeled mean wave direction aligned well with observations at all the buoy locations, attesting to the model’s adequacy in accurately simulating the mean wave direction. The results of the peak period yielded slightly higher errors but still showed good agreement with observations. These results demonstrate the model’s adequacy in simulating and predicting wave parameters within the model domain and signify that it can be used to accurately represent the wave field for the south coast of Portugal. Furthermore, the validation of the model during this month confirmed the findings of the calibration results, giving confidence to the model. However, it is still crucial to constantly verify model results with observations [68], and, thus, all future runs of this study are validated with in situ buoy observations.
3.3. Effects of Hydrodynamic Forcing on Wave Propagation
3.3.1. Waves Coming from the W-SW
To assess the influences of the various hydrodynamic inputs on wave propagation during a storm with predominantly W-SW waves, a time series of the significant wave height is exhibited in Figure 5. Buoy observations are shown on the left axis, while the range in the relative error between all the modeled results (run IDs from Table 4) and buoy observations are plotted on the right. This allows for an analysis of model’s ability to accurately capture wave propagation throughout the simulation and to assess the variability between the model runs that implemented various hydrodynamic forcings.

Figure 5.
Time series of Hs at the (a) Faro Ocean, (b) Faro Coast, (c) Cadiz, and (d) Sines buoys during a storm with waves coming from W-SW to test the variability in the modeled Hs due to hydrodynamic forcing. Black lines show buoy observations (left axis), and shaded areas indicate the range of the relative error across the seven model runs (Table 4), with overpredictions in red and underpredictions in blue.
In general, it can be stated that when Hs was high (above ~3 m), all the models underpredicted Hs (Figure 5). Off the south coast, the peak of the storm occurred on 22 October 2023, as shown by the results of the Faro Ocean Buoy, Faro Coast Buoy, and Cadiz Buoy (Figure 5a–c). At the Faro Ocean Buoy and Cadiz Buoy (Figure 5a,c), all the models underpredicted Hs for these peaks but then tended to overpredict Hs for the remainder of the simulation. However, at the Faro Coast Buoy (Figure 5b), all the models overpredicted Hs during the highest peak, with some models overpredicting Hs by nearly 1 m, with a relative error of approximately 20%. At the Cadiz Buoy, a relative error of 100% is observed during low wave conditions on 29 October 2023. At this time, the measured Hs was 0.5 m, while model predictions overestimated it at 1 m. Although this error seems to be high, the absolute difference is small and within a reasonable range. The Faro Coast Buoy and Sines Buoy yielded model results most similar to observations. At the Faro Coast Buoy, Hs stayed relatively low throughout the simulation, with values ranging between 0 and 2 m. Hs reached the highest off the west coast at the Sines Buoy, with values reaching nearly 10 m on 5 November 2023. The models were not able to capture this extreme wave height. However, they matched the observations quite well during the simulation and tended to overestimate Hs when Hs was low and underestimate Hs for higher values. In terms of the variance between the model results, Figure 5 shows more variability at the Faro Coast (Figure 5b) and Cadiz (Figure 5c) toward the end of the simulation, when Hs was low. The largest variability between the models in the relative error at these two locations was 37.71% and 29.84%, respectively. The smallest variability between the models is seen at the Sines Buoy (Figure 5d), with a maximum variance between the relative error of the models of 7.51%.
To summarize these errors during the simulation, boxplots were created showing the error in Hs (m) between each modeled simulation and the observed values according to the Hs class. On one hand, in the Gulf of Cadiz (Faro Ocean, Faro Coast, and Cadiz), Hs classes were defined as low (0–1 m), medium (1–3 m), and high (greater than 3 m). On the other hand, off the west coast of the Iberian Peninsula (Sines), the threshold for high waves is greater than 4 m [69].
The boxplots of the W-SW in Figure 6 demonstrate the model’s tendency to overpredict Hs (error > 0) across all the simulations. At the Faro Ocean Buoy, the runs with no hydrodynamic input, SOMA water level only, and depth-averaged velocity of the entire water column demonstrate larger errors compared to those of the runs incorporating the current velocity from the upper layers of the water column. The CMEMS model produced lower errors compared to all the modeled runs at this location. At the Faro Coast Buoy, the runs incorporating the current velocity from the upper layers of the water column produced higher errors under low and medium wave conditions. However, in high wave conditions, the runs incorporating the SOMA current velocity from the upper layers of the water column performed better. At this location, the median error across all the simulations is 0, with all the models both slightly overpredicting and slightly underpredicting Hs. The error produced by CMEMS at this location was low for low and medium waves but high for high wave conditions, with significant underpredictions in Hs. At the Cadiz Buoy, the distribution in the error for all the models was quite high for the high-Hs class. The time series in Figure 5 demonstrate that this condition occurred during the peak of the storm on 22 October 2023, when the range in the relative error for all the models ranged between approximately −10% and 50%. The errors at Sines were small for all the simulations, with the median error being very close to 0 for all the model runs when waves were between 1 and 4 m. Under higher wave conditions (above 4 m), the models tended to underpredict Hs, which is also apparent in the time series in Figure 5.
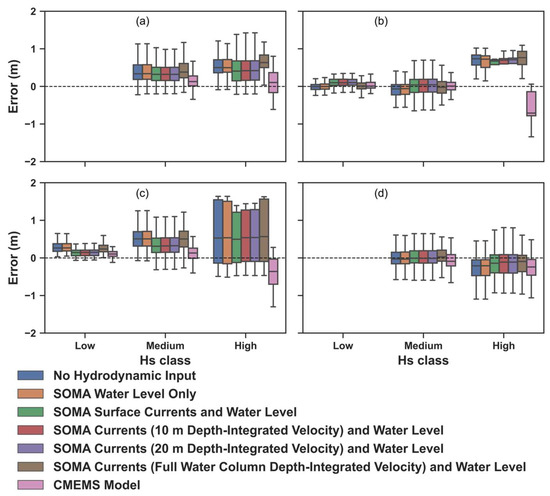
Figure 6.
Boxplots of absolute errors in Hs during the W-SW storm at the (a) Faro Ocean Buoy, (b) Faro Coast Buoy, (c) Cadiz Buoy, and (d) Sines Buoy to evaluate model errors by Hs class. The boxes depict the 25th to 75th percentiles, the dashed line is the median, and the whiskers show the 5th to 95th percentiles.
To quantify the error more precisely between specific model runs and observations, Table 7 presents the metrics of RMSE, BIAS, MSS, and R. The run IDs are referenced in Table 4. The best metric values (the lowest values of RMSE and BIAS and highest values of MSS and R) among all the simulations are highlighted in bold.

Table 7.
Error metrics of the significant wave height for each model run that implemented the various hydrodynamic forcings for the simulation with westerly waves. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
Table 7 demonstrates small variability in the statistics metrics between uncoupled runs and runs that implemented the different hydrodynamic forcings from SOMA. RMSE and BIAS values stayed quite low, ranging from 0.242 m to 0.594 m and from 0.005 to 0.502, respectively. MSS and Pearson’s Correlation Coefficient were high, ranging from 0.862 to 0.982 and from 0.923 and 0.968, respectively. When comparing the SWAN runs that implemented varying hydrodynamic forcings from SOMA, Run 3 (SOMA Surface Currents and Water Level) performed better than all the other simulations by achieving the highest number of “best” metric values for all the buoys. At the Faro Coast Buoy, the run with the SOMA water level only (Run 2) performed very well, with an RMSE of 0.242 m and an MSS of 0.958. This result is consistent with Wang and Elahi’s [16] finding that water levels play a more significant role in the modulation of the significant wave height in shallower waters, whereas the current velocity has more influence on wave propagation in the deep ocean. In comparison to the control run of the study without any hydrodynamic forcing (Run 1), all the simulations performed better, implying that adding hydrodynamic forcing improves the results. At the Faro Ocean Buoy, the RMSE was reduced by 0.054 m, or approximately 10%, when the surface currents and water level were implemented in the model (Run 3). The RMSE was reduced by 0.004 m at the Faro Coast Buoy with the case of the SOMA water level only. At this buoy location, the other runs produced less accurate results. At the Cadiz Buoy, the RMSE was reduced by 0.164 m (~28%) in the run with the SOMA surface currents and water level. In Sines, this same run reduced the RMSE by 0.029 m. Overall, the metrics presented in Table 7 reveal improvements to the model with the addition of hydrodynamic forcing, particularly in the case of the surface currents and water level. Table 7 shows better performance from the CMEMS model at all the buoy locations for the simulation with westerly waves. This can be due to the fact that CMEMS assimilates wave data from satellite results, leading to a more accurate representation of the model’s wave field [49].
To test how statistically significant the modeled runs incorporating hydrodynamic forcing from SOMA were compared to the run without SOMA input, Table 8 presents results of the DM statistic along with the p-value across all the buoy locations.

Table 8.
Diebold–Mariano statistical analysis to test the statistical significance of each hydrodynamically forced run compared to the run without hydrodynamic forcing during the W-SW storm.
Table 8 demonstrates that on average, across all the locations, modeled runs that surpassed the DM threshold of 1.96 were the run with the SOMA surface currents and water level, SOMA depth-averaged velocity for the upper 10 m of the water column, and SOMA depth-averaged velocity for the upper 20 m of the water column (Runs 3–5), with DM values of 6.911, 6.810, and 6.844, respectively. The CMEMS model also achieved a DM score of above 1.96, with a value of 5.789. This indicates that on average, these four modeled results are statistically significant and performed better than the baseline run without SOMA input. The mean DM across all the locations was highest for Run 3, which further supports the conclusion that model runs forced with the SOMA surface current velocity and water level yielded the highest improvement from the run without SOMA input during the W-SW storm. The runs of the SOMA water level only (Run 2) and depth-averaged velocity from the entire water column (Run 6) achieved a DM statistic of 0.426 and −0.339, respectively, and were therefore not statistically different from the run without SOMA input. In terms of the spatial variability, DM values varied slightly across buoy locations, with slightly worse, but not statistically significant, performance at the Faro Coast Buoy for the runs incorporating SOMA currents from the upper layers of the water column (Runs 3, 4, and 5), with values of −1.344, −1.751, and −1.711, respectively. Locations further offshore (Faro Ocean, Cadiz, and Sines) resulted in improved performance from these runs.
Across all the locations, the p-value is quite low, with values much lower than the threshold of 0.05, except at Faro Coast and Cadiz. This result coincides with the statistics presented in Table 7, which demonstrated that the RMSE did not differ significantly across model runs at these locations. For an overall summary of the p-values across all the locations, a combined method from Fisher [70] was performed for all the model runs. The overall results of the DM analysis for the W-SW storm demonstrate that runs forced with current velocity from the uppermost layers of the water column were the most statistically significant compared to the run without hydrodynamic forcing.
For a visual representation of how wave propagation in the computational domain changed due to the addition of hydrodynamic forcing, Figure 7 shows spatial maps of the difference in Hs between each simulation and the simulation without hydrodynamic forcing during the westerly storm. The 2D maps represent the average difference in Hs during the westerly storm period, with overlaying velocity vectors representing the average current velocity direction as well as the mean wave direction during the storm. For a complete evaluation of the magnitude of the current velocity over time, the time series of the current velocities at four locations within the domain are shown in Figure 8.
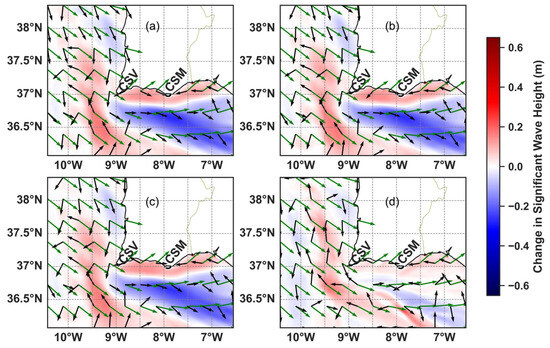
Figure 7.
The 2D spatial maps depicting the average change in Hs during the W-SW storm due to the (a) surface current velocity and water level forcing, (b) 10 m depth-averaged current velocity and water level forcing, (c) 20 m depth-averaged current velocity and water level forcing, and (d) depth-averaged current velocity from the entire water column and water level forcing. The black arrows represent the mean current velocity direction, and the green arrows represent the mean wave direction. Key coastal areas of Cape São Vicente (CSV) and Cape Santa Maria (CSM) are highlighted.
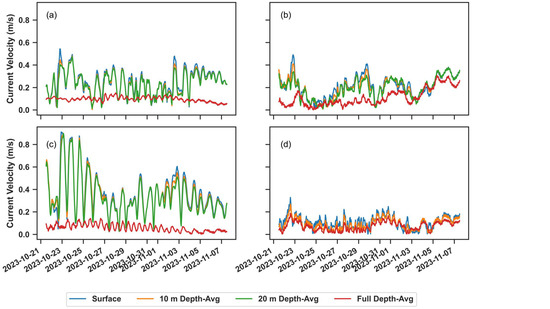
Figure 8.
Time series of SOMA current velocities at the locations of the (a) Faro Ocean Buoy, (b) Faro Coast Buoy, (c) Cadiz Buoy, and (d) Sines Buoy during the storm with westerly waves (21 October 2023–7 November 2023).
The magnitude of the change in Hs for each simulation, as shown in Figure 7, was very similar for the simulations forced with SOMA surface currents, SOMA 10 m depth-averaged velocity, and SOMA 20 m depth-averaged velocity, whereas the change in Hs for the simulation forced with depth-averaged velocity for the full water column was much smaller. The change in Hs was the highest for the simulation forced with surface currents (Figure 7a) and then reduced slightly as the depth increased, as shown from Figure 7ba–d. This is consistent with the time series of the velocity, as shown in Figure 8, as the magnitude of the depth-averaged velocity of the entire water column was always smaller compared to velocities more toward the surface. The magnitude of the change in Hs was higher off the south coast compared to the change in Hs off the west coast. Figure 7a–c shows decreases in Hs of approximately 0.4 m when the current velocity direction and mean wave direction were aligned. Close to the shoreline on the southern coast, increases in Hs were observed, as the average current velocity direction was easterly and the mean wave direction was westerly (opposing currents). Along the west coast, decreases in Hs were also observed due to the southerly direction of the waves (following currents). The time series of the current velocity in Figure 8 show higher velocity values at Faro Ocean, Faro Coast, and Cadiz compared to Sines, which further justify why changes in Hs are higher off the south coast compared to changes in Hs off the west coast. The magnitude of the velocity was also higher in the southeast domain, with values reaching close to 1 m/s, as shown in the time series plot at the Cadiz Buoy in Figure 8c. This further corresponded to a decrease in Hs of approximately 20 cm for all the simulations forced with the surface velocity as well as the depth-averaged velocity up to 10 m and 20 m. The enhancement of changes in the significant wave height due to stronger current velocity fields has been detected in other coupled wave–hydrodynamic models [7,8]. The increases in Hs closer to the shore, as shown in Figure 7, can also be attributed to the implementation of the dynamic SOMA water levels in the runs, underscoring the significant effects that varying water levels have on wave propagation in nearshore areas. The time series of the water levels at the Faro Ocean Buoy, Faro Coast Buoy, Cadiz Buoy, and Sines Buoy are shown in Appendix A (Figure A4).
3.3.2. Waves Coming from the E-SE
For the simulation with waves coming from the E-SE (February 2023), Figure 9 shows a time series of the significant wave height, with buoy observations on the left axis and the relative error percentage between the envelope of all the modeled results from Table 4 and observations on the right axis.
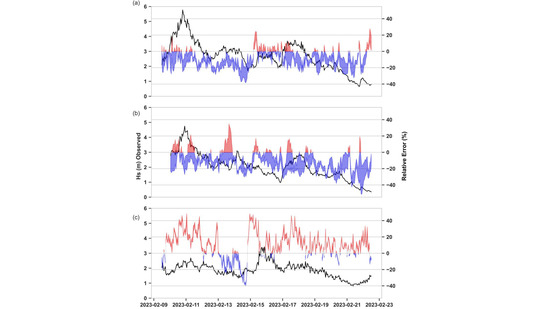
Figure 9.
Time series of Hs at the (a) Faro Ocean, (b) Faro Coast, and (c) Sines buoys during a storm with waves coming from the E-SE to test variability in modeled Hs due to hydrodynamic forcing. Black lines show buoy observations (left axis), and shaded areas indicate the range of the relative error across the seven model runs (Table 4), with overpredictions in red and underpredictions in blue.
Similar to the simulation with westerly waves, Figure 9 shows an underestimation of Hs when the observed values were high (above 3 m) and an overprediction for lower Hs values. All the models show a consistent slight underprediction at the Faro Ocean Buoy and Faro Coast Buoy. The models were able to capture wave propagation more accurately at the Sines Buoy and tended to slightly overestimate Hs. It should be noted that in situ data from the Cadiz Buoy were only available for three days of this simulation (19 February 2023–22 February 2023) and, thus, were not included in this analysis.
A boxplot showing the Hs error by Hs class during the E-SE storm is shown in Figure 10, with the same criteria used during the W-SW storm to define the Hs class.
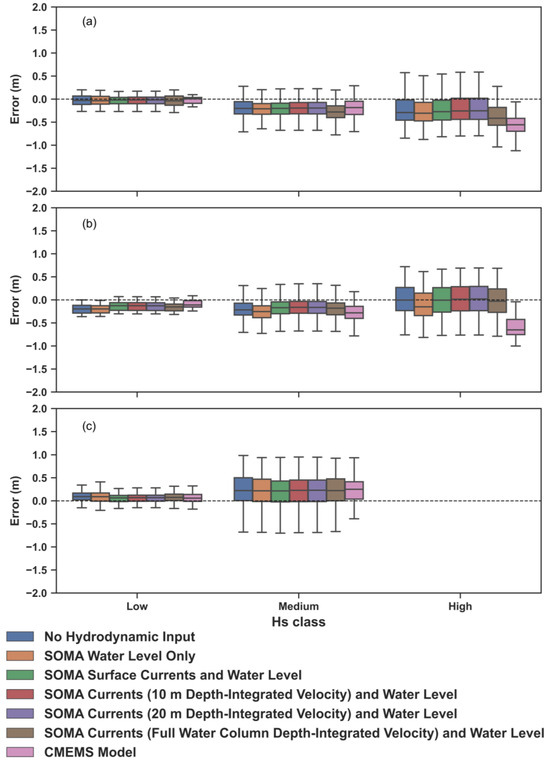
Figure 10.
Boxplots of absolute errors in Hs during the E-SE storm at the (a) Faro Ocean Buoy, (b) Faro Coast Buoy, and (c) Cadiz Buoy to evaluate model errors by Hs class. The boxes depict the 25th to 75th percentiles, the dashed line is the median, and the whiskers show the 5th to 95th percentiles.
Compared to the W-SW storm, the range of modeled Hs errors for the E-SE storm was much smaller. Across all the simulations, errors were close to 0 under low-wave conditions, but the range in the error increased with higher wave heights. At the Faro Ocean Buoy, all the simulations tended to underpredict Hs under both medium- and high-wave conditions. This underprediction also occurred closer to the shore at the Faro Coast Buoy for low- and medium-wave conditions. However, under high-wave conditions at this location, the median value of the error was close to 0, indicating that all the models both underpredicted and overpredicted Hs. At the Sines Buoy, all the models generally overpredicted Hs in cases of medium wave heights (1–4 m). Overall, the range in the error was quite similar among all the simulations, with slight improvements in those forced with the current velocity from the upper layers of the water column. The results in Figure 10, furthermore, demonstrate better performance from all the simulations compared to the CMEMS model, which tended to underpredict Hs for all the wave conditions.
To quantify more precisely how each model differed from observations, the statistics are summarized in Table 9.

Table 9.
Error metrics of the significant wave height for each model run that implemented the various hydrodynamic forcings for the simulation with easterly waves. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
The SWAN simulations performed very well in the simulation with easterly waves, which is reflected in the very low RMSE and BIAS values and very high MSS and R values across all the locations. RMSE values ranged from 0.288 m to 0.352 m, while BIAS values ranged from −0.195 m to 0.170 m. The simulations that included the current velocity up to a specific depth of the water column and water level forcing from SOMA (Runs 3–5) outperformed the run without any hydrodynamic input (Run 1). These model simulations reduced RMSE by approximately 0.2 m compared to the run without any hydrodynamic input for all the buoy locations. Runs 3–5 achieved the highest MSS value at the Faro Coast Buoy, with a value of 0.974. Run 4 (SOMA depth-averaged velocity up to 10 m and water level) resulted in the lowest RMSE values at both the Faro Ocean Buoy and Faro Coast Buoy. Run 4 produced the highest number of “best” metric values at all the locations, which indicates that the run with the depth-averaged velocity up to the first 10 m of the water column produced the most accurate results for the easterly wave simulation. The simulations performed better than CMEMS at all the locations, with the exception of the Sines Buoy, despite the fact that CMEMS assimilates wave observations and our simulations do not.
To further support these findings, the results of the DM test on the statistical significance are shown in Table 10.

Table 10.
Diebold–Mariano statistical analysis to test the statistical significance of each hydrodynamically forced run compared to the run without hydrodynamic forcing during the E-SE storm.
The DM test in Table 10 demonstrates that all the modeled runs, except for the run of the SOMA water level only (Run 2) and the CMEMS model, are statistically different from the run without SOMA input. The mean DM across all the locations was statistically significant (> 1.96) for Runs 2–6, implying that all the modeled runs that incorporated the current velocity from SOMA were significant. However, the run with the depth-averaged velocity for the entire water column (Run 6) performed worse than the baseline run without SOMA input due to a negative DM value (−2.186). The high DM values of 6.425, 6.999, and 6.991 for Run 3, Run 4, and Run 5, respectively, imply better performance from model runs incorporating the current velocity from the upper layers of the water column. The run with the SOMA depth-averaged velocity for the upper 10 m of the water column (Run 4) achieved the highest DM statistic, with a value of 6.999, which was also the same conclusion reached in the standard statistic analysis shown in Table 9. The very low p-values across all the simulations and all the locations also demonstrate strong evidence for statistical difference compared to the run without SOMA input.
To further analyze how the current velocity and water levels impacted Hs over the entire spatial domain, Figure 11 shows spatial maps of the difference in Hs between each simulation and the simulation without hydrodynamic forcing during the easterly storm. The time series of the current velocities at the four buoy locations are shown in Figure 12.
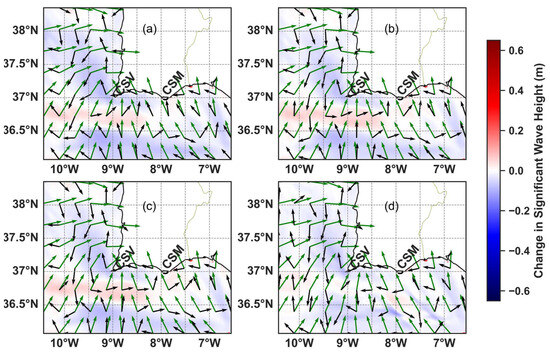
Figure 11.
The 2D spatial maps depicting the average change in Hs during the E-SE storm due to the (a) surface current velocity and water level forcing, (b) 10 m depth-averaged current velocity and water level forcing, (c) 20 m depth-averaged current velocity and water level forcing, and (d) depth-averaged current velocity from the entire water column and water level forcing. The black arrows represent the mean current velocity direction, and the green arrows represent the mean wave direction during the E-SE storm. Key coastal areas of Cape São Vicente (CSV) and Cape Santa Maria (CSM) are highlighted.
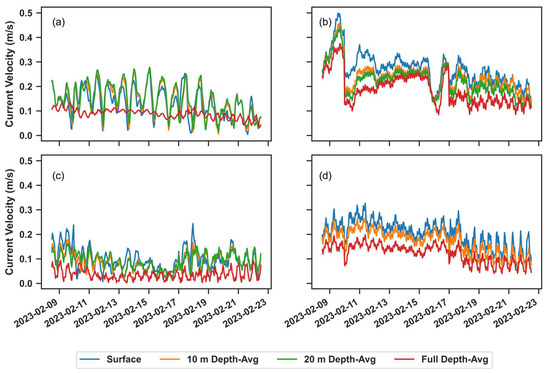
Figure 12.
Time series of SOMA current velocities at the locations of the (a) Faro Ocean Buoy, (b) Faro Coast Buoy, (c) Cadiz Buoy, and (d) Sines Buoy during the storm with easterly waves (8 February 2023–22 February 2023).
The simulation with waves coming from the E-SE resulted in higher changes in Hs compared to the storm with waves coming from the W-SW. The highest average change in Hs was observed on the southeast coast, where the average Hs during the storm increased by 0.623 m or 209% when comparing the run with no hydrodynamic input and all the SWAN simulations forced with SOMA hydrodynamics. The increase in Hs along this shoreline is attributed to varying water levels from SOMA, which are shown in Appendix A (Figure A5). Furthermore, Figure 12b demonstrates that the velocity magnitude closer to the coast was much higher compared to that offshore. There was not much variability between the changes in Hs for the simulations forced with the varying depth-averaged velocities for the E-SE storm. All the 2D spatial maps show significant increases in Hs at the coast, which highlight the impact that varying water levels have on Hs closer to the coastline. It is noted that in all the spatial maps in Figure 11, where the current flowed opposite to the easterly mean wave direction, increases in Hs were observed. When the currents and waves flowed easterly, decreases in Hs were observed. In general, the velocity magnitude was much smaller for the easterly simulation compared to velocity magnitude during the westerly simulation. However, the same effect still occurred where waves and currents in opposing directions resulted in increases in Hs and following currents resulted in decreases in Hs. The magnitude of these changes in Hs ranged from approximately 10–20 cm offshore to more than 0.6 m near the coast. Areas with larger magnitudes of velocity also resulted in greater changes in Hs. Opposing currents occurred more frequently off the southwest coast, and following currents occurred predominantly off the south coast and west coast.
3.3.3. Wave Propagation in Shallow Waters
To evaluate how waves propagate further into the domain up to nearshore areas, Figure 13 shows the time series results at the Armona Buoy for the simulation when data at this buoy were available.
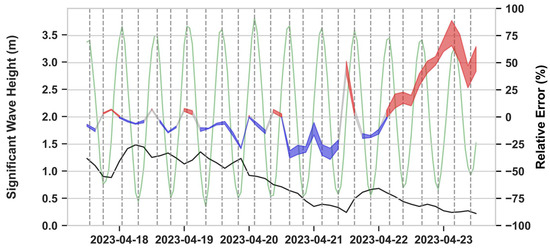
Figure 13.
Time series of significant wave height at Armona Buoy. The black line represents the significant wave height of in situ buoy observations (left axis), and shaded areas indicate the range of relative error across the seven model runs (Table 4), with overpredictions in red and underpredictions in blue. The green line represents the tidal level (from SOMA), with the high and low tides marked with the vertical dashed line.
Figure 13 shows a slight underprediction in Hs during the highest peaks of Hs on 18 April 2023, 19 April 2023, and 20 April 2023 and a slight overprediction of Hs for the lowest peaks of Hs on these days. There were several time instances during the simulation where the models and observations were in perfect agreement. The variability between model runs was quite small, with the variability in relative error ranging from approximately 1% to 5% throughout the simulation. This variability became larger toward the end of the simulation on 22 April 2023, when Hs started to decrease, and the variability in the relative error between the models became more spread out, with differences between errors ranging around 30%. All the models overpredicted Hs after this decrease in Hs on 22 April 2023. The statistics metrics for all buoy stations with available data during the simulation time are shown in Table 11.

Table 11.
Error metrics of significant wave height for the simulation 17 April 2023–23 April 2023. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
Table 11 shows very good metric scores amongst all simulations, especially at Armona Buoy, which is a very good indicator of how waves propagate further into the domain up to nearshore areas. The RMSE did not vary much between simulations at Armona Buoy. At Faro Coast Buoy, the largest reduction in RMSE when comparing with the run without any hydrodynamic input was for the simulation with the SOMA depth-averaged currents up 10 m of the water column and water level with a reduction of 0.015 m. At Cadiz Buoy the simulation with surface currents and water level (Run 3) reduced the RMSE by 0.008 m in comparison to the run without any hydrodynamic input (Run 1). All simulations performed better than the CMEMS model. However, CMEMS achieved a slightly lower BIAS value at Armona Buoy. The simulation that received the highest number of the “best” error metrics was the run with SOMA surface currents and water level (Run 3).
To further support these findings, the DM test for the simulation in low wave conditions is shown in Table 12.

Table 12.
Diebold-Mariano statistical analysis to test statistical significance of each hydrodynamically forced run during the simulation from 17 April 2023–23 April 2023.
Overall, Table 12 demonstrates that the mean DM statistic values for all simulations across all locations was less than 1.96, which implies that the hydrodynamically forced runs were not statistically significant during the simulation with low wave conditions. The CMEMS model was the only modeled run with statistical significance as it resulted in a mean DM value of −2.642, but this implies that it performed worse than the baseline run without SOMA input. Model performance was least significant at Armona Buoy, which is reflected in the absolute values of the DM statistics being less than 1.96 and the very high p-values > 0.05. This is further justified in both the time series of Figure 12 and the statistics analysis of Table 9. Contrary to what was found in the strong westerly and easterly storms, the run with SOMA Water Level only and the depth-averaged velocity of the entire water column (Run 2 and Run 6) yielded the best results at Faro Coast Buoy with DM values of 4.802 and 1.964. At Cadiz Buoy the best performance was from the run with SOMA surface currents and water level (Run 3) with a DM statistic of 2.277. Overall, the run with SOMA surface currents and water level still performed the best across all locations with a mean DM statistic of 1.387, which further validates the conclusion that model results improve with this model configuration. The results of the DM analysis during this simulation also underscore the small variability amongst simulations during low wave conditions.
3.3.4. Main Findings of the Hydrodynamically Forced Simulations
The results show overall improvements in wave model accuracy when forced with current velocity and water level. In the storm with waves coming from W-SW, reduction in RMSE ranged from 1.6% (Faro Coast Buoy) to 27.6% (Cadiz Buoy) and reduction in BIAS ranged from 12.5% (Faro Ocean Buoy) to 80% (Faro Coast Buoy) when comparing Hs results to the run with no hydrodynamic input (Run 1). The largest improvement was observed at Cadiz Buoy where RMSE was reduced by 16.4 cm and BIAS was reduced by 17.9 cm for the run with surface currents and water level. The magnitude of improvement at Faro Coast Buoy was smaller, with a reduction in RMSE of only 0.4 cm for the run with surface currents and water level (Run 3) and a reduction in BIAS of 3 cm for the run that implemented the depth-averaged velocity of the entire water column and water level (Run 6). At Faro Ocean Buoy the RMSE and BIAS were reduced by 5.4 cm and 5.1 cm, respectively for the run with surface currents and water level (Run 3). At Sines Buoy this same run reduced the RMSE by 2.9 cm and the run with the depth-averaged velocity for the entire water column (Run 5) reduced the BIAS by 8.6 cm. The DM-statistic, which is widely used to determine the statistical significance between forecasting models, demonstrated that all runs forced with current velocity from the surface layer and depth-averaged velocity from the upper 10 m and 20 m of the water column are statistically different compared to the run without SOMA input. The run with surface currents and water level was the most significant with a DM value of 6.911.
For the storm with waves coming from E-SE, RMSE was reduced by approximately 6% at all buoy locations, corresponding to a reduction in RMSE by 2 cm. At Faro Ocean and Faro Coast buoys the run that achieved the lowest reduction in RMSE was the run with the depth-averaged velocity up to 10 m of the water column (Run 4). At Sines Buoy, the run that achieved the lowest reduction in RMSE was the run with surface currents and water level (Run 3). The BIAS had a more significant improvement where it was reduced by 17% or 3 cm at Faro Coast Buoy and Sines Buoy. At Faro Ocean Buoy it was reduced by 5% or 1.6 cm. The magnitude of improvement of just a few centimeters is a common conclusion reached in previous literature, where improvements of only a few centimeters have been observed [7,8,9]. However, these small improvements are still statistically significant for runs incorporating current velocity from the upper layers of the water column according to the DM-statistic result (< 1.96) as well as the very low p-value (p < 0.05). This further signifies the higher influence that the upper layers of the water column have on wave propagation in this region. Including current velocity layers from the deepest parts of the water column, where the current velocity is weaker, reduces the overall magnitude of the depth-averaged 2D current field, making it less representative of the currents that actually influence wave propagation.
In this study, the simulation with waves coming from E-SE produced the most accurate results, even better than the CMEMS model, which was used to force the model with wave conditions at the boundary. The smallest differences were seen when the significant wave height was smaller, which is evident in the April 2023 simulation. This result is similar to the finding from Causio et al. [9] who found that coupling between hydrodynamic and wave models was most effective in periods with higher wave activity.
In terms of the spatial distribution of the effects of currents and water levels on wave propagation in the southwest Iberian Peninsula, the storm with waves from W-SW resulted in larger areas within the computational domain with increases in Hs. This is likely due to the westward circulation on the southern coast interacting with the westerly waves. Further offshore on the south coast, waves and currents flowed in the same direction, which resulted in decreases in Hs. In the storm with E-SE waves, decreases in Hs occurred over a broader area within the computational domain due to the water circulation and waves flowing in the same easterly direction. The observed changes in the distribution of wave energy can be explained by the Doppler effect associated with wave–current interaction. When the current opposes the wave, the energy is compressed and the wave height steepens. On the other hand, when a current and wave flow in the same direction, the wavelength is stretched, reducing the wave height. These changes in wave energy distribution are consistent with results of other studies on wave–current interactions [7,8,15,16,17,18,19,20,21].
For both storms, Hs increased along the southern coastline east of Cape Santa Maria toward Spain, underscoring the influence of wave–current interactions along this dynamic coastal zone. The consistent increase of Hs in this nearshore area across all model scenarios indicate the crucial role that both wave–current interaction and water level modulation have on wave propagation along this complex coastal geometry. Along the southwest coast, increases in Hs were observed just north of Cape São Vicente for the W-SW storm only. As the ocean circulation patterns and geomorphology of this region are both complex, accounting for all variables such as current velocity and water levels in wave propagation models for this study area is crucial. Previous studies that have developed wave models for this region have neglected these imperative forcing variables, thus overlooking crucial processes that affect sediment transport rates, which have further implications on marine structures [3,4,5] and the shoreline [1].
Hydrodynamic forcing on the wave model resulted in significant changes in the wave field based on the direction of the waves and currents along with current velocity magnitude. The interaction between the dominant westerly waves in winter and the Portugal Coastal Countercurrent that flows westward at this time resulted in increases in Hs close to shore off the south coast, but decreases in Hs further offshore where the Azores Current flows easterly. As the current velocity magnitude is stronger for surface currents, hydrodynamic forcing of the wave model with this current velocity field resulted in larger changes in Hs throughout the computational domain. In contrast, in the case of easterly waves, the magnitude of changes in Hs was smaller as these waves are less energetic. Decreases in Hs were observed along the south coast where the Portugal Coastal Countercurrent flowed in the same direction. Increases in Hs were observed offshore due to the interaction with the eastward Azores Current. For both storms, increases in Hs were observed very close to shore, especially east of Cape Santa Maria. This occurred for all depth scenarios, underscoring the significance of modulating water levels along with wave–current interactions in shallow waters.
Figure 14 quantifies the impact that both the magnitude of current velocity along with the wave–current angle difference had on changes in Hs for both the westerly and easterly storms. It compares the average change in Hs between simulations without hydrodynamic input and simulations forced with surface current velocity and water levels. Results for simulations forced with depth-averaged velocities are shown in Appendix A (Figure A6 and Figure A7).
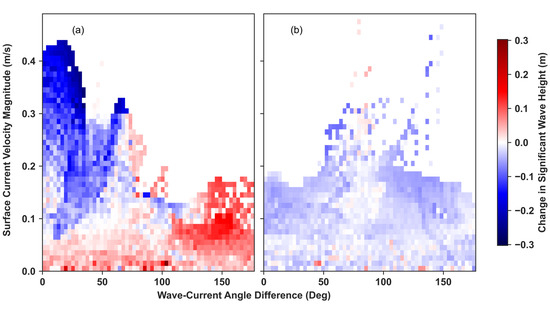
Figure 14.
Changes in Hs due to the combination of wave–current angle difference and surface current velocity magnitude for the (a) westerly storm and (b) easterly storm.
Results of the westerly storm (Figure 14a) demonstrated larger decreases in Hs due to following currents (wave–current angle difference < 30°) and smaller increases in Hs in the case of opposing currents (wave–current angle difference between 150° and 180°). The velocity magnitude for the case of following currents was much higher compared to the velocity of opposing currents, which further justifies the larger changes in Hs. The easterly storm (Figure 14b) did not have the same effect as both the current velocity magnitude and resulting changes in Hs were smaller. The effects of the currents during this storm resulted in mostly decreases in Hs independent of the wave–current angle difference. This result is consistent with a study by Barnes et al. [10], who also found that when current velocity was less than 0.5 m/s, decreases in Hs were observed regardless of the wave–current angle difference. The increase in Hs as shown in the spatial map of Figure 11a reveal that these increases occur near the coastline, which is due to the inclusion of water levels from SOMA. Figure 11 and Figure 14 both reveal slight increases in Hs when waves and currents meet at right angles. These changes in the wave field have also been observed by Wei et al. [3] who implemented a numerical flume model to study wave–current interaction.
While the differences between simulations at all time periods were relatively small, the simulation that included surface currents and water levels consistently achieved results that were most similar to observations. This model configuration also proved to be the most statistically significant according to the DM test. The improved performance of the model when incorporating surface currents is consistent with previous studies who have used surface currents in their wave models [7,8,10]. This highlights the necessity of including the coupling when simulating waves in this study area.
Limitations arise from the two-way coupling between wave and ocean circulation models that use depth-integrated velocities over an unstructured mesh. As these 2D models do not compute velocity at each vertical grid point, the computational time is much faster, but this two-way coupling ignores the influence of current velocity from the most significant layers attributing to wave propagation i.e., the surface layer. It is crucial to quantify current velocity over the vertical direction of the water column, and to properly compute the 2D current field attributed to wave propagation. The overall findings of this work demonstrate that simply computing the depth-averaged velocity over the entire water column yields less accurate results of wave propagation, and thus it is imperative to extract current velocity from a specific depth when coupling ocean circulation models with wave propagation models.
4. Conclusions
The wave model SWAN has been implemented, calibrated, and validated for the southern coast of the Iberian Peninsula. The standalone SWAN setup achieved results very similar to buoy observations, with low RMSE values ranging from 0.156 m to 0.407 m and low BIAS values ranging from −0.016 m to 0.255 m at several buoy stations during the validation period. It thus can be used to accurately represent wave characteristics on the south coast of Portugal. Improvements to this model have been investigated by assessing several model configurations that include various hydrodynamic forcing conditions from a previously developed model (SOMA). This was achieved by extracting water levels and a 2D current velocity field at different depths throughout the water column and testing the results under two storm conditions that are typical for the study region. When the wave direction and current velocity followed the same direction, the significant wave height decreased by approximately 10 cm. In cases of opposing currents, the significant wave height increased by approximately 20 cm.
For the E-SE storm, Hs increased significantly along the southeast coast due to the temporally varying water levels provided by SOMA. The coupling of wave and hydrodynamic models can capture these physical processes that would otherwise be missed in standalone wave or hydrodynamic models. This is especially crucial for the south coast of Portugal, given the dynamic nature of the coastline and the presence of rip currents in some areas, which pose a hazard.
The effects of this hydrodynamic forcing on the wave model showed small differences over the average time of the simulation periods between the results that varied the 2D current velocity field, but, overall, statistically significant improvements were made with the addition of the current velocity and water level from SOMA. The configuration that produced the best overall results was SOMA surface currents and the water level. This configuration will be used for all future operational runs of the wave model. The findings from this study present novel results on how water circulation impacts the wave field on the south coast of Portugal according to numerical model results.
Adding hydrodynamic forcing was demonstrated to be statistically significant for the wave model implemented on the southwest coast of the Iberian Peninsula. These results hold value for developers of shoreline protection models who require accurate representations of wave–current interactions. They can further be used in marine energy converter models, as wave energy is a valuable renewal energy resource. These findings further have applications to the design of coastal and offshore structures, as both wave and hydrodynamic loadings can damage these sites.
The main limitation of this study is that a one-way coupling approach was implemented, as opposed to a two-way coupling mechanism, to simulate the complex processes between surface currents and waves. However, it was imperative to evaluate precisely where in the water column the current velocity had the strongest influence on wave propagation. Therefore, the effects of currents on waves have been quantified, but updates to the current field due to waves have not been accounted for. Thus, future work will develop a fully integrated coupled system between SWAN with SOMA that uses surface currents and water level forcing as inputs for the wave model and radiation stress computed by SWAN as input for SOMA, allowing for the complete interaction between these complex processes. Future work will further assess the influences of wave dynamics on water circulation by evaluating the effects of radiation stress and bottom orbital velocities. In addition, simulations will be run over SOMA’s level 2 computational grid at a finer resolution of 1 km to evaluate the impacts of wave–current interactions in shallower water at a higher resolution. This was not performed for this study due to the high computational cost. The results of this work demonstrate the robustness of the model and the impacts that wave–current interactions have off the southwest coast of the Iberian Peninsula and, furthermore, set the stage for future developments on the study of wave–current interactions at a finer resolution near the coastline.
Author Contributions
Conceptualization, L.M., J.L.G., and F.M.; methodology, L.M., J.L.G., and F.M.; software, L.M.; validation, L.M.; formal analysis, L.M.; investigation, L.M.; data curation, L.M.; writing—original draft preparation, L.M.; writing—review and editing, L.M., J.L.G., and F.M.; visualization, L.M.; supervision, J.L.G. and F.M.; project administration, F.M.; funding acquisition, F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Portuguese Foundation of Science and Technology (FCT) to CIMA (grant number UID/00350/2025 CIMA: https://doi.org/10.54499/UID/00350/2025) and ARNET (grant number LA/P/0069/2020); CEEC INST. (10.54499/CEECINST/00146/2018/CP1493/CT0012); the EU-H2020 NAUTILOS project (grant number 101000825), and the EU-HEUROPE THETIDA project (grant number 101095253).
Data Availability Statement
The wave model results along with the hydrodynamic data used to force the wave model are openly available at https://cima-somathredds.ualg.pt/thredds/catalog/catalog.html. In-situ data at Faro Ocean, Cadiz, and Sines buoys for model validation were obtained from https://marineinsitu.eu/dashboard/. Restrictions apply to the availability of the data at Faro Coast and Armona buoys. Data were obtained from Instituto Hidrográfico and CIMA at the University of Algarve.
Acknowledgments
The authors would like to thank Erwan Garel from CIMA at the University of Algarve for providing wave data from the Armona Buoy as well as Instituto Hidrográfico for providing wave data from the Faro Coast Buoy.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
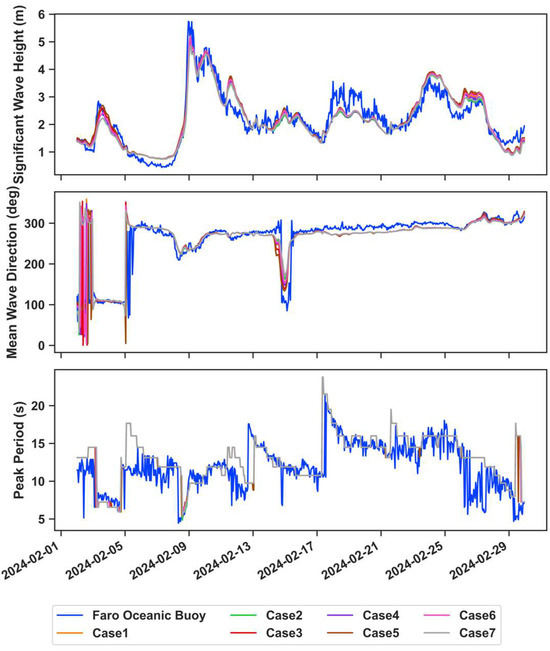
Figure A1.
Time series of Hs, Dir, and Tp for each model configuration during the calibration period (February 2024) at the Faro Oceanic Buoy.
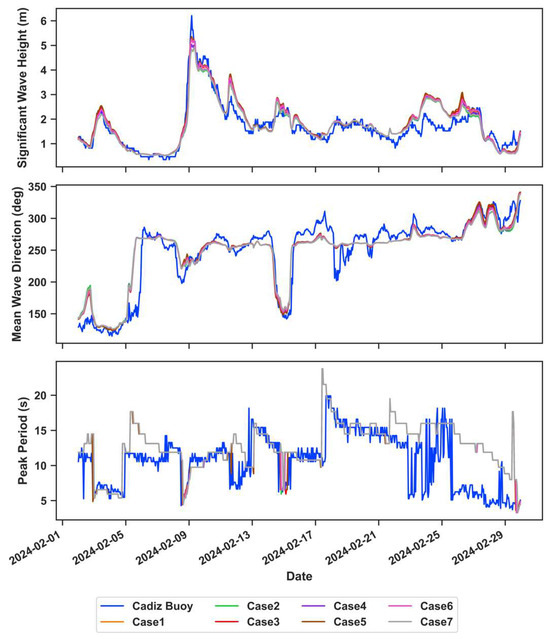
Figure A2.
Time series of Hs, Dir, and Tp for each model configuration during the calibration period (February 2024) at the Cadiz Buoy.
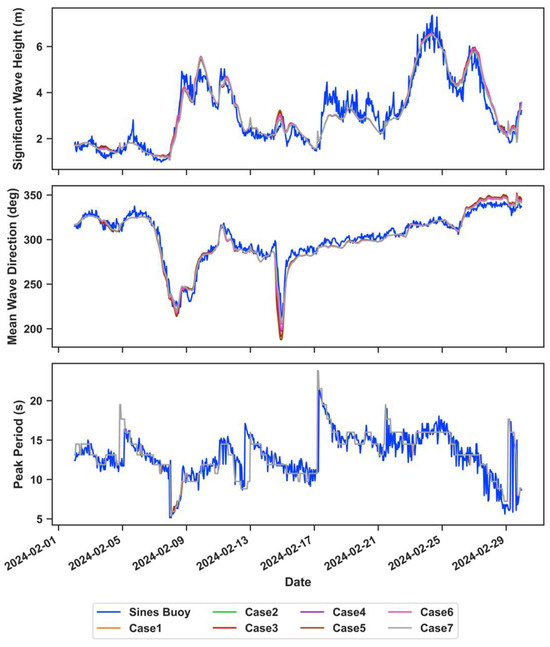
Figure A3.
Time series of Hs, Dir, and Tp for each model configuration during the calibration period (February 2024) at the Sines Buoy.

Table A1.
Error metrics of the mean wave direction, comparing the model results of each calibration setting with buoy observations. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
Table A1.
Error metrics of the mean wave direction, comparing the model results of each calibration setting with buoy observations. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
| Faro Ocean Buoy | Cadiz Buoy | Sines Buoy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (Deg.) | BIAS (Deg.) | MSS | R | RMSE (Deg.) | BIAS (Deg.) | MSS | R | RMSE (m) | BIAS (m) | MSS | R | |
| Case 1 | 38.067 | 1.631 | 0.893 | 0.801 | 20.933 | 0.729 | 0.957 | 0.932 | 6.857 | −1.781 | 0.985 | 0.976 |
| Case 2 | 41.279 | 3.578 | 0.865 | 0.760 | 21.722 | 0.318 | 0.953 | 0.927 | 6.058 | −1.641 | 0.988 | 0.979 |
| Case 3 | 31.859 | −0.904 | 0.930 | 0.866 | 20.648 | 1.005 | 0.959 | 0.932 | 7.607 | −1.882 | 0.982 | 0.972 |
| Case 4 | 37.551 | 1.481 | 0.895 | 0.806 | 21.276 | 0.638 | 0.956 | 0.929 | 6.751 | −1.755 | 0.985 | 0.976 |
| Case 5 | 30.589 | −2.218 | 0.936 | 0.878 | 20.394 | 1.202 | 0.961 | 0.934 | 8.232 | −1.953 | 0.979 | 0.968 |
| Case 6 | 37.340 | 1.282 | 0.897 | 0.809 | 20.718 | 0.684 | 0.958 | 0.934 | 6.700 | −1.823 | 0.986 | 0.977 |
| Case 7 | 41.633 | 3.735 | 0.861 | 0.755 | 21.500 | 0.249 | 0.954 | 0.930 | 5.974 | −1.684 | 0.988 | 0.979 |

Table A2.
Error metrics of the peak period, comparing the model results of each calibration setting with buoy observations. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
Table A2.
Error metrics of the peak period, comparing the model results of each calibration setting with buoy observations. Values in bold indicate the lowest (RMSE or BIAS) or highest (MSS or R) among all the cases.
| Faro Buoy | Cadiz Buoy | Sines Buoy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (s) | BIAS (s) | MSS | R | RMSE (s) | BIAS (s) | MSS | R | RMSE (s) | BIAS (s) | MSS | R | |
| Case 1 | 2.812 | 1.020 | 0.780 | 0.635 | 3.955 | 1.976 | 0.702 | 0.540 | 1.948 | 0.142 | 0.869 | 0.754 |
| Case 2 | 2.839 | 1.034 | 0.776 | 0.628 | 3.958 | 1.998 | 0.700 | 0.540 | 1.947 | 0.144 | 0.869 | 0.754 |
| Case 3 | 2.812 | 1.026 | 0.779 | 0.634 | 3.900 | 1.917 | 0.711 | 0.553 | 1.948 | 0.142 | 0.868 | 0.753 |
| Case 4 | 2.812 | 1.021 | 0.780 | 0.635 | 3.955 | 1.978 | 0.701 | 0.540 | 1.948 | 0.142 | 0.869 | 0.754 |
| Case 5 | 2.769 | 0.988 | 0.787 | 0.646 | 3.888 | 1.907 | 0.714 | 0.556 | 1.948 | 0.145 | 0.868 | 0.753 |
| Case 6 | 2.806 | 1.033 | 0.781 | 0.637 | 3.985 | 2.025 | 0.697 | 0.535 | 1.945 | 0.150 | 0.869 | 0.755 |
| Case 7 | 2.833 | 1.047 | 0.777 | 0.631 | 4.010 | 2.053 | 0.692 | 0.529 | 1.945 | 0.151 | 0.869 | 0.754 |

Table A3.
Sensitivity tests for directional spreading.
Table A3.
Sensitivity tests for directional spreading.
| Sensitivity Test | Directional Spreading | Simulation Timeframe |
|---|---|---|
| 1 | Degree E30 N30 S30 W40 | February 2024 |
| 2 | Degree E40 N40 S40 W40 | February 2024 |
| 3 | Power E2 N2 S3 W4 | February 2024 |
| 4 | Power E1.5 N1.5 S1.5 W1.5 | February 2024 |
| 5 | Power E2 N2 S3 W3 | February 2024 |
| 6 | Power E3 N3 S3 W3 | February 2024 |
| 7 | Power E15 N15 S15 W15 | February 2024 |
| 8 | Power E2 N4 S3 W4 | February 2024 |
| 9 | Power E4 N4 S4 W4 | February 2024 |
| 10 | Power E2 N2 S2 W4 | February 2024 |
| 11 | Power E2 N2 S2 W3 | February 2024 |
| 12 | Power E2 N2 S3 W4 | November 2023 |
| 13 | Power E2 N2 S2 W4 | November 2023 |
| 14 | Power E2 N2 S2 W3 | November 2023 |
| 15 | Power E2 N2 S2 W4 | 21 October 2023–11 July 2023 (westerly storm) |
| 16 | Power E2 N2 S2 W4 | 8 February 2023–22 February 2023 (easterly storm) |

Table A4.
Error metrics of the significant wave height during the calibration period (February 2024). Directional spreading refers to values for directional spreading for each segment on each side (E = east, N = north, S = south, and W = west). The simulation cases with the best metrics are highlighted in bold.
Table A4.
Error metrics of the significant wave height during the calibration period (February 2024). Directional spreading refers to values for directional spreading for each segment on each side (E = east, N = north, S = south, and W = west). The simulation cases with the best metrics are highlighted in bold.
| Faro Ocean Buoy | Cadiz Buoy | Sines Buoy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Directional Spreading | RMSE (m) | BIAS (m) | MSS | R | RMSE (m) | BIAS (m) | MSS | R | RMSE (m) | BIAS (m) | MSS | R |
| Degree E30 N30 S30 W40 | 0.404 | −0.070 | 0.955 | 0.916 | 0.370 | 0.082 | 0.958 | 0.923 | 0.421 | −0.022 | 0.978 | 0.956 |
| Degree E40 N40 S40 W40 | 0.415 | −0.027 | 0.952 | 0.908 | 0.424 | 0.154 | 0.945 | 0.907 | 0.398 | −0.025 | 0.980 | 0.960 |
| Power E2 N2 S3 W4 | 0.348 | −0.107 | 0.966 | 0.941 | 0.280 | −0.032 | 0.976 | 0.954 | 0.387 | 0.007 | 0.981 | 0.962 |
| Power E1.5 N1.5 S1.5 W1.5 | 0.390 | −0.050 | 0.958 | 0.920 | 0.374 | 0.103 | 0.957 | 0.923 | 0.401 | −0.014 | 0.980 | 0.960 |
| Power E2 N2 S3 W3 | 0.359 | −0.104 | 0.964 | 0.936 | 0.292 | −0.015 | 0.974 | 0.950 | 0.394 | 0.001 | 0.980 | 0.961 |
| Power E3 N3 S3 W3 | 0.359 | −0.102 | 0.964 | 0.936 | 0.291 | −0.013 | 0.974 | 0.950 | 0.410 | −0.001 | 0.979 | 0.959 |
| Power E15 N15 S15 W15 | 0.515 | −0.346 | 0.926 | 0.920 | 0.434 | −0.302 | 0.940 | 0.939 | 0.447 | −0.004 | 0.975 | 0.951 |
| Power E2 N4 S3 W4 | 0.349 | −0.104 | 0.966 | 0.940 | 0.279 | −0.031 | 0.976 | 0.954 | 0.414 | 0.003 | 0.979 | 0.958 |
| Power E4 N4 S4 W4 | 0.355 | −0.125 | 0.965 | 0.940 | 0.276 | −0.066 | 0.977 | 0.957 | 0.414 | 0.001 | 0.979 | 0.958 |
| Power E2 N2 S2 W4 | 0.346 | −0.072 | 0.967 | 0.939 | 0.297 | 0.026 | 0.973 | 0.948 | 0.388 | 0.009 | 0.981 | 0.962 |
| Power E2 N2 S2 W3 | 0.354 | −0.068 | 0.965 | 0.935 | 0.314 | 0.041 | 0.970 | 0.943 | 0.394 | 0.003 | 0.980 | 0.961 |

Table A5.
Error metrics of the significant wave height during the validation period (November 2023). Directional spreading refers to values for directional spreading for each segment on each side (E = east, N = north, S = south, and W = west). The simulation configuration with the best metrics is highlighted in bold.
Table A5.
Error metrics of the significant wave height during the validation period (November 2023). Directional spreading refers to values for directional spreading for each segment on each side (E = east, N = north, S = south, and W = west). The simulation configuration with the best metrics is highlighted in bold.
| Faro Ocean Buoy | Faro Coast Buoy | Cadiz Buoy | Sines Buoy | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Directional Spreading | RMSE | BIAS | MSS | R | RMSE | BIAS | MSS | R | RMSE | BIAS | MSS | R | RMSE | BIAS | MSS | R |
| E2 N2 S3 W4 | 0.341 | 0.058 | 0.956 | 0.93 | 0.217 | −0.145 | 0.950 | 0.947 | 0.251 | 0.054 | 0.957 | 0.942 | 0.335 | −0.024 | 0.989 | 0.982 |
| E2 N2 S2 W4 | 0.357 | 0.092 | 0.953 | 0.93 | 0.204 | −0.121 | 0.956 | 0.948 | 0.300 | 0.118 | 0.942 | 0.933 | 0.322 | −0.013 | 0.990 | 0.983 |
| E2 N2 S2 W3 | 0.368 | 0.101 | 0.950 | 0.922 | 0.183 | −0.093 | 0.964 | 0.951 | 0.328 | 0.149 | 0.931 | 0.925 | 0.328 | −0.022 | 0.990 | 0.983 |

Table A6.
Error metrics of the significant wave height during the storm with westerly waves with the directional spreading set at power E2 N2 S2 W4.
Table A6.
Error metrics of the significant wave height during the storm with westerly waves with the directional spreading set at power E2 N2 S2 W4.
| Level 1 Simulation 21 October 2023 12:00:00–7 November 2023 12:00:00–Waves Coming From the West | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Faro Oceanic Buoy | Faro Coast Buoy | Cadiz Buoy | Sines Buoy | |||||||||||||
| Run ID | RMSE (m) | BIAS (m) | MSS | R | RMSE (m) | BIAS (m) | MSS | R | RMSE (m) | BIAS (m) | MSS | R | RMSE (m) | BIAS (m) | MSS | R |
| 1 | 0.539 | 0.426 | 0.898 | 0.922 | 0.283 | −0.127 | 0.945 | 0.933 | 0.517 | 0.417 | 0.890 | 0.927 | 0.406 | −0.046 | 0.981 | 0.967 |
| 2 | 0.540 | 0.426 | 0.898 | 0.922 | 0.284 | −0.127 | 0.945 | 0.932 | 0.516 | 0.417 | 0.890 | 0.927 | 0.406 | −0.046 | 0.981 | 0.967 |
| 3 | 0.459 | 0.339 | 0.921 | 0.927 | 0.255 | 0.011 | 0.952 | 0.919 | 0.375 | 0.250 | 0.937 | 0.935 | 0.390 | 0.019 | 0.983 | 0.968 |
| 4 | 0.461 | 0.341 | 0.921 | 0.928 | 0.256 | 0.018 | 0.952 | 0.920 | 0.381 | 0.258 | 0.935 | 0.935 | 0.394 | 0.020 | 0.983 | 0.967 |
| 5 | 0.462 | 0.343 | 0.921 | 0.928 | 0.257 | 0.020 | 0.952 | 0.921 | 0.385 | 0.262 | 0.935 | 0.936 | 0.391 | −0.165 | 0.983 | 0.975 |

Table A7.
Error metrics of the significant wave height during the storm with easterly waves with the directional spreading set at power E2 N2 S2 W4.
Table A7.
Error metrics of the significant wave height during the storm with easterly waves with the directional spreading set at power E2 N2 S2 W4.
| Faro Oceanic Buoy | Faro Coast Buoy | Sines Buoy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Run ID | RMSE (m) | BIAS (m) | MSS | R | RMSE (m) | BIAS (m) | MSS | R | RMSE (m) | BIAS (m) | MSS | R |
| 1 | 0.385 | −0.265 | 0.964 | 0.962 | 0.367 | −0.266 | 0.954 | 0.958 | 0.356 | 0.162 | 0.901 | 0.878 |
| 2 | 0.385 | −0.265 | 0.964 | 0.962 | 0.368 | −0.266 | 0.954 | 0.958 | 0.356 | 0.162 | 0.901 | 0.878 |
| 3 | 0.373 | −0.275 | 0.966 | 0.969 | 0.358 | −0.254 | 0.955 | 0.956 | 0.333 | 0.118 | 0.912 | 0.880 |
| 5 | 0.360 | −0.255 | 0.969 | 0.969 | 0.352 | −0.241 | 0.957 | 0.955 | 0.341 | 0.135 | 0.908 | 0.880 |
Figure A4.
Time series of water levels at the (a) Faro Ocean Buoy, (b) Faro Coast Buoy, (c) Cadiz Buoy, and (d) Sines Buoy during the storm with westerly waves (21 October 2023–7 November 2023).
Figure A5.
Time series of water levels at the (a) Faro Ocean Buoy, (b) Faro Coast Buoy, (c) Cadiz Buoy, and (d) Sines Buoy during the storm with easterly waves (8 February 2023–22 February 2023).

Figure A6.
Changes in Hs due to the combination of the wave–current angle difference and surface current velocity magnitude during the W-SW storm due to (a) the surface current velocity and water level forcing, (b) 10 m depth-averaged current velocity and water level forcing, (c) 20 m depth-averaged current velocity and water level forcing, and (d) depth-averaged current velocity from the entire water column and water level forcing.
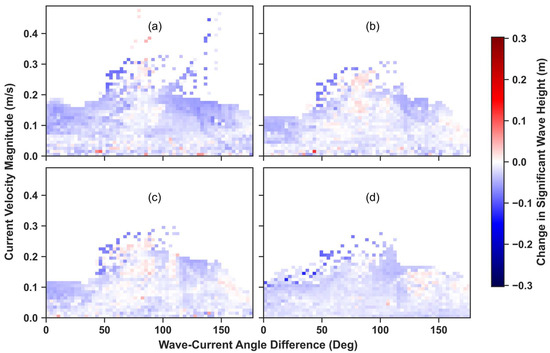
Figure A7.
Changes in Hs due to the combination of the wave–current angle difference and surface current velocity magnitude during the E-SE storm due to (a) the surface current velocity and water level forcing, (b) 10 m depth-averaged current velocity and water level forcing, (c) 20 m depth-averaged current velocity and water level forcing, and (d) depth-averaged current velocity from the entire water column and water level forcing.
References
- Scala, P.; Manno, G.; Cozar, L.C.; Ciraolo, G. COAST-PROSIM: A Model for Predicting Shoreline Evolution and Assessing the Impacts of Coastal Defence Structures. Water 2025, 17, 269. [Google Scholar] [CrossRef]
- Apsley, J.M.; Zhang, X.; Damian, I.E.; Iacchetti, M.F.; Liao, Z.; Stansby, P.; Li, G.; Li, G.; Wolgamot, H.; Gaudin, C.; et al. Integrated Hydrodynamic-Electrical Hardware Model for Wave Energy Conversion with M4 Ocean Demonstrator. In Proceedings of the European Wave and Tidal Energy Conference, Bilbao, Spain, 3–7 September 2023. [Google Scholar]
- Wei, K.; Hu, K. CFD Modeling of Orthogonal Wave-Current Interactions in a Rectangular Numerical Wave Basin. Adv. Bridge Eng. 2024, 5, 17. [Google Scholar] [CrossRef]
- Gudmestad, O.T. Modelling of Waves for the Design of Offshore Structures. J. Mar. Sci. Eng. 2020, 8, 293. [Google Scholar] [CrossRef]
- Zhang, X.; Simons, R.; Zheng, J.; Zhang, C. A Review of the State of Research on Wave-Current Interaction in Nearshore Areas. Ocean Eng. 2022, 243, 110202. [Google Scholar] [CrossRef]
- Marsooli, R.; Orton, P.M.; Mellor, G.; Georgas, N.; Blumberg, A.F. A Coupled Circulation-Wave Model for Numerical Simulation of Storm Tides and Waves. J. Atmos. Ocean. Technol. 2017, 34, 1449–1467. [Google Scholar] [CrossRef]
- Calvino, C.; Dabrowski, T.; Dias, F. Current Interaction in Large-Scale Wave Models with an Application to Ireland. Cont. Shelf Res. 2022, 245, 104798. [Google Scholar] [CrossRef]
- Barnes, M.A.; Rautenbach, C. Toward Operational Wave-Current Interactions Over the Agulhas Current System. J. Geophys. Res. Oceans 2020, 125, e2020JC016321. [Google Scholar] [CrossRef]
- Causio, S.; Ciliberti, S.A.; Clementi, E.; Coppini, G.; Lionello, P. A Modelling Approach for the Assessment of Wave-Currents Interaction in the Black Sea. J. Mar. Sci. Eng. 2021, 9, 893. [Google Scholar] [CrossRef]
- Marechal, G.; Ardhuin, F. Surface Currents and Significant Wave Height Gradients: Matching Numerical Models and High-Resolution Altimeter Wave Heights in the Agulhas Current Region. J. Geophys. Res. Oceans 2021, 126, e2020JC016564. [Google Scholar] [CrossRef]
- Clementi, E.; Oddo, P.; Drudi, M.; Pinardi, N.; Korres, G.; Grandi, A. Coupling Hydrodynamic and Wave Models: First Step and Sensitivity Experiments in the Mediterranean Sea. Ocean Dyn. 2017, 67, 1293–1312. [Google Scholar] [CrossRef]
- Elahi, M.W.E.; Wang, X.H.; Salcedo-Castro, J.; Ritchie, E.A. Influence of Wave–Current Interaction on a Cyclone-Induced Storm Surge Event in the Ganges–Brahmaputra–Meghna Delta: Part 1—Effects on Water Level. J. Mar. Sci. Eng. 2023, 11, 328. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Changes in the Form of Short Gravity Waves on Long Waves and Tidal Currents. J. Fluid Mech. 1960, 8, 565–583. [Google Scholar] [CrossRef]
- Wolf, J.; Prandle, D. Some observations of wave–current interaction. Coast. Eng. 1999, 37, 471–485. [Google Scholar] [CrossRef]
- Kumar, A.; Hayatdavoodi, M. On Wave–Current Interaction in Deep and Finite Water Depths. J. Ocean Eng. Mar. Energy 2023, 9, 455–475. [Google Scholar] [CrossRef]
- Wang, X.H.; Elahi, M.W.E. Influence of Wave–Current Interaction on a Cyclone-Induced Storm-Surge Event in the Ganges-Brahmaputra-Meghna Delta: Part 2—Effects on Wave. J. Mar. Sci. Eng. 2023, 11, 298. [Google Scholar] [CrossRef]
- Dodet, G.; Bertin, X.; Bruneau, N.; Fortunato, A.B.; Nahon, A.; Roland, A. Wave-Current Interactions in a Wave-Dominated Tidal Inlet. J. Geophys. Res. Ocean. 2013, 118, 1587–1605. [Google Scholar] [CrossRef]
- Fragkou, A.K.; Old, C.; Venugopal, V.; Angeloudis, A. Thetis-SWAN: A Python-Interfaced Wave–Current Interactions Coupled System. Environ. Model. Softw. 2024, 177, 106034. [Google Scholar] [CrossRef]
- Zhang, X.; Simons, R.; Zheng, J.; Zhang, C. Investigation on the Turbulent Structures in Combined Wave-Current Boundary Layers. Ocean Eng. 2024, 306, 118073. [Google Scholar] [CrossRef]
- Zhang, X.; Simons, R. Experimental Investigation on the Structure of Turbulence in the Bottom Wave-Current Boundary Layers. Coast. Eng. 2019, 152, 103511. [Google Scholar] [CrossRef]
- Hashemi, M.R.; Grilli, S.T.; Neill, S.P. A Simplified Method to Estimate Tidal Current Effects on the Ocean Wave Power Resource. Renew. Energy 2016, 96, 257–269. [Google Scholar] [CrossRef]
- Saruwatari, A.; Ingram, D.M.; Cradden, L. Wave-Current Interaction Effects on Marine Energy Converters. Ocean Eng. 2013, 73, 106–118. [Google Scholar] [CrossRef]
- Dietrich, J.C.; Tanaka, S.; Westerink, J.J.; Dawson, C.N.; Luettich, R.A.; Zijlema, M.; Holthuijsen, L.H.; Smith, J.M.; Westerink, L.G.; Westerink, H.J. Performance of the Unstructured-Mesh, SWAN+ ADCIRC Model in Computing Hurricane Waves and Surge. J. Sci. Comput. 2012, 52, 468–497. [Google Scholar] [CrossRef]
- Silva, D.; Bento, A.R.; Martinho, P.; Guedes Soares, C. High Resolution Local Wave Energy Modelling in the Iberian Peninsula. Energy 2015, 91, 1099–1112. [Google Scholar] [CrossRef]
- Rusu, L.; Pilar, P.; Guedes Soares, C. Hindcast of the Wave Conditions along the West Iberian Coast. Coast. Eng. 2008, 55, 906–919. [Google Scholar] [CrossRef]
- Horta, J.; Oliveira, S.; Moura, D.; Ferreira, Ó. Nearshore Hydrodynamics at Pocket Beaches with Contrasting Wave Exposure in Southern Portugal. Estuar. Coast. Shelf Sci. 2018, 204, 40–55. [Google Scholar] [CrossRef]
- Relvas, P.; Barton, E.D.; Dubert, J.; Oliveira, P.B.; Peliz, Á.; da Silva, J.C.B.; Santos, A.M.P. Physical Oceanography of the Western Iberia Ecosystem: Latest Views and Challenges. Prog. Oceanogr. 2007, 74, 149–173. [Google Scholar] [CrossRef]
- Peliz, Á.; Dubert, J.; Santos, A.M.P.; Oliveira, P.B.; Le Cann, B. Winter Upper Ocean Circulation in the Western Iberian Basin—Fronts, Eddies and Poleward Flows: An Overview. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 621–646. [Google Scholar] [CrossRef]
- Mills, L.; Janeiro, J.; Martins, F. Baseline Climatology of the Canary Current Upwelling System and Evolution of Sea Surface Temperature. Remote Sens. 2024, 16, 504. [Google Scholar] [CrossRef]
- Álvarez-Salgado, X.A.; Figueiras, F.G.; Perez, F.F.; Groom, S.; Nogueira, E.; Borges, A.V.; Chou, L.; Castro, C.G.; Moncoiffé, G.; Rios, A.F.; et al. The Portugal Coastal Counter Current off NW Spain: New Insights on Its Biogeochemical Variability. Prog. Oceanogr. 2003, 56, 281–321. [Google Scholar] [CrossRef]
- Relvas, P.; Barton, E.D. Mesoscale Patterns in the Cape São Vicente (Iberian Peninsula) Upwelling Region. J. Geophys. Res. Oceans 2002, 107, 3164. [Google Scholar] [CrossRef]
- Ferreira, Ó.; Kupfer, S.; Costas, S. Implications of Sea-Level Rise for Overwash Enhancement at South Portugal. Nat. Hazards 2021, 109, 2221–2239. [Google Scholar] [CrossRef]
- Fernandes, M.; Fernandes, C.; Barroqueiro, T.; Agostinho, P.; Martins, N.; Alonso-Martirena, A. Extreme Wave Height Events in Algarve (Portugal): Comparison between HF Radar Systems and Wave Buoys. In Proceedings of the 5th Jornadas Engenharia Hidrográfica, Lisboa, Portugal, 19–21 June 2018. [Google Scholar]
- Almeida, L.P.; Ferreira, Ó.; Vousdoukas, M.I.; Dodet, G. Historical Variation and Trends in Storminess along the Portuguese South Coast. Nat. Hazards Earth Syst. Sci. 2011, 11, 2407–2417. [Google Scholar] [CrossRef]
- Mota, P.; Pinto, J.P. Wave Energy Potential along the Western Portuguese Coast. Renew. Energy 2014, 71, 8–17. [Google Scholar] [CrossRef]
- Ferreira, Ó.; Matias, A.; Pacheco, A. The East Coast of Algarve: A Barrier Island Dominated Coast. Thalassas 2016, 32, 75–85. [Google Scholar] [CrossRef]
- Islek, F.; Yuksel, Y. Inter-Comparison of Long-Term Wave Power Potential in the Black Sea Based on the SWAN Wave Model Forced with Two Different Wind Fields. Dyn. Atmos. Ocean. 2021, 93, 101192. [Google Scholar] [CrossRef]
- Islek, F.; Yuksel, Y.; Sahin, C.; Guner, H.A.A. Long-Term Analysis of Extreme Wave Characteristics Based on the SWAN Hindcasts over the Black Sea Using Two Different Wind Fields. Dyn. Atmos. Ocean. 2021, 94, 101165. [Google Scholar] [CrossRef]
- Lei, Z.; Wu, W.; Gu, Y.; Zhai, F.; Li, P. A General Method to Determine the Optimal Whitecapping Dissipation Coefficient in the SWAN Model. Front. Mar. Sci. 2023, 10, 1298727. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A Third-Generation Wave Model for Coastal Regions, Part I, Model Description and Validation A Third-Generation Wave Model for Coastal Regions 1. Model Description and Validation. J. Geophys. Res. Ocean. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Booij, N.; Holthuijsen, L.H.; Ris, R.C. The “SWAN” Wave Model For Shallow Water. In Coastal Engineering 1996; American Society of Civil Engineers: Reston, VA, USA, 1997. [Google Scholar]
- Rogers, E.W.; Babanin, A.V.; Wang, D.W. Observation-Consistent Input and Whitecapping Dissipation in a Model for Wind-Generated Surface Waves: Description and Simple Calculations. J. Atmos. Ocean. Technol. 2012, 29, 1329–1346. [Google Scholar] [CrossRef]
- Janeiro, J.; Neves, A.; Martins, F.; Relvas, P. Integrating Technologies for Oil Spill Response in the SW Iberian Coast. J. Mar. Syst. 2017, 173, 31–42. [Google Scholar] [CrossRef]
- Martins, F.; Leitão, P.; Silva, A.; Neves, R. 3D Modelling in the Sado Estuary Using a New Generic Vertical Discretization Approach. Oceanol. Acta 2001, 24, 51–62. [Google Scholar] [CrossRef]
- Braunschweig, F.; Leitao, P.C.; Fernandes, L.; Pina, P.; Neves, R.J.J. The Object Oriented Design of the Integrated Water Modelling System MOHID. In Developments in Water Science; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Burchard, H.; Bolding, K.; Villarreal, M.R. GOTM, A General Ocean Turbulence Model: Theory, Implementation and Test Cases; European Commission: Brussel, Belgium, 1999. [Google Scholar]
- Mendonça, F.; Martins, F.; Janeiro, J. SMS-Coastal, a New Python Tool to Manage MOHID-Based Coastal Operational Models. J. Mar. Sci. Eng. 2023, 11, 1606. [Google Scholar] [CrossRef]
- Kallos, G.; Nickovic, S.; Papadopoulos, A.; Jovic, D.; Kakaliagou, O.; Misirlis, N.; Boukas, L.; Mitikou, N.; Sakellaridis, G.; Papageorgiou, J.; et al. The Regional Weather Forecasting System SKIRON: An Overview. In Proceedings of the International Symposium on Regional Weather Prediction on Parallel Computer Environments, Athens, Greece, 15–17 October 1997; pp. 109–122. [Google Scholar]
- Toledano, C.; Ghantous, M.; Lorente, P.; Dalphinet, A.; Aouf, L.; Sotillo, M.G. Impacts of an Altimetric Wave Data Assimilation Scheme and Currents-Wave Coupling in an Operational Wave System: The New Copernicus Marine IBI Wave Forecast Service. J. Mar. Sci. Eng. 2022, 10, 457. [Google Scholar] [CrossRef]
- Gomez, B.; Aouf, L.; Dalphinet, A.; Louis, L.; Alonso, A.; Garcia, M.; Valdecasas, J.M.; Ciliberti, S.; Aznar, R.; Sotillo, M.G. Atlantic-Iberian Biscay Irish-IBI Production Centre IBI_ANALYSISFORECAST_WAV_005_005; Copernicus Marine Service: Toulouse, France, 2024. [Google Scholar]
- Herbers, T.H.C.; Elgar, S.; Guza, R.T. Directional Spreading of Waves in the Nearshore. J. Geophys. Res. Oceans 1999, 104, 7683–7693. [Google Scholar] [CrossRef]
- Wehde, H.; Schuckmann, K.V.; Pouliquen, S.; Grouazel, A.; Bartolome, T.; Tintore, J.; De, M.; Alonso-Munoyerro, A.; Carval, T.; Racapé, V. In Situ TAC Multiparameter Products: INSITU_GLO_PHYBGCWAV_DISCRETE_MYNRT_013_030 INSITU_ARC_PHYBGCWAV_DISCRETE_MYNRT_013_031 INSITU_BAL_PHYBGCWAV_DISCRETE_MYNRT_013_032 INSITU_IBI_PHYBGCWAV_DISCRETE_MYNRT_013_033 INSITU_BLK_PHYBGCWAV_DISCRETE_MYNRT_013_034 INSITU_MED_PHYBGCWAV_DISCRETE_MYNRT_013_035 INSITU_NWS_PHYBGCWAV_DISCRETE_MYNRT_013_036; Copernicus Marine Service: Toulouse, France, 2024. [Google Scholar]
- De Alfonso Alonso-Muñoyerro, A.; Manzano Muñoz, F.; Gallardo, A.; Hammarklint, T.; Perivoliotis, L.; Bekiari, M.; Carval, T. Copernicus Marine Environment Monitoring Service In-Situ TAC CMEMS Element Real Time Quality Control for WAVES; Copernicus In Situ TAC: Toulouse, France, 2020. [Google Scholar] [CrossRef]
- SWAN Team. User Manual Cycle III Version 41.31A; Delft University of Technology: Delft, The Netherlands, 2020. [Google Scholar]
- Edwards, K.L.; Rogers, W.E.; Siqueira, S.; Gay, P.; Wood, K. A Cost-Benefit Analysis of SWAN with Source Term Package ST6; Naval Research Laboratory (NRL) Oceanography Division: Washington, DC, USA, 2018.
- Cavaleri, L.; Bertotti, L. The Miami 1981 Wave Model Intercomparison Test. II Nuovo C. C 1982, 5, 159–188. [Google Scholar] [CrossRef]
- Ardhuin, F.; Rogers, E.; Babanin, A.V.; Filipot, J.F.; Magne, R.; Roland, A.; van der Westhuysen, A.; Queffeulou, P.; Lefevre, J.M.; Aouf, L.; et al. Semiempirical Dissipation Source Functions for Ocean Waves. Part I: Definition, Calibration, and Validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Zieger, S.; Babanin, A.V.; Erick Rogers, W.; Young, I.R. Observation-Based Source Terms in the Third-Generation Wave Model WAVEWATCH. Ocean Model. 2015, 96, 2–25. [Google Scholar] [CrossRef]
- Couvelard, X.; Lemarié, F.; Samson, G.; Redelsperger, J.L.; Ardhuin, F.; Benshila, R.; Madec, G. Development of a Two-Way-Coupled Ocean-Wave Model: Assessment on a Global NEMO(v3.6)-WW3(v6.02) Coupled Configuration. Geosci. Model Dev. 2020, 13, 3067–3090. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- O’Donncha, F.; Hartnett, M.; Nash, S.; Ren, L.; Ragnoli, E. Characterizing Observed Circulation Patterns within a Bay Using HF Radar and Numerical Model Simulations. J. Mar. Syst. 2015, 142, 96–110. [Google Scholar] [CrossRef]
- Willmott, C.I. On The Validation Of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Korkidis, P.; Dounis, A. Wavelet Multiresolution Analysis-Based Takagi–Sugeno–Kang Model, with a Projection Step and Surrogate Feature Selection for Spectral Wave Height Prediction. Mathematics 2025, 13, 2517. [Google Scholar] [CrossRef]
- Majidi, A.G.; Ramos, V.; Amarouche, K.; Rosa Santos, P.; das Neves, L.; Taveira-Pinto, F. Assessing the Impact of Wave Model Calibration in the Uncertainty of Wave Energy Estimation. Renew. Energy 2023, 212, 415–429. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, H.; Chen, G.; Yang, J. Assessing the Performance of SWAN Model for Wave Simulations in the Bay of Bengal. Ocean. Eng. 2023, 285, 115295. [Google Scholar] [CrossRef]
- Aydoğan, B.; Ayat, B. Performance Evaluation of SWAN ST6 Physics Forced by ERA5 Wind Fields for Wave Prediction in an Enclosed Basin. Ocean Eng. 2021, 240, 109936. [Google Scholar] [CrossRef]
- Sapiega, P.; Zalewska, T.; Struzik, P. Application of SWAN Model for Wave Forecasting in the Southern Baltic Sea Supplemented with Measurement and Satellite Data. Environ. Model. Softw. 2023, 163, 105624. [Google Scholar] [CrossRef]
- Mendes, D.; Oliveira, T.C.A. Deep-Water Spectral Wave Steepness Offshore Mainland Portugal. Ocean Eng. 2021, 236, 109548. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers, 13th ed.; Oliver and Boyd: London, UK, 1958. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).