An Orthogonal Geometry-Based Algorithm for Accurate Mesoscale Eddy Detection
Abstract
1. Introduction
2. Algorithm Comparison
2.1. Highlights
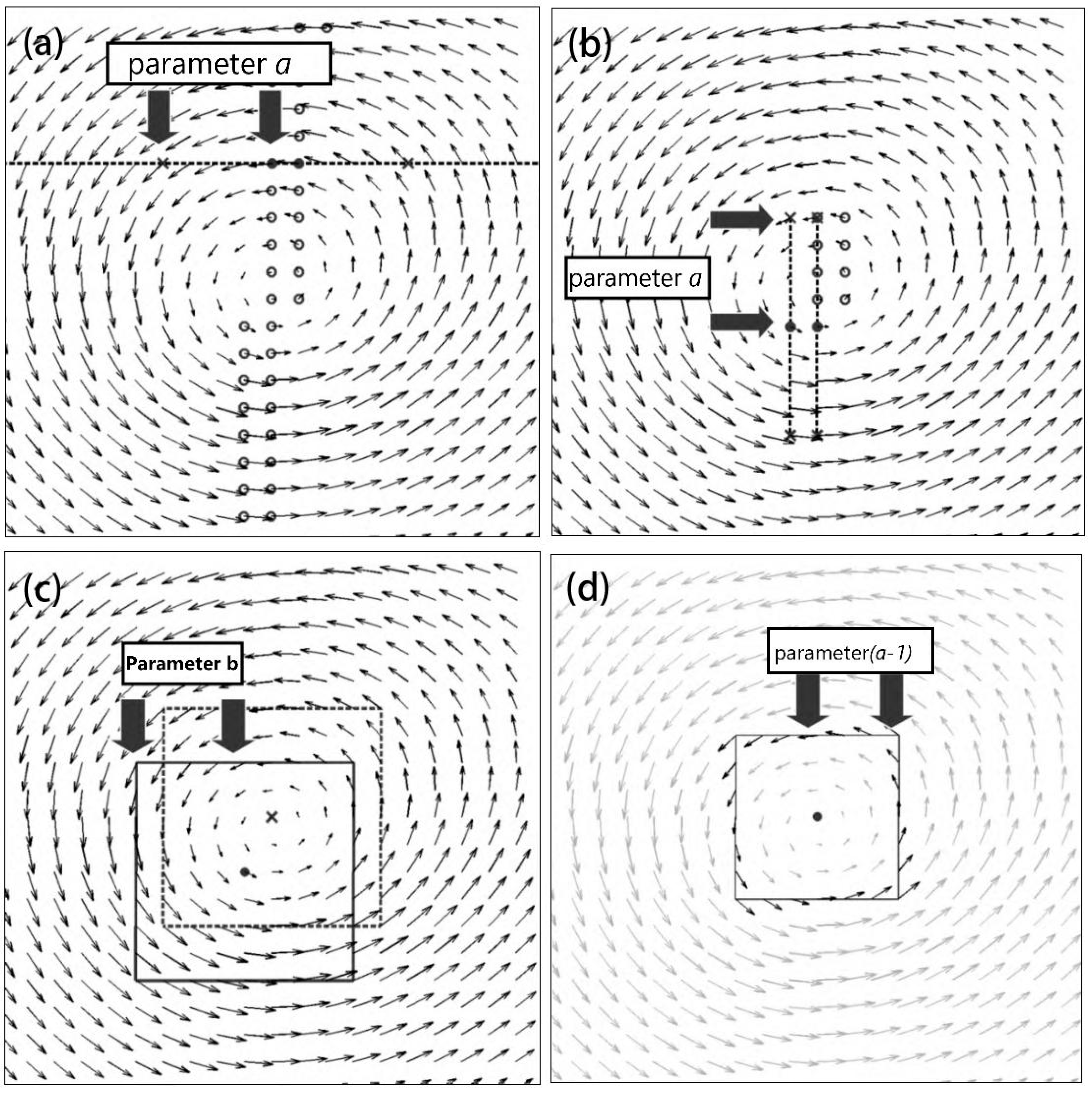
2.2. VG Algorithm
2.3. OG Algorithm
- (1)
- Orthogonal Transformation: Initially, following the acquisition of the flow field data for analysis, an orthogonal transformation is applied to the north–south velocity component () and the east–west velocity component (). To enhance the geometric signature of mesoscale eddies, we apply a fixed 90° counterclockwise orthogonal rotation to the original velocity field. The transformation is implemented using the standard 2D rotation matrix:
- (2)
- Preliminary screening of each eddy center: in consideration of the horizontal scale characteristics of ocean eddies, an appropriate window size (11 × 11 in this study) is selected to systematically traverse the entire vector field (illustrated in (Figure 3.)). Utilizing the characteristic that the velocity at each eddy center is minimal, the point with the smallest absolute velocity value within each sliding window is designated as a potential each eddy center (). This step is designed to efficiently filter potential each eddy center locations.
- (3)
- Refined positioning and verification: following the initial detection of each eddy center, a smaller sliding window is redefined using the golden ratio (with a size of 7 × 7 in this study), ensuring that the distance between the boundaries of the new window and the original window exceeds a predetermined distance threshold (, as depicted in (Figure 4). Additionally, the number of velocity direction vectors within the new window must surpass a preset threshold (). To determine the precise location of each eddy center, we employ a least-squares fitting method based on the radial flow assumption. For each point () in the 7 × 7 window, with coordinates () and transformed velocity components (), we assume that the velocity vectors radiate from or converge toward a common center . This leads to the linear relationship:
- To ensure the exclusion of each pseudo eddy center that is failed to satisfy the closure conditions, the following constraints are implemented:
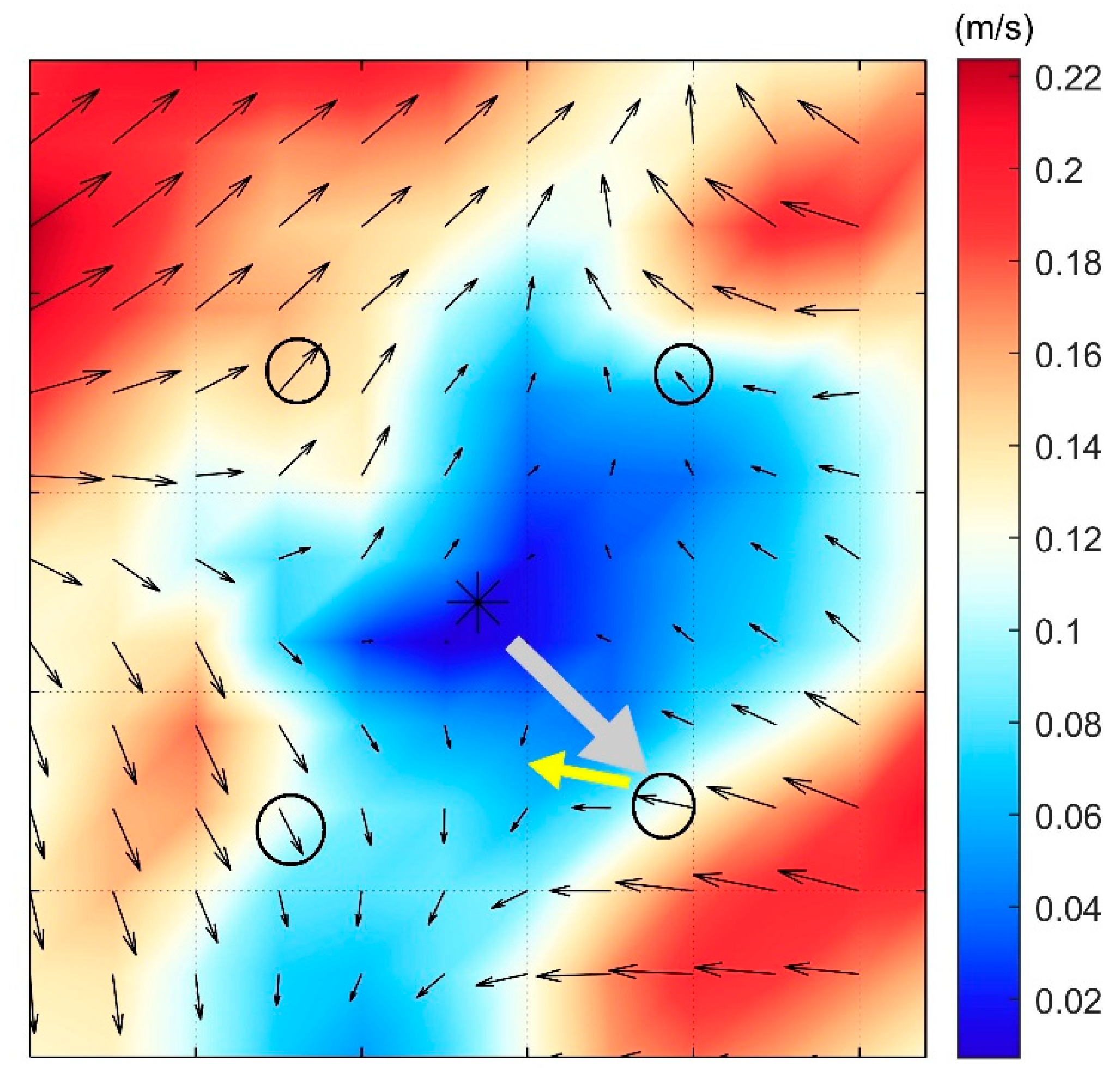
- It is essential to verify that each flow field box contains at least one data point in each directional vector (as illustrated in (Figure 4));
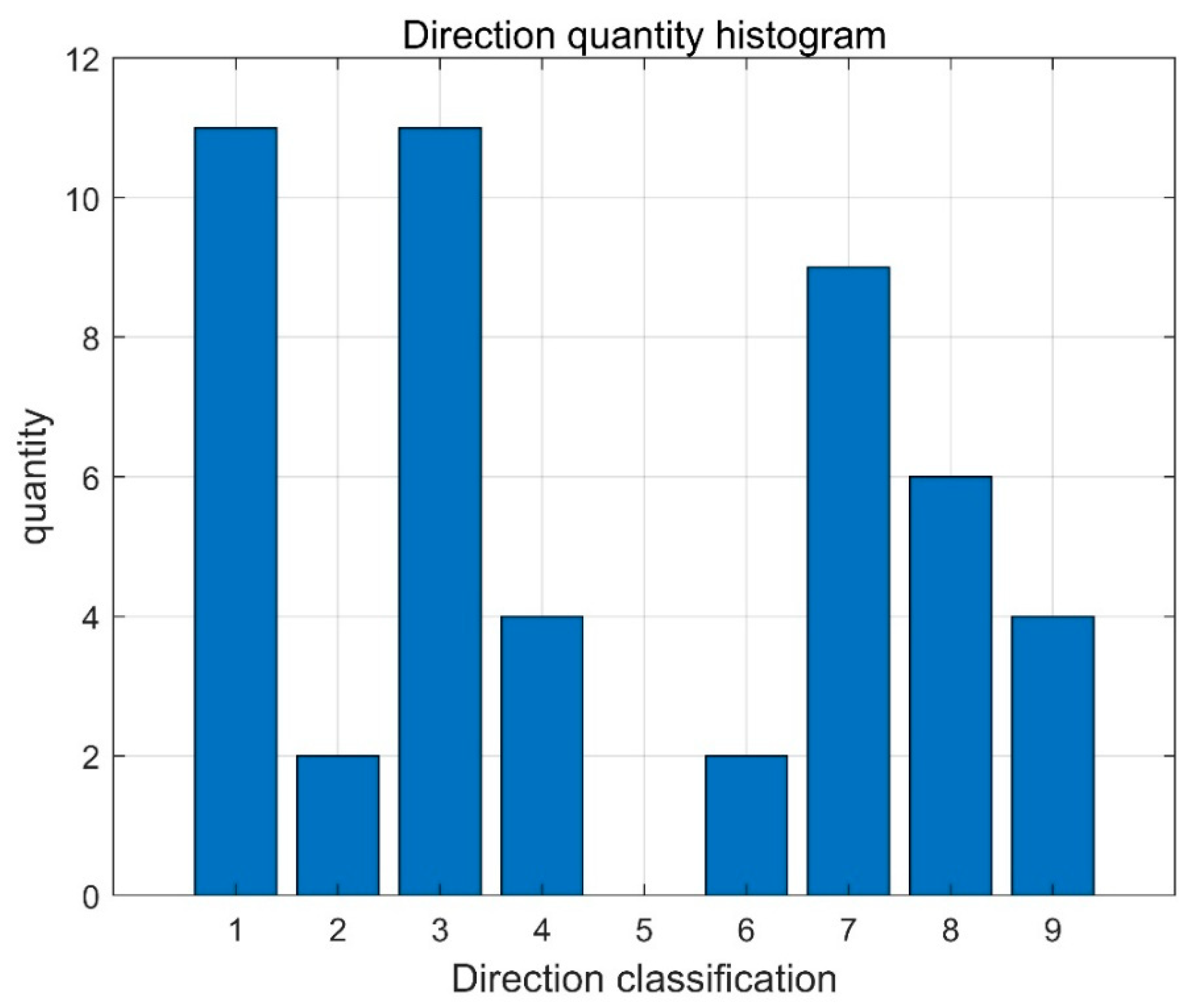
- The grid points , , , and , located in the northeast, southeast, northwest, and southwest quadrants relative to each eddy center , are selected. The dot product of the vector extending from each eddy center to these four points with the directional vectors of these points is calculated by by the gray and yellow arrows (as depicted in (Figure 5)). A notably small dot product value or one approaching 180° indicates that the vector direction of these points is nearly parallel to the vector connecting each eddy center to that point, suggesting an absence of conditions conducive to a closed flow field (as depicted in (Figure 5)).
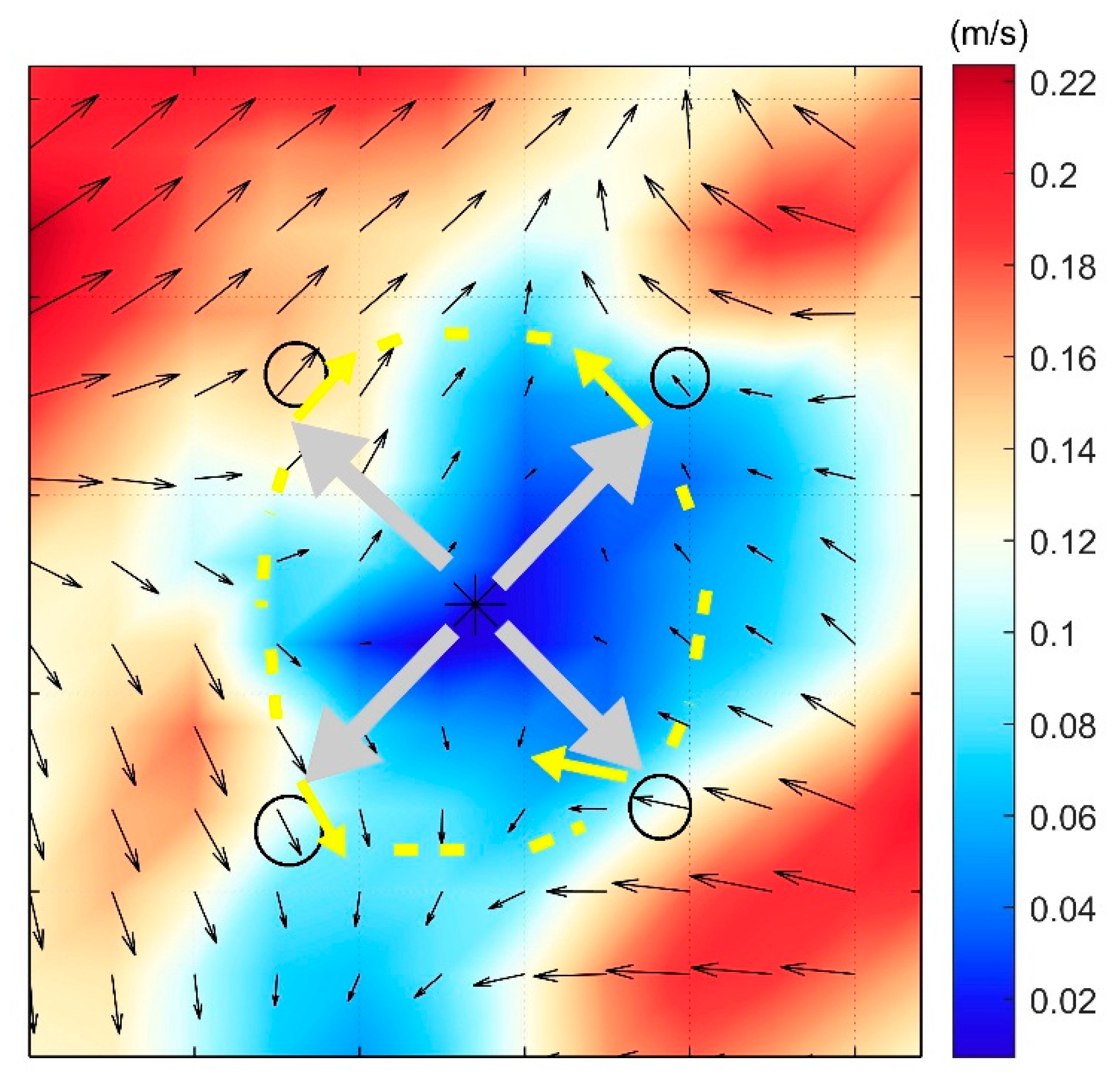
- The cross product from each eddy center to these four points is calculated as indicated by the gray and yellow arrows (as shown in (Figure 6)). Consistency in the signs of the cross products signifies uniformity in the direction of the streamlines, thereby satisfying the closure condition. Conversely, if any point fails to meet this criterion, the corresponding each eddy center is excluded (as shown in (Figure 6)).
3. Dataset-Based Evaluation
3.1. Dataset Construction
3.2. Evaluation Methodology
3.3. Detection Accuracy Across Different Types of Eddies
3.4. Each Eddy Center Localization Accuracy
3.5. Spatial and Seasonal Generalization
3.6. Quantitative Sensitivity Analysis of Key Parameters
4. Results Analysis
4.1. Result Verification
4.2. Comparison of Each Eddy Center
4.3. Eddies Clustering
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global Heat and Salt Transports by Eddy Movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed]
- Nencioli, F.; Dong, C.; Dickey, T.; Washburn, L.; McWilliams, J.C. A Vector Geometry-Based Eddy Detection Algorithm and Its Application to a High-Resolution Numerical Model Product and High-Frequency Radar Surface Velocities in the Southern California Bight. J. Atmos. Ocean. Technol. 2010, 27, 564–579. [Google Scholar] [CrossRef]
- Okubo, A. Horizontal Dispersion of Floatable Particles in the Vicinity of Velocity Singularities Such as Convergences. Deep Sea Res. Oceanogr. Abstr. 1970, 17, 445–454. [Google Scholar] [CrossRef]
- Wang, G.; Su, J.; Chu, P.C. Mesoscale Eddies in the South China Sea Observed with Altimeter Data. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Chaigneau, A.; Pizarro, O. Eddy Characteristics in the Eastern South Pacific. J. Geophys. Res. Ocean. 2005, 110, C06005. [Google Scholar] [CrossRef]
- Ari Sadarjoen, I.; Post, F.H. Detection, Quantification, and Tracking of Vortices Using Streamline Geometry. Comput. Graph. 2000, 24, 333–341. [Google Scholar] [CrossRef]
- Chaigneau, A.; Gizolme, A.; Grados, C. Mesoscale Eddies off Peru in Altimeter Records: Identification Algorithms and Eddy Spatio-Temporal Patterns. Prog. Oceanogr. 2008, 79, 106–119. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global Observations of Nonlinear Mesoscale Eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Vu, B.L.; Stegner, A.; Arsouze, T. Angular Momentum Eddy Detection and Tracking Algorithm (AMEDA) and Its Application to Coastal Eddy Formation. J. Atmos. Ocean. Technol. 2018, 35, 739–762. [Google Scholar] [CrossRef]
- Faghmous, J.H.; Frenger, I.; Yao, Y.; Warmka, R.; Lindell, A.; Kumar, V. A Daily Global Mesoscale Ocean Eddy Dataset from Satellite Altimetry. Sci. Data 2015, 2, 150028. [Google Scholar] [CrossRef] [PubMed]
- Mason, E.; Pascual, A.; McWilliams, J.C. A New Sea Surface Height–Based Code for Oceanic Mesoscale Eddy Tracking. J. Atmos. Ocean. Technol. 2014, 31, 1181–1188. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic Mass Transport by Mesoscale Eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef] [PubMed]
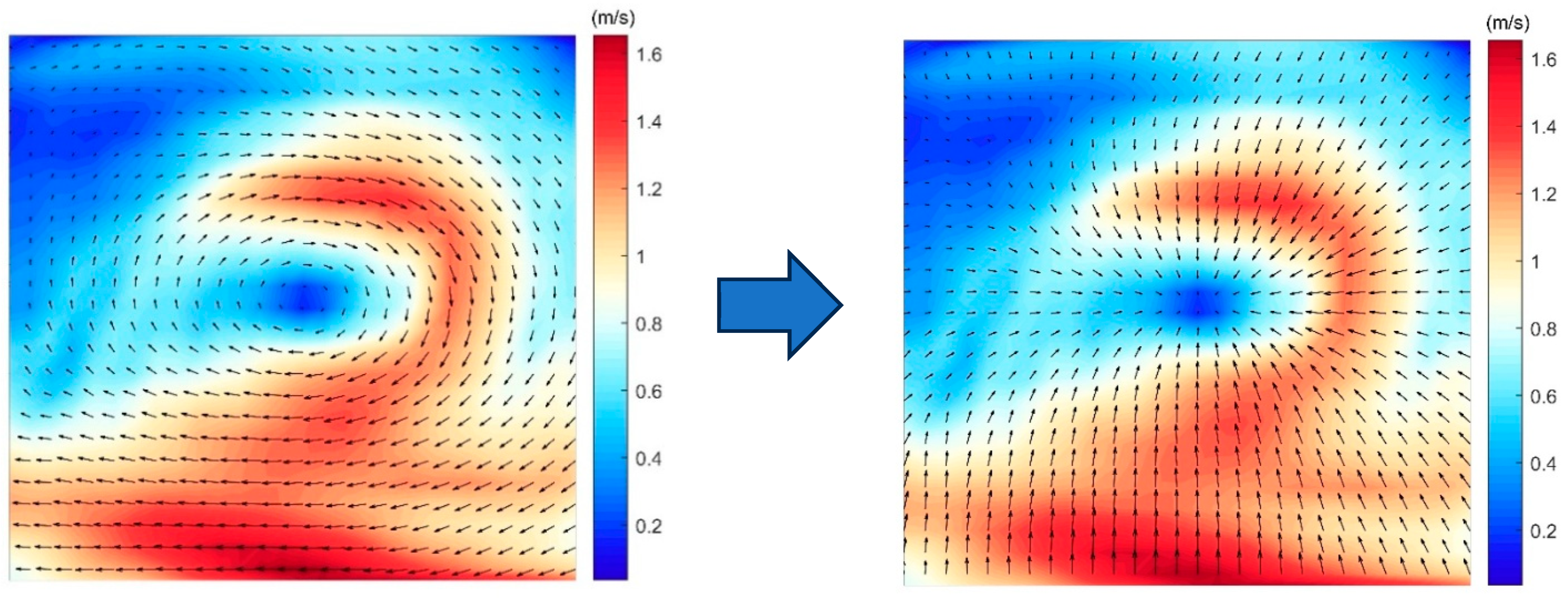
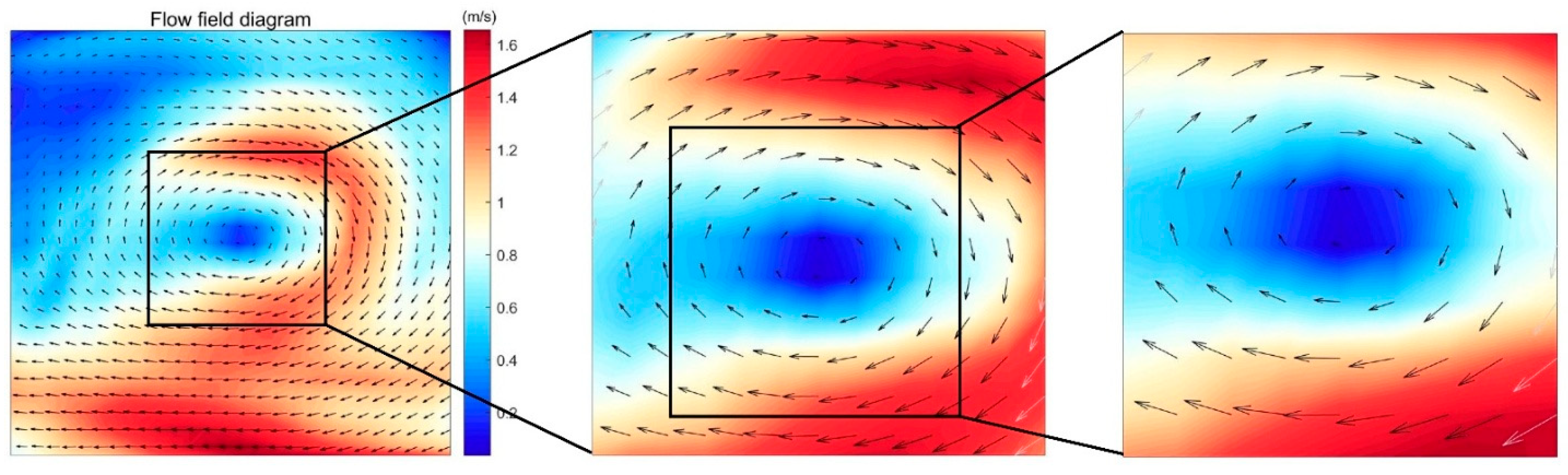
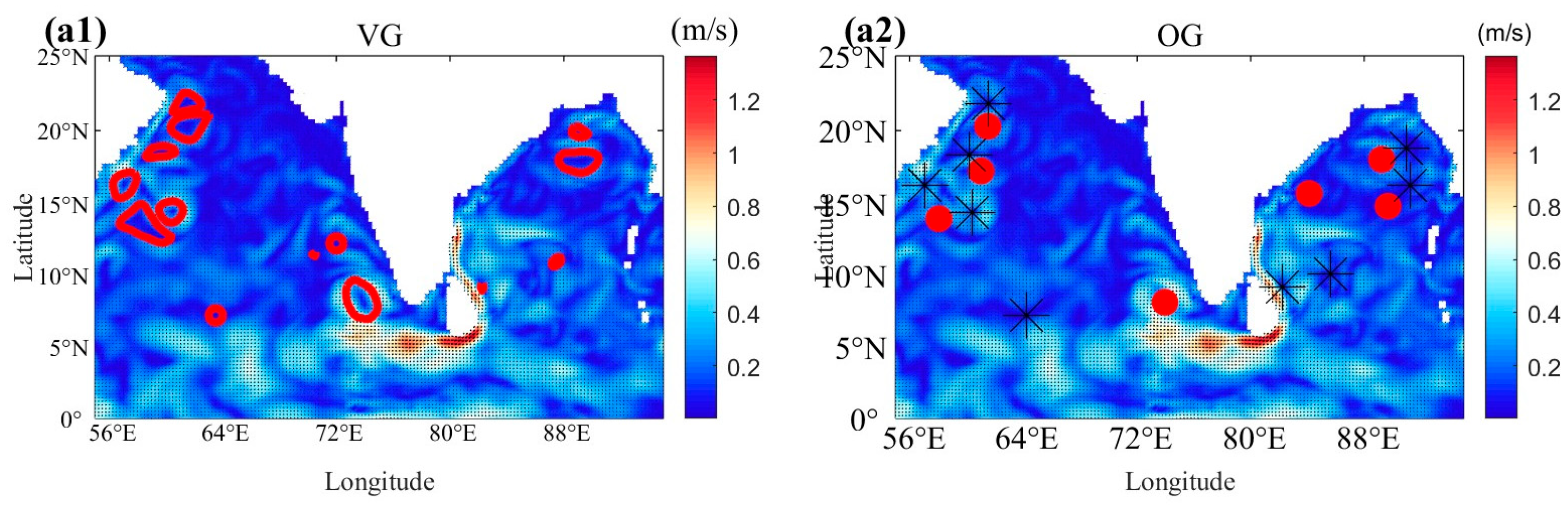
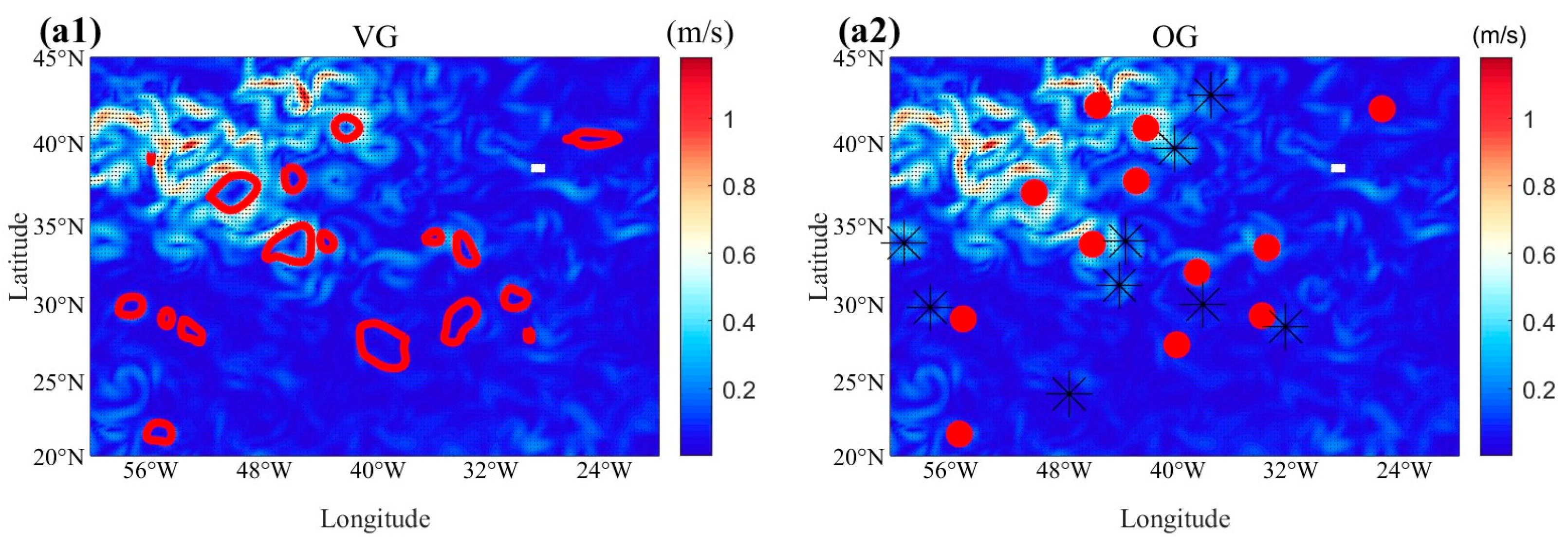
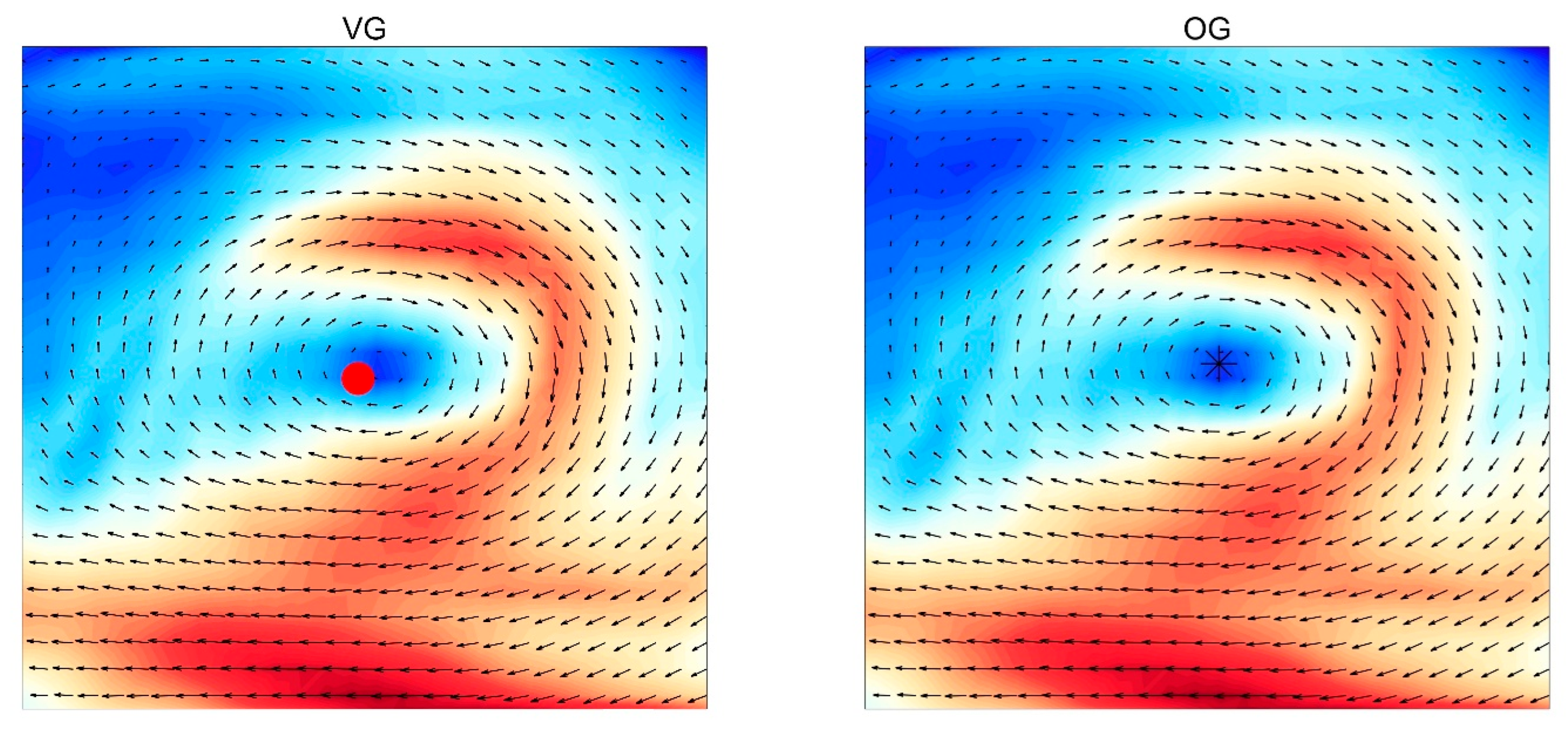
 ) are used to indicate eddies.
) are used to indicate eddies.
 ) are used to indicate eddies.
) are used to indicate eddies.
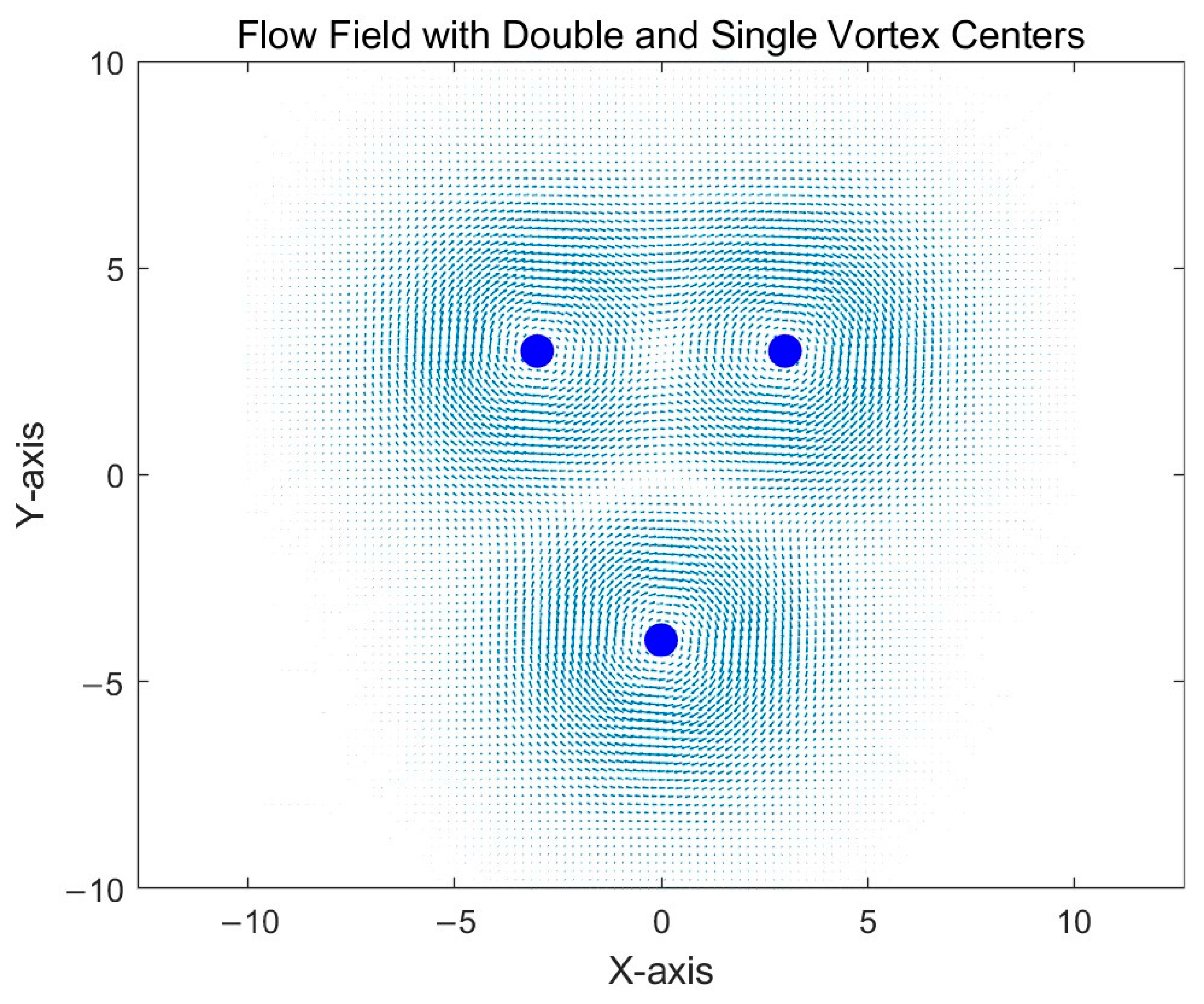
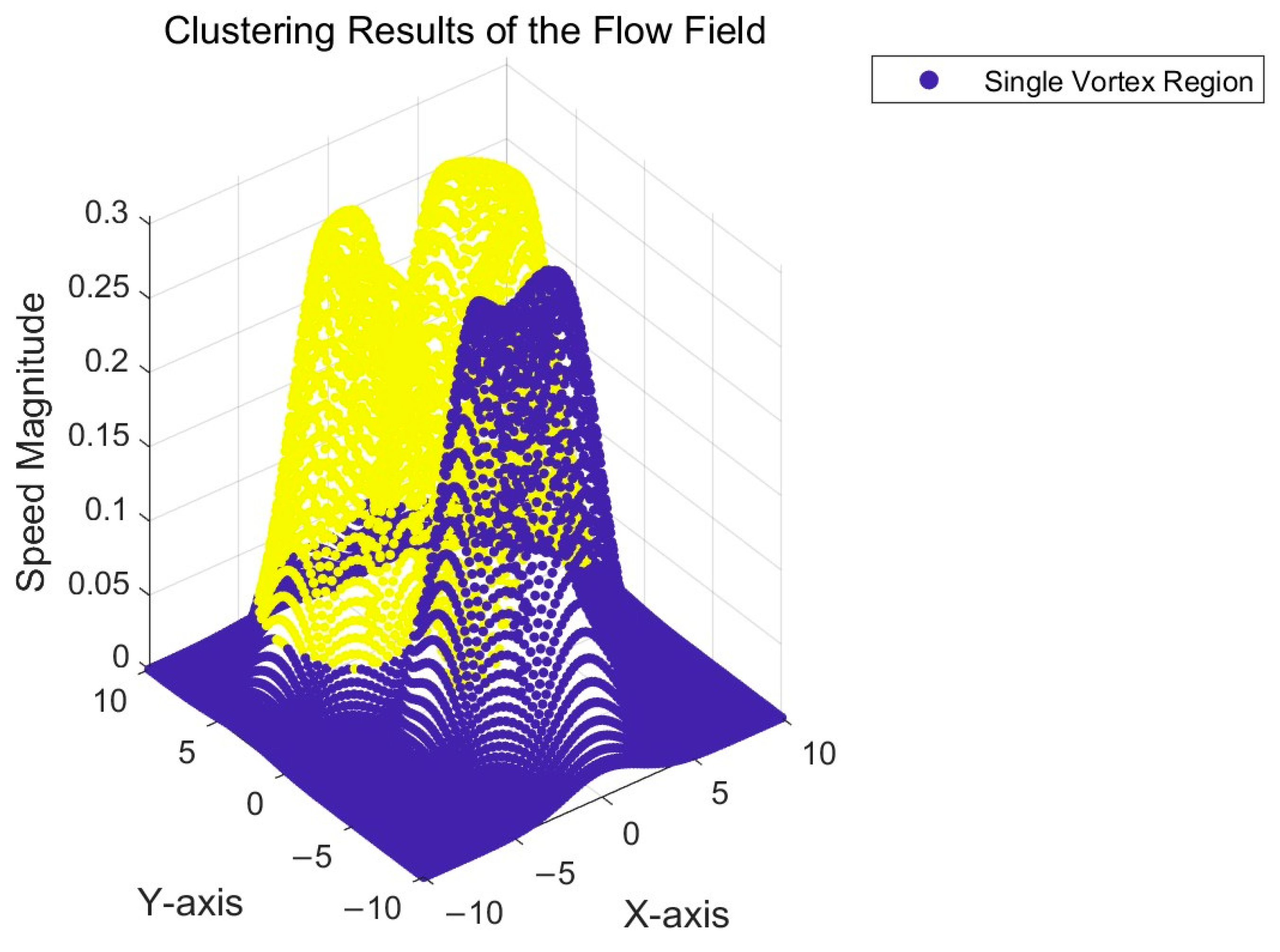
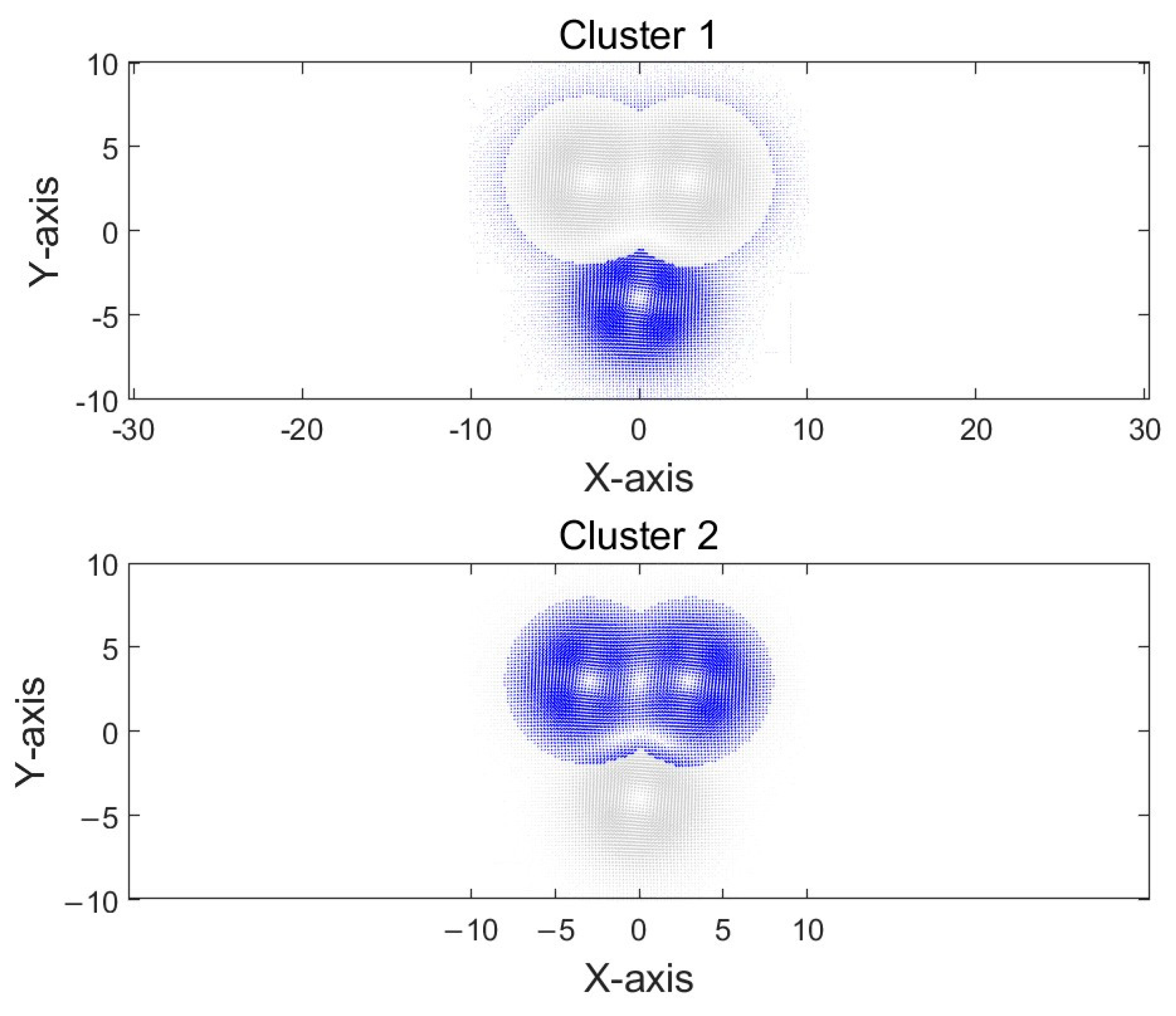
| Type of Eddies | Number of Sample 2 | VG Algorithm (%) | OG Algorithm (%) |
|---|---|---|---|
| Standard eddies | 200 | 92.4 | 96.8 |
| Eccentric eddies | 200 | 78.2 | 91.5 |
| Dual-core eddies | 200 | 46.8 | 88.7 |
| Overall | 600 | 72.5 | 92.3 |
| Type of Eddies | VG Algorithm (km) | OG Algorithm (km) |
|---|---|---|
| Standard eddies | 1.2 | 0.8 |
| Eccentric eddies | 2.7 | 1.5 |
| Dual-core eddies | 7.4 | 4.2 |
| Overall | 3.7 | 2.2 |
| Region | Date | VG Algorithm | OG Algorithm |
|---|---|---|---|
| Northwest Pacific | 1 January | 11 | 17 |
| 1 April | 14 | 23 | |
| 1 July | 17 | 21 | |
| 1 October | 13 | 13 | |
| North Indian Ocean | 1 January | 14 | 16 |
| 1 April | 8 | 10 | |
| 1 July | 9 | 10 | |
| 1 October | 8 | 6 | |
| North Atlantic Ocean | 1 January | 16 | 21 |
| 1 April | 6 | 7 | |
| 1 July | 10 | 17 | |
| 1 October | 14 | 24 |
| Method Category | Parameter Configuration | Valid Matches | Mean Bias (°) |
|---|---|---|---|
| OG Algorithm | 9 × 9/5 × 5 | 3 | 0.254 |
| 11 × 11/7 × 7 | 13 | 0.292 | |
| 15 × 15/9 × 9 | 10 | 0.479 | |
| VG Algorithm | a = 3 b = 2 | 10 | 0.472 |
| a = 4 b = 3 | 10 | 0.458 | |
| a = 5 b = 4 | 4 | 0.319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Yang, J.; Song, J. An Orthogonal Geometry-Based Algorithm for Accurate Mesoscale Eddy Detection. J. Mar. Sci. Eng. 2025, 13, 2242. https://doi.org/10.3390/jmse13122242
Cai Y, Yang J, Song J. An Orthogonal Geometry-Based Algorithm for Accurate Mesoscale Eddy Detection. Journal of Marine Science and Engineering. 2025; 13(12):2242. https://doi.org/10.3390/jmse13122242
Chicago/Turabian StyleCai, Yu, Jingyi Yang, and Jun Song. 2025. "An Orthogonal Geometry-Based Algorithm for Accurate Mesoscale Eddy Detection" Journal of Marine Science and Engineering 13, no. 12: 2242. https://doi.org/10.3390/jmse13122242
APA StyleCai, Y., Yang, J., & Song, J. (2025). An Orthogonal Geometry-Based Algorithm for Accurate Mesoscale Eddy Detection. Journal of Marine Science and Engineering, 13(12), 2242. https://doi.org/10.3390/jmse13122242






