Influence of Layout on Offshore Wind Farm Efficiency and Wake Characteristics in Turbulent Environments
Abstract
1. Introduction
2. Numerical Methods and Validation
2.1. Numerical Method
2.1.1. Momentum Theory and the Betz Limit
2.1.2. Dynamic Wake Meandering Wake Model
2.1.3. Damage Equivalent Load Method
2.1.4. Entropy Generation Theory
2.2. Numerical Validation
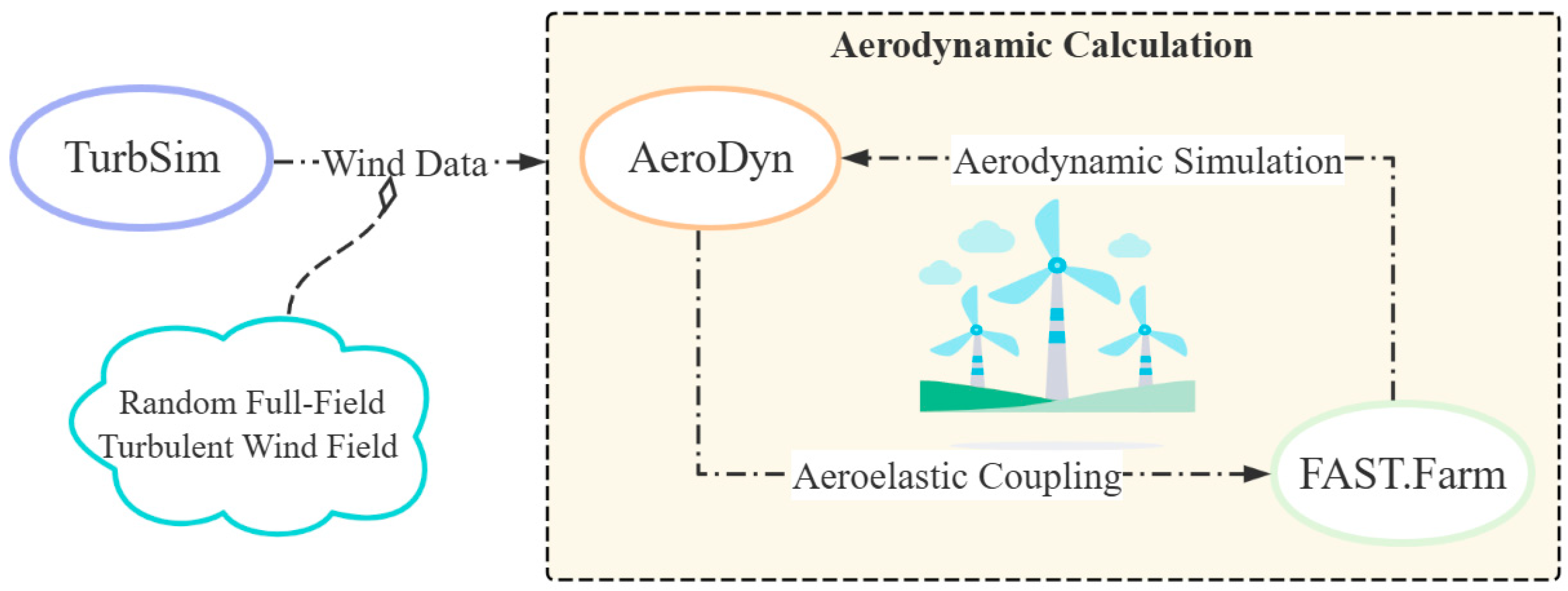
2.2.1. Introduction to FAST.Farm
2.2.2. Validation of Turbulent Wind Field
2.2.3. Grid Sensitivity Analysis
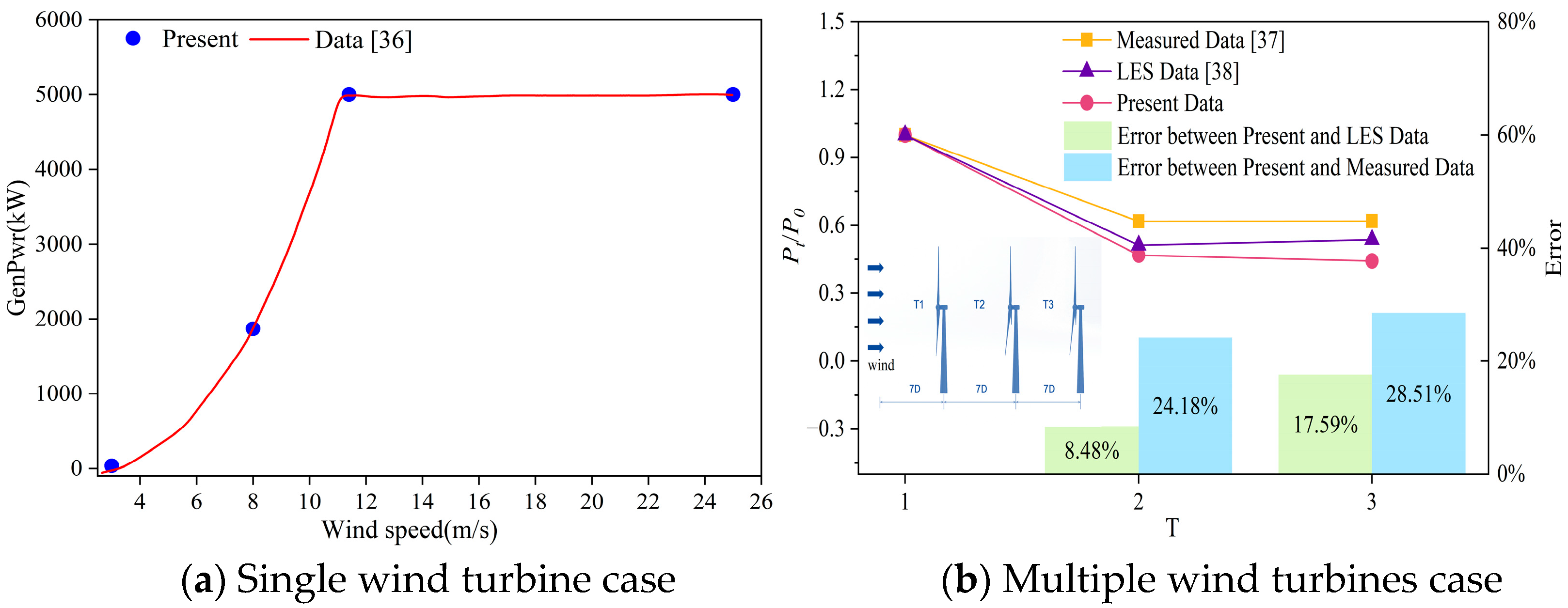
2.2.4. Validation of Single and Multiple Wind Turbines Power Performance
3. Optimization of Wind Farm Layout Design
3.1. Numerical Model
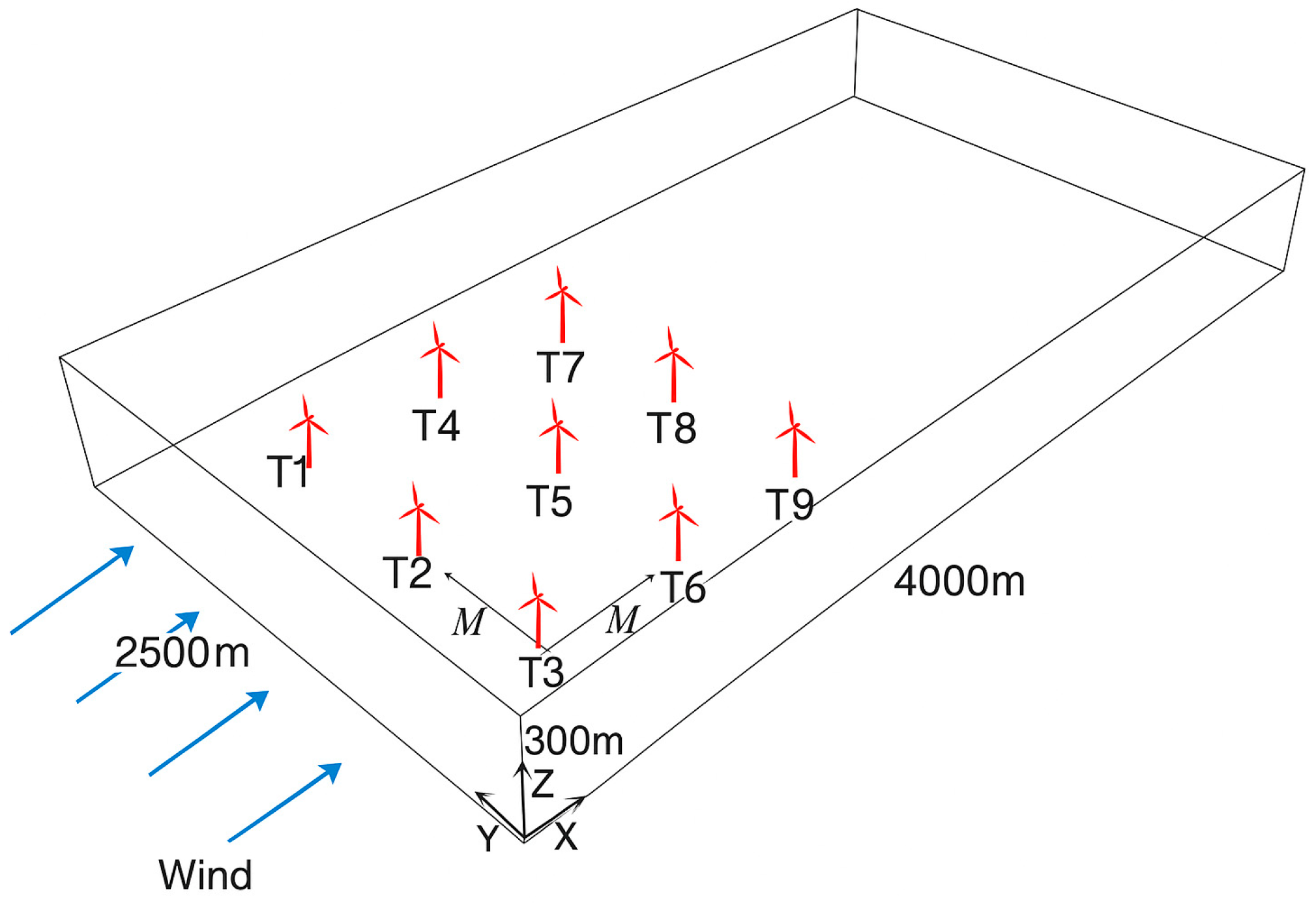
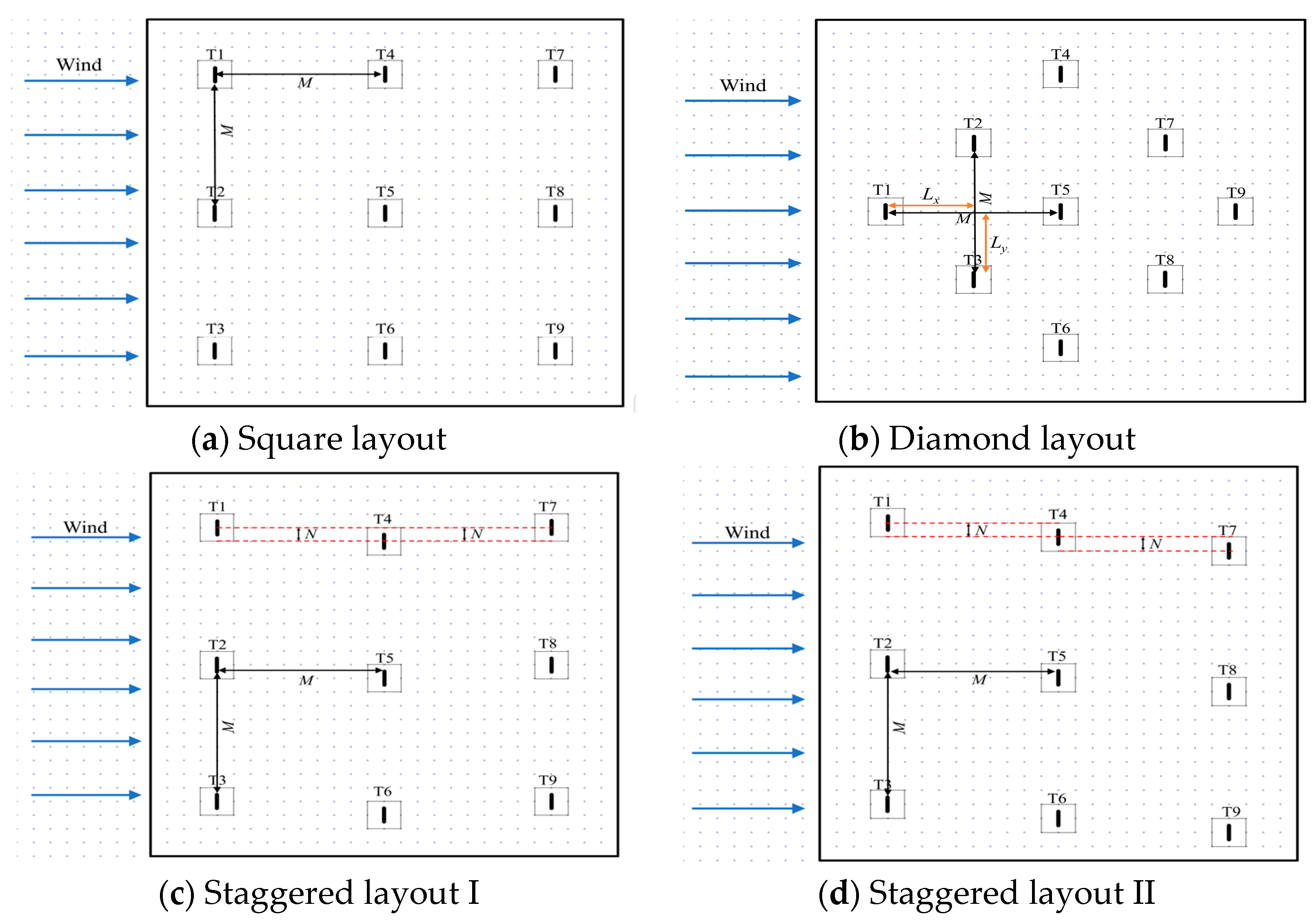
3.2. Wind Farm Layout
4. Results and Discussion
4.1. Square Layout Case
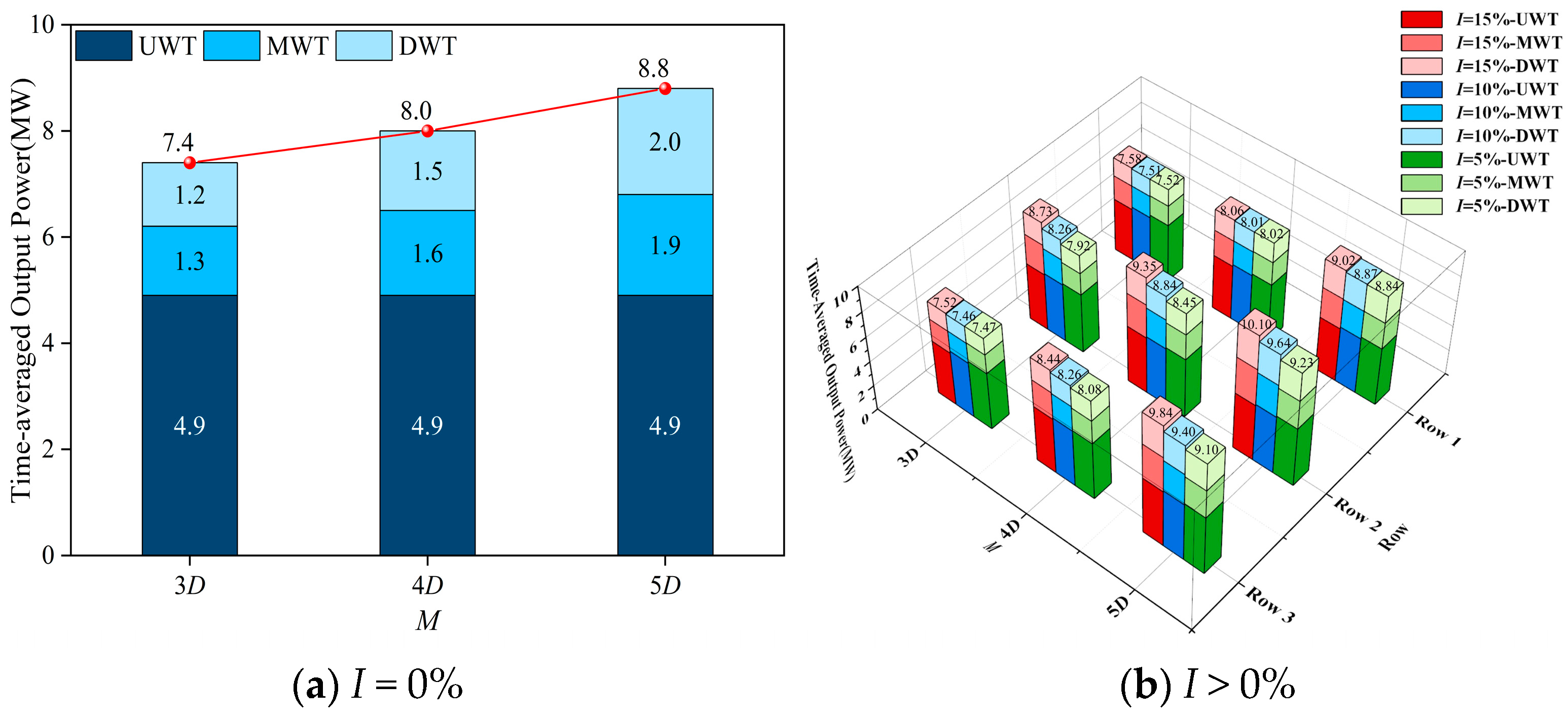
4.1.1. Power Performance
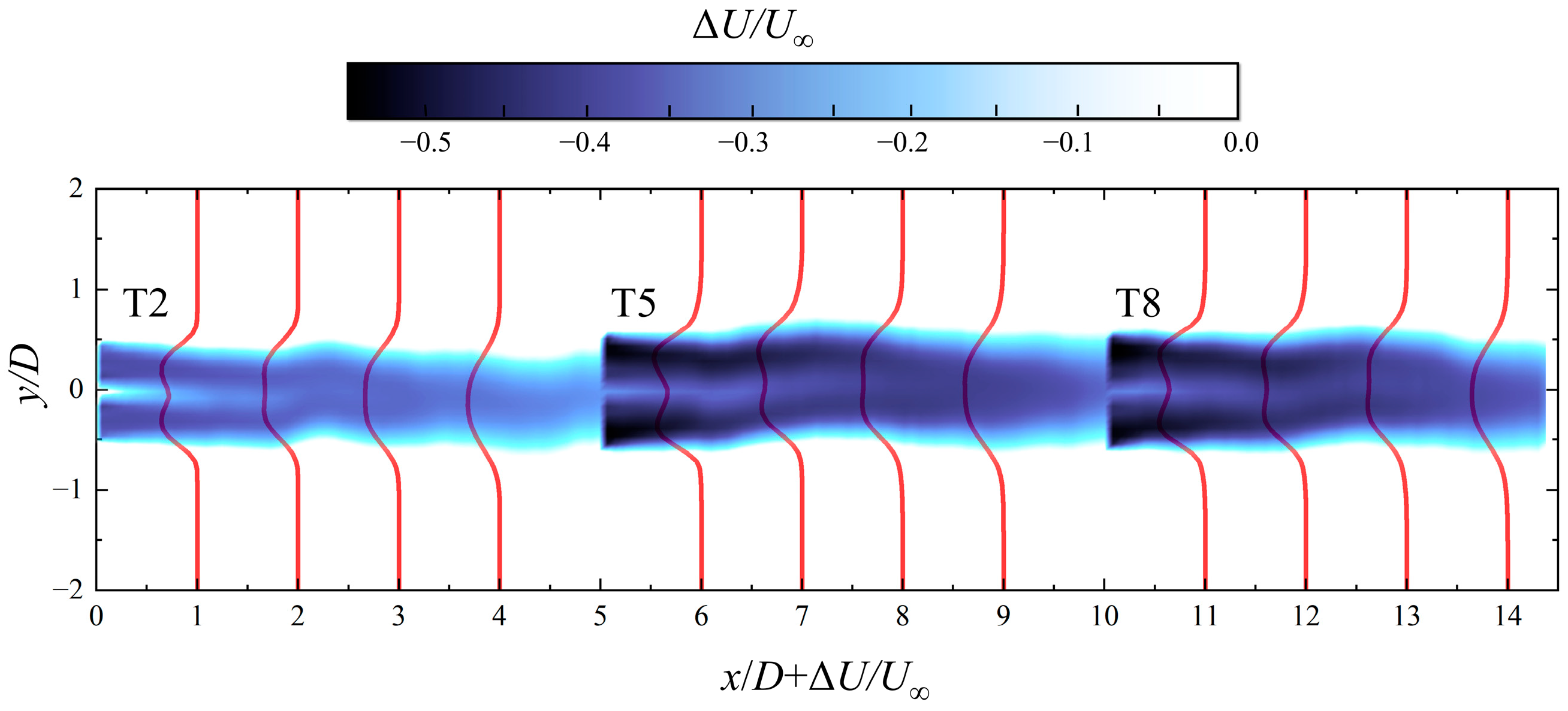
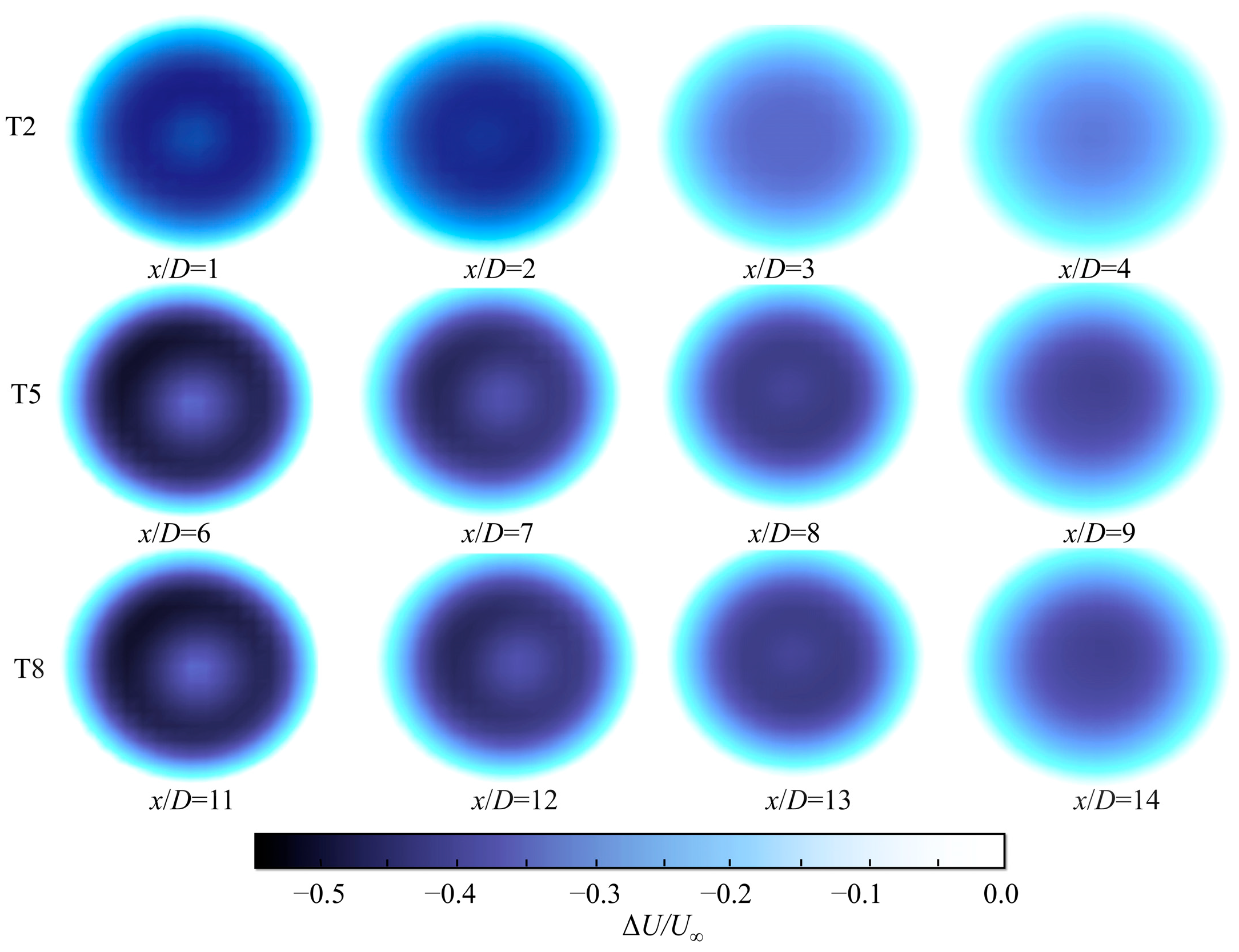
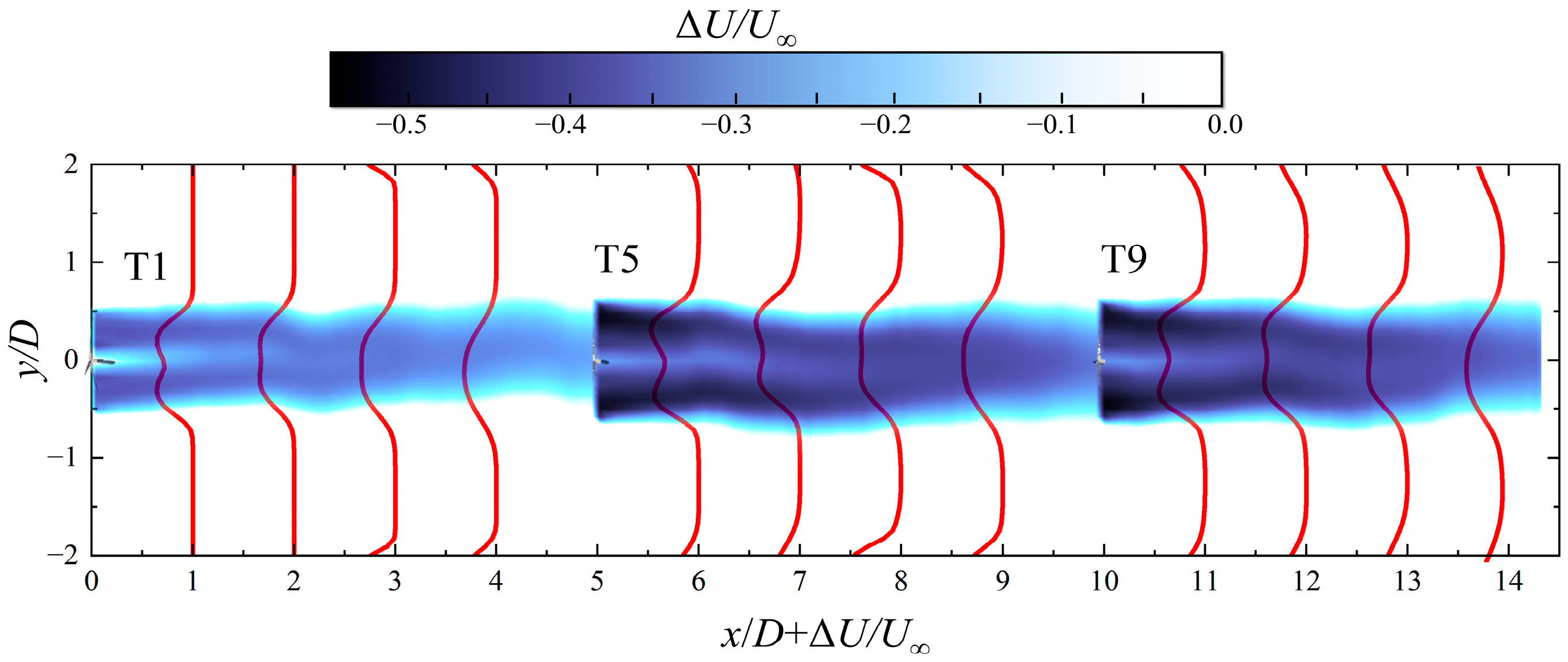
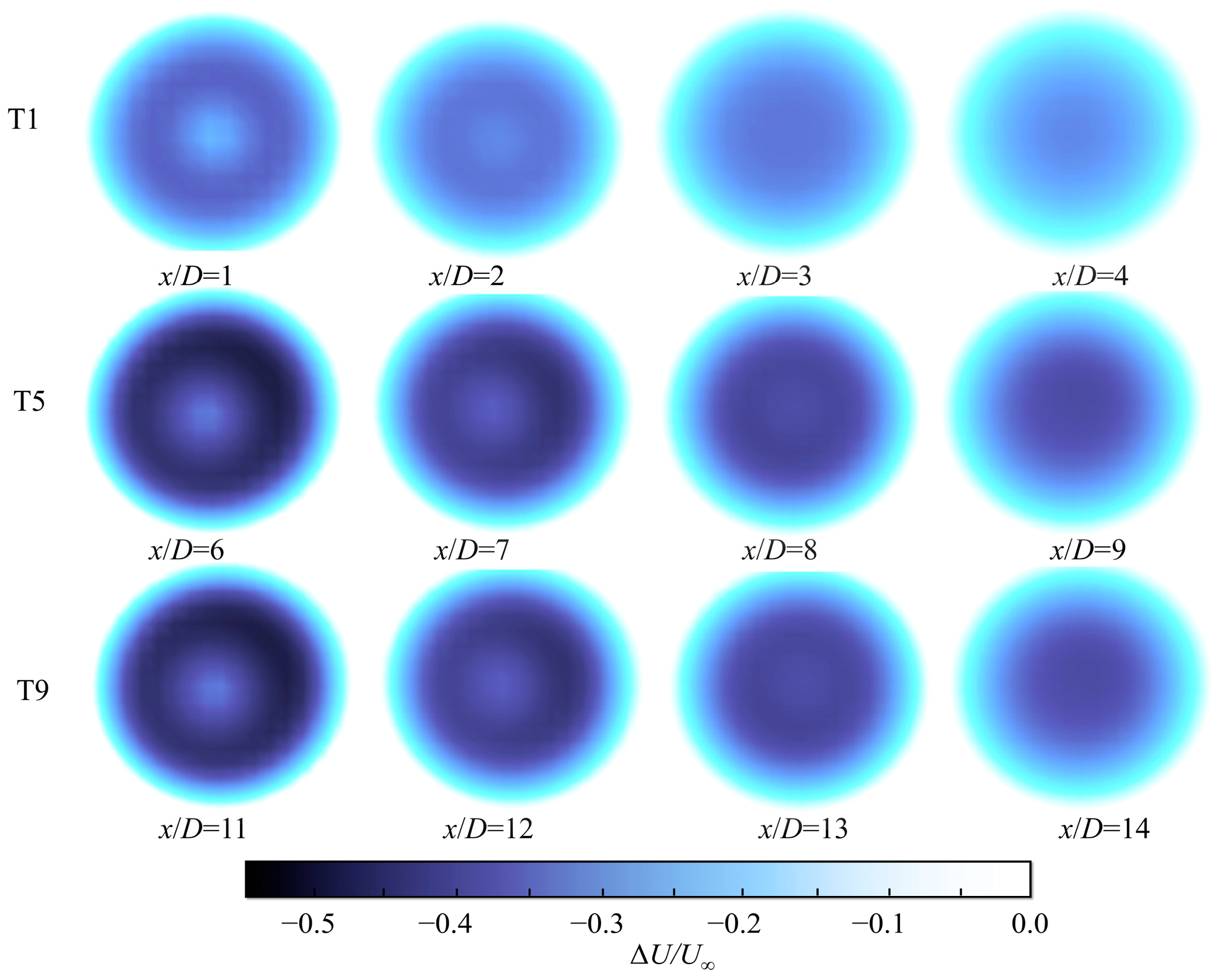
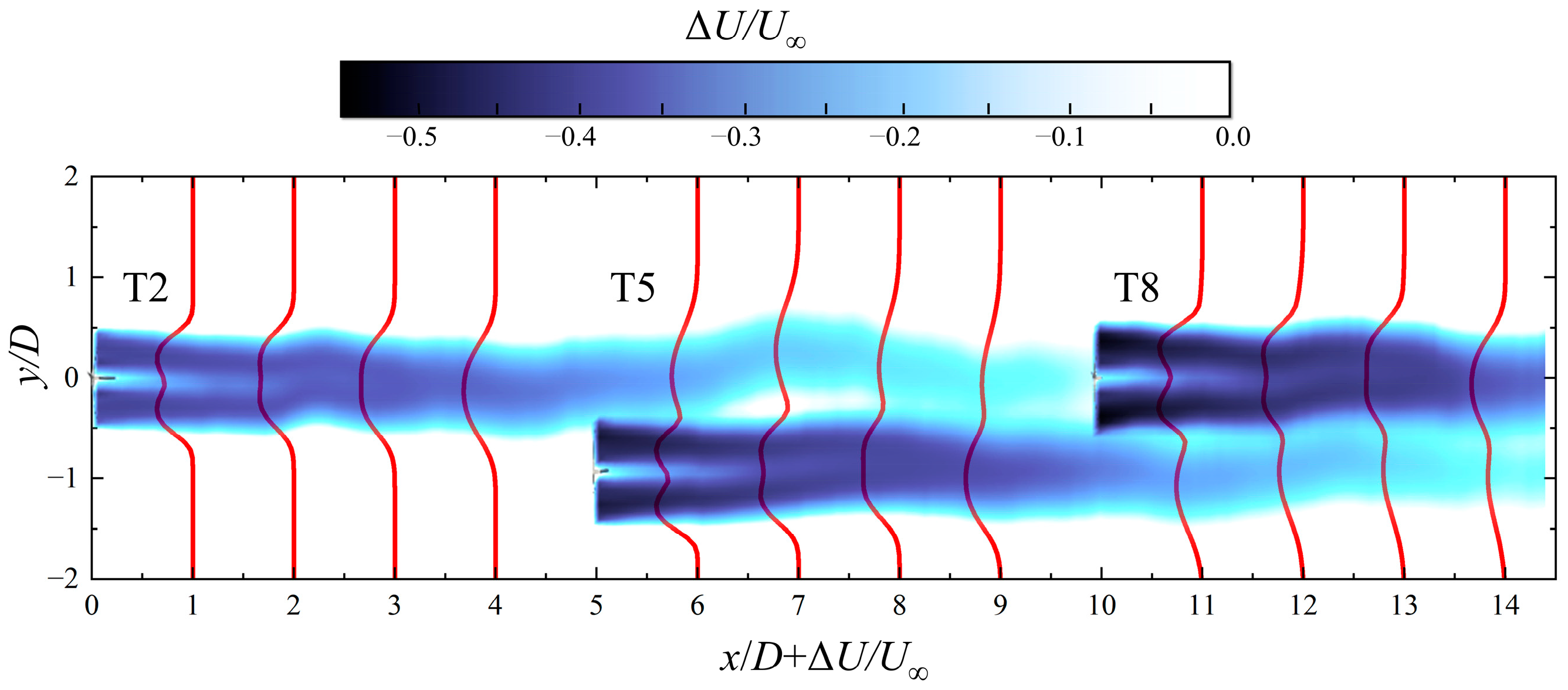
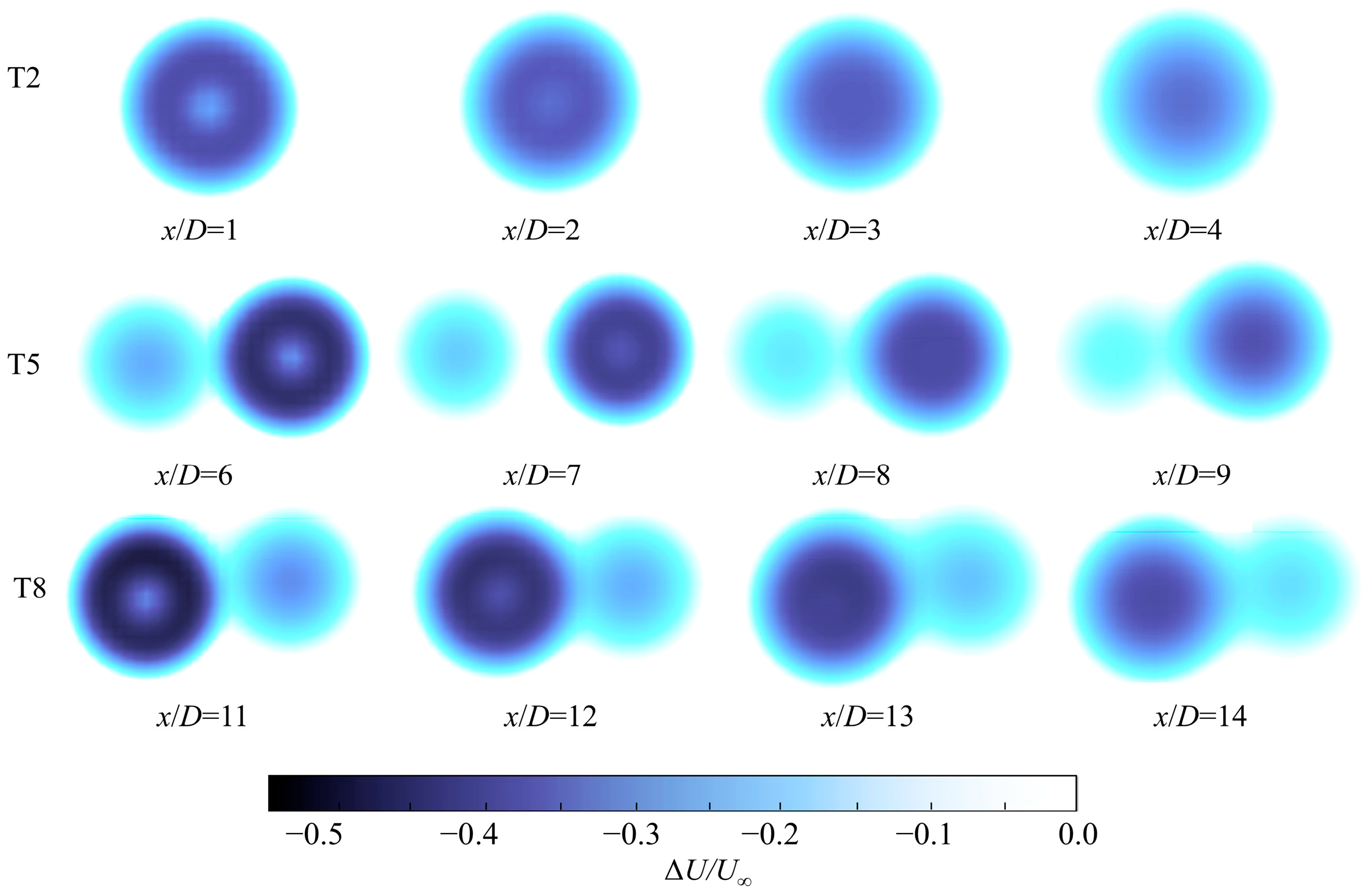
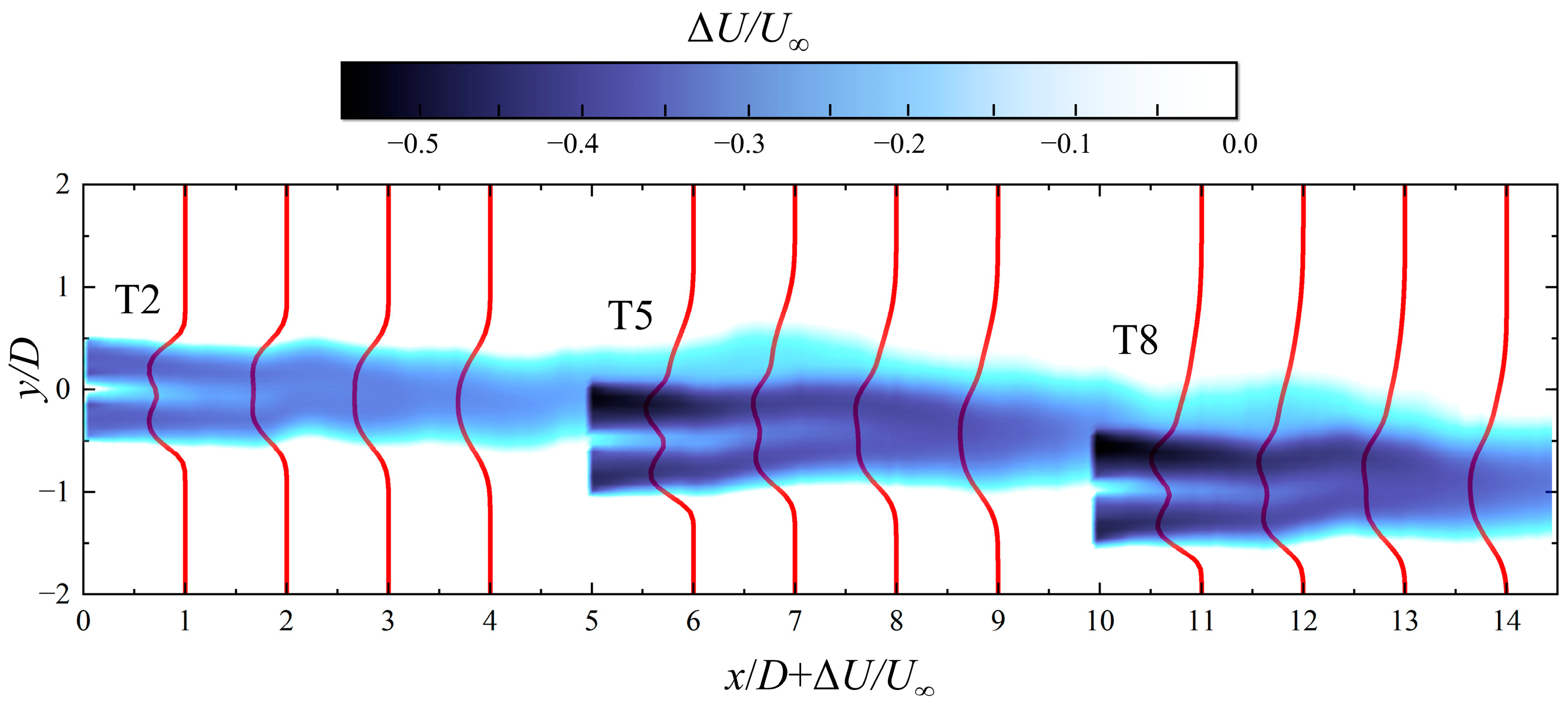
4.1.2. Wake Characteristic
4.2. Power and Wake Analysis for Diamond Layout Case
4.2.1. Power Performance
4.2.2. Wake Characteristic
4.3. Staggered Layout Case
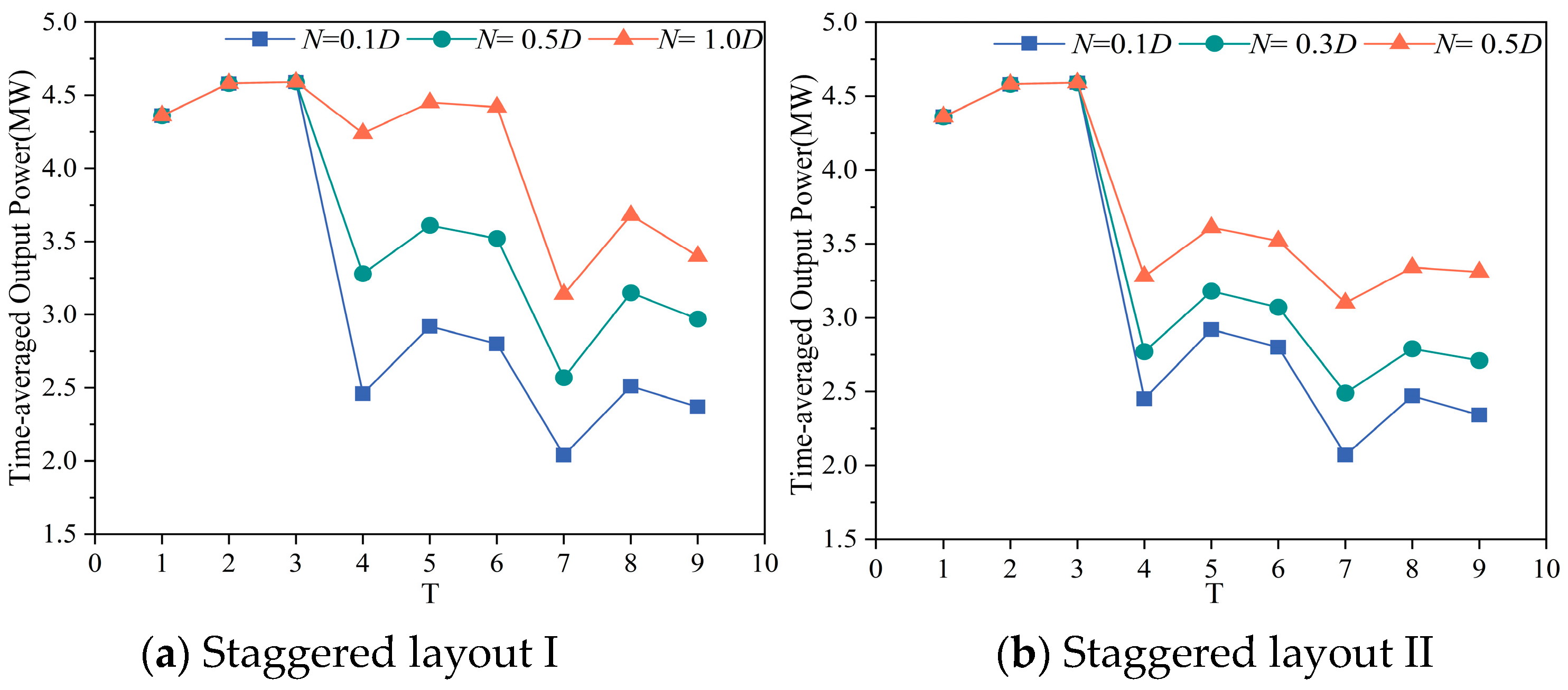
4.3.1. Power Performance
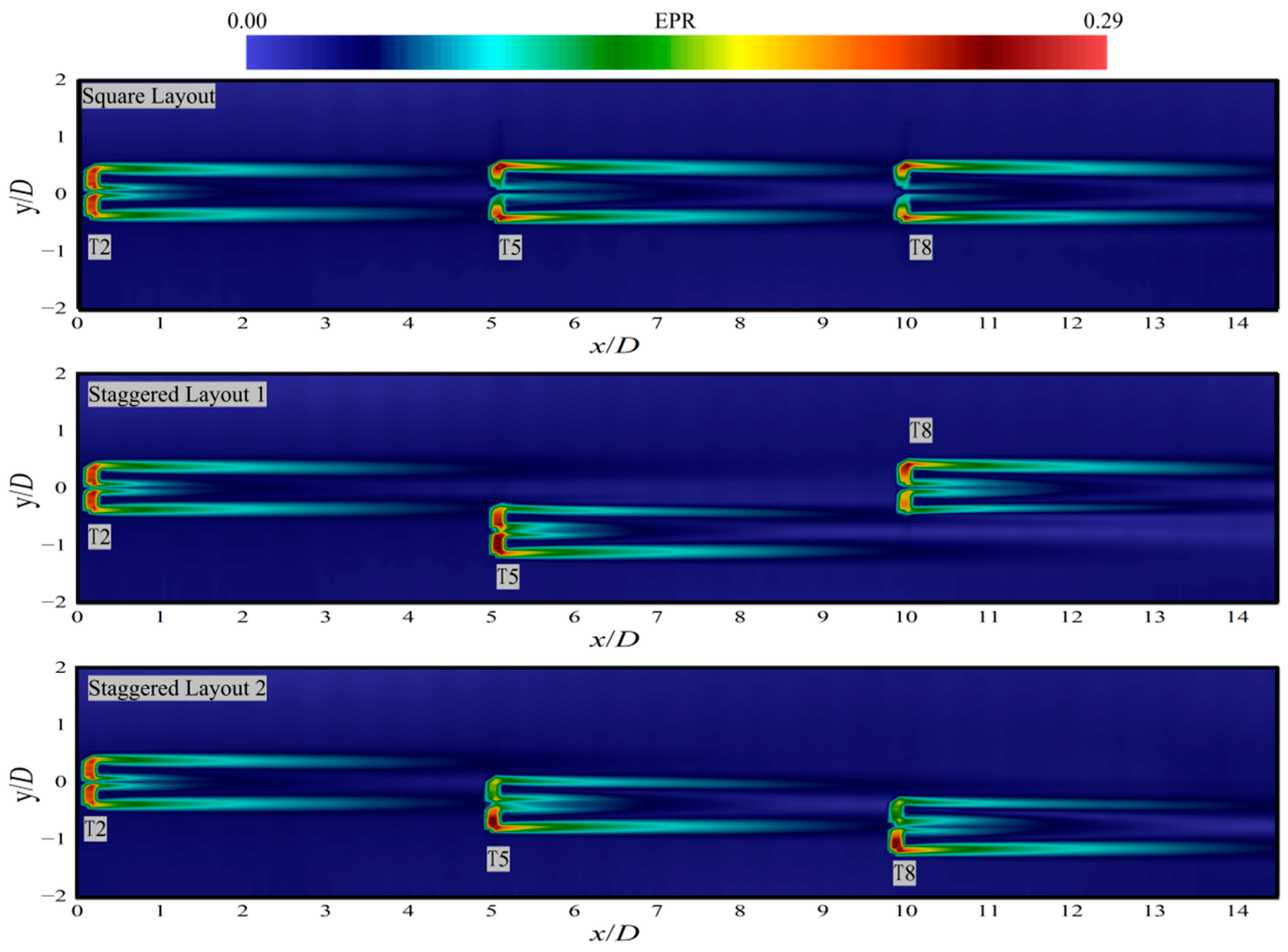
4.3.2. Wake Characteristic
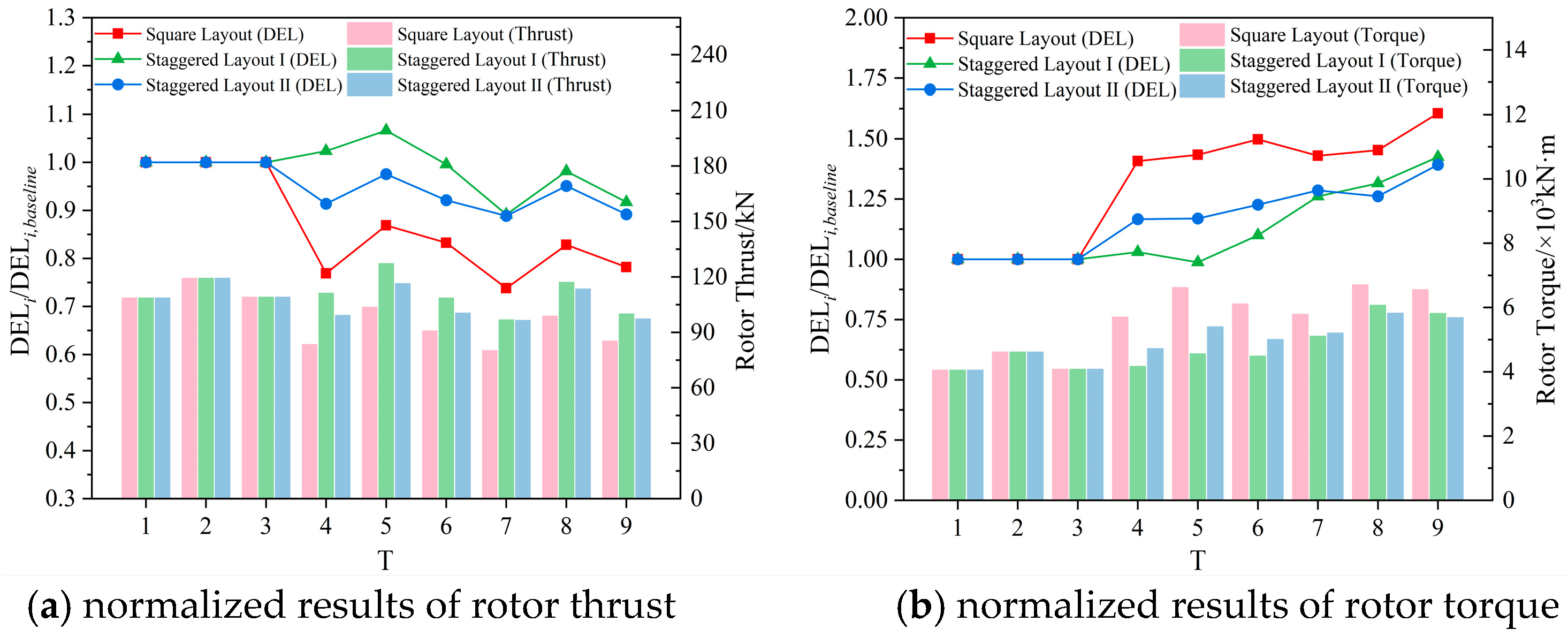
4.4. Rotor Thrust and Fatigue Load Analysis
4.5. Wake Entropy Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Steen, M.; Mäkitie, T.; Hanson, J.; Normann, H.E. Developing the industrial capacity for energy transitions: Resource formation for offshore wind in Europe. Environ. Innov. Soc. Transit. 2024, 53, 2210–4224. [Google Scholar] [CrossRef]
- Bai, H.; Zhang, J.H.; Ma, G.; Sun, K.; Kang, W.H.; Lai, Y.; Chen, Y.; Zhu, R.H. Structural modeling and optimization design of 15MW semi-submersible floating wind turbine platform based on intelligent algorithms. Energy 2025, 335, 137947. [Google Scholar] [CrossRef]
- Zhang, J.H.; Liu, Z.C.; Sun, K.; Chea, C.P.; Wei, M.Y.; Zhang, Y.W.; Lin, Z.B.; Geng, Y. Vibration control and parametric optimization of tuned liquid column damper for offshore wind turbines during shutdown. Energy 2025, 338, 138831. [Google Scholar] [CrossRef]
- Xu, X.; Wang, F.; Gaidai, O.; Næss, A.; Xing, Y.; Wang, J.L. Bivariate statistics of floating offshore wind turbine dynamic response under operational conditions. Ocean Eng. 2022, 257, 111657. [Google Scholar] [CrossRef]
- Sun, H.; Gao, X.; Yang, H. Experimental study on wind speeds in a complex-terrain wind farm and analysis of wake effects. Appl. Energy 2020, 272, 115215. [Google Scholar] [CrossRef]
- Su, H.; Meng, H.; Qu, T.; Lei, L. Wind tunnel experiment on the influence of array configuration on the power performance of vertical axis wind turbines. Energy Convers. Manag. 2021, 241, 114299. [Google Scholar] [CrossRef]
- Daaou Nedjari, H.; Guerri, O.; Saighi, M. CFD wind turbines wake assessment in complex topography. Energy Convers. Manag. 2017, 138, 224–236. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, Á.G.; Serrano-González, J.; Burgos-Payán, M.; Riquelme-Santos, J.M. Multi-objective optimization of a uniformly distributed offshore wind farm considering both economic factors and visual impact. Sustain. Energy Technol. Assess. 2022, 52, 102148. [Google Scholar] [CrossRef]
- Sahebzadeh, S.; Rezaeiha, A.; Montazeri, H. Impact of relative spacing of two adjacent vertical axis wind turbines on their aerodynamics. J. Phys. Conf. Ser. 2020, 1618, 042002. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Yang, H.R.; Zhao, Y.S.; Han, Z.L.; Zhou, D.; Zhang, J.H.; Tu, J.H.; Chen, M.S. A novel wake control strategy for a twin-rotor floating wind turbine: Mitigating wake effect. Energy 2024, 287, 129619. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, Z.H.; Yu, M.X.; Zhou, D.; Zhu, H.B.; Duan, L.; Tu, J.H.; Han, Z.L. Research on aerodynamic characteristics of three offshore wind turbines based on large eddy simulation and actuator line model. J. Mar. Sci. Eng. 2024, 12, 1341. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, P.; Zhou, Y.Z.; Guan, R.H.; Li, R.N. Insight into the impact of turbine-array configurations on the power output and wake effects of a finite-size wind farm. Renew. Energy 2025, 255, 123745. [Google Scholar] [CrossRef]
- Liu, S.Y.; Li, Q.S.; Lu, B.; He, J. Impact of incoming turbulence intensity and turbine spacing on output power density: A study with two 5 MW offshore wind turbines. Appl. Energy 2024, 371, 123648. [Google Scholar] [CrossRef]
- Yue, H.; Zhang, H.F.; Zhu, Q.C.; Ai, Y.F.; Tang, H.; Zhou, L. Wake dynamics of a wind turbine under real-time varying inflow turbulence: A coherence mode perspective. Energy Convers. Manag. 2025, 332, 119729. [Google Scholar] [CrossRef]
- Cao, L.C.; Ge, M.W.; Gao, X.X.; Du, B.; Li, B.; Huang, Z.; Liu, Y. Wind farm layout optimization to minimize the wake induced turbulence effect on wind turbines. Appl. Energy 2022, 323, 119599. [Google Scholar] [CrossRef]
- Wang, Y.; Chai, Y.F.; Gao, Z.T.; Zheng, X.B.; Hu, R.F.; Zheng, J.; Liu, H.Y.; Huang, H.J.; Gou, T. Effects of inflow turbulent coherent structures on a small-scale wind turbine in the atmospheric boundary layer of long corridor terrains: An example study in the Hexi corridor. PRX Energy 2024, 3, 043001. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Hu, Y.L.; Li, T.; Pan, J.; Yu, Z.Z.; Yang, Q.S. Numerical investigation of yaw-controlled wake effects on fatigue load distribution in downstream wind turbines. Ocean Eng. 2025, 341, 122455. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Yang, H.R.; Wang, R.Z.; Zhang, K.; Zhou, D.; Zhu, H.B.; Zhang, P.Y.; Han, Z.L.; Cao, Y.; Tu, J.H. Effects of combined platform rotation and pitch motions on aerodynamic loading and wake recovery of a single-point moored twin-rotor floating wind turbine. Energy 2025, 320, 135137. [Google Scholar] [CrossRef]
- Lin, M.; Porté-Agel, F. Wake meandering of wind turbines under dynamic yaw control and impacts on power and fatigue. Renew. Energy 2024, 223, 120003. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, M.S.; Tang, Q.H.; Zha, R.S. Investigating effects of pitch motions on aerodynamics and wake characteristics of a floating offshore wind turbine. Energy Convers. Manag. 2025, 326, 119402. [Google Scholar] [CrossRef]
- Song, K.; Huan, H.T.; Wei, L.C.; Liu, C.X. Investigation of the effect of blade angle of Archimedes spiral hydrokinetic turbine based on hydrodynamic performance and entropy production theory. Ocean Eng. 2025, 324, 120731. [Google Scholar] [CrossRef]
- He, G.F.; Sun, H.Y.; He, R.Y. A novel analytical wake model for floating offshore wind turbines with pitch motion effects. Renew. Energy 2026, 256, 124090. [Google Scholar] [CrossRef]
- Betz, A. Wind-Energie und ihre Ausnutzung durch Windmühlen; Vandenhoeck & Ruprecht: Göttingen, Germany, 1926. [Google Scholar]
- Yu, J.H. Wind Farm Wake Modeling and Analysis of Wind Impacts in a Wind Farm. Ph.D. Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 2016. [Google Scholar]
- Sutherland, H.J. On the Fatigue Analysis of Wind Turbines; Sandia National Laboratories Report SAND99-0089; Sandia National Laboratories: Albuquerque, NM, USA, 1999. [Google Scholar]
- Downing, S.D.; Socie, D.F. Simple rainflow counting algorithms. Int. J. Fatigue 1982, 4, 31–40. [Google Scholar] [CrossRef]
- McEvily, A.J.; Ishihara, S.; Endo, M. On the causes of deviation from the Palmgren-Miner rule. J. ASTM Int. 2004, 1, JAI19025. [Google Scholar] [CrossRef]
- Stanley, A.P.; King, J.; Bay, C.; Ning, A. A model to calculate fatigue damage caused by partial waking during wind farm optimization. Wind Energy Sci. 2022, 7, 433–454. [Google Scholar] [CrossRef]
- IEC 61400-13:2015; Wind Turbines—Part 13: Measurement of Mechanical Loads. International Electrotechnical Commission: Geneva, Switzerland, 2015.
- Herwig, H.; Köck, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Jonkman, J.; Shaler, K. FAST.Farm User’s Guide and Theory Manual; Technical Report NREL/TP-5000-78485; National Renewable Energy Laboratory: Golden, CO, USA, 2013. [Google Scholar]
- Doubrawa, P.; Annoni, J.R.; Jonkman, J.M. Optimization-Based calibration of FAST.Farm parameters against large-eddy simulations. In Proceedings of the Wind Energy Symposium (AIAA), Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Shaler, K.; Jonkman, J.; Hamilton, N. Effects of inflow spatiotemporal discretization on wake meandering and turbine structural response using FAST.Farm. J. Phys. Conf. Ser. 2019, 1256, 012023. [Google Scholar] [CrossRef]
- Shaler, K.; Jonkman, J.M. FAST.Farm response to varying wind inflow and discretization. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, X.S.; Wang, S.S.; Xing, Y.H.; Dou, P.; Ji, R.W.; Zhang, P.; Yang, P.Y. Investigating the influence of yaw control on wind farm dynamic characteristics for three conceptual floating offshore wind turbines. Ocean Eng. 2025, 342, 113597. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Barthelmie, R.J.; Hansen, K.; Frandsen, S.T.; Rathmann, O.; Schepers, J.G.; Schlez, W.; Phillips, J.; Rados, K.; Zervos, A.; Politis, E.S. Modelling and measuring flow and wind turbine wakes in large wind farms offshore. Wind Energy 2010, 12, 431–444. [Google Scholar] [CrossRef]
- Mou, L.; Fernando, P.A. Large-eddy simulation of a wind-turbine array subjected to active yaw control. Wind Energy Sci. 2022, 7, 2215–2230. [Google Scholar] [CrossRef]
- Liu, S.Y.; Li, Q.S.; Lu, B.; He, J.Y. Analysis of NREL-5MW wind turbine wake under varied turbulence conditions. Renew. Energy 2024, 224, 131148. [Google Scholar] [CrossRef]
- Cañadillas, B.; Foreman, R.; Steinfeld, G.; Robinson, N. Cumulative interactions between the global blockage and wake effects as observed by an engineering model and Large-Eddy Simulations. Energies 2023, 16, 2949. [Google Scholar] [CrossRef]
- Ning, X.; Wan, D. LES study of wake meandering in different atmospheric stabilities and its effects on wind turbine aerodynamics. Sustainability 2019, 11, 6939. [Google Scholar] [CrossRef]
- Meng, H.; Zhang, X.; Zhang, L.; Wang, L.; Zhang, Y. Analytical and numerical study on centrifugal stiffening effect of wind turbine blades. Renew. Energy 2022, 186, 1078–1094. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Zhang, X.; Li, H.; Zhang, L. Stress characteristics of horizontal-axis wind turbine blades under yaw fluctuations. Appl. Sci. 2023, 13, 8418. [Google Scholar] [CrossRef]

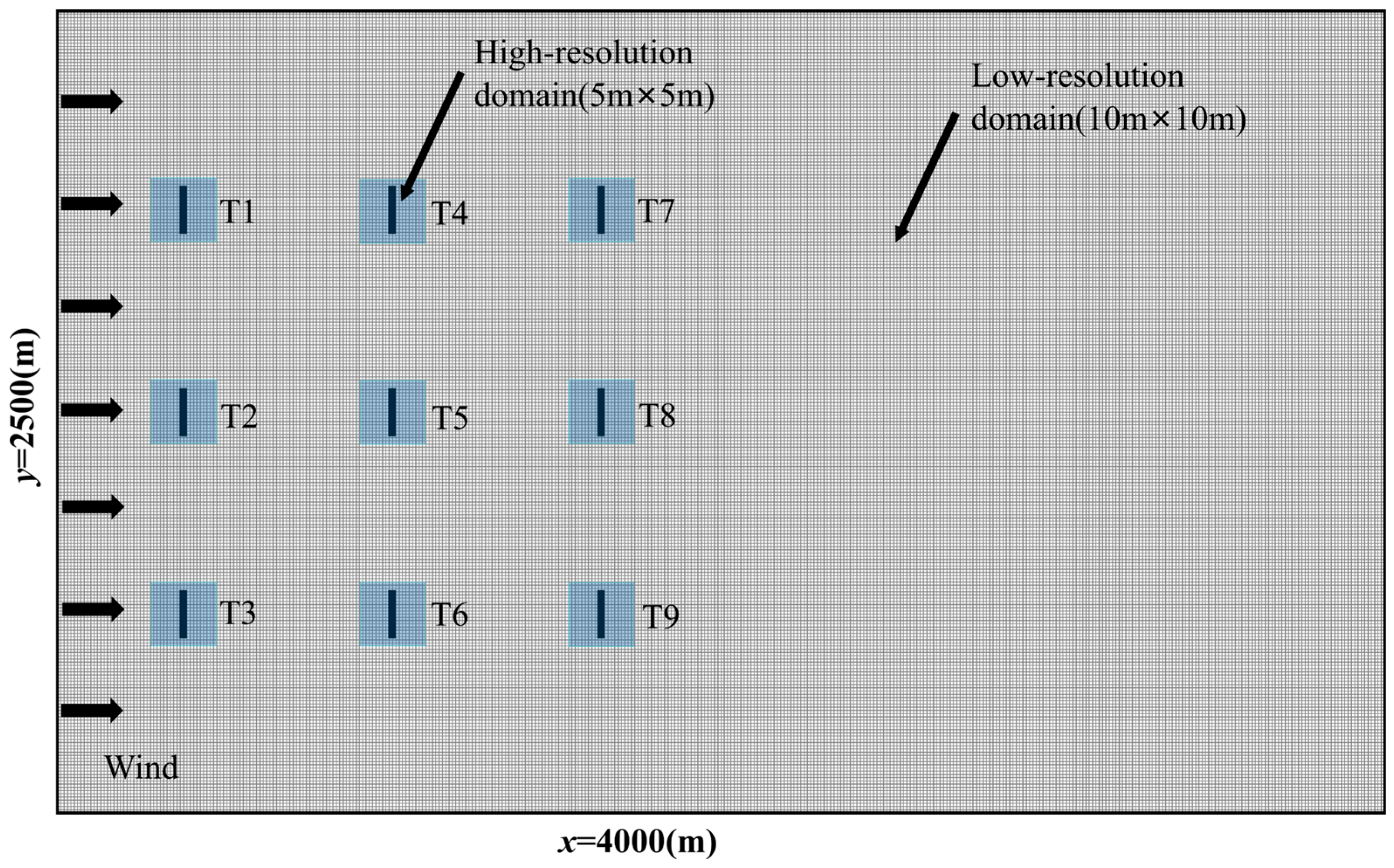

| Low-Resolution Domain Mesh Size(m) | High-Resolution Domain Mesh Size(m) | Output Power (MW) | Output Power Comparison Ratio (%) | |
|---|---|---|---|---|
| Mesh1 | 10 | 5 | 5.28 | 99.81 |
| Mesh2 | 10 | 10 | 5.23 | 98.87 |
| Mesh3 | 20 | 10 | 5.22 | 98.68 |
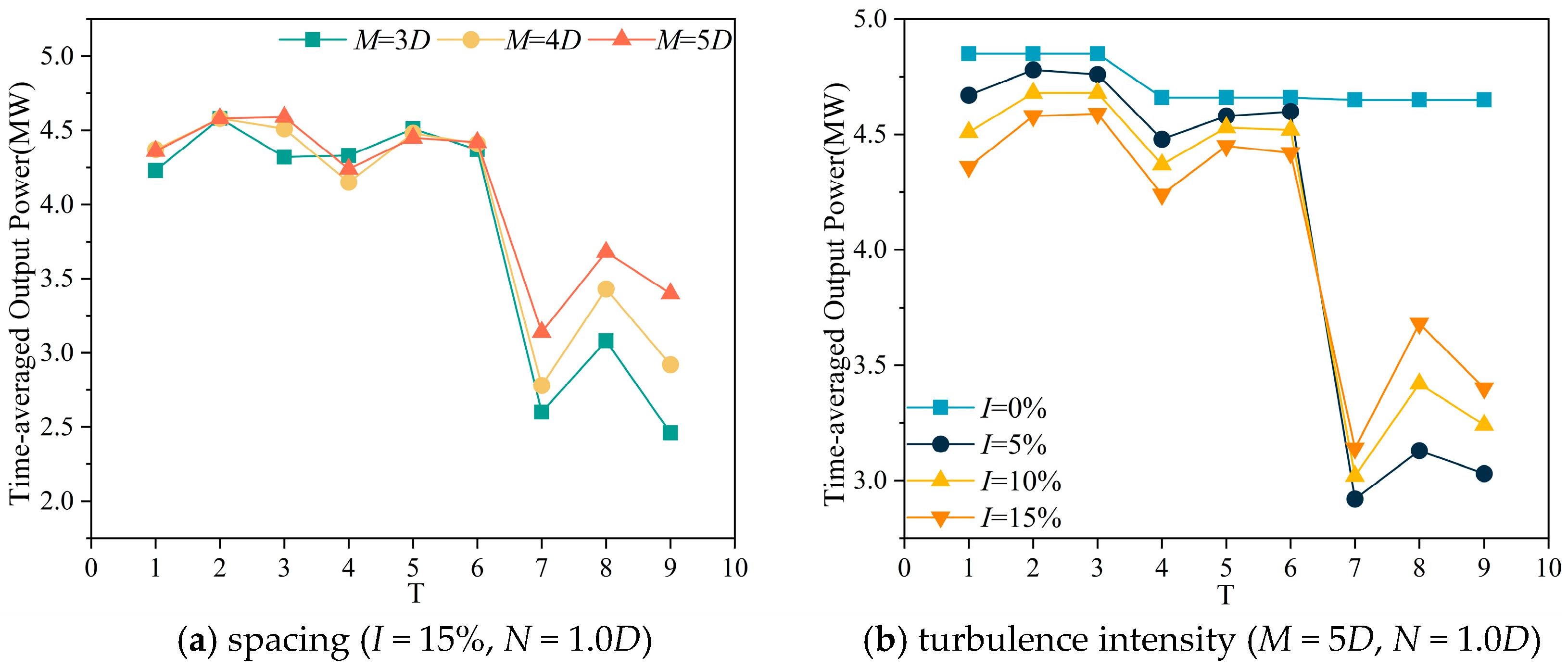
| M | I | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D | 0% | 4.85 | 4.85 | 4.85 | 1.32 | 1.32 | 1.32 | 1.27 | 1.27 | 1.27 | 22.32 |
| 5% | 4.63 | 4.78 | 4.65 | 1.57 | 1.72 | 1.51 | 1.32 | 1.42 | 1.31 | 22.89 | |
| 10% | 4.42 | 4.67 | 4.49 | 1.73 | 2.03 | 1.63 | 1.36 | 1.56 | 1.34 | 23.23 | |
| 15% | 4.23 | 4.58 | 4.32 | 1.91 | 2.38 | 1.79 | 1.44 | 1.77 | 1.41 | 23.83 | |
| 4D | 0% | 4.85 | 4.85 | 4.85 | 1.61 | 1.61 | 1.61 | 1.49 | 1.49 | 1.49 | 23.85 |
| 5% | 4.66 | 4.78 | 4.66 | 1.81 | 2.00 | 1.84 | 1.55 | 1.67 | 1.58 | 24.56 | |
| 10% | 4.52 | 4.68 | 4.62 | 1.91 | 2.32 | 1.99 | 1.58 | 1.84 | 1.65 | 25.10 | |
| 15% | 4.37 | 4.58 | 4.51 | 2.04 | 2.65 | 2.16 | 1.65 | 2.12 | 1.77 | 25.84 | |
| 5D | 0% | 4.85 | 4.85 | 4.85 | 1.86 | 1.86 | 1.86 | 2.03 | 2.03 | 2.03 | 26.22 |
| 5% | 4.67 | 4.78 | 4.76 | 2.08 | 2.25 | 2.21 | 2.09 | 2.20 | 2.13 | 27.17 | |
| 10% | 4.51 | 4.68 | 4.68 | 2.23 | 2.57 | 2.46 | 2.13 | 2.39 | 2.26 | 27.91 | |
| 15% | 4.36 | 4.58 | 4.59 | 2.41 | 2.89 | 2.77 | 2.23 | 2.63 | 2.48 | 28.94 |
| M | I | T1 | T2 | T3 | T4 | T5 | T6 | T7 | T8 | T9 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3D | 0% | 4.85 | 4.85 | 4.85 | 4.85 | 1.31 | 4.85 | 1.31 | 1.31 | 1.26 | 29.42 |
| 5% | 4.78 | 4.74 | 4.74 | 4.63 | 1.71 | 4.64 | 1.59 | 1.55 | 1.40 | 29.78 | |
| 10% | 4.68 | 4.63 | 4.65 | 4.43 | 2.03 | 4.48 | 1.79 | 1.69 | 1.55 | 29.91 | |
| 15% | 4.58 | 4.53 | 4.56 | 4.25 | 2.38 | 4.31 | 2.01 | 1.84 | 1.76 | 30.20 | |
| 4D | 0% | 4.85 | 4.85 | 4.85 | 4.85 | 1.60 | 4.85 | 1.59 | 1.59 | 1.47 | 30.49 |
| 5% | 4.78 | 4.70 | 4.70 | 4.72 | 1.99 | 4.66 | 1.80 | 1.85 | 1.66 | 30.85 | |
| 10% | 4.68 | 4.55 | 4.58 | 4.52 | 2.31 | 4.60 | 2.03 | 1.92 | 1.83 | 31.02 | |
| 15% | 4.58 | 4.42 | 4.46 | 4.38 | 2.65 | 4.48 | 2.25 | 2.06 | 2.11 | 31.37 | |
| 5D | 0% | 4.85 | 4.85 | 4.85 | 4.85 | 1.86 | 4.85 | 1.86 | 1.86 | 2.03 | 31.84 |
| 5% | 4.78 | 4.65 | 4.65 | 4.66 | 2.25 | 4.74 | 2.10 | 2.03 | 2.19 | 32.05 | |
| 10% | 4.68 | 4.46 | 4.51 | 4.50 | 2.57 | 4.64 | 2.27 | 2.13 | 2.39 | 32.14 | |
| 15% | 4.58 | 4.29 | 4.34 | 4.34 | 2.89 | 4.54 | 2.48 | 2.27 | 2.63 | 32.36 |
| N | M = 3D | M = 4D | M = 5D | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I = 0% | I = 5% | I = 10% | I = 15% | I = 0% | I = 5% | I = 10% | I = 15% | I = 0% | I = 5% | I = 10% | I = 15% | ||
| Staggered Layout I | 0.1D | 22.50 | 23.13 | 23.49 | 24.09 | 24.10 | 24.88 | 25.37 | 26.08 | 26.50 | 26.62 | 27.47 | 28.61 |
| 0.5D | 28.10 | 28.46 | 28.78 | 29.20 | 29.60 | 30.00 | 30.42 | 30.89 | 33.20 | 31.42 | 32.05 | 32.61 | |
| 1.0D | 35.40 | 34.84 | 34.64 | 34.46 | 36.50 | 35.97 | 35.80 | 35.62 | 42.48 | 36.94 | 36.96 | 36.84 | |
| Staggered Layout II | 0.1D | 22.80 | 23.30 | 23.63 | 24.20 | 24.30 | 25.00 | 25.44 | 26.12 | 26.50 | 26.69 | 27.48 | 28.56 |
| 0.3D | 26.10 | 26.43 | 26.65 | 27.10 | 27.40 | 27.87 | 28.23 | 28.73 | 28.90 | 29.33 | 29.88 | 30.53 | |
| 0.5D | 31.90 | 31.77 | 31.77 | 31.84 | 32.70 | 32.56 | 32.68 | 32.79 | 33.30 | 33.36 | 33.57 | 33.68 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Huang, J.; Zhang, Z.; Chen, K.; Shen, Z.; Tu, J.; Han, Z. Influence of Layout on Offshore Wind Farm Efficiency and Wake Characteristics in Turbulent Environments. J. Mar. Sci. Eng. 2025, 13, 2137. https://doi.org/10.3390/jmse13112137
Wang G, Huang J, Zhang Z, Chen K, Shen Z, Tu J, Han Z. Influence of Layout on Offshore Wind Farm Efficiency and Wake Characteristics in Turbulent Environments. Journal of Marine Science and Engineering. 2025; 13(11):2137. https://doi.org/10.3390/jmse13112137
Chicago/Turabian StyleWang, Guanyu, Junnan Huang, Zhihao Zhang, Kang Chen, Zhuang Shen, Jiahuang Tu, and Zhaolong Han. 2025. "Influence of Layout on Offshore Wind Farm Efficiency and Wake Characteristics in Turbulent Environments" Journal of Marine Science and Engineering 13, no. 11: 2137. https://doi.org/10.3390/jmse13112137
APA StyleWang, G., Huang, J., Zhang, Z., Chen, K., Shen, Z., Tu, J., & Han, Z. (2025). Influence of Layout on Offshore Wind Farm Efficiency and Wake Characteristics in Turbulent Environments. Journal of Marine Science and Engineering, 13(11), 2137. https://doi.org/10.3390/jmse13112137