Evaluating Gas Saturation in Unconventional Gas Reservoirs Using Acoustic Logs: A Case Study of the Baiyun Depression in the Northern South China Sea
Abstract
1. Introduction
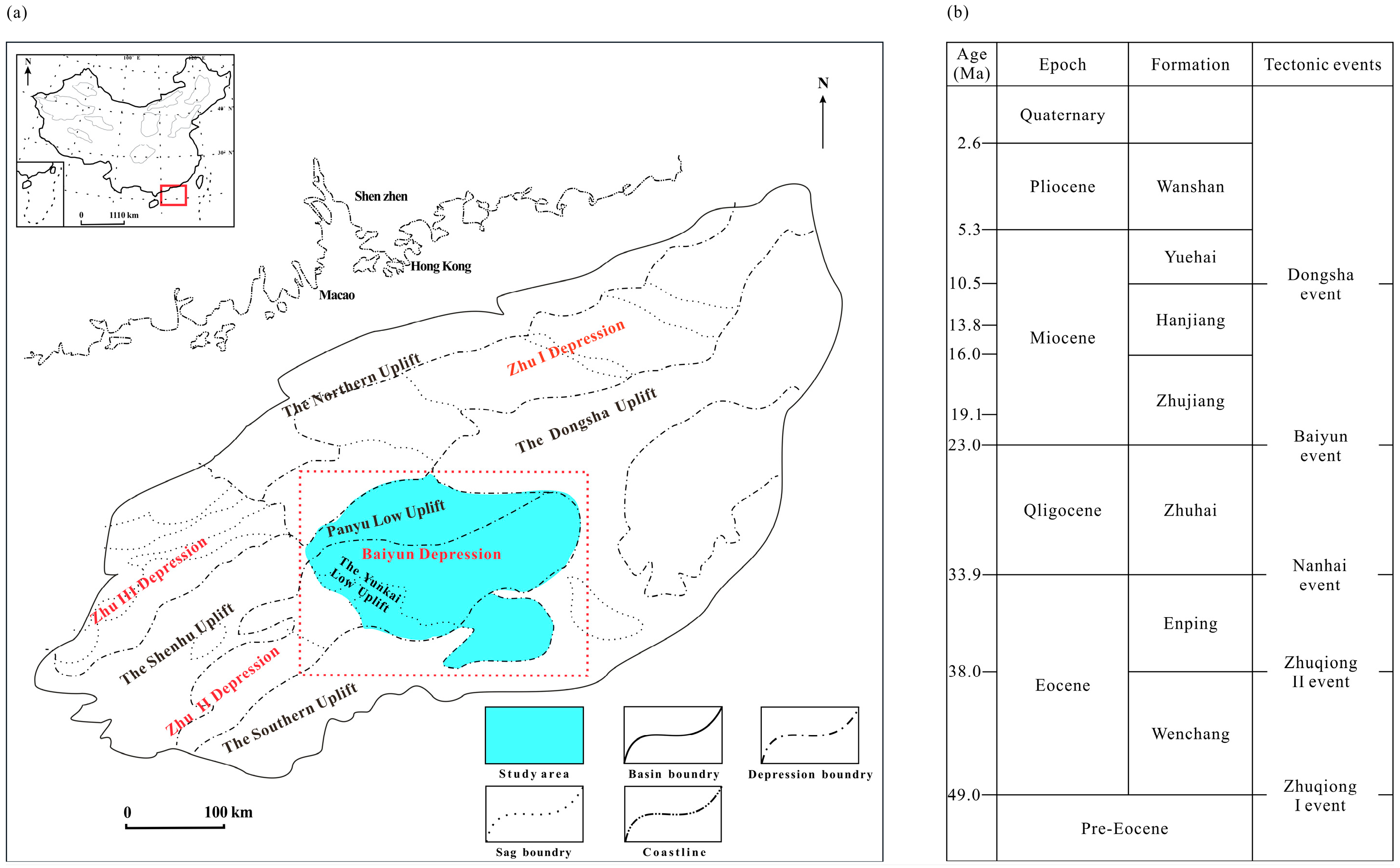
2. Geological Setting
3. Data and Method
3.1. Geophysical Logging Data
3.2. Method
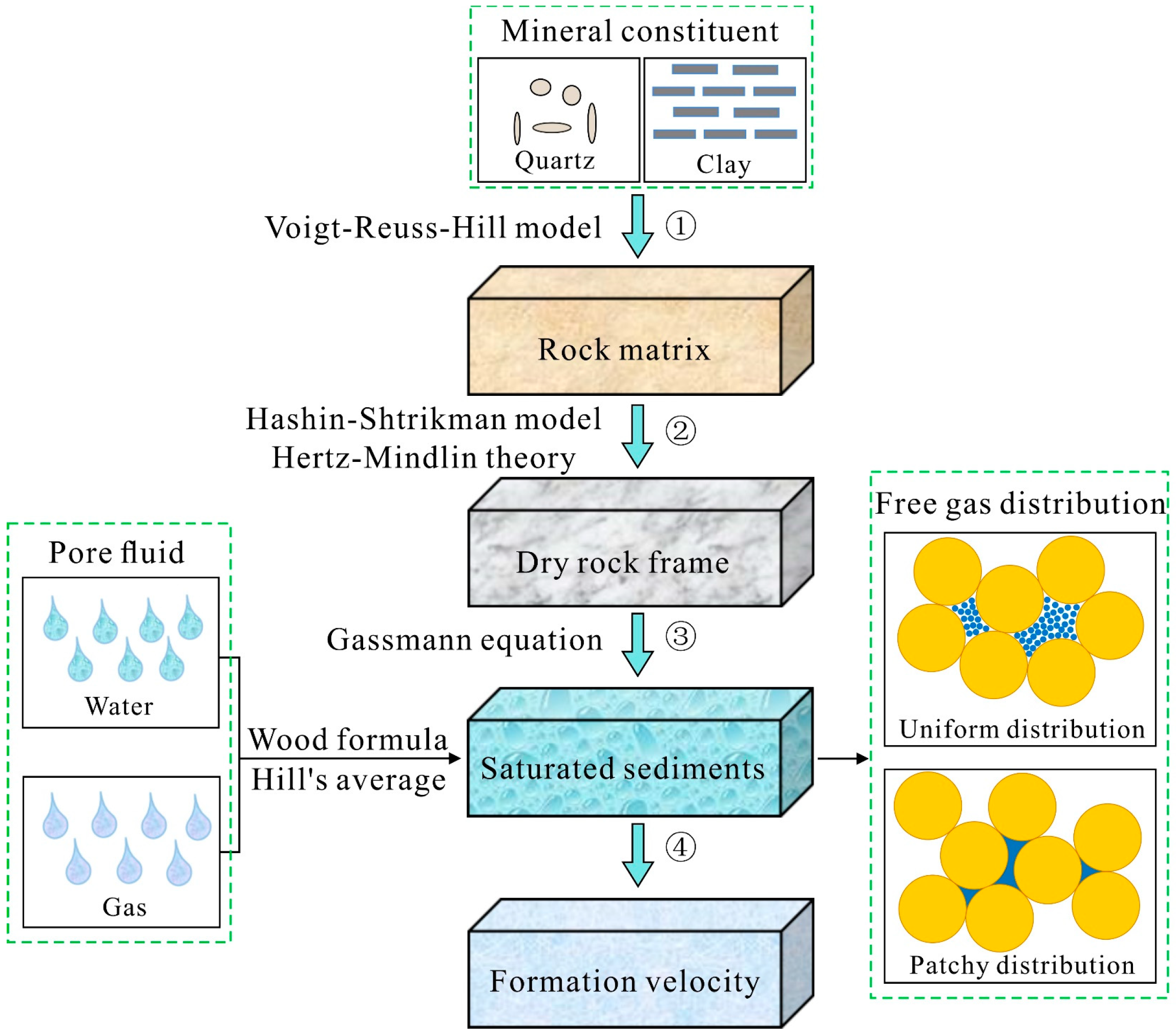
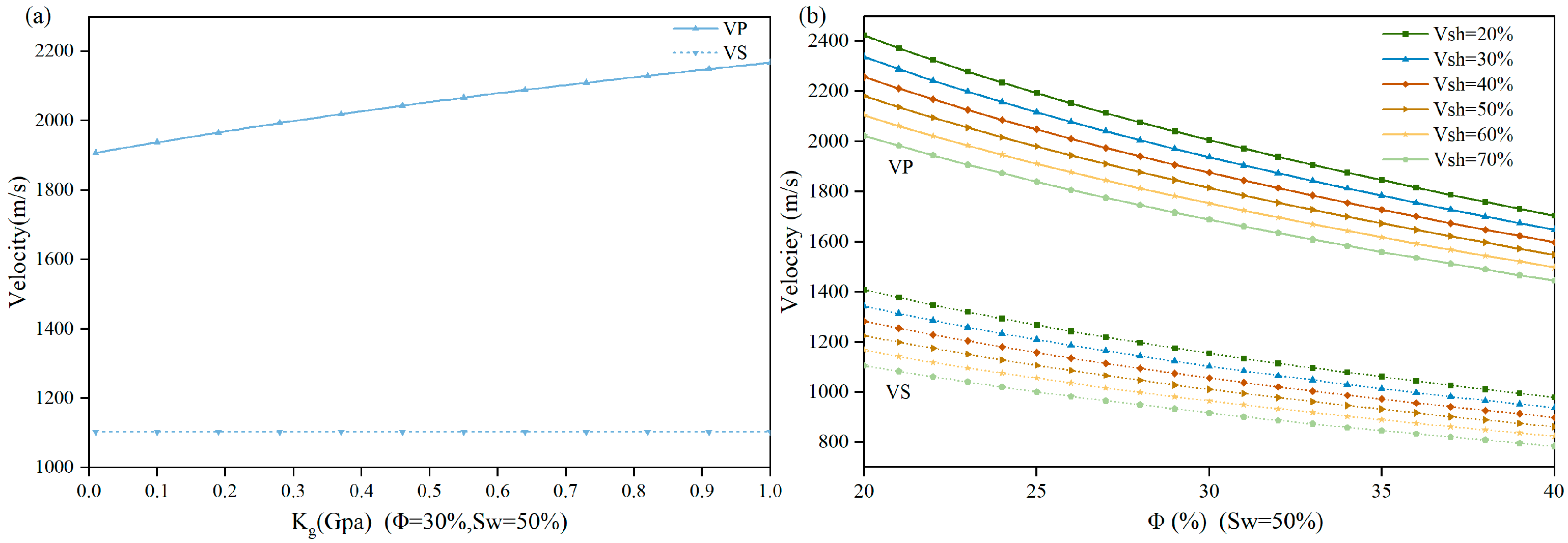
3.2.1. Rock Physics Modeling
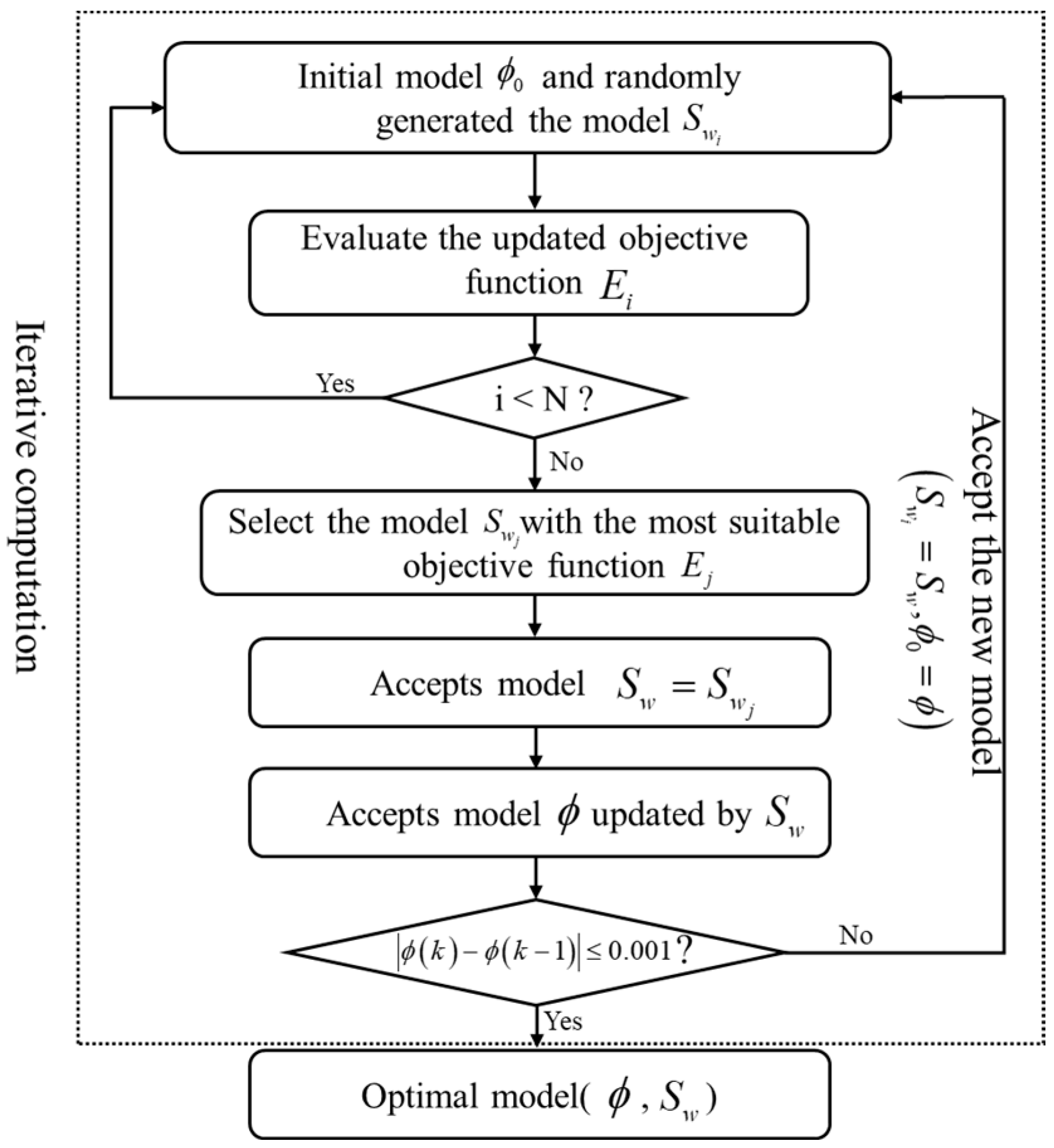
3.2.2. Saturation Predicted from Velocities
4. Results
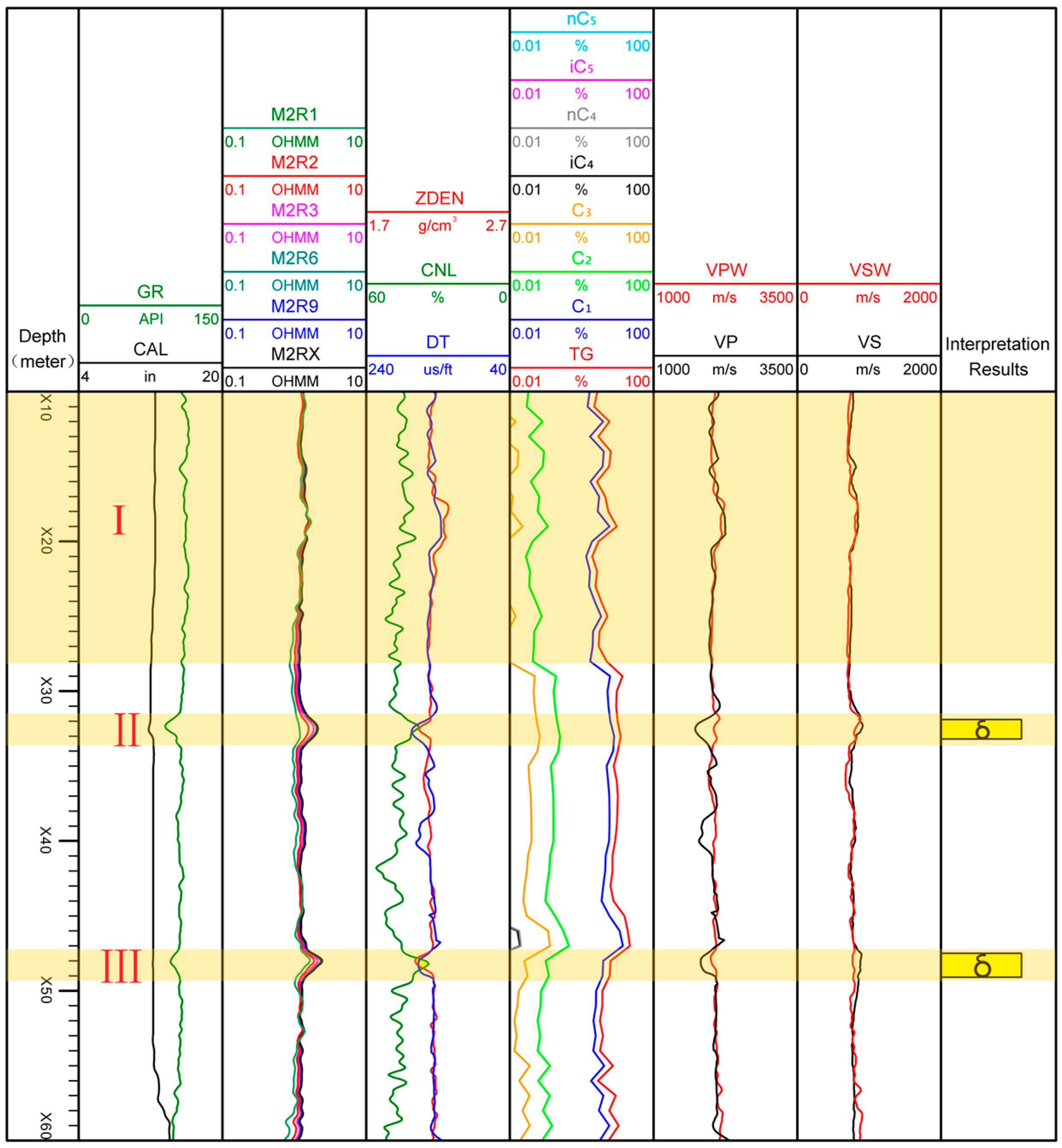
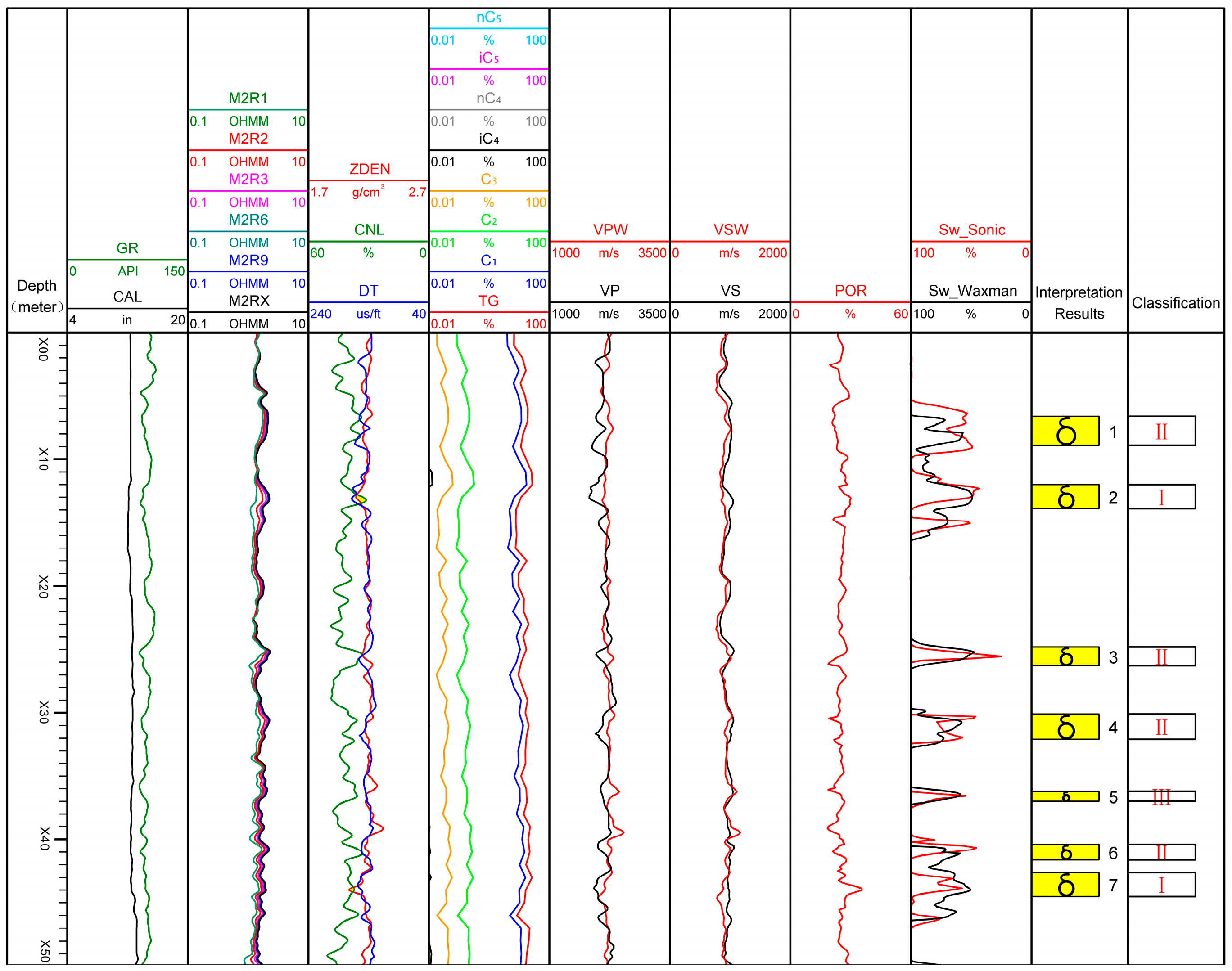
4.1. Logging Response of Gas-Bearing Sandstone Reservoirs
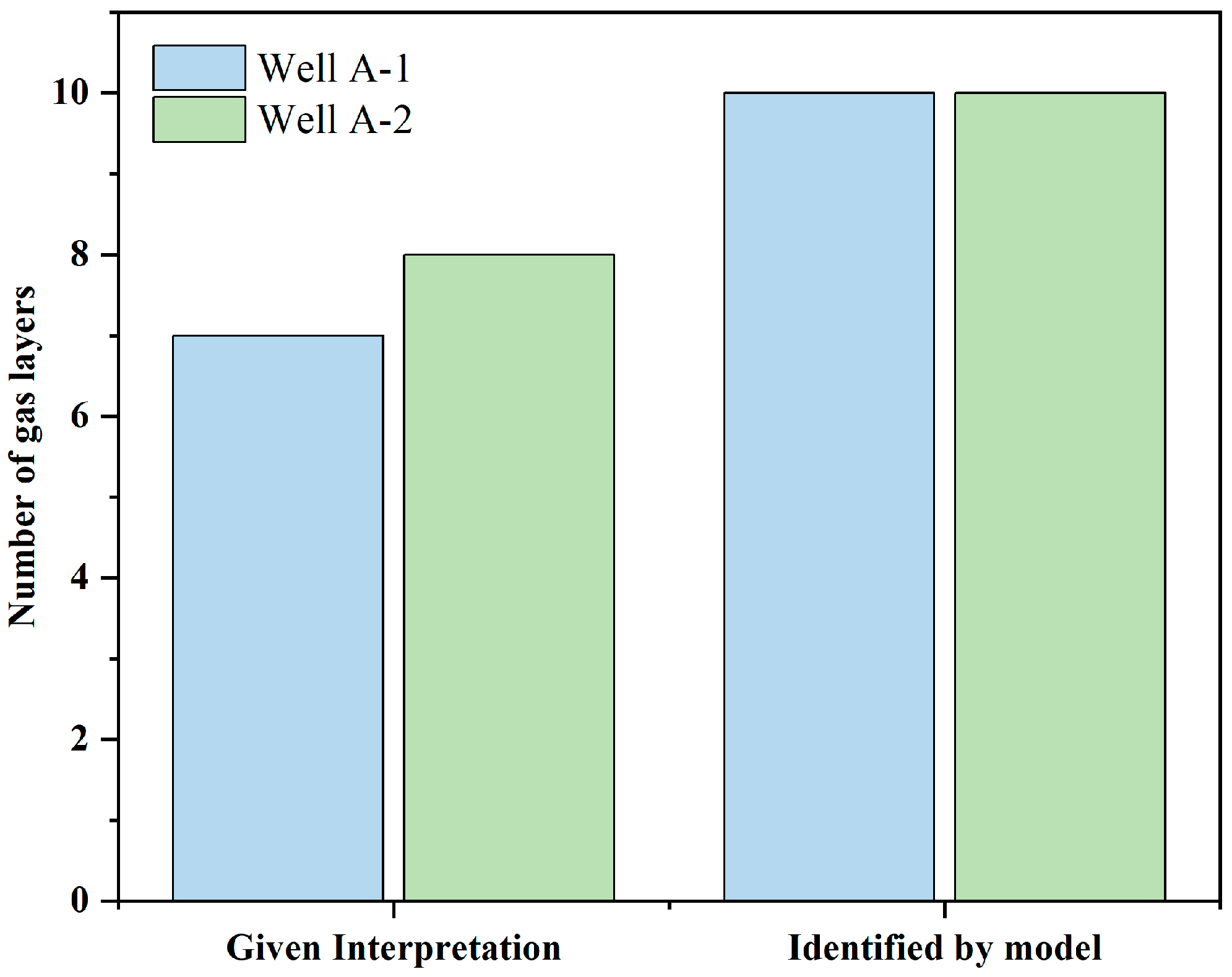
4.2. The Identification Results of the Gas Reservoirs
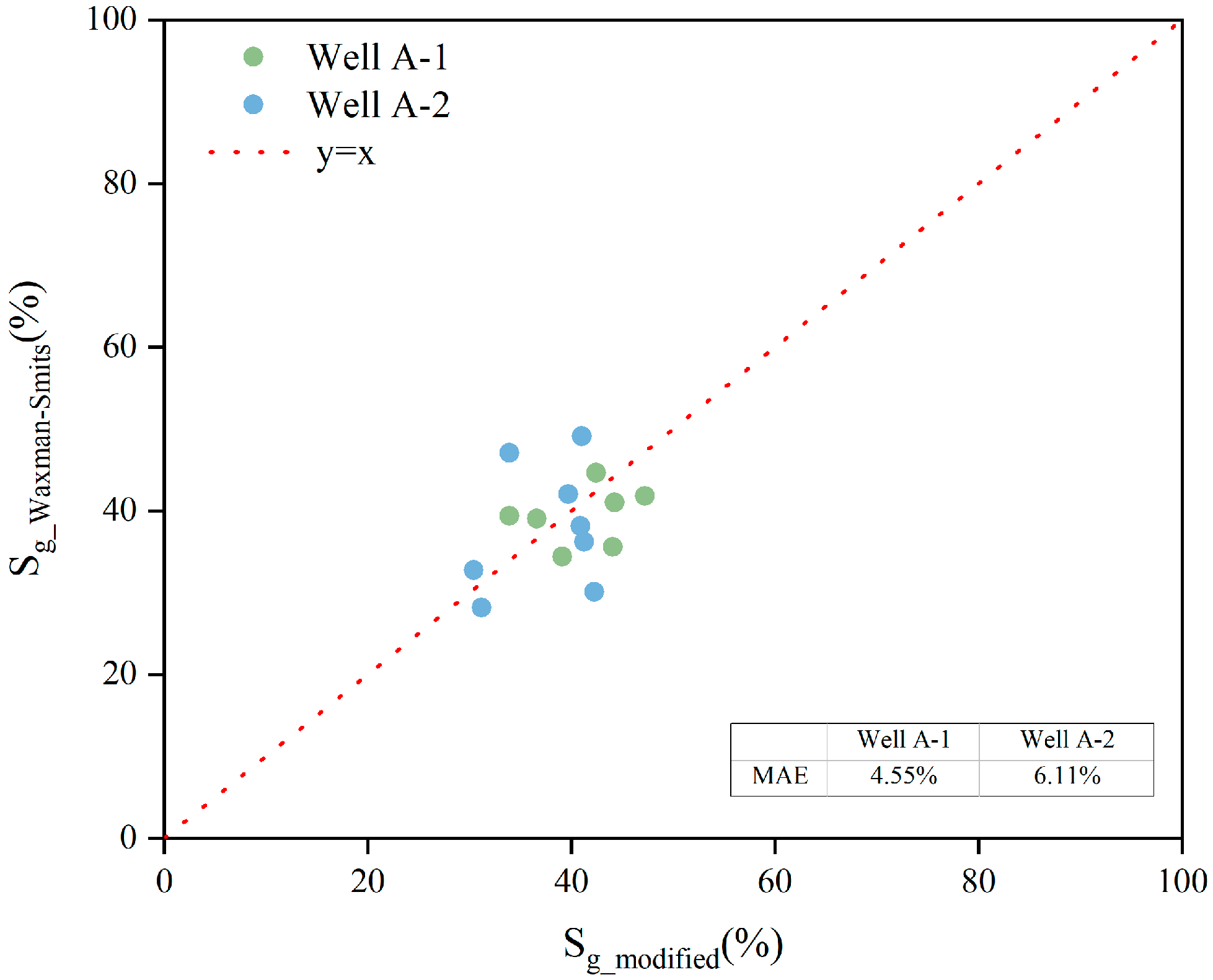
4.3. Evaluation Results of the Saturation
5. Discussion
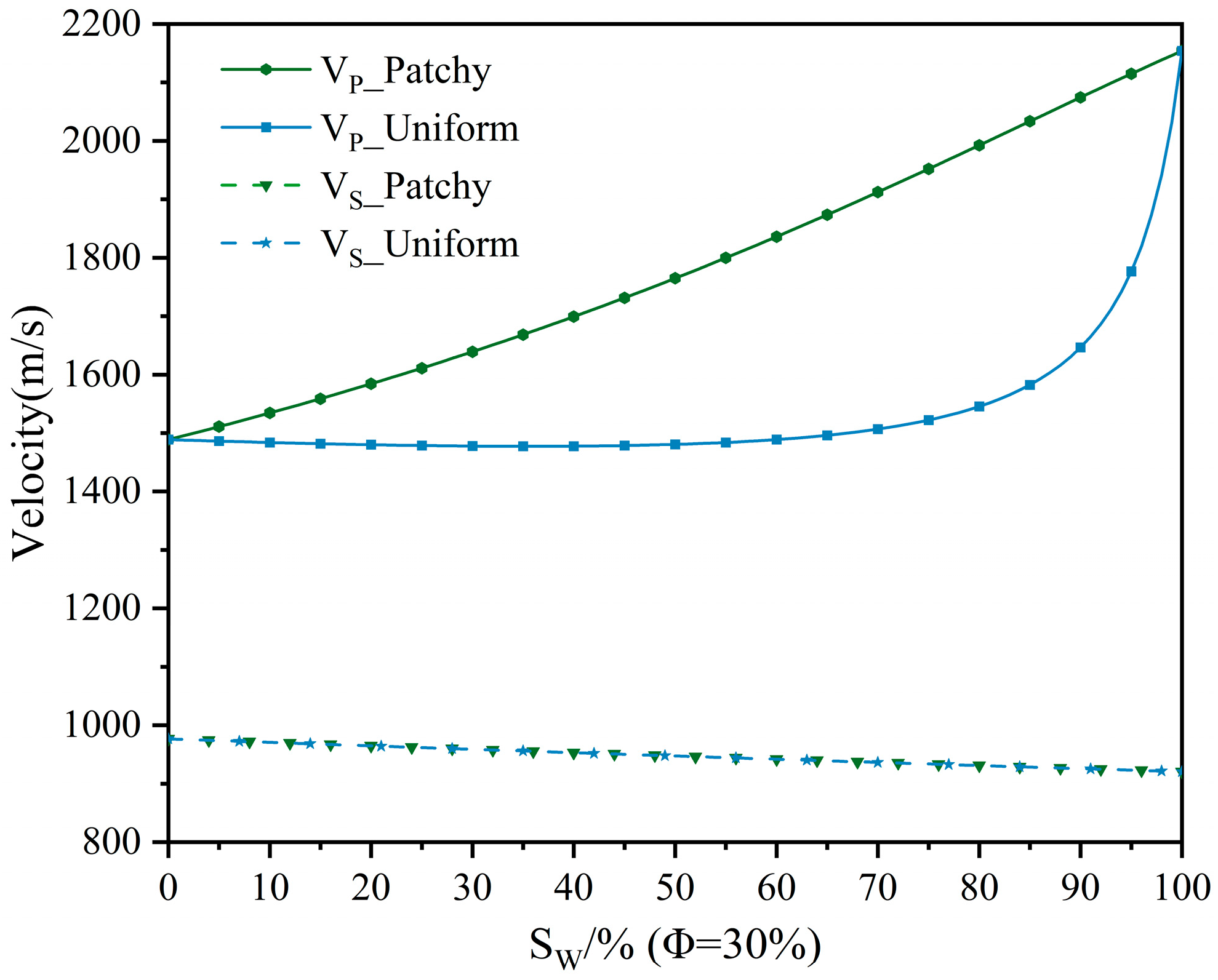
5.1. The Validity of the Model
5.2. Uncertainty Analysis of Gas Saturation Prediction
6. Conclusions
- (1)
- The rock physics model of shallow unconsolidated formations established by the Voigt-Reuss-Hill boundary model, Hertz-Mindlin theory, and Gassmann-Hill model achieves a good application effect in the shallow gas reservoirs of the PRMB. Compared to the velocities simulated with water-saturated, the compressional velocity in the gas-bearing reservoirs decreases significantly, and the shear remains essentially identical or decreases slightly, showing obvious gas-bearing characteristics. In the gas-free formations, the simulated velocity basically aligns with the measured velocity.
- (2)
- Compared with the assumption of uniform distribution in the Wood equation, the patchy distribution has better applicability. The results indicate that the gas saturation calculated from the array acoustic logging data ranges from 33.92% to 47.20% in Well A-1 and from 30.41% to 42.27% in Well A-2. These estimates demonstrate a certain degree of comparability with the saturation evaluated from the resistivity.
- (3)
- In Class I gas layers, the acoustic logging data are greatly influenced by the gas, resulting in a certain error in the saturation evaluation. However, for Class II and Class III gas layers, the method for saturation evaluation based on array acoustic logs and the shallow unconsolidated rock physics model shows good applicability, with an average improvement of 3.99% compared to the results from resistivity. This study provides a new path to evaluate gas saturation using non-electrical methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Aydin, H.; Merey, S. The effect of gas production from deeper conventional gas reservoirs on shallower gas hydrate layer stability: A case study in the conditions of the Sakarya gas field, Western Black Sea. J. Nat. Gas Sci. Eng. 2021, 94, 104103. [Google Scholar] [CrossRef]
- Zou, C.N.; Chen, Y.P.; Kong, L.F.; Sun, F.J.; Chen, S.S.; Dong, Z. Underground coal gasification and its strategic significance to the development of natural gas industry in China. Pet. Explor. Dev. 2019, 46, 205–215. [Google Scholar] [CrossRef]
- Zou, C.N.; Zhao, Q.; Chen, J.J.; Li, J.; Yang, Z.; Sun, Q.P.; Lu, J.L.; Zhang, G.X. Natural gas in China: Development trend and strategic forecast. Nat. Gas Ind. B 2018, 5, 380–390. [Google Scholar] [CrossRef]
- Davis, A.M. Shallow gas: An overview. Cont. Shelf Res. 1992, 12, 1077–1079. [Google Scholar] [CrossRef]
- Floodgate, G.D.; Judd, A.G. The origins of shallow gas. Cont. Shelf Res. 1992, 12, 1145–1156. [Google Scholar] [CrossRef]
- Müller, S.; Reinhardt, L.; Franke, D.; Gaedicke, C.; Winsemann, J. Shallow gas accumulations in the German North Sea. Mar. Pet. Geol. 2018, 91, 139–151. [Google Scholar] [CrossRef]
- Ren, J.F.; Cheng, C.; Xiong, P.F.; Kuang, Z.G.; Liang, J.Q.; Lai, H.F.; Chen, Z.G.; Chen, Y.; Li, T.; Jiang, T. Sand-rich gas hydrate and shallow gas systems in the Qiongdongnan Basin, northern South China Sea. J. Pet. Sci. Eng. 2022, 215, 110630. [Google Scholar] [CrossRef]
- Schroot, B.M.; Schüttenhelm, R.T.E. Expressions of shallow gas in the Netherlands North Sea. Neth. J. Geosci. 2003, 82, 91–105. [Google Scholar] [CrossRef]
- Cox, D.R.; Huuse, M.; Newton, A.M.; Sarkar, A.D.; Knutz, P.C. Shallow gas and gas hydrate occurrences on the northwest Greenland shelf margin. Mar. Geol. 2021, 432, 106382. [Google Scholar] [CrossRef]
- de Bruin, G.; ten Veen, J.; Wilpshaar, M.; Versteijlen, N.; Geel, K.; Verweij, H.; Carpentier, S. Origin of shallow gas in the Dutch North Sea—Seismic versus geochemical evidence. Interpretation 2022, 10, SB63–SB76. [Google Scholar] [CrossRef]
- Horozal, S.; Chae, S.; Kim, D.H.; Seo, J.M.; Lee, S.M.; Han, H.S.; Cukur, D.; Kong, G.-S. Seismic evidence of shallow gas in sediments on the southeastern continental shelf of Korea, East Sea (Japan Sea). Mar. Pet. Geol. 2021, 133, 105291. [Google Scholar] [CrossRef]
- Lee, S.H.; Chough, S.K. Distribution and origin of shallow gas in deep-sea sediments of the Ulleung Basin, East Sea (Sea of Japan). Geo-Mar. Lett. 2002, 22, 204–209. [Google Scholar] [CrossRef]
- Milkov, A.V. Methanogenic biodegradation of petroleum in the West Siberian Basin (Russia): Significance for formation of giant Cenomanian gas pools. AAPG Bull. 2010, 94, 1485–1541. [Google Scholar] [CrossRef]
- Hadavimoghaddam, F.; Ostadhassan, M.; Sadri, M.A.; Bondarenko, T.; Chebyshev, I.; Semnani, A. Prediction of water saturation from well log data by machine learning algorithms: Boosting and super learner. J. Mar. Sci. Eng. 2021, 9, 666. [Google Scholar] [CrossRef]
- Mondal, S.R.; Ghosh, R.; Ojha, M.; Maiti, S. Well log evaluation of the gas-bearing reservoirs in the Bombay offshore basin, Gulf of Cambay, western coast of India. Explor. Geophys. 2024, 55, 191–212. [Google Scholar] [CrossRef]
- Peng, C.; Zou, C.C.; Zhou, T.N.; Li, K.; Yang, Y.Q.; Zhang, G.H.; Wang, W.W. Factors affecting coalbed methane (CBM) well productivity in the Shizhuangnan block of southern Qinshui basin, North China: Investigation by geophysical log, experiment and production data. Fuel 2017, 191, 427–441. [Google Scholar] [CrossRef]
- Shedid, S.A.; Saad, M.A. Comparison and sensitivity analysis of water saturation models in shaly sandstone reservoirs using well logging data. J. Pet. Sci. Eng. 2017, 156, 536–545. [Google Scholar] [CrossRef]
- Xiao, L.; Zou, C.C.; Mao, Z.Q.; Shi, Y.J.; Jin, Y.; Guo, H.P.; Hu, X.X. Estimation of water saturation from nuclear magnetic resonance (NMR) and conventional logs in low permeability sandstone reservoirs. J. Pet. Sci. Eng. 2013, 108, 40–51. [Google Scholar] [CrossRef]
- Tohidi, E.; Hesan, M.; Azad, A.; Abbasi, M.; Sadeghnejad, S. Implementing pore size distribution into saturation height function modelling of reservoir rock types: A case study on a carbonate gas reservoir. Gas Sci. Eng. 2024, 121, 205188. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, N.Y.; Liu, C.L.; Zou, C.C.; Liu, Y.; Sun, J.Y.; Li, Y.L.; Hu, G.W. Research progress on global marine gas hydrate resistivity logging and electrical property experiments. J. Mar. Sci. Eng. 2022, 10, 645. [Google Scholar] [CrossRef]
- Lan, X.X.; Zou, C.C.; Peng, C.; Wu, C.W.; Zhang, Y.Y.; Wang, S.Y. Numerical Simulation of Electrical Properties for Pore-Scale Hydrate-Bearing Sediments with Different Occurrence Patterns and Distribution Morphologies. J. Mar. Sci. Eng. 2023, 11, 1169. [Google Scholar] [CrossRef]
- Simandoux, P. Dielectric measurements on porous media, application to the measurements of water saturation: Study of behavior of argillaceous formations. Rev. L’institut Fr. Pet. 1963, 18, 193–215. [Google Scholar]
- Waxman, M.H.; Smits, L.J.M. Electrical conductivities in oil-bearing shaly sands. Soc. Pet. Eng. J. 1968, 8, 107–122. [Google Scholar] [CrossRef]
- Clavier, C.; Coates, G.; Dumanoir, J. Theoretical and experimental bases for the dual-water model for interpretation of shaly sands. Soc. Pet. Eng. J. 1984, 24, 153–168. [Google Scholar] [CrossRef]
- Poupon, A.; Leveaux, J. Evaluation of water saturation in shaly formations. In Proceedings of the SPWLA Annual Logging Symposium, Dallas, TX, USA, 2–5 May 1971; p. SPWLA-1971-O. [Google Scholar]
- Gohari Nezhad, A.; Emami Niri, M. Enhancing water saturation predictions from conventional well logs in a carbonate gas reservoir with a hybrid CNN-LSTM model. J. Pet. Explor. Prod. Technol. 2025, 15, 89. [Google Scholar] [CrossRef]
- Coates, G.R.; Gardner, J.S.; Miller, D. Applying pulse-echo NMR to shaly sand formation evaluation. In Proceedings of the SPWLA Annual Logging Symposium, Tulsa, OK, USA, 19–22 June 1994; p. SPWLA-1994-B. [Google Scholar]
- Zhang, P.J.; Pan, B.Z.; Guo, Y.H.; Zhang, L.H.; Si, Z.W.; Xu, F.; Zhu, M.Y.; Li, Y. Study on an improved saturation parameter method based on joint inversion of NMR and resistivity data in porous media. Pet. Sci. 2025, 22, 2312–2314. [Google Scholar] [CrossRef]
- Qian, J.; Wang, X.J.; Collett, T.S.; Guo, Y.Q.; Kang, D.J.; Jin, J.P. Downhole log evidence for the coexistence of structure II gas hydrate and free gas below the bottom simulating reflector in the South China Sea. Mar. Pet. Geol. 2018, 98, 662–674. [Google Scholar] [CrossRef]
- Shi, W.; Wang, X.; Shi, Y.; Feng, A.; Zou, Y.; Young, S. Application of dipole array acoustic logging in the evaluation of shale gas reservoirs. Energies 2019, 12, 3882. [Google Scholar] [CrossRef]
- Yuan, H.M.; Han, D.H.; Wang, Y. A review of rock physical models for elastic properties characterization of gas hydrate bearing sediments. J. Pet. Sci. Eng. 2022, 218, 111013. [Google Scholar] [CrossRef]
- Guo, Z.; Lv, X.; Liu, C.; Chen, H.; Cai, Z. Characterizing gas hydrate–bearing marine sediments using elastic properties—Part 1: Rock physical modeling and inversion from well logs. J. Mar. Sci. Eng. 2022, 10, 1379. [Google Scholar] [CrossRef]
- Helgerud, M.B.; Dvorkin, J.; Nur, A.; Sakai, A.; Collett, T. Elastic-wave velocity in marine sediments with gas hydrates: Effective medium modeling. Geophys. Res. Lett. 1999, 26, 2021–2024. [Google Scholar] [CrossRef]
- Tinivella, U. A method for estimating gas hydrate and free gas concentrations in marine sediments. Boll. Geofis. Teor. Appl. 1999, 40, 19–30. [Google Scholar]
- Lee, M.W. Biot–Gassmann theory for velocities of gas hydrate-bearing sediments. Geophysics 2002, 67, 1711–1719. [Google Scholar] [CrossRef]
- Ghosh, R.; Ojha, M. Amount of gas hydrate estimated from rock physics analysis based on morphology and intrinsic anisotropy in area B, Krishna Godavari offshore basin, expedition NGHP-02. Mar. Pet. Geol. 2021, 124, 104856. [Google Scholar] [CrossRef]
- Pan, H.J.; Li, H.B.; Chen, J.Y.; Riedel, M.; Holland, M.; Zhang, Y.; Cai, S.J. Quantification of gas hydrate saturation and morphology based on a generalized effective medium model. Mar. Pet. Geol. 2020, 113, 104166. [Google Scholar] [CrossRef]
- Pan, H.J.; Li, H.B.; Chen, J.Y.; Zhang, Y.; Cai, S.J.; Huang, Y.C.; Zheng, Y.; Zhao, Y.; Deng, J. A unified contact cementation theory for gas hydrate morphology detection and saturation estimation from elastic-wave velocities. Mar. Pet. Geol. 2020, 113, 104146. [Google Scholar] [CrossRef]
- Qu, L.; Zou, C.C.; Lu, Z.Q.; Yu, C.Q.; Li, N.; Zhu, J.C.; Zhang, X.H.; Yue, X.Y.; Gao, M.Z. Elastic-wave velocity characterization of gas hydrate-bearing fractured reservoirs in a permafrost area of the Qilian Mountain, Northwest China. Mar. Pet. Geol. 2017, 88, 1047–1058. [Google Scholar] [CrossRef]
- Shankar, U.; Gupta, D.K.; Bhowmick, D.; Sain, K. Gas hydrate and free gas saturations using rock physics modelling at site NGHP-01-05 and 07 in the Krishna–Godavari Basin, eastern Indian margin. J. Pet. Sci. Eng. 2013, 106, 62–70. [Google Scholar] [CrossRef]
- Xiao, K.; Zou, C.C.; Lu, Z.Q.; Deng, J.Z. Gas hydrate saturations estimated from pore-and fracture-filling gas hydrate reservoirs in the Qilian Mountain permafrost, China. Sci. Rep. 2017, 7, 16258. [Google Scholar] [CrossRef]
- Jin, J.; Hu, J.; Li, L.; Li, J.; Zhu, Z.; Wang, X.; Zhou, J.; Wang, W. Submarine Slides and Their Influence on Gas Hydrate and Shallow Gas in the Pearl River Mouth Basin. J. Mar. Sci. Eng. 2025, 13, 308. [Google Scholar] [CrossRef]
- Wang, X.; Qiu, N.; Zhang, X.; Wang, Z.; Li, Z. Analysis of Hydrocarbon Enrichment in Tight Sandstone Reservoirs in the Eastern Baiyun Depression. Appl. Sci. 2024, 14, 10703. [Google Scholar] [CrossRef]
- Gao, Y.D.; Wang, X.D.; Xu, L.Y.; Zhang, Y.L.; Li, K.S.; Zhang, B.; Chen, C. Natural gas exploration history and main controlling factors for formation of large and medium gas fields in Baiyun Sag. China Offshore Oil Gas 2025, 37, 1–15. [Google Scholar]
- Ping, H.W.; Chen, H.H.; Zhu, J.Z.; George, S.C.; Mi, L.J.; Pang, X.; Zhai, P.Q. Origin, source, mixing, and thermal maturity of natural gases in the Panyu lower uplift and the Baiyun depression, Pearl River Mouth Basin, northern South China Sea. AAPG Bull. 2018, 102, 2171–2200. [Google Scholar] [CrossRef]
- Ping, H.W.; Chen, H.H.; Zhai, P.Q.; Zhu, J.Z.; George, S.C. Petroleum charge history in the Baiyun depression and Panyu lower uplift in the Pearl River Mouth Basin, northern South China Sea: Constraints from integration of organic geochemical and fluid inclusion data. AAPG Bull. 2019, 103, 1401–1442. [Google Scholar] [CrossRef]
- Li, H.; Sun, L.P.; Wang, X.C. Multivariate information fusion modeling method and its application in seismic pre-stack inversion of shallow gas reservoir. Gas Sci. Eng. 2025, 139, 205615. [Google Scholar] [CrossRef]
- Zhan, L.S.; Kang, D.J.; Lu, H.L.; Lu, J.A. Characterization of coexistence of gas hydrate and free gas using sonic logging data in the Shenhu Area, South China Sea. J. Nat. Gas Sci. Eng. 2022, 101, 104540. [Google Scholar] [CrossRef]
- Jiang, W.M.; Li, Y.; Yang, C.; Xiong, Y.Q. Organic geochemistry of source rocks in the Baiyun sag of the Pearl River Mouth Basin, south China sea. Mar. Pet. Geol. 2021, 124, 104836. [Google Scholar] [CrossRef]
- Ping, H.W.; Chen, H.H.; Zhai, P.Q.; Zhu, J.Z.; Xiong, W.L.; Kong, L.T.; Gong, S.; Vergara, T.J.; George, S.C. Evidence for deeply buried, oil-prone source rocks in the Baiyun depression, Pearl River Mouth Basin, northern South China Sea. AAPG Bull. 2021, 105, 749–783. [Google Scholar] [CrossRef]
- Fu, J.; Zhang, Z.T.; Chen, C.; Wang, T.G.; Li, M.J.; Ali, S.; Lu, X.L.; Dai, J.H. Geochemistry and origins of petroleum in the Neogene reservoirs of the Baiyun Sag, Pearl River Mouth Basin. Mar. Pet. Geol. 2019, 107, 127–141. [Google Scholar] [CrossRef]
- Lu, X.L.; Li, M.J.; Li, Y.C.; Yang, Y.C.; Yang, H.Z.; Wang, N.; Ran, Z.C.; Ali, S. Early Oligocene marine transgression and organic matter accumulation recorded in the upper Eocene to lower Oligocene Enping Formation of the Baiyun Sag, Pearl River Mouth Basin, South China Sea. J. Asian Earth Sci. 2024, 259, 105909. [Google Scholar] [CrossRef]
- Sun, R.; Li, Z.; Zhao, Z.G.; Yang, H.Z.; Wang, X.Y.; Zhao, Z. Characteristics and origin of the Lower Oligocene marine source rocks controlled by terrigenous organic matter supply in the Baiyun Sag, northern South China Sea. J. Pet. Sci. Eng. 2020, 187, 106821. [Google Scholar] [CrossRef]
- Sun, Q.L.; Alves, T.M.; Wu, S.G.; Zhao, M.H.; Xie, X.N. Early Miocene magmatism in the Baiyun Sag (South China Sea): A view to the origin of intense post-rift magmatism. Gondwana Res. 2023, 120, 127–144. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Zhu, H.T.; Yang, X.H.; Zeng, H.L.; Xia, C.C.; Chen, Y. Using seismic geomorphology and detrital zircon geochronology to constrain provenance evolution and its response of Paleogene Enping Formation in the Baiyun Sag, Pearl River Mouth Basin, South China sea: Implications for paleo-Pearl River drainage evolution. J. Pet. Sci. Eng. 2019, 177, 663–680. [Google Scholar] [CrossRef]
- Jin, J.P.; Wang, X.J.; Zhang, Z.Y.; He, M.; Magee, C.; Li, J.; Li, Y.P.; Li, S.Z.; Luan, Z.D.; Zhang, G.X. Shallow gas and gas hydrate accumulations influenced by magmatic complexes in the Pearl River Mouth Basin, South China Sea. Mar. Geol. 2022, 453, 106928. [Google Scholar] [CrossRef]
- Gao, J.W.; Peng, X.C.; Wu, S.G.; Lüdmann, T.; McIntosh, K.; Ma, B.J.; Xu, Z.Y. Different expressions of the crustal structure across the Dongsha Rise along the northeastern margin of the South China Sea. J. Asian Earth Sci. 2019, 171, 187–200. [Google Scholar] [CrossRef]
- Jiang, W.M.; Chen, C.; Long, Z.L.; Li, Y.; Yang, C.; Xiong, Y.Q. Geochemical characteristics and possible sources of crude oils in the Baiyun deep-water area of the Pearl River Mouth Basin, South China Sea. Mar. Pet. Geol. 2022, 135, 105410. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Ren, J.Y.; Pang, X.; Yang, L.L.; Zheng, J.Y. Structural style, formation of low angle normal fault and its controls on the evolution of Baiyun Rift, northern margin of the South China Sea. Mar. Pet. Geol. 2018, 89, 687–700. [Google Scholar] [CrossRef]
- Wang, B.; Guo, T.; Wang, H.; Tan, B. Extracting near-borehole P and S reflections from array sonic logging data. J. Geophys. Eng. 2011, 8, 308–315. [Google Scholar] [CrossRef]
- Xiang, M.; Wang, Z.W.; Liu, J.H. Extracting array acoustic logging signal information by combining fractional Fourier transform and Choi–Williams distribution. Appl. Acoust. 2015, 90, 111–115. [Google Scholar] [CrossRef]
- Abe, J.S.; Edigbue, P.I.; Lawrence, S.G. Rock physics analysis and Gassmann’s fluid substitution for reservoir characterization of “G” field, Niger Delta. Arab. J. Geosci. 2018, 11, 656. [Google Scholar] [CrossRef]
- Dvorkin, J.; Prasad, M.; Sakai, A.; Lavoie, D. Elasticity of marine sediments: Rock physics modeling. Geophys. Res. Lett. 1999, 26, 1781–1784. [Google Scholar] [CrossRef]
- Feng, Q.X.; Jiang, L.; Liu, M.Q.; Wan, H.; Chen, L.; Xiao, W. Fluid substitution in carbonate rocks based on the Gassmann equation and Eshelby–Walsh theory. J. Appl. Geophys. 2014, 106, 60–66. [Google Scholar] [CrossRef]
- Yan, F.Y.; Han, D.H. Effect of pore geometry on Gassmann fluid substitution. Geophys. Prospect. 2016, 64, 1575–1587. [Google Scholar] [CrossRef]
- Smith, T.M.; Sondergeld, C.H.; Rai, C.S. Gassmann fluid substitutions: A tutorial. Geophysics 2003, 68, 430–440. [Google Scholar] [CrossRef]
- Dvorkin, J.; Moos, D.; Packwood, J.L.; Nur, A.M. Identifying patchy saturation from well logs. Geophysics 1999, 64, 1756–1759. [Google Scholar] [CrossRef]
- Dvorkin, J.; Nur, A. Acoustic signatures of patchy saturation. Int. J. Solids Struct. 1998, 35, 4803–4810. [Google Scholar] [CrossRef]
- Knight, R.; Dvorkin, J.; Nur, A. Acoustic signatures of partial saturation. Geophysics 1998, 63, 132–138. [Google Scholar] [CrossRef]
- Reuß, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM-J. Appl. Math. Mech. Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Gassmann, F. Elastic waves through a packing of spheres. Geophysics 1951, 16, 673–685. [Google Scholar] [CrossRef]
- Batzle, M.; Wang, Z. Seismic properties of pore fluids. Geophysics 1992, 57, 1396–1408. [Google Scholar] [CrossRef]
- Lee, M.W.; Collett, T.S. Amount of gas hydrate estimated from compressional-and shear-wave velocities at the JAPEX/JNOC/GSC Mallik 2L-38 gas hydrate research well. Bull. Geol. Surv. Can. 1999, 544, 313–322. [Google Scholar]
- Cook, A.E.; Waite, W.F. Archie’s saturation exponent for natural gas hydrate in coarse-grained reservoirs. J. Geophys. Res. Solid Earth 2018, 123, 2069–2089. [Google Scholar] [CrossRef]
- Lee, M.W.; Collett, T.S. Gas hydrate saturations estimated from fractured reservoir at Site NGHP-01-10, Krishna-Godavari Basin, India. J. Geophys. Res. Solid Earth 2009, 114, B07102. [Google Scholar] [CrossRef]
- Chen, J.; Hu, G.W.; Bu, Q.T.; Wu, N.Y.; Liu, C.L.; Chen, Q.; Li, C.F.; Wan, Y.Z.; Wang, Z.H.; Zhao, W.G. Elastic wave velocity of marine sediments with free gas: Insights from CT-acoustic observation and theoretical analysis. Mar. Pet. Geol. 2023, 150, 106169. [Google Scholar] [CrossRef]
- Chen, J.; Hu, G.W.; Bu, Q.T.; Liu, C.L.; Dong, L.; Wan, Y.Z.; Mao, P.X.; Guo, Y.; Wang, Z.H. Elastic wave velocities of hydrate-bearing sands containing methane gas bubbles: Insights from CT-acoustic observation and theoretical analysis. J. Nat. Gas Sci. Eng. 2021, 88, 103844. [Google Scholar] [CrossRef]
- Mavko, G.; Mukerji, T. Bounds on low-frequency seismic velocities in partially saturated rocks. Geophysics 1998, 63, 918–924. [Google Scholar] [CrossRef]
- Brie, A.; Pampuri, F.; Marsala, A.F.; Meazza, O. Shear sonic interpretation in gas-bearing sands. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 22–25 October 1995; SPE: Danbury, CT, USA, 1995; p. SPE-30595-MS. [Google Scholar]
- Pan, H.J.; Li, H.B.; Chen, J.Y.; Zhang, Y.; Liu, X.B.; Cai, S.J.; Cao, C.J. Evaluation of gas hydrate resources using hydrate morphology-dependent rock physics templates. J. Pet. Sci. Eng. 2019, 182, 106268. [Google Scholar] [CrossRef]
- Yu, H.; Ba, J.; Carcione, J.; Li, J.S.; Tang, G.; Zhang, X.Y.; He, X.Z.; Ouyang, H. Rock physics modeling of heterogeneous carbonate reservoirs: Porosity estimation and hydrocarbon detection. Appl. Geophys. 2014, 11, 9–22. [Google Scholar] [CrossRef]
- Yu, H.; Li, J.S.; Yan, X.F.; Xu, G.C.; Jin, X.; Xu, B. Microscopic pore structure characterization of heterogeneous carbonate reservoirs and gas detection: A case study from limestone gas reservoirs on the right bank block of Amu Darya River. Geophys. Prospect. Pet. 2017, 56, 472–482. [Google Scholar] [CrossRef]
- Ghosh, R.; Ojha, M.; Kumar, P. Review of rock physics theories for quantifying gas hydrate and associated uncertainties. J. Asian Earth Sci. 2023, 256, 105828. [Google Scholar] [CrossRef]
- Voigt, W. Ueber die Beziehung zwischen den beiden Elasticitätsconstanten isotroper Körper. Ann. Phys. 1889, 274, 573–587. [Google Scholar] [CrossRef]
- Hill, R. On discontinuous plastic states, with special reference to localized necking in thin sheets. J. Mech. Phys. Solids 1952, 1, 19–30. [Google Scholar] [CrossRef]
- Dvorkin, J.; Nur, A. Elasticity of high-porosity sandstones: Theory for two North Sea data sets. Geophysics 1996, 61, 1363–1370. [Google Scholar] [CrossRef]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 16, 259–268. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Nur, A.; Mavko, G.; Dvorkin, J.; Galmudi, D. Critical porosity: A key to relating physical properties to porosity in rocks. Lead. Edge 1998, 17, 357–362. [Google Scholar] [CrossRef]
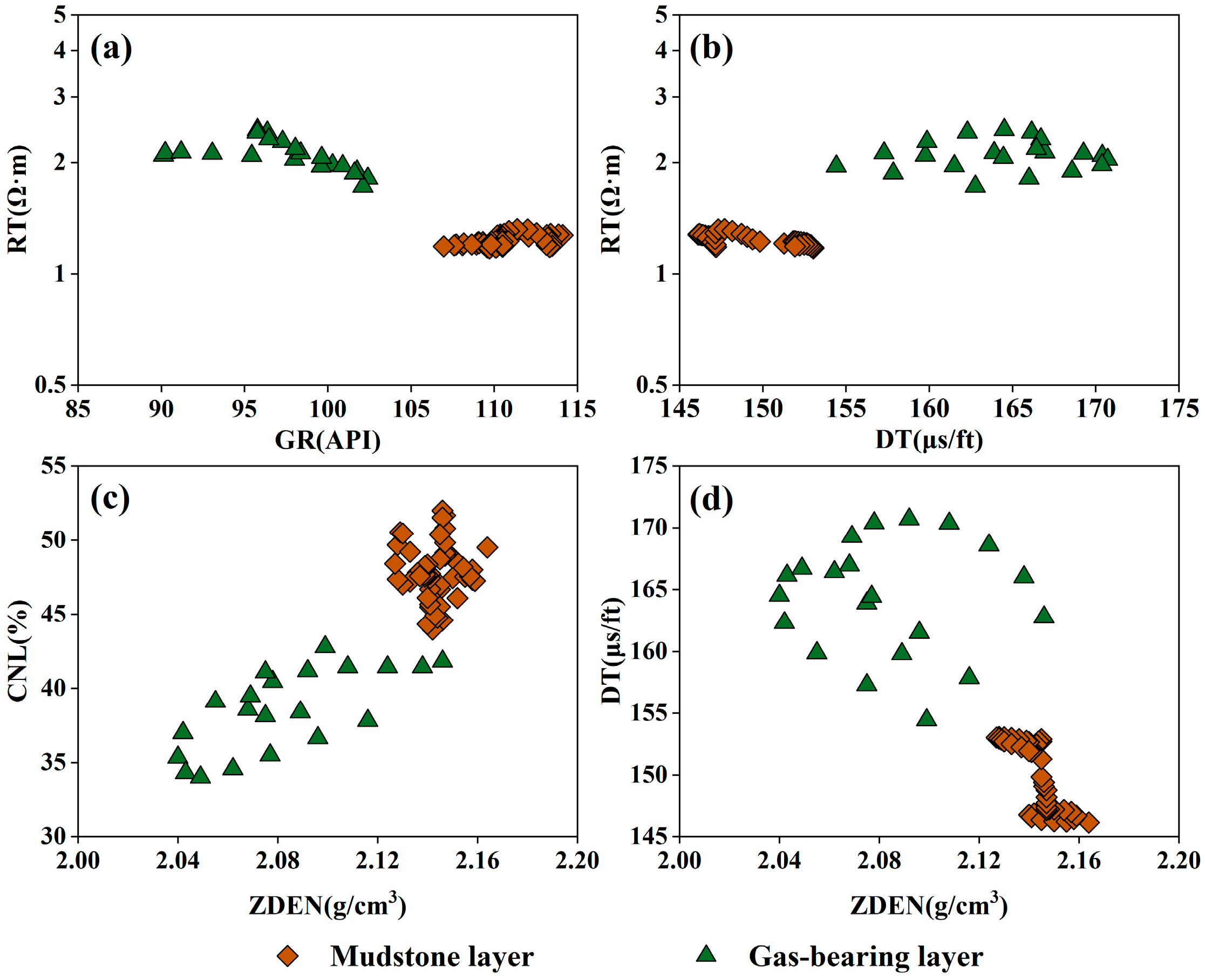
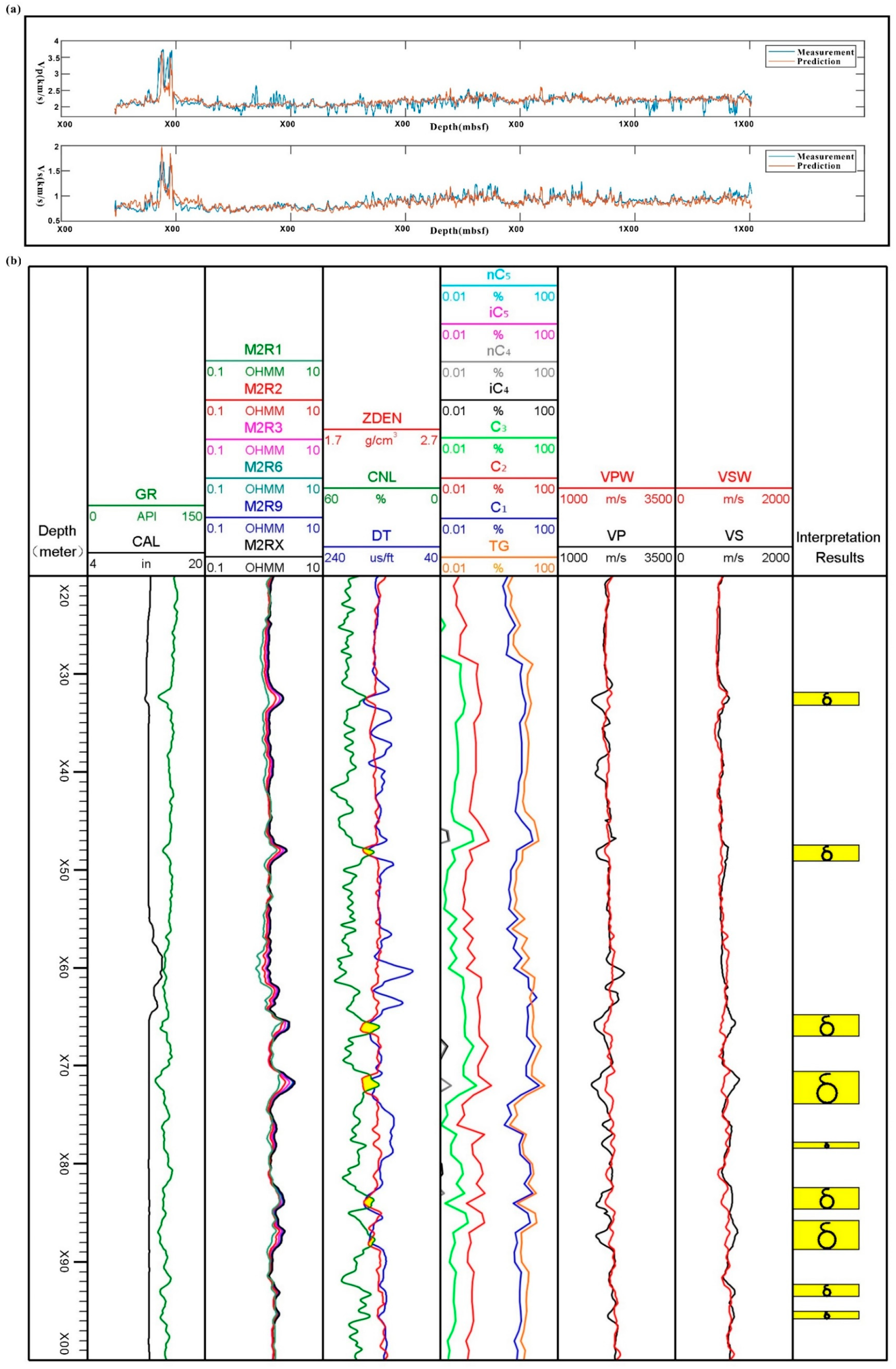
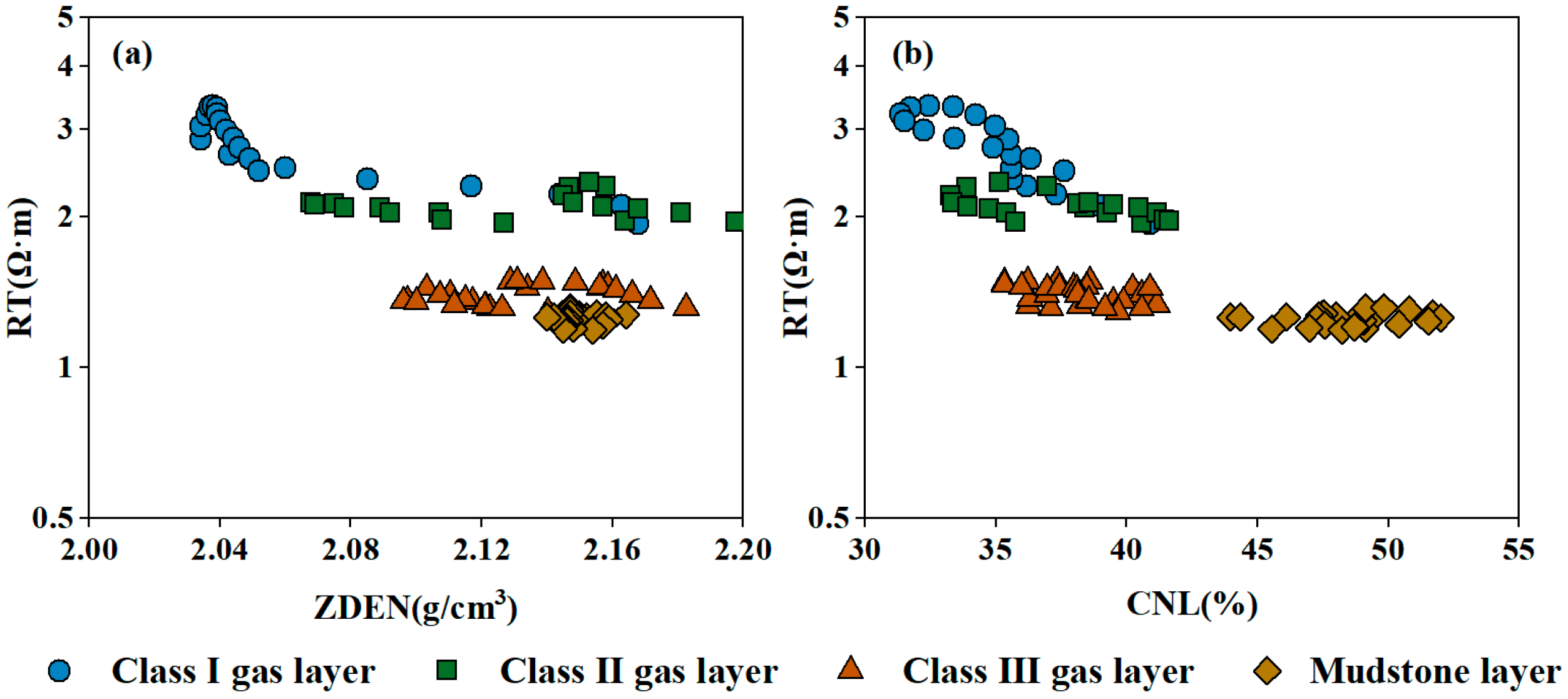


| Code | Name of Well Log | Unit |
|---|---|---|
| GR | Natural gamma ray | API |
| CAL | Caliper | inch |
| M2R1~M2RX | Array induction resistivity | Ohm·m |
| P16H~P40H | Phase-shift resistivity | Ohm·m |
| ZDEN | Density | g/cm3 |
| CNL | Compensated neutron | porosity unity |
| DT | Acoustic interval transit time | μs/ft |
| C1, C2, …TG | Mud logging | % |
| DST | Drill stem test | - |
| VP, VS | Array acoustic logging | m/s |
| Constituent | Bulk Modulus (GPa) | Shear Modulus (GPa) | Density (g/cm3) |
|---|---|---|---|
| Quartz | 36 | 45 | 2.65 |
| Clay | 20.9 | 6.85 | 2.58 |
| Water | 2.5 | 0 | 1.032 |
| Methane gas | 0.1 | 0 | 0.23 |
| Parameters | Types/Values |
|---|---|
| Matrix composition | Quartz and clay |
| Critical porosity | 40% |
| Coordination number | 8.5 |
| Convergence tolerance | 0.1% |
| Type | Resistivity (Ω·m) | Crossover of Neutron–Density Logging |
|---|---|---|
| Class I | >2 | Clear crossover (marked by the yellow filling in the figure) |
| Class II | >2 | Weak crossover (with no filling in the figure) |
| Class III | 1.2–2 | Weak crossover (with no filling in the figure) |
| Well Name | Layer Number | Gas Saturation (%) | Absolute Error | Mean | |
|---|---|---|---|---|---|
| Modified Method | Waxman–Smits | Absolute Error | |||
| A-1 | 1 | 39.12% | 34.41% | 4.71% | 4.55% |
| 2 | 42.44% | 44.67% | 2.23% | ||
| 3 | 47.20% | 41.84% | 5.36% | ||
| 4 | 36.60% | 39.04% | 2.44% | ||
| 5 | 44.26% | 41.03% | 3.23% | ||
| 6 | 44.07% | 35.61% | 8.46% | ||
| 7 | 33.92% | 39.36% | 5.44% | ||
| A-2 | 8 | 39.72% | 42.06% | 2.34% | 6.11% |
| 9 | 41.04% | 49.12% | 8.08% | ||
| 10 | 31.2% | 28.19% | 3.01% | ||
| 11 | 33.92% | 47.06% | 13.14% | ||
| 12 | 40.88% | 38.16% | 2.72% | ||
| 13 | 41.26% | 36.19% | 5.07% | ||
| 14 | 30.41% | 32.77% | 2.36% | ||
| 15 | 42.27% | 30.11% | 12.16% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, J.; Zou, C.; Peng, C.; Xiao, L.; Qiao, K.; Lan, X.; Shen, W.; Zhang, Y.; Zhang, H. Evaluating Gas Saturation in Unconventional Gas Reservoirs Using Acoustic Logs: A Case Study of the Baiyun Depression in the Northern South China Sea. J. Mar. Sci. Eng. 2025, 13, 2078. https://doi.org/10.3390/jmse13112078
Shu J, Zou C, Peng C, Xiao L, Qiao K, Lan X, Shen W, Zhang Y, Zhang H. Evaluating Gas Saturation in Unconventional Gas Reservoirs Using Acoustic Logs: A Case Study of the Baiyun Depression in the Northern South China Sea. Journal of Marine Science and Engineering. 2025; 13(11):2078. https://doi.org/10.3390/jmse13112078
Chicago/Turabian StyleShu, Jiangbo, Changchun Zou, Cheng Peng, Liang Xiao, Keyu Qiao, Xixi Lan, Wei Shen, Yuanyuan Zhang, and Hongjie Zhang. 2025. "Evaluating Gas Saturation in Unconventional Gas Reservoirs Using Acoustic Logs: A Case Study of the Baiyun Depression in the Northern South China Sea" Journal of Marine Science and Engineering 13, no. 11: 2078. https://doi.org/10.3390/jmse13112078
APA StyleShu, J., Zou, C., Peng, C., Xiao, L., Qiao, K., Lan, X., Shen, W., Zhang, Y., & Zhang, H. (2025). Evaluating Gas Saturation in Unconventional Gas Reservoirs Using Acoustic Logs: A Case Study of the Baiyun Depression in the Northern South China Sea. Journal of Marine Science and Engineering, 13(11), 2078. https://doi.org/10.3390/jmse13112078







