Heterogeneous Coupled Control of Ventilated Supercavitating Vehicles

Abstract

This study addresses the control challenge of ventilated supercavitating vehicles during depth-change maneuvers, where variations in speed and depth induce unsteady cavity evolution and nonlinear planing forces. An unsteady cavity evolution model based on the independent cross-sectional expansion principle was developed and integrated with vehicle dynamics to form a heterogeneous coupled motion framework. A DQN-based controller was designed to maintain cavity length under unsteady conditions, while an ADRC-based pitch controller achieved decoupled attitude control, with depth tracking realized through cascaded outer-loop feedback. Numerical simulations were performed on the established heterogeneous coupled motion model under depth-change maneuvers. The results show that the proposed approach maintains the cavity length within ±10% of the commanded value and achieves rapid and stable depth tracking. The proposed modeling and control framework offers an effective approach to enhance the maneuverability and robustness of ventilated supercavitating vehicles in complex hydrodynamic environments.

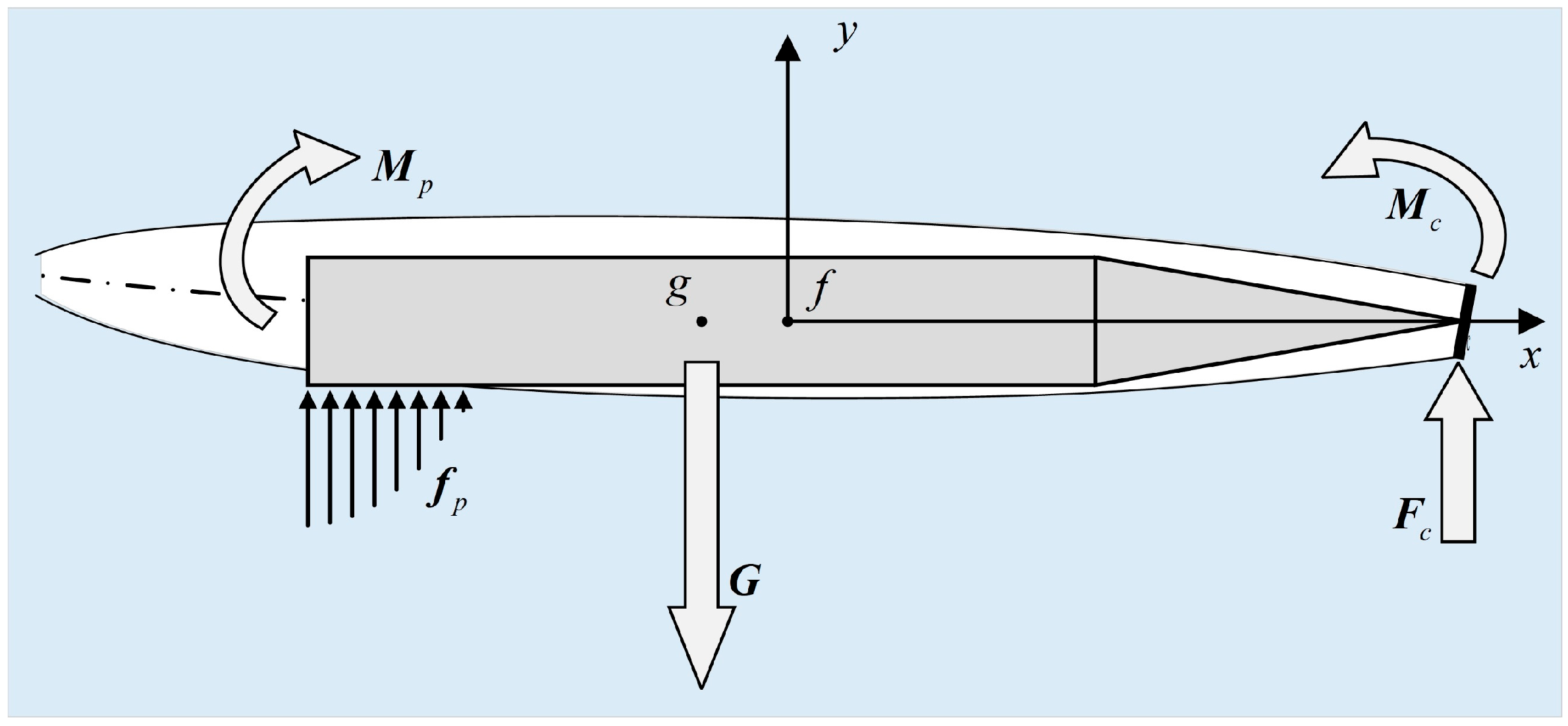
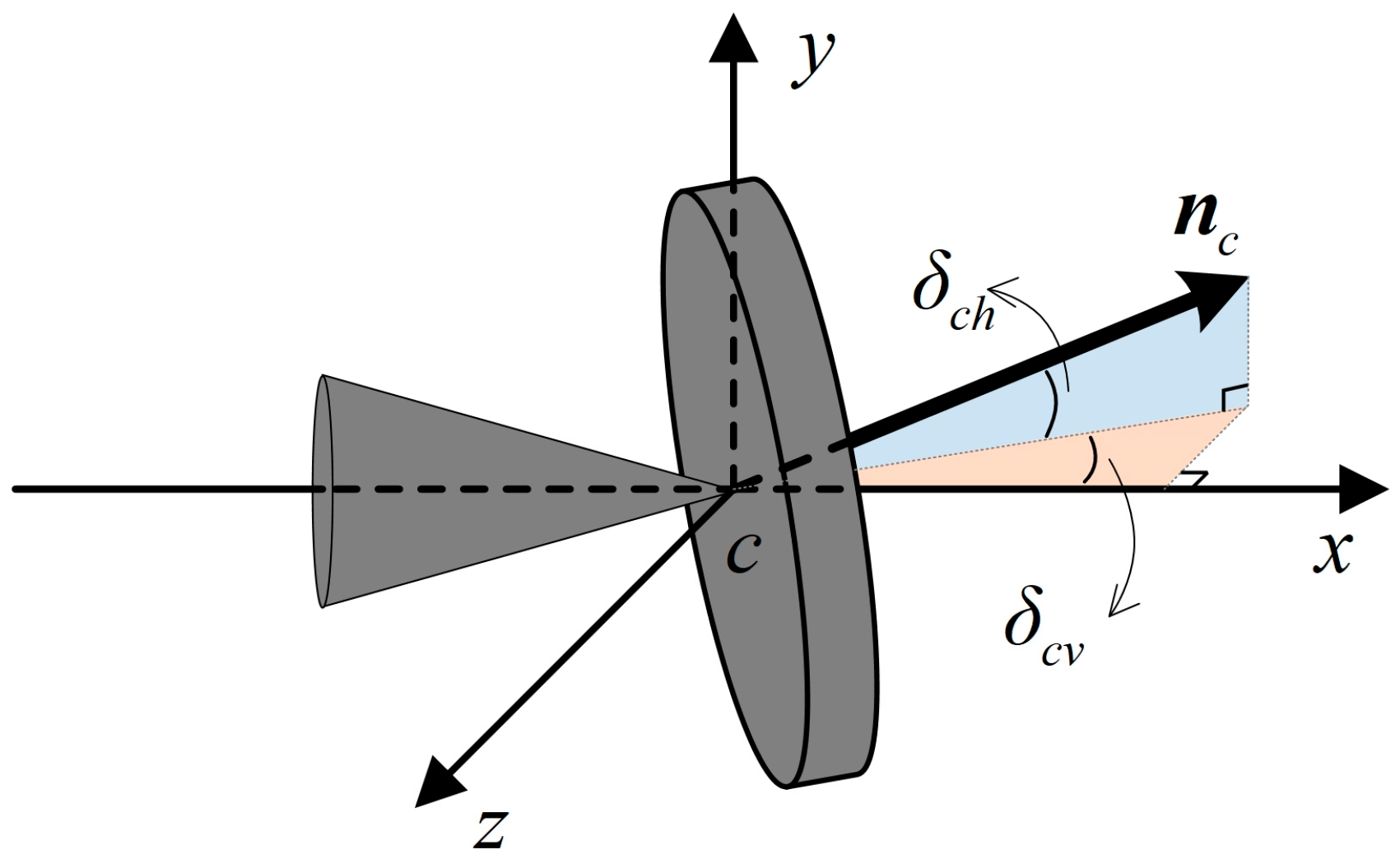
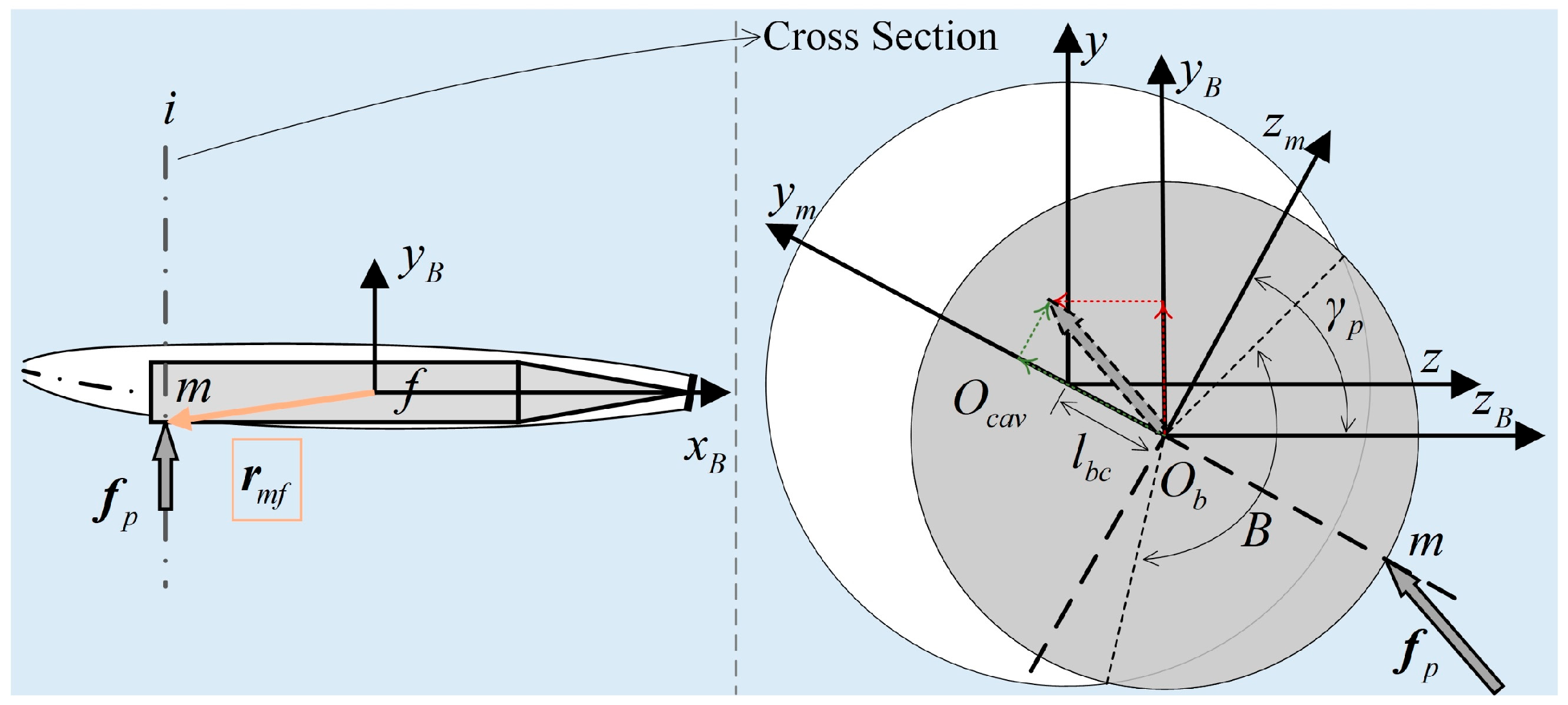
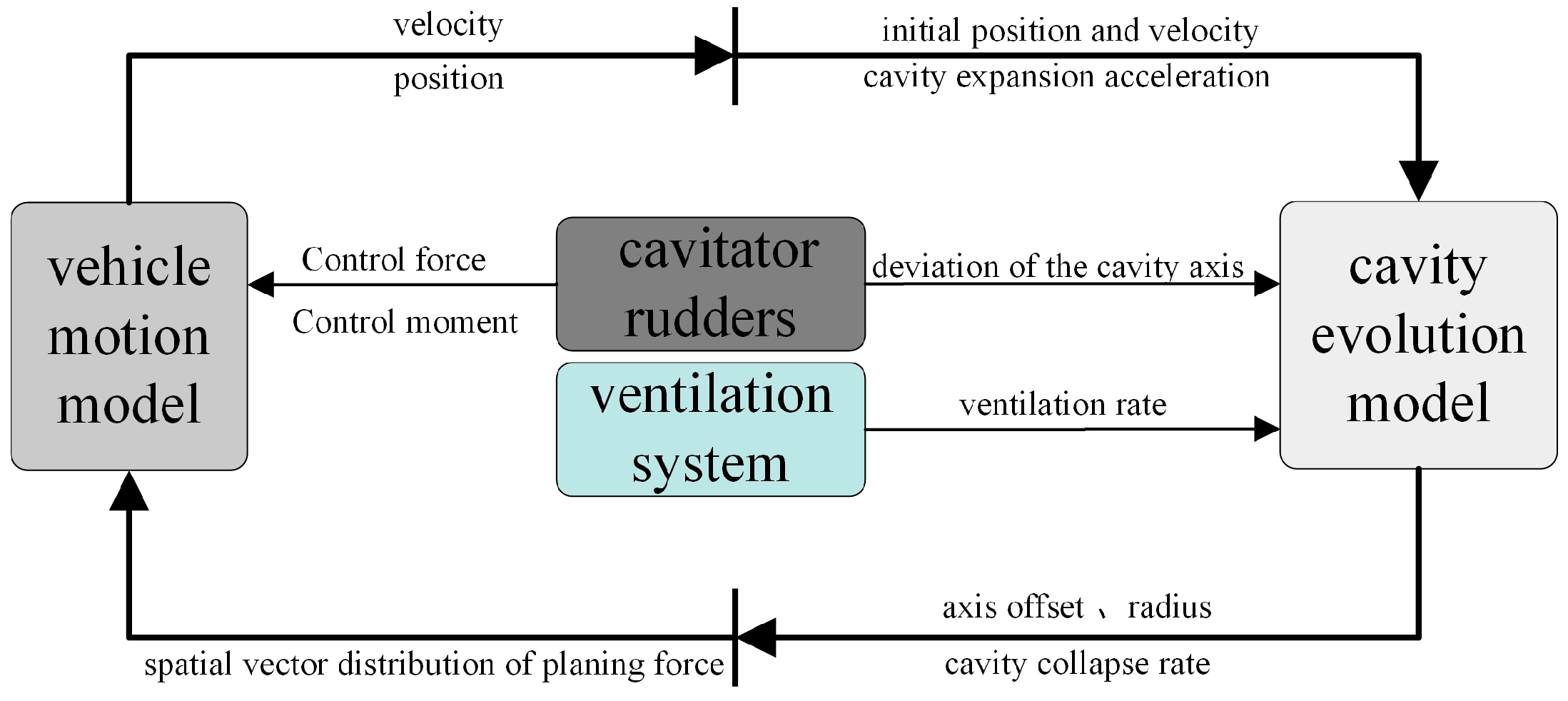
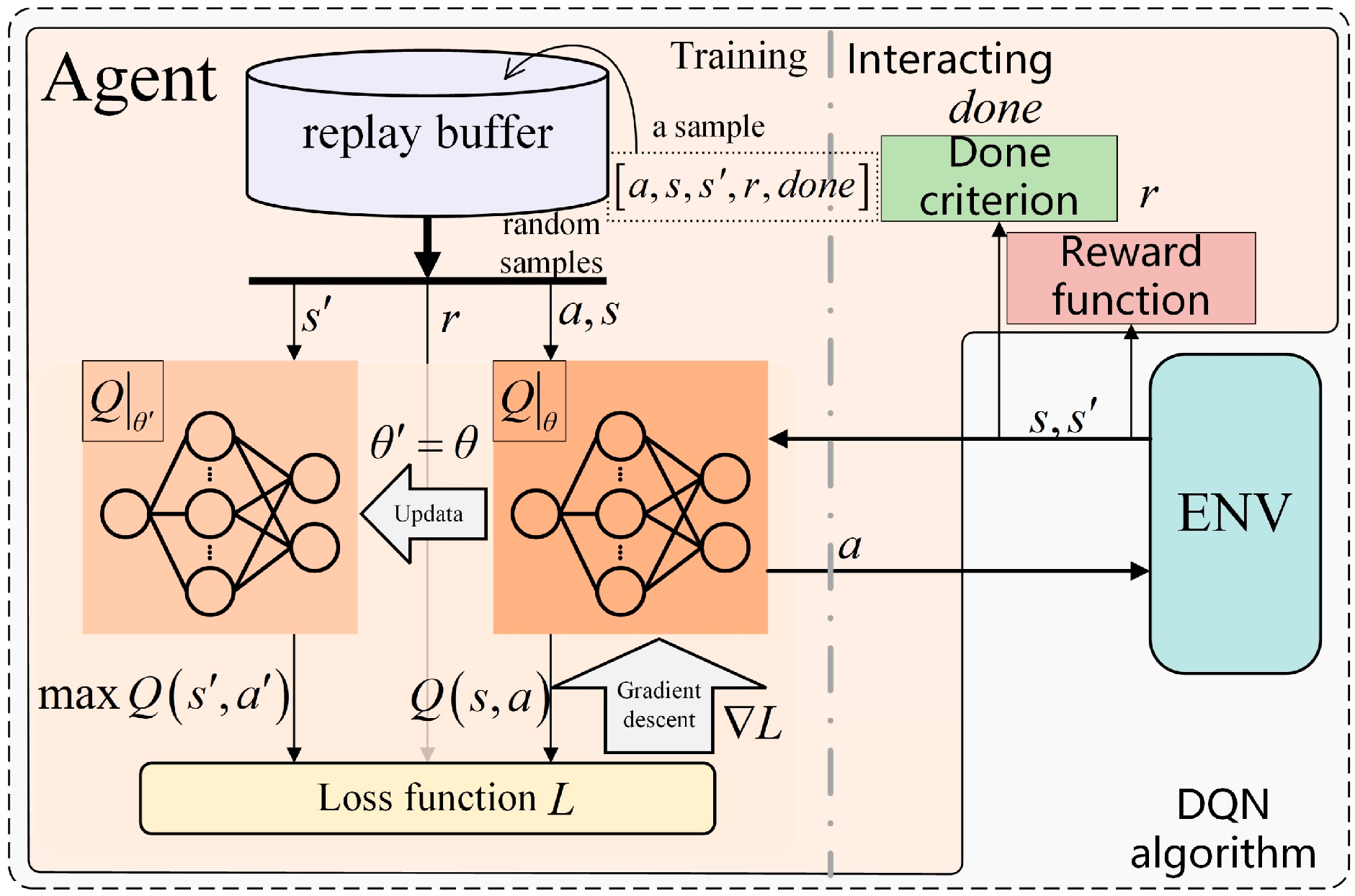
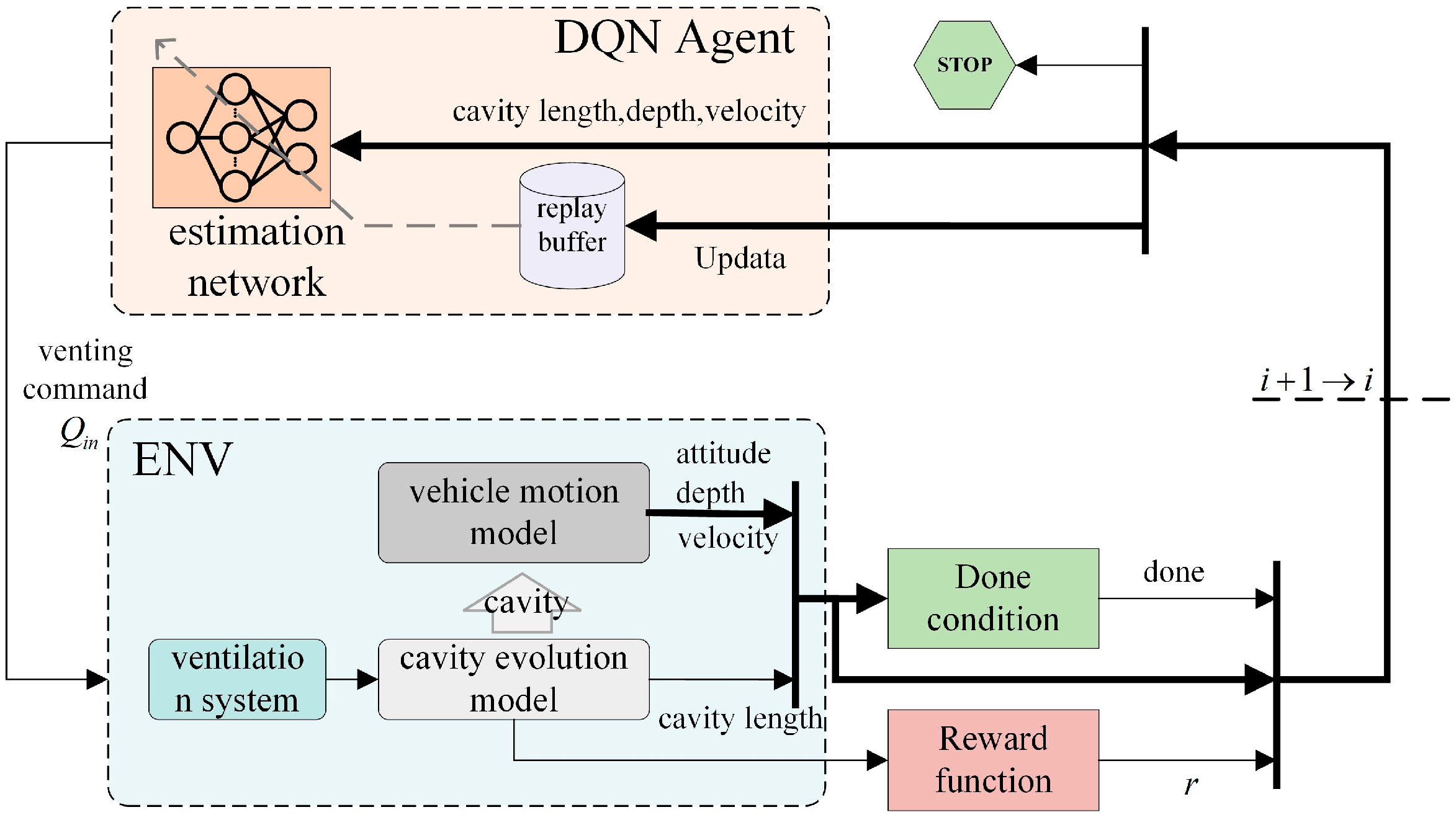
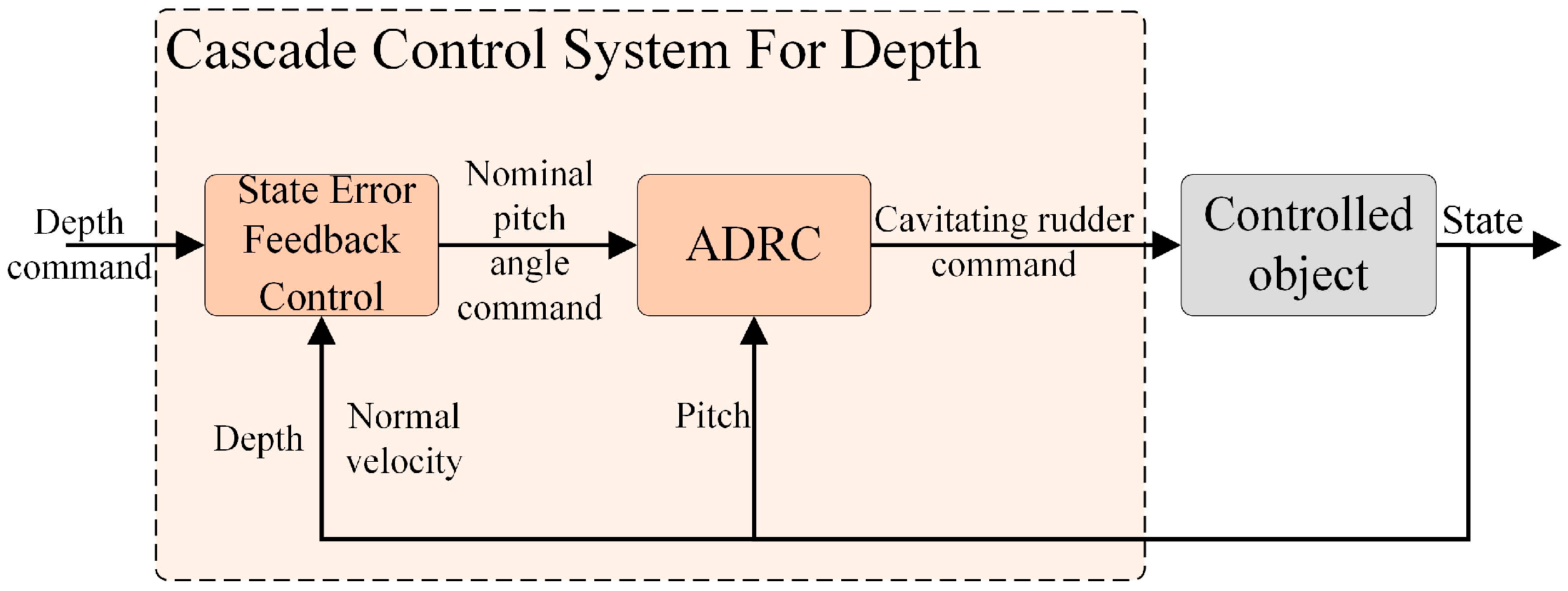
1. Introduction

Ventilated supercavitating vehicles have attracted significant attention from researchers worldwide because of their ability to achieve extremely high underwater speeds. Extensive research has been conducted on model development and control design for these vehicles. However, the mechanical coupling effects among gas-solid-liquid multiphase flows are highly complex, and the underlying mechanisms remain unclear. High-fidelity modeling and robust stabilization control design continue to be core challenges in this field. To date, much work has focused on establishing accurate dynamic models and designing controllers with strong robustness for supercavitating underwater vehicles.

With respect to cavity evolution models, Logvinovich [1] proposed the cross-sectional independent expansion principle, which provides a theoretical framework for analyzing the effects of the vehicle angle of attack and gravity on the cavity shape. This principle has been extensively validated through experiments and remains the fundamental theoretical basis for accurate cavity prediction to date. Furthermore, Yu. N. Savchenko [2] experimentally confirmed the validity of the cross-sectional independent expansion principle. Many researchers have subsequently conducted studies on cavity flow patterns and the coupled forces between the cavity and the vehicle on the basis of this principle. In terms of cavity flow pattern prediction, Serebryakov [3] derived differential equations and boundary conditions for steady and unsteady cavity flows by employing slender body theory and integral conservation laws. Building upon the cross-sectional independent expansion principle and differential equations for steady cavity flows, Y. N. Savchenko [4] investigated cavity shape by simplifying the steady cavity flow differential equations into algebraic equations. They derived an approximate formula for the drag coefficient of disk cavitators and developed predictive formulas for the length and diameter of axisymmetric cavities at low cavitation numbers. On the other hand, Paryshev [5] extended the unsteady cavity flow differential equations by incorporating pressure variations and dynamic characteristics within the cavity, employing integral transformations to obtain a sixth-order nonlinear differential equation system describing cavity dynamics.

With respect to the coupled forces between a cavity and vehicle, Paryshev [5] addressed the interaction by modeling any vehicle cross-section in contact with the cavity as equivalent to a cylinder submerged in a cylindrical water surface. Vasin and Paryshev [6] on the basis of potential flow theory, incorporated fluid viscosity and surface friction resistance and presented a formula for calculating the steady-state glide force of forward-moving vehicles under conditions of a low wetting ratio and high Froude number. In terms of supercavitating vehicle modeling, [7] Kirschner et al. [8] developed a six-degree-of-freedom (6-DOF) model of a supercavitating vehicle and subsequently simplified it. Dzielski and Kurdila [9] established a two-degree-of-freedom (2-DOF) longitudinal plane model, which, while simplified, retains most typical characteristics of supercavitating vehicles and has become a benchmark model that is widely cited in the literature. Vanek et al. [10] considered the hysteresis effect between cavity flow patterns and vehicle states, also known as the cavity memory effect, improved the glide force calculation, and developed a time-delay model for supercavitating vehicles.

In recent years, significant efforts have been devoted to improving the modeling of supercavitating vehicles, with numerous numerical and experimental studies addressing various aspects of their hydrodynamics and control. Jiang [11] experimentally investigated the drag characteristics and flow physics of ventilated supercavitating bodies with different geometries, systematically examining the influence of ventilation rates on drag behavior and analyzing the formation mechanisms and hydrodynamic characteristics of both bubbly and clear supercavities under different Froude numbers. Pham and Ahn et al. [12,13,14] carried out numerical simulations to assess the effects of forebody length, cavitator angle, and control fin sweep angle on supercavity dynamics, providing both qualitative and quantitative insights into cavity shape evolution, hydrodynamic performance, gas leakage mechanisms, and internal pressure distribution under varying vehicle and control surface configurations. Shao [15] employed high-speed digital inline holography (DIH) to investigate how gas leakage under different cavity closure modes affects the stability of ventilated supercavities, and proposed ventilation control strategies that enhance cavity stability.Despite these advances, early studies on the dynamics and control of supercavitating vehicles were often constrained by computational limitations. As a result, they typically assumed steady vehicle motion and employed simplified cavity evolution models and glide force calculations, which reduced model accuracy and neglected important nonlinear coupling effects. Such simplifications limit the ability to predict vehicle performance under complex maneuvering conditions, highlighting the need for more comprehensive modeling approaches.

In terms of supercavitating vehicle control, Y. Savchenko [2] analyzed the stability characteristics of vehicles enveloped by cavities and proposed four stable operating modes, laying the groundwork for subsequent control research on supercavitating vehicles. Dzielski and Kurdila [9] introduced their benchmark model and presented a state feedback control law using only the cavitator rudder angle as the control input, although without extensive explanation. They also suggested controlling the vehicle by simultaneously using both the vehicle’s stern rudder and the cavitator rudder angles as control inputs. Shao et al. [16], on the basis of a 6-DOF model, categorized the supercavitating vehicle’s dynamics into two states: with and without glide force. Controllers were designed for each state using linear quadratic regulator (LQR) theory, and the switching between control laws was achieved by monitoring the glide depth at the vehicle’s tail. Balas et al. [17] conducted studies on the benchmark model by transforming it into a bimodal system to confirm controllability. They implemented a twoloop control architecture, where the inner loop employed feedback linearization and the outer loop used dynamic inversion. Although this approach demonstrated satisfactory tracking performance, it imposed impractical demands on the rudder’s capabilities. Building upon Balas’s work, Vanek et al. [18] introduced a control strategy that combines inner-loop feedback linearization with outer-loop receding horizon control (RHC) for the benchmark model. While this method sacrifices some tracking accuracy, it significantly reduces the rudder performance requirements. Subsequently, Vanek transformed the benchmark model into a linear parameter-varying (LPV) framework and designed controllers accordingly. Lin et al. [19,20], on the basis of the benchmark model, designed controllers using robust pole placement methods and applied the circle criterion theorem for nonlinear system analysis. They demonstrated that robust pole placement effectively expands the domain of attraction of the supercavitating vehicle states, thus ensuring system stability; however, actuator saturation occurs as the domain of attraction expands. Sanabria et al. [21,22] developed a supercavitating vehicle dynamic model on the basis of experimental data and designed controllers using a mixed sensitivity approach, incorporating control strategies to avoid the generation of glide forces. Zou Wang and colleagues Zou et al. [23,24,25,26], on the basis of Logvinovich’s cavity cross-sectional independent expansion principle, studied cavity dynamics and established an unsteady ventilated supercavity model. They also investigated the ballistics, guidance, and control of supercavitating vehicles on the basis of the coupled model of unsteady ventilated supercavities and the vehicle. Sun Mingwei et al. Sun et al. [27] divided the benchmark model into inner and outer loops according to variable rates of change and used the circle criterion theorem to guarantee the absolute stability of the inner loop.

In summary, most control-oriented ventilated supercavity motion models focus on 2-DOF systems, assume steady cavity evolution, overlooks the influence of variations in vehicle motion, and thus weaken the coupling between heterogeneous control channels.

On the basis of the principle of cross-sectional independent cavity expansion, this study introduces an unsteady evolution model for ventilated cavities by spatially discretizing the cavity into multiple slices. The cavity evolution at each slice is computed according to local environmental and motion parameters, thereby completing the coupling relationships among heterogeneous channels. For each slice, the immersion relationship between the vehicle and the cavity cross-section is analyzed. Using the spatial distribution of glide forces derived from [5], the total glide force and moment are obtained through integration. Combined with the vehicle’s dynamics, a 6-DOF heterogeneous coupled motion model of the ventilated supercavitating vehicle is developed.

Building upon this model and addressing the coupling effects of heterogeneous channels, a control framework integrating ventilated cavity loop reinforcement learning and cavitator rudder-motion loop active disturbance rejection control (ADRC) is proposed. A deep Q-network (DQN) algorithm is employed to train an intelligent cavity length controller under staged ventilation conditions, effectively maintaining the cavity length during depth variation maneuvers. Moreover, ADRC is used to achieve effective observation and dynamic compensation of the overall disturbance, including glide forces, realizing decoupled control of the pitch channel. This approach is supported by outer-loop error feedback control to achieve accurate depth tracking.

2. Model Development

2.1. Cavity Evolution Model

The cavity evolution model consists of two components: the cavity cross-sectional expansion model and the cavity axis deviation model. The former characterizes the variation in the cavity’s cross-sectional area under the influence of the pressure differential between the cavity interior and the surrounding fluid. The latter describes the deviation of the cavity axis induced by gravity and the angle of attack of the cavitator.

G. V. Logvinovich [1] proposed the principle of Independent Cross-Section Expansion (ICSEP), which is illustrated in Figure 1. Its essence is that, for a supercavity generated by a high-speed body, each fixed cross-section of the cavity expands according to the same law relative to the trajectory of the cavitator’s center. The expansion law depends on the local flow conditions at the instant when the cavitator passes through the plane of the given cross-section, and is almost independent of the body’s motion before or after that moment.The mathematical formulation of this cross-sectional evolution constitutes the cavity evolution model, which consists of two components: the cavity cross-sectional expansion model and the cavity axis deviation model. The former characterizes the variation in the cavity cross-sectional area caused by the pressure difference between the cavity interior and the surrounding fluid, as expressed in Equation (1) the latter describes the deviation of the cavity axis induced by gravity and the cavitator’s angle of attack, as expressed in Equation (2).

The present ICSEP-based model is derived under the following main assumptions:

• The flow is incompressible and irrotational, and viscous effects are negligible.
• The cavity is steady and axisymmetric, corresponding to a fully developed supercavity.
• The internal cavity pressure is spatially uniform.

Although viscous, compressible, and transient effects are not explicitly modeled, it is recognized that these factors may exert noticeable influence only when the cavity is not fully developed or when the cavitator operates at a large angle of attack.

The cavity cross-sectional expansion model is given by:

$$\left\{\begin{array}{c}\ddot{S}=-k\Delta p/\rho \\ {\dot{S}}_0=2\pi C_x{R}_n{v}_{\infty }/a\end{array}\right.$$

(1)

where $k=4\pi C_x/a^2$, $\Delta p$ is the pressure difference between the inside and outside the cavity, $C_x$ is the drag coefficient of the cavitator, $a$ is an empirical constant (typically between $0.01~0.02$), $R_n$ is the radius of the cavitator, $v_{\infty }$ is the freestream velocity, and $S$ is the cross-sectional area of the cavity.

The cavity axis deviation model is given by:

$$\left\{\begin{array}{c}{\dot{h}}_y\left(x\right)={\dot{h}}_g\left(x\right)+{\dot{h}}_{\alpha }\left(x\right)\\ {\dot{h}}_z\left(x\right)={\dot{h}}_{\beta }\left(x\right)\hfill \end{array}\right.$$

(2)

where

$$\left\{\begin{array}{c}{\dot{h}}_g\left(x\right)=gV\left(x\right)/\pi v_{\infty }{r}_x^2\left(x\right)\\ {\dot{h}}_{\alpha }\left(x\right)=-F_y/{\rho }_{in}\pi v_{\infty }^2{r}_x^2\left(x\right)\\ {\dot{h}}_{\beta }\left(x\right)=-F_z/{\rho }_{in}\pi v_{\infty }^2{r}_x^2\left(x\right)\end{array}\right.$$

(3)

where ${\dot{h}}_g\left(x\right)$ is the deviation velocity induced by gravitational effects, ${\dot{h}}_{\alpha }\left(x\right)$ is the deviation velocity caused by the cavitator angle of attack, ${\dot{h}}_{\beta }\left(x\right)$ is the deviation velocity due to the sideslip angle, $g$ is the gravitational acceleration, $V\left(x\right)$ is the cumulative volume of the first n cavity cross-sections, $r_x^2$ is the cavity radius, ${\rho }_{in}$ is the gas density inside the cavity, $F_y$ is the component of the cavitator force along the body-fixed $y$-axis, and $F_z$ is the component of the cavitator force along the $z$-axis.

On the basis of the cavity shape obtained from the previous evolution step, it is necessary to compute the internal pressure of the cavity $p_c$ at the current time step to proceed with the next stage of cavity expansion. Thus, a governing equation is introduced to relate the internal cavity pressure $p_{\infty }$ to the ventilation rate ${\dot{Q}}_{in}$ and the gas leakage rate ${\dot{Q}}_{out}$.

Assuming a uniform pressure distribution inside the cavity, the internal pressure is calculated using the following equation:

$${\displaystyle \frac{d\left[p_c\left(t\right)V\left(t\right)\right]}{dt}}=p_{\infty }\left[{\dot{Q}}_{in}-{\dot{Q}}_{out}\left(t\right)\right]$$

(4)

where $p_c$ is the internal pressure of the cavity, $V$ is the cavity volume, $p_{\infty }$ is the freestream pressure, ${\dot{Q}}_{in}$ is the ventilation mass flow rate, and ${\dot{Q}}_{out}$ is the gas leakage mass flow rate, which is computed as:

$${\dot{Q}}_{out}=\left\{\begin{array}{c}0.015\pi v_{\infty }{R}_n^2\left({\displaystyle \frac{{\sigma }_v}{{\sigma }_c}}-1\right),F\ge 1.5\\ {\displaystyle \frac{0.27v_{\infty }{D}_n^2}{{\sigma }_c\left({\sigma }_c^{3}F{r}_n^4-2\right)}},F<1.5\end{array}\right.$$

(5)

where $F={\sigma }_c\sqrt{{\sigma }_c}F{r}_n^2$ is the criterion for the reentrant jet condition, $D_n$ is the cavitator diameter, $F{r}_n=v_{\infty }/\sqrt{g{D}_n}$ is the Froude number, ${\sigma }_c$ is the cavitation number, and ${\sigma }_v$ is the vapor cavitation number.

The unsteady evolution process of the supercavity is shown in Figure 1, and the corresponding computational procedure can be summarized as follows:

• Step 1: Set the simulation time step $\mathrm{d}t$, total simulation duration $T$, and time interval for adding new spatial slices $n\mathrm{d}t$. Let the slice counter be $i$ and the number of simulation step be $j$. Initialize the cavity volume $vo{l}_0=0$, slice index $i=0$ and time step counter $j=0$.
• Step 2: If $n$ is divisible by $j$, increment the slice counter $i++$. Add a new spatial slice $i$, and initialize its local cavity cross-sectional properties $I_j^i$ on the basis f the current cavitator position ${\mathit{Pos}}_j$, velocity ${\mathit{V}}_j$, and freestream pressure $p_{\infty j}$.
• Step 3: Using the current cavity volume $Vo{l}_j$, ventilation rate ${\left.{\dot{Q}}_{in}\right|}_j$, and gas leakage rate ${\left.{\dot{Q}}_{out}\right|}_j$, iteratively solve for the internal cavity pressure ${\left.p_c\right|}_{j+1}$, according to Equation (4).
• Step 4: Advance the simulation time step $j++$. On the basis of the pressure difference across each cavity cross-section $\Delta p_j^k$, update the cross-sectional area $S_j^k$ using Equation (1), where $k=1,\dots i$.
• Step 5: Calculate the cavity volume $Vo{l}_j$ by integrating the cross-sectional areas $S_j^k$ of all slices. Then, on the basis of the cavitator angle of attack ${\left.{\alpha }_n\right|}_j$, update the cavity axis offset $h_j^k$ using Equation (2), where $k=1,\dots i$.
• Step 6: Check whether the current simulation time $j\mathrm{d}t$ exceeds the total simulation duration $T$. If yes, terminate the simulation; otherwise, return to Step 2.

2.2. Dynamic Model of the Vehicle

This section presents an analysis of the primary external forces acting on the vehicle, as illustrated in Figure 2. These forces include the vehicle’s weight, the control force generated by the fore cavitator, and the hydrodynamic drag from the wetted aft region. On the basis of the principles of linear and angular momentum, a motion model of a supercavitating underwater vehicle is established.

2.2.1. Gravity

The representation of gravity in the vehicle body-fixed coordinate system is given by:

$${\left[\begin{array}{l}{X}_G\\ Y_G\\ Z_G\end{array}\right]}_B={\mathit{T}}_L^B{\left[\begin{array}{c}0\\ -G\\ 0\end{array}\right]}_L=G\left[\begin{array}{c}-\sin \theta \\ -\cos \theta \cos \phi \\ \cos \theta \sin \phi \end{array}\right]$$

(6)

where ${\mathit{T}}_L^B$ denotes the transformation matrix from the launch coordinate system to the body-fixed coordinate system, $\theta$ is the pitch angle and $\phi$ is the roll angle.

$${\left[\begin{array}{c}{M}_{Gx}\\ M_{Gy}\\ M_{Gz}\end{array}\right]}_B={\mathit{r}}_{gf}^B\times {\left[\begin{array}{l}{X}_G\\ Y_G\\ Z_G\end{array}\right]}_B=\left[\begin{array}{c}-z_g{Y}_G+y_g{Z}_G\\ z_g{X}_G-x_g{Z}_G\\ -y_g{X}_G+x_g{Y}_G\end{array}\right]$$

(7)

In the equation, ${\mathit{r}}_{gf}^B=[x_g,y_g,z_g]$ represents the vector from the vehicle’s geometric center $f$ to its center of mass $g$, as expressed in the body-fixed coordinate system.

2.2.2. Forces on the Cavitator

The velocity of the cavitator center point expressed in the body-fixed coordinate system is given by:

$${\mathit{v}}_c^B={\mathit{v}}_f^B+\mathsf{\omega }\times {\mathit{r}}_{cf}^B=\left[\begin{array}{c}\cos \alpha \cos \beta V-{\omega }_z{y}_c+{\omega }_y{z}_c\\ -\sin \alpha \cos \beta V+{\omega }_z{x}_c-{\omega }_x{z}_c\\ \sin \beta V-{\omega }_y{x}_c+{\omega }_x{z}_c\end{array}\right]$$

(8)

where ${\mathit{v}}_f^B$ denotes the vehicle velocity expressed in the body-fixed coordinate system, $\mathsf{\omega }=\left[{\omega }_x,{\omega }_y,{\omega }_z\right]$ is the vehicle angular velocity in the body-fixed coordinate system, and ${\mathit{r}}_{cf}^B=\left[x_c,y_c,z_c\right]$ is the vector from the vehicle’s geometric center $f$ to the cavitator center point $c$, as expressed in the body-fixed coordinate system.

As shown in Figure 3, the normal direction of the cavitator expressed in the body-fixed coordinate system is given by:

$${\mathit{n}}_c^B={[\cos {\delta }_{ch}\cos {\delta }_{cv},\sin {\delta }_{ch},-\cos {\delta }_{ch}\sin {\delta }_{cv}]}^T$$

(9)

where ${\delta }_{ch}$ represents the cavitator horizontal rudder angle and ${\delta }_{cv}$ represents the cavitator vertical rudder angle.

The normal hydrodynamic force acting on the cavitator can be expressed as:

$$F_{xn}=C_{xn}{\displaystyle \frac{1}{2}}\rho v_{n}V{S}_c$$

(10)

where $C_{xn}$ is the cavitator frontal drag coefficient, $v_n$ is the normal velocity component at the cavitator center, and $S_n$ is the cavitator area.

The force exerted on the cavitator, as expressed in the body-fixed coordinate system, is given by:

$${\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]}_B=F_{xn}\cdot {\mathit{n}}_c^B$$

(11)

The moment generated by the cavitator, as expressed in the body-fixed coordinate system, is given by:

$${\left[\begin{array}{c}{M}_{cx}\\ M_{cy}\\ M_{cz}\end{array}\right]}_B={\mathit{r}}_{cf}^B\times {\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]}_B$$

(12)

2.2.3. Planing Force

On the basis of the methodology proposed in [5], the planing force and moment acting on each spatial slice are analyzed under varying immersion azimuth angles. This approach yields the spatial vector distribution of the hydrodynamic planing forces.

For the $i\text{-}\mathrm{th}$ spatial cross-section, the nominal wall thickness $\epsilon$, immersion depth $h$, and immersion angle $B$ can be expressed on the basis of the following geometric relationships:

$$\left\{\begin{array}{c}{\epsilon }^i=R_{cav}^i-R_{body}^i\\ h^i=l_{bc}^i-{\epsilon }^i\\ \cos B^i=\left({\epsilon }^i-h^i\right)/\left({\epsilon }^i+h^i\right)\end{array}\right.$$

(13)

where $R_{cav}$ is the radius of the cavitation cross-section, $R_{body}$ is the radius of the vehicle cross-section, and $l_{bc}$ is the distance between the centers of the cavitation $O_{cav}$ and the centers of the vehicle cross-sections $O_b$.

The time derivatives of the nominal wall thickness $\epsilon$, immersion depth $h$, and immersion angle $B$ are given by:

$$\left\{\begin{array}{c}{\displaystyle \frac{\mathrm{d}{\epsilon }^i}{\mathrm{d}t}}=-V_R^i\hfill \\ {\displaystyle \frac{\mathrm{d}{h}^i}{\mathrm{d}t}}=V_R^i+V_n^i\hfill \\ {\displaystyle \frac{\mathrm{d}{B}^i}{\mathrm{d}t}}={\displaystyle \frac{\left({\epsilon }^i-h^i\right)V_n^i+\left(2V_R^i+V_n^i\right)\left({\epsilon }^i+h^i\right)}{{\left({\epsilon }^i+h^i\right)}^2\sin B^i}}\hfill \end{array}\right.$$

(14)

where $V_R$ represents the contraction rate of the cavitation cross-section and $V_n$ denotes the separation velocity between the centers of the cavitation $O_{cav}$ and the centers of the vehicle cross-sections $O_b$.

As shown in Figure 4, on the basis of geometric relationships, the planing force expressed in the immersion coordinate system is given by:

$$\left\{\begin{array}{c}{\left.F_{py}^i\right|}_m=\rho S_{body}^i{\sin }^2{\displaystyle \frac{B^i}{2}}\left[\left(1+{\cos }^2{\displaystyle \frac{B^i}{2}}\right){\displaystyle \frac{\mathrm{d}{V}_{ym}^i}{\mathrm{d}t}}+2{\displaystyle \frac{\mathrm{d}{V}_R^i}{\mathrm{d}t}}\right]\\ +\rho S_{body}^i\sin B^i{\displaystyle \frac{\mathrm{d}{B}^i}{\mathrm{d}t}}\left({\displaystyle \frac{1+\cos B^i}{2}}{V}_{ym}^i+V_R^i\right)\\ {\left.F_{pz}^i\right|}_m=\rho S_{body}^i{\sin }^4{\displaystyle \frac{B^i}{2}}{\displaystyle \frac{\mathrm{d}{V}_{zm}^i}{\mathrm{d}t}}+\rho S_{body}^i{\sin }^2{\displaystyle \frac{B^i}{2}}{\displaystyle \frac{\mathrm{d}{B}^i}{\mathrm{d}t}}\hfill \end{array}\right.$$

(15)

where $\rho$ denotes the fluid density, $S_{body}$ represents the cross-sectional area of the vehicle, and $V_{ym}$ and $V_{zm}$ are the components of the vehicle’s cross-sectional velocity in the immersion coordinate system, respectively.

The sectional planing force is transformed into the body-fixed coordinate system as follows:

$${\left[\begin{array}{c}{Y}_p^i\\ Z_p^i\end{array}\right]}_B=\left[\begin{array}{cc}\cos {\gamma }_p^i& \sin {\gamma }_p^i\\ -\sin {\gamma }_p^i& \cos {\gamma }_p^i\end{array}\right]{\left[\begin{array}{c}{F}_{py}^i\\ F_{pz}^i\end{array}\right]}_m$$

(16)

where ${\gamma }_p$ is the angle of clockwise rotation from the immersion coordinate system to the vehicle cross-sectional coordinate system.

The sectional planing moment expressed in the body-fixed coordinate system is given by:

$${\left[\begin{array}{c}{M}_{px}^i\\ M_{py}^i\\ M_{pz}^i\end{array}\right]}_B={\mathit{r}}_{mf}^{iB}\times {\left[\begin{array}{c}0\\ Y_P^i\\ Z_P^i\end{array}\right]}_B=\left[\begin{array}{c}-Y_P^i{z}_m^i+Z_P^i{y}_m^i\\ -Z_P^i{x}_m^i\\ Y_P^i{x}_m^i\end{array}\right]$$

(17)

In the equation, ${\mathit{r}}_{mf}^B=\left[x_m,y_m,z_m\right]$ represents the position vector from the vehicle’s center of mass $f$ to the point of sectional force application $m$, as expressed in the body-fixed coordinate system.

The total planing force and moment in the body-fixed coordinate system are obtained by integrating the spatial distribution vectors of the sectional planing forces as follows:

$${\left[\begin{array}{c}{X}_p\\ Y_p\\ Z_p\\ M_{px}\\ M_{py}\\ M_{pz}\end{array}\right]}_B={\displaystyle \sum _i\left[\begin{array}{c}{X}_p^i\\ Y_p^i\\ Z_p^i\\ M_{px}^i\\ M_{py}^i\\ M_{pz}^i\end{array}\right]}$$

(18)

2.2.4. Dynamic Model

Using the vehicle’s center of mass $f$ as the reference point, the momentum and moment equations in the body-fixed coordinate system are expressed as:

$$\left\{\begin{array}{l}{\displaystyle \frac{\mathsf{\delta }\mathit{Q}}{\mathsf{\delta }t}}+\mathsf{\omega }\times \mathit{Q}=\mathit{F}\\ {\displaystyle \frac{\mathsf{\delta }\mathit{K}}{\mathsf{\delta }t}}+\mathsf{\omega }\times \mathit{K}+{\mathit{v}}_f\times \mathit{Q}=\mathit{M}\end{array}\right.$$

(19)

where $\mathit{Q}=m{\mathit{v}}_g$ denotes the linear momentum of the vehicle, ${\mathit{v}}_g$ is the velocity of the center of mass, $\mathit{K}={\mathit{J}}_f\mathsf{\omega }+{\mathit{r}}_{gf}\times m{\mathit{v}}_f$ represents the angular momentum of the vehicle, ${\mathit{J}}_f$ is the inertia tensor about the center of mass, ${\mathit{v}}_f$ is the angular velocity of the center of mass, and $\mathit{F}$ and $\mathit{M}$ are the total external force and moment acting on the vehicle, respectively.

On the basis of the force analysis presented in the previous section, a dynamic model of the supercavitating vehicle is established.

$${\mathit{A}}_m\left[\begin{array}{c}{\dot{v}}_x\\ {\dot{v}}_y\\ {\dot{v}}_z\\ {\dot{\omega }}_x\\ {\dot{\omega }}_y\\ {\dot{\omega }}_z\end{array}\right]=-{\mathit{A}}_{v\omega }{\mathit{A}}_m\left[\begin{array}{c}{v}_x\\ v_y\\ v_z\\ {\omega }_x\\ {\omega }_y\\ {\omega }_z\end{array}\right]+\left[\begin{array}{c}{X}_G+X_c\\ Y_G+Y_c+Y_p\\ Z_g+Z_c+Z_p\\ M_{Gx}+M_{cx}+M_{px}\\ M_{Gy}+M_{cy}+M_{py}\\ M_{Gz}+M_{cz}+M_{pz}\end{array}\right]$$

(20)

where ${\mathit{A}}_m$ denotes the mass-inertia matrix and ${\mathit{A}}_{v\omega }$ represents the Coriolis and centripetal matrix constructed from the velocity and angular velocity.

2.3. Analysis of the Heterogeneous Coupling Model

As illustrated in Figure 5 the proposed heterogeneous coupled dynamic model integrates three core subsystems: the cavity evolution model, the six-degree-of-freedom vehicle motion model, and the control subsystem. In this framework, the interactions among these components are established through bidirectional feedback, leading to a complex coupling between vehicle dynamics and cavity evolution. Vehicle motion significantly influences cavity development, as the vehicle’s instantaneous velocity, attitude, and acceleration determine the boundary conditions of each cavity cross-section, affecting the expansion rate and the overall shape of the cavity. Meanwhile, the geometric parameters of the cavity, such as its length, maximum radius, and contraction rate, dictate the spatial distribution of sliding forces on the vehicle’s wetted surface, which in turn feed back into the vehicle’s six-degree-of-freedom dynamics and affect its acceleration and attitude.

Control inputs further contribute to this coupled behavior. The DQN-based ventilation controller regulates the gas injection rate based on the vehicle’s depth and cavity state to maintain the target cavity length, which indirectly modulates sliding force distribution and vehicle motion. Simultaneously, the ADRC-based attitude controller manipulates the cavitator rudder to generate control moments for depth and attitude regulation. However, rudder deflections alter the local flow and pressure fields near the cavitator, inducing secondary perturbations in cavity evolution. Consequently, this two-layer interaction forms a strongly nonlinear feedback loop in which vehicle motion, cavity dynamics, and control inputs continuously influence one another. Such intricate couplings highlight the challenges of controlling ventilated supercavitating vehicles and emphasize the necessity of a decoupled intelligent control framework to maintain system stability and performance.

3. Intelligent Control Design for Cavity Length

3.1. Principle of the DQN

The DQN is a reinforcement learning algorithm designed for discrete action spaces. As shown in Figure 6, the DQN agent consists of an experience replay buffer, a Q-estimation network, a target Q-network, and a loss function. During interaction with the environment, the agent continuously updates the network parameters on the basis of the observed environmental states to improve control performance.

The environment receives the agent’s action $a$ and, on the basis of the current state $s$, returns the next state $s^{\prime }$, reward $r\left(s^{\prime }\right)$, and a done flag $done\left(s^{\prime }\right)$ indicating episode termination. The evaluation network $Q\left(s,a|\theta \right)$ estimates the next action $a^{\prime }$ from the current state $s^{\prime }$ using an ε-greedy policy, forming an interaction loop between the agent and the environment.

Each step’s sample data $\left[a,s,s^{\prime },r,done\right]$ are stored in the agent’s experience replay buffer. Mini-batches of samples are randomly drawn from this buffer, and the loss function $L\left(\theta \right)$ is computed using both the target network $Q\left(s^{\prime },a^{\prime }|{\theta }^{\prime }\right)$ and the evaluation network $Q\left(s,a|\theta \right)$. The evaluation network parameters are then updated via gradient descent on the basis of this loss. Periodically, the target network parameters ${\theta }^{\prime }$ are updated by copying from the evaluation network $\theta$. This process enables evaluation network training during the interaction between the agent and the environment.

Here, $Q\left(s,a|\theta \right)$ and $Q\left(s^{\prime },a^{\prime }|{\theta }^{\prime }\right)$ represent the evaluation network and the target network, respectively. Their calculation formulas are as follows:

$$\begin{array}{l}Q\left(s_t,a_t\right)=r+\gamma \underset{a}{\max }Q\left(s_{t+1},a_{t+1}\right)\\ Q\left({s^{\prime }}_t,{a^{\prime }}_t\right)=r+\gamma \underset{a^{\prime }}{\max }Q\left({s^{\prime }}_{t+1},{a^{\prime }}_{t+1}\right)\end{array}$$

(21)

where $\gamma$ represents the reward discount factor.

The expressions for the loss function $L\left(\theta \right)$ and its gradient $\nabla L\left(\theta \right)$ are given by:

$$\left\{\begin{array}{l}L\left(\theta \right)=E\left[{\left(\begin{array}{l}r+\\ \gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },a^{\prime }|{\theta }^{\prime }\right)-\\ Q\left(s,a|\theta \right)\end{array}\right)}^2\right]\\ \nabla L\left(\theta \right)=E\left[\left(\begin{array}{l}r+\\ \gamma \max Q\left(s^{\prime },a^{\prime }|{\theta }^{\prime }\right)-\\ \underset{a^{\prime }}{Q\left(s,a|\theta \right)\nabla Q\left(s,a|\theta \right)}\end{array}\right)\right]\end{array}\right.$$

(22)

where $E\left(·\right)$ denotes the expectation (mean) operator.

3.2. Design of a DQN-Based Controller for Ventilated Cavity Length Regulation

The problem of cavity length regulation is embedded into a reinforcement learning framework, wherein the ventilated supercavitating vehicle’s heterogeneous coupled dynamics model is integrated to construct the interaction environment by defining appropriate reward functions and termination conditions. Each training episode corresponds to a simplified motion scenario characterized by a constant forward speed and a uniform descent rate, during which the controller is trained to maintain the cavity length.

As shown in Figure 7, an agent is designed on the basis of the DQN algorithm. The discrete ventilation levels of the vehicle are defined as the output actions of the agent, whereas the environmental state consists of the vehicle’s depth, speed, and cavity length. The reward and termination flags are computed using a carefully designed reward function $f_r\left(s\right)$ and a stopping criterion $f_{done}\left(s,t\right)$. During training, the sampled interaction data $\left[a,s,s^{\prime },r,done\right]$ are stored in the agent’s experience replay buffer for updating the network parameters.

The reward function is designed as follows:

$$r=f_r\left(s\right)=20\left(1-10\left|L_{cav}-L_{cav}^r\right|\right)\Delta t$$

(23)

In the equation, $r$ denotes the reward at each step, $L_{cav}$ represents the current cavity length, $L_{cav}^r$ is the target cavity length, and $\Delta t$ corresponds to the time step duration within a single episode.

The termination condition function is defined such that the training episode ends when the cavity length error exceeds a predefined threshold or when the simulation duration for a single episode is reached.

$$done=f_{done}\left(s,t\right)=\left\{\begin{array}{cc}1\hfill & L_{\mathrm{cav}}^e>2\\ 1\hfill & t>5\\ 0\hfill & else\end{array}\right.$$

(24)

where $L_{cav}^e=\left|L_{cav}-L_{cav}^r\right|$ represents the absolute value of the cavity length error and $t$ denotes the current time within the episode.

4. Longitudinal Profile Depth Controller Design

4.1. Active Disturbance Rejection Control Technique

The ADRC framework, as shown in Figure 8, consists of three main components: the tracking differentiator, the extended state observer, and the state error feedback control law.

Consider a nonlinear second-order controlled system expressed as:

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2\hfill \\ {\dot{x}}_2=f\left(x_1,x_2,u,\chi \right)+b_{0}u\hfill \\ y=x_1\hfill \end{array}\right.$$

(25)

where $f$ includes all forces excluding the known control input $b_{0}u$, including modeled terms, unknown control effects $\left(b-b_0\right)u$, unmodeled dynamics, and external disturbances $\chi$.

4.1.1. Tracking Differentiator

Under the assumption of a slowly varying reference input $v\left(t\right)$, when the time constant $T$ is sufficiently small, the first-order inertial system $1/\left(1+Ts\right)$ can be approximated by a pure time delay $e^{-Ts}$. Consequently, the classical differential signal is expressed as:

$$y={\displaystyle \frac{s}{Ts+1}}v={\displaystyle \frac{1}{T}}\left(1-{\displaystyle \frac{1}{Ts+1}}\right)v\approx {\displaystyle \frac{1}{T}}\left(v\left(t\right)-v\left(t-T\right)\right)$$

(26)

Owing to the inherent filtering characteristics of the first-order inertial element, the noise disturbances in Equation (26) are primarily introduced by the term $v\left(t\right)$. Equation (26) can be further reformulated as follows:

$$\begin{array}{c}y={\displaystyle \frac{1}{{\tau }_2-{\tau }_1}}\left({\displaystyle \frac{1}{{\tau }_{1}s+1}}-{\displaystyle \frac{1}{{\tau }_{2}s+1}}\right)v\approx {\displaystyle \frac{\left(v\left(t-{\tau }_1\right)-v\left(t-{\tau }_2\right)\right)}{{\tau }_2-{\tau }_1}}\\ 0<{\tau }_1<{\tau }_2\end{array}$$

(27)

When both ${\tau }_1$ and ${\tau }_2$ approach zero, Equation (27) reduces to a second-order oscillatory system, which is expressed as:

$$\underset{\begin{array}{l}{\tau }_1\to \tau \\ {\tau }_2\to \tau \end{array}}{\lim }{\displaystyle \frac{y\left(s\right)}{v\left(s\right)}}=\underset{\begin{array}{l}{\tau }_1\to \tau \\ {\tau }_2\to \tau \end{array}}{\lim }{\displaystyle \frac{1}{{\tau }_2-{\tau }_1}}\left({\displaystyle \frac{1}{{\tau }_{1}s+1}}-{\displaystyle \frac{1}{{\tau }_{2}s+1}}\right)={\displaystyle \frac{s}{{\tau }^{2}s+2\tau s+1}}$$

(28)

Therefore, the state-space realization of the second-order oscillatory tracking differentiator is given by:

$$\left\{\begin{array}{c}{\dot{v}}_1=v_2\hfill \\ {\dot{v}}_2=-a^2\left(v_1-r\left(t\right)\right)-2a{v}_2\hfill \\ y=v_2\hfill \end{array}\right.$$

(29)

Equation (29) enables tracking of a noisy input signal under the constraint imposed by the fast factor $a$ and extracting its differential signal $v_2$. The tracking differentiator serves to filter and denoise the original command $r$ while also reasonably shaping the transient response $v_1$ according to the speed limitations of the controlled system, balancing between overshoot and response speed at the command input and facilitating the extraction of the differential signal $v_2$, which further improves the control performance.

4.1.2. Extended State Observer

For a system with input u and output y, the disturbance is incorporated into the observer design. An extended state observer (ESO) is constructed, as shown in Equation (30), to enable real-time estimation of both system states and the total disturbance.

$$\left\{\begin{array}{c}e=y-z_1\hfill \\ {\dot{z}}_1=z_2+{\beta }_1\cdot e\hfill \\ {\dot{z}}_2=z_3+{\beta }_2\cdot e+b_0\cdot u\hfill \\ {\dot{z}}_3={\beta }_3\cdot e\hfill \end{array}\right.$$

(30)

The ESO augments the system disturbance into an additional state variable. By utilizing the system input $u$ and output $y$, the ESO effectively enables real-time estimation $z_i,i=1,2,3$ of the motion states $x_1$, $x_2$ and the total disturbance $f$. This estimation serves as the foundation for the subsequent state error feedback control law.

4.1.3. State Error Feedback Control Law

According to the reference signals $v_1$ and $v_2$ and the estimated states $z_1$, $z_2$, and $z_3$, a feedback control law is designed as follows:

$$u={\displaystyle \frac{k_p\left(v_1-z_1\right)+k_w\left(v_2-z_2\right)-z_3}{b_0}}$$

(31)

By substituting into the system model given in Equation (25), the closed-loop dynamics can be expressed as:

$$\begin{array}{cc}\hfill {\dot{x}}_2& =f+k_p\left(v_1-z_1\right)+k_w\left(v_2-z_2\right)-z_3\hfill \\ & =k_p\left(v_1-x_1\right)+k_w\left(v_2-x_2\right)+\left(k_{p}e+k_w{e}_2+e_3\right)\hfill \\ & \approx k_p\left(v_1-x_1\right)+k_w\left(v_2-x_2\right)\hfill \end{array}$$

(32)

Thus, under the control law defined in Equation (31), the original system is transformed via “dynamic compensation linearization” into a cascaded integrator structure. The transfer function from the reference input $v_1\left(t\right)$ to the system output $x_1\left(t\right)$ can be approximated as:

$${\displaystyle \frac{x_1\left(s\right)}{v_1\left(s\right)}}={\displaystyle \frac{k_{w}s+k_p}{s^2+k_{w}s+k_p}}$$

(33)

The state error feedback control law is formulated on the basis of the estimated disturbance $z_3$, enabling dynamic compensation and system linearization.

4.2. Depth Controller Design

The disturbance estimation and compensation process of the ADRC enables decoupled control across different channels. This section addresses the depth control problem of a tailless supercavitating vehicle. First, an inner-loop pitch angle controller is designed using ADRC, incorporating the sliding force as an estimated and compensated disturbance. This approach enables channel decoupling and control decoupling between the ventilation–cavity loop and the cavitator rubber–motion loop. An outer-loop cascaded depth controller is subsequently developed on the basis of the error feedback. The overall control architecture is shown in Figure 9.

On the basis of (20), assuming that the lateral and transverse motion parameters are small perturbations and that the axial velocity remains constant, the longitudinal profile dynamics equation of the supercavitating vehicle can be simplified as follows:

$$\left[\begin{array}{c}{\dot{v}}_y\\ {\dot{\omega }}_z\end{array}\right]=\left[\begin{array}{c}{b}_{11}\\ b_{21}\end{array}\right]{\delta }_{nh}-{\mathit{A}}_m^{-1}\left[\begin{array}{c}m{v}_x{\omega }_z+Y_G+Y_p\\ m{x}_g{v}_x{\omega }_z+M_{Gz}+M_{pz}\end{array}\right]$$

(34)

In this equation, the expressions for ${\mathit{A}}_m^{-1}$, $b_{11}$, $b_{21}$, and $k$ are given by:

$$\begin{array}{cc} {\mathit{A}}_m^{-1}=\left[\begin{array}{cc}{\displaystyle \frac{1}{km}}& -{\displaystyle \frac{x_g}{k{J}_{zz}}}\\ -{\displaystyle \frac{x_g}{k{J}_{zz}}}& {\displaystyle \frac{1}{k{J}_{zz}}}\end{array}\right] & b_{11}=-{\displaystyle \frac{q{S}_n{C}_{xn}}{mk}}+{\displaystyle \frac{q{S}_n{x}_c{C}_{xn}{x}_g}{J_{zz}k}} \\ k=1-{\displaystyle \frac{x_g^{2}m}{J_{zz}}}& b_{21}={\displaystyle \frac{x_{g}q{S}_n{C}_{xn}-q{S}_n{x}_c{C}_{xn}}{J_{zz}k}}\end{array}$$

In the expressions, $q$ denotes the dynamic pressure of the vehicle, $S_n$ represents the cavitator area, and $C_{xn}$ is the cavitator drag coefficient.

Considering the pitch channel as a second-order system to be controlled,

$$\left\{\begin{array}{l}\dot{\theta }={\omega }_z\\ {\dot{\omega }}_z=b_0{\delta }_{nh}+f\left(\theta ,v_y,y,Y_p,M_{zp}\right)\end{array}\right.$$

(35)

In the equation, $b_0=b_{21}$ represents the control moment coefficient of the cavitator rudder, and $f\left(\theta ,v_y,y,Y_p,M_{zp}\right)$ denotes the disturbance term, which includes the effects of the skimming force.

The ADRC is designed as follows:

$$\left\{\begin{array}{c}{\dot{v}}_1=v_2\hfill \\ {\dot{v}}_2=-a_{TD}^2\left(v_1-r\left(t\right)\right)-2a_{TD}{v}_2\hfill \\ e=y-z_1\hfill \\ {\dot{z}}_1=z_2+{\beta }_1\cdot e\hfill \\ {\dot{z}}_2=z_3+{\beta }_2\cdot e+b_0\cdot {\delta }_{nh}\hfill \\ {\dot{z}}_3={\beta }_3\cdot e\hfill \\ {\delta }_{nh}=\left(k_p\left(v_1-z_1\right)+k_w\left(v_2-z_2\right)-z_3\right)/b_0\hfill \end{array}\right.$$

(36)

The ADRC’s overall input consists of the reference command $r\left(t\right)$ and the measured state response $y\left(t\right)$, while its output corresponds to the cavitator rudder deflection angle ${\delta }_{nh}$. The controller design parameters include the observer gains ${\beta }_i,i=1,2,3$, control gain $b_0$, and control gains $k_p$ and $k_w$.

On the basis of the ADRC for the pitch angle control, an outer-loop nested error feedback controller is implemented to achieve depth regulation and expressed as follows:

$${\theta }_c=K_p\left(y_{v1}^L-y^L\right)+K_i{\displaystyle \int \left(y_{v1}^L-y^L\right)\mathrm{d}t}+K_d\left(y_{v2}^L-v_y\right)$$

(37)

where $y^L$ denotes the longitudinal coordinate of the vehicle in the launch coordinate system, $y_{v1}^L$ represents the depth command filtered through the tracking differentiator to generate a smooth transition, $y_{v2}^L$ is the derivative of $y_{v1}^L$, and $v_y$ is the longitudinal velocity in the launch coordinate system, which can be approximated by the velocity in the body-fixed frame under small pitch angle assumptions.

4.3. Pitch Channel Closed-Loop Performance and Stability Analysis

As discussed previously, the essence of the ADRC lies in its ability to estimate and compensate for both disturbance and coupling terms. When the observer error converges to zero, the system can be regarded as an ideal second-order integrator under control. This section analyzes the closed-loop performance of the pitch channel. First, the stability of the ideal system is proven under the assumption of converged observer error. Then, the convergence property of the observer itself is examined, followed by an analysis of the tracking error convergence of the pitch channel throughout the process. Finally, the influence of the observer bandwidth on the overall convergence behavior is discussed.

4.3.1. Stability Analysis of the Ideal System

On the basis of Equations (35) and (36), by selecting the state vector $\mathit{X}={\left[\begin{array}{cc}\theta & {\omega }_z\end{array}\right]}^T$, the state-space representation of the pitch channel second-order system is established as follows:

$$\stackrel{.}{\mathit{X}}=\hat{\mathit{A}}\mathit{X}+\hat{\mathit{B}}{\delta }_{nh}+\mathit{f}$$

(38)

where

$$\begin{gathered} \begin{array}{cc} \widehat{A}=\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{G{y}_g}{J_{zz}-x_g^{2}m}}& 0\end{array}\right] & \widehat{B}=\left[\begin{array}{c}0\\ b_{21}\end{array}\right] \end{array} \\ f={\left[\begin{array}{cc}0& f\left(\theta ,v_y,y,Y_p,M_{zp}\right)\end{array}\right]}^T \end{gathered}$$

When the disturbance compensation exactly matches the disturbance, the disturbance-free and compensation-free state equation can be established as follows:

$${\hat{\mathit{X}}}^{*}=\hat{\mathit{A}}{\mathit{X}}^{\ast }+\hat{\mathit{B}}\left(k_p\left(v_1-z_1\right)+k_w\left(v_2-z_2\right)\right)/b_0={\mathit{A}}^{*}{\mathit{X}}^{*}$$

(39)

where

$${\mathit{A}}^{*}=\left[\begin{array}{cc}0& 1\\ -k_p& -k_w\end{array}\right]$$

(40)

The results reveal that under the action of the ADRC, the pitch channel is transformed into a double-integrator system. By tuning the parameters $k_p$ and $k_w$ to ensure that matrix ${\mathit{A}}^{*}$ is a Hurwitz matrix, the stability of the pitch control can be guaranteed.

4.3.2. Convergence Analysis of the ESO

On the basis of the characteristics of the disturbance, the following assumption is made:

Assumption 1.

The derivatives of the disturbance up to a certain order are bounded. That is, there exists a positive constant$M_{\alpha }$such that:

$$\underset{t\in \left[\left.t_0,+\infty \right)\right.}{\sup }‖{\displaystyle \frac{\mathrm{d}{f}^{\left(n\right)}\left(t\right)}{\mathrm{d}t}}‖<M_a,n\in {\mathbb{Z}}^{+}$$

(41)

Theorem 1.

Under the condition of Assumption 1, the ESO provides a bounded estimation of the disturbance, and it satisfies the following inequality:

$$\left|f\left(t\right)-z_3\left(t\right)\right|\le c_1\left(e^{-c_2{\omega }_0\left(t-t_0\right)}+{\displaystyle \frac{1}{{\omega }_0}}\right)$$

(42)

In this equation, $c_1$ and $c_2$ are constants independent of ${\omega }_0$, with the expression given by:

$$\left\{\begin{array}{c}{c}_1={\displaystyle \frac{‖{\mathit{T}}_1‖}{\sqrt{{\lambda }_{\min }\left({\mathit{P}}_o\right)}}}\max \left\{\sqrt{\mathit{V}\left(t_0\right)},{\displaystyle \frac{2{\lambda }_{\max }\left({\mathit{P}}_o\right)‖{\mathit{P}}_o‖{\mathit{M}}_o}{\sqrt{{\lambda }_{\min }\left({\mathit{P}}_o\right)}}}\right\}\\ c_2={\displaystyle \frac{1}{2{\lambda }_{\max }\left({\mathit{P}}_o\right)}}\end{array}\right.$$

Proof. 

On the basis of Equations (35) and (36), the observer state equation is established as follows. By selecting the state vector ${\mathit{X}}_o={\left[\begin{array}{ccc}\theta & {\omega }_z& f\end{array}\right]}^T$, the extended state equation can be constructed as:

$$\left\{\begin{array}{c}{\stackrel{.}{\mathit{X}}}_o={\mathit{A}}_o{\mathit{X}}_o+{\mathit{F}}_o\dot{f}+{{\mathit{B}}^{\prime }}_o{\delta }_{nh}\\ {\mathit{y}}_o={\mathit{C}}_o{\mathit{X}}_o\end{array}\right.$$

(43)

where

$$\begin{array}{cc} {\mathit{A}}_o=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right] & {{\mathit{B}}^{\prime }}_o=\left[\begin{array}{c}0\\ b_{21}\\ 0\end{array}\right] \\ {\mathit{F}}_o=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]& {\mathit{C}}_o=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\end{array}$$

The observer state equation is given by:

$$\stackrel{.}{\mathit{Z}}={\mathit{A}}_o\mathit{Z}+\mathit{L}{\mathit{C}}_o\left({\mathit{X}}_o-\mathit{Z}\right)+{{\mathit{B}}^{\prime }}_o{\delta }_{nh}$$

(44)

where

$$\begin{array}{cc} \mathit{Z}={\left[z_1,z_2,z_3\right]}^T & \mathit{L}={\left[{\beta }_1,{\beta }_2,{\beta }_3\right]}^T \end{array}$$

To simplify the controller parameter design, the observer bandwidth ${\omega }_o$ can be used to configure the observer parameters, which are expressed as:

$$\begin{array}{ccc}{\beta }_1=3{\omega }_o & {\beta }_2=3{\omega }_o^2 & {\beta }_3={\omega }_o^3\end{array}$$

The observer error equation is defined as ${\mathit{E}}_o={\mathit{X}}_o-\mathit{Z}$. On the basis of Equations (43) and (44), it follows that:

The estimation error is transformed via an invertible linear transformation into the standard form:

$$\begin{array}{cc}\mathit{\xi }={\mathit{T}}_1^{-1}{\mathit{E}}_o & {\mathit{T}}_1=\left[\begin{array}{ccc}{\omega }_o^{-2}\hfill & 0\hfill & 0\hfill \\ 0\hfill & {\omega }_o^{-1}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right]\end{array}$$

The estimation error equation is transformed into:

$$\begin{array}{cc}\stackrel{.}{\mathit{\xi }}& ={\mathit{T}}_1^{-1}\left({\mathit{A}}_o-\mathit{L}{\mathit{C}}_o\right){\mathit{T}}_1\mathit{\xi }+{\mathit{T}}_1^{-1}{\mathit{F}}_o\dot{f}\hfill \\ & ={\omega }_o{\mathit{A}}_1\xi +\stackrel{-}{\mathit{F}}\dot{f}\hfill \end{array}$$

(45)

where

$$\begin{array}{cc}{\mathit{A}}_1=\left[\begin{array}{lll}-3\hfill & 1\hfill & 0\hfill \\ -3\hfill & 0\hfill & 1\hfill \\ -1\hfill & 0\hfill & 0\hfill \end{array}\right] & \stackrel{-}{\mathit{F}}=\left[\begin{array}{l}0\hfill \\ 0\hfill \\ 1\hfill \end{array}\right]\end{array}$$

It is evident that ${\mathit{A}}_1$ is a Hurwitz matrix; therefore, a positive definite matrix ${\mathit{P}}_o$ such that:

$${\mathit{A}}_1^{\mathit{T}}{\mathit{P}}_o+{\mathit{P}}_o{\mathit{A}}_1=-\mathit{I}$$

(46)

Considering the Lyapunov equation $V_o\left(t\right)={\mathit{\xi }}^T{\mathit{P}}_o\mathit{\xi }$,

$${\lambda }_{\min }\left(P_o\right)\Vert \mathit{\xi }{\Vert }^2⩽V_o(t)⩽{\lambda }_{\max }\left(P_o\right)\Vert \mathit{\xi }{\Vert }^2$$

(47)

where ${\lambda }_{\min }\left({\mathit{P}}_o\right)$ and ${\lambda }_{\max }\left({\mathit{P}}_o\right)$ denote the maximum and minimum eigenvalues of matrix ${\mathit{P}}_o$, respectively. The analysis shows that:

$${\displaystyle \frac{d\sqrt{V_o}}{dt}}=-{\displaystyle \frac{{\omega }_o\Vert \mathit{\xi }{\Vert }^2}{2\sqrt{V_o}}}+{\displaystyle \frac{{\xi }^T{\mathit{P}}_o\overline{\mathit{F}}\dot{f}}{\sqrt{V_o}}}⩽-{\displaystyle \frac{{\omega }_o}{2{\lambda }_{\max }\left({\mathit{P}}_o\right)}}\sqrt{V_o}+{\displaystyle \frac{‖{\mathit{P}}_o‖\Vert \overline{\mathit{F}}\dot{f}\Vert }{\sqrt{{\lambda }_{\min }\left({\mathit{P}}_o\right)}}}$$

(48)

According to the Gronwall–Bellman inequality, it can be deduced that:

$$‖{\mathit{E}}_o‖=‖{\mathit{T}}_1‖‖\mathit{\xi }‖⩽{\displaystyle \frac{‖{\mathit{T}}_1‖}{\sqrt{{\lambda }_{\min }\left({\mathit{P}}_o\right)}}}\left(e^{-{\displaystyle \frac{{\omega }_o}{2{\lambda }_{\max }\left({\mathit{P}}_o\right)}}\left(t-t_0\right)}\sqrt{V_o\left(t_0\right)}+\right.\left.{\displaystyle \frac{2{\lambda }_{\max }\left({\mathit{P}}_o\right)‖{\mathit{P}}_o‖M_{\alpha }}{{\omega }_o\sqrt{{\lambda }_{\min }\left({\mathit{P}}_o\right)}}}\right)⩽c_1\left(e^{-c_2{\omega }_o\left(t-t_0\right)}+{\displaystyle \frac{1}{{\omega }_o}}\right)$$

(49)

Theorem 1 is thus proven. Equation (42) indicates that when the higher-order derivatives of the disturbance are bounded, the estimation error of the ESO also remains bounded. Moreover, the estimation error is inversely proportional to the observer bandwidth ${\omega }_o$; that is, a larger ${\omega }_o$ leads to a smaller estimation error. □

4.3.3. Tracking Error Analysis Between the Actual and Ideal Systems

Theorem 2.

Building upon Theorem 1, the tracking error$‖{\mathit{E}}_{\mathit{X}}(t)‖=‖\mathit{X}(t)-{\mathit{X}}^{*}(t)‖$of system (38) satisfies the following bound:

$$\underset{t\in \left[t_0,\infty \right)}{\sup }‖\mathit{X}(t)-{\mathit{X}}^{*}(t)‖⩽c_3\left(e^{-c_4\left(t-t_0\right)}+{\displaystyle \frac{1}{{\omega }_0}}\right)$$

(50)

where $c_3$ and $c_4$ are constants independent of ${\omega }_0$, with the expression given by:

$$\left\{\begin{array}{l}{c}_3={\displaystyle \frac{1}{\sqrt{{\lambda }_{\min }\left({\mathit{P}}^{*}\right)}}}\max \left\{\sqrt{V^{*}\left(t_0\right)},{\displaystyle \frac{2{\lambda }_{\max }\left({\mathit{P}}^{*}\right)‖{\mathit{P}}^{*}‖M_f}{\sqrt{{\lambda }_{\min }\left({\mathit{P}}^{*}\right)}}}\right\}\hfill \\ c_4={\displaystyle \frac{1}{2{\lambda }_{\max }\left({\mathit{P}}^{*}\right)}}\hfill \end{array}\right.$$

Proof. 

On the basis of Equations (36) and (38),

$$\begin{array}{l}\stackrel{.}{\mathit{X}}=\hat{\mathit{A}}\mathit{X}+\hat{\mathit{B}}\left(k_p\left(v_1-z_1\right)+k_w\left(v_2-z_2\right)\right)/b_0\\ -\hat{\mathit{B}}{z}_3/b_0+\mathrm{f}\end{array}$$

(51)

Let the tracking error be defined as:

$${\stackrel{.}{\mathit{E}}}_{\mathit{X}}=\stackrel{.}{\mathit{X}}-{\stackrel{.}{\mathit{X}}}^{*}={\mathit{A}}^{*}{\mathit{E}}_{\mathit{X}}-\hat{\mathit{B}}{z}_3/b_0+\mathit{f}$$

(52)

In the analysis, the matrix ${\mathit{A}}^{*}$ in the equation is a Hurwitz matrix. Therefore, there exists a positive definite matrix ${\mathit{P}}^{*}$ such that:

$${\left({\mathit{A}}^{*}\right)}^T{\mathit{P}}^{*}+{\mathit{P}}^{*}{\mathit{A}}^{*}=-\mathit{I}$$

(53)

Considering the Lyapunov equation $V^{*}\left(t\right)={\mathit{E}}_{\mathit{X}}^T{\mathit{P}}_o{\mathit{E}}_{\mathit{X}}$,

$${\lambda }_{\min }\left({\mathit{P}}^{*}\right){‖{\mathit{E}}_{\mathit{X}}‖}^2⩽V^{*}⩽{\lambda }_{\max }\left({\mathit{P}}^{*}\right){‖{\mathit{E}}_{\mathit{X}}‖}^2$$

(54)

The analysis reveals that:

$${\displaystyle \frac{d\sqrt{V^{*}}}{ dt}}⩽-{\displaystyle \frac{{‖{\mathit{E}}_{\mathit{X}}‖}^2}{2\sqrt{V^{*}}}}+{\displaystyle \frac{{\mathit{E}}_{\mathit{X}}^T{\mathit{P}}^{*}}{\sqrt{V^{*}}}}\left(-\hat{\mathit{B}}{z}_3/b_0+\mathit{f}\right)⩽-{\displaystyle \frac{1}{2{\lambda }_{\max }\left({\mathit{P}}^{*}\right)}}\sqrt{V^{*}}+{\displaystyle \frac{‖{\mathit{P}}^{*}‖‖-\hat{\mathit{B}}{z}_3/b_0+\mathit{f}‖}{\sqrt{{\lambda }_{\min }\left({\mathit{P}}^{*}\right)}}}$$

(55)

On the basis of Assumption 1 and Theorem 1, there exists a positive constant $M_f$ such that:

$$‖-\hat{\mathit{B}}{z}_3/b_0+\mathit{f}‖\le {\displaystyle \frac{M_f}{{\omega }_o}}$$

(56)

$$\sqrt{V^{*}}⩽e^{-{\displaystyle \frac{t-t_0}{2{\lambda }_{\max }}}\left({\mathit{P}}^{*}\right)}\sqrt{V^{*}\left(t_0\right)}+{\displaystyle \frac{2{\lambda }_{\max }\left({\mathit{P}}^{*}\right)‖{\mathit{P}}^{*}‖M_f}{{\omega }_o\sqrt{{\lambda }_{\min }\left({\mathit{P}}^{*}\right)}}}$$

(57)

Combining Equations (56) and (59) yields:

$$‖{\mathit{E}}_{\mathit{X}}‖⩽\sqrt{{\displaystyle \frac{V^{*}}{{\lambda }_{\min }\left({\mathit{P}}^{*}\right)}}}⩽{\displaystyle \frac{\left(e^{-\frac{t-t_0}{2{\lambda }_{\max }\left(P^{*}\right)}}\sqrt{V^{*}\left(t_0\right)}\right.\left.+\frac{2{\lambda }_{\max }\left({\mathit{P}}^{*}\right)‖{\mathit{P}}^{*}‖M_f}{{\omega }_0\sqrt{{\lambda }_{\min }\left({\mathit{P}}^{*}\right)}}\right)}{\sqrt{{\lambda }_{\min }\left({\mathit{P}}^{*}\right)}}}⩽c_3\left(e^{-c_c\left(t-t_0\right)}+{\displaystyle \frac{1}{{\omega }_0}}\right)$$

(58)

The proof of Theorem 2 is thus complete. Equation (50) indicates that the observer bandwidth ${\omega }_o$ is inversely proportional to the tracking error between the actual system and the ideal system; the larger ${\omega }_o$ is, the smaller the tracking error. □

5. Simulation Analysis and Validation

5.1. Simulation Setup

The initial position of the vehicle in the launch coordinate system is set to [0,0,0] m, and its initial velocity in the body-fixed frame is set to [70,0,0] m/s. The depth command is set to −5 m. The vehicle mass is 7.599 kg, the main moment of inertia is [1.0,2.058,2.058] kg·m², the diameter is 0.1 m, the length is 0.8 m, the cavitator diameter is 0.035 m, and the drag coefficient is 0.82. The ambient vapor pressure is set to 2450 pa, and the surface water pressure is 101,000 pa. The initial simulation depth and velocity are set to 0 m and 70 m/s, respectively.

The simulations were performed using a fixed-step, fourth-order Runge–Kutta integration scheme to solve the coupled differential equations governing vehicle motion and cavity evolution. The time step was set to 0.0001 s to ensure numerical stability and accuracy. Boundary effects and wave-induced disturbances were neglected to focus on the intrinsic dynamics of vehicle–cavity interactions.

5.2. Parametric Study of Cavity Evolution

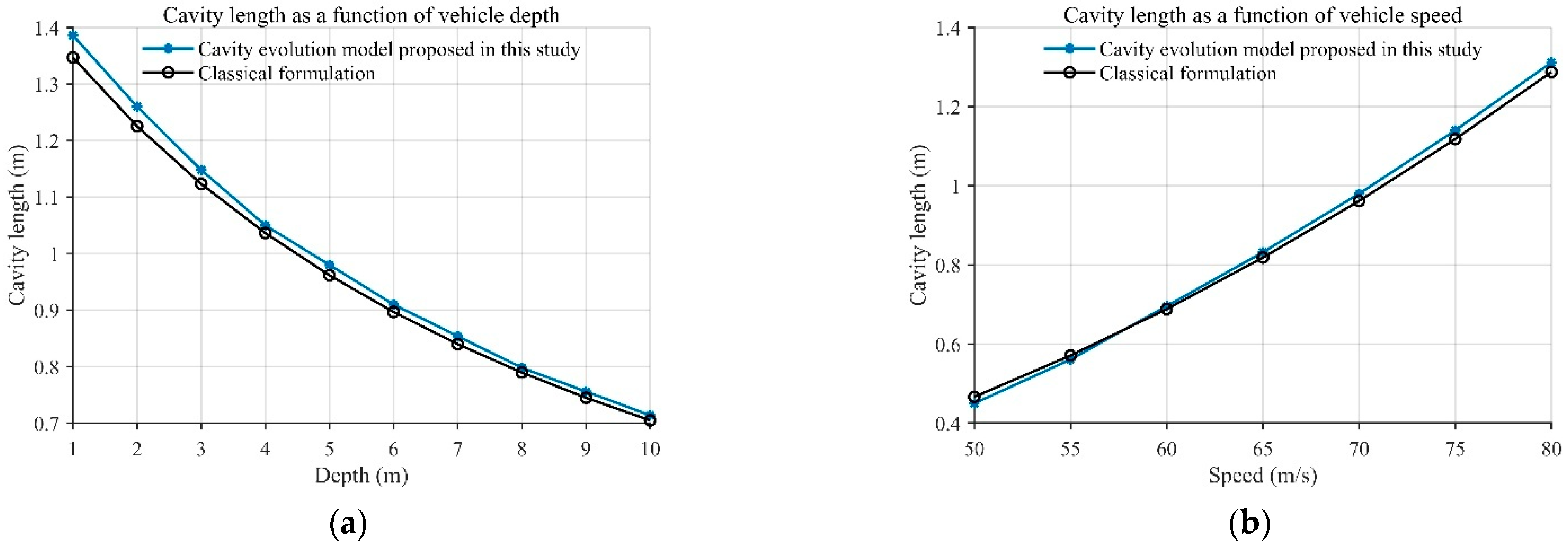
The cavity size plays a crucial role in governing the coupling between the vehicle and the cavity. To validate the effectiveness of the proposed cavity evolution model, a sensitivity analysis of cavity length was conducted and compared with a typical empirical correlation [4]. The results in Figure 10 indicate that the cavity length decreases with increasing operating depth and increases with increasing velocity. The observed trends are consistent with the empirical formula, thereby confirming the reliability of the proposed model.

5.3. Simulation Under Uncontrolled Conditions

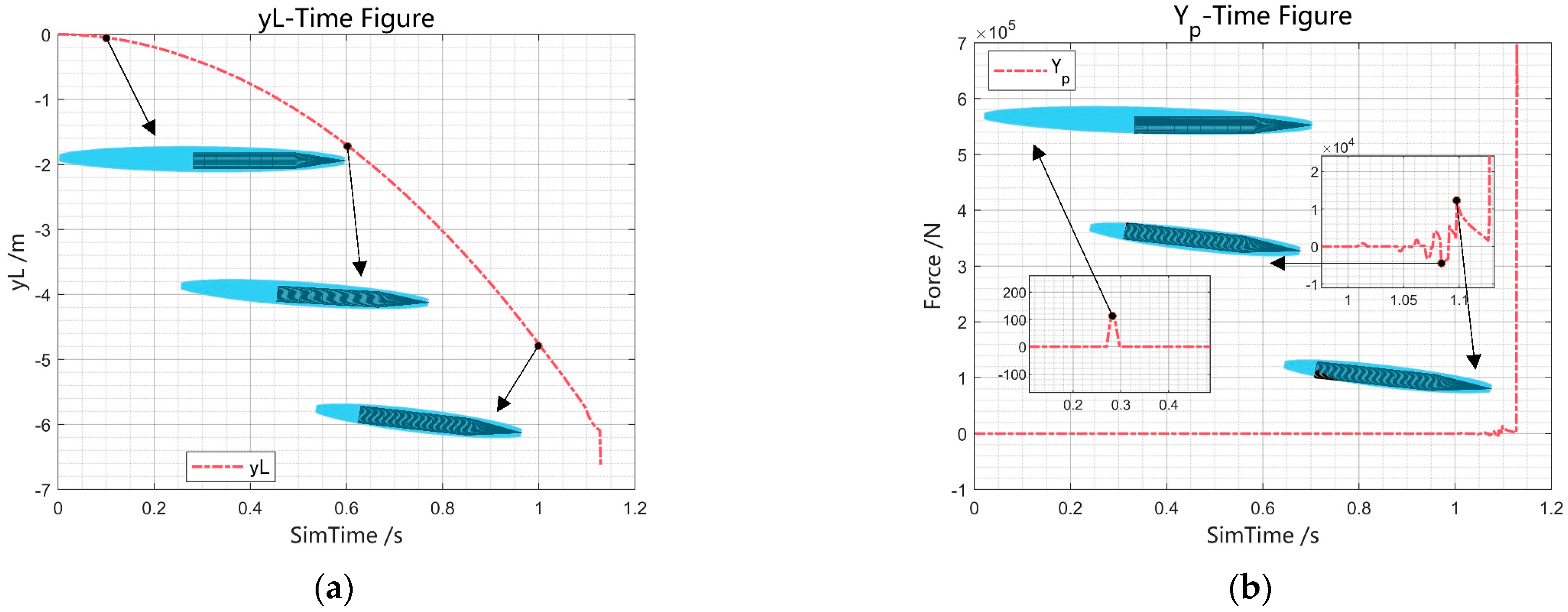
A 6-DOF simulation under uncontrolled conditions was conducted on the basis of the heterogeneous coupled motion model of the ventilated supercavitating vehicle. As shown in Figure 11, during the initial uncontrolled phase, the vehicle is not yet submerged and is subjected only to gravity: the pitch angular velocity remains zero, and the vehicle’s attitude is maintained; the velocity angle of attack decreases while the cavity axis gradually tilts upward; and the increasing depth leads to higher external pressure, causing the cavity length to shorten progressively. When the cavity contracts and the upward-tilted axis contacts the vehicle’s stern, there is a small positive normal slippage force and corresponding nose-down moment. The negative angular velocity lacks sufficient moment to be eliminated, resulting in the stern gradually pitching upward until submersion occurs and leading to a negative normal slippage force and a nose-up moment. This process introduces a periodic oscillation trend in both the vehicle’s attitude and normal velocity. As the cavity continues to contract and the vehicle submerges further, the amplitude of the slippage forces increases, ultimately leading to divergent motion of the vehicle.

To achieve stable motion and control of the ventilated supercavitating vehicle and in response to the divergence observed in uncontrolled simulations, a control strategy separating cavity length and attitude was developed. In the ventilation–cavity loop, a cavity length controller based on the DQN algorithm was designed to maintain the supercavitating state while preserving favorable characteristics of the slippage force, thereby alleviating the burden on attitude control. In the cavitator rudder–motion loop, a decoupled attitude controller based on ADRC was implemented to dynamically compensate for the “total disturbance,” including slippage forces, enabling precise attitude tracking.

5.4. Training of the Ventilation–Cavity Loop Controller

During training of the cavity-length control loop, the vehicle depth controller was assumed ideal. Each episode corresponded to maintaining cavity length during a simplified motion with constant forward speed and uniform depth change. To improve generalization, the initial vehicle depth, forward speed, and depth-change rate were randomly sampled within specified ranges for each episode.

The estimation networks $Q\left(a,s|\theta \right)$ and target networks $Q\left(a^{\prime },s^{\prime }|{\theta }^{\prime }\right)$ share the same architecture, consisting of an input layer with dimension $3\times 256$, two hidden layers each with dimension $256\times 256$, and an output layer of dimension $256\times 6$. The training was implemented in Python 3.10 using the PyTorch 2.8 framework, with the Adam optimizer and a learning rate of 0.001. The experience replay buffer had a capacity of 10,000 transitions, and the mini-batch size was set to 64. Training was conducted over 1000 episodes, with a reward discount factor of 0.1. The vehicle’s initial depth was randomly sampled within 0–20 m, the forward speed ranged from 55 to 85 m/s, and the depth-change rate varied between −2 and 2 m/s, allowing the controller to learn robust cavity-length regulation across a wide range of operating conditions. To ensure training stability, the target network was updated using a fixed-step soft update strategy (τ = 0.01), and the observed states were normalized prior to being fed into the network to accelerate convergence.

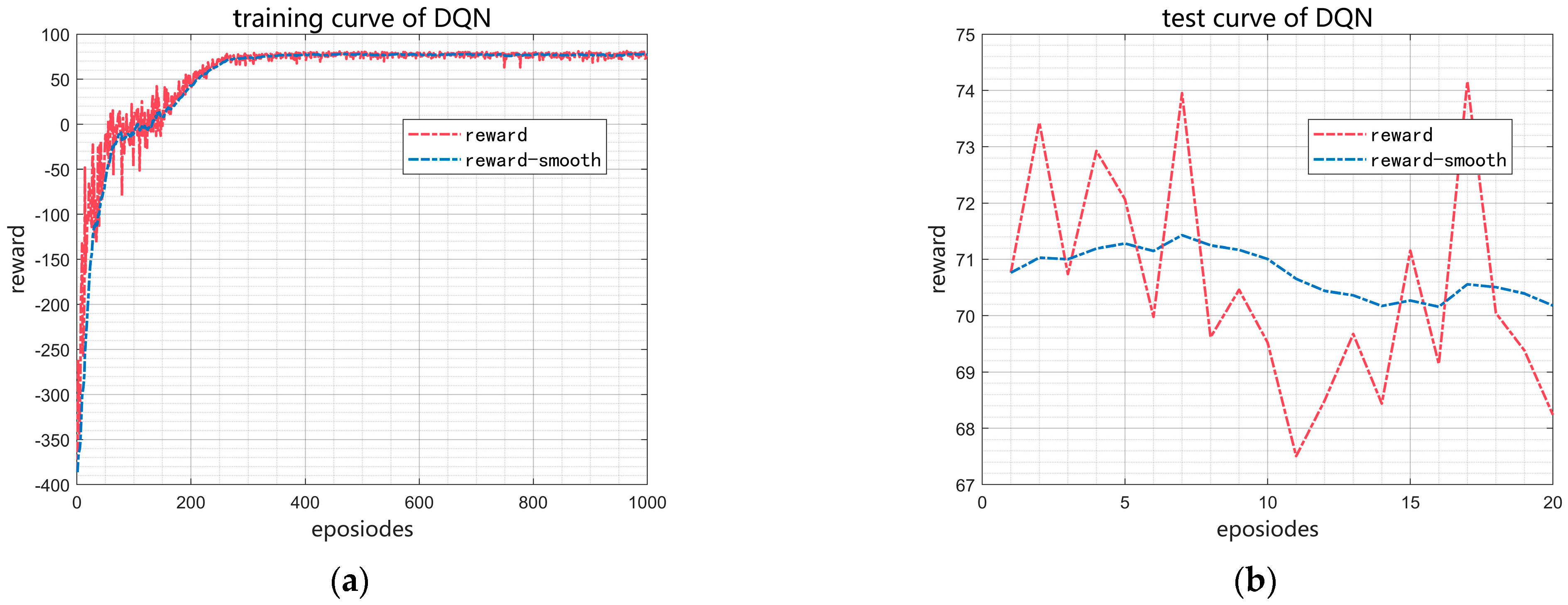
On the basis of the designed reward and termination functions, the maximum reward per step is determined to be $r_{\max }=20\Delta t$, resulting in a maximum cumulative reward of ${\displaystyle \sum r_{\max }}=100$ per episode. As shown in Figure 12, after 1000 training episodes, the agent’s reward stabilizes at approximately 74. During subsequent testing over 20 episodes, the average episode reward remains near 70, with a maximum of 74 and a minimum of 67. These results demonstrate that the reinforcement learning-based cavitation length controller exhibits strong stability and effective control performance.

During training, the vehicle’s speed was kept constant, and its depth varied uniformly. However, real-world operating conditions are typically much more complex. To further evaluate the robustness and generalization capability of the trained model, simulation experiments were designed in which both the vehicle’s speed and depth vary sinusoidally, in order to examine the DQN controller’s performance in maintaining the cavity length under more realistic conditions. The variation profiles of vehicle speed and ambient pressure are given in Equation (59). In these simulations, the trained DQN cavity length controller was used to maintain a cavity length of 1.8 m. As shown in Figure 13, the cavity length is maintained at approximately 1.8 m, with a maximum deviation of less than 0.1 m. These results demonstrate that the model can effectively handle moderate disturbances in vehicle speed and depth, maintaining a stable cavity length.

$$\left\{\begin{array}{l}V=70+5\sin \left(3t\right)\\ P_{\infty }=120000+20000\sin \left(3t\right)\end{array}\right.$$

(59)

5.5. Control Design for the Cavitator Rudder–Motion Loop

Assuming a constant cavity shape, the ADRC is designed on the basis of the simplified dynamic model given in (34). The design parameters are selected as follows: the fast convergence factor $a_{TD}$ is set to 10, and the observer parameters are chosen as ${\beta }_1=450$, ${\beta }_2=67500$, and ${\beta }_3=3375000$. The control gain is set to $b_0=-468.7$, and the control law parameters are configured as $k_p=225$, $k_{\omega }=45$. A sinusoidal pitch angle command is applied to evaluate the tracking performance.

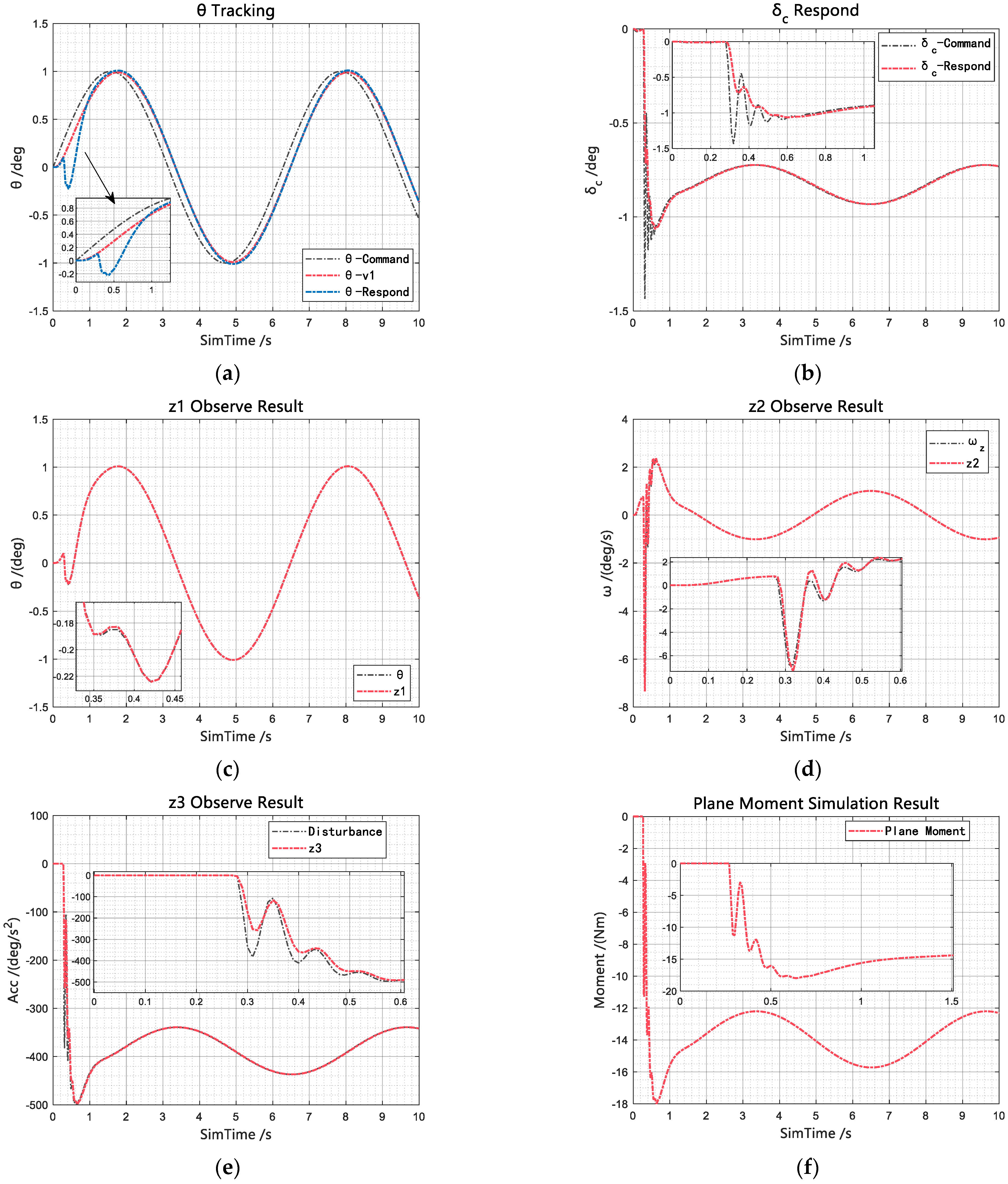
As shown in Figure 14, the ESO effectively estimates the current pitch angle $\theta$, pitch rate ${\omega }_z$, and total disturbance $f$. By incorporating the estimated states into the state error feedback control law, dynamic compensation-based linearization is achieved. The resulting system exhibits characteristics of a second-order cascaded integrator. Under the action of simply tuned control parameters, the pitch angle leads to satisfactory tracking performance.

The outer-loop error feedback controller is designed with the parameters set as $K_p=0.0524$, $K_i=0.0052$, and $K_d=0.0122$. The simulation results for the depth variation control are shown in Figure 15.

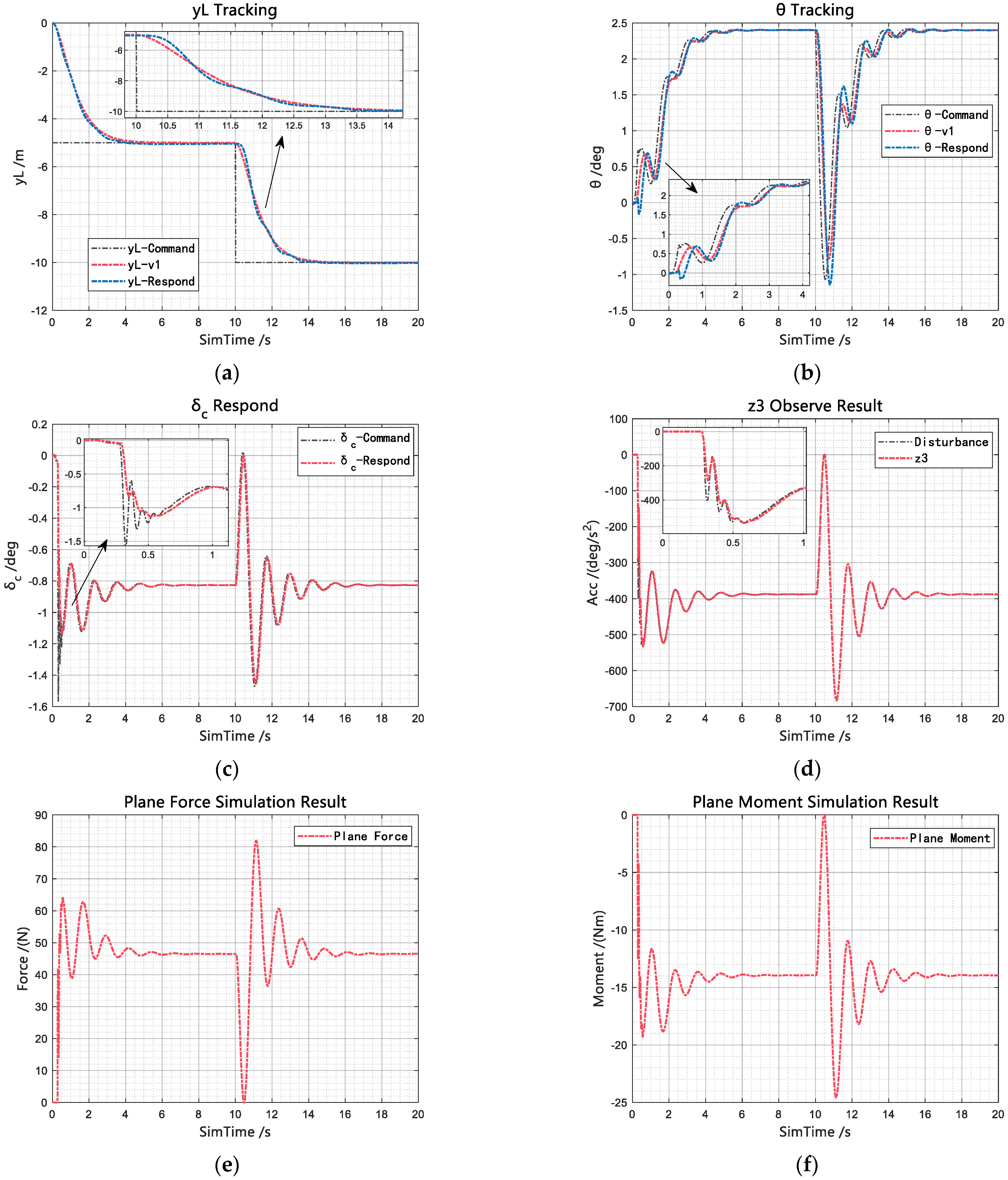
As shown in Figure 15, under the effective attitude angle regulation achieved by the inner-loop ADRC, the outer-loop error feedback controller achieves favorable control performance. Throughout the depth variation process, the depth command tracking differentiator, constrained by the selected fast factor, appropriately manages the transition process of the step inputs. This transition design is particularly essential for supercavitating vehicles characterized by pronounced dead zone nonlinearities. Significant fluctuations are observed in the hydrodynamic forces and moments, as shown in Figure 15c,d. Nevertheless, the control system exhibits strong disturbance rejection capabilities because of the accurate disturbance estimation provided by the extended state observer combined with real-time disturbance compensation via the state error feedback control law. Consequently, smooth and stable depth tracking control is realized without noticeable overshoot.

5.6. Depth Control Without Cavity Length Regulation

In this subsection, the coupling effect of vehicle depth maneuvers on cavity evolution is neglected. The ventilation rate is fixed, and only depth control is applied. The simulation results are presented in.

As shown in Figure 16, the cavity length decreases with decreasing depth. Around 1 s, the cavity length remains within the allowable range; however, by approximately 2.5 s, the cavity has contracted to nearly the length of the vehicle body. At this stage, the planing force calculation formula becomes completely invalid, and further vehicle dynamics computations are no longer meaningful.

These results clearly indicate that neglecting the influence of vehicle maneuvers on cavity evolution can lead to unrealistic predictions of vehicle dynamics. Therefore, it is necessary to incorporate a cavity length control loop to maintain the cavity within a reasonable range, thereby ensuring the fidelity and reliability of the vehicle dynamics model.

5.7. Depth Control of a Ventilated Supercavitating Vehicle

For comparative analysis, the parameters of the outer-loop depth controller were kept unchanged, while the inner-loop pitch angle control strategy was replaced with a classical PID controller, whose parameters are shown in Equation (60). This setup was used to compare the performance of the proposed cascaded ADRC scheme with that of the PID-based approach.

$${\delta }_{nh}=-0.35\left({\theta }_r-\theta \right)-0.275{\displaystyle \int \left({\theta }_r-\theta \right)}\mathrm{d}t$$

(60)

In the ventilation–cavity length control loop, the intelligent cavity length controller maintains the target cavity length by adjusting the ventilation rate according to the vehicle’s depth, velocity, and instantaneous cavity length. As shown in Figure 17b, during the depth maneuver, the ventilation rate increases gradually with depth, with local fluctuations caused by the discrete switching between different ventilation levels. Once the depth stabilizes, the ventilation rate becomes constant. As depicted in Figure 17a, under the ventilation control, the ventilated supercavity length remains stably regulated around the setpoint of 1.8 m throughout the maneuver, with a steady-state error of approximately 0.1 m. These results verify the high accuracy and robustness of the intelligent cavity length controller.

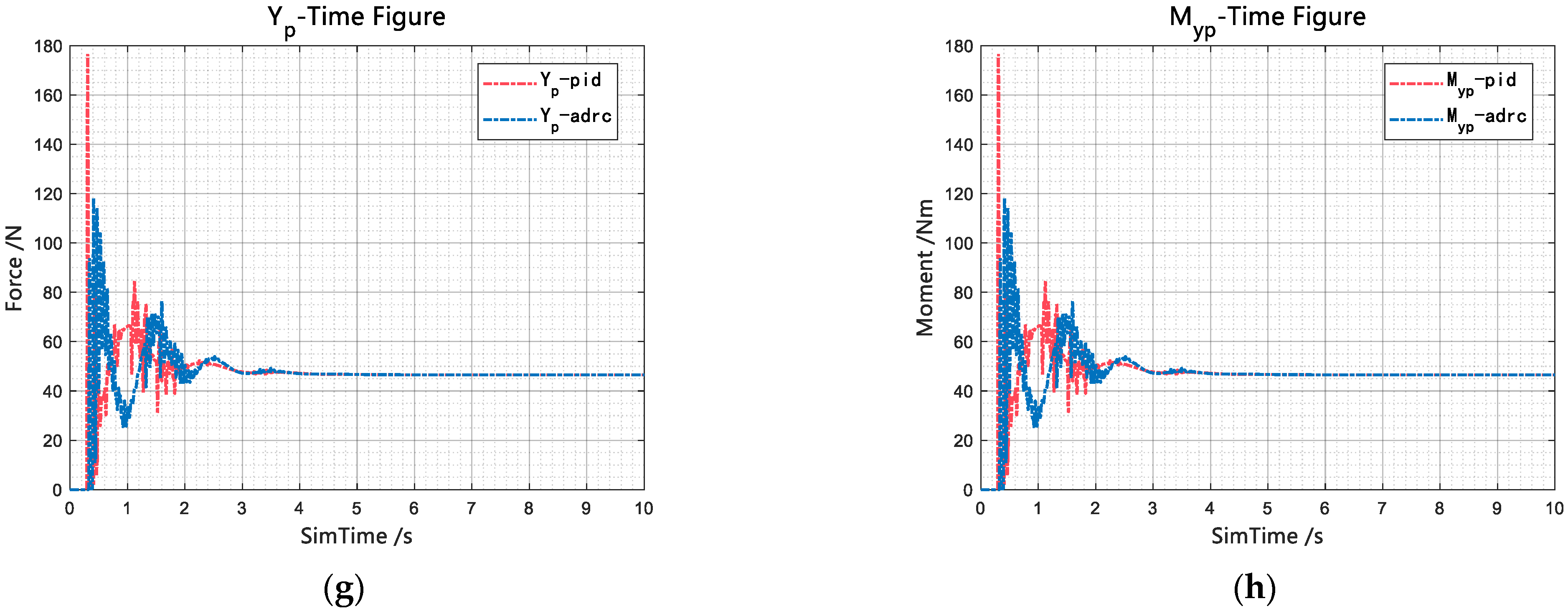
In the cavitator–motion control loop, the simulation results indicate that both PID-based and ADRC-based control strategies achieve satisfactory depth-tracking performance. However, when dealing with strong coupling effects and external disturbances, the ADRC-based control scheme exhibits superior dynamic characteristics. Compared with the PID controller, the ADRC reduces the peak glide force by approximately 30%, significantly enhancing the system’s stability and disturbance rejection capability.

Under the combined ADRC and reinforcement learning control framework, both cavity evolution and vehicle motion gradually stabilize during the depth-holding phase, with glide force oscillations effectively suppressed and a smooth transition achieved in depth control. As shown in Figure 17c,d, the vehicle closely follows the depth command throughout the maneuver, demonstrating high tracking precision and favorable dynamic performance. The rise time and settling time are approximately 3 s and 5 s, respectively, with no overshoot observed. After stabilization, the vehicle maintains a depth of 5 m with a steady-state error of about 0.05 m. Owing to the efficient cavity length regulation and the active disturbance rejection capability of the ADRC, the cascaded control system effectively balances translational maneuvering and attitude stabilization, suppresses excessive glide forces, avoids instability induced by heterogeneous coupling channels, and achieves robust and smooth depth maneuver control.

6. Conclusions

This study investigated the depth-change maneuver control of ventilated supercavitating vehicles. Due to high travel speeds, non-stationary cavity evolution, and the nonlinear and coupled nature of the control channels, the control of supercavitating vehicles remains one of the most challenging problems in fluid mechanics and control theory. To address these challenges, an unsteady cavity evolution model was developed based on the principle of independent cross-sectional expansion and the strip theory, and coupled with a six-degree-of-freedom vehicle dynamics model to establish a heterogeneous coupled framework. Compared with simplified models, this framework provides a more comprehensive representation of the interactions between cavity dynamics and vehicle motion, as well as the coupling among different motion channels.

To mitigate instabilities observed in uncontrolled simulations—such as cavity collapse, planing force oscillations, and attitude divergence—a decoupled intelligent control framework was proposed. Within this framework, a Deep Q-Network (DQN) controller was employed to stabilize cavity length, while an Active Disturbance Rejection Controller (ADRC) was applied to pitch control to suppress planing force fluctuations and improve depth-tracking performance. The decoupled control strategy, with the DQN managing the cavity-length loop and the ADRC controlling the motion loop, reduces system complexity while enhancing robustness.

Simulation results demonstrate that the proposed approach effectively maintains the cavity length near the desired setpoint, suppresses planing force oscillations, and achieves precise and stable depth control during maneuvers. Comparative simulations with a classical PID controller show that, while both PID- and ADRC-based strategies achieve similar depth-tracking performance, the ADRC outperforms PID in handling coupling effects and external disturbances, reducing the peak planing force by approximately 30%, thereby significantly improving system stability and disturbance rejection. Under the combined DQN–ADRC control framework, cavity evolution and vehicle motion stabilize once the depth reaches the commanded value, achieving smooth and reliable depth control with a rise time of approximately 3 s, a settling time of 5 s, and a steady-state error of around 0.05 m. The main contributions of this study are as follows:

• Heterogeneous Coupled Modeling: A six-degree-of-freedom heterogeneous coupled motion model for ventilated supercavitating vehicles was established, providing a more complete description of cavity–vehicle interactions and serving as a foundation for future maneuvering control studies.
• Decoupled Control Design: A separated control strategy was proposed, in which a DQN controller manages the cavity-length loop and an ADRC controller governs the attitude loop, enhancing system robustness and control efficiency.
• Intelligent Control Framework: A combined DQN-based cavity length control and ADRC-based depth control framework was developed and evaluated through simulations, demonstrating its effectiveness in maintaining cavity stability and achieving robust depth maneuver control.

In conclusion, this study holds significant scientific and engineering value in the modeling and control of ventilated supercavitating vehicles. It demonstrates both the novelty and practical potential of the proposed methodology while clearly identifying directions for future research.

7. Limitations and Future Work

Despite the progress achieved in this study, several limitations remain. First, the Independent Cross-Section Expansion Principle (ICSEP) is inherently an approximate method, and its applicability under complex maneuvering conditions still requires validation through high-fidelity CFD simulations or experimental studies. Second, this work only considers fully developed supercavitation, while the dynamics of partial cavitation and its coupling with vehicle motion have not been fully investigated. Third, the current control design primarily focuses on the longitudinal depth channel, and a complete six-degree-of-freedom (6-DOF) closed-loop control has yet to be realized. Moreover, the stability of the system under model uncertainties and time delays, as well as the generalization capability of reinforcement learning-based controllers in real-world environments, remains to be further explored. Finally, the robustness of the closed-loop system under communication delays and modeling uncertainties has not been systematically evaluated.

• Evaluating the applicability of the Independent Cross-Section Expansion Principle under diverse maneuvering conditions through high-fidelity numerical simulations and experimental validation;
• Extending the modeling framework to incorporate partially cavitating flows and their dynamic coupling effects;
• Developing a comprehensive six-degree-of-freedom control strategy to enhance maneuverability and robustness in complex hydrodynamic environments;
• Systematically investigating the stability and robustness of the closed-loop system under model uncertainties and time delays;
• Exploring the generalization, optimization, and transfer capabilities of reinforcement learning-based controllers in practical operating conditions.