A Low-Frequency Component Filtering Method for Heave Acceleration Signal of Marine Ship
Abstract
1. Introduction
- Compared with the expensive high sampling frequency data acquisition card, the proposed method uses a low sampling frequency data acquisition module. This allows the filtered acceleration signal to achieve similar signal accuracy as the high sampling frequency system at a lower sampling frequency. This hardware change not only reduces hardware costs but also reduces the burden of data storage and transmission, thereby improving the efficiency of data collection and making it more suitable for real-time monitoring systems of ship status.
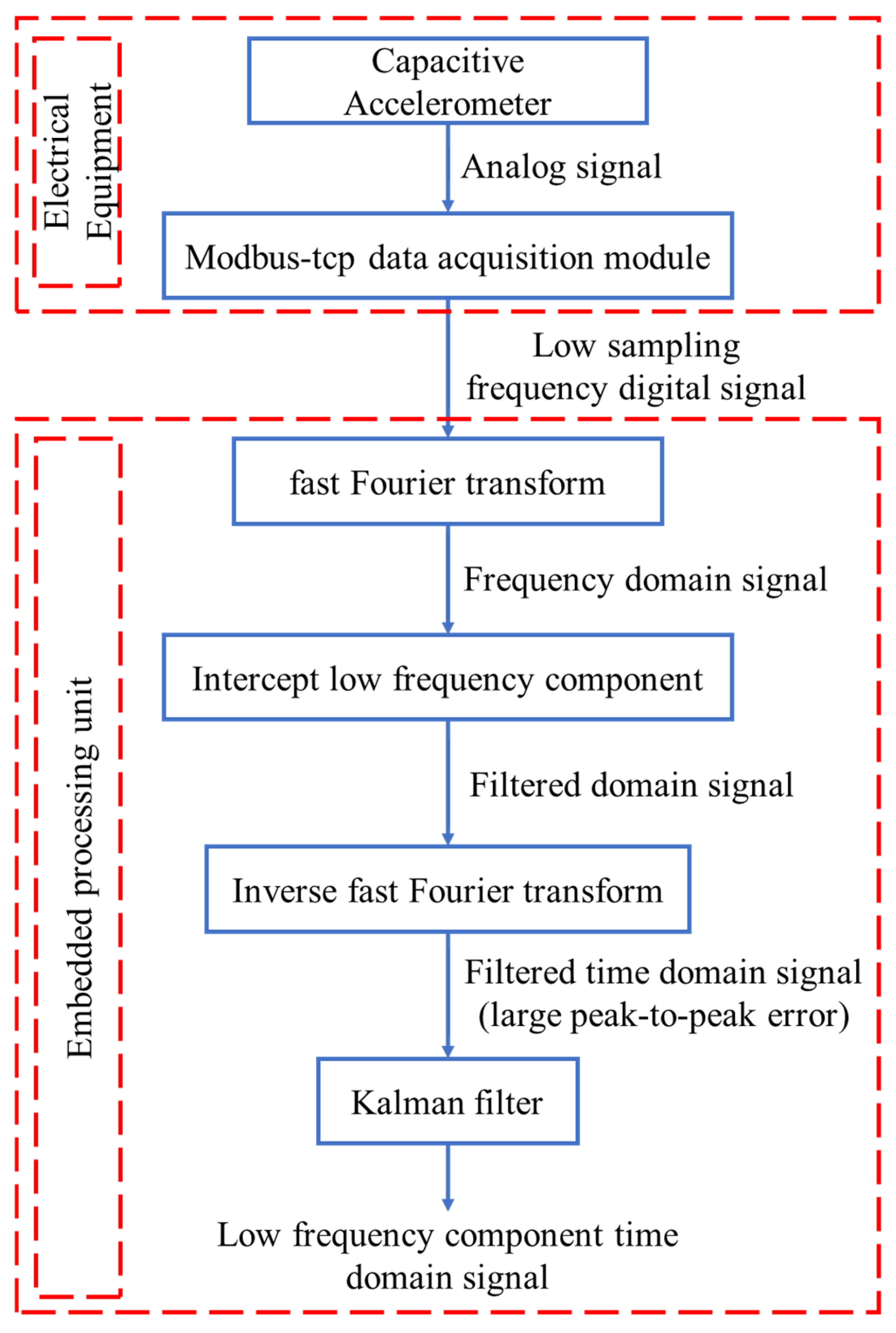
- Compared with the traditional filtering method, the proposed method uses digital filtering, which can flexibly adjust the ship heave acceleration under different sea conditions. Secondly, combined with Fast Fourier Transform, the noise component is effectively identified and suppressed, and the phase effect brought by the traditional filter is completely eliminated. Finally, the Kalman time domain filter is used to further suppress the imaginary error brought by the inverse Fourier transform and ensure the amplitude accuracy of the peak-to-peak value.
2. Preliminary Work
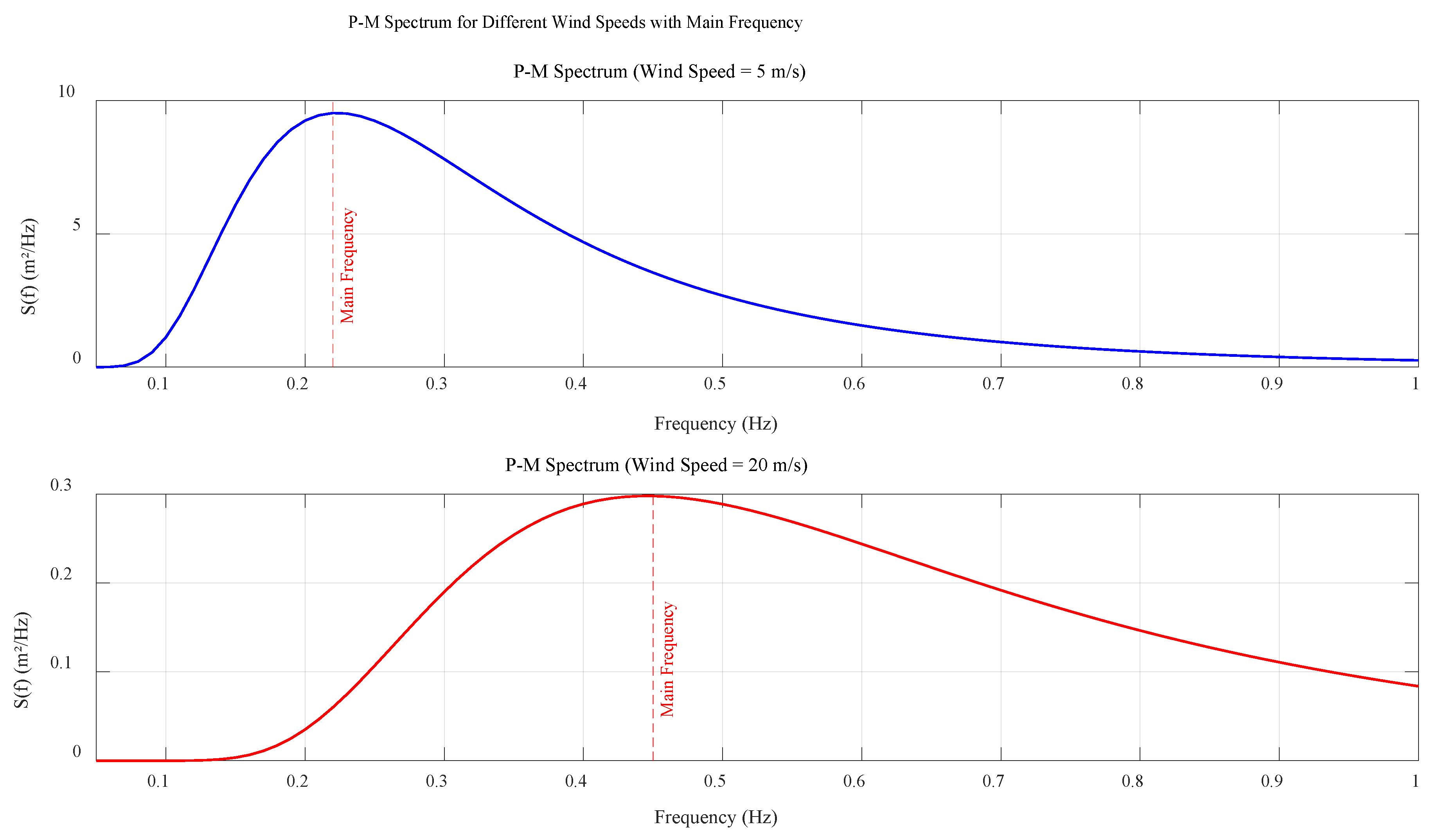
2.1. Low-Frequency Component Range of Ship Heave Acceleration
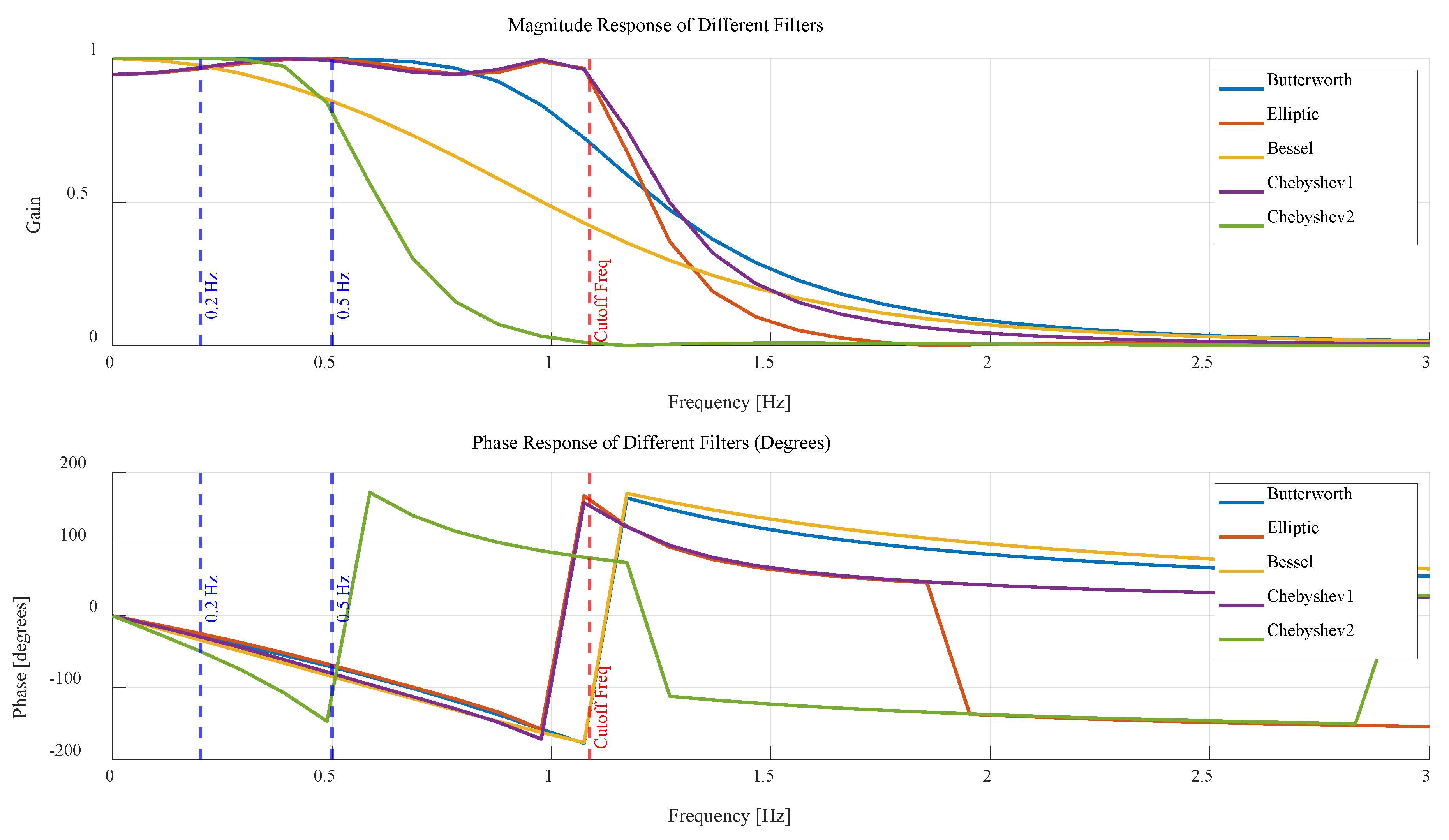
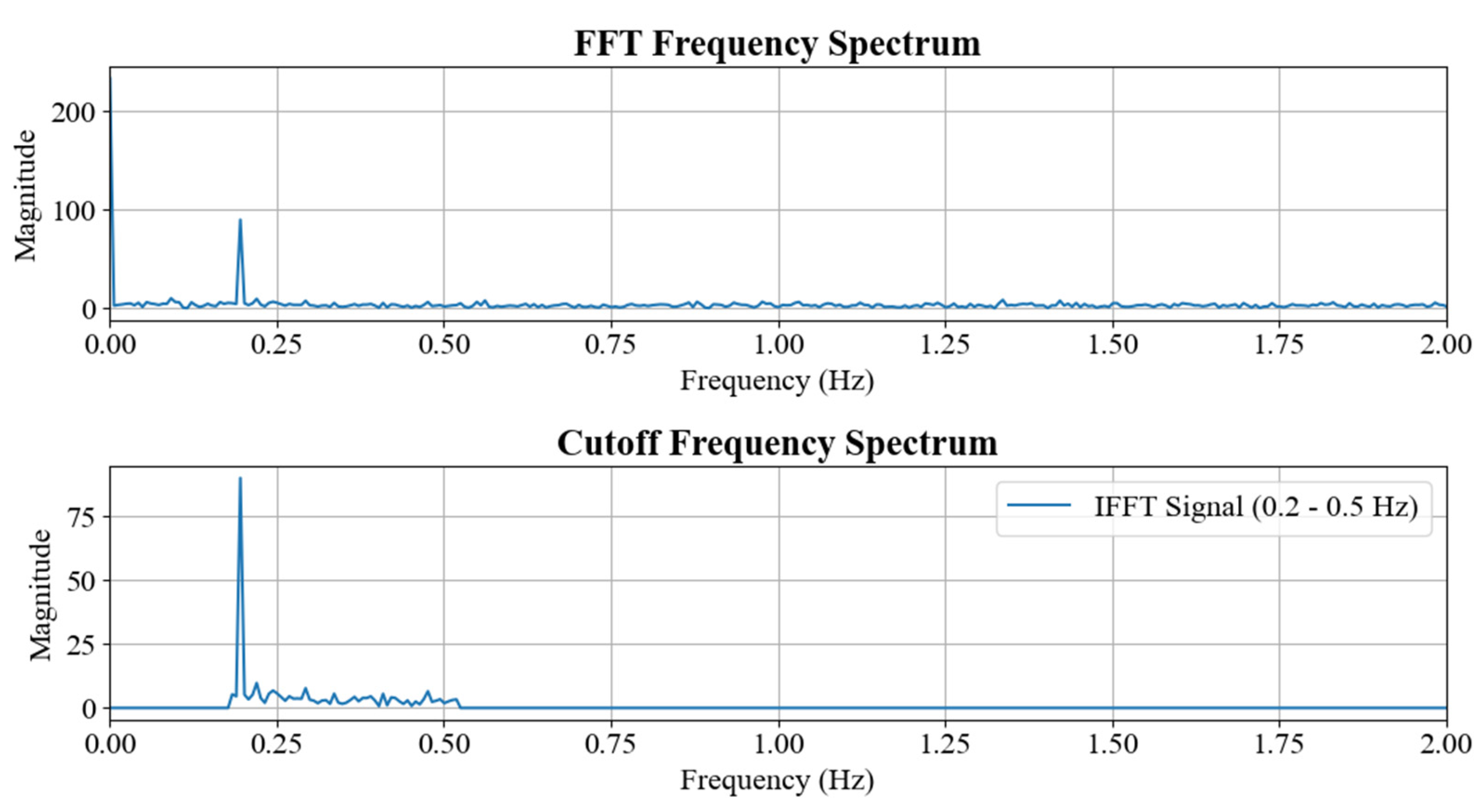
2.2. Low-Frequency Component Filters
3. Proposed Method
3.1. Low Sampling Frequency Data Acquisition Module
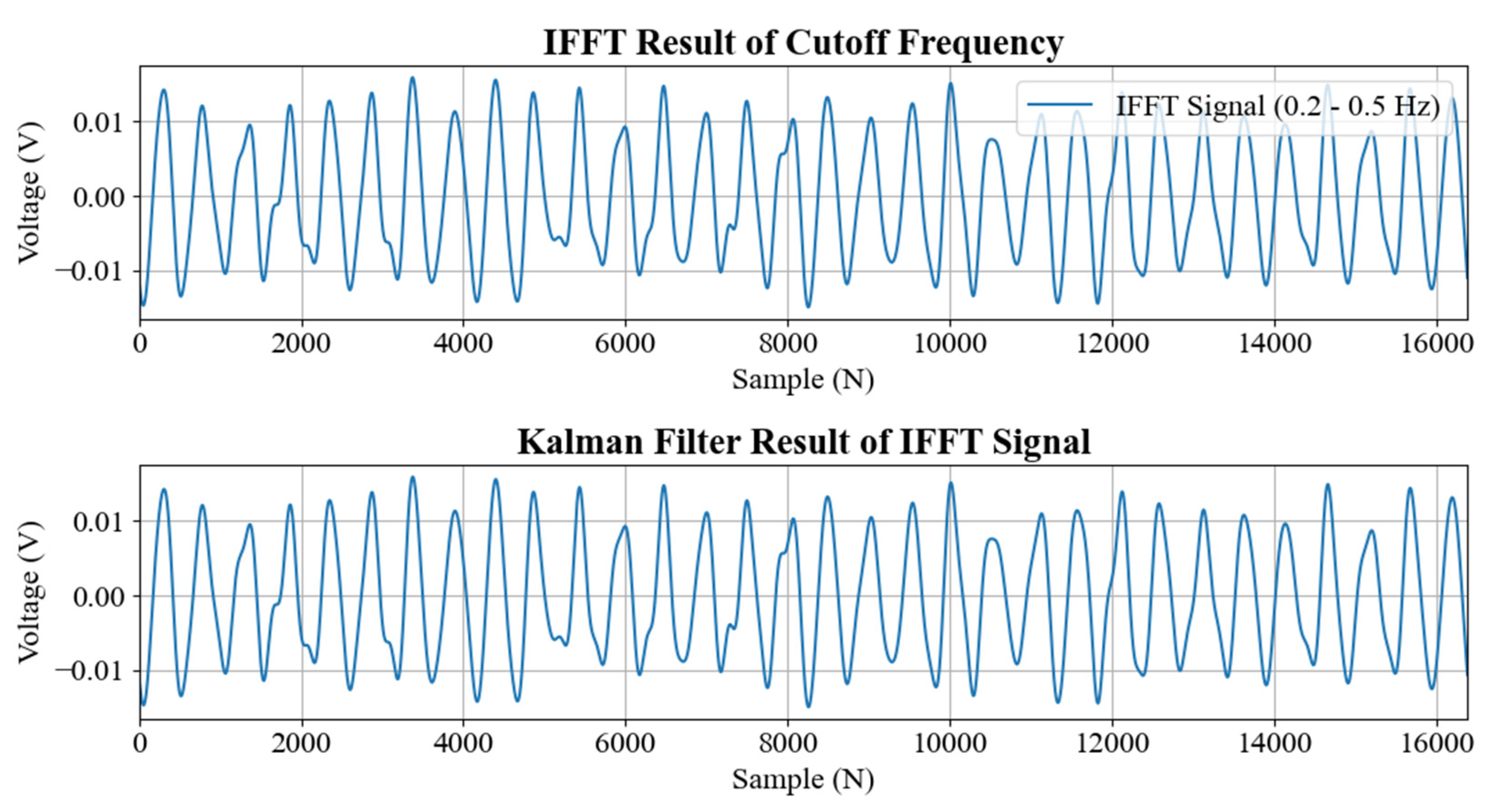
3.2. A Low-Frequency Component Filtering Method for Heave Acceleration Signal of Ships
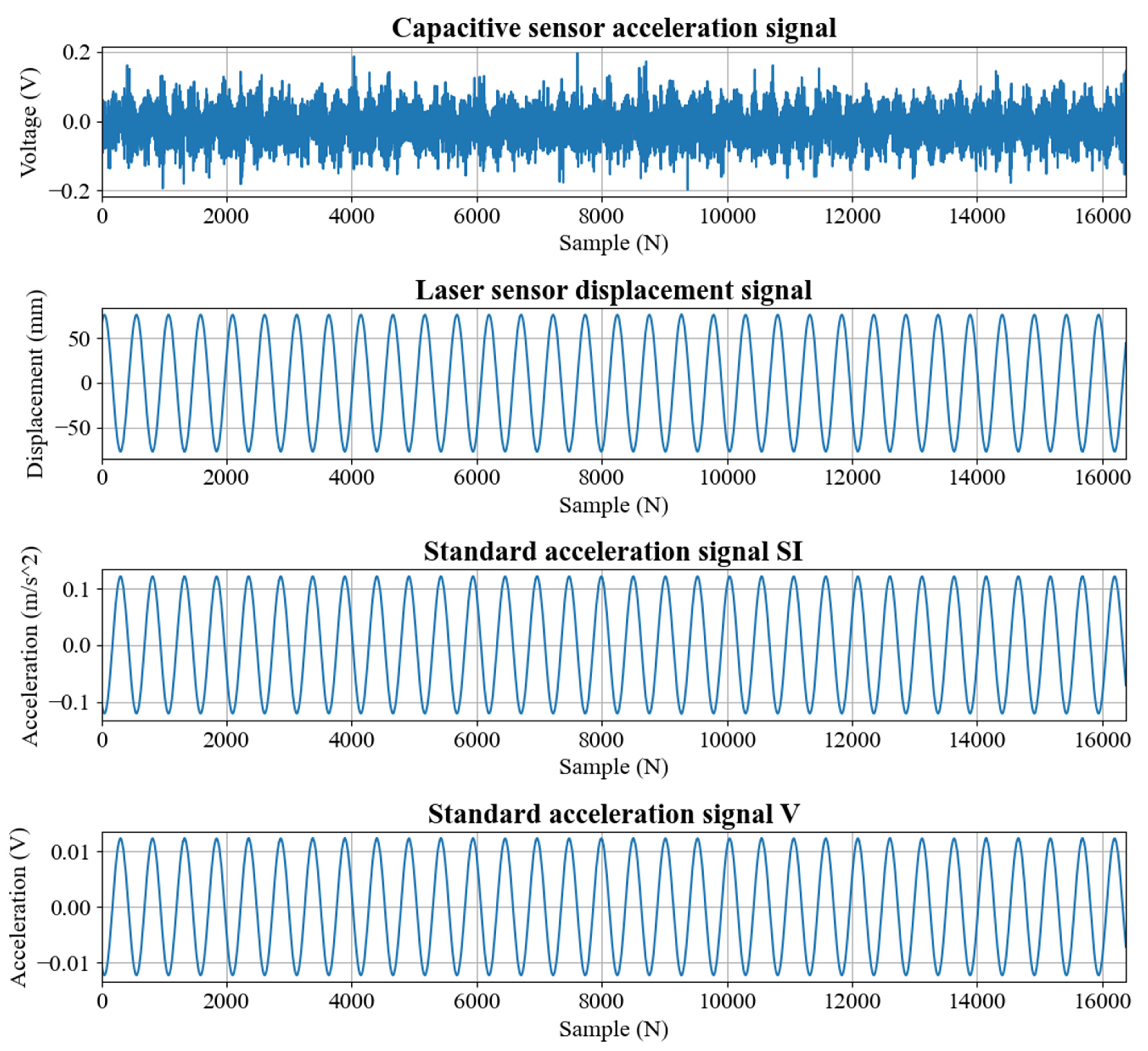
4. Experimental Results and Analysis
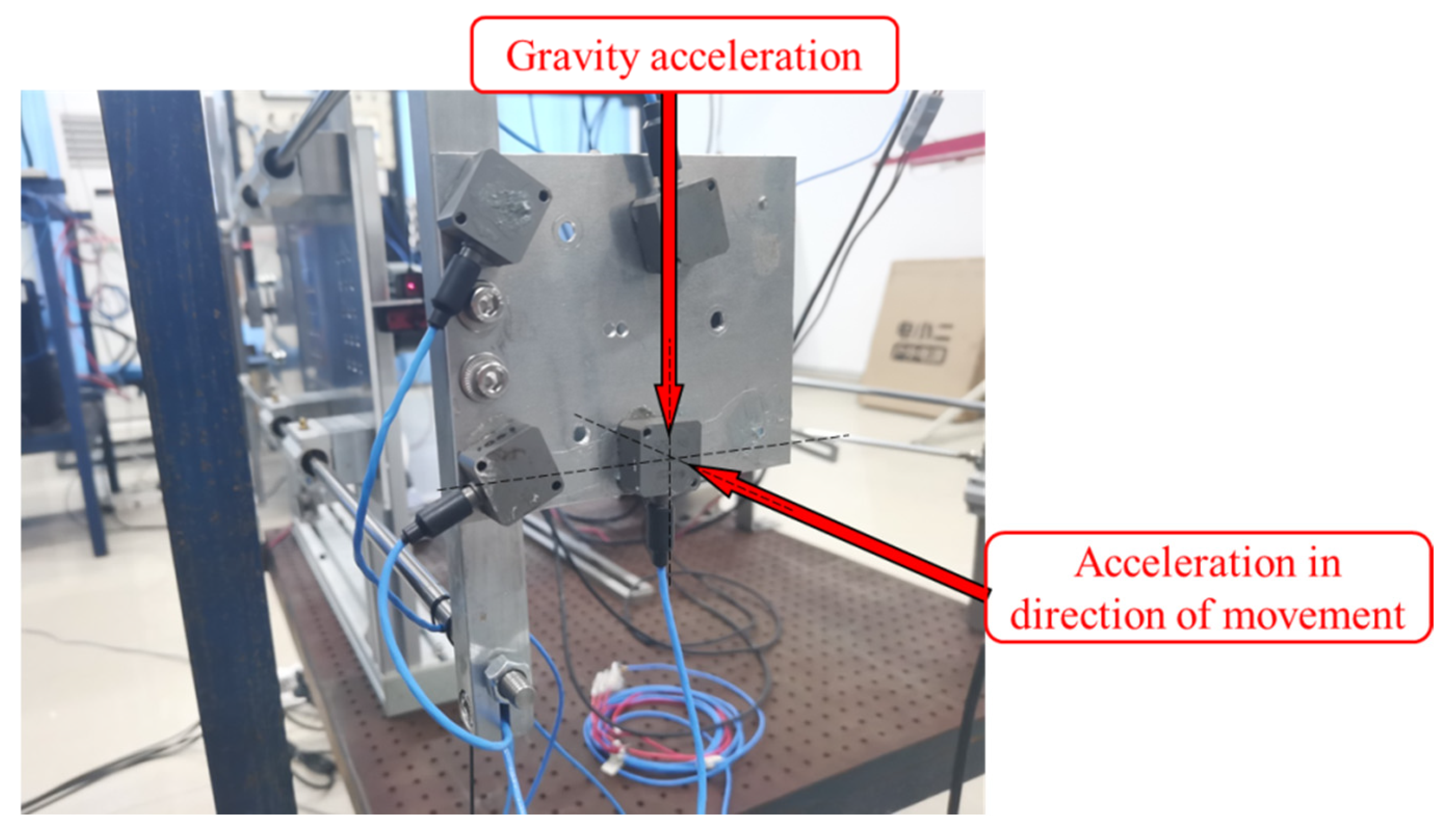
4.1. Horizontal Sine Motion Simulation Platform
4.2. Signal Acquisition System
4.3. Detailed Experimental Setup
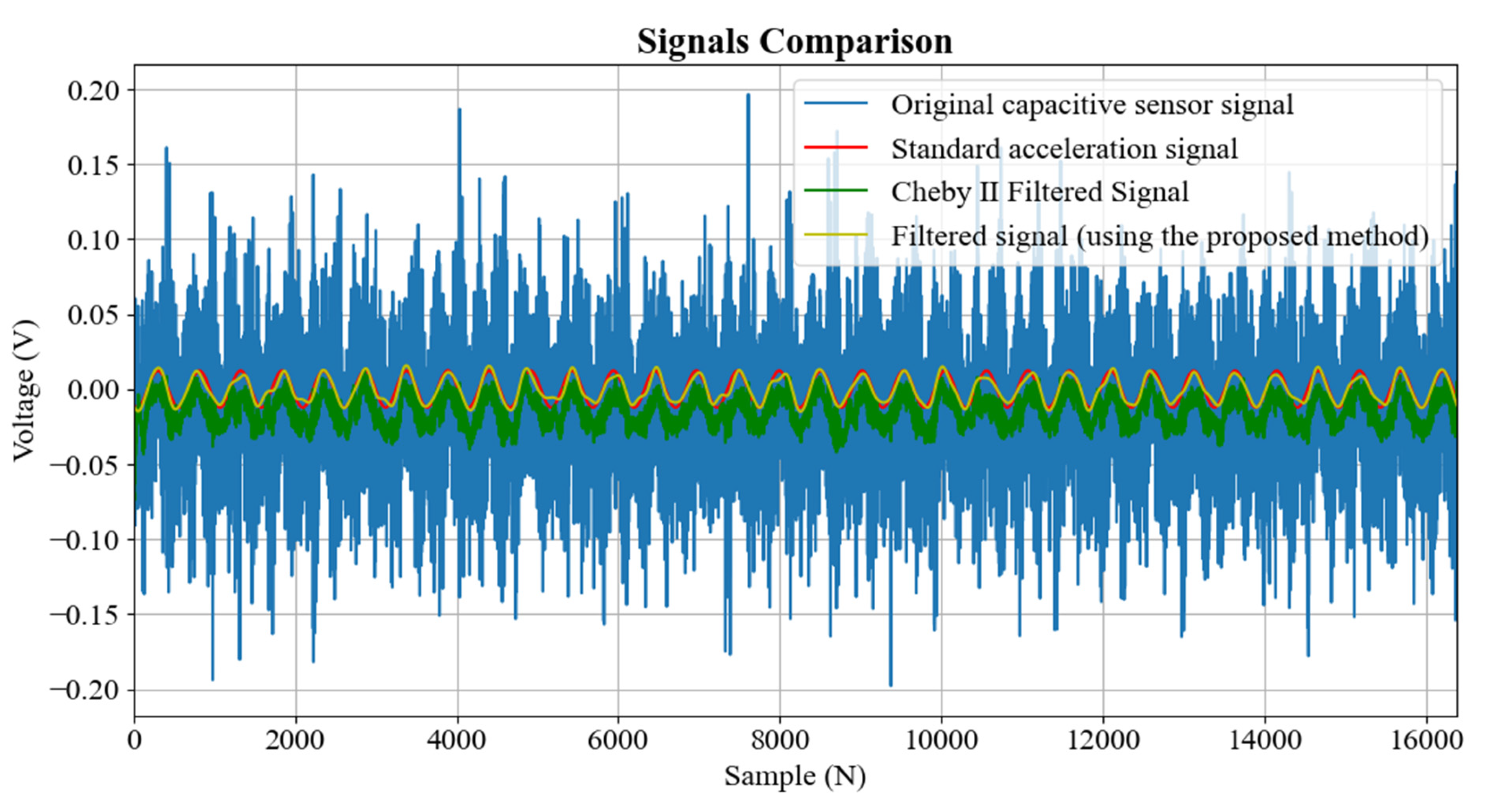
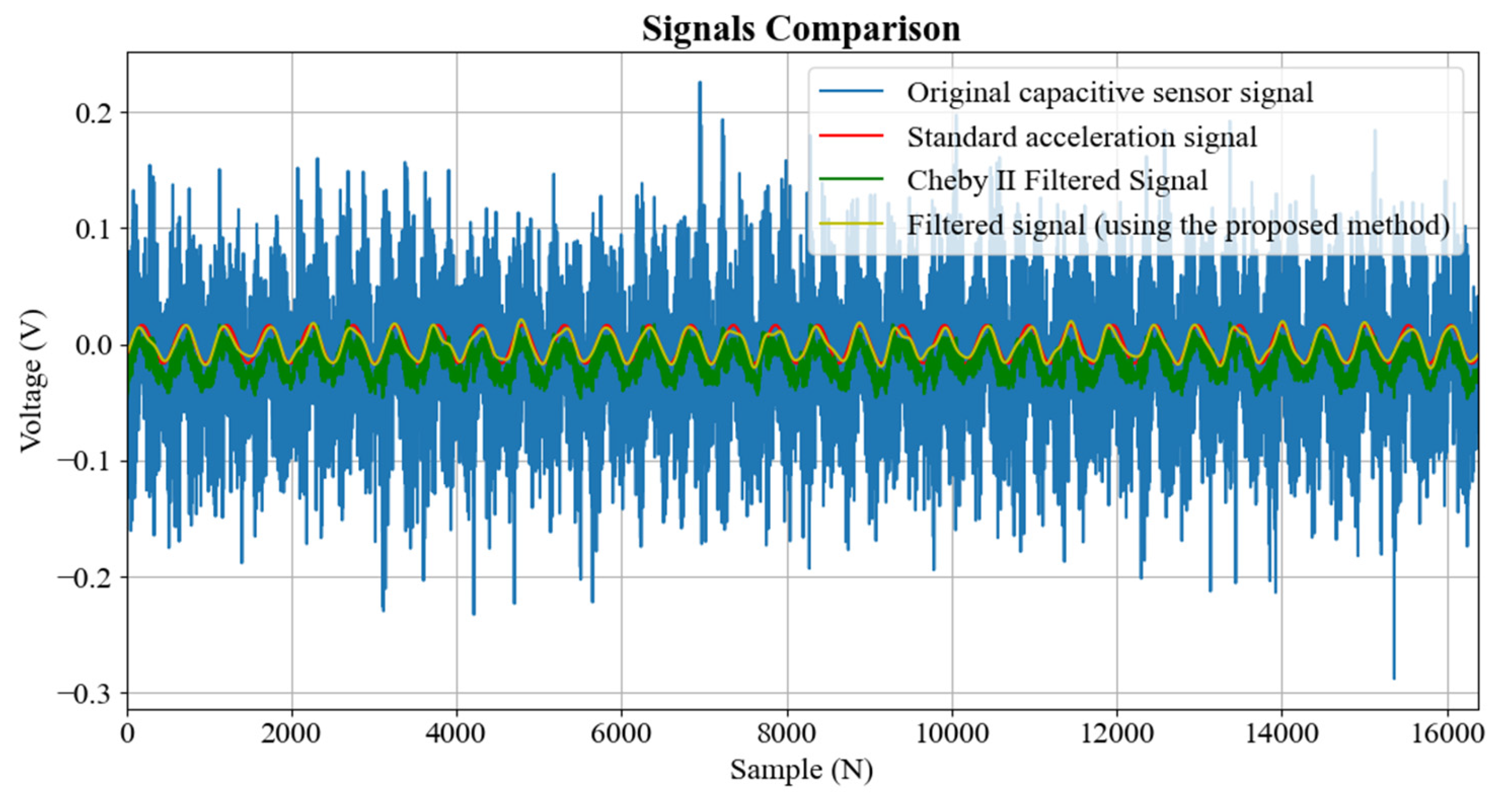
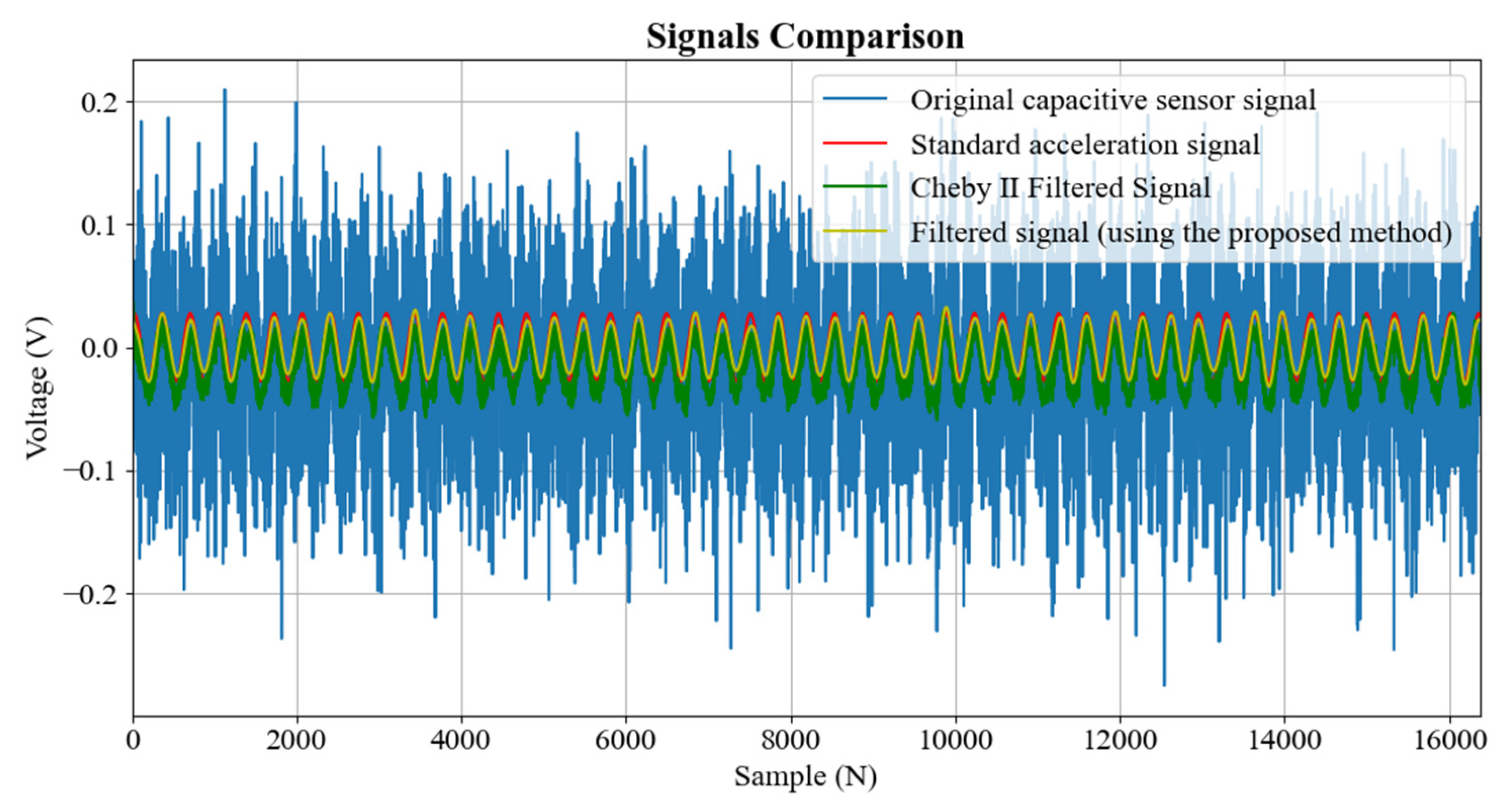
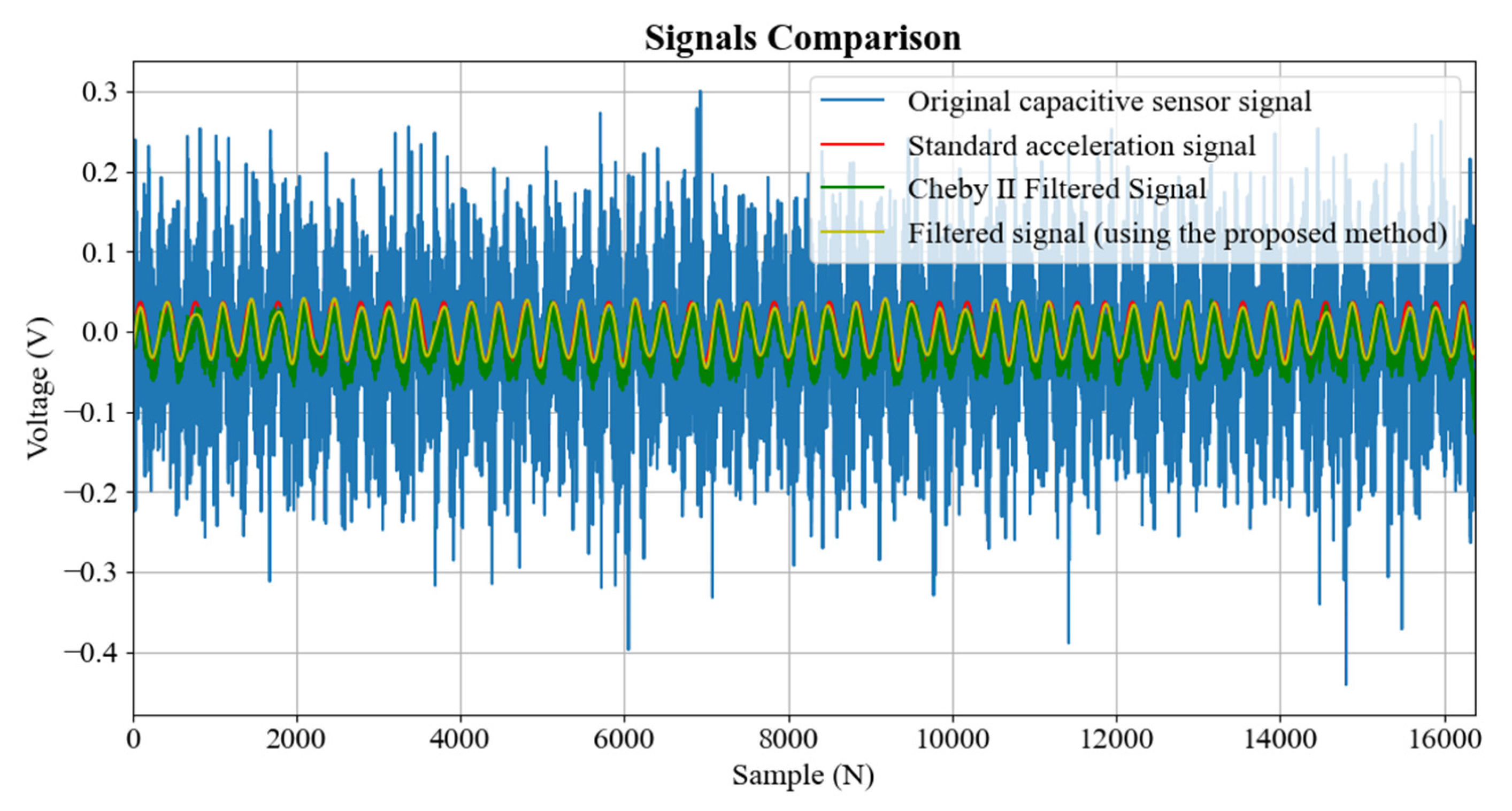
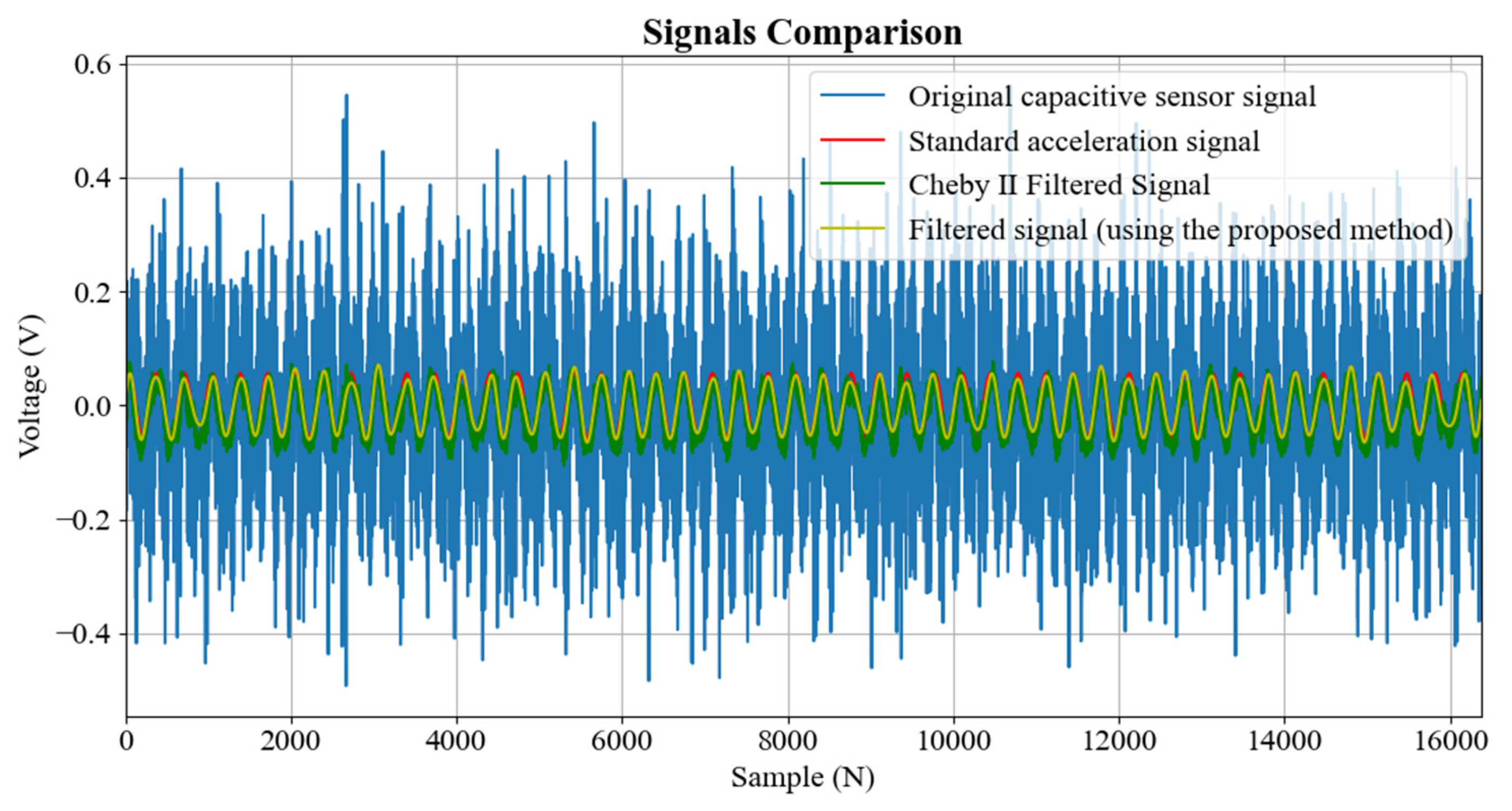
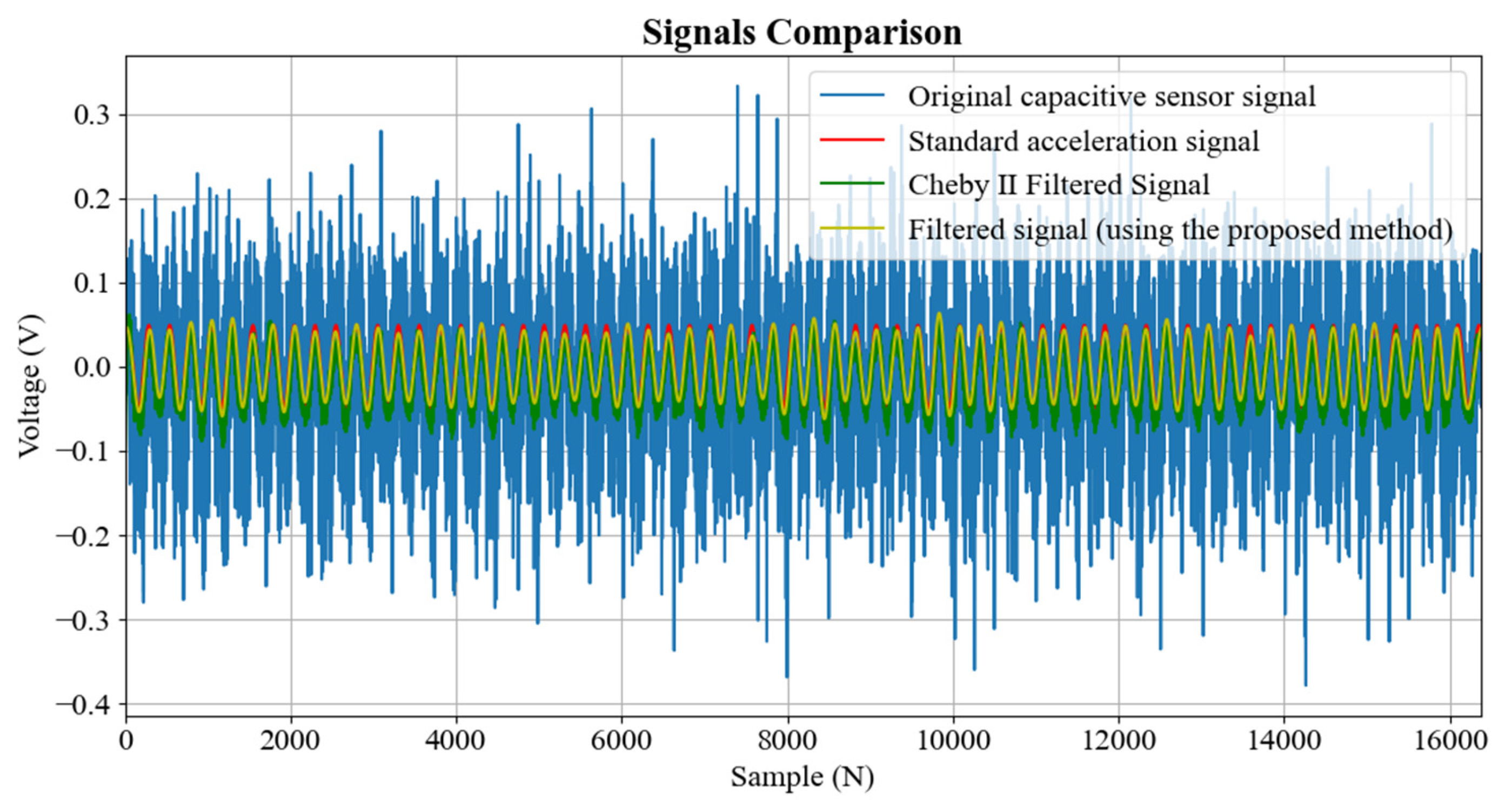
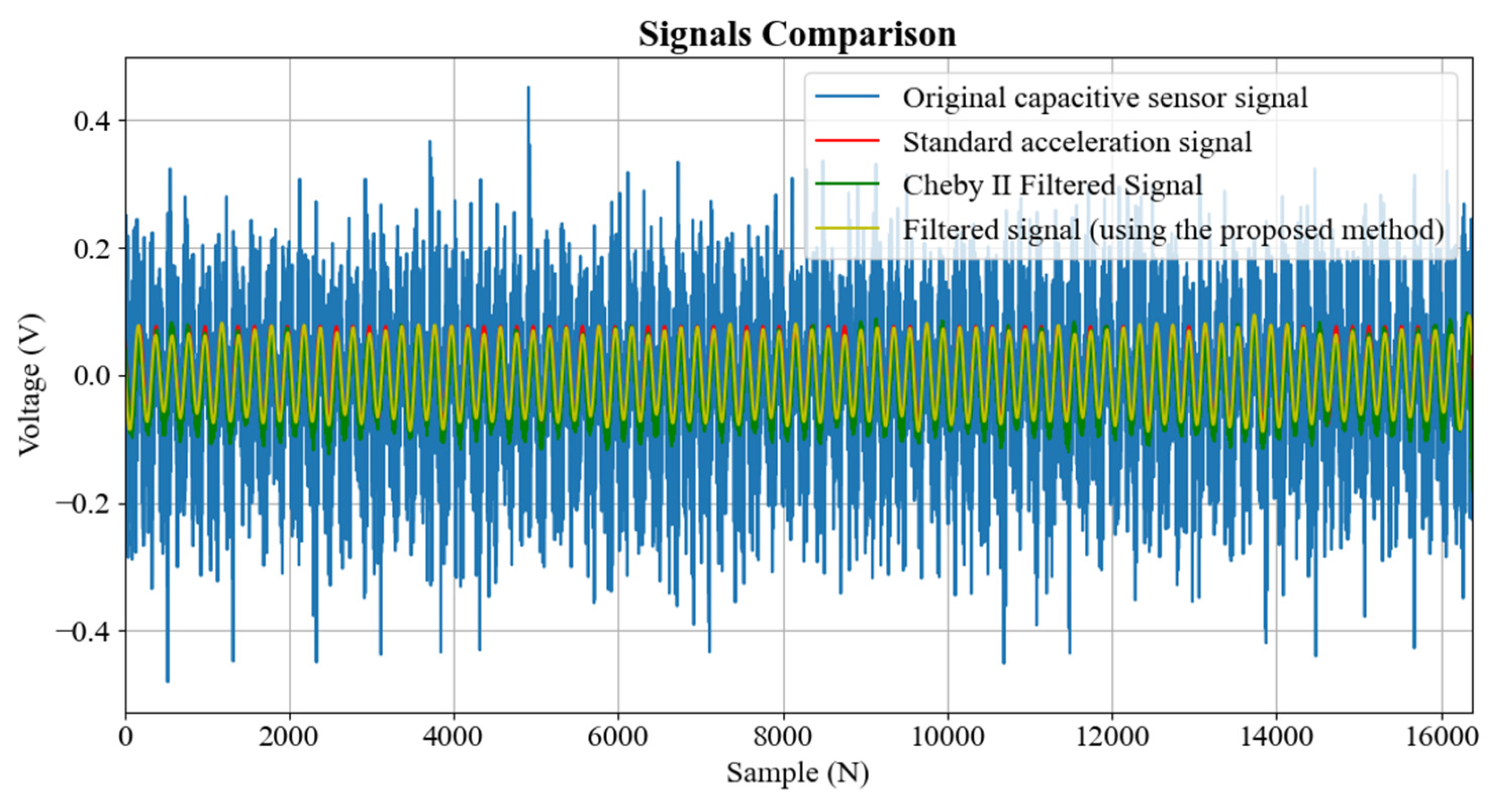
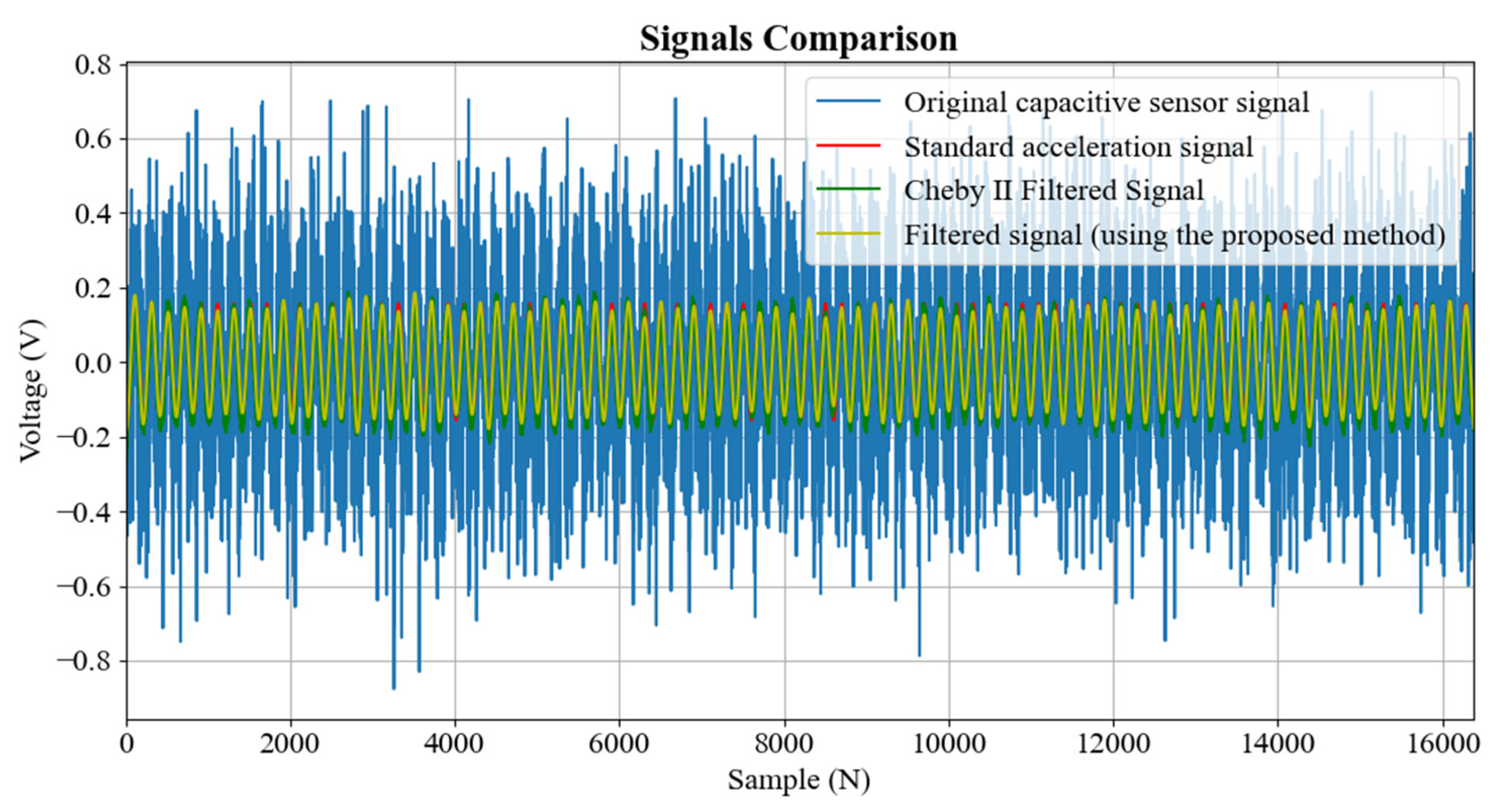
5. Results and Discussion
6. Conclusions
- (1)
- It can effectively process ultra-low frequency, small amplitude signals of 0.2 Hz–0.5 Hz and maintain high-precision acquisition under low sampling frequency conditions.
- (2)
- This method outperforms the traditional Chebyshev II filter in terms of filtering performance, mean square error (MSE) and correlation coefficient, especially in ultra-low frequency signals.
- (3)
- By using digital frequency domain filtering, the phase error and peak-to-peak error of the traditional filter are overcome, while the cost of analog-to-digital conversion is reduced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| P-M spectrum | Pierson–Moskowitz spectrum |
| PCI | Peripheral Component Interconnect |
| FFT | Fast Fourier Transform |
| DFT | Discrete Fourier Transform |
| TCP | Transmission Control Protocol |
| MSE | Mean Squared Error |
References
- Han, C.; Hu, X. An Absolute Displacement Measurement Method and Its Application in Ship Motion Measurement. J. Mar. Sci. Eng. 2023, 11, 931. [Google Scholar] [CrossRef]
- Han, C.; Hu, X.; Sun, D. The Influence of Ship Roll and Pitch on Absolute Measurement of Ship Heave Signals and Its Correction Method. Ocean Eng. 2025, 322, 120468. [Google Scholar] [CrossRef]
- Sawane, M.; Prasad, M. MEMS Piezoelectric Sensor for Self-Powered Devices: A Review. Mater. Sci. Semicond. Process. 2023, 158, 107324. [Google Scholar] [CrossRef]
- Preeti, M.; Guha, K.; Baishnab, K.L.; Sastry, A. Design and Analysis of a Capacitive MEMS Accelerometer as a Wearable Sensor in Identifying Low-Frequency Vibration Profiles. In Modern Techniques in Biosensors: Detection Methods and Commercial Aspects; Springer: Singapore, 2021; pp. 37–61. [Google Scholar]
- Singh, S.K.; Banerjee, B.P.; Lato, M.J.; Sammut, C.; Raval, S. Automated Rock Mass Discontinuity Set Characterisation Using Amplitude and Phase Decomposition of Point Cloud Data. Int. J. Rock Mech. Min. Sci. 2022, 152, 105072. [Google Scholar] [CrossRef]
- Liu, F.; Gao, S.; Chang, S. Displacement Estimation from Measured Acceleration for Fixed Offshore Structures. Appl. Ocean Res. 2021, 113, 102741. [Google Scholar] [CrossRef]
- Rahimi, H.; Nikkhah, A.A.; Hooshmandi, K. A Fast Alignment of Marine Strapdown Inertial Navigation System Based on Adaptive Unscented Kalman Filter. Trans. Inst. Meas. Control 2021, 43, 749–758. [Google Scholar] [CrossRef]
- Teodoro, M.F.; Pereira, C.; Henriques, P.; Canas, A. Prediction of Ship Movement Using a Kalman Filter Algorithm. Adv. Sci. Technol. 2024, 144, 93–100. [Google Scholar] [CrossRef]
- Song, K.-S.; Kim, S.-M.; Kwak, M.K.; Zhu, W. Development of a Control Algorithm for Active Control of Rolling Motion of a Ship Using a Gyrostabilizer. Ocean Eng. 2023, 280, 114669. [Google Scholar] [CrossRef]
- Majidiyan, H.; Enshaei, H.; Howe, D. Augmented Adaptive Filter for Real-Time Sea State Estimation Using Vessel Motions through Deep Learning. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Melbourne, Australia, 11–15 June 2023; American Society of Mechanical Engineers: New York, NY, USA, 2023; Volume 86878, p. V005T06A069. [Google Scholar]
- Jakovlev, S.; Eglynas, T.; Voznak, M.; Jusis, M.; Partila, P.; Tovarek, J.; Jankunas, V. Detecting Shipping Container Impacts with Vertical Cell Guides inside Container Ships during Handling Operations. Sensors 2022, 22, 2752. [Google Scholar] [CrossRef] [PubMed]
- Bossau, J.C.; Bekker, A. Line Detection Techniques to Pinpoint Slamming Impulses in Time-Frequency Images of Hull Acceleration Measurements. Ocean Eng. 2022, 249, 110841. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Han, B.; Liu, W.; Montewka, J.; Liu, R.W. Orientation-aware ship detection via a rotation feature decoupling supported deep learning approach. Eng. Appl. Artif. Intell. 2023, 125, 106686. [Google Scholar] [CrossRef]
- Guo, R.; Xiao, G.; Zhang, C.; Li, Q. A study on influencing factors of port cargo throughput based on multi-scale geographically weighted regression. Front. Mar. Sci. 2025, 12, 1637660. [Google Scholar] [CrossRef]
- Xiao, G.; Amamoo-Otoo, C.; Wang, T.; Li, Q.; Biancardo, S.A. Evaluating the impact of ECA policy on sulfur emissions from the five busiest ports in America based on difference in difference model. Front. Mar. Sci. 2025, 12, 1609261. [Google Scholar] [CrossRef]
- Fossen, T.I. Line-of-Sight Path-Following Control Utilizing an Extended Kalman Filter for Estimation of Speed and Course over Ground from GNSS Positions. J. Mar. Sci. Technol. 2022, 27, 806–813. [Google Scholar] [CrossRef]
- Han, C.; Hu, X. A Prediction Method of Ship Motion Based on LSTM Neural Network with Variable Step-Variable Sampling Frequency Characteristics. J. Mar. Sci. Eng. 2023, 11, 919. [Google Scholar] [CrossRef]
- Han, H.; Jeon, S.; Kim, Y.; Lee, C.; Lee, D.; Lee, G.; Lee, S. Monitoring of the Cavitation Inception Speed and Sound Pressure Level of the Model Propeller Using Accelerometer Attached to the Model Ship in the Cavitation Tunnel. Ocean Eng. 2022, 266, 112906. [Google Scholar] [CrossRef]
- Jakovlev, S.; Voznak, M. Auto-Encoder-Enabled Anomaly Detection in Acceleration Data: Use Case Study in Container Handling Operations. Machines 2022, 10, 734. [Google Scholar] [CrossRef]
- Murgano, E.; Caponetto, R.; Pappalardo, G.; Cafiso, S.D.; Severino, A. A Novel Acceleration Signal Processing Procedure for Cycling Safety Assessment. Sensors 2021, 21, 4183. [Google Scholar] [CrossRef]
- Ma, Q.; Cui, M.; Li, F.; Zhou, L.; Ding, S. Towards Automatic Identification of Ship-Ice Contact Using Acceleration Measurement. Ocean Eng. 2024, 306, 118038. [Google Scholar] [CrossRef]
- Pierson, W.J., Jr.; Moskowitz, L. A Proposed Spectral Form for Fully Developed Wind Seas Based on the Similarity Theory of SA Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Park, M.-H.; Yeo, S.; Choi, J.-H.; Lee, W.-J. Review of noise and vibration reduction technologies in marine machinery: Operational insights and engineering experience. Appl. Ocean Res. 2024, 152, 104195. [Google Scholar] [CrossRef]
- Ning, X.; Zhao, J.; Xu, J. The Heave Motion Estimation for Active Heave Compensation System in Offshore Crane. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016; IEEE: New York, NY, USA, 2016; pp. 1327–1332. [Google Scholar]
- Hu, Y.; Tao, L. Real-Time Zero Phase Filtering for Heave Measurement. In Proceedings of the 2013 IEEE 11th International Conference on Electronic Measurement & Instruments, Harbin, China, 16–19 August 2013; IEEE: New York, NY, USA, 2013; Volume 1, pp. 321–326. [Google Scholar]
- Ben, Y.; Gao, Q.; Wei, T.; Gong, S.; Li, Q. Real-Time Heave Motion Measurement by Adaptive Band-Pass Filter Based on Strapdown INS. Ocean Eng. 2022, 262, 112278. [Google Scholar] [CrossRef]






| Performance | English | SI |
|---|---|---|
| Sensitivity (±5%) | 1000 mV/g | 101.9 mV/(m/s2) |
| Measurement Range | ±2 g pk | +19.6 m/s2 pk |
| Frequency Range (±5%) | 0 to 250 Hz | 0 to 250 Hz |
| Frequency Range (+10%) | 0 to 350 Hz | 0 to 350 Hz |
| Resonant Frequency | ≥1.3 kHz | ≥1.3 kHz |
| Phase Response (10 Hz) | <2.5° | <2.5° |
| Broadband Resolution (0.5 to 100 Hz) | 0.25 mg rms | 0.0025 m/s2 rms |
| Non-Linearity | ≤1% | ≤1% |
| Transverse Sensitivity | ≤3% | ≤3% |
| Motion Parameters | Range |
|---|---|
| Amplitude A | [±50 mm, ±150 mm] |
| Reciprocating frequency f | [0.05 Hz, 1 Hz] |
| Equipment | Purpose |
|---|---|
| sine motion platform | Simulate the heave motion of ships |
| acceleration sensor | Measuring acceleration signals |
| ART data acquisition module | Analog-to-digital conversion |
| 24 V DC power | Power supply for acquisition module |
| Wireless router | Digital signal wirelessly transmitted |
| Frequency / Amplitude | Filtered Signal (Using Chebyshev II) | Filtered Signal (Using the Proposed Method) | ||
|---|---|---|---|---|
| MSE | Correlation Coefficient | MSE | Correlation Coefficient | |
| 0.2 Hz/±75 mm | 0.00024012 | 0.80365028 | 0.00000646 | 0.95607133 |
| 0.2 Hz/±100 mm | 0.00410815 | 0.83907569 | 0.00386112 | 0.96365433 |
| 0.2 Hz/±150 mm | 0.00922387 | 0.82917477 | 0.00895778 | 0.95203325 |
| 0.3 Hz/±75 mm | 0.00027744 | 0.92173587 | 0.00001544 | 0.98315985 |
| 0.3 Hz/±100 mm | 0.00033731 | 0.90836091 | 0.00003594 | 0.97360001 |
| 0.3 Hz/±150 mm | 0.00046533 | 0.90699737 | 0.00007744 | 0.97523929 |
| 0.4 Hz/±75 mm | 0.00037730 | 0.93607822 | 0.00004478 | 0.98169825 |
| 0.4 Hz/±100 mm | 0.00045627 | 0.94400958 | 0.00007990 | 0.98140774 |
| 0.4 Hz/±150 mm | 0.00066728 | 0.94856887 | 0.00017795 | 0.98232436 |
| 0.5 Hz/±75 mm | 0.00041660 | 0.96536633 | 0.00011006 | 0.98145660 |
| 0.5 Hz/±100 mm | 0.00058184 | 0.96532077 | 0.00024993 | 0.97599686 |
| 0.5 Hz/±150 mm | 0.00083354 | 0.97082588 | 0.00025992 | 0.98946692 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Hu, X.; Han, C.; Chen, X. A Low-Frequency Component Filtering Method for Heave Acceleration Signal of Marine Ship. J. Mar. Sci. Eng. 2025, 13, 1919. https://doi.org/10.3390/jmse13101919
Sun D, Hu X, Han C, Chen X. A Low-Frequency Component Filtering Method for Heave Acceleration Signal of Marine Ship. Journal of Marine Science and Engineering. 2025; 13(10):1919. https://doi.org/10.3390/jmse13101919
Chicago/Turabian StyleSun, Dejian, Xiong Hu, Chongyang Han, and Xinqiang Chen. 2025. "A Low-Frequency Component Filtering Method for Heave Acceleration Signal of Marine Ship" Journal of Marine Science and Engineering 13, no. 10: 1919. https://doi.org/10.3390/jmse13101919
APA StyleSun, D., Hu, X., Han, C., & Chen, X. (2025). A Low-Frequency Component Filtering Method for Heave Acceleration Signal of Marine Ship. Journal of Marine Science and Engineering, 13(10), 1919. https://doi.org/10.3390/jmse13101919







