A Pipeline Hoop Stress Measurement Method Based on Propagation Path Correction of LCR Waves
Abstract
1. Introduction
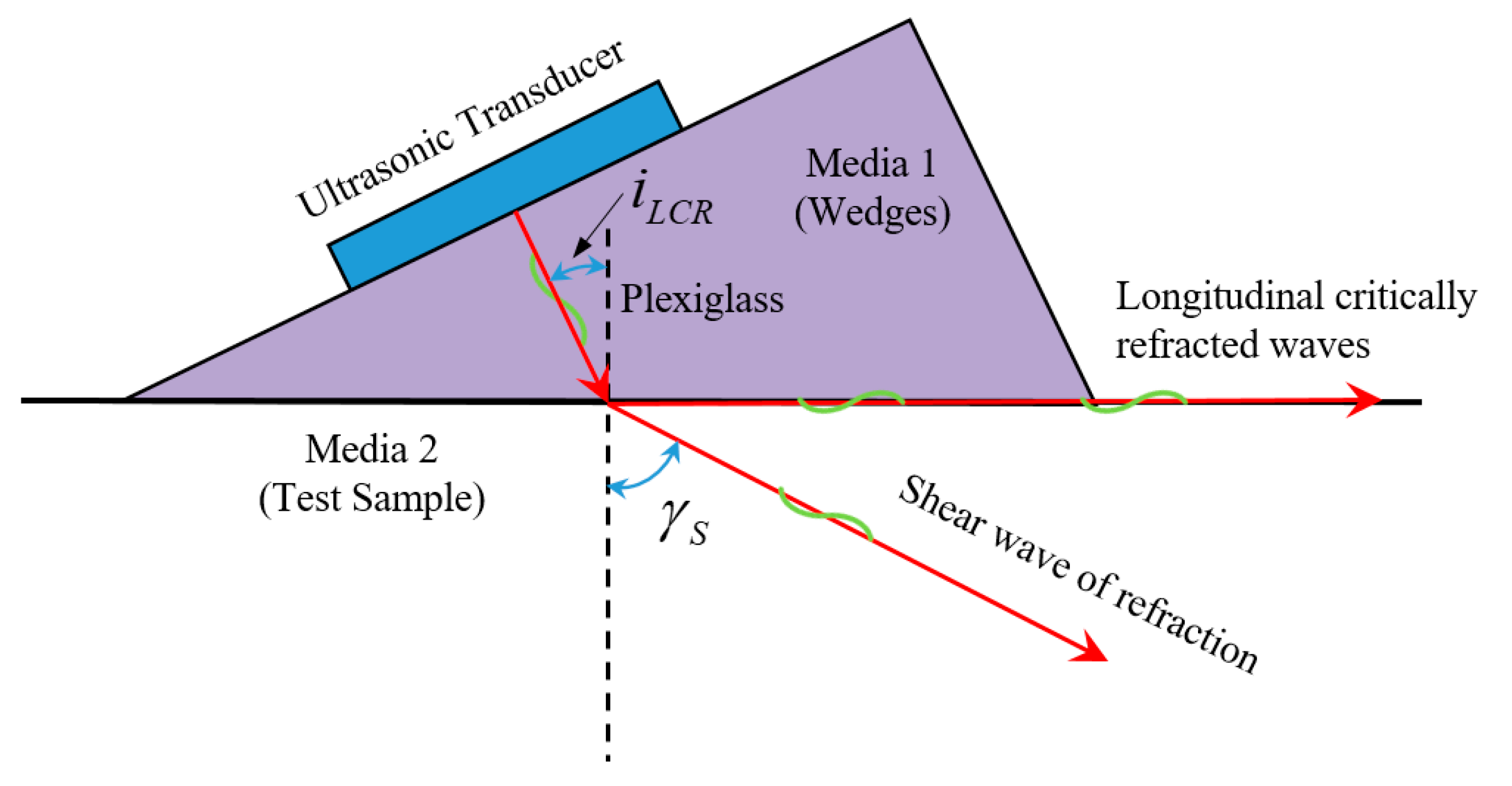
2. Measurement Theory
3. Simulation Analysis
4. Model Building
5. Experimental Setup
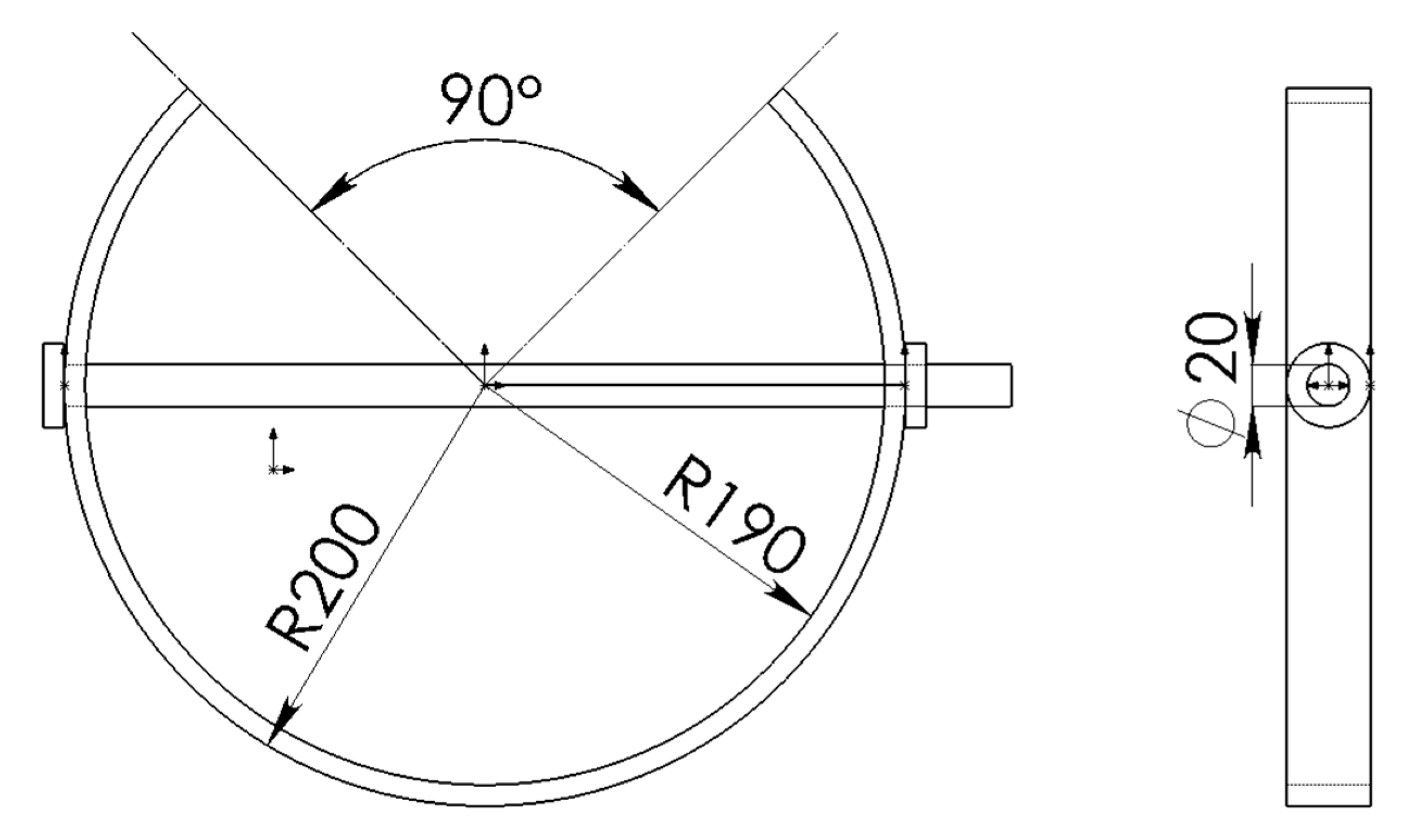
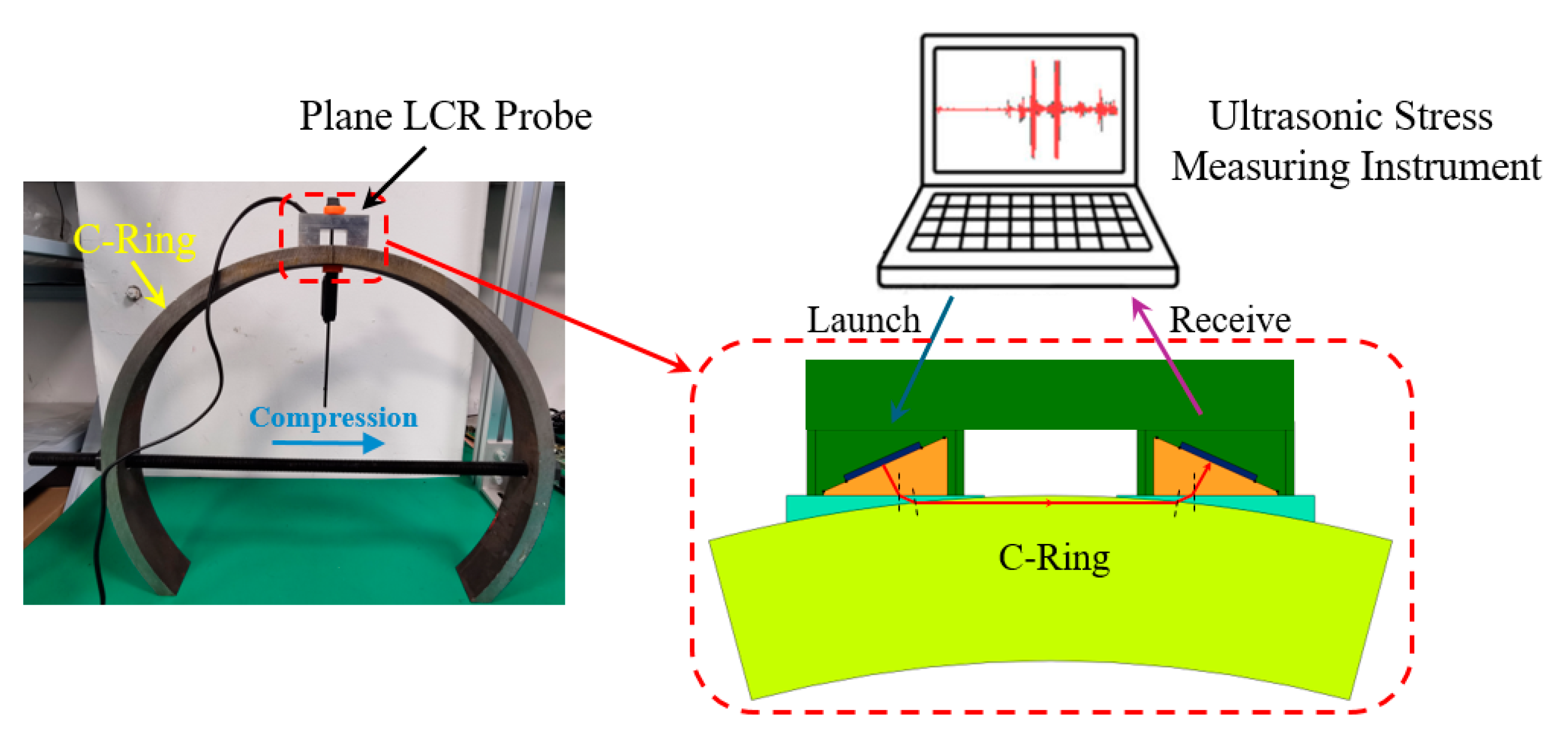
5.1. C-Ring Device
5.2. C-Ring Hoop Stress Correction
6. Results and Discussion
6.1. C-Ring Measurement
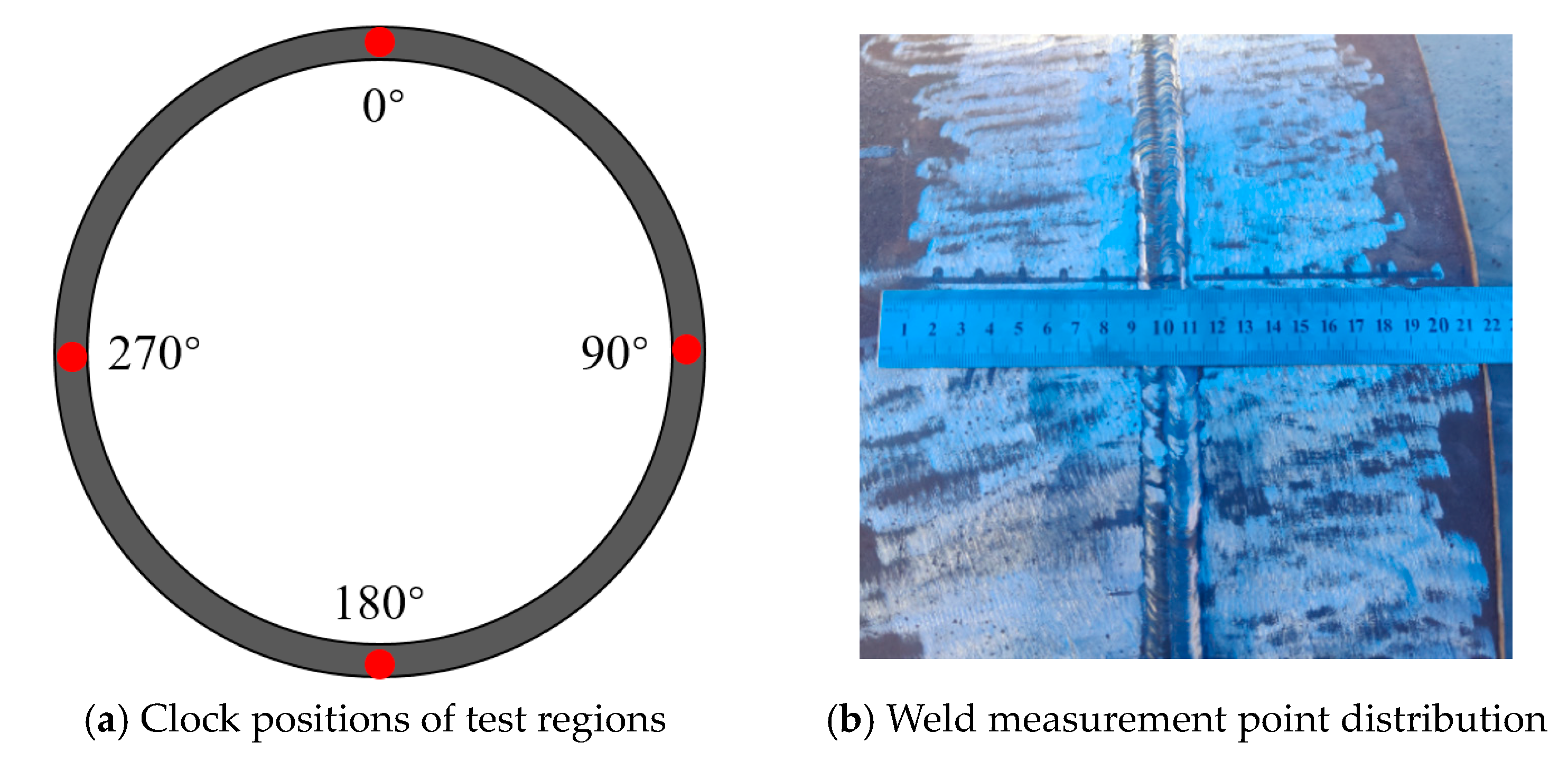
6.2. Case Study
7. Conclusions
- (1)
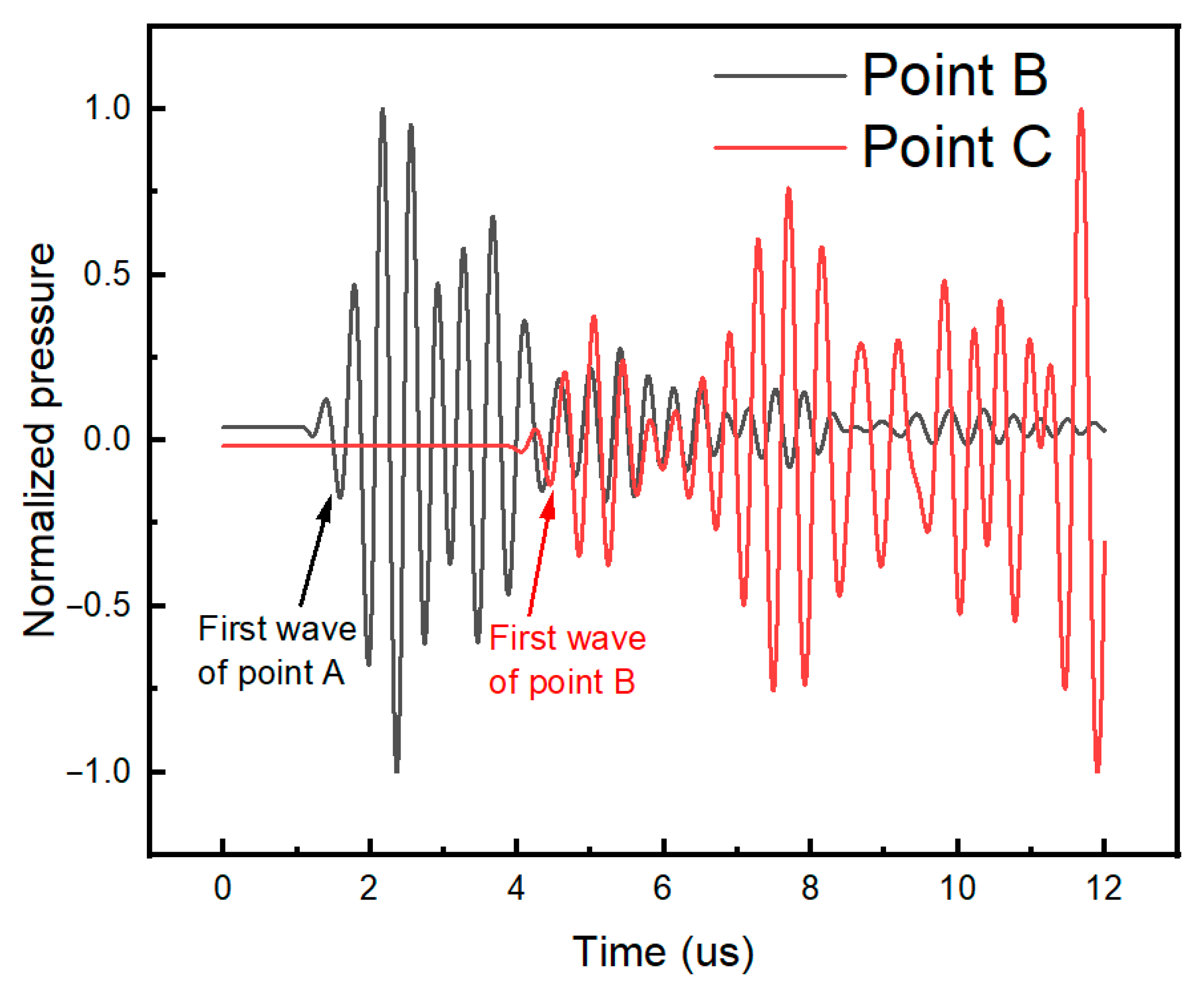
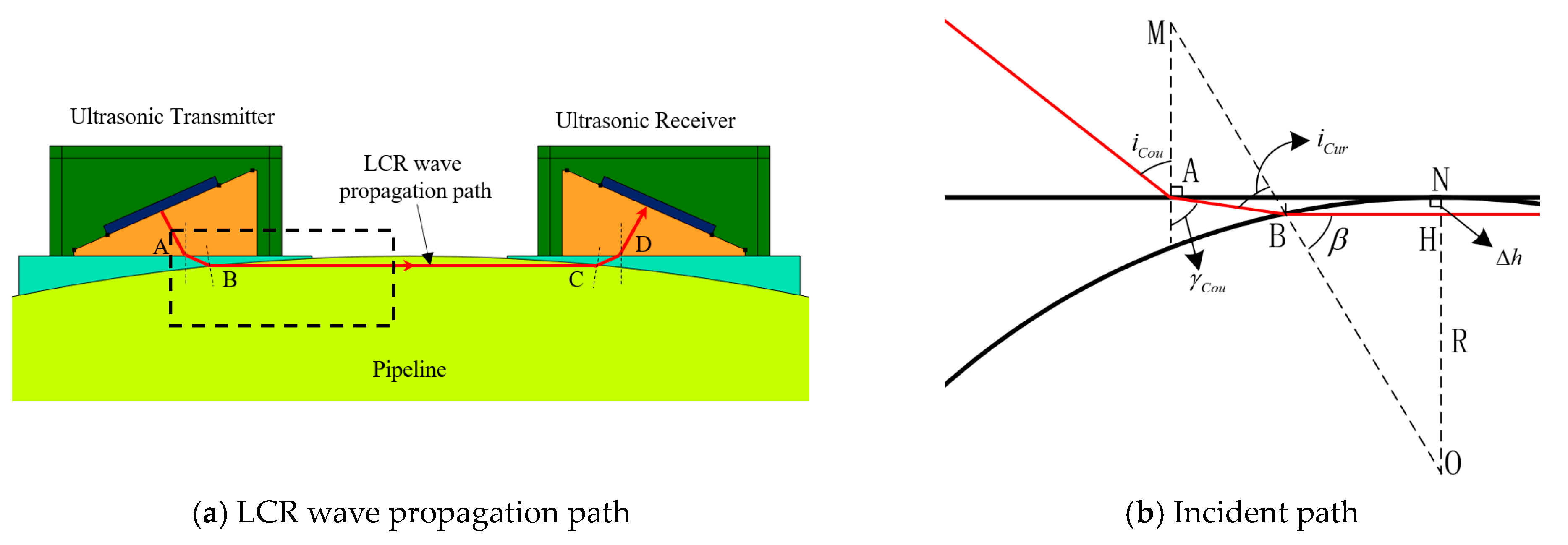
- Ultrasonic waves propagated in the near-field region within the wedge and exhibited quasi-plane wave characteristics without diffusion. After oblique incidence through the coupling layer into the pipeline, the LCR wave propagated along the chordal direction.
- (2)
- Based on the ray tracing method, a mapping relationship between the geometric structure of the pipeline and the ultrasonic propagation path was established. A correction algorithm for pipeline hoop stress measurement, referred to as the LCR-HS method, was developed.
- (3)
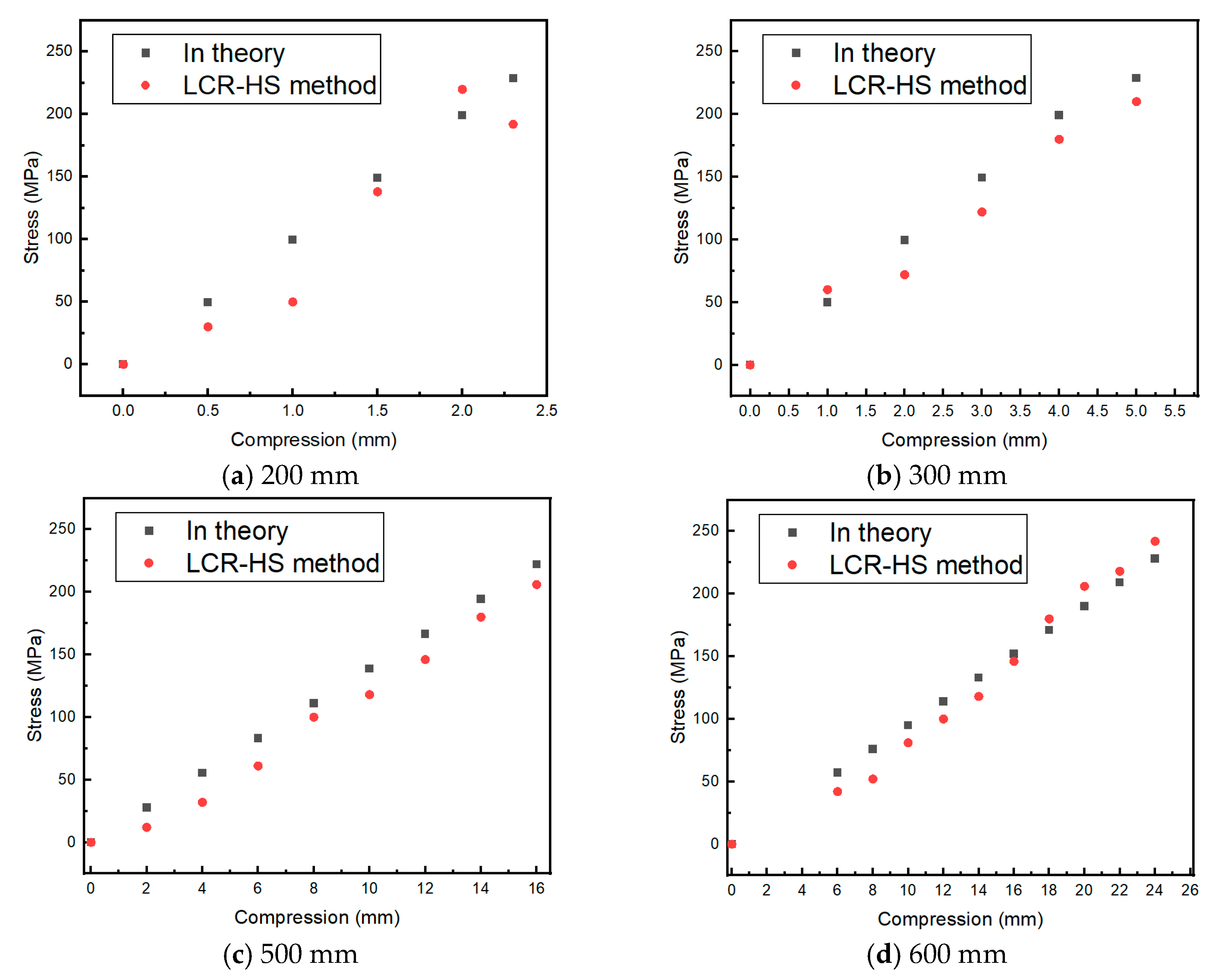
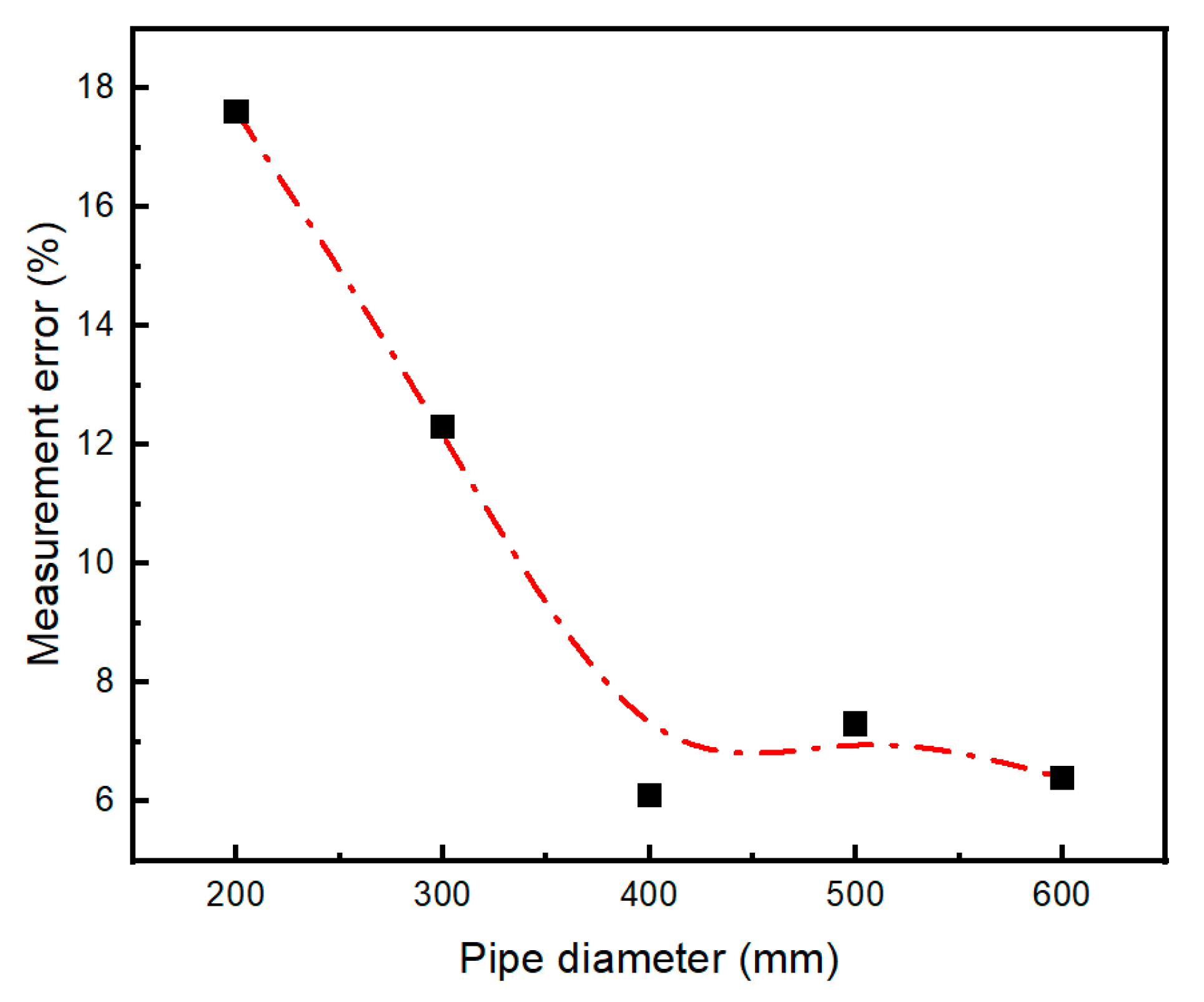
- Validation experiments using C-rings demonstrated that the measurement error decreased with increasing pipe diameter. When the diameter exceeds 338 mm, the error falls below 10%, and when it exceeds 400 mm, the error drops below 8% and gradually stabilized. Furthermore, a case study was conducted using the proposed method. Hoop stresses at the pipeline girth welds were obtained through both measurement and simulation, and the experimental results showed good agreement with the simulated data. The effectiveness and practicality of the proposed method were thus validated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Q.; Song, Y.; Zhang, X.; Dong, L.; Xi, Y.; Zeng, D.; Liu, Q.; Zhang, H.; Zhang, Z.; Yan, R.; et al. Evolution of corrosion prediction models for oil and gas pipelines: From empirical-driven to data-driven. Eng. Fail. Anal. 2023, 146, 107097. [Google Scholar] [CrossRef]
- Wasim, M.; Djukic, M.B. External corrosion of oil and gas pipelines: A review of failure mechanisms and predictive preventions. J. Nat. Gas Sci. Eng. 2022, 100, 104467. [Google Scholar] [CrossRef]
- Mondal, B.C.; Dhar, A.S. Burst pressure of corroded pipelines considering combined axial forces and bending moments. Eng. Struct. 2019, 186, 43–51. [Google Scholar] [CrossRef]
- Ozkan, I.F.; Mohareb, M. Testing and analysis of steel pipes under bending, tension, and internal pressure. J. Struct. Eng. 2009, 135, 187–197. [Google Scholar] [CrossRef]
- Mirzaee-Sisan, A.; Wu, G. Residual stress in pipeline girth welds- a review of recent data and modelling. Int. J. Press. Vessel. Pip. 2019, 169, 142–152. [Google Scholar] [CrossRef]
- Sun, M.; Fang, H.; Wang, N.; Du, X.; Zhao, H.; Zhai, K.-J. Limit state equation and failure pressure prediction model of pipeline with complex loading. Nat. Commun. 2024, 15, 4473. [Google Scholar] [CrossRef]
- Sun, M.; Fang, H.; Du, X.; Wang, W.; Li, X. Study on evaluation method of failure pressure for pipeline with axially adjacent defects. China Ocean Eng. 2023, 37, 598–612. [Google Scholar] [CrossRef]
- Arumugam, T.; Kumar, S.D.V.; Karuppanan, S.; Ovinis, M. The influence of axial compressive stress and internal pressure on a pipeline network: A review. Appl. Sci. 2023, 13, 3799. [Google Scholar] [CrossRef]
- Gou, R.; Zhang, Y.; Xu, X.; Sun, L.; Yang, Y. Residual stress measurement of new and in-service X70 pipelines by X-ray diffraction method. NDT E Int. 2011, 44, 387–393. [Google Scholar] [CrossRef]
- Same, S.A.; Khan, K.; Smyth, N.A. Comparison between a predicted and an experimentally measured residual stress field generated by side-punching of API X65 steel. Int. J. Press. Vessel. Pip. 2023, 203, 104943. [Google Scholar] [CrossRef]
- Damjanović, D.; Kozak, D.; Milinović, A.; Stojšić, J. Estimation of residual stresses in pipe-ring specimens by incremental hole drilling and X-ray diffraction method. Exp. Tech. 2024, 48, 129–139. [Google Scholar] [CrossRef]
- Peng, W.; Jiang, W.; Sun, G.; Yang, B.; Shao, X.; Tu, S.-T. Biaxial residual stress measurement by indentation energy difference method: Theoretical and experimental study. Int. J. Press. Vessel. Pip. 2022, 195, 104573. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, H.; Yang, Y.; Wang, S.; Wang, Z.; Wu, J.; Yang, C. Nondestructive testing method of residual stresses in metallic materials based on knoop indentation technique. Nondestruct. Test. Eval. 2025, 40, 188–205. [Google Scholar] [CrossRef]
- Liu, B.; Tian, R.; Yu, H.; He, L.; Yang, L.; Wang, F.; Geng, H.; Tian, Y. Research on the characteristics of weak magnetic internal detection signals for critical damage in pipeline stress based on density functional theory. Eng. Fail. Anal. 2024, 159, 108145. [Google Scholar] [CrossRef]
- He, G.; He, T.; Liao, K.; Deng, S.; Chen, D. Experimental and numerical analysis of non-contact magnetic detecting signal of girth welds on steel pipelines. ISA Trans. 2022, 125, 681–698. [Google Scholar] [CrossRef]
- Huang, Z.; Li, J.; Wang, L.; Lei, L.; Huang, X.; Yin, Z. Welding residual stress analysis of the X80 pipeline: Simulation and validation. Mech. Sci. 2024, 15, 305–314. [Google Scholar] [CrossRef]
- Song, W.; Pan, Q.; Xu, C.; Li, X.; Jin, X.; Li, H.; Liu, S. Residual stress nondestructive testing for pipe component based on ultrasonic method. In Proceedings of the 2014 IEEE Far East Forum on Nondestructive Evaluation/Testing, Chengdu, China, 20–23 June 2014; pp. 163–167. [Google Scholar] [CrossRef]
- Luo, C.; Chen, B.; Xia, L.; Xu, L.; Liu, X.; Zou, S.; Peng, D.; Gou, G. Residual stress measurement using EMAT for X80 pipeline steel: Effects of coating thickness and surface roughness under low surface preparation requirements. Materials 2024, 17, 5799. [Google Scholar] [CrossRef]
- Zhu, Z.; Gou, G.; Zhang, Z.; Ma, C.; Gao, W. Evaluate welding residual of 6082-T6 aluminum alloy welded plate by using ultrasonic method. Int. J. Mod. Phys. B 2019, 33, 1940038. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, J.; Gou, G.; Chen, H.; Li, P.; Gao, W. Residual stress measurement and calibration for A7N01 aluminum alloy welded joints by using longitudinal critically refracted (LCR) wave transmission method. J. Mater. Eng. Perform. 2016, 25, 4181–4189. [Google Scholar] [CrossRef]
- Guo, M.; Gou, G.; Chen, B.; Qiu, F.; Zhu, Z.; Jin, J.; Wu, X.; Gao, W.; Sun, S. Ultrasonic correction measurement for residual stress in 5083 aluminum alloy welded component of high-speed train. Metals 2023, 13, 137. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, J.; Gou, G.; Chen, H.; Li, P. Ameliorated longitudinal critically refracted—Attenuation velocity method for welding residual stress measurement. J. Mater. Process. Technol. 2017, 246, 267–275. [Google Scholar] [CrossRef]
- Gonçalves, V.V.; dos Santos, A.A., Jr. Effect of non-uniformity on time-of-flight measurement of critically refracted longitudinal waves for stress evaluations of carbon composite materials. Exp. Tech. 2022, 46, 1–15. [Google Scholar] [CrossRef]
- Liu, E.; Liu, Y.; Tan, J.; Gu, W.; Zheng, J.; Deng, S. Ultrasonic measurement method for three-dimensional assembly stress of aero-engine rotors. Mech. Syst. Signal Process. 2025, 222, 111796. [Google Scholar] [CrossRef]
- Li, P.; Xu, C.; Pan, Q.; Lu, Y.; Li, S. Denoising of LCR wave signal of residual stress for rail surface based on lifting scheme wavelet packet transform. Coatings 2021, 11, 496. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Z.; Qiao, M.; Ding, W.; Su, H. A depth gradient residual stress measurement method based on energy attenuation of LCR waves. IEEE Trans. Instrum. Meas. 2025, 74, 6003209. [Google Scholar] [CrossRef]
- Sun, L.; Shi, W.; Tian, X.; Li, J.; Zhao, B.; Wang, S.; Tan, J. A plane stress measurement method for CFRP material based on array LCR waves. NDT E Int. 2025, 151, 103318. [Google Scholar] [CrossRef]
- Javadi, Y.; Hloch, S. Evaluation of hoop residual stress variations in the thickness of dissimilar welded pipes by using the LCR ultrasonic waves. Teh. Vjesn. 2016, 23, 329–335. [Google Scholar] [CrossRef]
- Li, Y.; Li, S.; Zhou, Y.; Wan, W.; Guo, H.; Zhou, S.; Sun, L. Research on method for measuring two-dimensional stress in curved surface components using ultrasonic LCR waves. In Proceedings of the 2024 18th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Dongguan, China, 8–11 November 2024; pp. 405–409. [Google Scholar] [CrossRef]
- Egle, D.M.; Bray, D.E. Measurement of acoustoelastic and third-order elastic constants for rail steel. J. Acoust. Soc. Am. 1976, 60, 741–744. [Google Scholar] [CrossRef]
- ANSI/NACE TM0177-2016; Laboratory Testing of Metals for Resistance to Sulfide Stress Cracking and Stress Corrosion Cracking in H2S Environments. ANSI: Washington, DC, USA, 2016.
- Perić, M.; Garašić, I.; Gubeljak, N.; Tonković, Z.; Nižetić, S.; Osman, K. Numerical simulation and experimental measurement of residual stresses in a thick-walled buried-arc welded pipe structure. Metals 2022, 12, 1102. [Google Scholar] [CrossRef]
- Deng, D.; Kiyoshima, S. FEM prediction of welding residual stresses in a SUS304 girth-welded pipe with emphasis on stress distribution near weld start/end location. Comput. Mater. Sci. 2010, 50, 612–621. [Google Scholar] [CrossRef]
- Akbari, D.; Sattari-Far, I. Effect of the welding heat input on residual stresses in butt-welds of dissimilar pipe joints. Int. J. Press. Vessel. Pip. 2009, 86, 769–776. [Google Scholar] [CrossRef]


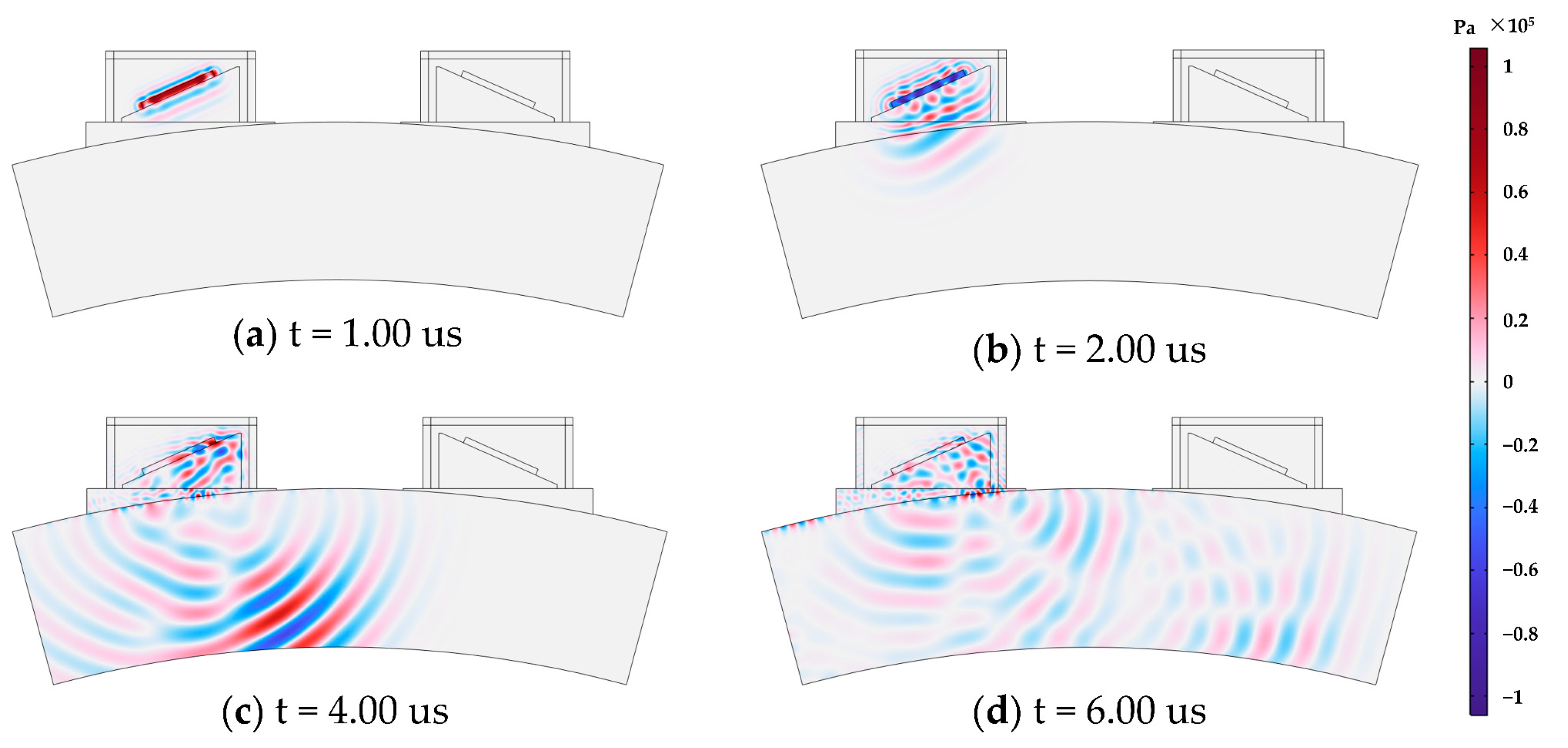
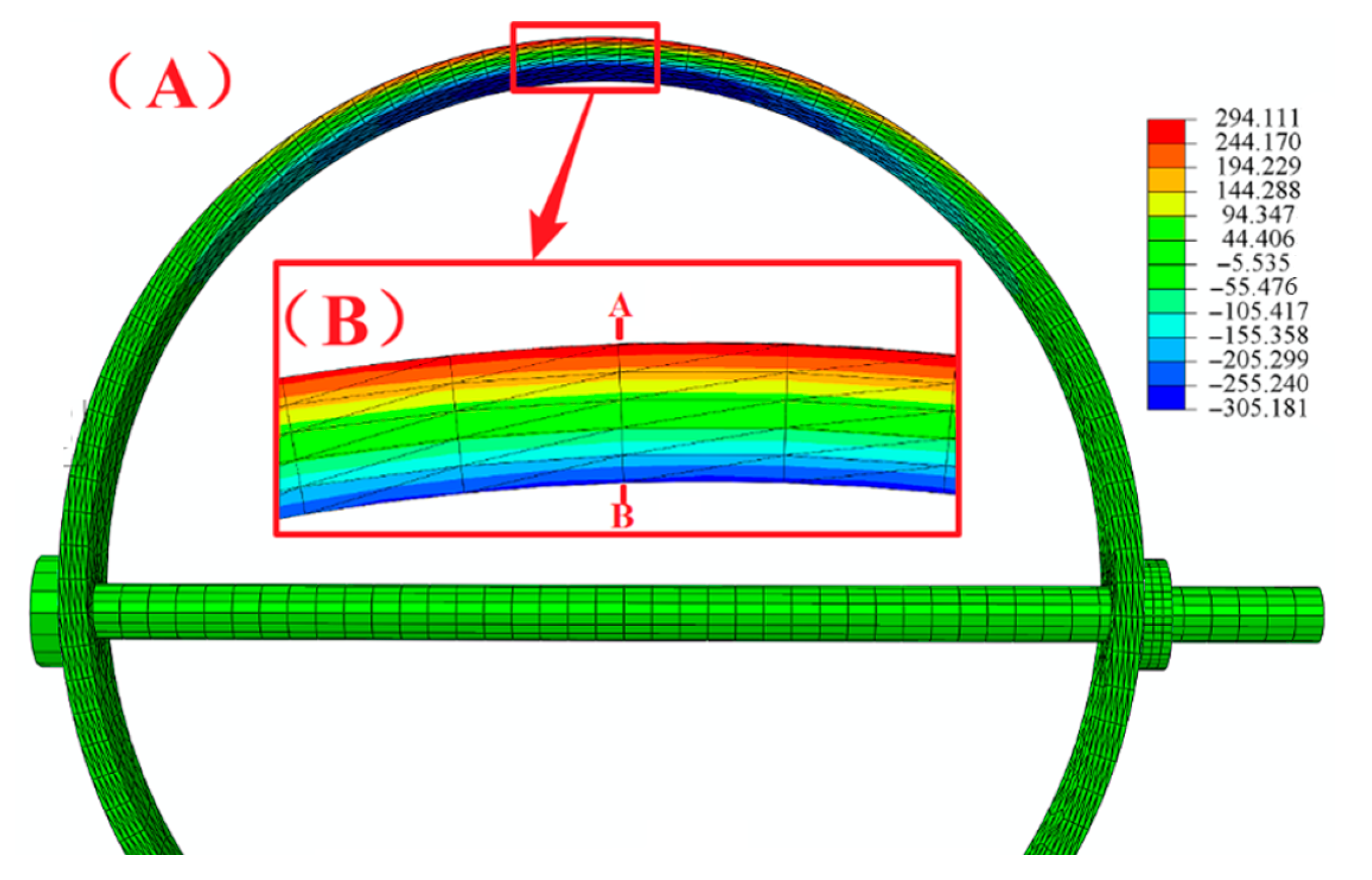




| Component | Density (kg/m3) | L-Wave Velocity (m/s) | Shear Wave Velocity (m/s) | Damping Ratio |
|---|---|---|---|---|
| Curved component | 2700 | 6300 | 3080 | 0.5 × 10−2 |
| Wedge | 1190 | 2700 | 1340 | 1 × 10−2 |
| Piezoelectric wafer | 7500 | 4620 | 1750 | / |
| Absorbing layer | 6580 | 1500 | 775 | 20 × 10−2 |
| Algorithm: An LCR-Wave Pipeline Hoop Stress Measurement Method | |
|---|---|
| Input: | Pipe diameter R, incident angle of ultrasonic transducer iCou, ultrasonic velocity of wedge VWedge, ultrasonic velocity of pipe VCur, ultrasonic velocity of coupling gel VCou, coefficient of plane stress KPla, detection distance of plane probe LPla |
| Begin: | |
| 1 | Initialize all parameters of the model |
| 2 | Assign values to input parameters |
| //Confirm parameters based on material properties and ultrasonic characteristics | |
| 3 | Angle of refraction in pipe β, is calculated by solving arcsin(β • VCou/VCur) + 90° = arcsin(siniCou • VCou/VWedge) + β |
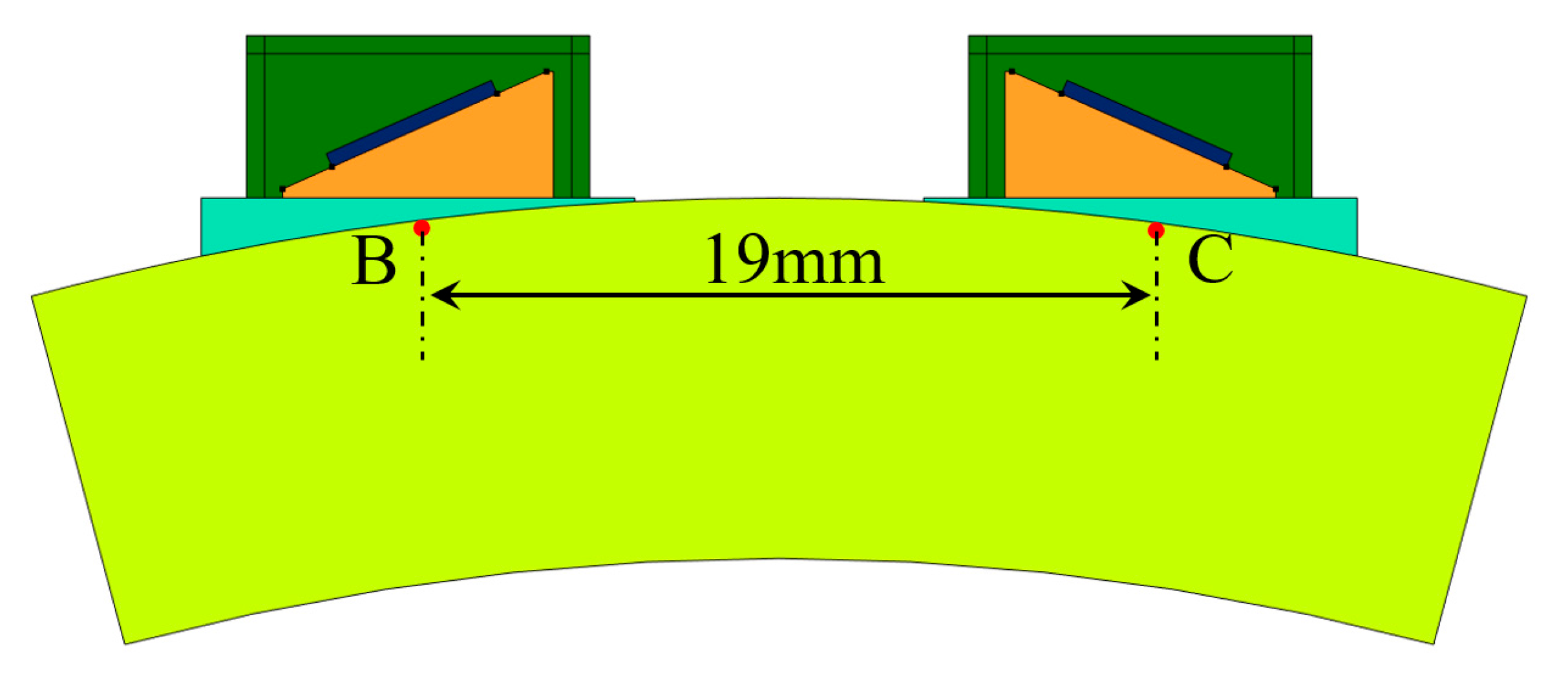
| 4 | Calculate effective distance of pipeline stress detection LCur = 2Rcosβ |
| //Establishing ultrasonic stress measurement system | |
| 5 | Collect data from the receiving probe |
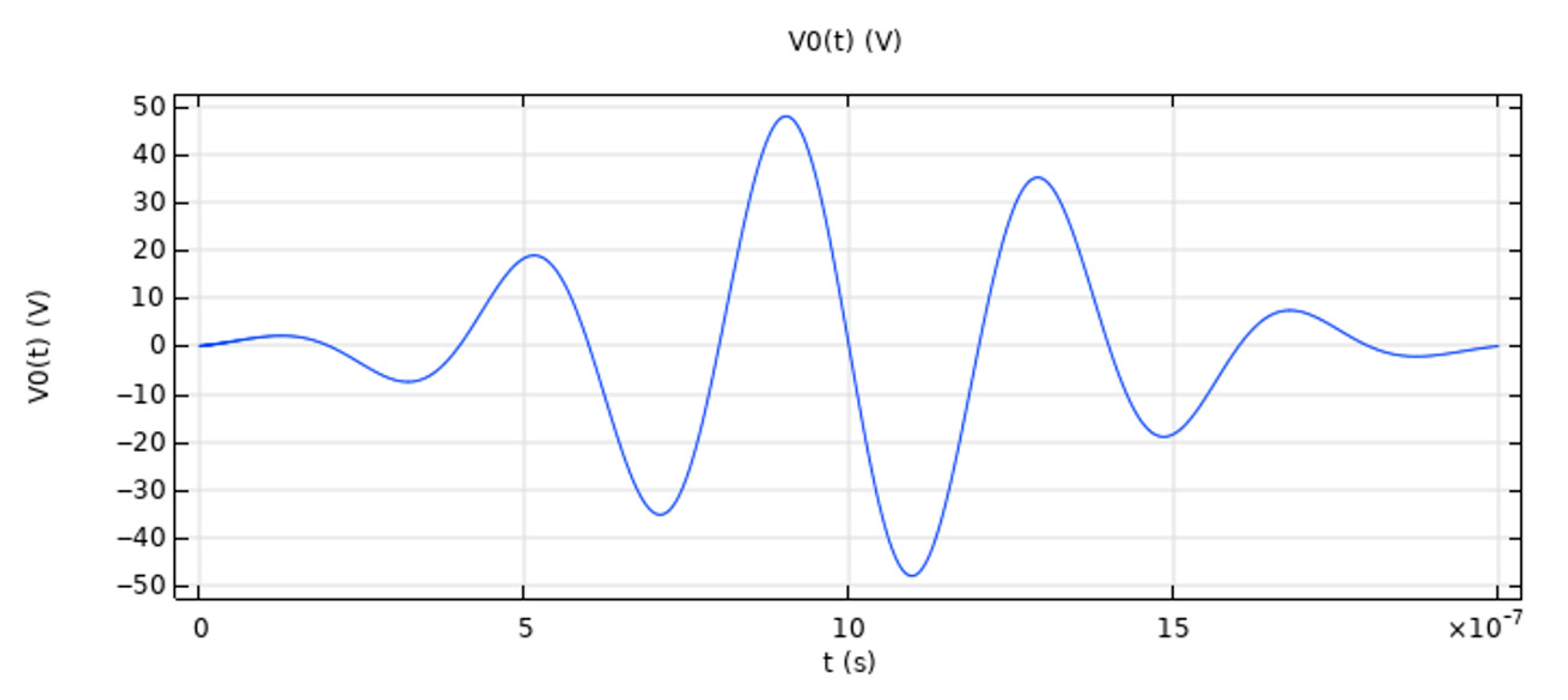
| 6 | Obtain LCR wave propagation time t1 |
| 7 | Calculate time of flight difference ΔtCur= t1 − t0 |
| 8 | Calculate hoop stress σhoop |
| Output: | Hoop stress values σhoop |
| Compression (mm) | Theoretical Stress (MPa) | LCR-HS Method | Uncorrected Planar Method | ||
|---|---|---|---|---|---|
| Measured (MPa) | Error (%) | Measured (MPa) | Error (%) | ||
| 2.56 | 55.59 | 45.99 | 17.28 | 24.23 | 56.42 |
| 4.57 | 99.24 | 94.94 | 4.34 | 50.02 | 49.60 |
| 6.46 | 140.28 | 156.50 | 11.56 | 82.45 | 41.22 |
| 8.62 | 187.19 | 195.81 | 4.60 | 103.16 | 44.89 |
| 10.44 | 226.71 | 212.87 | 6.11 | 112.15 | 50.53 |
| Pipe Diameter | 200 mm | 300 mm | 400 mm | 500 mm | 600 mm | |
|---|---|---|---|---|---|---|
| Repeatability | 100 MPa | 30.9 MPa | 20.7 MPa | 10.2 MPa | 10.1 MPa | 8.9 MPa |
| 150 MPa | 42.6 MPa | 22.8 MPa | 12.5 MPa | 11.8 MPa | 9.7 MPa | |
| 200 MPa | 38.7 MPa | 21.4 MPa | 11.8 MPa | 11.4 MPa | 10.7 MPa | |
| Average | 37.4 MPa | 21.6 MPa | 11.5 MPa | 11.1 MPa | 9.8 MPa | |
| Welding Technology | Welding Materials | Pipe Dimensions | |||
|---|---|---|---|---|---|
| Root Welding | Fill and Cover | ||||
| GMAW-STT-FCAW-S | ER50-6 | CHW-50C6 | E81T8-Ni2J | HOBART Fabshield | D1016 × 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Wang, B.; Qiu, F.; Luo, C.; Chen, J.; Gou, G. A Pipeline Hoop Stress Measurement Method Based on Propagation Path Correction of LCR Waves. J. Mar. Sci. Eng. 2025, 13, 1845. https://doi.org/10.3390/jmse13101845
Chen B, Wang B, Qiu F, Luo C, Chen J, Gou G. A Pipeline Hoop Stress Measurement Method Based on Propagation Path Correction of LCR Waves. Journal of Marine Science and Engineering. 2025; 13(10):1845. https://doi.org/10.3390/jmse13101845
Chicago/Turabian StyleChen, Bing, Binbin Wang, Feifei Qiu, Chunlang Luo, Jiakai Chen, and Guoqing Gou. 2025. "A Pipeline Hoop Stress Measurement Method Based on Propagation Path Correction of LCR Waves" Journal of Marine Science and Engineering 13, no. 10: 1845. https://doi.org/10.3390/jmse13101845
APA StyleChen, B., Wang, B., Qiu, F., Luo, C., Chen, J., & Gou, G. (2025). A Pipeline Hoop Stress Measurement Method Based on Propagation Path Correction of LCR Waves. Journal of Marine Science and Engineering, 13(10), 1845. https://doi.org/10.3390/jmse13101845








