Computational Fluid Dynamics Prediction of the Sea-Keeping Behavior of High-Speed Unmanned Surface Vehicles Under the Coastal Intersecting Waves
Abstract
1. Introduction
2. Geometry Modeling of the Fast Ship
3. Implement of the Intersecting Waves
3.1. Physical Modeling of the Numerical Tank
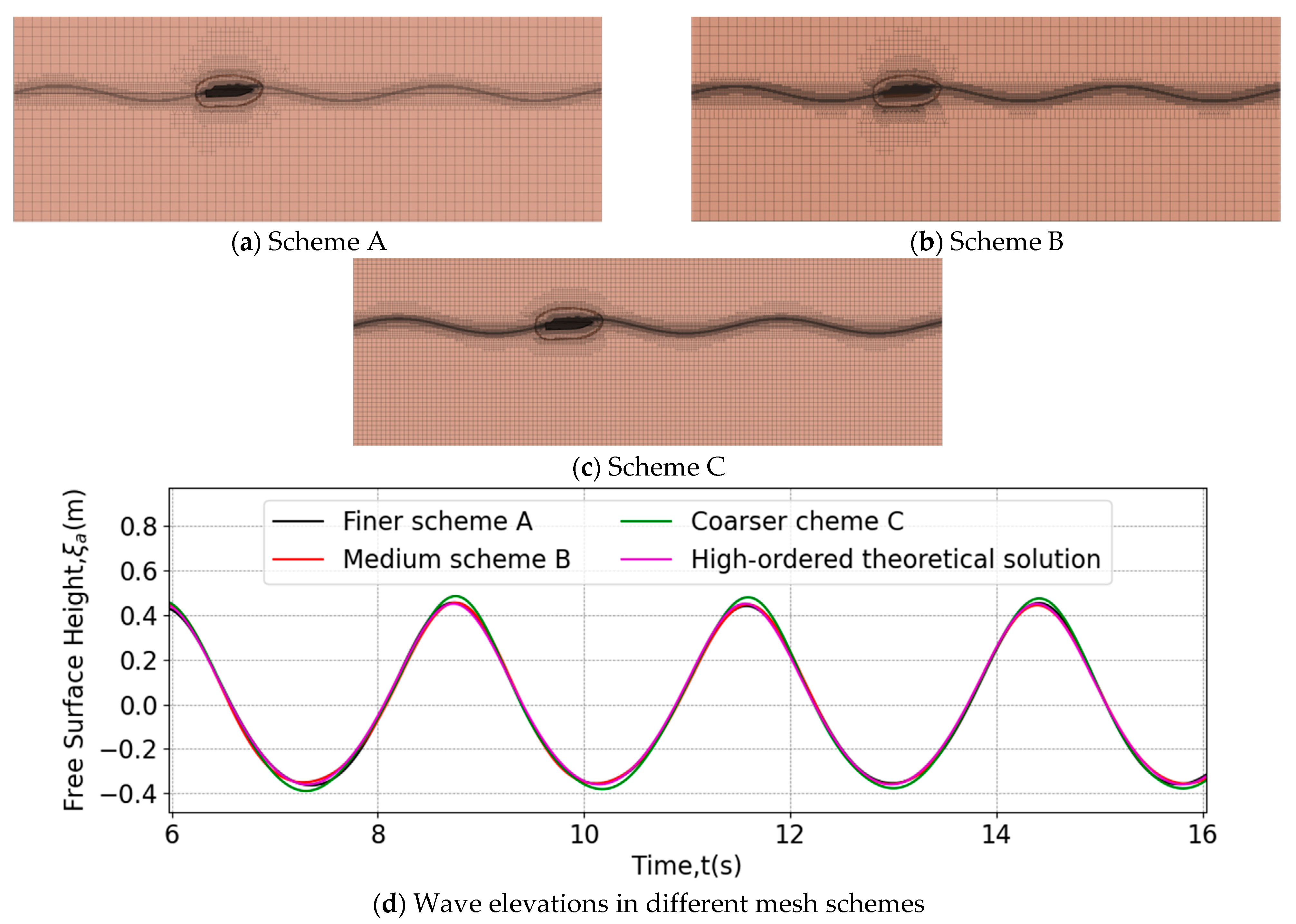
3.2. Meshing and Grid Verification of Numerical Region
3.3. Time Step Verification
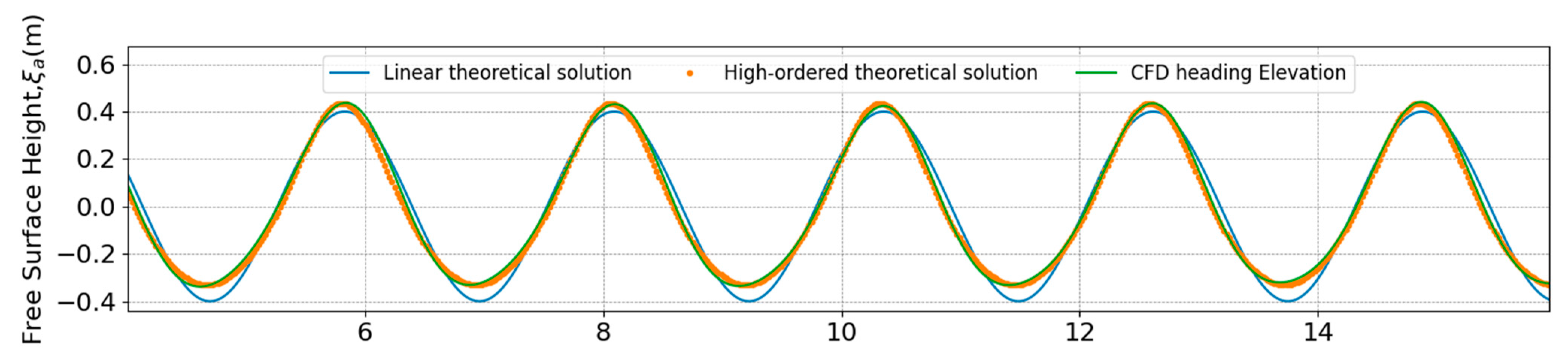
3.4. Validation of Numerical Model
3.5. Intersecting Waves Generating
3.6. Orthogonal Design of Parameters in Different Cases
4. Results of Intersecting Waves Encountering Simulation
4.1. Waves Analysis at Different Monitor Positions on the Navigating USV
4.2. FFT Analysis of Wave Height
4.3. USV Motions in Different Situations
4.3.1. Different Inclination Angles of Intersecting Waves
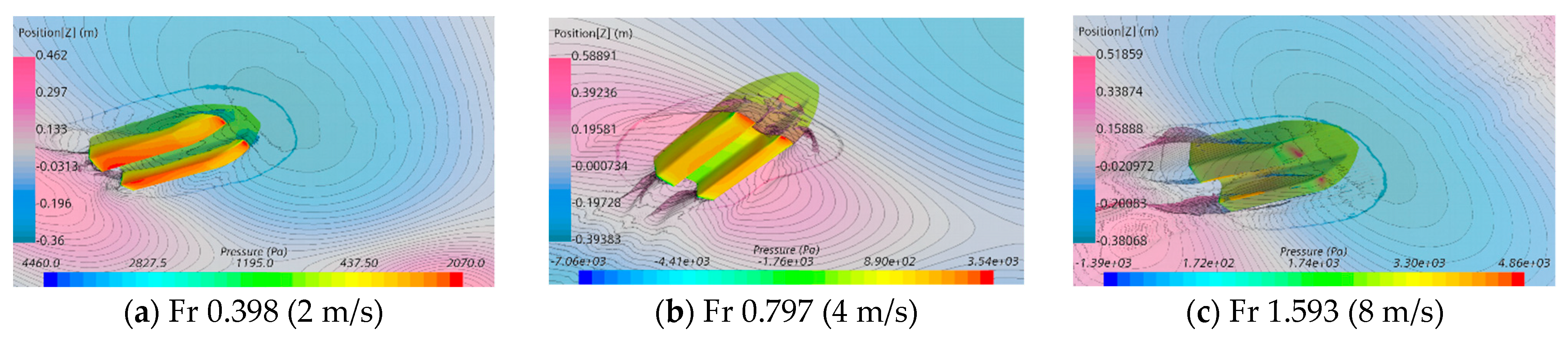
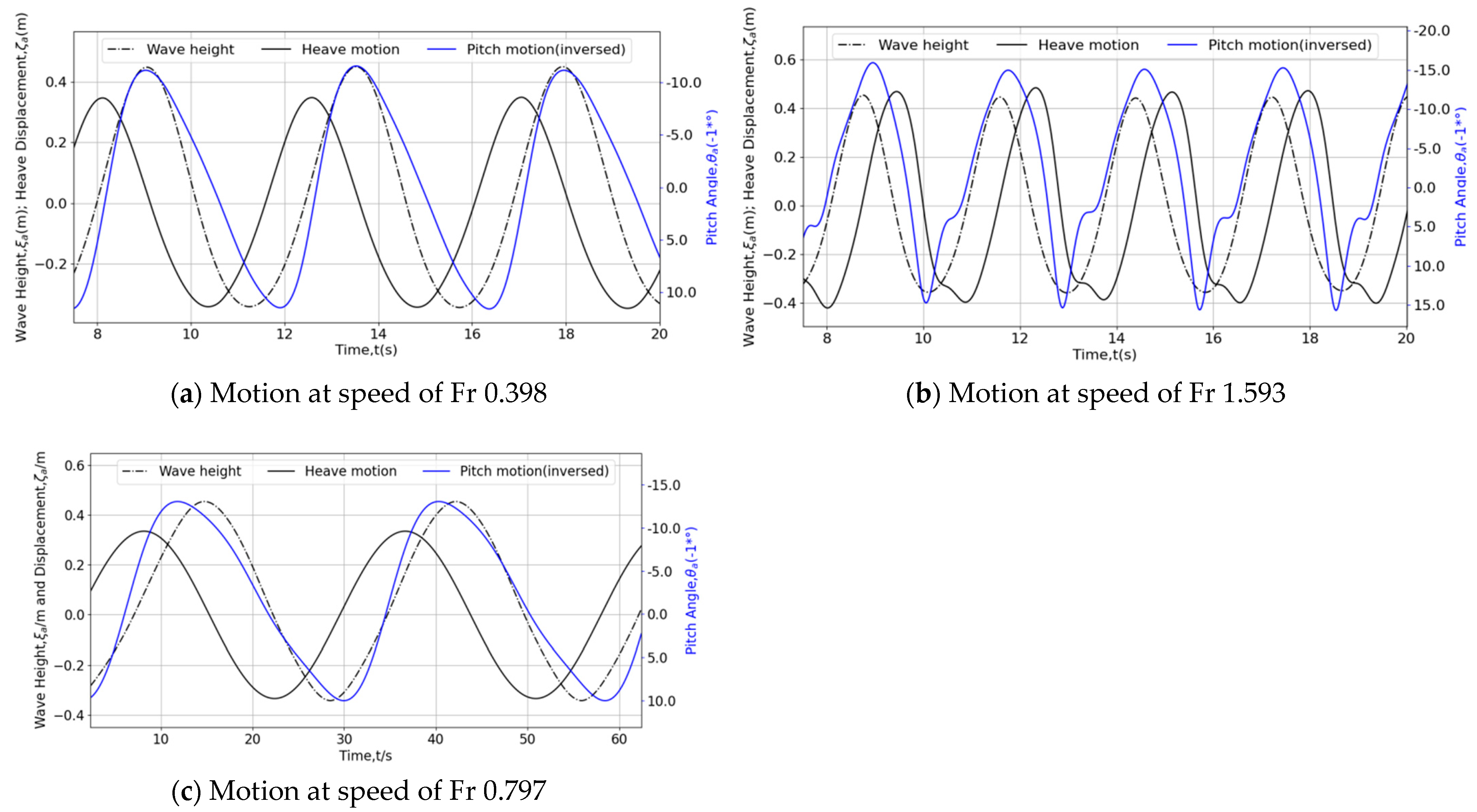
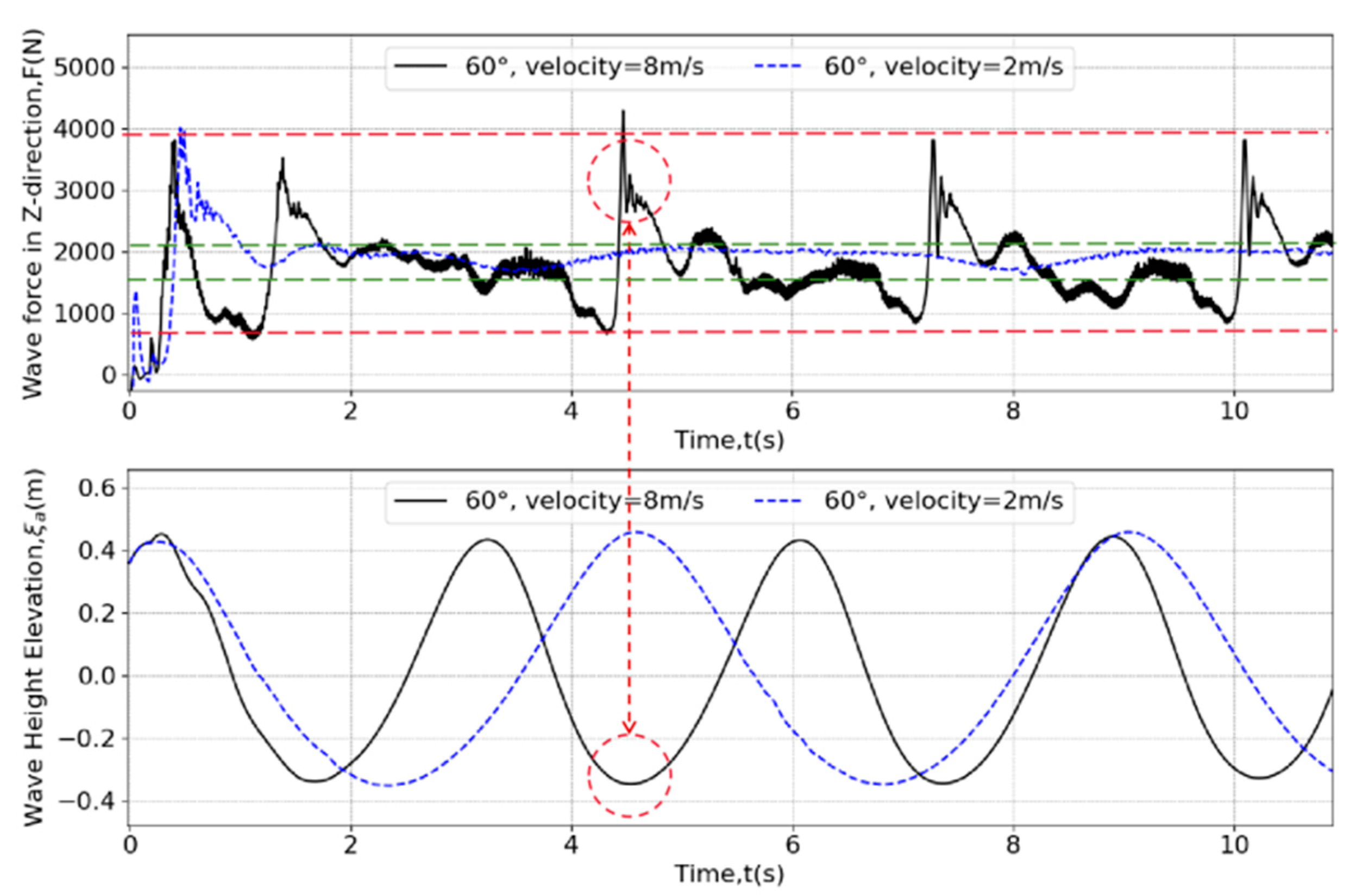
4.3.2. Different Navigating Speeds
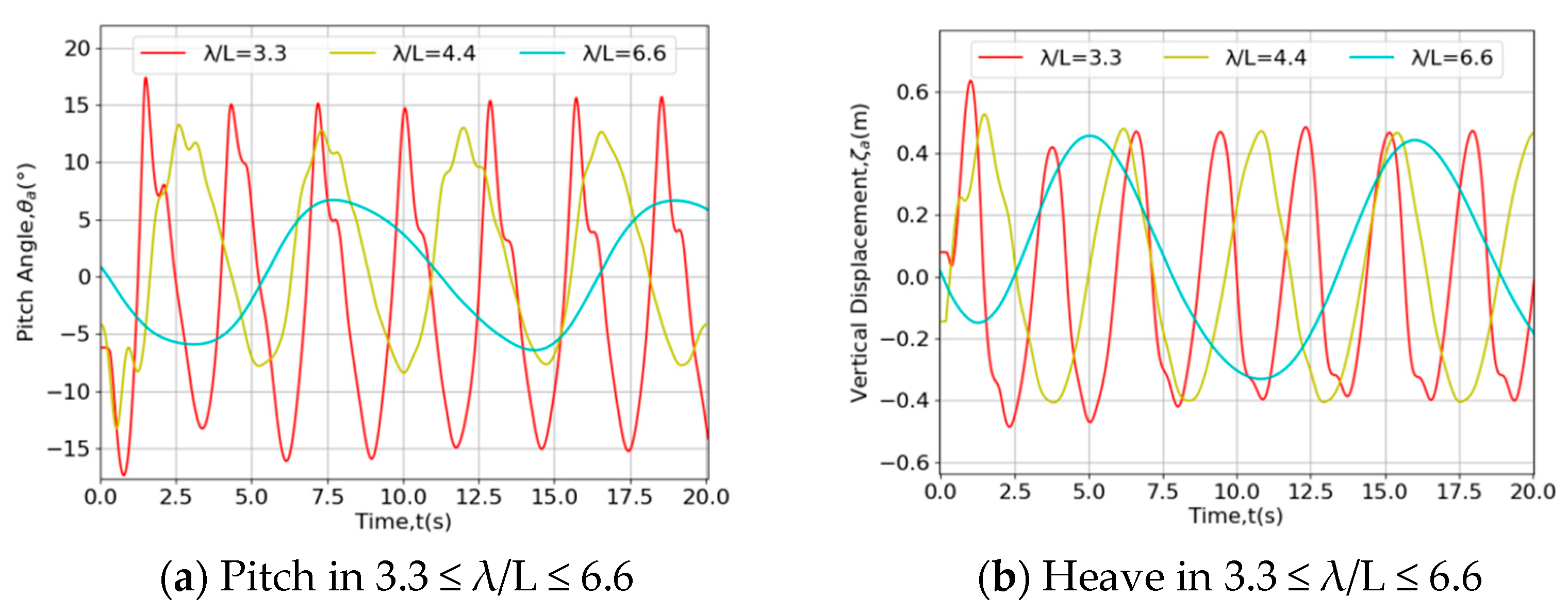
4.3.3. Different λ/L of Sub-Waves
5. Relevant Analysis of Response of USV in Wave
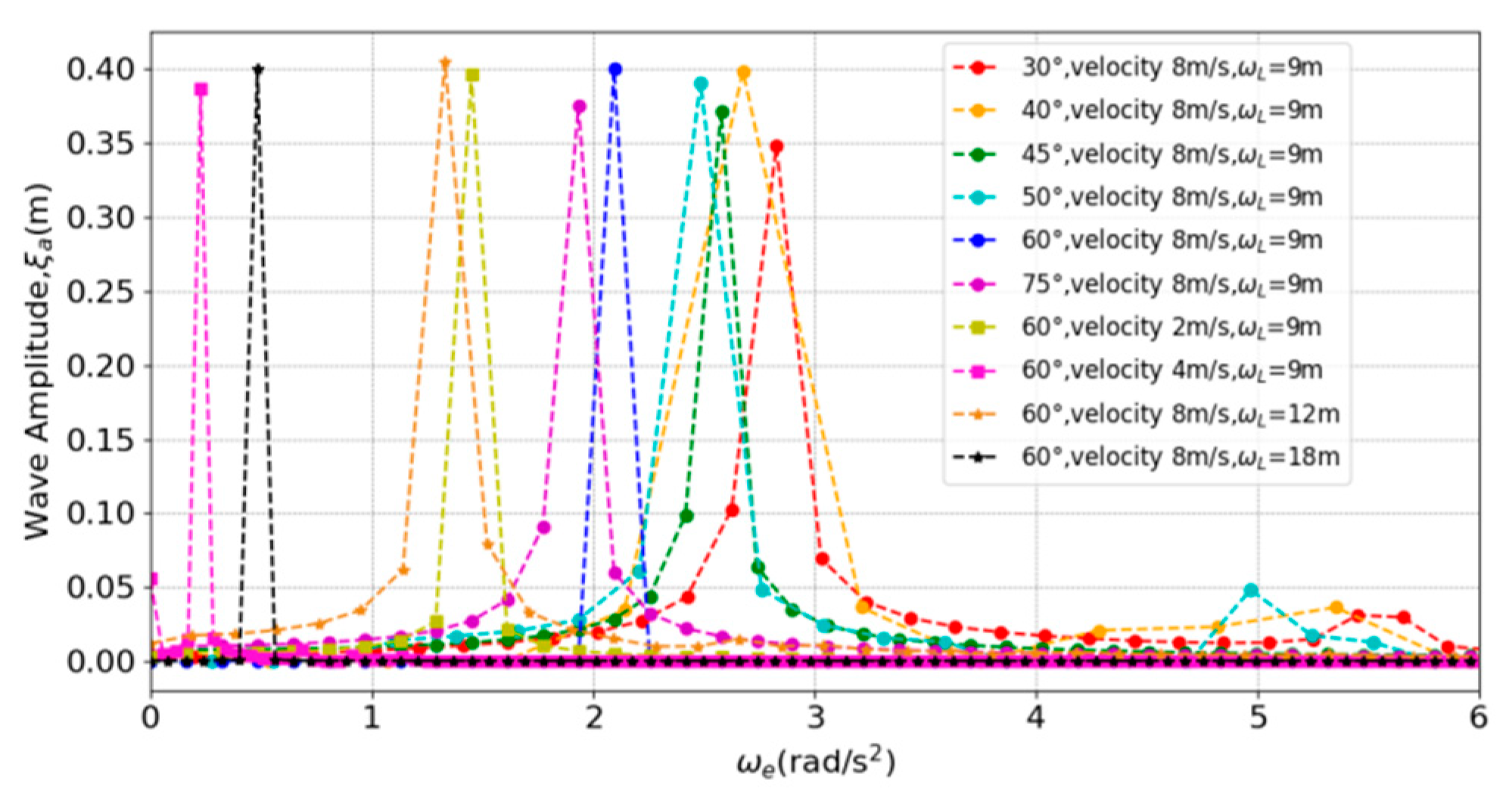
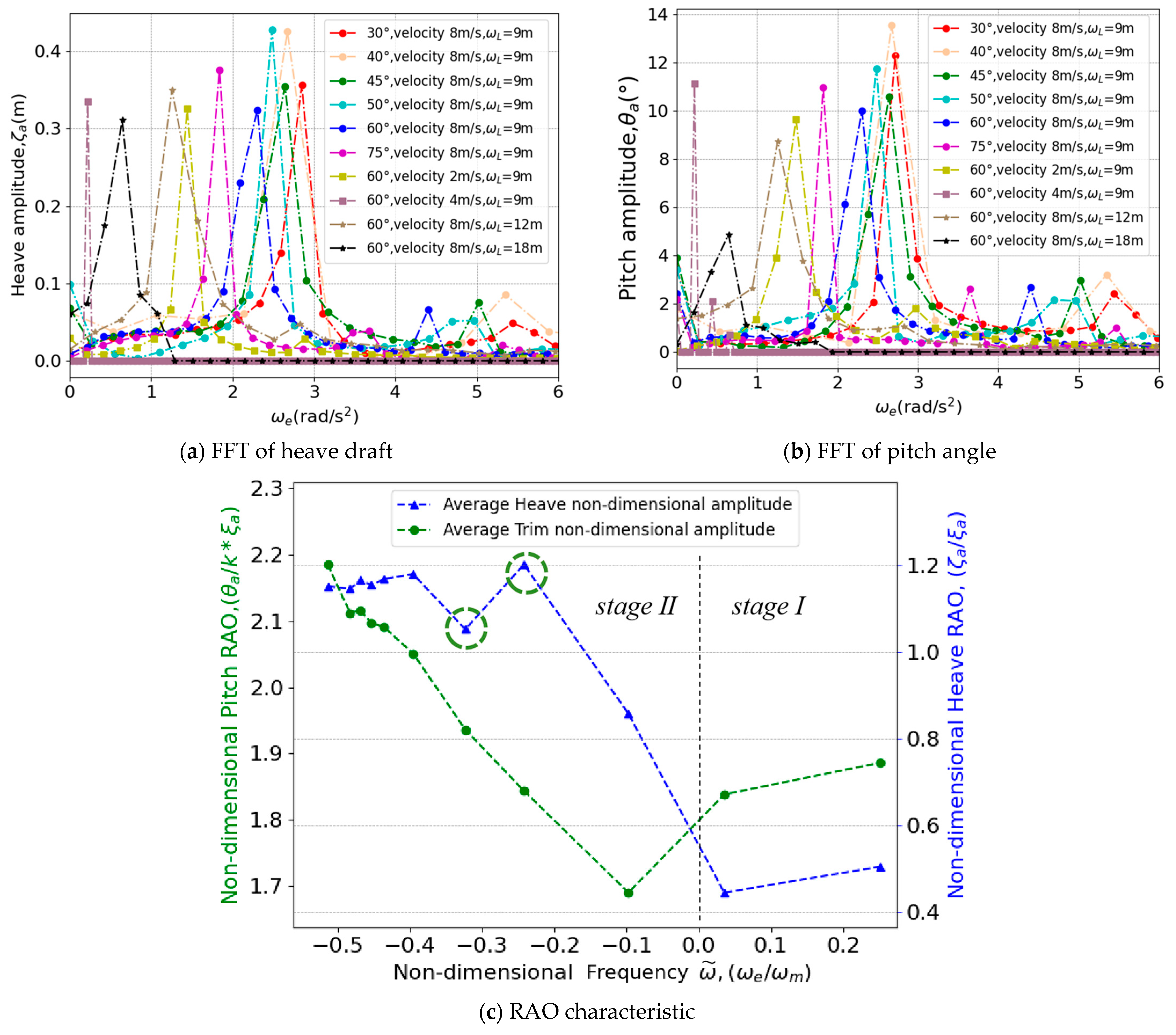
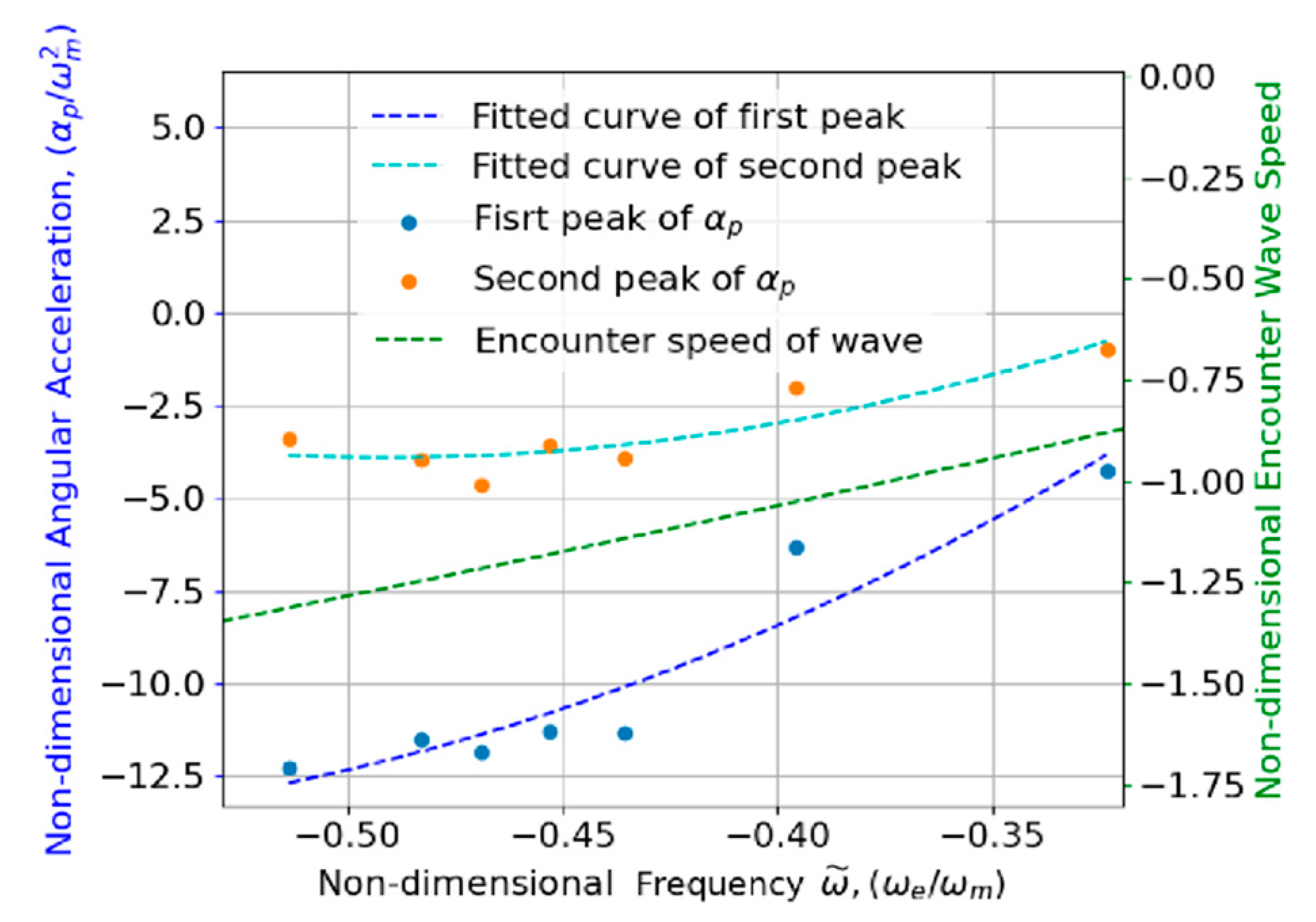
5.1. RAO Analysis of USV Motions with Encounter Frequency Perspective
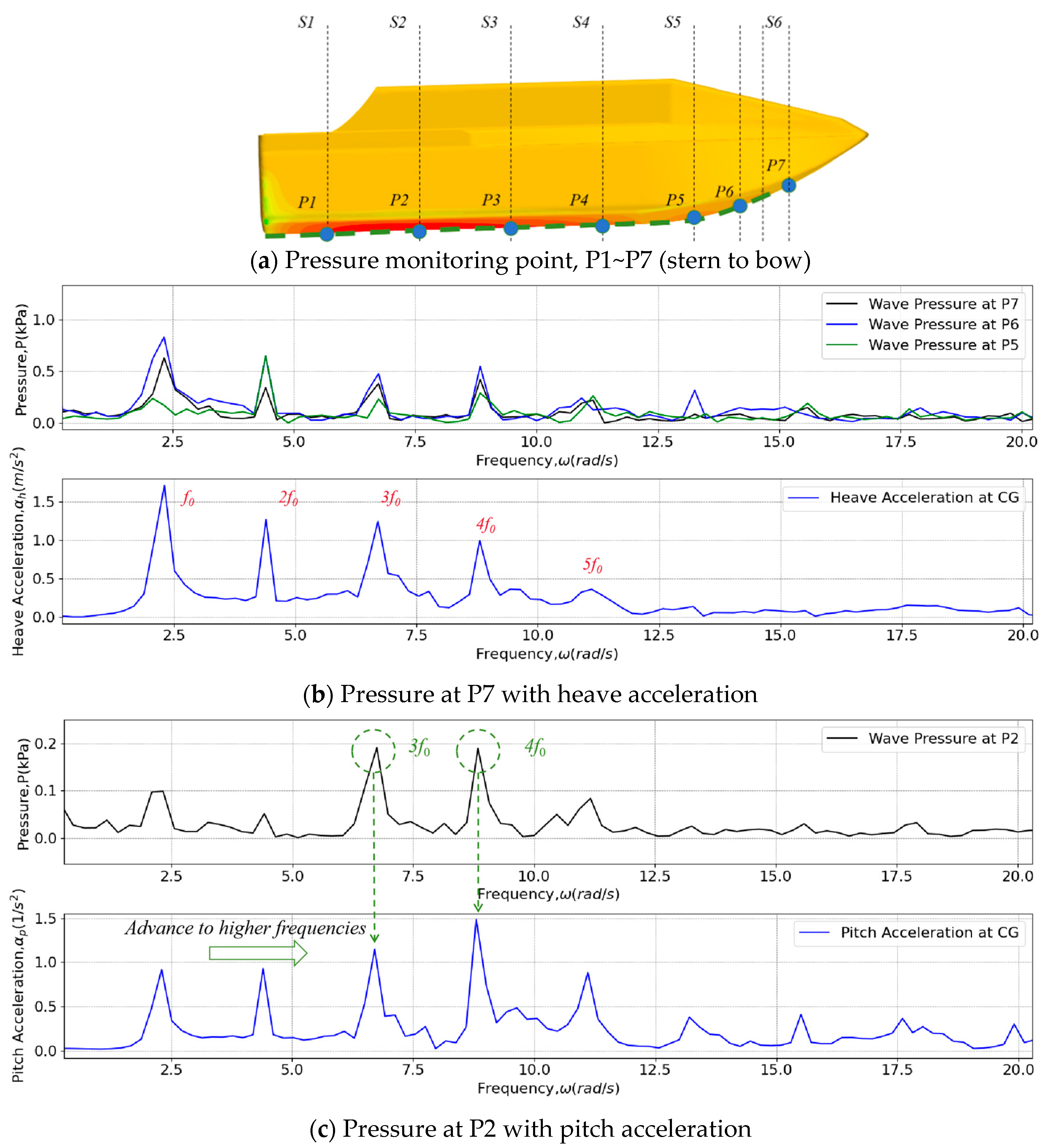
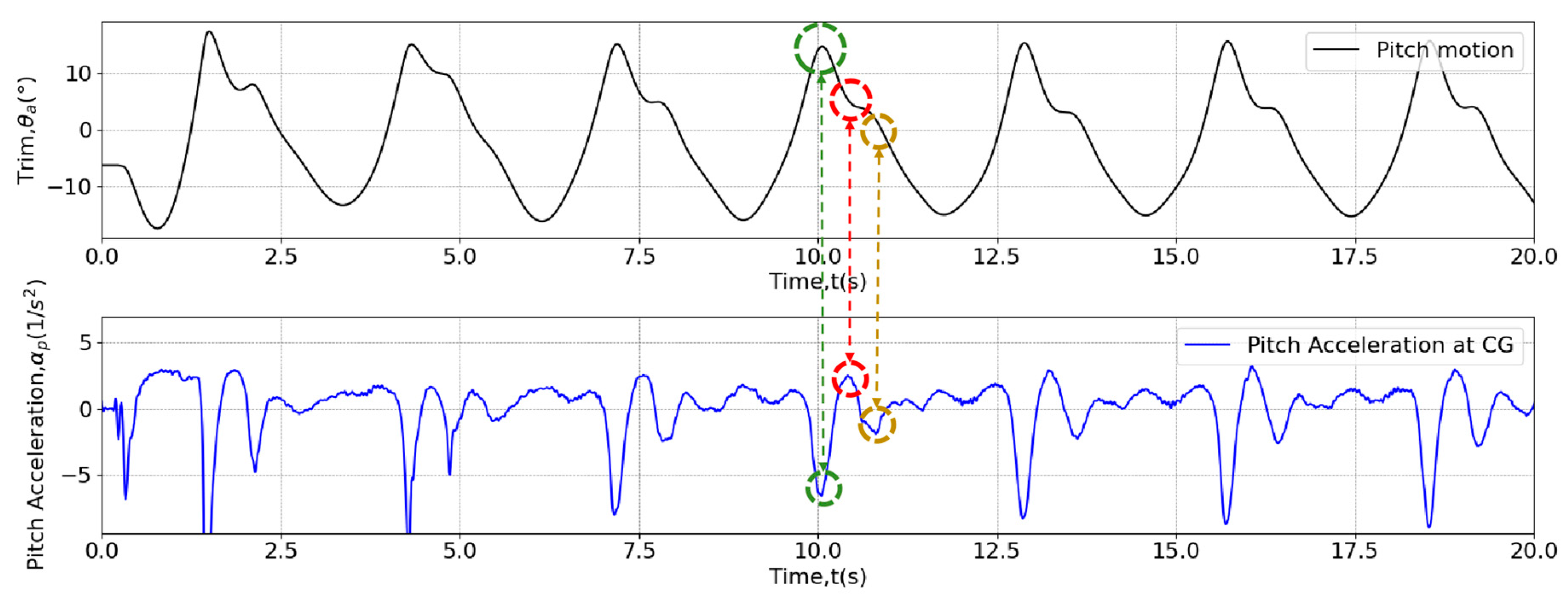
5.2. Relevant Analysis Between Pressure and Vertical Acceleration
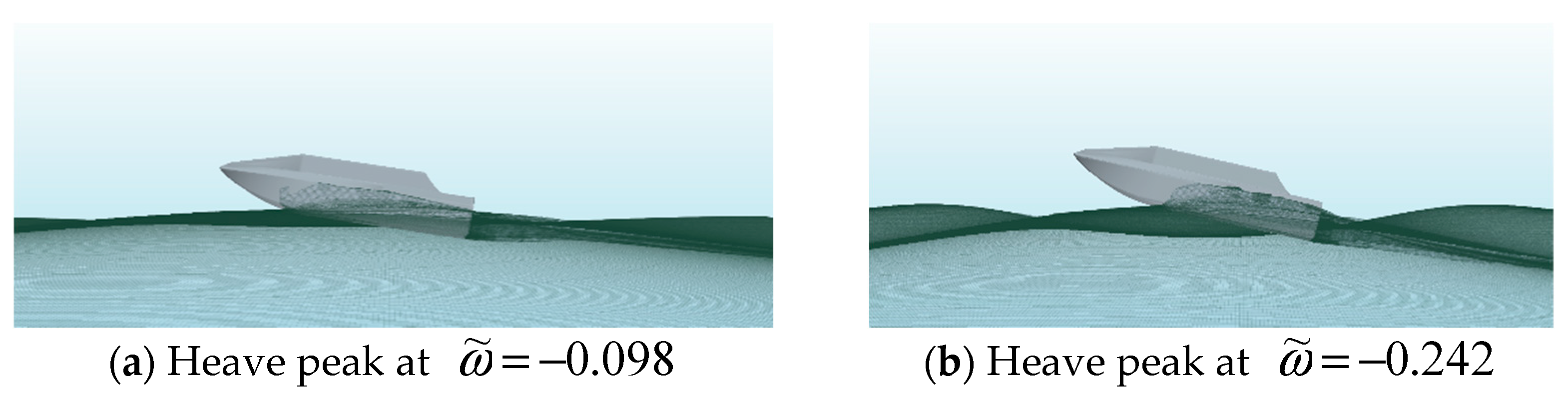
5.3. Severity Analysis of Vertical Pitch Response in Different Stages
6. Swaying Tests with PMM
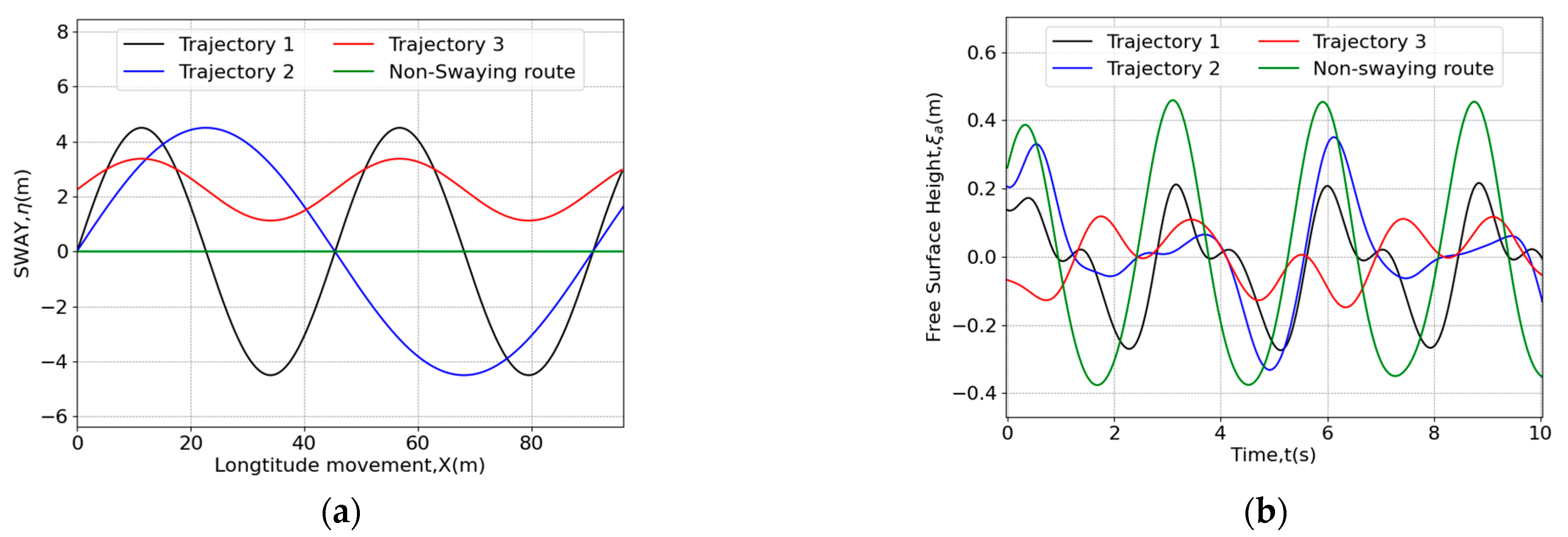
6.1. Encountered Waves of Different Swaying Routes
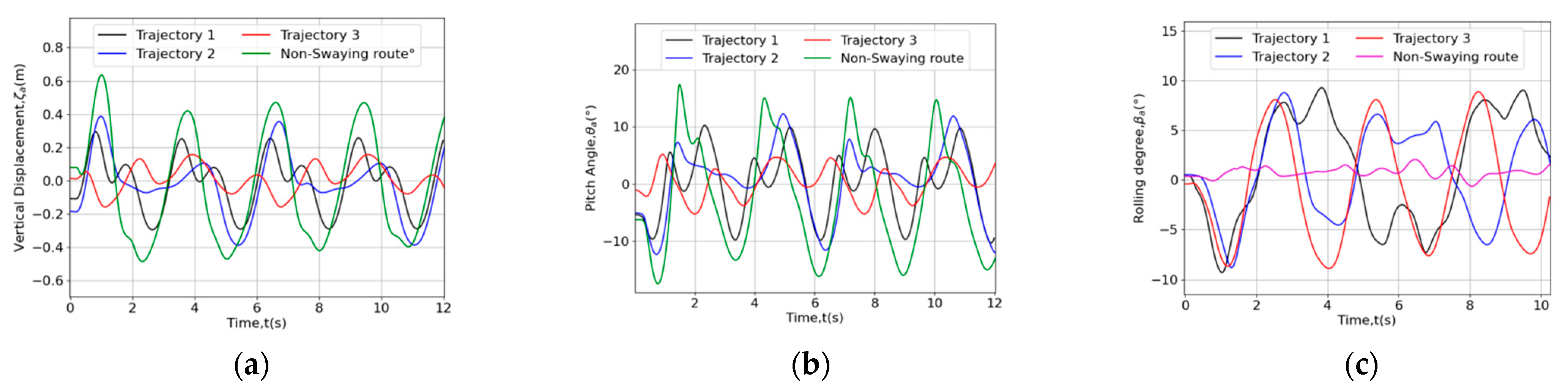
6.2. Sea-Keeping Response Comparisons
7. Conclusions
8. Future
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Wang, W.; Pakozdi, C.; Kamath, A.; Bihs, H. Representation of 3-h Offshore Short-Crested Wave Field in the Fully Nonlinear Potential Flow Model REEF3D::FNPF. J. Offshore Mech. Arct. Eng. 2022, 144, 041902. [Google Scholar] [CrossRef]
- Xiang, G.; Xiang, X.; Datla, R. Numerical study of a novel small waterplane area USV advancing in calm water and in waves using the higher-order Rankine source method. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2241892. [Google Scholar] [CrossRef]
- Townsend, J. The Application of Computational Fluid Dynamics to the Modelling and Design of High-Speed Boats; Swansea University: Swansea, UK, 2021. [Google Scholar]
- Sun, H.; Jing, F.; Jiang, Y. Zou, J; Zhuang, J; Ma, W. Motion prediction of catamaran with a semisubmersible bow in wave. Pol. Marit. Res. 2016, 23, 37–44. [Google Scholar] [CrossRef]
- Diez, M.; Broglia, R.; Durante, D.; Campana, E.F.; Stern, F. Validation of highfidelity uncertainty quantification of a high-speed catamaran in irregular waves. In Proceedings of the 13th International Conference on Fast Sea Transportation, FAST, Washington, DC, USA, 2–4 September 2015; pp. 1–4. [Google Scholar]
- Diez, M.; Broglia, R.; Durante, D.; Campana, E.F.; Stern, F. Statistical validation of a high-speed catamaran in irregular waves. In Proceedings of the 31st Symposium on Naval Hydrodynamics, Monterey, CA, USA, 11–16 September 2016; pp. 11–16. [Google Scholar]
- Xie, J. Investigation on nonlinear interactions of bidirectional waves. Dalian Univ. Technol. 2021, 003915. [Google Scholar]
- Cavaleri, L.; Bertotti, L.; Torrisi, L.; Bitner-Gregersen, E.; Serio, M.; Onorato, M. Rogue waves in crossing seas: The Louis Majesty accident. J. Geophys. Res. Ocean 2012, 117. [Google Scholar] [CrossRef]
- Adcock, T.A.A.; Taylor, P.H.; Yan, S.; Ma, Q.; Janssen, P. Did the Draupner wave occur in a crossing sea? Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 3004–3021. [Google Scholar] [CrossRef]
- Jiao, J.; Huang, S.; Soares, C.G. Numerical investigation of ship motions in cross waves using CFD. Ocean Eng. 2021, 223, 108711. [Google Scholar] [CrossRef]
- Huang, S.; Jiao, J.; Chen, C. CFD prediction of ship seakeeping behavior in bi-directional cross wave compared with in uni-directional regular wave. Appl. Ocean Res. 2021, 107, 102426. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, N.; Zhao, W.; Xia, J. Numerical prediction of seakeeping and slamming behaviors of a trimaran in short-crest cross waves compared with long-crest regular waves. Ocean Eng. 2023, 285, 115314. [Google Scholar] [CrossRef]
- Petrova, P.G.; Guedes Soares, C. Distributions of nonlinear wave amplitudes and heights from laboratory generated following and crossing bimodal seas. Nat. Hazards Earth Syst. Sci. 2014, 14, 1207–1222. [Google Scholar] [CrossRef]
- Sabatino, A.D.; Serio, M. Experimental investigation on statistical properties of wave heights and crests in crossing sea conditions. Ocean Dyn. 2015, 65, 707–720. [Google Scholar] [CrossRef]
- Ocaña-Blanco, D.; Castañeda-Sabadell, I.; Souto-Iglesias, A. CFD and potential flow assessment of the hydrodynamics of a kitefoil. Ocean Eng. 2017, 146, 388–400. [Google Scholar] [CrossRef]
- Kandasamy, M.; Ooi, S.K.; Carrica, P.; Stern, F.; Campana, E.F.; Peri, D.; Osborne, P.; Cote, J.; Macdonald, N.; de Waal, N. CFD validation studies for a high-speed foil-assisted semi-planing catamaran. J. Mar. Sci. Technol. 2011, 16, 157–167. [Google Scholar] [CrossRef]
- Amani, S. Numerical and Experimental Analysis of the Wind Forces Acting on a High-Speed Catamaran; University of Tasmania: Hobart, Australia, 2019. [Google Scholar]
- Haase, M.; Zurcher, K.; Davidson, G.; Binns, J.R.; Thomas, G.; Bose, N. Novel CFD-based full-scale resistance prediction for large medium-speed catamarans. Ocean Eng. 2016, 111, 198–208. [Google Scholar] [CrossRef]
- Phan, K.M.; Sadat, H. CFD study of extreme ship responses using a designed wave trail. Ocean Eng. 2023, 268, 113178. [Google Scholar] [CrossRef]
- Carrica, P.M.; Fu, H.; Stern, F. Computations of self-propulsion free to sink and trim and of motions in head waves of the KRISO Container Ship (KCS) model. Appl. Ocean Res. 2011, 33, 309–320. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Ma, N. Study on wave-induced motions of a turning ship in regular and long-crest irregular waves. Ocean Eng. 2021, 225, 108807. [Google Scholar] [CrossRef]
- Wang, W.; Bihs, H.; Kamath, A.; Arntsen, Ø.A. Multi-directional irregular wave modelling with CFD. In Proceedings of the Fourth International Conference in Ocean Engineering (ICOE2018), Chennai, India, 18–21 February 2018; Springer: Singapore, 2019; Volume 1, pp. 521–529. [Google Scholar]
- Li, J.; Wang, Z.; Liu, S. Experimental study of interactions between multi-directional focused wave and vertical circular cylinder, part II: Wave force. Coast. Eng. 2014, 83, 233–242. [Google Scholar] [CrossRef]
- Liu, S.; Ong, M.C.; Obhrai, C.; Seng, S. CFD simulations of regular irregular waves past a horizontal semi-submerged cylinder. J. Offshore Mech. Arctic. Eng. 2017, 140. [Google Scholar]
- Zhang, L.; Zhang, J.; Shang, Y. A practical direct URANS CFD approach for the speed loss and propulsion performance evaluation in short-crested irregular head waves. Ocean Eng. 2021, 219, 108287. [Google Scholar] [CrossRef]
- Kim, D.; Tahsin, T. CFD-based hydrodynamic analyses of ship course keeping control and turning performance in irregular waves. Ocean Eng. 2022, 248, 110808. [Google Scholar] [CrossRef]
- Judge, C.; Mousaviraad, M.; Stern, F.; Lee, E.; Fullerton, A.; Geiser, J.; Schleicher, C.; Merrill, C.; Weil, C.; Morin, J.; et al. Experiments and CFD of a high-speed deep-V planing hull–part II: Slamming in waves. Appl. Ocean Res. 2020, 97, 102059. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, D.; Gao, L.; Miao, Q. CFD computation of ship motions and added resistance for a high speed trimaran in regular head waves. Int. J. Nav. Archit. Ocean. Eng. 2011, 3, 105–110. [Google Scholar] [CrossRef]
- Nowruzi, L.; Enshaei, H.; Lavroff, J.; Kianejad, S.S.; Davis, M.R. CFD simulation of motion responses of a trimaran in regular head waves. Int. J. Marit. Eng. 2020, 162, A1. [Google Scholar] [CrossRef]
- Wang, S.; Guedes Soares, C. Review of ship slamming loads and responses. J. Mar. Sci. Appl. 2017, 16, 427–445. [Google Scholar] [CrossRef]
- Ardeshiri, S.; Mousavizadegan, S.H.; Kheradmand, S. Virtual simulation of PMM tests independent of test parameters. Brodogr. Int. J. Nav. Archit. Ocean Eng. Res. Dev. 2020, 71, 55–73. [Google Scholar] [CrossRef]
- Liu, J.; Chua, K.H.; Taskar, B.; Liu, D.; Magee, A.R. Virtual PMM captive tests using OpenFOAM to estimate hydrodynamic derivatives and vessel maneuverability. Ocean Eng. 2023, 286, 115654. [Google Scholar] [CrossRef]
- Zhu, Z.; Kim, B.S.; Wang, S.; Kim, Y. Study on Numerical PMM Tests in Incident Waves. In Proceedings of the 37th International Workshop on Water Waves and Floating Bodies, Giardini Naxos, Italy, 10–13 April 2022. [Google Scholar]
- Ma, C.; Hino, T.; Ma, N. Numerical investigation of the influence of wave parameters on maneuvering hydrodynamic derivatives in regular head waves. Ocean Eng. 2022, 244, 110394. [Google Scholar] [CrossRef]
- Ma, C.Q.; Ma, N.; Gu, X.C. Numerical simulation of PMM tests of a container ship in regular following waves. In Sustainable Development and Innovations in Marine Technologies; CRC Press: Boca Raton, FL, USA, 2019; pp. 197–204. [Google Scholar]
- Zhu, Z.; Kim, B.S.; Wang, S.; Kim, Y. Observation of the Wave Effect on Ship Manoeuvring Coefficients Based on Numerical PMM Approach. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Online, 5–10 June 2022; p. ISOPE-I-22-345. [Google Scholar]
- The Specialist Committee on Uncertainty Analysis. In Proceedings of the 26th International Towing Tank Conference 2011, Rio de Janeiro, Brazil, 28 August–3 September 2011.
- Reynolds, O. IV. On the Dynamical Theory of Incompressible Viscous Fluids andthe Determination of the Criterion. Philos. Trans. R. Lond. 1895, 186, 123–164. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-epsilon eddy viscosity model for high Reynolds number turbulent flows: Model development and validation. NASA Technical Memorandum 1994, 106721, 1–30. [Google Scholar]
- Kim, D.; Song, S.; Sant, T.; Demirel, Y.K.; Tezdogan, T. Nonlinear URANS model for evaluating course keeping and turning capabilities of a vessel with propulsion system failure in waves. Int. J. Nav. Archit. Ocean Eng. 2022, 14, 100425. [Google Scholar] [CrossRef]
- Terziev, M.; Tezdogan, T.; Demirel, Y.K.; Villa, D.; Mizzi, S.; Incecik, A. Exploring the effects of speed and scale on a ship’s form factor using CFD. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 147–162. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Ohmori, T. Finite-volume simulation of flows about a ship in maneuvering motion. J. Mar. Sci. Technol. 1998, 3, 82–93. [Google Scholar] [CrossRef]
- Ohmori, T.; Miyata, H. Oblique tow simulation by a finite-volume method. J. Soc. Nav. Archit. Jpn. 1993, 1993, 27–34. [Google Scholar] [CrossRef]
- Shabana, A.A. Computational Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Benek, J.A.; Steger, J.L.; Dougherty, F.C. Chimera: A Grid-Embedding Technique; Arnold Engineering Development Center, Air Force Systems Command, United States Air Force: Tullahoma, TN, USA, 1986. [Google Scholar]
- Field, P.L. Comparison of RANS and Potential Flow Force Computations for the ONR Tumblehome Hullfrom in Vertical Plane Radiation and Diffraction Problems. Va. Tech. 2013. [Google Scholar]
- ITTC Specialist Committee. Recommended procedures and guidelines-Practical Guidelines for Ship CFD Applications. In Proceedings of the 26th International Towing Tank Conference, Rio de Janeiro, Brasil, 5–10 September 2010. [Google Scholar]
- ITTC Manoeuvring Committee. Final report and recommendations to the 28th ITTC. In Proceedings of the 28th International Towing Tank Conference, Wuxi, China, 17–22 September 2017. [Google Scholar]
- Sezen, S.; Cakici, F. Numerical prediction of total resistance using full similarity technique. China Ocean Eng. 2019, 33, 493–502. [Google Scholar] [CrossRef]
- Li, H.; Zhao, N.; Zhou, J.; Chen, X.; Wang, C. Uncertainty Analysis and Maneuver Simulation of Standard Ship Model. J. Mar. Sci. Eng. 2024, 12, 1230. [Google Scholar] [CrossRef]
- Morabito, M.; Park, J.; van Rijsbergen, M. Quality systems group. In Proceedings of the 28th International Towing Tank Conference 2017, Wuxi, China, 17–22 September 2014. [Google Scholar]
- Gerhardt, F.; Young, J.; Minoura, M.; Bouscasse, B.; Hermundstad, O.A.; Nam, B.W.; Duan, W. Procedures and Guidelines. 2024. Available online: https://www.ittc.info/media/11894/75-02-07-025.pdf (accessed on 10 November 2024).
- De Luca, F.; Mancini, S.; Miranda, S.; Pensa, C. An extended verification and validation study of CFD simulations for planing hulls. J. Ship Res. 2016, 60, 101–118. [Google Scholar] [CrossRef]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998. [Google Scholar]
- Ec¸a, L.; Vaz, G.; Hoekstra, M. Code verification, solution verification and validation in RANS solvers. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 49149, pp. 597–605. [Google Scholar]
- Chen, Y.; Xu, S.; Shi, J.; Liu, X.; Hou, G. Hydrodynamic performance of small unmanned catamaran based on STAR-CCM+. Chin. J. Ship Res. 2023, 18, 73–82. [Google Scholar]
- Islam, H.; Soares, C.G. Uncertainty analysis in ship resistance prediction using OpenFOAM. Ocean Eng. 2019, 191, 105805. [Google Scholar] [CrossRef]
- Tasai, F. Damping force and added mass of ships heaving and pitching (continued). In Reports of Research Institute for Applied Mechanics; Research Institute for Applied Mechanics, Kyushu University: Fukuoka, Japan, 1960. [Google Scholar]
- Keuning, J.A. A calculation method for the heave and pitch motions of a hydrofoil boat in waves. Int. Shipbuild. Prog. 1979, 26, 217–232. [Google Scholar] [CrossRef]
- Gerritsma, J. Some notes on the calculation of pitching and heaving in longitudinal waves. Int. Shipbuild. Prog. 1956, 3, 255–264. [Google Scholar] [CrossRef]
- Katayama, T.; Ikeda, Y. A Study on Coupled Pitch and Heave Porpoising Instability of Planing Craft. J.-Kansai Soc. Nav. Archit. Jpn. 1997, 226, 227. [Google Scholar]
- Katayama, T.; Hinami, T.; Ikeda, Y. Longitudinal motion of a super high-speed planing craft in regular head waves. In Proceedings of the 4th Osaka Colloquium on Seakeeping Performance of Ships, Osaka, Japan, 17–21 October 2000; pp. 214–220. [Google Scholar]
- Irannezhad, M.; Eslamdoost, A.; Kjellberg, M.; Bensow, R.E. Investigation of ship responses in regular head waves through a Fully Nonlinear Potential Flow approach. Ocean Eng. 2022, 246, 110410. [Google Scholar] [CrossRef]
- Barrass, B.; Derrett, C.D.R. Ship Stability for Masters and Mates, 6th ed.; Butterworth-Heinemann: Oxford, UK, 2006. [Google Scholar]
- Biran, A.; López-Pulido, R. Ship Hydrostatics and Stability; Butterworth-Heinemann: Oxford, UK, 2003. [Google Scholar]
- Tupper, E.C.; Rawson, K.J. Basic Ship Theory, 5th ed.; Volume 2: Ship Dynamics and Design; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Oogushi, M. Ship Engineering Theory, 10th ed.; Kaibundo Shuppan: Tokyo, Japan, 1999. [Google Scholar]
- Boйткунский, Я.И.; Першиц, Р.Я.; Титoв, И.А. Справoчник пo теoрии кoрабля. Л: Судпрoмгиз. 1960; 228. [Google Scholar]
- Turkyilmazoglu, M. Maximum wave run-up over beaches of convex/concave bottom profiles. Cont. Shelf Res. 2022, 232, 104610. [Google Scholar] [CrossRef]
- Komar, P.D.; Gaughan, M.K. Airy wave theory and breaker height prediction. Coast. Eng. 1972, 1973, 405–418. [Google Scholar]
- Le Roux, J.P. An extension of the Airy theory for linear waves into shallow water. Coast. Eng. 2008, 55, 295–301. [Google Scholar] [CrossRef]
- Le Roux, J.P. Profiles of fully developed (Airy) waves in different water depths. Coast. Eng. 2008, 55, 701–703. [Google Scholar] [CrossRef]
- Wang, L.; Liu, W.; Lai, Z. Simulation method for simulating wave disturbance signals. Ship Eng. 2002, 4, 23–27. [Google Scholar]
- Hsu, J.R.C.; Tsuchiya, Y.; Silvester, R. Third-order approximation to short-crested waves. J. Fluid Mech. 1979, 90, 179–196. [Google Scholar] [CrossRef]
- Hsu, H.C.; Chen, Y.Y.; Hsu, J.R.C.; Tseng, W.-J. Nonlinear water waves on uniform current in Lagrangian coordinates. J. Nonlinear Math. Phys. 2009, 16, 47–61. [Google Scholar] [CrossRef]
- Waseda, T.; Tamura, H.; Kinoshita, T. Freakish sea index and sea states during ship accidents. J. Mar. Sci. Technol. 2012, 17, 305–314. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, X.-M. Global ship accidents and ocean swell-related sea states. Nat. Hazards Earth Syst. Sci. 2017, 17, 2041–2051. [Google Scholar] [CrossRef]
- Hammack, J.L.; Henderson, D.M.; Segur, H. Progressive waves with persistent two-dimensional surface patterns in deep water. J. Fluid Mech. 2005, 532, 1–52. [Google Scholar] [CrossRef]
- Elgar, S. Waves in oceanic and coastal waters. Oceanography 2007, 20, 133–135. [Google Scholar] [CrossRef]
- Liu, Z.; Fang, K. Two-layer Boussinesq models for coastal water waves. Wave Motion 2015, 57, 88–111. [Google Scholar] [CrossRef]
- Daripa, P.; Dash, R.K. A class of model equations for bi-directional propagation of capillary–gravity waves. Int. J. Eng. Sci. 2003, 41, 201–218. [Google Scholar] [CrossRef]
- Zaghi, S.; Broglia, R.; Di Mascio, A. Analysis of the interference effects for high-speed catamarans by model tests and numerical simulations. Ocean Eng. 2011, 38, 2110–2122. [Google Scholar] [CrossRef]
- Honaryar, A.; Ghiasi, M.; Liu, P.; Honaryar, A. A new phenomenon in interference effect on catamaran dynamic response. Int. J. Mech. Sci. 2021, 190, 106041. [Google Scholar] [CrossRef]
- Faltinsen, O.M. Hydrodynamics of High-Speed Marine Vehicles; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Bessho, M.; Komatsu, M.; Anjoh, M. On motions of a high speed planning boat in regular head sea. J. Soc. Nav. Archit. Jpn. 1974, 1974, 109–120. [Google Scholar] [CrossRef]
- Sun, H.; Huang, D.; Zou, J. Experimental investigation on resistances from stepped trimaran-planing boats. Huazhong Univ. Sci. Technol. 2012, 40, 86–89. [Google Scholar]
- Kim, Y.S.; Hwang, S.K. A Study on Air Resistance and Greenhouse Gas Emissions of an Ocean Leisure Planning Boat. J. Korean Soc. Mar. Environ. Energy 2013, 16, 202–210. [Google Scholar] [CrossRef]
- Shen, H.; Xiao, Q.; Zhou, J.; Su, Y.; Bi, X. Design of hydrofoil for the resistance improvement of planing boat based on CFD technology. Ocean Eng. 2022, 255, 111413. [Google Scholar] [CrossRef]
- Park, K.; Kim, D.J.; Kim, S.Y.; Seo, J.; Suh, I.; Rhee, S.H. Effect of waterjet intake plane shape on course-keeping stability of a planing boat. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 585–598. [Google Scholar] [CrossRef]
- Jinglei, Y.; Hanbing, S.; Xiaowen, L.; Wu, D. Experimental study on wave motion of partial air cushion supported catamaran. Int. J. Nav. Archit. Ocean Eng. 2023, 15, 100525. [Google Scholar] [CrossRef]

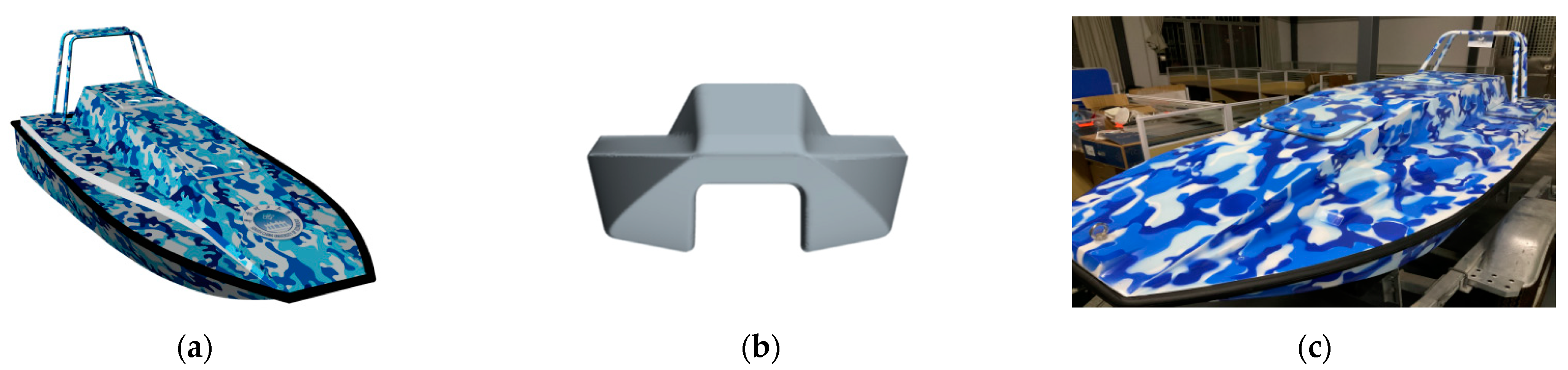
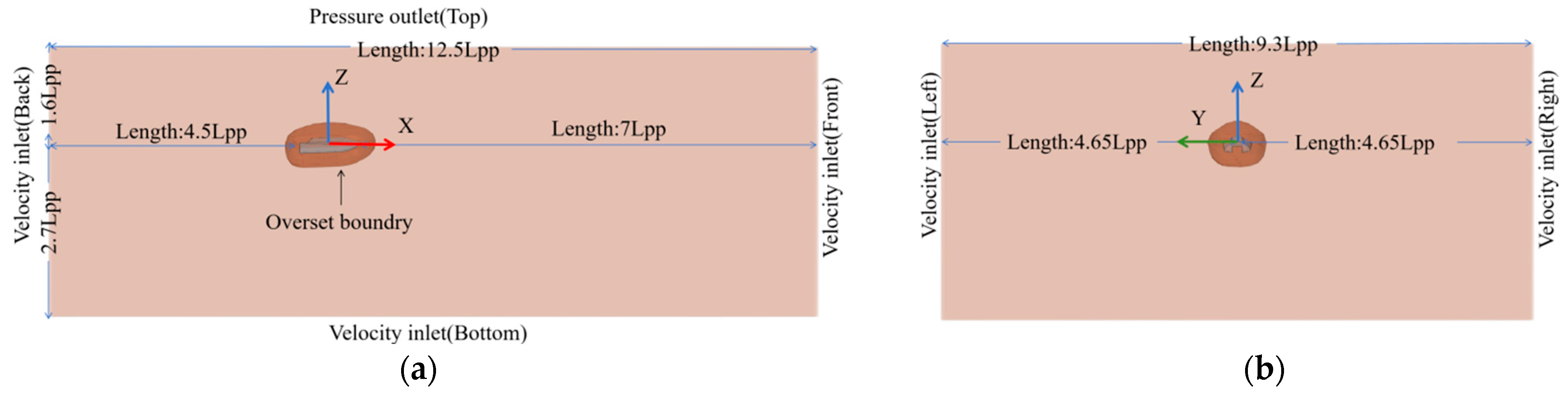

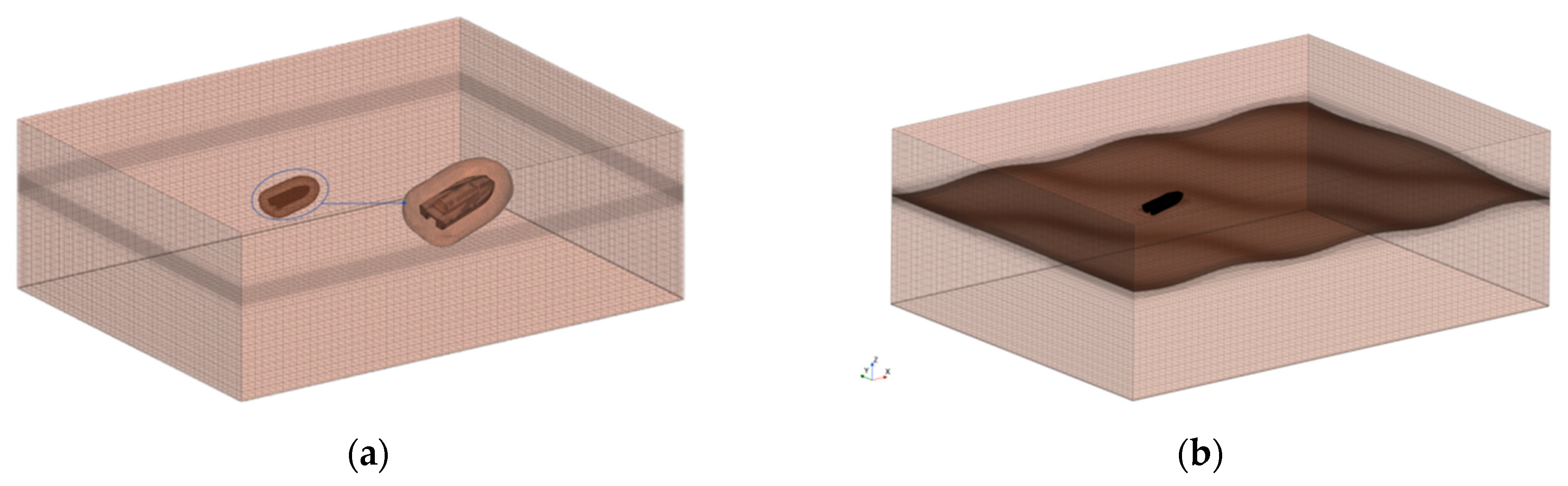
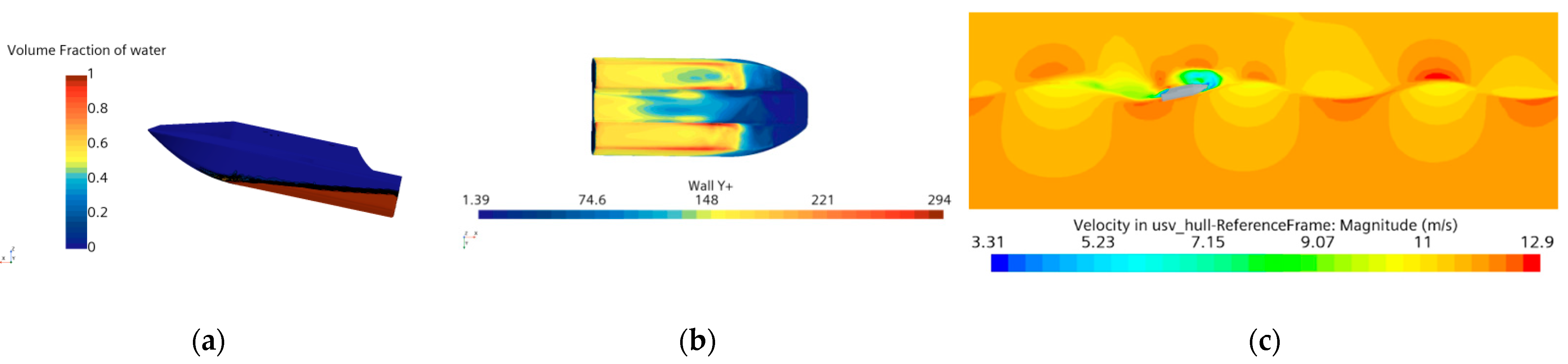
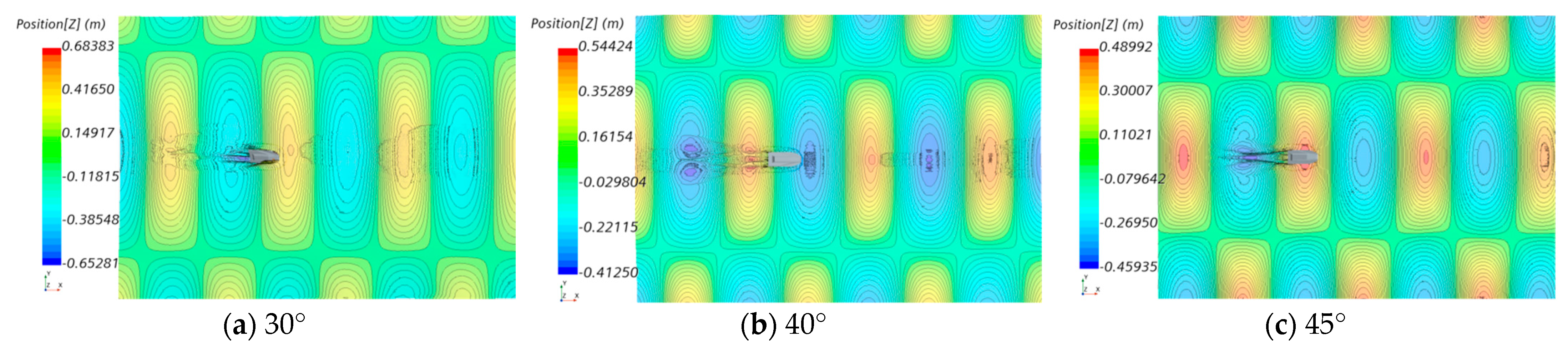
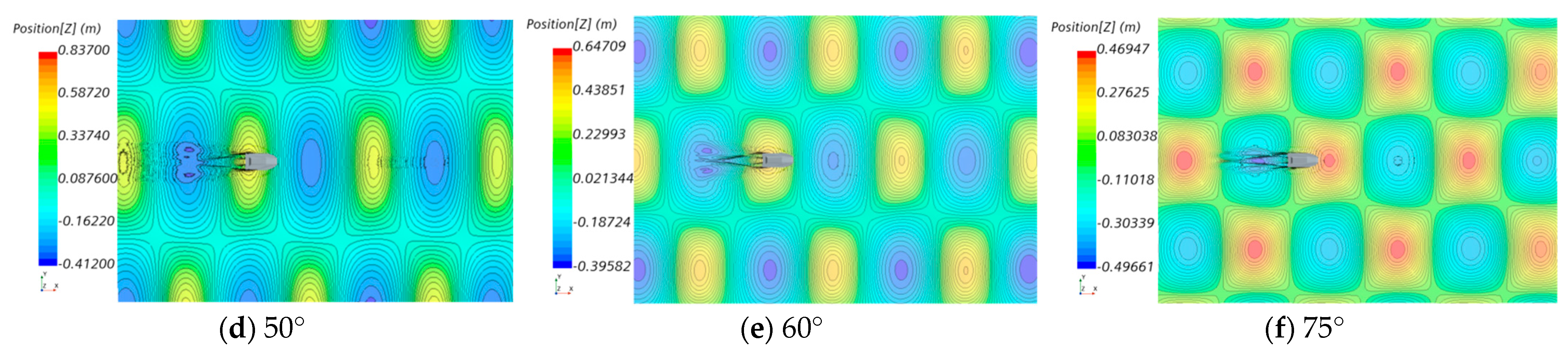









| Characteristic Item | Value |
|---|---|
| Scale (k) | 1:1 |
| Length between perpendiculars (Lpp)/m | 2.7283 |
| Beam overall (B)/m | 1.167 |
| Beam between center of demihull (Bd)/m | 0.8 |
| Demihull beam (Db)/m | 0.367 |
| Depth (D)/m | 0.729 |
| Draft (d)/m | 0.254 |
| Displacement (Δ)/kg | 208.5 |
| Vertical center of gravity from BL (VCG)/m | 0.433 |
| Longitude center of gravity form AP (LCG)/m | 1.0785 |
| Demihulls separation (Dp)/m | 0.415 |
| Demihull height (Dh)/m | 0.249 |
| Wave Amplitude/m | Pitching Amplitude/° | Maximum Slamming Force in Z-Direction/N | |
|---|---|---|---|
| Scheme A | 0.4363 | 16.273 | 2117.63 |
| Scheme B | 0.4065 | 15.278 | 1967.22 |
| Scheme C | 0.4012 | 15.052 | 1919.41 |
| (%) | 1.304 | 1.479 | 2.430 |
| (%) | 7.33 | 6.513 | 7.646 |
| (%) | 17.785 | 22.714 | 31.786 |
| (%) | 1.790 | 1.759 | 2.889 |
| Wave Amplitude/m | Pitching Amplitude/° | Maximum Slamming Force in Z-Direction/N | |
|---|---|---|---|
| Scheme A | 0.4128 | 15.625 | 2042.91 |
| Scheme B | 0.4065 | 15.278 | 1967.22 |
| Scheme C | 0.4022 | 15.049 | 1932.84 |
| (%) | 1.075 | 1.499 | 1.747 |
| (%) | 1.575 | 2.271 | 3.848 |
| (%) | 68.254 | 65.994 | 45.422 |
| (%) | 1.099 | 1.532 | 1.786 |
| (a) | |||||||||||
| Natural pitching tests and results | Natural heave tests and results | ||||||||||
| Initial Trim Angle /deg | −10 | −5 | 5 | 0 | 0 | 0 | |||||
| Initial Heave /m | 0 | 0 | 0 | −0.1 | −0.05 | 0.05 | |||||
| Empirical Formula Results/s | 1.12 | 1.12 | 1.12 | 1.21 | 1.21 | 1.21 | |||||
| EXP Results in design & fabrication/s | 1.253 | 1.251 | 1.250 | 1.304 | 1.301 | 1.303 | |||||
| CFD Results/s | 1.187 | 1.180 | 1.180 | 1.332 | 1.314 | 1.317 | |||||
| Error (%) | 5.27 | 5.68 | 5.60 | 2.15 | 0.99 | 1.07 | |||||
| (%) | 2.0 | 1.8 | 1.8 | 1.5 | 1.2 | 1.2 | |||||
| (%) | 6.12 | 3.97 | 4.51 | 1.42 | 1.18 | 1.16 | |||||
| (%) | 4.37 | 3.94 | 3.92 | 3.67 | 1.37 | 1.34 | |||||
| (b) | |||||||||||
| Initial condition | |||||||||||
| Trim Angle /deg | Heave /m | (%) | E (%) | (%) | E (%) | ||||||
| −10 | 0 | 7.78 | 5.27 | NaN | |||||||
| −5 | 0 | 5.88 | 5.68 | ||||||||
| 5 | 0 | 6.24 | 5.60 | ||||||||
| 0 | −0.1 | NaN | 4.21 | 2.15 | |||||||
| 0 | −0.05 | 2.17 | 0.99 | ||||||||
| 0 | 0.05 | 2.14 | 1.07 | ||||||||
| Wave | Inclination Angles of Wave Train 2θ/deg | Main Sub-Wavelength to Ship Length Ratio λ/L | Wave Amplitude/m | k1h = k2h (Criteria for Deep Water Waves) | Ship Navigating Speed (Fr) | Mesh Grid Mount/Million |
|---|---|---|---|---|---|---|
| Regular intersecting waves | 30 40 45 50 60 75 | 3.3 | 0.4 | 4.88 | 8 m/s (1.593) | 22 |
| Wave | 60 | 3.3 | 0.4 | 4.88 | 8 m/s (1.593) | 12, 25, 32 |
| Regular intersecting waves | 60 | 3.3 | 0.4 | 4.88 | 2 m/s (0.398), 4 m/s (0.797) | 22 |
| Wave | 60 | 4.4, 6.6 | 0.4 | 4.88 | 8 m/s (1.593) | 22 |
| Symbol Name | Signal |
|---|---|
| Wave amplitude | ξa |
| Heave amplitude | Za |
| Pitch amplitude | θa |
| Wave circular frequency | ω |
| Encounter frequency | ωe |
| Pitch natural frequency | ωm |
| Nondimensional wave frequency |
| Routes | Longitude Towing Speed, v0/m × s−1 | Lateral Moving Amplitude, y0/m | Swaying Period, T/s | Initial Lateral Position Offset from Original Route, b0/m |
|---|---|---|---|---|
| Trajectory 1 | 8 | 4.5 | 2.82 | 0 |
| Trajectory 2 | 8 | 4.5 | 5.64 | 0 |
| Trajectory 3 | 8 | 1.125 | 2.82 | 2.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, X.; Zheng, G.; Cai, R.; Chen, Y.; Xiao, G. Computational Fluid Dynamics Prediction of the Sea-Keeping Behavior of High-Speed Unmanned Surface Vehicles Under the Coastal Intersecting Waves. J. Mar. Sci. Eng. 2025, 13, 83. https://doi.org/10.3390/jmse13010083
Hong X, Zheng G, Cai R, Chen Y, Xiao G. Computational Fluid Dynamics Prediction of the Sea-Keeping Behavior of High-Speed Unmanned Surface Vehicles Under the Coastal Intersecting Waves. Journal of Marine Science and Engineering. 2025; 13(1):83. https://doi.org/10.3390/jmse13010083
Chicago/Turabian StyleHong, Xiaobin, Guihong Zheng, Ruimou Cai, Yuanming Chen, and Guoquan Xiao. 2025. "Computational Fluid Dynamics Prediction of the Sea-Keeping Behavior of High-Speed Unmanned Surface Vehicles Under the Coastal Intersecting Waves" Journal of Marine Science and Engineering 13, no. 1: 83. https://doi.org/10.3390/jmse13010083
APA StyleHong, X., Zheng, G., Cai, R., Chen, Y., & Xiao, G. (2025). Computational Fluid Dynamics Prediction of the Sea-Keeping Behavior of High-Speed Unmanned Surface Vehicles Under the Coastal Intersecting Waves. Journal of Marine Science and Engineering, 13(1), 83. https://doi.org/10.3390/jmse13010083







