An Analysis of the Effect of Cavitation on Rotor–Stator Interaction in a Bidirectional Bulb Tubular Pump
Abstract
1. Introduction
2. Experimental Setup
3. Numerical Simulation Setup
3.1. Governing Equations
3.2. Turbulence Model
3.3. Cavitation Model
3.4. Numerical Simulation Calculation Setup
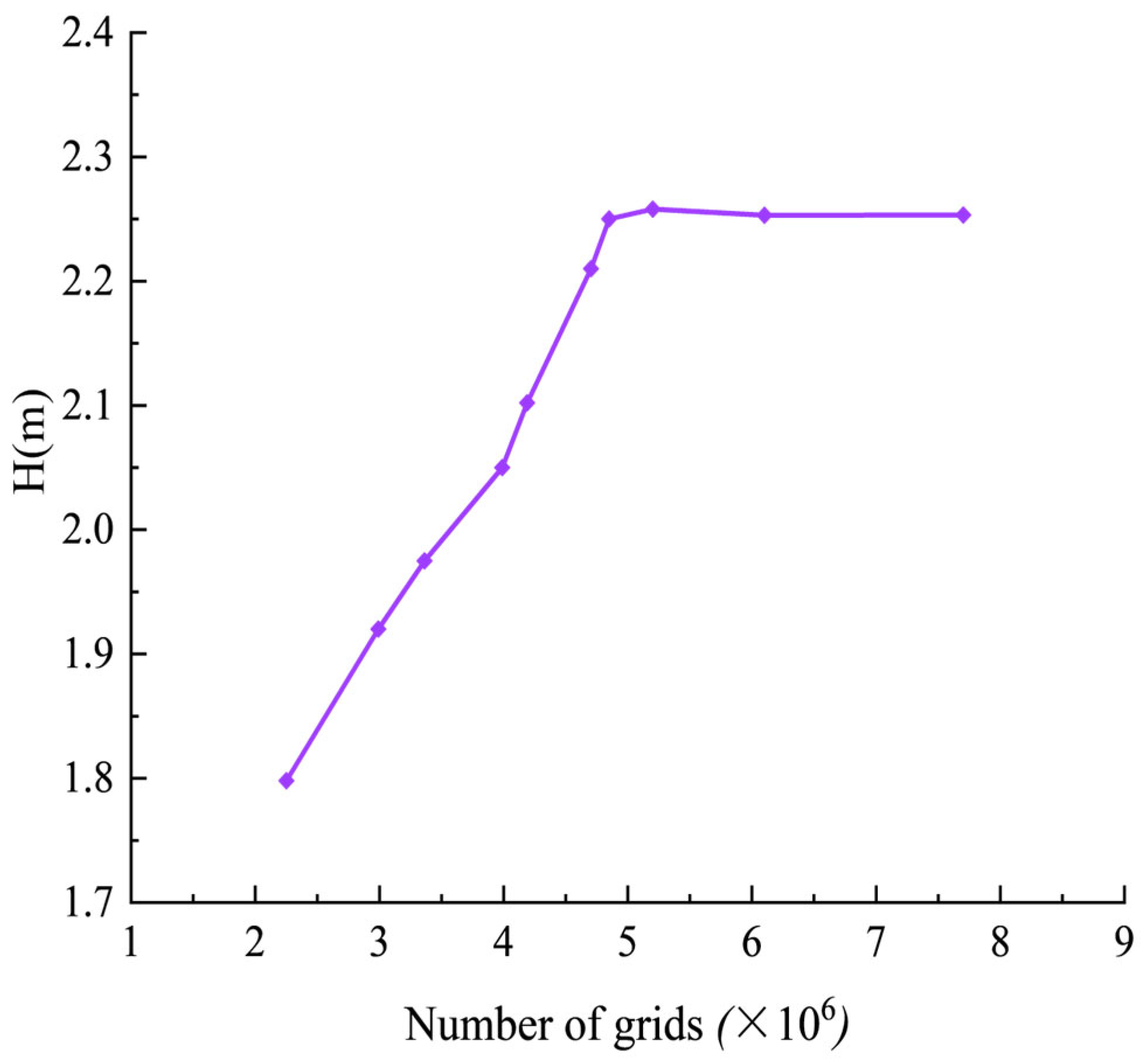
3.5. Grid Independence Analysis
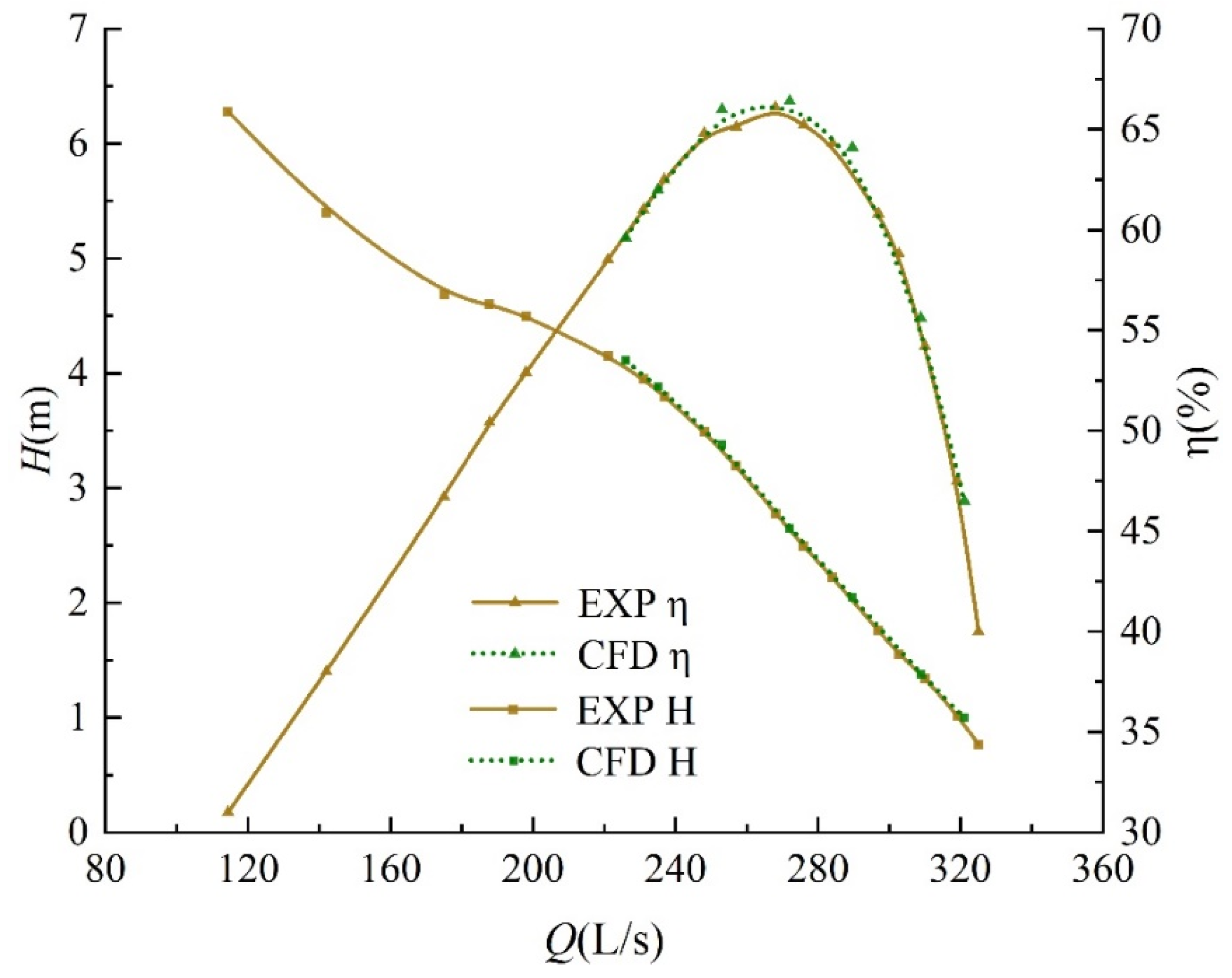
3.6. Verification of the Accuracy of External Characteristic Curves and Numerical Simulations
4. Results and Analysis
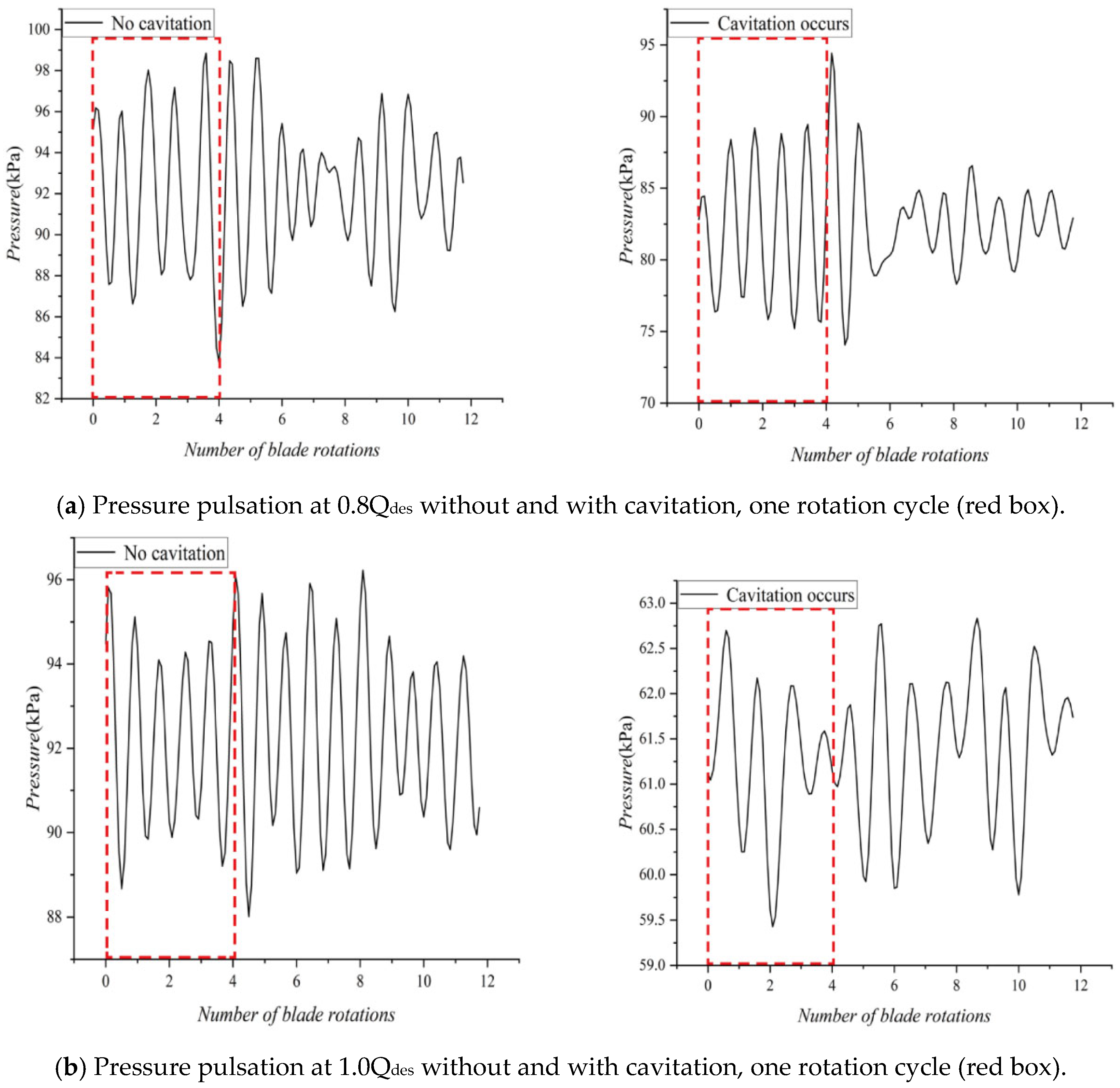
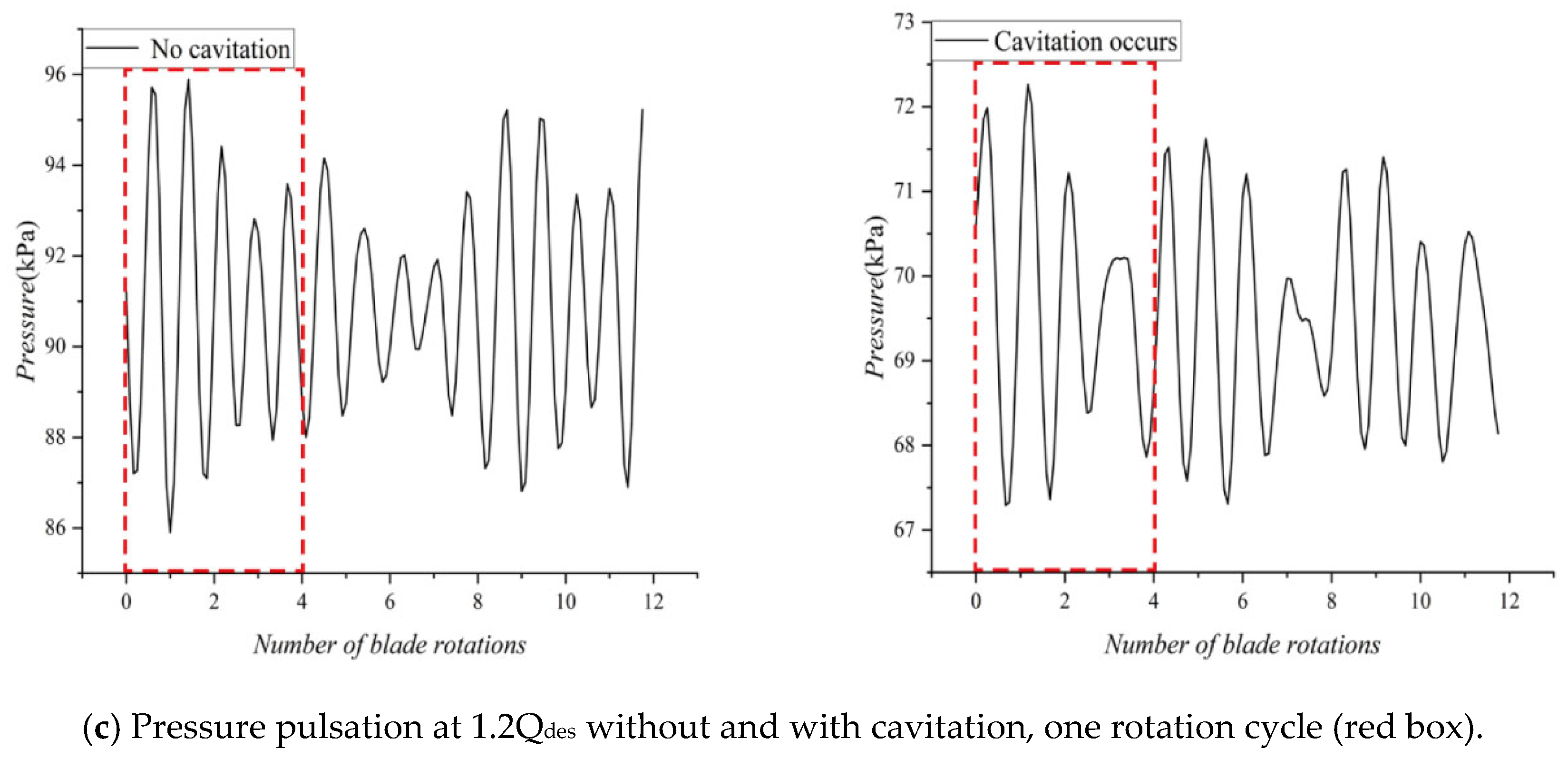
4.1. Time-Domain Analysis of Pressure Pulsation
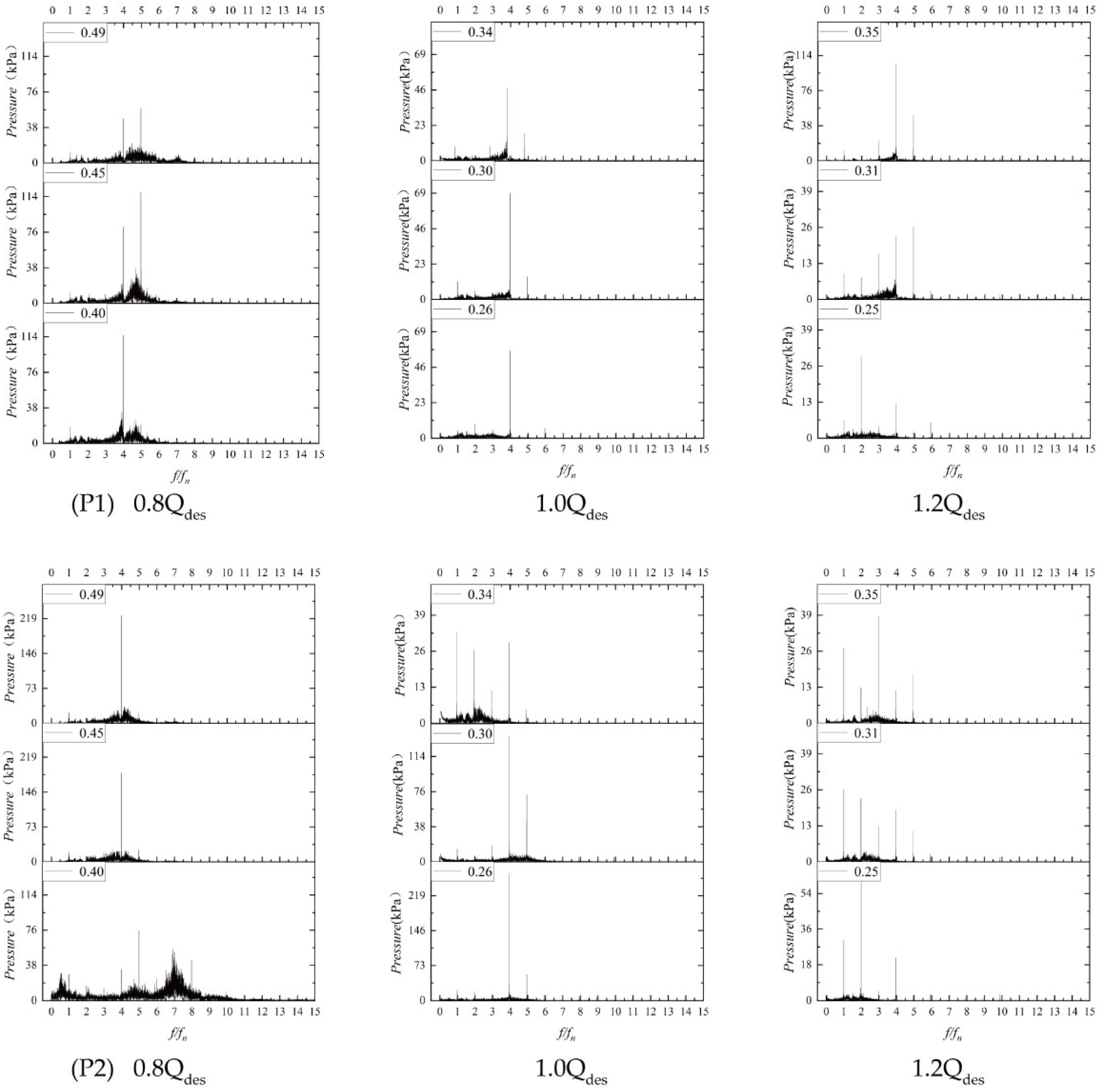
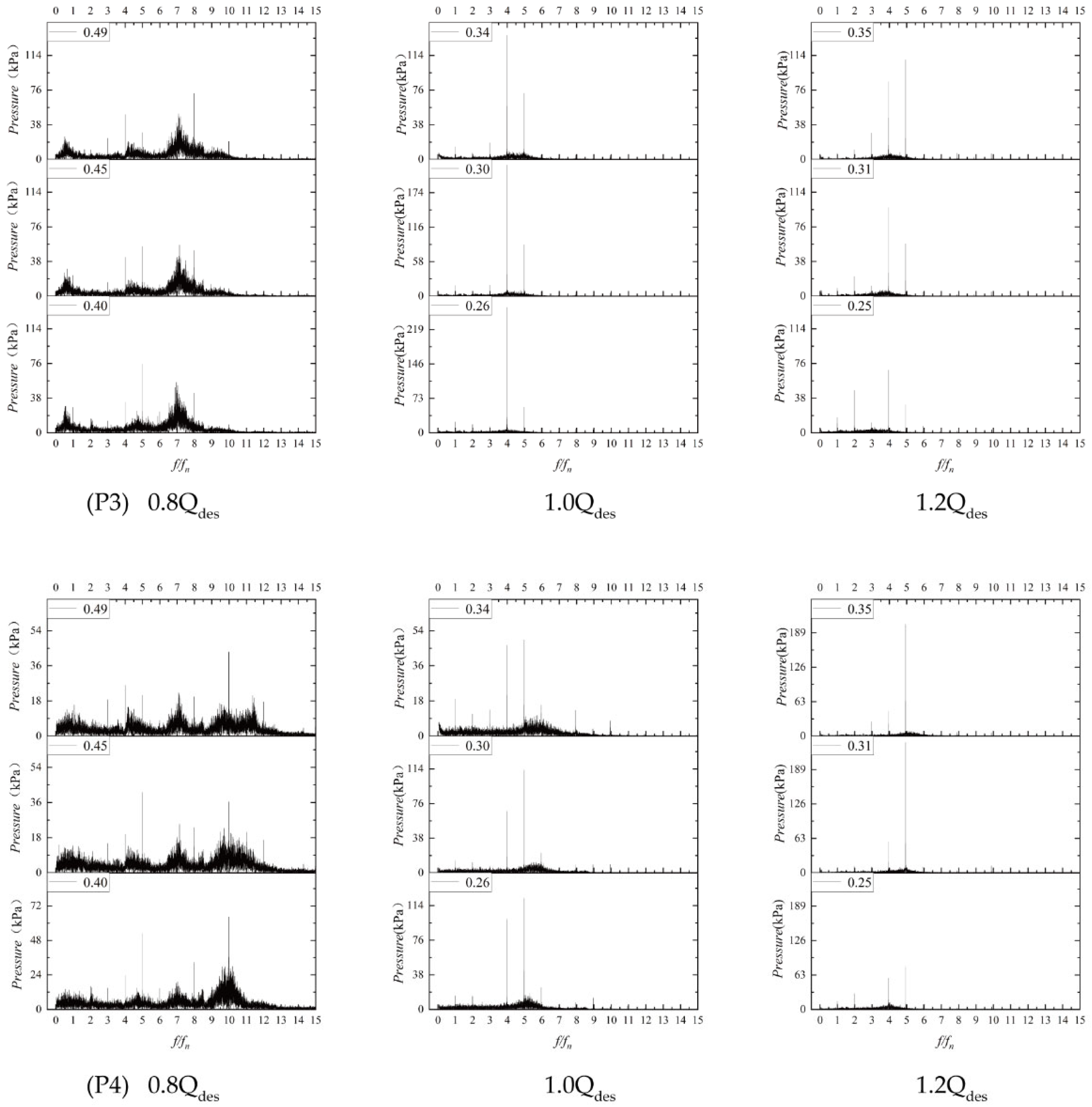
4.2. Analysis of Pressure Pulsation
4.3. Analysis of Flow Field at Low Flow Rates
5. Conclusions
- (1)
- Through the analysis of pressure pulsation data obtained from experiments at different locations before and after cavitation, it is observed that the emergence of cavitation enhances the rotor–stator interaction effect. Under certain operating conditions, the dominant and secondary frequencies observed before cavitation may switch under the influence of rotor–stator interaction after cavitation occurs;
- (2)
- As indicated by an analysis of the amplitude of the dominant frequency in the pressure pulsation frequency domain, rotor–stator interaction occurs in both the FVP and RVP. It has a more pronounced effect on pressure pulsation in the FVP compared to the RVP, particularly under low-flow conditions.
- (3)
- Through numerical simulation of the flow field, the presence of the front guide vanes in a bidirectional submerged tubular pump causes a certain deviation in the flow field during forward operation, resulting in unstable and non-smooth flow into the impeller, which exacerbates rotor–stator interaction within the FVP.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adu, D.; Jianguo, D.; Darko, R.O.; Boamah, K.B.; Emmanuel, A. Investigating the state of renewable energy and concept of pump as turbine for energy generation development. Energy Rep. 2020, 6 (Suppl. S6), 60–66. [Google Scholar] [CrossRef]
- Chen, J.; Huang, W. Risk and countermeasures of across river basins and long distance water transfer project. China Water Resour. 2006, 24, 11–14. [Google Scholar]
- Cavazzini, G.; Houdeline, J.B.; Pavesi, G.; Teller, O.; Ardizzon, G. Unstable behaviour of pump-turbines and its effects on power regulation capacity of pumped-hydro energy storage plants. Renew. Sustain. Energy Rev. 2018, 94, 399–409. [Google Scholar] [CrossRef]
- Feng, W.; Cheng, Q.; Guo, Z.; Qian, Z. Simulation of cavitation performance of an axial flow pump with inlet guide vanes. Adv. Mech. Eng. 2016, 8, 1–8. [Google Scholar] [CrossRef]
- Lu, J.; Yuan, S.; Parameswaran, S.; Yuan, J.; Ren, X.; Si, Q. Investigation on the vibration and flow instabilities induced by cavitation in a centrifugal pump. Adv. Mech. Eng. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Pavesi, G.; Cavazzini, G.; Ardizzon, G. Time-frequency characterization of rotating instabilities in a centrifugal pump with a vaned diffuser. Int. J. Rotating Mach. 2008, 2008, 202179. [Google Scholar] [CrossRef]
- Pavesi, G.; Cavazzini, G.; Ardizzon, G. Time–frequency characterization of the unsteady phenomena in a centrifugal pump. Int. J. Heat Fluid Flow 2008, 29, 1527–1540. [Google Scholar] [CrossRef]
- Khalifa, A.E.; Al-Qutub, A.M.; Ben-Mansour, R. Study of pressure fluctuations and induced vibration at blade-passing frequencies of a double volute pump. Arab. J. Sci. Eng. 2011, 36, 1333–1345. [Google Scholar] [CrossRef]
- Chalghoum, I.; Elaoud, S.; Kanfoudi, H.; Akrout, M. The effects of the rotor-stator interaction on unsteady pressure pulsation and radial force in a centrifugal pump. J. Hydrodyn. 2018, 30, 672–681. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, C.; Fu, T.; Zhang, T.; Feng, A.; Jin, Y. Numerical analysis and model test verification of energy and cavitation characteristics of axial flow pumps. Water 2022, 14, 2853. [Google Scholar] [CrossRef]
- Fei, Z.; Zhang, R.; Xu, H.; Feng, J.; Mu, T.; Chen, Y. Energy performance and flow characteristics of a slanted axial-flow pump under cavitation conditions. Phys. Fluids 2022, 34, 035121. [Google Scholar] [CrossRef]
- Zharkovskii, A.; Svoboda, D.; Borshchev, I.; Klyuyev, A.; Ivanov, E.; Shutsky, S. Axial-Flow Pump with Enhanced Cavitation Erosion Resistance. Energies 2023, 16, 1344. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R.; Alhamid, J. Experimental Investigation to Utilize Low-cost Sensors of Early Cavitation Prediction in Axial Pump Based on Acoustic and Vibration Approaches. J. Appl. Fluid Mech. 2024, 18, 16–31. [Google Scholar]
- Pei, J.; Meng, F.; Li, Y.; Yuan, S.; Chen, J. Effects of distance between impeller and guide vane on losses in a low head pump by entropy production analysis. Adv. Mech. Eng. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Chalghoum, I.; Kanfoudi, H.; Elaoud, S.; Akrout, M.; Zgolli, R. Numerical modeling of the flow inside a centrifugal pump: Influence of impeller–volute interaction on velocity and pressure fields. Arab. J. Sci. Eng. 2016, 41, 4463–4476. [Google Scholar] [CrossRef]
- Asim, T.; Mishra, R. Large-Eddy-Simulation-based analysis of complex flow structures within the volute of a vaneless centrifugal pump. Sādhanā 2017, 42, 505–516. [Google Scholar] [CrossRef]
- Cheng, Z.; Ma, Q.; Liu, H.; Dong, L.; Pan, Q. Influence of dynamic and static interference on the internal flow and vibration and noise characteristics of marine centrifugal pump. J. Appl. Fluid Mech. 2023, 16, 1989–2001. [Google Scholar]
- Ran, H.; Luo, X.; Zhu, L.; Zhang, Y.; Wang, X.; Xu, H. Experimental study of the pressure fluctuations in a pump turbine at large partial flow conditions. Chin. J. Mech. Eng. 2012, 25, 1205–1209. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, F. Investigation on hydrodynamic characteristics of coastal axial flow pump system model under full working condition of forward rotation based on experiment and CFD method. Ocean. Eng. 2022, 253, 111286. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; Ge, J.; Cao, W.; Zhang, Q.; Zhu, Y.; Chang, H. Internal flow characteristics of high-specific-speed centrifugal pumps with different number of impeller blades under large flow conditions. Machines 2023, 11, 138. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Zhang, D.; Shi, W.; Zang, J. Numerical Analysis of the Effect of Cavitation on the Tip Leakage Vortex in an Axial-Flow Pump. J. Mar. Sci. Eng. 2021, 9, 775. [Google Scholar] [CrossRef]
- Menter, F. Stress-Blended Eddy Simulation (SBES)—A New Paradigm in Hybrid RANS-LES Modeling. In Progress in Hybrid RANS-LES Modelling, Papers Contributed to the 6th Symposium on Hybrid RANS-LES Methods, Strasbourg, France, 26–28 September 2016; Springer International Publishing: Cham, Switzerland, 2018; pp. 27–37. [Google Scholar]
- Huang, R.; Ji, B.; Luo, X.; Zhai, Z.; Zhou, J. Numerical investigation of cavitation-vortex interaction in a mixed-flow waterjet pump. J. Mech. Sci. Technol. 2015, 29, 3707–3716. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, L.; Guo, P.; Hong, F. Numerical investigation of three dimensional cavitating performance of NACA66 hydrofoil base on different cavitation models. Chin. J. Hydrodyn. 2018, 33, 199–206. [Google Scholar]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]



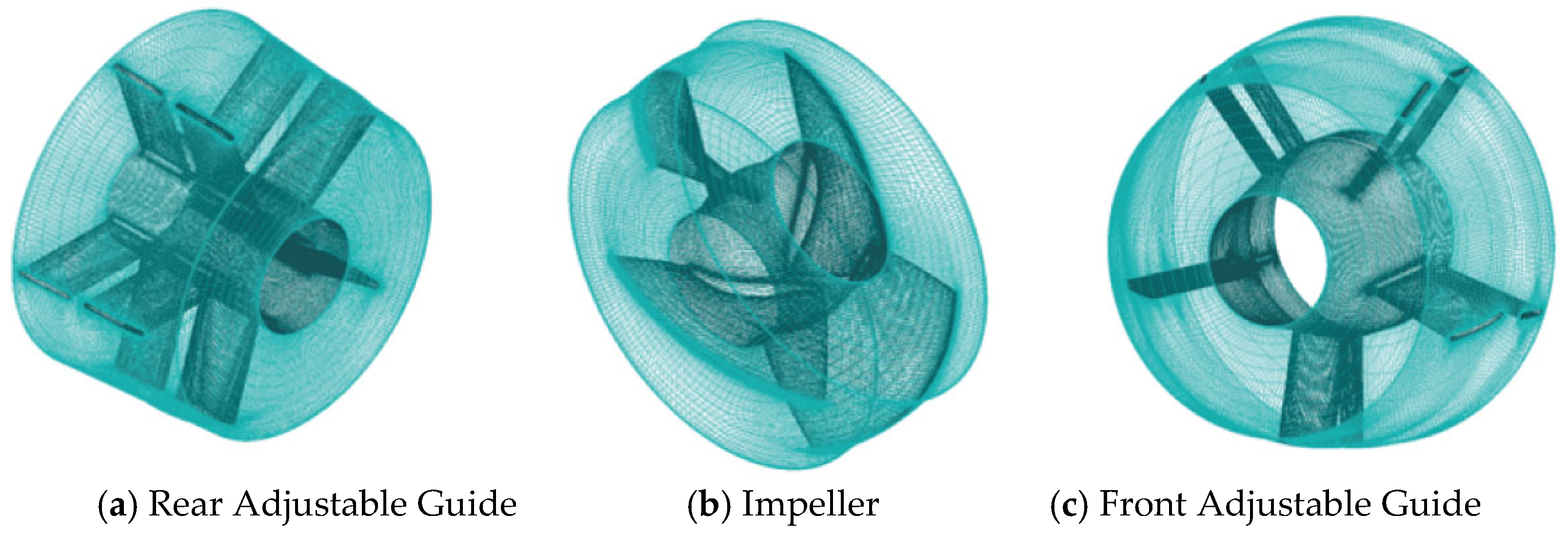


| Bidirectional Bulb Tubular Pump | Axial Flow Pump [19] | Centrifugal Pump [20] | |
|---|---|---|---|
| Design Flow Rate (L/s) | 285 | 203 | 2.78 |
| Design Head/m | 2.84 | 2.01 | 20 |
| Rotational Speed (r/min) | 1264 | 1000 | 980 |
| Diameter of Impeller (mm) | 300 | 300 | 425 |
| No Cavitation | Cavitation Occurs | |
|---|---|---|
| Inlet Pressure/atm | 0.93 | 0.83 |
| Flow Rate/(L⋅s−1) | 228 | 228 |
| Cavitation Number | 0.49 | 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Duan, W.; Liu, H.; Yang, X.; Hu, J.; Sun, D.; Yan, S. An Analysis of the Effect of Cavitation on Rotor–Stator Interaction in a Bidirectional Bulb Tubular Pump. J. Mar. Sci. Eng. 2025, 13, 138. https://doi.org/10.3390/jmse13010138
Zhou Y, Duan W, Liu H, Yang X, Hu J, Sun D, Yan S. An Analysis of the Effect of Cavitation on Rotor–Stator Interaction in a Bidirectional Bulb Tubular Pump. Journal of Marine Science and Engineering. 2025; 13(1):138. https://doi.org/10.3390/jmse13010138
Chicago/Turabian StyleZhou, Yucheng, Wenyong Duan, Haiyu Liu, Xiaodong Yang, Jing Hu, Dawang Sun, and Shikai Yan. 2025. "An Analysis of the Effect of Cavitation on Rotor–Stator Interaction in a Bidirectional Bulb Tubular Pump" Journal of Marine Science and Engineering 13, no. 1: 138. https://doi.org/10.3390/jmse13010138
APA StyleZhou, Y., Duan, W., Liu, H., Yang, X., Hu, J., Sun, D., & Yan, S. (2025). An Analysis of the Effect of Cavitation on Rotor–Stator Interaction in a Bidirectional Bulb Tubular Pump. Journal of Marine Science and Engineering, 13(1), 138. https://doi.org/10.3390/jmse13010138






