Abstract
With the increasing proportion of ships in logistics and the growing prosperity of traffic in maritime, negotiation and cooperative collision avoidance between ships is becoming more and more essential for navigational safety. This paper proposes a Model Predictive Control method that utilizes intention data of the target ship and a quaternion ship domain model to achieve collision avoidance while considering COLREGs, named IQMPC. Firstly, by utilizing the intention data of other ships, trajectories of the own ship and the target ship are well predicted to detect potential collision risks and take optimal avoidance actions in advance while risks exist. Secondly, the quaternion ship domain with its adjacent area is divided into four different parts to reflect the urgency of ship encounters. Collision risk evaluation functions are designed to determine avoidance actions conforming to COLREGs. Thirdly, several different ship encounter scenarios were simulated based on IQMPC to verify its capability.
1. Introduction
Based on the 2023 annual maritime accident investigation report by the European Maritime Safety Agency (EMSA), maritime traffic accidents between 2014 and 2022 resulted in a total of 6781 injuries and 604 fatalities. Human factors were identified as the most significant cause of maritime accidents, accounting for 59.1% of incidents. “Collision” was cited as the primary cause of fatalities, comprising 32.2% of the total deaths [1]. Actively developing Maritime Autonomous Surface Ships (MASS) and improving autonomous collision avoidance for ships are beneficial for reducing maritime accidents, ensuring navigation safety, and protecting the marine environment.
The International Regulations for Preventing Collisions at Sea (COLREGs) were proposed by the International Maritime Organization (IMO) in 1972 to safeguard maritime navigation safety and establish universally applicable international conventions for avoiding collisions between ships [2]. COLREGs explain encounter situations involving manned ships, but with the emergence of MASS, manned ships and MASS will coexist at sea for a long time. Therefore, researchers must consider how to design collision avoidance systems for MASS under the framework of COLREGs widely adopted by manned ships. COLREGs specify different responsibilities and actions for ships in various encounter situations [2]. However, there is no explicit quantitative description of when ships should take action or the urgency of the encounter situations in COLREGs. Many scholars have conducted extensive research on these issues, proposing concepts such as Time at Closest Point of Approach (TCPA) [3], Distance at Closest Point of Approach (DCPA) [4], and ship domain [5] to address these issues. Woerner [6] detailed the calculation methods of TPCA and DCPA that conformed to COLREGs. Minner [7] introduced a distance-only metric function for measuring safety values. Other works [8,9] also touched upon ship collision avoidance and action taking in recent years. Filip [10] focused on collision-avoidance action that shall be taken at an “ample time”, and made some progress by surveying practitioners and extracting their expert knowledge. As for ship domain, Fuji [11] firstly put forward the concept of ship domain in the maritime field, defining the area around a ship that should be clear. Goodwin [12] described a ship domain model for open waters based on radar simulator performance. Wang Ning [13] proposed a comprehensive fuzzy quaternion ship domain model considering various influencing factors using intelligent technology within a unified analytical framework. This model can dynamically adjust the shape of the domain to suit various water conditions. Zhang Liye et al. [14] proposed a ship domain named α-domain using the critical ship safety distance data. Silveira et al. [15] presented a polygonal ship domain method using AIS data. However, the aforementioned studies only describe encounter situations where other ships intrude into the domain of the own ship and construct collision risk assessment functions. When another ship is in the surrounding area with the own ship’s domain not being intruded upon, collision risk still exists due to ship operations and limitations. Therefore, a more comprehensive evaluation scheme for collision risk is necessary.
MASS has become a hotspot in the maritime field. Experts have proposed many algorithms for MASS autonomous collision avoidance, including: Artificial Potential Fields (APF), Velocity Obstacles (VO), and Model Predictive Control (MPC). APF, proposed by Khatib [16], conceptualized the influences of targets and obstacles on agent motion as artificial potential fields. Lv Hongguang [17] proposed an artificial potential field method based on prior path guidance that solved the unreachable and local optimal problem of APF. But it did not consider the COLREGs. VO can project moving objects into their velocity space and calculate velocity obstacle regions to evade obstacles [18]. Zheng H. et al. [19] and Yu D. et al. [20] also made new progress in the VO field, like using an UVO approach with a robust tube idea to handle the uncertainties, or combining the velocity obstacle and A* algorithms for anti-collision path planning. But most of the methods above do not consider the ship’s maneuvering characteristics in ship collision avoidance for encounter situations. Or the target ships will not change their headings during the voyage. These could be the limitations in certain navigation scenarios.
MPC is a very powerful method; it could consider multiple constraints, rolling optimization, and feedback correction. These advantages are very suitable for ship collision avoidance and solve the problems we mentioned above. We can employ a nonlinear ship dynamics model or compute an optimal ship trajectory though this method. Johansen et al. [21] utilized MPC in combination with COLREGs and ship dynamics to achieve autonomous collision avoidance. Hagen et al. [22] introduced a Scene-Based Model Predictive Control (SB-MPC) method by transition cost parameters to reduce the oscillatory motion of the own ship. Tengesdal et al. [23] conducted sea trials. He used a Kalman filter to calculate the probability of collision with nearby obstacles by Monte Carlo simulations and named this algorithm Probability SB-MPC. Some authors combined MPC with other methods [24,25]. But in these methods, the target ships keep their headings, the trajectories are straight lines, and this is not entirely in line with reality.
In recent years, with the development of communication technology [26,27], some collision avoidance studies based on MPC have begun to utilize the intention data of other ships [28,29]. By exchanging heading intention data between ships and knowing the trajectory, future collision risks can be predicted more accurately in advance. If risks exist, appropriate evasive action could be taken to reduce the probability of collision in the future. However, the expression of the severity of encounter situations is not clear enough in the methods we mentioned above. Collision risks generated by calculating multiple control commands at each sampling moment can significantly increase the computation burden, especially when the model and the scene are complex. We need to make good use of intention data in ship collision avoidance.
To address these challenges, this paper proposes a collision avoidance method based on MPC, utilizing a 3 degrees of freedom (DOF) surface ship dynamics model and intention data from the target ship to predict potential collision risks. Additionally, a quaternion ship domain with its adjacent area is employed to describe the urgency of encounter situations, ensuring that ships’ avoidance actions comply with COLREGs and could address immediate danger encounter situations effectively. By designing risk assessment functions, optimal collision avoidance behaviors are determined to reduce the probability of future collision accidents.
The merits of this paper are as follows:
- (1)
- Intention data of the target ships are included to predict their trajectories more accurately, which is beneficial to make more appropriate collision avoidance actions. The own ship predicts both its and the target ship’s motion trajectories, and calculates whether there is collision risk between them in the prediction horizon. If risk exists, the own ship takes avoidance action in advance. Compared to traditional collision avoidance algorithms which design the target ship trajectories based on a steady course, this method considers the intention data of the target ships, understanding the variations of their trajectories, which better aligns with reality.
- (2)
- Encounter situations are categorized into different urgency levels. A quaternion ship domain with its adjacent area is constructed into a safe zone, close-quarter avoidance zone, emergency avoidance zone, and prohibited zone. This distinguishes encounter situations with or without risks that reduce the computational burden of the collision risk generated by multiple control commands at each sampling moment. Moreover, a collision risk assessment function is designed to obtain an optimal heading offset for collision avoidance in different close-quarter situations and immediate danger situations. The own ship’s avoidance action complies with the COLREGs under close-quarter situations. When in immediate danger situations, the own ship could also exhibit good performance.
- (3)
- IQMPC is implemented for autonomous collision avoidance. IQMPC can calculate an optimal trajectory based on the intention data of the target ship, employing a nonlinear ship dynamics model and operational constraints. We constructed various encounter scenarios of head-on situations for simulation: the target ship in a close-quarter avoidance zone or an emergency avoidance zone, with or without the target ship’s intention data scenarios. And we also simulated the crossing and overtaking situations.
The main contents of this paper are as follows: Section 2 introduces the ship dynamics model and COLREGs considered in this paper. Section 3 presents the intention data of the target ship, the categorization of urgency levels and the principles of the algorithm. Section 4 shows the simulations of autonomous collision avoidance using IQMPC.
2. Ship Dynamics Model and COLREGs
2.1. Ship Dynamics Model
For this thesis, a 3-DOF model is used as Equation (1). x, y, and ψ are the position and heading of the ship in the North–East–Down (NED) coordinate frame:
where , , represent the derivative with respect to time. , and are the speed in the surge and sway direction. is the yaw rate in the body-fixed coordinate frame. , , and represent the derivative with respect to time. , , and represent the additional mass of the ship., , and are the hydrodynamic damping of the ship separately. and represent the force in the X-axis and Z-axis in Figure 1.
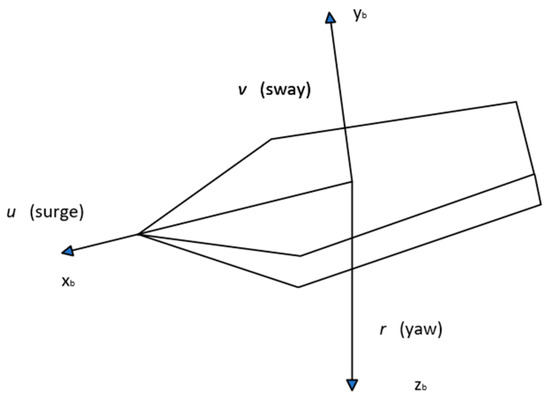
Figure 1.
The 3-DOF model for a surface ship.
2.2. COLREGs
In COLREGs, the encounter situations between two ships can be classified into: head-on or overtaking. Rule 13, Rule 14 and Rule 15 explain the situation of overtaking in Figure 2a, crossing in Figure 2b and head-on in Figure 2c in COLREGs [2]. Ships in different positions need to bear different avoidance responsibilities in Rule 16 and Rule 17. The method is designed based on these rules.
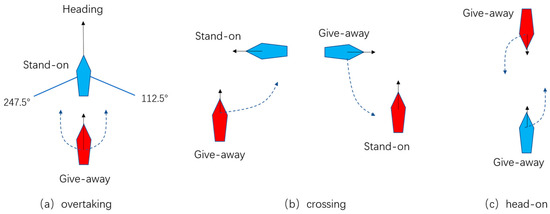
Figure 2.
Different situations. (a) Overtaking, (b) crossing, (c) head-on.
Rule 2 emphasizes the need to consider all dangers of navigation and collision, which may require departing from the rules to avoid immediate danger situations. This means ships could violate their duty to avoid collisions in immediate danger situations.
3. Collision Avoidance Using Intention Data and Quaternion Ship Domain Based on MPC
3.1. Intention Data of the Target Ship
In previous studies, Johansen et al. [21] and Hagen et al. [22] utilized straight-line predictions for the future states of the target ships within the prediction horizon. However, only considering straight-line prediction cannot meet the needs of the target ships that change their trajectories during navigation. This paper implements trajectory prediction based on route exchanges similar to Akdag et al. [23], utilizing the intention data of the target ship to enhance navigation safety. Assuming the target ship’s trajectory is shared via a communication system, the own ship can predict the future states of the target ship based on its speed and heading values from the intention data. This allows the own ship to assess whether there is a risk of collision while maintaining its heading in the prediction horizon. If there is no risk in the future, the own ship continues to maintain its heading; if risk exists, the own ship adopts heading offsets to avoid collision at this moment. The formula for calculating the future trajectory of the target ship is as follows:
where () indicates the current position of target ship at time , is the velocity component of the target ship along the X-axis, is the velocity component of the target ship along the Y-axis, is the resultant velocity of the target ship, is the heading angle of the target ship, and () is the position of the target ship during the prediction horizon.
Figure 3 illustrates the target ship’s trajectory navigating along a zigzag course, with a change in heading at t + 2. If at time t the own ship is unaware of the target ship’s intention when it changes course at t + 2, the own ship will predict the future trajectory of the target ship based on a straight-line trajectory. This may lead to an erroneous collision avoidance decision due to the prediction of collision risk. However, if the own ship is aware of the target ship’s intention data when it changes course at t + 2, the own ship predicts that there is no collision risk between the ships in the future, and there is no need to alter its heading. By utilizing intention data of the target ship to predict their trajectories, unnecessary evasive actions by the own ship can be avoided. Trajectory prediction based on intention data exchanging offers advantages over straight-line prediction.
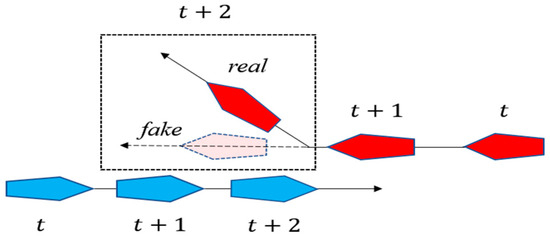
Figure 3.
The own ship’s prediction for the target ship without intention, considering that the target ship keeps a straight-line trajectory (fake). Comparing with the real trajectory of the target ship (red), the ship changes course at t + 2.
3.2. Safety Zone Division
Considering the characteristics of collision avoidance in open water, the quaternion ship domain and its adjacent area is selected as the basis for the collision risk model to describe the urgency level. The quaternion ship domain considers COLREGs, as well as factors such as good seamanship, ship maneuverability, ship length and speed, making it more suitable for ship collision avoidance. Taking the center of the own ship as the origin, the own ship coordinate system is established with the starboard beam direction as the positive Y-axis direction and the bow direction as the positive X-axis direction. In the own ship coordinate system, the boundary equation of the quaternion ship domain is :
where , , and are the radius length of the quaternion ship domain in the positive and negative directions of the Y-axis and the positive and negative directions of the X-axis. and are the symbol judgment functions. In the quaternion ship domain, the domain range presents a distribution where the front is larger than the back, and the right is larger than the left as in Figure 4. This is consistent with the common view in maritime practice that the danger ahead of a ship is greater than behind it, and the danger on the starboard side of a ship is greater than on the port side. Moreover, this aligns well with COLREGs and is more in line with actual situations. The Equations (3)–(5) refer to Wang Ning [13]. The radius of the quaternion ship domain , , and are shown as:
where L is the length of the ship, is the gain coefficient of the advance (AD) in the ship’s turning circle, and is the gain coefficient of the tactical diameter (DT). The coefficients and can be estimated using empirical formulas based on the size and speed of the ship:
where is the resultant speed of the own ship at time t. In Equation (5), the higher the speed of own ship, the greater the value of or . Similarly, the main determining variables L, and in Equation (4) affect , , and . This also indicates that the size of the quaternion ship field increases or decreases with increasing or decreasing ship size and speed. The quaternion ship field is dynamically changing based on the size of the ship and speed changes.
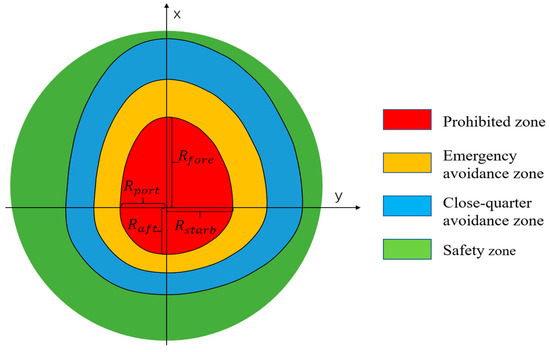
Figure 4.
Ship domain with its adjacent area.
To ensure the two ships can pass at a safe distance under different encounter situations, the own ship’s domain and its adjacent areas are set as follows: prohibited zone, emergency avoidance zone, close-quarter avoidance zone, and safety zone to describe the urgency of encounters:
Prohibited zone: The red area in Figure 4. Centered on the own ship’s quaternion ship domain, this area prohibits the entry of any other ships. Otherwise, a collision will occur.
Emergency avoidance zone: The yellow area in Figure 4. Centered on the own ship’s quaternion ship domain, it expands 1.5 times the domain radius and does not overlap with the prohibited zone. When the target ship appears in this area, there is a higher risk of collision between the ships, constituting an immediate danger situation. If the own ship is the stand-on ship, it can still take evasive action to reduce the risk of collision, ensuring navigation safety as the primary goal.
Close-quarter avoidance zone: The blue area in Figure 4. Centered on the own ship’s quaternion ship domain, expanding two times the domain radius, and does not overlap with the emergency avoidance zone. When the target ship appears in this area, the own ship’s avoidance responsibility is determined based on the target ship’s position according to COLREGs, while constantly observing the target ship’s actions.
Safety zone: The green area in Figure 4. and the outward expansion area. When the target ship appears outside the close-quarter avoidance zone, there is no collision risk between the ships.
The radius of the security domain, , needs to be determined based on the position of the target ship in Figure 5. is the distance between the ships and is the relative speed of the ships.
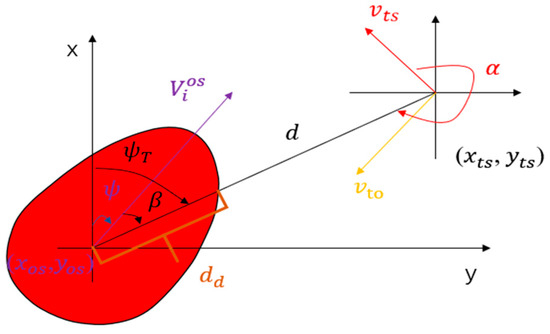
Figure 5.
The relative bearing angle β and the radius of the safe domain in red.
According to Woerner [6], The relative bearing angle is calculated as Equation (6):
where is the course angle of the target ship, and the course is 0° when the ship points in the direction of due north. The true azimuth of the ship concerning the target ship is calculated as:
The relative contact angle is calculated as:
where is the course angle of the target ship, and the course is 0° when the ship points in the direction of due north. The true azimuth of the ship concerning the target ship is calculated as:
where () is the own ship’s position and () is the target ship’s position. The overlapping part of the straight line with the quaternion ship domain can determine the radius of the safety domain . The radius of the target ship domain is a circle, and the encounter safe distance is:
3.3. Collision Risk Evaluation and Prediction
The own ship predicts its states and the target ship’s states at each time step , based on the ships’ courses and speeds at moment , where is the prediction horizon length. Each time step If the target ship appears in the safe zone in the prediction horizon in Figure 6, the distance between the two ships > ; if there is no risk, the own ship keeps its course. is the state of the own ship while keeping its course during the prediction horizon.
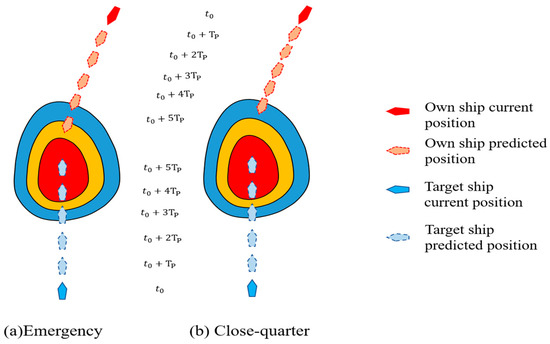
Figure 6.
Different encounter situations for the ships with the prediction that the target ship (red) will appear in different zones of the own ship (blue), when the own ship keeps its current course in the prediction horizon at .
If the distance between two ships < is within the prediction horizon, there will be a risk of collision. Because of the target ship’s different positions and speeds, it may appear in the emergency avoidance zone or the close-quarter avoidance zone of the own ship. The urgency of the situation also varies. The own ship selects different collision risk evaluation functions based on the zone in which the target ship appears within the prediction horizon.
where () is the state of the own ship while changing course and is the prediction of the distance between the ships for each time step. If the target ship only appears in the close-quarter avoidance zone, collision risk evaluation function Equation is used; if the target ship appears in the emergency avoidance zone, collision risk evaluation function Equation is used.
where p determines the importance of the time before the collision and shows that the risk of collision in the near future is greater than in the distant future. q determines the importance of the distance between two ships and increases as the speed of the own ship increases. COLREGs are considered in the equation, taking into account the avoidance responsibilities of the own ship in head-on situations when the target ship appears in the close-quarter avoidance zone. A penalty coefficient k(s) is designed to penalize violations of Rules 14. The s represents different scenarios for choosing different heading offsets. Equation (14) defines the encounter situation between two ships.
When the target ship appears in the emergency avoidance zone in the prediction horizon, the risk of collision between the two ships is high. So, the own ship needs to ensure the maximum distance between the ships in a short time. In consideration of this situation, the avoidance action temporarily violates Rules 14 to ensure safety.We define a set of finite heading offset . During the prediction horizon, the predicted states are based on the same heading offset as Figure 7. Maintaining a consistent avoidance angle enhances safety by providing clear and predictable navigation intentions to other ships. Meanwhile, it can reduce the computational burden of collision risk generated by multiple control commands at each sampling moment. By calculating the collision risk between ships under different heading offset values within the prediction horizon, the optimal avoidance trajectory with the minimum risk is determined, thus selecting the best avoidance course .
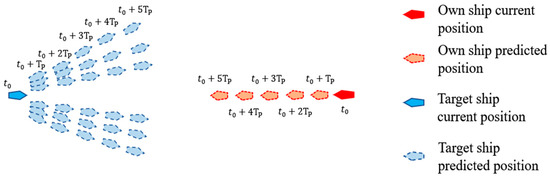
Figure 7.
Prediction of the trajectory if the own ship changes its course. The own ship is blue, the target ship is red.
3.4. IQMPC Collision Avoidance Algorithm
MPC is a control strategy used in engineering to optimize the performance of dynamic systems over a finite future time horizon. The basic principle involves predicting the future behavior of the system using a dynamic model, then computing the optimal control actions that minimize a predefined cost function. The system could adhere to some constraints like physical limitations or operational boundaries. MPC continuously repeats this process over time, updating predictions and control actions based on real-time measurements.
IQMPC is a method based on MPC to achieve ship collision avoidance. IQMPC can consider the real-time states of the ship and the intention data of the target ship. By predicting the ship’s trajectory over a future time span, it assists the ship in making more precise avoidance decisions while considering the constraints of inputs. From Equation (16) we get , and we use IQMPC to achieve collision avoidance.
The core of IQMPC is the optimal control problem, which is expressed as:
where is the cost function, the own ship’s state at time is , is the desired states of the own ship, represents the state error weight matrix, represents the input error weight matrix, and represents the terminal error weight matrix. is the initial states of the own ship at time , is the ship dynamics model as Equation (1), and are the constraints of the inputs. is the decision variable to achieve ship collision avoidance. The speed of the own ship during a collision is considered to be a constant value, so is designed as a constant value. The own ship’s target course is . If risk does not exist, the actual desired course is . The own ship keeps its course to move to its goal. If risk exists, the actual desired course is . The own ship needs to take course steering to avoid a collision.
The principles of the collision avoidance algorithm in this paper are illustrated in Figure 8. If the own ship reaches its goal position , the algorithm ends.
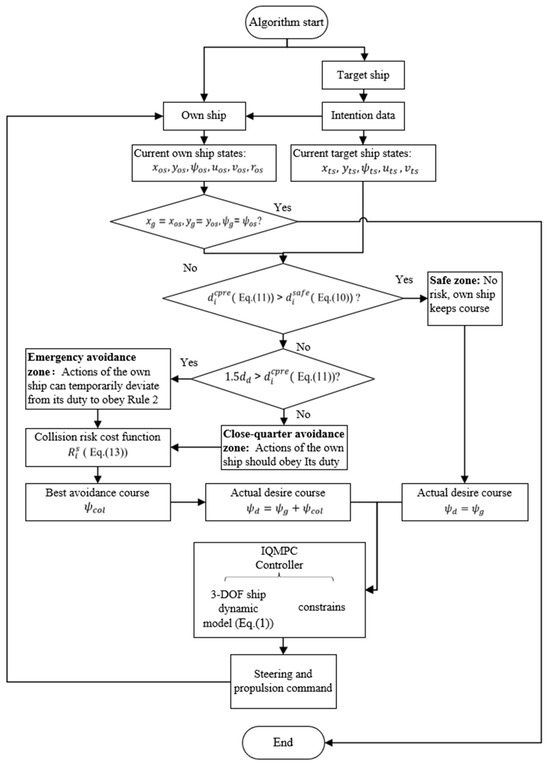
Figure 8.
Algorithm overview.
4. Simulation
As we mentioned in Section 2.2, the aporia of ship collision avoidance at sea is the head-on situation. So, this article validated the effectiveness of the designed ship collision avoidance algorithm by constructing head-on encounter scenarios. We also simulated the situations of crossing and overtaking. In the simulation scenarios, the own ship is controlled by IQMPC. The own ship and the target ship have their different initial positions, speeds and goals. They will meet as head-on, crossing and overtaking scenarios, but in different situations. All simulation experiments are based on MATLAB R2023a. Ship length , , , , , , . , , . Simulation length . , , , . , .
4.1. Close-Quarter Situation
In Figure 9a, the own ship’s initial position is (−10, −10), its goal is (140, 140) and its speed is 3 m/s. The target ship’s initial position is (117, 117), its goal is (−3, −3) and its speed is 2.8 m/s. The own ship and the target ship will meet in the close-quarter avoidance zone as the head-on situation in Figure 9a. This scenario is designed to verify the algorithm in close-quarter situations. The own ship takes a 35° heading offset in Figure 9b, and passes on the port side of the target ship.
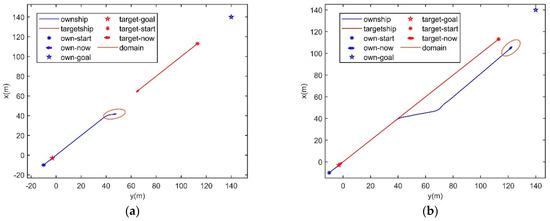
Figure 9.
Head-on situation simulation, when the ships meet in the close-quarter avoidance zone. (a) t = 26 s, (b) t = 60 s.
When there is no risk between the ships, the own ship keeps moving to its goal. The two ships maintain good distances during the encounter as in Figure 10. The own ship’s avoidance behaviors obey COLREGs for head-on situations. The variation of u is caused by the course changes, which accords with the actual ship dynamic characteristics. The ship’s safe domain is determined by the target ship’s position as in Figure 5.
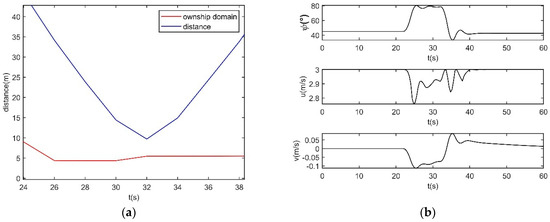
Figure 10.
Head-on situation simulation results, when the ships meet in the close-quarter avoidance zone. (a) Distance, (b) states.
4.2. Immediate Danger Situation
In Figure 11a, the own ship’s initial position is (−10, −10), its goal is (130, 130) and its speed is 3 m/s. The target ship’s initial position is (120, 120), its goal is (0, 0) and its speed is 2.8 m/s. Ships will meet in the emergency avoidance zone in immediate danger as in a head-on situation. This scenario is designed to verify the algorithm in immediate dangerous situations. At the same time, we make a comparison with close-quarter situations in Section 4.1. The own ship predicts that taking a −35° heading offset makes the optimal choice for collision avoidance, and it takes this action in Figure 11b. When there is no risk between the ships, the own ship keeps moving to its goal.
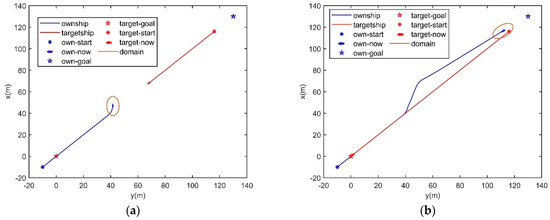
Figure 11.
Head-on situation simulation, when the ships meet in the emergency avoidance zone. (a) t = 26 s, (b) t = 60 s.
When two ships meet, the own ship predicts that they will form an immediate danger situation. The own ship chooses to execute the collision avoidance behavior that constitutes the maximum distance between the two ships. The actions obey Rule 2 in COLREGs. The own ship passes on the starboard side of the target ship with a good distance as in Figure 12.
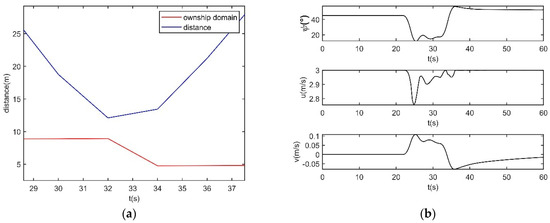
Figure 12.
Head-on situation simulation results, when the ships meet in the emergency avoidance zone. (a) Distance, (b) states.
4.3. With or Without Intention Data
In Figure 13 and Figure 14, the own ship’s initial position is (−10, −10), its goal is (140, 140) and its speed is 3 m/s. The target ship’s initial position is (117, 117), its goal is (−3, 63) and its speed is 2.8 m/s. The target ship will change course at a certain position (69, 69). If the own ship is unaware of the target ship’s change in direction and still predicts the target ship’s trajectory based on its original course, it may mistakenly assess a collision risk between the two ships in future moments, prompting the own ship to move starboard for avoidance as in Figure 13.
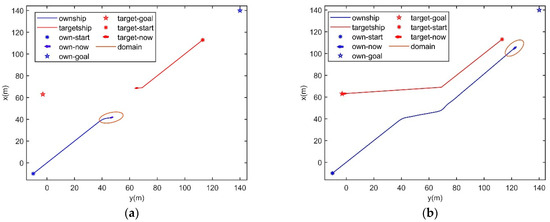
Figure 13.
Head-on situation simulation, when the own ship without intention data meets the target ship in the close-quarter avoidance zone. (a) t = 26 s, (b) t = 60 s.
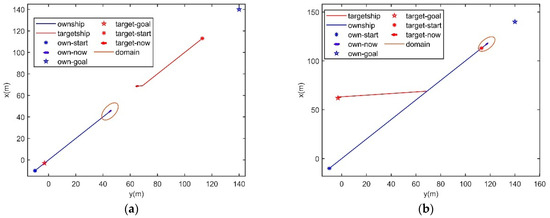
Figure 14.
Head-on situation simulation, when the own ship with intention data meets the target ship in the close-quarter avoidance zone. (a) t = 26 s, (b) t = 60 s.
In reality, when the target ship’s trajectory changes, there is no collision risk between ships. So, the own ship with intention data does not take avoidance action as in Figure 14. The own ship keeps its course, moving to its goal.
Therefore, comparing the two scenarios in Figure 13 and Figure 14, ship avoidance behavior utilizing intention data is more in line with reality. The own ship’s states and the target ship’s states are shown in Figure 15. By using the intention data, unnecessary collision avoidance behaviors have been reduced. In actual navigation, this method demonstrates higher navigation efficiency.
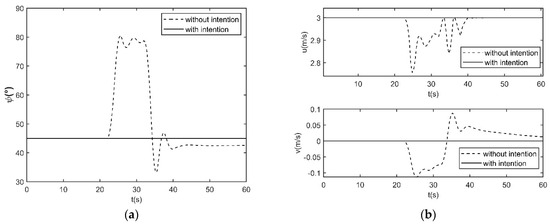
Figure 15.
Head-on situation simulation results, between the own ship with intention data or without intention data, in the close-quarter avoidance zone. (a) Distance, (b) states.
4.4. Overtaking
In Figure 16a, the own ship’s initial position is (−10, −10), its goal is (140, 140) and its speed is 3 m/s. The target ship’s initial position is (20, 20), its goal is (44, 44) and its speed is 0.6 m/s. The target ship’s speed is lower than the own ship’s speed, and the own ship is coming behind the target ship. Ships will meet in the close-quarter avoidance zone as an overtaking situation. The target ship is being overtaken. The own ship should take action to avoid a collision as in Figure 16b. When there is no risk between the ships, the own ship keeps moving to its goal. The two ships keep a good distance during the encounter as in Figure 17. The own ship’s behaviors obey the COLREGs of an overtaking situation.
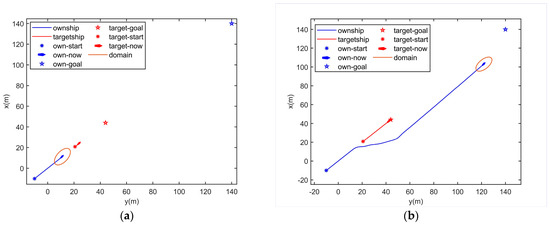
Figure 16.
Overtaking situation simulation results, when the ships meet in the close-quarter avoidance zone. (a) t = 10 s, (b) t = 60 s.
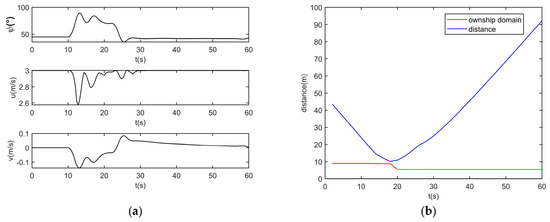
Figure 17.
Overtaking situation simulation results, when the ships meet in the close-quarter avoidance zone. (a) Distance, (b) states.
4.5. Crossing
In Figure 18a, the own ship’s initial position is (−10, −10), its goal is (140, 140) and its speed is 3 m/s. The target ship’s initial position is (−8, 98), its goal is (−22, 112) and its speed is 2.8 m/s. Ships will meet in the close-quarter avoidance zone as a crossing situation. The own ship is the give-away ship, and it takes action to avoid a collision as in Figure 18b. When there is no risk between the ships, the own ship keeps moving to its goal. The two ships keep a good distance during the encounter as in Figure 19. The ship using IQMPC knows its duty and the actions are obeying the COLERGs in different encounter situations.
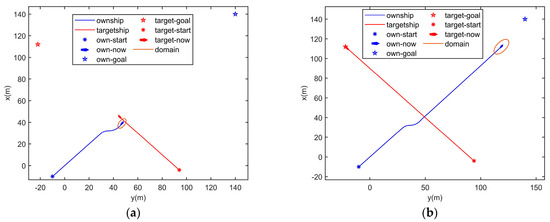
Figure 18.
Crossing situation simulation results, when the ships meet in the close-quarter avoidance zone. (a) t = 26 s, (b) t = 60 s.
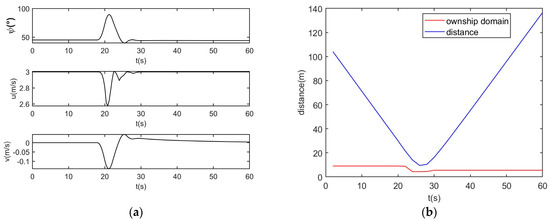
Figure 19.
Crossing situation simulation results, when the ships meet in the close-quarter avoidance zone. (a) Distance, (b) states.
5. Conclusions
This article has proposed an IQMPC collision avoidance method using intention data and quaternion ship domain. We aimed to categorize the encounter situations into different urgency levels through a quaternion ship domain with its adjacent area. We have designed a collision avoidance cost function to comply with COLREGs for different situations, and used IQMPC to compute an optimal trajectory for ship collision avoidance and position tracking. The ship’s collision avoidance behaviors follow the COLREGs. The method can also deal with immediate danger situations. The simulation results of different encounter situations show that the ships keep good states during encounters. In the simulations, the setting of sampling time affects the judgment of IQMPC in close-quarter situations and immediate danger situations. This method demonstrates the advantages of utilizing intention data. The size of the predicted horizon affects the ship’s estimation of future situations, which in turn affects the ship’s judgment, as well as the efficiency and computational burden of the algorithm. The performance of this method in different encounter situations meets our expectations for developing such a useful collision avoidance method
Due to unclear limitations on the conditions that constitute immediate danger in the COLREGs, determining whether a situation between two meeting ships poses an immediate danger often requires the captain’s experience. So, the expansion factor for distinguishing the emergency zone and close-quarter zone for MASS needs further experiments to obtain the best value. We focused on the main technical and operational requirements from COLREGs. Other requirements, like light and sound signals, are not considered in this method. Meanwhile, we do not consider the wind, ocean current forces, or waves in this study. We intend to consider these factors in future research. The conception of IQMPC is appropriate for overtaking and crossing encounter situations, but we mainly focused on head-on situations. We will enrich the encounter scenes in the upcoming work and explore multi-ship encounter situations in the future.
Author Contributions
Conceptualization, H.Z.; methodology, H.Z. and Q.S.; software, H.Z.; validation, H.Z., Q.S. and Y.S.; formal analysis, H.Z. and Y.S.; writing—original draft preparation, H.Z.; writing—review and editing, Y.C.; supervision, Y.C.; funding acquisition, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Dalian Maritime University Navigation College First-class Interdisciplinary Research Project, grant number 2023JXA02.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- EMSA. Annual Overview of Marine Casualties and Incidents. 2023, pp. 7–31. Available online: https://www.emsa.europa.eu/publications/item/5052-annual-overview-of-marine-casualties-and-incidents.html (accessed on 23 May 2024).
- International Maritime Organization. International Regulations for Preventing Collisions at Sea; International Maritime Organization: London, UK, 1972. [Google Scholar]
- Li, B.; Pang, F. An approach of vessel collision risk assessment based on the D–S evidence theory. Ocean Eng. 2013, 74, 16–21. [Google Scholar] [CrossRef]
- Chen, G.; Huang, Z.; Wang, W.; Yang, S. A novel dynamically adjusted entropy algorithm for collision avoidance in autonomous ships based on deep reinforcement learning. J. Mar. Sci. Eng. 2024, 12, 1562. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, Z. A review of ship collision avoidance system. Sci. Technol. Eng. 2019, 19, 32–39. [Google Scholar]
- Woerner, K. Multi-Contact Protocol-Constrained collision avoidance for autonomous marine vehicles. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016; pp. 294–301. [Google Scholar]
- Minne, P.K.E. Automatic Testing of Maritime Collision Avoidance Algorithms. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2017. [Google Scholar]
- Yim, J.; Park, D. Modeling evasive action to be implemented at the minimum distance for collision avoidance in a give-way situation. Ocean Eng. 2022, 263, 112210. [Google Scholar] [CrossRef]
- Gil, M. A concept of critical safety area applicable for an obstacle-avoidance process for manned and autonomous ships. Reliab. Eng. Syst. Saf. 2021, 214, 107806. [Google Scholar] [CrossRef]
- Filip, Z.; Mateusz, G.; Jakub, M. Declarative ship arenas under favourable conditions. Ocean Eng. 2025, 316, 119927. [Google Scholar]
- Fujii. Traffic capacity. J. Navig. 1971, 24, 543–552. [Google Scholar] [CrossRef]
- Goodwin, E. A statistical study of ship domains. J. Navig. 1975, 28, 328–344. [Google Scholar] [CrossRef]
- Wang, N. A novel analytical framework for dynamic quaternion ship domains. J. Navig. 2012, 66, 265–281. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Q. Probabilistic ship domain with applications to ship collision risk assessment. Ocean. Eng. 2019, 186, 106130. [Google Scholar] [CrossRef]
- Silveira, P.; Teixeira, A.P.; Soares, C.G. A method to extract the Quaternion Ship Domain parameters from AIS data. Ocean. Eng. 2022, 257, 111568. [Google Scholar] [CrossRef]
- Khatib, O. Real-Time obstacle avoidance for manipulators and mobile robots. Int. J. Robot. Res. 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Lv, H. Research on Multi Vessel Collision Avoidance Decision and Path Planning Based on Electronic Charts. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2019. [Google Scholar]
- Kuwata, Y.; Wolf, M.T.; Zarzhitsky, D. Safe maritime autonomous navigation with COLREGS, using Velocity Obstacles. IEEE J. Ocean. Eng. 2014, 39, 110–119. [Google Scholar] [CrossRef]
- Zheng, H.; Zhu, J.; Liu, C.; Dai, H. Regulation aware dynamic path planning for intelligent ships with uncertain velocity obstacles. Ocean Eng. 2023, 278, 114401. [Google Scholar] [CrossRef]
- Yu, D.; Roh, M. Method for anti-collision path planning using velocity obstacle and A* algorithms for maritime autonomous surface ship. Int. J. Nav. Archit. Ocean Eng. 2024, 16, 100586. [Google Scholar] [CrossRef]
- Johansen, T.A.; Perez, T.; Cristofaro, A. Ship collision avoidance and COLREGS compliance using Simulation-Based control behavior selection with predictive hazard assessment. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3407–3422. [Google Scholar] [CrossRef]
- Hagen, I.B.; Kufoalor, B.K.M.; Brekke, E.M. MPC-based collision avoidance strategy for existing marine vessel guidance systems. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation, Brisbane, QLD, Australia, 21–25 May 2018; pp. 7618–7623. [Google Scholar]
- Tengesdal, T.; Brekke, E.F.; Johansen, T.A. On collision risk assessment for autonomous ships using Scenario-Based-MPC. IFAC World Congr. 2020, 53, 14509–14516. [Google Scholar]
- Zhu, M.; Skulstad, R.; Zhao, L.; Zhang, H. MPC-based path planning for ship collision avoidance under COLREGS. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022; pp. 930–1935. [Google Scholar]
- Tang, Y.; Chen, L.; Mou, J.; Chen, P. Robust Model Predictive Control for Ship Collision Avoidance under Multiple Uncertainties. IEEE Trans. Transp. Electrif. 2024, 10, 10374–10387. [Google Scholar] [CrossRef]
- Liu, C.; Chu, X.; Wu, W.; Li, S. Human–machine cooperation research for navigation of maritime autonomous surface ships: A review and consideration. Ocean Eng. 2022, 246, 110555. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Jiang, L. Collision-avoidance navigation systems for Maritime Autonomous Surface Ships: A state of the art survey. Ocean Eng. 2021, 235, 109380. [Google Scholar] [CrossRef]
- Kjerstad, K. Collision avoidance system for ships utilizing other vessels’ intentions. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2020. [Google Scholar]
- Akdağ, M.; Fossen, T.I.; Johansen, T.A. Collaborative collision avoidance for autonomous ships using informed Scenario-Based Model Predictive Control. IFAC Pap. 2022, 55, 249–256. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).