Adaptive Transmission Interval-Based Self-Triggered Model Predictive Control for Autonomous Underwater Vehicles with Additional Disturbances
Abstract
1. Introduction
- (1)
- To improve communication efficiency, this paper proposes a novel self-triggered mechanism. This mechanism determines sampling instants using the self-triggered approach and calculates the actual state prediction error based on the sampled states. This method reduces conservatism in state-error estimations. Compared to the traditional self-triggered mechanisms [26,31,33] that determine triggering times based on the maximum-error bound, this approach can lower the triggering frequency.
- (2)
- The proposed algorithm’s theoretical properties are detailed. A minimum inter-triggering interval is specified to prevent Zeno behavior, and adequate conditions are established to guarantee both algorithm feasibility and closed-loop stability. These theoretical results enhance the literature by offering feasibility guarantees that were not addressed in [28,34].
2. Problem Statement
2.1. AUV Model
2.2. Design Objectives
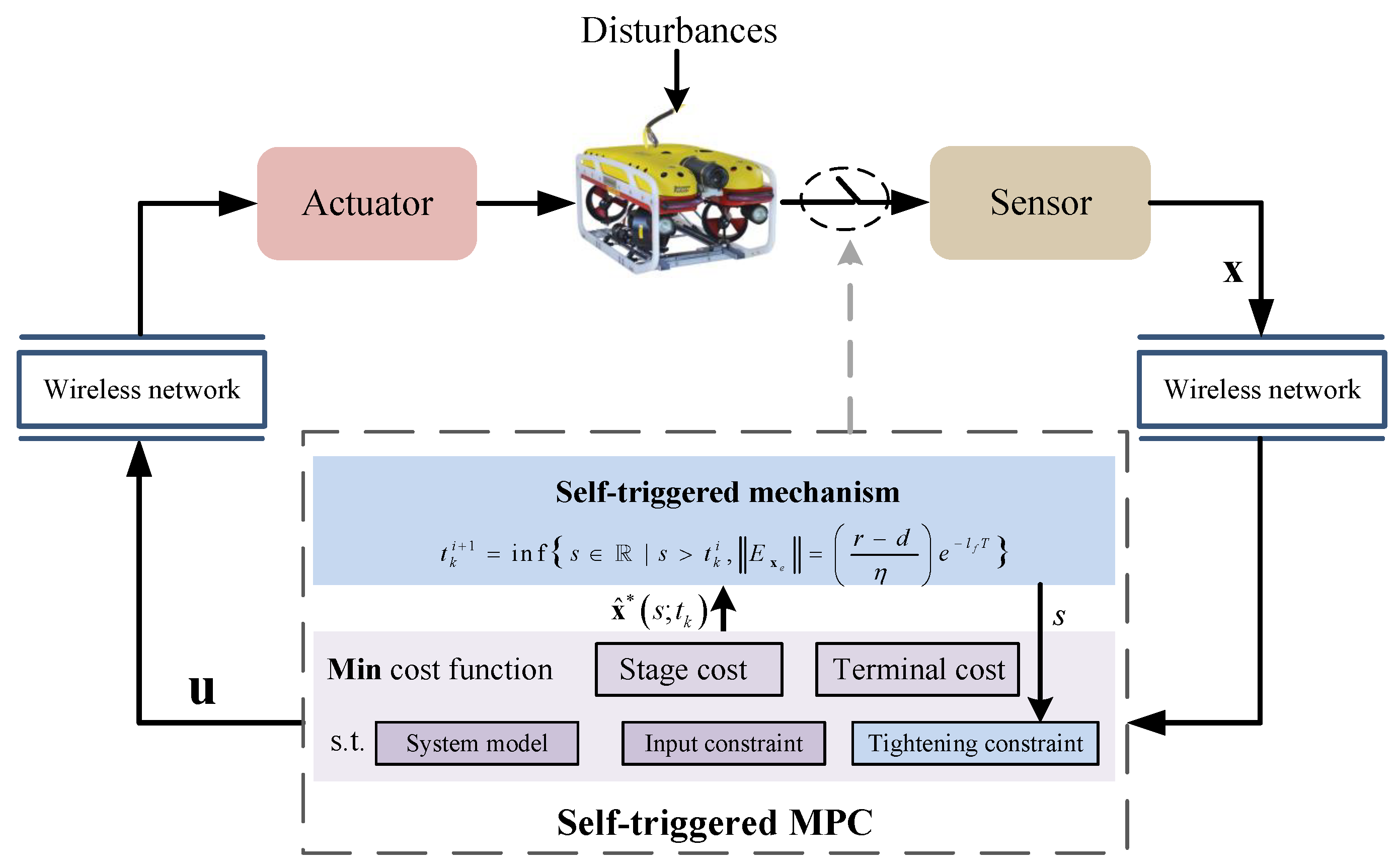
3. Main Results
3.1. Optimal-Control Problem
3.2. Self-Triggered Condition Design
| Algorithm 1 Self-triggered MPC algorithm |
| Input: Choose initial conditions T and initial state , |
| 1: if , then |
| 2: Utilize the locally stabilizing controller for the system outlined in System (4); |
| 3: else |
| 4: At time , determine the optimal-control inputs and the optimal state error |
| by solving (6). |
| 5: Based on the self-triggering condition (14), calculate the subsequent sampling instant |
| , and the combination of termination condition can be obtained . |
| 6: Implement the control for on the actual System (4). |
| 7: end if |
| 8: Update |
4. Recursive Feasibility and Stability Analysis
4.1. Recursive Feasibility Analysis
4.2. Stability Analysis
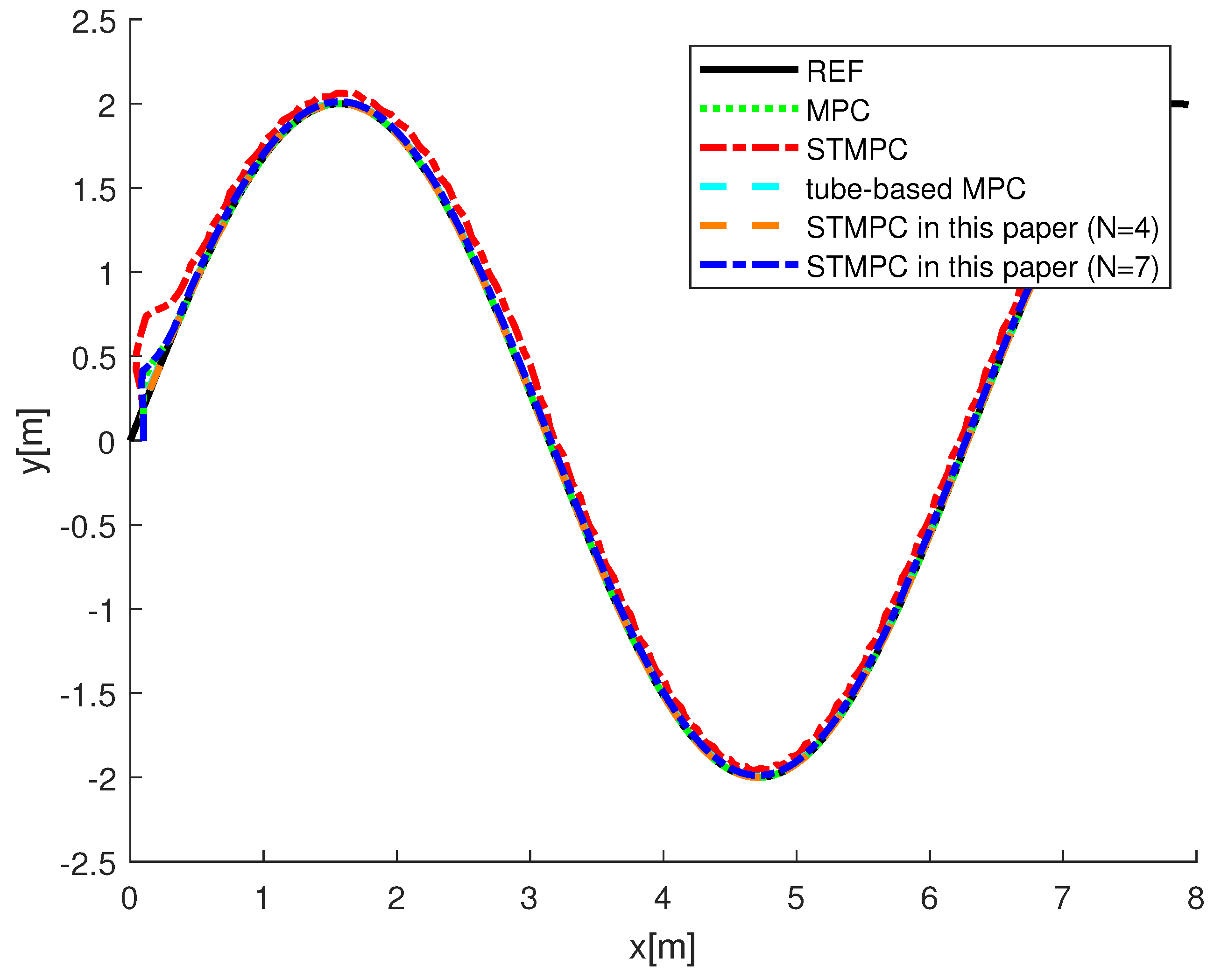
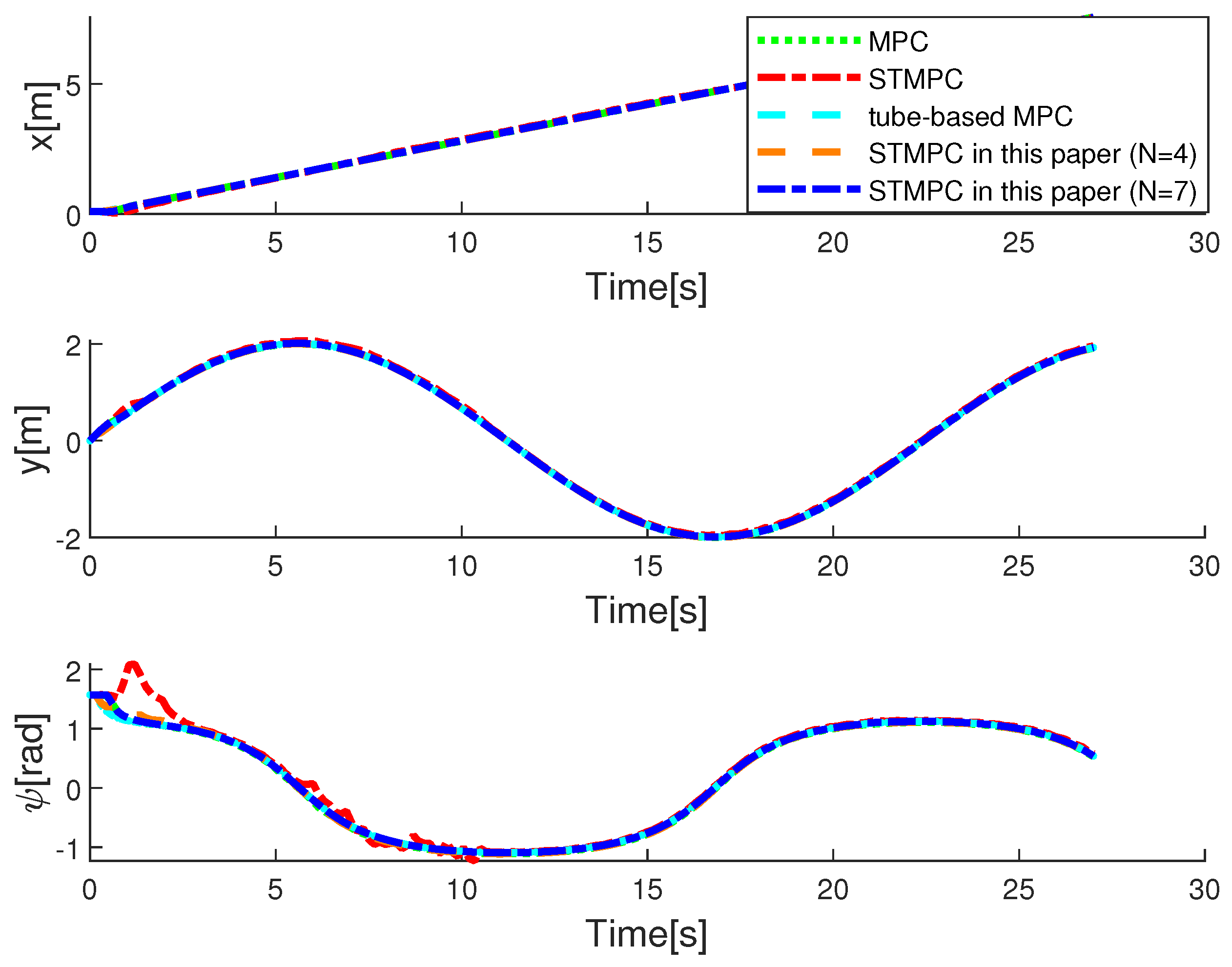
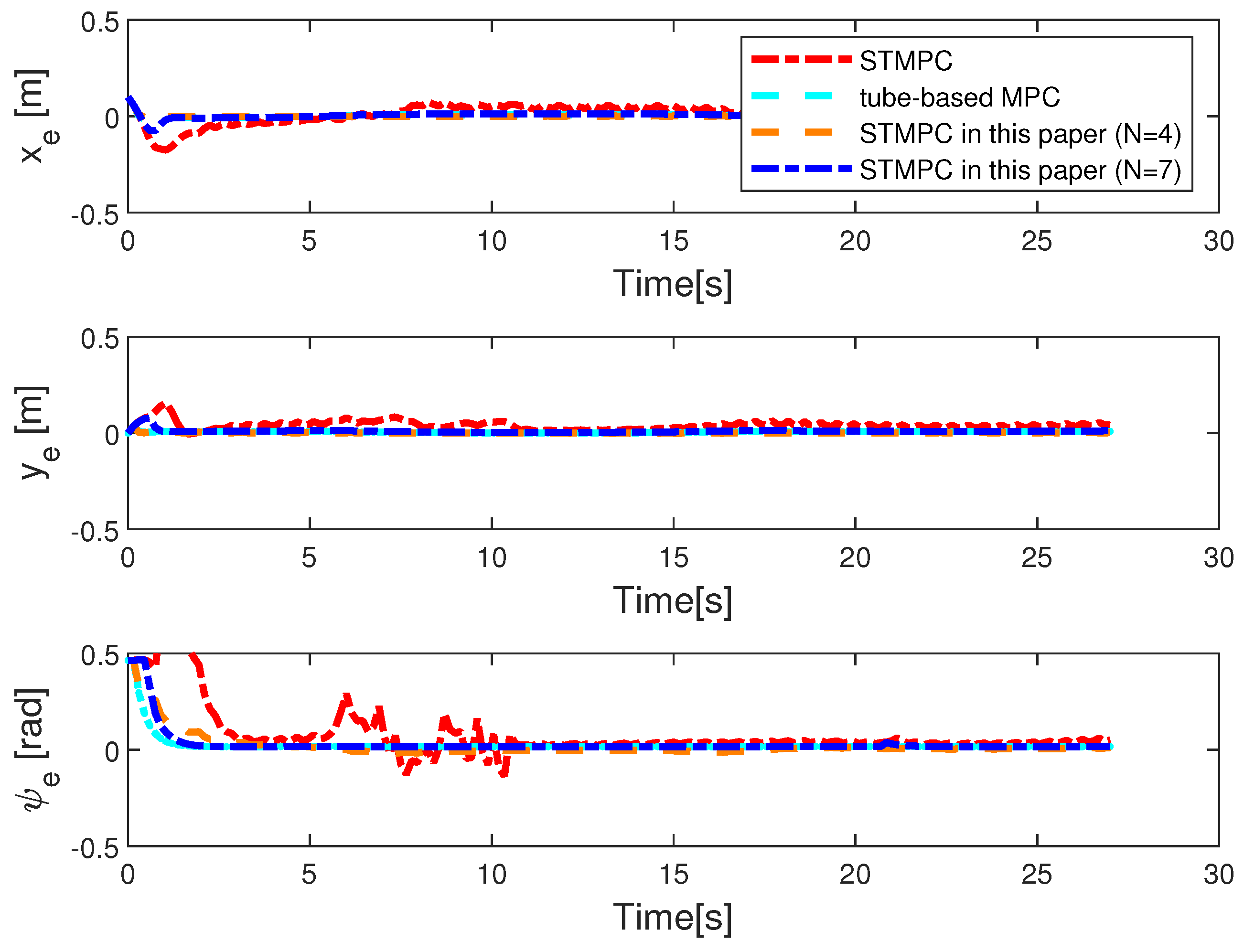
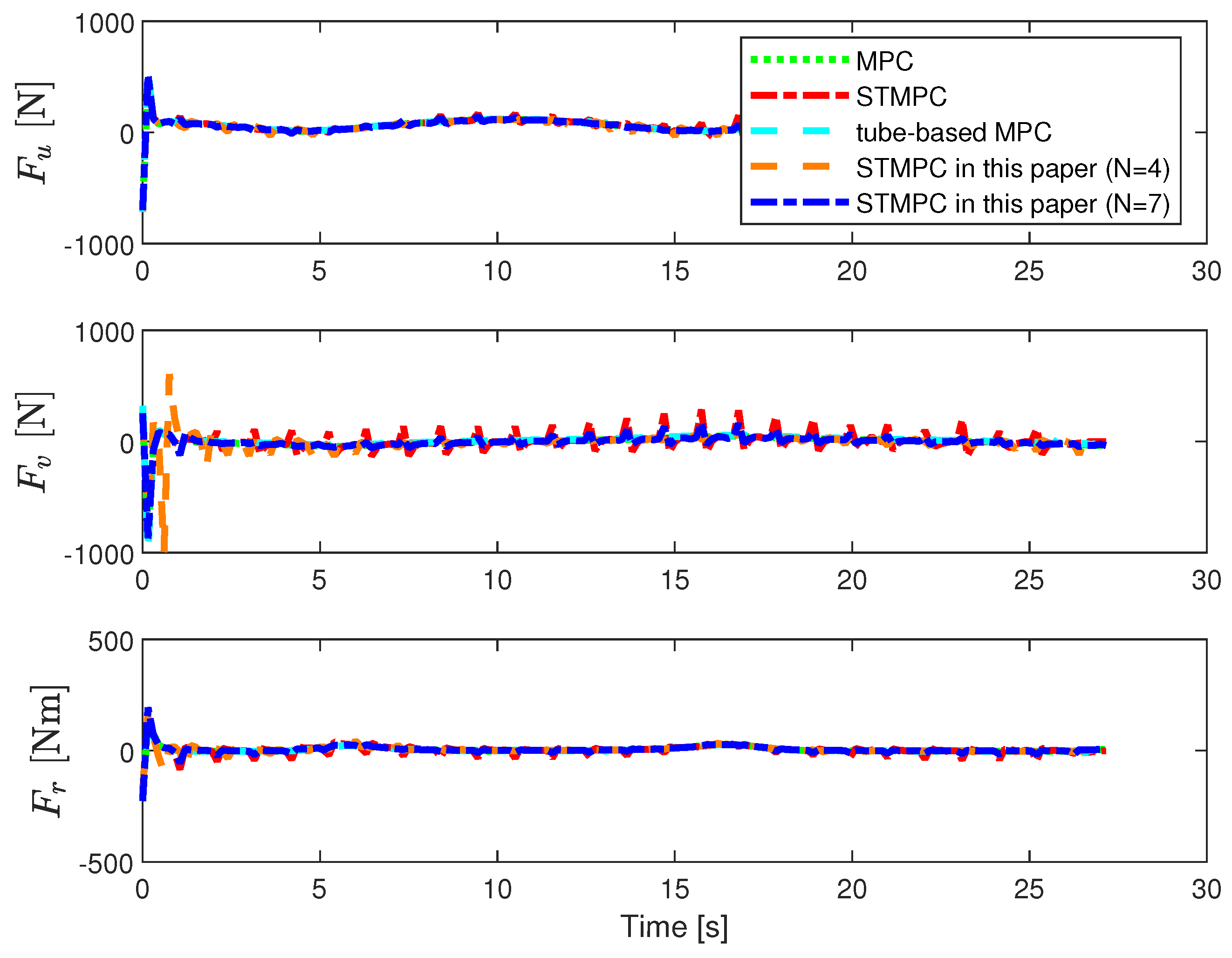
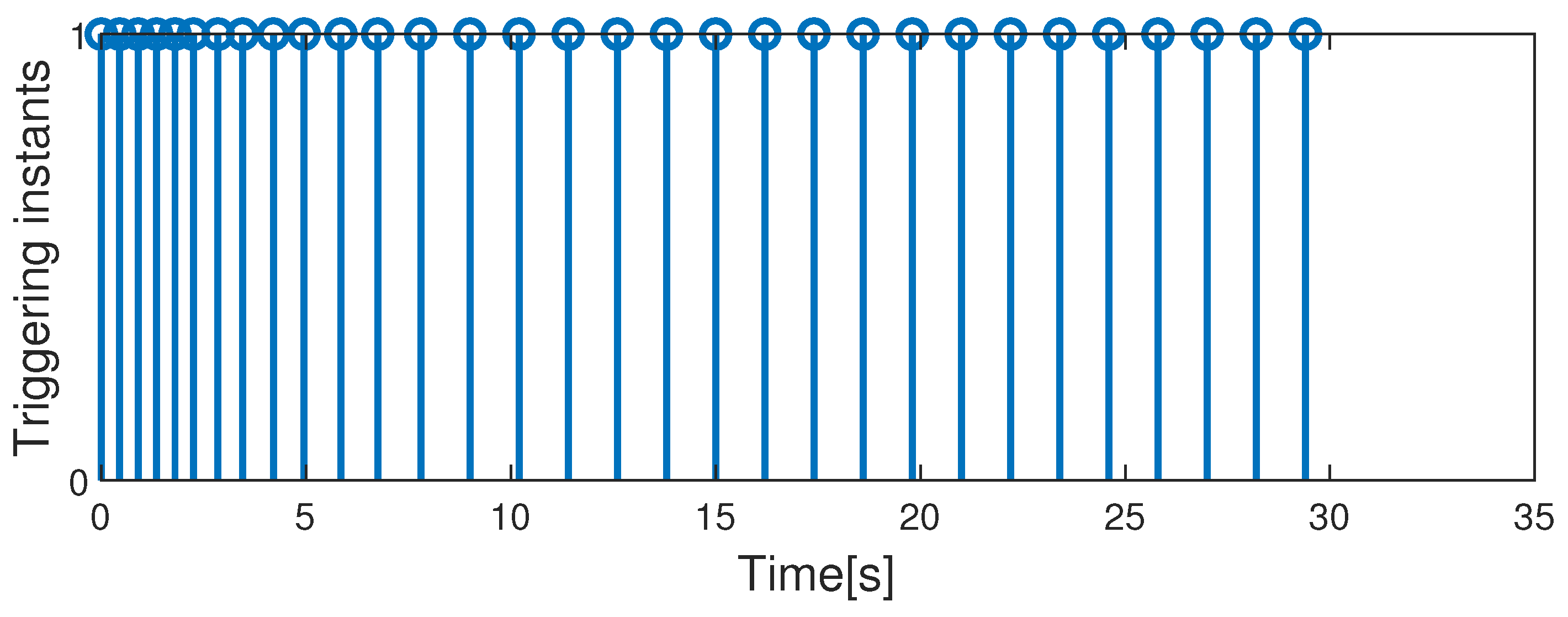
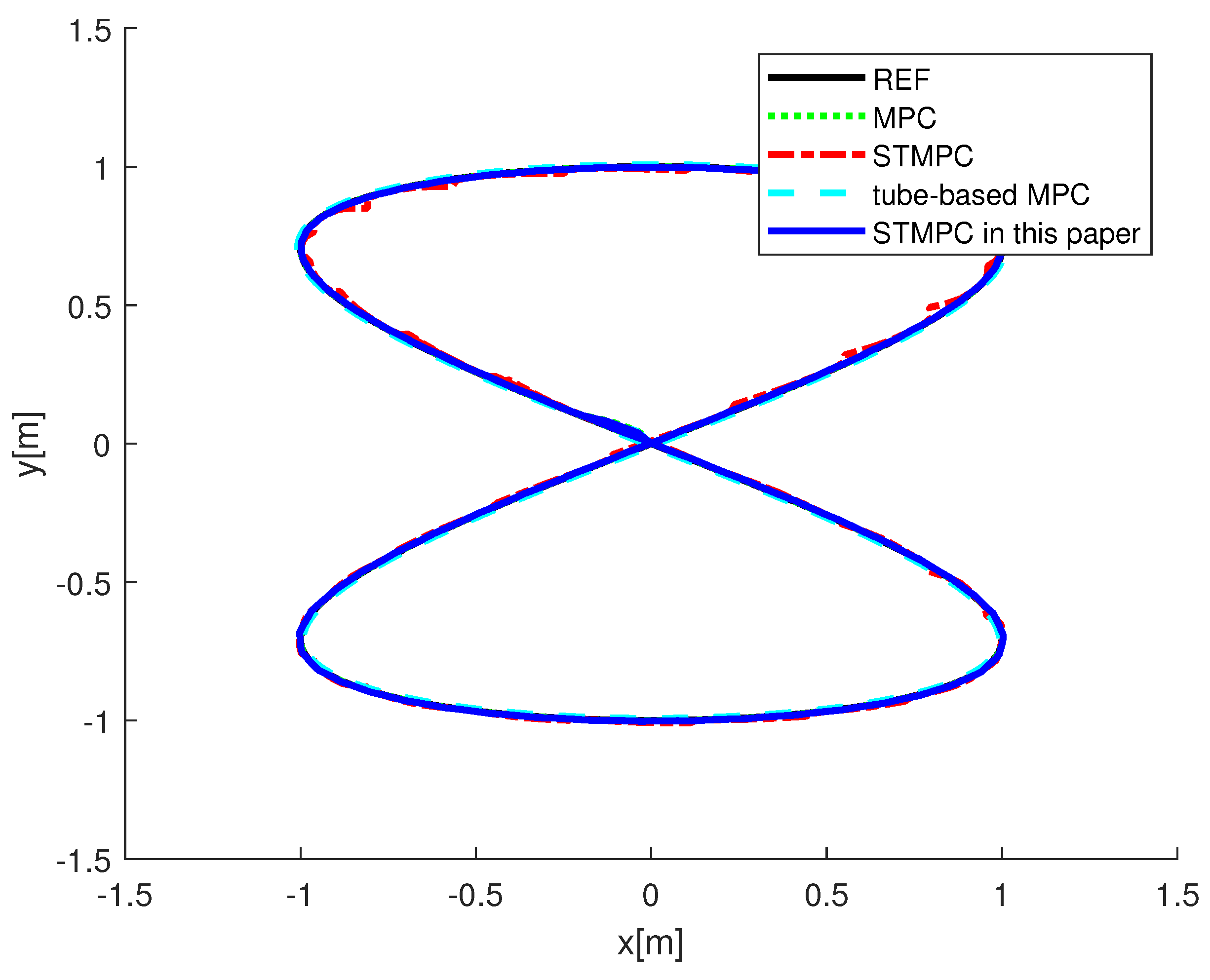
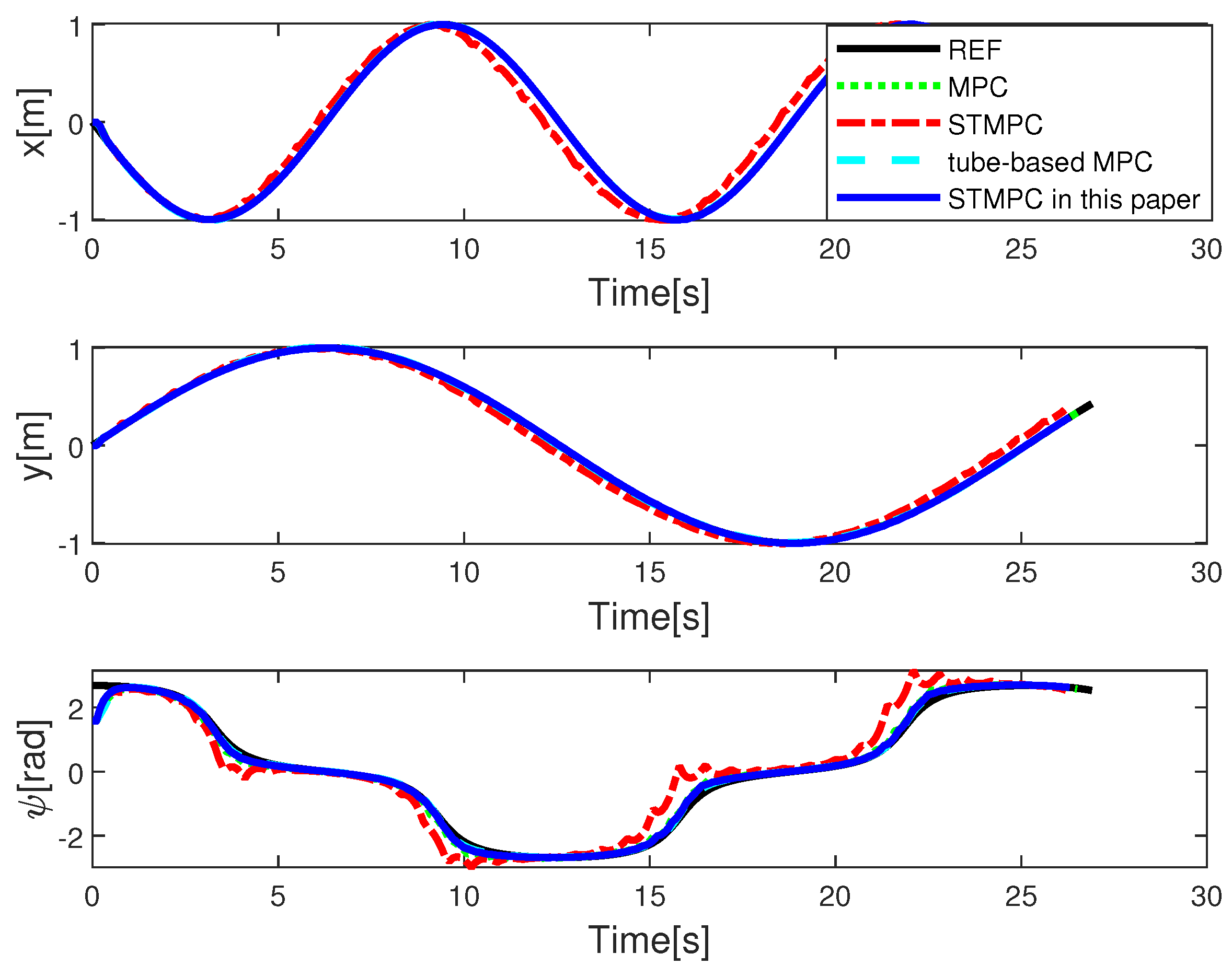
5. Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiang, X.; Lapierre, L.; Jouvencel, B. Smooth transition of AUV motion control: From fully-actuated to under-actuated configuration. Robot. Auton. Syst. 2015, 67, 14–22. [Google Scholar] [CrossRef]
- Zhang, F.; Marani, G.; Smith, R.N.; Choi, H.T. Future Trends in Marine Robotics. IEEE Robot. Autom. Mag. 2015, 22, 14–122. [Google Scholar] [CrossRef]
- Xiang, X.; Jouvencel, B.; Parodi, O. Coordinated Formation Control of Multiple Autonomous Underwater Vehicles for Pipeline Inspection. Int. J. Adv. Robot. Syst. 2010, 7, 75–84. [Google Scholar] [CrossRef]
- Ferri, G.; Munafò, A.; LePage, K.D. An Autonomous Underwater Vehicle Data-Driven Control Strategy for Target Tracking. IEEE J. Ocean. Eng. 2018, 43, 323–343. [Google Scholar] [CrossRef]
- Zhang, F.; Fratantoni, D.M.; Paley, D.A.; Lund, J.M.; Leonard, N.E. Control of coordinated patterns for ocean sampling. Int. J. Control 2007, 80, 1186–1199. [Google Scholar] [CrossRef]
- Refsnes, J.E.; Sorensen, A.J.; Pettersen, K.Y. Model-Based Output Feedback Control of Slender-Body Underactuated AUVs: Theory and Experiments. IEEE Trans. Control Syst. Technol. 2008, 16, 930–946. [Google Scholar] [CrossRef]
- Kim, J.; Joe, H.; Yu, S.c.; Lee, J.S.; Kim, M. Time-Delay Controller Design for Position Control of Autonomous Underwater Vehicle Under Disturbances. IEEE Trans. Ind. Electron. 2016, 63, 1052–1061. [Google Scholar] [CrossRef]
- Cui, R.; Zhang, X.; Cui, D. Adaptive sliding-mode attitude control for autonomous underwater vehicles with input nonlinearities. Ocean Eng. 2016, 123, 45–54. [Google Scholar] [CrossRef]
- Khodayari, M.H.; Balochian, S. Modeling and control of autonomous underwater vehicle (AUV) in heading and depth attitude via self-adaptive fuzzy PID controller. J. Mar. Sci. Technol. 2015, 20, 559–578. [Google Scholar] [CrossRef]
- Davila, J. Exact Tracking Using Backstepping Control Design and High-Order Sliding Modes. IEEE Trans. Autom. Control 2013, 58, 2077–2081. [Google Scholar] [CrossRef]
- Liao, Y.l.; Wan, L.; Zhuang, J.y. Backstepping dynamical sliding mode control method for the path following of the underactuated surface vessel. Procedia Eng. 2011, 15, 256–263. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, L.; Zhang, G.; Wang, C.; Chai, Y.; Mao, Z. Research on 3D trajectory tracking of underactuated AUV under strong disturbance environment. Comput. Electr. Eng. 2023, 111, 108924. [Google Scholar] [CrossRef]
- Choi, W.Y.; Lee, S.H.; Chung, C.C. Horizonwise Model-Predictive Control With Application to Autonomous Driving Vehicle. IEEE Trans. Ind. Inform. 2022, 18, 6940–6949. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M. Model Predictive Control: Theory, Computation, and Design; Nob Hill Publishing: Madison, WI, USA, 2017; Volume 2. [Google Scholar]
- Hao, L.Y.; Wu, Z.J.; Shen, C.; Cao, Y.; Wang, R.Z. Tube-Based Model Predictive Control for Constrained Unmanned Marine Vehicles With Thruster Faults. IEEE Trans. Ind. Inform. 2024, 20, 4606–4615. [Google Scholar] [CrossRef]
- Sun, Z.; Dai, L.; Liu, K.; Xia, Y.; Johansson, K.H. Robust MPC for tracking constrained unicycle robots with additive disturbances. Automatica 2018, 90, 172–184. [Google Scholar] [CrossRef]
- Wang, Q.; Duan, Z.; Lv, Y.; Wang, Q.; Chen, G. Distributed Model Predictive Control for Linear–Quadratic Performance and Consensus State Optimization of Multiagent Systems. IEEE Trans. Cybern. 2021, 51, 2905–2915. [Google Scholar] [CrossRef]
- Sun, Z.; Xia, Y.; Dai, L.; Liu, K.; Ma, D. Disturbance Rejection MPC for Tracking of Wheeled Mobile Robot. IEEE/ASME Trans. Mechatronics 2017, 22, 2576–2587. [Google Scholar] [CrossRef]
- Cao, Q.; Sun, Z.; Xia, Y.; Dai, L. Self-triggered MPC for trajectory tracking of unicycle-type robots with external disturbance. J. Frankl. Inst. 2019, 356, 5593–5610. [Google Scholar] [CrossRef]
- Li, H.; Shi, Y. Event-triggered robust model predictive control of continuous-time nonlinear systems. Automatica 2014, 50, 1507–1513. [Google Scholar] [CrossRef]
- Wang, M.; Sun, J.; Chen, J. Input-to-State Stability of Perturbed Nonlinear Systems With Event-Triggered Receding Horizon Control Scheme. IEEE Trans. Ind. Electron. 2019, 66, 6393–6403. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, C.; Xia, J.; Sun, J. Periodic Event-Triggered Robust Distributed Model Predictive Control for Multiagent Systems With Input and Communication Delays. IEEE Trans. Ind. Inform. 2023, 19, 11216–11228. [Google Scholar] [CrossRef]
- Yoo, J.; Johansson, K.H. Event-Triggered Model Predictive Control With a Statistical Learning. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2571–2581. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, P.; Zhang, Z.; Wang, M.; Chen, J. Periodic Event-Triggered MPC for Continuous-Time Nonlinear Systems With Bounded Disturbances. IEEE Trans. Autom. Control 2023, 68, 8036–8043. [Google Scholar] [CrossRef]
- Brunner, F.D.; Heemels, M.; Allgöwer, F. Robust self-triggered MPC for constrained linear systems: A tube-based approach. Automatica 2016, 72, 73–83. [Google Scholar] [CrossRef]
- Sun, Z.; Dai, L.; Liu, K.; Dimarogonas, D.V.; Xia, Y. Robust Self-Triggered MPC With Adaptive Prediction Horizon for Perturbed Nonlinear Systems. IEEE Trans. Autom. Control 2019, 64, 4780–4787. [Google Scholar] [CrossRef]
- Xie, H.; Dai, L.; Luo, Y.; Xia, Y. Robust MPC for disturbed nonlinear discrete-time systems via a composite self-triggered scheme. Automatica 2021, 127. [Google Scholar] [CrossRef]
- Hashimoto, K.; Adachi, S.; Dimarogonas, D.V. Self-Triggered Model Predictive Control for Nonlinear Input-Affine Dynamical Systems via Adaptive Control Samples Selection. IEEE Trans. Autom. Control 2017, 62, 177–189. [Google Scholar] [CrossRef]
- Luo, Y.; Xia, Y.; Sun, Z. Self-Triggered Model Predictive Control for Continue Linear Constrained System: Robustness and Stability. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 3612–3617. [Google Scholar]
- Cui, D.; Li, H. Dual Self-Triggered Model-Predictive Control for Nonlinear Cyber-Physical Systems. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 52, 3442–3452. [Google Scholar] [CrossRef]
- Su, Y.; Wang, Q.; Sun, C. Self-triggered robust model predictive control for nonlinear systems with bounded disturbances. IET Control Theory Appl. 2019, 13, 1336–1343. [Google Scholar] [CrossRef]
- Yang, H.; Li, Q.; Zuo, Z.; Zhao, H. Self-triggered MPC for nonholonomic systems with multiple constraints by adaptive transmission intervals. Automatica 2021, 133, 109870. [Google Scholar] [CrossRef]
- Hashimoto, K.; Adachi, S.; Dimarogonas, D.V. Distributed aperiodic model predictive control for multi-agent systems. IET Control Theory Appl. 2015, 9, 10–20. [Google Scholar] [CrossRef]
- He, N.; Shi, D.; Chen, T. Self-triggered model predictive control for networked control systems based on first-order hold. Int. J. Robust Nonlinear Control 2018, 28, 1303–1318. [Google Scholar] [CrossRef]
- Shen, C.; Shi, Y.; Buckham, B. Integrated Path Planning and Tracking Control of an AUV: A Unified Receding Horizon Optimization Approach. IEEE/ASME Trans. Mechatronics 2017, 22, 1163–1173. [Google Scholar] [CrossRef]
- Hao, L.Y.; Wang, R.Z.; Shen, C.; Shi, Y. Trajectory Tracking Control of Autonomous Underwater Vehicles Using Improved Tube-Based Model Predictive Control Approach. IEEE Trans. Ind. Inform. 2024, 20, 5647–5657. [Google Scholar] [CrossRef]
- Paulavičius, R.; Žilinskas, J. Analysis of different norms and corresponding Lipschitz constants for global optimization. Technol. Econ. Dev. Econ. 2006, 12, 301–306. [Google Scholar] [CrossRef]
- He, N.; Ma, K.; Li, H.; Li, Y. Resilient Self-Triggered Model Predictive Control of Discrete-Time Nonlinear Cyberphysical Systems Against False Data Injection Attacks. IEEE Intell. Transp. Syst. Mag. 2023, 2–15. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Eqtami, A.; Heshmati-alamdari, S.; Dimarogonas, D.V.; Kyriakopoulos, K.J. Self-triggered Model Predictive Control for nonholonomic systems. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 638–643. [Google Scholar]
- Yan, Z.; Yang, H.; Zhang, W.; Gong, Q.; Zhang, Y.; Zhao, L. Robust nonlinear model predictive control of a bionic underwater robot with external disturbances. Ocean Eng. 2022, 253, 111310. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Hao, L.; Wang, R. Adaptive Transmission Interval-Based Self-Triggered Model Predictive Control for Autonomous Underwater Vehicles with Additional Disturbances. J. Mar. Sci. Eng. 2024, 12, 1489. https://doi.org/10.3390/jmse12091489
Zhang P, Hao L, Wang R. Adaptive Transmission Interval-Based Self-Triggered Model Predictive Control for Autonomous Underwater Vehicles with Additional Disturbances. Journal of Marine Science and Engineering. 2024; 12(9):1489. https://doi.org/10.3390/jmse12091489
Chicago/Turabian StyleZhang, Pengyuan, Liying Hao, and Runzhi Wang. 2024. "Adaptive Transmission Interval-Based Self-Triggered Model Predictive Control for Autonomous Underwater Vehicles with Additional Disturbances" Journal of Marine Science and Engineering 12, no. 9: 1489. https://doi.org/10.3390/jmse12091489
APA StyleZhang, P., Hao, L., & Wang, R. (2024). Adaptive Transmission Interval-Based Self-Triggered Model Predictive Control for Autonomous Underwater Vehicles with Additional Disturbances. Journal of Marine Science and Engineering, 12(9), 1489. https://doi.org/10.3390/jmse12091489






