Multi-Objective Optimization for Thrust Allocation of Dynamic Positioning Ship
Abstract
1. Introduction
- The TA optimization problem is approached from a multi-objective perspective, where the TA objective functions are built to simultaneously minimize the thrust allocation error, power consumption, and wear-and-tear of the thruster system, taking the thruster input parameters of the propeller speed, azimuth angle, and rudder angle as decision variables. This method enables system optimization with multiple objectives in mind and helps to integrate the impact of multiple factors on system performance.
- The MOPSO algorithm is introduced to solve the TA optimization problem. The MOPSO algorithm introduces the mechanism of crowding distance and roulette method to select the globally optimal particles, and improves the inertia weights and learning factors while incorporating mutation operations to enhance the local optimization capability. The proposed IMOPSO algorithm uniquely balances the conflicting objectives of reducing allocation error, minimizing power consumption, and minimizing wear-and-tear through its particle swarm optimization mechanism, Pareto-based multi-objective strategy, elitist preservation, and constraint handling capabilities. This makes it superior to traditional multi-objective algorithms in solving multi-objective optimization problems for ships. Simulations demonstrate that the proposed algorithm exhibits a notably fast iteration speed, excellent convergence performance, and the ability to maintain population diversity. Moreover, when compared to the single-objective PSO algorithm, the proposed IMOPSO TA algorithm can reduce the thrust allocation errors, the thruster power consumption, and the changing rate of thruster inputs.
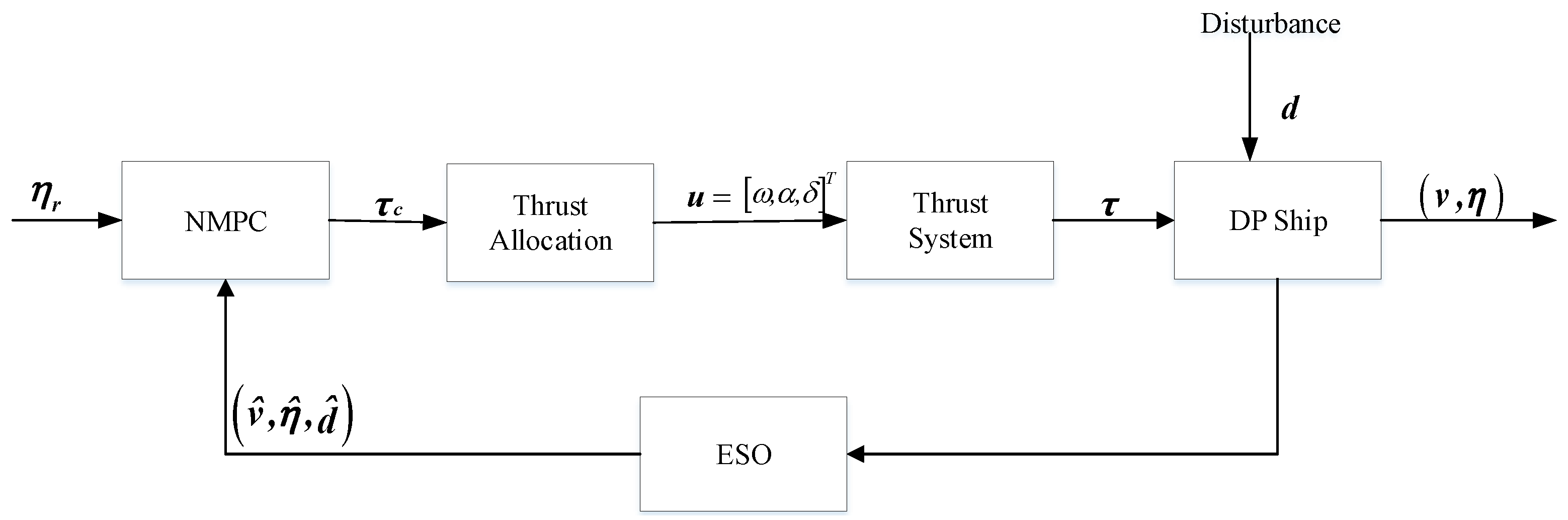
- Considering the TA under closed-loop control, a nonlinear model predictive control (NMPC) algorithm and extended state observer (ESO) are introduced. By utilizing the predictive power of NMPC and the ability of ESO to provide real-time estimation of uncertain model parameters and external disturbances, this combined approach enables accurate prediction of ship dynamics. This not only ensures TA execution accuracy but also optimizes performance by reducing allocation errors, power consumption, and equipment wear. Simulation results demonstrate the effectiveness of the proposed IMOPSO algorithm for TA in DP control systems, highlighting its potential to improve the safety, efficiency, and reliability of offshore operations.
2. Problem Formulation and Model
2.1. Preliminaries
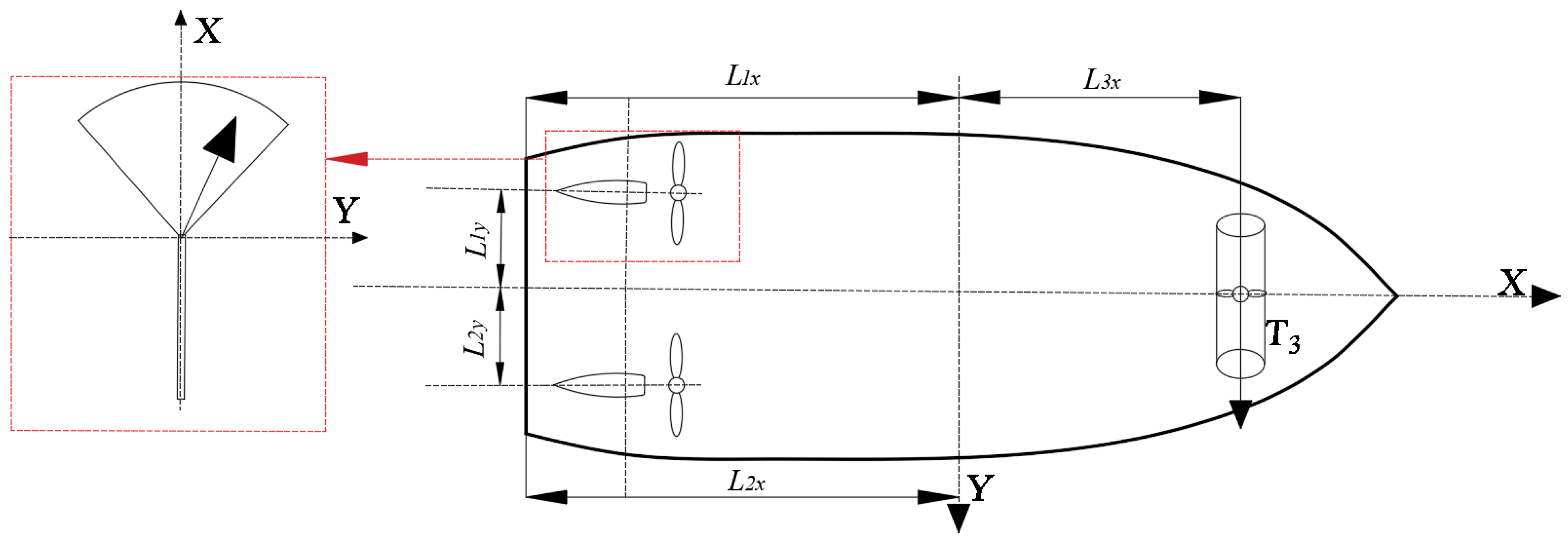
2.2. DP Ship Mathematical Model
2.3. Mathematical Model of Thrust Allocation
2.4. Multi-Objective Problem of Thrust Allocation
3. The Proposed Method
3.1. Improved MOPSO (IMOPSO) Algorithm
3.1.1. Creation of External Archives Repository
3.1.2. Determination of Individual and Global Optimal Solutions
3.1.3. Improvements during Particle Updates
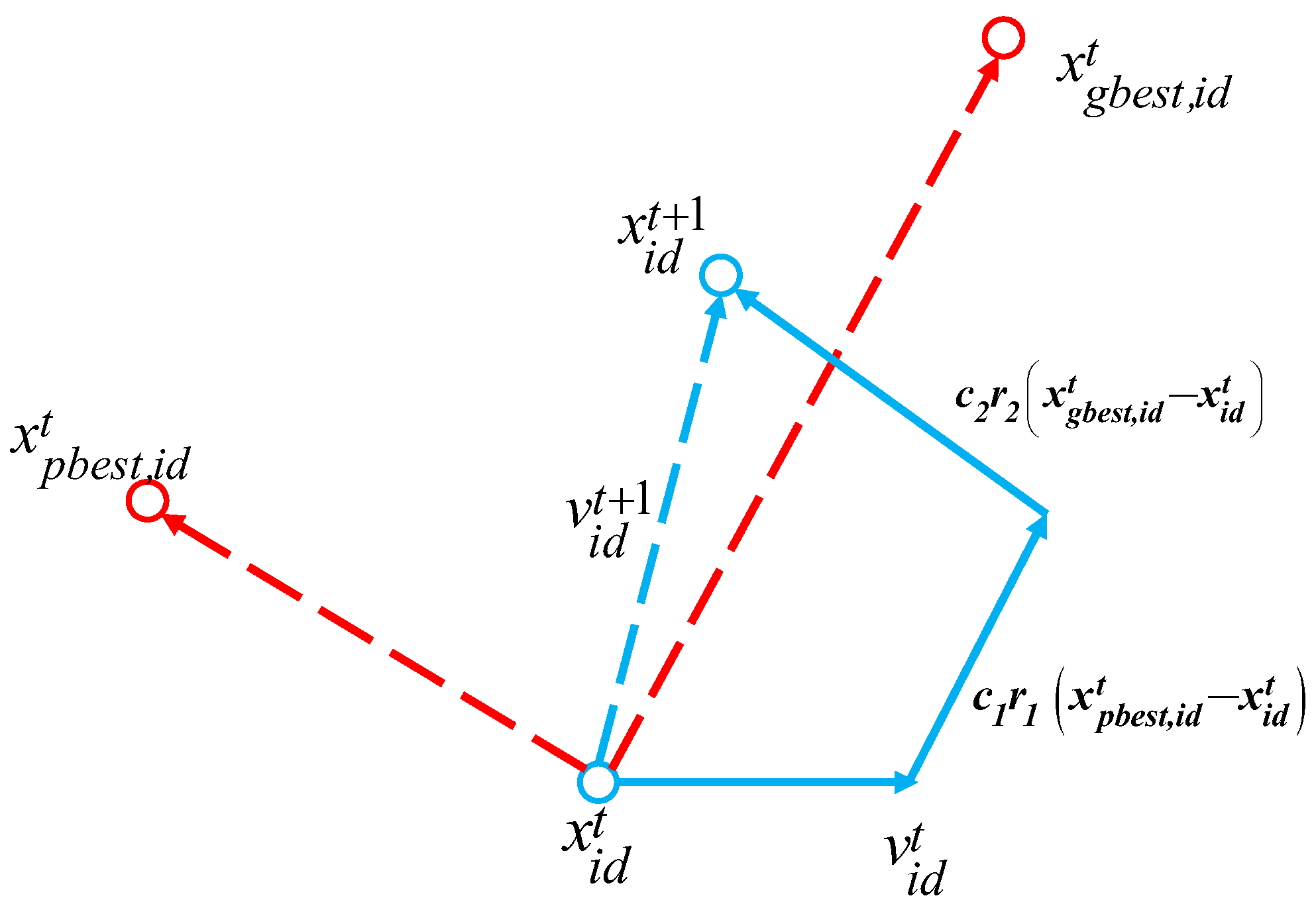
- Asynchronously changing learning rate: in the PSO algorithm, updating of particle velocity and position is defined as follows:The learning factor enables the particle to master the ability of self-learning and learning from other better particles in the optimization process, and gradually approach the optimal solution. Asynchronous change means that the two have inconsistent changes. By making the learning factors and change asynchronously, the change is as in Equation (18). This means that at the beginning of the optimization the particles are good at self-learning and relatively poor at social ability, and at the end of the optimization they are just the opposite; this practice can help the algorithm converge to the global optimal solution to prevent falling into the local optimum.The improved learning factor is defined as follows:where , and denote the velocity, the position, the individual best position, and the population best position of the i particles at t iterations in the d dimension, respectively. The and denote the velocity and position of the i-particle in the d-dimension at the iteration, respectively. is the inertia weight, and are random numbers uniformly distributed between [0, 1], and and are the individual learning factor and group learning factor.Figure 1 shows the path diagram of the particle update, in which the velocity update of the particle mainly consists of its own velocity , the self-knowledge part , and the social experience part ; the position update mainly consists of the particle’s current position and the updated velocity .
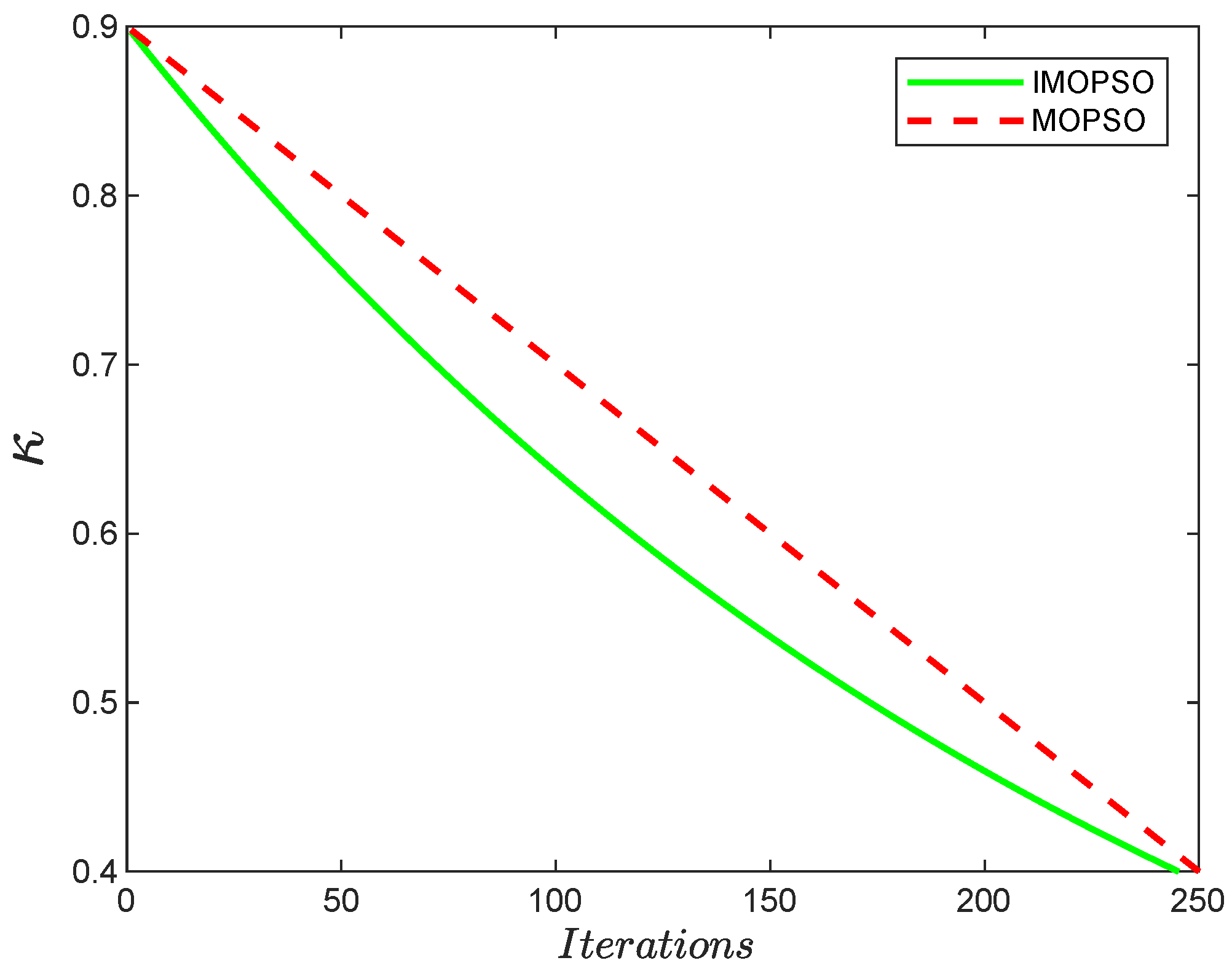
- Adjusting inertia weight: In PSO algorithm, the inertia weight usually changes dynamically with the current number of iterations t. The MOPSO algorithm usually employs a linear descent strategy to enhance the algorithm’s ability to find the optimum, and the weight change equation is defined as follows:where , are the maximum and minimum values of , respectively.However, the search accuracy of the linear descent strategy is not high. In the optimization process, it is better to focus on the global search at the beginning and then focus on the local search at a later stage, which not only improves the convergence speed of the algorithm but also improves the search accuracy of the algorithm. Therefore, this paper proposes an inertia weight exponentially decreasing strategy, and the improved weight change formula is defined asThe trend of with the number of iterations obtained from Equations (19) and (20) are shown in Figure 2.
- Mutation operation: The MOPSO algorithm can produce optimization results quickly due to its fast convergence rate. However, it may also cause particles fall into local optimal solutions; to overcome this drawback, the algorithm performs a mutation operation on the particles during the iteration process. At the beginning of the iteration, a large-scale search is required due to the large gap between the solution and the optimal solution sets in order to expand the search, increasing the probability that particle mutation is used to narrow the gap between the solution and the optimal solution sets. In the later stages of the iteration, the mutation probability of the particles is gradually reduced in order for the algorithm to converge quickly. Therefore, the mutation probability of the particle is gradually decreasing as the number of iterations increases. The mutation probability of a particle is defined aswhere is the mutation probability of the t-th iteration, m is the maximum number of iterations of the MOPSO algorithm, and is the conditioning factor.
3.2. IMOPSO Algorithm Procedure
| Algorithm 1 | IMOPSO algorithm optimization process |
| Input | Population size N. |
| Number of external archives . | |
| Maximum number of iterations m. | |
| Learning factors , , , . | |
| Conditioning factor . | |
| Output | The optimal solution of thruster input . |
| 1. | Initialize |
| 2. | Generate the velocity and position of each particle according to |
| the given constraints | |
| 3. | Assess the fitness value of every particle |
| 4. | Fill the of each particle with its current position |
| 5. | FOR : m |
| FOR : N | |
| Select | |
| Introduce a weighting matrix | |
| Update particle velocity | |
| Update particle position | |
| Perform boundary judgment | |
| IF | |
| Perform mutation operations | |
| END IF | |
| Update | |
| END FOR | |
| Add updated particles to | |
| Perform dominance analysis | |
| Retain non-dominated members | |
| Update grids and grid indexes | |
| Check repository fullness | |
| IF | |
| Extra= () | |
| Delete Extra | |
| END IF | |
| 6. | END FOR |
3.3. Performance Evaluation of IMOPSO
4. Numerical Simulations and Result Discussions
4.1. Simulation Parameter Settings
4.2. Simulation Results and Discussions
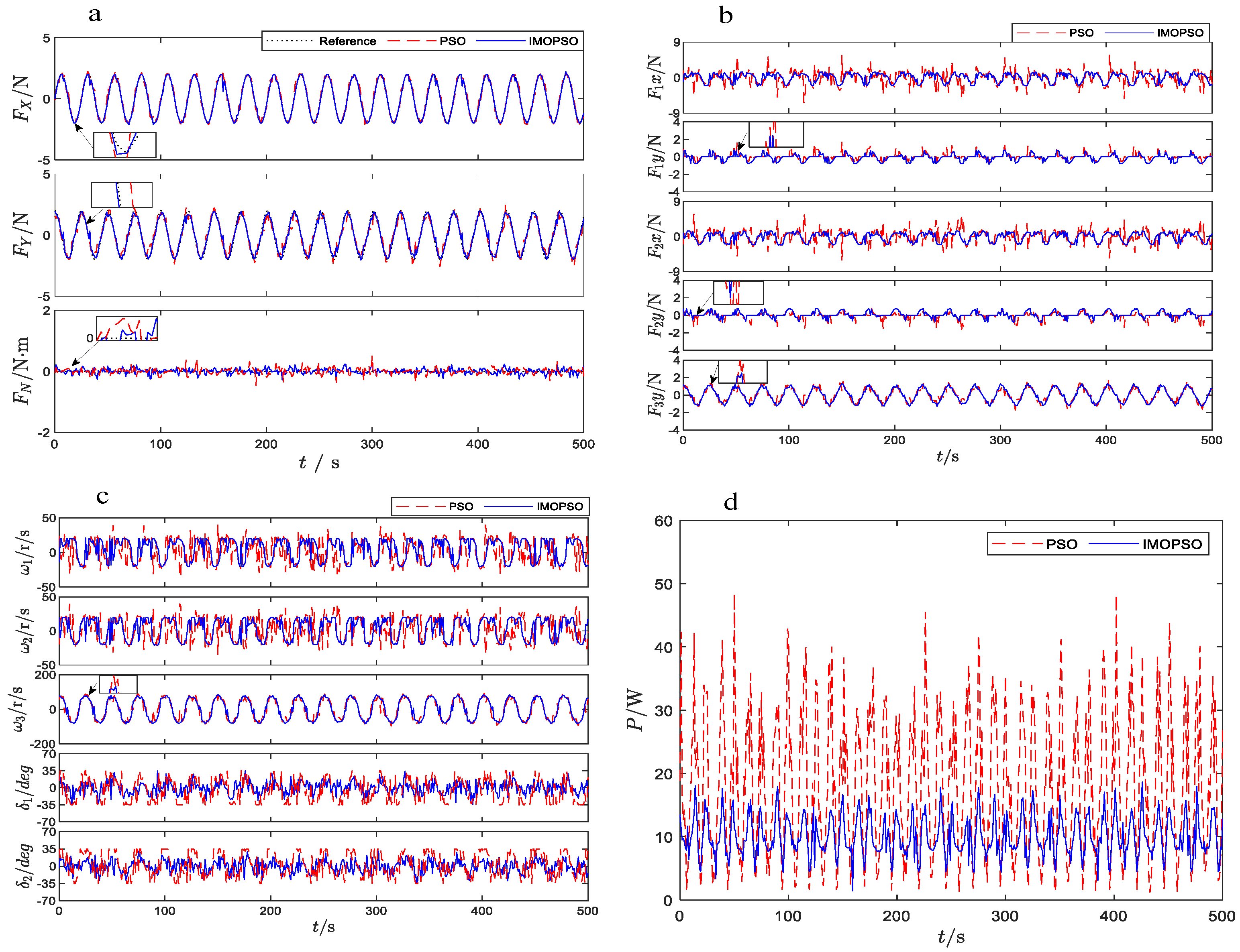
4.2.1. Thrust Allocation Performance Evaluation
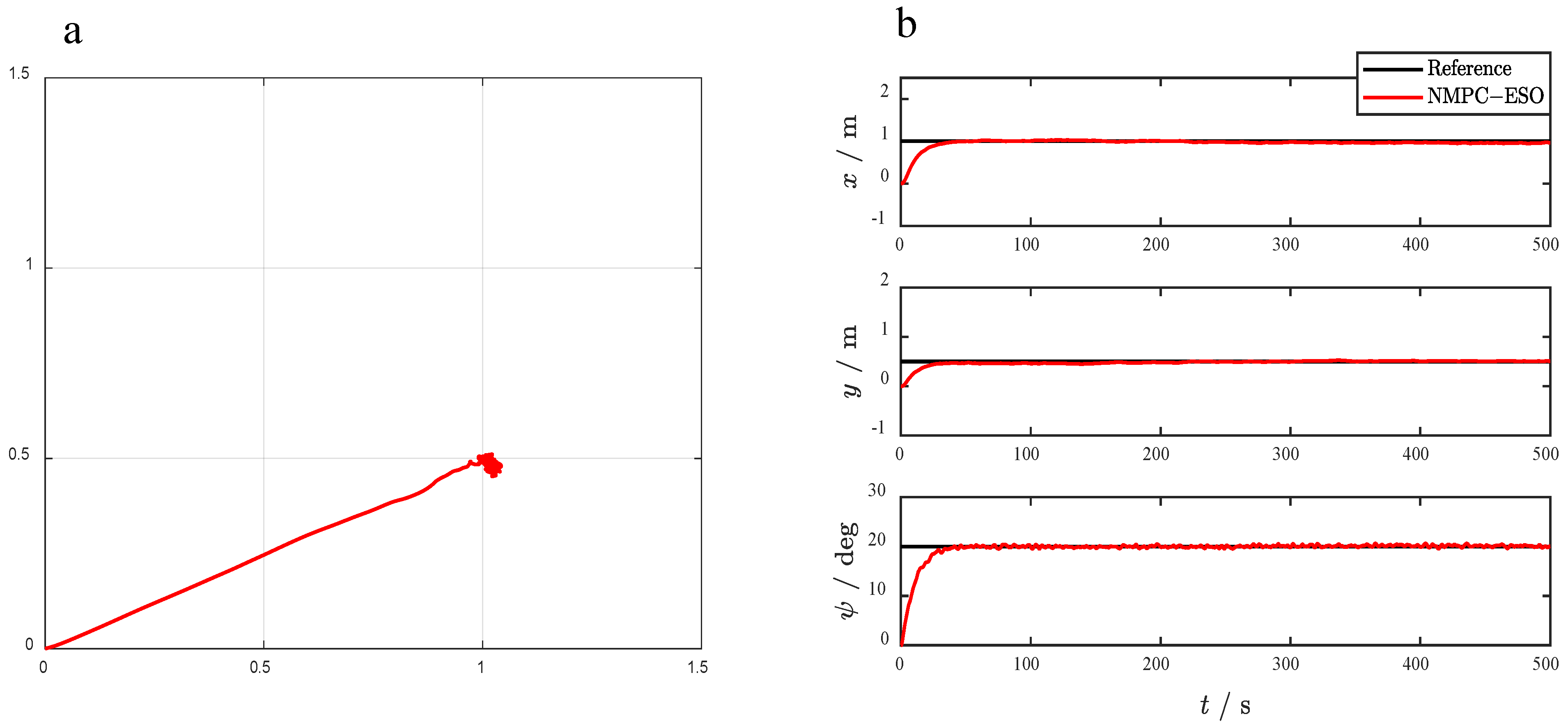
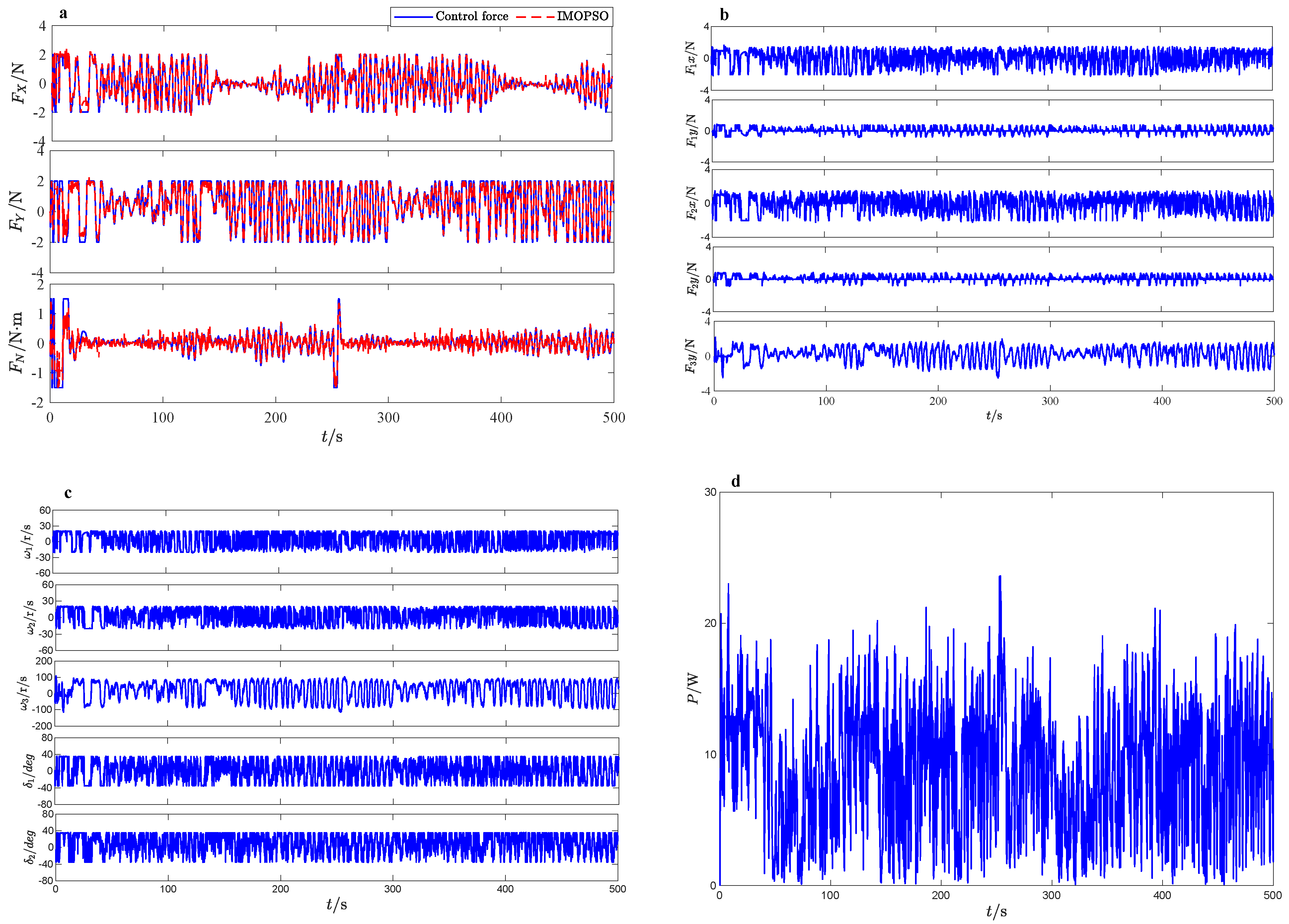
4.2.2. Closed-Loop Control and Thrust Allocation Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| TA | thrust allocation |
| DPS | dynamic positioning system |
| DP | dynamic positioning |
| MOP | multi-objective optimization problem |
| MOPSO | multi-objective particle swarm optimization |
| IMOPSO | improved multi-objective particle swarm optimization |
| LP | linear programming |
| QP | quadratic programming |
| SQP | sequential quadratic programming |
| PSO | particle swarm optimization |
| GA | genetic algorithm |
| ABC | artificial bee colony |
| MOFEPSO | multi-objective feasibility-enhanced particle swarm optimization algorithm |
| SOM | self-organizing map |
| ROV | remote operated vehicle |
| PF | Pareto front |
| SOP | single-objective optimization problem |
| IGD | inverse generation distance |
| HV | hyper volume |
| ESO | extended state observer |
| NMPC | nonlinear model predictive control |
| NSGA-II | nondominated sorting genetic algorithm II |
References
- Zhang, L.; Peng, X.; Wei, N.; Liu, Z.; Liu, C.; Wang, F. A thrust allocation method for DP vessels equipped with rudders. Ocean Eng. 2023, 285, 115342. [Google Scholar] [CrossRef]
- Bui, T.M.; Dinh, T.Q.; Marco, J.; Watts, C. Development and real-time performance evaluation of energy management strategy for a dynamic positioning hybrid electric marine vessel. Electronics 2021, 10, 1280. [Google Scholar] [CrossRef]
- Witkowska, A.; Śmierzchalski, R. Adaptive dynamic control allocation for dynamic positioning of marine vessel based on backstep** method and sequential quadratic programming. Ocean Eng. 2018, 163, 570–582. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Y.; Gu, M.; Zhang, L.; Teng, Y.; Tian, F. Experimental Study on Adaptive Backstep** Synchronous following Control and Thrust Allocation for a Dynamic Positioning Vessel. J. Mar. Sci. Eng. 2024, 12, 203. [Google Scholar] [CrossRef]
- Zalewski, P. Convex optimization of thrust allocation in a dynamic positioning simulation system. Zesz. Nauk. Akad. Morskiej Szczecinie 2016, 48, 58–62. [Google Scholar] [CrossRef]
- Koschorrek, P.; Hahn, T.; Jeinsch, T. A thrust allocation algorithm considering dynamic positioning and roll dam** thrust demands using multi-step quadratic programming. IFAC-PapersOnLine 2018, 51, 438–443. [Google Scholar] [CrossRef]
- Zalewski, P. Constraints in allocation of thrusters in a dp simulator. Zesz. Nauk. Akad. Morskiej Szczecinie 2017, 52, 45–50. [Google Scholar]
- Fossen, T.I.; Sagatun, S.I. Adaptive control of nonlinear systems: A case study of underwater robotic systems. J. Robot. Syst. 1991, 8, 393–412. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I.; Tøndel, P. Efficient optimal constrained control allocation via multiparametric programming. J. Guid. Control Dyn. 2005, 28, 506–515. [Google Scholar] [CrossRef]
- Sørdalen, O.J. Optimal thrust allocation for marine vessels. Control. Eng. Pract. 1997, 5, 1223–1231. [Google Scholar] [CrossRef]
- Liang, C.C.; Cheng, W.H. The optimum control of thruster system for dynamically positioned vessels. Ocean. Eng. 2004, 31, 97–110. [Google Scholar] [CrossRef]
- De Wit, C. Optimal Thrust Allocation Methods for Dynamic Positioning of Ships. Master’s Thesis, Delft Institute of Applied Mathematics, Delft, The Netherlands, 2009. [Google Scholar]
- Chen, X.; Liu, B.; Le, G. A Multi-Objective Optimization of the Anchor-Last Deployment of the Marine Submersible Buoy System Based on the Particle Swarm Optimization Algorithm. J. Mar. Sci. Eng. 2023, 11, 1305. [Google Scholar] [CrossRef]
- Yang, J.; Zou, J.; Yang, S.; Hu, Y.; Zheng, J.; Liu, Y. A particle swarm algorithm based on the dual search strategy for dynamic multi-objective optimization. Swarm Evol. Comput. 2023, 83, 101385. [Google Scholar] [CrossRef]
- Wu, D.; Ren, F.; Zhang, W. An energy optimal thrust allocation method for the marine dynamic positioning system based on adaptive hybrid artificial bee colony algorithm. Ocean. Eng. 2016, 118, 216–226. [Google Scholar] [CrossRef]
- Guangchi, X.; Dawei, Z.; Kaiwei, Z. Multi-agent chaos particle swarm optimization algorithm of thrust allocation for dynamic positioning vessels. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Yan, H. Research on Optimization Algorithm of the Thrust Allocation for Dynamic Positioning Systems of ships. Master’s Thesis, Dalian Maritime University, Dalian, China, 2011. [Google Scholar]
- Ji, M.; Yi, B. The optimal thrust allocation based on QPSO algorithm for dynamic positioning vessels. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2014. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Bai, J.; Ma, L.; Shi, C.; Zhang, G.; Shi, J. Multi-objective optimization of marine nuclear power secondary circuit system based on improved multi-objective particle swarm optimization algorithm. Prog. Nucl. Energy 2023, 161, 104740. [Google Scholar] [CrossRef]
- Mou, J.; Zhu, Q.; Liu, Y.; Bai, Y. Multi-objective optimal thrust allocation strategy for automatic berthing of surface ships using adaptive non-dominated sorting genetic algorithm III. Ocean. Eng. 2024, 299, 117288. [Google Scholar] [CrossRef]
- Xuebin, L. Dynamic multiobjective optimization for thrust allocation in ship application. Ocean. Eng. 2020, 218, 108187. [Google Scholar] [CrossRef]
- Nasouri, M.; Bidhendi, G.N.; Hoveidi, H.; Amiri, M.J. Parametric study and performance-based multi-criteria optimization of the indirect-expansion solar-assisted heat pump through the integration of Analytic Network process decision-making with MOPSO algorithm. Sol. Energy 2021, 225, 814–830. [Google Scholar] [CrossRef]
- Li, G.; Zhou, T. A multi-objective particle swarm optimizer based on reference point for multimodal multi-objective optimization. Eng. Appl. Artif. Intell. 2022, 107, 104523. [Google Scholar] [CrossRef]
- Li, Y.; Lei, J. A feasible solution to the beam-angle-optimization problem in radiotherapy planning with a DNA-based genetic algorithm. IEEE Trans. Biomed. Eng. 2009, 57, 499–508. [Google Scholar] [PubMed]
- Wang, Y.; Cheng, H.; Wang, C.; Hu, Z.; Yao, L.; Ma, Z.; Zhu, Z. Pareto optimality-based multi-objective transmission planning considering transmission congestion. Electr. Power Syst. Res. 2008, 78, 1619–1626. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Deng, F.; Zhang, H.; Ding, Q.; Zhang, S.; Du, Z.; Yang, H. PSO and NNPC-based integrative control allocation for dynamic positioning ships with thruster constraints. Ocean. Eng. 2024, 292, 116553. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I.; Berge, S.P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming. IEEE Trans. Control. Syst. Technol. 2004, 12, 211–216. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zapotecas Martínez, S.; Coello Coello, C.A. A multi-objective particle swarm optimizer based on decomposition. In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation, Dublin, Ireland, 12–16 July 2011. [Google Scholar]
- Lindegaard, K.P.; Fossen, T.I. Fuel-efficient rudder and propeller control allocation for marine craft: Experiments with a model ship. IEEE Trans. Control. Syst. Technol. 2003, 11, 850–862. [Google Scholar] [CrossRef]
- Deng, F.; Yang, H.L.; Wang, L.J.; Yang, W.M. UKF based nonlinear offset-free model predictive control for ship dynamic positioning under stochastic disturbances. Int. J. Control. Autom. Syst. 2019, 17, 3079–3090. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, C. Anti-disturbance lyapunov-based model predictive control for trajectory tracking of dynamically positioned ships. J. Mar. Sci. Eng. 2023, 11, 281. [Google Scholar] [CrossRef]
- Tang, L.; Liu, J.; Wang, L.; Wang, Y. Robust fixed-time trajectory tracking control of the dynamic positioning ship with actuator saturation. Ocean. Eng. 2023, 284, 115199. [Google Scholar] [CrossRef]
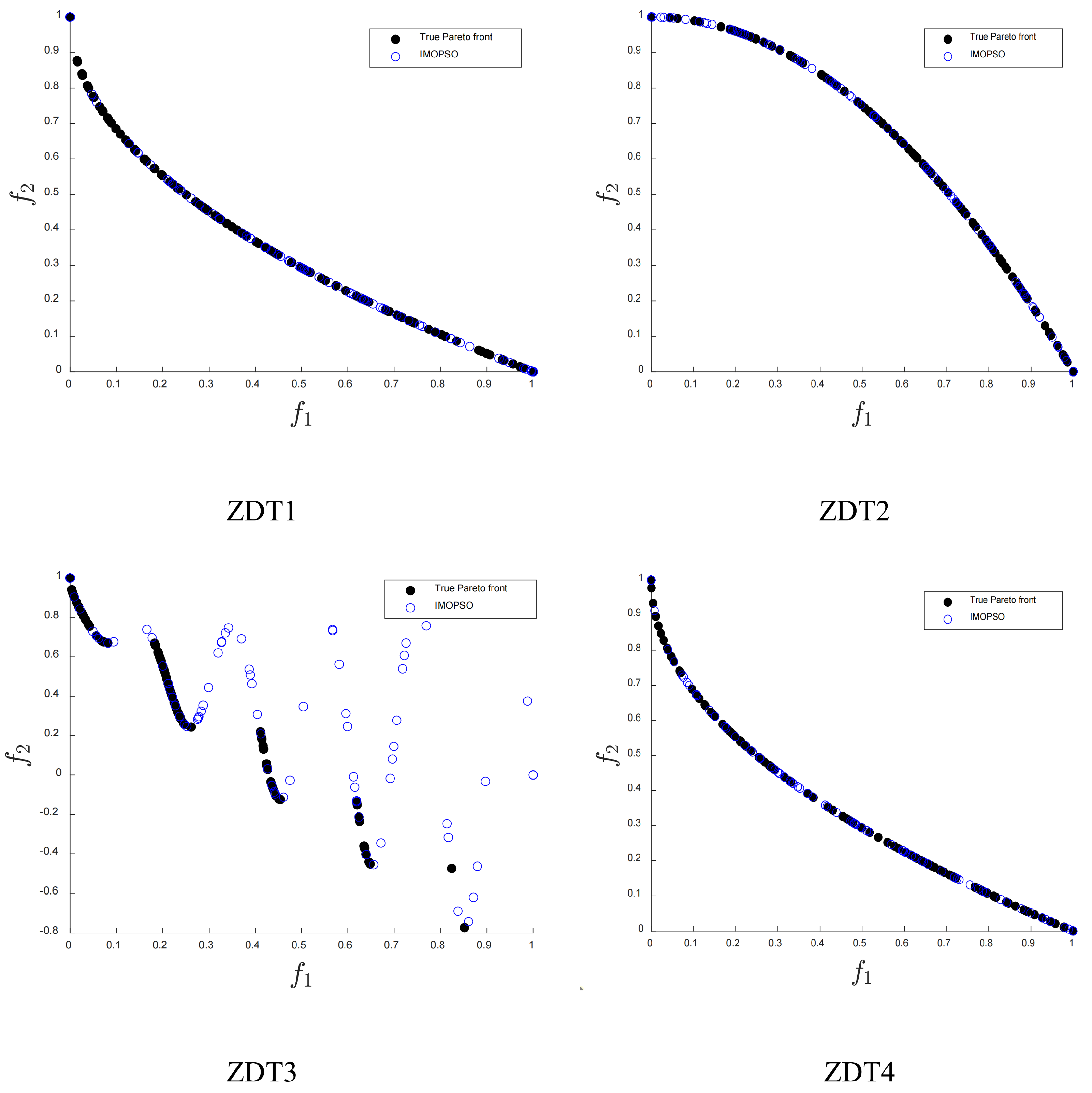
| Benchmark Function | Algorithm | HV | IGD | ||
|---|---|---|---|---|---|
| Mean | Std | Mean | Std | ||
| ZDT1 | IMOPSO | 7.1525 | 9.8272 | 8.7059 | 9.9005 |
| MOPSO | 7.0482 | 2.3940 | 1.8510 | 2.3014 | |
| NSGA-II | 4.5559 | 7.0696 | 2.5117 | 8.3138 | |
| ZDT2 | IMOPSO | 4.4018 | 8.7641 | 9.0600 | 1.0592 |
| MOPSO | 4.3842 | 2.0171 | 1.0955 | 1.7088 | |
| NSGA-II | 2.5952 | 6.9814 | 1.8818 | 1.3126 | |
| ZDT3 | IMOPSO | 5.9816 | 8.3284 | 9.6166 | 1.3557 |
| MOPSO | 5.8501 | 3.2777 | 1.4963 | 9.5468 | |
| NSGA-II | 5.0154 | 5.4232 | 2.9425 | 6.1269 | |
| ZDT4 | IMOPSO | 7.1356 | 7.6873 | 8.8606 | 7.7719 |
| MOPSO | 7.0876 | 2.8030 | 8.8071 | 1.2782 | |
| NSGA-II | 3.7631 | 1.6513 | 3.2794 | 1.8992 | |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| m | 23.8 | kg | 0.046 | m | |
| −2.0 | kg | −10.0 | kg | ||
| −0.0 | kg·m | −1.0 | kg·m2 | ||
| 1.76 | kg·m2 | −2 | kg/s | ||
| −7 | kg/s | −0.1 | kg·m/s | ||
| −0.1 | kg·m/s | −0.5 | kg·m/s |
| Thruster Number | Range of Propeller Speed (rad/s) and Rudder Angle (deg) | Change Rate of Propeller Speed (rad/s) and Rudder Angle (deg) | ||
|---|---|---|---|---|
| 0 |
| Parameter | Value | Unit |
|---|---|---|
| N· | ||
| N· | ||
| N· | ||
| N· | ||
| s | ||
| s | ||
| Algorithms | Total Algorithm Power Consumption (kW) |
|---|---|
| PSO | |
| IMOPSO |
| RMSE | PSO | IMOPSO | Improvement Percentage |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Q.; Deng, F.; Zhang, S.; Du, Z.; Yang, H. Multi-Objective Optimization for Thrust Allocation of Dynamic Positioning Ship. J. Mar. Sci. Eng. 2024, 12, 1118. https://doi.org/10.3390/jmse12071118
Ding Q, Deng F, Zhang S, Du Z, Yang H. Multi-Objective Optimization for Thrust Allocation of Dynamic Positioning Ship. Journal of Marine Science and Engineering. 2024; 12(7):1118. https://doi.org/10.3390/jmse12071118
Chicago/Turabian StyleDing, Qiang, Fang Deng, Shuai Zhang, Zhiyu Du, and Hualin Yang. 2024. "Multi-Objective Optimization for Thrust Allocation of Dynamic Positioning Ship" Journal of Marine Science and Engineering 12, no. 7: 1118. https://doi.org/10.3390/jmse12071118
APA StyleDing, Q., Deng, F., Zhang, S., Du, Z., & Yang, H. (2024). Multi-Objective Optimization for Thrust Allocation of Dynamic Positioning Ship. Journal of Marine Science and Engineering, 12(7), 1118. https://doi.org/10.3390/jmse12071118




