Analysis of the Bending Height of Flexible Marine Vegetation
Abstract
1. Introduction
2. Materials and Methods
2.1. Artificial Vegetation
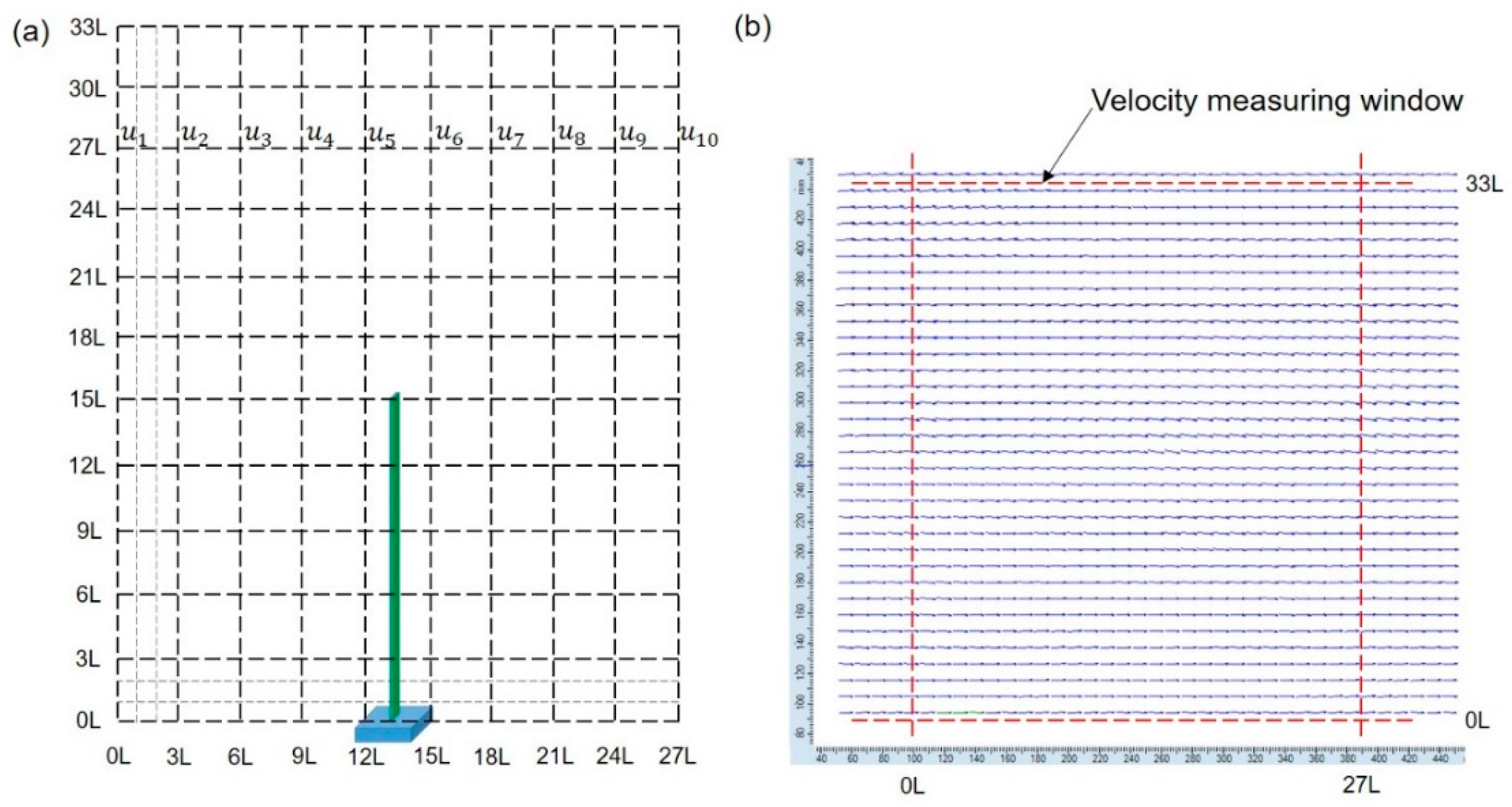
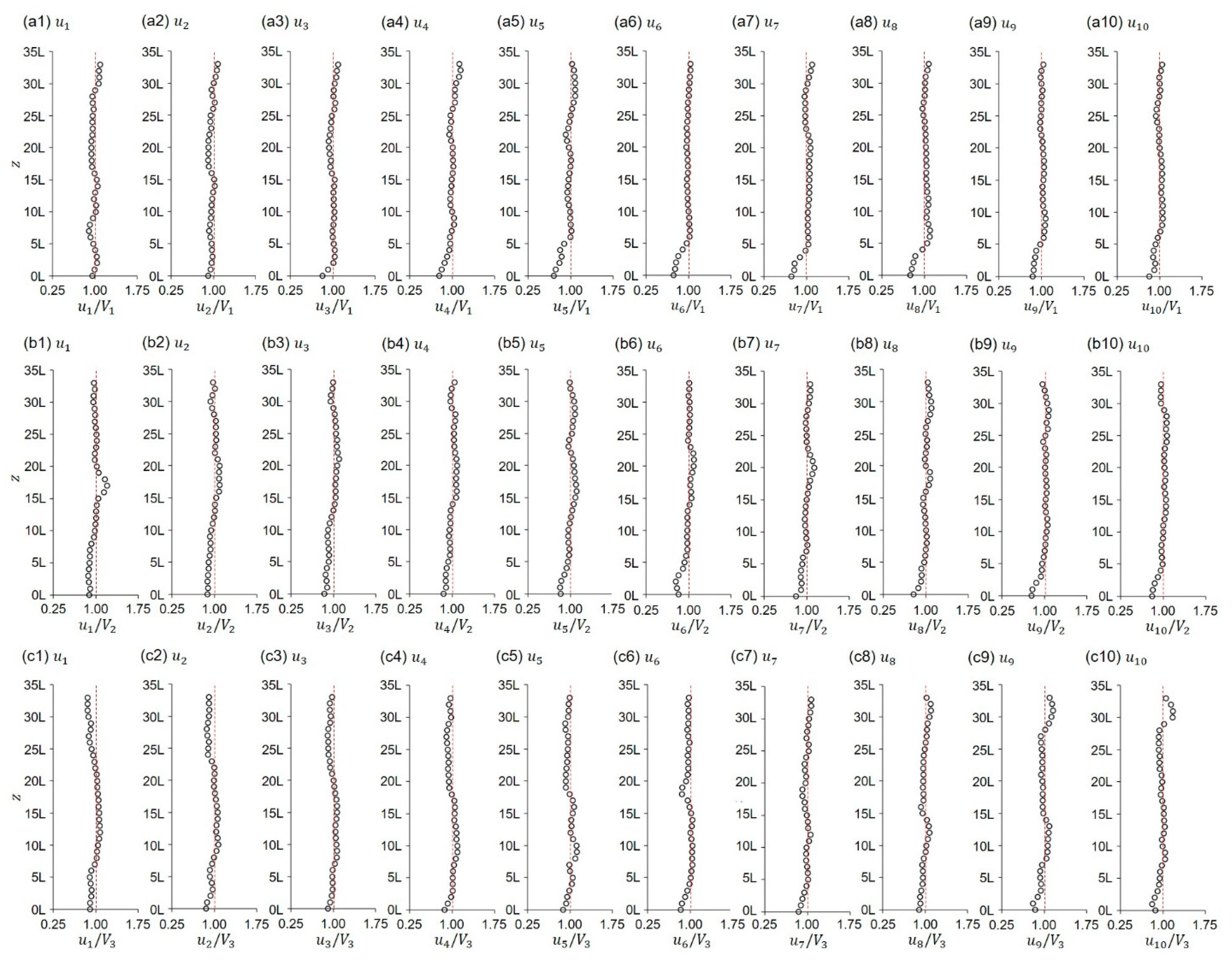
2.2. Experimental Setup
2.3. Fluid–Structure Interaction Simulation
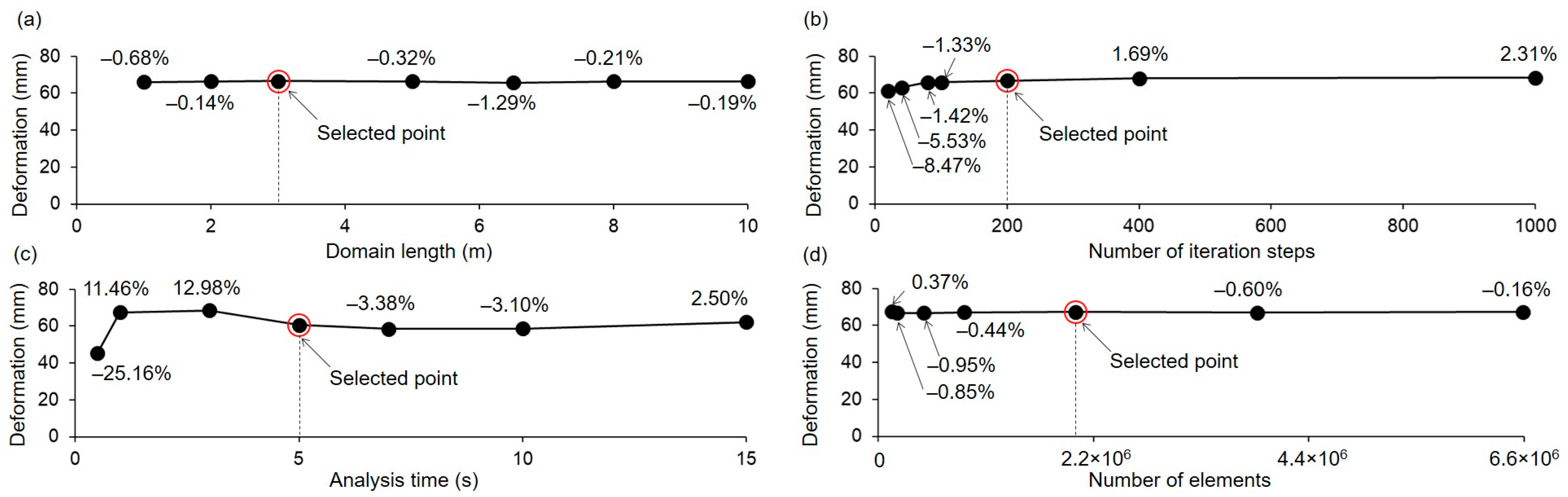
2.4. Simulation
3. Results
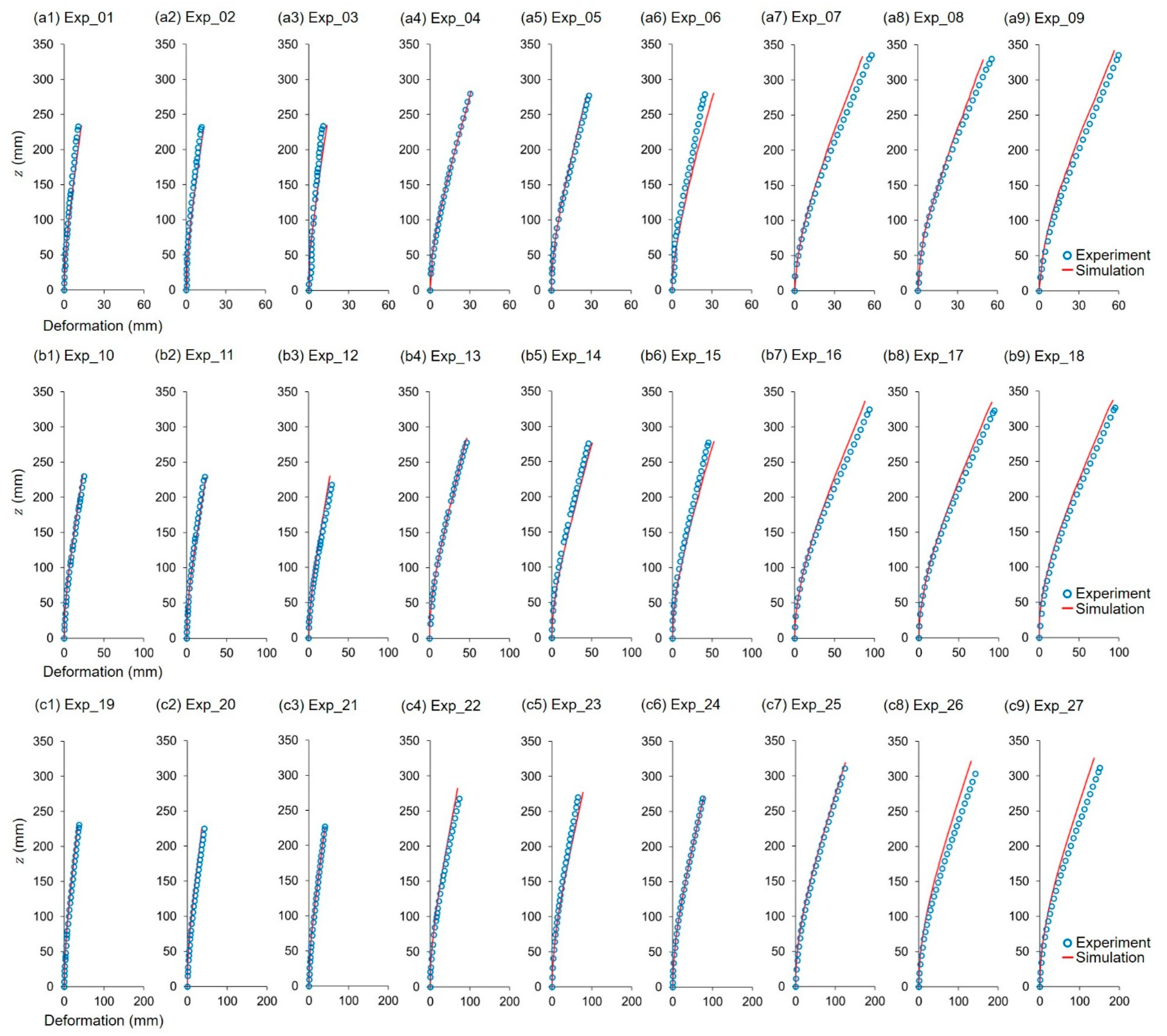
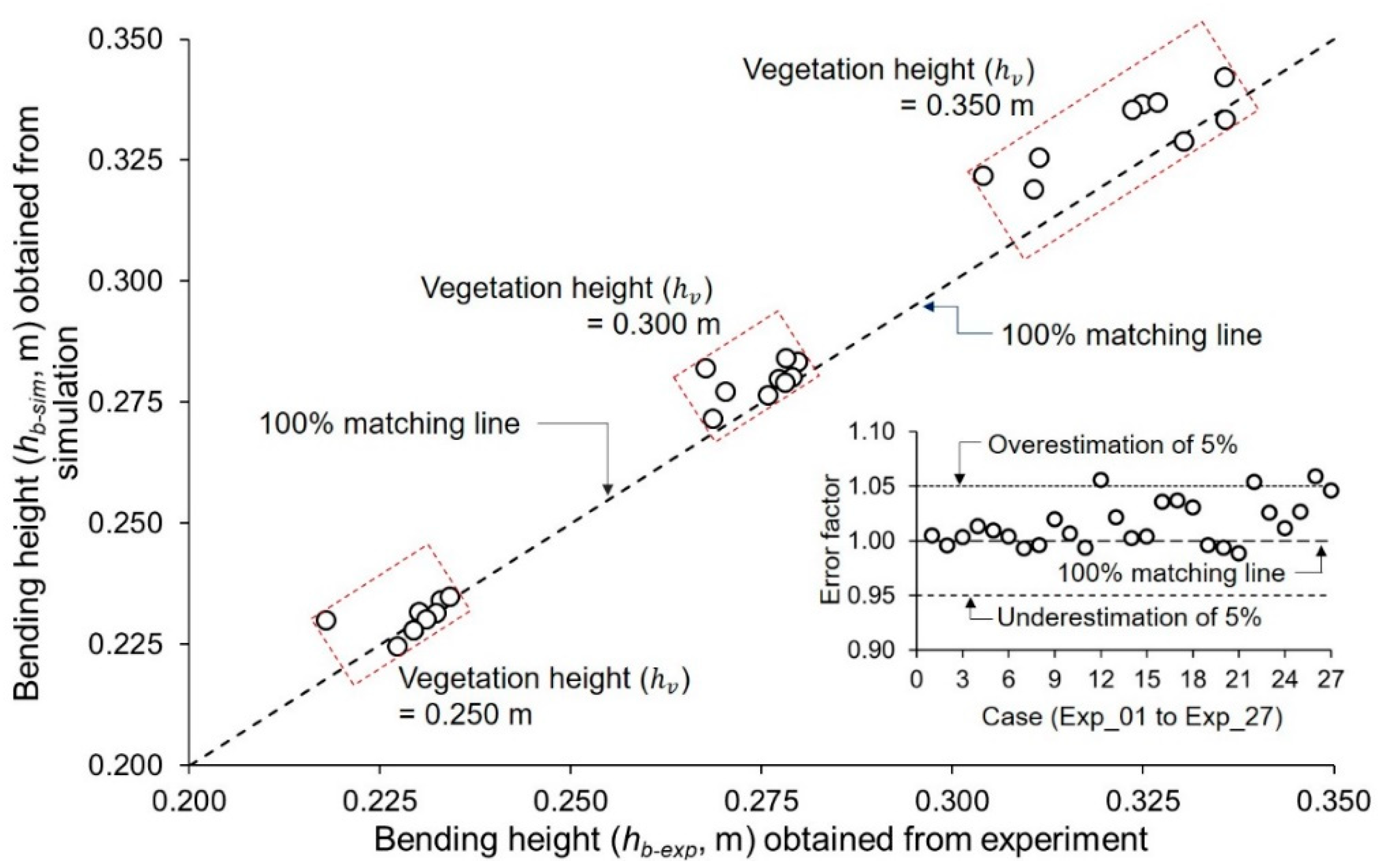
3.1. Experimental and Simulation Results
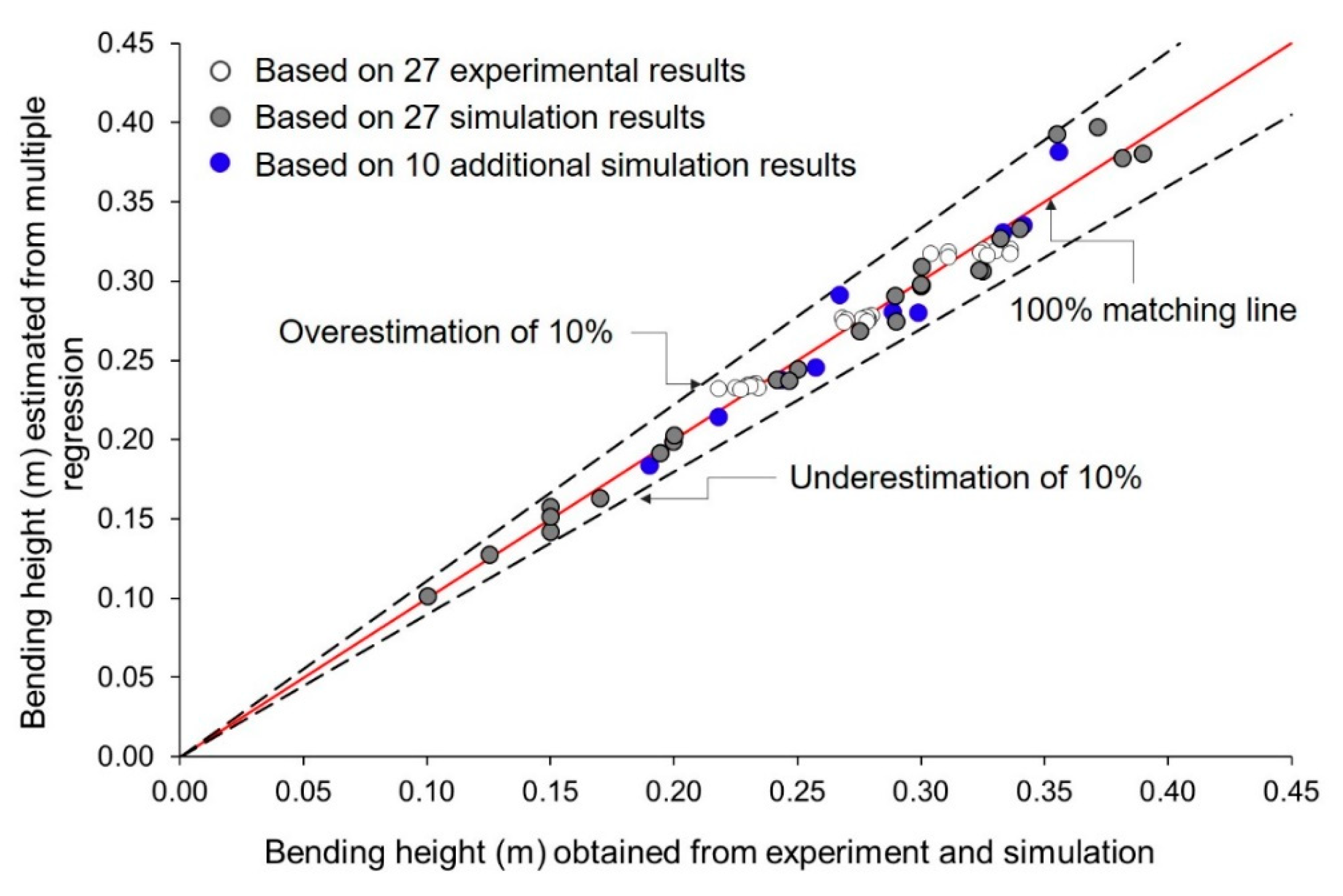
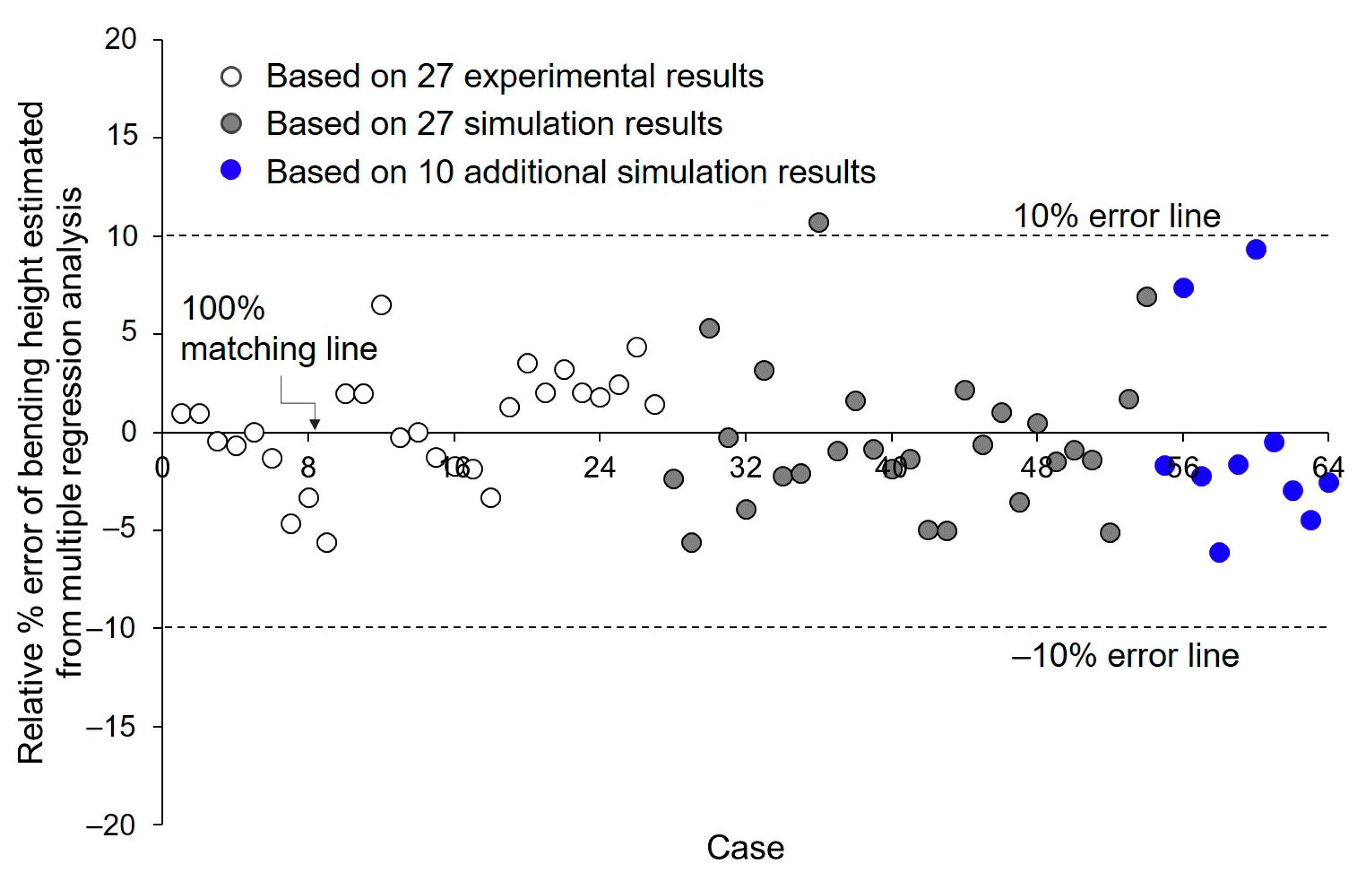
3.2. Regression Analysis
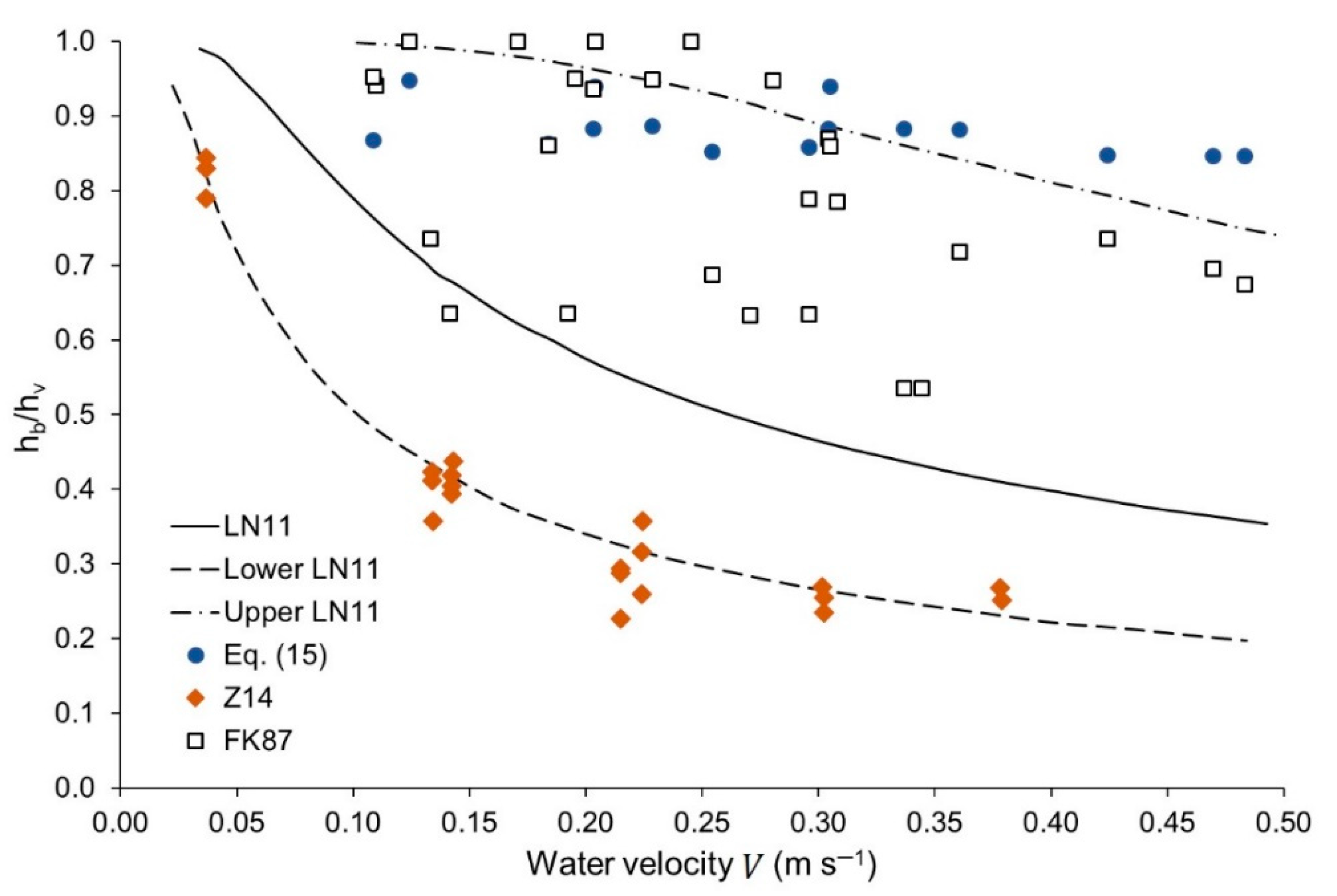
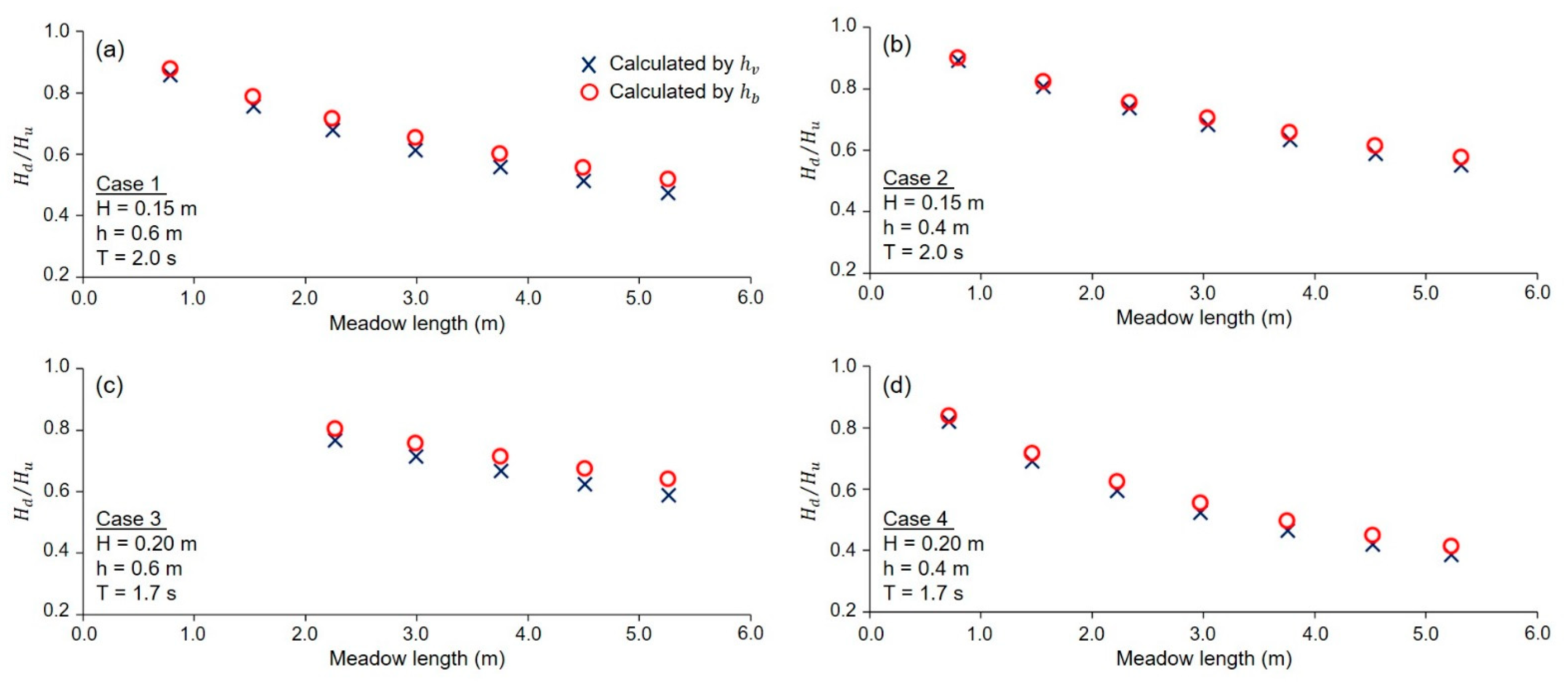
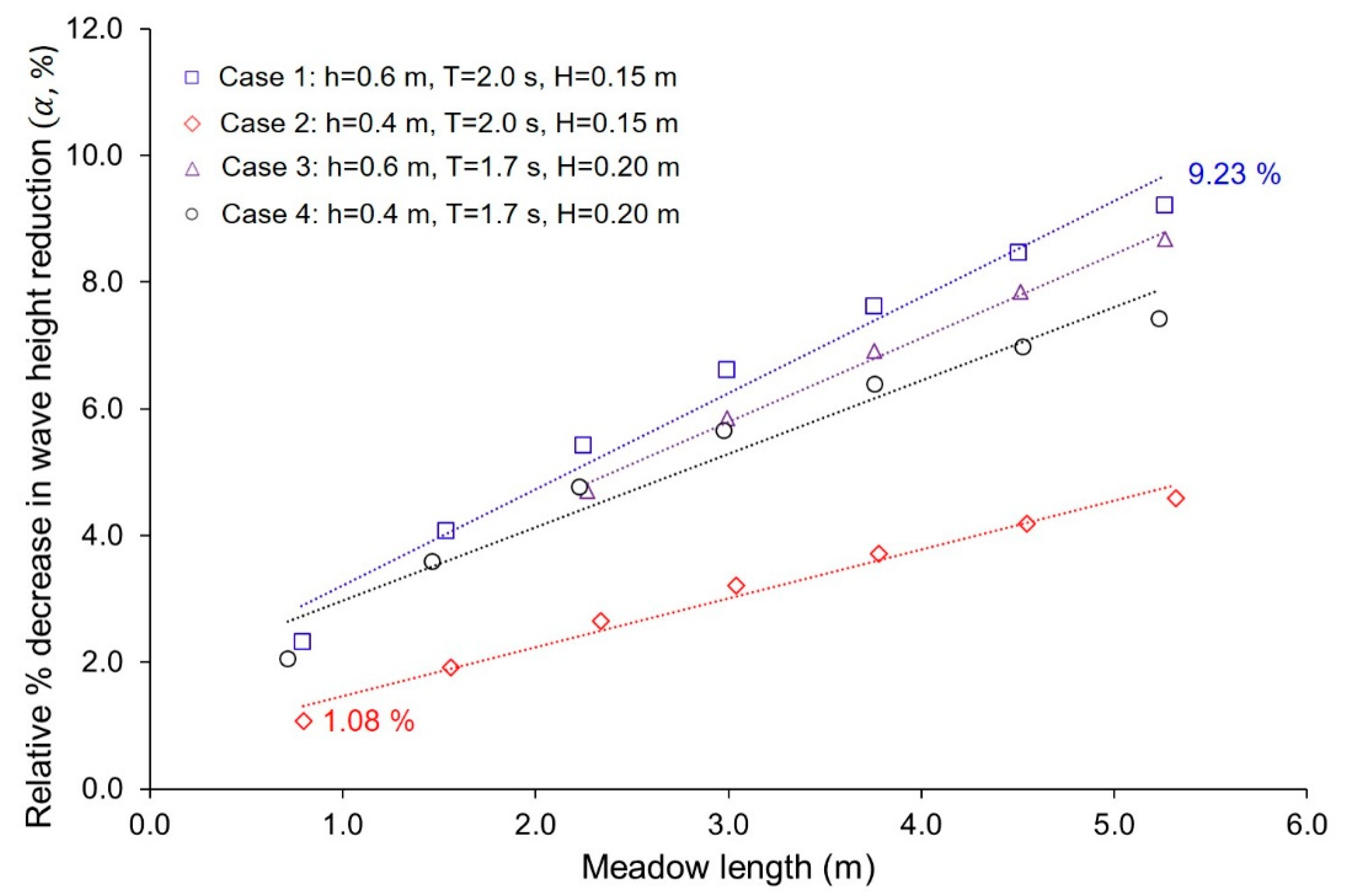
3.3. Effect of Bending Behavior on Wave Height
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ghaderpour, E.; Abbes, A.B.; Rhif, M.; Pagiatakis, S.D.; Farah, I.R. Non-stationary and unequally spaced NDVI time series analyses by the LSWAVE software. Int. J. Remote Sens. 2020, 41, 2374–2390. [Google Scholar] [CrossRef]
- He, Y.; Lee, E. Empirical relationships of sea surface temperature and vegetation activity with summer rainfall variability over the Sahel. Earth Interact. 2016, 20, 1–18. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Donat, M.G.; Burrows, M.T.; Moore, P.J.; Smale, D.A.; Alexander, L.V.; Benthuysen, J.A.; Feng, M.; Gupta, A.S.; Hobday, A.J.; et al. Longer and more frequent marine heatwaves over the past century. Nat. Commun. 2018, 9, 1324. [Google Scholar] [CrossRef]
- Jung, S.; Chau, V.T.; Kim, M.; Na, W.B. Artificial seaweed reefs that support the establishment of submerged aquatic vegetation beds and facilitate ocean macroalgal afforestation: A review. J. Mar. Sci. Eng. 2022, 10, 1184. [Google Scholar] [CrossRef]
- Barahimi, M.; Sui, J. Effects of submerged vegetation arrangement patterns and density on flow structure. Water 2023, 15, 176. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. Flow resistance of floodplain vegetation mixtures for modelling river flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- Stocker, B.D.; Tumber-Dávila, S.J.; Konings, A.G.; Anderson, M.C.; Hain, C.; Jackson, R.B. Global patterns of water storage in the rooting zones of vegetation. Nat. Geosci. 2023, 16, 250–256. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Liu, Y.; Li, Z.; Guo, L.; Xu, A.; Zhao, J. Effectiveness of vegetation cover pattern on regulating soil erosion and runoff generation in red soil environment, southern China. Ecol. Indic. 2021, 129, 107956. [Google Scholar] [CrossRef]
- Bai, G.; Xu, D.; Zou, Y.; Liu, Y.; Liu, Z.; Luo, F.; Wang, C.; Zhang, C.; Liu, B.; Zhou, Q.; et al. Impact of submerged vegetation, water flow field and season changes on sediment phosphorus distribution in a typical subtropical shallow urban lake: Water nutrients state determines its retention and release mechanism. J. Environ. Chem. Eng. 2022, 10, 107982. [Google Scholar] [CrossRef]
- Clarke, S.J. Vegetation growth in rivers: Influences upon sediment and nutrient dynamics. Prog. Phys. Geog. 2002, 26, 159–172. [Google Scholar] [CrossRef]
- Toromanovic, M.; Ibrahimpašić, J.; Topalić-Trivunović, L.; Šišić, I. Removal of organic pollutants from municipal wastewater by a horizontal pilot-scale constructed wetland utilizing Phragmites australis and Typha latifolia–Effectiveness monitoring per season. J. Chem. Technol. Environ. 2018, 10, 39–44. [Google Scholar] [CrossRef][Green Version]
- Wang, C.; Zheng, S.S.; Wang, P.F.; Qian, J. Effects of vegetations on the removal of contaminants in aquatic environments: A review. J. Hydrodyn. 2014, 26, 497–511. [Google Scholar] [CrossRef]
- John, B.M.; Shirlal, K.G.; Rao, S. Effect of artificial sea grass on wave attenuation- an experimental investigation. Aquat. Procedia 2015, 4, 221–226. [Google Scholar] [CrossRef]
- Morris, R.L.; Graham, T.D.J.; Kelvin, J.; Ghisalberti, M.; Swearer, S.E. Kelp beds as coastal protection: Wave attenuation of Ecklonia radiata in a shallow coastal bay. Ann. Bot. 2020, 125, 235–246. [Google Scholar] [CrossRef]
- Sánchez-González, J.F.; Sánchez-Rojas, V.; Memos, C.D. Wave attenuation due to Posidonia oceanica meadows. J. Hydraul. Res. 2011, 49, 503–514. [Google Scholar] [CrossRef]
- Sigren, J.M.; Figlus, J.; Armitage, A.R. Coastal sand dunes and dune vegetation: Restoration, erosion, and storm protection. Shore Beach 2014, 82, 5–12. [Google Scholar]
- Manousakas, N.; Salauddin, M.; Pearson, J.; Denissenko, P.; Williams, H.; Abolfathi, S. Effects of seagrass vegetation on wave runup reduction—A laboratory study. IOP Conf. Ser. Earth Environ. Sci. 2022, 1072, 012004. [Google Scholar] [CrossRef]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 56, 332–340. [Google Scholar] [CrossRef]
- Koftis, T.; Prinos, P.; Stratigaki, V. Wave damping over artificial Posidonia oceanica meadow: A large-scale experimental study. Coast. Eng. 2013, 73, 71–83. [Google Scholar] [CrossRef]
- Stratigaki, V.; Manca, E.; Prinos, P.; Losada, I.J.; Lara, J.L.; Sclavo, M.; Amos, C.L.; Cáceres, I.; Sánchez-Arcilla, A. Large-scale experiments on wave propagation over Posidonia oceanica. J. Hydraul. Res. 2011, 49, 31–43. [Google Scholar] [CrossRef]
- Cao, H.; Chen, Y.; Tian, Y.; Feng, W. Field investigation into wave attenuation in the mangrove environment of the South China Sea coast. J. Coastal Res. 2016, 32, 1417–1427. [Google Scholar] [CrossRef]
- Nowacki, D.J.; Beudin, A.; Ganju, N.K. Spectral wave dissipation by submerged aquatic vegetation in a back-barrier estuary. Limnol. Oceanogr. 2017, 62, 736–753. [Google Scholar] [CrossRef]
- Paquier, A.E.; Oudart, T.; Le Bouteiller, C.; Meulé, S.; Larroudé, P.; Dalrymple, R.A. 3D numerical simulation of seagrass movement under waves and currents with GPUSPH. Int. J. Sediment Res. 2021, 36, 711–722. [Google Scholar] [CrossRef]
- Yin, K.; Xu, S.; Huang, W.; Liu, S.; Li, M. Numerical investigation of wave attenuation by coupled flexible vegetation dynamic model and XBeach wave model. Ocean Eng. 2021, 235, 109357. [Google Scholar] [CrossRef]
- Twomey, A.J.; O’Brien, K.R.; Callaghan, D.P.; Saunders, M.I. Synthesising wave attenuation for seagrass: Drag coefficient as a unifying indicator. Mar. Pollut. Bull. 2020, 160, 111661. [Google Scholar] [CrossRef]
- Fonseca, M.S.; Cahalan, J.A. A preliminary evaluation of wave attenuation by four species of seagrass. Estuar. Coast. Shelf Sci. 1992, 35, 565–576. [Google Scholar] [CrossRef]
- Yiping, L.; Anim, D.O.; Wang, Y.; Tang, C.; Du, W.; Lixiao, N.; Yu, Z.; Acharya, K.; Chen, L. Laboratory simulations of wave attenuation by an emergent vegetation of artificial Phragmites australis: An experimental study of an open-channel wave flume. J. Environ. Eng. Landsc. Manag. 2015, 23, 251–266. [Google Scholar] [CrossRef][Green Version]
- Hashim, A.M.; Catherine, S.M.P. A Laboratory study on wave reduction by mangrove forests. APCBEE Procedia 2013, 5, 27–32. [Google Scholar] [CrossRef]
- He, F.; Chen, J.; Jiang, C. Surface wave attenuation by vegetation with the stem, root and canopy. Coast. Eng. 2019, 152, 103509. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 2011, 56, 2003–2017. [Google Scholar] [CrossRef]
- Losada, I.J.; Maza, M.; Lara, J.L. A new formulation for vegetation-induced damping under combined waves and currents. Coast. Eng. 2016, 107, 1–13. [Google Scholar] [CrossRef]
- Fonseca, M.S.; Kenworthy, W.J. Effects of current on photosynthesis and distribution of seagrasses. Aquat. Bot. 1987, 27, 59–78. [Google Scholar] [CrossRef]
- Zeller, R.B.; Weitzman, J.S.; Abbett, M.E.; Zarama, F.J.; Fringer, O.B.; Koseff, J.R. Improved parameterization of seagrass blade dynamics and wave attenuation based on numerical and laboratory experiments. Limnol. Oceanogr. 2014, 59, 251–266. [Google Scholar] [CrossRef]
- van Veelen, T.J.; Fairchild, T.P.; Reeve, D.E.; Karunarathna, H. Experimental study on vegetation flexibility as control parameter for wave damping and velocity structure. Coast. Eng. 2020, 157, 103648. [Google Scholar] [CrossRef]
- Folkard, A.M. Hydrodynamics of model Posidonia oceanica patches in shallow water. Limnol. Oceanogr. 2005, 50, 1592–1600. [Google Scholar] [CrossRef]
- Paul, M.; Bouma, T.J.; Amos, C.L. Wave attenuation by submerged vegetation: Combining the effect of organism traits and tidal current. Mar. Ecol. Prog. Ser. 2012, 444, 31–41. [Google Scholar] [CrossRef]
- Weitzman, J.S.; Zeller, R.B.; Thomas, F.I.M.; Koseff, J.R. The attenuation of current- and wave-driven flow within submerged multispecific vegetative canopies. Limnol. Oceanogr. 2015, 60, 1855–1874. [Google Scholar] [CrossRef]
- Atkins, M.D. Chapter 5–velocity field measurement using particle image velocimetry (PIV). In Application of Thermo-Fluidic Measurement Techniques: An Introduction; Kim, T., Lu, T.J., Song, S.J., Eds.; Butterworth-Heinemann: Cambridge, MA, USA, 2016; pp. 125–166. ISBN 978-012-809-731-1. [Google Scholar]
- Lee, Y.J.; Jung, S.; Na, W.B. Estimating movement and falling distances of underwater free-falling cuboid models for marine habitat enhancement structures considering horizontal water flow. Ocean Eng. 2022, 262, 112172. [Google Scholar] [CrossRef]
- Pauls, J.P.; Bartnikowski, N.; Jansen, S.H.; Lim, E.; Dasse, K. Chapter 13–Preclinical evaluation. In Mechanical Circulatory and Respiratory Support; Gregory, S.D., Stevens, M.C., Fraser, J.F., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 407–438. ISBN 978-012-810-491-0. [Google Scholar]
- Chen, S.N.; Sanford, L.P.; Koch, E.W.; Shi, F.; North, E.W. A nearshore model to investigate the effects of seagrass bed geometry on wave attenuation and suspended sediment transport. Estuar. Coast. 2007, 30, 296–310. [Google Scholar] [CrossRef]
- Axisa, F.; Antunes, J. Modelling of Mechanical Systems: Fluid Structure Interaction; Butterworth-Heinemann: Jordan Hill, Oxford, UK, 2007; pp. 1–44. ISBN 978-075-066-847-7. [Google Scholar]
- Lee, K.; Huque, Z.; Kommalapati, R.; Han, S.E. The evaluation of aerodynamic interaction of wind blade using fluid structure interaction method. J. Clean Energy Technol. 2015, 3, 270–275. [Google Scholar] [CrossRef]
- El Maani, R.; Radi, B.; El Hami, A. Vibratory reliability analysis of an aircraft’s wing via fluid-structure interactions. Aerospace 2017, 4, 40. [Google Scholar] [CrossRef]
- Hirschhorn, M.; Tchantchaleishvili, V.; Stevens, R.; Rossano, J.; Throckmorton, A. Fluid–structure interaction modeling in cardiovascular medicine—A systematic review 2017–2019. Med. Eng. Phys. 2020, 78, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Kamakoti, R.; Shyy, W. Fluid-structure interaction for aeroelastic applications. Prog. Aerosp. Sci. 2004, 40, 535–558. [Google Scholar] [CrossRef]
- Sederstrom, D.R. Methods and Implementation of Fluid-Structure Interaction Modeling into an Industry-Accepted Design Tool. Ph.D. Thesis, University of Denver, Denver, FL, USA, 2016; pp. 1–30. [Google Scholar]
- Kim, D.; Jung, S.; Na, W.B. Evaluation of turbulence models for estimating the wake region of artificial reefs using particle image velocimetry and computational fluid dynamics. Ocean Eng. 2021, 223, 108673. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent User’s Guide Release 2020 R1; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Tadepalli, S.C.; Erdemir, A.; Cavanagh, P.R. Comparison of hexahedral and tetrahedral elements in finite element analysis of the foot and footwear. J. Biomech. 2011, 44, 2337–2343. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Inc. ANSYS Fluent Theory Guide Release 2020 R1; ANSYS Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Drevon, D.; Fursa, S.R.; Malcolm, A.L. Intercoder reliability and validity of WebPlotDigitizer in extracting graphed data. Behav. Modif. 2016, 41, 323–339. [Google Scholar] [CrossRef] [PubMed]
- Buckingham, E. The principle of similitude. Nature 1915, 96, 396–397. [Google Scholar] [CrossRef]
- Dumka, P.; Chauhan, R.; Singh, A.; Singh, G.; Mishra, D. Implementation of Buckingham’s Pi theorem using Python. Adv. Eng. Softw. 2022, 173, 103232. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J.; Ondiviela, B.; Trinogga, J.; Bouma, T.J. Large-scale 3-D experiments of wave and current interaction with real vegetation. Part 2: Experimental analysis. Coast. Eng. 2015, 106, 73–86. [Google Scholar] [CrossRef]
- Henderson, S.M. Motion of buoyant, flexible aquatic vegetation under waves: Simple theoretical models and parameterization of wave dissipation. Coast. Eng. 2019, 152, 103497. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Kirby, J.T.; Hwang, P.A. Wave diffraction due to areas of energy dissipation. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 67–79. [Google Scholar] [CrossRef]
- Liu, S.; Xu, S.; Yin, K. Optimization of the drag coefficient in wave attenuation by submerged rigid and flexible vegetation based on experimental and numerical studies. Ocean Eng. 2023, 285, 115382. [Google Scholar] [CrossRef]
- Mullarney, J.C.; Henderson, S.M. Wave-forced motion of submerged single-stem vegetation. J. Geophys. Res. Oceans 2010, 115, C12061. [Google Scholar] [CrossRef]


| Vegetation † Shape | Density | Young’s Modulus (MPa) | Material Type | References | ||
|---|---|---|---|---|---|---|
| Height (m) | Width or Diameter (mm) | Thickness (mm) | ||||
| 0.15–0.50 | 10 | ~0.2 | 900 ± 20 | 540 ± 10 | Polyethylene | [35] |
| 0.30 | 12 | – | 32 | – | Polyethylene | [18] |
| 0.30 | 12 | – | – | – | Wooden dowel | |
| 0.55 | – | 1.0 | 550–700 | 903 | Polypropylene | [20] |
| 0.10–0.15 | 1.8–2.2 | – | – | – | Cable ties | [36] |
| 0.10–0.30 | 1.8–2.2 | – | – | – | Poly ribbon | |
| 0.55 | 10 | 1.0 | 550–700 | 903 | PVC | [19] |
| 0.21 | 4.0 | 0.1 | 800 | 600 | Polyethylene | [13] |
| 0.16 | 10 | 0.25 | – | 300 | LDPE | [37] |
| 0.07 | 6.35 | – | – | – | Wooden dowel | |
| 0.07 | 38.1 | – | – | – | PVC | |
| 0.45 | – | – | – | 645 ± 10 | HDPE | [29] |
| 0.45 | – | – | – | 3530 ± 390 | PVC | |
| 0.45 | – | – | – | 196 ± 49 | Polyethylene | |
| 0.30 | 5.0 | – | 350 | 2917 | Bamboo dowel | [34] |
| 0.30 | 5.0 | – | 998 | 0.56 | Silicon sealant | |
| Property | Magnitude | Unit |
|---|---|---|
| Density | 1040 | kg m−3 |
| Coefficient of Thermal Expansion | 0.00016 | °C−1 |
| Young’s Modulus | 2.73 × 109 | Pa |
| Poisson’s Ratio | 0.395 | - |
| Bulk Modulus | 4.3333 × 109 | Pa |
| Shear Modulus Tensile Yield Strength | 9.7849 × 108 3.45 × 107 | Pa Pa |
| Tensile Ultimate Strength | 4.31 × 107 | Pa |
| No. | Height (m) | Width (m) | Inlet Velocity (m s−1) | No | Height (m) | Width (m) | Inlet Velocity (m s−1) |
|---|---|---|---|---|---|---|---|
| Exp_01 | 0.250 | 0.020 | 0.089 | Exp_15 | 0.300 | 0.010 | 0.123 |
| Exp_02 | 0.250 | 0.015 | 0.089 | Exp_16 | 0.350 | 0.020 | 0.123 |
| Exp_03 | 0.250 | 0.010 | 0.089 | Exp_17 | 0.350 | 0.015 | 0.123 |
| Exp_04 | 0.300 | 0.020 | 0.089 | Exp_18 | 0.350 | 0.010 | 0.123 |
| Exp_05 | 0.300 | 0.015 | 0.089 | Exp_19 | 0.250 | 0.020 | 0.155 |
| Exp_06 | 0.300 | 0.010 | 0.089 | Exp_20 | 0.250 | 0.015 | 0.155 |
| Exp_07 | 0.350 | 0.020 | 0.089 | Exp_21 | 0.250 | 0.010 | 0.155 |
| Exp_08 | 0.350 | 0.015 | 0.089 | Exp_22 | 0.300 | 0.020 | 0.155 |
| Exp_09 | 0.350 | 0.010 | 0.089 | Exp_23 | 0.300 | 0.015 | 0.155 |
| Exp_10 | 0.250 | 0.020 | 0.123 | Exp_24 | 0.300 | 0.010 | 0.155 |
| Exp_11 | 0.250 | 0.015 | 0.123 | Exp_25 | 0.350 | 0.020 | 0.155 |
| Exp_12 | 0.250 | 0.010 | 0.123 | Exp_26 | 0.350 | 0.015 | 0.155 |
| Exp_13 | 0.300 | 0.020 | 0.123 | Exp_27 | 0.350 | 0.010 | 0.155 |
| Exp_14 | 0.300 | 0.015 | 0.123 |
| Case | (m) | PIV Measurement | FSI Simulation | |||
|---|---|---|---|---|---|---|
| (m) | Rel. % Difference (%) | (m) | Rel. % Difference (%) | Rel. % Error (%) | ||
| Exp_01 | 0.250 | 0.233 | –6.80 | 0.234 | –6.40 | +0.43 |
| Exp_02 | 0.250 | 0.232 | –7.20 | 0.231 | –7.60 | –0.43 |
| Exp_03 | 0.250 | 0.234 | –6.40 | 0.235 | –6.00 | +0.43 |
| Exp_04 | 0.300 | 0.280 | –6.67 | 0.283 | –5.67 | +1.07 |
| Exp_05 | 0.300 | 0.277 | –7.67 | 0.280 | –6.67 | +1.08 |
| Exp_06 | 0.300 | 0.279 | –7.00 | 0.280 | –6.67 | +0.36 |
| Exp_07 | 0.350 | 0.336 | –4.00 | 0.333 | –4.86 | –0.89 |
| Exp_08 | 0.350 | 0.330 | –5.71 | 0.329 | –6.00 | –0.30 |
| Exp_09 | 0.350 | 0.336 | –4.00 | 0.342 | –2.29 | +1.79 |
| Exp_10 | 0.250 | 0.230 | –8.00 | 0.232 | –7.20 | +0.87 |
| Exp_11 | 0.250 | 0.229 | –8.40 | 0.228 | –8.80 | –0.44 |
| Exp_12 | 0.250 | 0.218 | –12.80 | 0.230 | –8.00 | +5.50 |
| Exp_13 | 0.300 | 0.278 | –7.33 | 0.284 | –5.33 | +2.16 |
| Exp_14 | 0.300 | 0.276 | –8.00 | 0.276 | –8.00 | +0.00 |
| Exp_15 | 0.300 | 0.278 | –7.33 | 0.279 | –7.00 | +0.36 |
| Exp_16 | 0.350 | 0.325 | –7.14 | 0.337 | –3.71 | +3.69 |
| Exp_17 | 0.350 | 0.324 | –7.43 | 0.335 | –4.29 | +3.40 |
| Exp_18 | 0.350 | 0.327 | –6.57 | 0.337 | –3.71 | +3.06 |
| Exp_19 | 0.250 | 0.231 | –7.60 | 0.230 | –8.00 | –0.43 |
| Exp_20 | 0.250 | 0.225 | –10.00 | 0.228 | –8.80 | +1.33 |
| Exp_21 | 0.250 | 0.227 | –9.20 | 0.225 | –10.00 | –0.88 |
| Exp_22 | 0.300 | 0.268 | –10.67 | 0.282 | –6.00 | +5.22 |
| Exp_23 | 0.300 | 0.270 | –10.00 | 0.277 | –7.67 | +2.59 |
| Exp_24 | 0.300 | 0.269 | –10.33 | 0.272 | –9.33 | +1.12 |
| Exp_25 | 0.350 | 0.311 | –11.14 | 0.319 | –8.86 | +2.57 |
| Exp_26 | 0.350 | 0.304 | –13.14 | 0.322 | –8.00 | +5.92 |
| Exp_27 | 0.350 | 0.311 | –11.14 | 0.326 | –6.86 | +4.82 |
| Case | Density (kg m−3) | Young’s Modulus (Pa) | Vegetation Height (m) | Width (m) | Thickness (m) | Inlet Velocity (m s−1) | Bending Height (m) |
|---|---|---|---|---|---|---|---|
| Sim_01 | 1500 | 3.00 × 109 | 0.275 | 0.020 | 0.002 | 0.100 | 0.275 |
| Sim_02 | 2000 | 2.00 × 109 | 0.325 | 0.015 | 0.002 | 0.050 | 0.325 |
| Sim_03 | 500 | 1.00 × 109 | 0.150 | 0.030 | 0.003 | 0.200 | 0.150 |
| Sim_04 | 2500 | 5.00 × 108 | 0.200 | 0.040 | 0.002 | 0.150 | 0.200 |
| Sim_05 | 3000 | 1.50 × 109 | 0.175 | 0.005 | 0.001 | 0.250 | 0.170 |
| Sim_06 | 3500 | 5.00 × 109 | 0.300 | 0.050 | 0.005 | 0.300 | 0.300 |
| Sim_07 | 4000 | 3.00 × 109 | 0.400 | 0.040 | 0.003 | 0.400 | 0.389 |
| Sim_08 | 4500 | 7.00 × 109 | 0.250 | 0.030 | 0.002 | 0.250 | 0.250 |
| Sim_09 | 5000 | 2.00 × 109 | 0.450 | 0.010 | 0.001 | 0.175 | 0.355 |
| Sim_10 | 2200 | 1.80 × 109 | 0.300 | 0.030 | 0.003 | 0.200 | 0.300 |
| Sim_11 | 1000 | 1.20 × 109 | 0.200 | 0.020 | 0.003 | 0.300 | 0.200 |
| Sim_12 | 3000 | 2.50 × 109 | 0.300 | 0.020 | 0.003 | 0.100 | 0.300 |
| Sim_13 | 1750 | 3.00 × 109 | 0.350 | 0.030 | 0.002 | 0.250 | 0.340 |
| Sim_14 | 2250 | 1.75 × 109 | 0.250 | 0.025 | 0.002 | 0.300 | 0.241 |
| Sim_15 | 3000 | 2.50 × 109 | 0.150 | 0.005 | 0.001 | 0.200 | 0.150 |
| Sim_16 | 3500 | 1.00 × 109 | 0.325 | 0.015 | 0.002 | 0.150 | 0.323 |
| Sim_17 | 1000 | 2.00 × 109 | 0.125 | 0.010 | 0.002 | 0.250 | 0.125 |
| Sim_18 | 2000 | 7.50 × 108 | 0.300 | 0.030 | 0.003 | 0.100 | 0.300 |
| Sim_19 | 1500 | 5.00 × 108 | 0.150 | 0.020 | 0.002 | 0.200 | 0.150 |
| Sim_20 | 4000 | 2.00 × 109 | 0.250 | 0.025 | 0.002 | 0.300 | 0.246 |
| Sim_21 | 2500 | 3.00 × 109 | 0.300 | 0.010 | 0.003 | 0.400 | 0.290 |
| Sim_22 | 2750 | 2.50 × 109 | 0.350 | 0.010 | 0.002 | 0.250 | 0.332 |
| Sim_23 | 3750 | 5.00 × 109 | 0.400 | 0.030 | 0.002 | 0.175 | 0.381 |
| Sim_24 | 750 | 1.25 × 109 | 0.200 | 0.040 | 0.001 | 0.200 | 0.194 |
| Sim_25 | 1750 | 3.25 × 109 | 0.300 | 0.020 | 0.001 | 0.225 | 0.290 |
| Sim_26 | 2250 | 4.00 × 109 | 0.100 | 0.010 | 0.002 | 0.325 | 0.100 |
| Sim_27 | 1000 | 2.25 × 109 | 0.450 | 0.010 | 0.001 | 0.150 | 0.371 |
| Case | Wave Height H (m) | Water Depth h (m) | Wave Period T (s) | Current Velocity V (m s−1) |
|---|---|---|---|---|
| 1 | 0.15 | 0.60 | 2.00 | 0.30 |
| 2 | 0.15 | 0.40 | 2.00 | 0.30 |
| 3 | 0.20 | 0.60 | 1.70 | 0.30 |
| 4 | 0.20 | 0.40 | 1.70 | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chau, T.V.; Jung, S.; Kim, M.; Na, W.-B. Analysis of the Bending Height of Flexible Marine Vegetation. J. Mar. Sci. Eng. 2024, 12, 1054. https://doi.org/10.3390/jmse12071054
Chau TV, Jung S, Kim M, Na W-B. Analysis of the Bending Height of Flexible Marine Vegetation. Journal of Marine Science and Engineering. 2024; 12(7):1054. https://doi.org/10.3390/jmse12071054
Chicago/Turabian StyleChau, Than Van, Somi Jung, Minju Kim, and Won-Bae Na. 2024. "Analysis of the Bending Height of Flexible Marine Vegetation" Journal of Marine Science and Engineering 12, no. 7: 1054. https://doi.org/10.3390/jmse12071054
APA StyleChau, T. V., Jung, S., Kim, M., & Na, W.-B. (2024). Analysis of the Bending Height of Flexible Marine Vegetation. Journal of Marine Science and Engineering, 12(7), 1054. https://doi.org/10.3390/jmse12071054







