Abstract
As a flexible, autonomous and intelligent motion platform, underactuated surface vessels (USVs) are expected to be an ideal means of transport in dangerous and complex marine environments. The success and efficiency of maritime missions performed by USVs depend on their ability to accurately follow paths and remain robust against wind and wave disturbances. To this end, this paper focuses on accurate and robust path following control for USVs under wave disturbances. Model predictive control with a quasi-infinite horizon is proposed which converts the objective function from an infinite horizon to an approximate finite horizon, providing the convergence performance in long prediction horizons and reducing the computation load explicitly. To enhance robustness against disturbances, a fixed-time disturbance observer is applied to estimate the time-varying and bounded disturbances. The estimated value is provided to the controller input to form a robust control framework with disturbance feedforward compensation and predictive control feedback correction, which is substantially different from existing works. The convergence and optimality of the proposed algorithm are presented mathematically. Finally, we demonstrate the advantages of the algorithm in both theory and simulation.
1. Introduction
Maritime incidents have been a significant concern within the global maritime community since the inception of shipping. As indicated in [1], the total number of maritime accidents over the past 40 years is more than 63991 and there has been a reduction in the number of maritime incidents from 3152 in 1979 to 959 in 2001. Autonomous ships have the potential to significantly reduce the high rate of maritime accidents caused by human error, improving safety at sea [2]. Autonomous ships are most effective in complex heat, cold and deep-water environments. Path following control technology is a crucial aspect of autonomous underactuated surface vessels (USVs) performing maritime missions, as it determines the accuracy and autonomy of USVs navigating according to predetermined or self-planned paths [3].
A substantial amount of research has been conducted on the problem of USV path following with various control methods, including [4,5,6,7,8,9,10]. In particular, the line-of-sight (LOS) guidance law, initially developed by Fossen [4] for USV motion control, is a widely accepted guidance algorithm used in path following a USV. Reference [5] highlights the efficacy of the LOS guidance algorithm, which is a straightforward, intuitive and effective method that enables vessels to converge to the desired path in an efficient manner. The authors of [5] state that traditional autopilot can readily incorporate LOS, with the LOS angle being calculated through the minimization of the cross-track error. As long as the vessel is able to adhere to the LOS angle, its position will ultimately converge to the desired path [6]. Furthermore, the path tracking control algorithm is based on the traditional PID algorithm [7]. Qiu et al. [8] proposed an adaptive sliding mode control scheme for USVs based on a neural network, an auxiliary dynamic system, sliding mode control and an inverse stepping technique, which effectively addresses the issues of model uncertainty and input saturation. However, path following vehicles are affected by external ocean disturbances in practical applications, which reduce their accuracy [9,10]. The previous state-of-the-art studies have only emphasized path tracking accuracy, ignoring the effects of waves and wind. This leads to the generation of dynamic models that are not applicable to the actual ocean environment. Furthermore, there is an upper limit on the force output due to the input characteristics and physical properties of the USV thruster.
The vessel dynamic model incorporates both internal and external disturbances, which presents a significant challenge for controller design. To address this, different observers have been designed and applied. Gao et al. propose a finite-time trajectory tracking control approach for USVs with unknown dead-zones and unknown disturbances [11]. Han et al. introduce an active disturbance rejection controller that employs an extended state observer (ESO) to estimate states and disturbances [12]. Naghdi and Sadrnia in [13] propose a simple fuzzy system to modify the gain of linear ESO (LESO) to improve its performance. Li et al. in [14] investigate the path following problem for a USV in the presence of ocean currents, model uncertainties and input saturation. In [15], Seongik et al. propose a predefined-time and prescribed-performance control method for an unmanned planning hull system with input delay and unknown disturbance. In our previous work [16], we designed a path following controller for USVs and a disturbance observer to compensate for time-varying disturbances such as wind, waves and current. Furthermore, the authors of [17] conducted extensive research into model predictive control algorithms and robust high-speed multihull control. A robust anti-pitching control method with Kalman filter measurement is proposed in [17], which effectively solves the problem of excessive vertical movement of high-speed multihulls, as well as the difficulty of directly measuring surge and pitch angle speed. Despite the inherent complexity of designing a controller for this model given the time-varying disturbance of wind, waves, current and the physical model of the ship itself, the proposed disturbance observer combined with a robust controller provides a reliable solution.
To address this problem, Fu et al. [18] focus on the path following control problem for USVs in the presence of unknown time-varying environmental disturbances, using an enhanced adaptive integral line-of-sight guidance law that is suitable for any parametric paths and is capable of handling time-varying ocean currents. A disturbance observer is proposed in [19] as a means of estimating and compensating for disturbances in the designed controller for a highly nonlinear and strongly coupled ship’s path following model. The implementation of a model predictive control (MPC) law with a disturbance observer enables the effective mitigation of the effects of environmental disturbances and the provision of smooth control commands [20]. Furthermore, the proposed MPC approach in [20] is capable of achieving path following for underactuated surface ships, even in the presence of input saturation and parameter uncertainties. In standard finite horizon MPC, the prediction and control horizon lengths are often selected through tuning [21]. However, it is important to note that considering an infinite horizon, as demonstrated in [22], leads to more accurate results. In contrast to finite horizon model predictive control (FH-MPC), which is susceptible to a decrease in system performance with an increase in the horizon length, infinite horizon model predictive control (iH-MPC) exhibits a consistent level of performance, despite its increased complexity.
This paper presents a robust controller for USV path following with a disturbance observer. To this end, this paper proposes a quasi-infinite horizon model predictive control (QiH-MPC) scheme with a fixed-time disturbance observer for USV robust path following. The main contributions of this paper are summarized as follows:
- (1)
- In this paper, a state-of-the-art state space control model considering time-varying wave disturbances is established for USV path following, in which the states of tracking error, heading angle, heading angular velocity and disturbance are taken into account.
- (2)
- A QiH-MPC is proposed that provides convergence performance in long prediction horizons, and it explicitly reduces the computational burden due to the fact that it converts the objective function from an infinite horizon to an approximate finite horizon. Moreover, the convergence of the proposed algorithm is given mathematically.
- (3)
- Through the application of the fixed-time disturbance observer, the disturbance estimation is compensated in the controller input to form a robust control framework with disturbance feedforward compensation and predictive control feedback correction, which differs significantly from previous state-of-the-art works. This is of great value for the determination of optimal control actions for robust USV path following.
This paper is structured as follows. In Section 2, we present a description of the system model, including a USV path following description, a state space model of USV path following and QiH-MPC with a disturbance compensation framework. Section 3 presents the proposed controller for USV path following. Section 4 gives the fixed-time observer used for disturbance estimation. Section 5 gives the convergence analysis and Section 6 details the numerical simulation. This paper concludes in Section 7 and outlines future work.
2. System Modeling
2.1. Path following Description of USV
In this paper, we study the USV path following problem in Serret–Frenet (SF) coordinates (SFCs) [23], as shown in Figure 1. The origin of the coordinate system {SF} is located at the point on the given path which is closest to the origin of the body-fixed coordinate system {B}. is the given path, is the tangent direction of the given path, is the USV direction, is the heading angle formed by rotating the USV direction counterclockwise to the axis, is the desired heading angle formed by rotating the tangent direction of the path counterclockwise to the axis, is the tracking error and is the desired point.
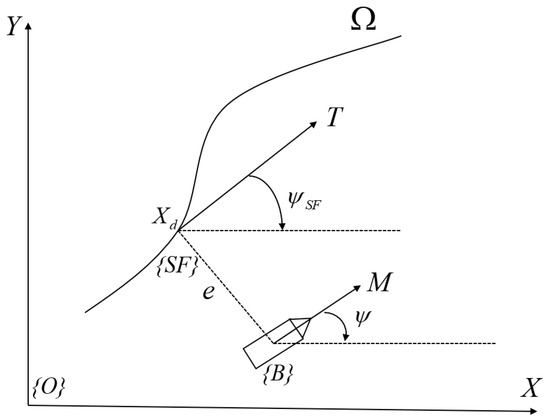
Figure 1.
Illustration of the coordinates in the earth frame (inertial frame) {O}, the surface vessel body-fixed frame {B} and the Serret–Frenet {SF} frame.
In Figure 1, the error dynamics based on the SFCs are given by
where , and are the surge, sway and yaw velocities; is the curvature of the desired path. In general, the control objective of USV path following is to drive tracking error and heading error to zero, thus accurately tracking the desired heading angle and the desired path.
Most problems pertaining to USV path following can be solved by tracking a straight line or a waypoint path, which can be segmented into several piecewise straight lines with low curvature. Furthermore, this solution can be derived with minimal control input, resulting in . Assuming that the ship is moving near the equilibrium point and disregarding the drift angle, we can deduce that surge velocity and sway velocity . This analysis enables the error dynamics (1) to be expressed in a compact form as
where is the tracking error, is the tracking heading error, is the USV speed and is the heading angle velocity.
2.2. State Space Model of USV Path Following
This paper investigates a ship featuring typical underactuated characteristics with a control rudder angle and the speed of the propeller thruster considered to be constant. This represents a significant and hitherto unrecognized threat to the stability of the ship, the reliability of its equipment and the safety of navigation. In extreme cases, the vessel can be capsized if the stability cannot be maintained.
Consequently, it is imperative to model and analyze the actuator and attitude kinematics. The Nomoto model [24] was employed to analyze ship maneuverability since it can model ship motion problems through easily obtained operational parameters. The Nomoto model is presented in detail below:
where is the heading angle, represents the constrained rudder angle and serves as the control input and and are the operational parameters, which can be obtained by the designated rotary and Z-type experiments. Equation (3) can be rewritten into a concise form as follows:
The heading deviation is defined as . If the desired path is a straight line or can be decomposed into multiple straight lines, we can derive that because for a straight line. Therefore, Formula (4) evolves into
Combined with the error dynamics of USV path following (2) and the sum of external bounded disturbance, it follows that
We can rewrite (6) into the form of a state space equation as
Remark 1.
The path following state space model in (7) describes the dynamics of USV path following with a control rudder angle as the input, where it is assumed that the speed of the propeller thruster is constant, featuring typical underactuated characteristics. By applying the following QiH-MPC to adjust the rudder angle of the controller, the positional and directional discrepancies between the current path and the target one are gradually reduced and ultimately eliminated.
2.3. QiH-MPC with Disturbance Compensation Framework
In conventional MPC, the time domain parameters of both prediction and control are adjustable, which directly affects the actual control performance [25]. The results will be better if an infinite horizon is considered, especially when the approximation of the desired minimization cost is more accurate. However, iH-MPC raises two concerns: (1) as the prediction and control time domain increase, the algorithm’s complexity grows, reducing real-time performance; and (2) although feedback correction enhances robustness, iH-MPC lacks the capability to effectively mitigate time-varying wave disturbances [26].
This paper presents QiH-MPC with a fixed-time disturbance observer for USV path following, which achieves optimal performance while also ensuring robustness. In detail, the objective function of infinite horizon prediction is constructed, and the terminal cost term is based on the linear quadratic regulator optimization theory. This maintains the performance of predictive control and reduces the amount of online optimization computation, which is substantially different from the existing works. The system control framework is shown in Figure 2, which includes the following:
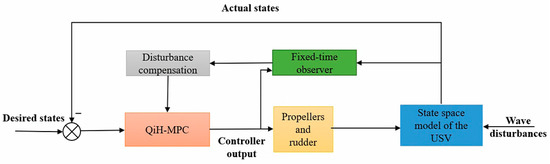
Figure 2.
USV path following with disturbance compensation framework based on QiH-MPC and fixed-time observer.
- (1)
- The feedback control strategy with QiH-MPC aims to obtain the optimal control law for USV path following. Specifically, the terminal cost term of finite time domain optimization in conventional MPC is re-constructed based on the linear quadratic regulator optimization. This approximation maintains the predictive performance of conventional MPC and reduces the amount of online computation significantly.
- (2)
- To improve the accuracy of the prediction model and the ability to suppress the wave disturbance, a fixed-time observer is proposed to estimate aggregate disturbances efficiently. The prediction model incorporates the estimation of aggregate disturbances, encompassing time-varying wave and nonlinear convolution terms of heading angle velocity, to improve the system’s resilience within a fixed time frame.
3. QiH-MPC for USV Path Following
MPC is an efficient computer control algorithm that utilizes model prediction, roll optimization and feedback correction to achieve excellent control performance and robustness. This paper focuses on the path following control of surface unmanned vehicles using iH-MPC. To implement MPC, the USV path following control model can be discretized as
where and are the discretized state and control variables; , and are system coefficient matrices; and is the discretized form of the estimated disturbance. is the output of the system. The discrete predictive control objective function within the finite-time horizon is defined as
where denotes the predictive horizon and control horizon; denote the corresponding predictive output and predictive input at the future sample instant based on the current sample instant . denote weighing matrices of the state and the control. It is clear that increasing the prediction horizon improves the prediction accuracy of the prediction model, thereby improving the steady-state and dynamic performance of the controller and the stability of the control system. However, this also increases the dimension of the optimization variable and computation load, leading to a deterioration in the real-time performance of the control system. As a result, a QiH-MPC scheme is designed in this section to accurately approximate the infinite horizon model predictive control with less computation, which can improve the robustness of the system while ensuring real-time performance.
Let and the objective function (9) evolve into
Moreover, we denote that
where is symmetric and positive semi-definite. To make (11) approximate a finite terminal cost term, consider a discrete Riccati equation (DRE) following LQR theory as
where is symmetric and positive semi-definite, is controllable and is observable. is the solution of (12). From [27], one can derive that there exists a unique solution for the matrix that minimizes . Thus, the obtained control law can be expressed as
where . Therefore, the dynamics of the closed-loop system can be written as
We proceed by constructing a Lyapunov function as , satisfying the following condition:
When we multiply both sides of (15) by on the left and on the right simultaneously, we derive that
which can be written as
Taking an accumulation from to for Equation (17), one follows
According to optimal control theory [28], the linear quadratic regulator optimization controller in the infinite horizon is closed-loop stable. Then, is established and Equation (18) can be expressed as
Based on (19), the discrete predictive control objective function (10) becomes a finite sum as
It is shown that is an expression of a finite sum that can be represented as
where .
Based on the above mathematical analysis, the problem of USV path following can be expressed in the following form:
The general form of the prediction output is obtained iteratively as
Based on the definition of and in (23), the discrete predictive control objective function evolves into
By differentiating for the objective function with respect to , the following equation holds according to the necessary conditions for generalized optimality:
Then, the optimal control sequence is
The model predictive control only selects the current instant as
where and is derived from Equation (26).
Remark 2.
It can be seen that controller form (26) performs the compensation for the wave disturbances by adding the integrated disturbance compensation matrix in the finite horizon. This significantly reduces the inaccuracy of the model prediction state and improves the robustness of the model predictive control. Furthermore, utilizing predicted states in the finite horizon allows for a precise estimation of infinite horizon predictive control, resulting in a substantial reduction in computation and facilitating practical applications.
4. Fixed-Time Observer (FTO) for Disturbance Estimation
The disturbance observer is capable of estimating both external and internal disturbances in the system, regardless of accurate modeling, thereby improving robustness. In contrast to the finite-time observer, the fixed-time disturbance observer for aggregate disturbance estimation ensures that the estimation error converges to zero within a fixed time. Furthermore, the upper bound of the convergence time is independent of the system’s initial state. As a result, this paper employs fixed-time observers for online estimation of aggregate disturbances for USV path following control, which can be incorporated into the QiH-MPC, forming a feed-forward and feedback integrated framework to improve its path following accuracy and robustness.
The fixed-time disturbance observer in this work was specifically designed for USV path following state space model (7). Incorporating the wave disturbance force and moment into the heading angular velocity is a deliberate choice, as the observer is more responsive to changes in wind and wave currents. We denote , and . Then, the USV path following model, with the added wave disturbance force and moment, can be expressed as
where denotes the aggregate bounded disturbance imposed by the disturbance force and moment. We define the tracking error as
where denotes the tracking error of the heading angle velocity; denotes the desired heading angle velocity. Combined with (28) and (29), one derives that
Following [29], we define a fixed-time disturbance observer as
where is the estimate of the disturbance. With the introduction of sliding mode auxiliary variables, is
Based on Equation (32), when and converge to zero, one derives accordingly. An auxiliary sliding mode differential equation is constructed based on the continuous fixed-time second-order sliding mode control algorithm, proposed as
where is an auxiliary variable, is the aggregate bounded disturbance and are positive constants, satisfying . denotes the initial instant of the system. Following [29], one derives that given a constant , when ,
We rewrite (34) in the following form:
By integrating both sides of Equation (35), it follows that
that is,
and, noting that ,
By multiplying both sides of Equation (38) with , it follows that
that is,
Thus, one derives that is decreasing. Due to the fact that and have opposite signs within the interval , then exhibits an increasing trend over the interval . When , it follows from (33) that
and
By integrating both sides of Equation (42), it follows that
and
Therefore, can reach zero at . Similarly, because and have opposite signs within the interval , it follows that exhibits an increasing trend over the interval . Then, is bounded as
where , is a constant to bound the disturbance as and is the initial time moment of the system. Based on (45), it follows that compared with the start point of for sliding system (33), the point of performs a faster convergence to zero, where
Reference [29] presented an estimation of trajectories in a finite time as
where , and and are the subsequent time moments. and is the symbol of the base of the natural logarithm. Then, the convergence time can be obtained:
Therefore, and must converge to zero within as
Then, the aggregate disturbance estimation can be obtained as
Remark 3.
By adding the disturbance estimation of wave forces and moments, it follows that the USV path following state space model becomes (7) exactly. The aggregate disturbances, including time-varying wave and nonlinear convolution terms of the heading angle velocity, are then introduced into the prediction model. To improve the accuracy of the prediction model and the ability to suppress the wave disturbance, the fixed-time observer above was employed to estimate aggregate disturbances efficiently, significantly enhancing the system’s robustness for external disturbances.
5. Convergence Analysis
Although the proposed QiH-MPC with a fixed-time disturbance observer can be briefly explained mathematically, it is essential to present a convergence and stability analysis. For the discretized form of USV path following control system (8), it is recommended to expressed it as a general form with
Since the control action in each period is obtained by solving optimization problem (22), we rewrite the objective function as
where and if and only if , and is bounded satisfying . Then, we present the following two assumptions that are easily satisfied based on the proposed QiH-MPC with a fixed-time disturbance observer:
Assumption 1.
, and is an equilibrium condition of USV path following control system (51).
Assumption 2.
Optimization problem (22) for each period has a feasible solution and the globally optimal solution can be obtained. Moreover, only the first optimal controller action is imposed on the system for the optimal control sequence .
Then, we present Theorem 1 about the convergence of the proposed Qi-MPC with a fixed-time disturbance observer as follows:
Theorem 1.
If Assumption 1 and Assumption 2 hold, then system (51) is stable at , and .
Proof of Theorem 1.
Based on the Lyapunov stability theory, it is necessary to determine a Lyapunov function of the system that is positive definite, and that has a negative definite time-derivative (i.e., the Lyapunov function is decreasing). We define the Lyapunov function as . It is obvious that is positive definite due to the fact that the form of is quadratic. Then,
For the end of optimization, we have the endpoint state constraint that . Then, one notes that . At the same time, we have . Then, it follows that
Based on the Lyapunov stability theory, USV path following control system (51) is stable at , and . □
6. Simulations
The proposed QiH-MPC for USV path following was verified in a MATLAB environment (v.2023b) on the author’s laptop with a 13th Gen Intel Core i9-13900HX processor (Intel, Santa Clara, CA, USA) and 16 GB DDR3 memory. The USV parameters are listed in Table 1. To elucidate the device characteristics under investigation, we present a block diagram of the control system of the USV SL-20Y in Figure 3, which can contribute to comprehending the system components and controller principles in detail.

Table 1.
Main details of the USV SL-20Y.
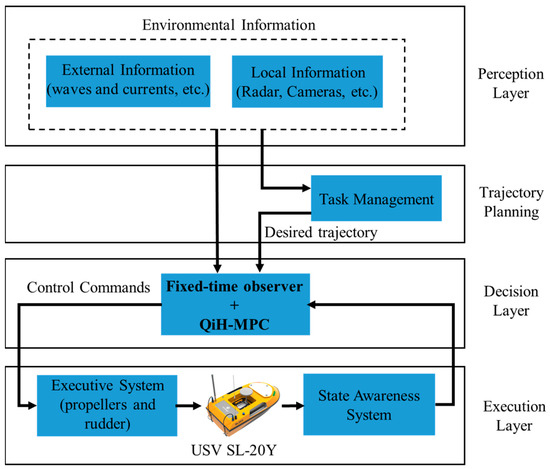
Figure 3.
USV SL-20Y path following block diagram based on QiH-MPC with fixed-time observer.
In this section, a simulation of the performance of QiH-MPC for USV path following is given first. Then, we make detailed comparisons between the proposed algorithm and conventional MPC. Finally, we present the performance of QiH-MPC with and without the fixed-time observer (FTO) to further show the effectiveness of the QiH-MPC with FTO.
6.1. Performance of QiH-MPC for USV Path Following
In this simulation, we give the performance of QiH-MPC for USV path following in detail. The maneuverability parameter and followability parameter are noted in Table 1. The speed of the USV is set as . The multi-segment linear tracking scenario is set up here, in which the initial values of the state are set as for the first target path and for the second target path. The sampling time is set as . The controller input is limited to and the rate of change of the controller input is constrained to . To verify the QiH-MPC controller performance, we set different parameters of the output error matrix and the input control matrix for this simulation. The results are shown in Figure 4 and Figure 5.
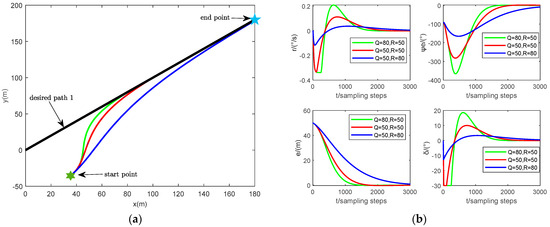
Figure 4.
(a) Simulation results for USV desired path 1 following; (b) the states and controller output for desired path 1 following.
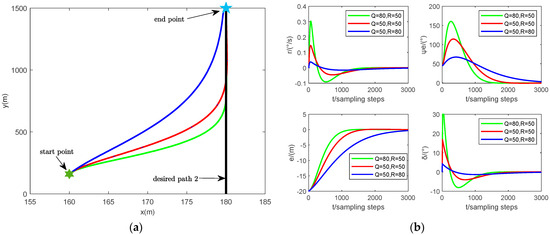
Figure 5.
(a) Simulation results for USV desired path 2 following; (b) the states and controller output for desired path 2 following.
The variation in the performance of the QiH-MPC path following controller is shown in Figure 4 and Figure 5. By setting two desired paths with different slopes, the QiH-MPC path following controller designed in this paper can be seen to be able to achieve accurate path following. Moreover, as the output error matrix increases and the input control matrix decreases, the tracking error converges more rapidly (see the tracking error state curve in Figure 4b and Figure 5b), such that the USV more aggressively follows the desired path (see the path following results in Figure 4a and Figure 5a). However, this is at the cost of a subsequent increase in the heading angular velocity, the heading angular error and the magnitude of rudder angle oscillations, which will make the USV less stable. Therefore, the parameter values of the output error matrix and the input control matrix must be chosen as a compromise between the efficiency and stability of path following.
6.2. Comparisons between Proposed Algorithm and Conventional MPC
In this simulation, we give the performance comparisons between the proposed algorithm and conventional MPC. A multi-segment linear tracking scenario is set up here, in which the initial values of the state are set as for the first target path and for the second target path. The controller input is limited to . To eliminate any uncertainty, the other parameters of QiH-MPC and conventional MPC are both set the same as in Section 6.1. The output error matrix and the input control matrix for this simulation. The results are shown in Figure 6 and Figure 7. Moreover, to further quantify the improvement in algorithm performance, the state and control quantities are further compared in terms of the maximum difference (absolute value), standard deviation and regulation time for the proposed QiH-MPC and conventional MPC.
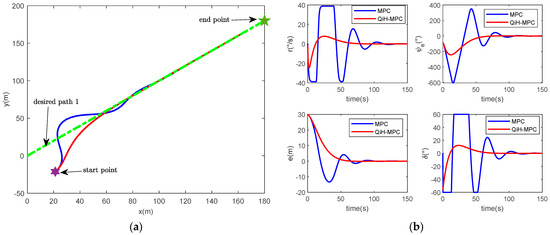
Figure 6.
Comparisons between QiH-MPC and conventional MPC for desired path 1 following: (a) USV path 1 following result; (b) the states and controller output simulation result for target path 1.
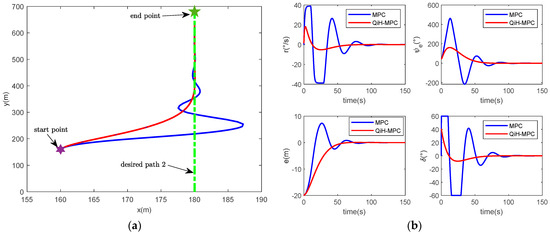
Figure 7.
Comparisons between QiH-MPC and conventional MPC for desired path 2 following: (a) USV path 2 following result; (b) the states and controller output simulation result for target path 2.
The results from QiH-MPC and conventional MPC for USV path following are shown in Figure 6 and Figure 7 by setting two desired paths with different slopes as well. Compared to conventional MPC, the QiH-MPC path following controller designed in this paper converges faster for each state variable and the controller input shows fewer oscillations; therefore, QiH-MPC achieves faster and more stable path following results.
Moreover, we present the regulation time, standard deviation and maximum difference comparison for the QiH-MPC and conventional MPC. For the regulation time, the tracking error of QiH-MPC is reduced by 44.1% for target path 1 and by 32.05% for target path 2, so QiH-MPC can track the target paths faster. For the standard deviation, the heading angle error of QiH-MPC is reduced by 59.17% for target path 1 and by 60.14% for target path 2; thus, QiH-MPC can track the target paths more stably. For the control quantity, the maximum difference is reduced by 43.13% for target 1 and by 59.21% for target path 2, so that the actuator of USV can track the desired paths more easily with the proposed QiH-MPC. Other detailed quantitative performance comparisons are shown in Table 2 and Table 3. The downward arrow denotes the percentage decrease of the variable corresponding to QiH-MPC in comparison to MPC.

Table 2.
Numerical comparisons between QiH-MPC and conventional MPC for target path 1 following.

Table 3.
Numerical comparisons between QiH-MPC and conventional MPC for target path 2 following.
6.3. Performance of QiH-MPC with and without FTO for USV Path Following
The proposed QiH-MPC implements the path following problem with and without the fixed-time observer under time-varying wave disturbances. The QiH-MPC parameters are set up following the same procedure as in Section 6.2. For the fixed-time observer, the parameters are set as , and . Waves are described by the two-parameter spectrum that is recommended by ITTC in [30] as
where denotes the power density, refers to the angular frequency of the wave, is the average period of the wave and is the significant wave height.
In this simulation, we give performance comparisons between the proposed algorithm QiH-MPC with and without FTO for USV path following. A multi-segment linear tracking scenario is set up here, in which the initial values of the state are set as for the first target path and for the second target path. Additionally, we positioned it 5 m away from the end of the current desired path, prompting the controller to follow to the next waypoint. To verify the constraint effect of the controller on different input control quantity, the controller input is limited to . To eliminate any uncertainty, the other parameters of QiH-MPC and conventional MPC are both set the same as in Section 6.1. The output error matrix and the input control matrix for this simulation. The results are shown in Figure 8 and Figure 9. Moreover, to further quantify the improvement in algorithm performance, the state and control quantities are further compared in terms of the maximum difference (absolute value) and standard deviation in Table 4 and Table 5. The downward arrow denotes the percentage decrease of the variable corresponding to QiH-MPC with FTO in comparison to QiH-MPC without FTO.
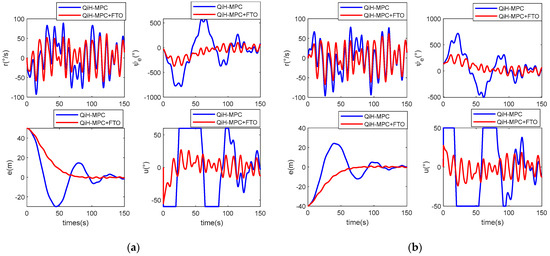
Figure 8.
(a) Performance of QiH-MPC with and without FTO for USV path 1 following; (b) performance of QiH-MPC with and without FTO for USV path 2 following.
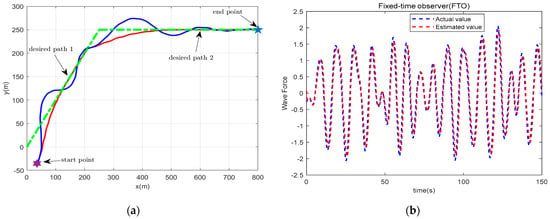
Figure 9.
(a) USV path following results of QiH-MPC with and without FTO; (b) the actual wave disturbances and their estimation based on FTO.

Table 4.
Performance details of QiH-MPC with and without FTO for USV path 1 following.

Table 5.
Performance details of QiH-MPC with and without FTO for USV path 2 following.
The results of QiH-MPC with and without FTO for USV path following are shown in Figure 8 and Figure 9. Clearly, the compensation of the state and control variables for wave disturbances is more effective using QiH-MPC with FTO designed in this paper, resulting in a significant reduction in the oscillations. In Figure 9a, one can verify that QiH-MPC with FTO performs with superior efficiency and stability in following the desired paths compared to QiH-MPC without FTO. And the wave disturbance can be estimated accurately by the FTO (see Figure 9b).
In Table 4 and Table 5, we present the maximum difference and standard deviation comparison for the QiH-MPC with and without FTO. For USV path 1 following, the maximum difference is reduced by 36.97% for the track error and by 23.03% for the controller input rudder angle. This allows the USV to follow the desired path more easily and efficiently with the proposed QiH-MPC with FTO. The standard deviation of USV path 2 following is reduced by 64.84% for the heading angle error and by 22.02% for the heading angle velocity with the proposed QiH-MPC with FTO. This contributes to the stability of the target paths. Further quantitative performance data can be found in Table 4 and Table 5.
7. Conclusions
This paper presents a QiH-MPC with a fixed-time disturbance observer for USV path following, taking into account the accuracy and robustness of the USV under wind and wave disturbances. The QiH-MPC provides convergence performance under long prediction horizons and reduces the computing load. The advantages of the algorithm are demonstrated from both theoretical and simulation aspects. Specifically, the proposed algorithm results in a 36% reduction in the maximum track error and a more than 23% reduction in the maximum difference of the controller input rudder angle. Furthermore, there is a reduction of over 64% in the standard deviation of the course angle error and of more than 22% in the standard deviation of the course angular velocity. These improvements enable the USV to track the desired path with greater efficiency and accuracy.
The work presented in this paper, however, is subject to certain limitations. Firstly, the model introduced here is not suitable for tracking paths with significant curvature due to its linearization approximation. Furthermore, the proposed disturbance observer proves ineffective in compensating for colored noise within wave disturbances. Therefore, future steps will consider real marine environments encompassing complex desired paths, diverse wave disturbances and multiple obstacle scenarios.
Author Contributions
W.L. performed the theoretical analysis and simulations, wrote the first and the last version of the draft paper. H.Z. contributed to the investigation, supervision, writing, review and the proposed approach was discussed with her. J.Z. contributed to the original draft and the literature review. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 62301489).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This work presents an extended version of a selected paper in the ICARM 2023 conference.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Luo, M.; Sung, S.H. Half-century research developments in maritime accidents: Future directions. Accid. Anal. Prev. 2019, 123, 448–460. [Google Scholar] [CrossRef]
- De Jiri, V.; Robert, G.H.; Osiris, A.V.B. The impact of autonomous ships on safety at sea—A statistical analysis. Reliab. Eng. Syst. Safe. 2021, 210, 107558. [Google Scholar]
- Wang, N.; Karimi, H.R.; Li, H.; Su, S. Accurate path following of disturbed surface vehicles: A finite-time control approach. IEEE Trans. Mechatron. 2019, 24, 1064–1074. [Google Scholar] [CrossRef]
- Fossen, T.; Breivik, M.; Skjetne, R. Line-of-sight path following of underactuated marine craft. IFAC Proc. Vol. 2003, 36, 211–216. [Google Scholar] [CrossRef]
- Gu, N.; Wang, D.; Peng, Z.; Wang, J.; Han, Q.L. Advances in line-of-sight guidance for path following of autonomous marine vehicles: An overview. IEEE Trans. Syst. Man Cyber. Syst. 2023, 53, 12–28. [Google Scholar] [CrossRef]
- Brhaug, E.; Pavlov, A.; Pettersen, K.Y. Integral LOS control for path following of underactuated marine surface vessels in the presence of constant ocean currents. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4984–4991. [Google Scholar]
- Paramesh, S.; Rajendran, S. A unified seakeeping and maneuvering model with a PID controller for path following of a KVLCC2 tanker in regular waves. Appl. Ocean Res. 2021, 116, 102860. [Google Scholar]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive sliding mode path following control for unmanned surface vehicle with modeling uncertainties and input saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef]
- Li, D.; Deng, H.; Pan, Z.; Yang, X. Collaborative obstacle avoidance algorithm of multiple bionic snake robots in fluid based on ib-lbm. ISA Trans. 2022, 122, 271–280. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Shen, L.; Yu, Y. Coordinated path following control of fixed wing unmanned aerial vehicles in wind. ISA Trans. 2022, 122, 260–270. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wang, N.; Zhang, W. Disturbance observer based finite-time trajectory tracking control of unmanned surface vehicles with unknown dead-zones. In Proceedings of the 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 263–268. [Google Scholar]
- Han, J. From pid to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Naghdi, M.; Sadrnia, M.A. A novel fuzzy extended state observer. ISA Trans. 2020, 102, 1–11. [Google Scholar] [CrossRef]
- Li, M.; Guo, C.; Yu, H. Filtered extended state observer based line-of-sight guidance for path following of unmanned surface vehicles with unknown dynamics and disturbances. IEEE Access 2019, 7, 178401–178412. [Google Scholar] [CrossRef]
- Seongik, H. Predefined-Time and prescribed-performance control methods combined with second-order terminal sliding mode control for an unmanned planning hull system with input delay and unknown disturbance. J. Mar. Sci. Eng. 2023, 11, 2191. [Google Scholar]
- Wei, L.; Fang, W.; Jie, B.; Han, Z. Model Predictive Control with Disturbance Observer for Unmanned Surface Vessels Path following. In Proceedings of the 8th IEEE International Conference on Advanced Robotics and Mechatronics, Sanya, China, 8–10 July 2023. [Google Scholar]
- Wei, L.; Jun, Z.; Wen, X. High-speed multihull anti-pitching control based on heave velocity and pitch angular velocity estimation. ISA Trans. 2024, 146, 380–391. [Google Scholar]
- Fu, M.; Wang, L. Disturbance observer based path following control of unmanned surface vessel with time-varying current. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 370–375. [Google Scholar]
- Liu, Y.; Li, C.; Wang, N. Nonlinear disturbance observer based backstepping finite-time sliding mode tracking control of underwater vehicles with system uncertainties and external disturbances. Nonlinear Dyn. 2017, 88, 465–476. [Google Scholar] [CrossRef]
- Fukushima, H.; Kon, K.; Matsuno, F. Model Predictive Formation Control Using Branch-and-Bound Compatible with Collision Avoidance Problems. IEEE Trans. Robot. 2013, 29, 1308–1317. [Google Scholar] [CrossRef]
- Ji, J.; Khajepour, A.; Melek, W.W.; Huang, Y. Path Planning and Tracking for Vehicle Collision Avoidance Based on Model 397 Predictive Control With Multi-constraints. IEEE Trans. Veh. Technol. 2017, 66, 952–964. [Google Scholar] [CrossRef]
- Gu, N.; Wang, D.; Peng, Z.; Liu, L. Observer-based finite-time control for distributed path maneuvering of underactuated unmanned surface vehicles with collision avoidance and connectivity preservation. IEEE Trans. Sys. Man and Cyber. Sys. 2021, 51, 5105–5115. [Google Scholar] [CrossRef]
- Skjetne, R.; Fossen, T. Nonlinear maneuvering and control of surface vessels. In Proceedings of the MTS/IEEE Oceans, Honolulu, HI, USA, 5–8 November 2001. [Google Scholar]
- Ren, R.Y.; Zou, Z.J.; Wang, Y.D. Adaptive Nomoto model used in the trajectory tracking problem of ships. J. Mar. Sci. Technol. 2018, 23, 888–898. [Google Scholar] [CrossRef]
- Li, R.; Huang, J.; Pan, X.; Hu, Q.; Huang, Z. Trajectory tracking of underactuated surface ships based on model predictive control with neural network. Int. J. Adv. Robot. Syst. 2020, 17, 172–185. [Google Scholar] [CrossRef]
- Greer, W.; Sultan, C. Infinite horizon model predictive control tracking application to helicopters. Aerosp. Sci. Technol. 2020, 98, 105675. [Google Scholar] [CrossRef]
- Vargas, F.J.; González, R.A. On the existence of a stabilizing solution of modified algebraic Riccati equations in terms of standard algebraic Riccati equations and linear matrix inequalities. IEEE Control Syst. Lett. 2020, 4, 91–96. [Google Scholar] [CrossRef]
- Tuffaha, A. The Stochastic Linear Quadratic Optimal Control Problem on Hilbert Spaces: The Case of Non-analytic Systems. Appl. Math. Optim. 2023, 87, 58. [Google Scholar] [CrossRef]
- Shun, A.; Longjin, W.; Yan, H. Robust fixed-time tracking control for underactuated AUVs based on fixed-time disturbance observer. Ocean Eng. 2022, 266, 112567. [Google Scholar]
- Liang, L.H.; Wen, Y. Rudder roll stabilization with disturbance compensation model predictive control. J. Mar. Sci. Tech. 2019, 24, 249–259. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).