Numerical Investigation on a High-Speed Transom Stern Ship Advancing in Shallow Water
Abstract
1. Introduction
2. Materials and Methods
2.1. Boundary Value Problem (BVP) of Steady Wave-Making Potential
2.1.1. Mixed Approximate Nonlinear Free Surface Boundary Condition
2.1.2. Transom Stern Boundary Condition
2.2. Resistance, Wave Elevation, Sinkage and Trim
3. Numerical Implementation
3.1. Rankine HOBEM
3.2. Approximate Nonlinear Free Surface Condition Iteration Algorithm
4. Numerical Results and Discussion
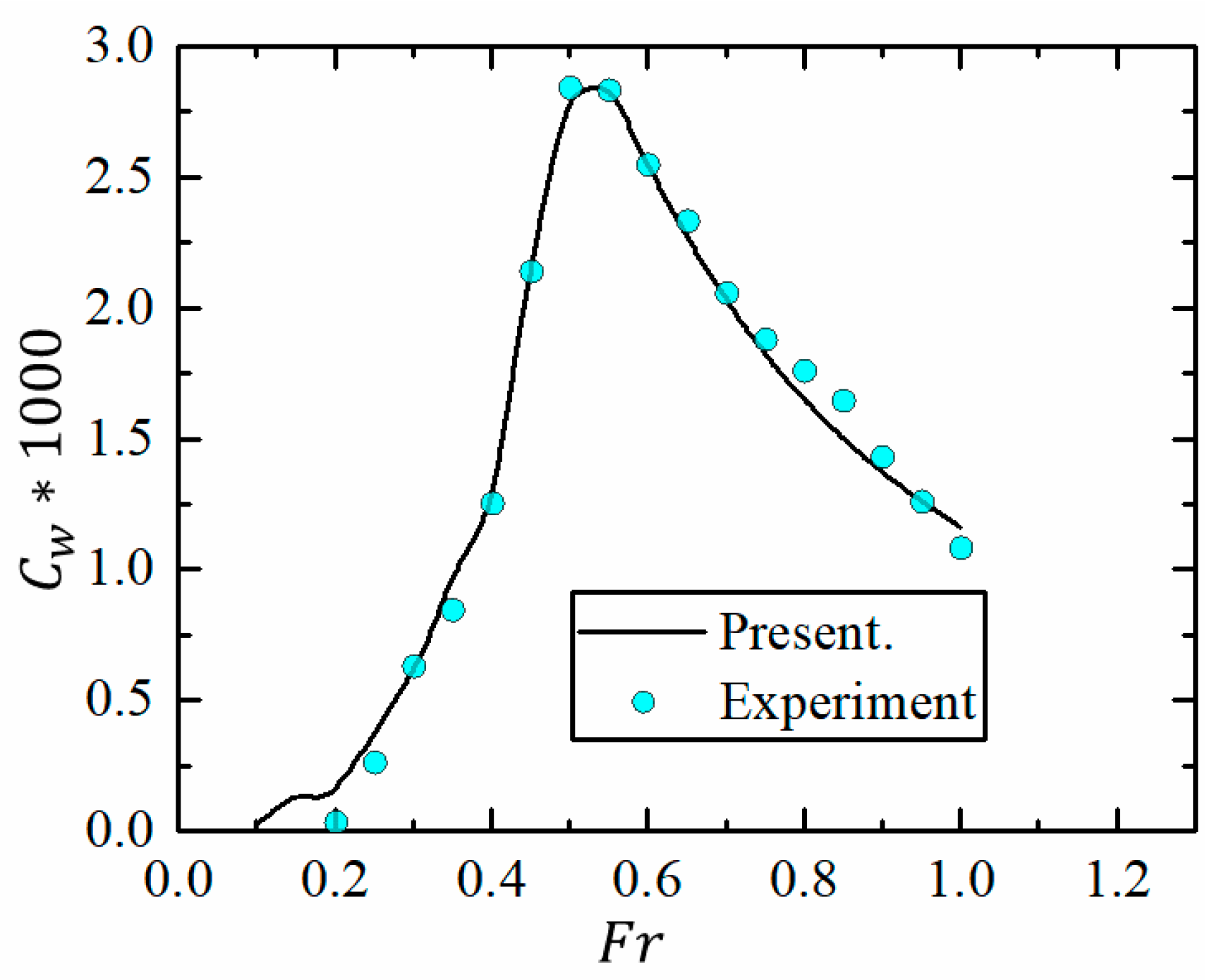
4.1. Validations in Deep Water
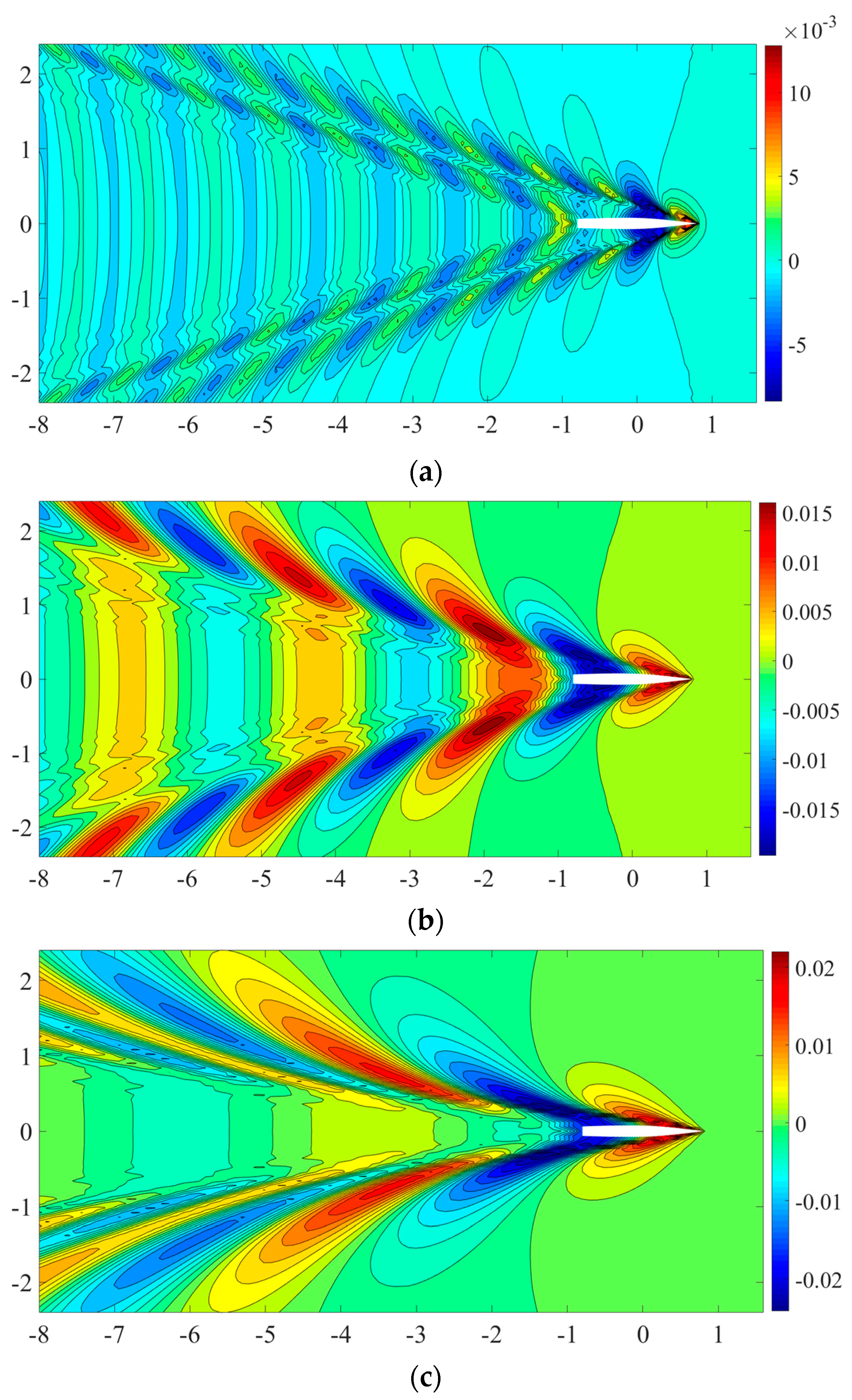
4.2. Numerical Results in Shallow Water
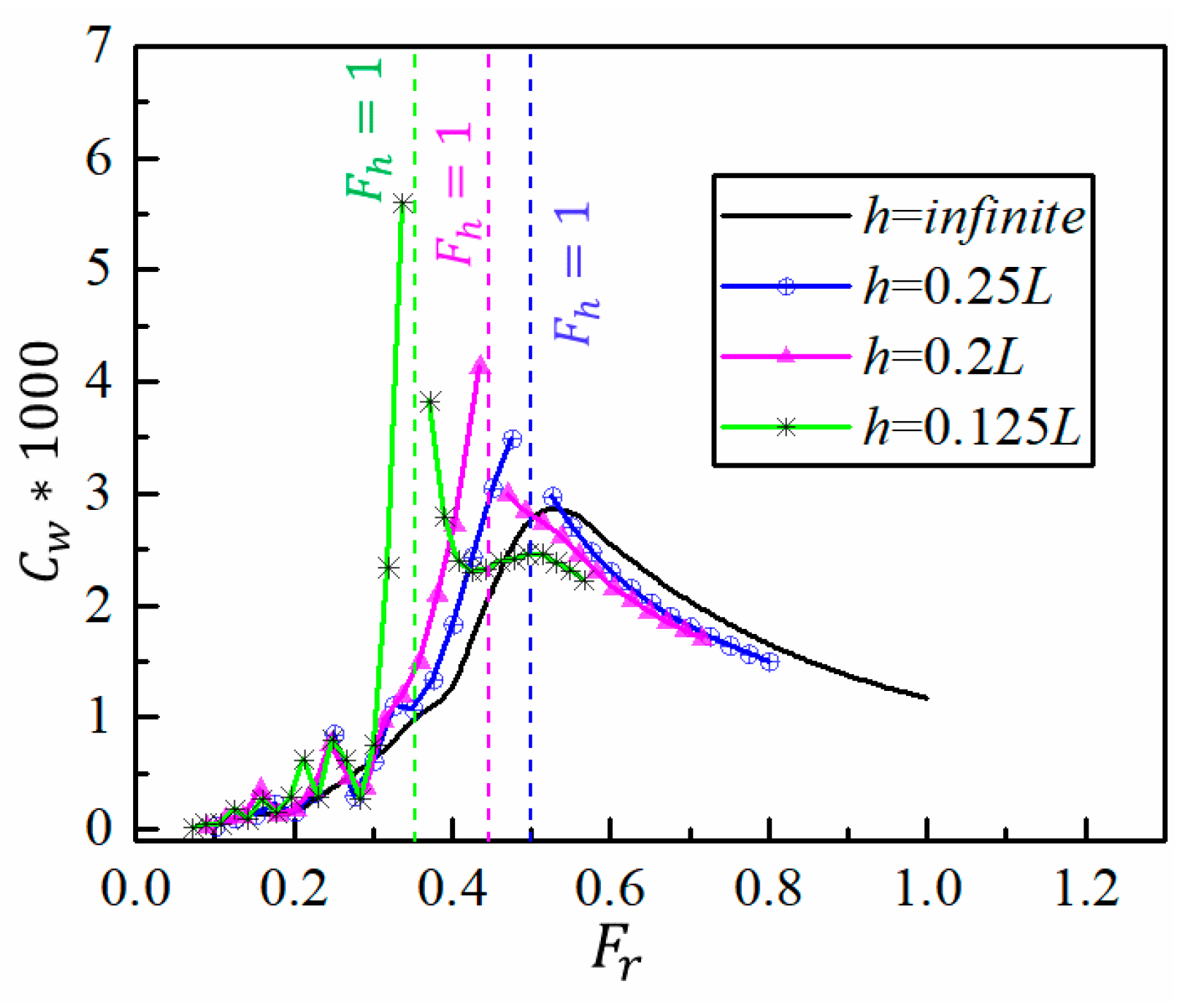
4.2.1. Wave-Making Resistance
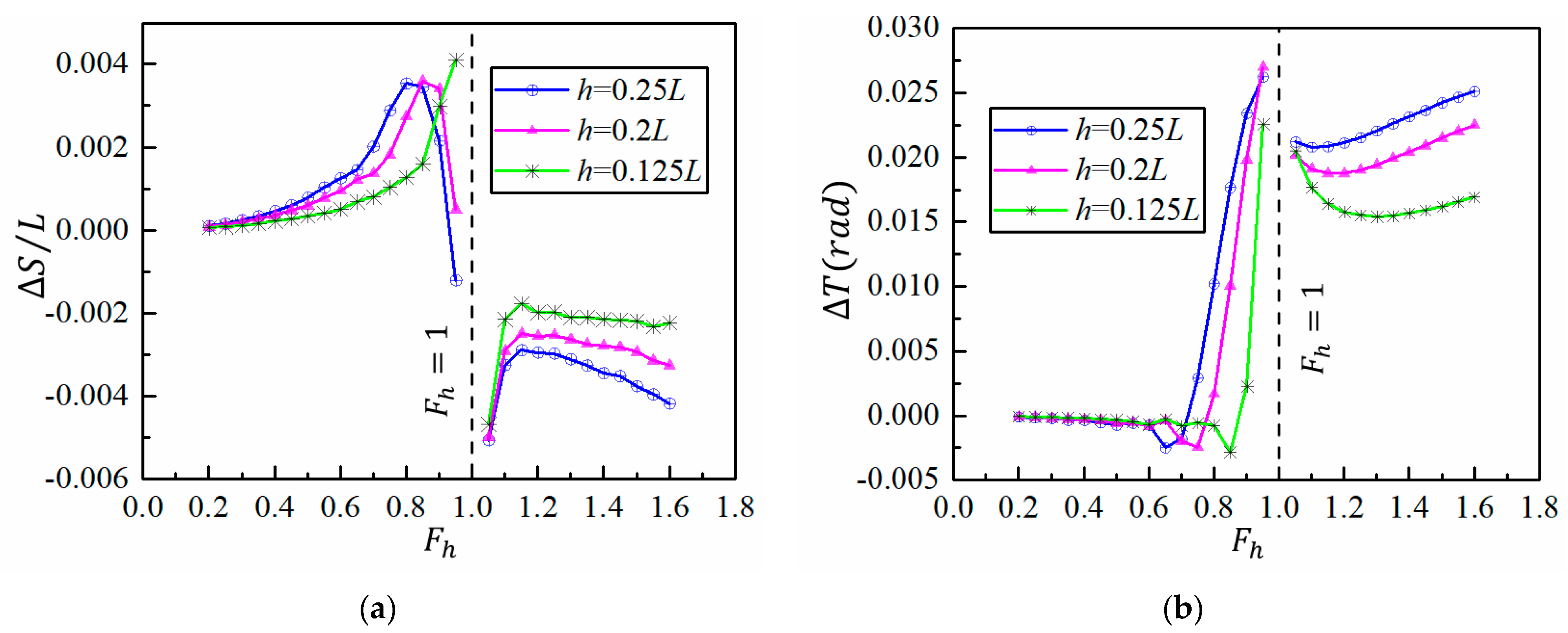
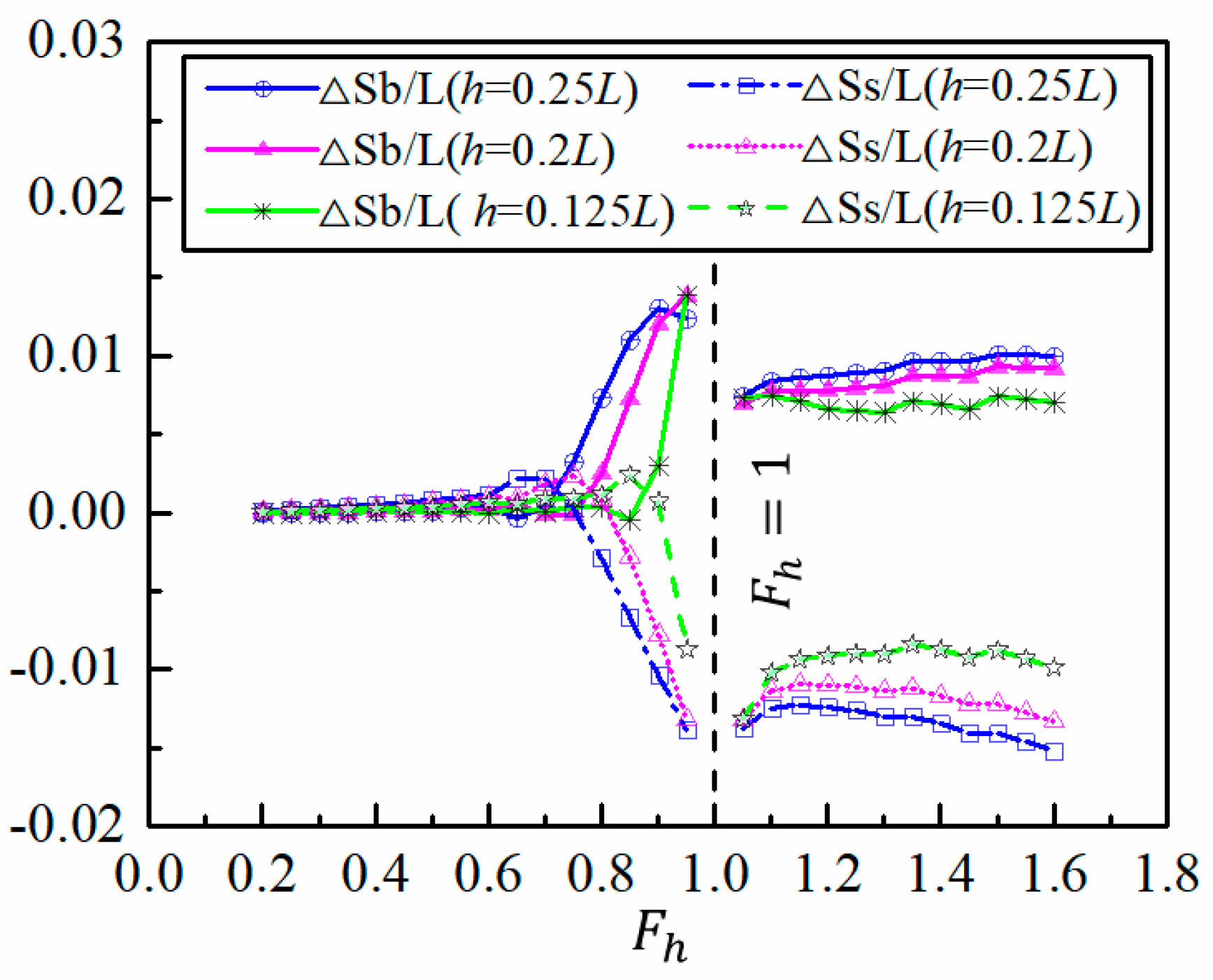
4.2.2. Sinkage and Trim
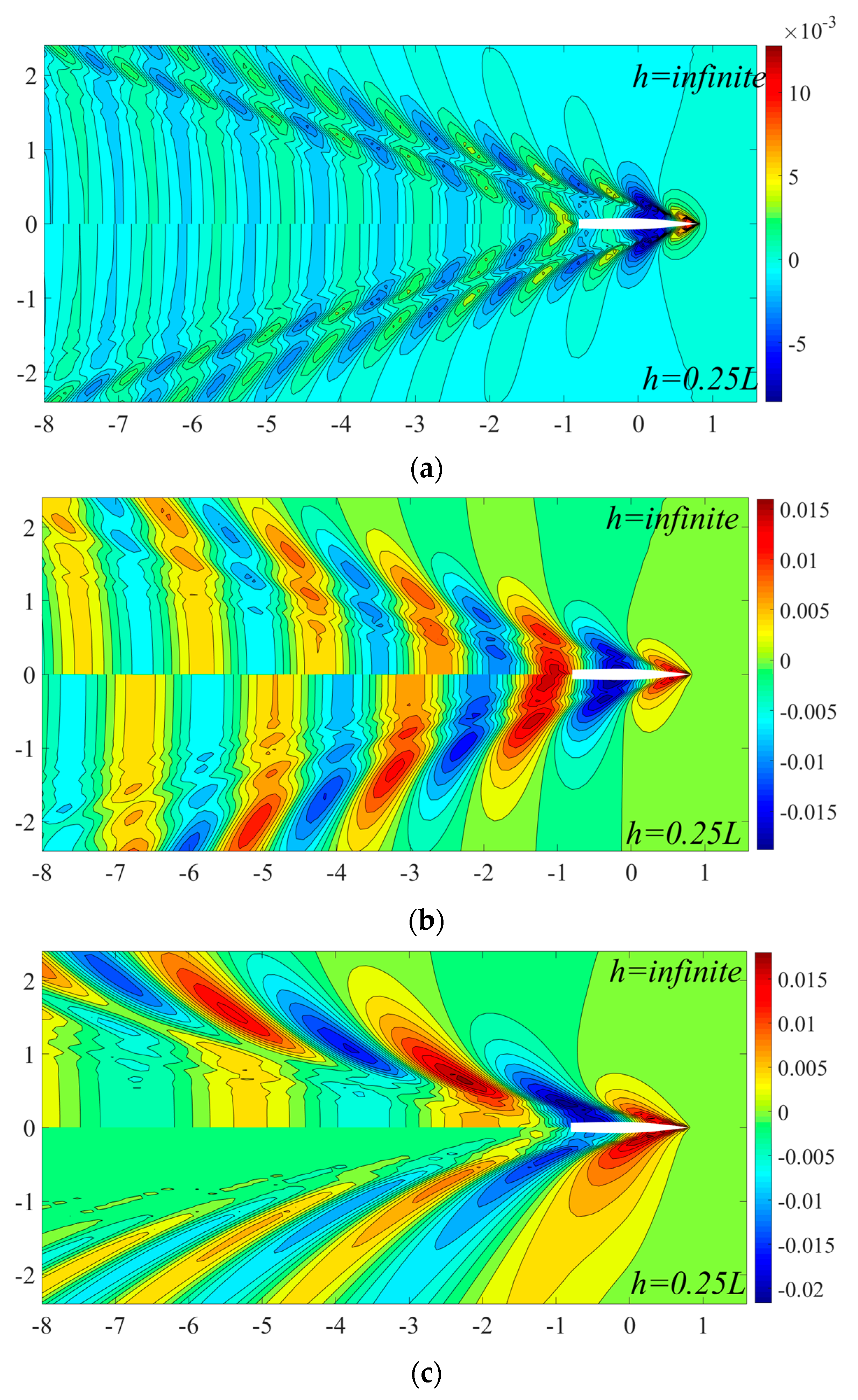
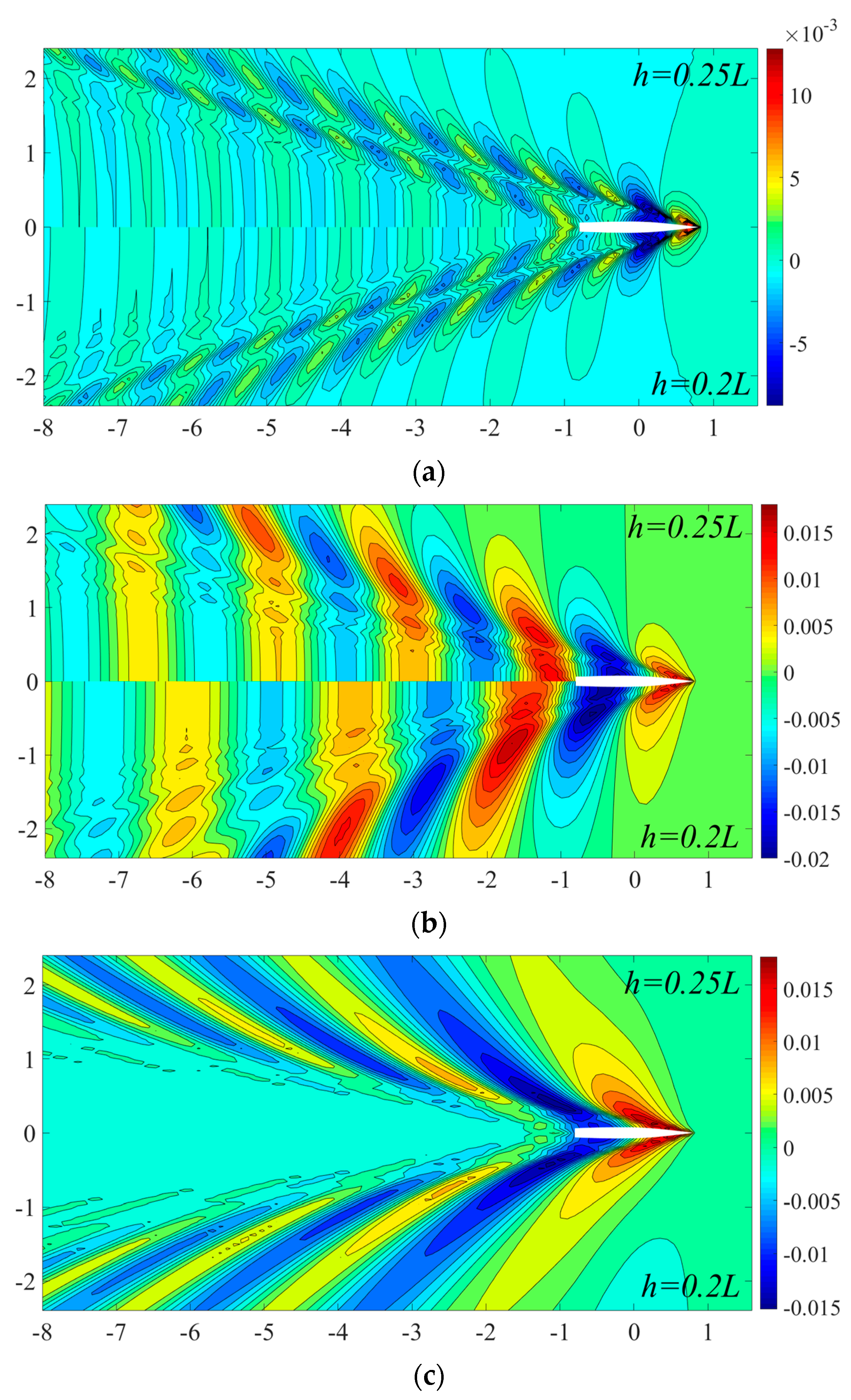
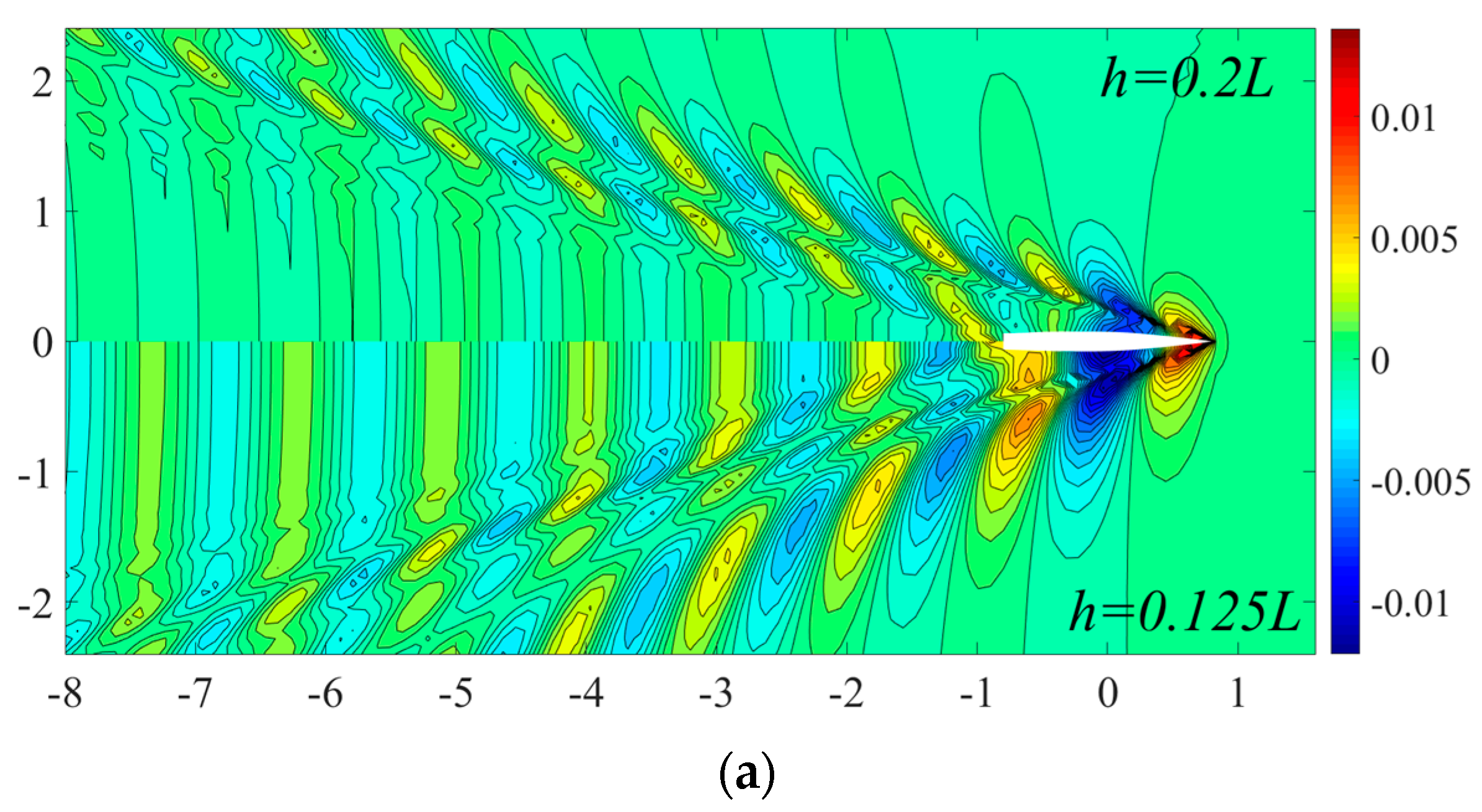
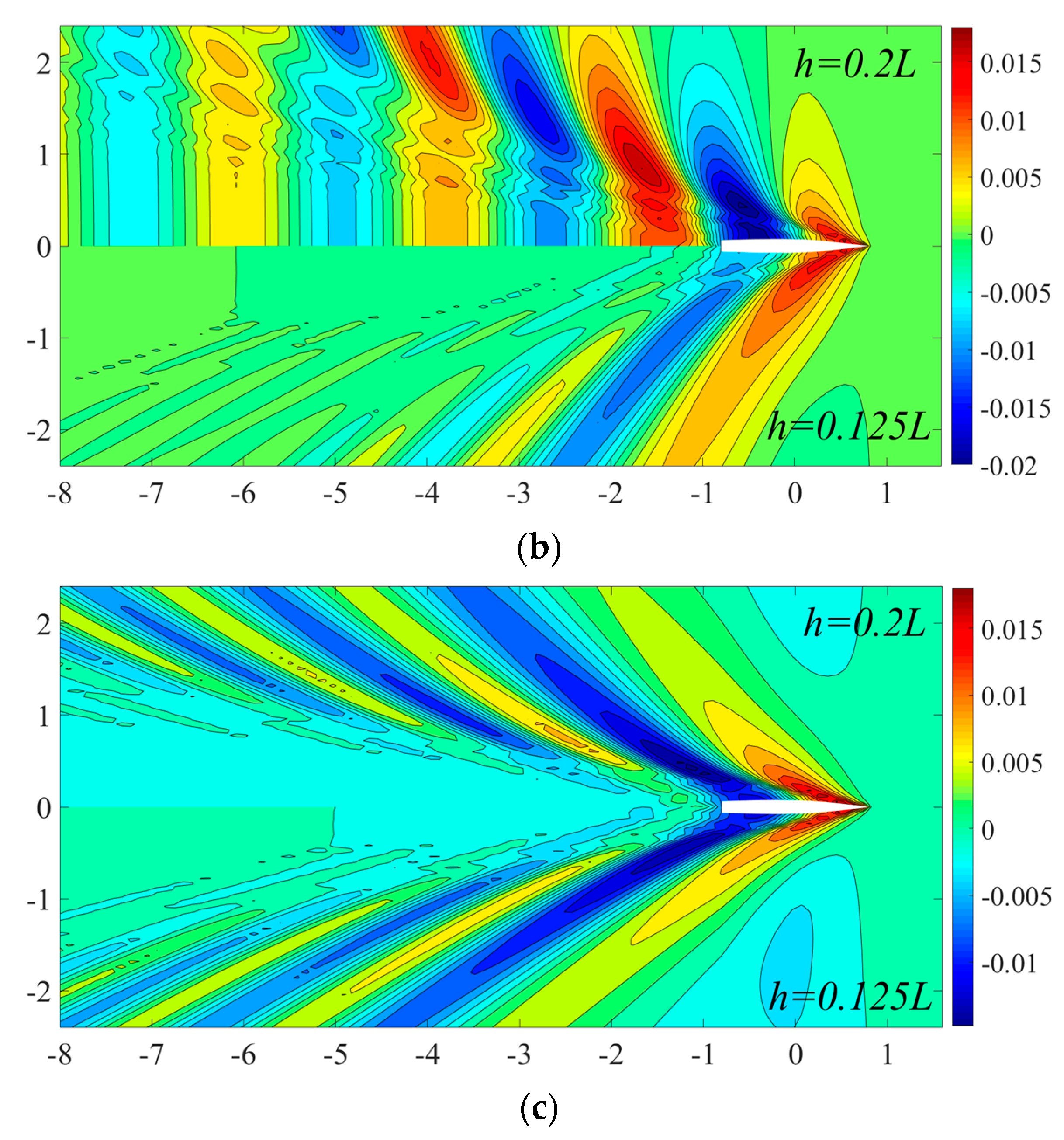
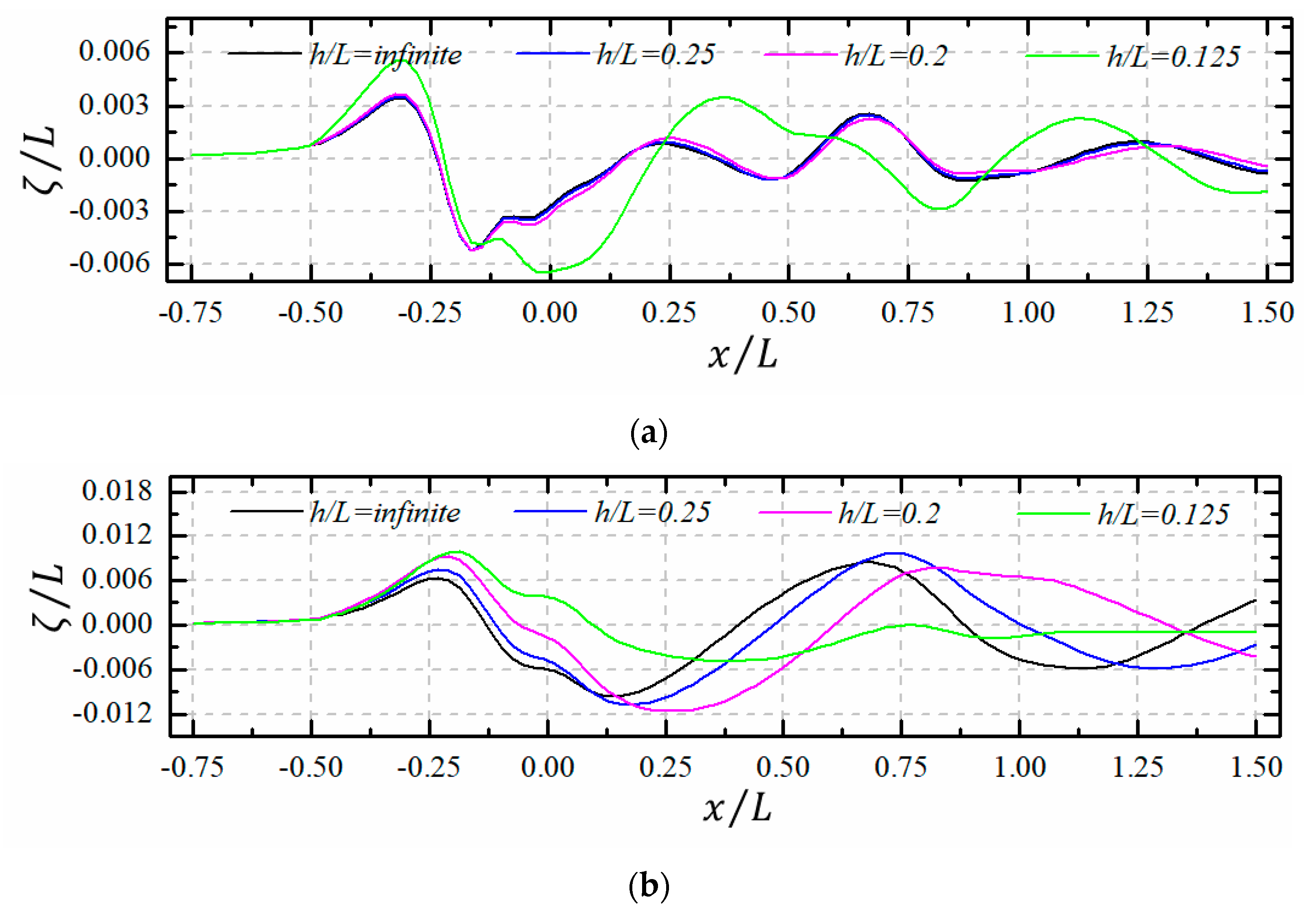
4.2.3. Wave Contour and Wave Profile
5. Conclusions
- (1)
- The computed results including wave-making resistance, singkage and trim in deep water show generally good agreement with test data, which demonstrates the stability and robustness of the present method. However, the errors at Fr ≤ 0.35 are larger than those in higher Fr, and the largest error even reaches about 75% compared with the experimental result in Fr = 0.2.
- (2)
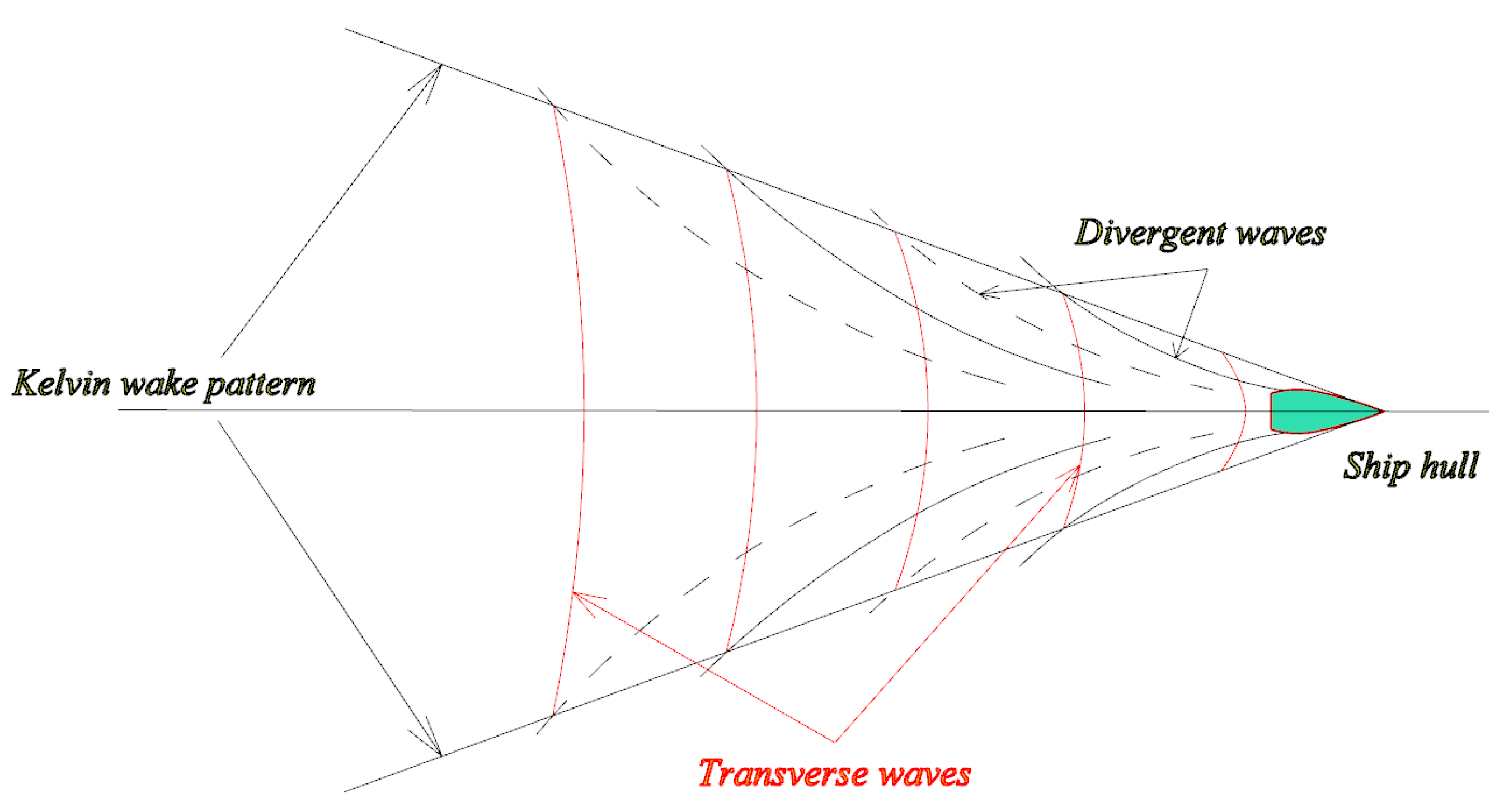
- In general, the reduction of water depth results in a drastic increase of wave-making resistance, sinkage, trim and wave elevation, the values increase sharply near the transcritical water depth Froude number Fh = 1.0 due to the combining transverse wave and diverging wave, and after that the results begin to decrease as the evanescent transverse at supercritical speed. However, when a ship advances at supercritical speed in shallow water, the wave-making resistance may even be smaller than that in deep water.
- (3)
- Near the transcritical water depth Froude number Fh = 1.0, the ship will experience a dramatically increased sinkage and trim, which implies that the forward speed should be restricted to avoid grounding.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lataire, E.; Vantorre, M.; Delefortrie, G. A prediction method for squat in restricted and unrestricted rectangular fairways. Ocean Eng. 2012, 55, 71–80. [Google Scholar] [CrossRef]
- Toxopeus, S.L.; Simonsen, C.D.; Guilmineau, E.; Visonneau, M.; Xing, T.; Stern, F. Investigation of water depth and basin wall effects on KVLCC2 in manoeuvring motion using viscous-flow calculations. J. Mar. Sci. Technol. 2013, 18, 471–496. [Google Scholar] [CrossRef]
- Castiglione, T.; He, W.; Stern, F.; Bova, S. URANS simulations of catamaran interference in shallow water. J. Mar. Sci. Technol. 2014, 19, 33–51. [Google Scholar] [CrossRef]
- Mucha, P.; Deng, G.; Gourlay, T.; el Moctar, O. Validation studies on numerical prediction of ship squat and resistance in shallow water. In Proceedings of the 4th MASHCON-International Conference on Ship Manoeuvring in Shallow and Confined Water with Special Focus on Ship Bottom Interaction, Hamburg, Germany, 23–25 May 2016; pp. 122–133. [Google Scholar]
- Terziev, M.; Tezdogan, T.; Oguz, E.; Gourlay, T.; Demirel, Y.K.; Incecik, A. Numerical investigation of the behaviour and performance of ships advancing through restricted shallow waters. J. Fluids Struct. 2018, 76, 185–215. [Google Scholar] [CrossRef]
- Gourlay, T.P.; Tuck, E.O. The maximum sinkage of a ship. J. Ship Res. 2001, 45, 50–58. [Google Scholar] [CrossRef]
- Scullen, D.C. Calculation of linear ship waves. ANZIAM J. 2010, 51, C316–C331. [Google Scholar] [CrossRef]
- Dawson, C.W. A practical computer method for solving ship-wave problems. In Proceedings of the Second International Conference on Numerical Ship Hydrodynamics, Berkeley, CA, USA, 19–21 September 1977; pp. 30–38. [Google Scholar]
- Yuan, Z.M.; Kellett, P. Numerical study on a KVLCC2 model advancing in shallow water. In Proceedings of the 9th International Workshop on Ship and Marine Hydrodynamics, Glasgow, UK, 26–28 August 2015. [Google Scholar]
- Yuan, Z.M. Ship hydrodynamics in confined waterways. J. Ship Res. 2019, 63, 16–29. [Google Scholar] [CrossRef]
- Yao, J.X.; Zou, Z.J. Calculation of ship squat in restricted waterways by using a 3D panel method. J. Hydrodyn. Ser. B 2010, 22, 489–494. [Google Scholar] [CrossRef]
- McTaggart, K. Ship squat prediction using a potential flow Rankine source method. Ocean Eng. 2018, 148, 234–246. [Google Scholar] [CrossRef]
- Raven, H.C. A Solution Method for the Nonlinear Ship Wave Resistance Problem. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1996. [Google Scholar]
- Raven, H.C. Numerical wash prediction using a free-surface panel code. In Proceedings of the RINA Symposium Hydrodynamics of High-Speed Craft: Wake Wash and Motions Control, London, UK, 7–8 November 2000; ISBN 0 903055 62 7. [Google Scholar]
- He, G.H. An iterative Rankine BEM for wave-making analysis of submerged and surfacepiercing bodies in finite water depth. J. Hydrodyn. 2013, 25, 839–847. [Google Scholar] [CrossRef]
- Algie, C.; Gourlay, T.; Lazauskas, L.; Raven, H.C. Application of potential flow methods to fast displacement ships at transcritical speeds in shallow water. Appl. Ocean Res. 2018, 71, 11–19. [Google Scholar] [CrossRef]
- Nakos, D.E.; Sclavounos, P.D. Kelvin wakes and wave resistance of cruiser-and transom-stern ships. J. Ship Res. 1994, 38, 9–29. [Google Scholar] [CrossRef]
- Gao, G. Numerical implementation of transom conditions for high-speed displacement ships. J. Ship Mech. 2006, 10, 1–9. [Google Scholar]
- Jensen, G.; Mi, Z.X.; Söding, H. Rankine source methods for numerical solutions of steady wave resistance problem. In Proceedings of the 16th Symposium on Naval Hydrodynamics, Berkeley, CA, USA, 13–18 July 1986. [Google Scholar]
- Molland, A.F.; Wellicome, J.F.; Couser, P.R. Resistance Experiments on a Systematic Series of High Speed Displacement Catamaran Forms: Variation of Length-Displacement Ratio and Breadth-Draught Ratio; Ship Science Report 71; University of Southampton: Southampton, UK, 1994. [Google Scholar]
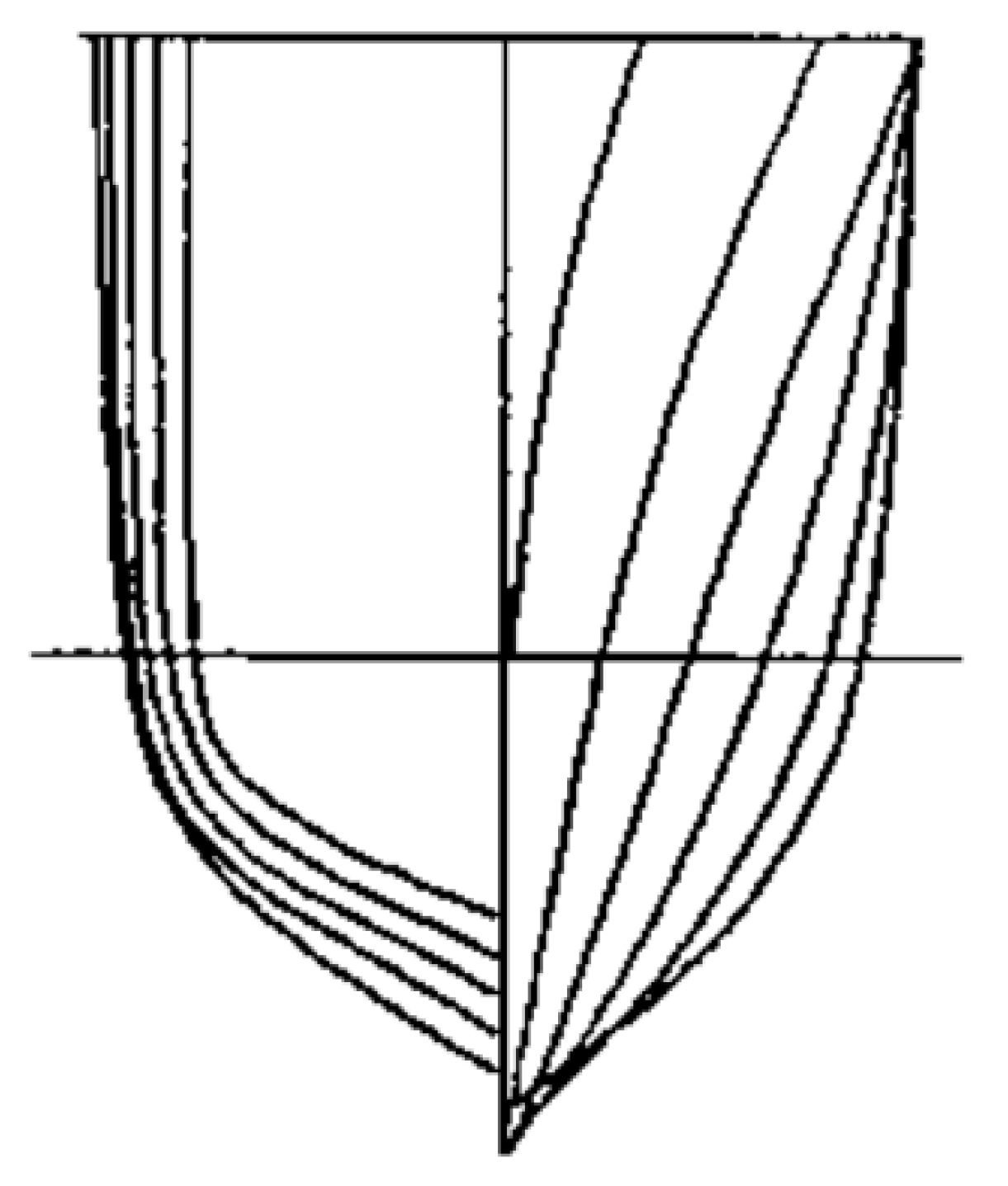


| Parameters | Value |
|---|---|
| ship length L (m) | 1.6 |
| ship width B (m) | 0.1538 |
| ship draft T (m) | 0.1026 |
| block coefficient CB | 0.397 |
| prismatic coefficient CP | 0.693 |
| midship section coefficient CM | 0.565 |
| Fr | Present | Experiment [19] | Errors (%) |
|---|---|---|---|
| 0.2 | 0.1583 | 0.039 | 75.36 |
| 0.25 | 0.3701 | 0.265 | 28.40 |
| 0.3 | 0.6110 | 0.632 | 3.44 |
| 0.35 | 0.9572 | 0.849 | 11.30 |
| 0.4 | 1.2809 | 1.256 | 1.94 |
| 0.45 | 2.1340 | 2.143 | 0.42 |
| 0.5 | 2.7706 | 2.846 | 2.72 |
| 0.55 | 2.8259 | 2.836 | 0.36 |
| 0.6 | 2.5512 | 2.551 | 0.01 |
| 0.65 | 2.2752 | 2.337 | 2.72 |
| 0.7 | 2.0349 | 2.061 | 1.28 |
| 0.75 | 1.8291 | 1.883 | 2.95 |
| 0.8 | 1.6549 | 1.764 | 6.60 |
| 0.85 | 1.5057 | 1.649 | 9.52 |
| 0.9 | 1.3758 | 1.434 | 4.23 |
| 0.95 | 1.2619 | 1.263 | 0.09 |
| 1.0 | 1.1626 | 1.087 | 6.50 |
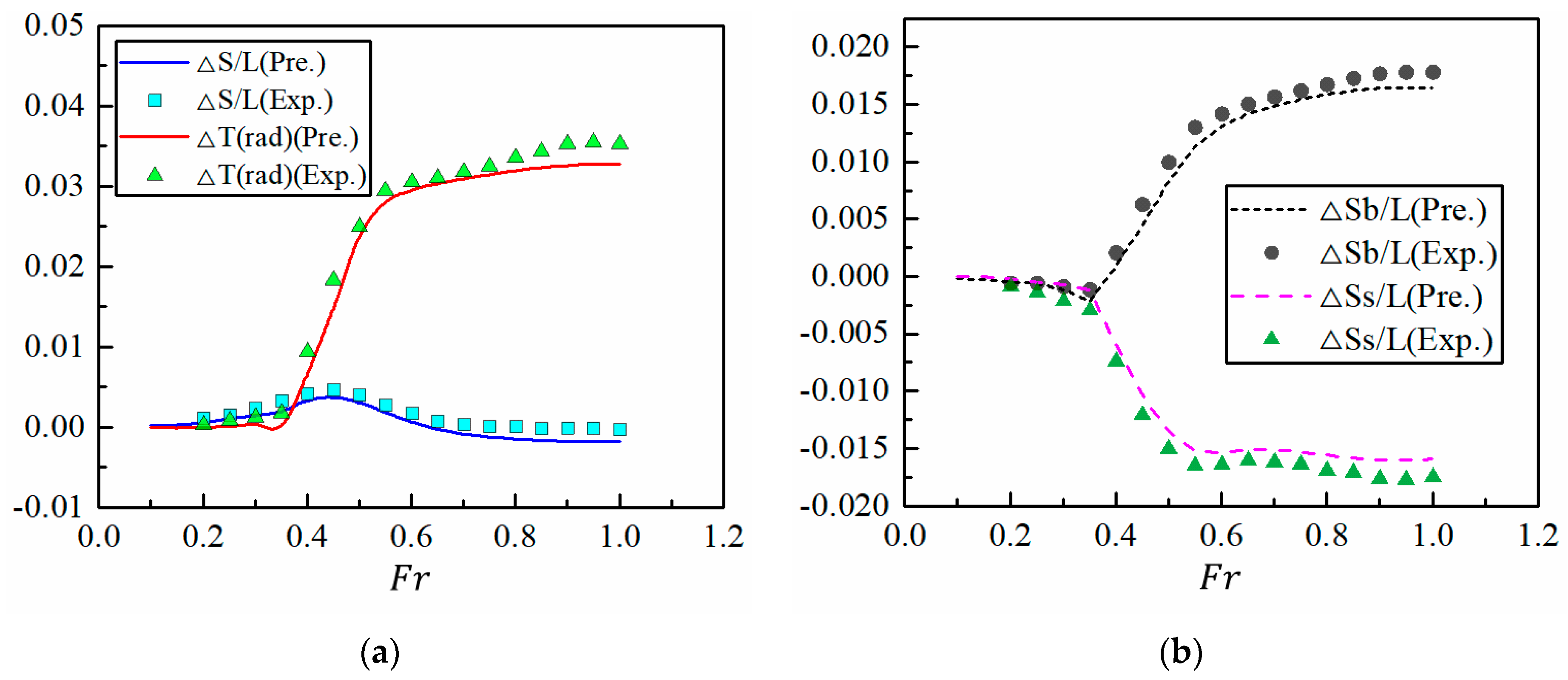
| Fr | Error (%) | |||
|---|---|---|---|---|
| ΔS/L | ΔT/L | ΔSb/L | ΔSs/L | |
| 0.2 | 12.65 | 18.50 | 3.15 | 38.40 |
| 0.25 | 6.05 | 44.29 | 0.30 | 18.43 |
| 0.3 | 7.54 | 8.74 | 2.28 | 24.18 |
| 0.35 | 7.71 | 35.25 | 4.54 | 15.83 |
| 0.4 | 3.24 | 1.53 | 12.37 | 2.45 |
| 0.45 | 2.77 | 0.88 | 4.27 | 1.71 |
| 0.5 | 3.31 | 6.52 | 1.99 | 1.11 |
| 0.55 | 5.33 | 5.96 | 1.52 | 0.86 |
| 0.6 | 18.85 | 3.87 | 0.82 | 0.66 |
| 0.65 | 40.83 | 2.88 | 0.61 | 0.62 |
| 0.7 | 14.68 | 3.14 | 0.55 | 0.69 |
| 0.75 | 11.16 | 3.63 | 0.51 | 0.71 |
| 0.8 | 10.90 | 5.36 | 0.54 | 0.85 |
| 0.85 | 9.28 | 6.38 | 0.65 | 0.80 |
| 0.9 | 9.73 | 8.38 | 0.79 | 1.03 |
| 0.95 | 9.68 | 8.50 | 0.80 | 1.08 |
| 1.0 | 8.67 | 7.66 | 0.83 | 1.00 |
| Fr | h/L = Infinite | h/L = 0.25 | h/L = 0.2 | h/L = 0.125 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | Value | Value | Value | ||||||
| Maximum | 0.3 | 0.00344 | −0.3225 | 0.00352 | −0.3225 | 0.0037 | −0.3225 | 0.00555 | −0.3225 |
| 0.4 | 0.00837 | 0.6900 | 0.00963 | 0.7350 | 0.00918 | −0.2100 | 0.00985 | −0.1875 | |
| 0.55 | 0.0096 | −0.1200 | 0.01176 | −0.0975 | 0.01071 | −0.1200 | 0.00951 | −0.1200 | |
| Minimum | 0.3 | −0.00522 | −0.1650 | −0.00524 | −0.1650 | −0.00526 | −0.1650 | −0.0065 | −0.0075 |
| 0.4 | −0.00959 | 0.1500 | −0.01075 | 0.1725 | −0.01161 | 0.2625 | −0.00486 | 0.3750 | |
| 0.55 | −0.01207 | 0.3750 | −0.00697 | 0.3975 | −0.00693 | 0.3975 | −0.00659 | 0.3975 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.-L.; Yang, B.-C.; Zhou, Z.-R. Numerical Investigation on a High-Speed Transom Stern Ship Advancing in Shallow Water. J. Mar. Sci. Eng. 2024, 12, 867. https://doi.org/10.3390/jmse12060867
Zhao Z-L, Yang B-C, Zhou Z-R. Numerical Investigation on a High-Speed Transom Stern Ship Advancing in Shallow Water. Journal of Marine Science and Engineering. 2024; 12(6):867. https://doi.org/10.3390/jmse12060867
Chicago/Turabian StyleZhao, Zhi-Lei, Bai-Cheng Yang, and Zhi-Rong Zhou. 2024. "Numerical Investigation on a High-Speed Transom Stern Ship Advancing in Shallow Water" Journal of Marine Science and Engineering 12, no. 6: 867. https://doi.org/10.3390/jmse12060867
APA StyleZhao, Z.-L., Yang, B.-C., & Zhou, Z.-R. (2024). Numerical Investigation on a High-Speed Transom Stern Ship Advancing in Shallow Water. Journal of Marine Science and Engineering, 12(6), 867. https://doi.org/10.3390/jmse12060867





