Abstract
Accurately assessing ice loads is a fundamental issue in the field of structural design for ships in ice-covered regions. In this paper, we conducted research on extreme ice load estimation for icebreaking ships, combining stochastic theory with numerical simulation. Firstly, using sea ice data from the Arctic region of the United States National Snow and Ice Data Center, a stochastic ice field model was established under Arctic sea ice conditions using non-parametric estimation and the rejection sampling method, and ice field data were generated stochastically. Then, based on the stochastic ice field data, a three-dimensional numerical model of the interaction between the ice field and the ship hull was established, and the reliability of the numerical model was verified by experimental results. Finally, based on the numerical model of the interaction between the ice field and the ship hull, asymptotic methods were used to study the extreme ice load estimation in different parts of the ship hull, revealing the variation law of the extreme ice load in different parts of the ship hull. This study provides basic theory and technical support for the structural design of ships in polar regions and has engineering application value.
1. Introduction
As the global economy develops, the demand for natural resources is increasing day by day in countries around the world. The Arctic has the world’s largest remaining oil and gas reserves [1]. Today, the extraction of these resources has resulted in a significant increase in what is known as destination-based shipping—the transportation of goods from the Arctic to non-Arctic destinations. In the coming decades, this type of transportation is expected to increase significantly, driven by new developments in oil and gas, such as the liquefied natural gas (LNG) projects in the Arctic. The use of trans-Arctic shipping routes is another type of Arctic shipping where goods are transported between non-Arctic destinations through Arctic waters. Compared to traditional non-Arctic shipping routes, trans-Arctic shipping may offer a range of advantages, with the most significant being distance savings. For example, for shipping between northern Europe and the Far East, trans-Arctic shipping along the Northern Sea Route (NSR) has reduced the distance by 40% compared to the traditional route through the Suez Canal [2].
Assessment of ice loads is a core issue in the design of ships for ice-covered areas, and icebreaking ships are the key pieces for ensuring the development of polar resources and Arctic shipping. The assessment of ice loads can be achieved through various methods, including theoretical analysis, empirical formulae, numerical simulation, and experimental methods, all of which can predict the resistance of ships in ice-covered areas to a certain extent. By using the physical parameters of ships and sea ice, as well as mechanical performance indicators of sea ice, ice loads can be evaluated [3]. However, sea ice is usually considered flat ice in these evaluation methods, and only the ice load at a specific moment and position during the navigation in ice-covered areas can be calculated, without reflecting the changes in the polar ice field. Nevertheless, the navigation of icebreaking ships in ice-covered areas is a continuous stochastic process, in which the physical parameters and types of sea ice within the ice field vary in time and space, although the ship’s hull parameters remain unchanged.
When a ship is moving in ice-covered waters, homogeneous sea ice conditions are never observed in reality. The sea ice conditions concerning the physical properties (i.e., microstructure, thickness, salinity, porosity, and density) and the mechanical properties (i.e., tensile, flexural, shear, uni- and multi-axial compression strength, elastic and strain modulus, Poisson’s ratio, fracture toughness, and friction) usually vary significantly. Many of these properties are not studied well [4]. These variations could be referred to as “external” statistics, i.e., the stochasticness of the ice-induced loads due to the variation in ice conditions [5].
Research by Mikko Suominen et al. shows that the properties and conditions of ice, as well as the ice loads on ships caused by working in sea ice, can be described by probability distributions. They analyzed the influence of the inverse coefficient of variation on the exponential distribution, lognormal distribution, and Weibull distribution [6]. Mikko Kotilainen et al. obtained data on sea ice thickness and icebreaker ship speed in the Baltic Sea and identified ice loads from the measurement data using a Rayleigh separator. Assuming that the ice loads are generated by a common stochastic process, they studied the relationship between the ship speed, ice thickness, and ice loads [7]. A. Suyuthi et al. performed statistical inference on the peak ice loads on the ship’s local structure using a set of special data provided by a full-scale measurement on a coast guard vessel during a winter voyage in 2007. They considered various methods for selecting statistical models for ice loads and estimating parameters, extended and analyzed each process, and verified the validity of some typical probability models [5,8]. Zhang Dayong et al. considered the uncertainty of ice loads in the process of ice resistance of offshore platform structures, established a simplified mechanical model using the Pushover method, and analyzed the probability models of resistance and ice loads using the K-S test [9]. Due to the extensive stochasticness in ice conditions, ice behavior, and contact scenarios, ice loads measured on the hull frames always show high stochastics. Typically, the load peaks are of concern. Probabilistic approaches are usually adopted to model the stochastic load peaks [10,11]. Extreme value statistics of ice loads, even in applications, have very often been based on asymptotic results. It is assumed that the epochal extremes, for example, yearly extreme wind speeds, are distributed according to the generalized (asymptotic) extreme value distribution with unknown parameters to be estimated on the basis of the observed data. The extreme values of ice loads are directly related to the reliability of the vessels since the ultimate limit states (ULSs) are generally based on extreme load effects [12]. Former studies of extreme ice load predictions are mainly based on the classic extreme value theory, which includes the peak amplitude approach [13], the asymptotic method [14,15], and the ACER method [16]. In the former method, statistical models are introduced to describe the parent (initial) distribution of loads based on the measured peak amplitudes of the ice-induced loads. When the parent distribution is known, the extreme value distribution is given in the form of the power of the encountered number of events [16].
The peak amplitude method among the three methods requires the ice load data to be a stationary stochastic process; the ACER method can predict the extreme ice loads well without considering the outliers, and the asymptotic method is based on asymptotic assumptions, and its evaluation effect depends on the time and quantity of ice load observation data. When using statistical models and methods to describe the interaction between icebreakers and sea ice, a sufficient amount of ice load sample data is required. These sample data can be obtained through shipboard monitoring, making the experimental data valuable but difficult to obtain. Full-scale experiments on ice–structure interaction processes are very valuable in gaining a first-hand understanding of ice loads. The measured peak ice load values are stochastic [17], and the results from full-scale (and model-scale) experiments often show a wide scatter, making analyzing the data challenging [18]. In brief, it is very unpredictable to repeat an experiment with the same parameterization due to the challenging environment and due to the inherent inhomogeneity of sea ice. The limited availability of experimental data on peak ice loads on structures is also a challenge [19]. With the development of numerical simulation technology, various methods such as finite element [20,21,22], discrete element [23,24,25,26], and smoothed particle hydrodynamics methods [27,28] have been applied to the numerical simulation of ship–ice interaction, and the simulation accuracy has gradually improved. The results of reliable numerical simulation also provide a source of data for load data statistics [29,30]. Here, we aim to increase the understanding of ice loads in ice–structure interaction by performing a statistical study on ice load data obtained by 2D combined finite–discrete element method (FEM-DEM) simulations. In more detail, we analyze the distribution of the data and seek error estimates for cases where only a low number of observations are available or the observed interaction processes are short [18]. The main objective of our work is to provide a reasonable extreme value estimation of ice-induced loads on ship hulls by utilizing available collected data from the full-scale measurements. This paper first conducts a statistical analysis of sea ice thickness data in the Arctic ice area and constructs a stochastic ice field that meets the environmental conditions of Arctic sea ice. Then, based on the stochastic ice field, the simulation process of the direct navigation and turning of icebreaking ships is carried out to obtain the ship ice load database. Finally, the distribution laws of ice loads on the ship’s bow and hull are studied, and the asymptotic method is used to predict the extreme ice load values on icebreaking ships in direct navigation and turning states in stochastic ice fields.
The present paper is organized as follows. Section 2 describes the method for generating a stochastic ice field based on the rejection sampling technique. Section 3 describes the numerical model and results of ice failure by an icebreaker. Section 4 shows the relevant results of the ship’s ice load distribution. Section 5 presents the related results of the extreme prediction of the ice load based on the asymptotic method. The advantages of the proposed approach are illustrated through relevant examples. The methods, results, and conclusions of this paper are expected to contribute to the development of reliability-based designs for ships operating in polar regions.
2. Establishment of a Stochastic Ice Field
Sea ice in the Arctic region exhibits complex diversity, with different distribution characteristics depending on the sea area and ice age. Arctic sea ice zones are classified into fixed ice zones and drift ice zones, as well as transitional ice zones based on their movement state, and based on their external shape, they can be classified into types such as flat ice, overlapping ice, piled ice, ice ridges, and icebergs. The distribution of sea ice thickness is different in the same temporal ice field. During winter voyages, icebreaking ships encounter different sea ice when navigating in polar regions. Many researchers have studied the icebreaking resistance of ships in the ice field and established many empirical and theoretical formulas. The more commonly used formulas for calculating icebreaking resistance are Lindqvist’s formula and Riska’s formula [31,32], both of which are semi-theoretical and semi-empirical formulas established based on real ship test data. In assessing the ice load of an icebreaking ship, it is related not only to the hull’s own parameters but also to the parameters characterizing the ice field. Among them, the sea ice thickness parameter becomes a parameter that must be considered in the icebreaking resistance assessment method. Therefore, selecting the Arctic sea ice thickness as a stochastic variable for the ice field and other parameters as deterministic parameters, this paper aims to establish a stochastic ice field model that conforms to the distribution characteristics of sea ice thickness in the Arctic ice zone. Based on the sea ice thickness data from the winter months of 2010–2019 in the Arctic provided by the US National Snow and Ice Data Center (NSIDC) [33,34], the probability density function of sea ice thickness is determined using non-parametric estimation, and the K-S test is used to verify whether the distribution of the sample data conforms to the hypothesized theoretical distribution. Then, using the Monte Carlo simulation method and the rejection sampling method to obtain a sufficient number of new datasets, a stochastic ice field data model can be constructed. Long-term data on other physical parameters, such as sea ice bending strength and uniaxial compression strength, are difficult to obtain temporarily and can be viewed as deterministic parameters using literature field test data.
2.1. Probability Density Function of Sea Ice Thickness
Based on the Arctic sea ice thickness data provided by the National Snow and Ice Data Center (NSIDC) in the United States, statistical analysis was performed on the sea ice thickness data. The frequency distribution histogram of the Arctic sea ice thickness sample data was plotted (Figure 1), where the vertical axis represents the value of the frequency divided by the group spacing (the number of individuals falling in each group of sample data is called the frequency, and the frequency divided by the total number of samples is the frequency). As shown in Figure 1, it can be seen that the sample data exhibits an asymmetric distribution with multiple peaks in many places. Based on the distribution characteristics, the probability density function of the sample data was estimated using kernel density estimation.
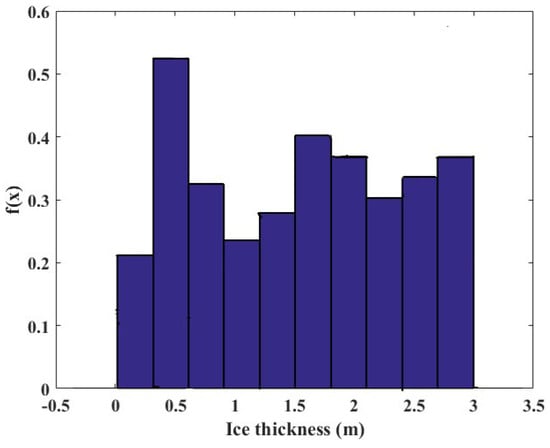
Figure 1.
Histogram of the frequency distribution of Arctic sea ice thickness.
The two main steps of kernel density estimation are determining the kernel function and the bandwidth h, where the choice of bandwidth h is crucial. For the kernel function , a Gaussian kernel function is used because it has good smoothness and excellent mathematical properties [35]. In this paper, a Gaussian kernel function is chosen, and its expression is as follows:
Combined with the definition formula of kernel density estimation, it can be obtained that
The estimation formula only contains the unknown parameter bandwidth h. Since the distribution of the sample data does not conform to normal distribution or other known distributions, it does not meet the conditions for applying the empirical rule proposed by Silverman [36], and therefore the plug-in method cannot be used to determine the appropriate bandwidth h. Cross-validation will be used to solve for the bandwidth h. The main principle of using cross-validation to select an appropriate bandwidth h is to minimize the integrated squared error (ISE). The calculation formula for ISE is as follows:
Equation (3) contains three terms, where the first two terms are related to the bandwidth h, while the third term is independent of the bandwidth h. Let and be the first two terms in Equation (3), and let be a function of the bandwidth h.
Therefore, selecting the bandwidth h to minimize Equation (3) is equivalent to selecting the bandwidth h to minimize Equation (4). Therefore, the appropriate bandwidth h is the solution .
For , it can be directly obtained from the definition of , which is
Among which, , is the selected kernel function. For , it is related to both the bandwidth h and the currently unknown term. Considering the definition of the mathematical expectation for continuous stochastic variables, we have the following:
At this point, we can use to estimate Equation (6). To obtain the expression , we first remove the i-th sample observation from the sample data X to form a new sample dataset . Then, using and the kernel density estimation method, we can obtain the expression for :
Therefore, the expression for is as follows:
By comparing the two methods of obtaining the bandwidth h mentioned above, it can be seen that the applicability of the plug-in method is limited. It requires the distribution of the sample data to be similar to a normal distribution or other known distributions to further determine the value of the bandwidth h, which limits its application. Compared with the plug-in method, although the cross-validation method has a larger computational cost and may not be easy to calculate with a large number of samples, the bandwidth h obtained is more theoretically and has a wider range of applications.
By substituting Equation (1) into the expression above, we can obtain
Substituting Equation (9) into Equation (5), we can obtain the first term of the function regarding the bandwidth h.
Thus, we can obtain the expression of function regarding the bandwidth h. Let be equal to a certain value, and we can then solve for the bandwidth . Therefore, the probability density function of Arctic sea ice thickness is as follows:
Plotting the obtained kernel density estimation function onto a histogram of frequency distribution, we can compare the trends between the two. As shown in Figure 2, it can be observed that within the range of [0, 3], the trend of the kernel density estimation function is consistent with the variation pattern of the sea ice thickness, exhibiting an asymmetric and non-unimodal distribution, and there are no outliers present.
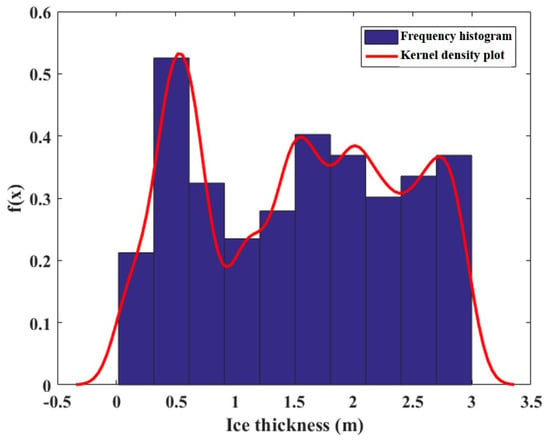
Figure 2.
Comparison of frequency histogram and kernel density estimation function.
2.2. Goodness-of-Fit Test
The probability density function of Arctic sea ice thickness in this paper cannot be directly obtained by an explicit expression of the distribution function. The K-S test is performed by comparing the values of and at the discrete point . Figure 3 shows the distribution function of sea ice thickness and the empirical cumulative distribution of the sample data. From the figure, it can be seen that has a stepwise increasing distribution, and with an increase in sample size, this stepwise property tends to become smoother. The fitting degree between and is good, and the curve is smooth without any outliers. Both show a consistent trend, gradually increasing from 0 to 1 monotonically, which conforms to the changing pattern of the distribution function of stochastic variables in nature. The maximum difference between the two occurs at , and the calculated test statistic is . By taking the confidence level and looking up the table based on the sample size n and confidence level , the critical value c is determined to be 0.0941. Since the test statistic is less than the critical value c, it can be concluded that the distribution law of Arctic sea ice thickness is consistent with the distribution function obtained by kernel density estimation in this paper.
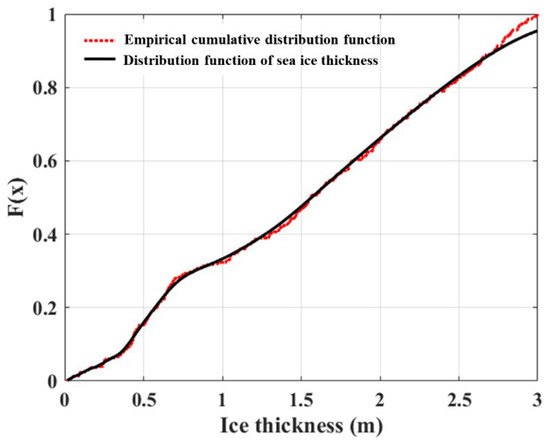
Figure 3.
Comparison of the sea ice thickness distribution function f and the empirical cumulative distribution function f based on the sample data.
2.3. Construction of a Stochastic Ice Field
Based on the probability density function of sea ice thickness in the Arctic region, stochastic numbers that follow the probability density function can be generated using Monte Carlo simulation. However, since the probability density function obtained by kernel density estimation in this study is a weighted average of several Gaussian kernel functions and each term is similar in form to a normal distribution, there is no explicit distribution function that can be used for the inverse transform method to generate new stochastic numbers directly. Therefore, the rejection sampling method is adopted in this study to generate the sea ice thickness data required for building a stochastic ice field. The finite element model established using this method will be more in line with reality, thus addressing the limitations of numerical simulations that use flat ice (with a fixed thickness) to build ice fields.
3. Numerical Simulation of the Ice Failure Process by an Icebreaker
3.1. Establishment of Numerical Model
To conduct a numerical simulation of the ice failure process of icebreakers in ice fields, the software LS-DYNA was used to simulate the submarine up-floating ice failure process. The research object selected was the icebreaker “Xuelong 2” [37,38], and the ice field was built using the ice thickness data obtained by the rejection sampling method. The “Xuelong 2” icebreaker has a total length of 116 m, a width of 22 m, a maximum draft of 7.8 m when fully loaded, a waterline entry angle of 40°, and a bow pillar inclination angle of 20° at the bow position. The waterline and longitudinal section of the ship are shown in Figure 4.
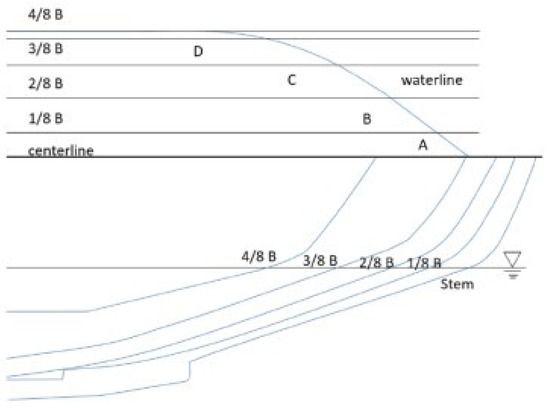
Figure 4.
Schematic diagram of waterline and longitudinal section of “Xuelong 2” icebreaker.
In the modeling process, referring to the waterline and longitudinal profile of the “Xuelong 2” icebreaker, a bottom-up modeling approach was used to sequentially establish key points that control the geometric shape of the ship’s bow, form smooth spline curves based on these key points, and preliminarily form the outline of the ship’s bow. According to these lines, the surface and body of the ship’s bow were formed. Secondly, the hull and stern of the icebreaker were established. Based on the total length of the icebreaker, appropriate key points were established, and the same approach was used to form the contours of the hull and stern. Finally, the complete model of the whole ship was established, as shown in Figure 5. A geometric model of an ice field is established by using a Monte Carlo method to generate stochastic ice thickness data ranging from 0 to 3 m, based on a 400 m × 300 m stochastic ice field, which models the real ice field, and considering fixed boundary conditions at the remote end. The specific process of establishing the ice field geometric model is as follows: (1) Let be the planar position coordinates of any point on the stochastic ice field, and let y be the thickness of the sea ice. (2) On the plane, with a fixed z coordinate, 61 key points are generated regularly at intervals of 5 m. The z coordinate is then increased by 5 m, and the above steps are repeated. This process is repeated until 4941 key points, each with a y-value obtained from the Monte Carlo method, are generated at regular intervals of 5 m. (3) Based on the regularity of the key point numbering, a loop command is used to connect the key points into regular lines, which are then used to form several curved surfaces. The entire irregular surface is dragged down 10 m along the negative y-axis to form a volume, and Boolean operations are performed on the working plane at to remove excess parts, thereby creating a geometric model of a stochastic ice field. See Figure 6 for an example. The use of an appropriate material model is one of the conditions for ensuring the accuracy of numerical simulation. This paper mainly studies the variation in ice loads caused by sea ice during the ice failure process of icebreakers, without considering the issue of hull damage. The numerical model treats the icebreaker as a rigid body [39].
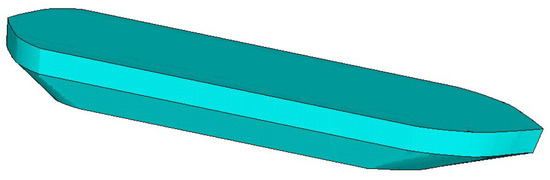
Figure 5.
Geometric model of icebreaker.
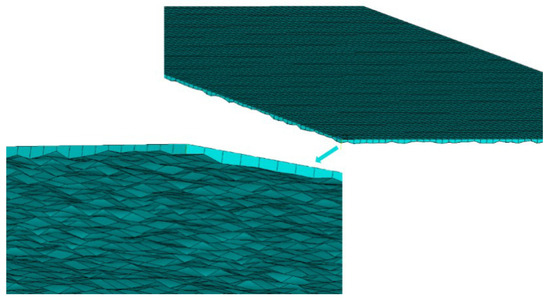
Figure 6.
Geometric model of a stochastic ice field.
Sea ice is regarded as an elastic brittle material, and the material model parameters defining the ice field are shown in Table 1 [40,41]. In this paper, the node separation method is used to simulate sea ice failure. The node separation method is an improvement of the traditional Lagrange unit. A fracture criterion is used for all spatial locations of the overlap of the node family (constraints on the relative degrees of freedom). The fracture characteristics of the material are described as when a node of the mechanical state meets the fracture criterion. This is where the node family is dissociated, and force is no longer transmitted between two nodes. The node separation method solves the problem of mesh fracture and forms the fracture mechanism of sea ice. Sea ice is modeled using an elastic–brittle model, and the failure of sea ice materials uses a strength criterion. When the stress reaches the permissible strength, damage to the sea ice occurs and crack development begins.

Table 1.
Parameters of the ice material model.
The finite element model of the icebreaker adopts 3D solid element SOLID164 and the mapping mesh partition method. The force situation of the icebreaker is different in the straight-line and turning states, and finite element models are generated for different navigation states. The finite element models of the icebreaker in the straight-line and turning states are shown in Figure 7. The first one contains 16,384 solid elements and 18,785 nodes, and the second one contains 19,456 solid elements and 22,049 nodes. The finite element model of a certain ice floe in a stochastic ice field adopts 3D solid element SOLID164 and the mapping mesh partition method. The finite element model of one ice floe is shown in Figure 8, which contains 129,600 elements and 174,484 nodes. For the stochastic ice field, this paper sets the contact surface with the icebreaker as a free end and the boundaries in the other three directions as fixed ends, thus simulating an infinite ice field as much as possible. When the icebreaker is breaking the ice in a straight line in the ice area, the buoyancy of seawater generated in this numerical model is balanced with the gravity of sea ice and the icebreaker, so the buoyancy and gravity are not considered in the vertical direction. When the icebreaker travels straight or turns in the ice area, the contact process mainly includes the initial contact between the icebreaker and sea ice when the sea ice is not yet broken; when the ice load accumulates to a certain degree, the sea ice breaks, and most of the broken pieces slide down along the bow surface of the icebreaker, while a small part of it moves along the hull to the stern and eventually separates from the hull. In the numerical model, automatic surface-to-surface contact is used to express the dynamic physical process of icebreaking by the icebreaker well.
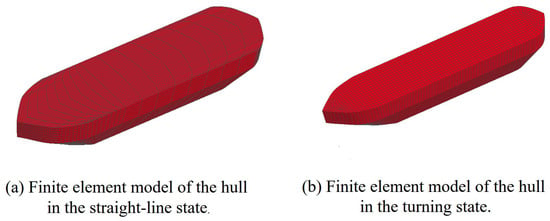
Figure 7.
Finite element model of the icebreaker.

Figure 8.
Finite element model of a certain ice floe in a stochastic ice field.
3.2. Numerical Model Validation
To optimize the numerical simulation process, this paper compared the numerical simulation results with different mesh accuracies with element numbers 137312, 145984, and 156576, respectively. Table 2 shows the average values of ice load peaks corresponding to different mesh accuracies. The average values of the ice load peaks under the first and third mesh accuracies are 2.69% and 1.68% different from those under the second mesh accuracy, respectively. Considering this comprehensively, the second mesh accuracy will be adopted to verify the numerical model of the interaction between icebreaker and sea ice. The element number of the icebreaker’s finite element model in the turning state is 3072 higher than that in the straight state. To ensure the simulation accuracy and computational efficiency, the element number of the icebreaker’s finite element model in both straight and turning states in the analysis of the stochastic ice field is controlled within the above-mentioned range.

Table 2.
Average values of ice load peaks under different numbers of elements.
The experimental data of the Xuelong 2 (Figure 4) model ship sailing in the ice tank in the literature [37] are used in this paper for comparison with the results of the numerical model and to verify the reliability of the numerical model. The tests were performed in the new ice tank at the Ice Engineering Laboratory of Tianjin University, which is 40 (long) × 6 (wide) × 2.0 (deep) with a cooling system sending cold air from the top of the insulated room that can be cooled down to an air temperature of −22 °C. The shape of the model vessel was determined by reducing the linear dimensions of the icebreaker with a geometric scaling factor (set as 40 in the present tests). For the present tests, the inertial, gravitational, and elastic forces are important, so Froude and Cauchy scaling laws were used. The model ice used in this model test is urea ice. The model ice is made by adding a certain proportion of urea to the water and then freezing it. The urea added to the model ice is similar to the salt water bubbles in the prototype sea ice, which is equivalent to making the ice easier to melt, increasing the porosity of the model ice, decreasing the strength of the model ice, and better meeting the requirements of the scaling ratio. To obtain detailed information on the distribution and variation of the ice load on the bow area, a tactile sensor was used in the tests. In order to comparatively analyze the distribution of the ice load on the hull of the icebreaker during navigation, the bow of the ship (which can be targeted only at half the ship width due to symmetry) was divided into four critical areas, namely, areas A, B, C, and D, on average. The model test data acquisition is output from the test cells, each of which has a size of 31.2 mm × 10.0 mm. The numerical simulation data are output according to the four critical regions. Figure 9 shows the distribution of extreme ice loads in the bow region of the icebreaker, where (a) represents the model test results and (b) represents the numerical simulation results. From Figure 9, it can be seen that the numerical simulation and model test obtained similar characteristics of the extreme value load distribution. The extreme ice loads obtained from the numerical simulation and model test are 21.453 N and 19.7471 N for area A; 12.872 N and 4.3658 N for area B; 8.250 N and 7.5498 N for area C; and 8.625 N and 10.1939 N for area D. Although the numerical simulation results for area B are skewed larger than the model test results, the numerical simulation and model test results in areas A, C, and D remain similar. It can be proved that the numerical model for the icebreaking process of the icebreaking ship is reliable.
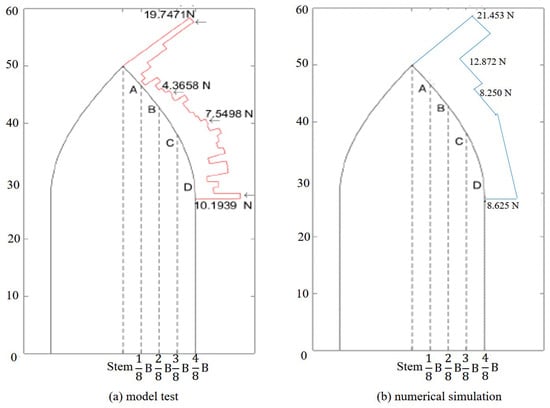
Figure 9.
Extreme ice load distribution in the bow area.
3.3. Numerical Model Results
3.3.1. Straight Navigation
Figure 10 shows the numerical simulation of the icebreaking process in the straight navigation of the icebreaker. When s, the icebreaker comes into contact with the sea ice, and the forward momentum and self-gravity cause the sea ice to bend and compress. When the ice load accumulates to a certain value, the sea ice begins to break. It should be noted that ice failure occurs at the contact between the icebreaker and the sea ice [23]. The reason is that the ice field finite element model in this paper is simplified to some extent, and the physical environmental conditions of real sea ice are very complex, with many special properties such as salinity and density. When s, the bow of the icebreaker has already entered the ice field completely, and the bending deformation of the ice field reaches the maximum value. Due to the lack of buoyancy, the broken sea ice sinks along the bow of the icebreaker. When s, the icebreaker has fully entered the ice field, and a large amount of sea ice sinks. Some of the sea ice enters the body of the icebreaker along the bow. Radial and circumferential cracks are usually induced in the bow of an icebreaker during straight navigation. During the entire icebreaking process, the sea ice mainly undergoes compression and bending failure, and, from time to time, this is helped by the shear failure of the ice, which is similar to the actual icebreaking process.
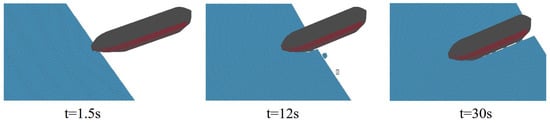
Figure 10.
Numerical simulation of the icebreaking process of an icebreaker.
Figure 11 shows the time history of the overall ice load on a straight-running icebreaker in a stochastic ice field. As seen from the figure, the icebreaker comes into contact with the stochastic ice field at s, and the ice load starts to act on the icebreaker. With time, the ice load gradually accumulates and reaches its first peak at s, followed by an unloading phenomenon, and a new cycle begins. The peak ice load during the whole process is N. The thickness distribution of the sea ice has certain stochastics, which makes the variation trend of the ice load closer to the real situation, and each peak ice load in the process of icebreaking has significant differences.
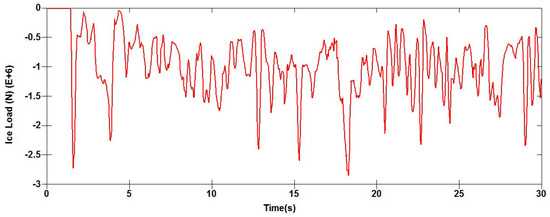
Figure 11.
Time history curve of the overall ice load on the icebreaker in straight navigation in a certain stochastic ice field.
3.3.2. Rotation Navigation
Figure 12 and Figure 13 show the turning and breaking ice process of the icebreaker in a stochastic ice field and the corresponding time history curve of the overall ice load. As can be seen from the figures, the time history curve of ice load during the turning state also has several peaks, which is consistent with the variation in ice load during the icebreaking process. As the rotational motion continues, the contact area between the ship’s hull and the sea ice gradually increases. Due to the structural differences between the hull and the bow, the failure mode of sea ice is mainly crushing, resulting in higher ice loads compared to the bow area. Before s, the effective contact area between the icebreaker and the stochastic ice field gradually increases, and the peak value of the ice load shows an increasing trend. From s to s, the rate of increase of the contact area between the icebreaker and the stochastic ice field begins to decrease, and the peak value of the ice load shows a decreasing trend. From s to s, the icebreaker’s moving state begins to approach the straight-line state, making the trend of the peak value of the ice load similar to that during straight-line movement. The maximum value of the overall ice load during the entire icebreaking process is N.
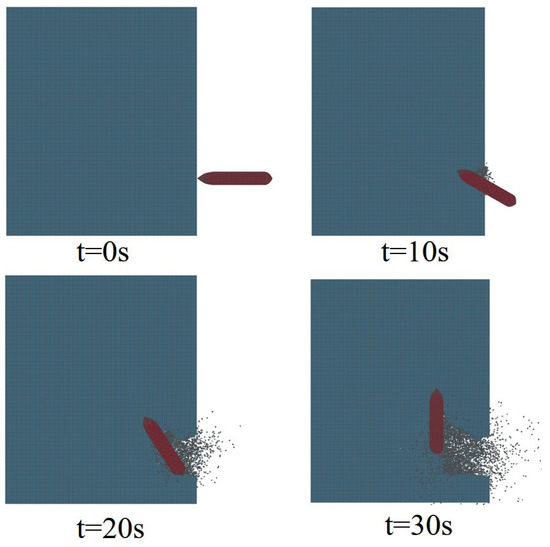
Figure 12.
Turning process of an icebreaker in a stochastic ice field at a certain ice field.
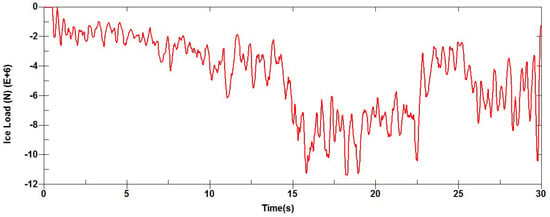
Figure 13.
Time history curve of ice load in turning case.
4. Distribution of Ice Loads on the Hull
When an icebreaker is breaking ice in polar regions, the local ice loads on different parts of the icebreaker can reflect the force situation in different positions on the hull, which is also of great significance for the design of the hull. During straight-line movement in an ice field, the bow of the icebreaker is the main part that collides with sea ice, and the force state of the hull and stern during the icebreaking process will not change significantly. Therefore, according to the characteristics of the force under straight-line movement, the icebreaker is divided into eight different areas, as shown in Figure 14. When the icebreaker is turning in an ice field, the force situation of the icebreaker is completely different from that during straight-line movement, and the bow, hull, and stern will all participate in the icebreaking process. Therefore, according to the characteristics of the force under the turning state, the icebreaker model is divided into 20 different areas, as shown in Figure 15.
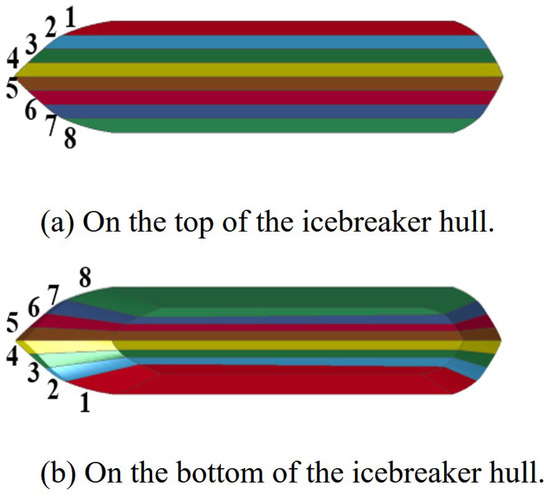
Figure 14.
Division of regions on the icebreaker during straight-line movement.
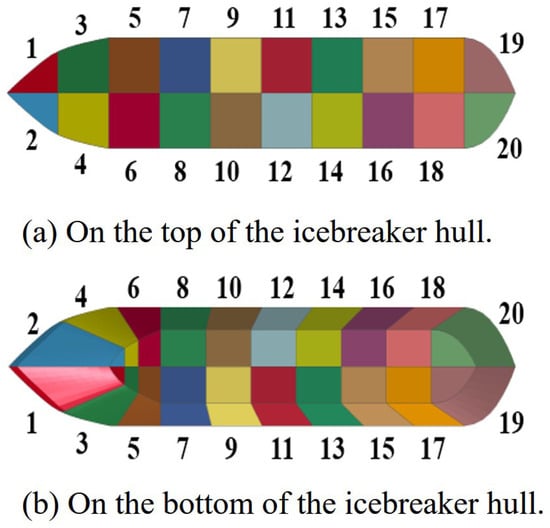
Figure 15.
Division of regions on the icebreaker during the turning state.
4.1. Straight-Line Icebreaking Case
Figure 16 shows the distribution of maximum ice loads on different parts of the icebreaker while moving in a stochastic ice field. Symmetrical parts are annotated with the same graphics. As can be seen from the figure, the maximum ice load occurs at position 4, with a value of N. The distribution trend of the ice load shows high middle and low ends, which is caused by the dominant role of the middle part of the hull in the icebreaking process.
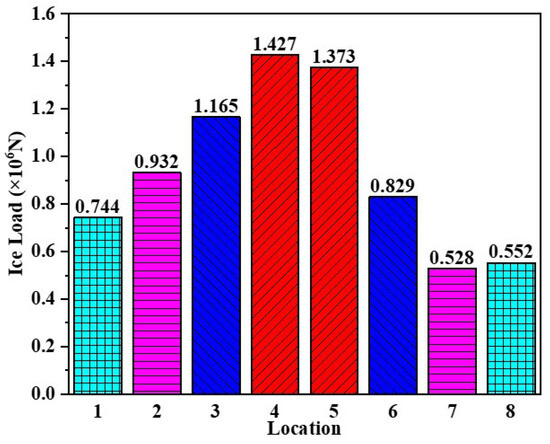
Figure 16.
Extreme ice loads on different parts of the icebreaker during straight-line icebreaking.
4.2. Ship’s Turning Icebreaking Case
Figure 17 shows the distribution of extreme ice loads on different parts of the icebreaker during rotational icebreaking in a stochastic ice field. Symmetrical parts are annotated with the same graph. It can be seen from the figure that the extreme ice loads on the non-icebreaking areas (3, 5, 7, 9, 11, 13, 15, 17, 19) of the icebreaker are close to zero. The extreme ice loads in the icebreaking areas show a trend of increasing first and then decreasing along the hull. The maximum extreme ice load appears at position 16, which is N. During icebreaking, due to the inclination of the bow area (1, 2, 3, 4), the failure mode of sea ice is mainly bending, resulting in relatively small numerical values. As the rotational motion continues, the contact area between the ship’s hull (6, 8, 10, 12, 14, 16) and the sea ice gradually increases. Due to the structural differences between the hull and the bow, the failure mode of sea ice is mainly crushing, resulting in higher ice loads compared to the bow area. When the icebreaker approaches a rotational angle of 90 degrees, its navigation trajectory approximates the straight-line icebreaking form.
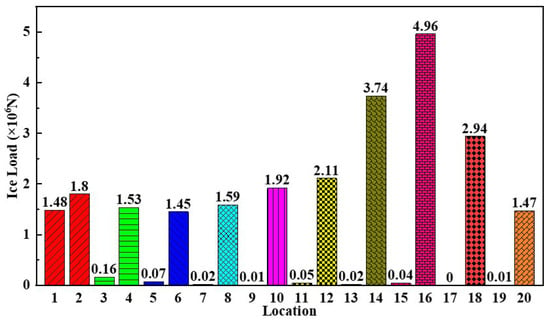
Figure 17.
Extreme ice loads on different parts of the icebreaker during rotational icebreaking.
5. Estimation of Ship Ice Load Extreme Values
Based on the generation of stochastic ice fields and numerical simulation of the icebreaking process of an icebreaker, a large number of ice load time history curves generated during straight-line and rotational motion of an icebreaker in ice fields can be obtained. This method was used to obtain 48 ice load time history curves, each with a time range of (0, 30) s. Using the asymptotic method, the extreme ice loads on different parts of the ship were estimated during straight-line and rotational icebreaking, and the possible range of variation of ice load extreme values was determined.
5.1. Asymptotic Method
The progressive method, also known as the time window method, can be used when the initial distribution function is difficult to determine. Similarly, this method regards the icebreaking process of a ship as a stochastic process with a duration of . The difference from the peak amplitude method is that a time interval t is set, and the duration range is uniformly divided into K segments, with the peak ice load values of each segment denoted as , where . Utilizing these peak ice load values, the extreme value type I distribution is used to approximate the extreme value distribution function of the ice load.
The expression for the extreme value type I distribution is as follows:
In the formula, a and b are parameters that can be determined using maximum likelihood estimation or least squares estimation. The estimation formula for the parameters is Equation (15):
where is the Euler constant and . Therefore, for a small transcendental probability , in conjunction with Equations (13)–(15), the extreme value of the ice load can be estimated. The estimated value of the ice load’s extreme value is Equation (16):
5.2. Estimation of Ice Load Extremes in Straight-Line Motion
In this study, the time interval t was set to 8 s, and the interval (0, 637) was uniformly divided into parts. The peak ice load was determined for each small interval, resulting in 80 ice load peak data samples. The sample data were then substituted into Equation (15), which gives and . Assuming a transcendental probability of and substituting it into Equation (16), the ice load extreme for region 4, when an icebreaker moves straight in a stochastic ice field, can be estimated, which gives an estimated result of kN.
It is worth noting that among the 25479 ice load sample data obtained, the ice load extreme in region 4 was 2718.8 kN. During all the numerical simulations of the straight-line motion of the icebreaker, only 3 samples had ice loads greater than kN, accounting for 0.01% of all the sample data, and 213 samples had ice loads greater than kN, accounting for 0.8% of all the sample data. Using frequency approximation instead of probability, it can be considered an extremely small probability event. Therefore, the estimated results obtained by both methods are acceptable. From a numerical point of view, the peak amplitude method is more conservative than the asymptotic method. In practical consideration of the ship design for straight-line motion, the estimated results of the peak amplitude method can be used for region 4, but it may lead to a lower material utilization efficiency. Alternatively, only the results obtained by the asymptotic method can be considered, but this may result in smaller estimated ice load extremes. The best approach is to comprehensively consider the results obtained by both methods and assume that the ice load extreme in region 4 ranges between and , which can ensure that the mechanical performance of the ship’s material is fully utilized and avoid underestimating the ice load extremes.
The asymptotic method was used to estimate the ice load extremes in regions 1–8 of the icebreaker, and the estimated results are shown in Figure 18. From the figure, it can be seen that the variation trend of the estimated results has a certain symmetry. The estimated results first decrease from the middle of the bow towards both sides and then become flat at regions 1 and 8. Regions 1 and 8 are transition zones located at the junction of the bow and hull and need to have a certain resistance to ice loads.
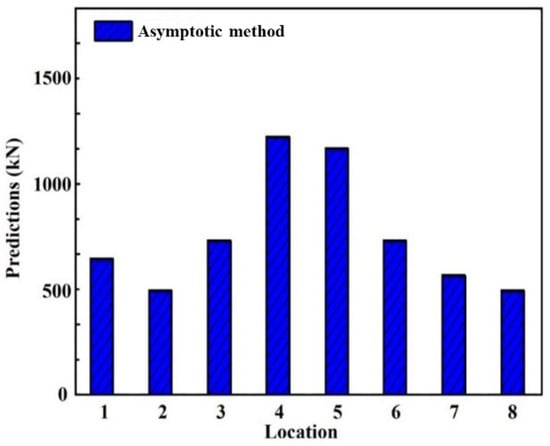
Figure 18.
Estimated ice load extremes in different regions.
5.3. Estimation of Ice Load Extremes in the Rotational Case
The asymptotic method is used to estimate the extreme ice loads at the bow, midship, and stern of the icebreaking ship in a rotational state. Regions 2, 16, and 20 are selected to represent the bow, midship, and stern of the icebreaking ship, respectively. This provides some reference for the force situation of the icebreaking ship in a rotational state.
Figure 19 shows the estimated extreme ice loads for regions 2, 16, and 20 of the icebreaking ship in a rotational state. From the figure, it can be seen that the extreme ice load in region 16 located at the midship is greater than those in regions 2 and 20 located at the bow and stern. The estimated result in region 16 is 51.3% higher than that in region 2 and 45.4% higher than that in region 20. The main reason is that in the rotational process of the icebreaking ship, the failure mode of the sea ice at the midship is dominated by compression failure, leading to a larger value of ice load. At the bow and stern, there is a certain inclination angle forming a conical hull structure, making the failure mode of the sea ice dominated by bending failure. The extreme ice loads at the bow and stern are almost the same, with a difference of 17.4%.
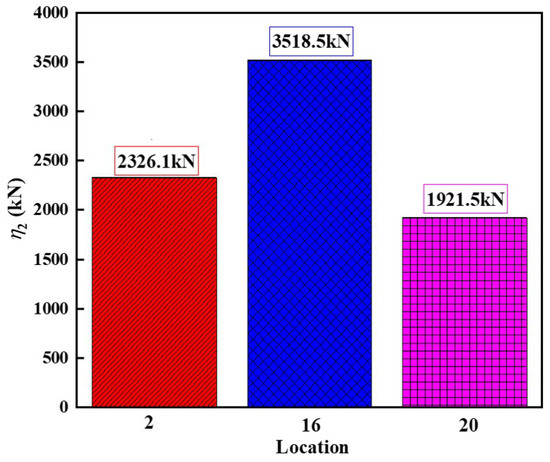
Figure 19.
Estimated maximum ice loads in regions 2, 16, and 20 during ship rotation.
6. Conclusions
In this study, based on probability and statistical analysis, a probability distribution function of sea ice thickness in the Arctic was determined. A stochastic ice field was constructed by using Monte Carlo simulation to generate a sufficient number of sea ice thickness samples. Then, a numerical model of ice–ship interaction was built based on the parameters of the “Xuelong 2” and the stochastic ice field model. The validity of the numerical model was verified by experimental results. Finally, the ice load time history data were obtained based on the numerical model, and the extreme ice loads on the icebreaker in straight and rotational motion states in the ice field were estimated using the asymptotic method. The following conclusions were drawn:
(1) It is feasible to use the acceptance–rejection sampling method to generate a random thickness ice field and combine it with finite element numerical simulation of the icebreaking process for assessing icebreaking resistance.
(2) In the straight state of the ship motion in the ice field, the local ice loads at the bow showed a high trend but were smaller in both the midhull and stern areas. In the rotational state, the ice loads at the ship’s midship were significantly higher than those at the bow and stern, mainly because the primary failure mode of sea ice at the midship was crushing. The ice load on the hull reaches its maximum value when the ship is turned about 45°.
(3) The asymptotic method is applicable for estimating the extreme ice loads of icebreaking ships, and the estimated results reflect the changing trends of ice loads in different regions.
The limitation of the work in this paper is that only the sea ice thickness was chosen as a stochastic parameter of the ice field, while other sea ice mechanical parameters were regarded as deterministic parameters. However, in practice, the mechanical parameters of sea ice are also highly stochastic, and in the future it will be necessary to include the stochastic variations of these parameters in the collection and statistics of other mechanical parameters of sea ice and in the establishment of the stochastic ice field model.
Author Contributions
Conceptualization, Supervision, L.L.; Writing—original draft, Data curation, L.L. and G.H.; Methodology, Funding acquisition, L.L. and S.J.; Writing—review and editing, L.L. and S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 51609054), State Key Laboratory of Structural Analysis for Industrial Equipment in Dalian University of Technology (Grant No. GZ22115), and Heilongjiang Provincial Key Laboratory of Polar Environment and Ecosystem (HPKL-PEE) (Grant No. 2021007). This support is gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding authors.
Acknowledgments
This research was supported by the School of Civil Engineering of the Harbin Institute of Technology. The authors would like to express sincere gratitude to those who supported this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gautier, D.L.; Bird, K.J.; Charpentier, R.R.; Grantz, A.; Houseknecht, D.W.; Klett, T.R.; Moore, T.E.; Pitman, J.K.; Schenk, C.J.; Schuenemeyer, J.H.; et al. Assessment of Undiscovered Oil and Gas in the Arctic. Science 2009, 324, 1175–1179. [Google Scholar] [CrossRef]
- Vanhatalo, J.; Huuhtanen, J.; Bergström, M.; Helle, I.; Mäkinen, J.; Kujala, P. Probability of a ship becoming beset in ice along the Northern Sea Route—A Bayesian analysis of real-life data. Cold Reg. Sci. Technol. 2021, 184, 103238. [Google Scholar] [CrossRef]
- Lu, W.; Lubbad, R.; Høyland, K.; Løset, S. Physical model and theoretical model study of level ice and wide sloping structure interactions. Cold Reg. Sci. Technol. 2014, 101, 40–72. [Google Scholar] [CrossRef]
- Timco, G.; Weeks, W. A review of the engineering properties of sea ice. Cold Reg. Sci. Technol. 2010, 60, 107–129. [Google Scholar] [CrossRef]
- Suyuthi, A.; Leira, B.; Riska, K. Statistics of local ice load peaks on ship hulls. Struct. Saf. 2013, 40, 1–10. [Google Scholar] [CrossRef]
- Suominen, M.; Kujala, P. Variation in short-term ice-induced load amplitudes on a ship’s hull and related probability distributions. Cold Reg. Sci. Technol. 2014, 106–107, 131–140. [Google Scholar] [CrossRef]
- Kotilainen, M.; Vanhatalo, J.; Suominen, M.; Kujala, P. Predicting ice-induced load amplitudes on ship bow conditional on ice thickness and ship speed in the Baltic Sea. Cold Reg. Sci. Technol. 2017, 135, 116–126. [Google Scholar] [CrossRef]
- Suyuthi, A.; Leira, B.; Riska, K. A generalized probabilistic model of ice load peaks on ship hulls in broken-ice fields. Cold Reg. Sci. Technol. 2014, 97, 7–20. [Google Scholar] [CrossRef]
- Zhang, D.; Li, G.; Yue, Q. Statistical properties of structural global resistance and extreme response of offshore platform in ice zone. J. Ship Mech. 2013, 17, 112–117. [Google Scholar] [CrossRef]
- Li, F.; Lu, L.; Suominen, M.; Kujala, P. Short-term statistics of ice loads on ship bow frames in floe ice fields: Full-scale measurements in the Antarctic ocean. Mar. Struct. 2021, 80, 103049. [Google Scholar] [CrossRef]
- Zhang, J.; Gaidai, O.; Wang, K.; Xu, J.; Ye, R.; Xu, X. A stochastic method for the prediction of icebreaker bow extreme stresses. Appl. Ocean Res. 2019, 87, 95–101. [Google Scholar] [CrossRef]
- Sinsabvarodom, C.; Chai, W.; Leira, B.J.; Høyland, K.V.; Naess, A. Uncertainty assessments of structural loading due to first year ice based on the ISO standard by using Monte-Carlo simulation. Ocean Eng. 2020, 198, 106935. [Google Scholar] [CrossRef]
- Ralph, F.; Jordaan, I. Probabilistic Methodology for Design of Arctic Ships. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; Volume 6, p. V006T07A010. [Google Scholar] [CrossRef]
- Suyuthi, A.; Leira, B.; Riska, K. Short term extreme statistics of local ice loads on ship hulls. Cold Reg. Sci. Technol. 2012, 82, 130–143. [Google Scholar] [CrossRef]
- Suominen, M.; Kujala, P.; Kotilainen, M. The Encountered Extreme Events and Predicted Maximum Ice-Induced Loads on the Ship Hull in the Southern Ocean. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015; p. V008T07A040. [Google Scholar] [CrossRef]
- Chai, W.; Leira, B.J.; Naess, A. Probabilistic methods for estimation of the extreme value statistics of ship ice loads. Cold Reg. Sci. Technol. 2018, 146, 87–97. [Google Scholar] [CrossRef]
- Daley, C.; Tuhkuri, J.; Riska, K. The role of discrete failures in local ice loads. Cold Reg. Sci. Technol. 1998, 27, 197–211. [Google Scholar] [CrossRef]
- Ranta, J.; Polojärvi, A.; Tuhkuri, J. Scatter and error estimates in ice loads—Results from virtual experiments. Cold Reg. Sci. Technol. 2018, 148, 1–12. [Google Scholar] [CrossRef]
- Timco, G.; Johnston, M. Ice loads on the caisson structures in the Canadian Beaufort Sea. Cold Reg. Sci. Technol. 2004, 38, 185–209. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, Z.; Tian, T.; Li, X.; Zhao, G. Numerical Simulation on the Resistance Performance of Ice-Going Container Ship Under Brash Ice Conditions. China Ocean Eng. 2018, 32, 51–61. [Google Scholar] [CrossRef]
- Kim, M.C.; Lee, S.K.; Lee, W.J.; Wang, J.Y. Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions. Int. J. Nav. Archit. Ocean 2013, 5, 116–131. [Google Scholar] [CrossRef]
- Wang, C.; Hu, X.; Tian, T.; Guo, C.; Wang, C. Numerical simulation of ice loads on a ship in broken ice fields using an elastic ice model. Int. J. Nav. Archit. Ocean 2020, 12, 414–427. [Google Scholar] [CrossRef]
- Xie, C.; Zhou, L.; Ding, S.; Liu, R.; Zheng, S. Experimental and numerical investigation on self-propulsion performance of polar merchant ship in brash ice channel. Ocean Eng. 2023, 269, 113424. [Google Scholar] [CrossRef]
- Ji, S. Discrete Element Modeling of Ice Loads on Ship and Offshore Structures. In Proceedings of the 7th International Conference on Discrete Element Methods, Dalian, China, 1–4 August 2016; Springer: Singapore, 2017; Volume 188, pp. 45–54. [Google Scholar] [CrossRef]
- Yang, B.; Sun, Z.; Zhang, G.; Wang, Q.; Zong, Z.; Li, Z. Numerical estimation of ship resistance in broken ice and investigation on the effect of floe geometry. Mar. Struct. 2021, 75, 102867. [Google Scholar] [CrossRef]
- Polojärvi, A.; Gong, H.; Tuhkuri, J. 3D DEM Simulations on a Ship Traveling Through an Ice Floe Field. In Proceedings of the 26th International Conference on Port and Ocean Engineering under Arctic Conditions, Virtual, 14–18 June 2021; Available online: https://www.researchgate.net/publication/353637541_3D_DEM_Simulations_on_a_Ship_Traveling_Through_an_Ice_Floe_Field (accessed on 14 June 2021).
- Liu, R.; Xue, Y.; Lu, X. Coupling of Finite Element Method and Peridynamics to Simulate Ship-Ice Interaction. J. Mar. Sci. Eng. 2023, 11, 481. [Google Scholar] [CrossRef]
- Liu, R.; Xue, Y.; Lu, X.; Cheng, W. Simulation of ship navigation in ice rubble based on peridynamics. Ocean Eng. 2018, 148, 286–298. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, M.; Zhou, L.; Garme, K.; Burman, M. A machine learning-based method for prediction of ship performance in ice: Part I. ice resistance. Mar. Struct. 2022, 83, 103181. [Google Scholar] [CrossRef]
- Zhong, K.; Ni, B.Y.; Li, Z.; Xu, X.; Wei, H.; Li, H.; Xue, Y. Direct measurements and CFD simulations on ice-induced hull pressure of a ship in floe ice fields. Ocean Eng. 2023, 272, 113523. [Google Scholar] [CrossRef]
- Lindqvist, G. A Straightforward Method for Calculation of Ice Resistance of Ships. In Proceedings of the 10th International Conference on Port and Ocean Engineering under Arctic Conditions, Luleå, Sweden, 12–16 June 1989; pp. 722–735. Available online: https://www.researchgate.net/publication/285085985_A_straightforward_method_for_calculation_of_ice_resistance_of_ships (accessed on 12 June 1989).
- Riska, K.; Wilhelmson, M.; Englund, K.; Leiviskä, T. Performance of Merchant Vessels in Ice in the Baltic; Helsinki University of Technology, Ship Laboratory: Espoo, Finland, 1997; Available online: http://urn.fi/URN:NBN:fi:bib:me:I00018353900 (accessed on 1 December 1997).
- Maness, J.; Duerr, R.; Dulock, M.; Fetterer, F.; Hicks, G.; Merredyth, A.; Sampson, W.; Wallace, A. Revealing our melting past: Rescuing historical snow and ice data. GeoResJ 2017, 14, 92–97. [Google Scholar] [CrossRef]
- Marcianesi, F.; Aulicino, G.; Wadhams, P. Arctic sea ice and snow cover albedo variability and trends during the last three decades. Pol. Sci. 2021, 28, 100617. [Google Scholar] [CrossRef]
- Ouyang, Z.L.; Zou, Z.J.; Zou, L. Adaptive hybrid-kernel function based Gaussian process regression for nonparametric modeling of ship maneuvering motion. Ocean Eng. 2023, 268, 113373. [Google Scholar] [CrossRef]
- Silverman, B. Density Estimation for Statistics and Data Analysis; Routledge: London, UK, 2018; pp. 1–175. [Google Scholar] [CrossRef]
- Huang, S. Model Test Study on the Distribution and Evolution of the Ice Load on Ship Hull during the Navigation Process. Master’s Thesis, Tianjin University, Tianjin, China, 2017. [Google Scholar] [CrossRef]
- Huang, Y.; Huang, S.; Sun, J. Experiments on navigating resistance of an icebreaker in snow covered level ice. Cold Reg. Sci. Technol. 2018, 152, 1–14. [Google Scholar] [CrossRef]
- Truong, D.D.; Jang, B.S. Estimation of ice loads on offshore structures using simulations of level ice-structure collisions with an influence coefficient method. Appl. Ocean Res. 2022, 125, 103235. [Google Scholar] [CrossRef]
- Ye, L.; Wang, C.; Guo, C.; Chang, X. Peridynamic model for submarine surfacing through ice. Chin. J. Ship Res. 2018, 488, 51–59. [Google Scholar] [CrossRef]
- Li, L.; Shkhinek, K. Dynamic interaction between ice and inclined structure. Mag. Civ. Eng. 2014, 45, 71–79. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).