Effect of Sampling Rate in Sea Trial Tests on the Estimation of Hydrodynamic Parameters for a Nonlinear Ship Manoeuvring Model

Abstract

This paper explores the impact of sampling rates during sea trials on the estimation of hydrodynamic parameters in a nonlinear manoeuvring model. Sea trials were carried out using an offshore patrol vessel and test data were collected. A nonlinear manoeuvring model is introduced to characterise the ship’s manoeuvring motion, and the truncated least squares support vector machine is employed to estimate nondimensional hydrodynamic coefficients and their corresponding uncertainties using the 25°–25° zigzag test. To assess the influence of the sampling rates, the training set is resampled offline with 14 sampling rates, ranging from 0.2 Hz to 5 Hz, encompassing a rate 10 times the highest frequency component of the signal of interest. The results show that the higher sampling rate can significantly diminish the parameter uncertainty. To obtain a robust estimation of linear and nonlinear hydrodynamic coefficients, the sampling rate should be higher than 10 times the highest frequency component of the signal of interest, and 3–5 Hz is recommended for the case in this paper. The validation is also carried out, which indicates that the proposed truncated least square support vector machine can provide a robust parameter estimation.

1. Introduction

As the global commercial ship fleet grows in size and number, there is an increasing demand for a thorough understanding of surface ship manoeuvrability, which is essential for safe navigation in bustling canals and ports. The recent fast development of autonomous ships has increased the demand for accurate prediction of a vessel’s manoeuvring motions because the onboard control system has to give commands based on the manoeuvrability of the ships, especially for collision avoidance. Possessing a thorough understanding of ship manoeuvrability offers significant advantages in terms of improving safety and efficiency. Additionally, it plays an important role in shaping the control systems for autonomous surface ships.

Mathematical manoeuvring models have long served as the conventional approach for simulating and forecasting ship behaviour. Ship manoeuvring models constitute a vital component within all existent bridge and desktop manoeuvring simulators [1]. The manoeuvring models are derived from Newton’s second law, considering the ship as a rigid body in motion through the water. Consequently, the pivotal task involves ascertaining the forces exerted upon the vessel. Abkowitz [2] introduced the renowned Abkowitz model, assuming that hydrodynamic forces are dependent on the ship’s motion variables, including speed, acceleration, and rudder action. The hydrodynamic forces on the ship are formulated as a polynomial function of manoeuvring and control parameters using the Taylor series. The main drawback is that an excessive number of hydrodynamic parameters complicates the determination of values through experimental methods. Indeed, some parameters, especially high-order nonlinear hydrodynamic coefficients, are meaningless and hard to explain and measure physically [3]. Therefore, the revised version of the Abkowitz model was proposed and the sensitivity analyses of each hydrodynamic coefficient were carried out [3]. The obtained model was used to simulate the sea trials of the “ESSO OSAKA” ship.

In the MMG model [4], hydrodynamic forces are individually investigated for the hull, propeller, and rudder, including their interactions. This approach significantly reduces the number of hydrodynamic coefficients. Other important versions of manoeuvring models include the vectorial model [5] and the generic manoeuvring model [6], just to name a few. No matter which model is chosen, determining the values of hydrodynamic coefficients is an unavoidable and challenging task.

The captive model test stands as a widely employed method for determining hydrodynamic coefficients in manoeuvring models, with endorsement by the International Towing Tank Conference. Scaled ship models are commonly attached to a Planar Motion Mechanism (PMM) that guides the model through predefined motions, with hydrodynamic forces and moments recorded via force gauges. Sutulo and Guedes Soares [6] employed captive-model tests to delineate ship manoeuvring forces through a multifactor regression model. Ross et al. [7] established a nonlinear manoeuvring model for the R/V Gunnerus through PMM tests, subsequently utilising the obtained model to forecast sea trials in the time domain [8]. In Ref. [9], a series of model experiments was conducted to ascertain hydrodynamic coefficients using a planar motion mechanism (PMM). The results indicate that the experimental coefficients yielded superior manoeuvring characteristics in both turning circle trajectories and zigzag manoeuvres.

The PMM tests of the DTC in the shallow water were conducted within the towing tank at Flanders Hydraulics Research [10]. These tests provided essential data used to predict the hydrodynamic coefficients of the bare hull operating in shallow water [11]. The primary advantage of employing PMM tests lies in the high quality of the obtained data, with the added benefit of environmental disturbances being effectively eliminated within the laboratory. Alternatively, free-running ship model tests offer a more cost-effective approach for assessing ship manoeuvrability [12,13,14]. They can be used to carry out the manoeuvring tests as recommended by ITTC [15], such as the turning test, zigzag test, and spiral and reverse spiral tests. Data acquisition during free-running ship model tests involves the utilization of onboard sensors, including the Global Positioning System (GPS), Inertial Measurement Unit (IMU), encoder, and anemometers.

Park et al. [16] examined the uncertainties associated with outdoor free-running model tests, aiming to evaluate the manoeuvrability of a damaged surface combatant. Costa et al. [17] introduced the identification and validation of hydrodynamic coefficients related to surge, sway, and yaw motions. This was achieved through zigzag and turning tests conducted on a free-running ship model. Xu et al. [18] studied the impact of shallow water on the vessel steering model through experimentation with a free-running ship model. Mucha et al. [19] conducted an experimental investigation on the manoeuvring capabilities of a free-running inland waterway ship under extremely shallow water conditions. The experimental data include results from repeatability studies, serving as potential validation for manoeuvring simulations. Chillcce and El Moctar [20] developed a data-driven system identification method for the parameters of a mathematical manoeuvring model. The proposed method is simple and robust, where the physical properties of hydrodynamic forces are considered. The free-running manoeuvre tests were used for validation. Ouyang et al. [21,22] applied the local Gaussian process regression method to describe the ship manoeuvring motion based on the free-running test data, and an adaptive hybrid-kernel function was proposed to improve the prediction accuracy. Xu and Guedes Soares [23] conducted an experimental investigation on the manoeuvring capabilities of a free-running inland waterway ship under extremely shallow water conditions. The experimental data include results from repeatability studies, serving as potential validation for manoeuvring simulations. The popularity of free-running ship model tests is rising, driven by advancements in sensor accuracy and cost reductions, making them widely employed for manoeuvrability investigations.

Sea trials play a crucial role in ensuring the effective manoeuvring and overall performance of a ship before it is put into service [24,25,26]. These trials provide an opportunity to assess the vessel’s handling characteristics, responsiveness, and stability in real-world maritime conditions. One of the primary reasons sea trials are of paramount importance is that they allow us to validate the ship’s design and construction against the theoretical models and simulations used during its development. Through sea trials, any discrepancies or unexpected issues in the ship’s manoeuvrability can be identified and addressed, ensuring that the vessel meets safety standards and operates efficiently.

Sea trials represent a direct approach for examining the manoeuvring characteristics of surface ships, circumventing the scale effects associated with ship models [27,28,29]. Guedes Soares et al. [30] conducted comprehensive manoeuvring trials on a 45 m fast catamaran equipped with waterjet propellers, operating in both deep and shallow waters at Froude numbers up to 0.56. The recorded data included trajectories, standard kinematic parameters, and the relative wind velocity vector. The trials involved executing circles at different speeds and rudder angles, spirals, zigzags, and stopping manoeuvres on the Atlantic coast of Portugal to study the full-scale manoeuvring characteristics of two fast patrol vessels [31]. Yun et al. [32] investigated the manoeuvrability of a tug-barge using sea trial tests. Pipchenko et al. [33] emphasised the necessity of correcting hydrodynamic coefficients based on trial data. They employed an objective function that considers both kinematic and dynamic components to determine hydrodynamic coefficients for an ultra-large container ship using sea trials, a conclusion echoed in Ref. [34]. Consequently, the system identification method is proposed to refine coefficients and search for optimal values through sea trials [1,35,36,37]. Perez and Fossen [38] summarised practical frequency-domain estimation algorithms, incorporating constraints on model structure and parameters to enhance the search for approximating parametric models [30].

The Support Vector Machine (SVM), a kernel-based method, gained prominence in the modelling of ship maneuvers [39]. SVMs offer several advantages when applied to system identification tasks. One notable advantage of SVMs lies in their ability to handle nonlinear relationships and high-dimensional data. This makes SVMs well-suited for complex system identification problems where the underlying dynamics may be intricate and difficult to model with traditional linear approaches. SVMs also excel in situations with limited data, as they can effectively generalise from a sparse dataset. Furthermore, SVMs provide a robust solution to outliers, contributing to their resilience in the presence of noisy data. Wang et al. [40] used nu-SVR for ship maneuvering motion in a user-friendly manner. Pei et al. [41] proposed an online model identification and manoeuvring prediction for marine crafts using an adaptive event-triggered mechanism. Xu et al. [18] identified the ship steering models based on the free-running ship model tests.

However, SVMs do have some limitations for system identification. One major drawback is their sensitivity to the choice of kernel functions and tuning parameters, which can impact the model’s performance and generalization ability. Additionally, SVMs might become computationally intensive, especially when dealing with large datasets, making real-time applications challenging. Suykens et al. [42] suggested that the size of the training set for the least square support vector machine (LS-SVM) should be restricted below 2000 data points. Therefore, a novel version of SVM, the truncated LS-SVM, was proposed for the big data application. This method has been successfully used for maneuvering modelling using PMM tests conducted in various conditions, including deep water [43], shallow water [11,44], and free-running ship model tests [18].

Other than the above methods, there are still many system identification technologies used for ship manoeuvring modelling. For example, Yoon and Rhee [45] used the Estimation-Before-Modelling (EBM) Technique to estimate the hydrodynamic parameters based on sea trial data. Perera et al. [46] used the extended Kalman filter (EKF) for the vessel steering model with unstructured uncertainties. Revestido Herrero and Velasco González [47] proposed a two-step identification method and a prediction error method with the Unscented Kalman Filter (UKF) performed for the obtention of the manoeuvring parameters. Gavrilin and Steen [48] discussed the global sensitivity of the hydrodynamic coefficients using the variance decomposition from full-scale trials. As can be observed from the published papers, many topics have been discussed for the sea trials. However, few papers focus on the quality of sea trial test data and their effect on the identified hydrodynamic coefficients. It is well known that system identification is a data-driven approach, and its success largely depends on the quality of the data.

The primary contribution of this work is to discuss the impact of sampling rate during sea trials on the estimation of the hydrodynamic coefficient. The truncated LS-SVM is used to estimate the nondimensional hydrodynamic coefficients and corresponding parameter uncertainties through diverse training sets. These training sets undergo resampling at 14 rates, spanning from 0.2 Hz to 5 Hz, with the inclusion of the recommended sampling rate, set at 10 times the highest frequency component of the signal of interest. By observing the obtained parameters and uncertainty, it can be concluded that the increment of the sampling rate can significantly diminish the parameter uncertainty, and the recommended sampling rate is also given in this paper.

2. Simplified Nonlinear Manoeuvring Mode

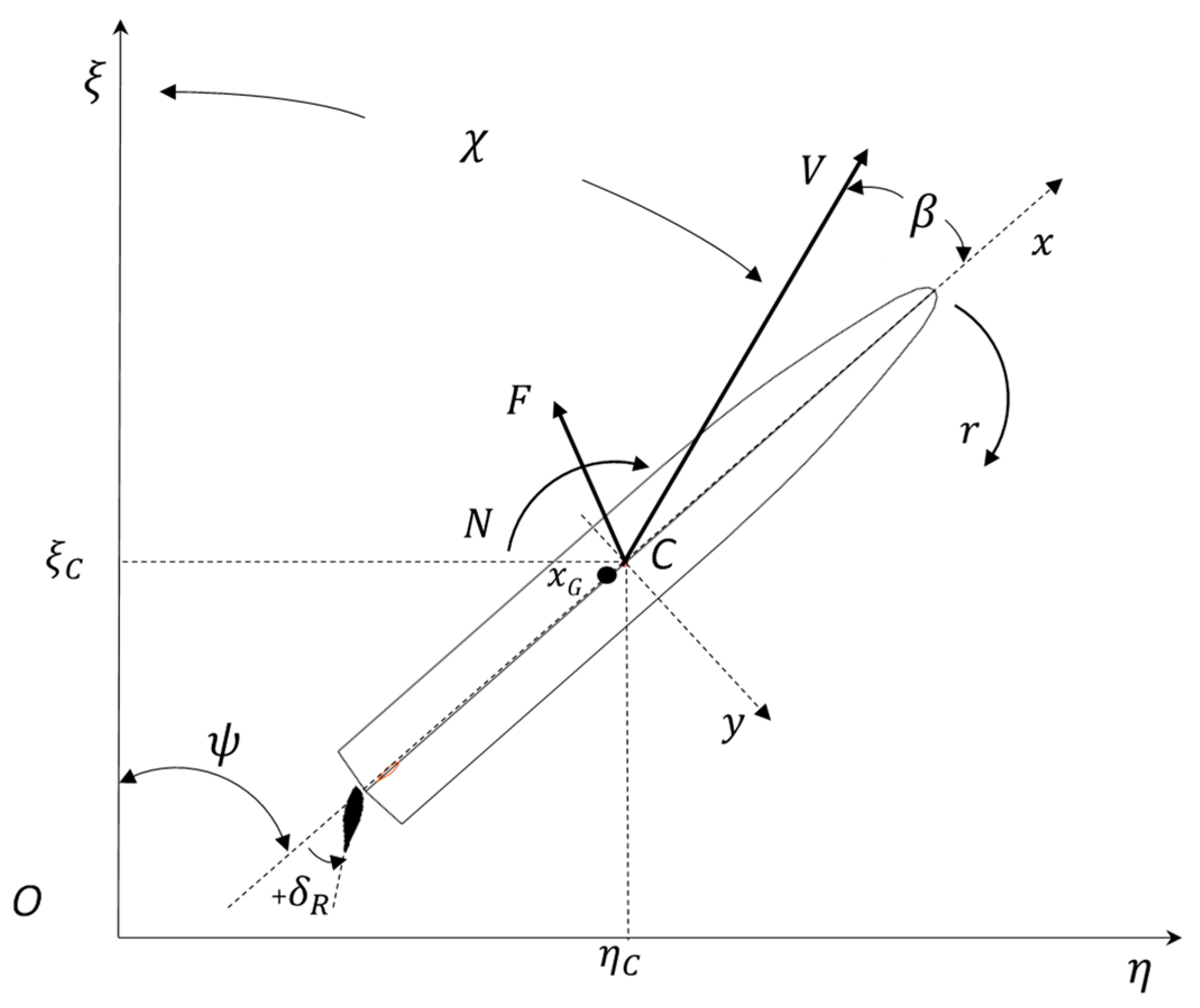
The ship kinematic model in three degrees of freedom (3DOF) is a mathematical representation that describes the motion of a ship in a simplified manner, considering three main degrees of freedom: surge, sway, and yaw motion. This model assumes a rigid-body approximation. The equations governing the ship’s 3DOF kinematics are derived from principles of physics and fluid dynamics, allowing for the prediction and analysis of the vessel’s motion in response to applied forces and moments. The 3DOF ship kinematic model serves as a valuable tool in maritime engineering, naval architecture, and ship control systems, facilitating the understanding and simulation of ship dynamics for various applications such as navigation, manoeuvring, and control system design.

For this present work, as presented in Figure 1, the 3DOF models can be used to describe the manoeuvring motions [49]:

$$\begin{gathered} \left(m+{\mu }_{11}\right)\dot{u}-mvr-m{x}_g{r}^2=X_q+X_p, \\ \left(m+{\mu }_{22}\right)\dot{v}+\left(m{x}_g+{\mu }_{26}\right)\dot{r}+mur=Y_q, \\ \left(m{x}_g+{\mu }_{62}\right)\dot{v}+\left(I_{zz}+{\mu }_{66}\right)\dot{r}+m{x}_{g}ur=N_q, \end{gathered}$$

(1)

where $u$, v, and r are the surge velocity, sway velocity, and yaw rate. The dotted variables are the accelerations. $m$ is the ship mass. The ${\mu }_{ij}$ are the added mass coefficients. $X_p$ is the propulsion forces of the propeller. $X_q,Y_q, N_q$are the hydrodynamic forces and moment. The hydrodynamic forces on the hull and rudder can be represented as follows [5]:

$$\begin{gathered} X_q={X^{\prime }}_q\left(u^{\prime },v^{\prime },{\delta }_R\right)\frac{\rho V^2}{2}LT, \\ {Y}_q={Y^{\prime }}_q\left(u^{\prime },v^{\prime },{\delta }_R\right)\frac{\rho V^2}{2}LT, \end{gathered}$$

(2)

where $\rho$ is the water density, V is the ground speed, and L is the length of ships.

$$\begin{gathered} N_q={N^{\prime }}_q\left(u^{\prime },v^{\prime },{\delta }_R\right)\frac{\rho V^2}{2}{L}^{2}T, \\ {X^{\prime }}_q={X^{\prime }}_{uu}{u}^{\prime 2}+{X^{\prime }}_{vr}{v}^{\prime }{r}^{\prime }+{X^{\prime }}_{\delta \delta }{\delta }_R^2 \\ {Y^{\prime }}_q={Y^{\prime }}_v{v}^{\prime }+{Y^{\prime }}_r{r}^{\prime }+{Y^{\prime }}_{vvr}{v^{\prime }}^2{r}^{\prime }+{Y^{\prime }}_{\delta }{\delta }_R \\ {N^{\prime }}_q={N^{\prime }}_v{v}^{\prime }+{N^{\prime }}_{r}r+{N^{\prime }}_{vvr}{v^{\prime }}^2{r}^{\prime }+{N^{\prime }}_{\delta }{\delta }_R \end{gathered}$$

(3)

where ${X^{\prime }}_{uu}$ … ${N^{\prime }}_{\delta }$ are the hydrodynamic parameters; $u^{\prime }$, $v^{\prime }$, and $r^{\prime }$ are the nondimensional velocity components, defined as

$$u^{\prime }=\frac{u}{V};v^{\prime }=\frac{v}{V};{ r}^{\prime }=\frac{rL}{V}$$

(4)

The model expressed in Equation (1) is extended with the kinematic equations needed for the transformation of the velocity components from the ship coordinate frame to the earth coordinate frame, given as

$$\begin{gathered} \dot{\xi }=u \mathrm{c}\mathrm{o}\mathrm{s}\psi -v \mathrm{s}\mathrm{i}\mathrm{n}\psi , \\ \dot{\eta }=u \mathrm{s}\mathrm{i}\mathrm{n}\psi +v \mathrm{c}\mathrm{o}\mathrm{s}\psi \end{gathered}$$

(5)

As presented in Figure 1, the ship has a length between perpendiculars of 76.8 m, a beam of 12.3 m, a draught of 3.77 m, and a mass of 1800 tonnes. The block coefficient is 0.499. The rudders’ area is 8 m². The properties of mass/inertia are estimated using the empirical equations, and they are given as follows: $I_{zz}=6.6952\times {10}^8 \mathrm{k}\mathrm{g}{\mathrm{m}}^2,{\mu }_{11}=4.4619\times {10}^4 \mathrm{k}\mathrm{g}$, ${\mu }_{22}=1.0289\times {10}^6$ kg, ${\mu }_{26}={\mu }_{62}=-1.3479\times {10}^6 \mathrm{k}\mathrm{g}\mathrm{m}$, ${\mu }_{66}=3.0692\times {10}^8 \mathrm{k}\mathrm{g}{\mathrm{m}}^2$. The nominal approach speed is $V_0=6.17$ m/s.

3. Sea Trials of an Offshore Patrol Vessel

Full-scale trials present a myriad of challenges stemming from various sources, encompassing uncertainties related to both weather and wave conditions, as well as those associated with the onboard sensors and equipment constituting the data acquisition setup. The intricacies involved in conducting these trials extend beyond mere technical considerations; they involve a substantial investment of time and financial resources. The preparatory phase alone entails the meticulous selection of actual ships, a comprehensive examination and analysis of the inherent sensing and data network capabilities of each vessel, and an assessment of the requisite technological specifications for external data acquisition setups. Furthermore, the planning and budgeting processes for the data acquisition setup and subsequent ship sea trials demand a level of detail that is commensurate with the scale and complexity of the undertaking.

Executing full-scale sea trials within predetermined weather and wave conditions remains a formidable challenge owing to the inherent unpredictability of maritime environments. This challenge is exacerbated by the need for precise alignment between planned conditions and the actual occurrences during the trials. Consequently, it is not surprising that the availability of reliable data from full-scale sea trials is notably scarce. The scarcity underscores the formidable nature of these trials, emphasising the critical importance of overcoming both technical and logistical hurdles to extract meaningful insights and advance our understanding of maritime systems. Despite the hurdles, the pursuit of accurate and comprehensive data through full-scale trials remains a paramount objective in advancing maritime technology and safety.

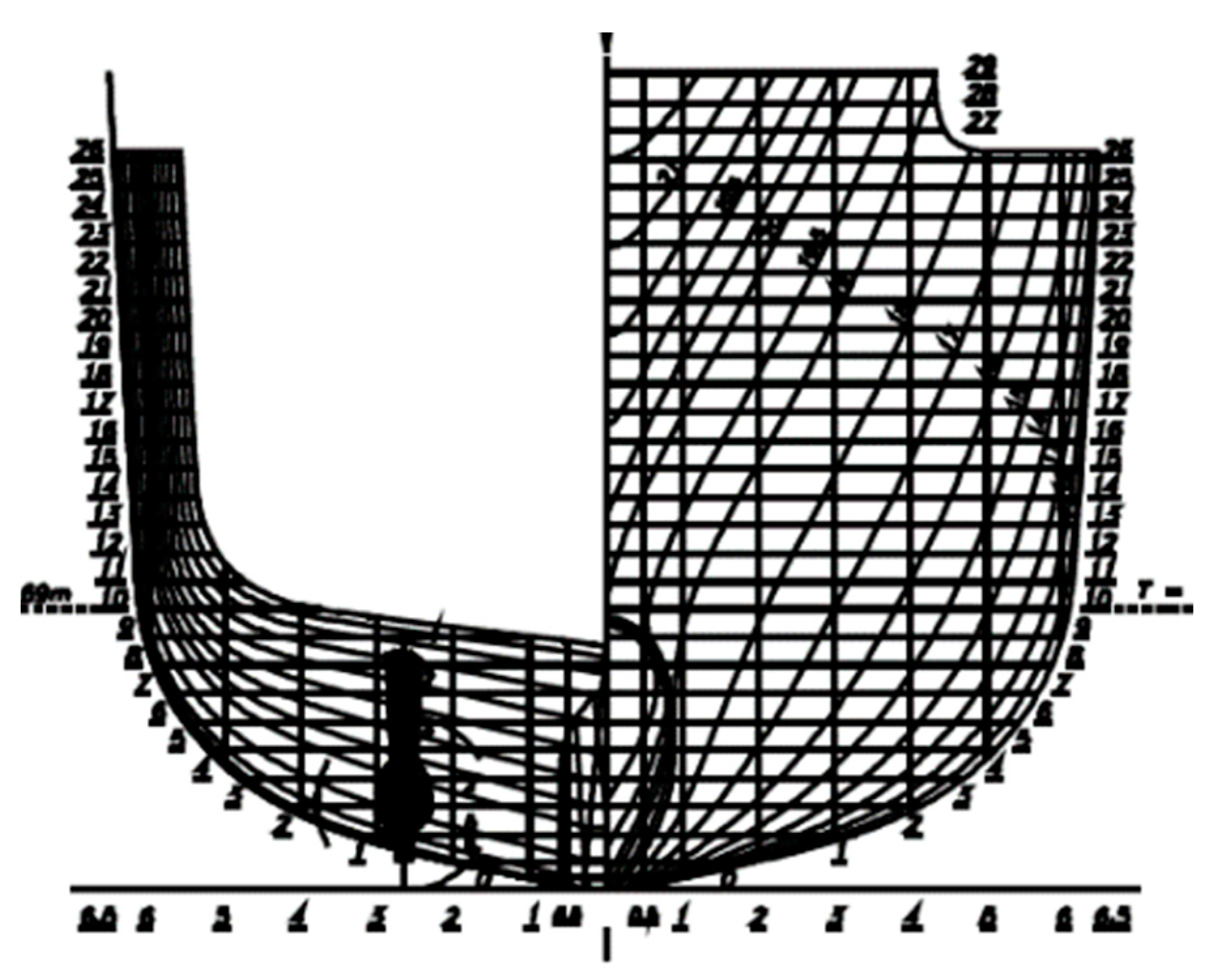
While the majority of current research centres around the analysis of commercial ship hulls, there is a noticeable lack of studies dedicated to naval hull types, as illustrated in Figure 2. This difference in attention is particularly significant considering the characteristics of naval surface ships, which often possess slenderer and faster designs compared to the more commonly studied commercial monohulls. The emphasis on commercial vessels may stem from their widespread application in the shipping industry, but overlooking naval hulls neglects the unique challenges and requirements posed by military vessels. Understanding the intricacies of naval hull types is crucial not only for optimising their performance but also for enhancing maritime security and defence capabilities. Consequently, there is a pressing need to redirect research efforts toward the comprehensive exploration of naval hulls, encompassing their hydrodynamics, structural integrity, and overall performance to fill the existing gap in our understanding of these critical maritime components. Such an inclusive approach will contribute significantly to advancing naval architecture and promoting advancements in both military and civilian marine technology.

The success of full-scale trials and the reliability of the collected data depend on numerous factors, with the quality of instrumentation emerging as a main factor. The significance of precise and sophisticated instruments cannot be overstated, as they are closely related to obtaining accurate and meaningful results. Unfortunately, conducting full-scale trials, particularly those with a scientific focus, entails substantial costs and consumes a significant amount of time. Moreover, these trials are typically conducted at the expense of diverting resources from regular ship operations, further emphasising the importance of optimising every aspect of the testing process. It is a challenging task with the absence of standardised, off-the-shelf equipment sets in the market. Consequently, each research group has to develop its own system, often utilising sensors repurposed from other applications. These sensors are connected to a controller featuring port modules. The data collected during testing are recorded on a computer, providing a comprehensive repository of measured parameters. In navigating these challenges, the quest for innovation and efficiency becomes paramount, pushing researchers to continually refine and optimise their instrumentation systems to enhance the effectiveness and accessibility of full-scale trials.

This project and the coordination of the sea trials involved researchers from CENTEC and CINAV, as well as interactions with Navy Operational Command, Navy Directorate of Ships, and the designated ship, an Offshore Patrol Vessel (OPV), whose lines plan is in Figure 2 with a corresponding image in Figure 3, operated by the Portuguese Navy with a level of sensing technology and integration that may be considered to be fully integrated digital networks of sensors.

The trials were performed in two campaigns. The data used in this work are part of wide data collection from a series of manoeuvres in waves performed at different velocities. This trial campaign took about 7 h and was performed at about 200 nautical miles from Portugal’s mainland in the Atlantic Ocean. In total, it meant at least 3 days of preparation and execution.

This work uses data from the first campaign performed, Beaufort 6, as well as Douglas 4 and the wind and sea states. During the trials, the following parameters were registered: the instantaneous World Geodetic System (WGS-84) geographical coordinates of the vessel; the speed over the ground; the course over the ground; the heading; the heave, roll, and pitch angles and the corresponding accelerations; accelerations in surge and sway; the relative and true wind vector; the engine’s rpm; the engine power and torque; the ship log speed; and the instantaneous propeller pitch.

In this ship, it is possible to have the same signal from two systems, allowing redundancy as shown in the “source” column of

Table 1. List of parameters collected during full-scale sea trials and the respective ship.

ID	Variables	Name	Signal Source	Sampling Rate (Hz)
1	u	Speed relative to water	ECDIS *	2 Hz
2	V	Speed Over Ground (SOG)	ECDIS, PorTable 10 Hz GPS unit	2 Hz/10 Hz
3	$\psi$	Heading angle	ECDIS, Portable IMU **	2 Hz/10 Hz
4	r	Rate of yaw	PMS ***, Portable IMU	10 Hz
5	$\chi$	Course Over Ground (COG)		2 Hz
6	$\xi ,\eta$	Cartesian coordinates	ECDIS, PorTable 10 Hz GPS unit	2 Hz
7	$\delta ;$	Rudder angle	PMS	10 Hz
8	WGS-84	Instant geographic coordinates	ECDIS and PorTable 10 Hz GPS unit	2 Hz/10 Hz
9	$\varphi$	Roll angle	Ship Gyro, Portable IMU	2 Hz/10 Hz
10	n	Shaft rotation (rpm)	PMS	2 Hz
11	$\theta$	Pitch angle	Ship Gyro, Portable IMU	2 Hz/10 Hz
12	$V_w,{\chi }_w$	Relative wind speed and direction	ECDIS, PMS, Portable Wi-Fi Meteo Station	2 Hz/0.5 Hz
13	$w$	Velocity of heave	Ship Gyro and Portable IMU	2 Hz/10 Hz
14	$\dot{u}$$, \dot{v}$, $\dot{w,}$	Inertial 6 DOF accelerations	Ship Gyro and Portable IMU	2 Hz/10 Hz
15	$\dot{\varphi }$$, \dot{\theta },$$\dot{\dot{\psi }}$	Inertial 6 DOF angle rate	Ship Gyro and Portable IMU	2 Hz/10 Hz

* ECDIS—Electronic Chart Display and Information System; ** IMU—Inertial Measurement Unit; *** PMS—Platform Management System.

. Part of the variables can be obtained by onboard sensors (e.g., GPS position and time, rudder angle, anemometer, SOG, COG) as redundancy to portable external sensors provided by CENTEC. The critical part is to obtain the rudder angle in real-time by digital signal (non-redundant signal).

The setup for these full-scale sea trials used the ship’s own sensor’s raw data as redundant (except for rudder deflection) to the parallel set. The sensors installed on the navy ship include the IXSea Octans Mk III Fibre Optic Gyrocompass (FOG), 10 Hz high-precision GPS unit, wireless weather station “Davis Vantage”, National Instruments cRIO 9037 with the CRio modules, and a laptop PC. The real-time monitoring and acquisition system developed by CENTEC was running on a laptop and communicating with various sensors, as presented in Figure 4.

It is possible to have part of the signals of Table 1 from the ECDIS system in this ship, which can provide data (GPS, anemometer, odometer, gyrocompass) from the navigation network (NN) in the NMEA protocol. However, this method required a separate and sequential start of data recording for each sensor; therefore, data synchronization for all the sensors is required when in the post-processing process. In addition to the onboard sensors mentioned, data acquisition during sea trials also incorporates various instruments to capture a comprehensive range of information. These may include hydrodynamic sensors like pressure sensors and accelerometers, which provide valuable insights into the ship’s interaction with waves, wave-induced motions, and the effects of propulsion systems. Furthermore, environmental sensors such as weather stations contribute essential data on wind speed, direction, and atmospheric conditions, allowing researchers to account for external factors influencing the ship’s performance. Acoustic sensors may be employed to analyse underwater noise and assess the ship’s impact on marine life. The integration of these diverse sensors enables a holistic understanding of the ship’s behaviour, aiding in the refinement of design, propulsion systems, and navigation strategies. This multidimensional data acquisition approach is crucial for enhancing the accuracy and reliability of sea trial tests, ultimately contributing to the optimization of maritime technology and safety.

4. Truncated LS-SVM

The truncated LS-SVM [11,43,44,50] was proposed to reduce the parameter uncertainty due to the noise in the training data. The truncated LS-SVM is derived based on the classical LS-SVM, introduced in Ref. [42], and it is defined as:

$$\underset{\mathit{A}}{\underbrace{\left[\begin{array}{cc}0& \overrightarrow{1}\\ \overrightarrow{1}& K(\cdot )+C^{-1}I\end{array}\right]}} \underset{\mathit{\theta }}{\underbrace{\left[\begin{array}{c}b\\ \overrightarrow{\alpha }\end{array}\right]}}=\underset{\mathit{Y}}{\underbrace{\left[\begin{array}{c}0\\ \overrightarrow{Y}\end{array}\right]}}$$

(6)

where $K(x_k\cdot x_i)=\phi {(x_k)}^T\phi (x_i)$, $i=1,\cdots ,N$ is the kernel function, and its dimensions increase dramatically with the size of training set. The large size of the kernel matrix will make the obtained parameters unstable and sensitive to noise. Therefore, the singular values decomposition is introduced:

$$\mathit{A}={\displaystyle \sum _{i=1}^n{u}_i{\sigma }_i{v}_i^T}=\mathit{U}\Sigma {\mathit{V}}^T$$

(7)

Then, substituting into Equation (6) gives:

$$\mathit{\theta }={\left(\mathit{U}\Sigma {\mathit{V}}^T\right)}^{-1}Y={\displaystyle \sum _{i=1}^n\frac{v_i{u_i}^T}{{\sigma }_i}}Y$$

(8)

Assume that the output data, Y, is populated with noise $\delta y$, then the error of the estimated parameter with the noise can be obtained:

$$\delta \mathit{\theta }=\widehat{\mathit{\theta }}-\mathit{\theta }={\displaystyle \sum _{i=1}^n\frac{v_i{u_i}^T}{{\sigma }_i}}\delta y$$

(9)

With the Picard condition [51], the error in the output data can be magnified dramatically when the singular values are small. It can dominate the solutions; therefore, to obtain a robust estimation, it is preferred to neglect the smaller singular values in the matrix Ʃ. The truncated matrix is defined as:

$${\mathit{A}}_r={\mathit{U}}_r{\Sigma }_r{{\mathit{V}}_r}^T$$

(10)

The constant parameter, r, indicates the number of singular values to be kept for matrix A. In this paper, the L-curve [52] is used to search for the optimal value.

The error propagation matrix is used to quantify the noise effect, indicating that the random measurement errors in the output, y, propagate to the identified parameters. It is defined as:

$${\mathit{V}}_{\widehat{\theta }}=\left[\frac{\partial \widehat{\mathit{\theta }}}{\partial y}\right]{\mathit{V}}_y{\left[\frac{\partial \widehat{\mathit{\theta }}}{\partial y}\right]}^T$$

(11)

The standard error, ${\sigma }_{\widehat{\theta }}$, is the square root of the diagonal of the error propagation matrix. The confidence intervals are given:

$$\widehat{\theta }-t_{1-a/2}{\sigma }_{\widehat{\theta }}\le \theta \le \widehat{\theta }+t_{1-a/2}{\sigma }_{\widehat{\theta }}$$

(12)

where ${\sigma }_{\widehat{\theta }}$ is the standard error, which can be calculated based on the error propagation matrix. $1-a$ is the desired confidence level, and t is the Student t-statistic.

5. Hydrodynamic Coefficient Estimation and Validation

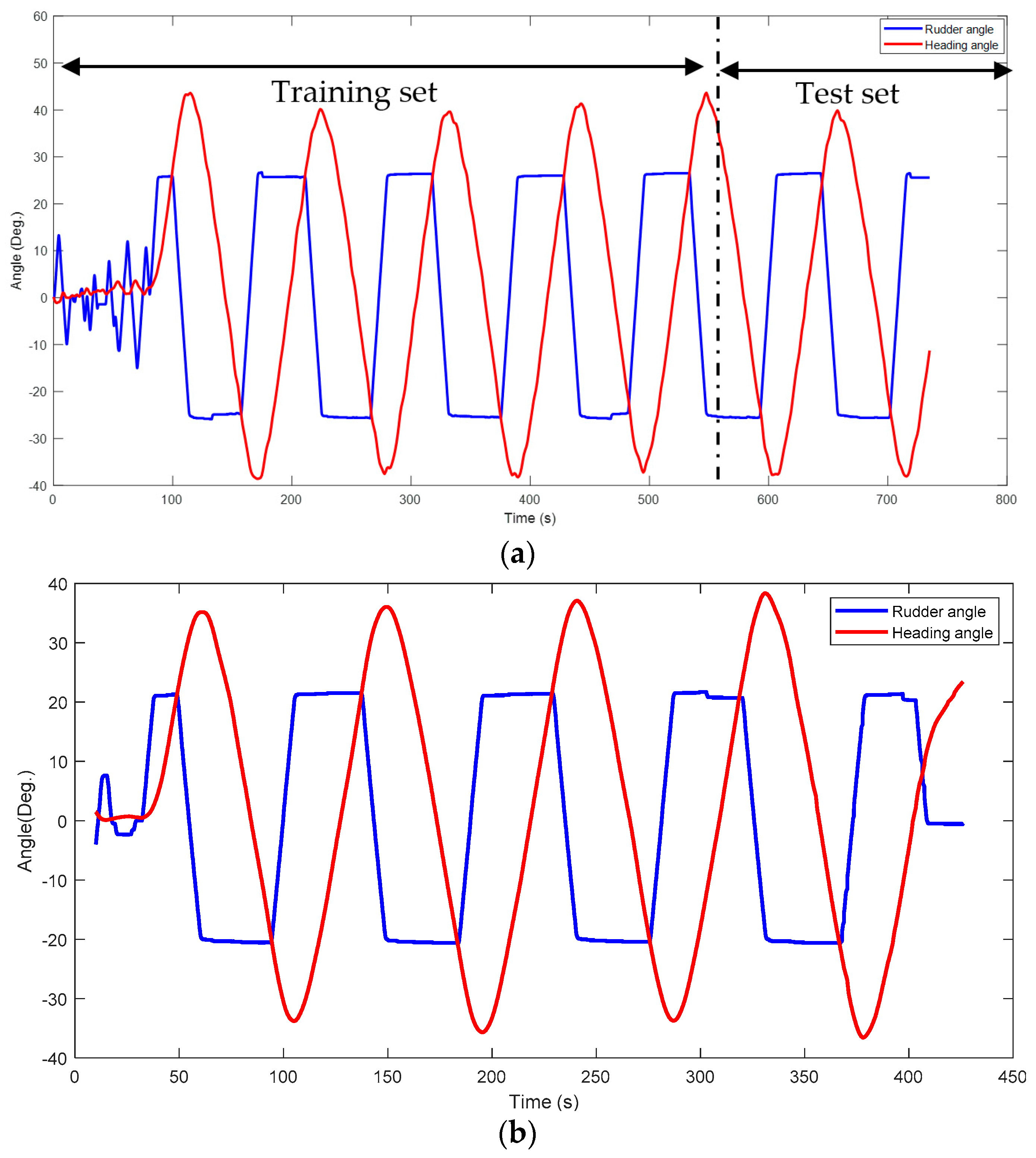
The hydrodynamic coefficients of the manoeuvring model will be identified, and the uncertainty due to the noise will be discussed. The sea trial, 25°–25° zigzag, is used for the training set, where the last portion of data (t = 540–740 s) and a new zigzag 20°–20° is kept as the validation, as presented in Figure 5. There are four rudder executions in the test set, and the ship is in the stage of stable steering motions. During the test, the rudder angle can change from the port to the starboard; therefore, the response of the ship can be activated and can provide rich information compared to the turning circle tests, where the rudder angle is a constant value during the tests. The main reason for choosing the zigzag test as the training data is that it can provide more information compared with the turning tests. The turning test can be considered as one constant step signal input for the ship at starboard or port; however, the zigzag can activate the dynamic motion of the ship on both sides with a constant rudder angle input signal.

In this section, the effect of the sampling rate of sea trials on the estimated parameters will be discussed. Therefore, the yaw angle measured during the zigzag test is transformed into the frequency domain using the Fast Fourier Transform (FFT), as presented in Figure 6. It can be noted that the predominant frequency of the yaw motion of the navy ship during the 25°–25° zigzag manoeuvre is 0.009 Hz. This can also be observed in Figure 5a, which shows that the vessel requires approximately 108 s to complete one cycle of oscillation. The maximum frequency is 0.03 Hz.

The significance of the sampling rate for the success of parameter estimation is widely acknowledged. Typically, the sampling rate is determined by the highest frequency component of the signal of interest. Generally, a sampling rate that is 10 times greater than the highest frequency component of the signal of interest is selected in practical applications. Consequently, this paper selects 14 sampling rates ranging from 0.2 Hz to 5 Hz.

The hydrodynamic coefficients will be identified based on the resampled training data. The input matrix, X, contains the hydrodynamic terms as indicated in Equation (3). Therefore, the input variables for the surge, sway, and yaw models are defined as: $X_{surge}=\left[u_i^2,v_i{r}_i,{\delta }_i^2\right]$, $X_{sway}=\left[v_i,r_i,v_i^2{r}_i,{\delta }_i\right]$, and $X_{yaw}=\left[v_i,r_i,v_i^2{r}_i,{\delta }_i\right]$, where i is the number of the data points. In order to implement using LS-SVM as presented in Equation (6), the first step is to build the kernel matrix, $K(x_k\cdot x_i)=\phi {(x_k)}^T\phi (x_i)$, $i=1,\cdots ,N$. In this paper, the linear kernel function will be used; therefore, $K(x_k\cdot x_i)={x_k}^T{x}_i$, $i=1,\cdots ,N$. The output variables for the surge, sway, and yaw models are equal to the left-hand term of Equation (1). The corresponding parameter uncertainty is calculated using the above Equation (12). Since the size of the training set is much larger than the hydrodynamic coefficients to be identified, therefore, the Student t-statistic is chosen: 1.96 for the 95% confidence intervals, and 1.28 for 80% confidence intervals.

The identified hydrodynamic coefficients of the surge model are given in Figure 7. There are only three non-dimensional parameters ($X_{uu}$, $X_{vr}$, and $X_{\delta \delta }$) to be determined. The original training set is resampled using 14 different sampling rates, ranging from 0.2 Hz to 5 Hz, where the 10 times highest frequency component (0.3 Hz) of the yaw motion is also included. It can be observed that the hydrodynamic coefficients converge with the increase in the sampling rate. The parameter, $X_{uu}$, increases largely with the sampling rate and arrives at a stage of slow increase around the 3 Hz sampling rate. The value of the nondimensional parameter, $X_{uu}$, is −0.0044.

From the figure, it can be observed that the large sampling rate has a significant effect on the identified value, but slightly reduces the parameter uncertainty. The nondimensional parameter, $X_{vr}$, decreases with the sampling rate and converges to −0.11. When the sampling rate is 2 Hz, it enters the stable stage, and the value changes slightly even if the sampling rate increases a lot. The parameter uncertainty also decreases with the sampling rate. For the above two parameters, they do not converge when the 10 times highest frequency component (0.3 Hz) is used. For the nondimensional parameter, $X_{\delta \delta }$, it can converge to the final value, −0.019, at the 0.3 Hz sampling rate. However, the parameter uncertainty can still be improved when using a large sampling rate, as indicated in Figure 7.

The identified nondimensional hydrodynamic parameters for the sway model are presented in Figure 8. It can be found that all the parameters ($Y_v$, $Y_r$, $Y_{vvr}$, and $Y_{\delta }$) converge to the final values ($Y_v$ = −0.199, $Y_r$ = 0.147, $Y_{vvr}$ = 0.256, and $Y_{\delta }$ = −0.087) with the increase of the sampling rate, and the corresponding parameter uncertainty is also decreased. It is worth mentioning that the linear hydrodynamic coefficients ($Y_v$, $Y_r$, and $Y_{\delta }$) converged fast with a small sampling rate.

When the sampling rate is 0.3 Hz, the identified values are already very close to the final values ($Y_v$ = −0.206, $Y_r$ = 0.148, and $Y_{\delta }$ = −0.0859), but it is not the same case for the nonlinear hydrodynamic coefficient $Y_{vvr}$ ($Y_{vvr}$ = 0.09). $Y_v$ is the hydrodynamic sway force when the sway velocity is one, and it should be a negative value considering the physical property. Therefore, the linear hydrodynamic coefficients can be identified using the recommended sampling rate (10 times the highest frequency component), but for the nonlinear hydrodynamic coefficients, it is recommended to increase the sampling rate; in this paper, the minimum of 3 Hz sampling rate is recommended for the identification of nonlinear hydrodynamic coefficient, $Y_{vvr}$.

The same pattern can be observed for the identified nondimensional hydrodynamic parameters in the yaw model, as given in Figure 9. All parameters ($N_v$, $N_r$, $N_{vvr}$, and $N_{\delta }$) converge to the final values ($N_v$ = 0.042, $N_r$ = −0.002, $N_{vvr}$ = −0.0395, and $N_{\delta }$ = −0.0149). $N_r$ is the hydrodynamic yaw moment when the yaw rate is one, and it should be a negative small value considering the physical property. When the sampling rate is 0.3 Hz, the identified values of the linear hydrodynamic coefficients are very close to the final values, ($N_v$ = 0.043, $Y_r$ = −0.002, and $Y_{\delta }$ = 0.0148), which indicates that the training set contains enough information to activate the response of linear yaw motion.

However, for the nonlinear hydrodynamic coefficient, $N_{vvr}$, the identified value is $N_{vvr}$ = −0.014, which has a large difference from the final value. Therefore, more information is required for the training set. The sampling rate of around 3 Hz is recommended for the estimation of the nonlinear hydrodynamic coefficient, $N_{vvr}$. For all the parameters, the large sampling rate can significantly reduce uncertainty.

From the above analysis, it can be concluded that a sampling rate 10 times higher than the highest frequency component of the signal of interest is the minimum recommended sampling rate for the parameter estimation of ship manoeuvring models. To some extent, it can be used to provide an estimation for the linear hydrodynamic coefficients, but the obtained results have significant parameter uncertainty. However, it is not recommended to be used for the estimate of the nonlinear parameters. To obtain a robust estimation for the most nonlinear hydrodynamic coefficients, it is recommended to measure the data during the sea trials at more than the 3–5 Hz sampling rate.

In the last part, the validation of the obtained nondimensional hydrodynamic coefficients will be carried out using the test set. The nondimensional hydrodynamic coefficients are given in

Table 2. The estimated nondimensional hydrodynamic coefficients and uncertainty with the 5 Hz sampling rate.

Coef.	Values	Deviation (%)	Coef.	Values	Deviation (%)
$X_{uu}$	−1.99 × 10−3	7.10	$Y_{\delta }$	−8.68 × 10−2	0.48
$X_{vr}$	−1.12 × 10−1	1.35	$N_v$	4.22 × 10−2	0.62
$X_{\delta \delta }$	−1.88 × 10−2	3.95	$N_r$	−1.97 × 10−3	5.49
$Y_v$	−1.99 × 10−1	0.83	$N_{vvr}$	−3.95 × 10−2	6.35
$Y_r$	1.47 × 10−1	0.46	$N_{\delta }$	1.49 × 10−2	0.44
$Y_{vvr}$	2.56 × 10−1	6.19

, and they are estimated based on the data measured using a 5 Hz sampling rate.

The manoeuvring models specified in Equation (5) will be employed, utilising nondimensional hydrodynamic coefficients to compute hydrodynamic forces and moments on the right side of the equations. The left side of the equations is determined directly through the accelerations recorded during the sea trials. The anticipated surge, lateral forces, and yaw moments are depicted in Figure 10. The figure demonstrates that the predicted forces and moments align well with the experimental results. The coefficients of determination (R2) are 0.8505, 0.9960, and 0.9912, respectively. Figure 11 illustrates the validation of the derived manoeuvring models through a novel zigzag 20°–20° test. The predictive results exhibit strong agreement with the experimental data, with coefficients of determination (R2) of 0.71, 0.94, and 0.91, respectively.

6. Conclusions

This paper examines the impact of the sampling rate employed during sea trials on the estimation of nondimensional hydrodynamic coefficients using truncated LS-SVM. The 25°–25° zigzag test was conducted with a naval vessel, and the sea trial data were partitioned into two sets: one for training the model and another reserved for validation. To explore the influence of the sampling rate, the training set underwent offline resampling at 14 different rates, ranging from 0.2 Hz to 5 Hz, encompassing the recommended sampling rate of 10 times the highest frequency component of the signal of interest.

The results reveal an important impact of the sea trial sampling rate on the estimation of hydrodynamic parameters, and the conclusions can be summarised as:

• As the sampling rate increases, the identified hydrodynamic coefficients converge towards constant values. Notably, a higher sampling rate can significantly reduce parameter uncertainty.
• The rate of 10 times the highest frequency component is deemed the minimum recommended sampling rate for estimating linear hydrodynamic coefficients, and it results in a somewhat larger parameter uncertainty.
• Consequently, for robust estimation of both linear and most nonlinear parameters, a sampling rate above 3–5 Hz is recommended, with these values contingent on the highest frequency component of the signal. It also should be noted that some nonlinear hydrodynamic coefficients do not converge even when the sampling rate is larger than 5 Hz.
• The outcomes are employed to predict surge, sway forces, and yaw moment, demonstrating good agreement with experimental data.