Discrimination of Internal Solitary Waves from Coarse Time Resolution Field Observational Data by Using Wavelet Analysis
Abstract
1. Introduction
2. Data and Methods
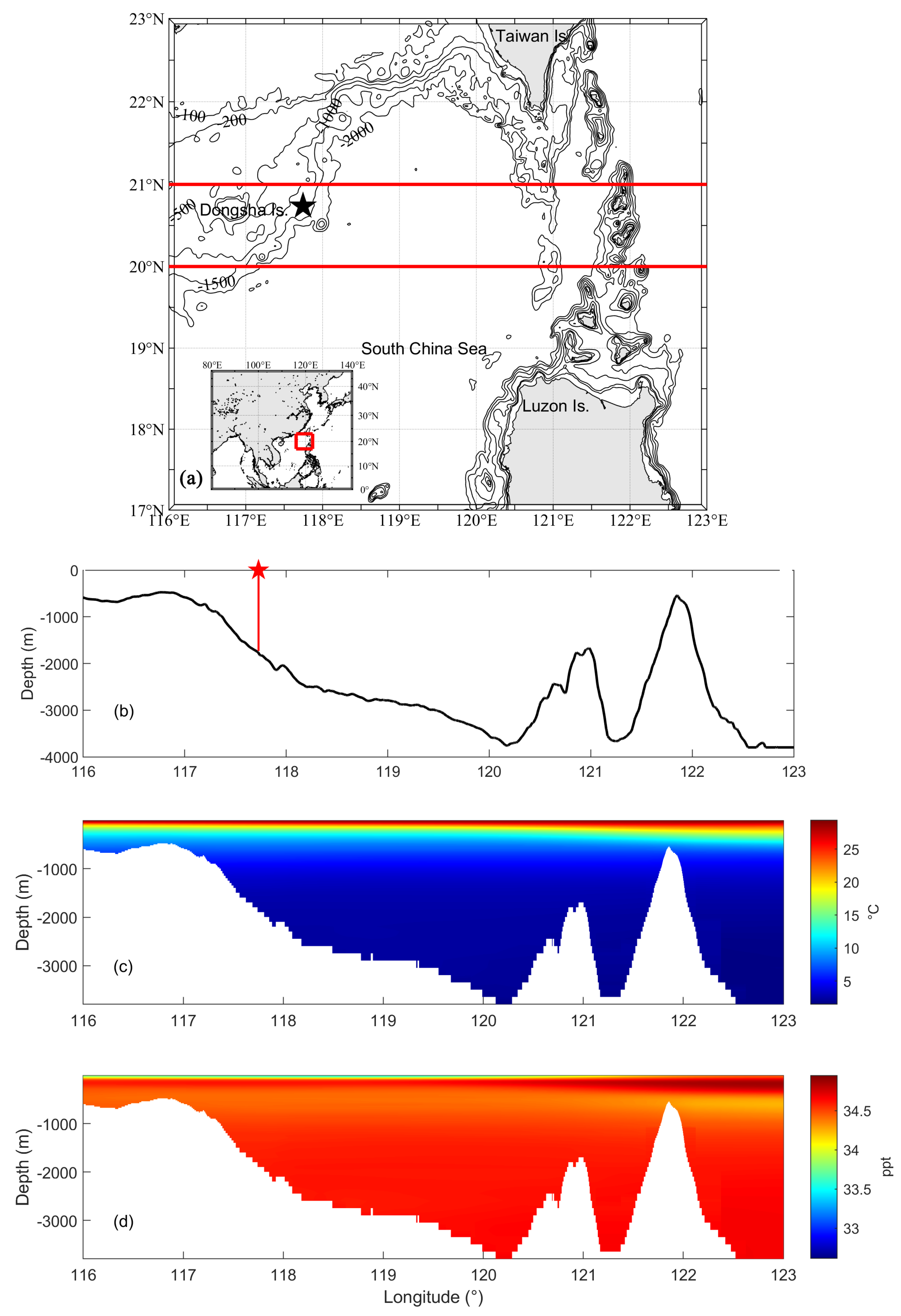
2.1. Field Observation
2.2. Continuous Wavelet Transformation
2.3. Setup of the Numerical Model
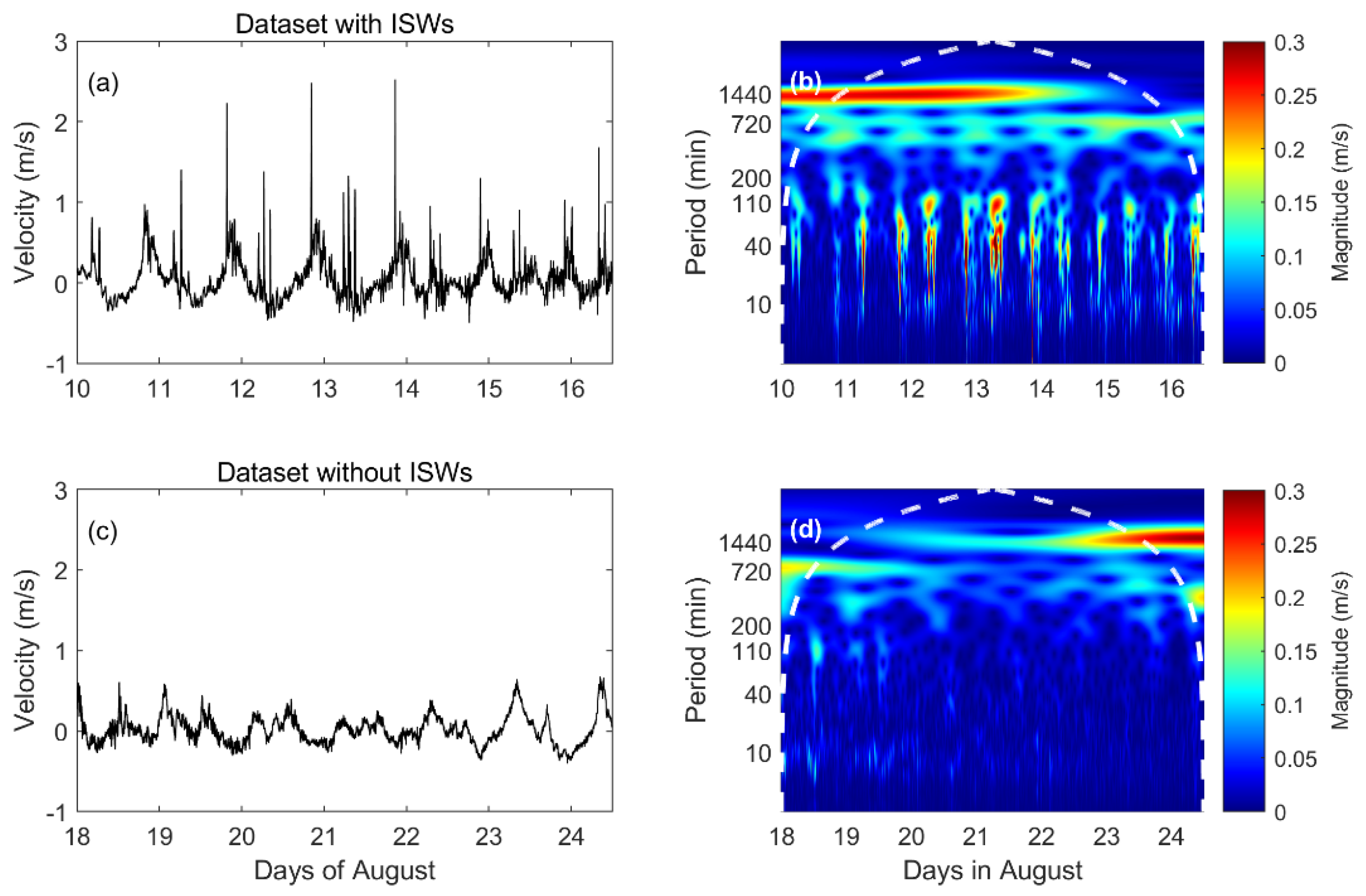
3. Results
- (1)
- Selection of Velocity Time−Series Data
- (2)
- Reduction of Wavelet Components
- (3)
- Hard Threshold Application
- (4)
- Signal Reconstruction
- (5)
- Peak Value Localization
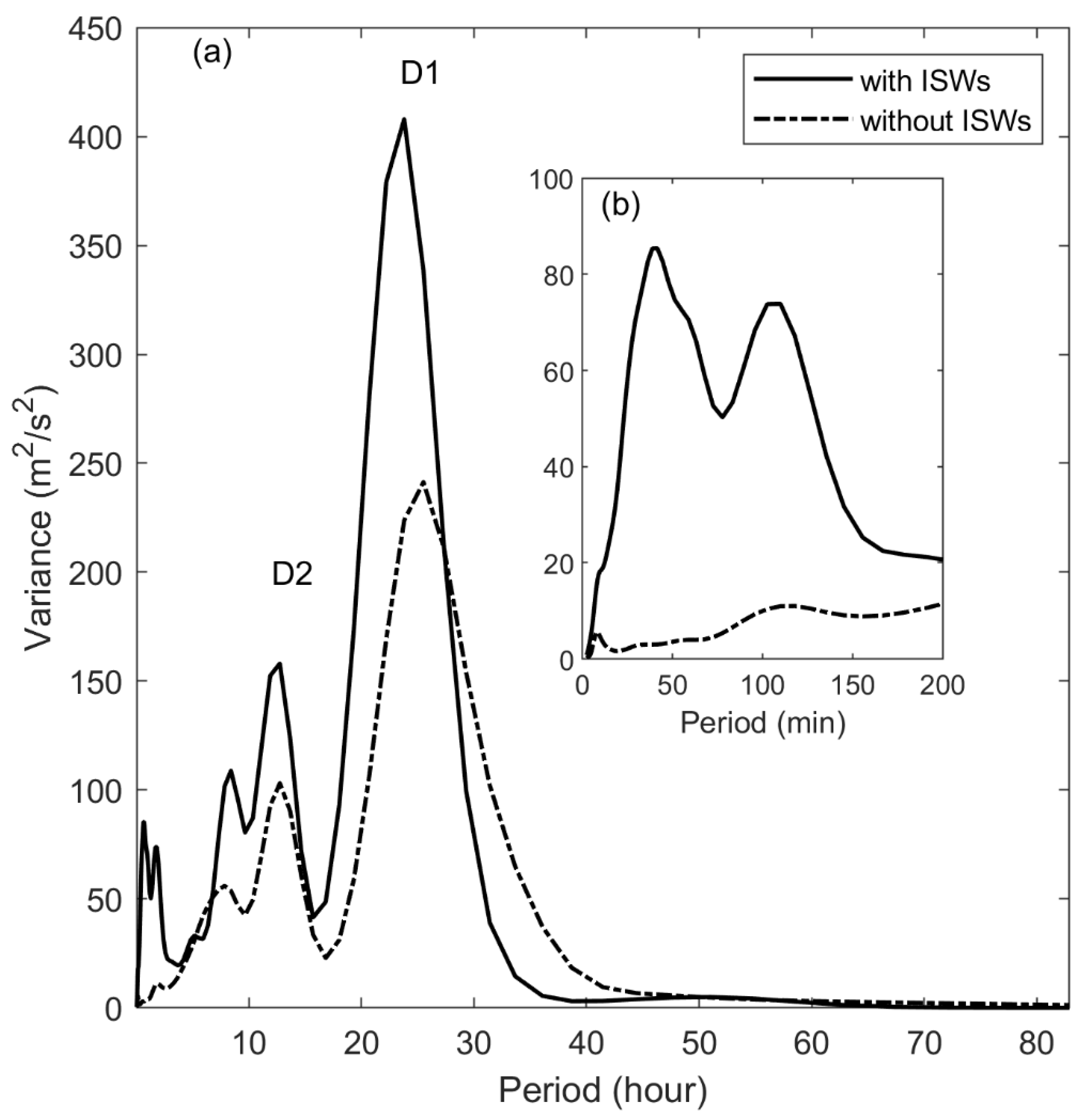
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cai, S.Q.; Gan, Z.J.; Long, X.M. Some characteristics and evolution of the internal soliton in the northern South China Sea. Chin. Sci. Bull. 2002, 47, 21–27. [Google Scholar] [CrossRef]
- Alford, M.; Peacock, T.; Mackinnon, J.; Nash, J.; Buijsman, M.; Centuroni, L.; Chao, S.; Chang, M.; Farmer, D.; Fringer, O.; et al. The formation and fate of internal waves in the South China Sea. Nature 2015, 521, 65–69. [Google Scholar] [CrossRef]
- Huang, X.; Chen, Z.; Zhao, W.; Zhang, Z.; Zhou, C.; Yang, Q.; Tian, J. An extreme internal solitary wave event observed in the northern South China Sea. Sci. Rep. 2016, 6, 30041. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, Q.; Xiong, X.; Yuan, Y.; Xie, H.; Guo, Y.; Yu, L.; Yun, S. Dynamic and Statistical Features of Internal Solitary Waves on the Continental Slope in the Northern South China Sea Derived From Mooring Observations. J. Geophys. Res. Oceans 2019, 124, 4078–4097. [Google Scholar] [CrossRef]
- Ramp, S.R.; Park, J.H.; Yang, Y.J.; Bahr, F.; Jeon, C. Latitudinal Structure of Solitons in the South China Sea. J. Phys. Oceanogr. 2019, 49, 1747–1767. [Google Scholar] [CrossRef]
- Xu, J.; Xie, J.; Chen, Z.; Cai, S.; Long, X. Enhanced mixing induced by internal solitary waves in the South China Sea. Cont. Shelf Res. 2012, 49, 34–43. [Google Scholar] [CrossRef]
- Cai, S.; Long, X.; Gan, Z. A method to estimate the forces exerted by internal solitons on cylindrical piles. Ocean Eng. 2003, 30, 673–689. [Google Scholar] [CrossRef]
- Xie, J.; Xu, J.; Cai, S. A numerical study of the load on cylindrical piles exerted by internal solitary waves. J. Fluids Struct. 2011, 27, 1252–1261. [Google Scholar] [CrossRef]
- Hu, J.; Kawamura, H.; Hong, H.; Kobashi, F.; Wang, D. 3≈6 Months Variation of Sea Surface Height in the South China Sea and Its Adjacent Ocean. J. Oceanogr. 2001, 57, 69–78. [Google Scholar] [CrossRef]
- Wu, R.; Li, C. Upper ocean response to the passage of two sequential typhoons. Deep Sea Res. Part I 2018, 132, 68–79. [Google Scholar] [CrossRef]
- Pun, I.-F.; Chan, J.; Lin, I.; Chan, K.; Price, J.; Ko, D.; Lien, C.; Wu, Y.; Huang, H. Rapid Intensification of Typhoon Hato (2017) over Shallow Water. Sustainability 2019, 11, 3709. [Google Scholar] [CrossRef]
- Chen, G.; Hou, Y.; Chu, X. Mesoscale eddies in the South China Sea: Mean properties, spatiotemporal variability, and impact on thermohaline structure. J. Geophys. Res. 2011, 116, C06018. [Google Scholar] [CrossRef]
- Nan, F.; Xue, H.; Yu, F. Kuroshio intrusion into the South China Sea: A review. Prog. Oceanogr. 2015, 137, 314–333. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, J.; Qiu, B.; Zhao, P.; Chang, D.; Wu, D.; Wan, X. Observation 3D structure, generation and dissipation of oceanic mesoscale eddies in the South China Sea. Sci. Rep. 2016, 6, 24349. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Liu, Z.; Zhao, Y.; Wang, M. Seasonal variability of tides in the deep northern South China Sea. Sci. China Earth Sci. 2019, 62, 671–683. [Google Scholar] [CrossRef]
- Zu, T.; Gan, J.; Erofeeva, S.Y. Numerical study of the tide and tidal dynamics in the South China Sea. Deep Sea Res. Part I 2008, 55, 137–154. [Google Scholar] [CrossRef]
- Lai, Z.G.; Jin, G.Z.; Huang, Y.M.; Chen, H.Y.; Shang, X.D.; Xiong, X.J. The Generation of Nonlinear Internal Waves in the South China Sea: A Three−Dimensional, Nonhydrostatic Numerical Study. J. Geophys. Res. 2019, 124, 8949–8968. [Google Scholar] [CrossRef]
- Lamb, K.G.; Lien, R.-C.; Diamessis, P.J. Internal Solitary Waves and Mixing. In Encyclopedia of Ocean Sciences; Academic Press: Cambridge, MA, USA, 2019; pp. 533–541. [Google Scholar]
- Huang, X.D.; Zhang, Z.W.; Zhang, X.J.; Qian, H.B.; Zhao, W.; Tian, J.W. Impacts of a Mesoscale Eddy Pair on Internal Solitary Waves in the Northern South China Sea revealed by Mooring Array Observations. J. Phys. Oceanogr. 2017, 47, 1539–1554. [Google Scholar] [CrossRef]
- Jackson, C. Internal wave detection using the moderate resolution Imaging spectroradiometer (MODIS). J. Geophys. Res. 2007, 112, C11012. [Google Scholar] [CrossRef]
- Zhao, Z. Internal tide radiation from the Luzon Strait. J. Geophys. Res. Oceans 2014, 119, 5434–5448. [Google Scholar] [CrossRef]
- Giese, G.S.; Hollander, R.B.; Fancher, J.E.; Giese, B.S. Evidence of coastal seiche excitation by tide-generated internal solitary waves. Geophys. Res. Lett. 1982, 9, 1305–1308. [Google Scholar] [CrossRef]
- Giese, G.S.; Hollander, R.B. The relationship between coastal seiches at Palawan Island and tide-generated internal waves in the Sulu Sea. J. Geophys. Res. 1987, 92, 5151–5156. [Google Scholar]
- Giese, G.S.; Chapman, D.C.; Black, P.G.; Fornshell, J.A. Causation of large-amplitude coastal seiches on the Caribbean coast of Puerto Rico. J. Phys. Oceanogr. 1990, 20, 1449–1458. [Google Scholar] [CrossRef][Green Version]
- Zhang, X.; Huang, X.; Zhang, Z.; Zhou, C.; Tian, J.; Zhao, W. Polarity Variations of Internal Solitary Waves over the Continental Shelf of the Northern South China Sea: Impacts of Seasonal Stratification, Mesoscale Eddies, and Internal Tides. J. Phys. Oceanogr. 2018, 48, 1349–1365. [Google Scholar] [CrossRef]
- Zhang, S.; Alford, M.; Mickett, J. Characteristics, generation and mass transport of nonlinear internal waves on the Washington continental shelf. J. Geophys. Res. Oceans 2015, 120, 741–758. [Google Scholar] [CrossRef]
- Cui, Z.; Liang, C.; Lin, F.; Jin, W.; Ding, T.; Wang, J. The observation and analysis of the internal solitary waves by mooring system in the Andaman Sea. J. Mar. Sci. 2020, 38, 16–25. [Google Scholar]
- Huang, S.; Huang, X.; Zhao, W.; Chang, Z.; Xu, X.; Yang, Q.; Tian, J. Shear Instability in Internal Solitary Waves in the Northern South China Sea Induced by Multiscale Background Processes. J. Phys. Oceanogr. 2022, 52, 2975–2994. [Google Scholar] [CrossRef]
- Bai, Y.; Song, H.; Guan, Y.; Yang, S. Estimating depth of polarity conversion of shoaling internal solitary waves in the northeastern South China Sea. Cont. Shelf Res. 2017, 143, 9–17. [Google Scholar] [CrossRef]
- Gong, Q.; Chen, L.; Diao, Y.; Xiong, X.; Sun, J.; Lv, X. On the identification of internal solitary waves from moored observations in the northern South China Sea. Sci. Rep. 2023, 13, 3133. [Google Scholar] [CrossRef]
- Shaw, P.; Ko, D.; Chao, S. Internal solitary waves induced by flow over a ridge: With applications to the northern South China Sea. J. Geophys. Res. 2009, 114, C02019. [Google Scholar]
- Xing, J.; Davies, A. Nonlinear effects of internal tides on the generation of tidal mean flow at the Hebrides shelf edge. Geophys. Res. Lett. 2001, 28, 3939–3942. [Google Scholar] [CrossRef]
- Van Haren, H. On the nature of internal wave spectra near a continental slope. Geophys. Res. Lett. 2002, 29, 121615. [Google Scholar] [CrossRef]
- Van Haren, H. Current spectra under varying stratification conditions in the central North Sea. J. Sea Res. 2004, 51, 77–91. [Google Scholar] [CrossRef]
- Van Haren, H. Tidal and near-inertial peak variations around the diurnal critical latitude. Geophys. Res. Lett. 2005, 32, L23611. [Google Scholar] [CrossRef]
- Carter, G.; Gregg, M. Persistent near-diurnal internal waves observed above a site of M2 barotropic-to-baroclinic conversion. J. Phys. Oceanogr. 2006, 36, 1136–1147. [Google Scholar] [CrossRef]
- Torrence, C.; Gilbert, P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Detto, M.; Joseph, W.; Calderón, O.; Helene, C. Resource acquisition and reproductive strategies of tropical forest in response to the El Niño–Southern Oscillation. Nat. Commun. 2018, 9, 913. [Google Scholar] [CrossRef]
- Liu, P.C. Wavelet spectrum analysis and ocean wind waves. Wavel. Geophys. 1994, 4, 151–166. [Google Scholar]
- Hawkins, J.; Warn−Varnas, A.; Christov, I. Fourier, scattering, and wavelet transforms: Application to internal gravity waves with comparisons to linear tidal data. In Nonlinear Time Series Analysis in the Geosciences; Donner, R., Barbosa, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 112, pp. 223–244. [Google Scholar]
- Xu, J.; He, Y.; Chen, Z.; Zhan, H.; Wu, Y.; Xie, J.; Shang, X.; Ning, D.; Fang, W.; Cai, S. Observations of different effects of an anti-cyclonic eddy on internal solitary waves in the South China Sea. Prog. Oceanogr. 2020, 188, 102422. [Google Scholar] [CrossRef]
- Moradi, M. Wavelet transform approach for denoising and decomposition of satellite-derived ocean color time-series: Selection of optimal mother wavelet. Adv. Space Res. 2022, 69, 2724–2744. [Google Scholar] [CrossRef]
- Daubechies, I.; Paul, T. Time-frequency localisation operators: A geometric phase space approach II. The use of dilations and translations. Inverse Probl. 1988, 4, 661–680. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S.C. Higher-order properties of analytic wavelets. IEEE Trans. Signal Process. 2009, 57, 146–160. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S.C. Generalized Morse wavelets as a superfamily of analytic wavelets. IEEE Trans. Signal Process. 2012, 60, 6036–6041. [Google Scholar] [CrossRef]
- Marshall, J.; Hill, C.; Perelman, J.; Adcroft, A. Hydrostatic, quasi-hydrostatic, and nonhydrostatic ocean modeling. J. Geophys. Res. 1997, 102, 5733–5752. [Google Scholar] [CrossRef]
- Xie, X.; Liu, Q.; Zhao, Z.; Shang, X.; Cai, S.; Wang, D.; Chen, D. Deep sea currents driven by breaking internal tides on the continental slope. Geophys. Res. Lett. 2018, 45, 6160–6166. [Google Scholar] [CrossRef]
- Stanley, J.; Holman, R.A.; Barth, J.A.; Suanda, S.H. Shore−Based Video Observations of Nonlinear Internal Waves across the Inner Shelf. J. Atmos. Ocean. Tech. 2014, 31, 714–728. [Google Scholar]
- Lien, R.-C.; D’Asaro, E.A.; Henyey, F. High–Frequency Internal Waves on the Oregon Continental Shelf. J. Phys. Oceanogr. 2007, 37, 1956–1967. [Google Scholar]




| Date | 10 August | 11 August | 12 August | 13 August | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ISW-induced velocity | 0.66 | 0.87 | 1.71 | 1.92 | 2.29 | 1.36 | 1.81 | 1.63 | 2.27 | 1.02 |
| Reconstructed velocity | 0.65 | 0.84 | 1.68 | 1.87 | 2.18 | 1.19 | 1.76 | 1.47 | 1.62 | 0.83 |
| Ratio of ISW-induced velocity/reconstructed velocity (%) | 98.0 | 96.9 | 98.0 | 97.4 | 95.1 | 87.8 | 97.3 | 90.2 | 71.4 | 81.5 |
| Date | 14 August | 15 August | 16 August | Mean Ratio (%) | ||||||
| ISW−induced velocity | 1.02 | 0.91 | 1.11 | 0.74 | 1.05 | 1.03 | 0.69 | 1.85 | 0.94 | |
| Constructed velocity | 0.81 | 0.81 | 1.05 | 0.67 | 0.98 | 0.93 | 0.69 | 1.67 | 0.86 | |
| Ratio of ISW−induced velocity/reconstructed velocity (%) | 80.0 | 88.9 | 94.6 | 90.8 | 93.3 | 90.5 | 100 | 90.5 | 90.9 | 91.4 |
| Date | 22 July | 23 July | 24 July | 25 July | 26 July | Mean Ratio (%) | |||
| ISW-induced velocity | 0.14 | 0.25 | 0.2 | 0.18 | 0.23 | 0.32 | 0.12 | 0.19 | |
| Reconstructed velocity | - | 0.25 | 0.2 | 0.12 | 0.11 | 0.18 | 0.14 | 0.21 | |
| Ratio of ISW-induced velocity/reconstructed velocity (%) | - | 100.0 | 100.0 | 66.7 | 47.8 | 56.3 | 116.7 | 110.5 | 85.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Chen, S.; Gong, Y.; Chen, Z.; Cai, S.; Li, D. Discrimination of Internal Solitary Waves from Coarse Time Resolution Field Observational Data by Using Wavelet Analysis. J. Mar. Sci. Eng. 2024, 12, 307. https://doi.org/10.3390/jmse12020307
Xu J, Chen S, Gong Y, Chen Z, Cai S, Li D. Discrimination of Internal Solitary Waves from Coarse Time Resolution Field Observational Data by Using Wavelet Analysis. Journal of Marine Science and Engineering. 2024; 12(2):307. https://doi.org/10.3390/jmse12020307
Chicago/Turabian StyleXu, Jiexin, Shaomin Chen, Yankun Gong, Zhiwu Chen, Shuqun Cai, and Daning Li. 2024. "Discrimination of Internal Solitary Waves from Coarse Time Resolution Field Observational Data by Using Wavelet Analysis" Journal of Marine Science and Engineering 12, no. 2: 307. https://doi.org/10.3390/jmse12020307
APA StyleXu, J., Chen, S., Gong, Y., Chen, Z., Cai, S., & Li, D. (2024). Discrimination of Internal Solitary Waves from Coarse Time Resolution Field Observational Data by Using Wavelet Analysis. Journal of Marine Science and Engineering, 12(2), 307. https://doi.org/10.3390/jmse12020307







