Abstract
Predicting earthquakes through reasonable methods can significantly reduce the damage caused by secondary disasters such as tsunamis. Recently, machine learning (ML) approaches have been employed to predict laboratory earthquakes using stick-slip dynamics data obtained from sheared granular fault experiments. Here, we adopt the combined finite-discrete element method (FDEM) to simulate a two-dimensional sheared granular fault system, from which abundant fault dynamics data (i.e., displacement and velocity) during stick-slip cycles are collected at 2203 “sensor” points densely placed along and inside the gouge. We use the simulated data to train LightGBM (Light Gradient Boosting Machine) models and predict the gouge-plate friction coefficient (an indicator of stick-slips and the friction state of the fault). To optimize the data, we build the importance ranking of input features and select those with top feature importance for prediction. We then use the optimized data and their statistics for training and finally reach a LightGBM model with an acceptable prediction accuracy (R2 = 0.94). The SHAP (SHapley Additive exPlanations) values of input features are also calculated to quantify their contributions to the prediction. We show that when sufficient fault dynamics data are available, LightGBM, together with the SHAP value approach, is capable of accurately predicting the friction state of laboratory faults and can also help pinpoint the most critical input features for laboratory earthquake prediction. This work may shed light on natural earthquake prediction and open new possibilities to explore useful earthquake precursors using artificial intelligence.
1. Introduction
Reliable prediction of earthquakes, a long-standing goal of earthquake research, is a prerequisite for reducing losses from earthquake disasters. Although many efforts have been made in the past, earthquake prediction is still in its infancy due to the inherent complexity of the underlying earthquake physics. In recent years, artificial intelligence, especially machine learning (ML), has become the mainstream tool for data analysis in various fields. The ML approaches can explore inner patterns from large data volumes and fit nonlinear mapping relationships between different variables in high dimensions. While various earthquake sources and propagation models have been developed, the intricate physics from earthquake nucleation to dynamic rupture poses tremendous challenges for accurate and reliable modelling and forecasting. In particular, integrating various heterogeneous fault data and extracting complex hidden patterns beyond simplified physical laws demands advanced data-driven approaches. Data collected from natural earthquakes typically includes seismic catalogues, earthquake waveforms, surface deformation, electromagnetic fields, temperature fields, gravity fields, and observations of changes in underground fluids and geochemical compositions [1]. Therefore, the ML algorithms, with a solid ability to capture underlying unknown nonlinear patterns, may thus be appropriate for earthquake prediction exploration.
There is evidence that machine learning has been used for the prediction of disasters such as earthquakes and tsunamis. Asencio-Cortés et al. [2] studied the sensitivity of 19 earthquake catalogue features to machine learning prediction models and explored the impact of different types of earthquake catalogues on the prediction target. Asim et al. [3] expanded the earthquake catalogue to include 60 entries by calculating statistical features within a fixed time window. The study used 60 earthquake characteristics and the mRMR criterion to extract relevant features. A prediction system was developed using SVR and HNN, with EPSO optimizing weights. This system, applied to Hindu Kush, Chile, and Southern California, showed improved prediction performance compared to previous studies. Allen and Melgar [4] constructed various decoders for seismic data using deep neural networks to predict earthquake magnitudes in the next seven days. Brykov et al. [5] employed different machine learning classifiers to predict events in specific areas with magnitudes equal to or greater than a certain threshold, showcasing strong predictive capabilities. Furthermore, Corbi et al. [6] effectively trained a machine learning prediction model capable of detecting sliding events by analysing recorded fault deformation data. In addition to the features based on earthquake catalogues mentioned above, machine learning models for natural earthquake prediction are also utilized to explain the earthquake process, such as earthquake magnitude changes analysis [7,8] and investigation of the underlying processes driving earthquake occurrence [9,10]. In this type of work, input data from catalogues of past events are crucial since they may directly affect how well ML models will perform. However, due to the limited number of periodic cycles of historical events recorded from many natural faults, reliable prediction of natural earthquakes using ML is still challenging.
As an alternative, it has been recognized that laboratory rock shearing experiments exhibiting stick-slips can generate patterns similar to the intermittent dynamics of natural earthquakes [11]. However, in contrast to natural earthquakes, laboratory earthquakes have the advantages of controllable seismogenic conditions, easy monitoring of frictional dynamics, highly repeatable earthquake processes, and abundant periodic cycles, and thus have been extensively employed to explore the physics of earthquakes [12,13,14,15,16]. The frictional dynamics data obtained in the stick-slip experiments can enable ML applications in laboratory earthquake prediction. For example, Rouet-Leduc et al. [17] revealed a correlation between the acoustic emission signal released in a laboratory shear test and the macroscopic shear stress based on a random forest model; Bolton et al. [18] classified the acoustic emission signals in laboratory shear experiments by an unsupervised K-cluster method and predict the occurrence time, duration, and magnitude of laboratory earthquakes using the data trained with classified features. Wang et al. [19] used a deep-learning transformer model to predict fault characteristics like displacement and friction using acoustic emission signals. The ML-based laboratory earthquake prediction may pave the way for developing appropriate approaches and procedures for natural earthquake prediction. However, due to the limitations of monitoring equipment, some laboratory experiments can only collect limited types of signals with restricted quantities. Particularly, the local friction dynamic information (displacement, velocity) inside the fault is difficult to acquire directly during the experiment because of the restriction of sensor location in the physical model. As a result, the datasets utilized in the existing ML work are usually small, i.e., using no more than a few sensor points, and thus the generalization ability of the ML models in these applications may be limited.
Complementary to physical laboratory experiments, numerical simulations of laboratory-scale sheared granular fault experiments have also been conducted to explore earthquake physics in recent years [20,21,22,23,24,25,26,27]. Setting up dense monitoring points both on the shearing plate and inside the gouge in the numerical model allows for collecting sufficient macroscopic and microscopic friction dynamics data during stick-slip cycles with spatial resolutions that are practically impossible in physical experiments. Numerical simulation can enable a more detailed investigation of laboratory earthquake predictions with various seismic features and also the interaction between these features leading to recurring slip events. For example, Ren et al. [28] used the rigid particle-based discrete element method (DEM) to simulate a sheared stick-slip experiment containing a granular gouge and, thereby, collected friction dynamics data of different particles to train a series of XGBoost [29] models for predicting the system’s macroscopic friction. They found that the fault dynamics responses at different locations have entirely different contributions to the overall stick-slip behaviour and incorporating more statistical features of the friction dynamics signals in training can improve prediction accuracy. However, only the velocity signals from one or two particles in the DEM simulation are utilized in each training. Ma et al. [30] also trained an XGBoost model using data and their statistics from a DEM-simulated sheared granular fault gouge to investigate the relations between the microslips and macroscopic friction and suggested that the trained ML model can well distinguish the recharge and drop stages of the entire system.
Very recently, the state-of-the-art combined finite-discrete element method (FDEM) has been applied as an improvement of the traditional rigid particle-based DEM for sheared granular fault simulations [31,32,33]. The FDEM inherits the merits of both the finite element method (FEM) and the DEM and has proven to be a powerful tool for simulating granular materials (see the introduction of the FDEM in Text S1 of Supplementary Material) [34]. In an FDEM realization of the sheared granular fault system, the DEM module is responsible for processing the particle–particle and particle–plate interactions, and the FEM module allows for simulating the deformation of both particles and shearing plates. A combination of the FEM and the DEM is superior to traditional DEM simulations where only rigid particles and plates are allowed (see Figure S1 in Supplementary Material for the comparison between the FDEM and the DEM). Gao et al. [31] mentioned that compared to the DEM, the FDEM could easily realize the explicit representation of granular fault systems and thus better capture more detailed and realistic fault microscopic dynamics data in both particles and shearing plates during stick-slip cycles. In our previous work, we have thoroughly validated the appropriateness of the FDEM for simulating laboratory earthquakes [31]. Based on our FDEM simulated sheared granular fault data, Wang et al. [35] trained a convolutional encoder-decoder using the kinematic energy of the numerical model and successfully transferred the trained ML model to predict the frictions of physical laboratory experiments. The transfer learning practice demonstrates great potential for training laboratory earthquake ML prediction models using FDEM simulations.
In this work, continuing with the FDEM simulated 2D granular fault system under stick-slip shearing, we further probe into the fault dynamics data collected at 2203 “sensor” points (i.e., displacements and velocities in both x and y directions at each sensor point) densely distributed both on the shearing plates and inside the gouge. We train and test LightGBM [36] models using the time-series data obtained at these sensor points as input features and the gouge-plate normalized shear stress (shear stress divided by the applied constant normal stress) as the label (i.e., prediction target). The main purpose of this study is to investigate whether the regular fault dynamics data (displacements and velocities) contain effective information on the instantaneous shear stress of the fault and to explore how the input features could be optimized to better predict the fault friction state when a large number of fault dynamics data are available.
This paper is organized as follows. Section 2 briefly introduces the FDEM model, the LightGBM, and SHAP value approaches. In Section 3, we first determine the optimal number of input features that are representative of the fault system through a series of ML training and testing using different numbers of sensor data. We then filter the 8812 input features (2203 × 4) to alleviate the possibility of feature correlation based on the obtained optimal number and the importance ranking of input features. We train the LightGBM model using the optimized (filtered) dataset and test its prediction performance. Following this, we also expand the optimized feature data by calculating their statistics to form a new input feature dataset and check the performance of the newly trained LightGBM model. In Section 4, the SHAP value analysis is carried out as a preliminary trial to discuss the contribution of input features to the prediction results. The conclusions are given at the end.
2. Methods
2.1. FDEM Simulation of Stick-Slips
In this study, a laboratory-scale sheared granular fault system is simulated using the FDEM to produce fault dynamics data and macroscopic shear stress fluctuations associated with stick-slip processes. The FDEM model, which was first referenced by Gao et al. [31], consists of two shearing plates and one granular fault gouge and is realized according to the laboratory photoelastic experiment conducted by Geller et al. [37] (Figure 1). The gouge, confined between two identical deformable plates, consists of 2817 bidisperse circular particles with diameters of either 1.2 or 1.6 mm. The material and numerical simulation parameters are shown in Table S1 of the Supplementary Material. All particles are randomly generated and placed between the two plates. Each plate is 570 mm × 250 mm in width and height, and to induce friction, numerous half-circular “teeth” are created on the plates along the gouge-plate boundary. We apply the shear loading and normal pressure through two stiff bars attached to the top end of the upper plate and the bottom end of the lower plate, respectively. The bottom stiff bar is fixed in the shear direction (x direction), so it can only move in the vertical direction (y direction) under a constant normal pressure P = 28 kPa. The granular gouge is sheared by pushing the top stiff bar horizontally towards the right-hand side (x direction) at a constant velocity V = 5.0 × 10−4 m/s with its vertical movement fixed. A detailed illustration of the model geometry and parameter selection is presented in Text S2 of the Supplementary Material. As in our previous work [31], we calibrated the FDEM simulation by comparing its equivalent seismic moments with those obtained from the laboratory experiments by Geller et al. [37]. Figure S2 (Supplementary Material) shows that the FDEM simulation generates slip events with magnitudes adequately following the Gutenberg-Richter distribution [38]. These prove that the FDEM model can simulate the stick-slip behaviour in sheared granular gouges with sufficient accuracy.
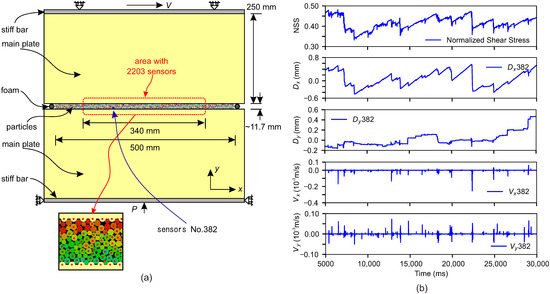
Figure 1.
(a) Schematic of the FDEM model and the sensor locations. (b) Exemplar fault dynamics data such as (from top to bottom) the normalized gouge-plate shear stress, and the x and y displacements and velocities collected at sensor No. 382. “NSS” is short for normalized shear stress.
To track the frictional dynamics signals during shearing and to avoid the edge effect, the 2203 “sensor” points are placed at the centres of the particles and the half-circular teeth that cover the middle segment of the granular gouge layer with a span of ~340 mm in the x direction (Figure 1a). We thus collect a total of 8812 (2203 × 4, i.e., Vx, Vy, Dx, and Dy at each sensor point) items of time-series data. The sensors on the two plates (i.e., on the half-circular teeth) are numbered first starting from 0 to 285, followed by the ones on the particles. The sensors on the bottom plate are numbered with even numbers (i.e., 0, 2, …, 284), and the sensors on the top plate are numbered with odd numbers (i.e., 1, 3, …, 285). The sensor numbers on the particles are then followed in a sequence from left to right and bottom to top. We set a time step of 10−7 s and run the model for almost 3.0 × 108 time steps with a total running time of ~30 s. The model reaches a steady state after the first 3 s, and the data collected after 5 s are used here for ML analysis. The normalized gouge-plate shear stress and the x and y velocity (Vx, Vy) and displacement (Dx, Dy) at the 2203 sensor points are recorded every 1 ms. Figure 1b presents the time series of the normalized shear stress (NSS) and the exemplar displacement and velocity data recorded at a selected sensor at No. 382, manifesting the repetitive generation of slip events and recharging processes.
2.2. LightGBM (Light Gradient Boosting Machine) Approach
The dense microscopic fault dynamics data collected at different sensor locations in the granular fault system may reflect the macroscopic stick-slip behaviour differently. Some of these data likely significantly contribute to the ML model’s prediction performance, while others are merely redundant information due to potential feature correlations [39,40]. Therefore, filtering important input features and alleviating feature correlation are crucial in training ML prediction models, especially when abundant data are available.
This study employs the LightGBM (Light Gradient Boosting Machine) approach [36] to select important input features and train prediction models. LightGBM is built based on the Gradient Boosting Decision Tree (GBDT) and is one of the most versatile ML algorithms. Unlike other GBDT algorithms adopting a pre-sorting method for node splitting, LightGBM uses the histogram of input features to substantially reduce its memory consumption and computational cost [36]. Before training the model, we first convert the input feature data at each time instant into a histogram in the form of , where xi is the bin vector of input features and yi is the corresponding bin values. Then, the K additive tree functions in the LightGBM algorithm are represented as
where fk represents the classification and regression tree (CART) model; wq(x) is the score of the leaf node; q(x) is the specific leaf node; is the prediction value; F is the set space that contains all trees. We utilize the root mean square error (RMSE) loss function during training. RMSE is a widely used evaluation metric that quantifies the disparity between predicted values and actual observations. By minimizing RMSE, our objective is to enhance the model performance in predicting the label. The mathematical expression of RMSE can be illustrated as
where i, from 1 to n, denotes the index of input instances, n is the number of instances, and yi and are the ground truth and prediction, respectively. Consequently, the objective function of all K additive trees can be simplified as
where t, from 1 to K, denotes the index of the tth tree, and is the regularization value of the tth tree. To train the model, residuals are calculated in each iteration relative to the previous tree. The prediction for the tth iteration is the summation of the previous tree’s prediction, i.e.,
where is the summation of all the predicted values before the tth tree; is the predicted value of the tth tree. One base decision tree is sequentially chosen and added to the ensemble model to reduce each iteration’s residual by minimizing the objection function during each iteration. The objection function of the tth iteration is
where is the regularization value of the tth tree. The LightGBM model can be continuously optimized through the growth process of the tree model for constructing feature splits. A detailed explanation of LightGBM is presented in Text S3 (Supplementary Material), and the typical structure of LightGBM is shown in Figure 2.
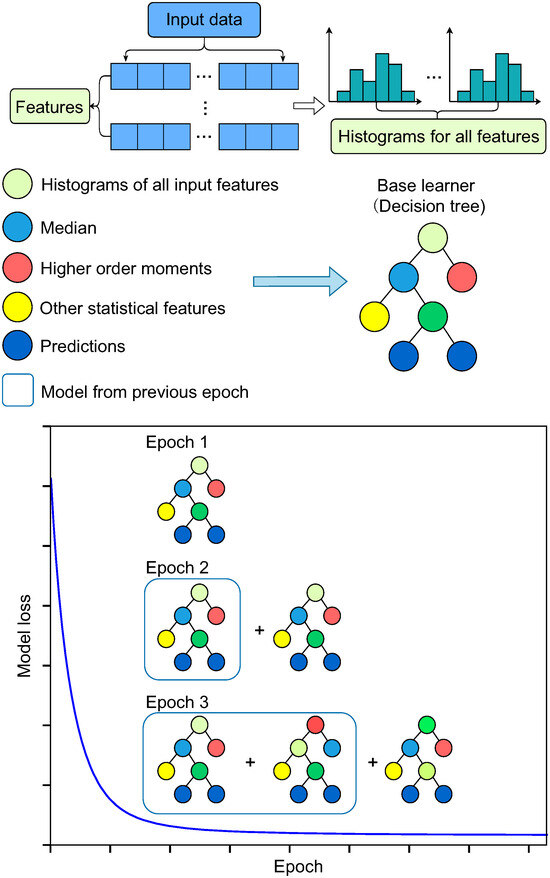
Figure 2.
Schematic of LightGBM based on the gradient boosting decision tree (GBDT).
To fully use the input data and consider the commonly used training data proportion in ML, we clip the first 80% of each item of the collected time-series data (5–25 s) as the training dataset and the remaining 20% (25–30 s) for testing. In order to find the optimal hyperparameters, we divide the training dataset into five non-overlapping folds, i.e., using the first four folds for training and the last one for validation. The hyperparameters of the LightGBM model are tuned using grid search [41] and Bayesian optimization [42,43]. We first employ the Bayesian optimization to narrow the range of hyperparameters from a large solution space to a certain degree, and then use the grid search method to search for optimal hyperparameters in a small solution space. The optimal hyperparameters are selected from the group with the lowest training loss in cross-validation, as shown in Table S2 in the Supplementary Material. We use R2, a normalized parameter ranging from 0 to 1 (from bad to good in terms of prediction accuracy), to calculate the gap between the prediction results and ground truth, i.e.,
where denotes the mean of the ground truth. The R2 is a relative indicator of a machine learning model’s prediction performance. Since we are comparing different machine learning models’ performance on the same testing dataset in the present paper, the R2 can satisfy our needs.
It is worth noting that for time-series data, the LightGBM works differently from deep-learning approaches, where a consecutive segment of time-series data from each input feature is often used. Here, we make a “now” prediction, and instead, the LightGBM models are trained step by step in temporal space, i.e., all input feature data points from the same time instant are collected and trained in each time step using a histogram-based algorithm to predict the normalized shear stress at the same time instance. Thus, temporal relationships between adjacent data points in each time-series feature are not considered in our LightGBM model. To achieve decent results, appropriate feature engineering should be conducted for time-series data to improve the prediction accuracy of LightGBM models. This can be completed by filtering the input feature data based on their importance ranking according to the information gained in training, which measures the predictive ability of a feature on the target by counting the number of times an input feature has been used in node splitting in a decision tree [44]. Additionally, the LightGBM approach can effectively preserve each feature’s physical meaning, allowing for straightforward interpretations of prediction models compared to deep learning. Upon acquiring a decent LightGBM model, the SHAP value approach [44], as will be illustrated next, can be employed to quantitatively trace back and interpret the contribution of input features to the prediction results.
2.3. SHAP (Shapley Additive exPlanation) Value
Interpretation of input features is a crucial part of the applications of ML models to real-world problems since it facilitates our understanding of the underlying physics in the trained model and also helps evaluate whether the model could meet the initial expectation. After obtaining the best ML model, the contribution of each input feature can be quantified using the SHAP value approach, a method developed from cooperative game theory [44]. The SHAP value is an additive feature attribution method. Specifically, at a time instant, the summation of the SHAP values of all input features is equal to the predicted value minus the mean predicted value of all input features, i.e.,
Here, j, from 1 to p, denotes the index of input feature; represents the model prediction of input instant x; represents the contribution of model prediction from input feature j; is the weight of input feature j; xj denotes the contribution of input feature j; Xj represents the set of model prediction of feature j; is the average contribution of prediction for feature j. By calculating the SHAP values, the evolution of the contributions of each input feature on the prediction results with respect to time can be obtained.
3. Predictions
This section demonstrates how the input features can be optimized to achieve better prediction performance. The purpose is to identify the appropriate procedure upon which the information in input features can be fully excavated. With the appropriate procedure, the laboratory slip events can be accurately and efficiently predicted when abundant frictional dynamics data are available.
3.1. Input Feature Data Optimization
As mentioned earlier, the fault dynamics data collected at 2203 densely distributed sensor points may contain redundant and correlated information. Here, we filter the data by first exploring the optimal number of input features that are representative of the fault system from an ML prediction viewpoint. This is achieved by training and testing a series of LightGBM models using data from an increasing number of sensor points, say, 1, 5, 10, 20, 50, 100, 200, 500, 1000, 1500, and 2203. For each of these numbers, we randomly draw data from all the 2203 sensor points using the specified number of sensors and then use the selected data to train a LightGBM model and test its performance. The procedure is repeated ten times for each number (except 2203 since all data are used) to alleviate uncertainty. Note that for each sensor, all four items of time-series data, i.e., Vx, Vy, Dx, and Dy, are used in the training and testing.
The testing performance of each trained LightGBM model in terms of R2 and the required number of epochs for convergence in training are presented in Figure 3a,b. It is manifest that the prediction accuracy of the trained LightGBM models is poor when the number of sensor data used is less than 10. The accuracy significantly improves when the sensor number exceeds 20 (Figure 3a). As the number continues to increase, the R2 mainly hovers around 0.8, while the models’ training expense significantly increases (Figure 3b). Particularly, we reach an R2 of 0.82 for the LightGBM model trained using all the 2203 sensor data without screening (Figure 3a); however, the time needed in training is very demanding, i.e., the training takes an epoch of ~3300 upon convergence (Figure 3b). These results demonstrate that the dense fault dynamics data at various sensor points on the shearing plates and inside the gouge do contain effective information regarding the shear stress of the fault, and the LightGBM model trained using a decent amount of sensor data can adequately capture the complex relations between microscopic frictional dynamics in the sheared granular fault system and the macroscopic slip events. In the meantime, this also confirms that the data from the 2203 sensors indeed have redundant information.
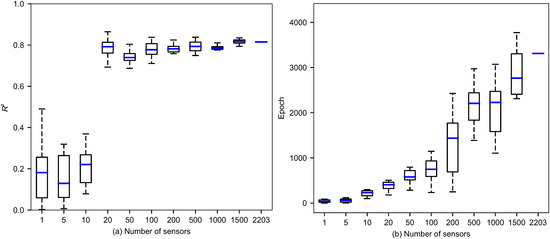
Figure 3.
Box plots of the LightGBM model performance trained using the data from an increasing number of sensors. The training and testing are repeated ten times for each sensor number to obtain the statistics. (a) Statistics of the testing R2 of the ten LightGBM models trained under each sensor number. (b) Statistics of the required training epochs for convergence for the ten LightGBM models trained under each sensor number. Note that the model trained using all the 2203 sensor data is not repeated, and the results are indicated by a single blue bar.
Compromising the training efficiency and prediction accuracy, we choose an optimal number of sensor points of ~20 for feature filtering, corresponding to ~80 (~20 × 4) input features. To optimize the 8812 input features, we calculate and rank the importance values of each input feature based on the LightGBM model trained using all the 2203 sensor data. Finally, we choose a list of 88 features with top rankings as the optimized feature dataset. In contrast, the remaining features mainly have importance values in more than one order smaller than the largest one. Note that the exact number of sensors related to these 88 selected features is more than 22 since maybe only 1–2 items of time-series data from one sensor have been selected to form the optimized feature dataset. Due to space limitations, only the top 50 optimized input features are presented in Figure 4.
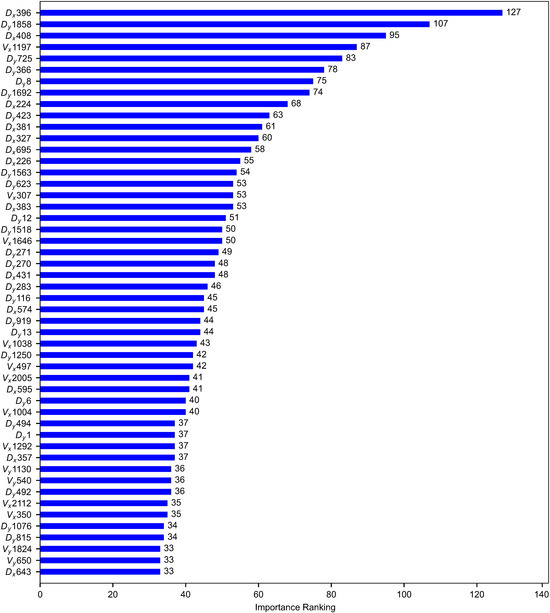
Figure 4.
The top 50 optimized input features with higher importance values. For the names of these input features located on the left side of the horizontal bar, the symbols Vx, Vy, Dx, and Dy represent the velocity and displacement in the x and y directions, and the number following the symbol indicates the sensor ID mentioned in Section 2.1. The importance value of each input feature is given on the right side of the horizontal bar.
3.2. Prediction Using Optimized Data
We proceed by retraining and testing a LightGBM model using the 88 optimized input features. As shown in Figure 5a, the ML model trained on the optimized features generates an R2 of 0.90 and RMSE of 0.0045 for testing, outperforming the previous model trained using all 8812 input features (Figure 3a). This demonstrates that although only 88 input features are used here, the trained model can achieve a better prediction accuracy than the one trained using all data. In other words, the fault dynamics information in the 88 optimized input features is sufficient to represent the dynamics of the entire sheared granular fault system; in contrast, the remaining unused features are mainly redundant to the prediction of normalized shear stress. It is also worth noting here that the training efficiency is significantly improved, as evidenced by the fact that the RMSE converges after only ~100 epochs (see inset of Figure 5a), which contrasts the ~3300 epochs needed to converge in the previous training where all input features are used (Figure 3b). Additionally, the RMSE evolution on the testing set shows no significant degradation, indicating no sign of overfitting. In general, training LightGBM models on the optimized feature data can reduce the chance of model overfitting, improve prediction accuracy, and enhance training efficiency.
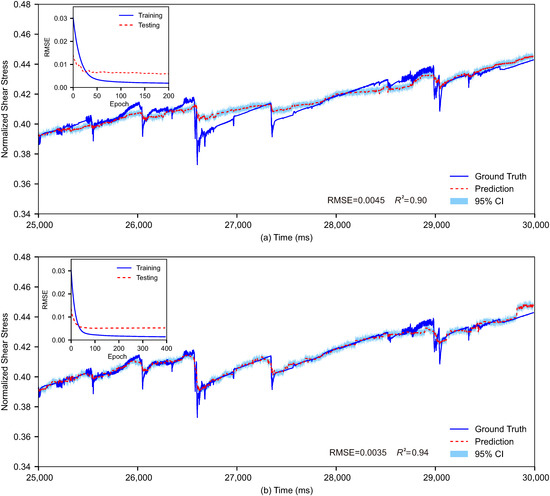
Figure 5.
The prediction results of the two trained LightGBM models, together with the 95% confidence intervals (light blue shaded region). (a) Performance of the model trained with the optimized sensor data on the testing set. (b) Performance of the model trained with the optimized sensor data and their statistics on the testing set. The inset in each subfigure presents the evolution of RMSE for the corresponding model during training and testing.
3.3. Prediction Using Optimized Data and Their Statistics
In laboratory-earthquake-related ML practices, to fully exploit the underlying information from the obtained fault dynamics data and to achieve better prediction performance, the statistics of raw data are also commonly used as input features to train the prediction models [17,28,45]. Here, on top of the 88 optimized time-series data, we use the sliding time window approach to calculate 8 statistical parameters, such as the mean, variance, skewness, kurtosis, quartile, 1st percentile, 91st percentile, and median of the data located in each window, for each item of the time-series data and comprises a total of 792 input features (88 × 9) for ML training and testing. The size of the sliding window used to calculate the statistics is 300 ms, which is chosen based on the fact that the periods of most stick-slip cycles are within the range of 300 ms in our FDEM simulated results. Adjacent sliding windows overlap each other by 299 ms. Again, we train and test a LightGBM model using the 792 new input features and obtain an improved R2 = 0.94 and RMSE = 0.0035 for testing. As shown in Figure 5b, the predicted normalized shear stress shows a very good match with the actual values. Although the training takes more epochs (~200) before reaching stable results (inset of Figure 5b) than the previous training using only the 88 optimized feature data (inset of Figure 5a), compared with the first case using all the 8812 input features (Figure 3), the result of this model is notably superior in terms of both prediction accuracy and training efficiency.
Through the above progressive adjustment of the input features from raw data to the optimized data and to their statistics, the prediction performance of the trained LightGBM models has been gradually improved. Particularly, the statistics-based input features provide an in-depth excavation of the raw data, which helps to better capture the distribution characteristics and variation trends of the data, thereby improving the model’s performance. We also provide a precise visualization of the predictive performance of the two LightGBM models (models related to Figure 5a,b) on the testing dataset in Figure S3 of the Supplementary Material.
One may easily argue that when statistics-based features are used, there are cases where slip events are predicted prior to actual events (e.g., the slip event at 29.0 s in Figure 5b), i.e., an artificial smoothing effect. However, as shown in Figure 5a, without using statistics-based features, there are also predicted slips before the actual slip events, e.g., the same slip event at 29.0 s. Therefore, we would attribute the smoothing largely to prediction inaccuracy. Given the complexity of our FDEM-simulated irregular stick-slip cycles, a precise prediction is challenging. Nevertheless, the model trained using the statistics-based features indeed improves the prediction accuracy, as is clearly evidenced by the increased R2 from Figure 5a to Figure 5b.
4. Discussion
The above ML analyses based on the dense fault dynamics data extracted from the FDEM simulated sheared granular fault system demonstrate that upon appropriate optimization of input features, we can achieve acceptable performance and accuracy for laboratory earthquake prediction using LightGBM. However, ML models are often called “black boxes”, which means that although we may reach accurate predictions, the mechanism behind the models remains elusive. To probe into the working mechanism of the LightGBM prediction model, we evaluate the role each input feature plays in the prediction using the SHAP value approach, which quantifies the direct contribution of an input feature to the predicted value at each instant of time. Specifically, the positive SHAP value of an input feature results in an increase in the predicted normalized shear stress at that time and vice versa. Based on the last LightGBM model with the highest prediction accuracy—the one trained using the optimized data and their statistics (i.e., 792 input features), we calculate the SHAP values of each input feature at each instant of time.
Due to space limitations, we first plot in Figure 6 the top 50 input features with large cumulative magnitudes of the yielded SHAP values (in descending order). The cumulative magnitude of SHAP values is the summation of the magnitudes (absolute values) of all yielded SHAP values for an input feature, indicating a feature’s overall contribution to prediction at all times. The actual SHAP value versus the corresponding feature value (relative value from low to high, denoted by the colour bar) at each instant of time is presented in Figure 6. An enlarged version listing the top 200 input features is presented in Figure S4 in the Supplementary Material. These plots show that the different microscopic fault dynamics data types have completely distinct contributions to the predicted normalized shear stress.
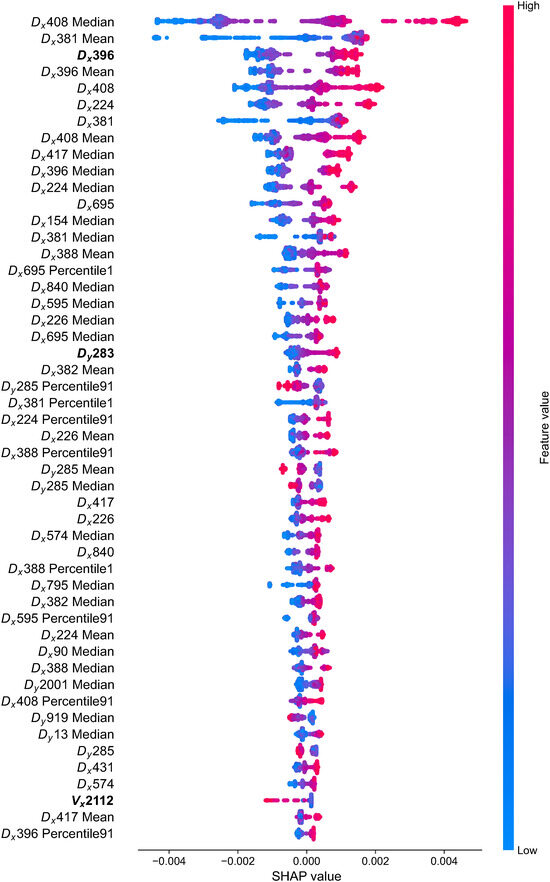
Figure 6.
The SHAP value versus feature value at each instant of time for the top 50 input features with relatively larger cumulative magnitudes of the yielded SHAP values. The results are based on the last LightGBM model trained using the optimized input features and their statistics. Typical input features analysed in Figure 7 are marked in bold.
The top input features shown in Figure 6 (e.g., the top 10–15) yield both positive and negative SHAP values. The behaviour of this type of input feature is further detailed in Figure 7a by the temporal evolution of the SHAP value of an exemplar Dx at sensor No. 396, alongside the change of Dx and the normalized shear stress for comparison. As shown in Figure 7a, the changing trend of the SHAP value is roughly consistent with the feature value, i.e., during the stick stages, both the feature value and SHAP value increase, and sudden drops occur at slips for both. Moreover, the larger the feature value is, the higher the generated SHAP value will be (although imprecisely). The rough consistency between the input feature and the corresponding SHAP value in both the stick and slip stages is commonplace for the majority of the top input features, especially the ones related to Dx and its statistics, e.g., the data collected at sensors with No. 224, 408, and 417, among many others (Figure S4). This agrees with our intuitive understanding that features with better prediction capability should have similar evolution patterns and pace to the prediction target. However, not all Dx-related features exhibit similar evolution patterns to the predicted target. As shown in Figure S5 of the Supplementary Material, the correlation between the listed Dx features and the normalized shear stress is considerably weak. Nevertheless, the SHAP value provides a powerful approach that helps filter the Dx-related features with high correlations and contributions to the prediction target.
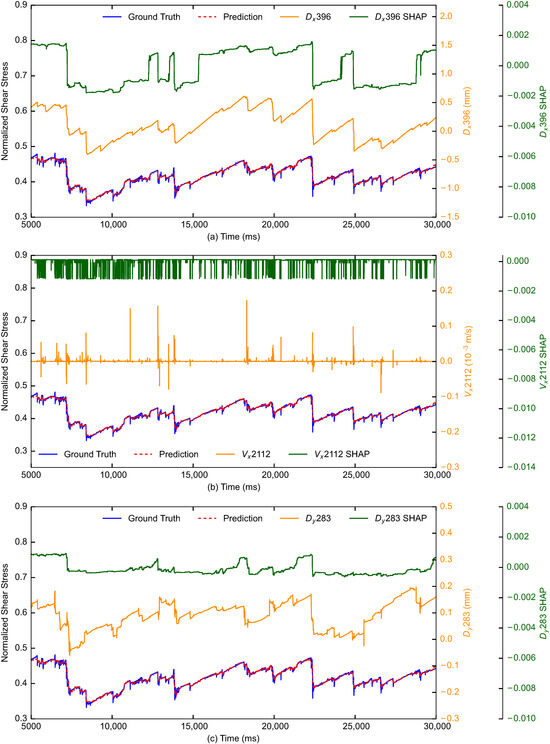
Figure 7.
The evolution of SHAP values of typical features with respect to time for the LightGBM model trained using the optimized data and their statistics (i.e., 792 input features). (a) The evolution of SHAP values of Dx at sensor No. 396, where the increase/decrease in SHAP value has a similar trend to Dx. (b) The evolution of SHAP values of Vx at sensor No. 2112, where spikes occur at slips and cause a sharp drop in its SHAP value. (c) The evolution of SHAP values of Dy at sensor No. 283, where Dy shows a slight increase during the stick phases and sudden drop at slips; however, it mainly only causes a sharp increase in its SHAP value when a slip occurs.
There are also input features that mainly yield negative SHAP values, e.g., the Vx of sensor No. 2112 (Figure 6). As detailed in Figure 7b regarding its temporal evolution versus the SHAP value and normalized shear stress, when a slip occurs, a negative SHAP value will be generated, together with a spike in Vx (can be positive or negative). However, during the stick phases, Vx is very small, and the yielded SHAP value is mainly around zero, thus having no distinct contribution to the prediction. These demonstrate that this type of input feature (Vx) mainly contributes to the prediction results at slips by bringing down the predicted normalized shear stress. Similar phenomena can also be found in the Vx of a few other sensors, e.g., the ones with No. 406, 1004, and 1888 (Figure S4).
On the contrary, a small number of input features behave the opposite, e.g., the Dy of sensor No. 283 (Figure 6). Specifically, when a slip occurs, this type of feature mainly generates positive SHAP values and pushes up the predicted normalized shear stress (Figure 7c). During stick phases, although we can also witness an increase in these feature values (similar to Dx), they mainly have minor contributions to the prediction results, i.e., the yielded SHAP values are mainly around zero or of a small negative value. These input features include the Dy of sensors with No. 8, 12, and 285 (Figure S4). It is worth noting that the Vy of sensors barely has notable contributions to the prediction results, as there are only 4 input features related to Vy on the top 200 feature list shown in Figure S4.
The SHAP values of input features can help uncover local friction dynamics’ role in laboratory earthquake prediction. From the above analyses, we find that the input features related to Dx mainly occupy the top of the list shown in Figure 6 (or Figure S4), simply because these top features evolve at a similar pace to the normalized shear stress in both the stick and slip phases. This is followed by the input features related to Dy. However, compared with Dx, the magnitudes of the yielded SHAP values are relatively smaller. We suspect this may be partially caused by the fact that the input features related to Dy only contribute to the prediction results at slips. We can observe a small number of input features related to Vx on the list in Figure 6 (or Figure S4), and they also only contribute to the prediction results at slips. We barely see input features related to Vy in Figure S4. Details of the sensor numbers and their locations are presented in Figure 8. Locations of the sensors related to the top 200 input features listed in Figure S4 are also presented in Figure 8 (coloured). All these demonstrate that, in general, the input features related to displacements contribute more to the prediction results than those associated with velocity. In addition, the features related to the shearing direction (i.e., the x direction) can better reflect the friction dynamics of the system and thus have higher contributions to the prediction results than those in the y direction.
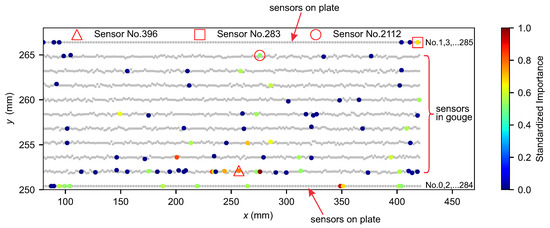
Figure 8.
Sensor locations and their numbers in the granular gouge fault system. The sensors related to the top 200 input features presented in Figure S4 are coloured according to their normalized importance values.
Through the SHAP value analysis, accurate evaluations of the contribution of each feature to the predicted normalized shear stress can be obtained. Therefore, the LightGBM prediction model combined with the SHAP value analysis can quantify the impact of microscopic fault dynamics data on the macroscopic stick-slip response in a sheared granular fault system. The above analysis also implies that for natural earthquakes, and even tsunami prediction, the displacement data (or equivalent data) monitored near the fault may be more valuable than velocity data, and the data resolved along the fault shearing direction are more valuable than those perpendicular to the fault. With the SHAP value analysis, we can further optimize the earthquake prediction. The arrangement of natural earthquake sensor positions is a key factor. By introducing our model, we can optimize this arrangement. Specifically, we can select the positions corresponding to the most important features based on the analysis results of the model and arrange sensors at these positions. In this way, we can make the most of limited resources and improve the accuracy and efficiency of earthquake prediction.
It is worth noting that due to the large dimension of the dense fault dynamics data used in the present research (say, 8812), dimensionality reduction on the input features is necessary. The LightGBM approach employed here could achieve our goal of effectively filtering the redundant information from a large number of fault dynamics data and preserving the original physical meanings of the final optimized data, which facilitates the interpretability of the prediction model. Therefore, the LightGBM model together with the SHAP value analysis can efficiently and accurately predict laboratory earthquakes based on dense fault dynamics data and may also help explore valuable precursors for upcoming slip events.
5. Conclusions
In this paper, we have simulated a sheared granular fault system using the FDEM to collect fault dynamics data (Vx, Vy, Dx, and Dy) at 2203 “sensor” points during stick-slip cycles and trained a series of LightGBM models by optimizing and excavating the input features. The prediction performance of these models is tested upon the generation of stick-slips characterized by the normalized shear stress between the shearing plates and gouge. The purpose is to explore the appropriate ML model training procedure and achieve better laboratory earthquake predictions when abundant fault dynamics data are available. The SHAP values of input features are also calculated to quantify the contribution of each input feature to the prediction results.
The ML study uses the sensor data as input features and the gouge-plate normalized shear stress as the label, and the first 80% of the time-series proportion is reserved for training and the remaining 20% for testing. We first optimize the 8812 input features by randomly selecting an increasing number of sensor data and training and testing the LightGBM models’ performance. When the number of sensors used in training exceeds 20, the R2 mainly hovers around 0.8, while the models’ training expense significantly increases. We choose an optimal number of sensor points of ~20 by considering both the model’s prediction accuracy and training efficiency. Then, 88 input features with top importance are selected as the optimized dataset based on the LightGBM model trained using all the 8812 input features. Following this, the LightGBM model trained using the optimized dataset yields an R2 of 0.90; however, the training efficiency is remarkably enhanced. Then, to fully use the underlying fault dynamics information, by calculating the 8 statistical parameters of the 88 optimized features, we compose an enlarged dataset with 792 input features and retrain a LightGBM model with a significantly improved prediction accuracy of R2 = 0.94. Based on the final trained LightGBM model, we extract the SHAP values of each input feature and compare them with the normalized shear stress. We find that the input features related to displacements contribute more to the prediction results than those associated with velocity, and the ones in the x direction (fault shearing direction) can better reflect the friction dynamics of the system than those in the y direction.
The analyses demonstrate that the dense fault dynamics data obtained from the gouge and plates contain the necessary information to train appropriate ML models so that the fault friction state can be adequately predicted. However, the dense fault dynamics data may contain redundant information and increase training expenses. Using ML approaches to screen out correlated information and optimize the data can facilitate the training process and achieve better prediction results. Additionally, appropriate utilization of the statistics of the fault dynamics data may help extract important hidden information from the data and enhance the prediction performance. Finally, the SHAP values obtained with the trained LightGBM model can quantify the contribution of each input feature to the prediction results.
The data collection process from earthquake sensors is vital. Aim to gather information from sensors that are rich in earthquake catalogues and closely tied to earthquake occurrences. Trying to gather data from sensors deployed in locations that the machine learning model considers to be of high importance will significantly aid in earthquake prediction. This study offers useful guidance for this process. Constructing a prediction model requires diligent data screening, feature extraction, and model optimization. These steps help to create a reliable representation of complex physical processes. This research provides an effective example of how to create an efficient prediction framework. The SHAP value analysis emphasizes the importance of features such as displacement and displacement statistics. This insight offers a fresh viewpoint for exploring potent earthquake precursor signals and setting up early warning systems. Our work has broad applications. While it can predict laboratory earthquakes, its framework, methods, and conclusions provide a solid base for forecasting modelling processes to natural faults. This broadens the potential for employing machine learning in natural earthquake prediction. This work can shed light on natural earthquake prediction in terms of selecting valuable monitoring data and training appropriate ML models and also opens new possibilities to explore valuable precursors for earthquake prediction.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/jmse12020246/s1. Text S1: Brief introduction of FDEM; Text S2: Supplementary explanation of FDEM model setup; Text S3: Light Gradient Boosting Machine (LightGBM); Figure S1: Numerical representation of the granular fault system using DEM and FDEM. (a) In DEM, the plates are simplified by a set of bonded particles, and the gouge layer is composed of a series of rigid particles. Therefore, both the gouge particles and the shearing plates cannot deform. (b) In FDEM, the plates are explicitly represented, and both plates and particles are further discretized into finite elements to capture their detailed deformation and movement; Figure S2: Probability density distribution of the seismic moment of all slip events, where the detailed calculation of the moment is explained by Gao et al. [31]. The results agree with the physical experiment data collected in Geller et al. [37]. The probability density distribution is consistent with the Gutenberg-Richter distribution and is predicted to scale as (the power −3/2 is within the range of −1.4 to −1.8 observed in natural earthquakes; Figure S3: Performance of the two LightGBM models trained with different datasets. (a) Training with optimized sensor data. (b) Training with optimized sensor data and their statistics; Figure S4: The SHAP value versus the feature value at each instant of time for the top 200 input features with relatively larger cumulative magnitudes of the yielded SHAP values. The results are based on the last LightGBM model trained using the optimized dataset and their statistics; Figure S5: Evolutions of Dx for several sensors and their comparison with the normalized shear stress. (a) Normalized shear stress. (b) Dx of sensor No. 95. (c) Dx of sensor No. 295. (d) Dx of sensor No. 1832; Table S1: Material and numerical simulation parameters; Table S2: The optimal hyperparameters of the LightGBM model trained using 8812 features; References [31,32,33,34,35,36,37,38,39,40,41,42,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60] are citied in the Supplementary Materials.
Author Contributions
W.H.: conceptualization, methodology, software, investigation, formal analysis, writing original draft. K.G.: conceptualization, resources, funding acquisition, supervision, writing review and editing. Y.F.: validation, writing review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (42374070), the National Key R&D Program of China (2022YFF0800601), and the Guangdong Provincial Key Laboratory of Geophysical High-resolution Imaging Technology (2022B1212010002).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in the paper will be available upon request to the corresponding author. The Supplementary Material includes an expanded explanation of the FDEM method and model setup and a brief introduction to the LightGBM approach.
Acknowledgments
We sincerely thank two anonymous reviewers for their critical comments and constructive suggestions, which have greatly improved the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meng, M.; Ge, H.; Shen, Y.; Ji, W.; Wang, Q. Rock Fabric of Tight Sandstone and Its Influence on Irreducible Water Saturation in Eastern Ordos Basin. Energy Fuels 2023, 37, 3685–3696. [Google Scholar] [CrossRef]
- Asencio-Cortés, G.; Martínez-Álvarez, F.; Morales-Esteban, A.; Reyes, J. A Sensitivity Study of Seismicity Indicators in Supervised Learning to Improve Earthquake Prediction. Knowl.-Based Syst. 2016, 101, 15–30. [Google Scholar] [CrossRef]
- Asim, K.M.; Idris, A.; Iqbal, T.; Martínez-Álvarez, F. Earthquake Prediction Model Using Support Vector Regressor and Hybrid Neural Networks. PLoS ONE 2018, 13, e0199004. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.M.; Melgar, D. Earthquake Early Warning: Advances, Scientific Challenges, and Societal Needs. Annu. Rev. Earth Planet. Sci. 2019, 47, 361–388. [Google Scholar] [CrossRef]
- Brykov, M.N.; Petryshynets, I.; Pruncu, C.I.; Efremenko, V.G.; Pimenov, D.Y.; Giasin, K.; Sylenko, S.A.; Wojciechowski, S. Machine Learning Modelling and Feature Engineering in Seismology Experiment. Sensors 2020, 20, 4228. [Google Scholar] [CrossRef] [PubMed]
- Corbi, F.; Bedford, J.; Sandri, L.; Funiciello, F.; Gualandi, A.; Rosenau, M. Predicting Imminence of Analog Megathrust Earthquakes with Machine Learning: Implications for Monitoring Subduction Zones. Geophys. Res. Lett. 2020, 47, e2019GL086615. [Google Scholar] [CrossRef]
- Asim, K.M.; Martínez-Álvarez, F.; Basit, A.; Iqbal, T. Earthquake Magnitude Prediction in Hindukush Region Using Machine Learning Techniques. Nat. Hazards 2016, 85, 471–486. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Beroza, G.C. A Machine-Learning Approach for Earthquake Magnitude Estimation. Geophys. Res. Lett. 2020, 47, e2019GL085976. [Google Scholar] [CrossRef]
- Beroza, G.C.; Segou, M.; Mousavi, S.M. Machine Learning and Earthquake Forecasting-Next Steps. Nat. Commun. 2021, 12, 4761. [Google Scholar] [CrossRef]
- Johnson, C.W.; Johnson, P.A. Learning the Low Frequency Earthquake Activity on the Central San Andreas Fault. Geophys. Res. Lett. 2021, 48, e2021GL092951. [Google Scholar] [CrossRef]
- Brace, W.F.; Byerlee, J.D. Stick-Slip as a Mechanism for Earthquakes. Science 1966, 153, 990–992. [Google Scholar] [CrossRef] [PubMed]
- Tinti, E.; Scuderi, M.M.; Scognamiglio, L.; Di Stefano, G.; Marone, C.; Collettini, C. On the Evolution of Elastic Properties During Laboratory Stick-Slip Experiments Spanning the Transition from Slow Slip to Dynamic Rupture. J. Geophys. Res. Solid Earth 2016, 121, 8569–8594. [Google Scholar] [CrossRef]
- Leeman, J.R.; Saffer, D.M.; Scuderi, M.M.; Marone, C. Laboratory Observations of Slow Earthquakes and the Spectrum of Tectonic Fault Slip Modes. Nat. Commun. 2016, 7, 11104. [Google Scholar] [CrossRef] [PubMed]
- Rouet-Leduc, B.; Hulbert, C.; Bolton, D.C.; Ren, C.X.; Riviere, J.; Marone, C.; Guyer, R.A.; Johnson, P.A. Estimating Fault Friction from Seismic Signals in the Laboratory. Geophys. Res. Lett. 2018, 45, 1321–1329. [Google Scholar] [CrossRef]
- Bolton, D.C.; Shreedharan, S.; Rivière, J.; Marone, C. Acoustic Energy Release During the Laboratory Seismic Cycle: Insights on Laboratory Earthquake Precursors and Prediction. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018975. [Google Scholar] [CrossRef]
- Bolton, D.C.; Shreedharan, S.; McLaskey, G.C.; Rivière, J.; Shokouhi, P.; Trugman, D.T.; Marone, C. The High-Frequency Signature of Slow and Fast Laboratory Earthquakes. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024170. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Hulbert, C.; Lubbers, N.; Barros, K.; Humphreys, C.J.; Johnson, P.A. Machine Learning Predicts Laboratory Earthquakes. Geophys. Res. Lett. 2017, 44, 9276–9282. [Google Scholar] [CrossRef]
- Bolton, D.C.; Shokouhi, P.; Rouet-Leduc, B.; Hulbert, C.; Rivière, J.; Marone, C.; Johnson, P.A. Characterizing Acoustic Signals and Searching for Precursors During the Laboratory Seismic Cycle Using Unsupervised Machine Learning. Seismol. Res. Lett. 2019, 90, 1088–1098. [Google Scholar] [CrossRef]
- Wang, K.; Johnson, C.W.; Bennett, K.C.; Johnson, P.A. Predicting Future Laboratory Fault Friction through Deep Learning Transformer Models. Geophys. Res. Lett. 2022, 49, e2022GL098233. [Google Scholar] [CrossRef]
- Hazzard, J.F.; Mair, K. The Importance of the Third Dimension in Granular Shear. Geophys. Res. Lett. 2003, 30, 1708. [Google Scholar] [CrossRef]
- Abe, S.; Mair, K. Grain Fracture in 3D Numerical Simulations of Granular Shear. Geophys. Res. Lett. 2005, 32, L05305. [Google Scholar] [CrossRef]
- Mair, K.; Hazzard, J.F. Nature of Stress Accommodation in Sheared Granular Material: Insights from 3D Numerical Modeling. Earth Planet. Sci. Lett. 2007, 259, 469–485. [Google Scholar] [CrossRef]
- Mair, K.; Abe, S. 3D Numerical Simulations of Fault Gouge Evolution During Shear: Grain Size Reduction and Strain Localization. Earth Planet. Sci. Lett. 2008, 274, 72–81. [Google Scholar] [CrossRef]
- Griffa, M.; Ferdowsi, B.; Guyer, R.A.; Daub, E.G.; Johnson, P.A.; Marone, C.; Carmeliet, J. Influence of Vibration Amplitude on Dynamic Triggering of Slip in Sheared Granular Layers. Phys. Rev. E 2013, 87, 012205. [Google Scholar] [CrossRef]
- Ferdowsi, B. Discrete Element Modeling of Triggered Slip in Faults with Granular Gouge. Application to Dynamic Earthquake Triggering. Ph.D. Thesis, ETH-Zürich, Zürich, Switzerland, 2014. [Google Scholar]
- Dorostkar, O.; Guyer, R.A.; Johnson, P.A.; Marone, C.; Carmeliet, J. On the Micromechanics of Slip Events in Sheared, Fluid-Saturated Fault Gouge. Geophys. Res. Lett. 2017, 44, 6101–6108. [Google Scholar] [CrossRef]
- Wang, C.; Elsworth, D.; Fang, Y. Influence of Weakening Minerals on Ensemble Strength and Slip Stability of Faults. J. Geophys. Res. Solid Earth 2017, 122, 7090–7110. [Google Scholar] [CrossRef]
- Ren, C.X.; Dorostkar, O.; Rouet-Leduc, B.; Hulbert, C.; Strebel, D.; Guyer, R.A.; Johnson, P.A.; Carmeliet, J. Machine Learning Reveals the State of Intermittent Frictional Dynamics in a Sheared Granular Fault. Geophys. Res. Lett. 2019, 46, 7395–7403. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme Gradient Boosting. R Package Version 0.4-2 2015, 1, 1–4. [Google Scholar]
- Ma, G.; Mei, J.; Gao, K.; Zhao, J.; Zhou, W.; Wang, D. Machine Learning Bridges Microslips and Slip Avalanches of Sheared Granular Gouges. Earth Planet. Sci. Lett. 2022, 579, 117366. [Google Scholar] [CrossRef]
- Gao, K.; Euser, B.J.; Rougier, E.; Guyer, R.A.; Lei, Z.; Knight, E.E.; Carmeliet, J.; Johnson, P.A. Modeling of Stick-Slip Behavior in Sheared Granular Fault Gouge Using the Combined Finite-Discrete Element Method. J. Geophys. Res. Solid Earth 2018, 123, 5774–5792. [Google Scholar] [CrossRef]
- Gao, K.; Guyer, R.; Rougier, E.; Ren, C.X.; Johnson, P.A. From Stress Chains to Acoustic Emission. Phys. Rev. Lett. 2019, 123, 048003. [Google Scholar] [CrossRef]
- Gao, K.; Guyer, R.A.; Rougier, E.; Johnson, P.A. Plate Motion in Sheared Granular Fault System. Earth Planet. Sci. Lett. 2020, 548, 116481. [Google Scholar] [CrossRef]
- Munjiza, A.; Lei, Z.; Divic, V.; Peros, B. Fracture and Fragmentation of Thin Shells Using the Combined Finite-Discrete Element Method. Int. J. Numer. Methods Eng. 2013, 95, 478–498. [Google Scholar] [CrossRef]
- Wang, K.; Johnson, C.W.; Bennett, K.C.; Johnson, P.A. Predicting Fault Slip Via Transfer Learning. Nat. Commun. 2021, 12, 7319. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Gutenberg, B.; Richter, C.F. Magnitude and Energy of Earthquakes. Nature 1955, 176, 795. [Google Scholar] [CrossRef]
- Khosravikia, F.; Clayton, P. Machine Learning in Ground Motion Prediction. Comput. Geosci. 2021, 148, 104700. [Google Scholar] [CrossRef]
- Ren, C.X.; Peltier, A.; Ferrazzini, V.; Rouet-Leduc, B.; Johnson, P.A.; Brenguier, F. Machine Learning Reveals the Seismic Signature of Eruptive Behavior at Piton De La Fournaise Volcano. Geophys. Res. Lett. 2020, 47, e2019GL085523. [Google Scholar] [CrossRef] [PubMed]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Martinez-Cantin, R. Bayesopt: A Bayesian Optimization Library for Nonlinear Optimization, Experimental Design and Bandits. J. Mach. Learn. Res. 2014, 15, 3735–3739. [Google Scholar]
- Victoria, A.H.; Maragatham, G. Automatic Tuning of Hyperparameters Using Bayesian Optimization. Evol. Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.G.; Lee, S.-I. Consistent Individualized Feature Attribution for Tree Ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Johnson, P.A.; Rouet-Leduc, B.; Pyrak-Nolte, L.J.; Beroza, G.C.; Marone, C.J.; Hulbert, C.; Howard, A.; Singer, P.; Gordeev, D.; Karaflos, D.; et al. Laboratory Earthquake Forecasting: A Machine Learning Competition. Proc. Natl. Acad. Sci. USA 2021, 118, e2011362118. [Google Scholar] [CrossRef]
- Dorostkar, O.; Guyer, R.A.; Johnson, P.A.; Marone, C.; Carmeliet, J. On the role of fluids in stick-slip dynamics of saturated granular fault gouge using a coupled computational fluid dynamics-discrete element approach. J. Geophys. Res. Solid Earth 2017, 122, 3689–3700. [Google Scholar] [CrossRef]
- Geller, D.A.; Ecke, R.E.; Dahmen, K.A.; Backhaus, S. Stick-Slip Behavior in a Continuum-Granular Experiment. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2015, 92, 060201. [Google Scholar] [CrossRef]
- Euser, B.; Rougier, E.; Lei, Z.; Knight, E.E.; Frash, L.P.; Carey, J.W.; Viswanathan, H.; Munjiza, A. Simulation of Fracture Coalescence in Granite via the Combined Finite–Discrete Element Method. Rock Mech. Rock Eng. 2019, 52, 3213–3227. [Google Scholar] [CrossRef]
- Lei, Q.; Gao, K. Correlation between Fracture Network Properties and Stress Variability in Geological Media. Geophysical Research Letters 2018, 45, 3994–4006. [Google Scholar] [CrossRef]
- Lei, Z.; Rougier, E.; Knight, E.E.; Munjiza, A.A.; Viswanathan, H. A generalized anisotropic deformation formulation for geomaterials. Comput. Part. Mech. 2016, 3, 215–228. [Google Scholar] [CrossRef]
- Lei, Z.; Rougier, E.; Munjiza, A.; Viswanathan, H.; Knight, E.E. Simulation of discrete cracks driven by nearly incompressible fluid via 2D combined finite-discrete element method. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1724–1743. [Google Scholar] [CrossRef]
- MiDi, G. On dense granular flows. Eur. Phys. J. E 2004, 14, 341–365. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K. NBS contact detection algorithm for bodies of similar size. Int. J. Numer. Methods Eng. 1998, 43, 131–149. [Google Scholar] [CrossRef]
- Munjiza, A.; Rougier, E.; John, N.W.M. MR linear contact detection algorithm. Int. J. Numer. Methods Eng. 2006, 66, 46–71. [Google Scholar] [CrossRef]
- Munjiza, A.A. Discrete Elements in Transient Dynamics of Fractured Media. Ph.D. Thesis, Swansea University, Swansea, UK, 1992. [Google Scholar]
- Munjiza, A.A. The Combined Finite-Discrete Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Munjiza, A.A.; Knight, E.E.; Rougier, E. Computational Mechanics of Discontinua; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Munjiza, A.A.; Rougier, E.; Knight, E.E. Large Strain Finite Element Method: A Practical Course; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Okubo, K.; Bhat, H.S.; Rougier, E.; Marty, S.; Schubnel, A.; Lei, Z.; Knight, E.E.; Klinger, Y. Dynamics, radiation and overall energy budget of earthquake rupture with coseismic off-fault damage. J. Geophys. Res. Solid Earth 2019, 124, 11771–11801. [Google Scholar] [CrossRef]
- Rougier, E.; Munjiza, A.; Lei, Z.; Chau, V.T.; Knight, E.E.; Hunter, A.; Srinivasan, G. The combined plastic and discrete fracture deformation framework for FDEM. Int. J. Numer. Methods Eng. 2019, 121, 1020–1035. [Google Scholar] [CrossRef]
- Tatone, B.S.A.; Grasselli, G. A calibration procedure for two-dimensional laboratory-scale hybrid finite–discrete element simulations. Int. J. Rock Mech. Min. Sci. 2015, 75, 56–72. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).