Underwater SSP Measurement and Estimation: A Survey
Abstract
1. Introduction
- We have conducted a survey on sound speed field construction indicating that it can be obtained by two kinds of methods: direct measurement method and inversion method.
- We have summarized the recognized mainstream underwater sound speed empirical formulas and compared their application scenarios.
- We have conducted research on advanced global commercial temperature, conductivity, and depth profiler (CTD), and compared their performance indicators.
- We have summarized three frameworks for constructing sound speed fields: matched field processing (MFP), compressive sensing (CS), and deep learning (DL). We have also compared the performance of different sound field construction methods.
- We have reviewed the development of constructing sound speed fields, identified current problems to be solved, and identified the trends of future development.
2. Methods for Constructing Underwater Acoustic Velocity Fields
2.1. Direct Measurement Methods
- (1)
- Wilson empirical formula [8]:where t is the temperature in °C, S is the salinity in ‰, and p is the pressure in kg/cm3. The W.D. Wilson formula can be applied over the range of temperature [−4 °C, 30 °C], salinity , and pressure [ kg/cm3].
- (2)
- Leroy empirical formula [11]:where t is the temperature in °C, S is the salinity in ‰, and Z is the depth in m. Leroy’s empirical formula can be applied over the range of temperature , ], salinity , and depth up to 8000 m.
- (3)
- Medwin empirical formula [12]: In 1975, Medwin proposed a simplified formula based on the Wilson empirical formula:where , and Z have the same meaning and unit with Leroy’s empirical formula. The Medwin empirical formula can be applied over the range of temperature ], salinity , and depth up to 1000 m.
- (4)
- Del Grosso empirical formula [13]: In 1974, Del Grosso summarized the empirical formula for calculating sound speed under conditions with high salinity:where , and p have the same meaning and unit with the Wilson empirical formula. Del Grosso’s empirical formula is applicable to the following ranges: temperature ], salinity , and pressure kg/cm3].
- (5)
- Chen–Millero empirical formula [14]: In 1977, Chen and Millero, transmitting Wilson’s data to more accurately measured sound speed data, proposed the Chen–Millero empirical formula by studying Wilson’s measurements data:where t and S have the same meaning and unit with the Medwin empirical formula, p is the pressure in bar. represents the sound speed value in a purified water environment. The parameters and can be obtained by checking the table in the literature [15]. The Chen–Millero empirical formula can be applied with the following ranges: temperature ], salinity , and pressure up to 1000 bar. In 1994, Millero and Li made a more accurate correction within the low-temperature range based on the Chen–Millero empirical formula and proposed the Chen–Millero–Li formula [16], which has been recommended by the United Nations Educational, Scientific and Cultural Organization (UNESCO) as the international standard formula for calculating underwater sound speed.
- (6)
- Coppens empirical formula [17]: In 1981, Coppens extrapolated the Del Grosso’s formula in the ranges of high salt, low salt, and low temperature, and then proposed the Coppens empirical formula:where t is the temperature in °C, S is the salinity in ‰, and Z is the depth in m. Coppens empirical formula can be applied within the ranges of temperature ], salinity , and depth up to 4000 m. The application condition of mainstream sound speed empirical formula is given in Table 1.
2.2. Sound Speed Inversion Method
3. Inversion Technology of Underwater SSP
3.1. MFP for SSP Inversion
3.1.1. EOF-Based MFP Method
3.1.2. MFP Method Based on Dictionary Learning
3.2. CS for SSP Inversion
3.3. DL for SSP Inversion
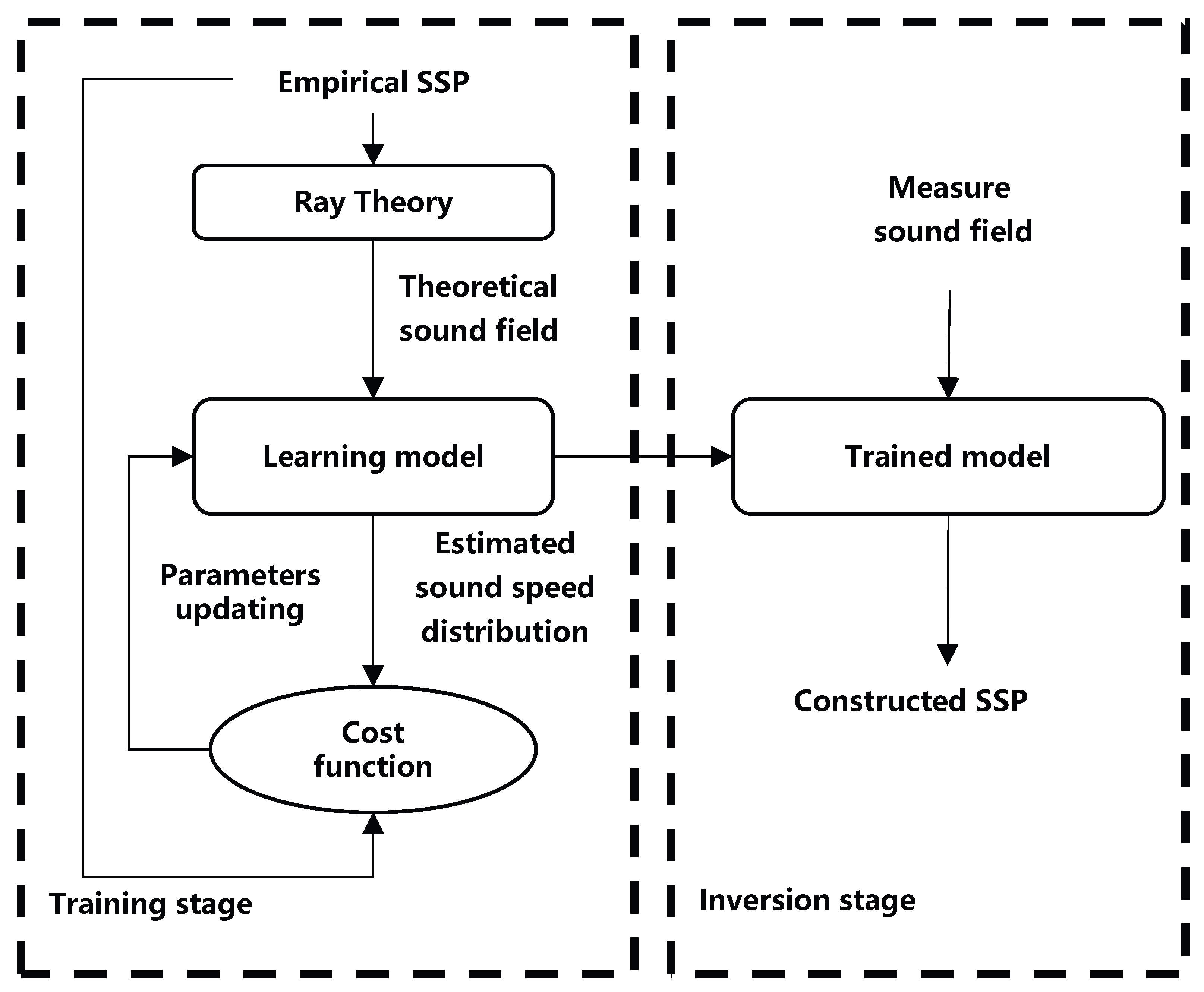
3.3.1. Neural Network Inversion of SSP Based on Sound Field Observation Data
3.3.2. Constructing SSPs Using Neural Networks Without Sound Field Observation Data
3.3.3. Typical Sound Field Measurement Mode
4. Comparison of Methods for Constructing Underwater SSPs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PNTC | Positioning, navigation, timing and communication |
| AUVs | Autonomous underwater vehicles |
| ROVs | Remotely operated vehicles |
| MFP | Matched field processing |
| CS | Compressive sensing |
| DL | Deep learning |
| SSPs | Sound speed profiles |
| SVP | Sound velocity profiler |
References
- Lin, B.; Zhang, Z.; Han, X.; Liu, L.; Liu, Z.; Che, Y. Key Technologies for Space-Air-Ground-Ocean Integrated Networks towards Maritime Emergency: An Overview. Mob. Commun. 2020, 44, 19–26. [Google Scholar]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics: Chapter 1; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; pp. 3–4. [Google Scholar] [CrossRef]
- Munk, W.; Wunsch, C. Ocean acoustic tomography: A scheme for large scale monitoring. Deep. Sea Res. Part Oceanogr. Res. Pap. 1979, 26, 123–161. [Google Scholar] [CrossRef]
- Munk, W.; Wunsch, C. Ocean acoustic tomography: Rays and modes. Rev. Geophys. 1983, 21, 777–793. [Google Scholar] [CrossRef]
- Munk, W.; Worcester, P.; Wunsch, C. Ocean Acoustic Tomography; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Lasky, M. Review of undersea acoustics to 1950. J. Acoust. Soc. Am. 1977, 61, 283–297. [Google Scholar] [CrossRef]
- Overview of the Development of Ocean Survey Instruments Abroad. Mar. Sci. Technol. Inf. 1977, 5, 24–44. (In Chinese)
- Wilson, D.W. Equation for the Speed of Sound in Sea Water. J. Acoust. Soc. Am. 1977, 32, 1357. [Google Scholar] [CrossRef]
- Wang, D.; Shang, E. Marine Acoustic; China Science Publishing and Media Ltd. (CSPM): Beijing, China, 2013. (In Chinese) [Google Scholar]
- Zhang, L.; Ye, S.; Zhou, S.; Liu, F.; Han, Y. Review of Measurement Techniques for Temperature, Salinity and Depth Profile of Sea Water. Mar. Sci. Bull. 2017, 36, 481–489. (In Chinese) [Google Scholar]
- Claude, L.C. Development of Simple Equations for Accurate and More Realistic Calculation of the Speed of Sound in Seawater. J. Acoust. Soc. Am. 1969, 46, 216–226. [Google Scholar]
- Medwin, H. Speed of sound in water: A simple equation for realistic parameters. J. Acoust. Soc. Am. 1975, 58, 1318–1319. [Google Scholar] [CrossRef]
- Del-Grosso, V.A. New equation for the speed of sound in natural waters (with comparisons to other equations). J. Acoust. Soc. Am. 1974, 56, 1084. [Google Scholar] [CrossRef]
- Chen, C.T.; Millero, F.J. Speed of sound in seawater at high pressures. J. Acoust. Soc. Am. 1977, 62, 1129–1135. [Google Scholar] [CrossRef]
- Huang, C.; Lu, X.; Wang, K.; Shen, J.; Zhang, B.; Zhai, G. A method of exactly determining the sound velocity in deep water based on salt information from WOA13 model and XBT data. Mar. Sci. Bull. 2016, 35, 554–561. [Google Scholar]
- Millero, F.J.; Li, X. Comments on "On equations for the speed of sound in sea water". J. Acoust. Soc. Am. 1994, 93, 255–275. [Google Scholar]
- Coppens, B.A. Simple equations for the speed of sound in Neptunian waters. J. Acoust. Soc. Am. 1981, 69, 862–863. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, J.; Zhou, C. Determination of the Optimal Sound Velocity Formula for Multibeam Sounding Systems. J. Ocean. Phy. Taiwan Strait. 2001, 4, 411–419. [Google Scholar]
- Chen, C.; Wu, B.; Wang, S. Research on optimization selection of computation formulas for underwater sound velocity. Ship Sci. Technol. 2014, 36, 77–80. [Google Scholar]
- Sea-Bird Scientific. SBE CTDs Profiling. Available online: https://www.seabird.com/profiling/family?productCategoryId=54627473767 (accessed on 12 December 2023).
- YSI, Inc. SonTek CastAway-CTD. Available online: https://www.ysi.com/castaway-ctd (accessed on 12 December 2023).
- Ocean Seven Ocean Seven 320 Plus WOCE-CTD. Available online: https://www.idronaut.it/multiparameter-ctds/oceanographic-ctds/os320plus-oceanographic-ctd/ (accessed on 12 December 2023).
- RBR, Ltd. RBR CT and CTD Instruments. Available online: https://rbr-global.com/support/documentation/ (accessed on 12 December 2023).
- Sea & Sun Technology, GmbH. Sea & Sun Technology CTD Probes. Available online: https://www.sea-sun-tech.com/product-category/probes/ctd-probes/ (accessed on 12 December 2023).
- Tsurumi-Seiki Co., L. eXpendable Conductivity, Temperature and Depth Product Code: XCTD. Available online: https://tsurumi-seiki.co.jp/en/product/e-sku-2/ (accessed on 12 December 2023).
- Ocean Physics Technology. OST Series CTD. Available online: https://www.oceanphysics.cn/index.php?a=shows&catid=69&id=81 (accessed on 12 December 2023).
- Trampp, D.A. Upper Ocean Characteristics in the Tropical Indian Ocean from AXBT and AXCTD Measurements; Technical Report; Naval Postgraduate School: Monterey, CA, USA, 2012. [Google Scholar]
- Shi, X.; Su, Q. Development Status of Expendable Marine Instruments and Equipment. Acoust. Electron. Eng. 2015, 4, 46–48. [Google Scholar]
- Cheng, F.; Chen, S.; Jin, S.; Sun, W. An Expanding Method of Sound Velocity Profiles Via EOF in Marginal Deepwater Areas. Hydrogr. Surv. Charting 2016, 36, 26–29. (In Chinese) [Google Scholar]
- Huang, W.; Lu, J.; Li, S.; Xu, T.; Wang, J.; Zhang, H. Fast Estimation of Full Depth Sound Speed Profile Based on Partial Prior Information. In Proceedings of the 2023 IEEE 6th International Conference on Electronic Information and Communication Technology (ICEICT), Qingdao, China, 21–24 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 479–484. [Google Scholar] [CrossRef]
- AML Oceanographic Ltd. MVP300 Operation and Maintenance Manual. Available online: https://amloceanographic.com/moving-vessel-profiler-for-uncrewed-systems-vessels (accessed on 12 December 2023).
- Wang, Y.; Yi, X. A Towed Multi-parameter Profile Measurement System. Oceanography; Technical report; CNKI: Beijing, China, 2005. [Google Scholar]
- Products, D.U.T. CZT1-3A Towed Multi-Parameter Profile Measurement System. 715 Research Institute of China: Hangzhou, China, 2010. [Google Scholar]
- Ren, Q.; Yu, F.; Wei, C.; Tang, Y.; Lu, N. Development and Application of A Moving Multi-parameter Profile Measurement System. Hydrogr. Surv. Charting 2022, 42, 33–36. (In Chinese) [Google Scholar]
- Cornuelle, B.; Munk, W.; Worcester, P. Ocean acoustic tomography from ships. J. Geophys. Res. Ocean. 1989, 94, 6232–6250. [Google Scholar] [CrossRef]
- Tolstoy, A.; Diachok, O.; Frazer, L. Acoustic tomography via matched field processing. J. Acoust. Soc. Am. 1991, 89, 1119–1127. [Google Scholar] [CrossRef]
- Zhang, Z. A Study on Inversion for Sound Speed Profile in Shallow Water (in Chinese). Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2002. [Google Scholar]
- Zhang, W.; Yang, S.e.; Huang, Y.w.; Li, L. Inversion of sound speed profile in shallow water with irregular seabed. In Proceedings of the Advances in Ocean Acoustics: Proceedings of the 3rd International Conference on Ocean Acoustics (OA2012), Beijing, China, 21–25 May 2012; 1495; AIP: Melville, NY, USA, 2012; pp. 392–399. [Google Scholar] [CrossRef]
- Zhang, W. Inversion of Sound Speed Profile in Three-dimensional Shallow Water. Ph.D. Thesis, Chapter 2. Harbin Engineering University, Harbin, China, 2013. (In Chinese). [Google Scholar]
- Zheng, G.Y.; Huang, Y.W. Improved Perturbation Method for Sound Speed Profile Inversion. J. Harbin Eng. Univ. 2017, 38, 371–377. [Google Scholar] [CrossRef]
- Zhang, Z.M. The Study for Sound Speed Inversion in Shallow Water on Application of Genetic and Simulated Annealing Algorithms. Master’s Thesis, Chapter 4. Harbin Engineering University, Harbin, China, 2005. [Google Scholar] [CrossRef]
- Tang, J.F.; Yang, S.E. Sound speed profile in ocean inverted by using travel time. J. Harbin Eng. Univ. 2006, 27, 733–737. [Google Scholar] [CrossRef]
- Sun, W.C.; Bao, J.Y.; Jin, S.H.; Xiao, F.M.; Cui, Y. Inversion of Sound Velocity Profiles by Correcting the Terrain Distortion. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 349–355. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, W.; Xu, Y. Inversion of the sound speed with radiated noise of an autonomous underwater vehicle in shallow water waveguides. IEEE J. Ocean. Eng. 2015, 41, 204–216. [Google Scholar] [CrossRef]
- Bianco, M.; Gerstoft, P. Dictionary learning of sound speed profiles. J. Acoust. Soc. Am. 2017, 140, 1749–1758. [Google Scholar] [CrossRef]
- Bianco, M.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef]
- Bianco, M.; Gerstoft, P. Compressive Acoustic Sound Speed Profile Estimation. J. Acoust. Soc. Am. 2016, 139, EL90–EL94. [Google Scholar] [CrossRef]
- Choo, Y.; Seong, W. Compressive sound speed profile inversion using beamforming results. Remote Sens. 2018, 10, 704. [Google Scholar] [CrossRef]
- Stephan, Y.; Thiria, S.; Badran, F. Inverting Tomographic Data with Neural Nets. In Proceedings of the Challenges of Our Changing Global Environment, San Diego, CA, USA, 9–12 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 1501–1504. [Google Scholar]
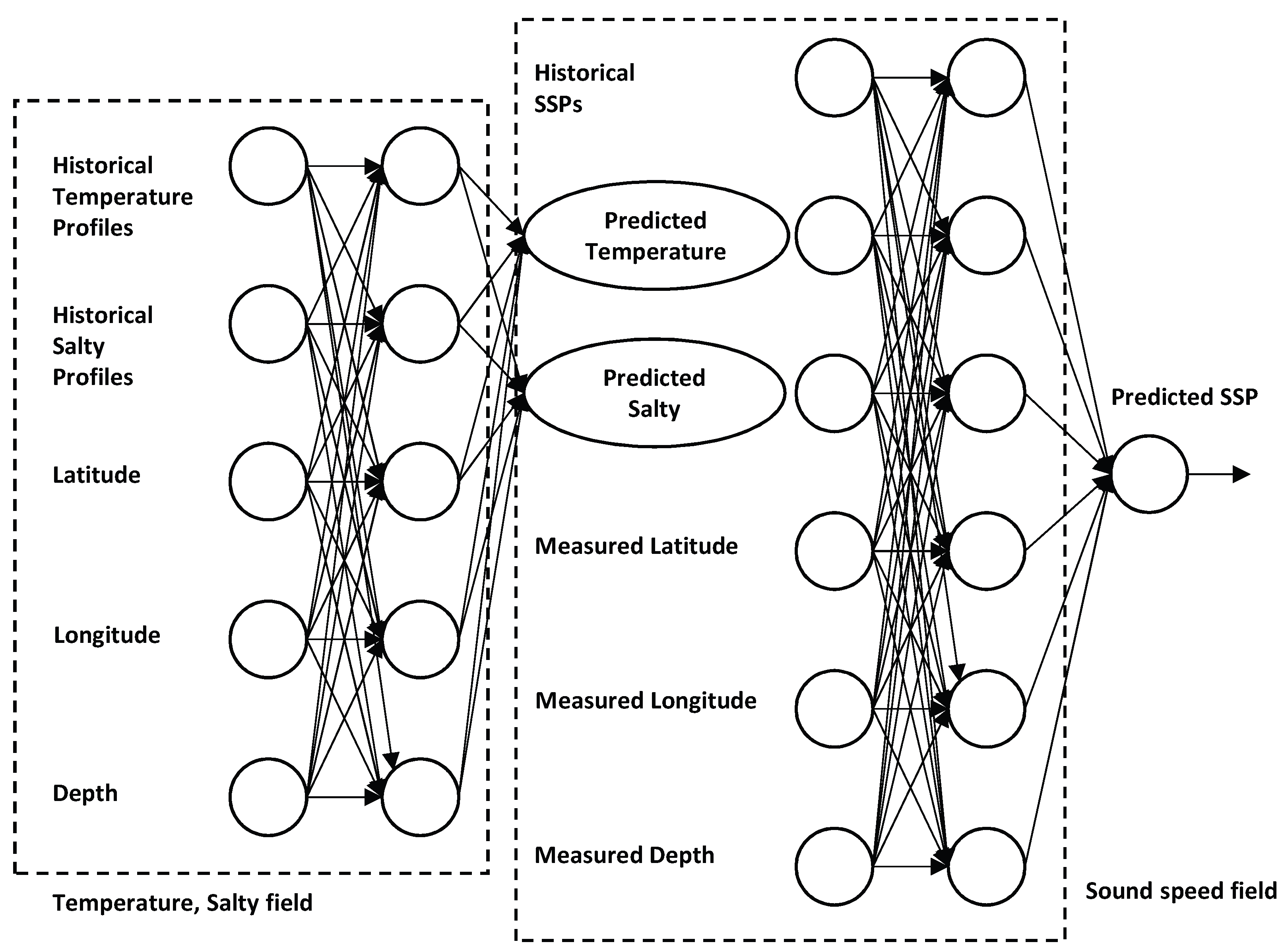
- Huang, W.; Liu, M.; Li, D.; Yin, F.; Chen, H.; Zhou, J.; Xu, H. Collaborating Ray Tracing and AI Model for AUV-Assisted 3-D Underwater Sound-Speed Inversion. IEEE J. Ocean. Eng. 2021, 46, 1372–1390. [Google Scholar] [CrossRef]
- Huang, W.; Li, D.; Jiang, P. Underwater Sound Speed Inversion by Joint Artificial Neural Network and Ray Theory. In Proceedings of the Proceedings of the Thirteenth ACM International Conference on Underwater Networks & Systems (WUWNet’18), Shenzhen, China, 3–5 December 2018; ACM: New York, NY, USA, 2018; pp. 1–8. [Google Scholar] [CrossRef]
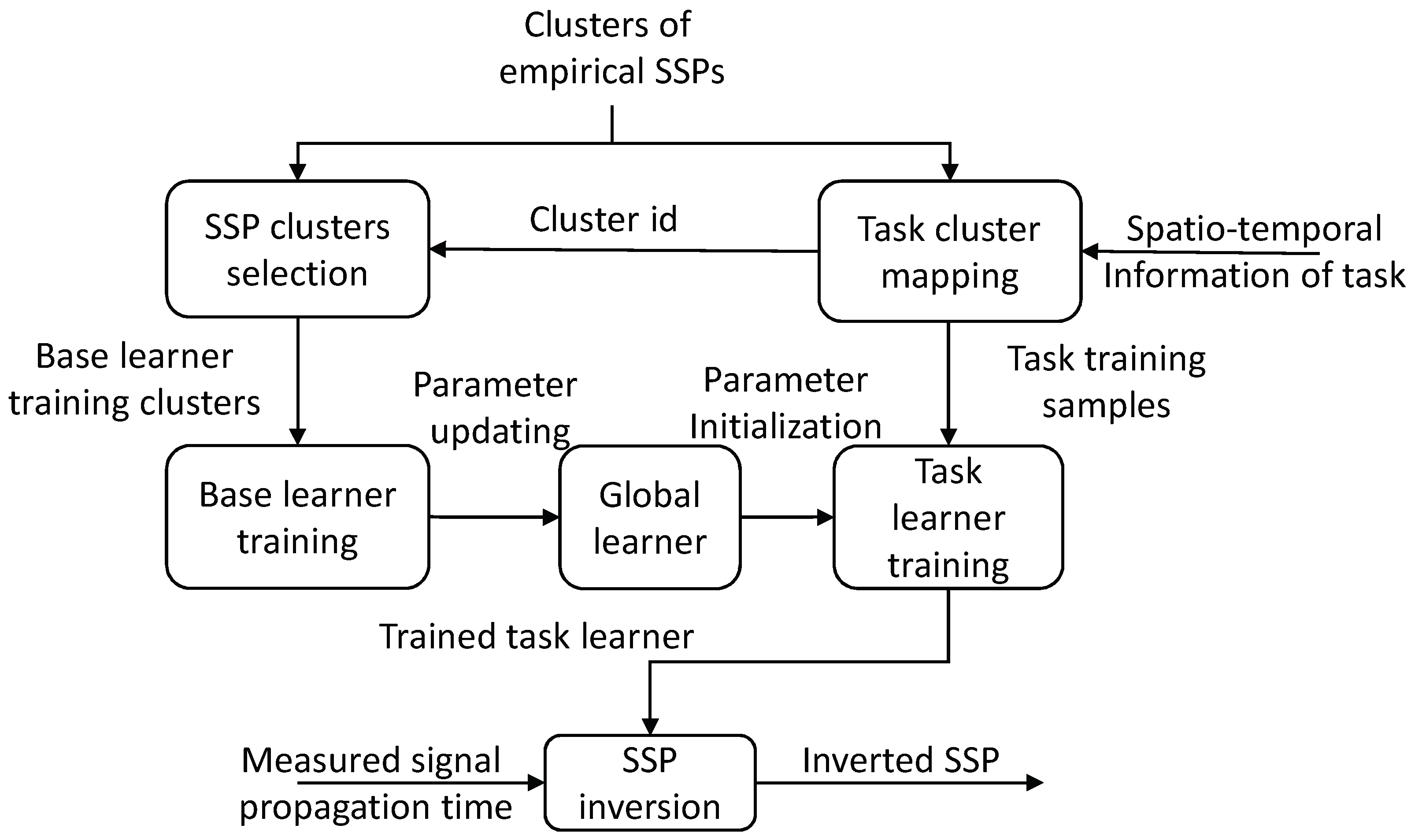
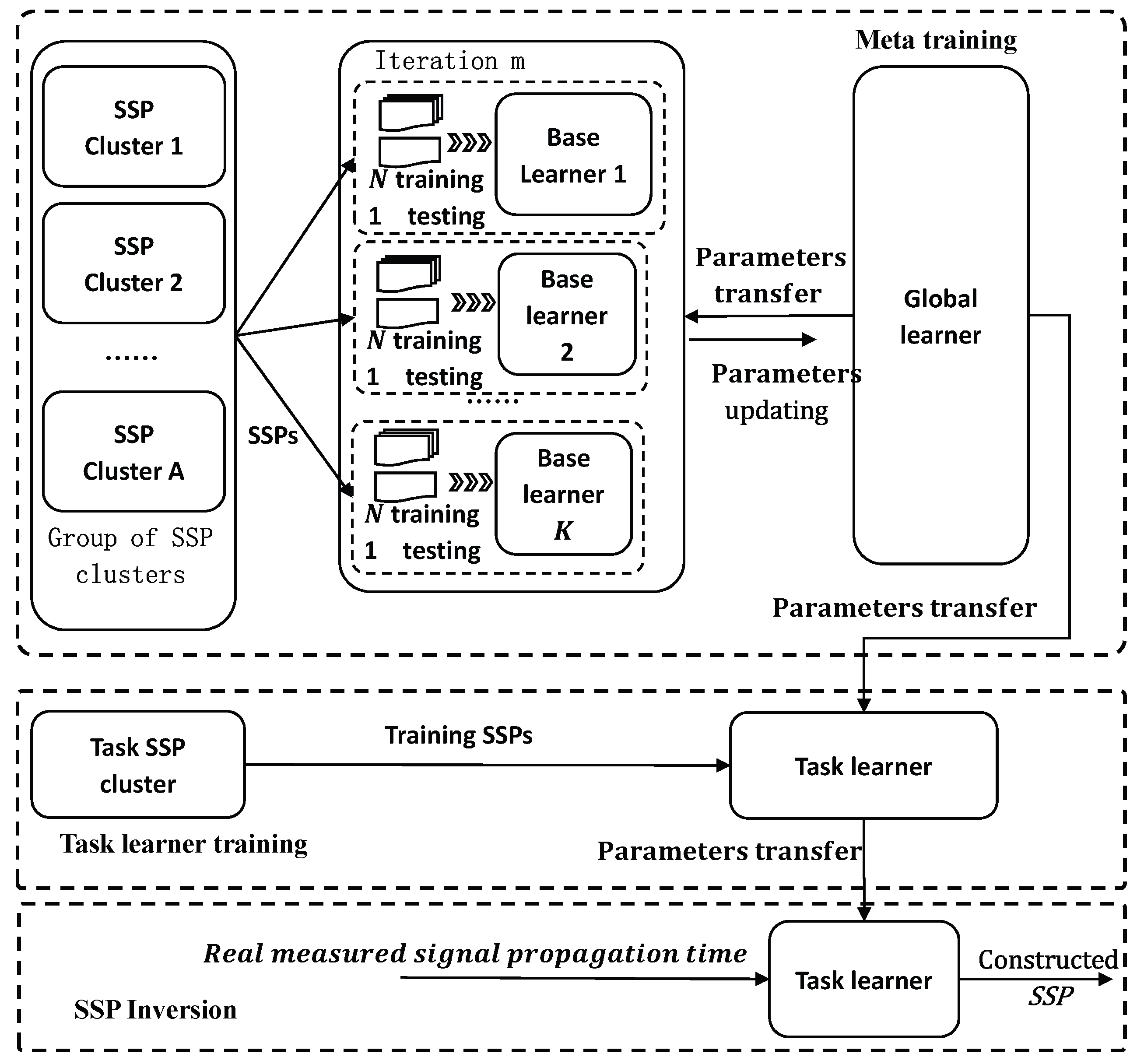
- Huang, W.; Li, D.; Zhang, H.; Xu, T.; Yin, F. A meta-deep-learning framework for spatio-temporal underwater SSP inversion. Front. Mar. Sci. 2023, 10. [Google Scholar] [CrossRef]
- Yu, X.; Xu, T.; Wang, j. Sound Velocity Profile Prediction Method Based on RBF Neural Network. In Proceedings of the In Proceedings of China Satellite Navigation Conference (CSNC), Chengdu, China, 23–25 May 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–8. [Google Scholar]
- Wang, J. Research on Theory and Method of Marine Precise Acoustic Data Processing. Ph.D. Thesis, Shandong University, Weihai, China, 2022. (In Chinese). [Google Scholar]
- Li, Q.; Shi, J.; Zhenglin, L.; Yu, L.; Zhang, K. Acoustic sound speed profile inversion based on orthogonal matching pursuit. Acta Oceanol. Sin. 2022, 38, 149–157. [Google Scholar] [CrossRef]
- Li, F.; Zhang, R. Inversion for sound speed profile by using a bottom mounted horizontal line array in shallow water. Chin. Phys. Lett. 2010, 27, 084303. [Google Scholar] [CrossRef]
- Li, Z.; He, L.; Zhang, R.; Li, F.; Yu, Y.; Lin, P. Sound speed profile inversion using a horizontal line array in shallow water. Sci. China Phys. Mech. Astron. 2015, 58, 1–7. [Google Scholar] [CrossRef]
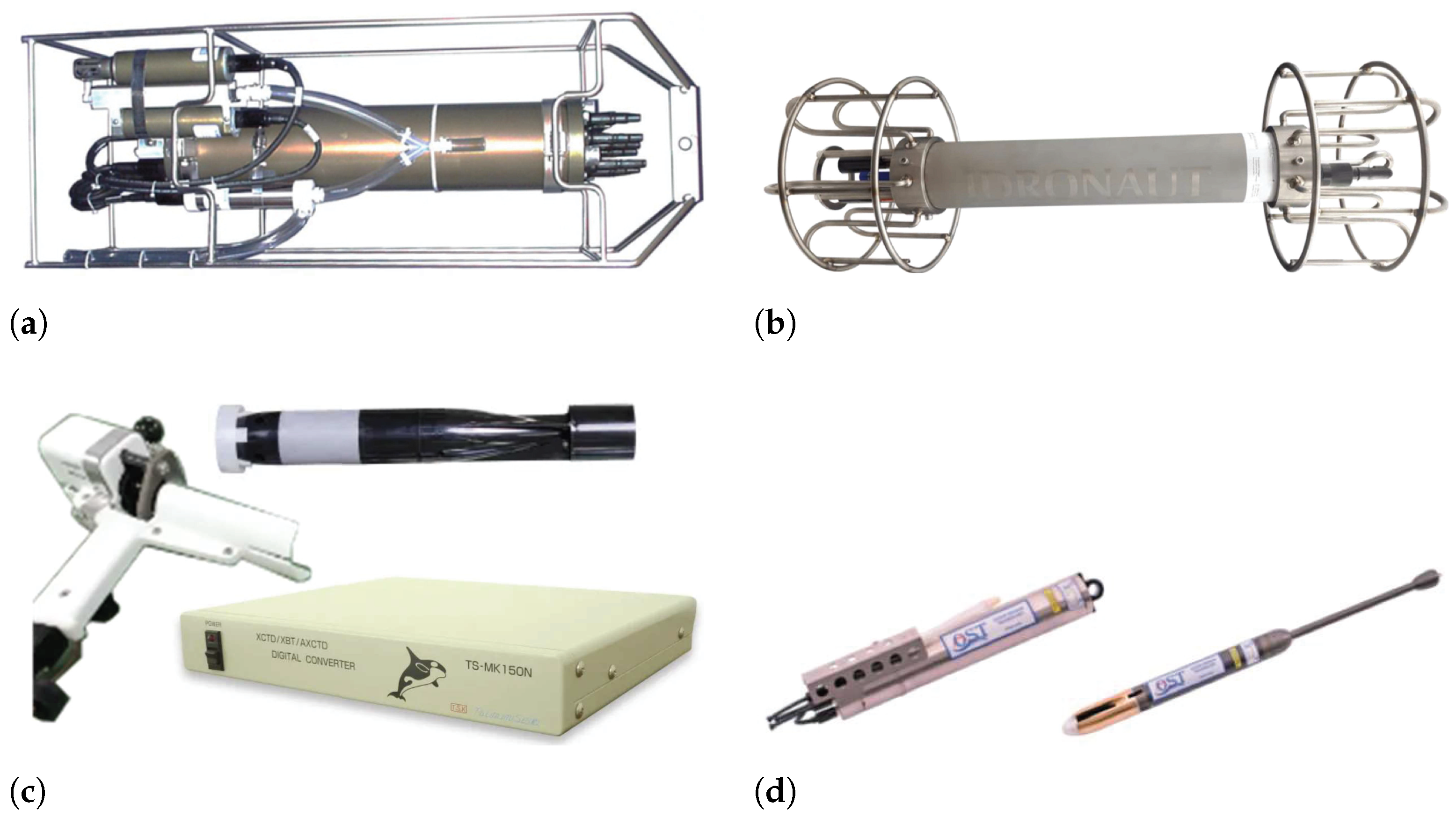
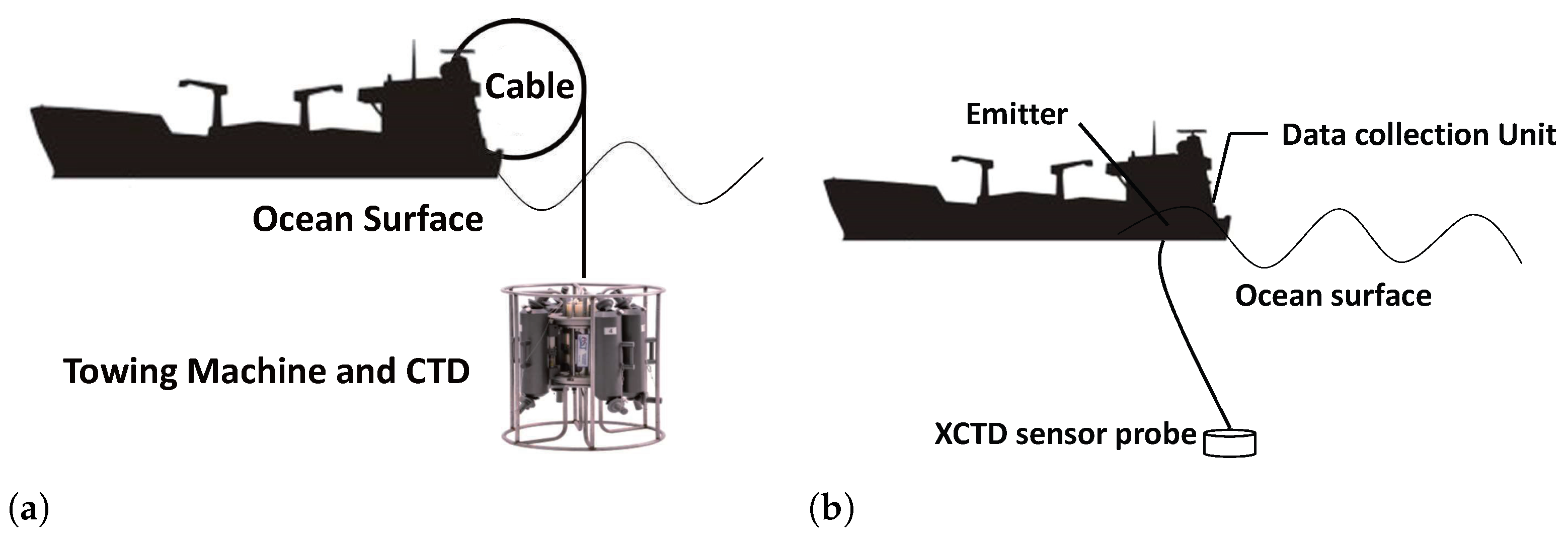





| Empirical Formula | Proposed Year | Application Range | ||
|---|---|---|---|---|
| Temperature | Salinity | Depth/Pressure | ||
| Wilson empirical formula [8] | 1960 | [−4 °C, 30 °C] | [0, 1000 kg/cm3] | |
| Leroy empirical formula [11] | 1969 | [−2 °C, 34 °C] | [0, 8000 m] | |
| Del Grosso empirical formula [13] | 1974 | [0, 30 °C] | [0, 1000 kg/cm3] | |
| Medwin empirical formula [12] | 1975 | [0, 35 °C] | [0, 45‰] | [0, 1000 m] |
| Chen–Millero empirical formula [14] | 1977 | [0, 40 °C] | [0, 1000 bar] | |
| Coppens empirical formula [17] | 1981 | [0, 35 °C] | [0, 4000 m] | |
| Model | OST15D [26] | SBE911plus [20] | OS320plus [22] | CTD90M [24] | RBR Concerto3 [23] | XCTD-4N [25] | |
|---|---|---|---|---|---|---|---|
| Temperature (°C) | Range | [−5, 35] | [−5, 35] | [−5, 45] | [−2, 36] | [−5, 35] | [−2, 35] |
| Accuracy | |||||||
| Resolution | 0.0001 | 0.0002 | 0.0001 | 0.0005 | <0.00005 | 0.01 | |
| Stability | /year | /month | - | - | /year | - | |
| Conductivity (S/m) | Range | [0, 7] | [0, 7] | [0, 7] | [0, 30] | [0, 8.5] | [0, 6] |
| Accuracy | |||||||
| Resolution | 0.00001 | 0.00004 | 0.00001 | 0.0005 | <0.0001 | 0.0015 | |
| Stability | /month | /month | - | - | /year | - | |
| Pressure ( kPa) | Range | [0, 7] | [0, 10.5] | [0, 10] | [0, 6] | [0, 6] | [0, 1.85] |
| Accuracy | range | range | range | range | range | - | |
| Resolution | range | range | range | range | range | - | |
| Stability | range/year | range/year | - | - | range/year | - | |
| Department | Oceans Center | Sea Bird | Idronaut | SST | RBR | TSK | |
| Country | China | the U.S. | Italy | Germany | Canada | Japan | |
| Method | Sonar Data | Accuracy | Time Consumption | Advantage | Disadvantage | |
|---|---|---|---|---|---|---|
| Preparation | Construction | |||||
| CTD/SVP [20,21,22,23,24,26] | no | high | - | very long | accurate | very long period; high economic costs |
| XCTD [25,27,28,29,30] | no | high | - | long | accurate; portable | long period; limited depth coverage |
| EOF-MFP [36,37,38,39,40,41,42,43,44] | yes | good | very short | medium | near real-time | complex optimization object searching |
| Dictionary learning [45,46] | yes | good | short | medium | near real-time | complex optimization object searching |
| CS [47,48] | yes | medium | short | short | sparse representation low storage space; not bad real-time | accuracy loss by linear representation |
| ANN [49,51] | yes | good | long | very short | real-time | complex preparation stage; weak noise reistance; overfitting problem |
| AEFMNN [50] | yes | good | long | very short | real-time; good robustness | complex preparation stage; overfitting problem |
| TDML [52] | yes | good | very long | very short | real-time; anti-overfitting | complex preparation stage |
| RBF [53,54] | no | low | long | very short | real-time; no sonar data | weak time and space resolution ability |
| SOM [55] | no | low | long | very short | real-time; no sonar data | insufficient accuracy in the deep-ocean part and seasonal thermocline |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Wu, P.; Lu, J.; Lu, J.; Xiu, Z.; Xu, Z.; Li, S.; Xu, T. Underwater SSP Measurement and Estimation: A Survey. J. Mar. Sci. Eng. 2024, 12, 2356. https://doi.org/10.3390/jmse12122356
Huang W, Wu P, Lu J, Lu J, Xiu Z, Xu Z, Li S, Xu T. Underwater SSP Measurement and Estimation: A Survey. Journal of Marine Science and Engineering. 2024; 12(12):2356. https://doi.org/10.3390/jmse12122356
Chicago/Turabian StyleHuang, Wei, Pengfei Wu, Jiajun Lu, Junpeng Lu, Zhengyang Xiu, Zhenpeng Xu, Sijia Li, and Tianhe Xu. 2024. "Underwater SSP Measurement and Estimation: A Survey" Journal of Marine Science and Engineering 12, no. 12: 2356. https://doi.org/10.3390/jmse12122356
APA StyleHuang, W., Wu, P., Lu, J., Lu, J., Xiu, Z., Xu, Z., Li, S., & Xu, T. (2024). Underwater SSP Measurement and Estimation: A Survey. Journal of Marine Science and Engineering, 12(12), 2356. https://doi.org/10.3390/jmse12122356






