A Vessel Position Precision Analysis Based on a Two-Star Combined Approach
Abstract
1. Introduction
2. Positioning Model Based on the Two-Star Combination Method
- Star Sensor Base Coordinate System (s-system): This is the coordinate system fixed to the star sensor.
- Vessel Coordinate System (b-system): This system is theoretically fixed to the vessel but may have installation errors.
- Geographical Coordinate System (n-system): This system is aligned with geographical coordinates.
- Earth-Centered Inertial Coordinate System (i-system): This system is aligned with the Earth-centered inertial frame.
- Earth-Centered Fixed Coordinate System (e-system): This system is aligned with the fixed frame relative to the Earth.
3. Positioning Accuracy Model
3.1. Positioning Accuracy Model
- When the angular separation is greater than the difference in zenith distances and less than the sum of the zenith distances, the two circles intersect at two points, resulting in two possible solutions for two-star positioning.
- When the sum of the zenith distances equals the angular separation, or the absolute difference of the zenith distances equals the angular separation, the two circles are tangent to each other, providing a single solution for two-star positioning.
- When the sum of the zenith distances is less than the angular separation, or the difference in zenith distances is greater than the angular separation, the two circles do not intersect. In this case, the double-star positioning model has no solution.
3.2. Algorithm Flow
- (1)
- Experimental Preparation: Complete the calibration of the INS and the calibration of installation errors between the INS and the star sensor.
- (2)
- Observation of Navigation Star 1: Obtain the elevation angle, azimuth angle, right ascension, declination, and GHA for the celestial body in the s-system.
- (3)
- Transformation to Geographical Coordinates: Convert the right ascension and declination to the n-system using the latitude, longitude, and GHA.
- (4)
- Conversion to Geographical Coordinates: Convert the observed elevation angle to the n-system using the attitude provided by the INS.
- (5)
- Interpolation of Navigation Star 1 Data: Find the closest available elevation angle information for Navigation Star 1 at the current time and perform secondary interpolation. Since right ascension and declination change very slowly; no interpolation is needed for this.
- (6)
- Selection of Navigation Star 2: Find Navigation Star 2 between the current time and the interpolation time. Combine Navigation Star 1 and Navigation Star 2, using the observation time of Navigation Star 2 as the reference time.
- (7)
- Calculation of Angular Separation: Determine the angular separation between Navigation Star 1 and Navigation Star 2.
- (8)
- Evaluation of Star Separation and Zenith Distance Relationship: Calculate the relationship between the angular separation and the two zenith distances, and evaluate whether Navigation Star 1 and Navigation Star 2 can be combined to complete the two-star positioning.
- (9)
- Solution Determination: If the conditions are met, solve for the two-star positioning solution. If the conditions are not met, discard this combination and repeat steps 1 through 7.
4. Experiments
4.1. Navigation Star Selection for Simulation Experiment
4.2. Comparison of Numerical Solution Accuracy with Other Closed Analytic Methods
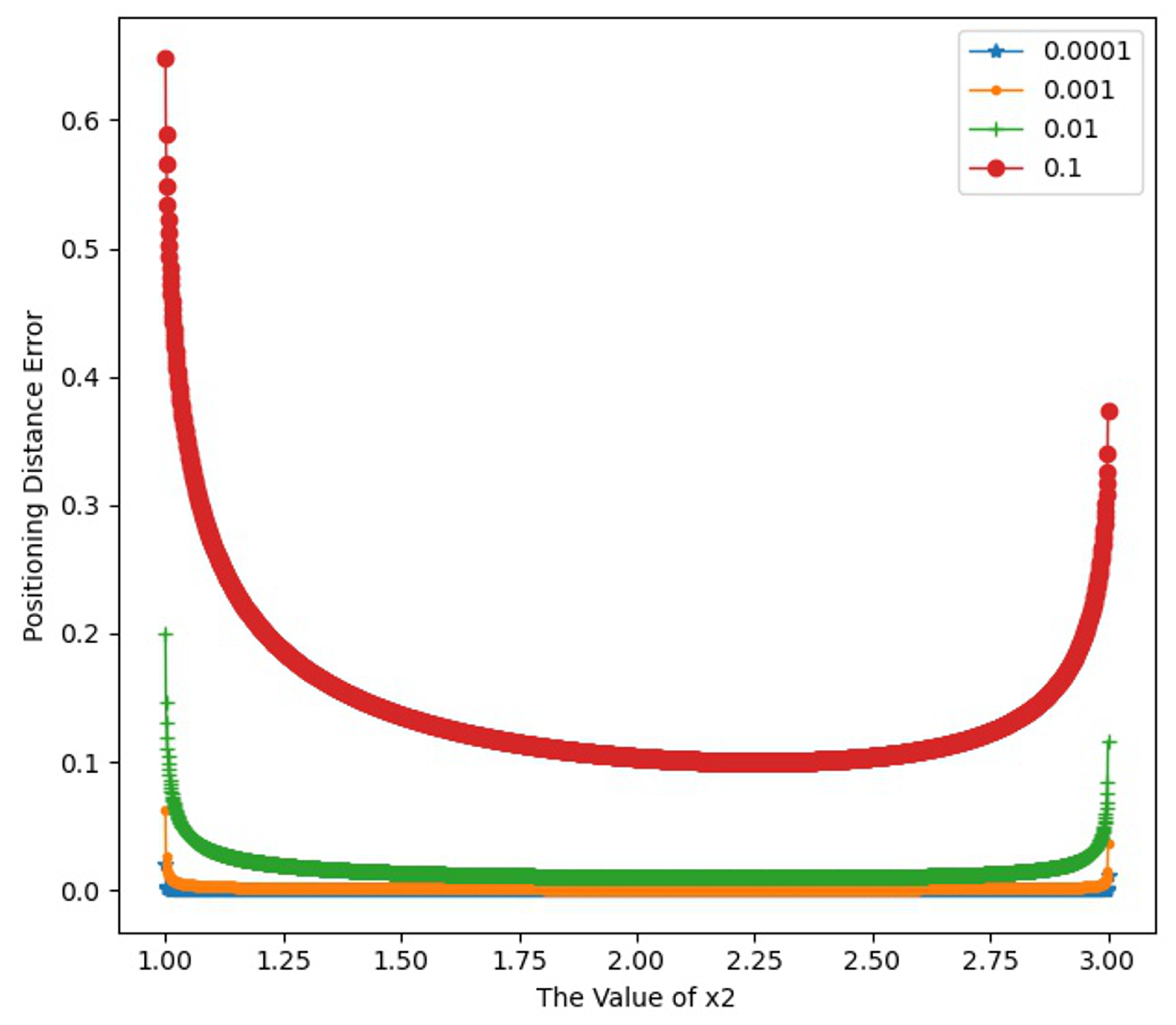
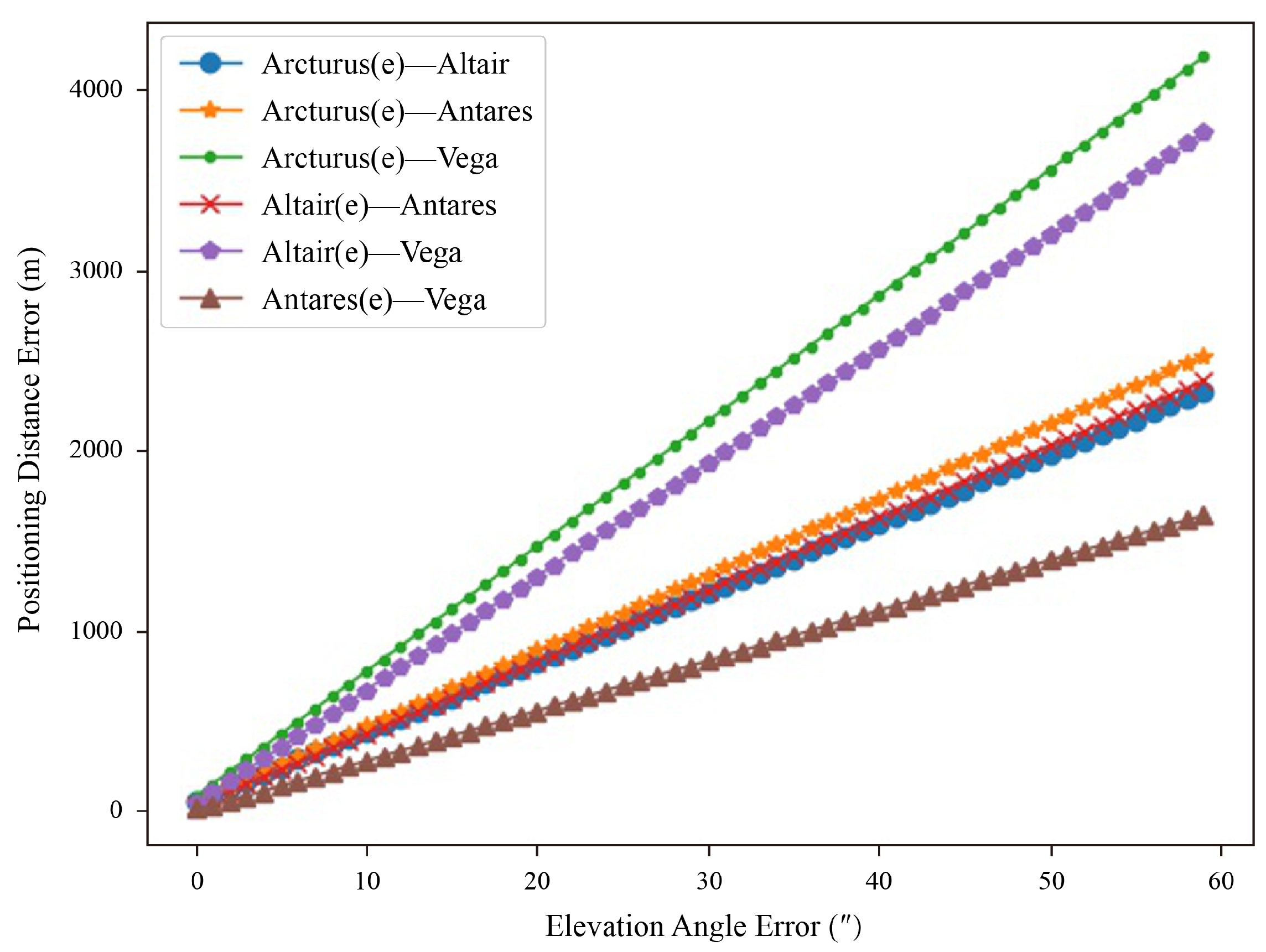
4.3. Simulation Analysis of Positioning Accuracy
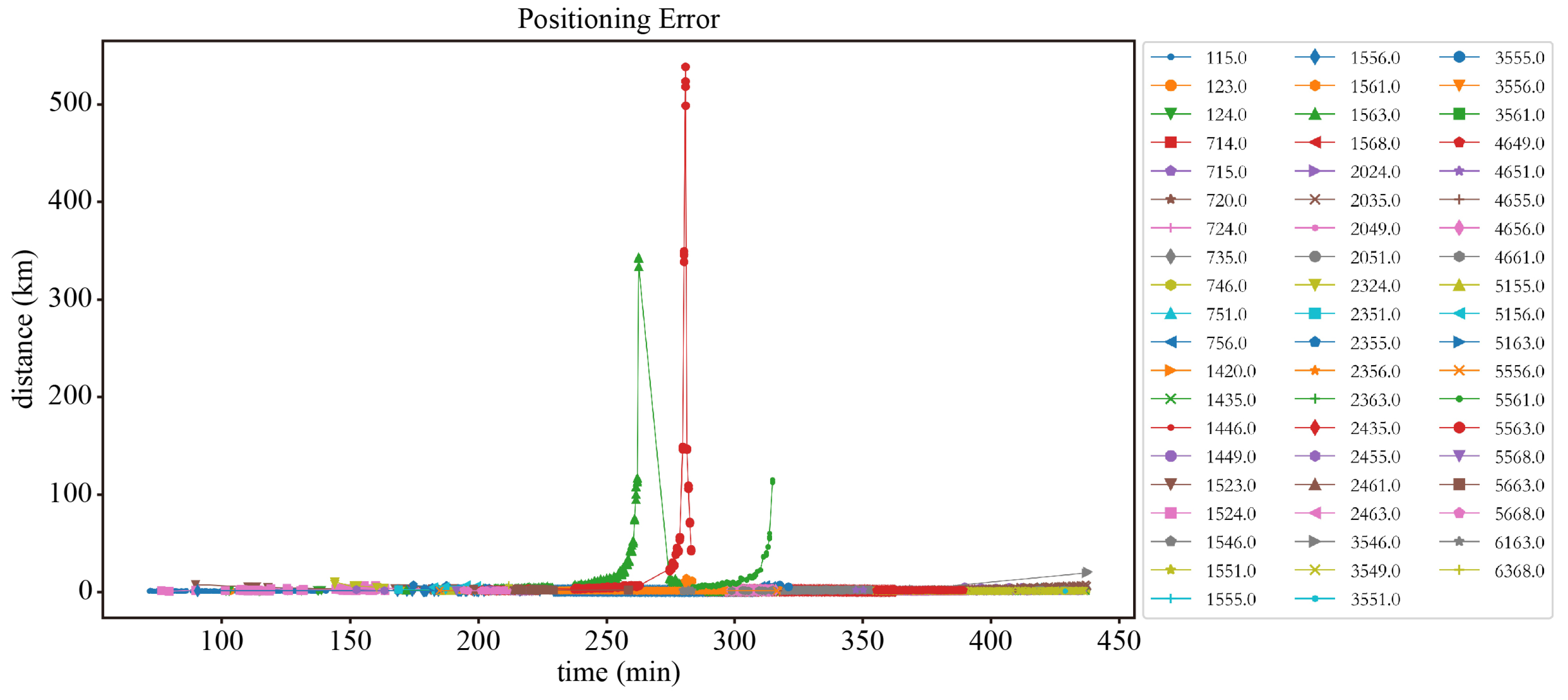
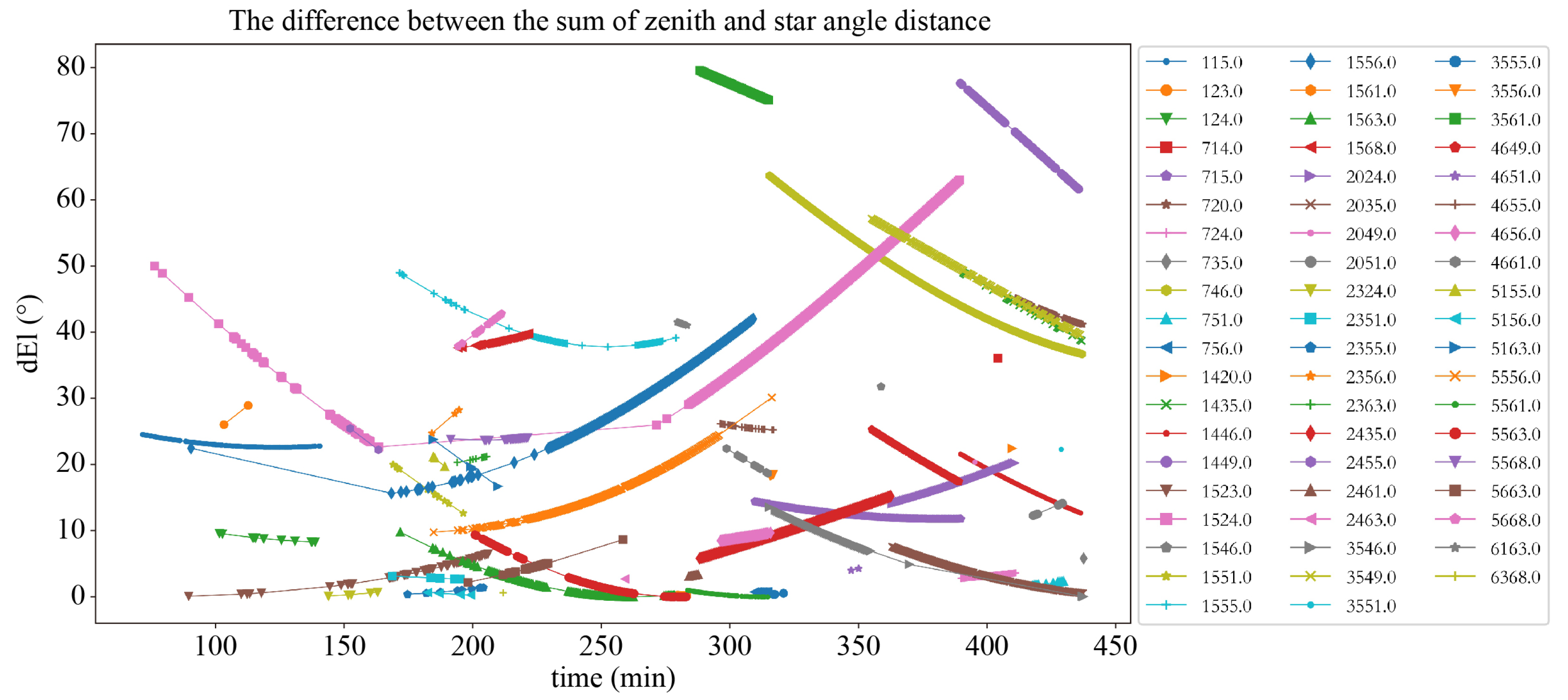
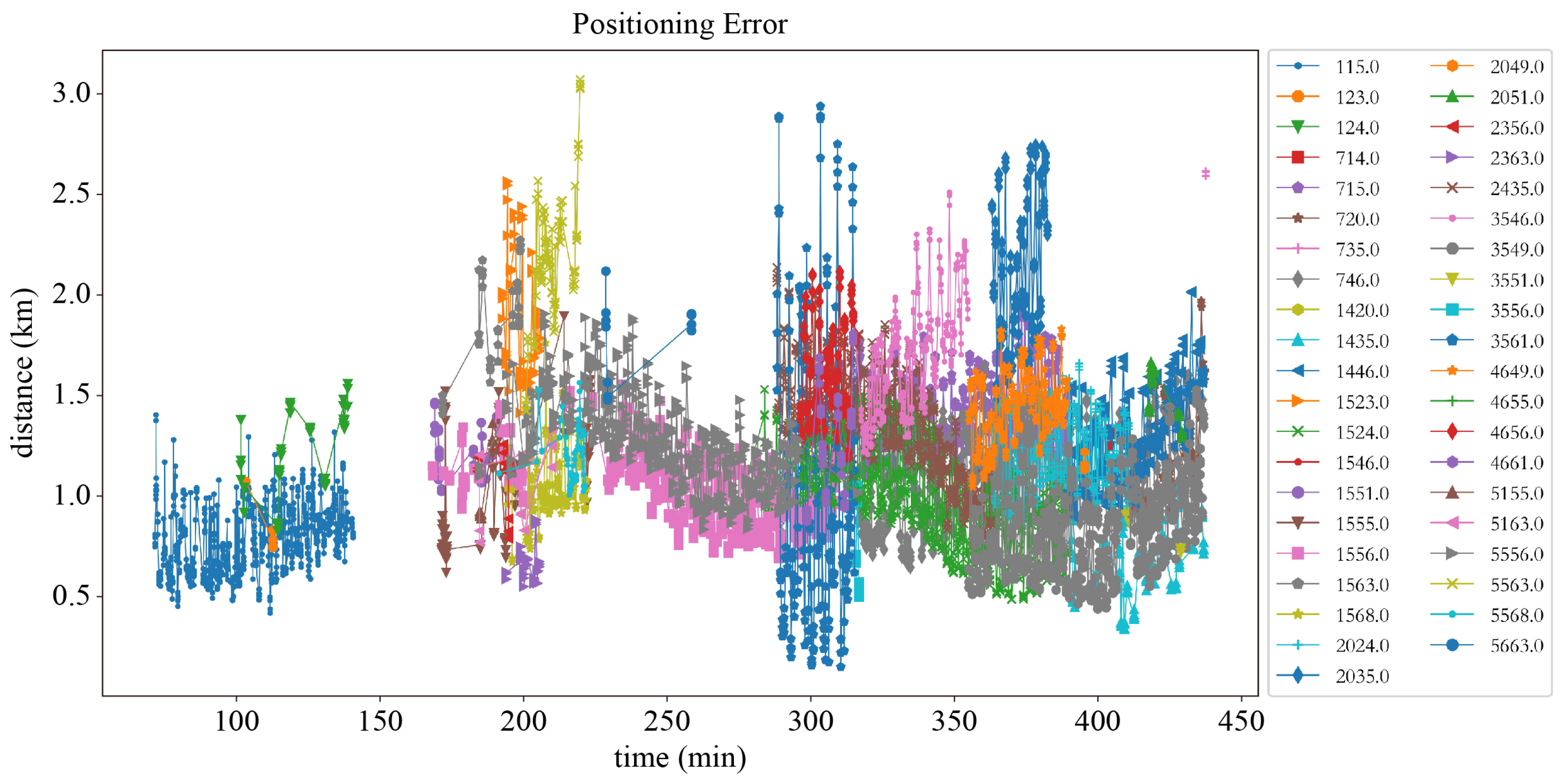
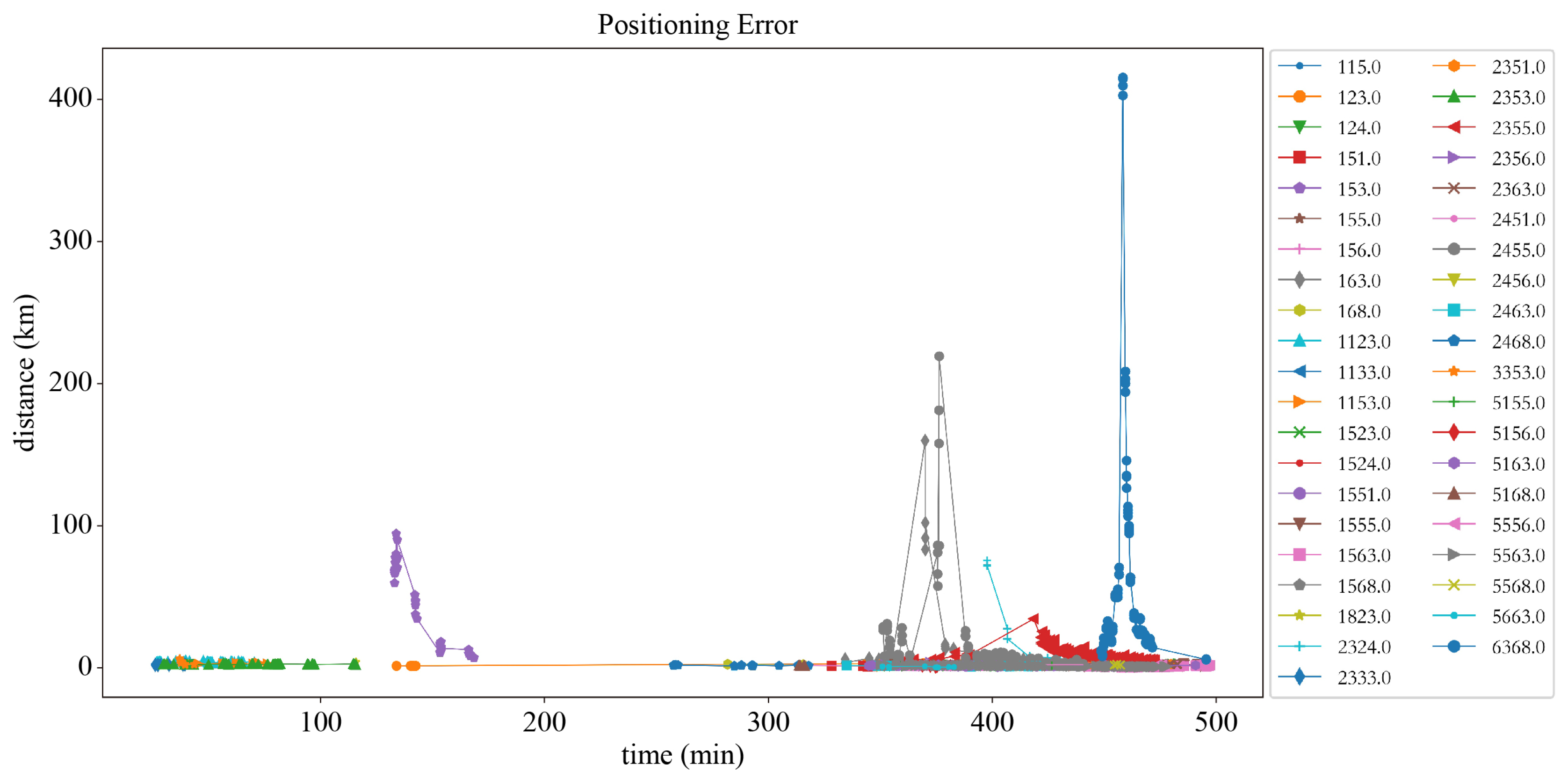
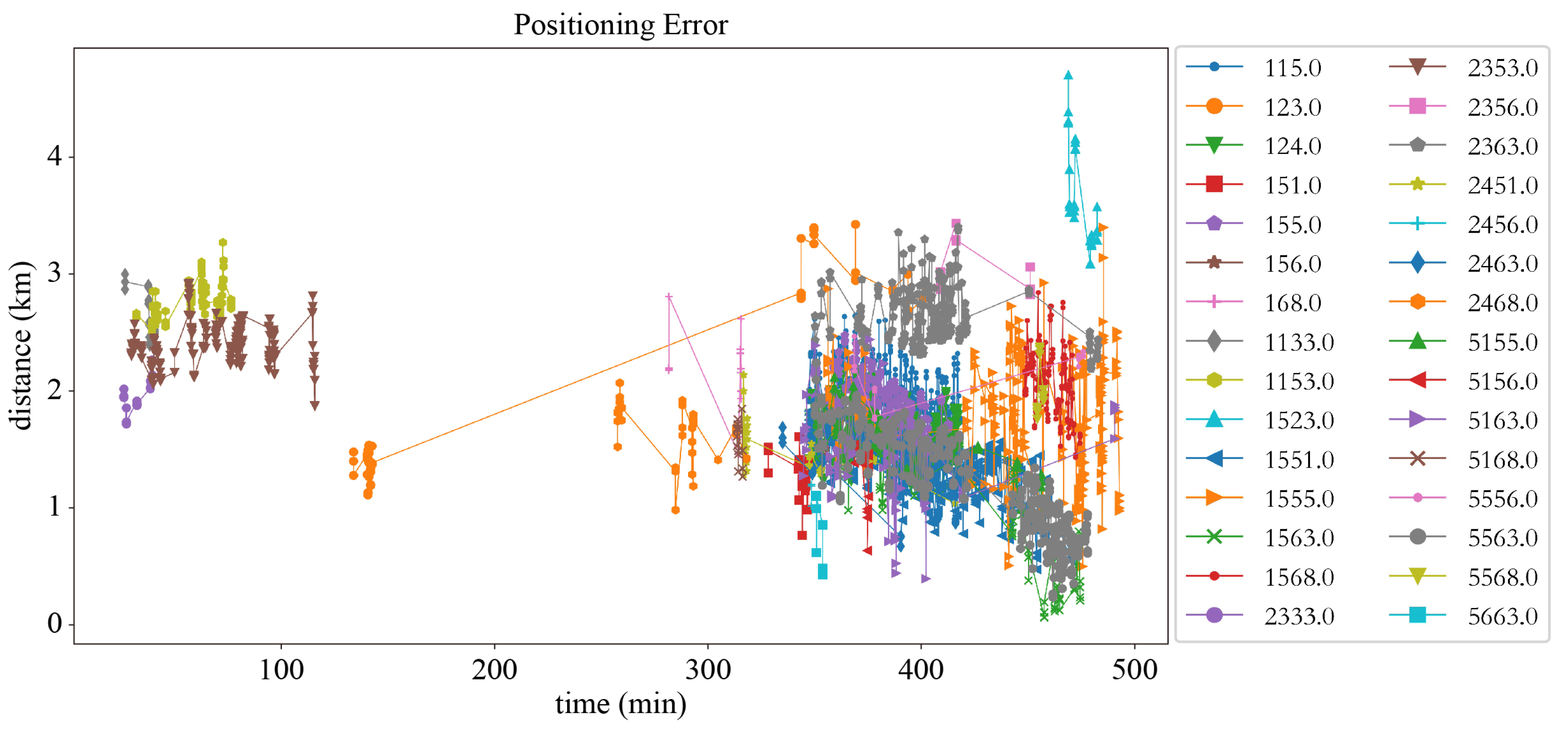
4.4. Ground-Based Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Howell, S.P. Practical Celestial Navigation; Rowman & Littlefield: Lanham, MD, USA, 2023. [Google Scholar]
- Critchley-Marrows, J.J.; Mortari, D. A Return to the Sextant—Maritime Navigation Using Celestial Bodies and the Horizon. Sensors 2023, 23, 4869. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zhang, M. Inertial navigation system gyroscopic on-line calibration assisted by marine star sensor based on forgetting factor selection of a Sage-Husa filter. J. Mar. Eng. Technol. 2022, 21, 1–8. [Google Scholar] [CrossRef]
- Rad, A.M.; Nobari, J.H.; Nikkhah, A.A. Optimal attitude and position determination by integration of INS, star tracker, and horizon sensor. IEEE Aerosp. Electron. Syst. Mag. 2014, 29, 20–33. [Google Scholar] [CrossRef]
- Zheng, X.; Huang, Y.; Mao, X.; He, F.; Ye, Z. Research status and key technologies of all-day star sensor. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1510, p. 012027. [Google Scholar]
- Han, J.; Wang, C.; Li, B. High accuracy method of positioning based on multi-star-sensor. In Proceedings of the 2016 Seventh International Conference on Intelligent Control and Information Processing (ICICIP), Siem Reap, Cambodia, 1–4 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 236–242. [Google Scholar]
- Nguyen, V.S.; Im, N. Development of computer program for solving astronomical ship position based on circle of equal altitude equation and SVD-least square algorithm. J. Navig. Port Res. 2014, 38, 89–96. [Google Scholar] [CrossRef]
- Pierros, F. Stand-alone celestial navigation positioning method. J. Navig. 2018, 71, 1344–1362. [Google Scholar] [CrossRef]
- Van Allen, J.A. An analytical solution of the two star sight problem of celestial navigation. Navigation 1981, 28, 40–43. [Google Scholar] [CrossRef]
- Tsai, K.C.; Tseng, W.K.; Chen, C.L.; Sun, Y.J. A Novel Analytical Solution Method for Celestial Positioning. J. Mar. Sci. Eng. 2022, 10, 771. [Google Scholar] [CrossRef]
- Zhao, X.; Jia, H.; Wu, J.; Ma, Z. Research of Computer Assisted Astronomical Positioning Algorithm. In Proceedings of the 2009 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–4. [Google Scholar]
- Chen, C.L.; Hsu, T.P.; Chang, J.R. A novel approach to determine the astronomical vessel position. J. Mar. Sci. Technol. 2003, 11, 6. [Google Scholar] [CrossRef]
- Nguyen, V.S.; Im, N.K.; Dao, Q.D. Azimuth method for ship position in celestial navigation. Int. J. E-Navig. Marit. Econ. 2017, 7, 55–62. [Google Scholar] [CrossRef]
- Nguyen Thai Duong, L.T.N. Determining Ship’s Position by the Celestial Altitude Difference Using the Least Squares Method. J. Hunan Univ. Nat. Sci. 2021, 48, 199–207. [Google Scholar]
- Tsou, M.C. Celestial navigation fix based on particle swarm optimization. Pol. Marit. Res. 2015, 22, 20–27. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Lu, G.; Wang, W.; Wang, A.G. An Optimization Model and Genetic Algorithm Solution for Automated Celestial Navigation of Ships. Appl. Mech. Mater. 2014, 548, 1277–1281. [Google Scholar] [CrossRef]
- Tsou, M.C. Genetic algorithm for solving celestial navigation fix problems. Pol. Marit. Res. 2012, 19, 53–59. [Google Scholar] [CrossRef]
- Li, C.h.; Chen, Z.l.; Liu, X.j.; Chen, B.; Zheng, Y.; Tong, S.; Wang, R.P. Adaptively robust filtering algorithm for maritime celestial navigation. J. Navig. 2022, 75, 200–212. [Google Scholar] [CrossRef]
- Khan, A.H.; Cao, X.; Li, S.; Katsikis, V.N.; Liao, L. BAS-ADAM: An ADAM based approach to improve the performance of beetle antennae search optimizer. IEEE/CAA J. Autom. Sin. 2020, 7, 461–471. [Google Scholar] [CrossRef]
- Bate, R.R.; Mueller, D.D.; White, J.E.; Saylor, W.W. Fundamentals of Astrodynamics; Courier Dover Publications: Mineola, NY, USA, 2020. [Google Scholar]
- Yang, S.; Feng, W.; Wang, S.; Li, J. A SINS/CNS integrated navigation scheme with improved mathematical horizon reference. Measurement 2022, 195, 111028. [Google Scholar] [CrossRef]
- Zheng, Z.; Han, S.; Zheng, K. An eight-position self-calibration method for a dual-axis rotational inertial navigation system. Sens. Actuators A Phys. 2015, 232, 39–48. [Google Scholar] [CrossRef]
- Lu, J.; Lei, C.; Liang, S.; Yang, Y. An all-parameter system-level calibration for stellar-inertial navigation system on ground. IEEE Trans. Instrum. Meas. 2017, 66, 2065–2073. [Google Scholar] [CrossRef]

| Observation GHA: 339.534° | |||
|---|---|---|---|
| Location: Longitude 91.532° W; Latitude 41.662° N | |||
| Star | Right Ascension (°) | Declination (°) | Elevation Angle (°) |
| Arcturus | −125.915 | 19.317 | 36.704 |
| Altair | −42.156 | 8.799 | 54.382 |
| Antares | −92.581 | −26.376 | 68.045 |
| Vega | −60.520 | 38.759 | 23.731 |
| James A. Van Allen Method (°) | King-Cheng Tsai Method (°) | Our Method (°) | ||||
|---|---|---|---|---|---|---|
| Star Combination | Position 1 | Position 2 | Position 1 | Position 2 | Position 1 | Position 2 |
| Arcturus—Altair | 41.661 | −2.148 | 41.6615 | −2.1484 | 41.66149 | −2.14840 |
| −91.532 | −95.605 | −91.5321 | −95.6052 | −91.53208 | −95.60520 | |
| Arcturus—Antares | 41.662 | 0.136 | 41.6621 | 0.1361 | 41.66208 | 0.13607 |
| −91.532 | −157.841 | −91.5325 | −157.8410 | −91.53248 | −157.84100 | |
| Arcturus—Vega | 41.661 | 29.334 | 41.6613 | 29.3340 | 41.66128 | 29.33396 |
| −91.532 | −86.95 | −91.5319 | −86.9504 | −91.53194 | −86.95039 | |
| Antares—Vega | 41.662 | 21.009 | 41.6621 | 21.0094 | 41.66207 | 21.00941 |
| −91.532 | −42.186 | −91.5320 | −42.1856 | −91.53200 | −42.18559 | |
| Altair—Vega | 41.662 | 62.295 | 41.6617 | 62.2952 | 41.66169 | 62.29522 |
| −91.532 | −55.55 | −91.5320 | −55.5504 | −91.53197 | −55.55036 | |
| Altair—Antares | 41.662 | −37.143 | 41.6621 | −37.1432 | 41.66207 | −37.14315 |
| −91.532 | −11.087 | −91.5318 | −11.0869 | −91.53176 | −11.08690 | |
| Star Combination | Position | James A. Van Allen Method (°) | King-Cheng Tsai Method (°) | Our Method (°) | Ours–James (″) | Ours-Tsai (″) |
|---|---|---|---|---|---|---|
| Arcturus—Altair | Position 1 | 41.661 | 41.6615 | 41.66149 | 1.7712 | −0.0288 |
| Position 2 | −2.148 | −2.1484 | −2.14840 | −1.4256 | 0.0144 | |
| Arcturus—Antares | Position 1 | 41.662 | 41.6621 | 41.66208 | 0.2772 | −0.0228 |
| Position 2 | 0.136 | 0.1361 | 0.13607 | 0.2412 | 0.0012 | |
| Arcturus—Vega | Position 1 | 41.661 | 41.6613 | 41.66128 | 0.9972 | −0.0228 |
| Position 2 | 29.334 | 29.3340 | 29.33396 | −0.144 | −0.024 | |
| Antares—Vega | Position 1 | 41.662 | 41.6621 | 41.66207 | 0.252 | 0.012 |
| Position 2 | 21.009 | 21.0094 | 21.00941 | 1.458 | 0.018 | |
| Altair—Vega | Position 1 | 41.662 | 41.6617 | 41.66169 | −1.1016 | 0.0384 |
| Position 2 | 62.295 | 62.2952 | 62.29522 | 0.7776 | −0.0024 | |
| Altair—Antares | Position 1 | 41.662 | 41.6621 | 41.66207 | 0.2412 | 0.0012 |
| Position 2 | −37.143 | −37.1432 | −37.14315 | −0.5328 | 0.0072 |
| Star Combination | Position | James A. Van Allen Method (°) | King-Cheng Tsai Method (°) | Our Method (°) | Ours–James (″) | Ours-Tsai (″) |
|---|---|---|---|---|---|---|
| Arcturus—Altair | Position 1 | −91.532 | −91.5321 | −91.53208 | −0.2952 | 0.0048 |
| Position 2 | −95.605 | −95.6052 | −95.60520 | −0.702 | 0.018 | |
| Arcturus—Antares | Position 1 | −91.532 | −91.5325 | −91.53248 | −1.728 | 0.012 |
| Position 2 | −157.841 | −157.8410 | −157.84100 | −0.0072 | −0.0072 | |
| Arcturus—Vega | Position 1 | −91.532 | −91.5319 | −91.53194 | 0.2268 | −0.0132 |
| Position 2 | −86.95 | −86.9504 | −86.95039 | −1.4184 | 0.0216 | |
| Antares—Vega | Position 1 | −91.532 | −91.5320 | −91.53200 | 0.0036 | 0.0036 |
| Position 2 | −42.186 | −42.1856 | −42.18559 | 1.4652 | 0.0252 | |
| Altair—Vega | Position 1 | −91.532 | −91.5320 | −91.53197 | 0.1116 | −0.0084 |
| Position 2 | −55.55 | −55.5504 | −55.55036 | −1.2996 | −0.0396 | |
| Altair—Antares | Position 1 | −91.532 | −91.5318 | −91.53176 | 0.864 | 0.024 |
| Position 2 | −11.087 | −11.0869 | −11.08690 | 0.3492 | −0.0108 |
| Star Combination | Two-Circle Position | Star Angular Distance (°) | The Sum of the Zenith (°) | The Difference of the Zenith (°) | Difference (°) |
|---|---|---|---|---|---|
| Arcturus—Altair | External | 74.617 | 88.443 | / | 13.826 |
| Arcturus—Antare | Internal | 53.784 | / | 28.037 | 25.747 |
| Arcturus—Vega | External | 56.518 | 59.641 | / | 3.123 |
| Altair—Antares | Internal | 57.519 | / | 11.752 | 45.767 |
| Altair—Vega | Internal | 33.690 | / | 28.802 | 4.888 |
| Antares—Vega | Internal | 67.115 | / | 40.554 | 26.561 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Zhuo, C.; He, T.; Liu, G.; Liu, Q. A Vessel Position Precision Analysis Based on a Two-Star Combined Approach. J. Mar. Sci. Eng. 2024, 12, 2347. https://doi.org/10.3390/jmse12122347
Wu Y, Zhuo C, He T, Liu G, Liu Q. A Vessel Position Precision Analysis Based on a Two-Star Combined Approach. Journal of Marine Science and Engineering. 2024; 12(12):2347. https://doi.org/10.3390/jmse12122347
Chicago/Turabian StyleWu, Yulin, Chao Zhuo, Tao He, Gangjun Liu, and Qingqing Liu. 2024. "A Vessel Position Precision Analysis Based on a Two-Star Combined Approach" Journal of Marine Science and Engineering 12, no. 12: 2347. https://doi.org/10.3390/jmse12122347
APA StyleWu, Y., Zhuo, C., He, T., Liu, G., & Liu, Q. (2024). A Vessel Position Precision Analysis Based on a Two-Star Combined Approach. Journal of Marine Science and Engineering, 12(12), 2347. https://doi.org/10.3390/jmse12122347






