Numerical Permeation Models to Predict the Annulus Composition of Flexible Pipes
Abstract
:1. Introduction
2. Modeling Principles
2.1. Mass Transport
2.2. Physical Parameters in Mass Transport
2.2.1. Dry Annulus
2.2.2. Flooded Annulus
2.2.3. Polymeric Barriers
2.3. Thermodynamic Equilibrium in the Annulus
2.4. Heat Transfer in Flexible Pipes
3. Numerical Model
3.1. Assumptions
- Non-ideal representation of the species behavior, as discussed in Section 2;
- Continuity in the annulus of the pipe, including at the layers’ interfaces. In contrast, the concentration of the species has a discontinuous distribution;
- Better agreement with experimental measurements, according to Last et al. [10].
- Equaling temperature and fugacity ;
- Equaling thermal conductivity and permeability ;
- Matching the specific heat capacity with the solubility coefficient ;
- Assuming density as unitary.
3.2. Two-Dimensional FE Model (2DFE)

3.3. Three-Dimensional FE Model (3DFE)
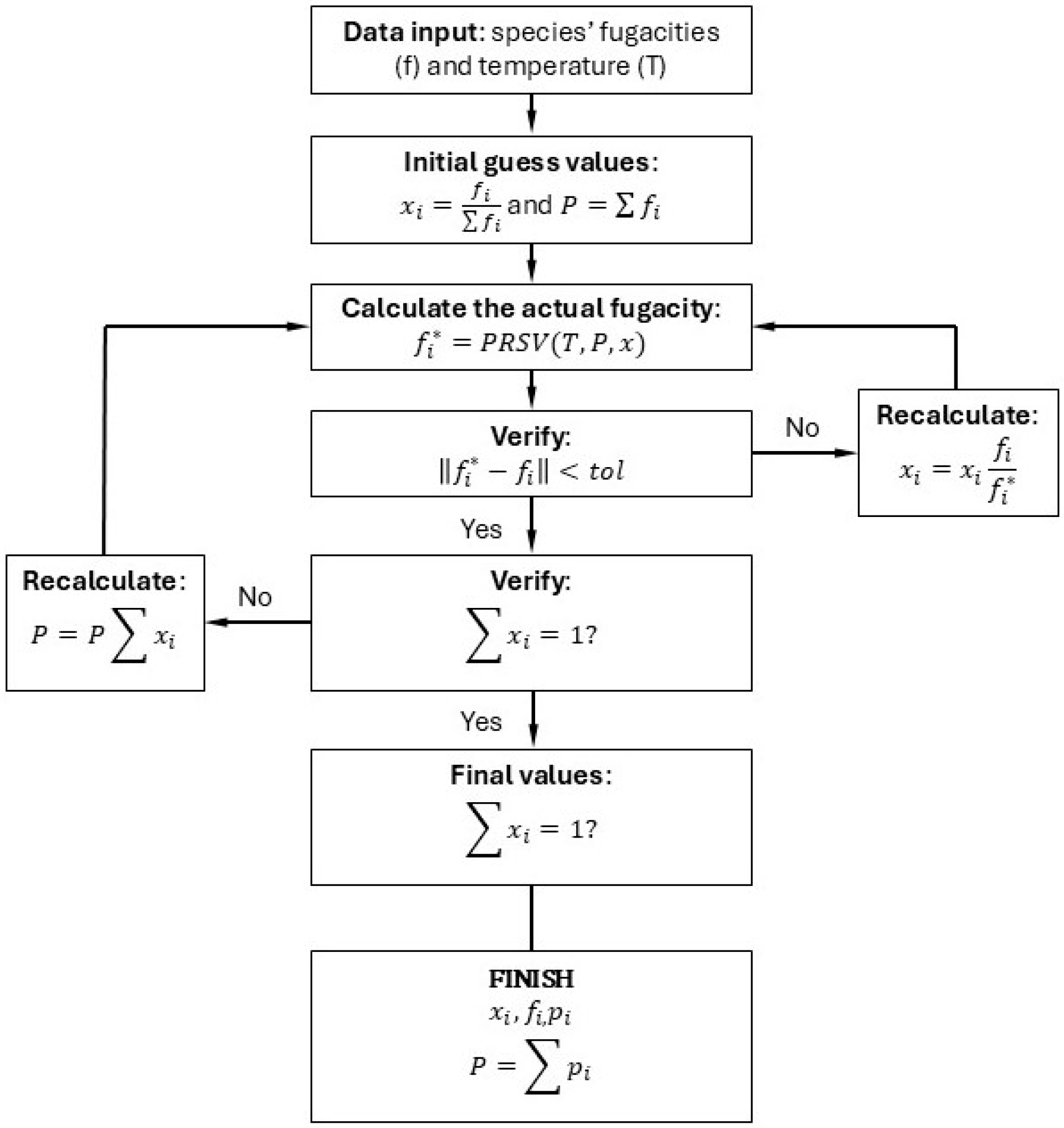
3.4. Implementation
4. Case Study
4.1. Description
- Internal and external temperatures of 60 °C and 5 °C, respectively;
- Internal and external pressures of 500 bar and 200 bar, respectively;
- CO2 and CH4 fugacities of 100 bar and 190 bar, respectively. These fugacities correspond to a bore composition of 60% CH4 and 40% CO2;
- Both wet and dry conditions;
- Total permeation analysis time of 2 years.
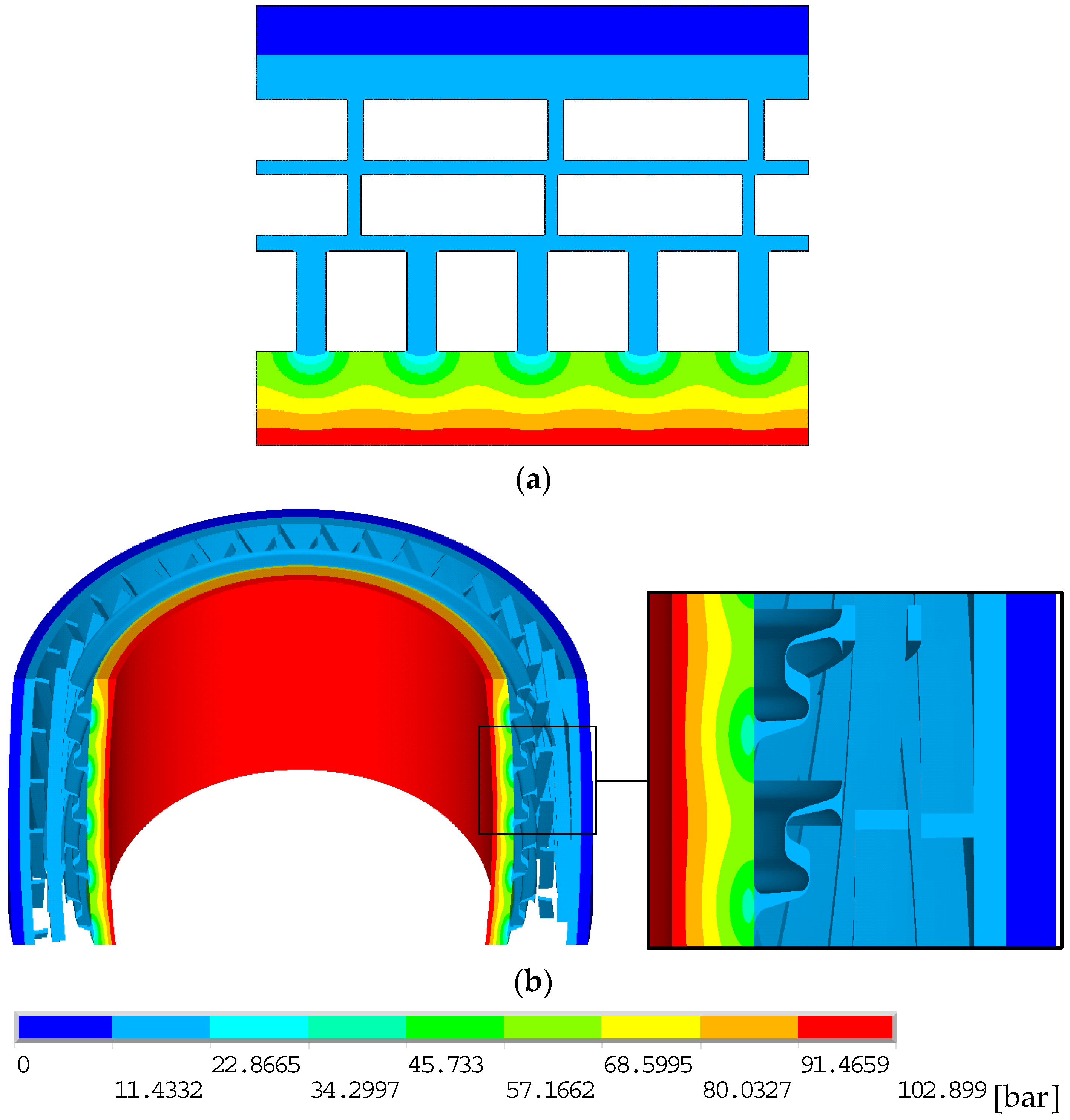
4.2. Thermal Analysis
4.3. Permeation Analyses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- API. API RP 17B: Recommended Practice for Flexible Pipe, 6th ed.; American Petroleum Institute: Washington, DC, USA, 2024. [Google Scholar]
- Revie, R.W.; Uhlig, H.H. Corrosion and Corrosion Control: An Introduction to Corrosion Science and Engineering, 4th ed.; Wiley-Interscience: Hoboken, NJ, USA, 2008; pp. 150–166. [Google Scholar]
- ANP. Stress Corrosion Due to CO2 (SCC-CO2). Security Alert 001. Agência Nacional do Petróleo. 2017. Available online: https://www.gov.br/anp/pt-br/assuntos/exploracao-e-producao-de-oleo-e-gas/seguranca-operacional/incidentes/arquivos-alertas-de-seguranca/alerta-01/alerta-de-seguranca_001_ssm_scc-co2_pt.pdf (accessed on 19 November 2024). (In Portuguese)
- Fonseca, D.; Tagliari, M.R.; Guaglianoni, W.C.; Tamborim, S.M.; Borges, M.F. Carbon Dioxide Corrosion Mechanisms: Historical Development and Key Parameters of CO2-H2O Systems. Int. J. Corros. 2024, 2024, 5537767. [Google Scholar] [CrossRef]
- de Motte, R.; Joshi, G.; Chehuan, T.; Legent, R.; Kittel, J.; Désamais, N. CO2-SCC in Flexible Pipe Carbon Steel Armour Wires. Corrosion 2022, 78, 547–562. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Fried, E.; Anand, L. The Mechanics and Thermodynamics of Continua; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Eide, J.T.W.; Muren, J. Lifetime assessment of flexible pipes. In Proceedings of the ASME 2014 33rd International Conference on Offshore Mechanics and Arctic Engineering (OMAE2014), San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Eriksen, M.; Engelbreth, K.I. Outer cover damages on flexible pipes—Corrosion and integrity challenges. In Proceedings of the ASME 2014 33rd International Conference on Offshore Mechanics and Arctic Engineering (OMAE2014), San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Kristensen, A.B. Diffusion in Flexible Pipes. Master’s Dissertation, Technical University of Denmark, Lingby, Denmark, 2000. [Google Scholar]
- Benjelloun-Dabaghi, Z.; Hemptinne, J.-C.; Jarrin, J.; Leroy, J.-M.; Aubry, J.-C.; Saas, J.N.; Condat, C.T. MOLDITM: A Fluid Permeation Model to Calculate the Annulus Composition in Flexible Pipes. Oil Gas Sci. Technol. 2002, 57, 177–192. [Google Scholar]
- Taravel-Condat, C.; Guichard, M.; Martin, J. MOLDITM: A Fluid Permeation Model to Calculate the Annulus Composition in Flexible Pipes—Validation With Medium Scale Tests, Full Scale Tests and Field Cases. In Proceedings of the OMAE03 22nd International Conference on Offshore Mechanics and Arctic Engineering, Cancun, Mexico, 8–13 June 2003. [Google Scholar]
- Last, S.; Groves, S.; Rigaud, J.; Taravel-Condat, C.; Wedel-Heinen, J.; Clements, R.; Buchner, S. Comparison of Models to Predict the Annulus Conditions of Flexible Pipe. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2002. [Google Scholar]
- Lefebvre, X.; Khvoenkova, N.; de Hemptinne, J.C.; Lefrançois, L.; Radenac, B.; Pignoc-Chicheportiche, S.; Plennevaux, C. Prediction of Flexible Pipe Annulus Composition by Numerical Modeling: Identification of Key Parameters. Sci. Technol. Energy Transit. 2022, 77, 1–11. [Google Scholar] [CrossRef]
- Ansys, Inc. Ansys® Mechanical APDL (Release 2023 R1); ANSYS, Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Frisch, H.L. Sorption and Transport of Penetrants in Glassy Polymers. Polym. Eng. Sci. 1980, 20, 2–13. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Poling, B.E.; O’Connell, J.P. Properties of Gases and Liquids, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Lewis, G.N.; Randal, M. Thermodynamics and the Free Energy of Chemical Substances, 1st ed.; McGraw-Hill Book Company: New York, NY, USA, 1923. [Google Scholar]
- Hemond, H.F.; Fechner, E.J. Chemical Fate and Transport in the Environment, 4th ed.; Elsevier: San Diego, CA, USA, 2022. [Google Scholar]
- Fuller, E.N.; Schettler, P.D.; Giddings, C.J. New method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 1966, 58, 19–27. [Google Scholar] [CrossRef]
- Chang, P.; Wilke, C.R. Some Measurements of Diffusion in Liquids. J. Phys. Chem. 1955, 59, 592–596. [Google Scholar] [CrossRef]
- Kontogeorgis, G.; Voutsas, E.; Yakoumis, I.; Tassios, D. An Equation of State for Associating Fluids. Ind. Eng. Chem. Res. 1996, 45, 4310–4318. [Google Scholar] [CrossRef]
- Diamond, L.W.; Akinfiev, N.N. Thermodynamic description of aqueous nonelectrolytes at infinite dilution over a wide range of state parameters. Geochim. Cosmochim. Acta 2003, 67, 613–629. [Google Scholar]
- Diamond, L.W.; Akinfiev, N.N. Solubility of CO2 in water from −1.5 to 100 °C and from 0.1 to 100 MPa: Evaluation of literature data and thermodynamic modeling. J. Chem. Thermodyn. 2003, 208, 265–290. [Google Scholar] [CrossRef]
- Flaconnèche, B.; Martin, J.; Klopffer, M.H. Permeability, Diffusion and Solubility of Gases in Polyethylene, Polyamide 11 and Poly (Vinylidene Fluoride). Oil Gas Sci. Technol. 2001, 56, 261–278. [Google Scholar] [CrossRef]
- Stryjek, R.; Vera, J. PRSV—An Improved Peng-Robinson Equation of State for Pure Compounds and Mixtures. Can. J. Chem. Eng. 1986, 64, 323–333. [Google Scholar] [CrossRef]
- Vieira, J.M.B. Numerical Models to Predict Gases Diffusion in the Annulus of Flexible Pipes. Master’s Dissertation, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil, 2023. Available online: http://www.coc.ufrj.br/pt/dissertacoes-de-mestrado/661-2022-5/10176-joao-marcos-bastos-vieira-3 (accessed on 19 November 2023). (In Portuguese).
- de Sousa, J.R.M.; de Sousa, F.J.M.; de Siqueira, M.Q.; Sagrilo, L.V.S.; de Lemos, C.A.D. A Theoretical Approach to Predict the Fatigue Life of Flexible Pipes. J. Appl. Math. 2012, 2012, 983819. [Google Scholar] [CrossRef]
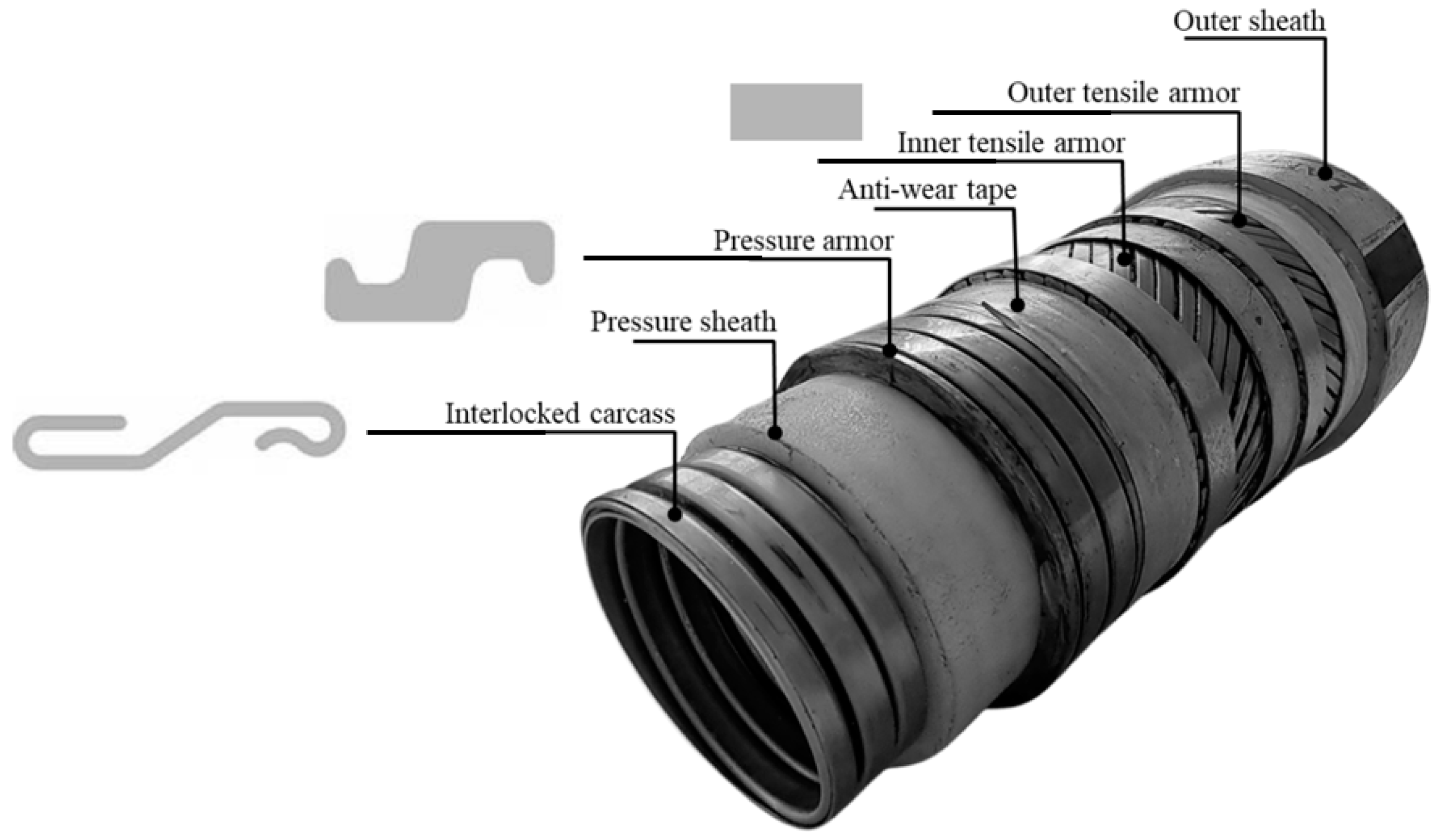











| No. | Layer (Material) | Properties |
|---|---|---|
| 1 | Inner carcass 1 (stainless steel) | Thickness = 7.5 mm; Width = -; No of wires = 1; Lay angle = 87.8°; intralayer gap, s = - |
| 2 | Pressure sheath (PA11) | Thickness = 9.3 mm |
| 3 | Pressure armor (carbon steel) | Thickness = 10.0 mm; Width = 10.5 mm; No. of wires = 2; Lay angle = 87.6°; intralayer gap, s = 3.9 mm |
| 4 | Antiwear tape (polymeric tape) | Thickness = 1.5 mm; Width = 60.0 mm; No. of tapes = 1; Lay angle = 79.7°; intralayer gap, s = 3.0 mm |
| 5 | Inner tensile armor (carbon steel) | Thickness = 6.0 mm; Width = 14.0 mm; No. of wires = 2; Lay angle = 35.0°; intralayer gap, s = 1.3 mm |
| 6 | Antiwear tape (polymeric tape) | Thickness = 1.5 mm; Width = 60.0 mm; No. of tapes = 1; Lay angle = 79.7°; intralayer gap, s = 3.0 mm |
| 7 | Outer tensile armor (carbon steel) | Thickness = 6.0 mm; Width = 14.0 mm; No. of wires = 2; Lay angle = −35.0°; intralayer gap, s = 1.7 mm |
| 8 | Anti-buckling tape (aramid fiber) | Thickness = 2.3 mm |
| 9 | Outer sheath (HDPE) | Thickness = 9.3 mm |
| Material | (W/mK) | Gas | (cm2/s) | (J/mol) | (cm3(STP)/cm3) | (J/mol) |
|---|---|---|---|---|---|---|
| Stainless steel | 15.0 | CO2 | - | - | - | - |
| CH4 | - | - | - | - | ||
| Carbon steel | 45.0 | CO2 | - | - | - | - |
| CH4 | - | - | - | - | ||
| Polymeric tape | 0.24 | CO2 | - | - | - | - |
| CH4 | - | - | - | - | ||
| Aramid fiber | 0.20 | CO2 | - | - | - | - |
| CH4 | - | - | - | - | ||
| PA11 | 0.24 | CO2 | 0.40 | 36,000 | 5.40 × 10−3 | −12,000 |
| CH4 | 4.50 | 45,000 | 7.50 × 10−2 | 0 | ||
| HDPE | 0.54 | CO2 | 0.20 | 32,000 | 3.00 × 10−3 | −15,000 |
| CH4 | 0.50 | 36,000 | 2.50 × 10−2 | −7000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vieira, J.M.B.; de Sousa, J.R.M. Numerical Permeation Models to Predict the Annulus Composition of Flexible Pipes. J. Mar. Sci. Eng. 2024, 12, 2294. https://doi.org/10.3390/jmse12122294
Vieira JMB, de Sousa JRM. Numerical Permeation Models to Predict the Annulus Composition of Flexible Pipes. Journal of Marine Science and Engineering. 2024; 12(12):2294. https://doi.org/10.3390/jmse12122294
Chicago/Turabian StyleVieira, João Marcos B., and José Renato M. de Sousa. 2024. "Numerical Permeation Models to Predict the Annulus Composition of Flexible Pipes" Journal of Marine Science and Engineering 12, no. 12: 2294. https://doi.org/10.3390/jmse12122294
APA StyleVieira, J. M. B., & de Sousa, J. R. M. (2024). Numerical Permeation Models to Predict the Annulus Composition of Flexible Pipes. Journal of Marine Science and Engineering, 12(12), 2294. https://doi.org/10.3390/jmse12122294






