Design Optimization of a Marine Propeller Shaft for Enhanced Fatigue Life: An Integrated Computational Approach
Abstract
1. Introduction
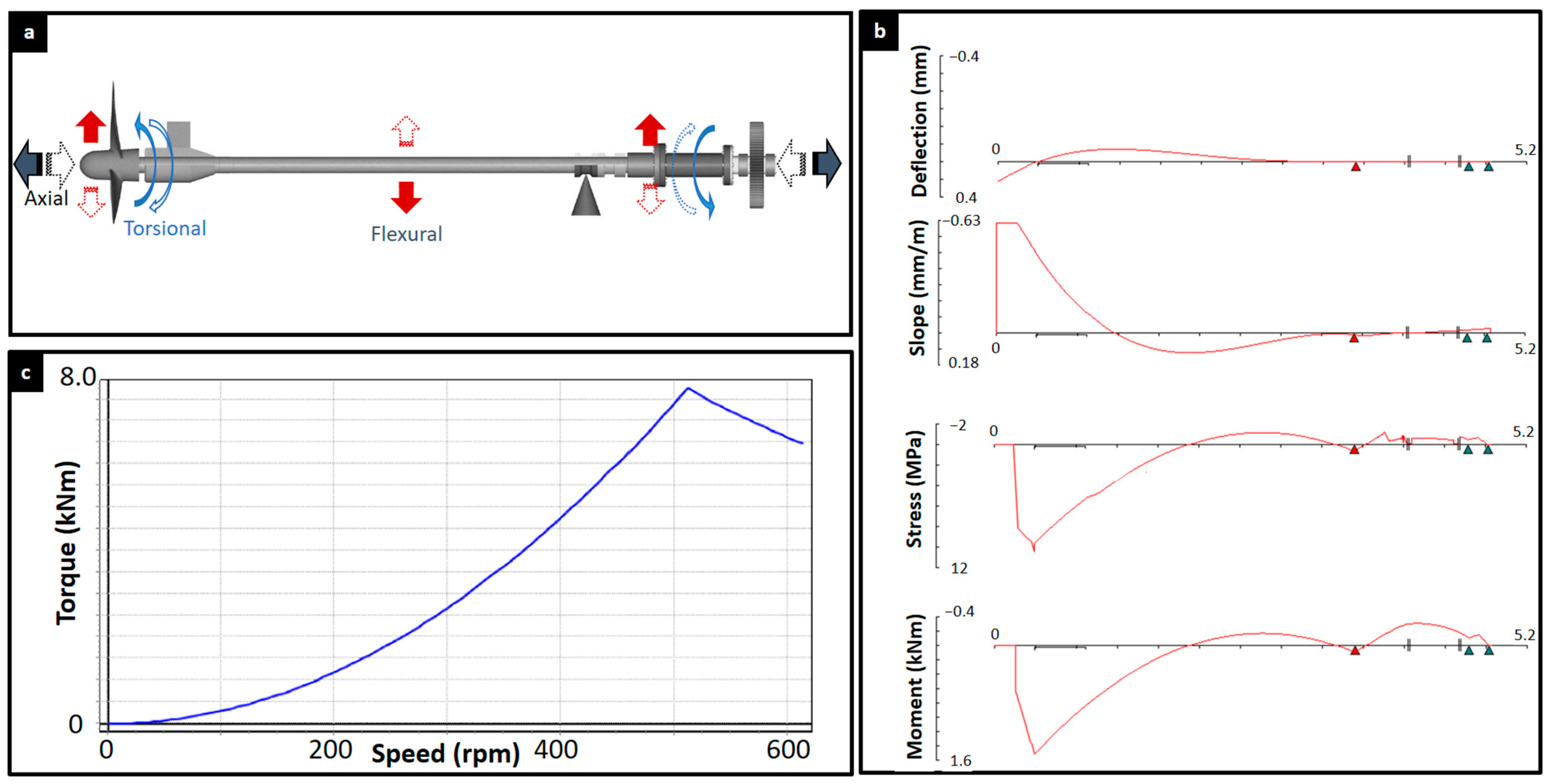
Configuration and Components of the Propulsion System
2. Materials and Methods
2.1. Methods for Calculating the Propeller Shaft Line
- Direct theoretical calculations to define the dimensions and operational speed ranges of the shaft.
- Simulation of the propeller line using ShaftDesigner software to analyze its dynamic behavior under operational conditions.
- Post-simulation evaluation in ShaftDesigner to estimate the service life of the propeller shaft.
- Analysis of torsional behavior using SolidWorks 2020 to evaluate the shaft’s performance under pure torsional loads.
- Simulations of proposed modifications or redesigns to assess improvements in load-bearing capacity.
2.2. Vibration Analysis on the Marine Propeller Shaft
2.3. Fatigue Life Cycles
2.3.1. Fatigue Strength Limit
2.3.2. Variable and Fluctuating Stresses
2.3.3. Fatigue Failure Under Fluctuating Combined Stresses
2.4. Component Analysis: Resistance and Failure in Operational Conditions
2.4.1. Keys and Keyseats
2.4.2. Shaft Fatigue Life
2.4.3. Computational Simulations of Shaft Strength Using Finite Elements
3. Results and Discussion
3.1. Direct Calculations of Shaft Diameter
3.2. Support Spacing Determination from Natural Frequency Calculations
3.2.1. Support Spacing from Natural Frequency Using the Ship Vibration Design Guide
3.2.2. Support Spacing Using Empirical Calculation Method
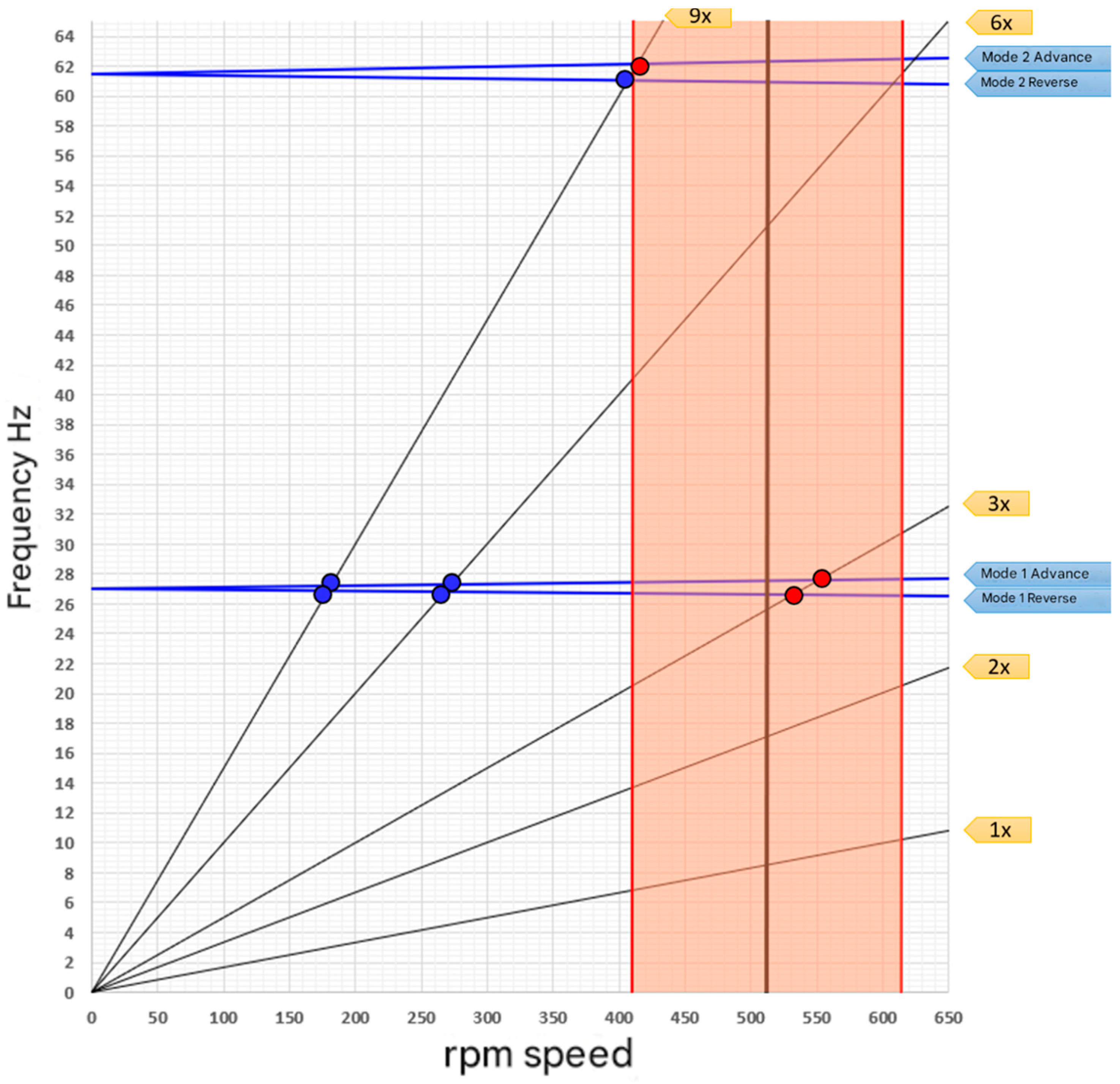
3.3. Whirling Vibrations Analysis
3.4. Dynamic Torsional and Bending Load Analysis
3.5. Fatigue Life Analysis
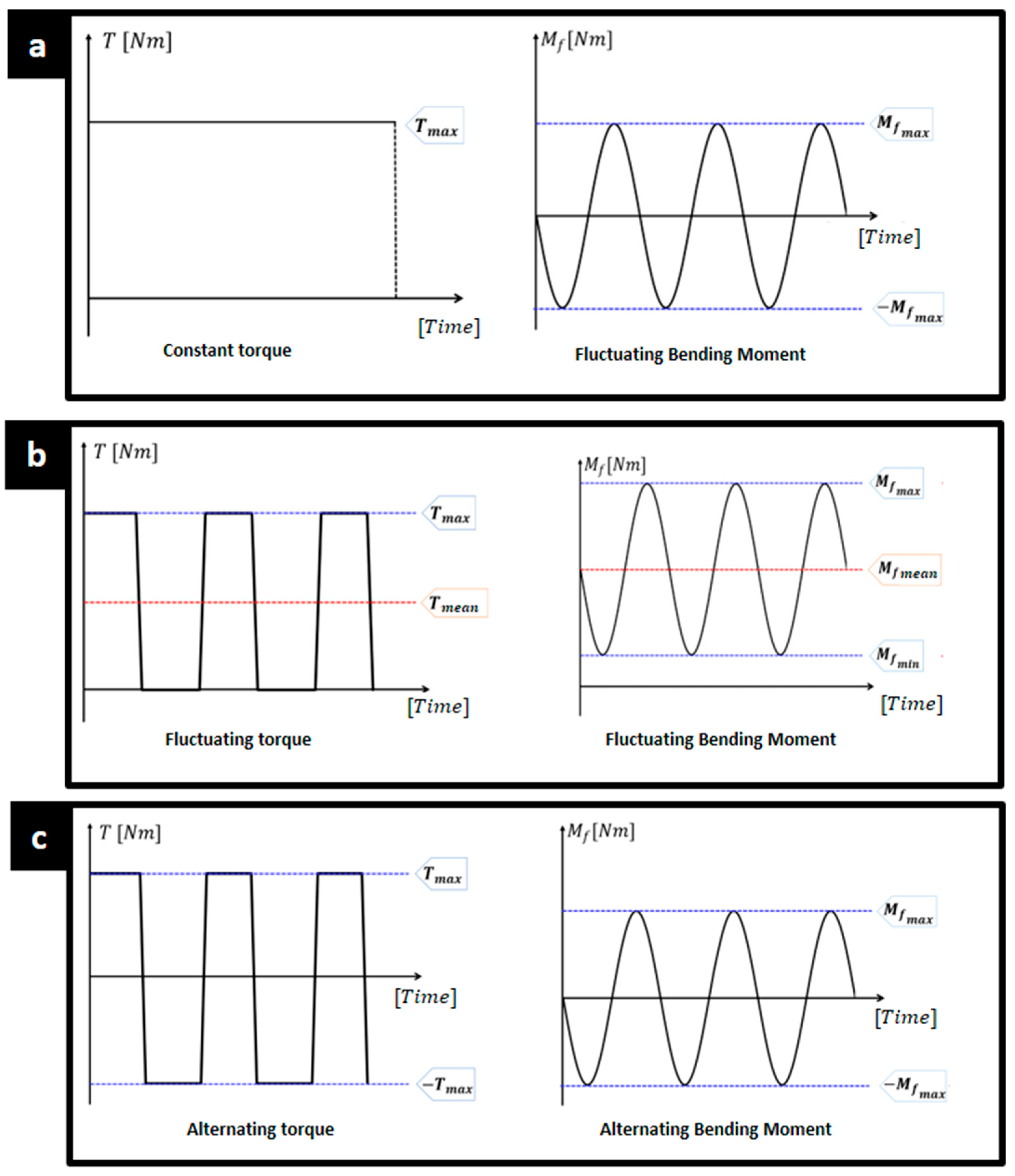
- Case 1: Continuous Operation at Constant Speed (Figure 7a).
- Constant torsional moment, alternating bending moment. Results indicate a safety factor of 3.06 and a life cycle of 373 × 106, suggesting infinite life.
- Case 2: Alternating Stationary and Operating Moments (Figure 7b).
- Fluctuating stresses. Safety factor of 2.59 and life cycle of 85.8 × 106. Reduced life compared to Case 1 due to increased fatigue from continuous operation.
- Case 3: Forward and Reverse Operation Cycles (Figure 7c).
- Torsional moment varies from maximum positive to maximum negative, bending moment alternates between ±1523.4 Nm. Safety factor of 1.5 and life cycle of 5.43 × 106, indicating higher loads and reduced safety.
3.6. Local Stress from Finite Element Simulations
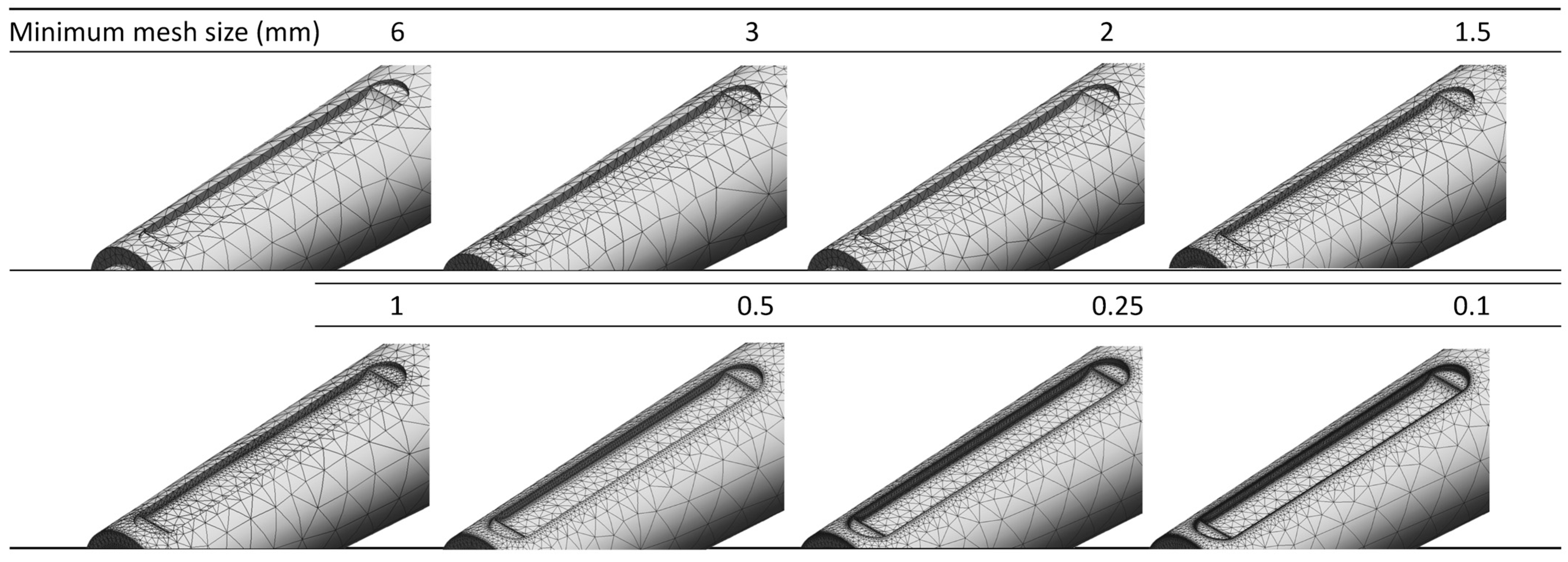
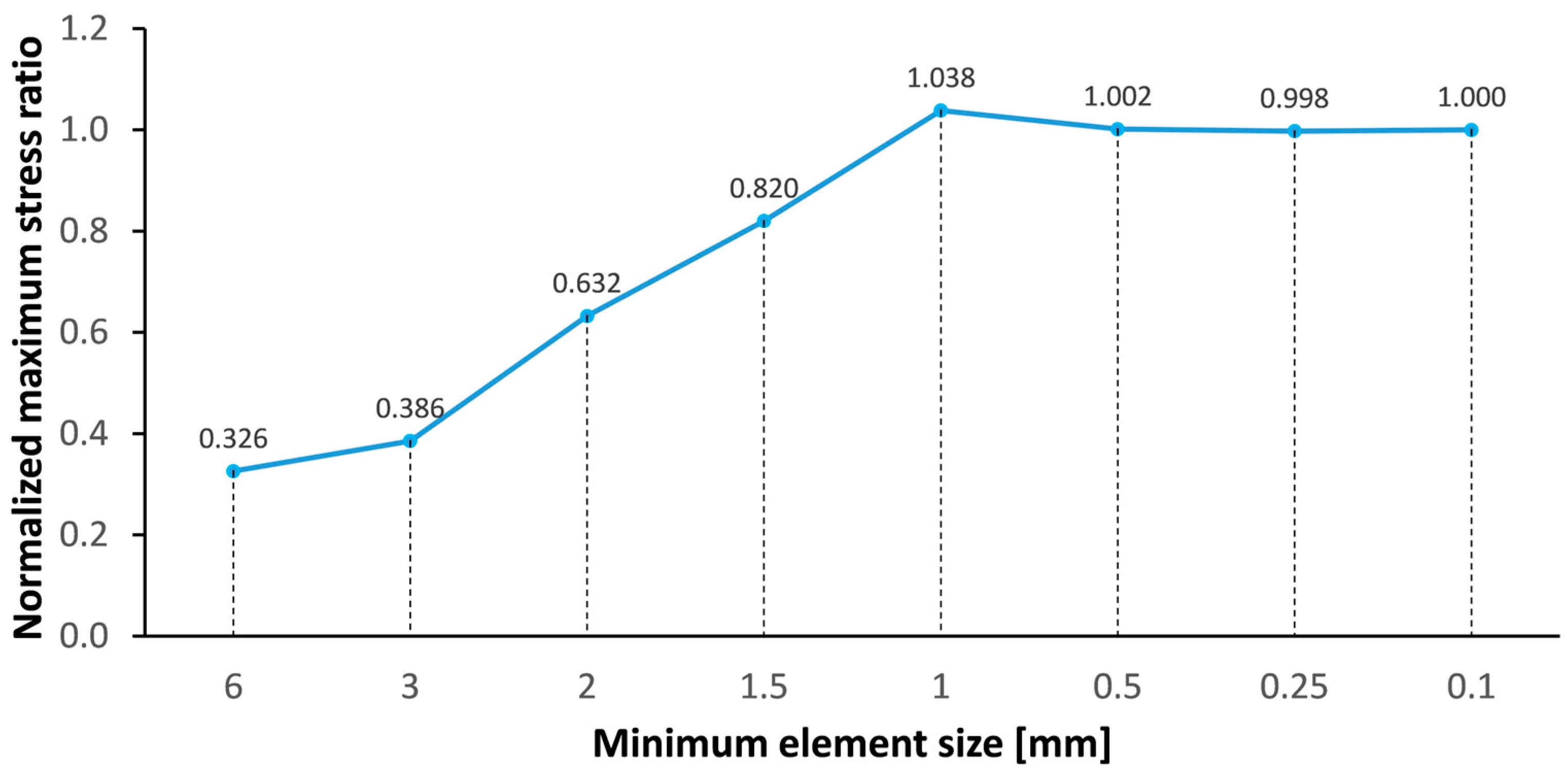
3.6.1. Meshing Sensitivity Analysis for Local Stresses
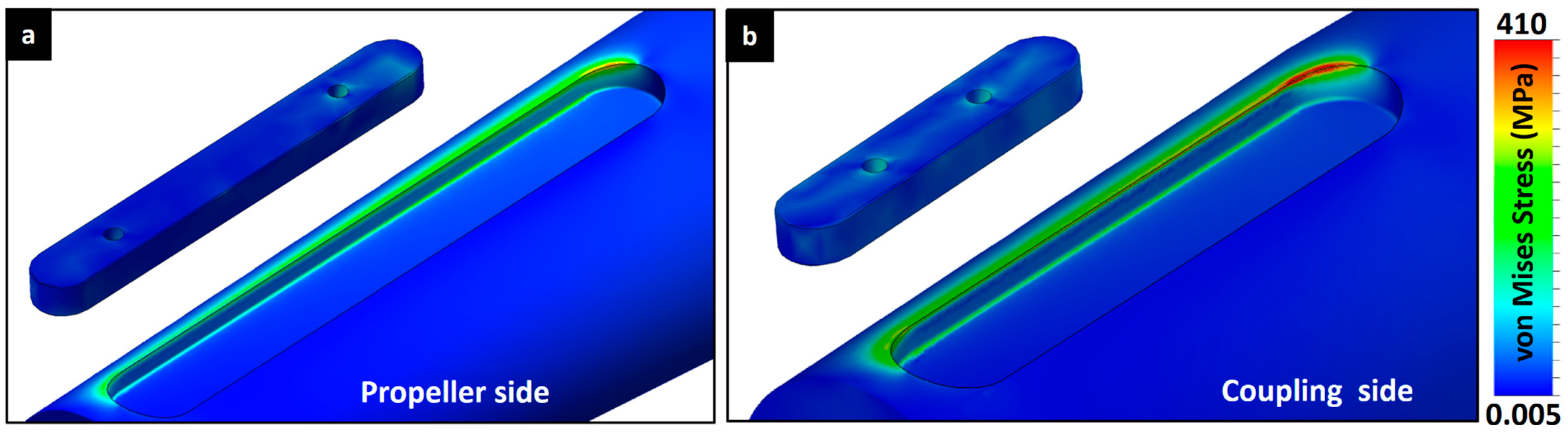
3.6.2. Maximum Stresses in Keyseats
3.6.3. Keyseat Redesign of Shaft
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description | Units of Measure |
| Tensile and compressive stress. | MPa | |
| Tension or compression load. | N | |
| Shaft cross-sectional area. | mm2 | |
| Displacement of a shaft point. | mm | |
| Original length of the shaft. | mm | |
| Modulus of elasticity of the material. | MPa | |
| Intermediate bending stress in the shaft. | MPa | |
| Maximum bending stress in the shaft. | MPa | |
| Shaft bending moment. | Nm | |
| Intermediate shaft radius. | M | |
| Moment of inertia of the cross-section. | mm4 | |
| Intermediate shaft diameter. | mm | |
| Outside diameter. | M | |
| Volumetric density of the material. | kg/m3 | |
| Acceleration of gravity. | m/s2 | |
| Outer radius. | M | |
| Intermediate shaft shear stress. | MPa | |
| Maximum shear stress in the shaft. | MPa | |
| Internal torque. | Nm | |
| Torsional moment on shaft surface. | Nm | |
| Polar moment of inertia of the cross-section. | mm4 | |
| Power. | kW | |
| Revolutions per minute. | RPM | |
| Angular velocity. | Rad/s | |
| Drive motor factor: 95 for electric drives and 100 for others. | ||
| Shaft component factor: 1.0 for shaft with integral flange, 1.1 with keyway or cylindrical connections, and 1.2 for shafts with longitudinal notches. | ||
| Power delivered to the shaft. | kW | |
| Ultimate stress of the material. | N/mm2 | |
| Elastic limit of the material. | N/mm2 | |
| Natural frequency. | Hz | |
| Excitation frequency. | Hz | |
| Number of propeller blades. | ||
| Vibration mode constant. | ||
| Mass per unit length. | kg/m | |
| Distance between supports. | m | |
| Critical operating speed. | RPM | |
| Fatigue resistance limit at critical location. | MPa | |
| Fatigue resistance limit at the rotating beam. | MPa | |
| Modification factor for surface condition. | ||
| Modification factor for size. | ||
| Modification factor for load. | ||
| Modification factor for temperature. | ||
| Reliability factor. | ||
| Modification factor for miscellaneous effects. | ||
| Minimum tensile strength. | MPa | |
| Shaft outside diameter. | mm | |
| Fatigue strength fraction. | ||
| True stress–true strain. | kpsi; MPa | |
| Constant to obtain the fatigue strength fraction. | ||
| Number of cycles to obtain the fatigue strength fraction. | ||
| Number of life cycles. | ||
| Constant to determine the failure cycles. | ||
| Constant to determine the failure cycles. | ||
| Fully reversed stress. | MPa | |
| Fatigue stress concentration factor for bending or fatigue. | ||
| Stress concentration factor. | ||
| Neuber’s constant. | Pulg. | |
| Notch radius. | mm | |
| Average stress. | MPa | |
| Alternating stress | MPa | |
| Maximum stress. | MPa | |
| Minimum stress. | MPa | |
| Ratio of amplitude. | ||
| Stress ratio | ||
| Fatigue concentration factor for bending loads. | ||
| Fatigue concentration factor for axial loads. | ||
| Fatigue concentration factor for torsional loads. | ||
| Alternating stress bending loads. | MPa | |
| Average stress bending loads. | MPa | |
| Alternating stress due to axial loads. | MPa | |
| Average stress due to axial loads. | MPa | |
| Shear stress due to torsional loads. | MPa | |
| Shear stress due to torsional loads. | MPa | |
| Alternating von Mises stress. | MPa | |
| Average von Mises stress | MPa | |
| Average shear stress due to direct shear. | MPa | |
| Applied force. | N | |
| Shear area. | mm2 | |
| Minimum shear area. | mm2 | |
| Shaft diameter at the center of the key. | Mm | |
| Average contact pressure stress. | MPa | |
| Lateral contact area of key with shaft keyway. | mm2 | |
| Minimum pressure area. | mm2 | |
| Ultimate stress of key. | MPa |
References
- Choi, S.-P.; Lee, J.-U.; Park, J.-B. Application of Deep Reinforcement Learning to Predict Shaft Deformation Considering Hull Deformation of Medium-Sized Oil/Chemical Tanker. J. Mar. Sci. Eng. 2021, 9, 767. [Google Scholar] [CrossRef]
- Arisoy, C.F.; Başman, G.; Şeşen, M.K. Failure of a 17-4 PH Stainless Steel Sailboat Propeller Shaft. Eng. Fail. Anal. 2003, 10, 711–717. [Google Scholar] [CrossRef]
- Zou, D.; Zhang, J.; Ta, N.; Rao, Z. The Hydroelastic Analysis of Marine Propellers with Consideration of the Effect of the Shaft. Ocean Eng. 2017, 131, 95–106. [Google Scholar] [CrossRef]
- Han, H.S.; Lee, K.H.; Park, S.H. Estimate of the Fatigue Life of the Propulsion Shaft from Torsional Vibration Measurement and the Linear Damage Summation Law in Ships. Ocean Eng. 2015, 107, 212–221. [Google Scholar] [CrossRef]
- Sitthipong, S.; Towatana, P.; Sitticharoenchai, A. Failure Analysis of Metal Alloy Propeller Shafts. Mater. Today Proc. 2017, 4, 6491–6494. [Google Scholar] [CrossRef]
- Vizentin, G.; Vukelic, G.; Murawski, L.; Recho, N.; Orovic, J. Marine Propulsion System Failures—A Review. J. Mar. Sci. Eng. 2020, 8, 662. [Google Scholar] [CrossRef]
- Ball, A. The Fracture of a Ship’s Propeller Shaft. Fract. Fract. Mech. 1985, 265–271. [Google Scholar] [CrossRef]
- Balyts’kyi, O.I.; Kawiak, M.; Kawiak, P. Assessment of the Fatigue Damage to the Propeller Shaft of a Sea Craft. Mater. Sci. 2013, 49, 130–133. [Google Scholar] [CrossRef]
- Lee, J.-W.; Vuong, Q.D.; Jeong, B.; Lee, J. Changes in Propeller Shaft Behavior by Fluctuating Propeller Forces during Ship Turning. Appl. Sci. 2022, 12, 5041. [Google Scholar] [CrossRef]
- Tuninetti, V.; Mariqueo, M. Performance of Combined Woven Roving and Mat Glass-Fiber Reinforced Polymer Composites Under Absorption Tower Lifting Loads. Polymers 2024, 16, 2937. [Google Scholar] [CrossRef]
- Tuninetti, V.; Fuentes, G.; Oñate, A.; Narayan, S.; Celentano, D.; García-Herrera, C.; Menacer, B.; Pincheira, G.; Garrido, C.; Valle, R. Computational Shape Design Optimization of Femoral Implants: Towards Efficient Forging Manufacturing. Appl. Sci. 2024, 14, 8289. [Google Scholar] [CrossRef]
- Tuninetti, V.; Sepúlveda, H. Computational Mechanics for Turbofan Engine Blade Containment Testing: Fan Case Design and Blade Impact Dynamics by Finite Element Simulations. Aerospace 2024, 11, 333. [Google Scholar] [CrossRef]
- Motley, M.R.; Nelson, M.; Young, Y.L. Integrated Probabilistic Design of Marine Propulsors to Minimize Lifetime Fuel Consumption. Ocean Eng. 2012, 45, 1–8. [Google Scholar] [CrossRef]
- Dong, C.; Yuan, C.; Bai, X.; Yan, X.; Mao, S. Reliability Evaluation of Marine Propulsion Shaft Based on Stress-Strength Interference Theory. In Proceedings of the 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Pantazopoulos, G.; Papaefthymiou, S. Failure and Fracture Analysis of Austenitic Stainless Steel Marine Propeller Shaft. J. Fail. Anal. Prev. 2015, 15, 762–767. [Google Scholar] [CrossRef]
- Afolabi, S.O.; Oladapo, B.I.; Ijagbemi, C.O.; Adeoye, A.O.M.; Kayode, J.F. Design and Finite Element Analysis of a Fatigue Life Prediction for Safe and Economical Machine Shaft. J. Mater. Res. Technol. 2019, 8, 105–111. [Google Scholar] [CrossRef]
- Ding, G.; Yan, X.; Gao, X.; Xiao, J. Experimental and Numerical Studies on Fatigue Characteristics of CFRP Shaft Tube. Appl. Sci. 2022, 12, 8933. [Google Scholar] [CrossRef]
- Rao, R.; Mohan, S.; Kumar, G. Determination of Fatigue Life of Surface Propeller by Using Finite Element Analysis. Int. J. Eng. Sci. 2016, 2492, 2492–2503. [Google Scholar]
- da Silva, F.A.C.; de Castro, P.M.S.T. Redesign of a Failed Hoisting Shaft of a Vertical Transfer Device. Eng 2023, 4, 1981–2002. [Google Scholar] [CrossRef]
- Song, M.H.; Pham, X.D.; Vuong, Q.D. Torsional Vibration Stress and Fatigue Strength Analysis of Marine Propulsion Shafting System Based on Engine Operation Patterns. J. Mar. Sci. Eng. 2020, 8, 613. [Google Scholar] [CrossRef]
- Huang, Z.; Wu, R.; Chen, J.; Xu, X.; Xie, Y. Study of Torsional Vibration Bifurcation Characteristics of Direct-Drive Wind Turbine Shaft System. Processes 2022, 10, 1700. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, G.; Wu, J.; Ma, K.; Fan, L. Vibration Fatigue Analysis of a Simply Supported Cracked Beam Subjected to a Typical Load. Appl. Sci. 2022, 12, 7398. [Google Scholar] [CrossRef]
- Vizentin, G.; Vukelić, G.; Srok, M. Common Failures of Ship Propulsion Shafts. Pomorstvo 2017, 31, 85–90. [Google Scholar] [CrossRef]
- Liu, G.; Shao, Y. Fatigue Life Calculation of Shaft System Based on Bend-Torsion Coupling. IOP Conf. Ser. Mater. Sci. Eng. 2019, 569, 022008. [Google Scholar] [CrossRef]
- Xu, X.L.; Yu, Z.W. Failure Analysis of a Marine Intermediate Shaft. Eng. Fail. Anal. 2021, 126, 105464. [Google Scholar] [CrossRef]
- Song, M.H.; Nam, T.K.; Lee, J.U. Self-Excited Torsional Vibration in the Flexible Coupling of a Marine Propulsion Shafting System Employing Cardan Shafts. J. Mar. Sci. Eng. 2020, 8, 348. [Google Scholar] [CrossRef]
- Wang, W.; Shang, Y.; Yao, Z. A Predictive Analysis Method of Shafting Vibration for the Hydraulic-Turbine Generator Unit. Water 2022, 14, 2714. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q.; Zhang, M.; Xie, Z. Numerical Prediction of Cavitation Fatigue Life and Hydrodynamic Performance of Marine Propellers. J. Mar. Sci. Eng. 2024, 12, 74. [Google Scholar] [CrossRef]
- Ju, H.J.; Choi, J.S. Experimental Study of Cavitation Damage to Marine Propellers Based on the Rotational Speed in the Coastal Waters. Machines 2022, 10, 793. [Google Scholar] [CrossRef]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Effect of Hull and Propeller Roughness during the Assessment of Ship Fuel Consumption. J. Mar. Sci. Eng. 2023, 11, 784. [Google Scholar] [CrossRef]
- He, T.; Xie, Z.; Tao, X.; Yang, K.; Jiao, J.; Huang, M.; Ma, W. Analysis of the Tribological and Dynamic Performance of the Self-Adapting Water-Lubricated Stern Bearing. Lubricants 2022, 10, 245. [Google Scholar] [CrossRef]
- Teng, Y.; Xie, L.; Zhang, H. Experimental Study on Vibration Fatigue Behavior of Aircraft Aluminum Alloy 7050. Materials 2022, 15, 7555. [Google Scholar] [CrossRef] [PubMed]
- Kwon, W.S.; Vuong, Q.D.; Choi, J.H.; Lee, J.U.; Lee, J.W.; Yoon, S.H.; Nyongesa, A.J.; Park, M.H.; Yang, S.K.; Lee, W.J. Study on the Propeller Rope Cutter Concerning Transient Torsional Vibration Due to Cutting Action. Appl. Sci. 2022, 12, 1628. [Google Scholar] [CrossRef]
- Lloyd’s, R. Rules and Regulations for the Classification of Naval Ships; Lloyd’s Register: London, UK, 2018. [Google Scholar]
- Zhang, G.; Zhao, Y.; Chu, W. Longitudinal Vibration Transmission Control of Marine Propulsion Shafting with Friction Damper Integrated into the Thrust Bearing. J. Mar. Sci. Eng. 2022, 10, 1555. [Google Scholar] [CrossRef]
- Noonan, E.F. Ship Vibration Design Guide; Ship Structure Committee publications; Ship Structure Committee: Washington, DC, USA, 1990. [Google Scholar]
- Martínez Muñoz, S. Diseño de La Línea de Ejes de Un Buque Oceanográfico; Universidad Politécnica de Cartagena: Cartagena, Spain, 2017. [Google Scholar]
- Budynas, R.G.; Nisbett, J.K. Diseño En Ingeniería Mecánica de Shigley, 9th ed.; McGraw Hill: New York, NY, USA, 2010; ISBN 9781626239777. [Google Scholar]
- Rothbart, H.A. Mechanical Design and Systems Handbook, 2nd ed.; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Bhushan, B. Introduction to Tribology, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2013; ISBN 9781119944539. [Google Scholar]
- Dokos, S.J. Sliding Friction Under Extreme Pressures—1. J. Appl. Mech. 2021, 13, A148–A156. [Google Scholar] [CrossRef]
- Pougis, A.; Philippon, S.; Massion, R.; Faure, L.; Fundenberger, J.-J.; Toth, L.S. Dry Friction of Steel under High Pressure in Quasi-Static Conditions. Tribol. Int. 2013, 67, 27–35. [Google Scholar] [CrossRef]
- Nassiraei, H.; Rezadoost, P. Stress Concentration Factors in Tubular T/Y-Joints Strengthened with FRP Subjected to Compressive Load in Offshore Structures. Int. J. Fatigue 2020, 140, 105719. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Zhang, D.; Zhang, X.; Shao, W. Research on Load Reverse Engineering and Vibration Fatigue Analysis Technology of Rapid Box Wagon. Materials 2022, 15, 8322. [Google Scholar] [CrossRef]
- Tuninetti, V.; Alzugaray, R.; González, J.; Valenzuela, M.; Jaramillo, A.; Diez, E. Root Cause and Vibration Analysis to Increase Veneer Manufacturing Process Efficiency: A Case Study on an Industrial Peeling Lathe. Eur. J. Wood Wood Prod. 2021, 79, 951–966. [Google Scholar] [CrossRef]
- Song, G.; Park, H.; Lee, T. The Effect of Rudder Existence on Propeller Eccentric Force. J. Mar. Sci. Eng. 2019, 7, 455. [Google Scholar] [CrossRef]
- Witek, L. Failure Analysis of Turbine Disc of an Aero Engine. Eng. Fail. Anal. 2006, 13, 9–17. [Google Scholar] [CrossRef]
- Venegas, I.; Oñate, A.; Pierart, F.G.; Valenzuela, M.; Narayan, S.; Tuninetti, V. Efficient Mako Shark-Inspired Aerodynamic Design for Concept Car Bodies in Underground Road Tunnel Conditions. Biomimetics 2024, 9, 448. [Google Scholar] [CrossRef] [PubMed]
- Rilling, S.; Ríos, I.; Gómez, Á.; Valenzuela, M.; Oñate, A.; Tuninetti, V. Optimized Infill Density through Topological Optimization Increases Strength of Additively Manufactured Porous Polylactic Acid. Int. J. Adv. Manuf. Technol. 2023, 129, 3739–3750. [Google Scholar] [CrossRef]
- Bustos, F.; Hinojosa, J.; Tuninetti, V. Computational Comparison of Performance of Different Steel Plate Shear Yielding Dampers. Buildings 2023, 13, 793. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Tuninetti, V.; Sepúlveda, H.; Betaieb, E.; Pincheira, G.; Gilles, G.; Duchêne, L.; Habraken, A.M. Accurate Numerical Prediction of Ductile Fracture and Micromechanical Damage Evolution for Ti6Al4V Alloy. Comput. Mech. 2024, 73, 177–198. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Bouffioux, C.; Jaramillo, A.F.; García-Herrera, C.M.; Hussain, T.; Duchêne, L.; Riu, G.; Josep Roa, J.; Flores, P.; Marie Habraken, A.; et al. Nanomechanical Characterization of the Deformation Response of Orthotropic Ti–6Al–4V. Adv. Eng. Mater. 2021, 23, 2001341. [Google Scholar] [CrossRef]
- Duchêne, L.; Bettaieb, A.B.; Tuninetti, V.; Habraken, A.M. Numerical Modeling and Digital Image Correlation Strain Measurements of Coated Metal Sheets Submitted to Large Bending Deformation. Key Eng. Mater. 2013, 554–557, 2424–2431. [Google Scholar] [CrossRef]
- Jardin, R.T.; Tuninetti, V.; Tchuindjang, J.T.; Duchêne, L.; Hashemi, N.; Tran, H.S.; Carrus, R.; Mertens, A.; Habraken, A.M. Optimizing Laser Power of Directed Energy Deposition Process for Homogeneous AISI M4 Steel Microstructure. Opt. Laser Technol. 2023, 163, 109426. [Google Scholar] [CrossRef]
- Dzionk, S.; Przybylski, W.; Ścibiorski, B. The Possibilities of Improving the Fatigue Durability of the Ship Propeller Shaft by Burnishing Process. Machines 2020, 8, 63. [Google Scholar] [CrossRef]
- Tuninetti, V.; Flores, P.; Valenzuela, M.; Pincheira, G.; Medina, C.; Duchêne, L.; Habraken, A.M. Experimental Characterization of the Compressive Mechanical Behaviour of Ti6Al4V Alloy at Constant Strain Rates over the Full Elastoplastic Range. Int. J. Mater. Form. 2020, 13, 709–724. [Google Scholar] [CrossRef]
- Flores, P.; Tuninetti, V.; Gilles, G.; Gonry, P.; Duchêne, L.; Habraken, A.M. Accurate Stress Computation in Plane Strain Tensile Tests for Sheet Metal Using Experimental Data. J. Mater. Process. Technol. 2010, 210, 1772–1779. [Google Scholar] [CrossRef]
- Kwon, J.D.; Cho, S.J.; Bae, Y.T. A Study on Fretting Fatigue Behavior of Degraded 1Cr-0.5Mo Steel. In Proceedings of the Advances in Fracture and Failure Prevention; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2004; Volume 261, pp. 1221–1226. [Google Scholar]
- Kravchenko, G.N.; Kravchenko, K.G. Assessment of Cyclic Crack Resistance of Surface Hardened Parts. IOP Conf. Ser. Mater. Sci. Eng. 2020, 862, 022042. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gómez, Á.; Bustos, F.; Oñate, A.; Hinojosa, J.; Gallo, C.; Habraken, A.; Duchêne, L. Computational Modeling of U-Shaped Seismic Dampers for Structural Damage Mitigation. Appl. Sci. 2024, 14, 10238. [Google Scholar] [CrossRef]




| Manufacturing Process | (MPa) | |
|---|---|---|
| Grinding | 1.58 | |
| Machining or cold rolling | 5.51 | |
| Hot rolling | 57.7 | |
| As-forged | 272 |
| Shaft Diameter | |
|---|---|
| Original marine propulsion shaft | 114 |
| By direct calculation (maximum torsional shear stress) | 103.8 |
| By Lloyd’s Register [34]: | |
| k = 1.0 | 96.3 |
| k = 1.1 | 105.9 |
| k = 1.2 | 115 |
| Parameter | Value |
|---|---|
| Young’s modulus of SAE 1030 steel (GPa) | 190 |
| Diameters (mm) | 106 y 114 |
| SAE 1030 steel density (kg/m)3 | 7850 |
| Number of blades | 3 |
| Working speed (RPM) | 511.5 |
| (first mode) | 9.87 |
| Case (a) | Case (b) | Case (c) | |
|---|---|---|---|
| Safety factor | 3.1 | 2.6 | 1.5 |
| Life cycles (×) | 373 | 86 | 5.43 |
| Simulation | Maximum Element Size (mm) | Minimum Element Size (mm) | Size Growth Coefficient | Normalized Maximum Stress Ratio |
|---|---|---|---|---|
| #1 | 30 | 6 | 1.8 | 0.33 |
| #2 | 30 | 3 | 0.39 | |
| #3 | 30 | 2 | 0.63 | |
| #4 | 30 | 1.5 | 0.82 | |
| #5 | 30 | 1 | 1.04 | |
| #6 | 30 | 0.5 | 1.00 | |
| #7 | 30 | 0.25 | 1.00 | |
| #8 | 30 | 0.1 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuninetti, V.; Martínez, D.; Narayan, S.; Menacer, B.; Oñate, A. Design Optimization of a Marine Propeller Shaft for Enhanced Fatigue Life: An Integrated Computational Approach. J. Mar. Sci. Eng. 2024, 12, 2227. https://doi.org/10.3390/jmse12122227
Tuninetti V, Martínez D, Narayan S, Menacer B, Oñate A. Design Optimization of a Marine Propeller Shaft for Enhanced Fatigue Life: An Integrated Computational Approach. Journal of Marine Science and Engineering. 2024; 12(12):2227. https://doi.org/10.3390/jmse12122227
Chicago/Turabian StyleTuninetti, Víctor, Diego Martínez, Sunny Narayan, Brahim Menacer, and Angelo Oñate. 2024. "Design Optimization of a Marine Propeller Shaft for Enhanced Fatigue Life: An Integrated Computational Approach" Journal of Marine Science and Engineering 12, no. 12: 2227. https://doi.org/10.3390/jmse12122227
APA StyleTuninetti, V., Martínez, D., Narayan, S., Menacer, B., & Oñate, A. (2024). Design Optimization of a Marine Propeller Shaft for Enhanced Fatigue Life: An Integrated Computational Approach. Journal of Marine Science and Engineering, 12(12), 2227. https://doi.org/10.3390/jmse12122227






