Operation Analysis of the Floating Derrick for Offshore Wind Turbine Installation Based on Machine Learning
Abstract
1. Introduction
2. Methodology and Validation
2.1. Theoretical Formulations
2.1.1. Wind Loads on the Impeller of Wind Turbine
2.1.2. Hydrodynamics of Multi-Body (Two Floating Bodies)
- (1)
- Floating body a is free, and floating body b is fixed;
- (2)
- Floating body a is fixed, and floating body b is free.
2.1.3. Lifting
2.2. BP Neural Network Theory
Error Back Propagation Process
2.3. Numerical Model and Validation
2.3.1. Numerical Model
- (1)
- The crane on the floating derrick is a rigid body as a whole, ignoring the deformation during its operation;
- (2)
- Compared with the large mass of the impeller, the mass of the sling is ignored in the numerical simulation.
2.3.2. Comparison Between Numerical and Experimental Results
3. Hydrodynamics Parameters of the Floating Derrick and Cargo Ship
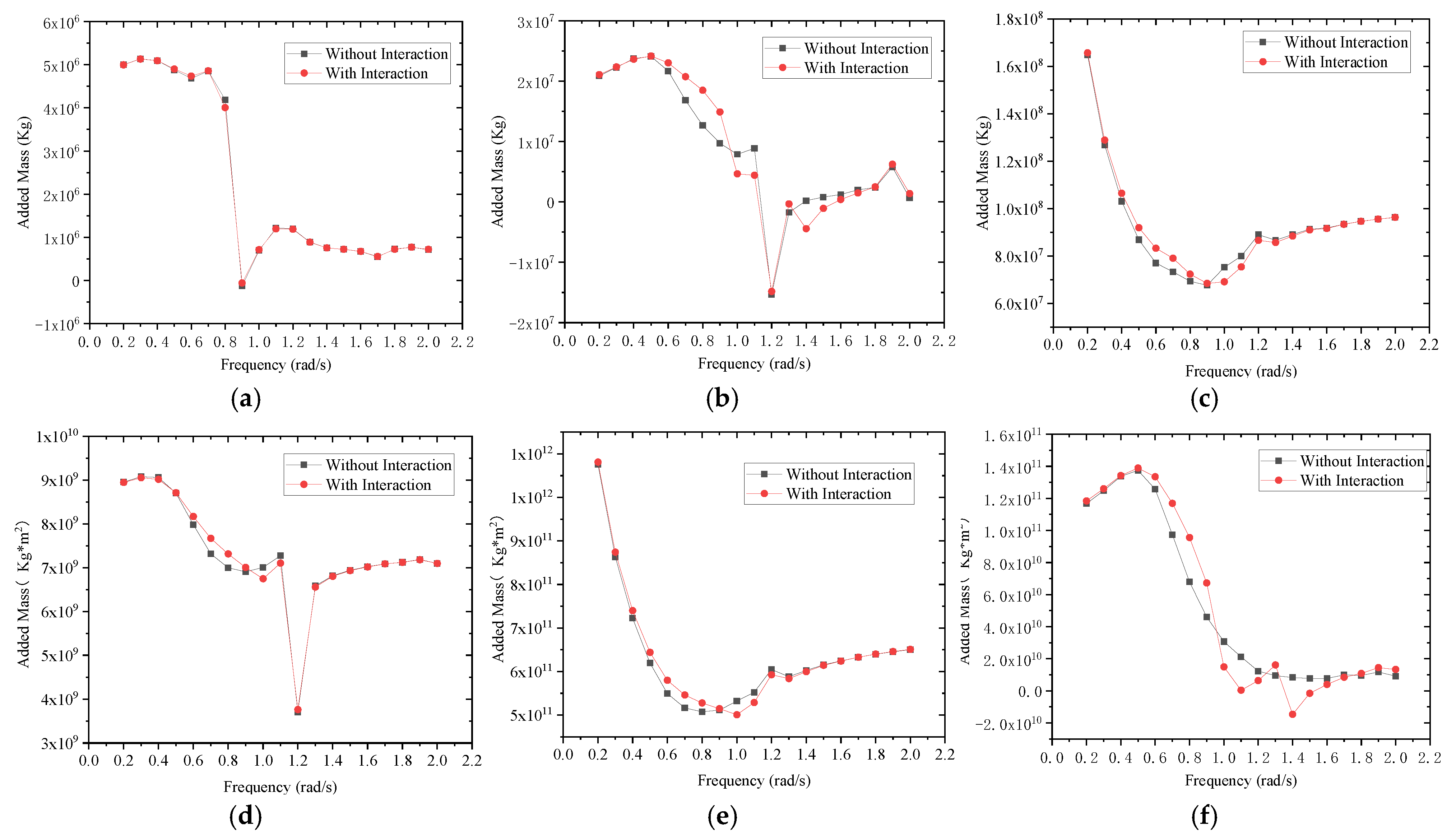
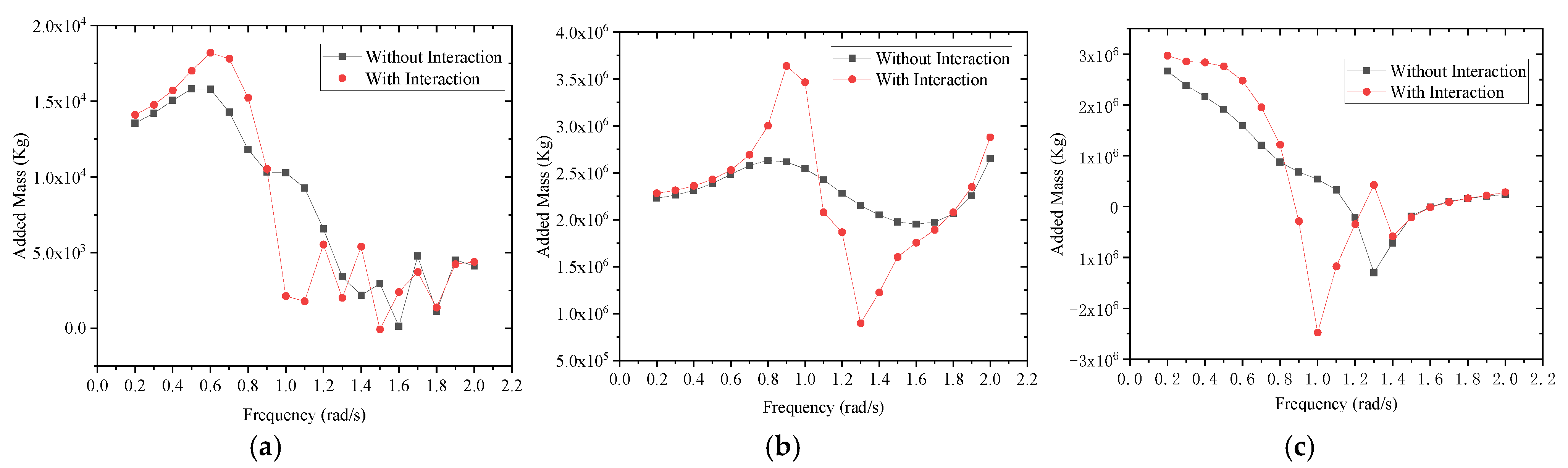
3.1. Added Mass
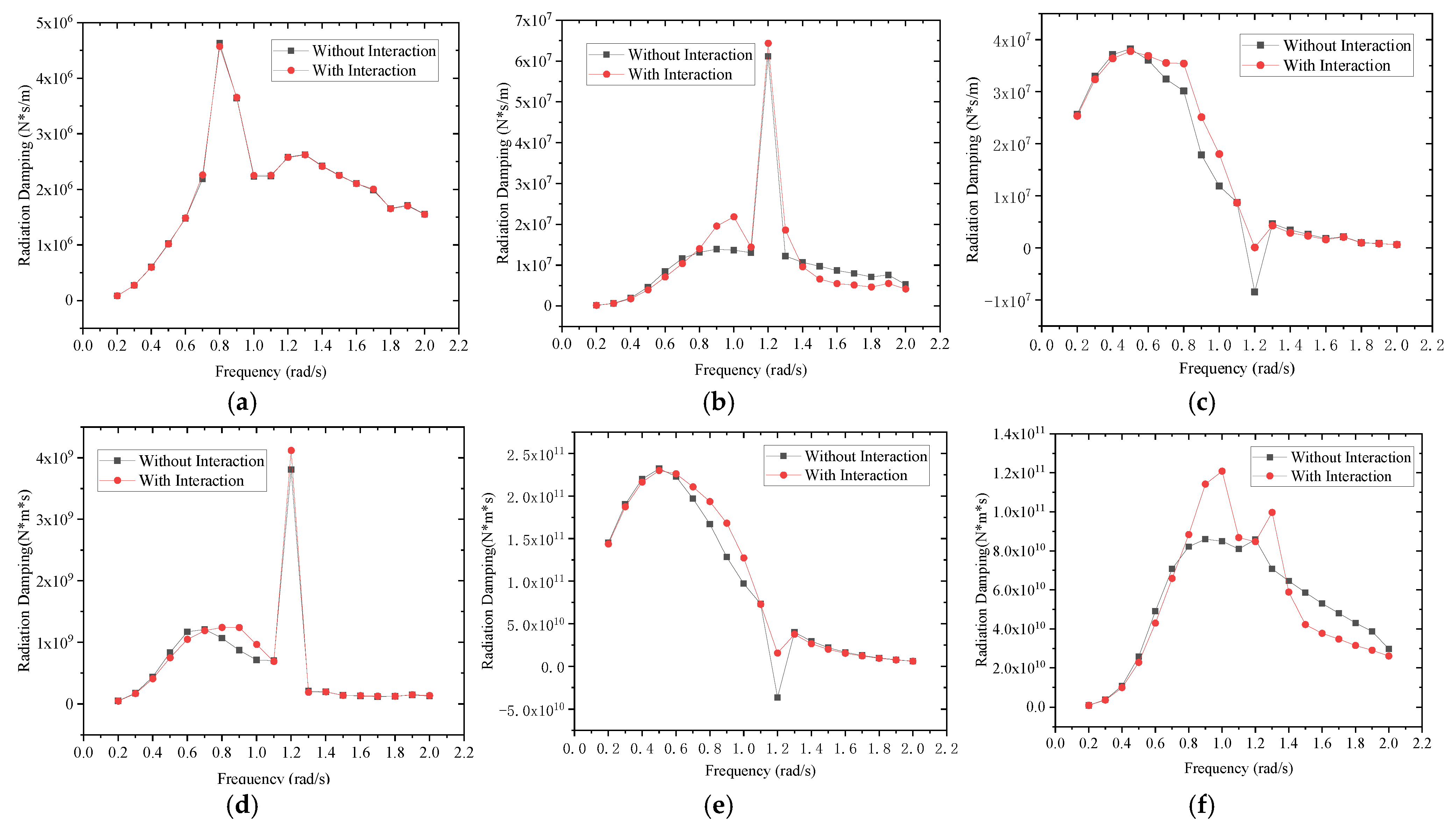
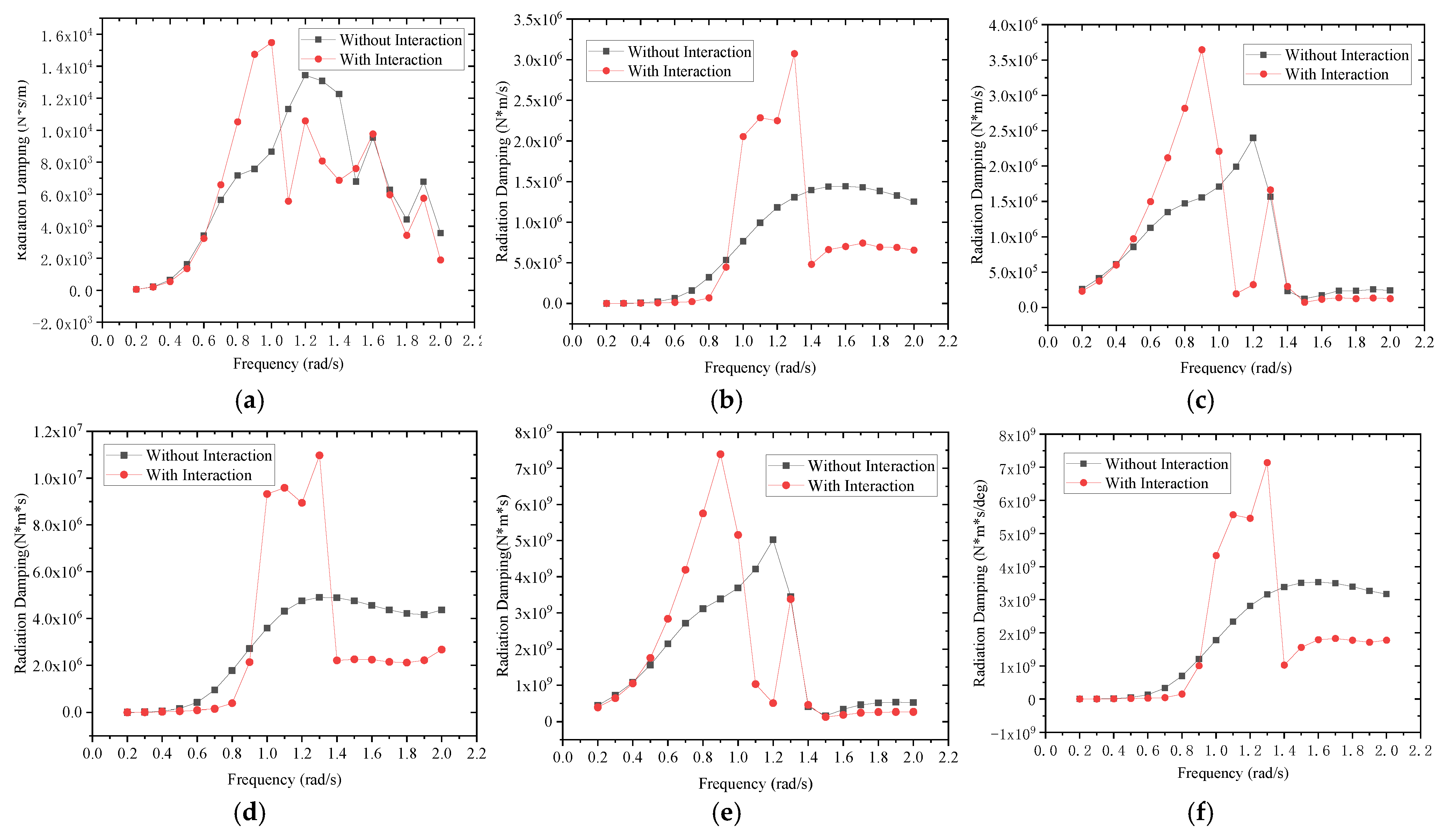
3.2. Radiation Damping
3.3. Response Amplitude Operator (RAO)
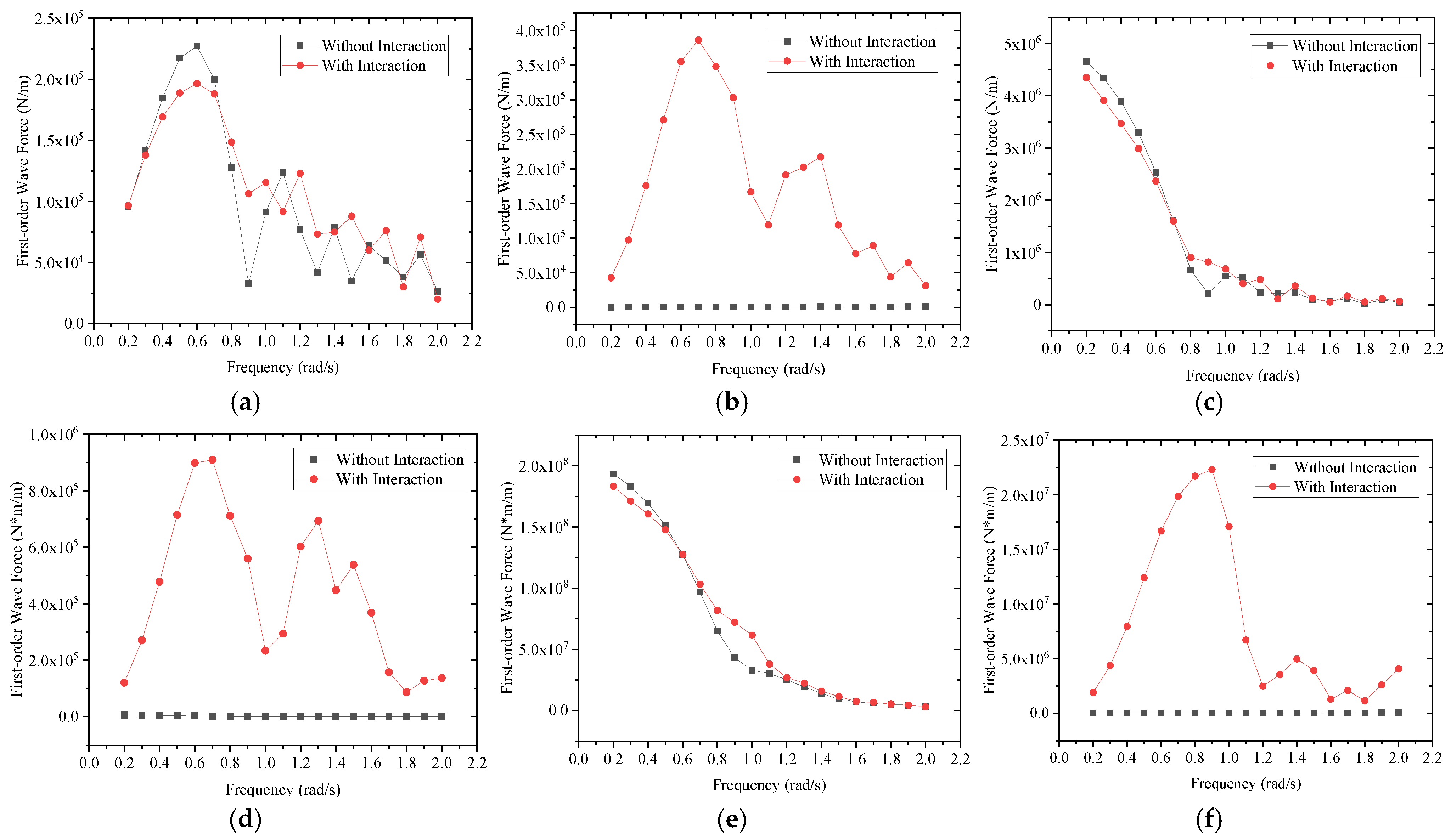
3.4. First-Order Wave Force
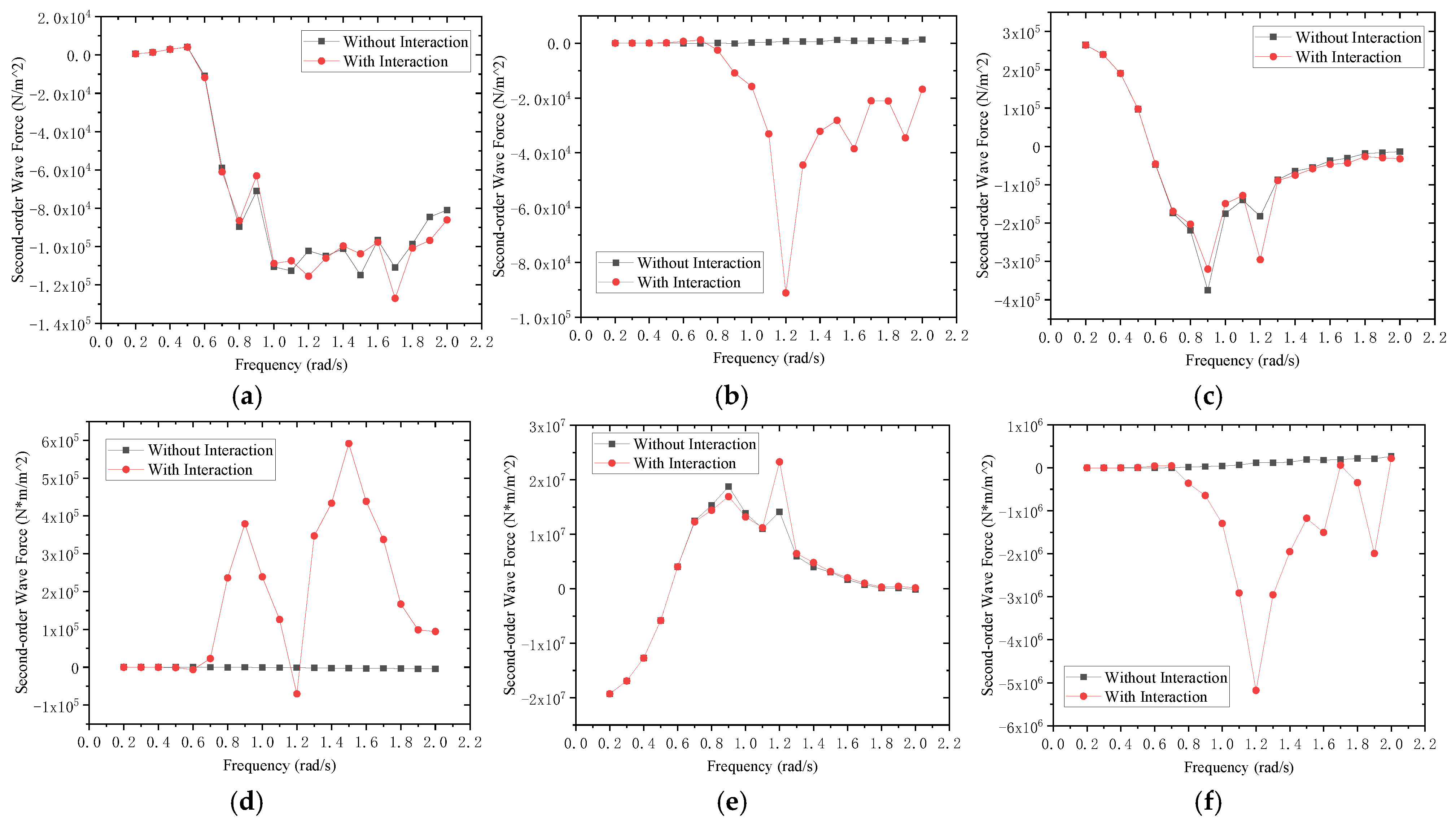
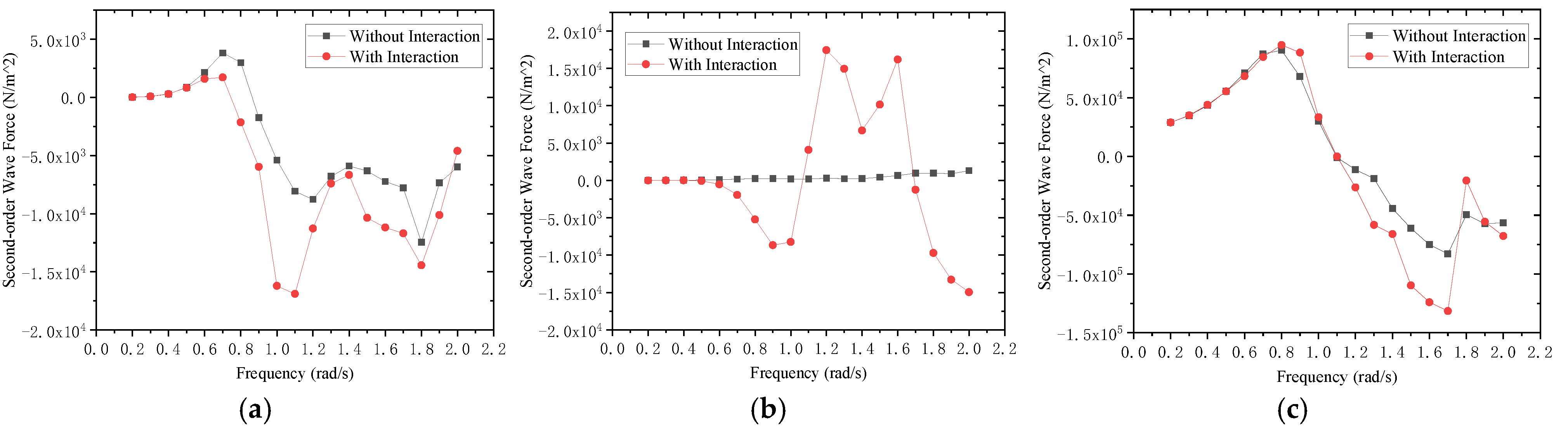
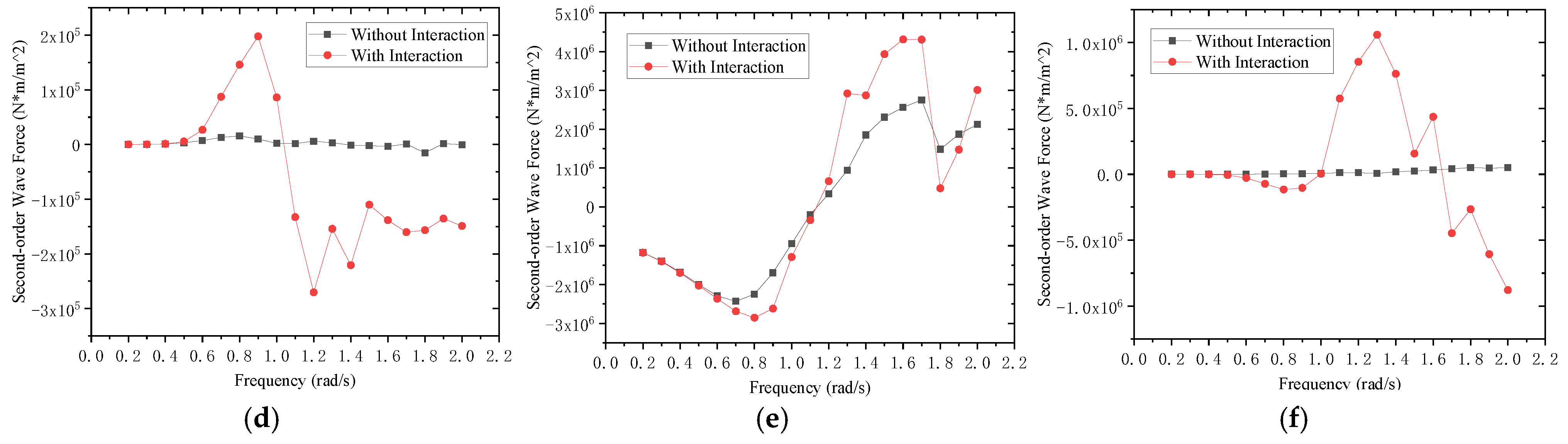
3.5. Second-Order Wave Force
4. Influencing Factors Analysis
4.1. Environmental and Lifting Parameters
4.2. Environmental Factors
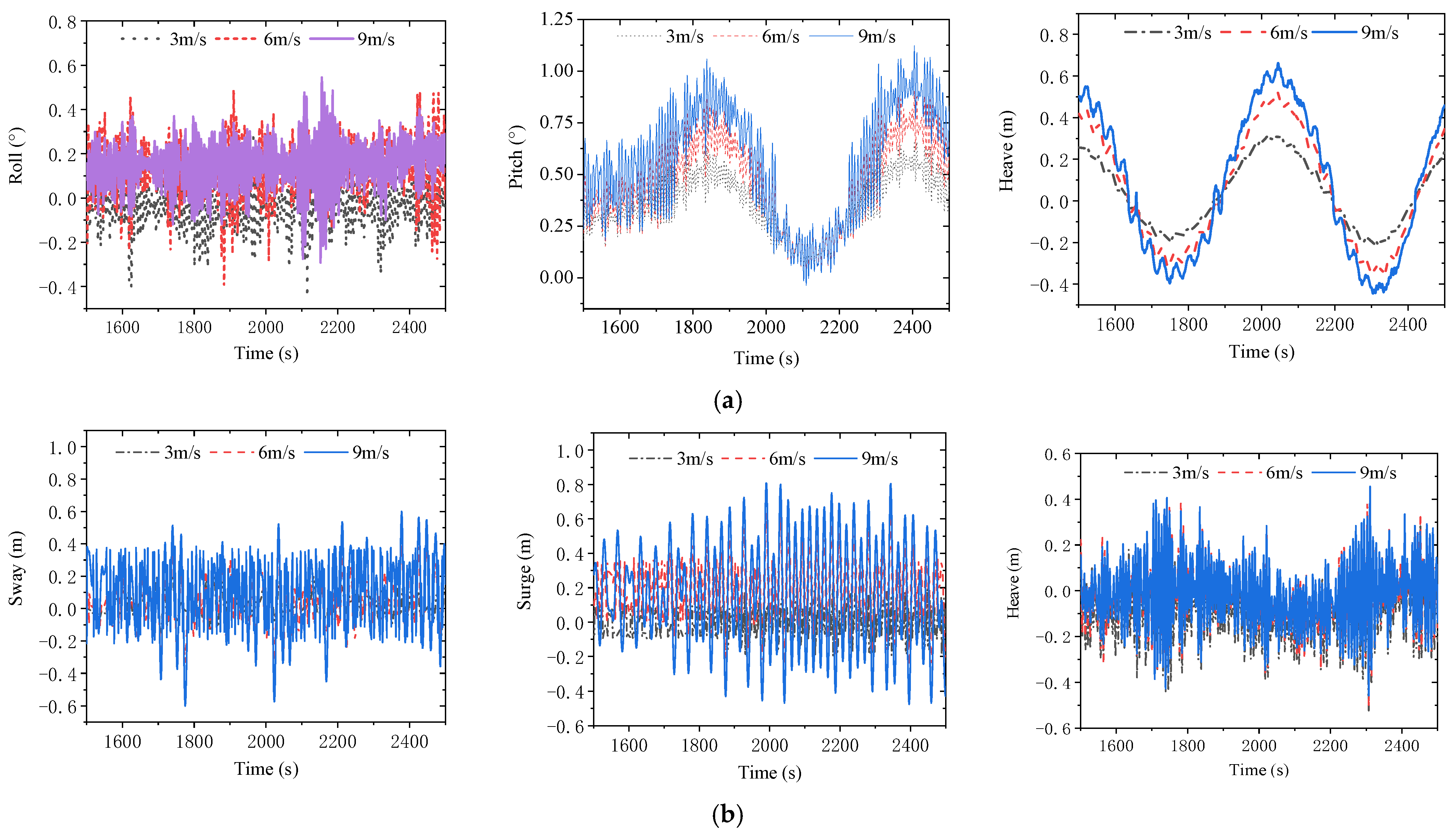
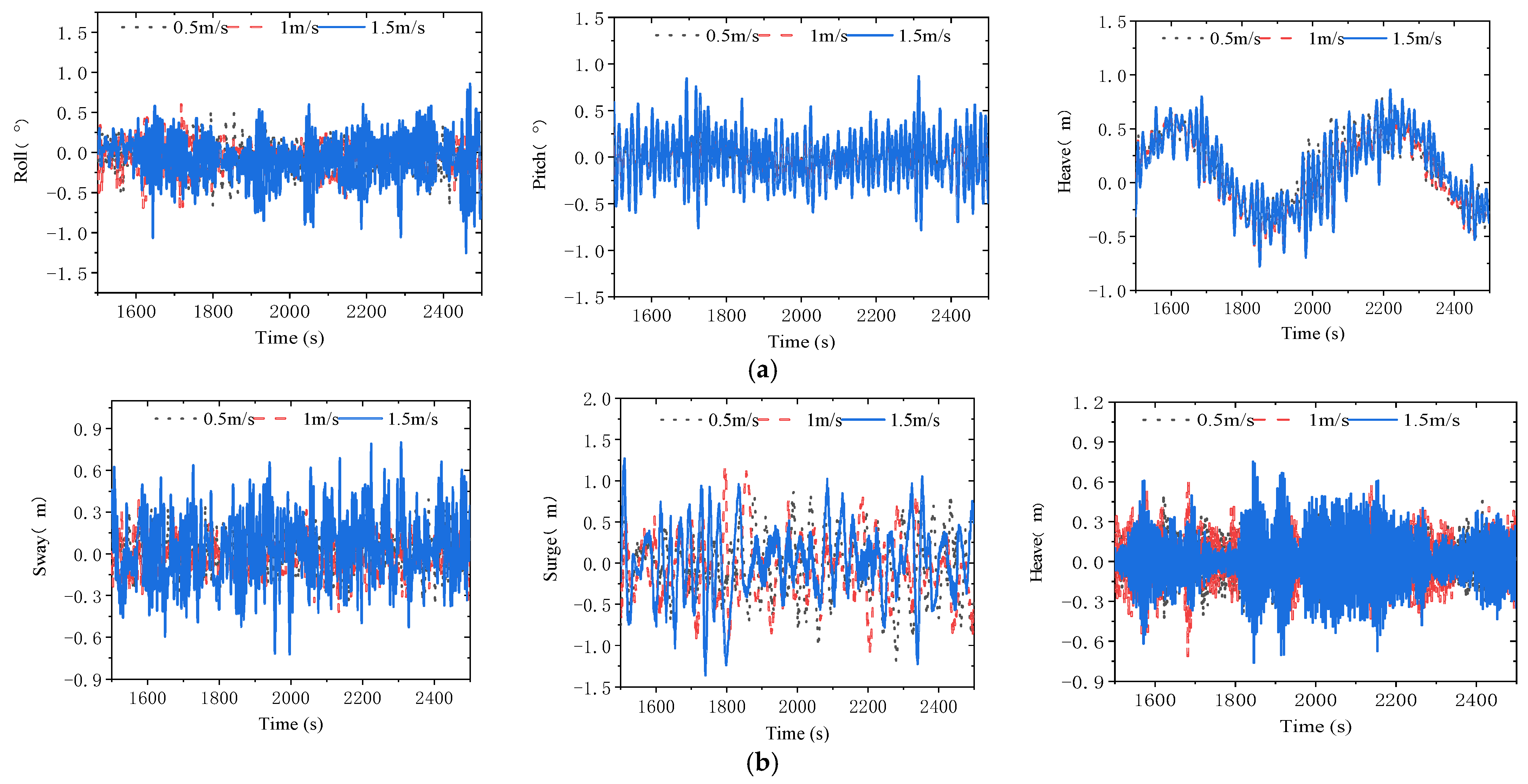
4.2.1. Wind Velocity
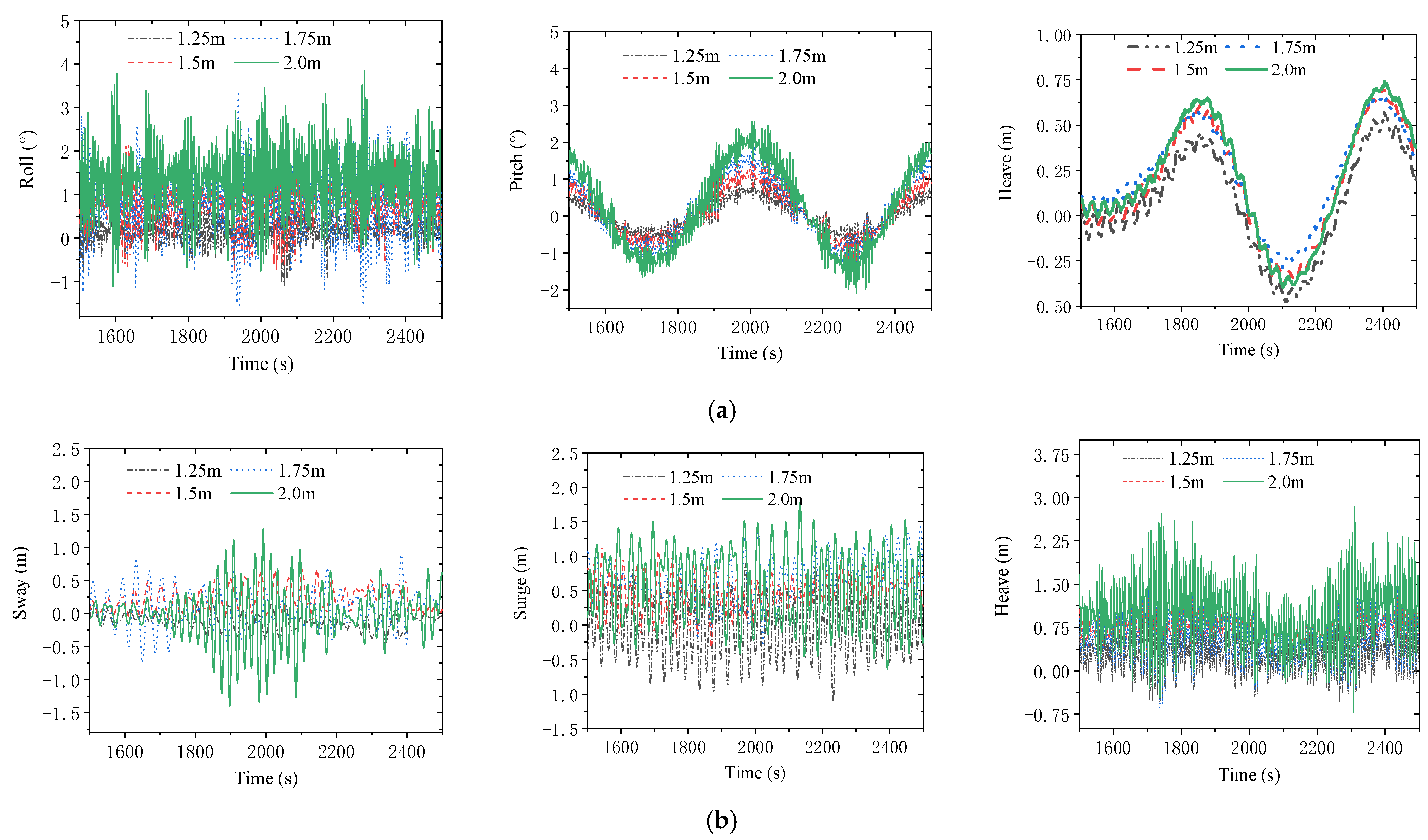
4.2.2. Wave Height
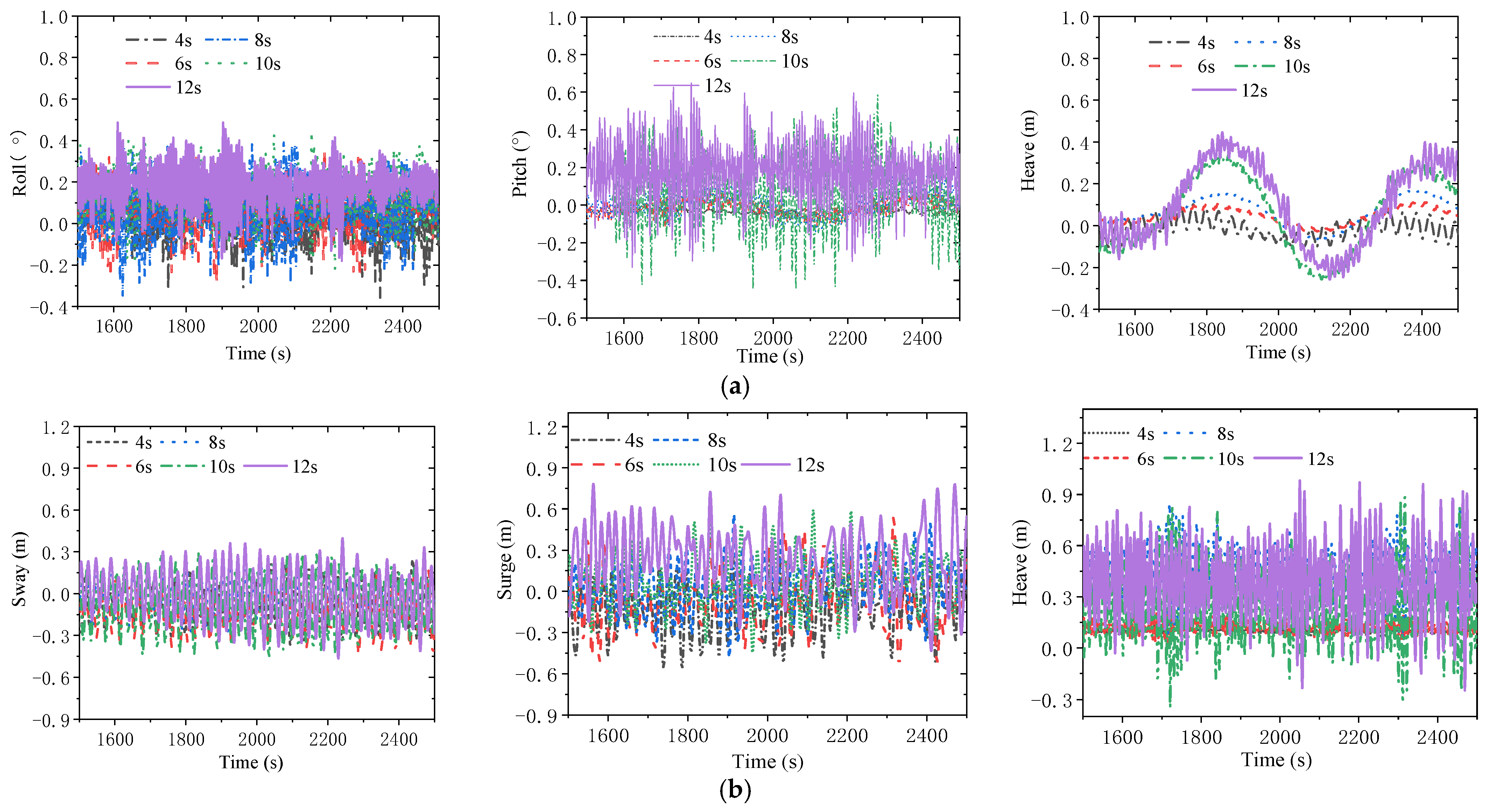
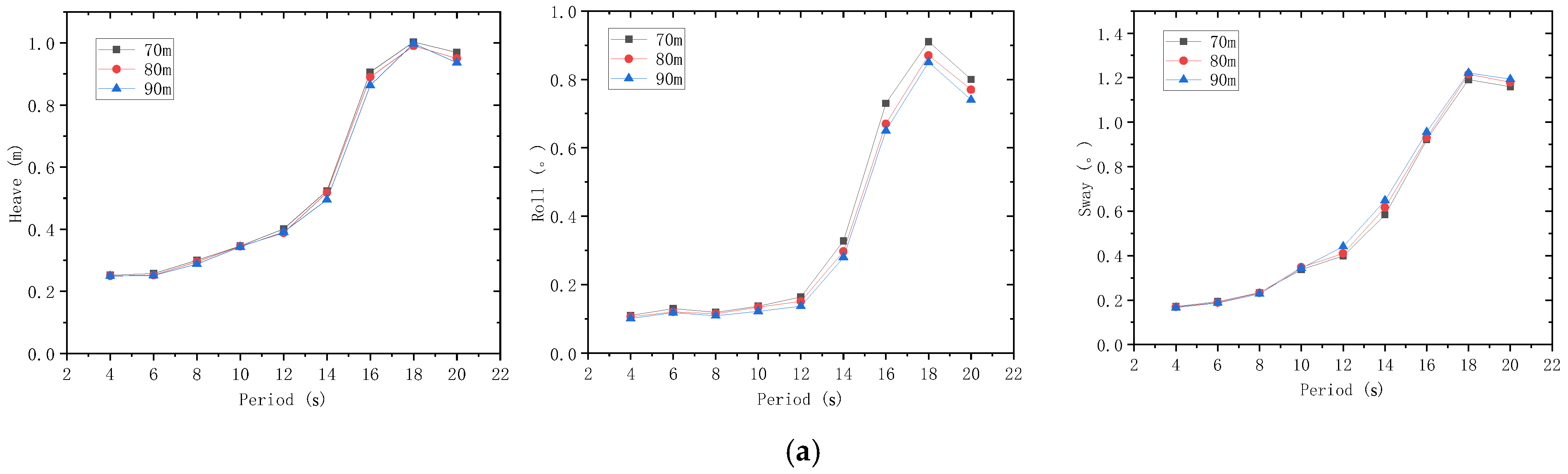
4.2.3. Spectral Peak Period
4.2.4. Current Velocity
4.3. Lifting Parameters
4.3.1. Lifting Heights
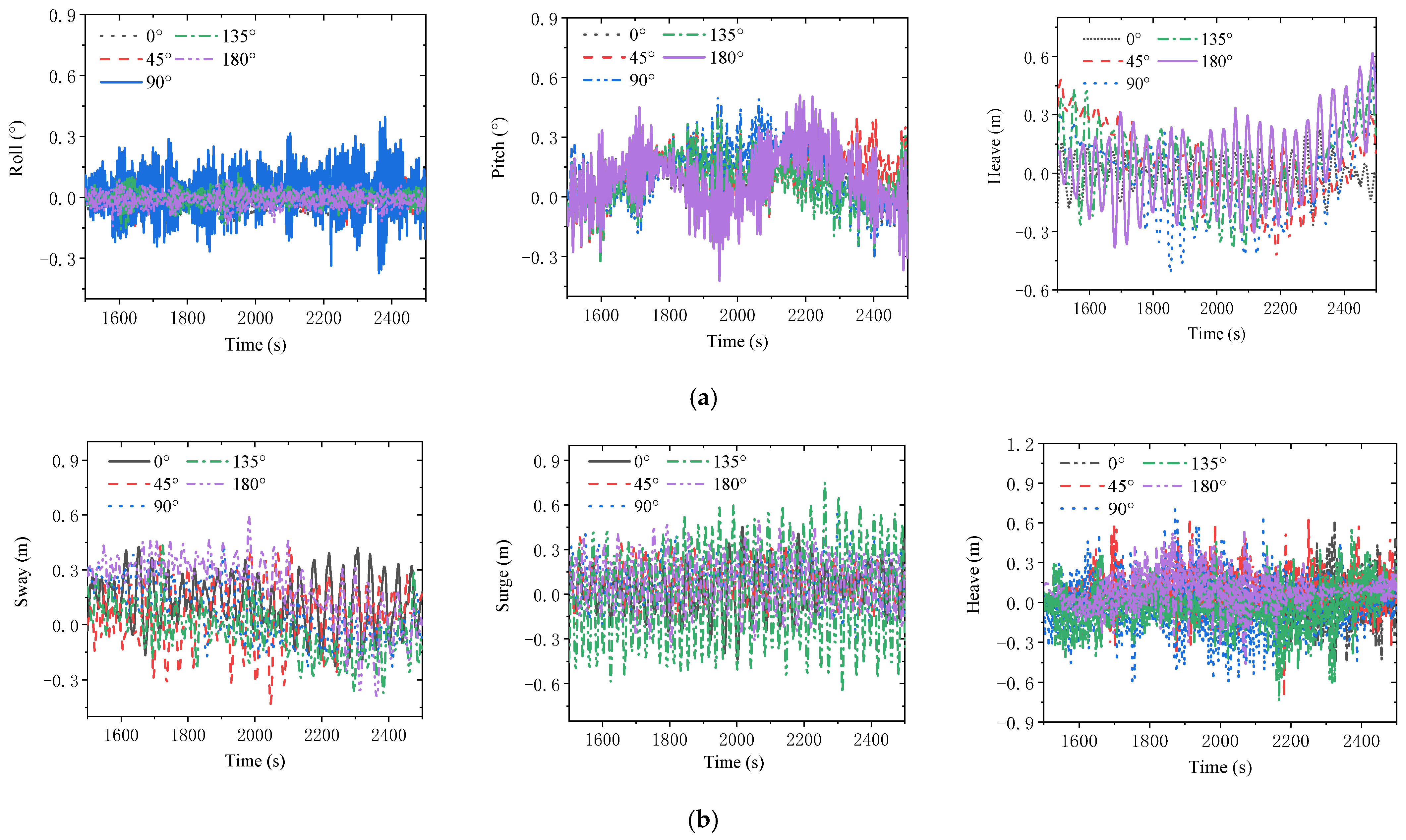
4.3.2. Boom Rotation Angle
5. Prediction Model of Floating Crane System Based on BP Neural Network
5.1. Selection and Pre-Treatment of Data Samples
5.2. Design of Network Structure Model
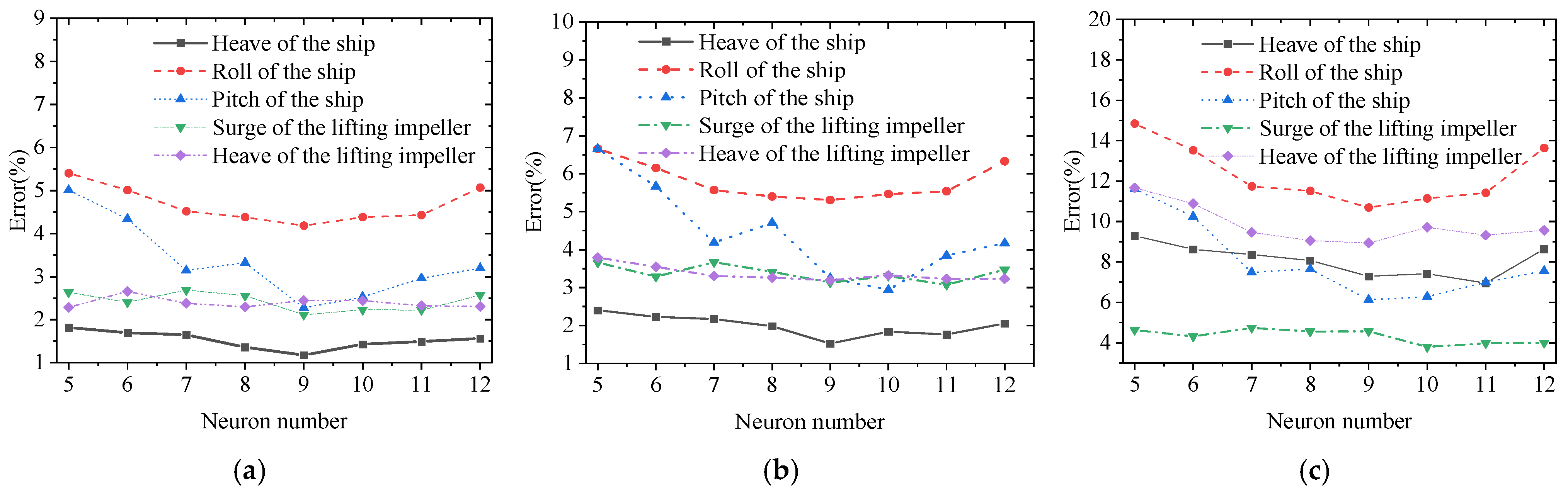
5.2.1. Determine the Number of Neurons
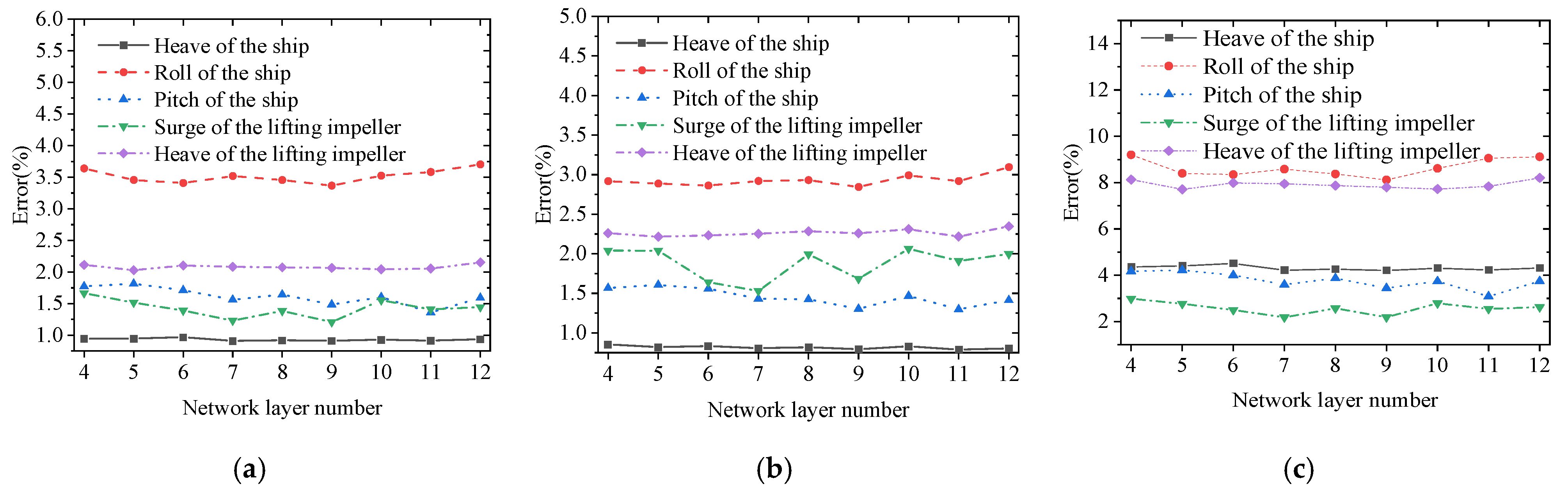
5.2.2. Determine the Number of the Network Layers
5.3. Model Training and Testing
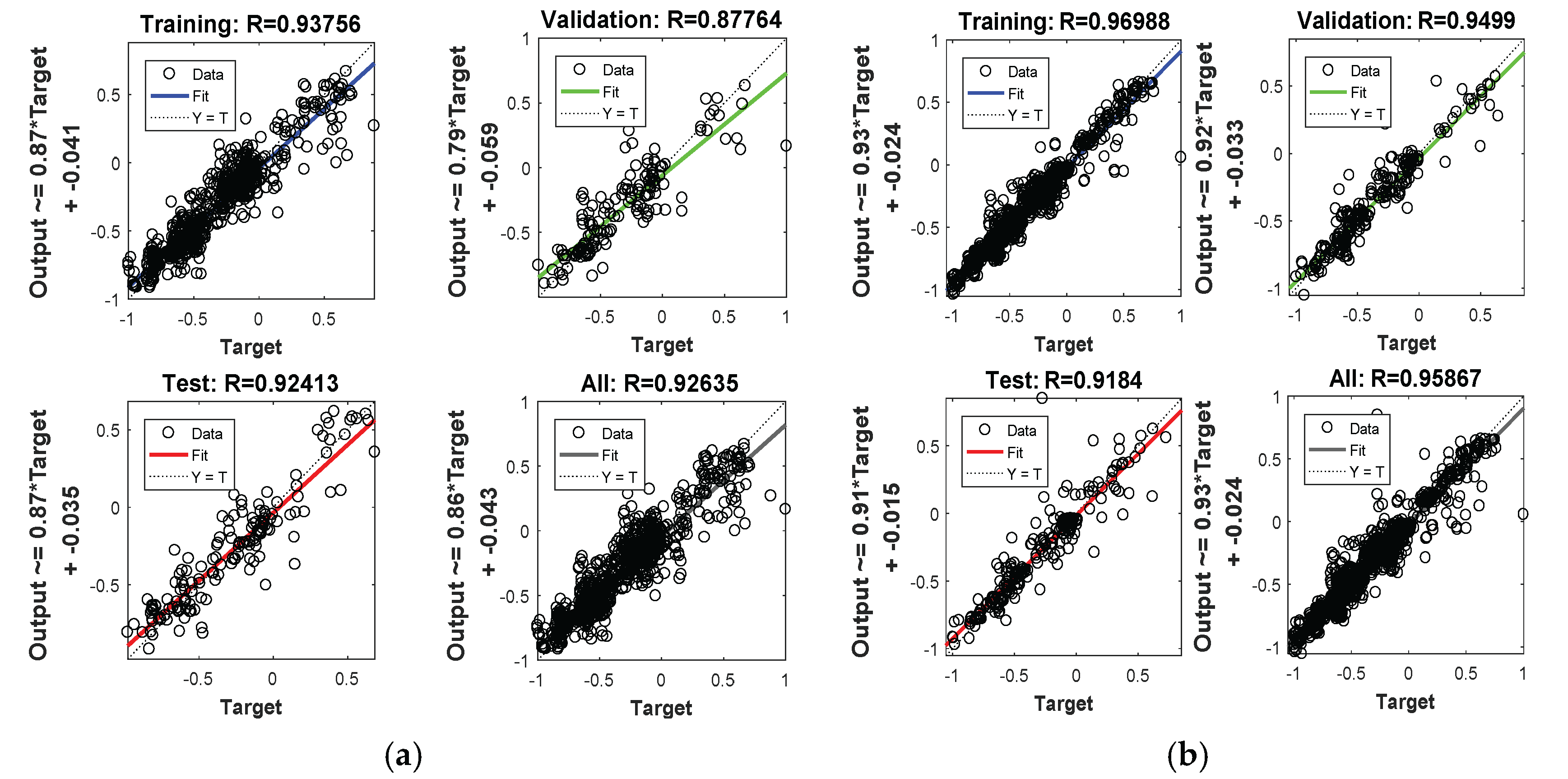
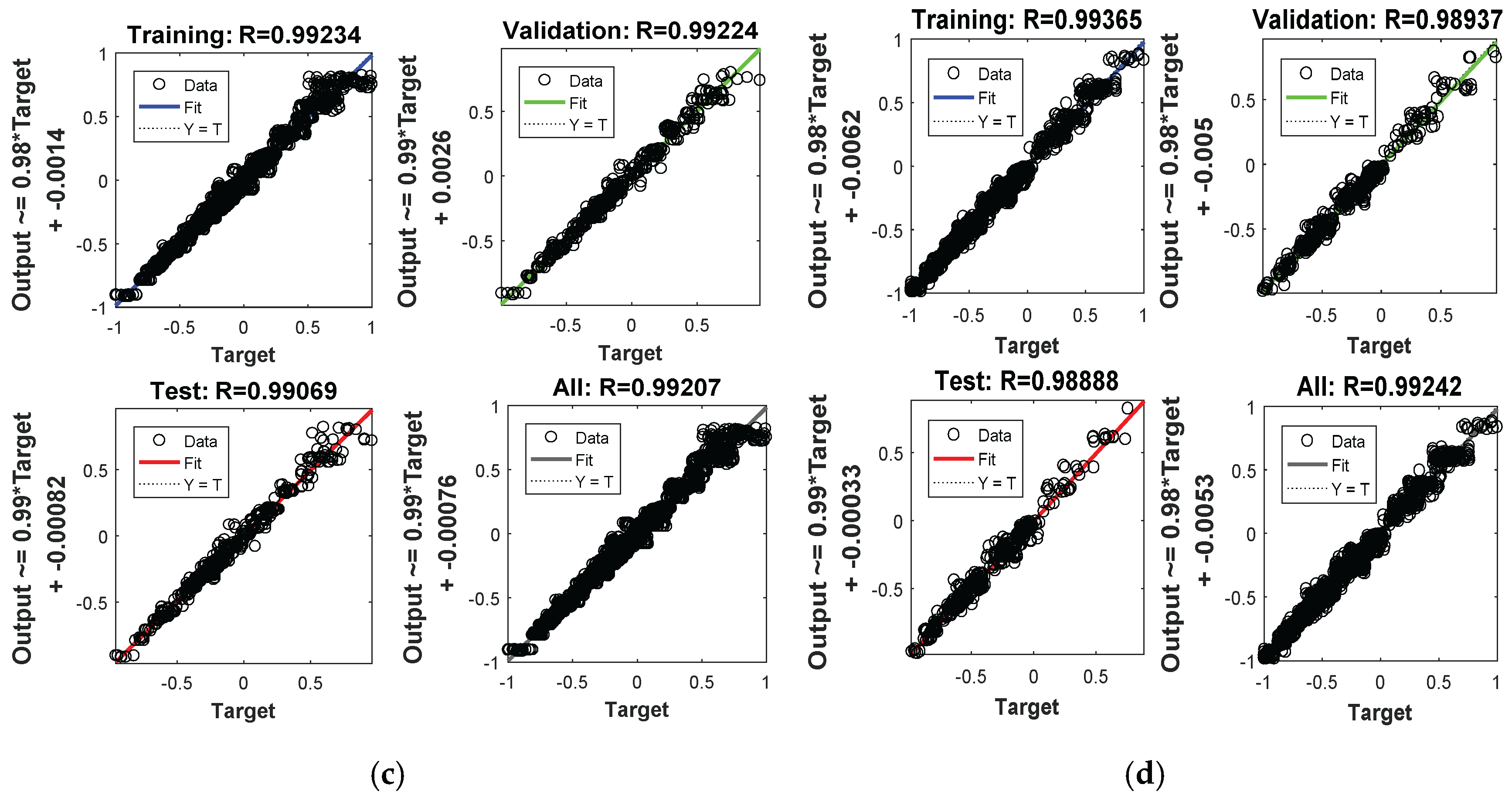
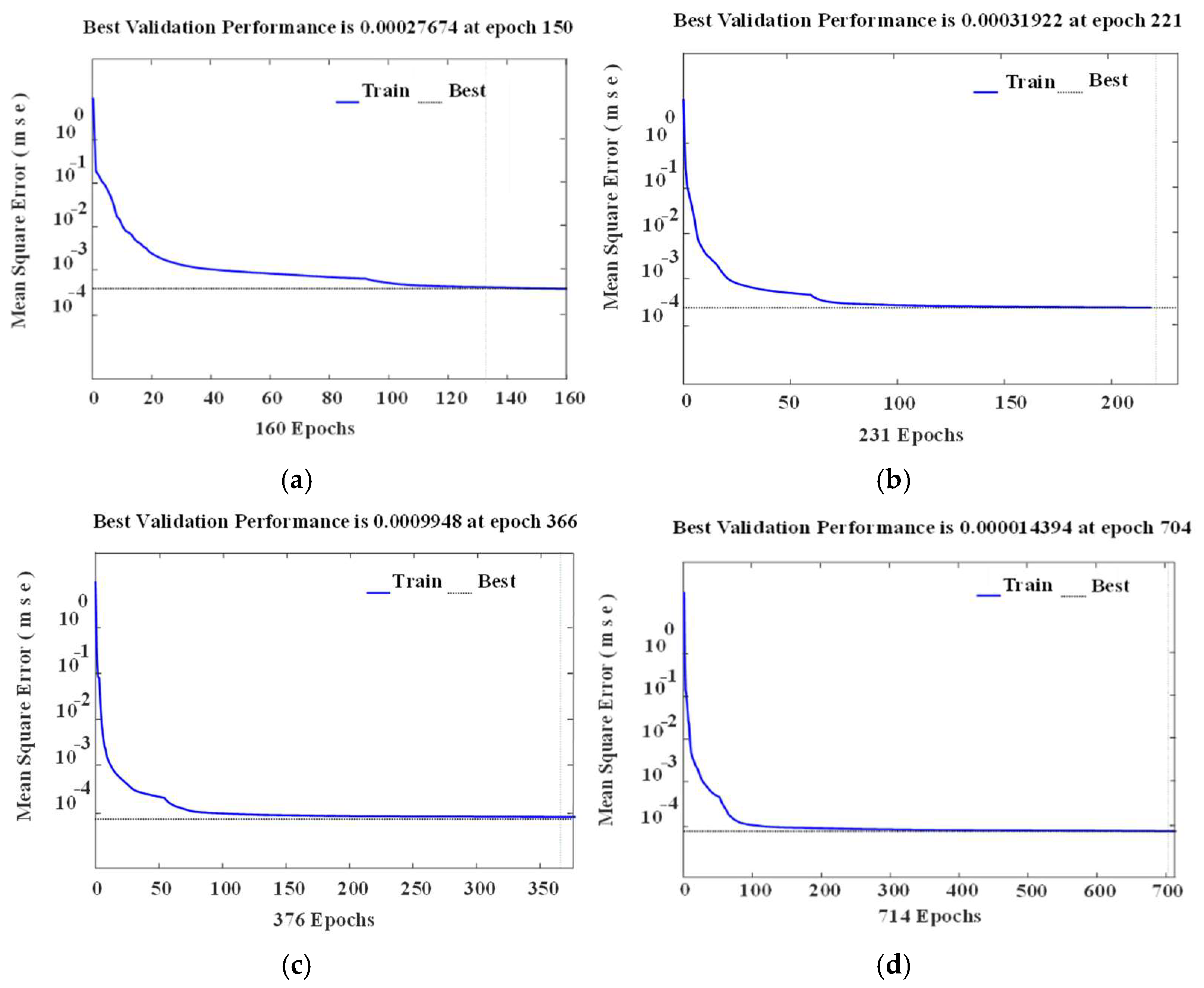
5.3.1. Network Model Training
5.3.2. Network Model Testing
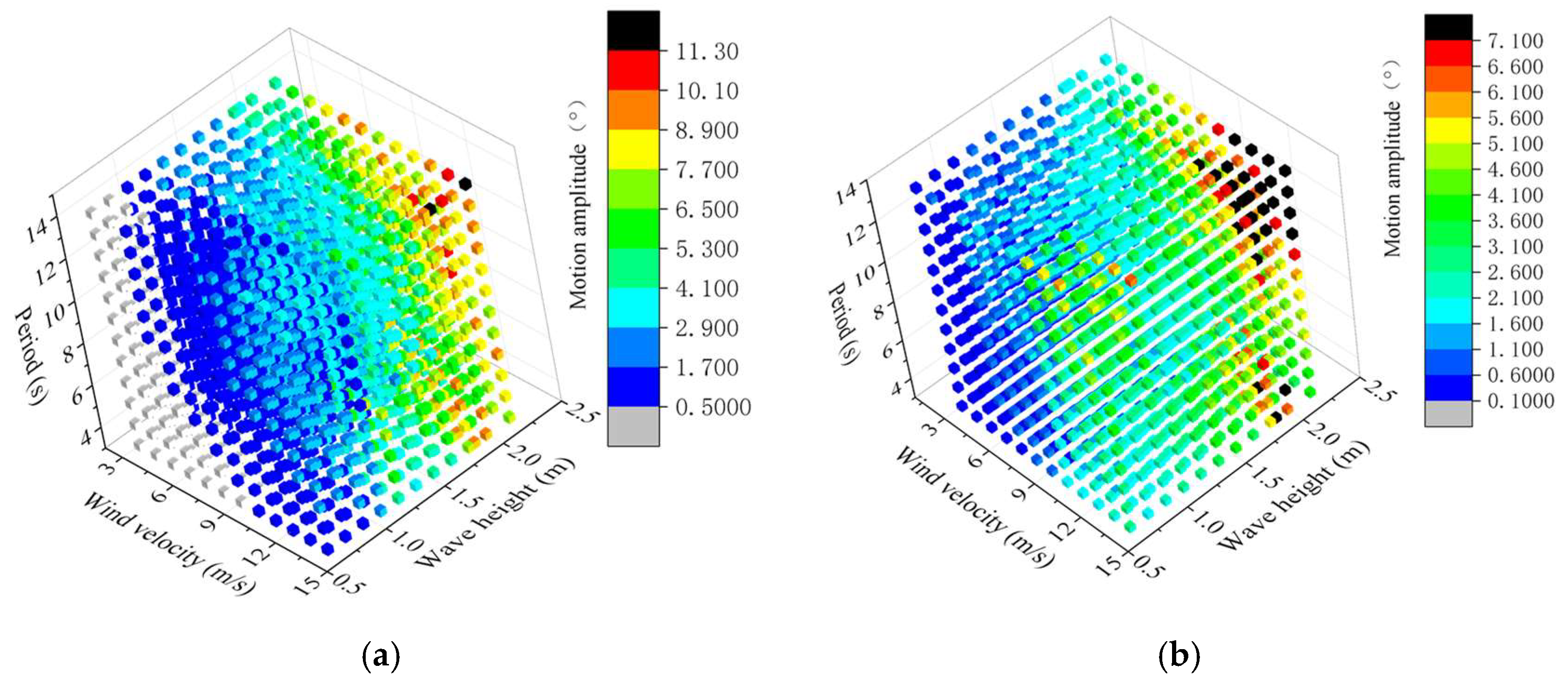
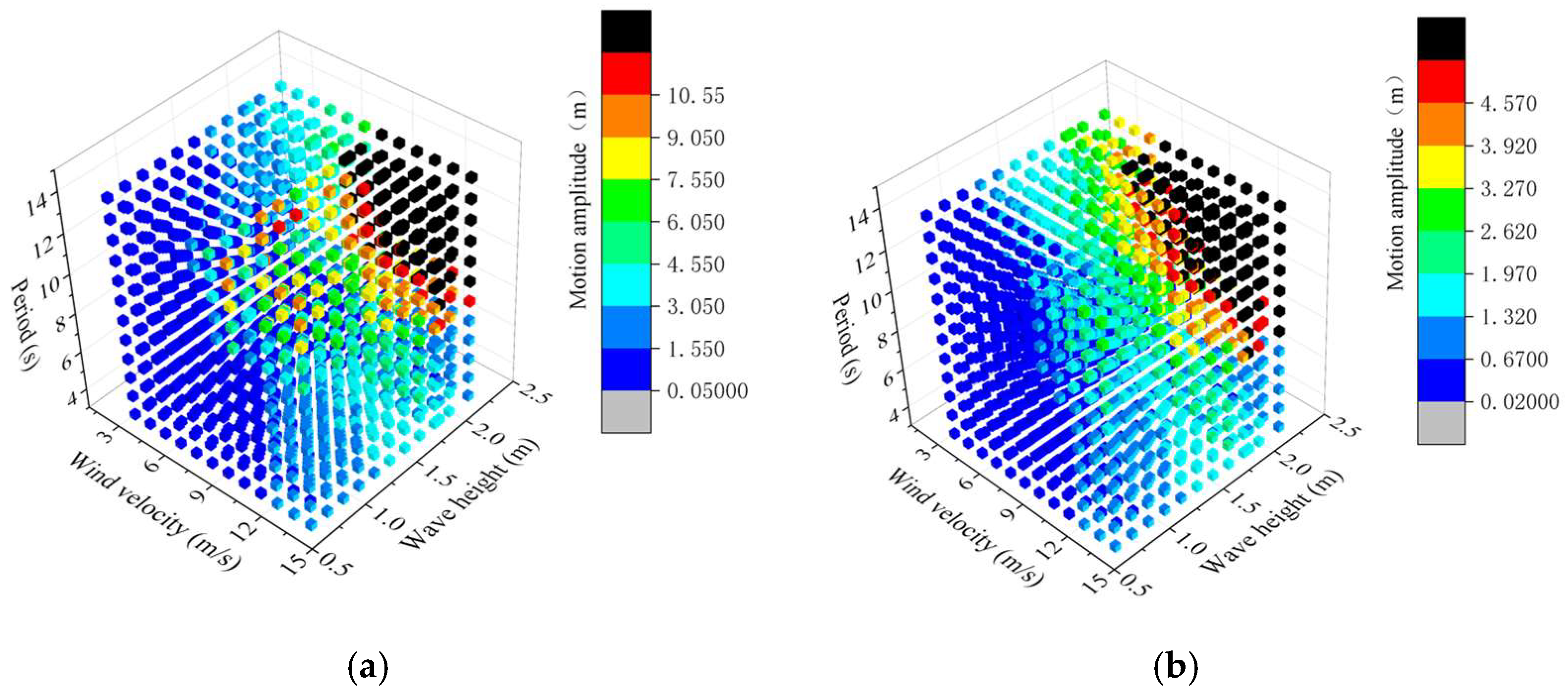
6. Prediction of Operation of the Floating Crane System
6.1. Environmental Data of a Wind Farm in the Eastern China Sea
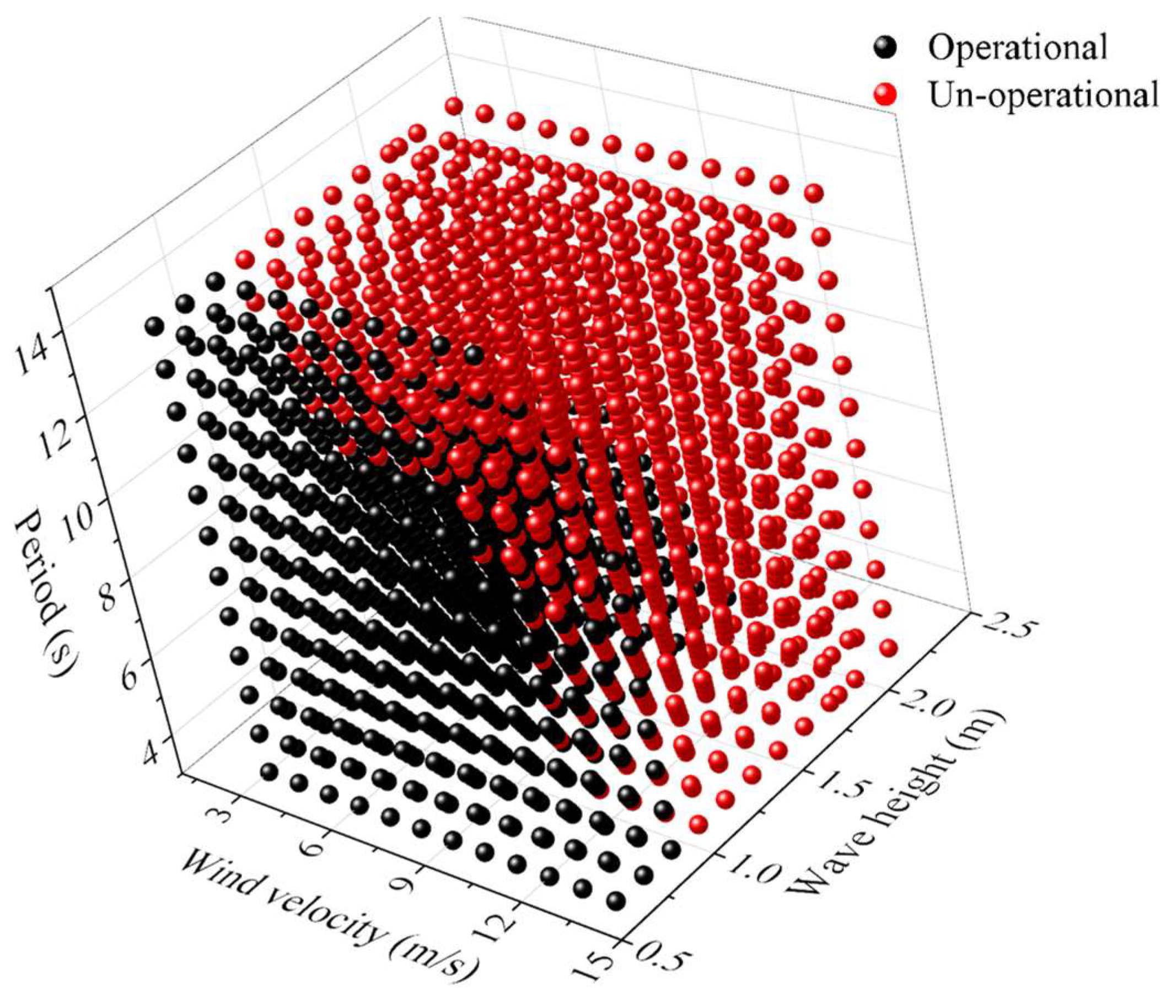
6.2. Motion Prediction and Operation Analysis
7. Conclusions
- (1)
- The cargo deck ship has a significant effect on the motion of the floating derrick, as the hydrodynamics parameters will be different considering the interaction of the cargo ship. The wind velocity under the wave in the direction of 180° mainly affects the pitch and heave motion of the ship and the sway and surge motion of the lifting. The wave height has a great influence on the sway and surge of the lifting objective. In the process of the lifting operation, the influence of the lifting height of the lifting object on the ship is mainly the pitch, and the influence on the impeller is mainly the surge and heave motion. The boom rotation angle is not the main influencing factor for the floating crane system. The coupling effect of the floating derrick with the lifting impeller is obvious, as the sloshing of the ship is transmitted to the lifting object through the sling, which aggravates the sloshing amplitude of the lifting object;
- (2)
- The BP neural network for the floating crane motion response prediction model is built, based on the evaluation indexes of the model performance under different parameters. It is determined that the neural network model with nine hidden layers and nine neurons in each hidden layer can give a good prediction with a small error. The BP neural network is verified to be effective and feasible for predicting the motions of the floating crane system;
- (3)
- Based on the environmental characteristics, the motions of the 1728 working cases are generated by the BP neural network. Combined with the Rules for Lifting Appliances of Ships and Offshore Installations [24] and the Noble Denton Guidelines for Marine Lifting Operation [25], the operation analysis of the floating crane system is performed. As the wind velocity does not exceed 10 m/s, the period does not exceed 10 s, and the significant wave height is within 1 m, the floating crane ship can safely carry out the lifting operation, and its operation efficiency will be improved accordingly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, J.; Li, C.; Wen, W.; Zhou, R.; Reppa, V. Deep Learning in Maritime Autonomous Surface Ships: Current Development and Challenges. J. Mar. Sci. Appl. 2023, 22, 584–601. [Google Scholar] [CrossRef]
- Kristensen, H.O. Statistical Analysis and Determination of Regression Formulas for Main Dimensions of Container Ships Based on IHS Fairplay Data; University of Southern Denmark: Odense, Denmark, 2013. [Google Scholar]
- Papanikolaou, A. Ship Design; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Gurgen, S.; Altın, İ.; Ozkok, M. Prediction of Main Particulars of a Chemical Tanker at Preliminary Ship Design Using Artificial Neural Network. Ships Offshore Struct. 2018, 13, 459–465. [Google Scholar] [CrossRef]
- Cepowski, T.; Chorab, P. Determination of Design Formulas for Container Ships at the Preliminary Design Stage Using Artificial Neural Network and Multiple Nonlinear Regression. Ocean Eng. 2021, 238, 109727. [Google Scholar] [CrossRef]
- Jeon, M.; Noh, Y.; Shin, Y.; Lim, O.K.; Lee, I.; Cho, D. Prediction of Ship Fuel Consumption by Using an Artificial Neural Network. J. Mech. Sci. Technol. 2018, 32, 5785–5796. [Google Scholar] [CrossRef]
- Kaplan, P. A Study of Prediction Techniques for Aircraft Carrier Motions at Sea. J. Hydronautics 1969, 3, 121–131. [Google Scholar] [CrossRef]
- Triantafyllou, M.; Bodson, M.; Athans, M. Real Time Estimation of Ship Motions Using Kalman Filtering Techniques. IEEE J. Ocean Eng. 1983, 8, 9–20. [Google Scholar] [CrossRef]
- Hui, L.; Chen, G.; Li, X.F. Analysis and Prediction of Ship Roll Motion Based on the Theory of Wavelet Transform. J. Dalian Marit. Univ. 2010, 36, 5–8. [Google Scholar] [CrossRef]
- Ma, J.; Li, G. Time Series Prediction of Ship Rolling. J. Beijing Inst. Mach. 2006, 4–7. [Google Scholar] [CrossRef]
- Li, G.; Kawan, B.; Wang, H.; Zhang, H. Neural-Network-Based Modeling and Analysis for Time Series Prediction of Ship Motion. Ship Technol. Res. 2017, 64, 30–39. [Google Scholar] [CrossRef]
- Gao, M.; Shi, G.; Li, S. Online Prediction of Ship Behavior with Automatic Identification System Sensor Data Using Bidirectional Long Short-Term Memory Recurrent Neural Network. Sensors 2018, 18, 4211. [Google Scholar] [CrossRef] [PubMed]
- Duan, W.-Y.; Huang, L.-M.; Han, Y.; Zhang, Y.-H.; Huang, S. A Hybrid AR-EMD-SVR Model for The Short-Term Prediction of Nonlinear and Non-Stationary Ship Motion. J. Zhejiang Univ.-SCIENCE A 2015, 16, 562–576. [Google Scholar] [CrossRef]
- Khan, A.; Bil, C.; Marion, K.E. Ship Motion Prediction for Launch and Recovery of Air Vehicles. In Proceedings of the OCEANS 2005 MTS/IEEE, Washington, DC, USA, 17–23 September 2005; Volume 2793, pp. 2795–2801. [Google Scholar]
- Cha, J.-H.; Roh, M.-I.; Lee, K.-Y. Dynamic Response Simulation of a Heavy Cargo Suspended by a Floating Crane Based on Multibody System Dynamics. Ocean Eng. 2010, 37, 1273–1291. [Google Scholar] [CrossRef]
- Van Trieu, P. Combined Controls of Floating Container Cranes. In Proceedings of the 2015 International Conference on Control, Automation and Information Sciences (ICCAIS), Changshu, China, 29–31 October 2015. [Google Scholar]
- Ardhiansyah, F.; Prastianto, R.W.; Murdjito; Suastika, K.; Nugroho, S. Dynamic Response of Floating Crane During Lifting Operation: A Parametric Study. In Applied and Computational Mathematics; Springer Proceedings in Mathematics & Statistics; Springer Nature: Singapore, 2024; Volume 455. [Google Scholar] [CrossRef]
- Nam, B.W.; Kim, N.W.; Hong, S.Y. Experimental and Numerical Study on Coupled Motion Responses of a Floating Crane Vessel and a Lifted Subsea Manifold in Deep Water. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 552–567. [Google Scholar] [CrossRef]
- Soner, O.; Akyuz, E.; Celik, M. Statistical Modelling of Ship Operational Performance Monitoring Problem. J. Mar. Sci. Technol. 2019, 24, 543–552. [Google Scholar] [CrossRef]
- An, J.; Yu, Y.; Cao, W.; Wu, M. Load Distribution and Optimization Method for Cooperative Lifting of Double Cranes Considering the Minimal Lifting Consumption. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 2969–2974. [Google Scholar]
- Cheng, N.; Chen, L.; Zeng, D. Ship Energy Efficiency Prediction Method Based on Data Mining Techniques. In Proceedings of the 2024 3rd Conference on Fully Actuated System Theory and Applications (FASTA), Shenzhen, China, 10–12 May 2024. [Google Scholar]
- Gao, Z. Research in Data Mining Technology of Ship Intelligent Energy Efficiency Management. Master’s Thesis, Dalian Maritime University, Dalian, China, 2019. [Google Scholar]
- DNV. User Guide for SIMA; SINTEF Ocean and DNV: Oslo, Norway, 2022. [Google Scholar]
- China Classification Society. Rules for Lifting Appliances of Ships and Offshore Installations; China Communications Press: Beijing, China, 2007. [Google Scholar]
- GL Noble Denton. Guidelines for Marine Lifting Operations; Technical Policy Board: Berlin, Germany, 2010. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Luo, X. Numerical Simulation and Experimental Study on Motion Responses of Lanjiang Crane Vessel Coupling System in Heading Waves. Master’s Thesis, Tianjin University, Tianjin, China, 2018. (In Chinese). [Google Scholar]

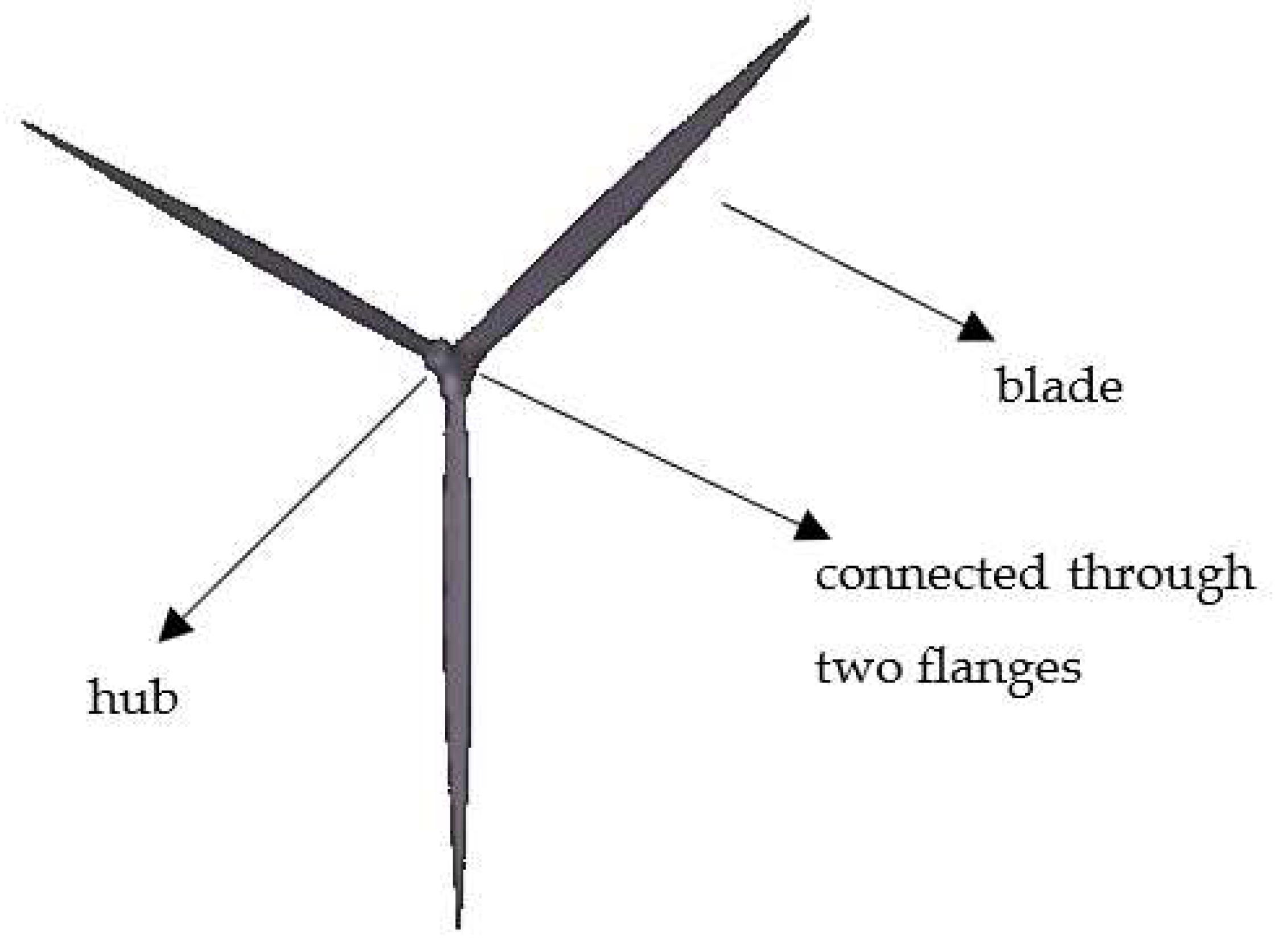

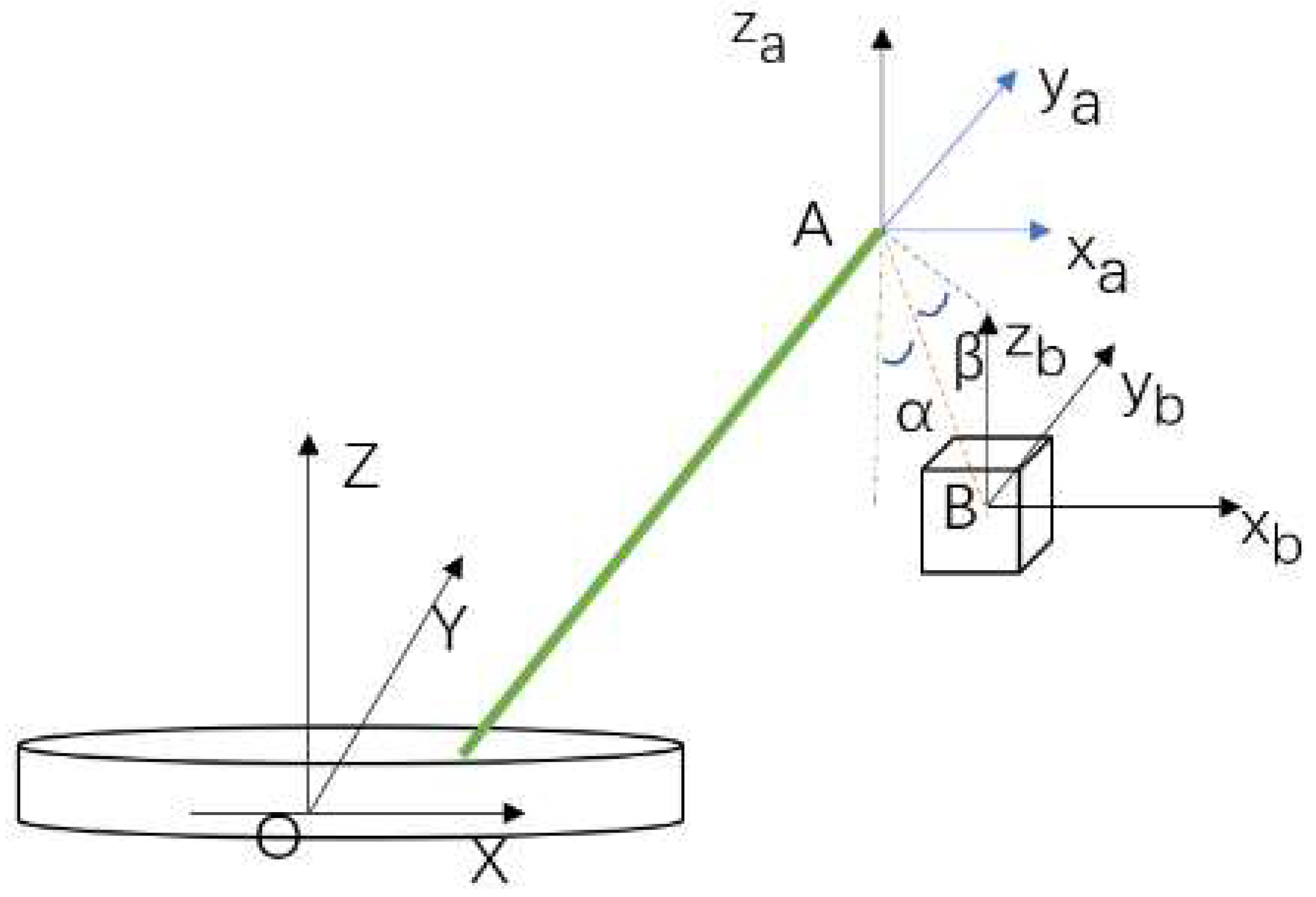
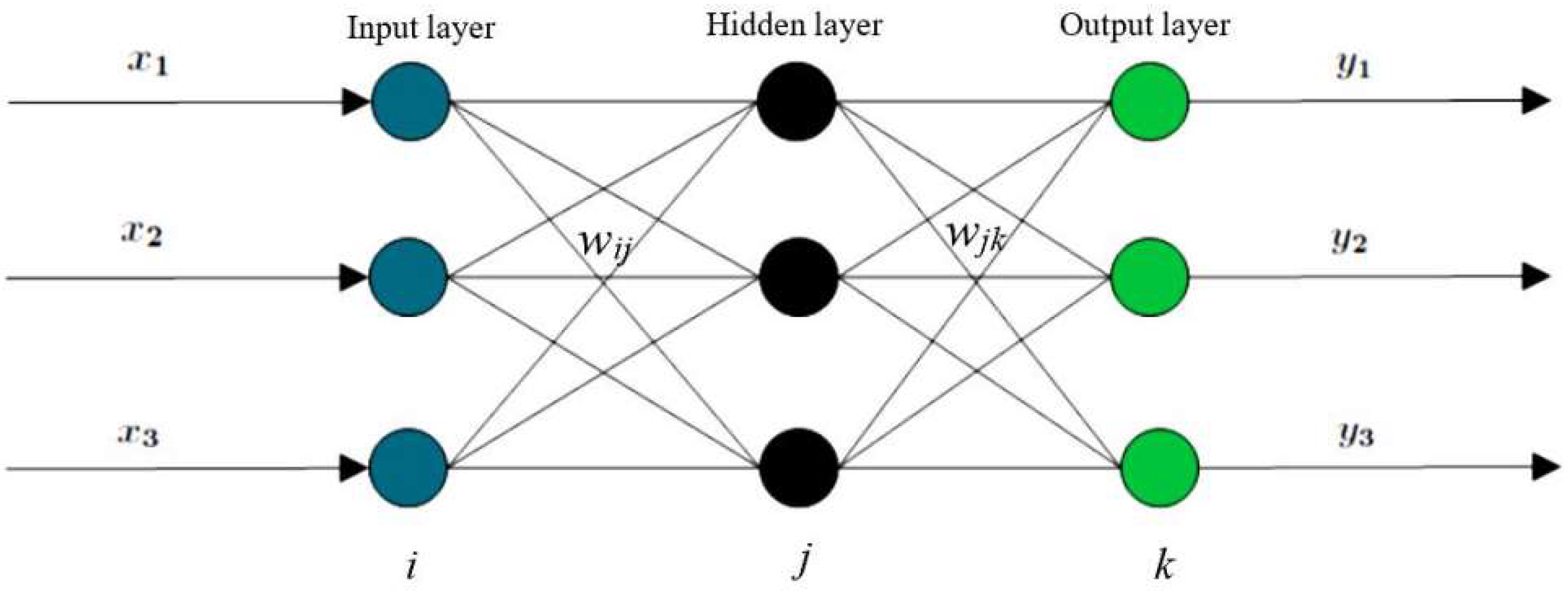




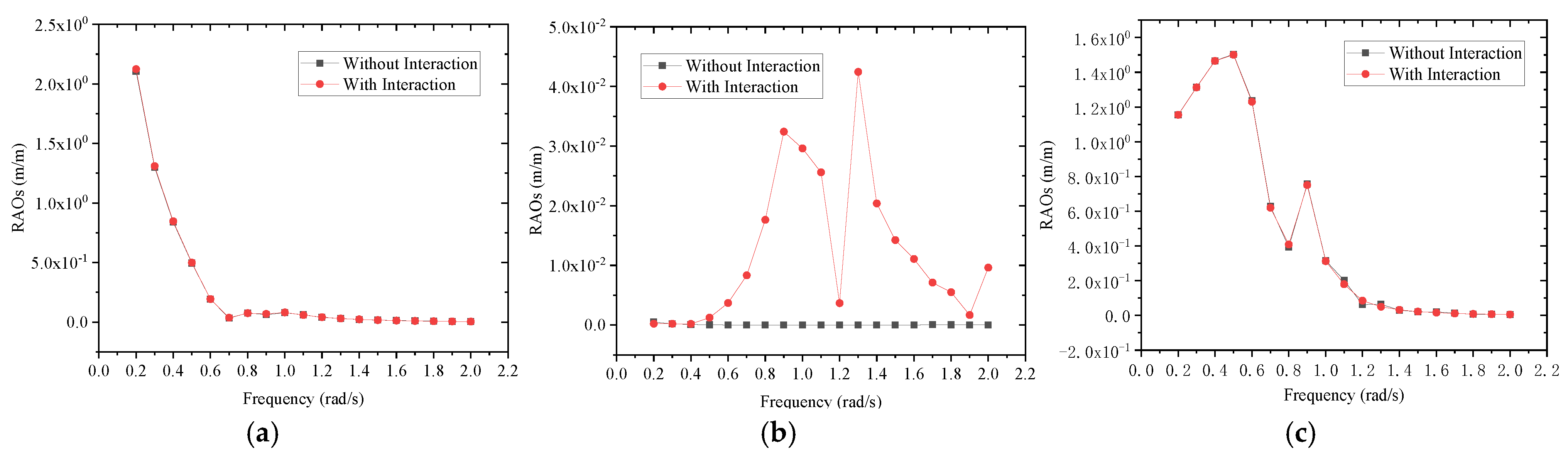
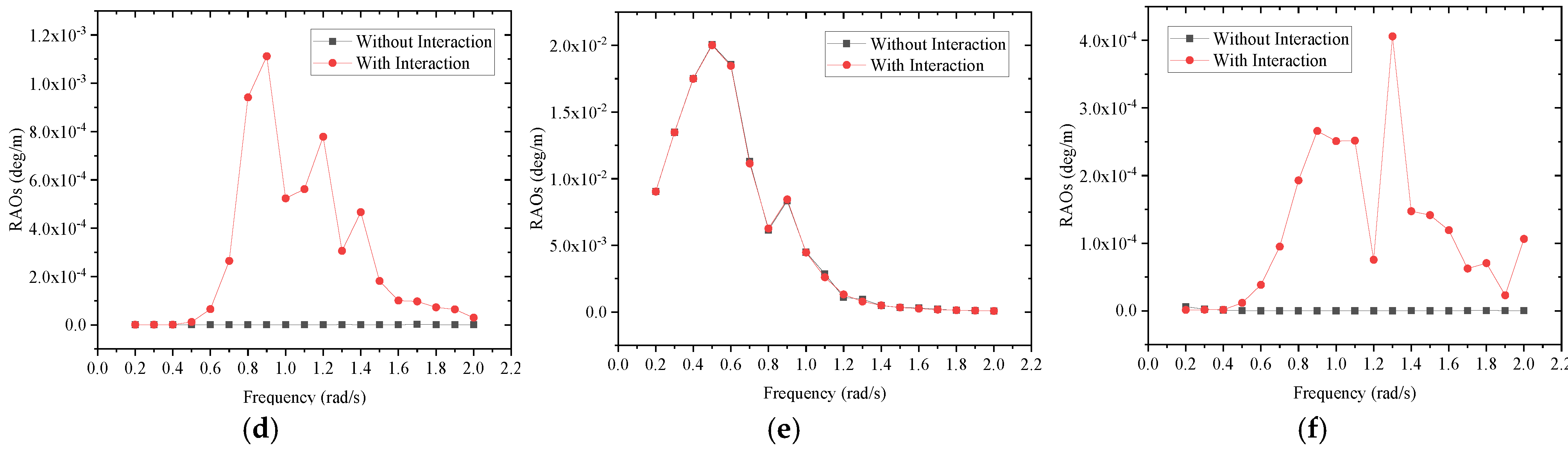
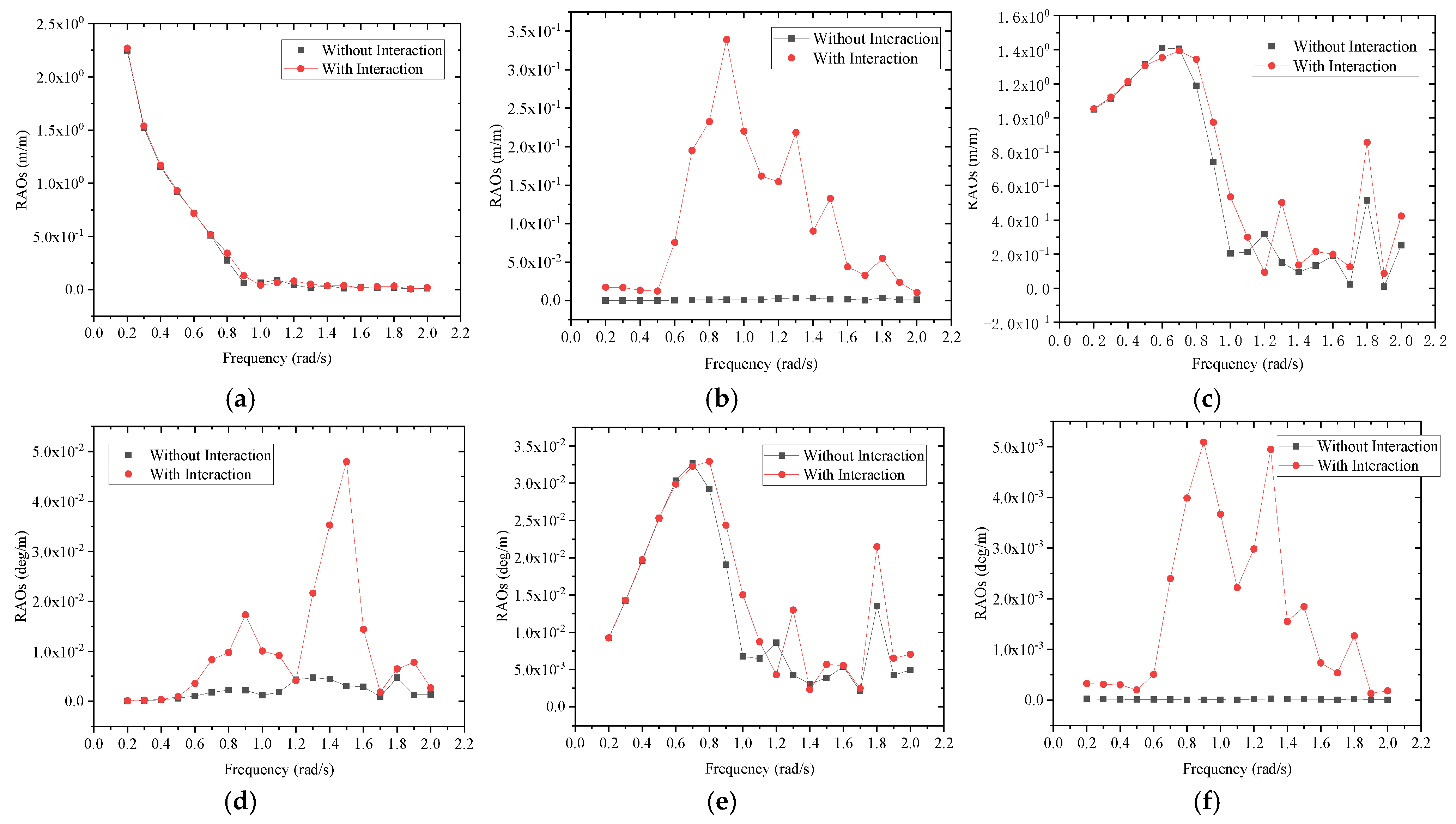
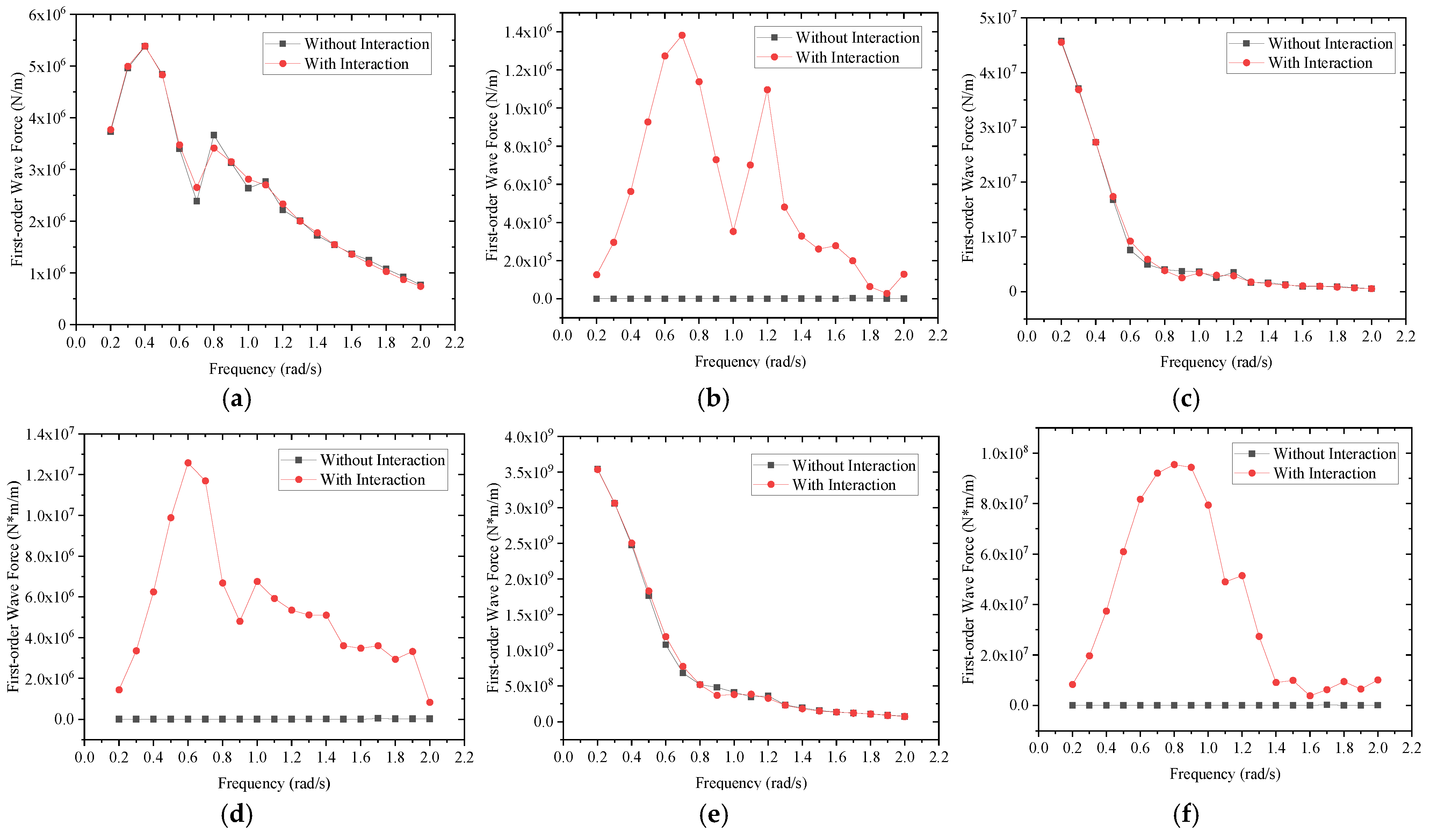


| Items | Variable | Unit | Ship Type | |
|---|---|---|---|---|
| Floating Derrick | Deck Cargo Ship | |||
| Length | m | 143 | 88 | |
| Waterline length | m | 141 | 86 | |
| Length between perpendiculars | m | 137 | 82 | |
| Width | B | m | 46.4 | 15 |
| Width of one sheet | b | m | - | 5.6 |
| Depth | D | m | 10.8 | 4 |
| Draft | d | m | 7.5 | 3 |
| Displacement | t | 40,682 | 1064 | |
| Vertical position of center of gravity | KG | m | 3.62 | 5.12 |
| Longitudinal position of center of gravity | LCG | m | 76.13 | 42.2 |
| Inertia radius of roll | m | 13.48 | 5.31 | |
| Inertia radius of pitch | m | 33.20 | 25.94 | |
| Inertia radius of yaw | m | 35.82 | 26.2 | |
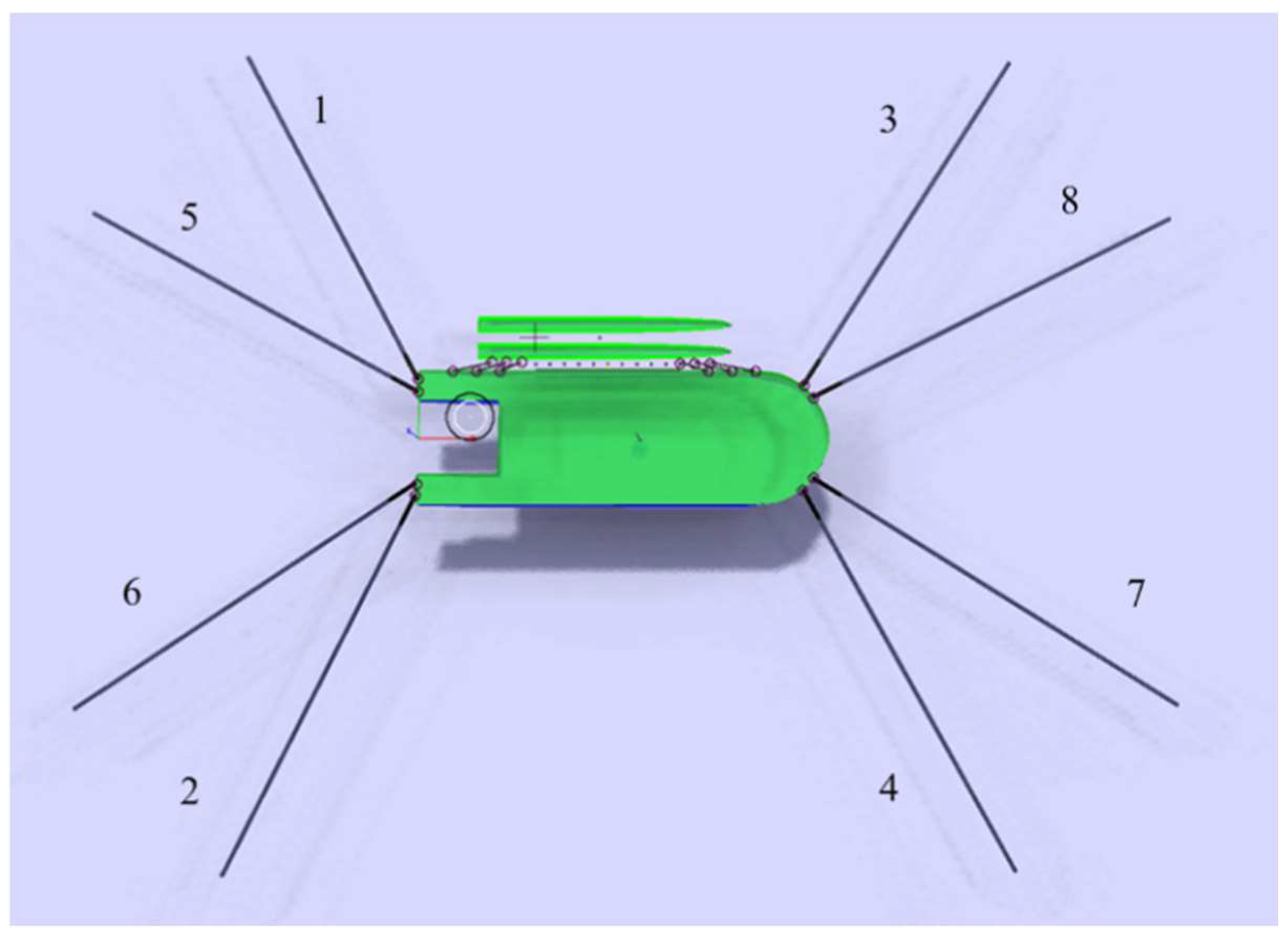
| Mooring Line Number | Pretension (kN) | Azimuth (deg) | Fairlead | ||
|---|---|---|---|---|---|
| X | Y | Z | |||
| 1 | 1100 | 120 | −76 | 20.05 | 3.3 |
| 2 | 1100 | −120 | −76 | −20.05 | 3.3 |
| 3 | 1100 | 60 | 56.5 | 18 | 3.3 |
| 4 | 1100 | −60 | 56.5 | −18 | 3.3 |
| 5 | 1100 | 150 | −76 | 15.85 | 3.3 |
| 6 | 1100 | −150 | −76 | −15.85 | 3.3 |
| 7 | 1100 | 30 | 60 | 14 | 3.3 |
| 8 | 1100 | −30 | 60 | −14 | 3.3 |
| Diameter m | Dry Weight kg/m | Wet Weight kg/m | Stiffness kN | Broken Strength kN |
|---|---|---|---|---|
| 0.076 | 123 | 98.4 | 6.75 × 106 | 8520 |
| Items | Unit | Value |
|---|---|---|
| Number of blades | - | 3 |
| Blade length | m | 61.5 |
| Impeller diameter | m | 126 |
| Hub diameter | m | 3 |
| Hub mass | Kg | 56,780 |
| Leaf mass | Kg | 17,740 |
| Items | Unit | Barge 1 | Barge 2 | |||
|---|---|---|---|---|---|---|
| Original Ship | Test Model | Original Ship | Test Model | |||
| Length | Loa | m | 207 | 2.5875 | 235.6 | 2.9450 |
| Length between perpendiculars | LBP | m | 194 | 2.4250 | 225 | 2.8125 |
| Breadth | B | m | 36 | 0.4500 | 46 | 0.5750 |
| Depth | D | m | 16 | 0.2000 | 24.1 | 0.3013 |
| Draft | d | m | 8.7 | 0.1088 | 11 | 0.1375 |
| Displacement | t | 49,444 | 0.0942 | 104,748.4 | 0.1996 | |
| Vertical position of center of gravity | KG | m | 11.8 | 0.1475 | 10.242 | 0.1280 |
| Center of gravity longitudinal position | LCG | m | 1.8 | 0.0225 | −2.0 | −0.0250 |
| Irregular Wave | Unit | Actual Value | Test Value |
|---|---|---|---|
| Significant wave height | m | 2.5 | 0.03 |
| Spectral periods | s | 10 | 1.1 |
| Direction | deg | 180° | 180° |
| Items | Value |
|---|---|
| Wave spectrum | JONSWAP |
| Wind spectrum | NPD |
| Wind velocity m/s | 3–9 |
| Current velocity m/s | 0.5–1.5 |
| Significant wave height m | 1.25–2.0 |
| Items | Value |
|---|---|
| Lifting height m | 70/80/90 |
| Hoisting arm elevation angle ° | 75 |
| Crane rotation velocity m/s | 0.2 |
| The boom rotation angle ° | 0/45/90/135/180 |
| Operating Condition Parameters | Value |
|---|---|
| Wave spectrum | JONSWAP |
| Wind spectrum | NPD |
| Lifting height m | 65/75/80/85/90/95 |
| Spectral peak period s | 4/6/8/10/12 |
| Wave height m | 0.65/0.8/0.95/1.1/1.25/1.4/1.55 |
| Wind velocity m/s | 3/5/7/9/12 |
| Boom rotation angle ° | 76/77/78/79/80 |
| Parameter | Heave Ship | Roll Ship | Pitch Ship | Surge Lifting Impeller | Heave Lifting Impeller |
|---|---|---|---|---|---|
| We (%) | 0.0361 | 0.3048 | 0.1529 | 0.4114 | 0.2510 |
| Wf (%) | 0.1149 | 0.2885 | 0.2743 | 0.2509 | 0.3198 |
| Wg (%) | 0.0151 | 0.0673 | 0.0433 | 0.0048 | 0.0262 |
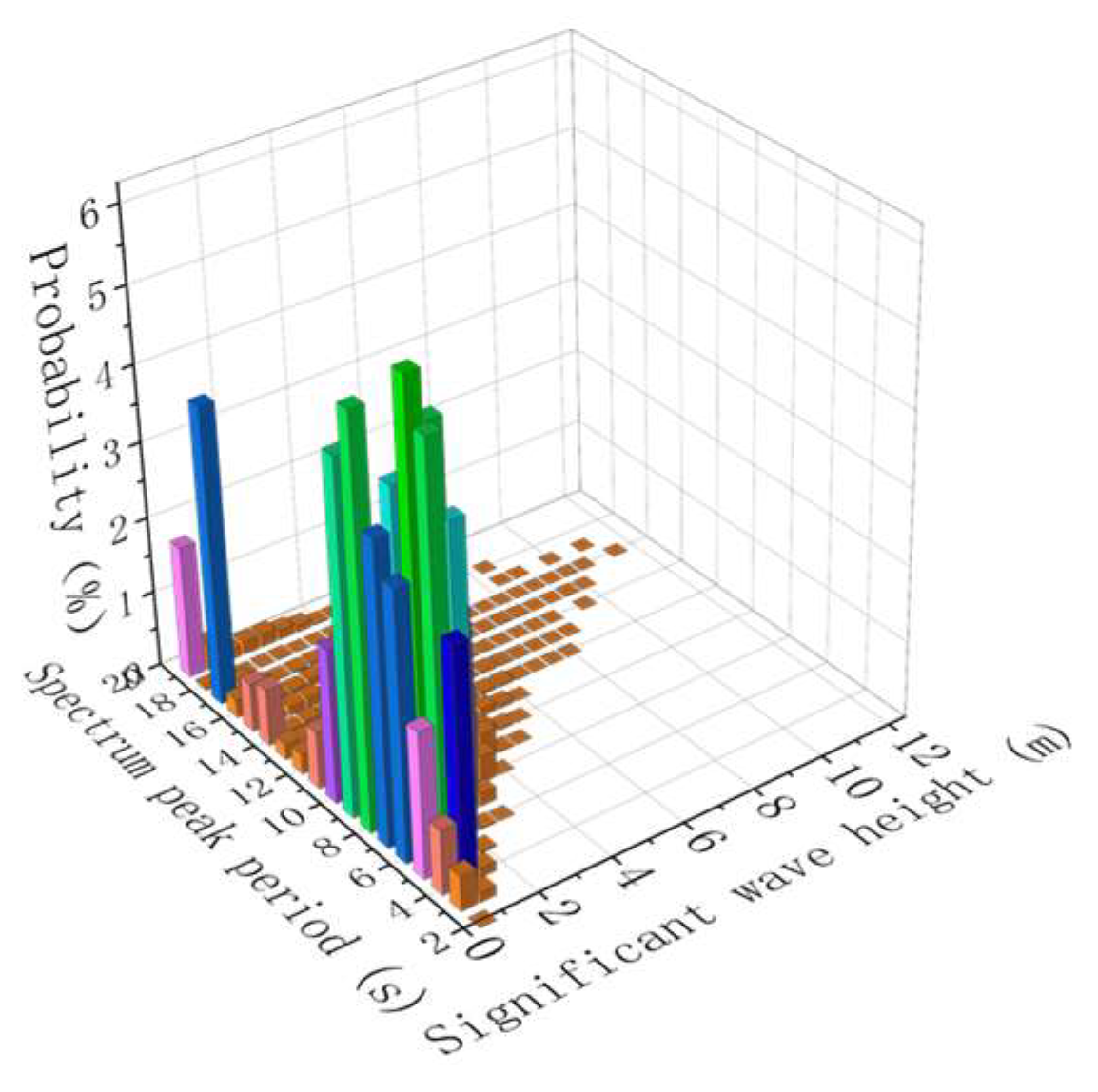
| Total | 0.3 | 16 | 35 | 60.5 | 64 | 135.3 | 160 | 144.8 | 158 | 122 | 51.1 | 32.3 | 11 | 1.8 | 3 | 3 | 4 | 2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| wave height/m | 3.00–3.50 | 0.8 | 0.3 | ||||||||||||||||
| 2.50–3.00 | 0.8 | 4 | 5 | 6 | 4 | ||||||||||||||
| 2.00–2.50 | 0.3 | 1 | 9 | 17 | 28 | 12 | 7 | ||||||||||||
| 1.50–2.00 | 0.5 | 2 | 6 | 15 | 26 | 35 | 22 | 6 | 3 | 6 | |||||||||
| 1.00–1.50 | 2 | 9 | 22 | 34 | 46 | 35 | 42 | 31 | 2 | 8 | 2 | 1 | |||||||
| 0.50–1.00 | 5 | 16 | 38 | 33 | 59 | 72 | 68 | 57 | 36 | 24 | 10 | 3 | |||||||
| 0.00–0.50 | 0.3 | 11 | 17 | 13 | 7 | 36 | 26 | 6 | 3 | 0.3 | 0.8 | 3 | 3 | 4 | 2 | ||||
| Period/s | 2.25 | 2.75 | 3.25 | 3.75 | 4.25 | 4.75 | 5.25 | 5.75 | 6.25 | 6.75 | 7.25 | 7.75 | 8.25 | 8.75 | 9.25 | 1025 | 10.75 | 11.25 | |
| Parameters | Value |
|---|---|
| Wave height m | 0.65–2.2 |
| Wind velocity m/s | 3–12 |
| Spectral peak period s | 2–12 |
| Current velocity m/s | 1.0 |
| Lifting height m | 70 |
| Boom rotation angle ° | 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Li, H.; Wang, S.; Shi, X. Operation Analysis of the Floating Derrick for Offshore Wind Turbine Installation Based on Machine Learning. J. Mar. Sci. Eng. 2024, 12, 2136. https://doi.org/10.3390/jmse12122136
Yu J, Li H, Wang S, Shi X. Operation Analysis of the Floating Derrick for Offshore Wind Turbine Installation Based on Machine Learning. Journal of Marine Science and Engineering. 2024; 12(12):2136. https://doi.org/10.3390/jmse12122136
Chicago/Turabian StyleYu, Jia, Honglong Li, Shan Wang, and Xinghua Shi. 2024. "Operation Analysis of the Floating Derrick for Offshore Wind Turbine Installation Based on Machine Learning" Journal of Marine Science and Engineering 12, no. 12: 2136. https://doi.org/10.3390/jmse12122136
APA StyleYu, J., Li, H., Wang, S., & Shi, X. (2024). Operation Analysis of the Floating Derrick for Offshore Wind Turbine Installation Based on Machine Learning. Journal of Marine Science and Engineering, 12(12), 2136. https://doi.org/10.3390/jmse12122136







