Case Study of Central Outlet Cap Used in Flow-Through Aquaculture Systems by Using Computational Fluid Dynamics
Abstract
1. Introduction
2. Model Design and Methods for Numerical Analysis and Simulation
2.1. Geometric Model and Boundary Conditions
2.2. Numerical Model Set Up
2.3. Definition of Orthogonal Array
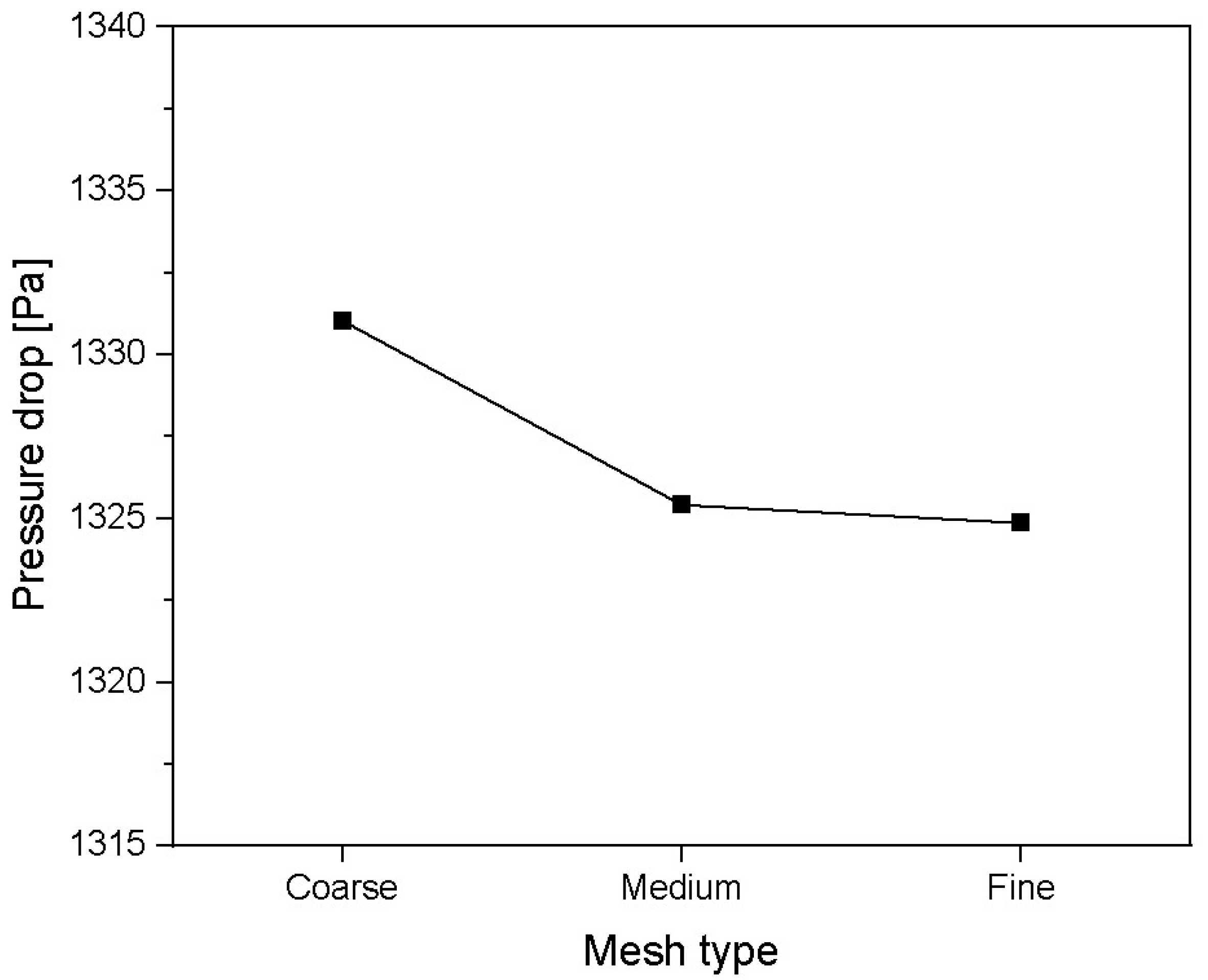
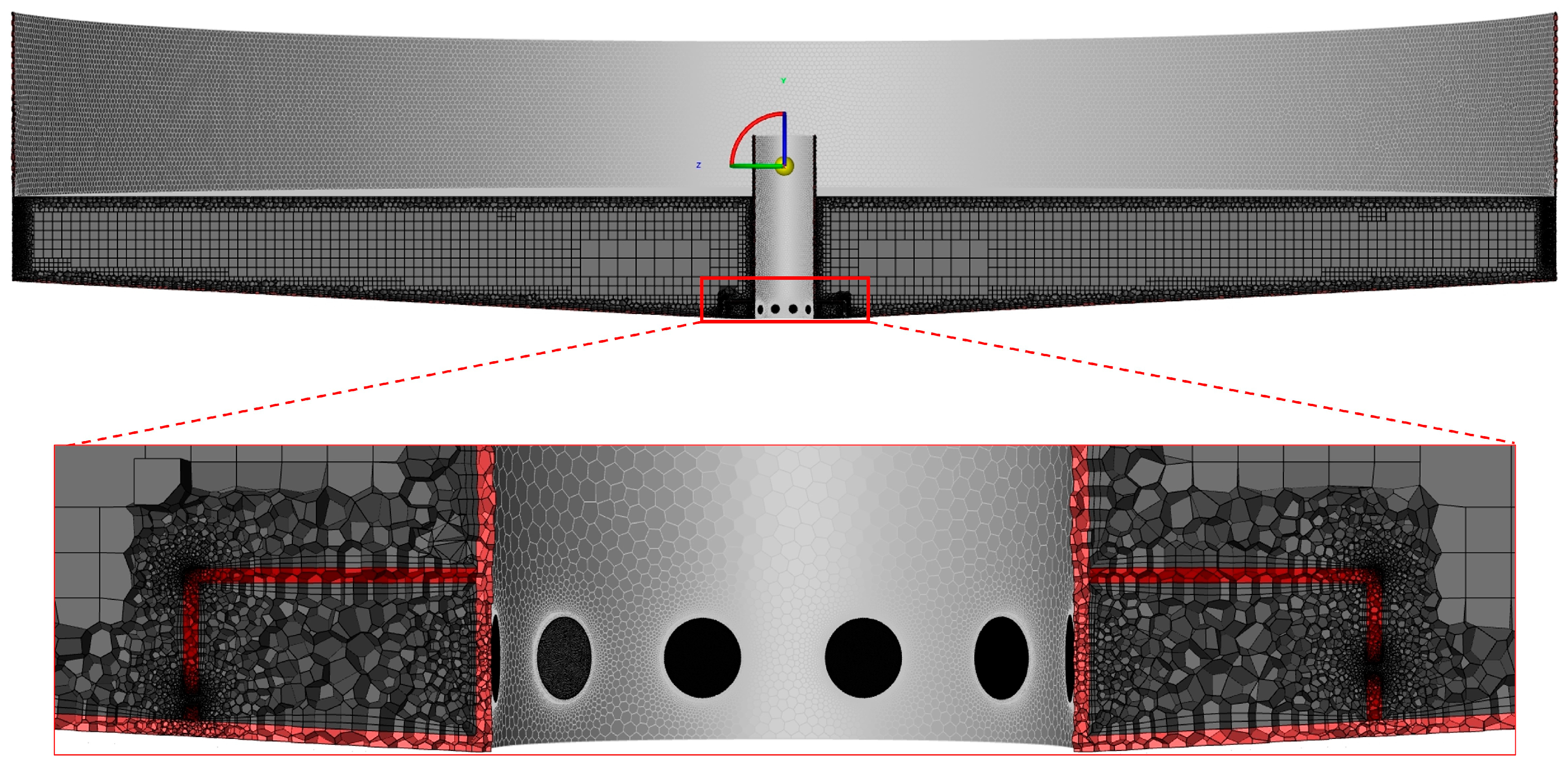
2.4. Grid Models
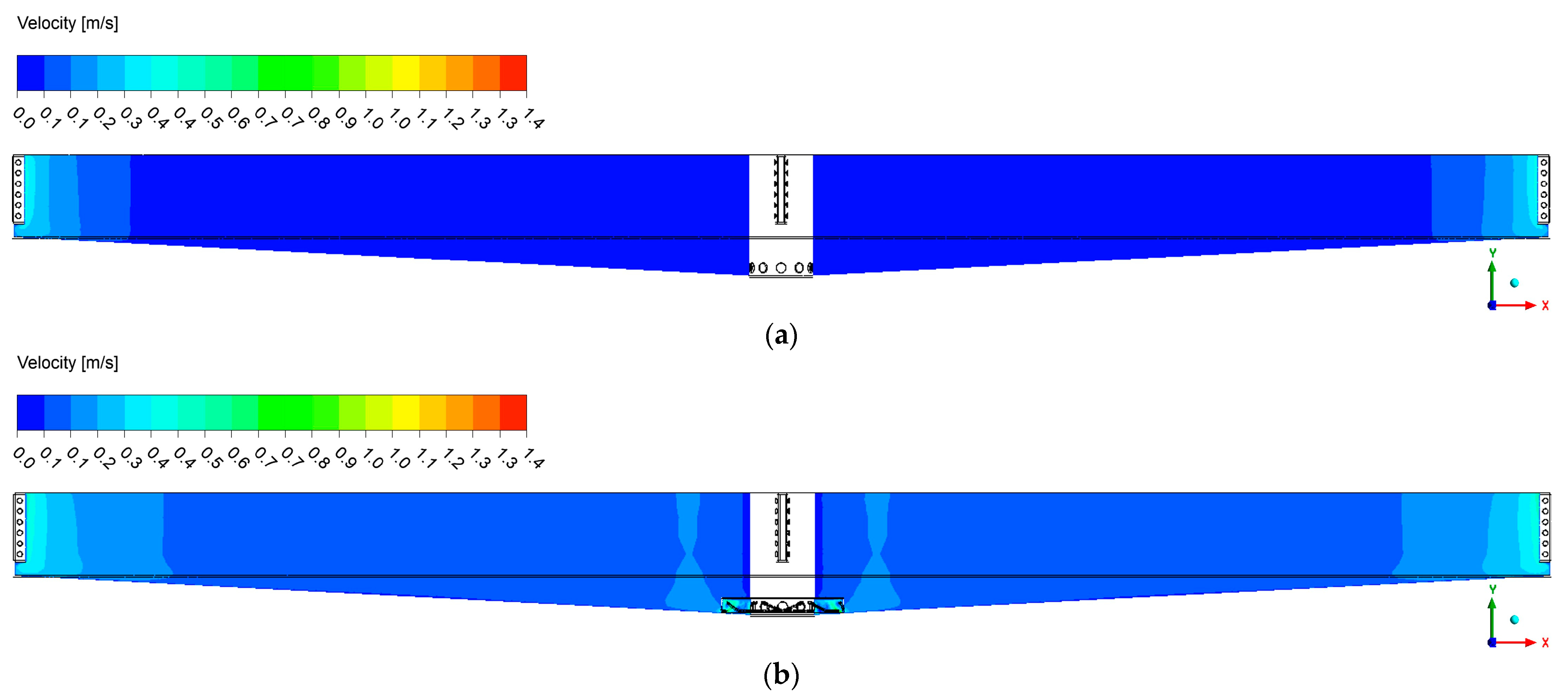
3. Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations (FAO). The State of World Fisheries and Aquaculture 2022. Towards Blue Transformation; FAO: Rome, Italy, 2022. [Google Scholar]
- Iber, B.T.; Kasan, N.A. Recent Advances in Shrimp Aquaculture Wastewater Management. Heliyon 2021, 7, e08283. [Google Scholar] [CrossRef] [PubMed]
- National Assembly Research Service (NARS). Current Status and Future Tasks of the Smart Aquaculture Industry; NARS: Seoul, Republic of Korea, 2019. [Google Scholar]
- Hoque, M.S.; Haque, M.M.; Nielsen, M.; Rahman, M.T.; Hossain, M.I.; Mahmud, S.; Mandal, A.K.; Frederiksen, M.; Larsen, E.P. Prospects and Challenges of Yellow Flesh Pangasius in International Markets: Secondary and Primary Evidence from Bangladesh. Heliyon 2021, 7, e08060. [Google Scholar] [CrossRef] [PubMed]
- Ciji, A.; Akhtar, M.S. Stress Management in Aquaculture: A Review of Dietary Interventions. Rev. Aquac. 2021, 13, 2190–2247. [Google Scholar] [CrossRef]
- Wells, R.M.G.; Pankhurst, N.W. Evaluation of Simple Instruments for the Measurement of Blood Glucose and Lactate, and Plasma Protein as Stress Indicators in Fish. J. World Aquac. Soc. 1999, 30, 276–284. [Google Scholar] [CrossRef]
- Yada, T.; Tort, L. Stress and Disease Resistance: Immune System and Immunoendocrine Interactions. In Fish Physiology; Elsevier: Amsterdam, The Netherlands, 2016; Volume 35, pp. 365–403. ISBN 1546-5098. [Google Scholar]
- Korean Statistical Information Service (KOSIS). Current Status of Aquaculture by Fish Type by Aquaculture Method. Available online: https://kosis.kr/statHtml/statHtml.do?orgId=101&tblId=DT_1EZ0008 (accessed on 3 December 2023).
- Yin, G.; Ong, M.C.; Lee, J.; Kim, T. Numerical Simulation of Oxygen Transport in Land-Based Aquaculture Tank. Aquaculture 2021, 543, 736973. [Google Scholar] [CrossRef]
- Xiong, Z.; He, M.; Zhu, W.; Sun, Y.; Hou, X. Analysis of Flow Field Characteristics of Aquaculture Cabin of Aquaculture Ship. J. Mar. Sci. Eng. 2023, 11, 390. [Google Scholar] [CrossRef]
- Wang, C.M.; Ma, M.; Chu, Y.; Jeng, D.-S.; Zhang, H. Developments in Modeling Techniques for Reliability Design of Aquaculture Cages: A Review. J. Mar. Sci. Eng. 2024, 12, 103. [Google Scholar] [CrossRef]
- Zhang, F.; Cui, M.; Liu, H.; Zhang, C. The Effect of Corner Structure on the Optimisation of Fishable Flow Field in Aquaculture Tanks. J. Mar. Sci. Eng. 2024, 12, 1185. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. A Review of the Hydroelastic Theoretical Models of Floating Porous Nets and Floaters for Offshore Aquaculture. J. Mar. Sci. Eng. 2024, 12, 1699. [Google Scholar] [CrossRef]
- Guo, Y.C.; Mohapatra, S.C.; Guedes Soares, C. Review of Developments in Porous Membranes and Net-Type Structures for Breakwaters and Fish Cages. Ocean Eng. 2020, 200, 107027. [Google Scholar] [CrossRef]
- Oca, J.; Masalo, I. Flow Pattern in Aquaculture Circular Tanks: Influence of Flow Rate, Water Depth, and Water Inlet & Outlet Features. Aquac. Eng. 2013, 52, 65–72. [Google Scholar] [CrossRef]
- An, C.-H.; Sin, M.-G.; Kim, M.-J.; Jong, I.-B.; Song, G.-J.; Choe, C. Effect of Bottom Drain Positions on Circular Tank Hydraulics: CFD Simulations. Aquac. Eng. 2018, 83, 138–150. [Google Scholar] [CrossRef]
- Saisorn, S.; Wongwises, S. Flow Pattern, Void Fraction and Pressure Drop of Two-Phase Air–Water Flow in a Horizontal Circular Micro-Channel. Exp. Therm. Fluid Sci. 2008, 32, 748–760. [Google Scholar] [CrossRef]
- Okafor, N.A.; Aimikhe, V.J.; Kinigoma, B. Modelling the effect of acceleration term on total pressure drop in horizontal gas pipelines. Pet. Coal 2019, 61, 1314. [Google Scholar]
- Mallya, Y.J. The Effects of Dissolved Oxygen on Fish Growth in Aquaculture. In The United Nations University Fisheries Training Programme, Final Project; United Nations University: Reykjavik, Iceland, 2007. [Google Scholar]
- Pastore, D.M.; Peterson, R.N.; Fribance, D.B.; Viso, R.; Hackett, E.E. Hydrodynamic Drivers of Dissolved Oxygen Variability within a Tidal Creek in Myrtle Beach, South Carolina. Water 2019, 11, 1723. [Google Scholar] [CrossRef]
- KWON, I.; KIM, T. Analysis of Land-Based Circular Aquaculture Tank Flow Field Using Computational Fluid Dynamics (CFD) Simulation. J. Korean Soc. Fish. Ocean Technol. 2020, 56, 395–406. [Google Scholar] [CrossRef]
- Ansys, Inc. Ansys Fluent 15.0 User’s Guide; Ansys Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Ansys, Inc. Ansys Fluent Theory Guide; Ansys Inc.: Canonsburg, PA, USA, 2011; Volume 794. [Google Scholar]
- Liu, H.-F.; Liu, Y.; Gui, F.; Sun, H.; Zhao, Y.-P. Quantitative Evaluation on the Suitable Flow Region inside the Shielding Device of Submersible Aquaculture Facility. Ocean Eng. 2023, 267, 113270. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Liu, H.-F.; Bi, C.-W.; Cui, Y.; Guan, C.-T. Numerical Study on the Flow Field inside and around a Semi-Submersible Aquaculture Platform. Appl. Ocean Res. 2021, 115, 102824. [Google Scholar] [CrossRef]
- Yang, C.; Yuan, H.; Bai, X.; Hao, Z.; Sun, Y.; Wu, D.; Johanning, L. Numerical Investigations on Fluid Characteristics around the Bottom-Fixed Aquacultural Farm. Ocean Eng. 2022, 266, 112689. [Google Scholar] [CrossRef]
- Rodrigues, H.C.; Papáček, Š.; Petera, K.; Herskovits, J.; Masaló, I.; Soares, M.; Araújo, A.L.; Oca, J.; Guedes, J.M.; Folgado, J.O. On the Optimization of Recirculated Aquaculture Systems. In EngOpt 2018 Proceedings of the 6th International Conference on Engineering Optimization; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Klebert, P.; Volent, Z.; Rosten, T. Measurement and Simulation of the Three-Dimensional Flow Pattern and Particle Removal Efficiencies in a Large Floating Closed Sea Cage with Multiple Inlets and Drains. Aquac. Eng. 2018, 80, 11–21. [Google Scholar] [CrossRef]
- Tsai, J.-T.; Chou, J.-H.; Liu, T.-K. Optimal Design of Digital IIR Filters by Using Hybrid Taguchi Genetic Algorithm. IEEE Trans. Ind. Electron. 2006, 53, 867–879. [Google Scholar] [CrossRef]
- Vázquez-Sánchez, A.Y.; Aguilar-Zárate, P.; Muñiz-Márquez, D.B.; Wong-Paz, J.E.; Rojas, R.; Ascacio-Valdés, J.A.; Martínez-Ávila, G.C.G. Effect of Ultrasound Treatment on the Extraction of Antioxidants from Ardisia Compressa Kunth Fruits and Identification of Phytochemicals by HPLC-ESI-MS. Heliyon 2019, 5, e03058. [Google Scholar] [CrossRef] [PubMed]
- Si, J.; Cheng, G.; Zhu, J. Optimisation of Multisource Injection of Carbon Dioxide into Goafs Based on Orthogonal Test and Fuzzy Comprehensive Theory. Heliyon 2019, 5, e01607. [Google Scholar] [CrossRef]
- Teng, D.; Li, Y.; Yang, H.; Wei, Z.; Li, Y. Genetic Algorithm for Sparse Optimization of Mills Cross Array Used in Underwater Acoustic Imaging. J. Mar. Sci. Eng. 2022, 10, 155. [Google Scholar] [CrossRef]
- Davidson, J.; Summerfelt, S.T. Solids Removal from a Coldwater Recirculating System—Comparison of a Swirl Separator and a Radial-Flow Settler. Aquac. Eng. 2005, 33, 47–61. [Google Scholar] [CrossRef]
- López-Rebollar, B.M.; Salinas-Tapia, H.; García-Pulido, D.; Durán-García, M.D.; Gallego-Alarcón, I.; Fonseca-Ortiz, C.R.; García-Aragón, J.A.; Díaz-Delgado, C. Performance Study of Annular Settler with Gratings in Circular Aquaculture Tank Using Computational Fluid Dynamics. Aquac. Eng. 2021, 92, 102143. [Google Scholar] [CrossRef]



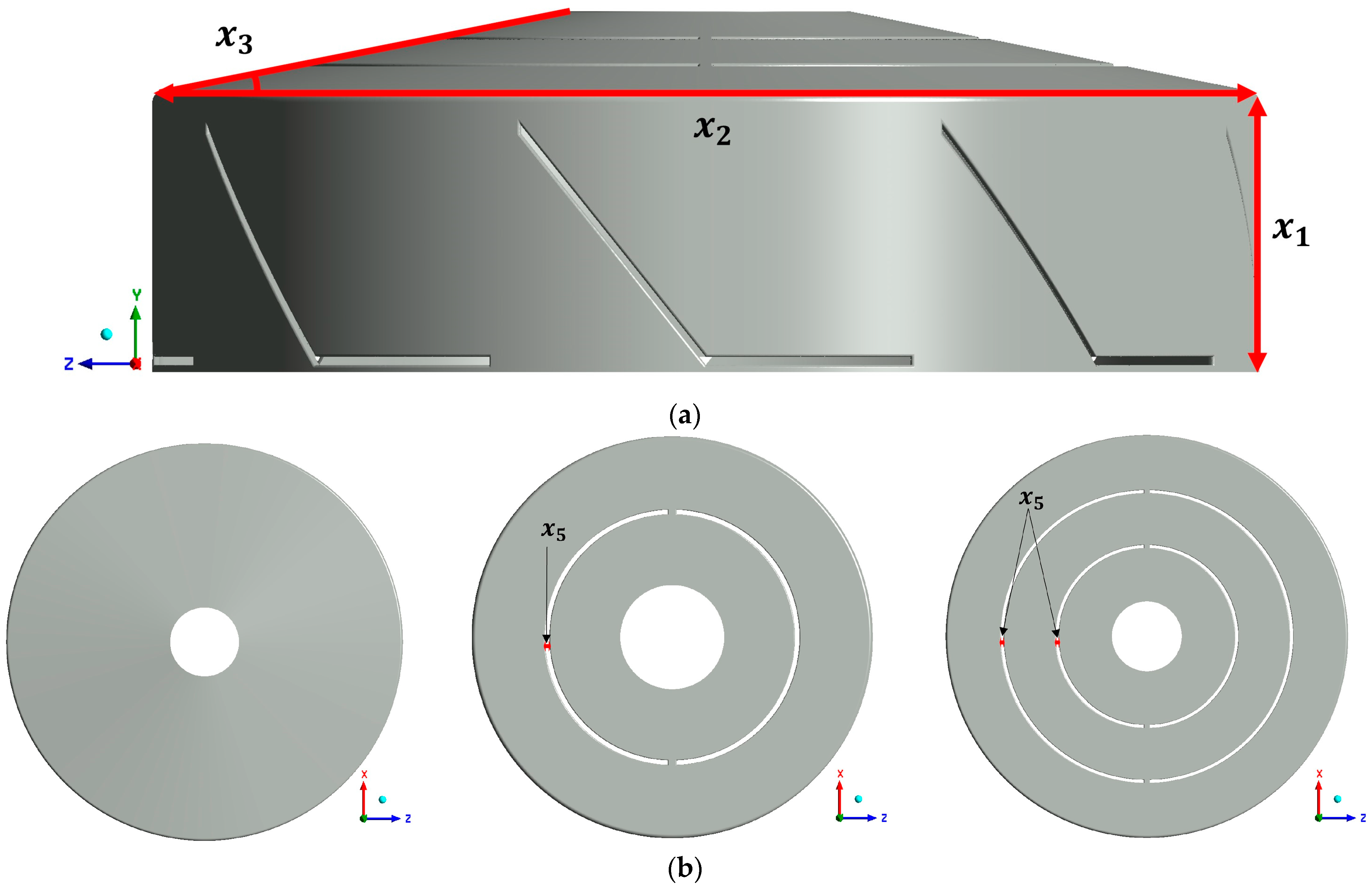

| Level | [mm] | [mm] | [°] | [mm] | |
|---|---|---|---|---|---|
| 1 | 50 | 400 | 0 | 0 | 3 |
| 2 | 125 | 800 | 7.5 | 1 | 6 |
| 3 | 200 | 1200 | 15 | 2 | 9 |
| Experimental Number | Variables Column | ||||
|---|---|---|---|---|---|
| 1 | 50 mm | 400 mm | 0° | 0 | 3 mm |
| 2 | 50 mm | 400 mm | 7.5° | 1 | 6 mm |
| 3 | 50 mm | 400 mm | 15° | 2 | 9 mm |
| 4 | 50 mm | 800 mm | 0° | 1 | 6 mm |
| 5 | 50 mm | 800 mm | 7.5° | 2 | 9 mm |
| 6 | 50 mm | 800 mm | 15° | 0 | 3 mm |
| 7 | 50 mm | 1200 mm | 0° | 2 | 9 mm |
| 8 | 50 mm | 1200 mm | 7.5° | 0 | 3 mm |
| 9 | 50 mm | 1200 mm | 15° | 1 | 6 mm |
| 10 | 125 mm | 400 mm | 0° | 0 | 6 mm |
| 11 | 125 mm | 400 mm | 7.5° | 1 | 9 mm |
| 12 | 125 mm | 400 mm | 15° | 2 | 3 mm |
| 13 | 125 mm | 800 mm | 0° | 1 | 9 mm |
| 14 | 125 mm | 800 mm | 7.5° | 2 | 3 mm |
| 15 | 125 mm | 800 mm | 15° | 0 | 6 mm |
| 16 | 125 mm | 1200 mm | 0° | 2 | 3 mm |
| 17 | 125 mm | 1200 mm | 7.5° | 0 | 6 mm |
| 18 | 125 mm | 1200 mm | 15° | 1 | 9 mm |
| 19 | 200 mm | 400 mm | 0° | 0 | 9 mm |
| 20 | 200 mm | 400 mm | 7.5° | 1 | 3 mm |
| 21 | 200 mm | 400 mm | 15° | 2 | 6 mm |
| 22 | 200 mm | 800 mm | 0° | 1 | 3 mm |
| 23 | 200 mm | 800 mm | 7.5° | 2 | 6 mm |
| 24 | 200 mm | 800 mm | 15° | 0 | 9 mm |
| 25 | 200 mm | 1200 mm | 0° | 2 | 6 mm |
| 26 | 200 mm | 1200 mm | 7.5° | 0 | 9 mm |
| 27 | 200 mm | 1200 mm | 15° | 1 | 3 mm |
| Experimental Number | Pressure Drop [Pa] | Experimental Number | Pressure Drop [Pa] | Experimental Number | Pressure Drop [Pa] |
|---|---|---|---|---|---|
| 1 | 1325.41523 | 10 | 659.465 | 19 | 594.73348 |
| 2 | 637.13841 | 11 | 596.37012 | 20 | 691.30139 |
| 3 | 584.4903 | 12 | 668.34447 | 21 | 597.20498 |
| 4 | 589.94417 | 13 | 585.31235 | 22 | 630.69791 |
| 5 | 577.98958 | 14 | 614.01653 | 23 | 587.17231 |
| 6 | 751.99647 | 15 | 606.39196 | 24 | 589.71031 |
| 7 | 580.17279 | 16 | 597.2357 | 25 | 583.21357 |
| 8 | 661.75538 | 17 | 594.46629 | 26 | 587.89079 |
| 9 | 585.91797 | 18 | 582.54783 | 27 | 611.24046 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Doh, J.; Lim, K.; Kwon, I.; Kim, T.; Kim, S. Case Study of Central Outlet Cap Used in Flow-Through Aquaculture Systems by Using Computational Fluid Dynamics. J. Mar. Sci. Eng. 2024, 12, 2006. https://doi.org/10.3390/jmse12112006
Lee J, Doh J, Lim K, Kwon I, Kim T, Kim S. Case Study of Central Outlet Cap Used in Flow-Through Aquaculture Systems by Using Computational Fluid Dynamics. Journal of Marine Science and Engineering. 2024; 12(11):2006. https://doi.org/10.3390/jmse12112006
Chicago/Turabian StyleLee, Jongjae, Jaehyeok Doh, Kihoon Lim, Inyeong Kwon, Taeho Kim, and Sanghoon Kim. 2024. "Case Study of Central Outlet Cap Used in Flow-Through Aquaculture Systems by Using Computational Fluid Dynamics" Journal of Marine Science and Engineering 12, no. 11: 2006. https://doi.org/10.3390/jmse12112006
APA StyleLee, J., Doh, J., Lim, K., Kwon, I., Kim, T., & Kim, S. (2024). Case Study of Central Outlet Cap Used in Flow-Through Aquaculture Systems by Using Computational Fluid Dynamics. Journal of Marine Science and Engineering, 12(11), 2006. https://doi.org/10.3390/jmse12112006








