Time Prediction in Ship Block Manufacturing Based on Transfer Learning
Abstract
1. Introduction
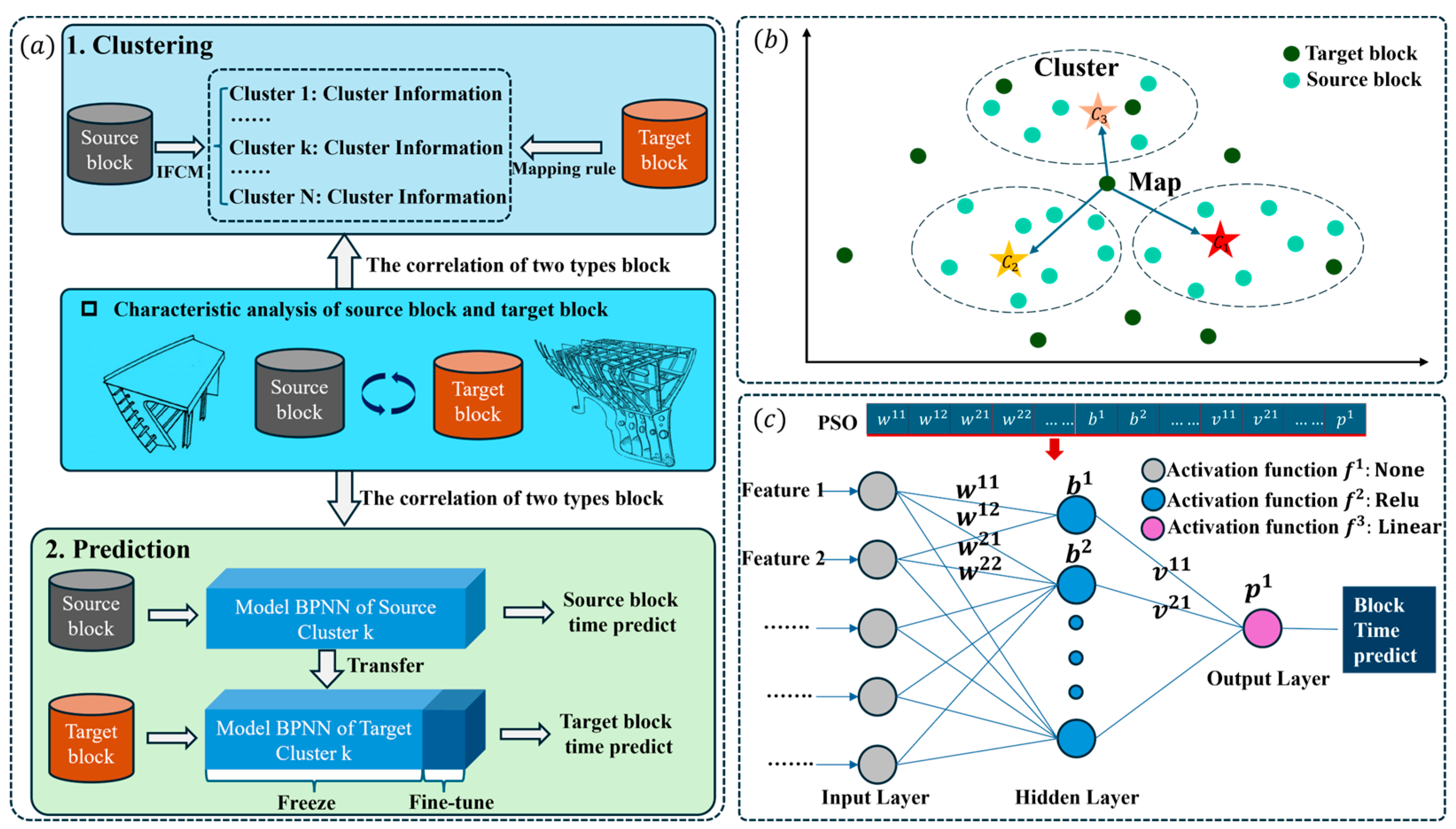
2. Proposed Method
2.1. Operational Process Description
2.2. Data Preprocessing
2.3. Block Clustering to Partition the Data Space
2.3.1. Define Features for Clustering
2.3.2. Block Clustering
2.4. Model Development
2.4.1. Model Prediction Effect Evaluation Indexes
2.4.2. PSO-BPNN Model of Source Domain Block
2.4.3. TR-PSO-BPNN Model of Target Domain Block
3. Experimental Evaluation
3.1. Dataset Description
3.2. Source Domain Block Time Prediction
3.3. Target Domain Block Time Prediction
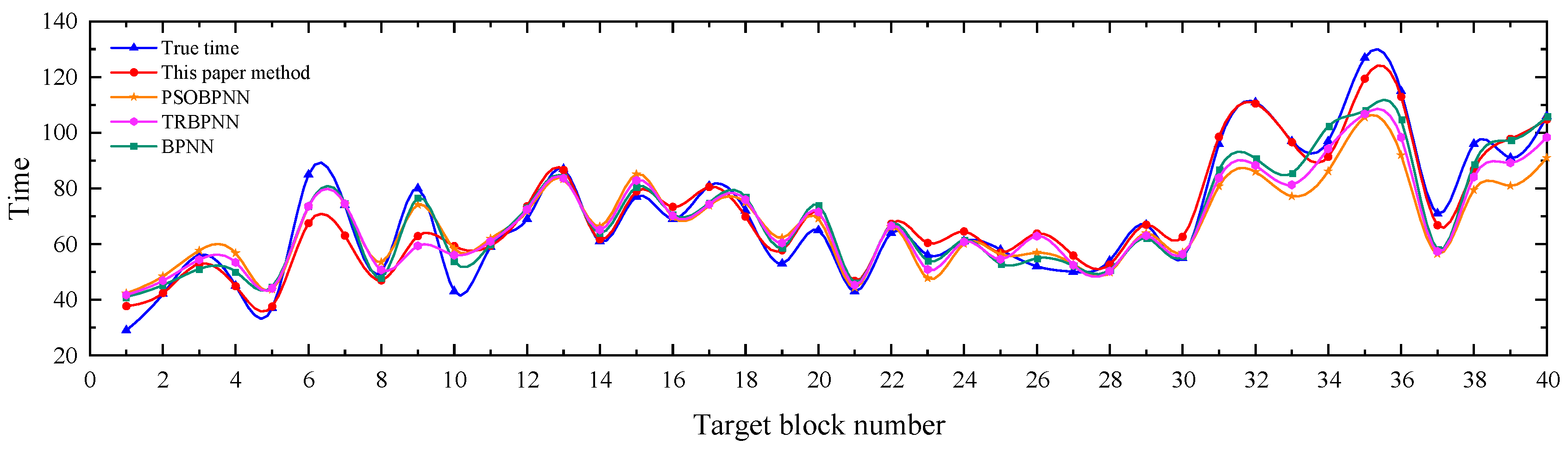
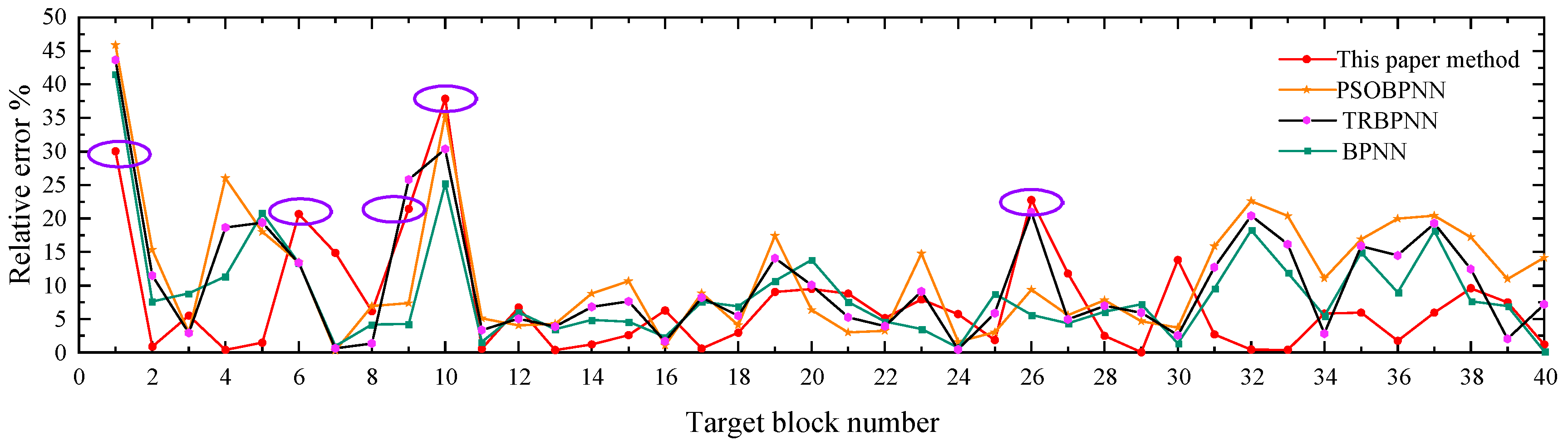
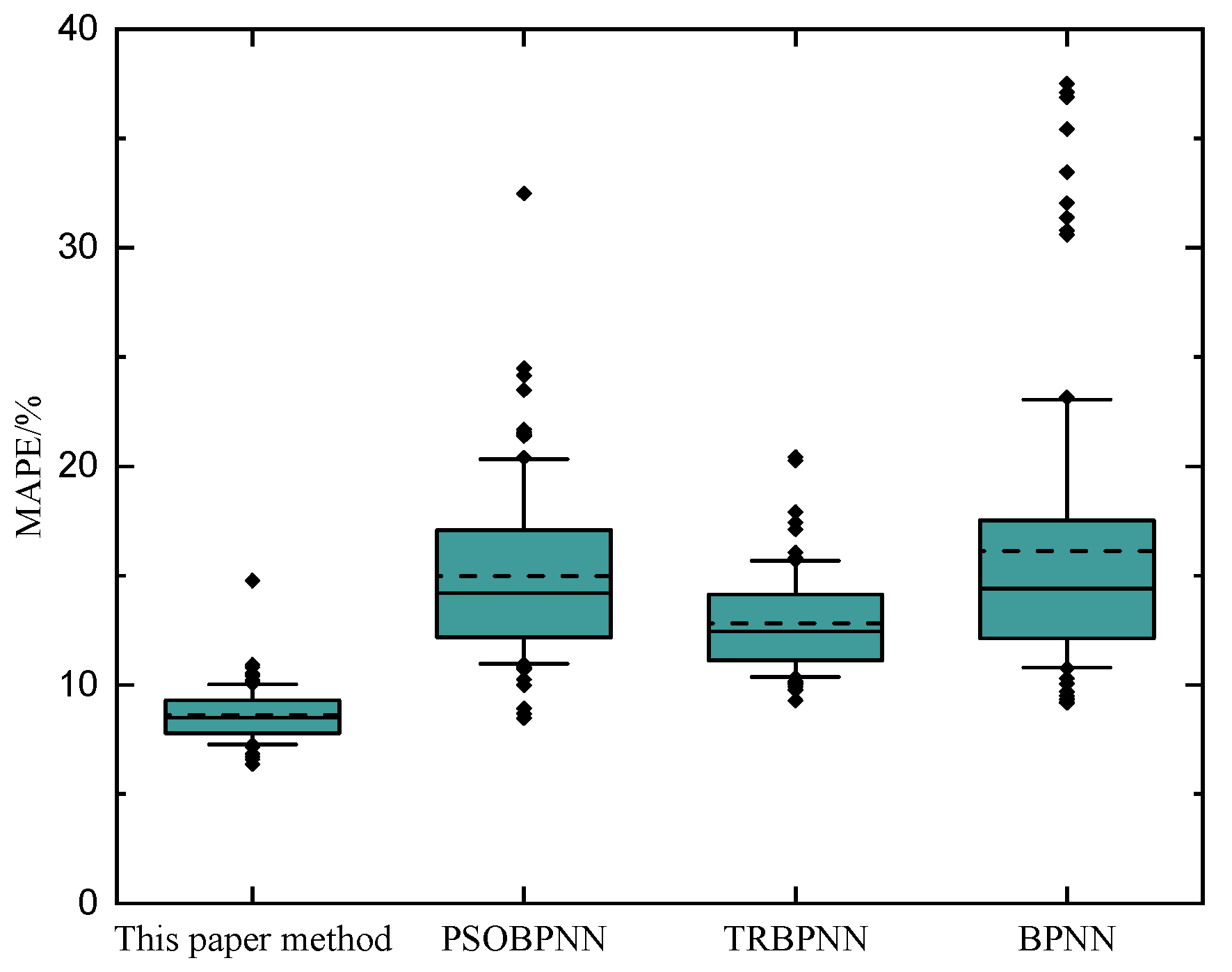
3.4. Comparison with Other Methods
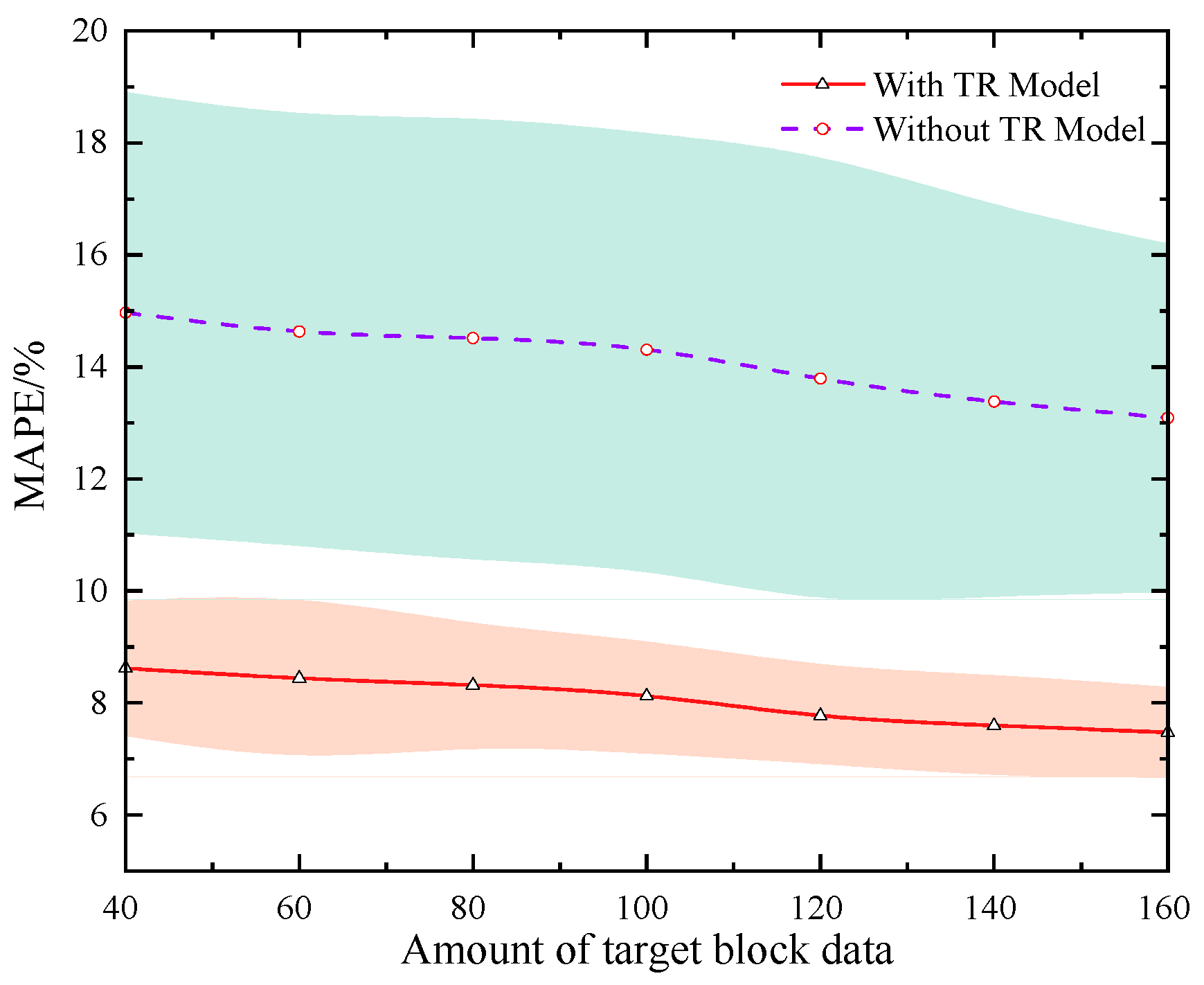
3.5. Comparison with Other Sample Capacities
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Back, M.G.; Lee, D.K.; Shin, J.G.; Woo, J.H. A study for production simulation model generation system based on data model at a shipyard. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 496–510. [Google Scholar] [CrossRef][Green Version]
- You-Ling, C.; Xiao-Jie, R.; Juan, T.; Hui-Cong, W. Labor hour estimation method based on difficulty coefficient of process in mass customization. Comput. Integr. Manuf. Syst. 2014, 20, 424–429. [Google Scholar]
- Kim, K.J.; Yun, W.G.; Kim, I.K. Estimating approximate construction duration of CFRD in the planning stage. KSCE J. Civ. Eng. 2016, 20, 2604–2613. [Google Scholar] [CrossRef]
- Choi, W.S.; Kim, D.H.; Nam, J.H.; Kim, M.J.; Son, Y.B. Estimating Production Metric for Ship Assembly Based on Geometric and Production Information of Ship Block Model. J. Mar. Sci. Eng. 2021, 9, 39. [Google Scholar] [CrossRef]
- Lei, Y.G.; Yang, B.; Jiang, X.W.; Jia, F.; Li, N.P.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Proc. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Wang, T.; Wang, J.B.; Zhang, X.J.; Liu, C. A Study on Prediction of Process Parameters of Shot Peen Forming Using Artificial Neural Network Optimized by Genetic Algorithm. Arab. J. Sci. Eng. 2021, 46, 7349–7361. [Google Scholar] [CrossRef]
- Yang, J.Y.; Kang, G.Z.; Liu, Y.J.; Kan, Q.H. A novel method of multiaxial fatigue life prediction based on deep learning. Int. J. Fatigue 2021, 151, 106356. [Google Scholar] [CrossRef]
- Rizaee, S.; Lei, Z. Duration Estimation of a Heavy Industrial Scaffolding Project: A Case Study. J. Constr. Eng. Manag. 2024, 150, 05024002. [Google Scholar] [CrossRef]
- Chang, J.T.; Kong, X.G.; Yin, L. A novel approach for product makespan prediction in production life cycle. Int. J. Adv. Manuf. Technol. 2015, 80, 1433–1448. [Google Scholar] [CrossRef]
- Kong, W.L.; Li, H. Combining adaptive time-series feature window and stacked bidirectional LSTM for predicting tool remaining useful life without failure data. Int. J. Adv. Manuf. Technol. 2022, 121, 7509–7526. [Google Scholar] [CrossRef]
- Chen, T.; Wang, Y.C. Estimating simulation workload in cloud manufacturing using a classifying artificial neural network ensemble approach. Robot. Comput. Integr. Manuf. 2016, 38, 42–51. [Google Scholar] [CrossRef]
- Chen, T. Incorporating fuzzy c-means and a back-propagation network ensemble to job completion time prediction in a semiconductor fabrication factory. Fuzzy Sets Syst. 2007, 158, 2153–2168. [Google Scholar] [CrossRef]
- Jeong, J.H.; Woo, J.H.; Park, J. Machine Learning Methodology for Management of Shipbuilding Master Data. Int. J. Nav. Archit. Ocean Eng. 2020, 12, 428–439. [Google Scholar] [CrossRef]
- Qu, S.P.; Jiang, Z.H. Man-hour calculation methods of the block assembly for shipbuilding. J. Harbin Eng. Univ. 2012, 33, 550–555. [Google Scholar]
- Zhu, H.; Woo, J.H. Hybrid NHPSO-JTVAC-SVM Model to Predict Production Lead Time. Appl. Sci. 2021, 11, 6369. [Google Scholar] [CrossRef]
- Li, J.H.; Sun, M.M.; Han, D.F.; Wang, J.X.; Mao, X.Z.; Wu, X.Y. A knowledge discovery and reuse method for time estimation in ship block manufacturing planning using DEA. Adv. Eng. Inform. 2019, 39, 25–40. [Google Scholar] [CrossRef]
- Liu, F.X.; Dai, Y.R. Product quality prediction method in small sample data environment. Adv. Eng. Inform. 2023, 56, 101975. [Google Scholar] [CrossRef]
- Kang, G.Q.; Wu, L.F.; Guan, Y.; Peng, Z. A Virtual Sample Generation Method Based on Differential Evolution Algorithm for Overall Trend of Small Sample Data: Used for Lithium-ion Battery Capacity Degradation Data. IEEE Access 2019, 7, 123255–123267. [Google Scholar] [CrossRef]
- Li, D.C.; Huang, W.T.; Chen, C.C.; Chang, C.J. Employing virtual samples to build early high-dimensional manufacturing models. Int. J. Prod. Res. 2013, 51, 3206–3224. [Google Scholar] [CrossRef]
- Li, D.C.; Lin, W.K.; Lin, L.S.; Chen, C.C.; Huang, W.T. The attribute-trend-similarity method to improve learning performance for small datasets. Int. J. Prod. Res. 2017, 55, 1898–1913. [Google Scholar] [CrossRef]
- El Bilali, A.; Taleb, A.; Bahlaoui, M.A.; Brouziyne, Y. An integrated approach based on Gaussian noises-based data augmentation method and AdaBoost model to predict faecal coliforms in rivers with small dataset. J. Hydrol. 2021, 599, 126510. [Google Scholar] [CrossRef]
- Zhuang, F.Z.; Qi, Z.Y.; Duan, K.Y.; Xi, D.B.; Zhu, Y.C.; Zhu, H.S.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Moreo, A.; Esuli, A.; Sebastiani, F. Lost in Transduction: Transductive Transfer Learning in Text Classification. ACM Trans. Knowl. Discov. Data 2022, 16, 1–21. [Google Scholar] [CrossRef]
- Zhuang, F.Z.; Luo, P.; Du, C.Y.; He, Q.; Shi, Z.Z.; Xiong, H. Triplex Transfer Learning: Exploiting Both Shared and Distinct Concepts for Text Classification. IEEE Trans. Cybern. 2014, 44, 1191–1203. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.S.; Ghamisi, P. Heterogeneous Transfer Learning for Hyperspectral Image Classification Based on Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3246–3263. [Google Scholar] [CrossRef]
- Wang, D.; Zheng, T.F. Transfer Learning for Speech and Language Processing. In Proceedings of the Asia-Pacific-Signal-and-Information-Processing-Association Annual Summit and Conference (APSIPA ASC), Hong Kong, China, 16–19 December 2015; pp. 1225–1237. [Google Scholar]
- Zhou, H.T.; Chen, J.; Dong, G.M.; Wang, R. Detection and diagnosis of bearing faults using shift-invariant dictionary learning and hidden Markov model. Mech. Syst. Signal Proc. 2016, 72–73, 65–79. [Google Scholar] [CrossRef]
- Mao, W.T.; Ding, L.; Tian, S.Y.; Liang, X.H. Online detection for bearing incipient fault based on deep transfer learning. Measurement 2020, 152, 107278. [Google Scholar] [CrossRef]
- Li, Q.; Shen, C.Q.; Chen, L.; Zhu, Z.K. Knowledge mapping-based adversarial domain adaptation: A novel fault diagnosis method with high generalizability under variable working conditions. Mech. Syst. Signal Proc. 2021, 147, 107095. [Google Scholar] [CrossRef]
- Yang, B.; Xu, S.C.; Lei, Y.G.; Lee, C.G.; Stewart, E.; Roberts, C. Multi-source transfer learning network to complement knowledge for intelligent diagnosis of machines with unseen faults. Mech. Syst. Signal Proc. 2022, 162, 108095. [Google Scholar] [CrossRef]
- Zhang, A.S.; Wang, H.L.; Li, S.B.; Cui, Y.X.; Liu, Z.H.; Yang, G.C.; Hu, J.J. Transfer Learning with Deep Recurrent Neural Networks for Remaining Useful Life Estimation. Appl. Sci. 2018, 8, 2416. [Google Scholar] [CrossRef]
- Sun, C.; Ma, M.; Zhao, Z.B.; Tian, S.H.; Yan, R.Q.; Chen, X.F. Deep Transfer Learning Based on Sparse Autoencoder for Remaining Useful Life Prediction of Tool in Manufacturing. IEEE Trans. Ind. Inform. 2019, 15, 2416–2425. [Google Scholar] [CrossRef]
- Hung, S.K.; Gan, J.Q. Small facial image dataset augmentation using conditional GANs based on incomplete edge feature input. PeerJ Comput. Sci. 2021, 7, e760. [Google Scholar] [CrossRef]
- Zhao, W. Research on the Deep Learning of the Small Sample Data based on Transfer Learning. In Proceedings of the International Conference on Green Energy and Sustainable Development (GESD), Chongqing, China, 27–28 May 2017. [Google Scholar]
- Chen, J.G.; Han, X.B.; Sun, T.; Zheng, Y.J. Analysis and prediction of battery aging modes based on transfer learning. Appl. Energy 2024, 356, 122330. [Google Scholar] [CrossRef]
- Li, J.H.; Guo, D.; Chen, Z.Y.; Li, X.; Li, Z.F. Transfer learning for collapse warning in TBM tunneling using databases in China. Comput. Geotech. 2024, 166, 105968. [Google Scholar] [CrossRef]
- Li, Y.; Wei, P.T.; Xiang, G.; Jia, C.F.; Liu, H.J. Gear contact fatigue life prediction based on transfer learning. Int. J. Fatigue 2023, 173, 107686. [Google Scholar] [CrossRef]
- Kretschmer, R.; Pfouga, A.; Rulhoff, S.; Stjepandic, J. Knowledge-based design for assembly in agile manufacturing by using Data Mining methods. Adv. Eng. Inform. 2017, 33, 285–299. [Google Scholar] [CrossRef]
- Deng, Z.H.; Jiang, Y.Z.; Chung, F.L.; Ishibuchi, H.; Choi, K.S.; Wang, S.T. Transfer Prototype-Based Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2016, 24, 1210–1232. [Google Scholar] [CrossRef]
- Sun, Y.; He, D.P.; Li, J. Research on the Fatigue Life Prediction for a New Modified Asphalt Mixture of a Support Vector Machine Based on Particle Swarm Optimization. Appl. Sci. 2021, 11, 11867. [Google Scholar] [CrossRef]
- Xiao, M.Z.; Luo, R.; Chen, Y.; Ge, X.M. Prediction model of asphalt pavement functional and structural performance using PSO-BPNN algorithm. Constr. Build. Mater. 2023, 407, 133534. [Google Scholar] [CrossRef]
- Geyer, P.; Schlüter, A.; Cisar, S. Application of clustering for the development of retrofit strategies for large building stocks. Adv. Eng. Inform. 2017, 31, 32–47. [Google Scholar] [CrossRef]
- Golizadeh, H.; Sadeghifam, A.N.; Aadal, H.; Abd Majid, M.Z. Automated tool for predicting duration of construction activities in tropical countries. KSCE J. Civ. Eng. 2016, 20, 12–22. [Google Scholar] [CrossRef]
- Min, C.; Bin, P.; Jian, L. Man-hour Calculation of Working Package using Error Back-propagation Artificial Neural Network. Shipbuild. China 2003, 44, 1–7. [Google Scholar]
- Ruy, W.S.; Kim, H.K.; Cho, Y.J.; Ko, D.E. Implementation of welding material quantity evaluation system combined with ship design CAD system. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 219–226. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Siam Review: Philadelphia, PA, USA, 1983; Volume 25. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Karch, J. Improving on Adjusted R-Squared. Collabra-Psychol. 2020, 6, 45. [Google Scholar] [CrossRef]




| No. | Feature Name | Data Type | Range |
|---|---|---|---|
| 1 | Block weight | Numeric | [120, 240] |
| 2 | Block projection area | Numeric | [110, 280] |
| 3 | Unit assembly block number | Numeric | [7, 28] |
| 4 | Block type | Enumeration | such as curved block, flat block, two-dimensional unit, and volume surface section |
| 5 | Slope type | Enumeration | such as I, X, Y, V, K, and U slopes |
| 6 | Welding seam type | Enumeration | such as butt weld, filet weld, and lap weld |
| Hyperparameters | Size of Value |
|---|---|
| The number of input layer nodes | 5 |
| The number of hidden layers | 1 |
| The number of hidden layer nodes | 4 |
| The number of output layer nodes | 1 |
| The total trainable parameters | 29 |
| Initialization minimum error | 1 × 105 |
| The loss function | Mean Square Error |
| The number of trainings | 200 |
| Minimum error of training target | 1 × 10−6 |
| Hyperparameters | Size of Value |
|---|---|
| Individual and group learning factors | 1.5 |
| Maximum number of iterations | 200 |
| Particle swarm size | 200 |
| Minimum value of inertia weight | 0.4 |
| Maximum value of inertia weight | 0.9 |
| Speed limit range | [−3, 3] |
| Location restrictions | [−5, 5] |
| Individual and group learning factors | 1.5 |
| Cluster1 | Cluster2 | Cluster3 | Cluster4 | |
|---|---|---|---|---|
| Source block count | 191 | 192 | 463 | 154 |
| Target block count | 31 | 47 | 96 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Lin, P.; Song, D.; Yan, Z.; Yang, B.; Zhou, L. Time Prediction in Ship Block Manufacturing Based on Transfer Learning. J. Mar. Sci. Eng. 2024, 12, 1977. https://doi.org/10.3390/jmse12111977
Li J, Lin P, Song D, Yan Z, Yang B, Zhou L. Time Prediction in Ship Block Manufacturing Based on Transfer Learning. Journal of Marine Science and Engineering. 2024; 12(11):1977. https://doi.org/10.3390/jmse12111977
Chicago/Turabian StyleLi, Jinghua, Pengfei Lin, Dening Song, Zhe Yan, Boxin Yang, and Lei Zhou. 2024. "Time Prediction in Ship Block Manufacturing Based on Transfer Learning" Journal of Marine Science and Engineering 12, no. 11: 1977. https://doi.org/10.3390/jmse12111977
APA StyleLi, J., Lin, P., Song, D., Yan, Z., Yang, B., & Zhou, L. (2024). Time Prediction in Ship Block Manufacturing Based on Transfer Learning. Journal of Marine Science and Engineering, 12(11), 1977. https://doi.org/10.3390/jmse12111977







