Abstract
Classifying modulated signals for non-cooperative underwater acoustic communication is challenging due to signal distortion caused by fading and multipath effects in the underwater acoustic channel. Our proposed method utilizes channel estimation parameters to measure and correct signal distortion, thereby enhancing the recognition performance of the received signal. Modulation classification experiments were conducted on a public dataset with various modulation schemes, as well as on the same dataset with simulated underwater acoustic channels. The results indicate that our method effectively mitigates the impact of the underwater acoustic channel on modulation signal classification, improves recognition accuracy, and is broadly applicable to a wide range of machine learning classifiers. Finally, we validated these findings using real underwater communication data.
1. Introduction
Researchers are increasingly focusing on underwater acoustic communication technology due to the critical demands of military advancements and the growing need to exploit marine resources. In many practical communication systems, variable modulation schemes offer significant advantages. For example, different schemes perform differently in terms of bandwidth utilization and data rate, and using a fixed scheme may not achieve optimal efficiency in various environments. Additionally, modulation schemes vary in their resistance to noise and interference. Moreover, flexible schemes enable dynamic resource allocation based on link conditions to meet performance requirements, whereas fixed schemes lack this flexibility. Thus, modulation identification is crucial in communication signal processing. In non-cooperative underwater communication, where prior information about the signals is absent, direct demodulation at the receiver is unfeasible. This process necessitates an initial step of modulation pattern recognition, which is followed by subsequent demodulation. Initially, scholars attempted to adapt modulation recognition algorithms from wireless radio signals for use in underwater acoustic communication; however, these efforts often lead to suboptimal identification results. Underwater acoustic communication signals typically operate at lower frequency bands, exhibit slower transmission rates, and involve shorter communication distances compared to wireless radio signals [1]. Moreover, the underwater acoustic communication environment is inherently more complex than the wireless communication environment. Unlike radio communication, which relies on electromagnetic waves, underwater communication utilizes sound waves for signal transmission. The complexity of the underwater communication channel is further exacerbated by factors such as the variable distribution of sound speed in the ocean, reflections of sound waves from the seabed and sea surface, as well as the refraction and scattering phenomena encountered during oceanic propagation [2]. Therefore, conducting research on modulation recognition for underwater acoustic communication signals and developing algorithms that are robust and adaptable to the underwater environment are crucial.
Initially, professionals relied on manual methods to recognize modulation modes. They extracted communication signal characteristics and compared them with their professional knowledge and empirical feature parameters. However, with advancements in wireless communication technology and the increase in communication rates, the efficiency and accuracy of manual modulation recognition methods have progressively declined. Consequently, researchers have developed automatic modulation mode recognition algorithms, particularly focusing on blind recognition of modulation signals without prior knowledge or with only partial prior knowledge. Modulation recognition algorithms can generally be categorized into two groups: decision-theoretic methods based on the maximum likelihood assumption and statistical methods based on feature extraction. The former involves extensive parameter calculations, requires prior knowledge, and is sensitive to impairments such as phase and frequency offset, making it unsuitable for non-cooperative underwater acoustic communication. Therefore, we will focus on the feature extraction method, which offers lower computational complexity and greater robustness.
In April 1969, C.S. Weave and four other authors published a technical report at Stanford University on automatic modulation signal recognition algorithms. They proposed using time-frequency domain features of signals for classification, which initiated research into communication signal modulation pattern recognition [3]. Subsequently, W.A. Gardner conducted studies on spectral correlation features for both analog and digital modulations [4,5,6]. Modulation types were classified by extracting the square spectrum of the modulation signal’s spectral correlation function [7].
Later studies on classifiers integrated methods from artificial intelligence. Whelchel used a neural network classifier for communication signal modulation pattern classification and achieved comparable results to the state-of-the-art maximum likelihood classifier at that time [8]. In 1992, Soliman introduced a method that uses statistical moments to identify the modulation order of MPSK signals. It was noted that for MPSK signals, the nth-order statistical moment is a monotonically increasing function of the modulation order M [9].
Subsequently, N. Ghani conducted feature research based on the square spectrum. In [10], the authors achieved the classification and identification of signals such as AM, FM, ASK, QPSK, SSB-USB, SSB-LSB, non-coherent FSK, continuous-phase FSK, BPSK, and CW by extracting parameters such as the number of peaks in the square spectrum and signal power spectrum. This overview provides a comprehensive account of the evolution of modulation signal recognition research, covering various approaches and techniques over the years.
In 1996, A.K. Nandi initiated research on features based on instantaneous statistical quantities. He proposed seven characteristics derived from instantaneous values in the time domain, frequency domain, and higher-order moments. Nandi successfully recognized both analog and digital modulation signals by employing a decision tree as a classifier [11]. Subsequently, Nandi shifted focus to classifiers and introduced a novel approach using Artificial Neural Networks (ANN) for modulation recognition [12]. Experimental results demonstrated that ANN outperformed decision trees in recognition across diverse channels and noise environments [13]. Nandi’s research significantly advanced the practical application of modulation recognition in communication signals.
C.J. Martre investigated the use of higher-order statistical moments to extract features and achieved intra-class recognition of QAM signals [14]. H. Xiaomin used Hellinger distance to express differences in constellation diagrams as classification features and successfully identified 15 modulation types, surpassing likelihood methods or key feature extraction methods at a signal-to-noise ratio of 5 dB [15].
In 2000, A. Swami conducted a study on higher-order cumulants for diagnostic signals. Swami proposed that computing the fourth-order cumulant of modulation signals could effectively accomplish modulation recognition, even in the presence of carrier phase and frequency offsets, demonstrating robustness [16]. The study assumed achieving signal preprocessing precision.
Traditional signal analysis often relies on Fourier transforms, which cannot simultaneously capture both time and frequency localized information of a signal. K.C. Ho introduced the use of wavelet transforms in communication signal diagnostics to enhance the representation of time-frequency locality in signal analysis [17].
After extracting higher-order cumulant features, O.A. Dobre employed the fourth-, sixth-, and eighth-order cyclic cumulants of signals to automatically classify MQAM, MPSK, and MASK modulations. This approach yielded favorable results at a signal-to-noise ratio of 5 dB [18]. This study exemplifies the ongoing advancements in modulation recognition, employing diverse methodologies to enhance the accuracy and robustness of signal classification techniques.
A. Fehske proposed a method for extracting the spectral coherence function of signals as characteristic features, which, when coupled with a neural network classifier, addresses the challenge of recognizing modulation signals [19]. In researching improved algorithms for higher-order and cyclic cumulants, this approach is noteworthy. To improve applicability and robustness in the channel context, W. Headley used a distributed data collection system to extract the spectral correlation function of signals. This ultimately led to the recognition of diagnostic signals in a Gaussian channel [20].
E. Like expanded the classification study of various signals based on the theory of cyclic spectra. By using higher-order cyclic cumulants as characteristic features, along with spatial diversity techniques, 12 modulation signals were successfully classified [21]. Later, A. Punchihew conducted research on identifying multi-carrier modulation signals. Punchihew was able to recognize CPOFDM signals in time-varying fading channels by leveraging the cyclic spectrum features of cyclic cumulants [22]. Deep learning (DL) has gained significant attention from researchers due to its exceptional data processing capabilities. DL has become increasingly popular in solving ACM problems. O’Shea is one of the most representative pioneers of applying DL to the modulation recognition problem. He demonstrated that the recognition rate of convolutional neural networks (CNNs) trained on baseband IQ data exceeded that of methods based on traditional cyclic moment features [23]. Deep learning has been frequently used to solve the modulation recognition problem in recent years, as it can mine deep features and learn from data, resulting in better results than traditional methods [24,25]. However, due to limitations in underwater data, such as the difficulty of obtaining a large number of high-quality samples and labeling them, traditional methods are still relied upon in underwater acoustic communication.
Modulation recognition technology has been well-developed in the radio field, but its application to underwater acoustic communication still presents significant challenges. The complex and variable underwater environment causes severe distortion of signal characteristics, complicating the development of reliable modulation recognition algorithms for underwater acoustic communication. Therefore, we will consider the classification of underwater modulated signals with channel modeling together. To minimize acoustic channel distortion, we estimate the underwater sound field based on the normal mode model with the existing environmental parameters. An equalization technique is then employed to restore the received signal, minimizing the impact of the acoustic channel on the modulation signal classification. This approach enhances the applicability of modulation classification algorithms in underwater acoustic environments. Our contributions are summarized as follows:
- We consider the classification of underwater modulated signals and channel estimation together.
- By estimating the acoustic channel parameters within a specific range, we can restore communication signals distorted by underwater transmission. This reduces the instances where the classical classification algorithm is not applicable due to the influence of the underwater acoustic environment on modulated signal classification, thereby enhancing the algorithm’s universality in underwater environments.
- The proposed method was validated through both simulation and real-world experiments, which confirmed the effectiveness of the approach. The results demonstrate that, when applying the classical classification algorithm, the recognition performance of modulated signals after restoration is significantly enhanced. Under ideal conditions, certain classifiers can achieve performance levels that closely approximate those observed without underwater channels, thus demonstrating the method’s ability to mitigate channel effects.
The remainder of the paper is structured as follows. Section 2 provides an overview of underwater acoustic channel estimation and the theoretical foundations of modulation recognition algorithms based on feature extraction. It outlines a methodology for computing communication signal features by inversely estimating underwater acoustic channel parameters, with the modified features serving as the basis for modulation recognition. Section 3 details the selection of the experimental dataset, experimental scenarios, and the procedures involved. Section 4 presents a comparative analysis of the experimental results and discusses the enhancement of modulation recognition performance achieved through our method. In Section 5, the significance of our work is discussed, along with the limitations of our approach and potential directions for future research.
2. Modulation Recognition Algorithm Based on Channel Parameter Inversion
This paper proposes a solution to the issue of classical manual feature-based modulation recognition methods failing to achieve satisfactory recognition accuracy due to the fading characteristics of the underwater acoustic channel. The proposed solution involves calculating the distortion caused by the communication signal as it passes through the underwater acoustic channel, quantifying its impact, and incorporating it into the feature extraction calculation. This reduces the influence of the channel on the extracted features, allowing for the restoration of accurate modulation signal features. The classical manual feature extraction method is then used to perform modulation classification. For this purpose, blind estimation of the underwater acoustic channel is a critical step in achieving the inversion of the communication signal parameters, which serves as the basis for modulation classification.
2.1. Model-Based Underwater Acoustic Channel Estimation
Underwater acoustic channel modeling is a method that translates the physical characteristics of signals in the ocean into mathematical models, allowing researchers to understand the operational performance of underwater acoustic systems through simulation. To capture the propagation patterns of sound waves in water, various approximation models are commonly used for acoustic propagation calculations. Typical models used to characterize the underwater acoustic channel include Ray Theory [26], Normal Mode [27], Parabolic Equation [28], and Wavenumber Integration. For this study, which focuses on shallow water environments, the Normal Mode model, which is better suited for such conditions, was employed.
Assuming that the signal spectrum at the sound source located at is , then the sound pressure signal at the receiving point can be expressed by the following inverse Fourier transform:
In the formula, is a key parameter in acoustic channel modeling and calculation, as it represents the channel transfer function between the source and the receiving point. It is obtained through the wave equation of sound pressure:
where is the injection of external force in time and space, that is, the source of the field, represents the displacement potential, and is the speed of sound. Then, the displacement potential is written as a part that separates the spatial and temporal variables, and it is transformed into the Helmholtz equation commonly used for solving the wave equation [29]:
In the formula, represents the Laplace operator, is the wave number of the medium, and is the Dirac delta function. The Normal Mode model calculates the vertical direction of the acoustic waveguide as the vibration of a series of strings with different modes, and the horizontal direction as the horizontal wavenumber corresponding to the mode. The sound field is expressed as the superposition of all the mode vibrations excited by the sound source. Thus, the channel transfer function is expressed as follows:
The mode function, , is dependent only on the source depth, is source depth, while is the distance-dependent function that represents the corresponding amplitude of the mode function. and represent the distance of the receiver from the sound source and the depth of the receiver, respectively. By solving the Helmholtz equation, we can obtain the modal equation and then solve for the mode function . The modal equation is obtained through solving as follows:
In the formula, is the horizontal wavenumber, corresponding to the m-th mode function, and also,
The orthogonality between different modes is used as a constraint condition:
where is the water depth and is the water density associated with depth. This is a problem of solving the eigenvalues of the Sturm-Liouville equation; the eigenfunctions are the modal functions of the equation, corresponding to the eigenvalues of the horizontal wavenumber . The amplitude expression of the modal function can be derived as follows:
Further, the channel transfer function is obtained by Equation (4). Finally, based on the obtained channel response, the source signal spectrum can be estimated by channel equalization. We use a zero-forcing equalizer based on the least squares method to obtain the source signal estimate after channel parameter inversion and extract the features of the estimated signal to perform modulation pattern recognition.
Here, and are the frequency domain expressions of and , respectively.
2.2. Modulation Identification Based on Channel Inversion
A modulation recognition algorithm based on feature extraction solves the problem from the perspective of pattern recognition. The whole process includes several steps; as shown in Figure 1, they are signal preprocessing, feature extraction, classifier training, classifier judgment, and modulation type judgment.
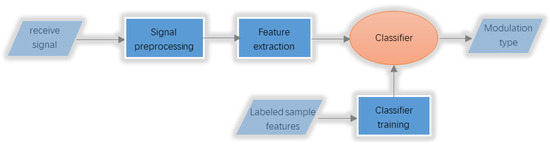
Figure 1.
Modulation recognition process based on feature extraction.
Extracting effective features is crucial in the modulation recognition process. Different types of modulation signals or communication environments may require the extraction of different kinds or multiple features to complete the modulation signal classification. Higher-order cumulants can serve as recognition features for modulation signals and can characterize some essential signal properties. They can detect the degree of difference between a Gaussian distribution and any random variable, eliminating Gaussian white noise in modulation signals and providing anti-noise advantages. These features have been proven effective in modulation recognition, and the classification features based on higher-order statistics are easy to calculate. When applicable conditions are met, they can achieve higher recognition accuracy with less data. Simultaneously, the system can recognize a wider range of signals. Therefore, this paper employs higher-order cumulants as the fundamental recognition features. In practice, the higher-order cumulants of the signal cannot be directly obtained and must be estimated based on signal sample data. Assuming that the received signal is represented by , the calculation expressions for order cumulant are as follows.
We use the , , , , of the ideal synchronization and power normalized signals as the classification features for the communication signals of several modulation methods that are commonly used in underwater communication, such as BPSK, QPSK, 8PSK, 16APSK, 16QAM, 32QAM, and 256QAM. To verify the generalization and universality of the method, we used various classifiers as the classification tools, including support vector machine (SVM) [30], decision tree [31], K-nearest neighbor (KNN), gradient boosting decision tree, Gaussian naive Bayes, and extreme gradient boosting (XGBoost), etc., and compared their classification results and work efficiency.
Figure 2 shows the process of modulation recognition through the extraction of signal features after the inversion calculation of Formula (9).
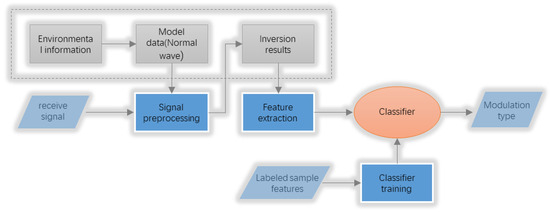
Figure 2.
Modulation identification process based on channel inversion.
3. Experiments and Results
3.1. Dataset Preparation
The dataset used for modulation recognition tasks is RML2016.10a, which is a public dataset described in [32]. We selected several commonly used modulation recognition methods for underwater communication to form the experimental dataset, including BPSK, QPSK, 8PSK, 16APSK, 16QAM, 32QAM, and 256QAM, each with 1000 I/Q data samples. This resulted in a total of 7000 data samples to be classified. The classification results of two transmission scenarios, with and without the acoustic channel, were considered in this study. The simulation of the acoustic channel is based on the Kraken software (Integrated in Acoustic Toolbox, version V2.2L), using the PekerisK environment model. One sound source is used at a depth of 25 m, and 11 receivers are vertically distributed between 0 and 100 m. The communication range between the sound source and the receiver array is 5 km. Figure 3 shows the simulated acoustic channel propagation loss based on the above environmental parameters. Figure 4 and Figure 5 show a comparison of modulation signals in the time domain with and without the acoustic channel. The blue and green curves represent the real and imaginary data of the I/Q signals, respectively. The figures clearly demonstrate that the acoustic channel introduces signal distortion.
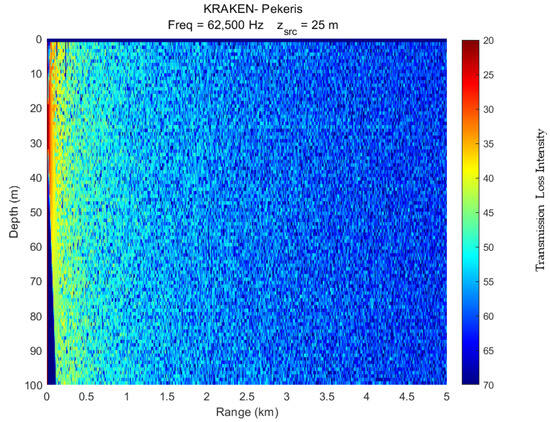
Figure 3.
Signal propagation loss in a simulated underwater acoustic channel.
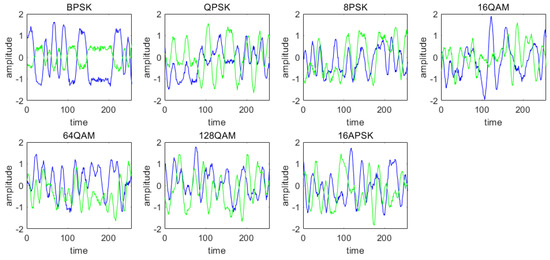
Figure 4.
I/Q time domain examples of 7 modulations without an underwater acoustic channel at 10 dB.
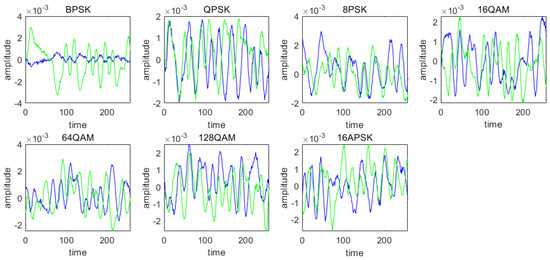
Figure 5.
I/Q time domain examples of 7 modulations through an underwater acoustic channel at 10 dB.
3.2. Modulation Recognition Experiment
To assess the effectiveness of the proposed scheme in reducing the impact of the acoustic channel, classification experiments were conducted on modulation signals that passed through both the AWGN and acoustic channels. The aim was to assess the impact of the multipath fading effect of the acoustic channel on the propagation of the communication signals and the improvement of the modulation classification results after the restoration of the transmitted signals by the channel parameters. Multiple classifiers were used for identification to compare the applicability of our method on different classifiers. The 7000 training and test samples were distributed in an 8:2 ratio. As the source position is difficult to obtain in practical engineering applications, and we used the source information as a necessary known condition when performing channel estimation, this can lead to errors. To make the experiment closer to the real scenario, we added random errors of approximately 30 m to 100 m to the source position during the channel estimation. The classification results of the AWGN and acoustic channels, and signal restoration after 10 dB and 2 dB are shown in Figure 6 and Figure 7, respectively. Figure 8 illustrates the comparison of modulation signal classification accuracy after the influence of the underwater acoustic channel and the restoration calculation at signal-to-noise ratios ranging from 2 to 10 dB. Both classifiers employ the relatively stable GBDT. Table 1 displays the classification results of modulation signals by different classifiers under the same conditions and dataset.
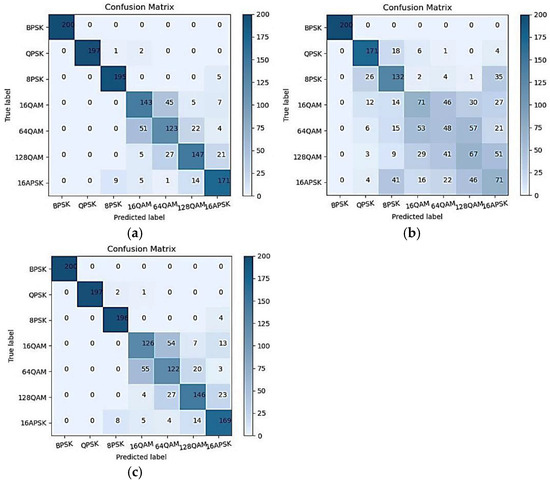
Figure 6.
Modulation confusion matrix for GBDT trained and tested on synthetic dataset with SNR = 10 dB: (a) Only under AWGN channel; (b) Under the underwater acoustic channel; (c) Under the underwater acoustic channel, but signals are restored.
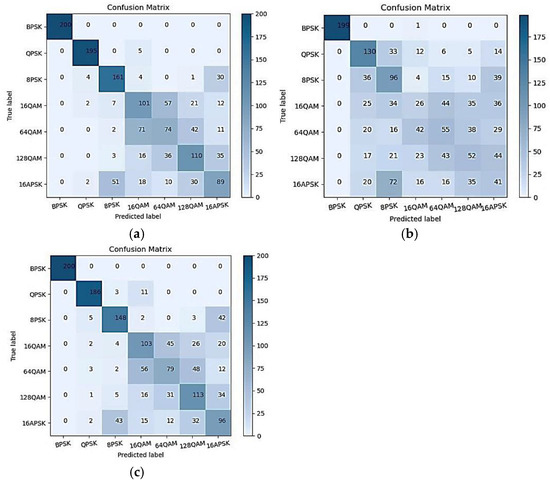
Figure 7.
Modulation confusion matrix for GBDT trained and tested on synthetic dataset with SNR = 2 dB: (a) Only under AWGN channel; (b) Under the underwater acoustic channel; (c) Under the underwater acoustic channel, but signals are restored.
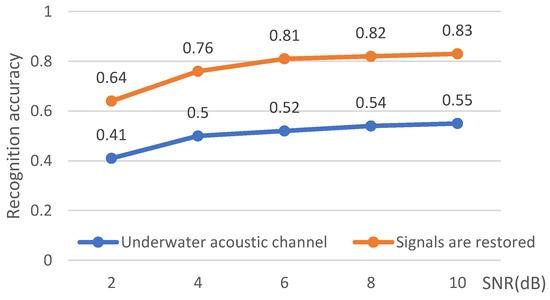
Figure 8.
Comparison of modulation signal classification accuracy from 2 to 10 dB.

Table 1.
The classification results of the proposed method are applied to different classifiers with SNR = 10 dB.
3.3. Five-Element Acoustic Dataset Experiment
Based on simulation experiments, we further validated the proposed method using the Five-Element Acoustic Underwater Dataset from the University of Texas. This dataset consists of 360 data packet transmission samples, each lasting approximately 0.5 s. It is particularly suited for the study of short-range underwater communication in shallow water channels, with communication distances of less than 1.25 km. The signals have a center frequency of 62.5 kHz, a bandwidth of 31.25 kHz, and a sampling rate of 200 kHz. It includes a variety of modulation schemes, such as BPSK, QPSK, and MQAM. The data was collected by Perrine’s team at the ARL Lake Travis test station on 6 November 2009. The lake has a maximum depth of approximately 37 m, with the receiver positioned at an immersion depth of 4.6 m on the test station. An omnidirectional transceiver was suspended from a small boat, with its depth adjustable between 1 and 8 m. Additional details on the experimental parameters and environmental settings are provided in reference [33,34]. Table 2 describes the parameters of the signal to be identified selected from the data packet.

Table 2.
Description of the five signals.
The experimental conditions were set to Position 1, where the boat travels a specified distance before stopping at a designated position for signal transmission. Initially, the raw data undergoes preprocessing to enhance the signal-to-noise ratio through noise reduction filtering and other techniques. Since preprocessing is not the primary focus of this paper, a detailed discussion is omitted, allowing for potential future optimization in this aspect of the work. Figure 9 and Figure 10 present the spectral and time-frequency representations of the transmitted data. Following preprocessing, the data was extracted according to the features outlined in Section 2.2. Subsequently, the recognition results were compared using several classifiers. Due to the limited amount of experimental data, the training and test samples were allocated in a 3:1 ratio. Table 3 presents the comparative outcomes of various classifiers for the direct classification of the University of Texas dataset and the classification following signal restoration.
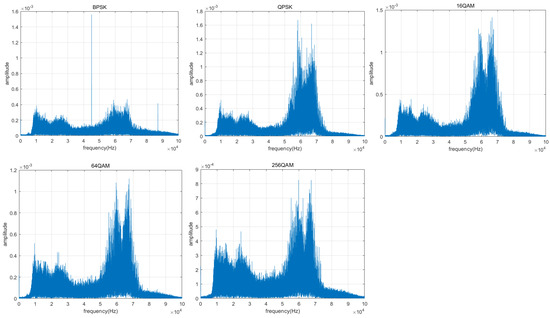
Figure 9.
Spectrum of the transmitted signal.
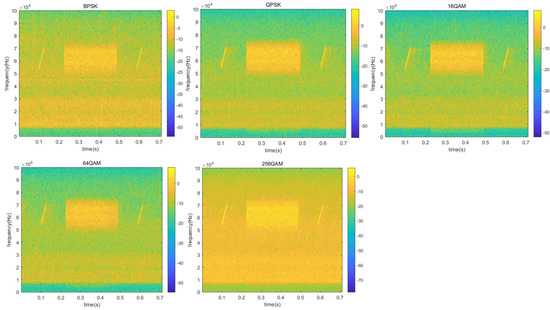
Figure 10.
Time-frequency diagram of the transmitted signal.

Table 3.
Classification results of applying the proposed method to the University of Texas dataset.
4. Discussion
Features are extracted based on the higher-order cumulants of the signal, forming feature vectors. Multiple classifiers are then used to perform modulation recognition on underwater acoustic communication signals. We compare the degradation in classification accuracy when the communication signal is affected by the acoustic channel to the improvement in classification accuracy after the received signal is restored. For the modulation recognition experiment, 7000 modulation signal samples commonly used for underwater communication were randomly selected from the publicly available dataset RML2016.10a. Out of these, 5600 samples were used for training and 1400 samples were used for testing.
The aim of our experiment was to verify the improvement in classification performance by reducing the impact of the acoustic channel. This is achieved by using channel parameter estimation to restore the signal distortion caused by the channel’s influence during transmission. We selected classical, noise-resistant higher-order cumulants for verification without extracting overly complex features, taking into account the computational complexity and practicality of the method. The classification results of the Gradient Boosting Decision Tree (GBDT) classifier are displayed in Figure 6 for three different scenarios, with a signal-to-noise ratio of 10 dB. By comparing the three confusion matrices, it is evident that the signal distortion is severe after transmission through the acoustic channel. This results in a significant decline in classification accuracy under the same feature extraction and classifier conditions, with a reduction of approximately 30% using the GBDT classifier. However, after restoring the received signal, the classification accuracy significantly improves and becomes comparable to the accuracy achieved without the influence of the acoustic channel. Using channel parameter estimation to estimate signal distortion and perform the corresponding restoration calculation has been shown to be effective in improving the modulation mode classification of underwater communication signals. Figure 7 shows the classification results of the GBDT classifier under the same scenario, but with a lower signal-to-noise ratio. Similarly, the classification result was effectively improved after the signal underwent restoration processing, following an impact on the signal by the acoustic channel. Figure 8 compares the accuracy of underwater modulation signal recognition using traditional features extracted at multiple signal-to-noise ratios from 2 dB to 10 dB, highlighting the improvement in recognition rate after signal restoration through channel estimation.
Table 1 presents a comparison of the classification results obtained from different classifiers across the three experimental scenarios mentioned above. The classifiers perform poorly on the signals transmitted through the acoustic channel, indicating that the underwater multipath fading effect has a significant impact on both the signal and the extracted features. In particular, the SVM classifier struggles to complete the classification task in this scenario, and the accuracy of most classifiers decreases by approximately 30%. The signal classification results after restoration processing have significantly improved across all classifiers, although performance variations remain. The top-performing classifiers nearly match the results obtained without the influence of the acoustic channel, while the lower-performing ones, such as Adaptive Boosting, show improvement in the classification of the restored signals but still fall short of the original signals by approximately 16%. The variation in performance may be attributed to the calculation process of signal restoration through channel parameters, which involves both solving and measurement errors for the actual scenario. Additionally, different classifier algorithms have varying strategies, resulting in different sensitivities to data and thus differing degrees of performance affected by errors.
Finally, we further verified that the restored signal enhances the accuracy of modulated signal recognition using experimental data collected by the University of Texas team at Lake Travis. Table 3 shows a significant improvement in the recognition rates of the restored signal across several classifiers. Notably, the performance of Random Forest, Decision Tree, GBDT, and Extreme Gradient Boosting is consistent with the trend of classification results on the simulated data in Section 3.2, indicating a certain level of stability. The processing results of the actual experimental data fully demonstrate the feasibility of the strategy to improve classification accuracy by mitigating the influence of the underwater acoustic channel on the signal.
Gaussian Naive Bayes and some other classifiers not listed performed poorly, likely due to differing sensitivity and adaptability of the classifiers to the dataset. These classifiers present very low recognition rates for the original, unrestored signals, with Gaussian Naive Bayes achieving only 20%. Although signal restoration results in some improvement, using classifiers that are unsuitable for the dataset does not yield optimal classification results. This suggests that future work should focus on classifier selection. Based on signal restoration, an artificial neural network tailored to the dataset could be developed for classification.
5. Conclusions
To improve the recognition performance of non-cooperative underwater acoustic communication signals, a method is proposed that uses channel estimation to calculate signal distortion and restore the signal. This approach aims to address the issue of low recognition accuracy caused by the acoustic channel’s impact on modulation recognition. The experimental results demonstrate that the classification accuracy of the restored modulation signal is significantly higher than that of the distorted signal that has passed through the acoustic channel. This improvement is observed across different classifiers, indicating the feasibility of restoring the signal for mitigating underwater multipath fading effect.
The modulation signals that have been processed exhibit varying levels of performance across different classifiers. The better-performing classifiers can achieve classification accuracy that is almost as good as that of the original signal, while the slightly inferior classifiers show some improvements but still exhibit a significant gap compared to the accuracy of the original signal. This suggests that future research could focus on classifiers, for example, by constructing an artificial neural network (ANN) classifier that is better suited to the current classification tasks. However, this study does not focus on this aspect; therefore, it has not been addressed yet and will be explored in future work. On the other hand, the next step should also consider conducting additional processing when extracting signal features to further achieve the purpose of noise resistance. For example, applying the ICA method to process asymmetric acoustic signals [35]. In addition, certain studies on optimizing channel estimation may also be helpful for the method proposed in this paper. For example, the method of dynamically estimating channel conditions discussed in [36] can further improve the accuracy of channel estimation, thereby optimizing the signal restoration results.
Errors in the solution equations can compromise the accuracy of the restored signal during channel estimation. Moreover, in practical engineering applications, the accuracy of channel estimation may be further degraded by measurement errors, which subsequently impact classification performance. Future work could aim to address this issue by optimizing the channel estimation process.
Author Contributions
Conceptualization, X.Y. and D.Z.; methodology, X.Y.; software, X.Y.; validation, X.Y., D.Z. and T.S.; formal analysis, X.Y.; investigation, X.Y.; resources, Z.W.; data curation, X.Y., D.Z. and T.S.; writing—original draft preparation, X.Y.; writing—review and editing, Z.W.; visualization, X.Y.; supervision, Z.W. and T.S.; project administration, D.Z. and T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, J.; Shen, T.S.; Zhao, D.X.; Zhang, F.T. Flow Sensing-Based Underwater Target Detection Using Distributed Mobile Sensors. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022; Volume 12, pp. 2681–2687. [Google Scholar]
- Yin, J.W. Underwater Acoustic Communication Principles and Signal Processing Technology; National Defense Industry Press: Arlington, TX, USA, 2011. [Google Scholar]
- Weaver, C.S.; Cole, C.A.; Krumland, R.B. The Automatic Classification of Modulation Types by Pattern Recognition; Stanford University: Stanford, CA, USA, 1969. [Google Scholar]
- Gardner, W.A. The spectral correlation theory of cyclostationary time-series. Signal Process. 1986, 11, 13–36. [Google Scholar] [CrossRef]
- Gardner, W.A. Spectral correlation of modulated signals: Part I—Analog modulation. IEEE Trans. Commun. 1987, 35, 584–594. [Google Scholar] [CrossRef]
- Gardner, W.A.; Brown, W.A.I.; Chen, C.K. Spectral correlation of modulated signals: Part II—Digital Modulation. IEEE Trans. Commun. 1987, 35, 595–601. [Google Scholar] [CrossRef]
- Gardner, W.A. A unifying view of second-order measures of quality for signal classification. IEEE Trans. Commun. 1980, 28, 807–816. [Google Scholar] [CrossRef]
- Whelchel, J.E.; McNeill, D.L.; Hughes, R.D. Signal Understanding: An Artificial Intelligence Approach to Modulation Classification. In Proceedings of the IEEE International Workshop on Tools for Artificial Intelligence, Fairfax, VA, USA, 23–25 October 1989; pp. 231–236. [Google Scholar]
- Soliman, S.S.; Hsue, S.Z. Signal Classification Using Statistical Moments. IEEE Trans. Commun. 1992, 40, 908–916. [Google Scholar] [CrossRef]
- Ghani, N.; Lamontagne, R. Neural networks applied to the classification of spectral features for automatic modulation recognition. In Proceedings of the MILCOM’93-IEEE Military Communications Conference, Boston, MA, USA, 11–14 October 1993; IEEE: New York, NY, USA, 1993; Volume 1, pp. 111–115. [Google Scholar]
- Azzouz, E.; Nandi, A.K. Automatic Modulation Recognition of Communication Signals; Kluwer Academic Publishers: New York, NY, USA, 1996. [Google Scholar]
- Azzouz, E.E.; Nandi, A.K. Modulation recognition using artificial neural networks. Signal Process. 1997, 56, 165–175. [Google Scholar]
- Nandi, A.K.; Azzouz, E.E. Algorithms for automatic Modulation recognition of communication signals. IEEE Trans. Commun. 1998, 46, 431–436. [Google Scholar] [CrossRef]
- Le Martret, C.J.; Boiteau, D. Modulation classification by means of different orders statistical moments. In Proceedings of the MILCOM 97 MILCOM 97 Proceedings, Monterey, CA, USA, 3–5 November 1997; IEEE: New York, NY, USA, 1997; Volume 3, pp. 1387–1391. [Google Scholar]
- Donoho, D.L.; Huo, X. Large-sample modulation classification using Hellinger representation. In Proceedings of the First IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Communications, Paris, France, 16–18 April 1997; IEEE: New York, NY, USA, 1997; pp. 133–136. [Google Scholar]
- Swami, A.; Sadler, B.M. Hierarchical digital modulation classification using cumulants. IEEE Trans. Commun. 2000, 48, 416–429. [Google Scholar] [CrossRef]
- Ho, K.C.; Prokopiw, W.; Chan, Y. Modulation identification of digital signals by the wavelet transform. IEEE Proc.-Radar Sonar Navig. 2000, 147, 169–176. [Google Scholar] [CrossRef]
- Dobre, O.A.; Bar-Ness, Y.; Su, W. Higher-order cyclic cumulants for high order modulation classification. In Proceedings of the IEEE Military Communications Conference. MILCOM 2003, Boston, MA, USA, 13–16 October 2003; IEEE: New York, NY, USA, 2003; Volume 1, pp. 112–117. [Google Scholar]
- Fehske, A.; Gaeddert, J.; Reed, J.H. A new approach to signal classification using spectral correlation and neural networks. In Proceedings of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, 2005. DySPAN 2005, Baltimore, MD, USA, 8–11 November 2005; IEEE: New York, NY, USA, 2005; pp. 144–150. [Google Scholar]
- Headley, W.C.; Reed, J.D.; da Silva, C.R. Distributed cyclic spectrum feature-based modulation classification. In Proceedings of the 2008 IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 31 March–3 April 2008; IEEE: New York, NY, USA, 2008; pp. 1200–1204. [Google Scholar]
- Like, E.; Chakravarthy, V.; Ratazzi, P.; Wu, Z. Signal classification in fading channels using cyclic spectral analysis. EURASIP J. Wirel. Commun. Netw. 2009, 2009, 879812. [Google Scholar] [CrossRef]
- Punchihewa, A.; Zhang, Q.; Dobre, O.A.; Spooner, C.; Rajan, S.; Inkol, R. On the Cyclostationarity of OFDM and Single Carrier Linearly Digitally Modulated Signals in Time Dispersive Channels: Theoretical Developments and Application. IEEE Trans. Wirel. Commun. 2010, 9, 2588–2599. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional radio modulation recognition networks. In Proceedings of the Engineering Applications of Neural Networks: 17th International Conference, EANN 2016, Aberdeen, UK, 2–5 September 2016; Proceedings 17. Springer International Publishing: New York, NY, USA, 2016; pp. 213–226. [Google Scholar]
- Zhang, F.; Luo, C.; Xu, J.; Luo, Y. An efficient deep learning model for automatic modulation recognition based on parameter estimation and transformation. IEEE Commun. Lett. 2021, 25, 3287–3290. [Google Scholar] [CrossRef]
- Zhang, F.; Luo, C.; Xu, J.; Luo, Y.; Zheng, F.C. Deep learning based automatic modulation recognition: Models, datasets, and challenges. Digit. Signal Process. 2022, 129, 103650. [Google Scholar] [CrossRef]
- Keller, J.B. Rays, waves and asymptotics. Bull. Amer. Math. Soc. 1978, 84, 727–750. [Google Scholar] [CrossRef]
- Pekeris, C.L. Theory of Propagation of Explosive Sound in Shallow Water; Geological Society of America: Boulder, CO, USA, 1948; p. 27. [Google Scholar]
- Hardin, R.H.; Tappert, F.D. Applications of the Split-Step Fourier Method to the Numerical Solution of Nonlinear and Variable Coefficient Wave Equations. SIAM Rev. 1973, 15, 423. [Google Scholar]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics; Springer: New York, NY, USA, 2011; pp. 457–527. [Google Scholar]
- Nello, C.; John, S.T. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; United Kingdom at the University Press: Cambridge, UK, 2000. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- O’Shea, T.J.; West, N. Radio machine learning dataset generation with gnu radio. In Proceedings of the GNU Radio Conference, Boulder, CO, USA, 12–16 September 2016; Volume 1. [Google Scholar]
- Perrine, K.A.; Nieman, K.F.; Henderson, T.L.; Lent, K.H.; Brudner, T.J.; Evans, B.L. University of Texas Applied Research Laboratory Nov. In Five-Element Acoustic Underwater Dataset; Technical Report; University of Texas: Austin, TX, USA, 2009. [Google Scholar]
- Perrine, K.A.; Nieman, K.F.; Henderson, T.L.; Lent, K.H.; Brudner, T.J.; Evans, B.L. Doppler estimation and correction for shallow underwater acoustic communications. In Proceedings of the 2010 Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2010; IEEE: New York, NY, USA, 2010; pp. 746–750. [Google Scholar]
- Spurek, P.; Tabor, J.; Rola, P.; Ociepka, M. ICA based on asymmetry. Pattern Recognit. 2017, 67, 230–244. [Google Scholar] [CrossRef]
- Ardizzon, F.; Casari, P.; Tomasin, S. A RNN-based approach to physical layer authentication in underwater acoustic networks with mobile devices. Comput. Netw. 2024, 243, 110311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).