Multi-Objective Optimization Design of a Mooring System Based on the Surrogate Model
Abstract
1. Introduction
2. Surrogate Models for the Optimization of FOWTs
2.1. Kriging Surrogate Modeling
2.1.1. Kriging Algorithm
2.1.2. Surrogate Modeling
2.2. Global Response Calculation of FOWTs
- (1)
- Aerodynamic Load
- (2)
- Fluid Loads
- (3)
- Mooring Line Tension
2.3. NSGA-II Algorithm
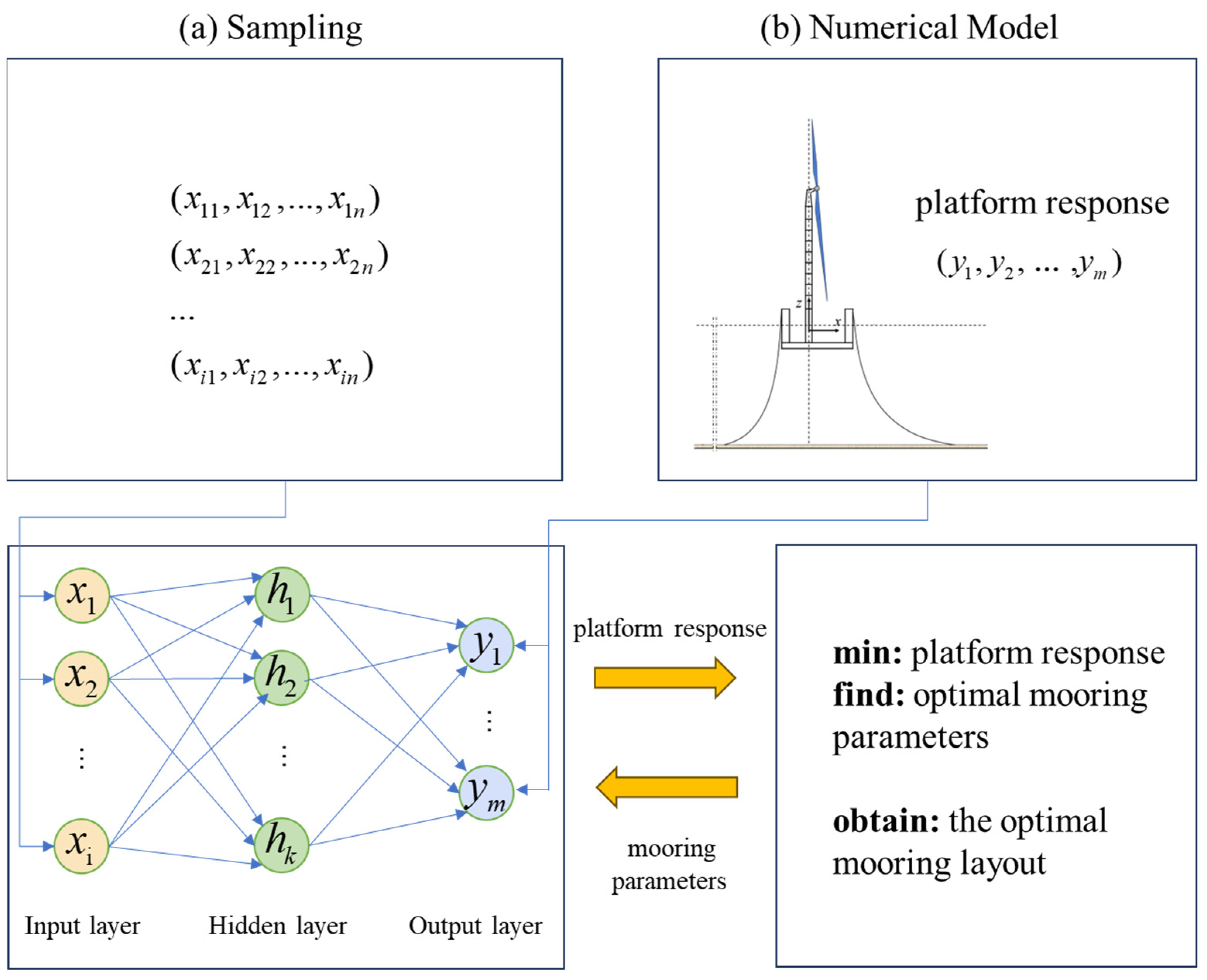
2.4. Optimization Process Based on the Surrogate Model
- (a)
- Sampling
- (b)
- Numerical Modeling
- (c)
- Kriging Surrogate Modeling
- (d)
- Mooring System Optimization
3. Case Study
3.1. The Parameters of the FOWT Model
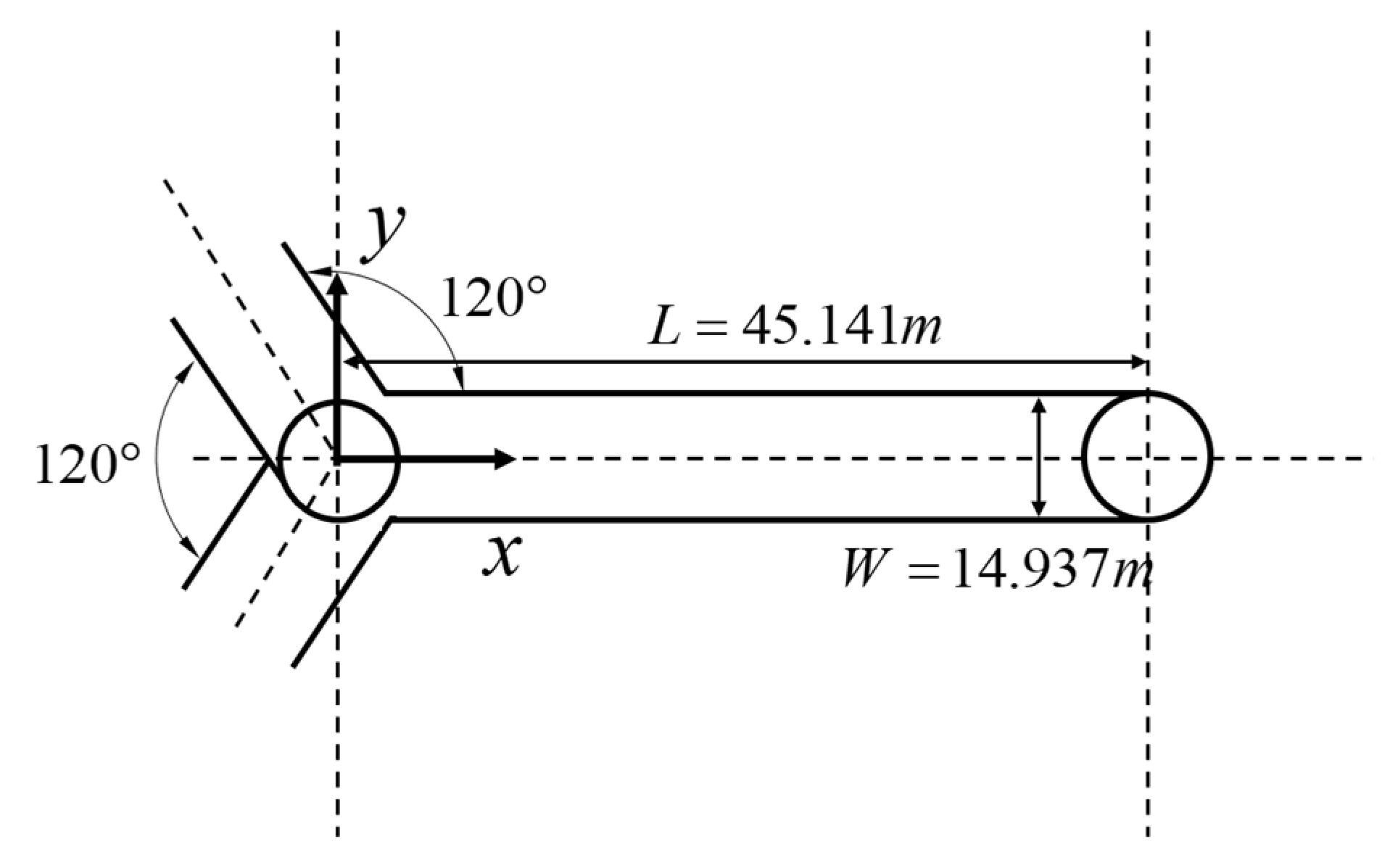
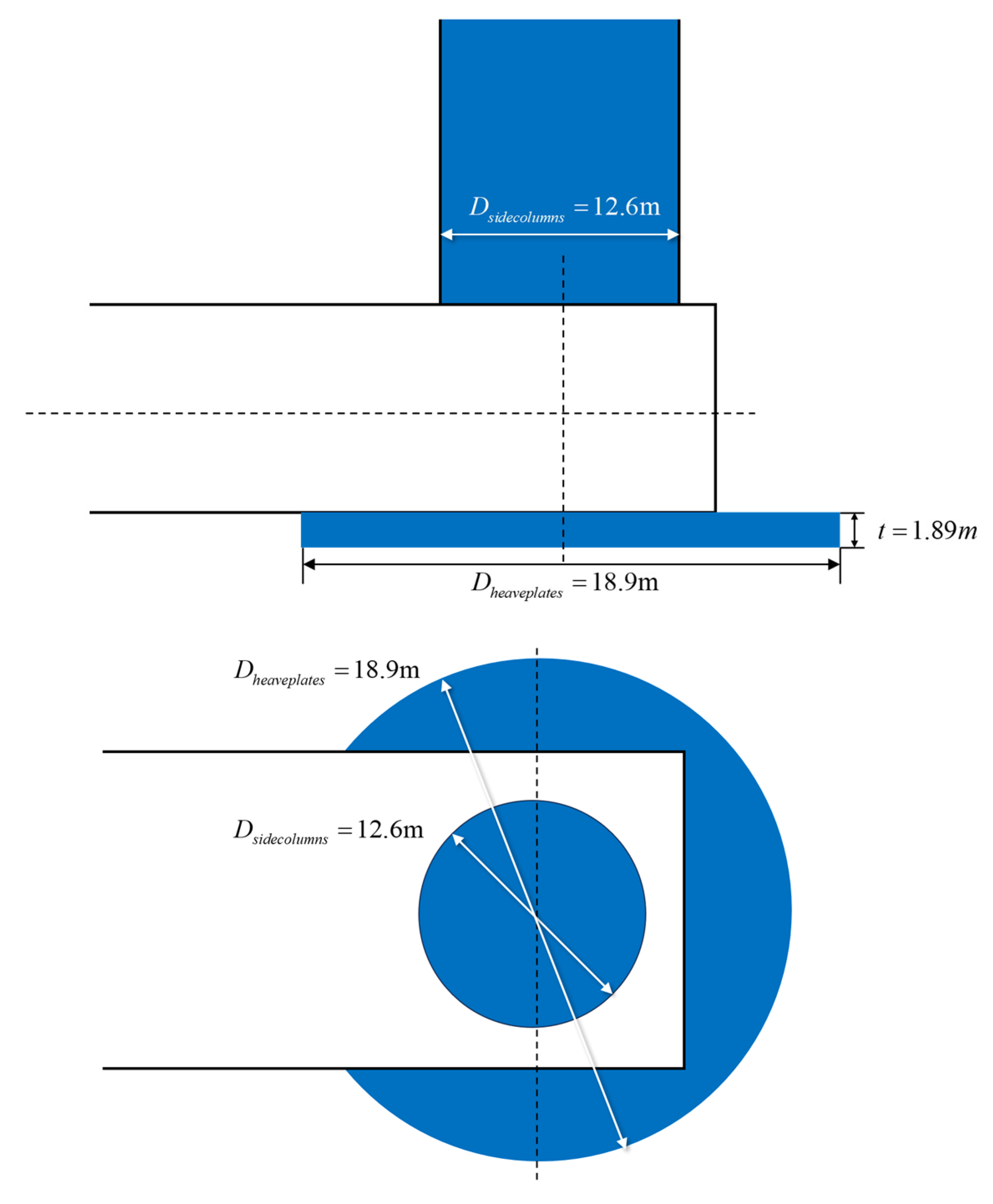
3.1.1. Semi-Submersible Platform
3.1.2. Wind Turbine and Tower
3.1.3. Initial Mooring System
3.2. Design Load Condition
3.3. Design Variables
3.4. Objective Function and Constraints
4. Results and Discussion
4.1. Surrogate Modeling and Validation
4.1.1. Sample Point Selection
4.1.2. Global Responses of the Sample Set
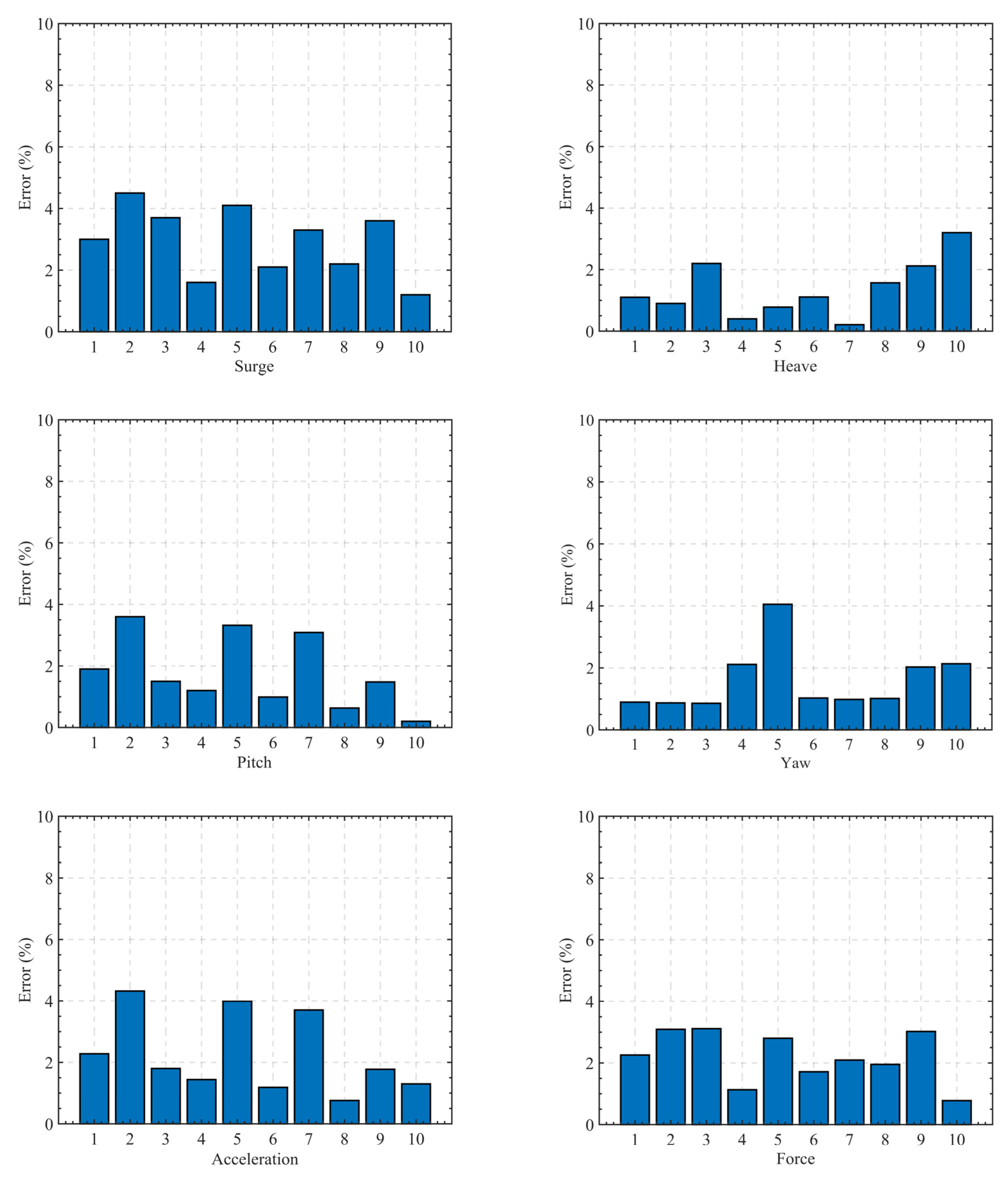
4.1.3. Reliability Analysis of Surrogate Model
4.2. Mooring System Optimization
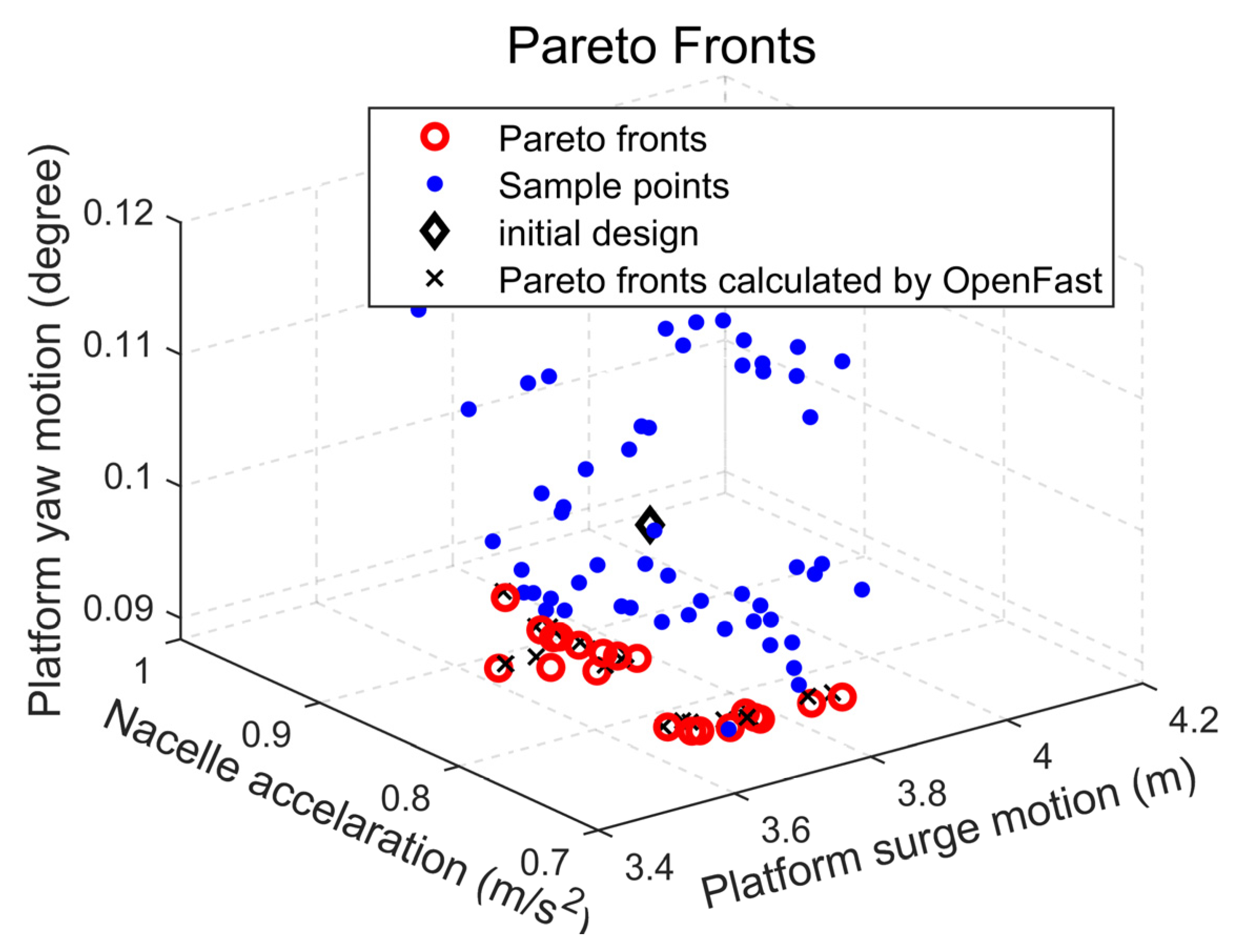
4.2.1. Pareto Solution
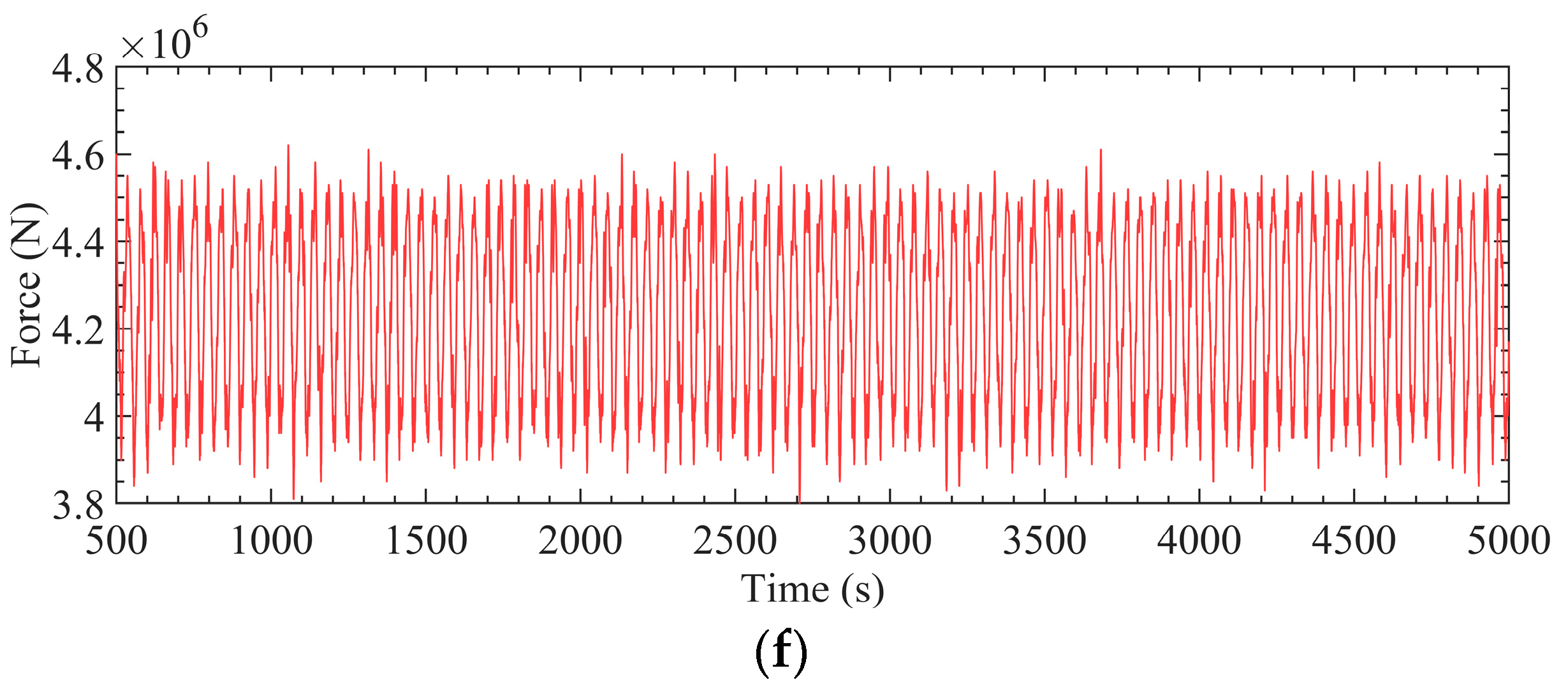
4.2.2. Results for Optimized Configurations Based on Time-Domain Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, Y.; Duan, Y.; Li, J.; Chen, M.; Zhang, X. Optimization of mooring systems for a 10 MW semisubmersible offshore wind turbines based on neural network. Ocean Eng. 2024, 296, 117020. [Google Scholar] [CrossRef]
- Ja’e, I.A.; Ali, M.O.A.; Yenduri, A.; Amaechi, C.V.; Nizamani, Z.; Nakayama, A. Optimization of mooring line design parameters using Mooring Optimization Tool for FPSO (MooOpT4FPSO) with the consideration of integrated design methodology. Ocean Eng. 2022, 264, 112499. [Google Scholar]
- Shafieefar, M.; Rezvani, A. Mooring optimization of floating platforms using a genetic algorithm. Ocean Eng. 2007, 34, 1413–1421. [Google Scholar] [CrossRef]
- Sclavounos, P.; Tracy, C.; Lee, S. Floating offshore wind turbines: Responses in a seastate pareto optimal designs and economic assessment. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; pp. 31–41. [Google Scholar]
- Philippe, M.; Babarit, A.l.; Ferrant, P. Comparison of time and frequency domain simulations of an offshore floating wind turbine. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; pp. 589–598. [Google Scholar]
- Karimi, M.; Buckham, B.; Crawford, C. A fully coupled frequency domain model for floating offshore wind turbines. J. Ocean Eng. 2019, 5, 135–158. [Google Scholar] [CrossRef]
- Karimi, M.; Hall, M.; Buckham, B.; Crawford, C. A multi-objective design optimization approach for floating offshore wind turbine support structures. J. Ocean Eng. 2017, 3, 69–87. [Google Scholar] [CrossRef]
- Brommundt, M.; Krause, L.; Merz, K.; Muskulus, M. Mooring system optimization for floating wind turbines using frequency domain analysis. Energy Procedia 2012, 24, 289–296. [Google Scholar] [CrossRef]
- Bruschi, N.; Ferri, G.; Marino, E.; Borri, C. Influence of clumps-weighted moorings on a spar buoy offshore wind turbine. Energies 2020, 13, 6407. [Google Scholar] [CrossRef]
- Barbanti, G.; Marino, E.; Borri, C. Mooring system optimization for a spar-buoy wind turbine in rough wind and sea conditions. In Proceedings of the XV Conference of the Italian Association for Wind Engineering: IN-VENTO 2018 25; Springer: Cham, Switzerland, 2019; pp. 87–98. [Google Scholar]
- Mockutė, A.; Marino, E.; Lugni, C.; Borri, C. Comparison of nonlinear wave-loading models on rigid cylinders in regular waves. Energies 2019, 12, 4022. [Google Scholar] [CrossRef]
- Mirzaei, M.; Maimun, A.; Priyanto, A.; Fitriadhy, A. Mooring pattern optimization using a genetic algorithm. J. Teknol. 2014, 66, 189–193. [Google Scholar] [CrossRef][Green Version]
- da Fonseca Monteiro, B.; Baioco, J.S.; Albrecht, C.H.; de Lima, B.S.L.P.; Jacob, B.P. Optimization of mooring systems in the context of an integrated design methodology. Mar. Struct. 2021, 75, 102874. [Google Scholar] [CrossRef]
- Koziel, S.; Bekasiewicz, A.; Couckuyt, I.; Dhaene, T. Efficient Multi-Objective Simulation-Driven Antenna Design Using Co-Kriging. IEEE Trans. Antennas Propag. 2014, 62, 5900–5905. [Google Scholar] [CrossRef]
- Chatterjee, T.; Chakraborty, S.; Chowdhury, R. A Critical Review of Surrogate Assisted Robust Design Optimization. Arch. Comput. Methods Eng. 2019, 26, 245–274. [Google Scholar] [CrossRef]
- Zhang, X.; Song, X.; Qiu, W.; Yuan, Z.; You, Y.; Deng, N. Multi-objective optimization of Tension Leg Platform using evolutionary algorithm based on surrogate model. Ocean Eng. 2018, 148, 612–631. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Cai, X.; Xie, J.; Wang, Y.; Zhang, N. Novel method for designing and optimising the floating platforms of offshore wind turbines. Ocean Eng. 2022, 266, 112781. [Google Scholar] [CrossRef]
- Sun, Y.; Denimal, E.; Yuan, J.; Salles, L.J.S.; Optimization, M. Geometric design of friction ring dampers in blisks using nonlinear modal analysis and Kriging surrogate model. Struct. Multidiscipl. Optim. 2022, 65, 98. [Google Scholar] [CrossRef]
- Thapa, M.; Missoum, S.J.S.; Optimization, M. Surrogate-based stochastic optimization of horizontal-axis wind turbine composite blades. Struct. Multidiscipl. Optim. 2022, 65, 41. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, T.; Duan, M.; Men, H. Multi-objective optimization of semi-submersible platforms based on a support vector machine with grid search optimized mixed kernels surrogate model. Ocean Eng. 2022, 260, 112077. [Google Scholar] [CrossRef]
- Augusto, O.B.; Dias, C.A.N.; Rossi, R. Practical method for mooring systems optimum design. Dev. Mar. Technol. 1998, 11, 1013–1021. [Google Scholar]
- Schmidt, H.; Thierauf, G. A combined heuristic optimization technique. Adv. Eng. Softw. 2005, 36, 11–19. [Google Scholar] [CrossRef]
- Jiang, Z.; Gu, M. Optimization of a fender structure for the crashworthiness design. Mater. Des. 2010, 31, 1085–1095. [Google Scholar] [CrossRef]
- Saka, M.P. Optimum design of steel frames using stochastic search techniques based on natural phenomena: A review. In Civil Engineering Computations: Tools and Techniques; Saxe-Coburg Publications: Stirlingshire, UK, 2007; Chapter 6; pp. 105–147. [Google Scholar]
- Sahab, M.G.; Toropov, V.V.; Gandomi, A.H. A review on traditional and modern structural optimization: Problems and techniques. In Metaheuristic Applications in Structures and Infrastructures; Elsevier Science: Amsterdam, The Netherlands, 2013; pp. 25–47. [Google Scholar]
- Rao, S.S. Engineering Optimization: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Krige, D.G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand. J. S. Afr. Inst. Min. Metall. 1951, 52, 201–203. [Google Scholar]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Multi-fidelity optimization via surrogate modelling. Proc. R. Soc. A 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- Qiao, D.; Zhou, Y.; Xu, B.; Qin, J.; Tang, G.; Lu, L.; Ou, J. Dynamic response analysis of a fully coupled aerodynamic-hydrodynamic-mooring-anchor floating offshore wind turbine. Ocean Eng. 2024, 312 Pt 1, 119085. [Google Scholar] [CrossRef]
- Low, Y.M.; Langley, R.S. Time and frequency domain coupled analysis of deepwater floating production systems. Appl. Ocean Res. 2006, 28, 371–385. [Google Scholar] [CrossRef]
- Xiong, L.; Yang, J.; Zhao, W. Dynamics of a taut mooring line accounting for the embedded anchor chains. Ocean Eng. 2016, 121, 403–413. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Benassai, G.; Campanile, A.; Piscopo, V.; Scamardella, A. Optimization of mooring systems for floating offshore wind turbines. Coast Eng. J. 2015, 57, 1550021. [Google Scholar] [CrossRef]



| Parameter | Unit | Value |
|---|---|---|
| Water depth | m | 200 |
| Displacement | m3 | 20,206 |
| Draft | m | 25.474 |
| Center of mass | m | −18.162 |
| Center of buoyancy | m | −16.757 |
| Platform mass | kg | |
| Moment of inertia about the x-axis | kg·m2 | 5.873 × 1010 |
| Moment of inertia about the y-axis | kg·m2 | 5.873 × 1010 |
| Moment of inertia about the z-axis | kg·m2 | 2.367 × 1010 |
| Parameter | Unit | #1 | #2 | #3 | ||
|---|---|---|---|---|---|---|
| x | m | −45.141 | 0 | −30.161 | ||
| y | m | 22.571 | 39.092 | −30.161 | ||
| z | m | 26.306 | −45.561 | −30.161 | ||
| Diameter | m | 18.900 | ||||
| Thickness | m | 1.890 | ||||
| A33 | kg | 2.679× 107 | ||||
| B33 | N/(m/s) | 1.02 × 106 | ||||
| Cd | - | 6.203 | ||||
| Cm | - | 6.437 | ||||
| Parameter | Unit | Value |
|---|---|---|
| Number of blades | - | 3 |
| Cut-in wind speed | m/s | 3 |
| Rated wind speed | m/s | 10.59 |
| Cut-out wind speed | m/s | 25 |
| Rotor diameter | m | 240 |
| Hub height | m | 150 |
| Minimum rotor speed | rpm | 5 |
| Maximum rotor speed | rpm | 7.56 |
| Parameter | Unit | Value |
|---|---|---|
| Tower mass | kg | 1.26 × 106 |
| Tower length | m | 129.49 |
| Base diameter of the tower | m | 10.00 |
| Top diameter of the tower | M | 6.50 |
| Parameter | Unit | Value |
|---|---|---|
| Number | - | 3 |
| Radius of anchor points from centerline | m | 837.6 |
| Radius of fairlead holes from centerline | m | 58 |
| Diameter | mm | 185 |
| Dry weight | kg/m | 685 |
| Stiffness | MN | 3270 |
| Length | m | 900 |
| Condition | Tp (s) | Hs (m) | Peak Enhancement Factor | Wind Speed (m/s) | Turbulence Intensity (%) |
|---|---|---|---|---|---|
| - | 12.51 | 5.5 | 1.0 | 10.59 | 5.5 |
| Design Variables | Variable Name | Initial Value | Lower Bound | Upper Bound |
|---|---|---|---|---|
| anchor point location Xanch | 900 | 500 | 1500 | |
| mooring line length | −837.6 | −500 | −1500 |
| No. | Parameter | Constraint |
|---|---|---|
| 1 | surge motion | |
| 2 | mooring line length | |
| 3 | catenary section length |
| No. | Length [m] | Coordinates [m] |
|---|---|---|
| 1 | 550 | −500 |
| 2 | 600 | −550 |
| 3 | 600 | −500 |
| 4 | 650 | −600 |
| 5 | 650 | −550 |
| 6 | 650 | −500 |
| 7 | 700 | −650 |
| 8 | 700 | −600 |
| 9 | 700 | −550 |
| 10 | 750 | −700 |
| 11 | 750 | −650 |
| 12 | 750 | −600 |
| 13 | 800 | −750 |
| 14 | 800 | −700 |
| 15 | 800 | −650 |
| 16 | 850 | −800 |
| 17 | 850 | −750 |
| 18 | 850 | −700 |
| 19 | 900 | −850 |
| 20 | 900 | −837.5 |
| 21 | 900 | −800 |
| 22 | 900 | −750 |
| 23 | 950 | −900 |
| 24 | 950 | −850 |
| 25 | 950 | −800 |
| 26 | 1000 | −950 |
| 27 | 1000 | −900 |
| 28 | 1000 | −850 |
| 29 | 1050 | −1000 |
| 30 | 1050 | −950 |
| 31 | 1050 | −900 |
| 32 | 1100 | −1050 |
| 33 | 1100 | −1000 |
| 34 | 1100 | −950 |
| 35 | 1150 | −1100 |
| 36 | 1150 | −1050 |
| 37 | 1150 | −1000 |
| 38 | 1200 | −1150 |
| 39 | 1200 | −1100 |
| 40 | 1200 | −1050 |
| 41 | 1250 | −1200 |
| 42 | 1250 | −1150 |
| 43 | 1250 | −1100 |
| 44 | 1300 | −1250 |
| 45 | 1300 | −1200 |
| 46 | 1300 | −1150 |
| 47 | 1350 | −1300 |
| 48 | 1350 | −1250 |
| 49 | 1350 | −1200 |
| 50 | 1400 | −1350 |
| 51 | 1400 | −1300 |
| 52 | 1400 | −1250 |
| 53 | 1450 | −1400 |
| 54 | 1450 | −1350 |
| 55 | 1450 | −1300 |
| 56 | 1500 | −1450 |
| 57 | 1500 | −1400 |
| 58 | 1500 | −1350 |
| No. | Surge [m] | Heave [m] | Pitch [°] | Yaw [°] | ACCE [m/s2] | VFair [N] |
|---|---|---|---|---|---|---|
| 1 | 3.720 | 2.060 | 0.109 | 0.095 | 0.857 | 4.752 × 106 |
| 2 | 3.640 | 2.011 | 0.111 | 0.098 | 0.864 | 4.757 × 106 |
| 3 | 4.060 | 2.073 | 0.131 | 0.099 | 0.880 | 4.405 × 106 |
| 4 | 3.620 | 2.004 | 0.110 | 0.093 | 0.845 | 4.771 × 106 |
| 5 | 4.030 | 2.092 | 0.124 | 0.094 | 0.960 | 4.438 × 106 |
| 6 | 4.100 | 2.105 | 0.138 | 0.097 | 0.918 | 4.362 × 106 |
| 7 | 3.640 | 2.030 | 0.111 | 0.098 | 0.851 | 4.787 × 106 |
| 8 | 4.000 | 2.141 | 0.126 | 0.096 | 0.932 | 4.429 × 106 |
| 9 | 3.900 | 2.153 | 0.138 | 0.097 | 0.956 | 4.349 × 106 |
| 10 | 3.690 | 2.038 | 0.110 | 0.092 | 0.825 | 4.795 × 106 |
| 11 | 4.090 | 2.131 | 0.128 | 0.095 | 0.894 | 4.442 × 106 |
| 12 | 3.600 | 2.133 | 0.135 | 0.089 | 0.927 | 4.383 × 106 |
| 13 | 3.740 | 2.039 | 0.109 | 0.091 | 0.801 | 4.804 × 106 |
| 14 | 3.770 | 1.948 | 0.126 | 0.089 | 0.931 | 4.429 × 106 |
| 15 | 3.900 | 2.092 | 0.133 | 0.091 | 0.874 | 4.415 × 106 |
| 16 | 3.700 | 2.039 | 0.109 | 0.090 | 0.801 | 4.809 × 106 |
| 17 | 3.690 | 2.057 | 0.123 | 0.091 | 0.868 | 4.490 × 106 |
| 18 | 4.000 | 2.185 | 0.131 | 0.089 | 0.904 | 4.365 × 106 |
| 19 | 3.780 | 2.025 | 0.108 | 0.091 | 0.795 | 4.805 × 106 |
| 20 | 3.810 | 1.921 | 0.120 | 0.089 | 0.863 | 4.533 × 106 |
| 21 | 3.550 | 2.013 | 0.119 | 0.090 | 0.849 | 4.450 × 106 |
| 22 | 4.000 | 2.149 | 0.132 | 0.095 | 0.889 | 4.357 × 106 |
| 23 | 3.850 | 1.990 | 0.109 | 0.094 | 0.817 | 4.812 × 106 |
| 24 | 3.850 | 2.164 | 0.123 | 0.090 | 0.884 | 4.534 × 106 |
| 25 | 4.000 | 2.082 | 0.134 | 0.090 | 0.945 | 4.410 × 106 |
| 26 | 3.810 | 2.027 | 0.108 | 0.094 | 0.777 | 4.810 × 106 |
| 27 | 3.910 | 2.046 | 0.118 | 0.093 | 0.789 | 4.480 × 106 |
| 28 | 3.700 | 1.946 | 0.129 | 0.093 | 0.940 | 4.388 × 106 |
| 29 | 3.810 | 1.945 | 0.106 | 0.092 | 0.850 | 4.825 × 106 |
| 30 | 3.750 | 2.087 | 0.121 | 0.089 | 0.880 | 4.538 × 106 |
| 31 | 4.000 | 2.068 | 0.127 | 0.091 | 0.875 | 4.396 × 106 |
| 32 | 3.860 | 1.988 | 0.108 | 0.087 | 0.809 | 4.816 × 106 |
| 33 | 3.880 | 2.086 | 0.118 | 0.087 | 0.779 | 4.481 × 106 |
| 34 | 3.800 | 1.979 | 0.128 | 0.086 | 0.931 | 4.394 × 106 |
| 35 | 3.740 | 1.873 | 0.108 | 0.087 | 0.843 | 4.825 × 106 |
| 36 | 3.680 | 2.011 | 0.122 | 0.087 | 0.878 | 4.537 × 106 |
| 37 | 4.000 | 2.159 | 0.131 | 0.087 | 0.890 | 4.423 × 106 |
| 38 | 3.820 | 2.026 | 0.108 | 0.087 | 0.765 | 4.812 × 106 |
| 39 | 3.720 | 2.036 | 0.121 | 0.087 | 0.881 | 4.538 × 106 |
| 40 | 4.000 | 2.211 | 0.128 | 0.087 | 0.875 | 4.402 × 106 |
| 41 | 3.830 | 2.077 | 0.107 | 0.088 | 0.766 | 4.833 × 106 |
| 42 | 3.640 | 2.032 | 0.118 | 0.092 | 0.842 | 4.526 × 106 |
| 43 | 3.600 | 1.862 | 0.125 | 0.091 | 0.812 | 4.447 × 106 |
| 44 | 3.850 | 1.967 | 0.107 | 0.087 | 0.796 | 4.825 × 106 |
| 45 | 3.760 | 2.006 | 0.120 | 0.087 | 0.836 | 4.526 × 106 |
| 46 | 4.100 | 2.121 | 0.132 | 0.091 | 0.867 | 4.428 × 106 |
| 47 | 3.840 | 1.949 | 0.107 | 0.090 | 0.804 | 4.837 × 106 |
| 48 | 3.550 | 1.934 | 0.120 | 0.090 | 0.828 | 4.554 × 106 |
| 49 | 4.000 | 2.119 | 0.129 | 0.089 | 0.841 | 4.454 × 106 |
| 50 | 3.700 | 2.102 | 0.109 | 0.0871 | 0.753 | 4.894 × 106 |
| 51 | 3.710 | 2.088 | 0.119 | 0.0886 | 0.818 | 4.554 × 106 |
| 52 | 3.800 | 2.141 | 0.129 | 0.084 | 0.865 | 4.439 × 106 |
| 53 | 3.830 | 1.938 | 0.107 | 0.084 | 0.837 | 4.822 × 106 |
| 54 | 3.980 | 1.969 | 0.114 | 0.084 | 0.794 | 4.570 × 106 |
| 55 | 3.600 | 1.954 | 0.121 | 0.084 | 0.851 | 4.442 × 106 |
| 56 | 3.840 | 1.989 | 0.108 | 0.085 | 0.776 | 4.835 × 106 |
| 57 | 3.870 | 2.177 | 0.117 | 0.084 | 0.787 | 4.541 × 106 |
| 58 | 3.800 | 2.050 | 0.127 | 0.084 | 0.873 | 4.444 × 106 |
| K-f1 | 23.784 | 50.000 |
| K-f2 | 23.784 | 47.880 |
| K-f3 | 6.484 | 5.221 |
| No. | Length [m] | Coordinates [m] |
|---|---|---|
| 1 | 702.4 | −624.3 |
| 2 | 758.5 | −625.5 |
| 3 | 882.0 | −796.0 |
| 4 | 951.3 | −837.6 |
| 5 | 1037.8 | −963.5 |
| 6 | 1106.9 | −994.0 |
| 7 | 1204.3 | −1100.8 |
| 8 | 1257.9 | −1123.8 |
| 9 | 1356.8 | −1220.3 |
| 10 | 1450.6 | −1358.7 |
| No. | Surge [m] | Heave [m] | Pitch [°] | Yaw [°] | ACCE [m/s2] | VFair /[N] |
|---|---|---|---|---|---|---|
| 1 | 3.720 | 2.060 | 0.109 | 0.098 | 0.857 | 4.75 × 106 |
| 2 | 3.640 | 2.011 | 0.111 | 0.096 | 0.864 | 4.76 × 106 |
| 3 | 4.060 | 2.073 | 0.131 | 0.097 | 0.880 | 4.41 × 106 |
| 4 | 3.620 | 2.004 | 0.110 | 0.092 | 0.845 | 4.77 × 106 |
| 5 | 4.030 | 2.092 | 0.124 | 0.095 | 0.96 | 4.44 × 106 |
| 6 | 4.100 | 2.105 | 0.138 | 0.089 | 0.918 | 4.36 × 106 |
| 7 | 3.640 | 2.030 | 0.111 | 0.091 | 0.851 | 4.79 × 106 |
| 8 | 4.001 | 2.141 | 0.126 | 0.089 | 0.932 | 4.43 × 106 |
| 9 | 3.901 | 2.153 | 0.138 | 0.091 | 0.956 | 4.35 × 106 |
| 10 | 3.690 | 2.038 | 0.110 | 0.090 | 0.825 | 4.80 × 106 |
| No. | Surge [m] | Heave [m] | Pitch [°] | Yaw [°] | ACCE [m/s2] | VFair /[N] |
|---|---|---|---|---|---|---|
| 1 | 3.831 | 2.082 | 0.111 | 0.099 | 0.876 | 4.85 × 106 |
| 2 | 3.803 | 2.029 | 0.114 | 0.097 | 0.901 | 4.90 × 106 |
| 3 | 4.210 | 2.118 | 0.132 | 0.098 | 0.895 | 4.54 × 106 |
| 4 | 3.677 | 2.012 | 0.111 | 0.094 | 0.857 | 4.82 × 106 |
| 5 | 4.195 | 2.108 | 0.128 | 0.099 | 0.998 | 4.56 × 106 |
| 6 | 4.186 | 2.128 | 0.139 | 0.090 | 0.928 | 4.43 × 106 |
| 7 | 3.760 | 2.034 | 0.114 | 0.092 | 0.882 | 4.88 × 106 |
| 8 | 4.088 | 2.174 | 0.126 | 0.09 | 0.939 | 4.51 × 106 |
| 9 | 4.040 | 2.198 | 0.140 | 0.093 | 0.972 | 4.48 × 106 |
| 10 | 3.734 | 2.103 | 0.110 | 0.092 | 0.835 | 4.83 × 106 |
| No. | Length [m] | Coordinates [m] | Surge [m] | Heave [m] | Pitch [°] | Yaw [°] | ACCE [m/s2] | VFair [N] |
|---|---|---|---|---|---|---|---|---|
| 1 | 626.6 | −604.6 | 3.510 | 1.998 | 0.105 | 0.0928 | 0.821 | 4.998 × 106 |
| 2 | 884.0 | −803.2 | 3.523 | 2.008 | 0.114 | 0.0976 | 0.818 | 4.556 × 106 |
| 3 | 882.8 | −809.6 | 3.537 | 2.003 | 0.112 | 0.0964 | 0.810 | 4.605 × 106 |
| 4 | 606.5 | −583.6 | 3.552 | 2.006 | 0.104 | 0.0923 | 0.837 | 4.995 × 106 |
| 5 | 606.5 | −583.6 | 3.553 | 2.006 | 0.104 | 0.0923 | 0.837 | 4.995 × 106 |
| 6 | 875.8 | −806.8 | 3.554 | 2.012 | 0.111 | 0.0960 | 0.806 | 4.639 × 106 |
| 7 | 881.9 | −815.3 | 3.562 | 2.002 | 0.110 | 0.0954 | 0.803 | 4.652 × 106 |
| 8 | 874.6 | −811.2 | 3.572 | 2.012 | 0.110 | 0.0912 | 0.798 | 4.679 × 106 |
| 9 | 875.5 | −816.0 | 3.588 | 2.009 | 0.109 | 0.0903 | 0.786 | 4.706 × 106 |
| 10 | 678.9 | −676.4 | 3.604 | 2.018 | 0.099 | 0.0917 | 0.801 | 5.202 × 106 |
| 11 | 873.2 | −826.0 | 3.652 | 2.013 | 0.107 | 0.0933 | 0.792 | 4.800 × 106 |
| 12 | 1381.2 | −1351.5 | 3.656 | 2.093 | 0.106 | 0.0890 | 0.768 | 5.035 × 106 |
| 13 | 1377.3 | −1356.3 | 3.658 | 2.086 | 0.105 | 0.0889 | 0.776 | 5.096 × 106 |
| 14 | 1389.9 | −1359.1 | 3.673 | 2.099 | 0.107 | 0.0887 | 0.767 | 5.033 × 106 |
| 15 | 1394.3 | −1350.8 | 3.678 | 2.104 | 0.108 | 0.0891 | 0.756 | 4.941 × 106 |
| 16 | 1400.8 | −1347.5 | 3.702 | 2.102 | 0.109 | 0.0896 | 0.752 | 4.870 × 106 |
| 17 | 1401.8 | −1357.9 | 3.716 | 2.094 | 0.108 | 0.0889 | 0.759 | 4.939 × 106 |
| 18 | 1219.7 | −1183.3 | 3.839 | 2.064 | 0.104 | 0.0889 | 0.763 | 4.921 × 106 |
| 19 | 1222.1 | −1190.1 | 3.860 | 2.069 | 0.104 | 0.0888 | 0.762 | 4.957 × 106 |
| 20 | 1225.8 | −1198.1 | 3.879 | 2.072 | 0.103 | 0.0888 | 0.761 | 4.994 × 106 |
| Surge [m] | Heave [m] | Pitch [°] | Yaw [°] | ACCE [m/s2] | VFair [N] | |
|---|---|---|---|---|---|---|
| 3.564 | 1.991 | 0.102 | 0.087 | 0.784 | 4.61 × 106 | |
| Error | 2.05% | 0.22% | 1.03% | 4.64% | 1.78% | 1.41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, X.; Zheng, P.; Qiao, D.; Zhao, X.; Zhou, Y.; Wang, L. Multi-Objective Optimization Design of a Mooring System Based on the Surrogate Model. J. Mar. Sci. Eng. 2024, 12, 1853. https://doi.org/10.3390/jmse12101853
Ye X, Zheng P, Qiao D, Zhao X, Zhou Y, Wang L. Multi-Objective Optimization Design of a Mooring System Based on the Surrogate Model. Journal of Marine Science and Engineering. 2024; 12(10):1853. https://doi.org/10.3390/jmse12101853
Chicago/Turabian StyleYe, Xiangji, Peizi Zheng, Dongsheng Qiao, Xin Zhao, Yichen Zhou, and Li Wang. 2024. "Multi-Objective Optimization Design of a Mooring System Based on the Surrogate Model" Journal of Marine Science and Engineering 12, no. 10: 1853. https://doi.org/10.3390/jmse12101853
APA StyleYe, X., Zheng, P., Qiao, D., Zhao, X., Zhou, Y., & Wang, L. (2024). Multi-Objective Optimization Design of a Mooring System Based on the Surrogate Model. Journal of Marine Science and Engineering, 12(10), 1853. https://doi.org/10.3390/jmse12101853






