Energy Efficiency Maximization for Multi-UAV-IRS-Assisted Marine Vehicle Systems
Abstract
1. Introduction
- In the multi-UIRS-assisted marine vehicle system, an energy efficiency maximization (EEM) optimization problem is formulated by jointly optimizing the association relationships between UIRSs and USVs, computation resources of USVs, multi-UIRS phase shifts, and multi-UIRS 3D trajectories, subject to the computation data demand threshold constraints.
- The formulated optimization problem is a mixed integer nonlinear programming problem with discrete variables, i.e., association relationships, and continuous variables, i.e., computation resources, phase shifts, and trajectories, which is well known to be NP-hard. To efficiently solve the challenging problem, we decompose the original problem into two layers to solve discrete and continuous variables, respectively.
- Then, we propose a CO-MATD3 algorithm, which is an integrated convex optimization and deep reinforcement learning algorithm designed to facilitate collaborative optimization. Specifically, in the inner layer, the Dinkelbach method and relaxation method are applied to optimize the association relationships. In the outer layer, a distributed cooperative deep reinforcement learning algorithm, i.e., the Multi-Agent Twin Delayed Deep Deterministic Policy Gradient (MATD3), is developed to optimize continuous variables.
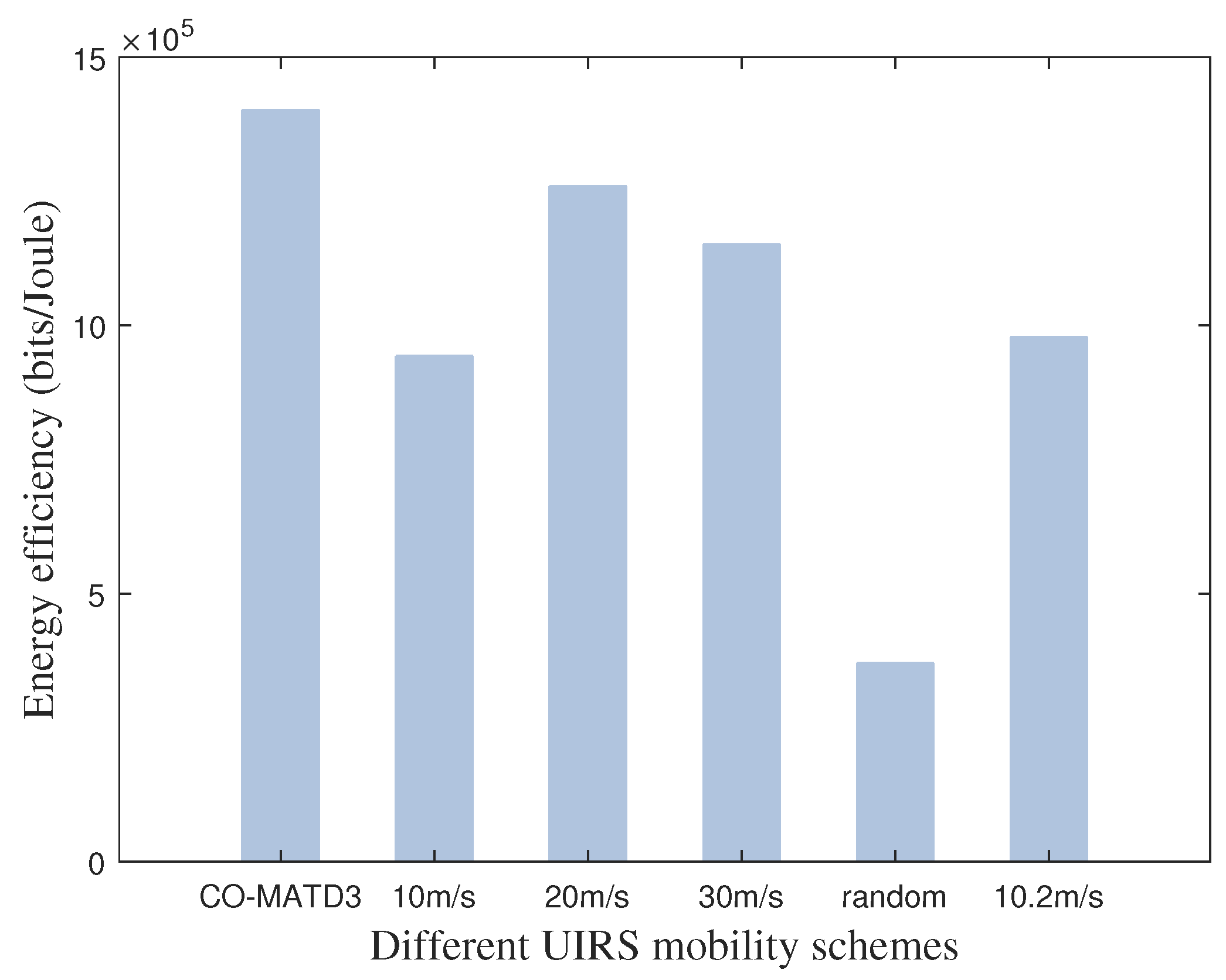
- Finally, the simulation results demonstrate the efficient training convergence and effectiveness of the proposed CO-MATD3 algorithm in optimizing energy efficiency. In addition, we find that our proposed CO-MATD3 algorithm has the capability to optimize multi-UIRS trajectories according to the dynamic locations of USVs to improve energy efficiency. The simulation results show that the performance of the proposed algorithm is superior to other benchmarks under different simulation conditions, such as the number of UIRSs, the number of USVs, computation resources, and transmission power.
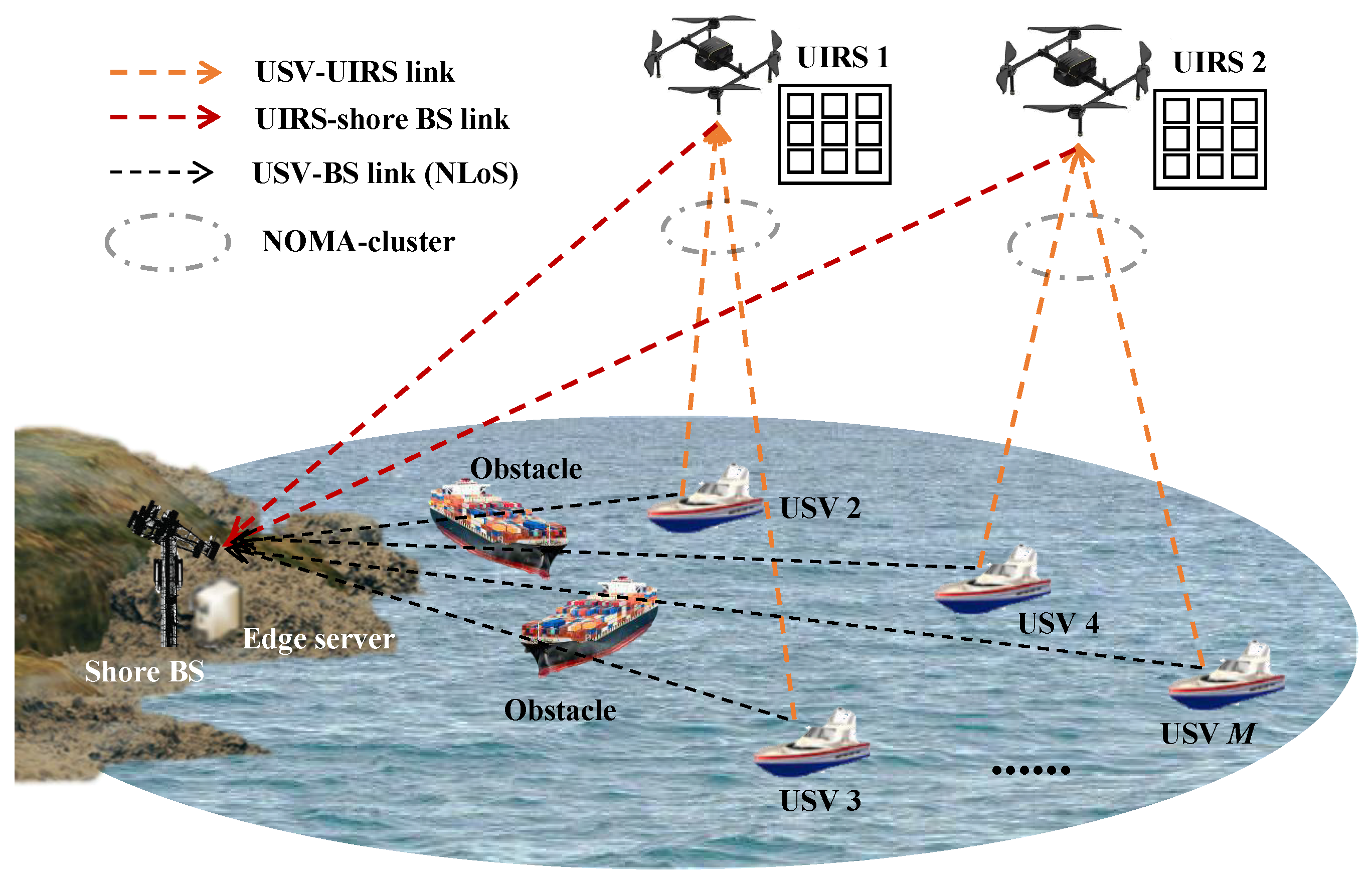
2. System Model And Problem Formulation
2.1. Network Model
2.2. Channel Model
2.3. Task Execution Model
2.4. Energy Consumption Model
2.5. Problem Formulation
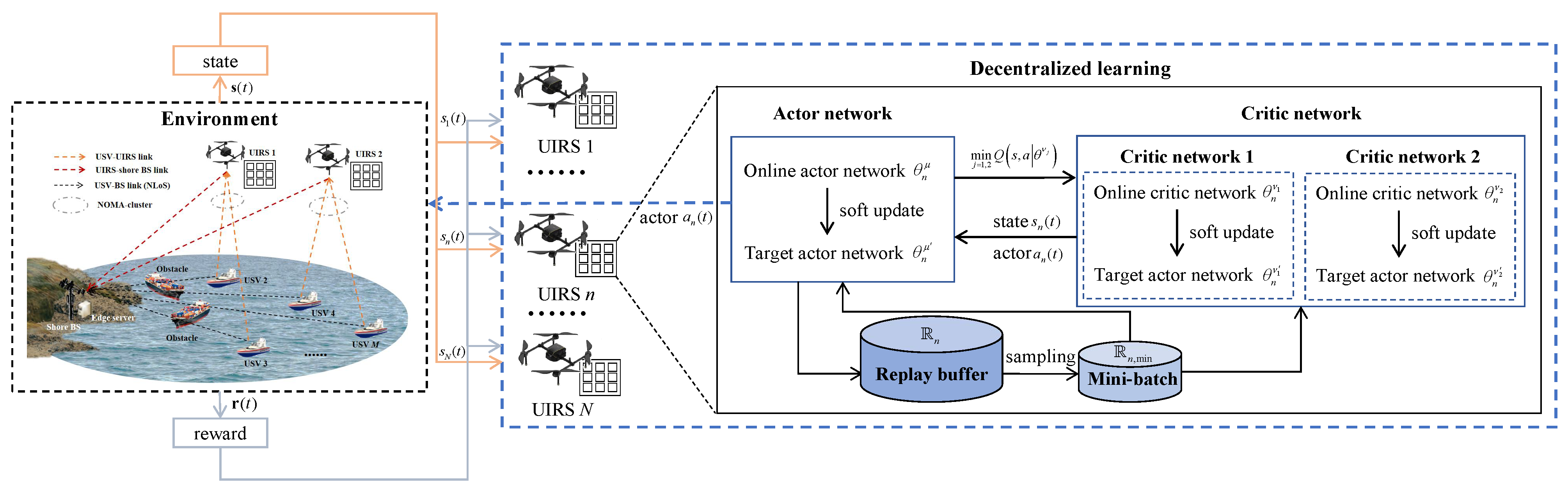
3. Proposed CO-MATD3 Algorithm
3.1. EEM-Inner Problem
3.2. EEM-Outer Problem
| Algorithm 1 CO-MATD3 algorithm for solving EEM problem. |
|
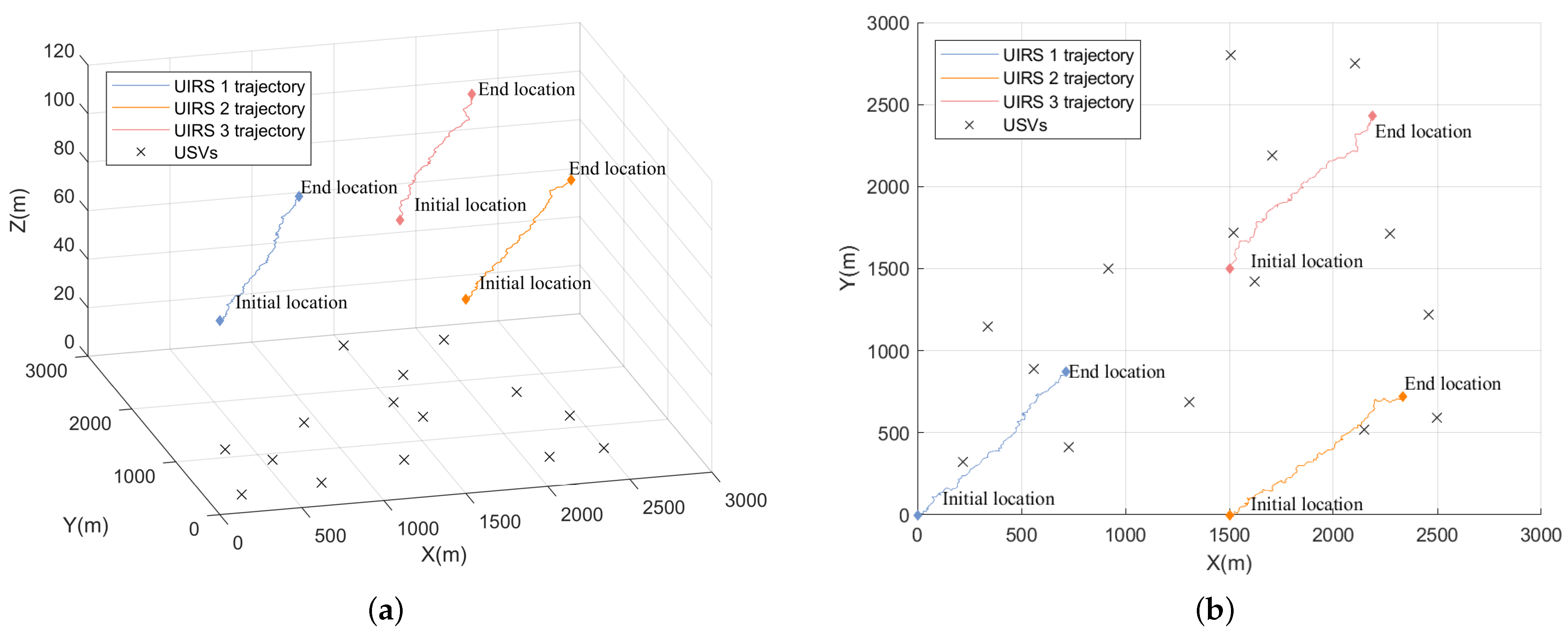
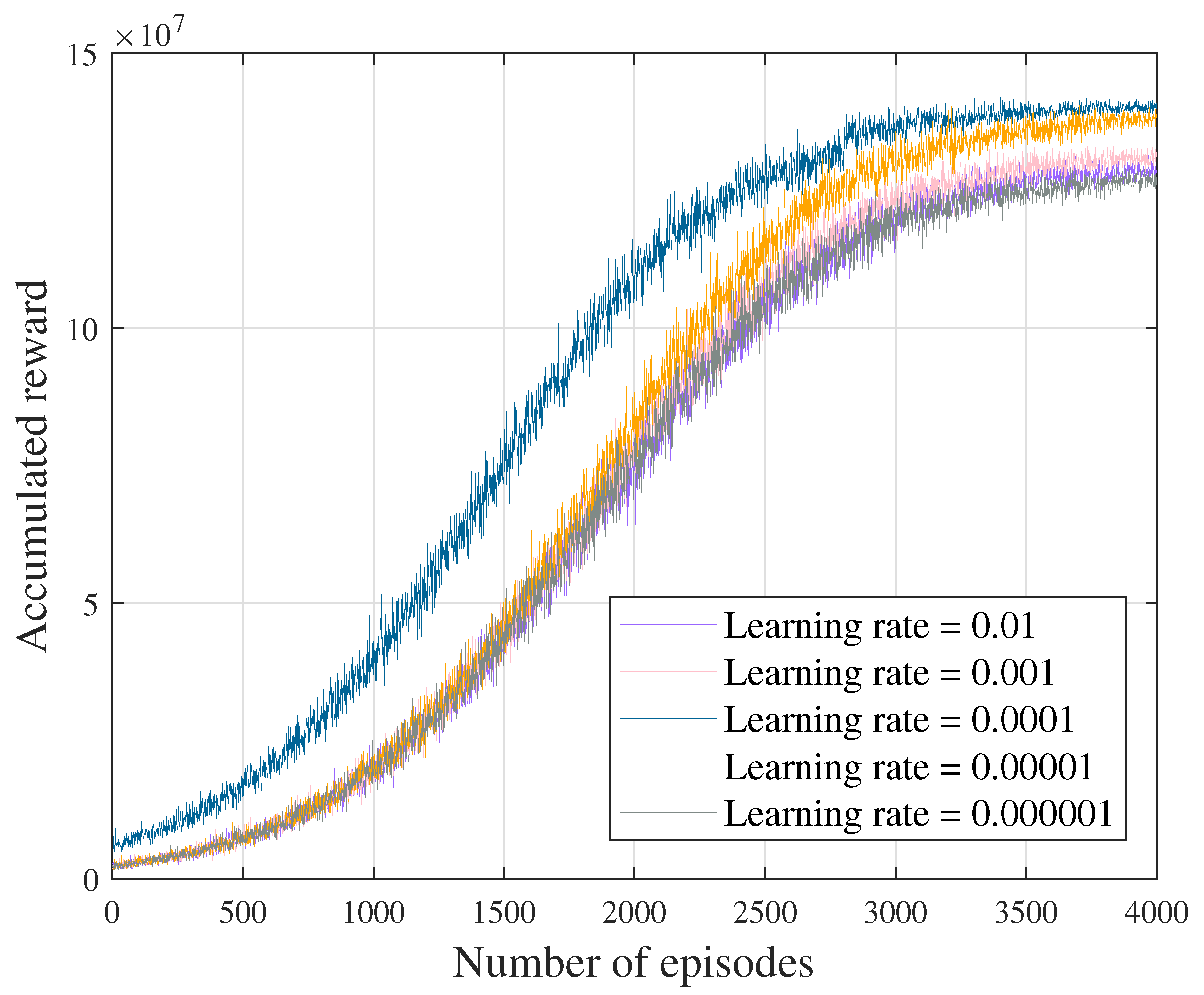
4. Numerical Results
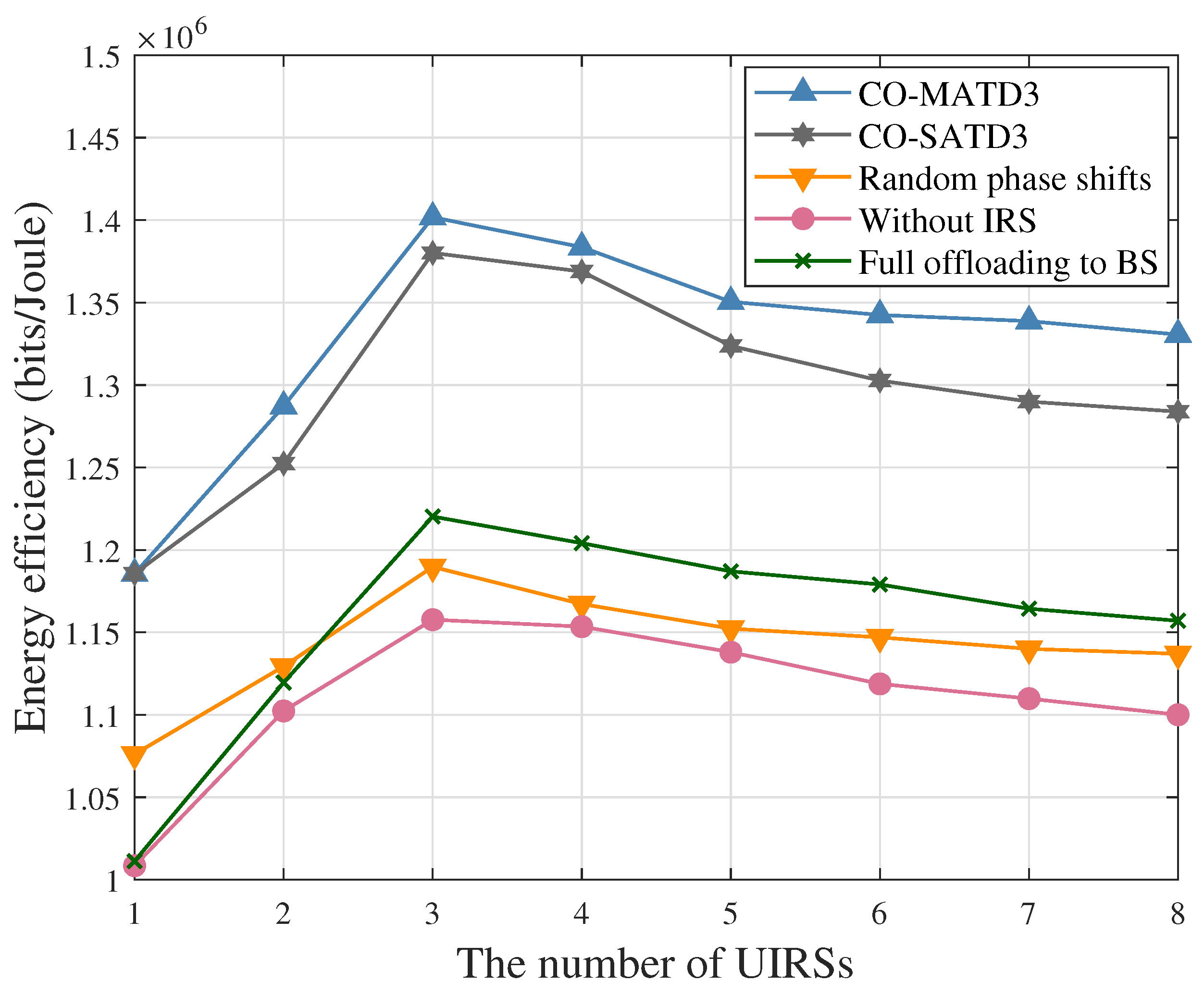
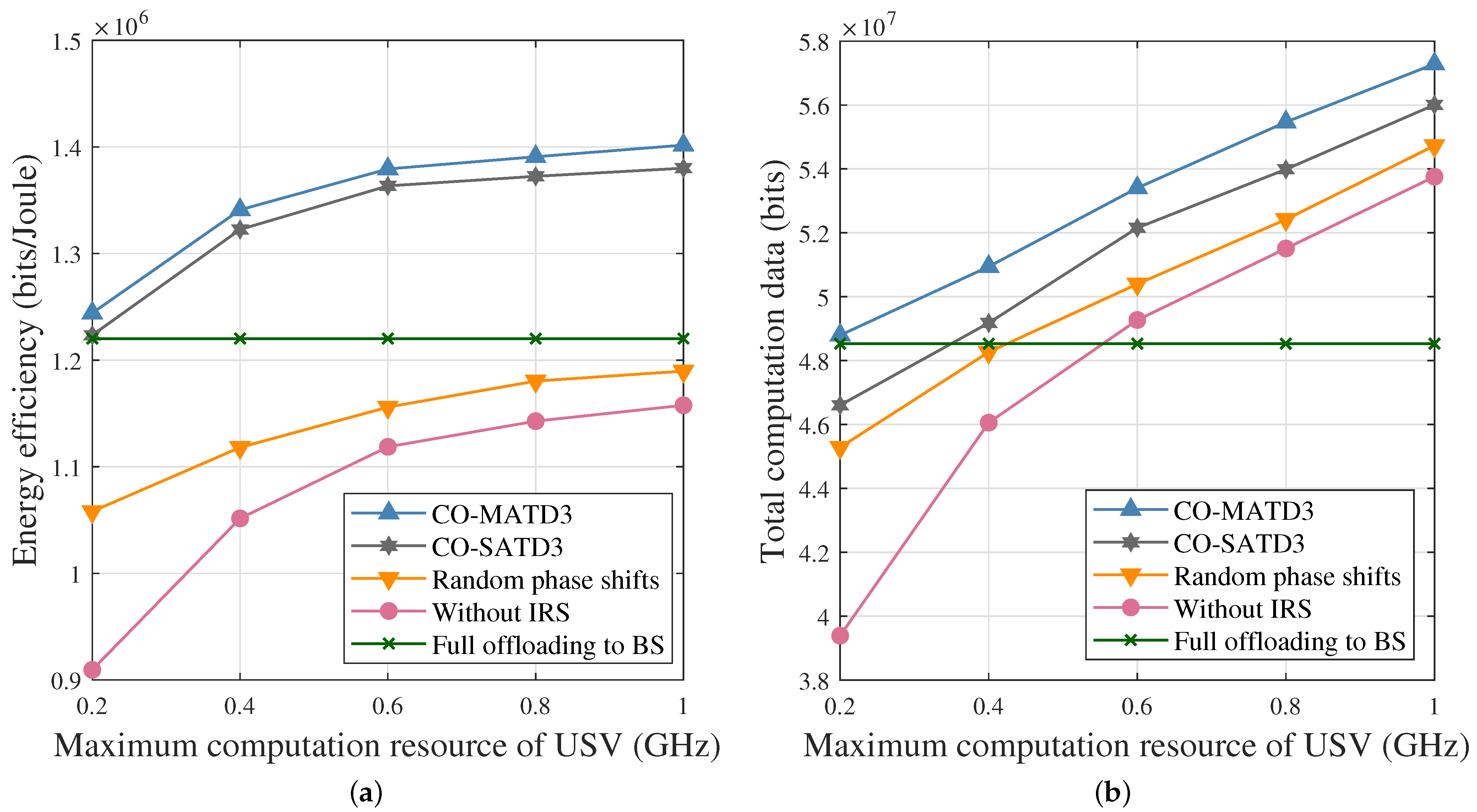
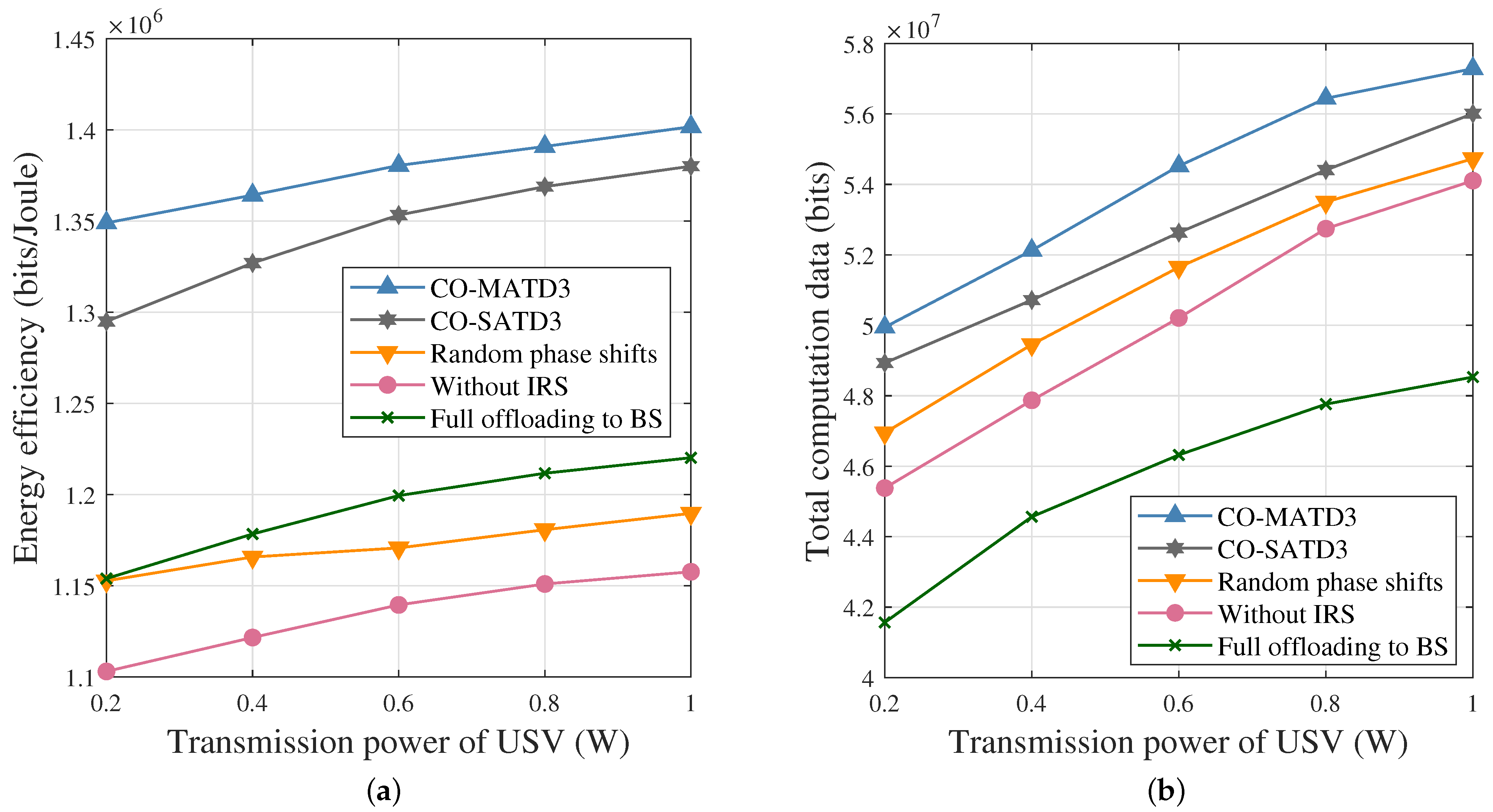
- Convex Optimization and Single-Agent TD3 (CO-SATD3). In this scheme, the SATD3 algorithm aims to optimize the EEM-Outer problem, while the EEM-Inner problem is optimized by Section 3.1. For the SATD3 algorithm, the shore BS acts as the agent to centrally manage the state and action information of USVs and UIRSs.
- Random phase shifts scheme. In this scheme, the phase shifts of the reflection elements are randomly selected in the constraint range.
- Without IRS scheme. This scheme involves a multi-UAV-assisted marine vehicle system without an IRS, in which each UAV acts as a decode-and-forward relay node to achieve data transmission from USVs to the shore BS.
- Full offloading to BS scheme. In this scheme, the computation tasks of USVs are fully offloaded to the shore BS for edge computing, while the USVs cannot process computation tasks locally.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, T.; Feng, W.; Chen, Y.; Wang, C.X.; Ge, N.; Lu, J. Hybrid satellite-terrestrial communication networks for the maritime Internet of Things: Key technologies, opportunities, and challenges. IEEE Internet Things J. 2021, 8, 8910–8934. [Google Scholar] [CrossRef]
- Xu, W.; Gu, L. UAV Relay Energy Consumption Minimization in an MEC-Assisted Marine Data Collection System. J. Mar. Sci. Eng. 2023, 11, 2333. [Google Scholar] [CrossRef]
- Su, X.; Meng, L.; Huang, J. Intelligent Maritime Networking with Edge Services and Computing Capability. IEEE Trans. Veh. Technol. 2020, 69, 13606–13620. [Google Scholar] [CrossRef]
- Dai, M.; Luo, Z.; Wu, Y.; Qian, L.; Lin, B.; Su, Z. Incentive Oriented Two-Tier Task Offloading Scheme in Marine Edge Computing Networks: A Hybrid Stackelberg-Auction Game Approach. IEEE Trans. Wirel. Commun. 2023, 22, 8603–8619. [Google Scholar] [CrossRef]
- Jung, S.; Jeong, S.; Kang, J.; Kang, J. Marine IoT Systems with Space–Air–Sea Integrated Networks: Hybrid LEO and UAV Edge Computing. IEEE Internet Things J. 2023, 10, 20498–20510. [Google Scholar] [CrossRef]
- Yang, H.; Lin, K.; Xiao, L.; Zhao, Y.; Xiong, Z.; Han, Z. Energy Harvesting UAV-RIS-Assisted Maritime Communications Based on Deep Reinforcement Learning Against Jamming. IEEE Trans. Wirel. Commun. 2024, 23, 9854–9868. [Google Scholar] [CrossRef]
- Dai, M.; Dou, C.; Wu, Y.; Qian, L.; Lu, R.; Quek, T.Q.S. Multi-UAV Aided Multi-Access Edge Computing in Marine Communication Networks: A Joint System-Welfare and Energy-Efficient Design. IEEE Trans. Commun. 2024, 72, 5517–5531. [Google Scholar] [CrossRef]
- Cai, Y.; Wei, Z.; Hu, S.; Liu, C.; Ng, D.W.K.; Yuan, J. Resource Allocation and 3D Trajectory Design for Power-Efficient IRS-Assisted UAV-NOMA Communications. IEEE Trans. Wirel. Commun. 2022, 21, 10315–10334. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Joint Active and Passive Beamforming Optimization for Intelligent Reflecting Surface Assisted SWIPT Under QoS Constraints. IEEE J. Sel. Areas Commun. 2020, 38, 1735–1748. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, L.; Cai, S.; Lian, Z.; Su, Y.; Xie, Z. Low-Complexity Algorithm for Maximizing the Weighted Sum-Rate of Intelligent Reflecting Surface-Assisted Wireless Networks. IEEE Internet Things J. 2024, 11, 10490–10499. [Google Scholar] [CrossRef]
- Xu, W.; Gu, L. Energy-Efficient Resource Optimization for IRS-Assisted VLC-Enabled Offshore Communication System. J. Mar. Sci. Eng. 2024, 12, 772. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Zhu, Y.; Mao, B.; Kato, N. A Dynamic Task Scheduling Strategy for Multi-Access Edge Computing in IRS-Aided Vehicular Networks. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1761–1771. [Google Scholar] [CrossRef]
- Li, Z.; Chen, M.; Yang, Z.; Zhao, J.; Wang, Y.; Shi, J.; Huang, C. Energy Efficient Reconfigurable Intelligent Surface Enabled Mobile Edge Computing Networks with NOMA. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 427–440. [Google Scholar] [CrossRef]
- Li, Y.; Wang, F.; Zhang, X.; Guo, S. IRS-Based MEC for Delay-Constrained QoS Over RF-Powered 6G Mobile Wireless Networks. IEEE Trans. Veh. Technol. 2023, 72, 8722–8737. [Google Scholar] [CrossRef]
- Chen, G.; Wu, Q.; Liu, R.; Wu, J.; Fang, C. IRS Aided MEC Systems with Binary Offloading: A Unified Framework for Dynamic IRS Beamforming. IEEE J. Sel. Areas Commun. 2023, 41, 349–365. [Google Scholar] [CrossRef]
- Yang, Y.; Gong, Y.; Wu, Y.C. Intelligent-Reflecting-Surface-Aided Mobile Edge Computing with Binary Offloading: Energy Minimization for IoT Devices. IEEE Internet Things J. 2022, 9, 12973–12983. [Google Scholar] [CrossRef]
- Aung, P.S.; Park, Y.M.; Tun, Y.K.; Han, Z.; Hong, C.S. Energy-Efficient Communication Networks via Multiple Aerial Reconfigurable Intelligent Surfaces: DRL and Optimization Approach. IEEE Trans. Veh. Technol. 2023, 73, 4277–4292. [Google Scholar] [CrossRef]
- Wang, C.; Chen, X.; An, J.; Xiong, Z.; Xing, C.; Zhao, N.; Niyato, D. Covert Communication Assisted by UAV-IRS. IEEE Trans. Commun. 2023, 71, 357–369. [Google Scholar] [CrossRef]
- Lu, H.; Zeng, Y.; Jin, S.; Zhang, R. Aerial Intelligent Reflecting Surface: Joint Placement and Passive Beamforming Design with 3D Beam Flattening. IEEE Trans. Wirel. Commun. 2021, 20, 4128–4143. [Google Scholar] [CrossRef]
- Truong, T.P.; Tuong, V.D.; Dao, N.N.; Cho, S. FlyReflect: Joint Flying IRS Trajectory and Phase Shift Design Using Deep Reinforcement Learning. IEEE Internet Things J. 2023, 10, 4605–4620. [Google Scholar] [CrossRef]
- Zhai, Z.; Dai, X.; Duo, B.; Wang, X.; Yuan, X. Energy-Efficient UAV-Mounted RIS Assisted Mobile Edge Computing. IEEE Wirel. Commun. Lett. 2022, 11, 2507–2511. [Google Scholar] [CrossRef]
- Ai, Q.; Qiao, X.; Liao, Y.; Yu, Q. Joint Optimization of USVs Communication and Computation Resource in IRS-Aided Wireless Inland Ship MEC Networks. IEEE Trans. Green Commun. Netw. 2022, 6, 1023–1036. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Long, K.; Nallanathan, A. Exploring Sum Rate Maximization in UAV-Based Multi-IRS Networks: IRS Association, UAV Altitude, and Phase Shift Design. IEEE Trans. Commun. 2022, 70, 7764–7774. [Google Scholar] [CrossRef]
- Li, Z.; Hua, M.; Wang, Q.; Song, Q. Weighted Sum-Rate Maximization for Multi-IRS Aided Cooperative Transmission. IEEE Wirel. Commun. Lett. 2020, 9, 1620–1624. [Google Scholar] [CrossRef]
- Rafieifar, A.; Ahmadinejad, H.; Razavizadeh, S.M.; He, J. Secure Beamforming in Multi-User Multi-IRS Millimeter Wave Systems. IEEE Trans. Wirel. Commun. 2023, 22, 6140–6156. [Google Scholar] [CrossRef]
- Pan, H.; Liu, Y.; Sun, G.; Wang, P.; Yuen, C. Resource Scheduling for UAVs-Aided D2D Networks: A Multi-Objective Optimization Approach. IEEE Trans. Wirel. Commun. 2024, 23, 4691–4708. [Google Scholar] [CrossRef]
- Deng, X.; Zhao, J.; Kuang, Z.; Chen, X.; Guo, Q.; Tang, F. Computation Efficiency Maximization in Multi-UAV-Enabled Mobile Edge Computing Systems Based on 3D Deployment Optimization. IEEE Trans. Emerg. Top. Comput. 2023, 11, 778–790. [Google Scholar] [CrossRef]
- Duo, B.; He, M.; Wu, Q.; Zhang, Z. Joint Dual-UAV Trajectory and RIS Design for ARIS-Assisted Aerial Computing in IoT. IEEE Internet Things J. 2023, 10, 19584–19594. [Google Scholar] [CrossRef]
- Waraiet, A.; Cumanan, K.; Ding, Z.; Dobre, O.A. Robust Design for IRS-Assisted MISO-NOMA Systems: A DRL-Based Approach. IEEE Wirel. Commun. Lett. 2024, 13, 592–596. [Google Scholar] [CrossRef]
- Zhang, T.; Wen, H.; Jiang, Y.; Tang, J. Deep-Reinforcement-Learning-Based IRS for Cooperative Jamming Networks Under Edge Computing. IEEE Internet Things J. 2023, 10, 8996–9006. [Google Scholar] [CrossRef]
- Zhan, C.; Hu, H.; Liu, Z.; Wang, Z.; Mao, S. Multi-UAV-Enabled Mobile-Edge Computing for Time-Constrained IoT Applications. IEEE Internet Things J. 2021, 8, 15553–15567. [Google Scholar] [CrossRef]
- Qin, X.; Na, Z.; Wen, Z.; Wu, X. Relaying IRS-UAV Assisted Covert Communications in Uplink C-NOMA Network. IEEE Commun. Lett. 2024, 28, 2136–2140. [Google Scholar] [CrossRef]
- Yu, J.; Li, Y.; Liu, X.; Sun, B.; Wu, Y.; Hin-Kwok Tsang, D. IRS Assisted NOMA Aided Mobile Edge Computing with Queue Stability: Heterogeneous Multi-Agent Reinforcement Learning. IEEE Trans. Wirel. Commun. 2023, 22, 4296–4312. [Google Scholar] [CrossRef]
- Mei, H.; Yang, K.; Liu, Q.; Wang, K. 3D-Trajectory and Phase-Shift Design for RIS-Assisted UAV Systems Using Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2022, 71, 3020–3029. [Google Scholar] [CrossRef]
- Zhao, T.; Li, F.; He, L. DRL-Based Secure Aggregation and Resource Orchestration in MEC-Enabled Hierarchical Federated Learning. IEEE Internet Things J. 2023, 10, 17865–17880. [Google Scholar] [CrossRef]
- Zhang, R.; Pang, X.; Lu, W.; Zhao, N.; Chen, Y.; Niyato, D. Dual-UAV Enabled Secure Data Collection with Propulsion Limitation. IEEE Trans. Wirel. Commun. 2021, 20, 7445–7459. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication with Rotary-Wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Pan, H.; Liu, Y.; Sun, G.; Fan, J.; Liang, S.; Yuen, C. Joint Power and 3D Trajectory Optimization for UAV-Enabled Wireless Powered Communication Networks with Obstacles. IEEE Trans. Commun. 2023, 71, 2364–2380. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| The number of reflecting elements on the UIRS n, | 10 |
| Time slot length, | 1 s |
| Channel bandwidth, W | 1 MHz |
| Channel gain at the reference distance, | dB |
| Noise power, | dBm |
| The Rician factor, | [6] |
| The antenna height of the USV m, | 5 m |
| The antenna height of the shore BS, | 35 m |
| Transmission power of the USV m, | 1 W |
| The maximum computation resources of the USV m, | 1 GHz |
| The CPU cycles required to process one bit of USV m, | 1000 cycles/bit |
| The effective switched capacitance of the USV m, | |
| The power of each reflecting element on the UIRS n, | W [34] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Lin, B.; Li, C.; Qi, S. Energy Efficiency Maximization for Multi-UAV-IRS-Assisted Marine Vehicle Systems. J. Mar. Sci. Eng. 2024, 12, 1761. https://doi.org/10.3390/jmse12101761
Zhang C, Lin B, Li C, Qi S. Energy Efficiency Maximization for Multi-UAV-IRS-Assisted Marine Vehicle Systems. Journal of Marine Science and Engineering. 2024; 12(10):1761. https://doi.org/10.3390/jmse12101761
Chicago/Turabian StyleZhang, Chaoyue, Bin Lin, Chao Li, and Shuang Qi. 2024. "Energy Efficiency Maximization for Multi-UAV-IRS-Assisted Marine Vehicle Systems" Journal of Marine Science and Engineering 12, no. 10: 1761. https://doi.org/10.3390/jmse12101761
APA StyleZhang, C., Lin, B., Li, C., & Qi, S. (2024). Energy Efficiency Maximization for Multi-UAV-IRS-Assisted Marine Vehicle Systems. Journal of Marine Science and Engineering, 12(10), 1761. https://doi.org/10.3390/jmse12101761






