Design and Performance Evaluation of an Enclosed Inertial Wave Energy Converter with a Nonlinear Stiffness Mechanism
Abstract
1. Introduction
2. Schematic Design and Modeling
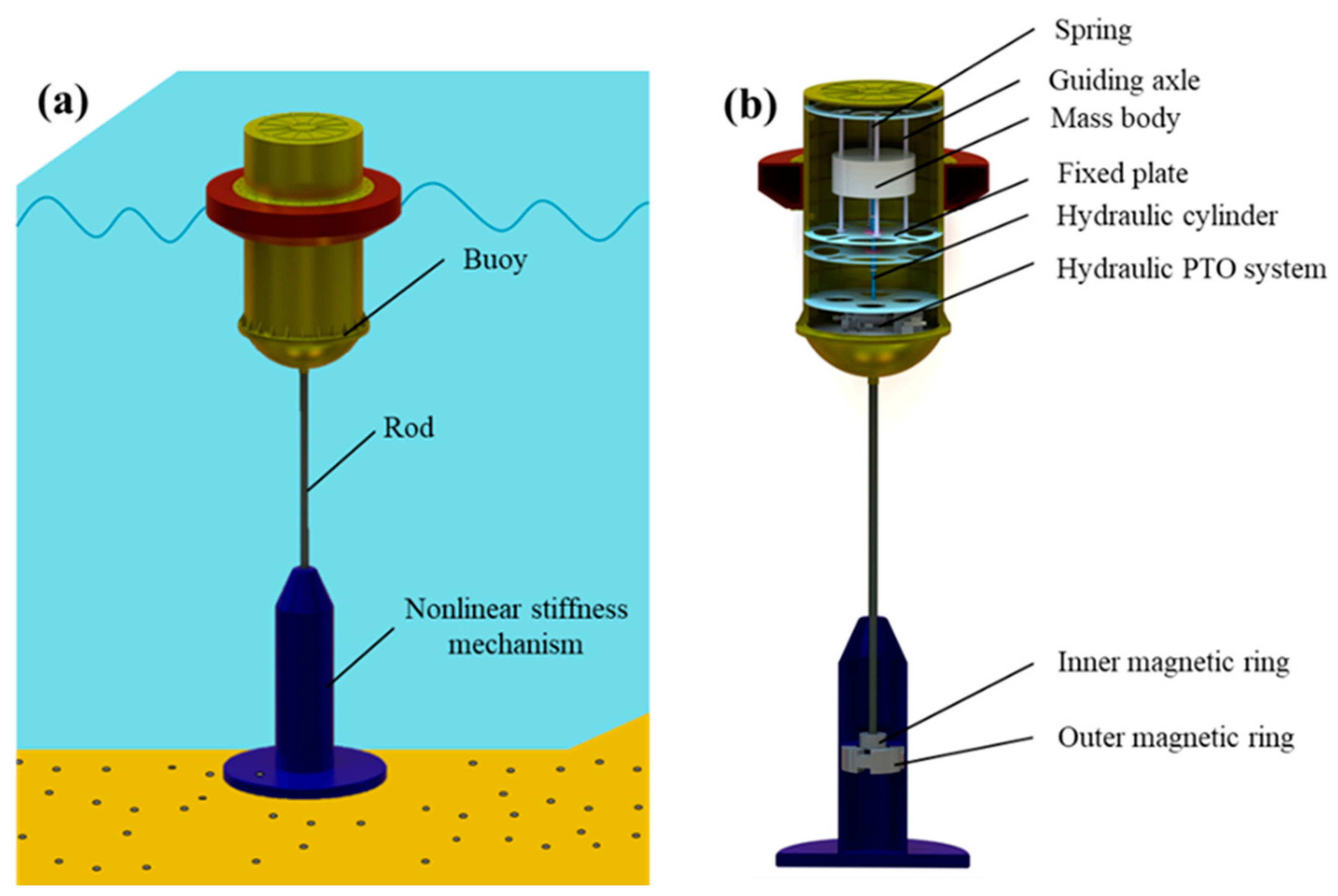
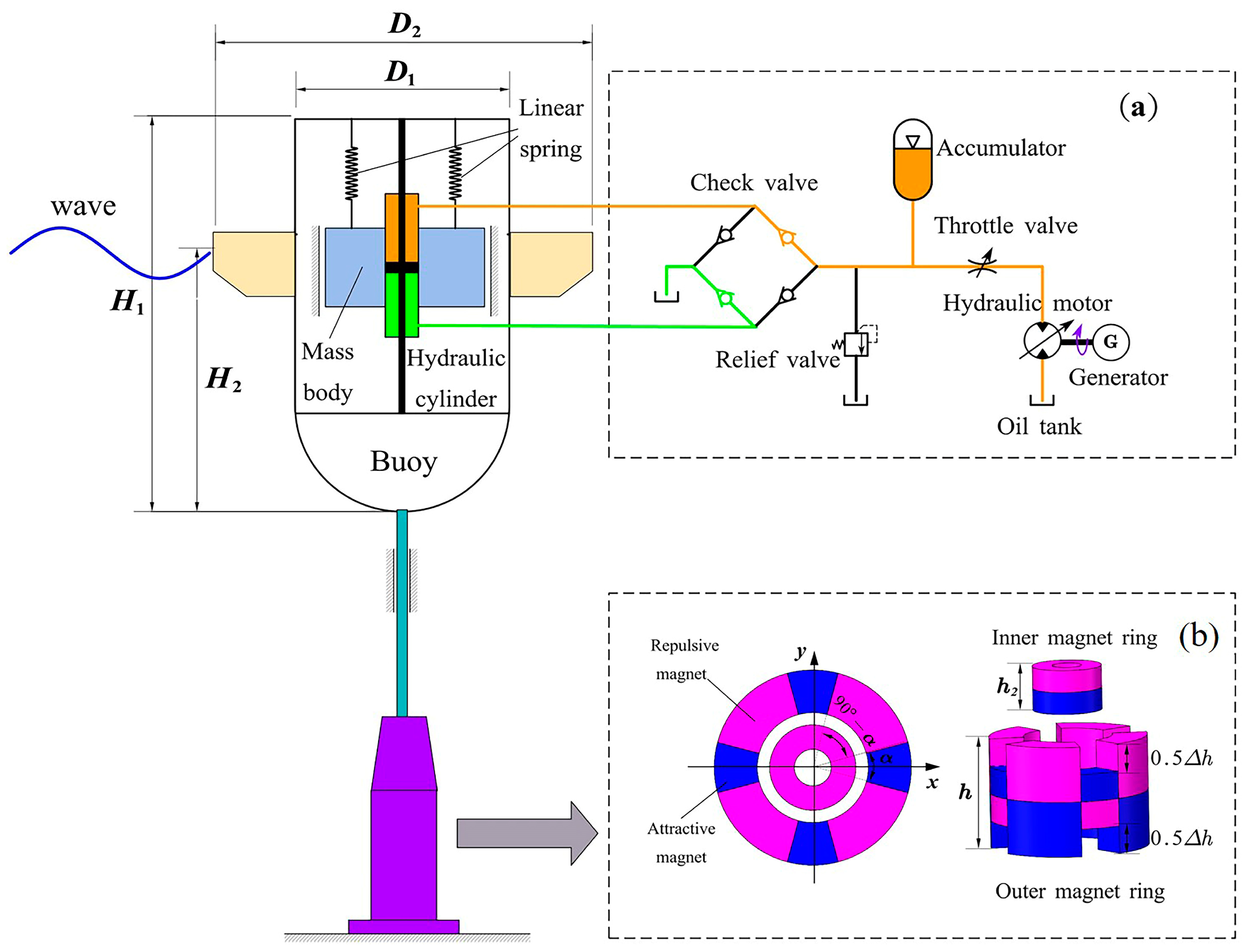
2.1. Schematic Design
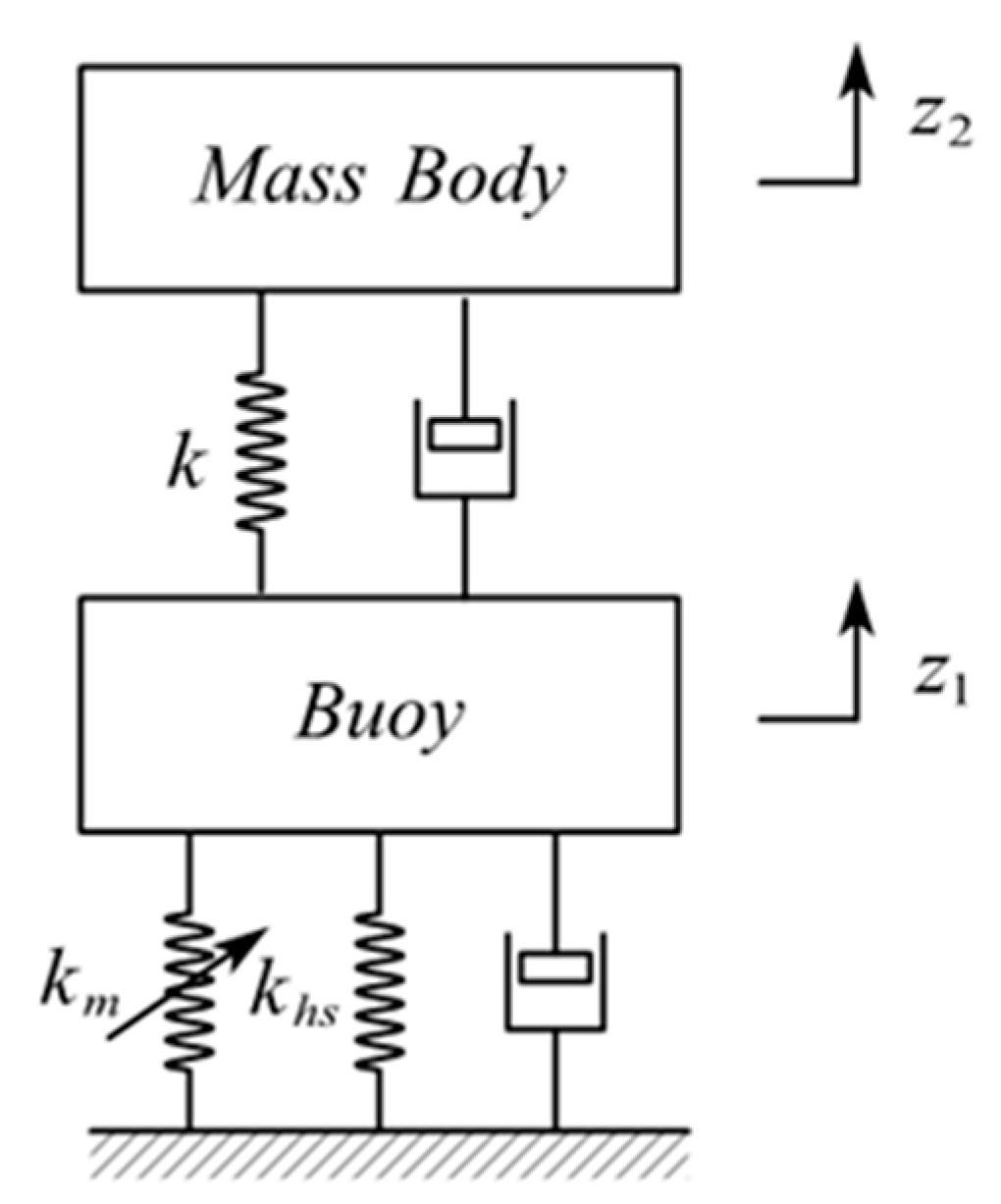
2.2. Mathematical Modeling
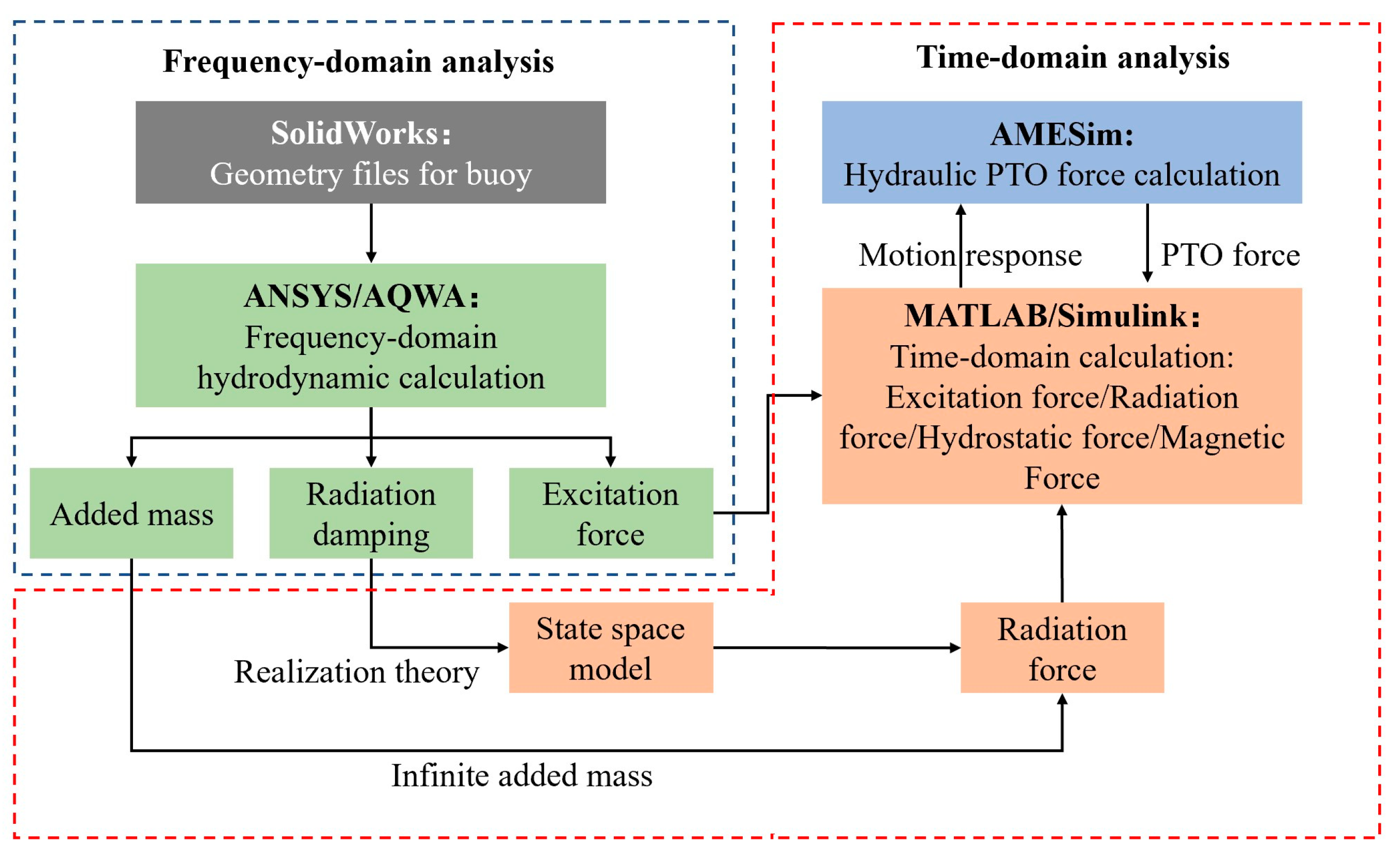
2.3. Software Application and Configuration
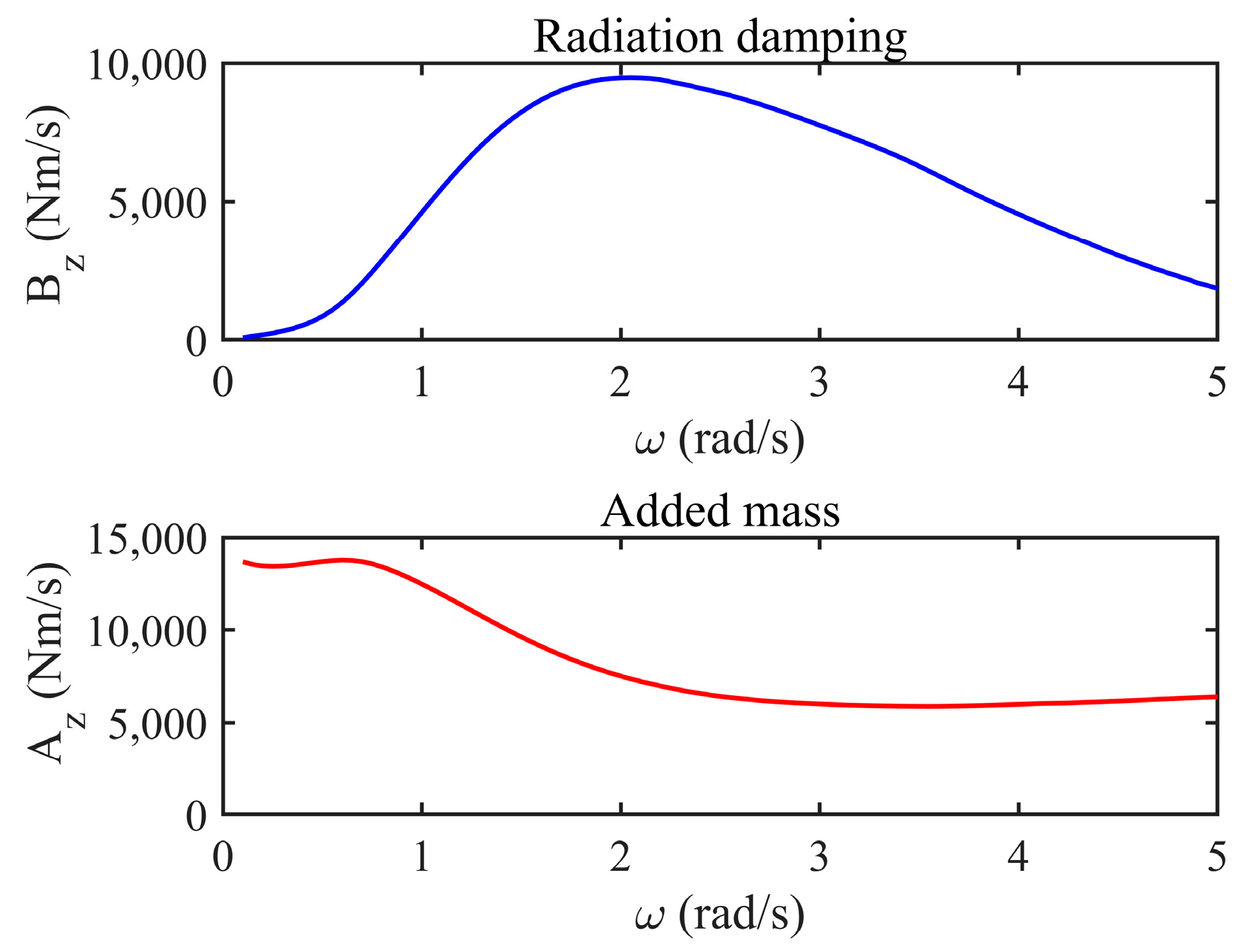
2.4. Validation of the Time-Domain Model
3. Results and Discussion
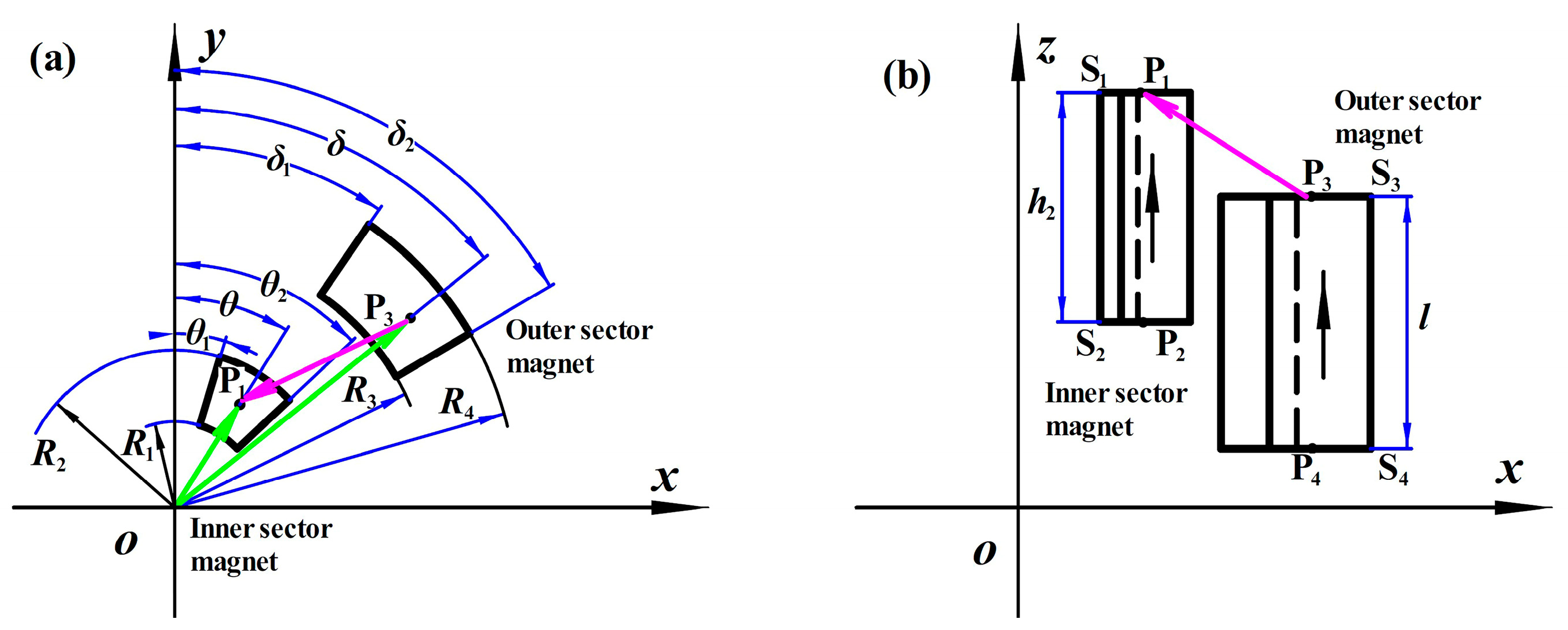
3.1. Mechanical Property Analysis of NSM
3.1.1. Structural Parameters
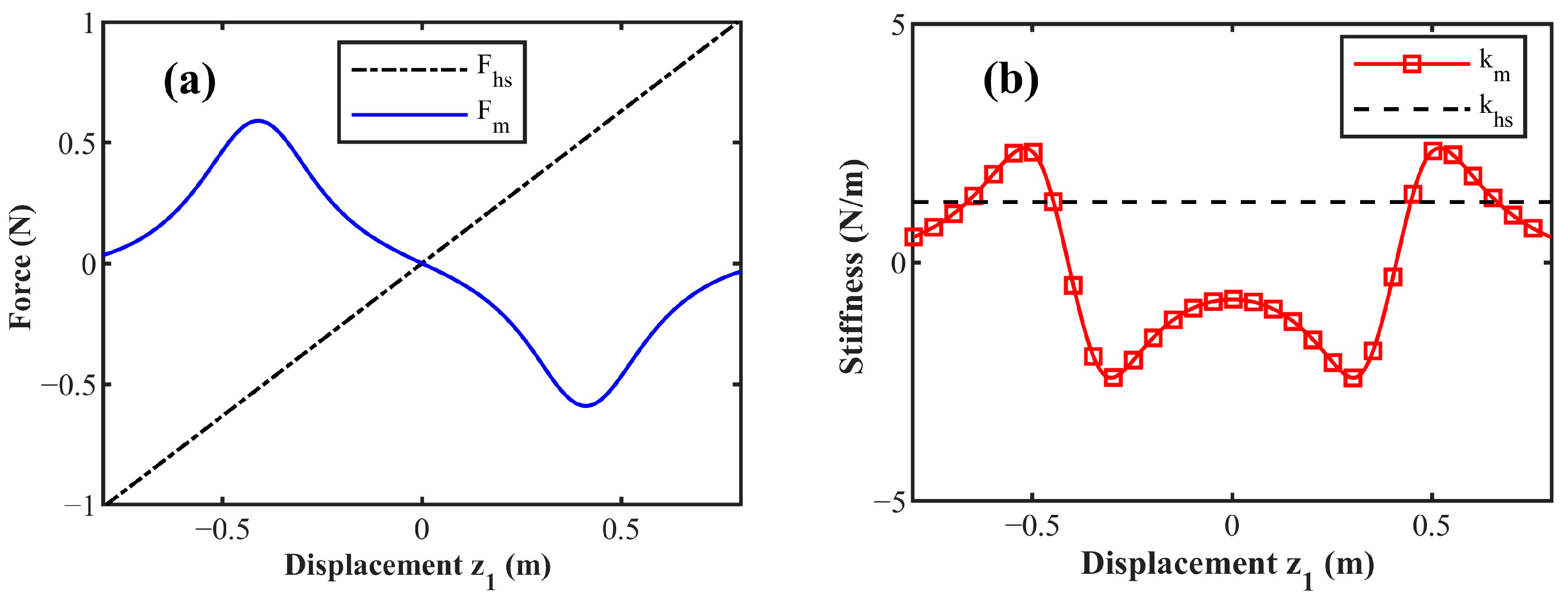
3.1.2. Magnetic Force and Stiffness of NSM
3.2. Effect of Nonlinear Stiffness Mechanism (NSM)
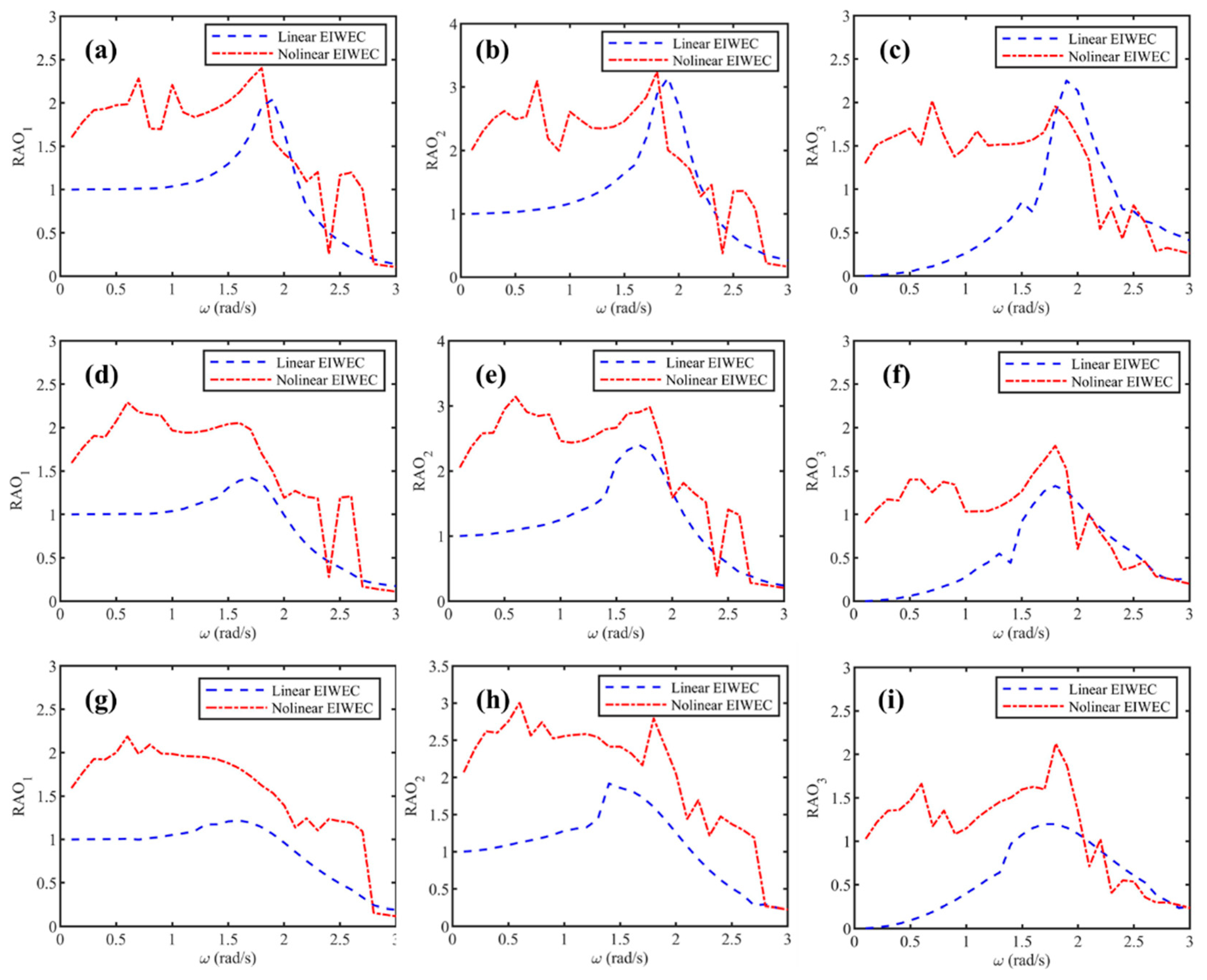
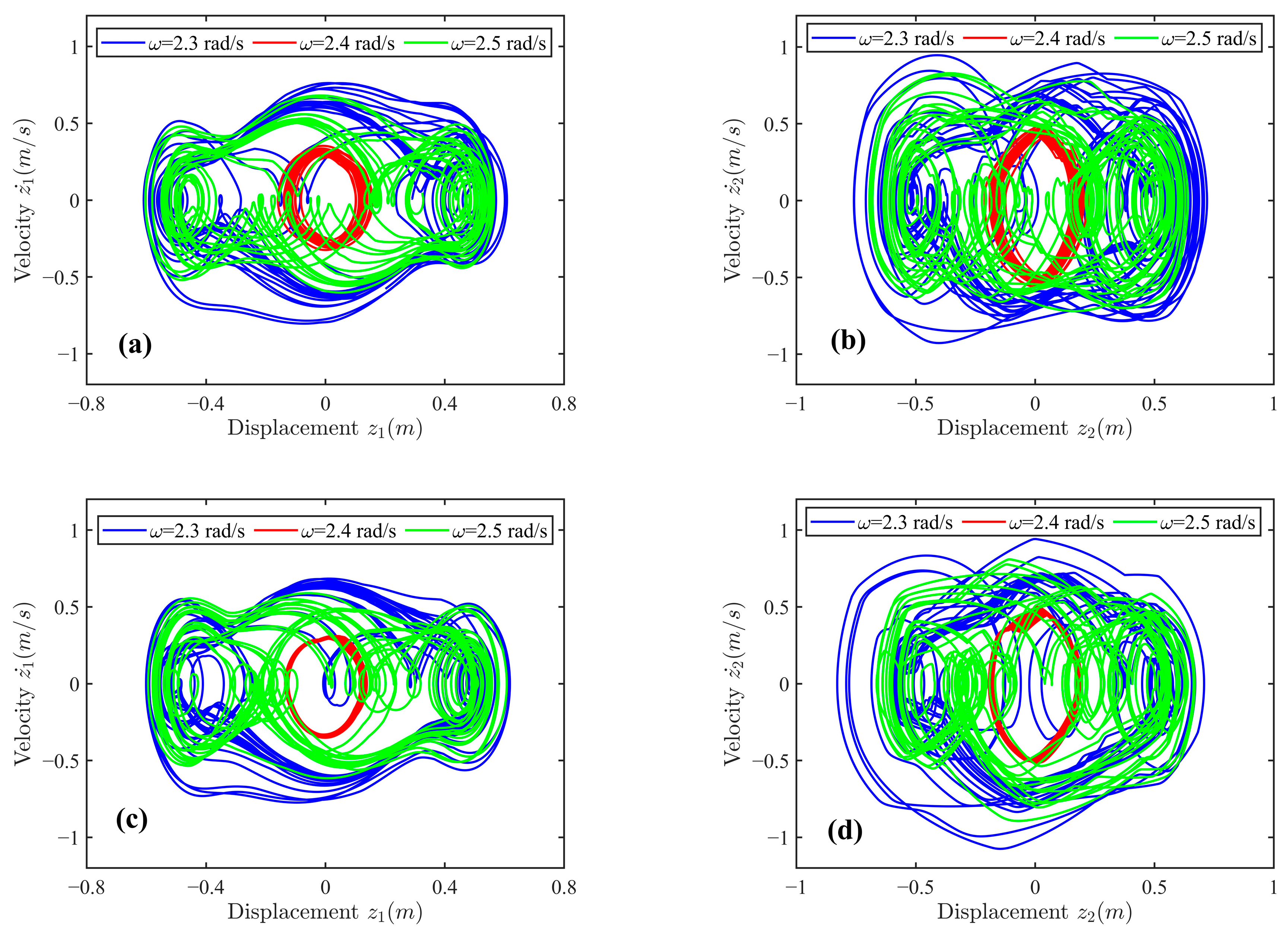
3.2.1. Motion Response Analysis
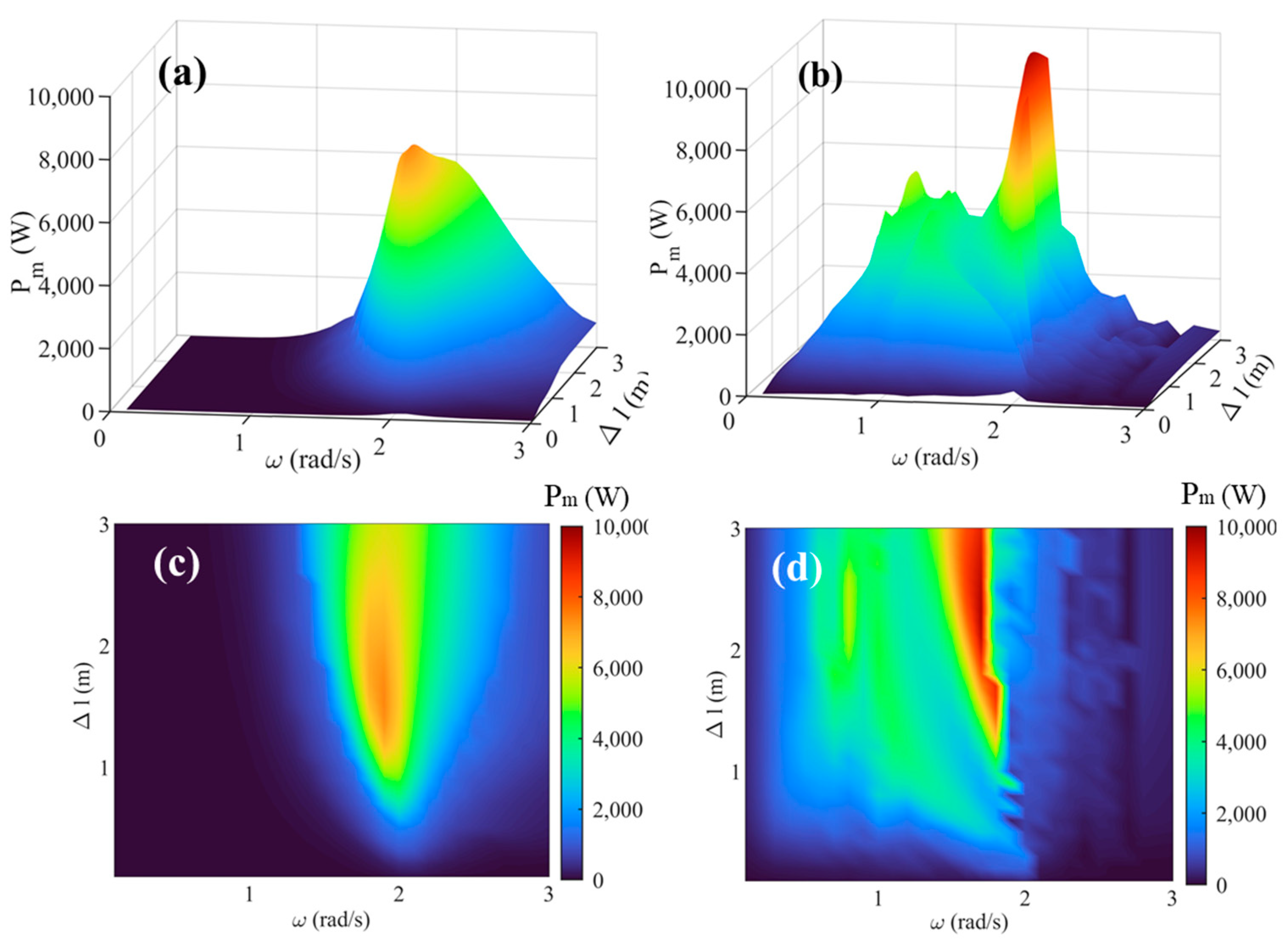
3.2.2. Output Power Analysis
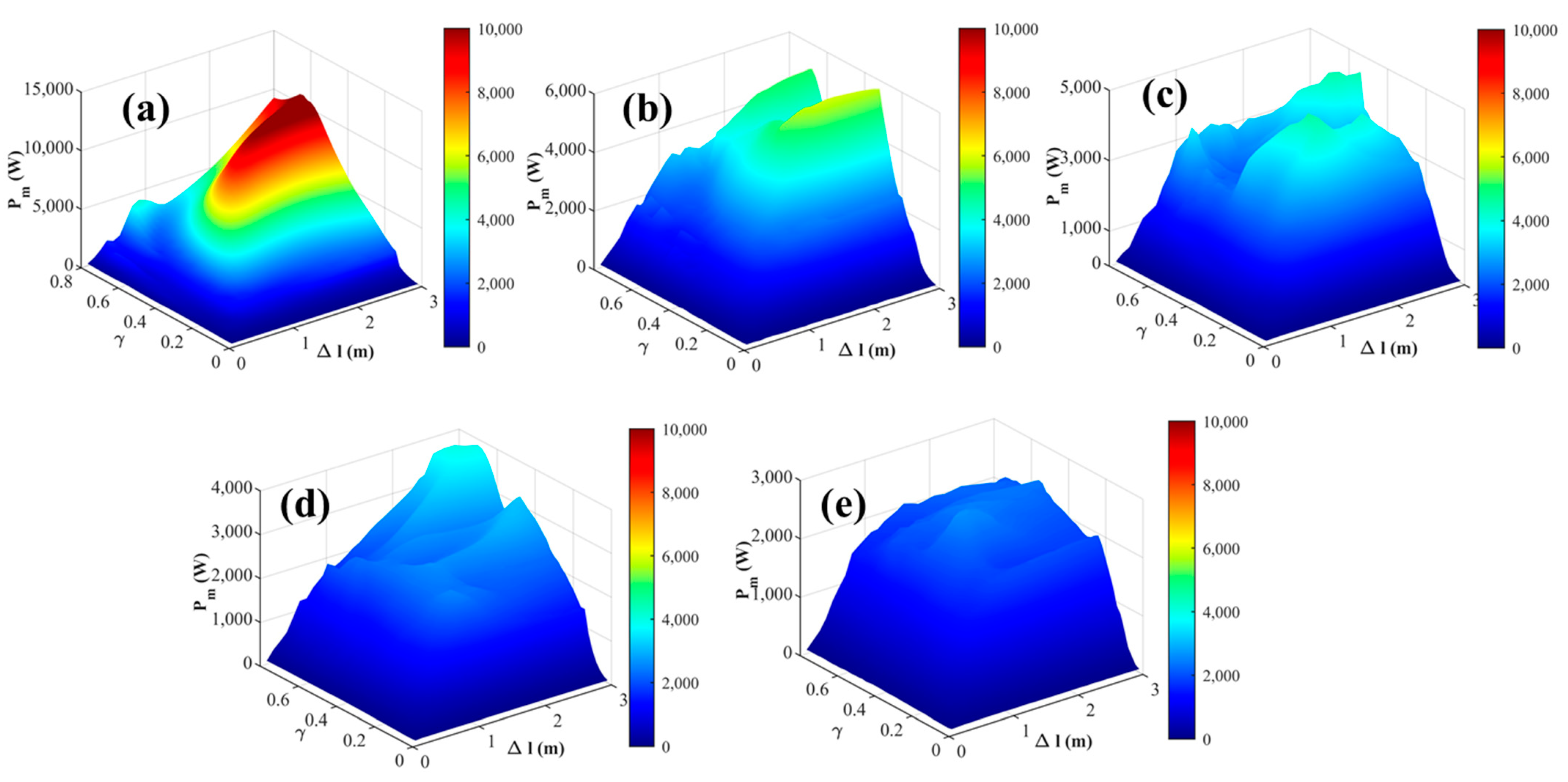
3.3. Effect of Mass Body and Linear Spring
3.4. Influence of Hydraulic PTO Parameters
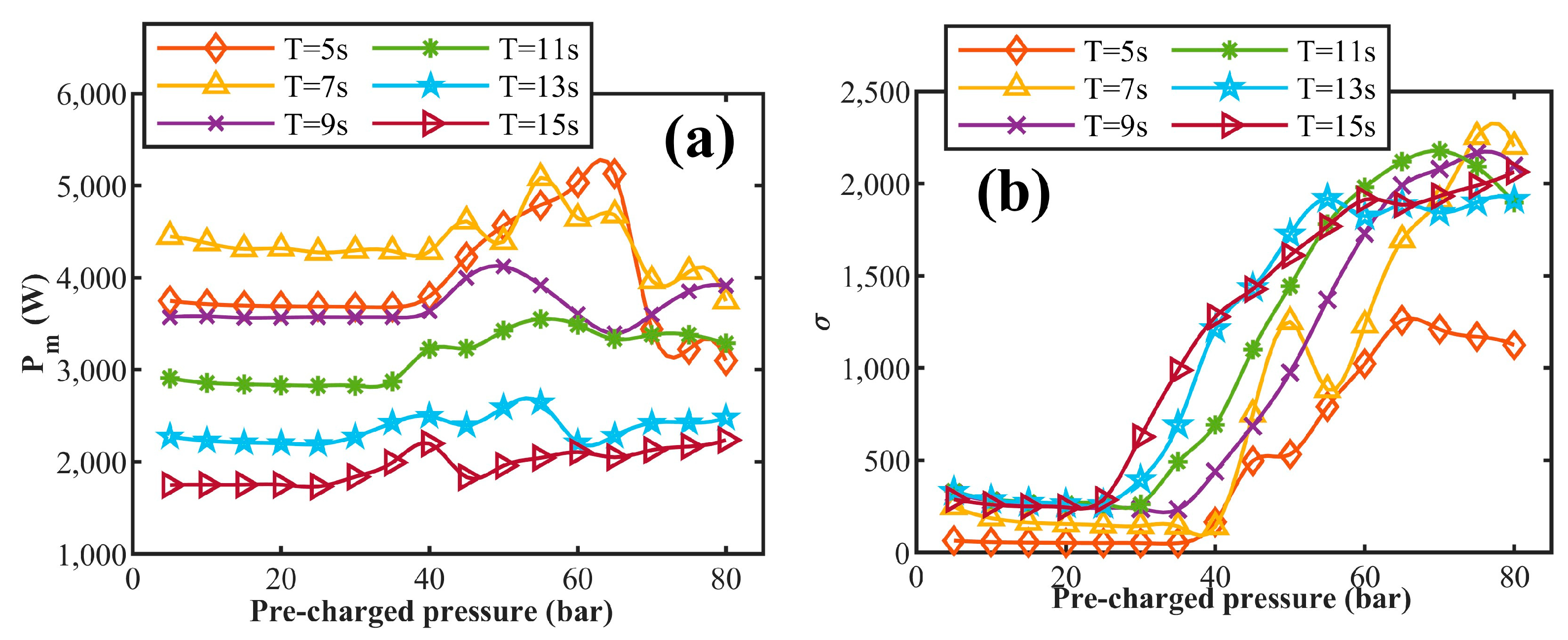
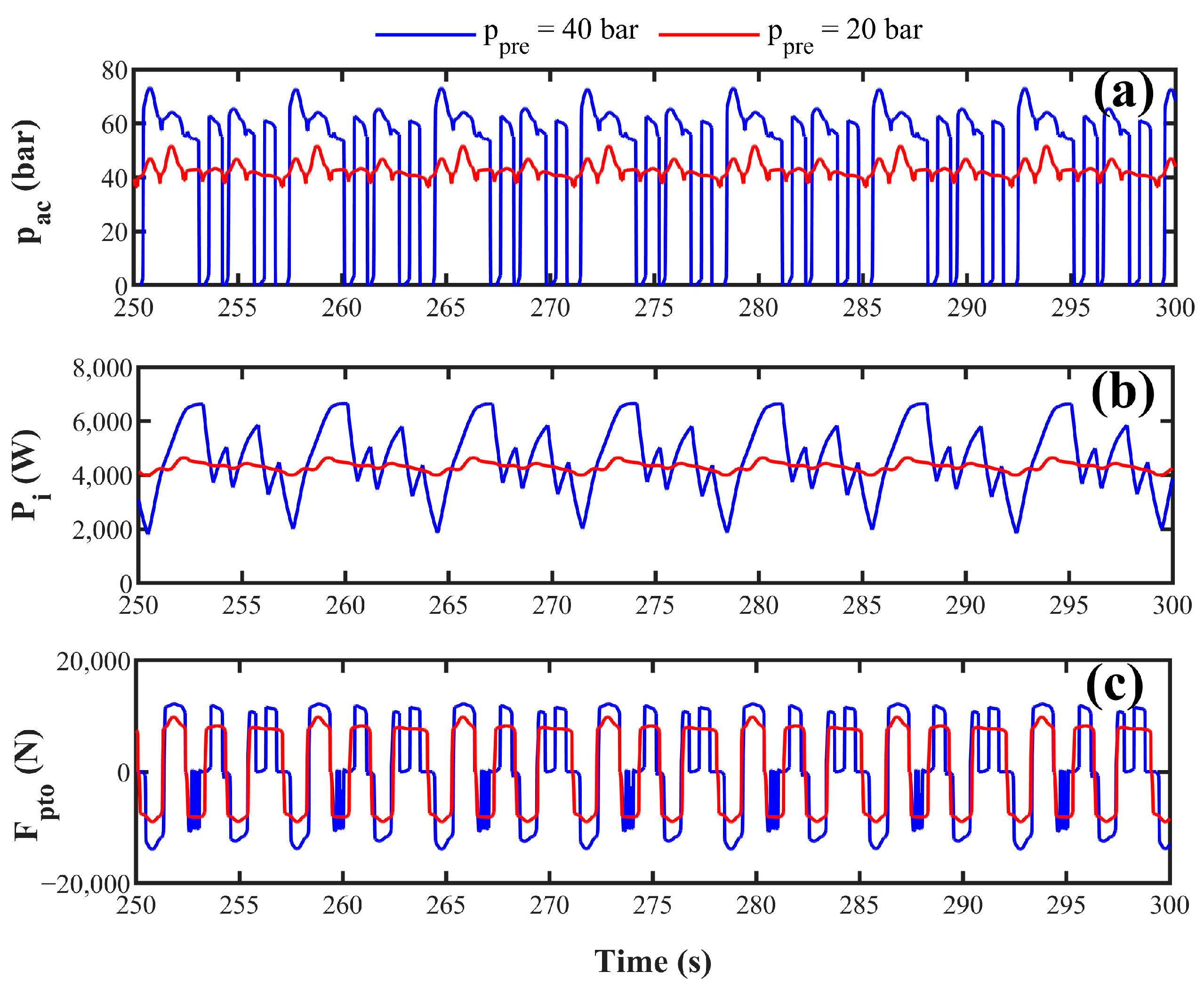
3.4.1. Effect of Pre-Charged Pressure of Accumulator
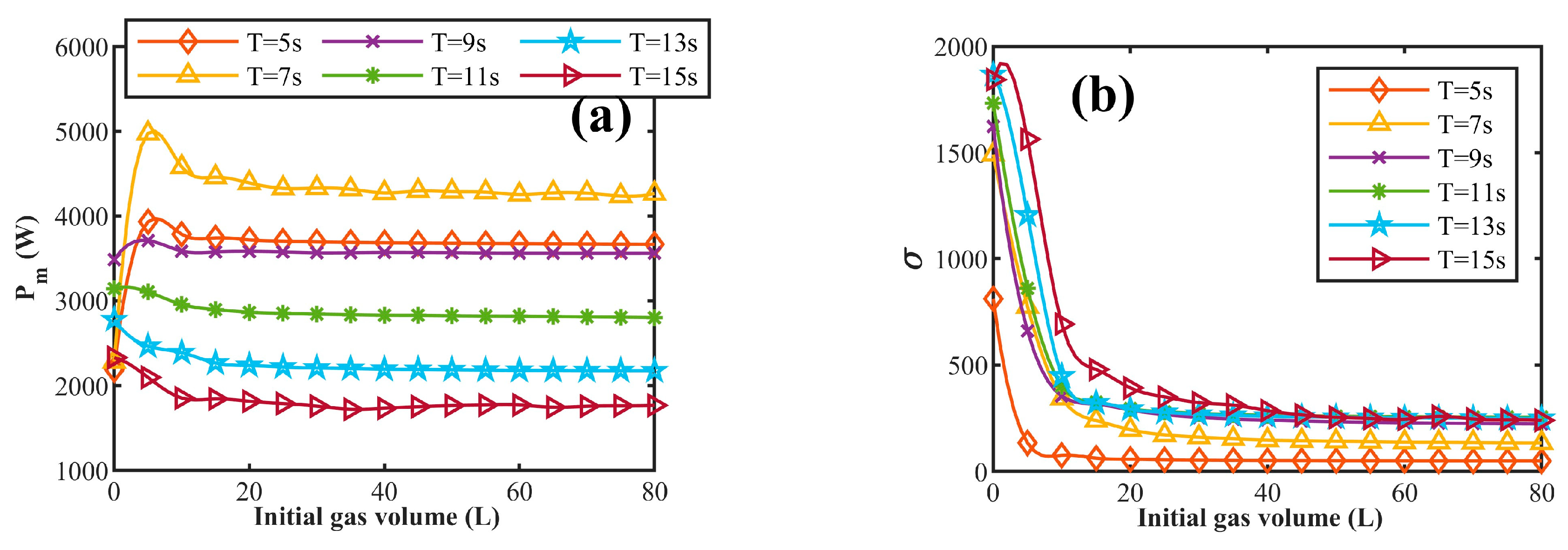
3.4.2. Effect of the Initial Gas Volume of the Accumulator
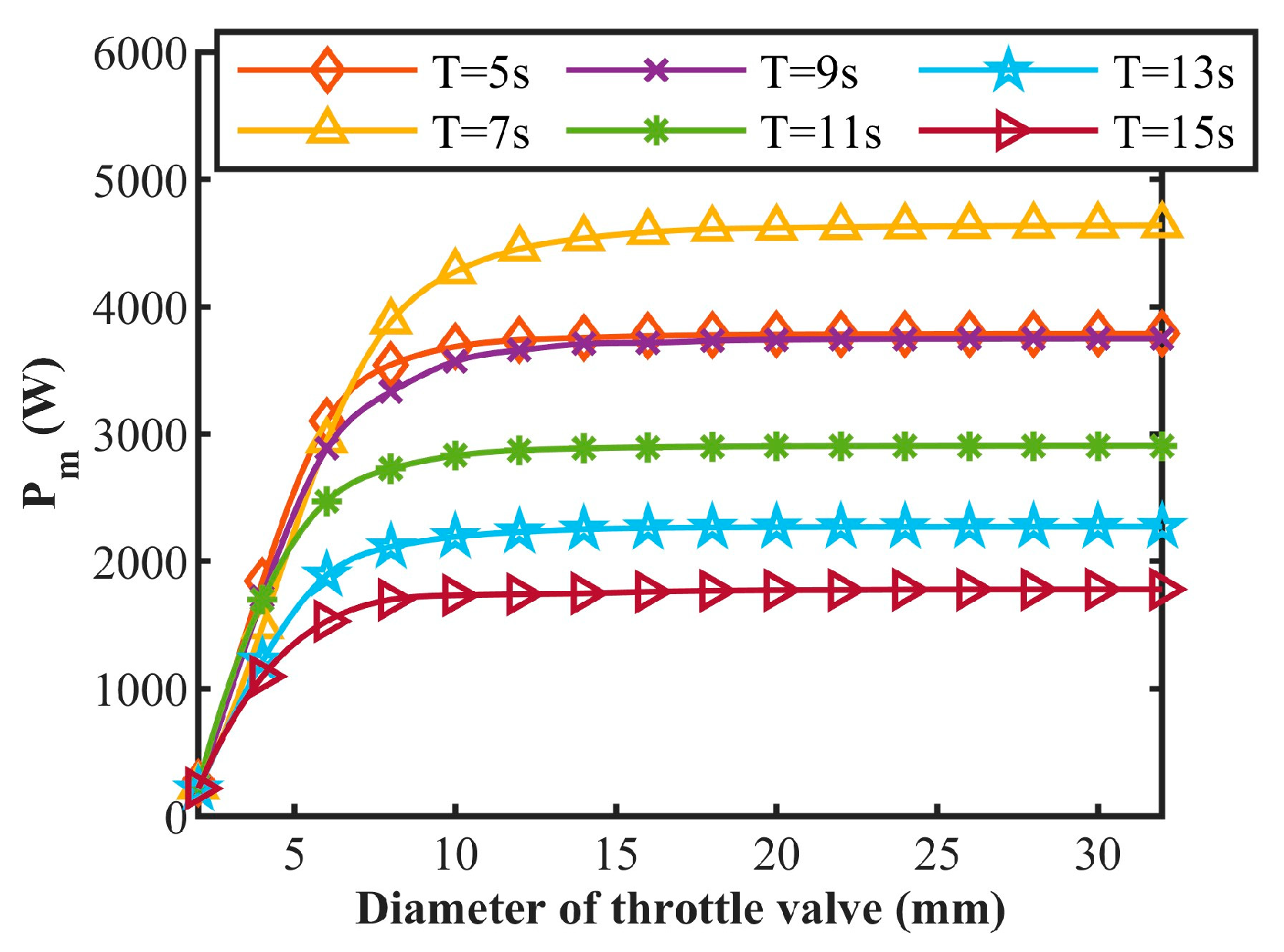
3.4.3. Effect of Diameter of Throttle Valve
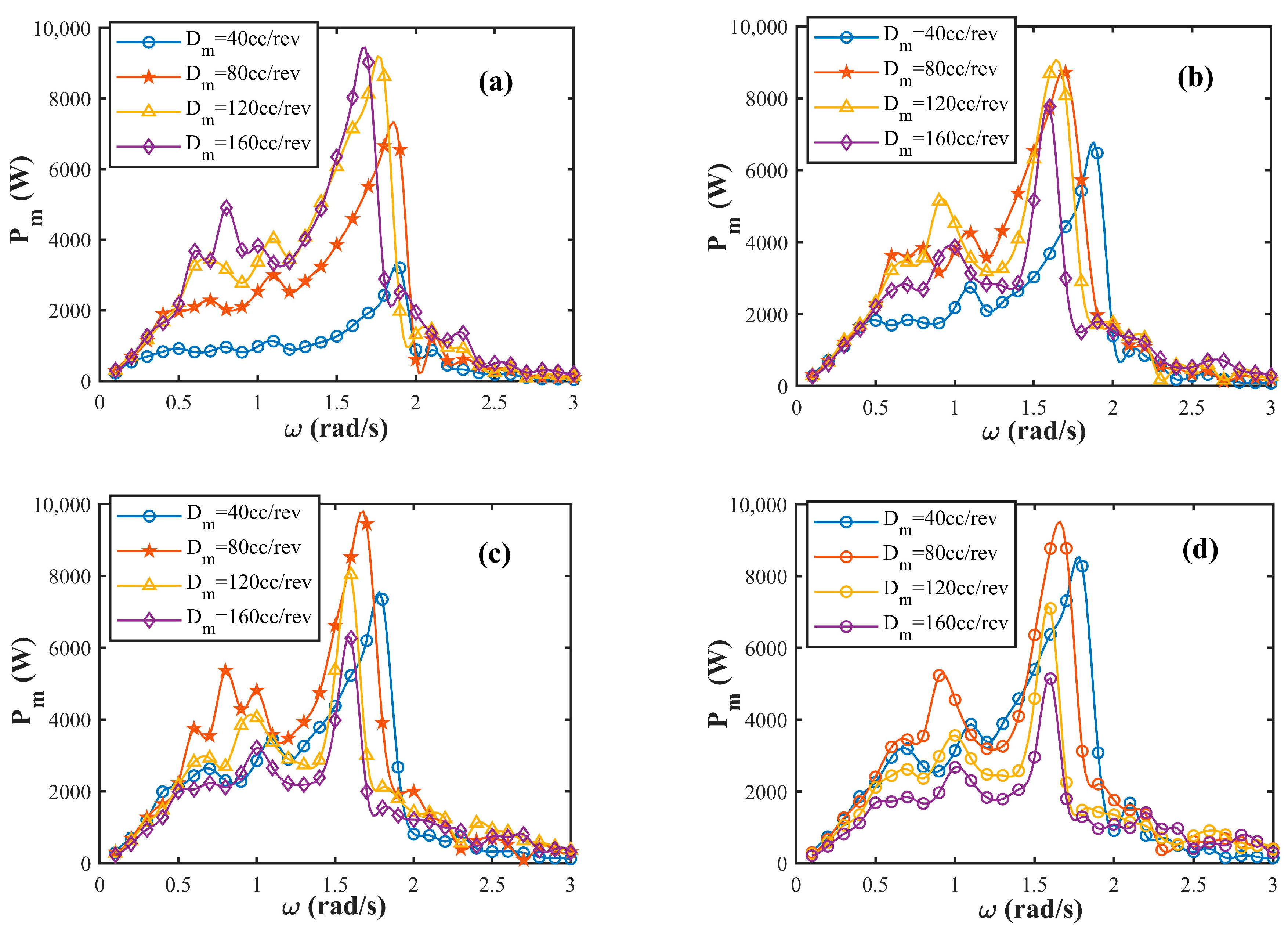
3.4.4. Effect of Displacement of the Hydraulic Motor and Load Resistance
4. Conclusions
- (1)
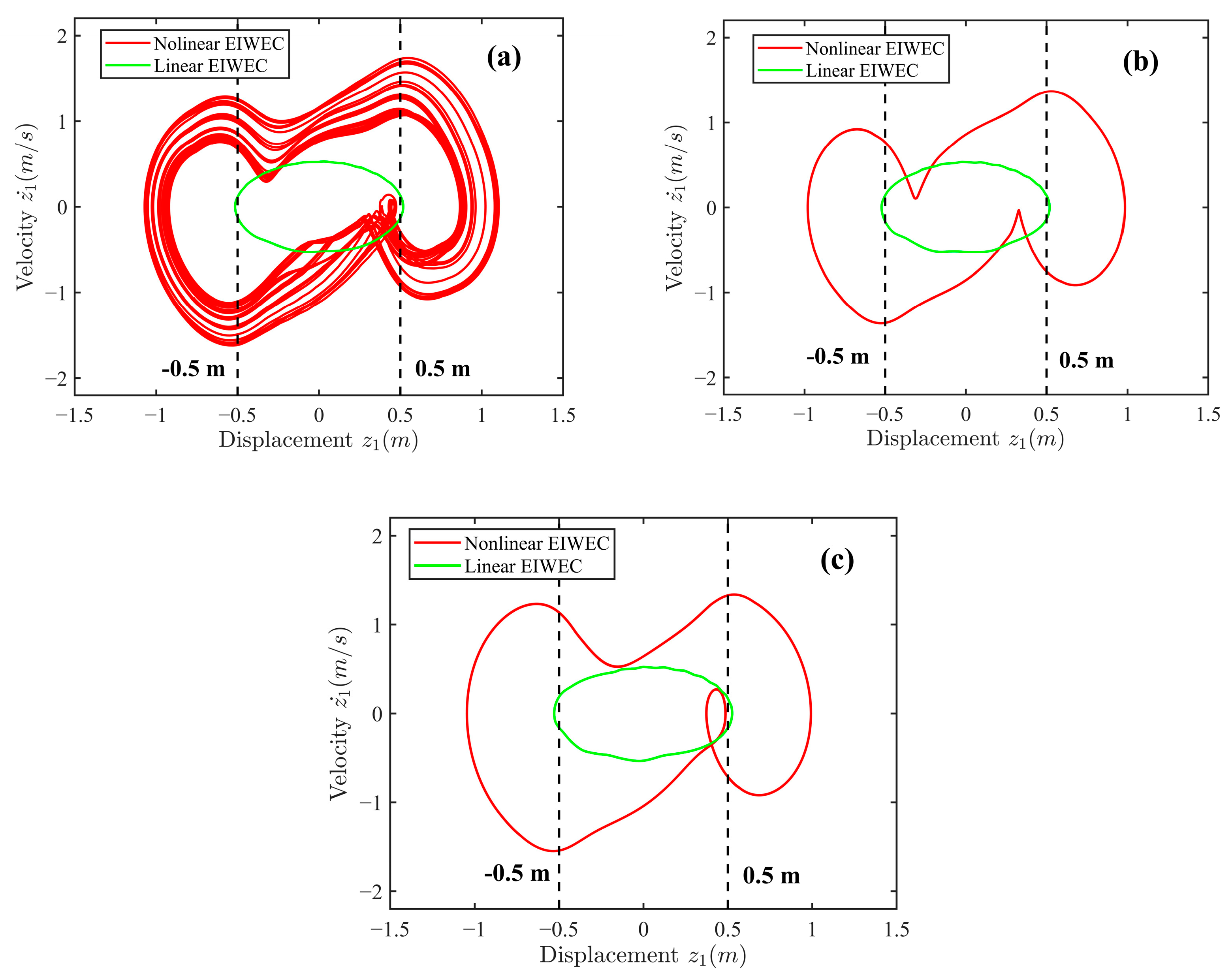
- Compared to linear EIWEC, the introduction of NSM increased the motion response of nonlinear EIWEC. The large amplitude relative motion provided favorable conditions for energy conversion.
- (2)
- The nonlinear negative stiffness property of the NSM reduced the intrinsic frequency and broadened the frequency bandwidth of the EIWEC. The effective frequency band shifted to a lower frequency range, and the output power of the nonlinear EIWEC was considerably enhanced.
- (3)
- Within the typical wave frequency range, the output power of the nonlinear EIWEC is insensitive to changes in the wave frequencies and linear spring stiffness. This not only increases the robustness of the system but also reduces the design difficulty of the linear spring.
- (4)
- Increasing the mass of the internal mass body and decreasing the stiffness of the linear spring will have a positive effect on enhancing the power performance of the system.
- (5)
- Choosing an accumulator with lower pre-charged pressure and larger gas initial volume can fully absorb the pressure and flow pulsations in the hydraulic PTO system, which is favorable to the smooth power output.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coyle, E.D.; Simmons, R.A. Understanding the Global Energy Crisis; Purdue University Press: West Lafayette, IN, USA, 2014; ISBN 1557536619. [Google Scholar]
- Bodansky, D. The United Nations framework convention on climate change: A commentary. Yale J. Int’l L. 1993, 18, 451. [Google Scholar]
- Schleussner, C.; Rogelj, J.; Schaeffer, M.; Lissner, T.; Licker, R.; Fischer, E.M.; Knutti, R.; Levermann, A.; Frieler, K.; Hare, W. Science and policy characteristics of the Paris Agreement temperature goal. Nat. Clim. Chang. 2016, 6, 827–835. [Google Scholar] [CrossRef]
- Davis, M.; Moronkeji, A.; Ahiduzzaman, M.; Kumar, A. Assessment of renewable energy transition pathways for a fossil fuel-dependent electricity-producing jurisdiction. Energy Sustain. Dev. 2020, 59, 243–261. [Google Scholar] [CrossRef]
- Vidal-Amaro, J.J.; Østergaard, P.A.; Sheinbaum-Pardo, C. Optimal energy mix for transitioning from fossil fuels to renewable energy sources—The case of the Mexican electricity system. Appl. Energy 2015, 150, 80–96. [Google Scholar] [CrossRef]
- Halkos, G.E.; Gkampoura, E. Reviewing usage, potentials, and limitations of renewable energy sources. Energies 2020, 13, 2906. [Google Scholar] [CrossRef]
- Guo, B.; Wang, T.; Jin, S.; Duan, S.; Yang, K.; Zhao, Y. A review of point absorber wave energy converters. J. Mar. Sci. Eng. 2022, 10, 1534. [Google Scholar] [CrossRef]
- Yue, W.; Wang, Z.; Ding, W.; Sheng, S.; Zhang, Y.; Huang, Z.; Wang, W. Feasibility of Co-locating wave energy converters with offshore aquaculture: The Pioneering case study of China’s Penghu platform. Ocean Eng. 2023, 288, 116039. [Google Scholar] [CrossRef]
- Clemente, D.; Rosa-Santos, P.; Ferradosa, T.; Taveira-Pinto, F. Wave energy conversion energizing offshore aquaculture: Prospects along the Portuguese coastline. Renew. Energy 2023, 204, 347–358. [Google Scholar] [CrossRef]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F. On the potential synergies and applications of wave energy converters: A review. Renew. Sustain. Energy Rev. 2021, 135, 110162. [Google Scholar] [CrossRef]
- Gallutia, D.; Fard, M.T.; Soto, M.G.; He, J. Recent advances in wave energy conversion systems: From wave theory to devices and control strategies. Ocean Eng. 2022, 252, 111105. [Google Scholar] [CrossRef]
- Tiron, R.; Mallon, F.; Dias, F.; Reynaud, E.G. The challenging life of wave energy devices at sea: A few points to consider. Renew. Sustain. Energy Rev. 2015, 43, 1263–1272. [Google Scholar] [CrossRef]
- Xue, G.; Qin, J.; Zhang, Z.; Huang, S.; Liu, Y. Experimental Investigation of Mooring Performance and Energy-Harvesting Performance of Eccentric Rotor Wave Energy Converter. J. Mar. Sci. Eng. 2022, 10, 1774. [Google Scholar] [CrossRef]
- Cordonnier, J.; Gorintin, F.; De Cagny, A.; Clément, A.H.; Babarit, A. SEAREV: Case study of the development of a wave energy converter. Renew. Energy 2015, 80, 40–52. [Google Scholar] [CrossRef]
- Pozzi, N.; Bracco, G.; Passione, B.; Sirigu, S.A.; Mattiazzo, G. PeWEC: Experimental validation of wave to PTO numerical model. Ocean Eng. 2018, 167, 114–129. [Google Scholar] [CrossRef]
- Khedkar, K.; Nangia, N.; Thirumalaisamy, R.; Bhalla, A.P.S. The inertial sea wave energy converter (ISWEC) technology: Device-physics, multiphase modeling and simulations. Ocean Eng. 2021, 229, 108879. [Google Scholar] [CrossRef]
- The Penguin Wave Energy Converter. Available online: https://wello.eu/the-penguin-2/ (accessed on 9 January 2024).
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Martins, P. Influence of platform design and power take-off characteristics on the performance of the E-Motions wave energy converter. Energy Conv. Manag. 2021, 244, 114481. [Google Scholar] [CrossRef]
- Scarcity of Resources, Climate Change. Available online: https://seaturns.com/ (accessed on 9 January 2024).
- Crowley, S.; Porter, R.; Taunton, D.J.; Wilson, P.A. Modelling of the WITT wave energy converter. Renew. Energy 2018, 115, 159–174. [Google Scholar] [CrossRef]
- Maheen, M.H.; Yang, Y. Wave energy converters with rigid hull encapsulation: A review. Sustain. Energy Technol. Assess. 2023, 57, 103273. [Google Scholar]
- Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Martins, P. Experimental performance assessment of geometric hull designs for the E-Motions wave energy converter. Ocean Eng. 2022, 260, 111962. [Google Scholar] [CrossRef]
- Ding, W.; Wang, K.; Mao, Z.; Cao, H. Layout optimization of an inertial energy harvester for miniature underwater mooring platforms. Mar. Struct. 2020, 69, 102681. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, L.; Yeung, R.W. Analysis and optimization of a Dual Mass-Spring-Damper (DMSD) wave-energy convertor with variable resonance capability. Renew. Energy 2019, 131, 1060–1072. [Google Scholar] [CrossRef]
- Falnes, J.; Kurniawan, A. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2020; ISBN 1108481663. [Google Scholar]
- Khasawneh, M.A.; Daqaq, M.F. Response behavior of bi-stable point wave energy absorbers under harmonic wave excitations. Nonlinear Dyn. 2022, 109, 371–391. [Google Scholar] [CrossRef]
- Khasawneh, M.A.; Daqaq, M.F. Experimental assessment of the performance of a bi-stable point wave energy absorber under harmonic incident waves. Ocean Eng. 2023, 280, 114494. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, Z.; Zhang, Y.; Huang, S.; Liu, Y.; Xue, G. Design and performance evaluation of novel magnetic tristable wave energy converter. Ocean Eng. 2023, 285, 115424. [Google Scholar] [CrossRef]
- Kurniawan, A.; Greaves, D.; Chaplin, J. Wave energy devices with compressible volumes. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140559. [Google Scholar] [CrossRef] [PubMed]
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy; Springer Nature: Berlin, Germany, 2017. [Google Scholar]
- Bracco, G.; Canale, M.; Cerone, V. Optimizing energy production of an inertial sea wave energy converter via model predictive control. Control Eng. Pract. 2020, 96, 104299. [Google Scholar] [CrossRef]
- Vissio, G.; Valério, D.; Bracco, G.; Beirão, P.; Pozzi, N.; Mattiazzo, G. ISWEC linear quadratic regulator oscillating control. Renew. Energy 2017, 103, 372–382. [Google Scholar] [CrossRef]
- Salcedo, F.; Ruiz-Minguela, P.; Rodriguez, R.; Ricci, P.; Santos, M. Oceantec: Sea trials of a quarter scale prototype. In Proceedings of the 8th European Wave and Tidal Energy Conference, Uppsala, Sweden, 7–10 September 2009; pp. 460–465. [Google Scholar]
- Sirigu, S.A.; Bracco, G.; Bonfanti, M.; Dafnakis, P.; Mattiazzo, G. On-board sea state estimation method validation based on measured floater motion. IFAC-PapersOnLine 2018, 51, 68–73. [Google Scholar] [CrossRef]
- Scapolan, M.; Tehrani, M.G.; Bonisoli, E. Energy harvesting using parametric resonant system due to time-varying damping. Mech. Syst. Signal Proc. 2016, 79, 149–165. [Google Scholar] [CrossRef]
- Giorgi, G.; Faedo, N. Performance enhancement of a vibration energy harvester via harmonic time-varying damping: A pseudospectral-based approach. Mech. Syst. Signal Proc. 2022, 165, 108331. [Google Scholar] [CrossRef]
- Yurchenko, D.; Alevras, P. Dynamics of the N-pendulum and its application to a wave energy converter concept. Int. J. Dyn. Control 2013, 1, 290–299. [Google Scholar] [CrossRef]
- Giorgi, G. Embedding parametric resonance in a 2:1 wave energy converter to get a broader bandwidth. Renew. Energy 2023, 222, 119928. [Google Scholar] [CrossRef]
- Schubert, B.W.; Sergiienko, N.Y.; Cazzolato, B.S.; Robertson, W.S.; Ghayesh, M.H. The true potential of nonlinear stiffness for point absorbing wave energy converters. Ocean Eng. 2022, 245, 110342. [Google Scholar] [CrossRef]
- Guo, B.; Ringwood, J.V. Non-linear modeling of a vibro-impact wave energy converter. IEEE Trans. Sustain. Energy 2020, 12, 492–500. [Google Scholar] [CrossRef]
- Zhang, H.; Xi, R.; Xu, D.; Wang, K.; Shi, Q.; Zhao, H.; Wu, B. Efficiency enhancement of a point wave energy converter with a magnetic bistable mechanism. Energy 2019, 181, 1152–1165. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, X.; Xiao, L.; Li, X.; Chen, L. Application of an adaptive bistable power capture mechanism to a point absorber wave energy converter. Appl. Energy 2018, 228, 450–467. [Google Scholar] [CrossRef]
- Liu, B.; Yi, H.; Levi, C.; Estefen, S.F.; Wu, Z.; Duan, M. Improved bistable mechanism for wave energy harvesting. Ocean Eng. 2021, 232, 109139. [Google Scholar] [CrossRef]
- Wang, L.; Tang, H.; Wu, Y. On a submerged wave energy converter with snap-through power take-off. Appl. Ocean Res. 2018, 80, 24–36. [Google Scholar] [CrossRef]
- Todalshaug, J.H.; ásgeirsson, G.S.; Hjálmarsson, E.; Maillet, J.; Möller, P.; Pires, P.; Guérinel, M.; Lopes, M. Tank testing of an inherently phase-controlled wave energy converter. Int. J. Mar. Energy 2016, 15, 68–84. [Google Scholar] [CrossRef]
- Corpower. Available online: https://www.corpowerocean.com/ (accessed on 9 January 2024).
- Li, M.; Jing, X. A bistable X-structured electromagnetic wave energy converter with a novel mechanical-motion-rectifier: Design, analysis, and experimental tests. Energy Conv. Manag. 2021, 244, 114466. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, S.; Xue, G.; Liu, Y. Influence of Hydraulic PTO Parameters on Power Capture and Motion Response of a Floating Wind-Wave Hybrid System. J. Mar. Sci. Eng. 2022, 10, 1660. [Google Scholar] [CrossRef]
- Choi, K.; Yang, D.; Park, S.; Cho, B. Design and performance test of hydraulic PTO for wave energy converter. Int. J. Precis. Eng. Manuf. 2012, 13, 795–801. [Google Scholar] [CrossRef]
- Gao, H.; Xiao, J. Effects of power take-off parameters and harvester shape on wave energy extraction and output of a hydraulic conversion system. Appl. Energy 2021, 299, 117278. [Google Scholar] [CrossRef]
- Liu, C.; Hu, M.; Zhao, Z.; Zeng, Y.; Gao, W.; Chen, J.; Yan, H.; Zhang, J.; Yang, Q.; Bao, G. Latching control of a raft-type wave energy converter with a hydraulic power take-off system. Ocean Eng. 2021, 236, 109512. [Google Scholar] [CrossRef]
- Xue, G.; Zhang, Z.; Qin, J.; Huang, S.; Liu, Y. Control Parameters Optimization of Accumulator in Hydraulic Power Take-Off System for Eccentric Rotating Wave Energy Converter. J. Mar. Sci. Eng. 2023, 11, 792. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, X.; Xiao, L.; Wei, H.; Chen, W. Evaluation of long-term power capture performance of a bistable point absorber wave energy converter in South China Sea. Ocean Eng. 2021, 237, 109338. [Google Scholar] [CrossRef]
- Newman, J.N. The exciting forces on fixed bodies in waves. J. Ship Res. 1962, 6, 10–17. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse Response Function and Ship Motions; David Taylor Model Basin: Washington, DC, USA, 1962. [Google Scholar]
- Ogden, D.; Ruehl, K.; Yu, Y.; Keester, A.; Forbush, D.; Leon, J.; Tom, N. Review of WEC-Sim development and applications. Int. Mar. Energy J. 2022, 5, 5–9. [Google Scholar] [CrossRef]
- Tampier, G.; Grueter, L. Hydrodynamic analysis of a heaving wave energy converter. Int. J. Mar. Energy 2017, 19, 304–318. [Google Scholar] [CrossRef]

| Parameter | Symbol | Value |
|---|---|---|
| Inner diameter of inner magnetic rings (m) | 0.2 | |
| External diameter of inner magnetic rings (m) | 0.5 | |
| Inner diameter of outer magnetic rings (m) | 0.6 | |
| External diameter of outer magnetic rings (m) | 1.0 | |
| Center angle of attractive magnet ( | 18 | |
| Center angle of repulsive magnet ( | 90° | 72 |
| Height difference between attractive and repulsive magnets (m) | 0.08 | |
| Height of inner magnetic ring (m) | 0.15 | |
| Permeability of vacuum (H/m) | ||
| Residual magnetic flux density (T) | 1.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Zhang, Z.; Song, X.; Huang, S.; Liu, Y.; Xue, G. Design and Performance Evaluation of an Enclosed Inertial Wave Energy Converter with a Nonlinear Stiffness Mechanism. J. Mar. Sci. Eng. 2024, 12, 191. https://doi.org/10.3390/jmse12010191
Qin J, Zhang Z, Song X, Huang S, Liu Y, Xue G. Design and Performance Evaluation of an Enclosed Inertial Wave Energy Converter with a Nonlinear Stiffness Mechanism. Journal of Marine Science and Engineering. 2024; 12(1):191. https://doi.org/10.3390/jmse12010191
Chicago/Turabian StyleQin, Jian, Zhenquan Zhang, Xuening Song, Shuting Huang, Yanjun Liu, and Gang Xue. 2024. "Design and Performance Evaluation of an Enclosed Inertial Wave Energy Converter with a Nonlinear Stiffness Mechanism" Journal of Marine Science and Engineering 12, no. 1: 191. https://doi.org/10.3390/jmse12010191
APA StyleQin, J., Zhang, Z., Song, X., Huang, S., Liu, Y., & Xue, G. (2024). Design and Performance Evaluation of an Enclosed Inertial Wave Energy Converter with a Nonlinear Stiffness Mechanism. Journal of Marine Science and Engineering, 12(1), 191. https://doi.org/10.3390/jmse12010191






