A Novel Configuration of Hybrid Reverse Osmosis, Humidification–Dehumidification, and Solar Photovoltaic Systems: Modeling and Exergy Analysis

Abstract

The pressing demand for clean water worldwide has increased attention to developing innovative desalination processes. In this work, the second law of thermodynamics is used to examine and assess two coupled desalination systems: a separation-based reverse osmosis (RO) system and a thermal desalination-based humidification–dehumidification (HDH) system. The HDH unit configuration used here is based on the working principle of the heat pump, where the process is open-air, open-water, and air-heated. The RO system is equipped with a pressure exchanger (PX) and has been examined under various operating circumstances, such as different feed water pressures, salinities, and flow rates. To improve the system’s sustainability, a solar photovoltaic system (PV) was integrated. An exergy model was used to precisely evaluate the system components and the hybrid systems by employing a proper exergy efficiency definition. The evaluation of the second law of thermodynamics for the RO–HDH–PX and RO–HDH–PX–PV systems indicated maximum efficiencies of 23% and 23.25%, respectively. A cost analysis was also performed on the hybrid RO–HDH–PX–PV desalination system using two approaches: the first included a battery storage system, whereas, in the second, the battery was not considered. When a battery storage system is included, the cost per cubic meter varies from USD 3.22 to USD 5.10. In contrast, it varies from USD 3.96 to USD 7.12 without a battery storage system.

1. Introduction

Water is one of the fundamental necessities required for life. Water scarcity and the growing demand for water are among the most pressing problems facing development, industry, and urbanization [1,2,3]. Around 1.2 billion people around the globe are affected by extreme water scarcity [4]. Much of the world’s water cannot be utilized directly for freshwater consumption, even in the small amounts in which it is primarily used as potable water [5,6]. Therefore, water desalinization may be the solution. One of the significant issues affecting current methods for generating freshwater is the high level of investment required for water treatment.

On the other hand, most traditional desalination systems rely on fossil fuels to power their operations. There is a necessity to develop more sustainable methods due to the environmental effect of these energy sources and their inherent unsustainability. In terms of performance and commercial viability, conventional systems remain superior to sustainable desalination alternatives. However, there is a significant potential that renewable energy-based desalination systems will surpass conventional plants over time [7]. High energy consumption is a major barrier to expanding the scale of the desalination systems used in industrial and commercial applications. This revelation gave rise to the integration of renewable energy sources with desalination techniques.

Thermal and membrane desalination technologies account for the vast majority of what is now available. The former technologies suffer from high costs, corrosion, and complicated installation procedures (e.g., multi-stage flash (MSF)). The latter are affected by membrane fouling, which necessitates the pre- and post-treatment of the water before it can be delivered to the desalination modules. There are various other less-well-known desalination methods, such as pervaporation, forward osmosis, and membrane distillation, each with benefits and drawbacks.

Many pilot desalination plants that use renewable energy sources have been established, and most have been running efficiently for years. Most of them use solar or geothermal energy to produce potable water, and they are each suited to their specific location [8]. Renewable-energy-powered desalination systems are not yet cost-competitive with conventional desalination systems. However, they are suitable in certain locations, and they are expected to become more widely viable soon. El-Ghonemy [9] examined renewable-energy-powered water desalination systems, focusing on recent developments in this field from both a technological and a financial perspective.

Different desalination technologies—mostly reverse osmosis (RO) and humidification–dehumidification (HDH) systems—have been integrated with solar photovoltaic (PV) systems to increase their sustainability. Shalaby [10] discussed RO desalination systems powered by solar energy and reported that photovoltaic (PV) energy is the renewable energy source most commonly utilized to power RO systems because it is more cost-effective than using solar organic Rankine cycles (ORCs). Herold and Neskakis [11] experimented with a PV–RO battery-based system that could produce 0.3 to 0.8 m³/day. With a feed pressure of 63 bar, the SEC was 15 kWh/m³. Additionally, an investigation by Mohamed et al. [12] examined the financial viability of a PV–RO system in two scenarios: with and without batteries. Even though the SEC dropped when the system with batteries was examined, the price rose from EUR 7.5 to EUR 8.3 per cubic meter owing to the high level of investment and expense required for replacement. Kettani and Bandelier [13] presented a techno-economic analysis of a PV-RO desalination system on a major scale. For a plant with a capacity of 275,000 m³/day, they estimated a freshwater cost of around USD 1 per cubic meter.

Conversely, a few research studies involving HDH systems with integrated solar PV systems were conducted. Wang et al. [14] demonstrated that a PV-powered HDD in which the power is supplied directly and indirectly by solar radiation is an economically feasible choice for desalination in remote areas. In addition, they discovered that forced convection improved the performance of this setup under the same operational conditions. Wang et al. [15] studied the effects of several variables on the rates of evaporation and condensation. The highest freshwater output was around 0.873 L/m²/d with forced convection and an evaporator temperature of 64.3 °C; this was higher than the 0.789 kg/m²/d obtained using a free convection process. From this study, it can be concluded that the integration of solar PV systems is more appropriate for small-scale HDH systems and is favorable for remote areas away from electric power supplies. Using thermal energy recovery (TES) technology, Giwa et al. [16] studied the various environmental circumstances that affected a PV–HDH system’s productivity. Using an HDH desalination unit that was combined with PV/T modules, Gabrielli et al. [17] investigated the effect of the design and the working environment on the performance of the system. In a theoretical study, Rafiei et al. [18] investigated how the operating circumstances affected the amount of freshwater produced by an HDH desalination system that used a solar dish concentrator and a PV/T system. Mahmoud et al. [19] hypothetically evaluated the performance of a hybrid solar distiller/HDH desalination system with incorporated PV panels and solar concentrators.

Many researchers have conducted such hybridization techniques. Narayan et al. [20] presented a hybrid HDH and reverse osmosis system to minimize energy consumption. Compared to conventional HDH systems, the GOR for this hybrid system was significantly increased to reach 20. Similarly, Kabeel and El-Said [21] examined a system that combined air heated HDH with a flash desalination system in a single stage. Solar collectors were used to heat both air and water at a laboratory scale [22]. In a separate study performed by the same authors [23], the system’s economic viability was examined. The hybrid system was more productive and cost-effective than the independent units. Also, from a financial perspective, Eslamimanesh et al. 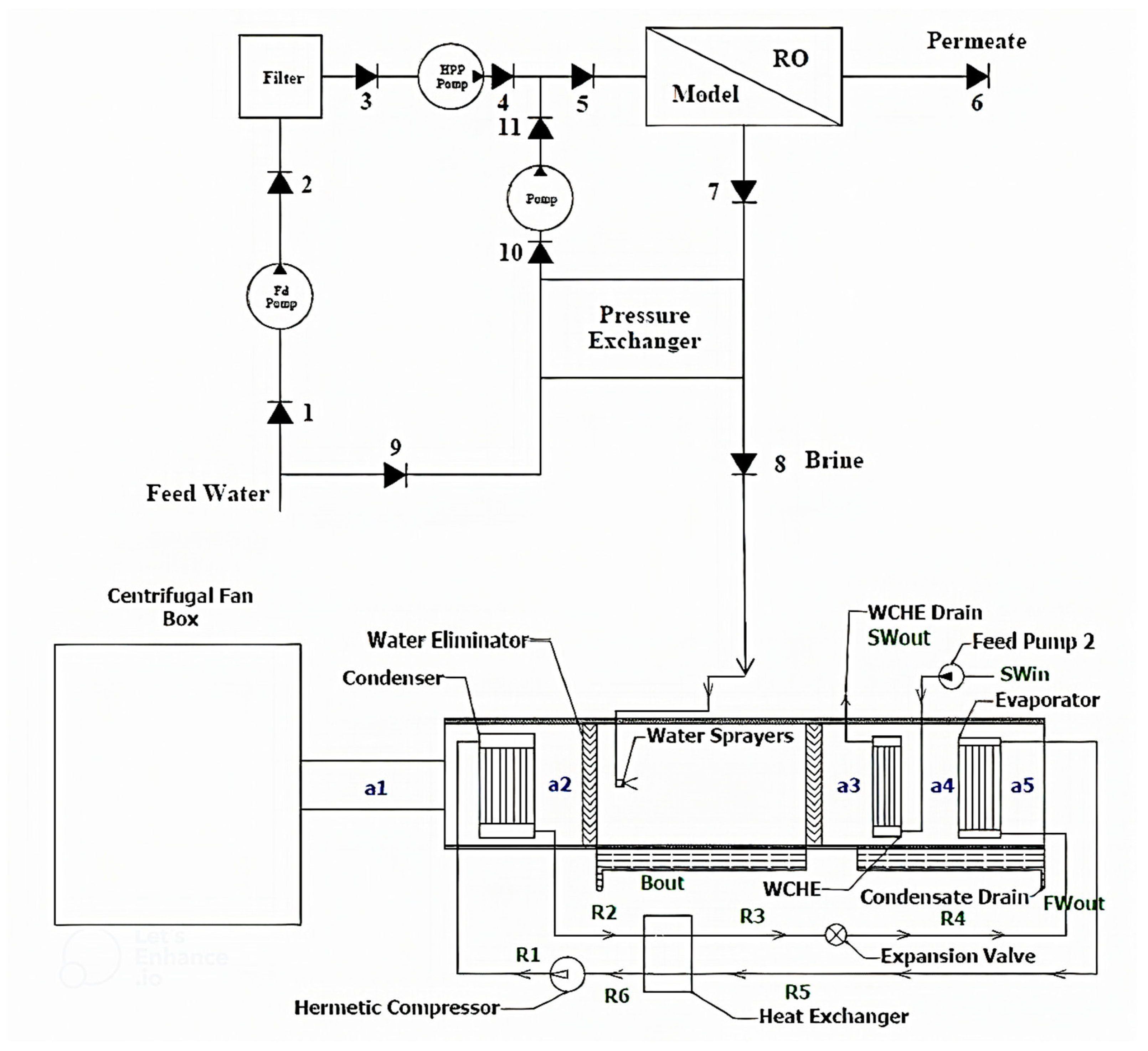[24] compared a pilot HDH system to an RO system. They recommended integrating an HDH system with an RO for the highest potential. A PV-powered HDH–RO system including thermal recovery (PV cooling) units, solar collectors (air and water), and a pressure exchanger was simulated by Abdelgaied et al. [25]. The collectors were employed to improve the HDH system’s efficiency, while the PV cooling units served a dual purpose: they both preheated the HDH system’s water and increased the PV system’s power output. With SEC values between 1.22 and 1.24 kWh/m³, the suggested system achieved a maximum hourly production of 192–200 L.

On the other hand, other researchers have investigated the hybridization of the HDH with the RO system using the second law of thermodynamics. The second law of thermodynamics, widely referred to as exergy, attempted to enhance the quality of the energy released through its exergy in a dead state or, in particular, with regard to the ambient environment. Al-Sulaiman et al. [26] examined a hybrid HDH–RO system theoretically, where they modeled the whole system thermodynamically and calculated exergy for all components, ignoring concentration change in HDH. They treated water as a real solution and analyzed its characteristics using Sharqawy et al. [27]. The entire unit exergy efficiency was stated to be 10–11.9%. Likewise, Jamil et al. [28] compared two HDH desalination systems, one using the OAOW process and the other using an OACW process. The combination of an RO and HDH unit was also investigated. According to the study, the HDH–RO with PX has the highest exergy efficiency at 3%. Furthermore, Ameri and Eshaghi [29] introduced a water desalination system combining RO with an HDH system, in which chemical exergy was considered. The stand-alone RO, HDH, and RO–HDH had exergy efficiencies of 0.064–0.724%, 7.95–12.66%, and 15.90–20.60%, respectively.

Many HDH and RO exergy studies have been found in the literature, but few examine the chemical exergy of flows or salt propagation into freshwater produced by HDH systems. In addition, few studies have examined the usage of solar PV systems with such hybrid RO–HDH and the effect of the PV integration on the hybrid system from an exergy analysis perspective. Consequently, this study aimed to propose a hybrid desalination system integrating two methods of desalination, RO and HDH. The novelty can be considered in the integration of the RO system with the HDH, which is driven by a heat pump. Moreover, the hybrid system is powered by a solar PV system, which is adequate for such a small-scale desalination system, as indicated by the Wang et al. [14] study. Using a pressure exchanger as an ERD, the RO system’s energy consumption was improved. Energy and exergy assessments are examined for the RO–HDH–PX–PV system. In addition, an advanced exergy model is used to evaluate system components through an appropriate exergy efficiency definition.

2. Description of Systems and Models

The water desalination system combines two different technologies (reverse osmosis and humidification–dehumidification processes) powered by a solar PV system. The reverse osmosis system includes a configuration using ERD (pressure exchanger), as shown in Figure 1. The feed water first enters the reverse osmosis system, which is equipped with a pressure exchanger to harness the energy of the brine flowing out of the reverse osmosis module. The brine flow collected from the reverse osmosis system is also used as a direct source to feed the humidification section of the HDH unit.

The main operating parameters of the hybrid RO–HDH desalination system are summarized in

Table 1. Operating conditions for RO–HDH hybrid system.

Parameters	Humidification–Dehumidification System	Reverse Osmosis System
Membrane type	-	SW30-4040
Air mass flow rate (kg/h)	936	-
Feedwater mass flow rate (kg/h)	219–345	383–602
Air inlet temperature (°C)	25	-
Water inlet temperature (°C)	25	25
Feedwater pressure (MPa)	0.15	5–6.5
Recovery ratio (%)	-	43.86
Feedwater Salinity (ppm)	Based on RO brine	35,000–45,000

.

2.1. Reverse Osmosis Desalination System

The RO system consists of a feed pump, feed water filters, a high-pressure pump, RO modules, a pressure exchanger, and a booster pump. The RO module consists of four pressure vessels, each fitted with six elements of SW30-4040 membranes (DuPont, Wilmington, DE, USA). The characteristics of this type of membrane are presented in

Table 2. Characteristics of the Film-Tec spiral wound membrane element used in the reverse osmosis system (DuPont, Wilmington, DE, USA).

Element Type	SW30-4040
Active area (m2)	7.4
Length of the element (m)	1016
Diameter of the element (mm)	99
Feed space (μm)	711.2
Feed flow rate range (m3/h)	0.1–3.6
Permeate flow (m3/d)	7.4
Stabilized salt rejection (%)	99.75
Maximum operating pressure (MPa)	6.9
Pure water permeability constant, A (kg/m2.s.Pa)	9.058 × 10−10
Salt permeability constant, B (kg/m2.s)	2.11 × 10−10

.

Variations in applied pressure, feedwater mass flow rate, and total dissolved salts affect system performance benchmarks, as will be discussed in the results and discussion section. The ranges used in this work are the following: the feedwater flow rate varied from 383 to 602 kg/h, while the feed pressure varied from 5 to 6.5 MPa. Two salinity concentrations will be considered for the feedwater: 35,000 ppm and 45,000 ppm. The brine from the RO system will feed the HDH system.

The thermodynamic properties of the material streams at the RO–PX desalination system for a feedwater flow rate of 602 kg/h are presented in

Table 3. Thermodynamic properties at different locations for the RO–PX unit at a feedwater flow rate of 602 kg/h.

Point	Temperature (°C)	Pressure (kPa)	Mass Flow Rate (kg/h)	Total Dissolved Salts (ppm)
1	25	101.325	240.64	35,000
2	25	500	240.64	35,000
3	25	486	240.64	35,000
4	25	6500	240.64	35,000
5	25	6500	601.61	35,000
6	25	101.325	257	62.69
7	25	6350	337.78	62290
8	25	150	337.78	62290
9	25	101.325	361	35,000
10	25	5706.7	361	35,000
11	25	6500	361	35,000

.

The permeate water flux is defined as follows [30]:

$$J_w=AA\times TCF\times FF\left[\left(P_f-P_p-\frac{{∆P}_f}{2}\right)-\left({\pi }_{bw}-{\pi }_p\right)\right]\times {10}^6$$

(1)

As AA is the water permeability coefficient, TCF is the temperature correction factor, which can be estimated using Equations (2) or (3) [31]. The FF is the fouling factor; it was assumed to be 0.85, while π is the osmatic pressure.

For T < 25 °C:

$$TCF=exp\left[2640\left(\left(\frac{1}{298}\right)-\frac{1}{T_f+273}\right)\right]$$

(2)

For T > 25 °C:

$$TCF=exp\left[3020\left(\left(\frac{1}{298}\right)-\frac{1}{T_f+273}\right)\right]$$

(3)

The salt flux estimated is:

$$J_s=B(C_{bw}-C_p)$$

(4)

The osmotic pressure is a mutually exclusive feature. Within this respect, the osmotic pressure is simply determined by the concentration of ions in the solution [32]. As a result of Vant’s Hoff equation:

$$\pi =iRTC$$

(5)

The number of ions released by a salt solution in a solvent is represented by Vant’s Hoff coefficient i in Equation (5).

Using Formula (6), we may determine the permeate solution’s mean velocity.

$$V_p=\frac{J_w-J_s}{{\rho }_p}$$

(6)

The film-theory method may be used to estimate the concentration polarization on the feed sidewall of the membrane [33]:

$$\frac{C_m-C_p}{C_{bw}-C_p}=exp\left(\frac{J_w}{K_m}\right)$$

(7)

where $K_M$ is defined as the mass transfer coefficient of the solute, as determined by Equation (8) [34]:

$$K_M=1.62\times {Re}^{0.33}\times {Sc}^{0.33}\times {\left(\frac{d_h}{L}\right)}^{0.33}$$

(8)

where Re denotes the Reynolds number and Sc denotes the Schmidt number, specified as follows:

$$Re=\frac{V\times \rho \times d_h}{mu}$$

(9)

$$Sc=\frac{mu}{\rho \times D_s}$$

(10)

The hydraulic diameter of rectangular ducts is equivalent to two times the duct’s height. Using a spacer, the hydraulic diameter of that duct may be obtained as follows [32]:

$$d_h=\frac{4\alpha }{\frac{2}{H}+(1-\alpha S_m)}$$

(11)

where $\alpha$ and Sm denote the spacer porosity and the spacer’s specific surface area, respectively, and H denotes the duct height.

For seawater, the following is the solute permeability coefficient [35]:

$$D_s=6.2725\times {10}^{-6}\times exp\left[0.1546\times {10}^{-3}\times C_f-\frac{2513}{273.15+T}\right]$$

(12)

The pressure drop across a rectangular duct is expressed as [30]:

$${∆\mathrm{P}}_{\mathrm{f}}=\frac{0.0033\times {\mathrm{Q}}_{\mathrm{avg}}\times \mathrm{l}\times \mathrm{m}\mathrm{u}}{\mathrm{W}\times {\mathrm{F}\mathrm{S}}^3}$$

(13)

As a result of the mass conservation law:

$$Q_f=Q_{bw}+Q_p$$

(14)

$$Q_f\times C_f=Q_{bw}\times C_{bw}+Q_p\times C_p$$

(15)

The efficiency of the pressure exchanger can be described as follows:

$${\eta }_{px}=\frac{Q_{bw,out}\times P_{bw,out}+Q_{f,out}\times P_{f,out}}{Q_{bw,in}\times P_{bw,in}+Q_{f,in}\times P_{f,in}}$$

(16)

The SW30-4040 membrane was employed to optimize the performance of the proposed RO system according to the characteristics of the element membrane shown in

Table 4. Characteristics of the Film-Tec spiral wound reverse osmosis membrane elements used in the model validation (DuPont, Wilmington, DE, USA).

Element Type	SW30-4040	SW30XLE-400i
Active area (m2)	7.4	37.2
Length of the element (m)	1016	1.016
Diameter of the element (mm)	99	201
Feed space (μm)	711.2	711.2
Feed flow rate range (m3/h)	0.1–3.6	19.3
Permeate flow (m3/d)	7.4	34
Stabilized salt rejection (%)	99.75	99.7
Maximum operating pressure (MPa)	6.9	8.3
Pure water permeability constant, A (kg/m2.s.Pa)	9.058 × 10−10	3.5 × 10−9
Salt permeability constant, B (kg/m2.s)	2.11 × 10−10	3.2 × 10−5

. The model developed to simulate the RO system was validated by Lu et al. [36]. However, this study utilized the SW30XLE-400i membrane (DuPont, Wilmington, DE, USA), whose characteristics are shown in Table 4. The validation was focused on the permeate concentration, indicating the feasibility of the developed model and allowing the use of the proposed model.

Table 5. Validation of the reverse osmosis system.

Parameters	Test 1		Test 2		Test 3
	Lu et al. [36]	Model Values	Lu et al. [36]	Model Values	Lu et al. [36]	Model Values
Feed water mass flow rate (m3/h)	264	264	264	264	264	264
Permeate water mass flow rate (m3/h)	120	120	120	120	120	120
Feed water concentration (ppm)	48,000	48,000	42,000	42,000	38,000	38,000
Feed water pressure (MPa)	8.1	8.1	7.3	7.3	6.7	6.7
Permeate water concentration (ppm)	380	383.1682	330	341.9592	300	318.8987

presents the validation of the reverse osmosis system.

2.2. Humidification–Dehumidification Desalination System

The humidification–dehumidification (HDH) system process is based on the working principle of a heat pump. The system used here is described by Tourab et al. [37] as open-air, open-water air-heated (OAOW-AH). The HDH desalination system consists of a heat pump condenser, evaporator, humidifier, and dehumidifier. In the humidification process, a parallel spraying system is used. The humidifier receives two streams where heat and mass are transferred; one is the hot air from a heat pump condenser and the other is salted water from the RO desalination system. Due to the heating process for air, the specific humidity decreases, thus improving the humidification process. The dehumidifier has two sections: the first includes a water-cooled heat exchanger and the second contains a heat pump evaporator. Therefore, moist air is dehumidified, and freshwater is collected.

The feedwater mass flow rate to the humidification process varied from 219 to 345 kg/h. In contrast, the air mass flow rate varied from 936 kg/h to 1440 kg/h.

Table 6. Thermodynamic properties at different locations for the HDH unit for a 936 kg/h flow of air and 219 kg/h flow of feed water.

Point	Temperature (°C)	Pressure (kPa)	Mass Flow Rate (kg/h)	Specific Enthalpy (kJ/kg)
a1	25	101.314	936	50.33
a2	50	101.314	936	62.57
a3	32.2	101.314	957.95	87.19
a4	31.4	101.314	957.95	86.69
a5	26.8	101.314	953.93	77.99
SWin	25	125	270	99.79
SWout	28.3	101.325	270	110.71
Fin	25	150	219.33	99.79
Bout	25	101.325	210.93	95.44
FWout	18.63	101.325	4.018	76.09

and

Table 7. Thermodynamic properties of the refrigerant at different locations for the heat pump cycle.

Point	Pressure (kPa)	Specific Enthalpy (kJ/kg)	Mass Flow Rate (kg/h)
R1	2000	468	57.6
R2	2000	275	57.6
R3	2000	268.71	57.6
R4	450	260.2	57.6
R5	450	418.3	57.6
R6	450	421.5	57.6

show some thermodynamic properties at different locations for the HDH unit and the heat pump. Where the calculations are based on a flow of air of 936 kg/h and a flow of water of 219 kg/h.

The mathematical modeling for the heat pump condenser, humidifier, dehumidifier, and reverse osmosis systems is solved using MATLAB 2015b. The following assumptions are considered:

• Fluid properties are constant: c_p,a, c_p,w, c_p,v, c_p,R, and h_fg, which are the specific heat at a constant pressure of air, water, vapor, and refrigerant, in addition to the latent heat of vaporization, respectively.
• Ambient temperature (T_amb): 25 °C.
• The pressure drop in the RO filter is 14 kPa.
• Isentropic efficiency of the pressure exchanger: 96%.
• Isentropic efficiency of all the pumps: 75%.

The model for the humidification–dehumidification system was already validated in previous works [3,37]. Some results are shown in

Table 8. Validation of HDH system.

Parameters	El-Maghlany et al. [3] Experimental Data	Model Values	Relative Error (%)
Feed seawater mass flow rate (kg/h)	132	132	0
Feed air flow mass rate (kg/min)	15.71	15.71	0
Inlet air temperature (°C)	25	25	0
Inlet feed water temperature (°C)	15	15	0
Inlet-specific enthalpy to heat pump condenser $h_{R,1}$ (kJ/kg)	470	485	3.19
Inlet-specific enthalpy to heat pump evaporator $h_{R,4}$ (kJ/kg)	275	290	5.45
Freshwater produced (kg/h)	3.22	3.18	1.24
The temperature of freshwater (°C)	20.6	19.85	3.64

.

Table 9. Specification and geometry of the HDH unit [3].

Parameters	Values
Heat pump condenser fins	195
Heat pump condenser volume (m3)	0.53 × 0.4 × 0.25
Fin pitch in the condenser (m)	0.02
Humidifier volume (m3)	0.53 × 0.4 × 1.5
Water-cooled heat exchanger fins	169
Water-cooled heat exchanger volume (m3)	0.53 × 0.4 × 0.2
Heat pump evaporator fins	177
Fin pitch in the evaporator (m)	0.02
Heat pump evaporator volume (m3)	0.53 × 0.4 × 0.2
Compressor power (kW)	2
Feed pump power (kW)	0.22

summarizes the HDH’s geometry as well as its characteristics.

2.3. Solar Energy Integration

The integration of a solar photovoltaic (PV) system enhances the sustainability of the hybrid desalination system and mitigates the ecological footprint attributed to the consumption of fossil-fuel-based energy sources.

According to the previous review, solar PV is the best and cheapest renewable source to power the RO system. So, in this section, an investigation of integrating a solar PV system with the RO–HDH–PX hybrid system will be introduced. Figure 2 shows the components of the solar PV system used for this purpose: solar PV modules, battery charger controller, battery storage system, and inverter.

Two approaches have been considered. The first approach employed batteries in the PV system to guarantee the energy supply throughout the day. The second approach was considered without using the battery. The location of Alexandria, Egypt, was chosen for the design of the PV system. The average annual amount of sunshine is about ten hours per day. [38]. The monthly solar direct normal irradiation over the year, DNI, has been obtained from the Global Solar Atlas [38]. The average daily solar energy input over the year, Gavg, was calculated from the DNI as 5.337 kWh/day/m².

The total energy consumption of the RO–HDH–PX hybrid system for the daily load operation and considering the first and second approaches (with and without battery usage) is shown in

Table 10. Energy consumption per day of the RO–HDH–PX hybrid system at different operating conditions.

Total Seawater Feed Flow Rate (m3/h)	383	438	492	547	602
At feed pressure, 5 MPa
Without battery usage (kWh/day)	15.7	16.2	16.7	17.13	17.6
Using battery (kWh/day)	37.8	38.9	40	41.1	42.2
At feed pressure, 6.5 MPa
Without battery usage (kWh/day)	16.7	17.3	17.9	18.5	19.1
Using battery (kWh/day)	40.1	41.504	43	44.4	45.8

. The values represent the maximum energy consumption at different seawater feed flow rate operating conditions.

2.3.1. Sizing of the PV System Panels

Here, a basic sizing to study the effect of the integration of the solar photovoltaic system with the RO–HDH–PX system is included.

The operating parameters of the PV module, Sunergy Solar SSM420-108, were obtained from the manufacturer data sheet as listed in

Table 11. Characteristics of the Sunergy Solar SSM420-108 PV module (Sunergy Solar, Huzhou, China).

Parameters	Value
Nominal output power (Pmmp)	420 W
Nominal voltage (Vmmp)	31.77 V
Nominal current (Immp)	13.15 A
Short circuit current (Isc)	14.05 A
Open circuit voltage (Voc)	37.81 V
Module efficiency ${\mathit{\eta }}_{\mathit{p}\mathit{v}}$	21.4%
Number of cells	108 cell
Module Dimensions	1722 × 1134 × 30 mm
Normal Operation Cell Temperature (NOCT)	41 °C $(\pm 3 °\mathrm{C})$

.

The size of the PV array can be calculated by:

$${PV}_{area}=\frac{E_L}{G_{av}·{\eta }_{pv}·{\eta }_B·{\eta }_{Inv}·TCF}$$

(17)

where E_L is the average daily energy yield, as given in Table 10, G_avg is the average solar energy input per day, and TCF is the temperature correction factor assumed to equal 0.8. ${\eta }_{pv}$ is the PV module efficiency, while ${\eta }_B$ and ${\eta }_{Inv}$ are the battery efficiency of 90% and inverter efficiency of 93%, respectively.

The peak solar insolation, PSI, is assumed to be 1000 W/m²; thus, the PV peak power is given as follows:

$$PV Peak Power={PV}_{area}·PSI·{\eta }_{pv}$$

(18)

Thus, after calculating the PV peak power, the number of solar PV modules could be estimated.

2.3.2. Battery Storage Capacity

The battery storage capacity can be calculated using Equation (19) [39], assuming that the DC bus voltage is 24 V.

$$Storage Capacity=\frac{N_c·E_L}{DOD·{\eta }_{out}}$$

(19)

N_C is the number of successive cloudy days at the location [38], which is seven days based on the chosen location, and DOD is the maximum depth of drain of the battery, which is 80%. Consequently, the ampere-hour could be obtained by dividing the storage capacity by the DC bus voltage. According to the battery ampere-hour, the total number of the battery could be estimated.

2.3.3. Battery Charge Controller

A battery charge controller is essential for the secure charging of batteries and the extension of their life span. It needs to handle the PV array’s short circuit current. The battery charger selection is based on the number of module strings and the short circuit current I_sc.

2.3.4. Inverter

The inverter installed needs to be able to withstand the maximum possible AC load. It might be chosen to be 20% over the estimated rated power of the AC loads.

2.3.5. Results of the Design

The results of the design are summarized in

Table 12. Results of the design of the solar system at different operating conditions.

Items	At Feed Pressure, 5 MPa		At Feed Pressure, 6.5 MPa
System approach	Without battery	Utilizing battery	Without battery	Utilizing battery
Number of solar PV module	11–12	25–28	11–13	27–31
Number of batteries (12 V–220 A)	-	75–84	-	80–91
Solar inverter capacity (kW)	3	3	3	3
Battery charger capacity (kW)	-	14.4	-	14.4

. The effect of different operating conditions has been considered.

3. Exergy Analysis

The exergy of a material stream consists mainly of a thermo-mechanical (physical) exergy part and a chemical exergy part. The thermo-mechanical part is defined as the maximum work produced when the temperature and pressure of the system are varied to the temperature and pressure of the surrounding environment (T₀, P₀) while maintaining the same concentration of all system elements. Therefore, a thermo-mechanical equilibrium with the environment is achieved. Chemical exergy is the amount of work that can be conducted when the concentration of each substance in the system varies to the concentration in the environment at the same pressure and temperature as the environment (T₀, P₀). As a result, a state of chemical equilibrium arises. The mathematical description of the flow exergy may be stated as considering the physical and chemical exergy as follows [40,41]:

$$e_f=\left(h-h_0\right)-T_0\left(s-s_0\right)+\sum _{i=1}^n{w}_i\left({\mu }_{i,0}-{\mu }_{i,0}^{\ast }\right)$$

(20)

where the properties denoted by “₀” are determined at the dead state temperature and pressure (T₀, P₀) but the initiation composition or concentration of the flow stream. ${\mu }_{i,0}$ is the chemical potential of “i” at T₀ and P₀ when the composition is that of the state under consideration and ${\mu }_{i,0}^{*}$ represents the chemical potential of “i” when, at T₀ and P₀, the system reaches chemical equilibrium with the environment. $w_i$ is the mass fraction of component “i”.

Exergy is not a conservative quantity in any existing system since exergy destruction (due to irreversibilities) occurs in every real system. It is necessary to determine the flow exergy at each state in the desalination plant before studying the system. The system is examined under steady-state conditions while disregarding the kinetic and potential energy of the fluid streams. So, the exergy balance is represented as follows:

$$\sum {Exergy}_{in}-\sum {Exergy}_{out}=Exergy destroyed$$

(21)

It is critical to clarify that the amount of energy consumed by any system or component should be positive. A negative exergy destroyed value indicates a negative entropy generation, which violates the second law of thermodynamics.

In calculating the specific exergy, the specific enthalpy, specific entropy, and chemical potential have been estimated using the correlations presented by Sharqawy et al. [42].

On the other hand, the specific exergy of the moist air can be determined using Equation (22) presented by Wepfer et al. [43]. Therefore, it may be defined as follows:

$$\begin{gathered} e_{ma}=\left(c_{pa}-{\omega c}_{pv}\right){·T}_0·\left(\frac{T}{T_0}-1-ln\frac{T}{T_0}\right)+\left(1+1.608·\omega \right){·R}_a·T_0·ln\frac{P}{P_0}+R_a·T_0\left[\left(1+1.608\omega \right)· \\ ln\frac{\left(1+1.608{·\omega }_0\right)}{\left(1+1.608·\omega \right)}+1.608·\omega ·ln\frac{\omega }{{\omega }_0}\right] \end{gathered}$$

(22)

In this equation, the physical exergy is referred to by the first two terms and the chemical exergy by the last term. The following parameter values were employed in this investigation: $c_{pa}$ = 1.003 kJ/kg.K, $c_{pv}$ = 1.872 kJ/kg.K, and $R_a$ = 0.287 kJ/kg.K.

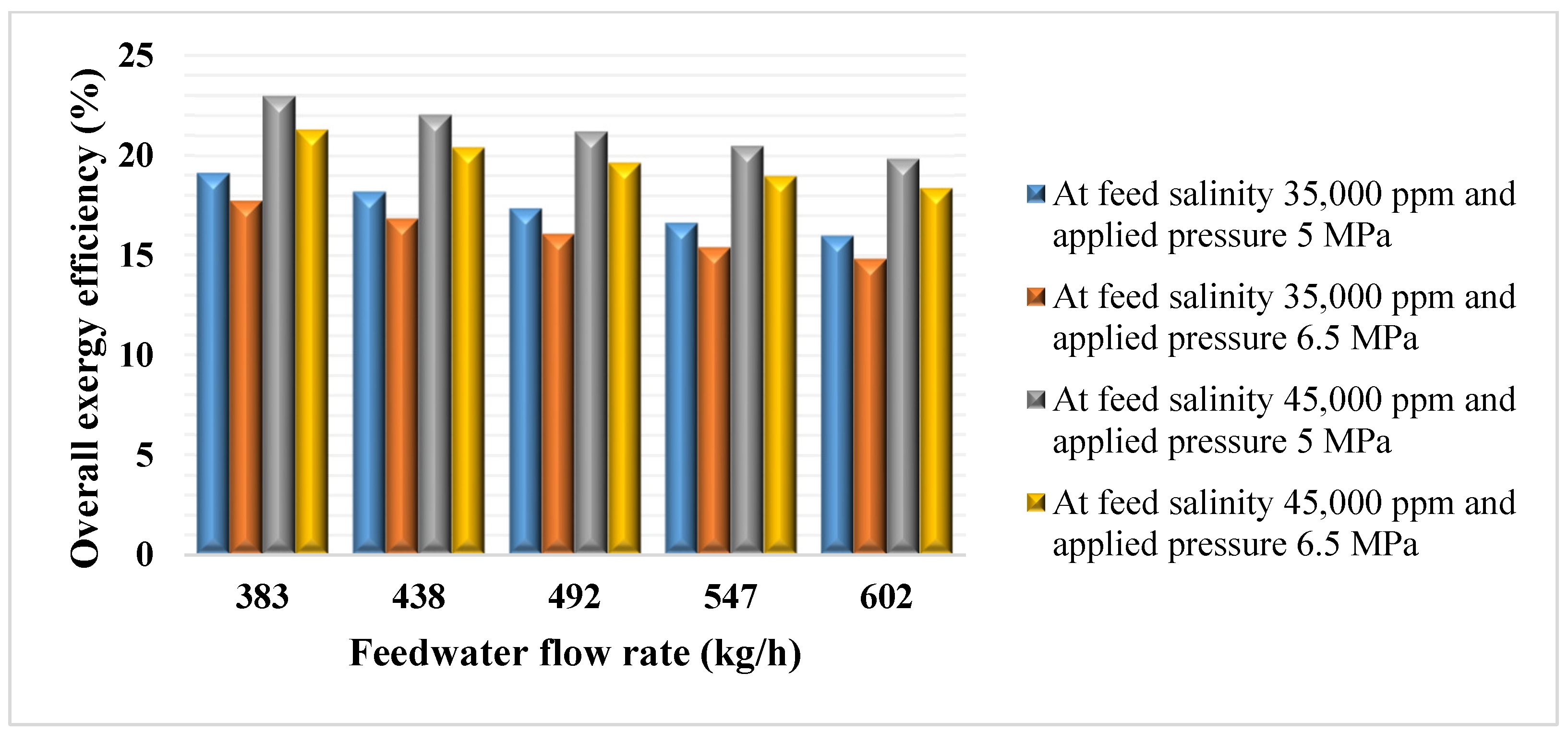
In this work, the values of the properties of the environment are as follows: T₀ = 25 °C, P₀ = 101.325 kPa, $\omega$₀ = 0.0099 kg vapor/kg dry air, and the concentration of salted feed water: TDS₀ = 35,000 ppm.

It is possible to define the exergy balance in terms of output exergetic effect and the required input or driven exergy expenditure, known as product and fuel exergy, respectively.

$${\dot{E}}_P={\dot{E}}_F-{\dot{E}}_D-{\dot{E}}_L$$

(23)

Finally, the exergy efficiency may be represented as follows:

$$\epsilon =\frac{{\dot{E}}_P}{{\dot{E}}_F}=1-\frac{{\dot{E}}_D+{\dot{E}}_L}{\sum {\dot{E}}_{in}}$$

(24)

3.1. Exergy Balance of the Desalination Systems

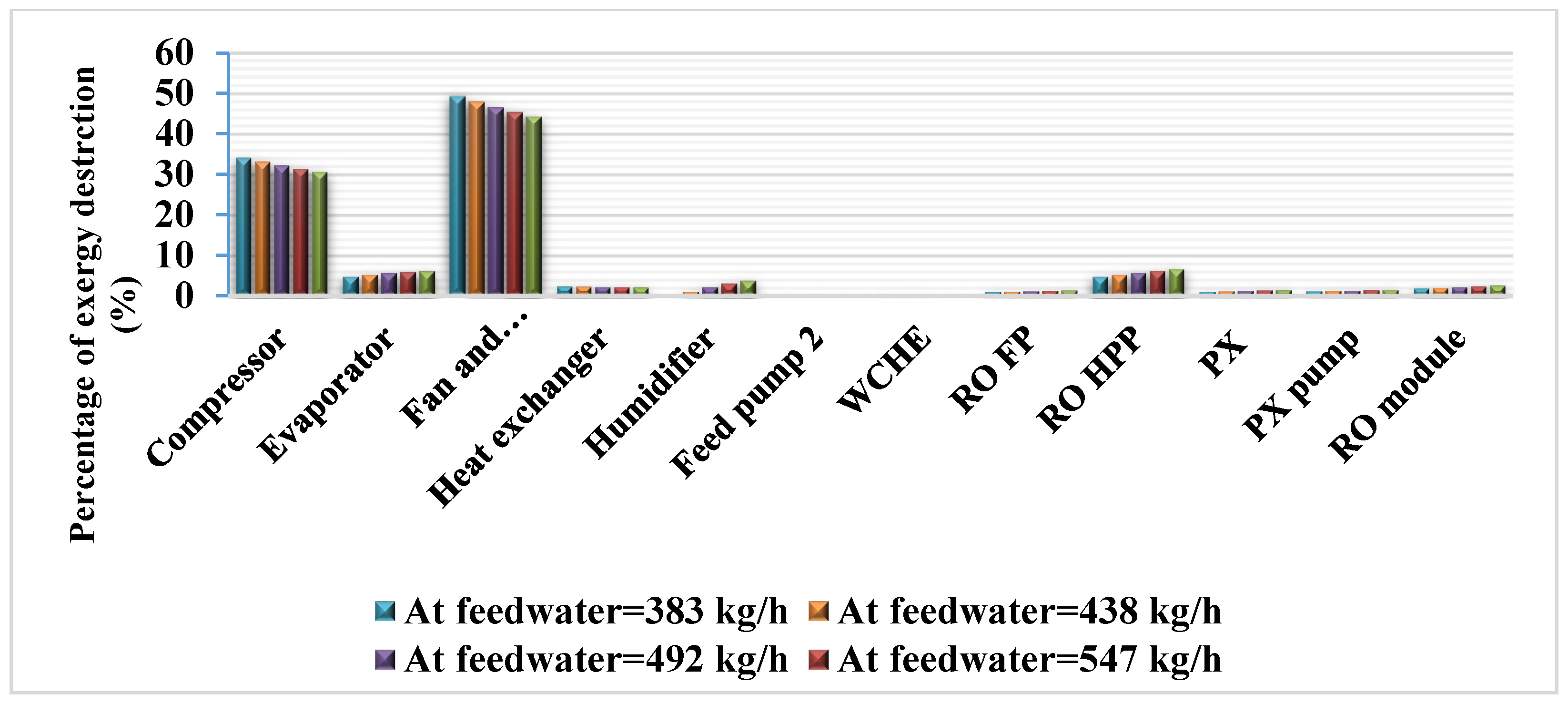
The exergy destroyed at the different components of the desalination systems is compiled in

Table 13. Exergy destruction at each component of the HDH, RO, and hybrid desalination systems.

Components	Exergy Balance
HDH system
Fan and Condenser	${\dot{E}}_{D,cond,fan}=\left({\dot{E}}_{x,R1}-{\dot{E}}_{x,R2}\right)+{\dot{W}}_{Fan}-\left({\dot{E}}_{x,a2}-{\dot{E}}_{x,a1}\right)$
Humidifier	${\dot{E}}_{D,humi}=\left({\dot{E}}_{x,a2}^{PH}-{\dot{E}}_{x,a3}^{PH}\right)-\left({\dot{E}}_{x,Bout}-{\dot{E}}_{x,Fin}\right)-\left({\dot{E}}_{x,a3}^{CH}-{\dot{E}}_{x,a2}^{CH}\right)$
Water-cooled heat exchanger	${\dot{E}}_{D,WCHE}=\left({\dot{E}}_{x,a3}-{\dot{E}}_{x,a4}\right)-\left({\dot{E}}_{x,Bout}-{\dot{E}}_{x,Fin}\right)$
Evaporator	${\dot{E}}_{D,E}=\left({\dot{E}}_{x,R5}-{\dot{E}}_{x,R4}\right)-\left({\dot{E}}_{x,a4}-{(\dot{E}}_{x,a5}+{\dot{E}}_{x,FWout})\right)$
Heat exchanger	${\dot{E}}_{D,HE}=\left({\dot{E}}_{x,R2}-{\dot{E}}_{x,R3}\right)-\left({\dot{E}}_{x,R5}-{\dot{E}}_{x,R6}\right)$
Compressor	${\dot{E}}_{D,comp}={\dot{W}}_{comp}-\left({\dot{E}}_{x,R1}-{\dot{E}}_{x,R6}\right)$
Overall HDH system exergy efficiency	${\epsilon }_{HDH}=\frac{{\dot{E}}_{x,a5}+{\dot{E}}_{x,FWout}}{{\dot{W}}_{comp}+{\dot{W}}_{Fan}+{\dot{W}}_{feed pump,1}+{\dot{W}}_{feed pump,2}+{\dot{E}}_{x,Fin}}$
HDH exergy losses	${\dot{E}}_L={\dot{E}}_{x,Bout}+{\dot{E}}_{x,SWout}$
RO system
Feed pump and Filter	${\dot{E}}_{D,FP}={\dot{W}}_{FP}-\left({\dot{E}}_{x,3}-{\dot{E}}_{x,1}\right)$
High-pressure pump	${\dot{E}}_{D,HPP}={\dot{W}}_{HPP}-\left({\dot{E}}_{x,4}-{\dot{E}}_{x,3}\right)$
Pressure exchanger pump	${\dot{E}}_{D, PX pump}={\dot{W}}_{PX,pump}-\left({\dot{E}}_{x,11}-{\dot{E}}_{x,10}\right)$
Reverse osmosis module without ERD	${\dot{E}}_{D,RO}=\left({\dot{E}}_{x,4}^{PH}-{\dot{(E}}_{x,5}^{PH}-{\dot{E}}_{x,7}^{PH})\right)-\left({\dot{(E}}_{x,5}^{CH}-{\dot{E}}_{x,7}^{CH})-{\dot{E}}_{x,4}^{CH}\right)$
Reverse osmosis module using pressure exchanger	${\dot{E}}_{D,RO}=\left({\dot{E}}_{x,5}^{PH}-{\dot{(E}}_{x,6}^{PH}-{\dot{E}}_{x,7}^{PH})\right)-\left({\dot{(E}}_{x,6}^{CH}-{\dot{E}}_{x,7}^{CH})-{\dot{E}}_{x,5}^{CH}\right)$
Pressure exchanger	${\dot{E}}_{D,PX}=\left({\dot{E}}_{x,7}-{\dot{E}}_{x,8}\right)-\left({\dot{E}}_{x,10}-{\dot{E}}_{x,9}\right)$
Overall RO–PX system exergy efficiency	${\epsilon }_{RO-PX}=\frac{{\dot{m}}_{permeate}.e_{permeate}^{CH}+{\dot{m}}_{brine}(e_{brine}^{PH}+e_{brine}^{CH}-e_{seawater}^{PH})}{{\dot{W}}_{pumps}+{\dot{m}}_{permeate}(e_{seawater}^{PH}-e_{permeate}^{PH})}$
Hybrid system
Overall RO–HDH–PX system exergy efficiency	${\epsilon }_{RO-HDH-PX}=\frac{{\dot{E}}_{P,tot}}{{\dot{E}}_{F,tot}}=\frac{{\dot{E}}_{x,permeate}+{\dot{E}}_{x,a5}+{\dot{E}}_{x,FWout}}{\sum {\dot{W}}_{tot}-({\dot{E}}_{x,SWout}-{\dot{E}}_{x,SWin})}$
Total exergy loss	${\dot{E}}_{loss}={\dot{E}}_{x,Bout}$

.

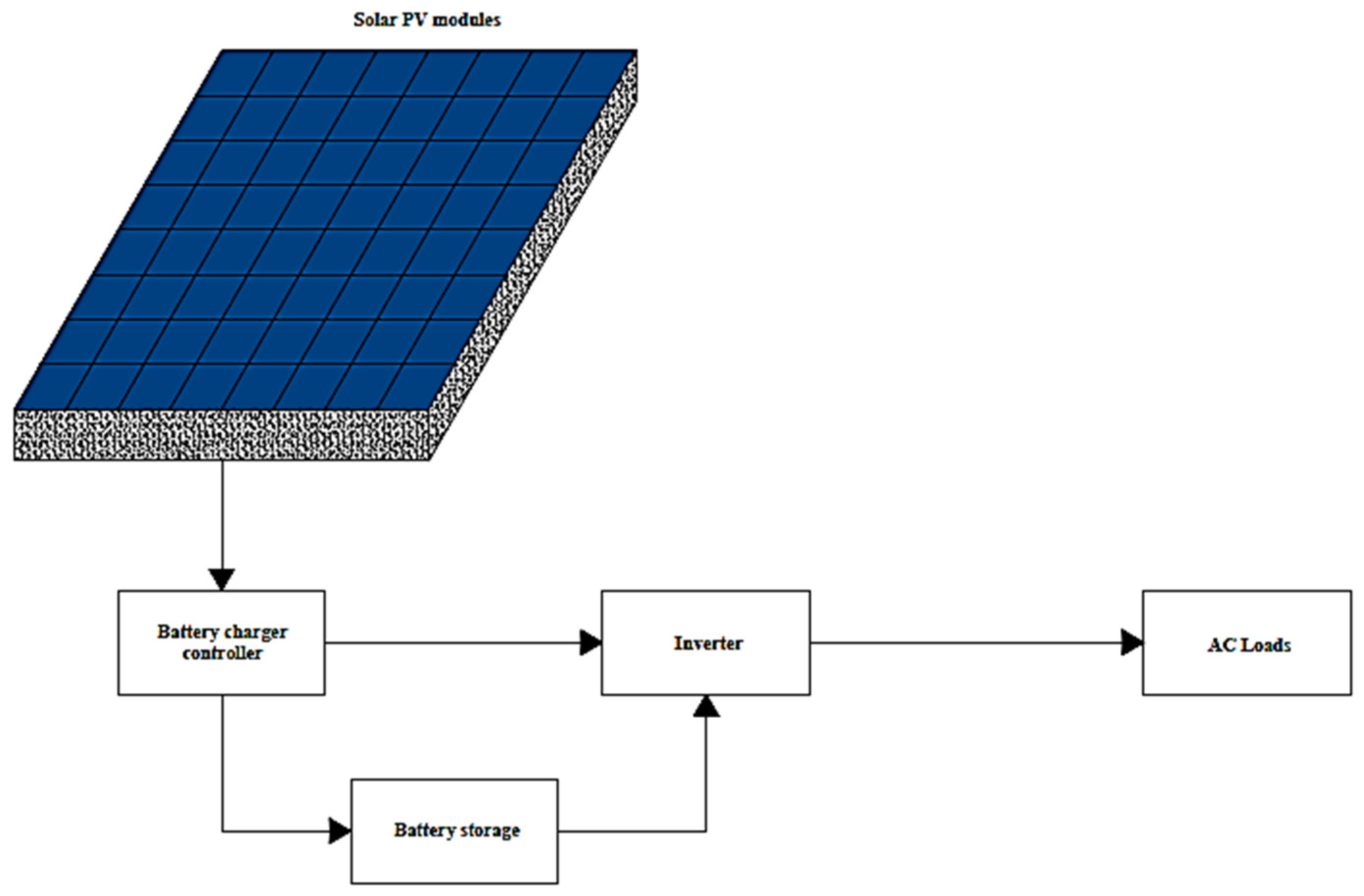
3.2. Exergy Analysis of the Solar PV Panel

The exergetic assessment of the solar PV system, assuming a steady-state flow process, can be obtained using Equation (23). Electrical and thermal energy are the two energy forms produced from solar radiation converted by solar cells. The potential of electrical energy is the main target. In contrast, thermal energy is wasted in the surrounding environment in the form of heat, causing exergy destruction.

The exergy efficiency of the PV module can be calculated using Equation (24).

The fuel exergy of a PV system includes only solar radiation exergy from the sun. The PV fuel exergy can be described as follows [44]:

$$E_{F,PV}=A_{pvm}.G\left[1-\frac{4}{3}\left(\frac{T_{amb}}{T_{sun}}\right)+\frac{1}{3}{\left(\frac{T_{amb}}{T_{sun}}\right)}^4\right]$$

(25)

where the sun temperature $T_{sun}$ is assumed to be 6000 K. $A_{pv,m}$ is the PV module area (m²) and G is the solar radiation intensity (W/m²) defined based on the chosen location.

The product exergy of the PV system can be calculated as [45]:

$$E_{P,PV}=E_{electrical}$$

(26)

The electrical exergy in the output electrical power of the PV module is given as follows [46]:

$$E_{electrical}=V_{OC}·I_{SC}·FF$$

(27)

FF denotes the fill factor, which can be determined using Equation (28). It indicates the most influential power transformation achieved by the PV module [47]. Meanwhile, $V_{OC}$ and $I_{SC}$ are the open-circuit voltage and short-circuit current of the PV module, respectively.

$$FF=\frac{I_m·V_m}{I_{SC}·V_{OC}}$$

(28)

where $I_m$ and $V_m$ are the maximum current and voltage delivered by the PV module, respectively.

However, the thermal exergy can be considered an exergy loss ${\dot{E}}_{thermal}$, which is given as follows:

$$E_{thermal}=Q_{pv,L}\left[1-\frac{T_{amb}}{{Tpv,}_m}\right]$$

(29)

where $Q_{pv,L}$ denotes the heat losses from the PV cells, which can be estimated by:

$$Q_{pv,L}=U_{pv}·A_{pvm}·\left(T_{pv,m}-T_{amb}\right)$$

(30)

where $U_{pv}$ is the overall heat transfer coefficient of the PV module and $T_{pv,m}$ the solar PV module temperature. The overall heat transfer coefficient $U_{pv}$ of a PV module includes convection and radiation losses that can be calculated by:

$$U_{pv}=h_{conv, pv}+h_{rad, pv}$$

(31)

The convective heat transfer coefficient is defined by [33], as follows:

$$h_{conv, pv}=2.8+3V_w$$

(32)

where $V_w$ is the wind speed [38].

The radiative heat transfer coefficient, as described by Watmuff et al. [48], is defined as follows:

$$h_{rad, pv}=ϵ\sigma \left(T_{sky}+T_{pv,m}\right)\left(T_{sky}^2+T_{pv,m}^2\right)$$

(33)

where the emissivity of the panel $ϵ$ is assumed to be 0.9, while $\sigma$ is Stefan Boltzmann’s Constant 5.67 × 10⁻⁸ W/m²K⁴ and $T_{sky}$ is the effective temperature of the sky defined by Watmuff et al. [48], as follows:

$$T_{sky}=T_{amb}-6$$

(34)

The solar PV module temperature, T_pv,m, can be determined using the nominal operating cell temperature, NOCT, which is defined as the temperature reached by open-circuited cells in a module under the conditions G = 800 W/m², $T_{amb}$ = 20 °C, and $V_w$ = 1 m/s [47].

$$T_{pv,m}=T_{amb}+\left(NOCT-20\right).\frac{G}{800}$$

(35)

Thus, the overall system exergy efficiency of the RO–HDH–PX system combined with the solar PV system can be defined as:

$${\epsilon }_{PV}=\frac{{\dot{E}}_{P,tot}}{{\dot{E}}_{F,tot}}=\frac{{\dot{E}}_{x,permeate}+{\dot{E}}_{x,a5}+{\dot{E}}_{x,FWout}+E_{P,PV}}{\sum {\dot{W}}_{tot}-\left({\dot{E}}_{x,SWout}-{\dot{E}}_{x,SWin}\right)+E_{F,PV}}$$

(36)

And, hence, the total exergy loss of the RO–HDH–PX system combined with the solar PV system is:

$${\dot{E}}_{loss}={\dot{E}}_{x,Bout}+E_{thermal}$$

(37)

4. Results

4.1. Exergy Analysis of the RO–HDH–PX System

The exergy analysis of the hybrid RO–HDH–PX system showed that the highest exergetic efficiency was obtained at feed salinity and pressure of 45,000 ppm and 5 MPa, as illustrated in Figure 3. The analysis indicated that the heat pump has a significant impact on the exergy destruction distribution, where the condenser and compressor were responsible for the highest exergy destruction, as shown in Figure 4 and Figure 5. However, no significant differences were observed in the exergy destruction of the different components as a function of operating conditions.

4.2. Exergy Analysis of the Stand-Alone Solar PV System

The variation in the exergetic efficiency and the exergy destruction over a year is shown in Figure 6. In the summer season, the exergy efficiency decreases due to the increase in the value of the irreversibilities with global radiation. In contrast, the exergetic efficiency has the highest values at the beginning and end of the year, when the value of the irreversibilities decreases. The maximum exergetic efficiency achieved was 24.06% in February, while the minimum was 16.49% in July (data from 2022).

4.3. Exergy Analysis of the RO–HDH–PX System Integrated with Solar PV

The hybrid RO–HDH–PX system combined with the solar PV system has been examined from an exergy analysis perspective. In the exergy analysis of the integrated hybrid system, the cooling capacity of the heat pump evaporator was considered as the product exergy in addition to the electrical energy produced by the solar PV system and freshwater produced by the RO and HDH systems. The integrated system RO–HDH–PX–PV has been investigated under different circumstances regarding feed water pressure, salinity, and mass flow rate. Moreover, the effect of solar irradiance variations over the year was included. However, as clarified in Section 4.2, the highest and lowest exergy efficiencies for the solar PV system were found in February and July; consequently, the overall exergy analysis for the whole system was conducted just for those months, which is the margin of the highest and lowest exergetic efficiency for the whole system.

The exergy efficiency has been affected by the integration with the PV system as a result of the exergy loss of the solar PV system throughout the year. Figure 7a–d shows the exergy efficiency of the RO–HDH–PX–PV system in February at different feed pressures, salinities, and mass flow rates. In contrast, Figure 8a–d shows the overall exergy efficiency in July. An increase of about 3% in exergy efficiency was observed in the RO–HDH–PX–PV system between February and July. Furthermore, the overall exergetic efficiency slightly improved as the percentage of increase varied from 1.25% to 2.15% compared to the RO–HDH–PX system. Meanwhile, in July, it slightly deteriorated compared to the RO–HDH–PX system by 0.15% to 1.12%. This was found to be consistent with the results indicated in the exergy analysis of the stand-alone solar PV system, where the addition of the product and fuel exergies of the solar PV system to the overall exergy analysis of the RO–HDH–PX system followed the same magnitude of increase and decrease in the exergy efficiency of the RO–HDH–PX–PV system in February and July during the year 2022, respectively.

4.4. Cost Analysis of the RO–HDH–PX–PV Hybrid Desalination System

The costs of the various components used in the desalination unit, based on the Egyptian market prices for 2022, are given in

Table 14. Estimated capital cost for the RO–HDH–PX–PV components (2022 Egyptian market).

System Components	Cost (USD)	System Components	Cost (USD)
RO system		Solar PV system
Seawater FP	750	Solar PV panel	0.188/W
Seawater HPP (4.5 MPa delivery pressure)	1500	Solar inverter	290
Seawater HPP (6.5 MPa delivery pressure)	2000	Battery	59.9/kWh
RO membrane Film-tec SW30-4040	464/element	Battery Charge Controller	375
Pressure exchanger	2000
HDH system
Centrifugal fan	100	Feed pump I	40
Flexible duct	15	Heat pump evaporator	40
Compressor	464	Piping	40
Heat pump condenser	50	Steel construction stands	150
Water eliminator	20	Insulated ducts	30
Control panel	25
Two water sprayers	5
Installation			10% of capital cost
Maintenance ($\mathbf{M}/\mathbf{y}\mathbf{r}$)			5% of capital cost/year

. To obtain the cost of the freshwater produced by these systems, other parameters must be taken into consideration: assuming installation costs to be 10% of the capital cost; expected lifetime, N, 10 years; inflation rate, dd, 15.637%; and interest rates ii, 11.75% (based on 2022 Egyptian economic statistics) [49,50]. In addition, a yearly maintenance cost, M/yr., of 5% of the capital cost has been considered.

The life cycle cost (LCC) of the hybrid system (RO–HDH–PX–PV) is the total of all current costs of the components RO, HDH, and PV, plus installation and present worth of the maintenance cost (MC), which is calculated using Equation (38).

$$MC=\left(\frac{M}{yr}\right)\times \left[\frac{1+ii}{1+dd}\right]\times \left\{\frac{1-{\left(\frac{1+ii}{1+dd}\right)}^N}{1-\left(\frac{1+ii}{1+dd}\right)}\right\}$$

(38)

All components are estimated to have a lifespan of 10 years, except for the batteries and RO membranes, which have a lifespan of 5 years. After five years, batteries and RO membranes must be replaced. The value of the additional set of batteries and RO membranes can be calculated using Equation (39), where CC_x is the present worth value of the batteries or RO membranes.

$${CC}_{x,PW}={CC}_x·{\left(\frac{1+ii}{1+dd}\right)}^N$$

(39)

Figure 9 shows the unit cost of freshwater for the hybrid RO–HDH–PX–PV system, with and without batteries, and at different feedwater operating pressures (5 MPa and 6.5 MPa). The analysis shows that the system implemented with battery storage has the lowest unit cost despite the extra cost of the storage system on the total cost. The reason is that the productivity of the unit without a storage system is low because it has only 10 h of operation. Also, it was observed that the unit cost of freshwater decreases as the feed pressure decreases, while energy consumption decreases (mainly due to the high-pressure pump). The minimum unit cost of freshwater for the system implemented with battery storage results in 3.22 USD/m³ at a feedwater pressure of 5 MPa.

5. Conclusions

In this study, a hybrid desalination system based on membrane and thermal desalination technologies (RO–HDH) has been investigated.

The hybrid system was examined at different feedwater pressures, salinity, and mass flow rates. The HDH system was optimized to accommodate hybridization with the RO unit, where the brine from the RO unit feeds the HDH unit. Furthermore, a solar PV system was used to power the proposed hybrid desalination system, which was designed and evaluated considering the operational and environmental conditions. The findings can be summarized as follows:

• The exergy analysis of the RO–HDH–PX system indicated that the condenser was responsible for the major exergy destruction, (from 43% to 49%, depending on the operation conditions). The highest exergy efficiency reached by the overall system was 23%.
• The exergy analysis for the solar PV system revealed that the exergy efficiency is much higher in winter than in summer (reaching 7.5%) due to the high thermal losses.
• The integration of the solar PV system increased the sustainability of the hybrid RO–HDH–PX system. The system implemented with battery storage showed a low freshwater cost compared to that without a battery. The unit cost of freshwater ranged from USD 3.22/m³ to USD 5.1/m³ when a battery was used; in contrast, it varied from USD 3.96/m³ to USD 7.1/m³ in the system without battery storage.