Abstract
Trajectory data holds pivotal importance in the shipping industry and transcend their significance in various domains, including transportation, health care, tourism, surveillance, and security. In the maritime domain, improved predictions for estimated time of arrival (ETA) and optimal recommendations for alternate routes when the weather conditions deem it necessary can lead to lower costs, reduced emissions, and an increase in the overall efficiency of the industry. To this end, a methodology that yields optimal route recommendations for vessels is presented and evaluated in comparison with real-world vessel trajectories. The proposed approach utilizes historical vessel tracking data to extract maritime traffic patterns and implements an A* search algorithm on top of these patterns. The experimental results demonstrate that the proposed approach can lead to shorter vessel routes compared to another state-of-the-art routing methodology, resulting in cost savings for the maritime industry. This research not only enhances maritime routing but also demonstrates the broader applicability of trajectory mining, offering insights and solutions for diverse industries reliant on trajectory data.
1. Introduction
Trajectory mining (TM) is a data mining technique used to extract knowledge from trajectory data, which refer to the sequence of spatial locations visited by an object over time [1]. Trajectory mining has been widely applied in various fields, including transportation, health care, tourism, surveillance, and security. In health care, it has been applied to study patient movements and predict disease outbreaks [2]. In tourism, it has been applied to understanding tourist movements to enhance tourist experiences [3,4] and the planning of infrastructure development [5]. In surveillance and security, it has been used to analyze the movement of people and vehicles to detect suspicious activities [6,7]. Above all, in transportation, trajectory mining has been employed to find the most efficient routes for vehicles based on historical trajectory data [8,9], to analyze and predict traffic congestion patterns to optimize traffic flow and reduce congestion [10], and to improve transportation systems overall.
Trajectory mining has emerged as a transformative field in data analysis [11], offering profound advantages across diverse industries by harnessing the power of movement data. In an era marked by an unprecedented proliferation of location-aware devices and systems, trajectory mining stands as a potent tool for extracting valuable insights from the patterns and behaviors of objects or entities as they move through time and space [12]. The long list of applications [13] showcases the ability of TM to drive data-informed decision making, reduce costs, and enhance safety and sustainability in an array of domains. As the world continues to generate vast volumes of movement data, trajectory mining remains a vital tool for unlocking actionable insights and shaping a more efficient, interconnected future.
The extraction of patterns from trajectory data has gained paramount importance in the maritime sector, revolutionizing the way vessels navigate the world’s oceans. At the heart of this transformation is the Automatic Identification System (AIS), which has enabled the collection of extensive trajectory data from ships. This real-time tracking system mandated by maritime regulations has ushered in an era of unprecedented transparency and safety at sea. AIS data provide a comprehensive record of vessel movements, including their positions, speed, and course overground, thereby enhancing navigation, safety, and efficiency. With AIS-derived trajectory data, shipping companies can optimize routes to minimize fuel consumption and reduce environmental impact, resulting in substantial cost savings and lower emissions. Furthermore, these data are instrumental in maritime security, allowing authorities to monitor vessel movements and detect any suspicious or unauthorized activities, thereby safeguarding national waters [14,15,16]. In addition to safety and efficiency, trajectory mining with AIS data holds immense promise for future advancements in maritime logistics, port management, and global trade. By analyzing historical and real-time trajectories, stakeholders can make informed decisions, improve port operations, and streamline the flow of goods worldwide. In summary, the availability of AIS-generated trajectory data has catapulted trajectory mining into a pivotal role within the maritime sector [17]. It not only ensures safer and more efficient sea voyages but also underpins global commerce, environmental stewardship, and national security on the high seas.
A prominent limitation in existing research on trajectory mining is the lack of a mechanism designed to effectively balance the tradeoff between exploration and exploitation of acquired data. Many approaches outlined in relevant literature tend to prioritize the exploitation of abundant data associated with historical routes at the expense of exploration. Consequently, this approach results in a biased and oversimplified strategy that merely “queries” the identified routes rather than integrating them to construct a comprehensive network. This ultimately yields a less informative scheme. In this direction, the proposed approach takes advantage of AIS data collected by multiple vessels over an extended time period, encompassing various seasons and weather conditions. Leveraging this rich repository of naval trajectory information, we build on a network abstraction that represents the intricate web of paths traversed by vessels. This network not only captures the historical behavior of vessels but also accounts for their responses to diverse environmental factors. To enhance the efficacy of route recommendations, we integrate this network information with real-time weather condition data, ensuring that the selected trajectories are optimized for prevailing environmental conditions. By employing sophisticated shortest-path algorithms, our approach identifies and recommends the most efficient routes for vessels, ultimately improving navigation, reducing fuel consumption, and enhancing overall maritime operations. This innovative fusion of historical naval path data, real-time weather insights, and advanced optimization techniques constitutes a powerful and adaptive approach to trajectory-based route planning in the maritime industry. This work presents the initial potential of an AIS-based routing optimization approach by extracting the shortest path between two waypoints and benchmarking the acquired results with readily available open-source libraries for navigation management that have been well-established within the maritime domain.
The contributions of the current work can be summarized as follows:
- The exploitability of AIS data in path planning and weather routing applications is limited. Therefore, this research builds on the exploitation of past vessel trajectories derived from AIS data and develops a fine-tuned grid of possible vessel routes.
- The development of an A* search algorithm for optimal path planning based on the historical vessel routes.
Section 2 provides an overview of research on trajectory mining in various fields and emphasizes on the works in the maritime domain and the problems they tackle. Section 3 provides an overview of the available data that were employed to build the network abstraction of the vessel paths. Section 4 describes the methodological approach that we propose for finding optimal paths using shortest-path principles based on the network information and introduces a grid-based approach that solves several inconsistencies and further improves the performance of our approach. Finally, Section 6 briefly discusses the main findings of our work and concludes the paper with suggestions for future research directions.
2. Related Work
The application of trajectory mining has its origins in the analysis of video data, aiming at the tracking of objects’ movement through the spatiotemporal analysis of their position in consecutive video frames [18] (e.g., ball movement in soccer videos). With the advent of GPS and the availability of the respective position data, applications quickly moved towards the modeling of the movement of real-world objects [19], such as persons or animals [20,21], vehicles [22], vessels [23], etc. Various data mining techniques have been applied to trajectory data, depending on the problem and the information carried by the trajectories, ranging from clustering and classification to anomaly detection and trajectory prediction. Related works are presented below, organized by technique and application domain, and their main requirements and results are discussed.
Classification From the early work on TraClass [21] that introduced the concept of trajectory partitioning, then applied clustering to trajectory segments to the more recent works on movelets [24], the process is almost always similar: (i) partition the trajectory into subtrajectories of either equal length or duration or based on changes in the trajectory properties, (ii) define a similarity or distance measure for comparison of subtrajectories that are considered the features that describe each trajectory, and (iii) expand this measure to calculate the similarity between a prototype trajectory (i.e., class representative) and all other trajectories. In a similar line, the authors of [25] proposed a shapelet-based [26] classification framework for the detection of specific search-and-rescue maneuvers performed by vessels. They employed a genetic algorithm to find the best shapelets to use as features and managed to significantly reduce the complexity of their approach without a significant loss in terms of accuracy. More recent approaches attempt to classify the trajectory as a whole, either extracting features from the distributions of speed, longitude, latitude, and course in the whole trajectory [27] or by examining the trajectories as images [28,29] and applying popular classification algorithms to them (from random forests to CNNs). In this line, the authors of [30] employed a segmentation and clustering approach to identify different types of travel patterns, such as regular commuting, leisure travel, and airport transportation based on data on ride-hailing passengers.
Clustering techniques are the most popular in trajectory mining since they allow for the creation of meaningful groups of trajectories or trajectory segments that share the same location, shape, or movement characteristics. TraClus [31], the first trajectory clustering algorithm, is based on a partition-and-group approach and a composite distance function for trajectory segments and combines the perpendicular, parallel, and angle distances. DBSCAN is a basic algorithm that was extended to capture the composite distance function. In [32], DBSCAN was incorporated into a holistic, modular framework (TREAD) that identifies vessel traffic patterns in real time to realize an informed decision-making procedure through causal analysis and pattern recognition. The authors of [33] were able to associate vessel types (containers, Ro-Ro, etc.) with route segments by utilizing geometry-based fuzzy membership functions. More recently, the authors of [34] presented another extended version of DBSCAN that, apart from the locational and directional features of the moving object, also considers its speed in an attempt to create clusters in which the objects move close to each other, almost in parallel, and with similar speeds. The authors of [35] conducted a comprehensive survey of trajectory clustering techniques, including spatial and time-dependent clustering, partition and group clustering, and semantic trajectory clustering. They also summarized the main distance and similarity measures that are used by the algorithms.
Outlier and anomaly detection techniques usually rely on clustering or classification in the first step in order to find the trajectories that lack a corresponding match within the dataset. The applications vary from object tracing to climate monitoring and road network management, and apart from classification and clustering, statistic-based and density-based techniques are also employed to find samples that diverge from the normal distribution [36,37]. Once again, a representation of the trajectory or subtrajectory in the first step and a distance or similarity measure in the second step are needed to group similar items together and detect outliers. The anomaly detection framework proposed in [38] provides a different approach that combines a maritime trajectory model as a basis comprising moving objects’ trajectory streams with a grid partitioning of the space to discover infrequent regions that contain outlying trajectory segments or segments that diverge from the main streams. In [39], a complex event recognition framework was introduced, utilizing event calculus for real-time outlier detection in AIS data streams corresponding to vessel trajectories.
Graph-based techniques have frequently been employed to trajectory data, especially in the transportation domain. Authors usually represent the movement trends of the monitored entities on a graph that contains POIs, entities (i.e., persons, vehicles, or vessels) as nodes, and their connectivity across spatiotemporal and semantic dimensions as edges in order to create a network or graph abstraction. Then they perform queries that extract frequent patterns from the graph. In [40], the authors exploited historical data of vessel trajectories in order to understand maritime routes and traffic. In the same context, the authors of [41] presented a methodology for extracting the navigation network of an area from AIS data. The nodes in the final graph represent points of interest with respect to the vessel trajectories, such as ports or points of major change in speed and direction (waypoints), and the edges are the result of the clustering of trajectory segments from multiple vessels. The segments share similar location, direction, and speed properties. In a slightly different approach, the authors of [42] employed a graph-based spatiotemporal convolutional network trained on past vehicle trajectories to predict vehicle trajectories in an autonomous driving scenario. The vehicles were considered the nodes of the graph, and their past trajectories were encoded as node features. The graph was fully connected, but the edges’ weights model the effect that each vehicle has on surrounding vehicles. The proposed approach allows for the simultaneous prediction of the future location of all vehicles at once.
Trajectory prediction is one of the most prominent tasks, with many applications in tourism, transportation, traffic management, etc. The comprehensive survey of human trajectory prediction reported in [43], the surveys of machine learning approaches for vehicle trajectory prediction presented in [44,45], and the recent survey of vessel trajectory prediction techniques [46,47] all agree that either physics- (turn rate, velocity, and acceleration) or statistics-based methods (Kalman filters and Monte Carlo methods) can be employed to predict the future position of a moving object, and they propose the use of deep learning techniques to implicitly capture the complex dynamics of motion, especially in the context of other moving objects, in order to predict the evolution of a trajectory. In [48], the authors proposed a transformer-based context-aware network that captures POI visiting sequences from trajectories, enriches them with semantic and social context, and predicts the next POI to be visited in an ongoing trajectory. Similarly, the authors of [49] proposed a spatiotemporal LSTM network that processes semantic trajectories from Foursquare and predicts the future locations of persons moving around a city. These works go beyond the traditional spatiotemporal representation of trajectories and capitalize on multiaspect semantic trajectories [50], which, in turn, creates new research opportunities in the trajectory mining domain.
All the techniques and approaches presented so far cover a wide range of applications of trajectory mining in various domains. In the maritime sector, trajectory mining techniques have been adopted recently to analyze vessel movements and improve vessel safety and efficiency. In [51], TM was used to analyze vessel movements in a port. The study used trajectory clustering to identify vessel behavior patterns, such as berthing, departure, and maneuvering. The results can be used to optimize port management and improve vessel safety. Another study [52] involved the application of trajectory mining to analyze the movement patterns of fishing vessels. The study used trajectory segmentation and clustering to identify different types of fishing behavior, such as trolling, drifting, and anchoring. The results can be used to improve fishing management and reduce overfishing.
The use of the Automatic Identification System (AIS) in vessels has created an enormous amount of trajectory data that can be employed in a multitude of ways. In the following section, we present a novel methodological approach that utilizes knowledge from historical trajectory data in order to support a routing optimization algorithm for the maritime sector. Preliminary experimental results demonstrate that AIS routing lowers the overall computational cost of traditional brute-force graph- and grid-based methods and ideally exploits the acquired historical routes by employing a tailor-made sea grid of alternative waypoints.
3. Data Overview and Processing
Raw AIS data are acquired by transmitters installed on board, synchronizing with the closest AIS station at fixed intervals, where they can be aggregated and stored in streams via a TCP/IP protocol. They consist of the vessel coordinates at a specific time, the vessel speed that corresponds to the overground speed (GPS speed), and the vessel overground heading. The specific dataset used in this work corresponds to approximately ≈ routes (round-trip voyages) of cargo ships (container ships) in the Mediterranean sea. A limited version of the dataset (trajectories) is depicted in Figure 1 for visualization purposes.
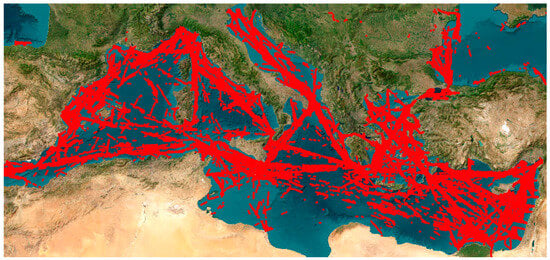
Figure 1.
Acquired AIS routes (sample).
To employ vessel trajectory patterns, a preprocessing step is required that can denoise the dataset and create geographic regions at sea (in the form of polygons) that indicate the traffic patterns of vessels. The extraction of traffic patterns is visualized in Figure 2.
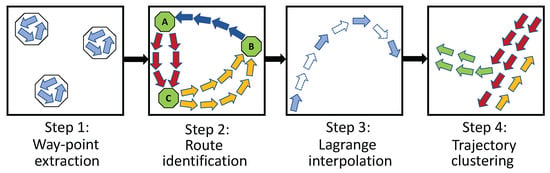
Figure 2.
Preprocessing steps for the extraction of maritime traffic routes.
Step 1. The first step is the extraction of waypoints. Waypoints are defined as regions at sea where vessels stop completely, indicating ports or anchorage areas. By identifying such areas, the origin and destination points of a vessel can be determined. To detect such points, the AIS positions with zero speed are kept. Then, the DBSCAN algorithm is employed to cluster together positions of high density close to each other and remove any possible outliers, e.g., single positions with zero speed farther away from the ports or anchorage areas that may have been produced due to GPS errors. Empirical experiments indicated that a value of = 2 km (an average radius of medium-sized ports) and a value of yield the best results when compared to the port database of the World Port Index1 (WPI). It is worth noting that the WPI does not contain information about anchorage areas; therefore, a unified method for identifying both ports and anchorage areas is required. Next, the resulting clusters are converted to convex hulls (the minimum bounding geometry that contains all positions of a cluster), and the final convex hulls are used as waypoints.
Step 2. The next step is the identification of the routes. In this step, we simply segment the trajectories of the vessels based on the waypoints to incorporate the origin–destination ports in the dataset. The result of this step is subtrajectories that start and end at a waypoint.
Step 3. The third step consists of interpolation of the AIS positions of each trajectory. The reason for this step is to fill the gaps that may arise in real vessel trajectories. Such gaps may affect the quality of the traffic patterns extracted with the proposed methodology, since they directly affect the quality of the clustering step that follows (Step 4). It is quite common to have such gaps in vessel trajectories because although vessels must carry an AIS transponder, the transponder does not need to be switched on [15]. This is a common tactic when vessels want to hide their tracks and conceal their whereabouts to avoid piracy attacks or perform an illegal act themselves (e.g., fishing in prohibited areas). AIS gaps in trajectories may also happen either due to poor weather condition; because the receivers are deliberately jammed; or, on rare occasions, because of packet collisions that take place when the AIS receivers are flooded with messages. To this end, Lagrange interpolation, a well-known and established algorithm was employed for each trajectory, which is preferred over Newton interpolation because it provides more accurate approximations. The interpolation itself is not the focus of our study; nevertheless, the various interpolation techniques can be used in the future to further study their effects on our approach.
Step 4. The fourth and final step is trajectory clustering. In this step, a modified iteration of the DBSCAN algorithm was utilized to cluster trajectories involving multiple vessels following the same route (from waypoint to waypoint). This clustering was based on various factors, including the geographical location, speed, and heading of the AIS positions. Specifically, the surveillance area was segmented into a grid with a resolution of —a resolution that matches the Copernicus Climate Change Service2 (C3S) and can be utilized in future studies to find optimal route recommendations. In each grid cell, the standard deviations of speed over ground, course over ground, and distance between AIS positions were calculated. We used the standard deviation because it measures the amount of variation or dispersion of a set of values. Positions with the lowest dispersions of speed, heading, and Haversine distance need to be grouped together. Then, a modified DBSCAN algorithm is employed to further cluster the AIS positions of each vessel type and origin–destination waypoints in each grid cell. The modified DBSCAN algorithm employs two more parameters other in addition to the and parameters, which remain the same: the s and c parameters, refer to the speed and the course over ground, respectively. The values of s and c used for the clustering are the previously calculated standard deviation values of speed and course over ground for each grid cell. is the standard deviation of the distance. is set to 6 because we need at least two three-position-length routes per itinerary. Three is the minimum number of positions a trajectory should have to be considered valid. Therefore, clusters with one route are not considered common and are excluded from the process. Then, the convex hulls per cluster are calculated. Consequently, numerous polygons emerged along each route, with each polygon representing the specific area where vessels operated with similar speeds and headings. An illustration of such polygons is depicted in Figure 3. More details about the preprcessing steps can be found in [34,41].
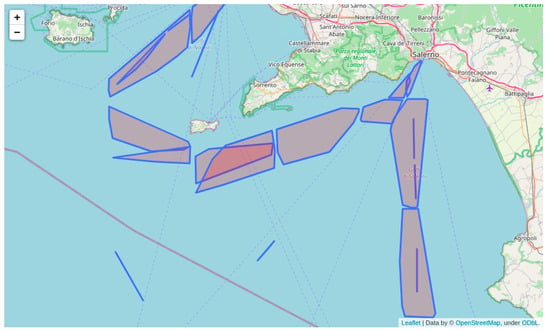
Figure 3.
Convex hull of AIS trajectory clusters.
4. Trajectory Mining and Ocean Path Planning
To the best of our knowledge, this is the first attempt to integrate assimilated experience modeled by AIS clusters of vessel trajectories with a routing optimization algorithm in the context of ocean route planning. The main concept and innovation behind this method is to group similar navigational patterns of past routes for a specific vessel type (such as container ships, LNG ships, passenger ships, RO-RO, etc.), creating a dense network that defines the navigational and operational boundaries in terms of speed and heading. This network of past routes can then be leveraged to significantly automate and expedite the decision-making process, proposing alternative optimal routes in terms of operational efficiency and environmental compliance for vessels with similar characteristics (Deadweight-DWT and Cargo Carrying Capacity-TEUs). Through this approach, we can develop a custom sea grid by identifying and querying the appropriate set of clusters (past trajectories) based on a specific origin and destination.
The upcoming sections provide a comprehensive demonstration of the key conceptual steps, mathematical modeling, and algorithmic procedures required to successfully implement the proposed methodology. Through this detailed explanation, readers can gain a clear understanding of how to effectively execute and utilize this approach.
4.1. Derivation of AIS Clusters Based on Shortest-Path Principles
In this section, we describe our methodological approach to extract AIS clusters from the initial dataset corresponding to clusters of past trajectory segments of cargo ships based on a predefined route (ORIGIN-DESTINATION) and locations. In the following, we demonstrate the algorithmic procedure to find an alternative path based on AIS data for an example voyage, from Venezia to Piraeus.
The process is initiated by acquiring a publicly available broad sea grid. Here, we utilized a sea grid with one degree of granularity (Figure 4). Based on this broad sea grid, we employ one of the most prominent shortest-path algorithms, namely the A* algorithm, to extract a rough approximation of the shortest path between our origin and the destination.
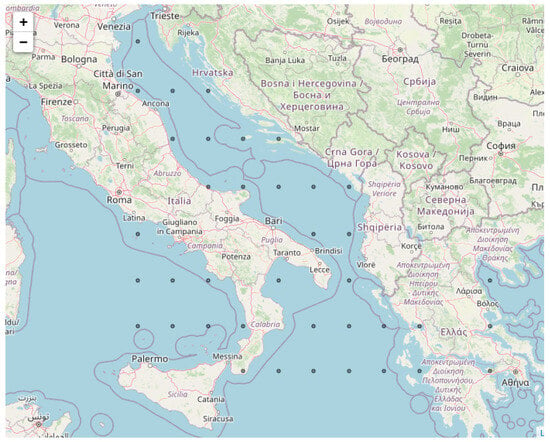
Figure 4.
Publicly available sea grid (1 degree of granularity).
The A* algorithm is heuristic search algorithm that is commonly used for path-finding and routing optimization problems. It is a best-first search algorithm that aims to find the shortest path between two points in a graph by combining both the actual cost of the path and an estimate of the remaining cost to reach the goal. This estimate is typically based on heuristics such as the Euclidean distance or the Manhattan distance between the current node and the goal node.
The theoretical backbone of A* is inextricably linked with the Bellman equation and optimality [53] in the sense that it is approximating, recursively, the functional equation that describes the optimal solution (here, the shortest path) as a function of the current state and all possible future states depending the current. The evaluation of the “optimal” state in each step of the algorithm is conducted by defining a value function (V, i.e., policy function).
A* incorporates a cost function that combines both the actual cost of the path from the start node to the current node, as denoted by , and an estimate of the remaining cost to the goal node, as denoted by . The cost function is defined as:
where n is the current node being evaluated. The algorithm uses this cost function to prioritize the exploration of nodes with lower values of , as these are likely to lead to a shorter path to the goal node. Furthermore, A* uses a priority queue to keep track of the nodes that have been evaluated but not yet expanded. The priority queue orders the nodes based on their values, with the node with the lowest value at the front of the queue. The algorithm proceeds by iteratively selecting the node with the lowest value from the priority queue, expanding it, and adding its neighboring nodes to the priority queue. The algorithm continues until the goal node is reached or the priority queue becomes empty, indicating that no path exists. By employing the A* algorithm on the aforementioned sea grid for the selected voyage, we obtain the result depicted in Figure 5.
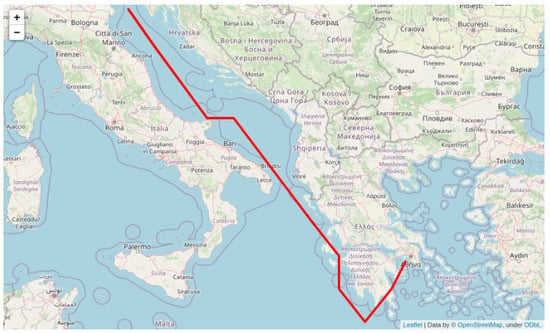
Figure 5.
Shortest-path route for Venezia–Piraeus based on A*.
As evidenced by the graph depicted above, the route has several inherent disadvantages and issues. Some of these issues include abrupt deviations in heading, waypoints located on land, and a lack of information regarding the speed adopted for each waypoint. These characteristics make the route suboptimal in terms of vessel utilization. To make this route feasible, it is necessary to invest significant time and resources in refining and adapting it. This would involve building a dynamic graph for each waypoint and generating a range of different possible pathways by taking into account constraints such as speed (estimated time of arrival (ETA) compliance) and distance from shore. However, this process would be time-consuming and computationally expensive and may require a substantial investment of resources.
To overcome this, we exploit the shortest-path route to derive the ideal set of AIS clusters containing past segments of trajectories undertaken by cargo ships, corresponding to the voyage of interest. Each cluster of AIS data is described by the convex hull (polygon) of the points (lat and lon coordinates) lying on the boundaries and contains the set of features referenced below, outlining the average, the minimum, and maximum, as well the standard deviations of the speed and heading of the trajectories comprising this specific cluster (Figure 6). In order to extract the set of clusters corresponding to this route, we utilize the centroid of each polygon and calculate the distance from each waypoint extracted by the shortest-path route employed by A*.
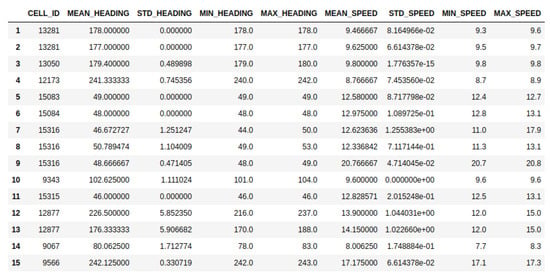
Figure 6.
Snapshot of features comprising AIS clusters.
The output of Algorithm 1 is a subset of clusters bounded by the shortest path initially employed by A* in terms of proximity, utilizing an arbitrary, broad sea grid. These clusters contain past trajectories segments of cargo ships corresponding to the specified origin–destination voyage (Venezia–Piraeus), see also Figure 7.
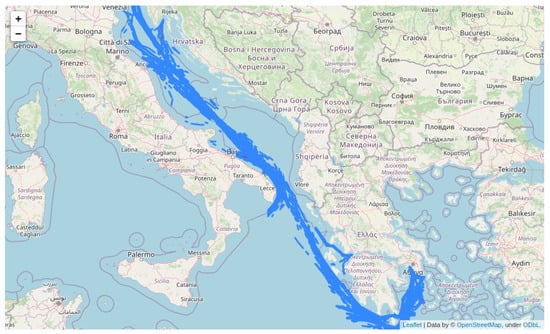
Figure 7.
Extracted AIS clusters corresponding to Venezia–Piraeus voyage.
| Algorithm 1 Algorithm for AIS cluster extraction based on a path. |
| Require: shortest path from A* A* based on sea grid Require: Convex Hull of clusters from initial processing Require: Centroids from Require: candidate AIS clusters list 1: for each do 2: for each do 3: if then 4: if then 5: add to 6: Return |
4.2. Building the Custom Grid
Utilizing the extracted polygons (AIS clusters) as a foundation, we aim to employ a tailor-made grid bounded by the convex hull of each cluster in order to construct a sea grid to be used as a basis for a routing optimization algorithm. To accomplish this goal, we initiate the process by constructing an adversary grid that is situated within the rectangular area defined by the latitude and longitude coordinates of both the starting and ending points of the selected voyage. The grid is constructed utilizing a user-defined granularity ( step here). Each point is added to the final constructed sea grid if it lies within the boundaries of the convex hull of the previously mentioned extracted AIS clusters. Algorithm 2 outlines the exact steps required to realize the aforementioned procedure.
| Algorithm 2 Algorithm for grid construction. |
| Require: Convex Hull of filtered clusters from initial processing Require: Rectangle defining bounding box for selected voyage ← 1: for each with step 0.1 do 2: for each with step 0.1 do 3: if (, ) ∈ then 4: add (, ) to 5: Return |
The employed sea grid with 0.1 degrees granularity is depicted in Figure 8.
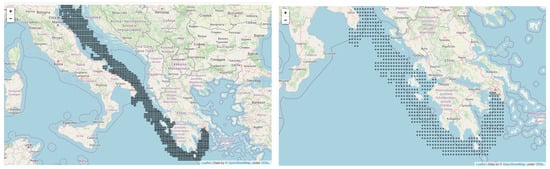
Figure 8.
Sea grid constructed based on past AIS trajectories.
By utilizing AIS clusters of past trajectories, we also have the option to employ a custom, adaptive sea grid based on a set of constraints like narrow sea passages, emission control areas (ECA/SECAs), piracy zones, sensitive aquaculture, etc.
In Figure 9, we demonstrate an example of a sea grid with 0.1 granularity that employs custom grid points (yellow point) to narrow sea passages, corresponding to the actual points belonging to AIS clusters.
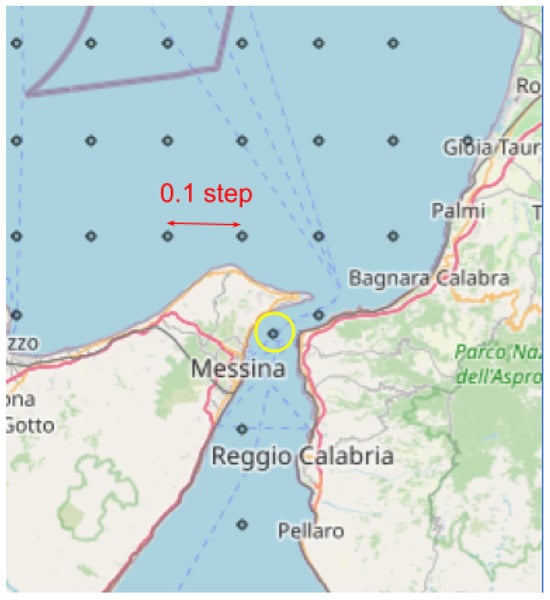
Figure 9.
Example of a custom grid on a narrow passage.
4.3. Shortest-Path Planning Based on Tailor-Made Employed Grid
Utilizing the sea grid extracted by adopting the consolidated algorithmic procedure described in Section 4.1 and Section 4.2, we are able to employ a routing optimization algorithm that incorporates past experience in its core functionality by bounding the search space of alternative routes. The shortest path employing the A* algorithm based on the predefined grid is depicted in Figure 10a. Each waypoint composing the alternative route belongs to a certain cluster (or set of clusters) (see Figure 10b) described by a set of inherent variables (e.g., mean, min, and max speed adopted inside the specific clusters; see also Figure 6). This set of features can be exploited accordingly to define speed adaptations/deviations, in alignment with certain types of constraints (estimated time of arrival (ETA) and/or charter party compliance) to which vessel operation is subject.
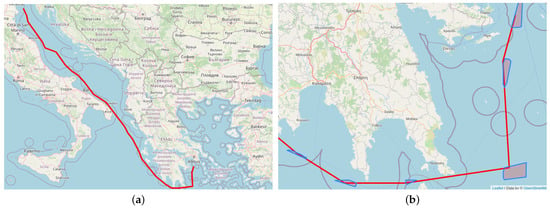
Figure 10.
Alternative route construction. (a) Extracted AIS shortest path for the VENEZIA–PIRAEUS voyage. (b) Clusters assigned to waypoints of alternative route segments.
5. Experimental Results
In this section, we showcase preliminary benchmarking results by comparing our proposed method with a open source library that is well-established amongst marine practitioners that extracts the shortest path between an origin and a destination (AtoBviaC). The aforementioned library is based on a grid employed by domain experts (captains, etc.) and is therefore highly subjective and influenced by personal experience and perspective, resulting in a “biased” grid of waypoints. Figure 11 alongside with the results depicted in Table 1 clearly exhibit the predominance of AIS routing (red polyline) when compared with AtoBviaC (blue polyline) in terms of shortest-path exploration by calculating the total distance traveled for a given voyage (e.g., Marseille–Piraeus).
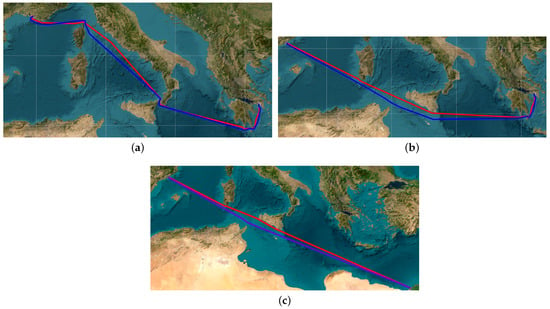
Figure 11.
Alternative route construction. (a) Marseille–Piraeus. (b) Barcelona–Piraeus. (c) Alexandria–Barcelona.

Table 1.
Route length comparison.
The accuracy of the AIS-based path-finding algorithm is attributed mainly to the rich and composite nature of the processed grid constrained by the corresponding clusters, which results in a versatile network of alternative waypoints to AtoBviaC’s user-defined, broad grid.
The identification of areas of interest by employing AIS-informed convex hulls corresponding to segments of historical routes allows us to build an "ideal" network of waypoints, regarding both route exploration and validation, that ultimately yields a more probable, in terms of optimal path-finding solution, scheme. This network automatically enables the inclusion of a variety of parameters regarding weather avoidance, bunkering planning, etc., and the further exploitation of AIS data by correlating events with a probability distribution that will be utilized in the context of a stochastic routing optimization algortihm.
6. Conclusions
Trajectory mining is a powerful data mining technique that has been widely applied in various fields, including transportation, health care, finance, and security. In the maritime sector, trajectory mining has been used to analyze vessel movements and improve vessel safety and efficiency. Similarly, the purpose of this research paper is to provide a novel methodological approach utilizing trajectory mining techniques for the maritime sector. Specifically, previous research reporting the extraction of maritime traffic patterns from AIS data in the form of convex hulls was exploited. Then, these convex hulls were further fine-tuned and segmented to increase their granularity, thus increasing the available vessel routes to be explored. Finally, an A* search algorithm was developed with a cost function optimized for the AIS-derived and fine-tuned routes in order to find the shortest available path. The implementation of such an algorithm allows us to revolutionize and redesign outdated routing optimization approaches by introducing a data-influenced methodological framework that aims to expedite and vastly optimize the routing problem by taking into account past experience mirrored by AIS data.
In future work, we plan to enrich the developed cost function to also include weather information and fuel consumption data that will ultimately result in an advanced weather routing application. Stochastic optimization by introducing reinforcement learning concepts is also included in our immediate plan to extend this research by identifying areas of interest that correspond to a probability distribution rather than discrete values based on the density of the acquired AIS grid.
Author Contributions
Conceptualization, I.V., D.K. and I.K.; methodology, D.K. and I.K.; software, D.K.; validation, I.K., I.Z.E. and T.V.; data curation, D.K. and I.K.; writing—original draft preparation, D.K.; writing—review and editing, D.K. and I.K. and I.Z.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by EU Horizon Project DT4GS (grant number 101056799).
Data Availability Statement
Data can be made available upon request to the first author.
Conflicts of Interest
Author Prof. Takis Varelas was employed by the company Danaos Shipping Co. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Notes
| 1 | https://msi.nga.mil/Publications/WPI, accessed on 2 January 2024. |
| 2 | https://climate.copernicus.eu/, accessed on 2 January 2024. |
References
- Bian, J.; Tian, D.; Tang, Y.; Tao, D. Trajectory data classification: A review. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–34. [Google Scholar] [CrossRef]
- Khodabandehloo, E.; Riboni, D. Collaborative trajectory mining in smart-homes to support early diagnosis of cognitive decline. IEEE Trans. Emerg. Top. Comput. 2020, 9, 1194–1205. [Google Scholar] [CrossRef]
- Zheng, W.; Li, M.; Lin, Z.; Zhang, Y. Leveraging tourist trajectory data for effective destination planning and management: A new heuristic approach. Tour. Manag. 2022, 89, 104437. [Google Scholar] [CrossRef]
- Park, S.; Yuan, Y.; Choe, Y. Application of graph theory to mining the similarity of travel trajectories. Tour. Manag. 2021, 87, 104391. [Google Scholar] [CrossRef]
- Chua, A.; Servillo, L.; Marcheggiani, E.; Moere, A.V. Mapping Cilento: Using geotagged social media data to characterize tourist flows in southern Italy. Tour. Manag. 2016, 57, 295–310. [Google Scholar] [CrossRef]
- Gamage, C.; Dinalankara, R.; Samarabandu, J.; Subasinghe, A. A comprehensive survey on the applications of machine learning techniques on maritime surveillance to detect abnormal maritime vessel behaviors. WMU J. Marit. Aff. 2023, 22, 447–477. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Y.; Chen, L.; Pei, J.; Han, J. Mining frequent trajectory patterns for activity monitoring using radio frequency tag arrays. IEEE Trans. Parallel Distrib. Syst. 2011, 23, 2138–2149. [Google Scholar] [CrossRef]
- Mao, Y.; Zhong, H.; Xiao, X.; Li, X. A segment-based trajectory similarity measure in the urban transportation systems. Sensors 2017, 17, 524. [Google Scholar] [CrossRef]
- Qiao, S.; Han, N.; Zhu, W.; Gutierrez, L.A. TraPlan: An effective three-in-one trajectory-prediction model in transportation networks. IEEE Trans. Intell. Transp. Syst. 2014, 16, 1188–1198. [Google Scholar] [CrossRef]
- Dokuz, A.S. Weighted spatio-temporal taxi trajectory big data mining for regional traffic estimation. Phys. A Stat. Mech. Its Appl. 2022, 589, 126645. [Google Scholar] [CrossRef]
- Smyth, C.S. Mining mobile trajectories. Geogr. Data Min. Knowl. Discov. 2001, 1, 337–361. [Google Scholar]
- Spaccapietra, S.; Parent, C.; Damiani, M.L.; de Macedo, J.A.; Porto, F.; Vangenot, C. A conceptual view on trajectories. Data Knowl. Eng. 2008, 65, 126–146. [Google Scholar] [CrossRef]
- Mazimpaka, J.D.; Timpf, S. Trajectory data mining: A review of methods and applications. J. Spat. Inf. Sci. 2016, 2016, 61–99. [Google Scholar] [CrossRef]
- Galdelli, A.; Mancini, A.; Ferrà, C.; Tassetti, A.N. A synergic integration of AIS data and SAR imagery to monitor fisheries and detect suspicious activities. Sensors 2021, 21, 2756. [Google Scholar] [CrossRef] [PubMed]
- Kontopoulos, I.; Chatzikokolakis, K.; Zissis, D.; Tserpes, K.; Spiliopoulos, G. Real-time maritime anomaly detection: Detecting intentional AIS switch-off. Int. J. Big Data Intell. 2020, 7, 85–96. [Google Scholar] [CrossRef]
- Varlamis, I.; Tserpes, K.; Sardianos, C. Detecting Search and Rescue missions from AIS data. In Proceedings of the 2018 IEEE 34th International Conference on Data Engineering Workshops (ICDEW), Paris, France, 16–20 April 2018; pp. 60–65. [Google Scholar]
- Kaklis, D.; Varelas, T.J.; Varlamis, I.; Eirinakis, P.; Giannakopoulos, G.; Spyropoulos, C.V. From STEAM to Machine: Emissions control in the shipping 4.0 era. In Proceedings of the SNAME International Symposium on Ship Operations, Management and Economics, SNAME, Athens, Greece, 7 March 2023; p. D011S001R002. [Google Scholar]
- Yu, X.; Xu, C.; Leong, H.W.; Tian, Q.; Tang, Q.; Wan, K.W. Trajectory-based ball detection and tracking with applications to semantic analysis of broadcast soccer video. In Proceedings of the Eleventh ACM International Conference on Multimedia, Berkeley, CA, USA, 2–8 November 2003; pp. 11–20. [Google Scholar]
- Brakatsoulas, S.; Pfoser, D.; Tryfona, N. Modeling, storing and mining moving object databases. In Proceedings of the International Database Engineering and Applications Symposium (IDEAS’04), Coimbra, Portugal, 7–9 July 2004; pp. 68–77. [Google Scholar]
- Giannotti, F.; Nanni, M.; Pinelli, F.; Pedreschi, D. Trajectory pattern mining. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007; pp. 330–339. [Google Scholar]
- Lee, J.G.; Han, J.; Li, X.; Gonzalez, H. TraClass: Trajectory classification using hierarchical region-based and trajectory-based clustering. Proc. VLDB Endow. 2008, 1, 1081–1094. [Google Scholar] [CrossRef]
- Brakatsoulas, S.; Pfoser, D.; Tryfona, N. Practical data management techniques for vehicle tracking data. In Proceedings of the 21st International Conference on Data Engineering (ICDE’05), Tokyo, Japan, 5–8 April 2005; pp. 324–325. [Google Scholar]
- de Vries, G.; van Someren, M. Clustering vessel trajectories with alignment kernels under trajectory compression. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2010, Barcelona, Spain, 20–24 September 2010; Proceedings, Part I 21. Springer: Berlin/Heidelberg, Germany, 2010; pp. 296–311. [Google Scholar]
- Ferrero, C.A.; Alvares, L.O.; Zalewski, W.; Bogorny, V. Movelets: Exploring relevant subtrajectories for robust trajectory classification. In Proceedings of the 33rd Annual ACM Symposium on Applied Computing, Pau, France, 9–13 April 2018; pp. 849–856. [Google Scholar]
- Kapadais, K.; Varlamis, I.; Sardianos, C.; Tserpes, K. A framework for the detection of search and rescue patterns using shapelet classification. Future Internet 2019, 11, 192. [Google Scholar] [CrossRef]
- Ye, L.; Keogh, E. Time series shapelets: A novel technique that allows accurate, interpretable and fast classification. Data Min. Knowl. Discov. 2011, 22, 149–182. [Google Scholar] [CrossRef]
- Luo, D.; Chen, P.; Yang, J.; Li, X.; Zhao, Y. A New Classification Method for Ship Trajectories Based on AIS Data. J. Mar. Sci. Eng. 2023, 11, 1646. [Google Scholar] [CrossRef]
- Kontopoulos, I.; Makris, A.; Zissis, D.; Tserpes, K. A Computer Vision Approach for Trajectory Classification. In Proceedings of the 22nd IEEE International Conference on Mobile Data Management (MDM), Toronto, ON, Canada, 15–18 June 2021; pp. 163–168. [Google Scholar]
- Kontopoulos, I.; Makris, A.; Tserpes, K. A Deep Learning Streaming Methodology for Trajectory Classification. ISPRS Int. J. Geo-Inf. 2021, 10, 250. [Google Scholar] [CrossRef]
- Liu, X.; Tian, Y.; Zhang, X.; Wan, Z. Identification of Urban Functional Regions in Chengdu Based on Taxi Trajectory Time Series Data. Int. J.-Geo-Inf. 2020, 9, 158. [Google Scholar] [CrossRef]
- Lee, J.G.; Han, J.; Whang, K.Y. Trajectory Clustering: A Partition-and-Group Framework. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data, ACM, Beijing, China, 11–14 June 2007; pp. 593–604. [Google Scholar]
- Pallotta, G.; Michele, V.; Karna, B. Vessel pattern knowledge discovery from AIS data: A framework for anomaly detection and route prediction. Entropy 2013, 15, 2218–2245. [Google Scholar] [CrossRef]
- Iphar, C.; Anne-Laure, J. A geometry-based fuzzy approach for long-term association of vessels to maritime routes. Ocean Eng. 2023, 281, 114755. [Google Scholar] [CrossRef]
- Kontopoulos, I.; Varlamis, I.; Tserpes, K. A distributed framework for extracting maritime traffic patterns. Int. J. Geogr. Inf. Sci. 2021, 35, 767–792. [Google Scholar] [CrossRef]
- Yuan, G.; Sun, P.; Zhao, J.; Li, D.; Wang, C. A Review of Moving Object Trajectory Clustering Algorithms. Artif. Intell. Rev. 2017, 47, 123–144. [Google Scholar] [CrossRef]
- Meng, F.; Yuan, G.; Lv, S.; Wang, Z.; Xia, S.T. An Overview on Trajectory Outlier Detection. Artif. Intell. Rev. 2019, 52, 2437–2456. [Google Scholar] [CrossRef]
- Belhadi, A.; Djenouri, Y.; Lin, J.C.W.; Cano, A. Trajectory Outlier Detection: Algorithms, Taxonomies, Evaluation, and Open Challenges. ACM Trans. Manag. Inf. Syst. (TMIS) 2020, 11, 1–29. [Google Scholar] [CrossRef]
- Lei, P.R. A Framework for Anomaly Detection in Maritime Trajectory Behavior. Knowl. Inf. Syst. 2016, 47, 189–214. [Google Scholar] [CrossRef]
- Pitsikalis, M.; Ioannis, K.; Alexander, A.; Elias, A.; Paul, D.; Jules-Edouard, P.; Richard, D.; Ray, C.; Camossi, E.; Jousselme, A.-L.; et al. Composite event patterns for maritime monitoring. In Proceedings of the 10th Hellenic Conference on Artificial Intelligence, Patras, Greece, 9–12 July 2018; Volume 281, pp. 1–4. [Google Scholar]
- Laddada, W.; Ray, C. Graph-based analysis of maritime patterns of life. In Proceedings of the GAST Workshop, 20th Journées Francophones Extraction et Gestion des Connaissances (EGC), Brussels, Belgium, 27–31 January 2020; pp. 1–14. [Google Scholar]
- Varlamis, I.; Kontopoulos, I.; Tserpes, K.; Etemad, M.; Soares, A.; Matwin, S. Building navigation networks from multi-vessel trajectory data. GeoInformatica 2021, 25, 69–97. [Google Scholar] [CrossRef]
- Sheng, Z.; Xu, Y.; Xue, S.; Li, D. Graph-based spatial-temporal convolutional network for vehicle trajectory prediction in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17654–17665. [Google Scholar] [CrossRef]
- Rudenko, A.; Palmieri, L.; Herman, M.; Kitani, K.M.; Gavrila, D.M.; Arras, K.O. Human Motion Trajectory Prediction: A Survey. Int. J. Robot. Res. 2020, 39, 895–935. [Google Scholar] [CrossRef]
- Liu, J.; Mao, X.; Fang, Y.; Zhu, D.; Meng, M.Q.H. A Survey on Deep-Learning Approaches for Vehicle Trajectory Prediction in Autonomous Driving. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics (ROBIO), Sanya, China, 27–31 December 2021; pp. 978–985. [Google Scholar]
- Huang, Y.; Du, J.; Yang, Z.; Zhou, Z.; Zhang, L.; Chen, H. A Survey on Trajectory-Prediction Methods for Autonomous Driving. IEEE Trans. Intell. Veh. 2022, 7, 652–674. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, X.; Xiao, Z.; Xu, H.; Qin, Z. Vessel Trajectory Prediction in Maritime Transportation: Current Approaches and Beyond. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19980–19998. [Google Scholar] [CrossRef]
- Zhang, M.; Pentti, K.; Mashrura, M.; Jinfen, Z.; Spyros, H. A machine learning method for the prediction of ship motion trajectories in real operational conditions. Ocean Eng. 2023, 283, 114905. [Google Scholar] [CrossRef]
- Xue, H.; Salim, F.; Ren, Y.; Oliver, N. MobTCast: Leveraging auxiliary trajectory forecasting for human mobility prediction. Adv. Neural Inf. Process. Syst. 2021, 34, 30380–30391. [Google Scholar]
- Sun, H.; Guo, X.; Yang, Z.; Chu, X.; Liu, X.; He, L. Predicting future locations with semantic trajectories. ACM Trans. Intell. Syst. Technol. (TIST) 2022, 13, 1–20. [Google Scholar] [CrossRef]
- Renso, C.; Bogorny, V.; Tserpes, K.; Matwin, S.; de Macedo, J.A.F. Multiple-aspect analysis of semantic trajectories (MASTER). Int. J. Geogr. Inf. Sci. 2021, 35, 763–766. [Google Scholar] [CrossRef]
- Chen, X.; Kamalasudhan, A.; Zhang, X. An application of convolutional neural network to derive vessel movement patterns. In Proceedings of the International Conference on Transportation Information and Safety (ICTIS), Liverpool, UK, 14–17 July 2019. [Google Scholar]
- Martha, F.; Gabriel, S.; Amilcar, S.; Stan, M. A Semi-Supervised Methodology for Fishing Activity Detection Using the Geometry behind the Trajectory of Multiple Vessels. Sensors 2022, 22, 6063. [Google Scholar]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).