Development of a Mobile Buoy with Controllable Wings: Design, Dynamics Analysis and Experiments
Abstract
1. Introduction
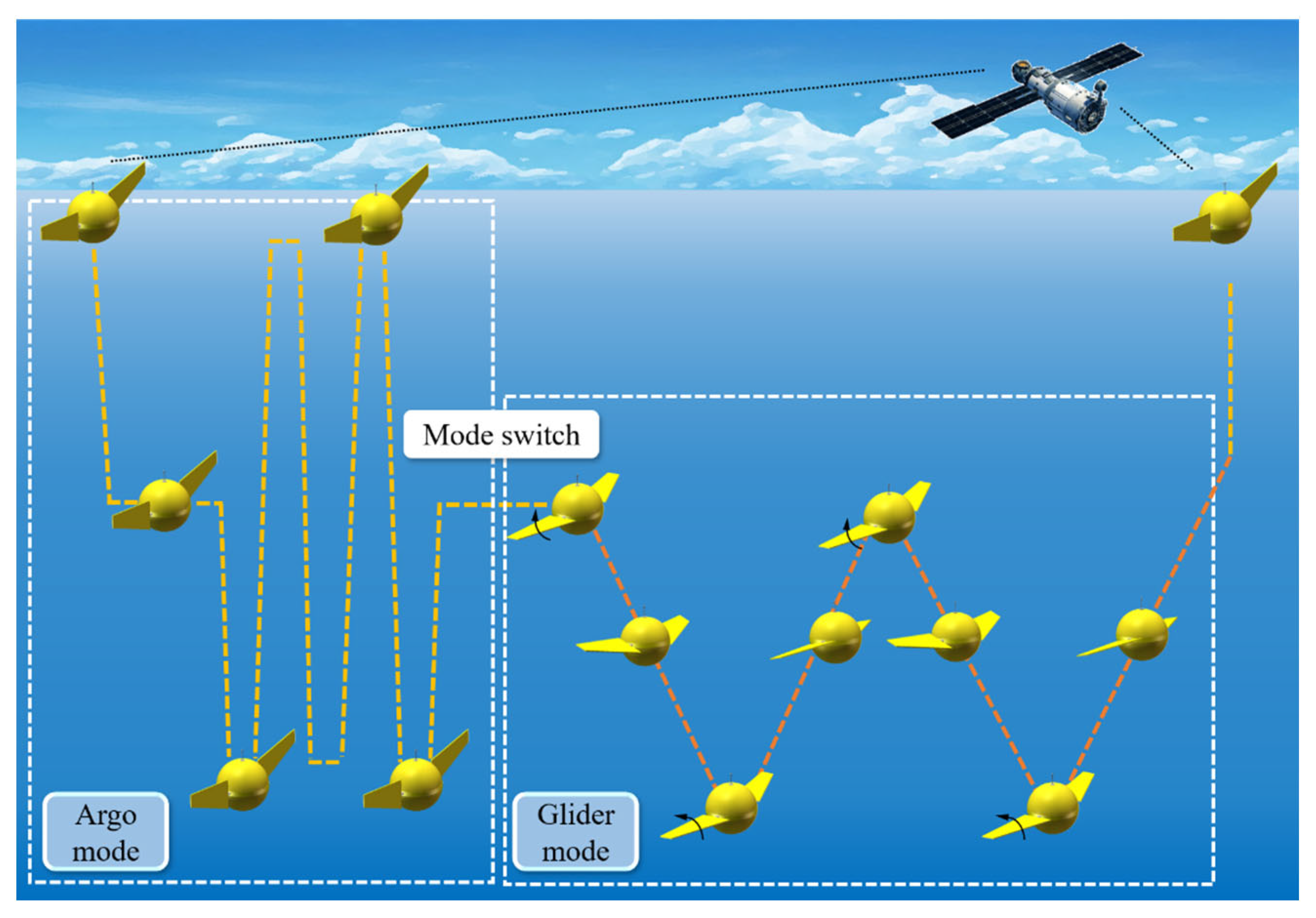
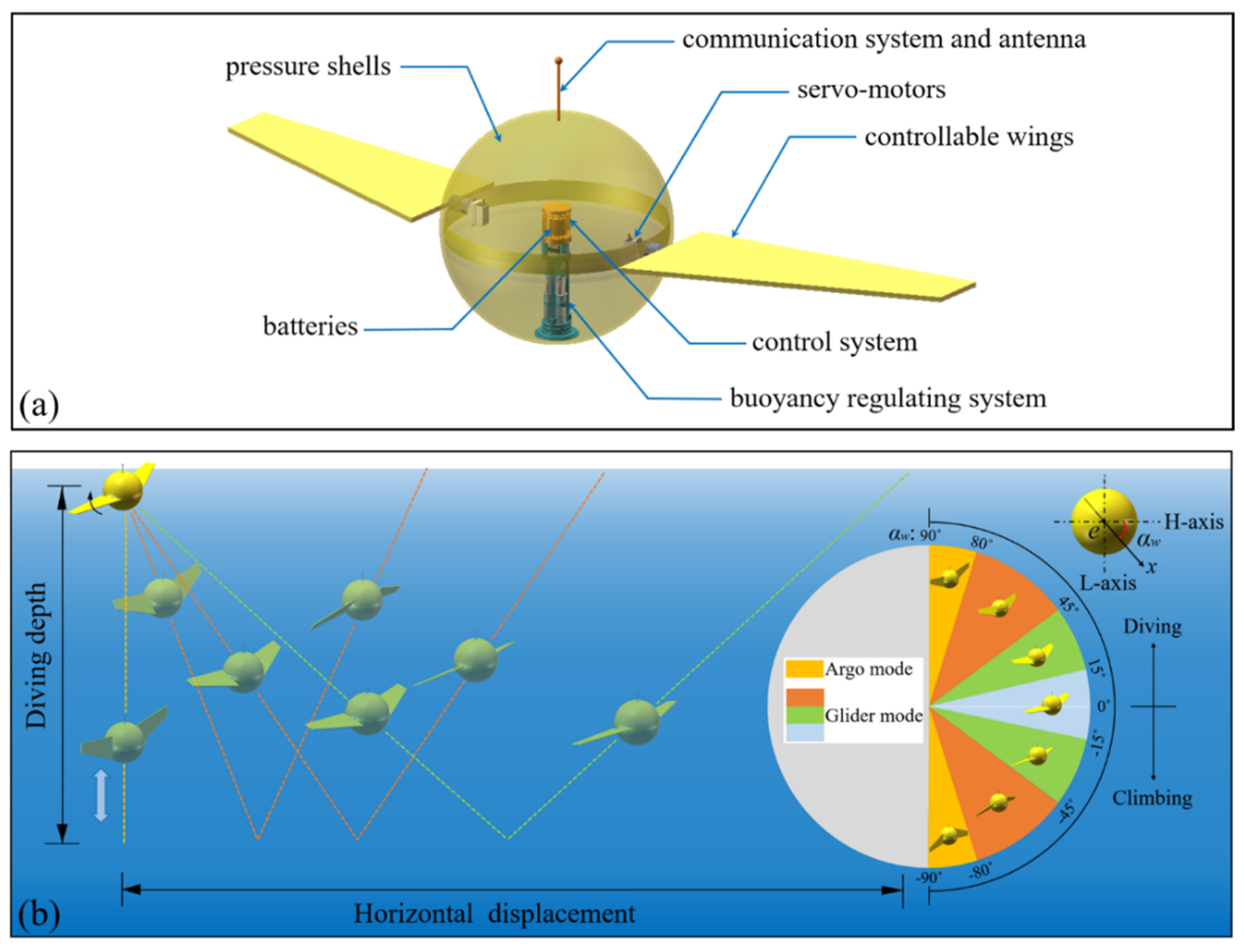
2. Mobile Buoy with Controllable Wings
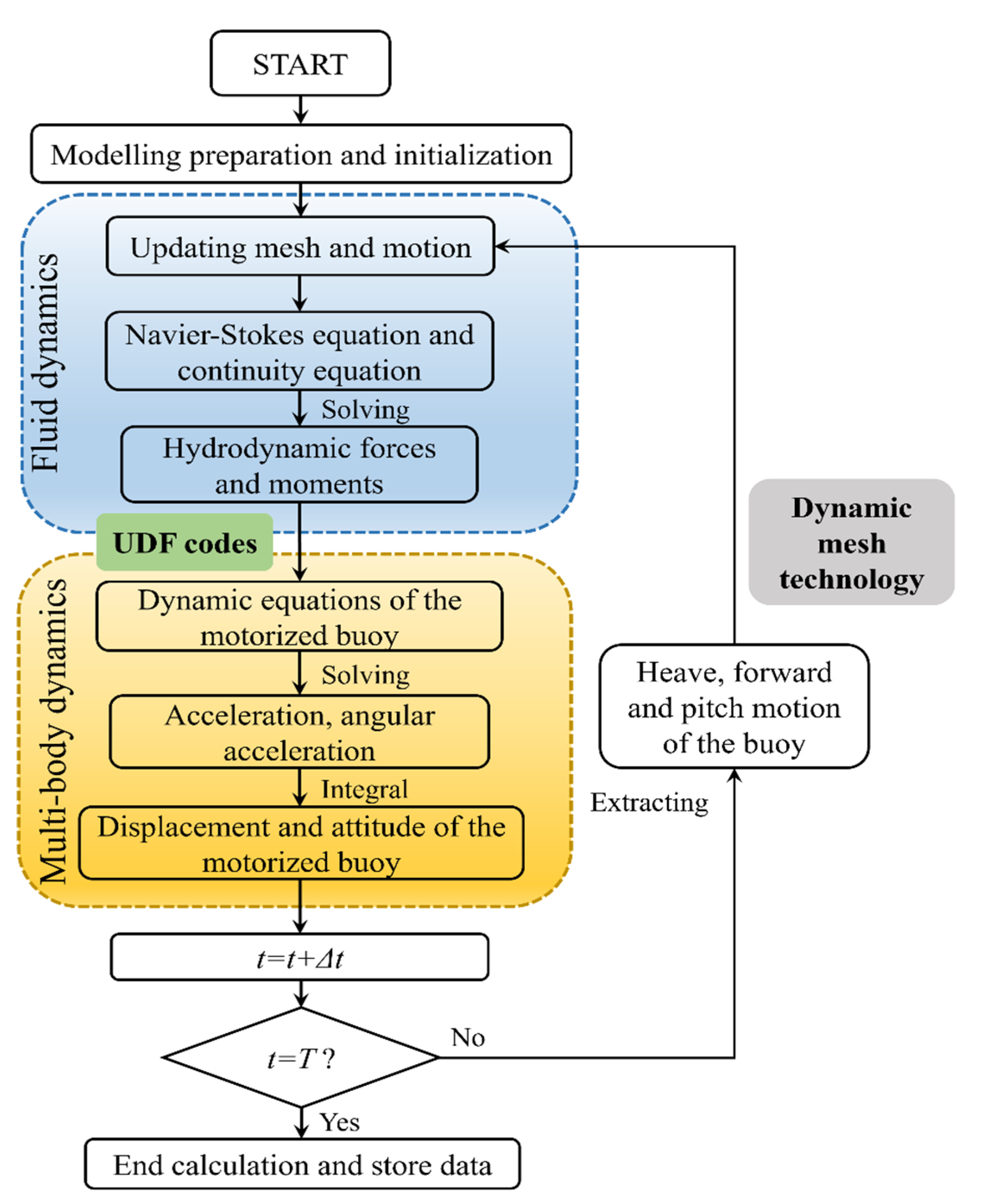
3. Fluid–Multibody Coupling Dynamics Model
3.1. Fluid–Multibody Coupling Analysis Method
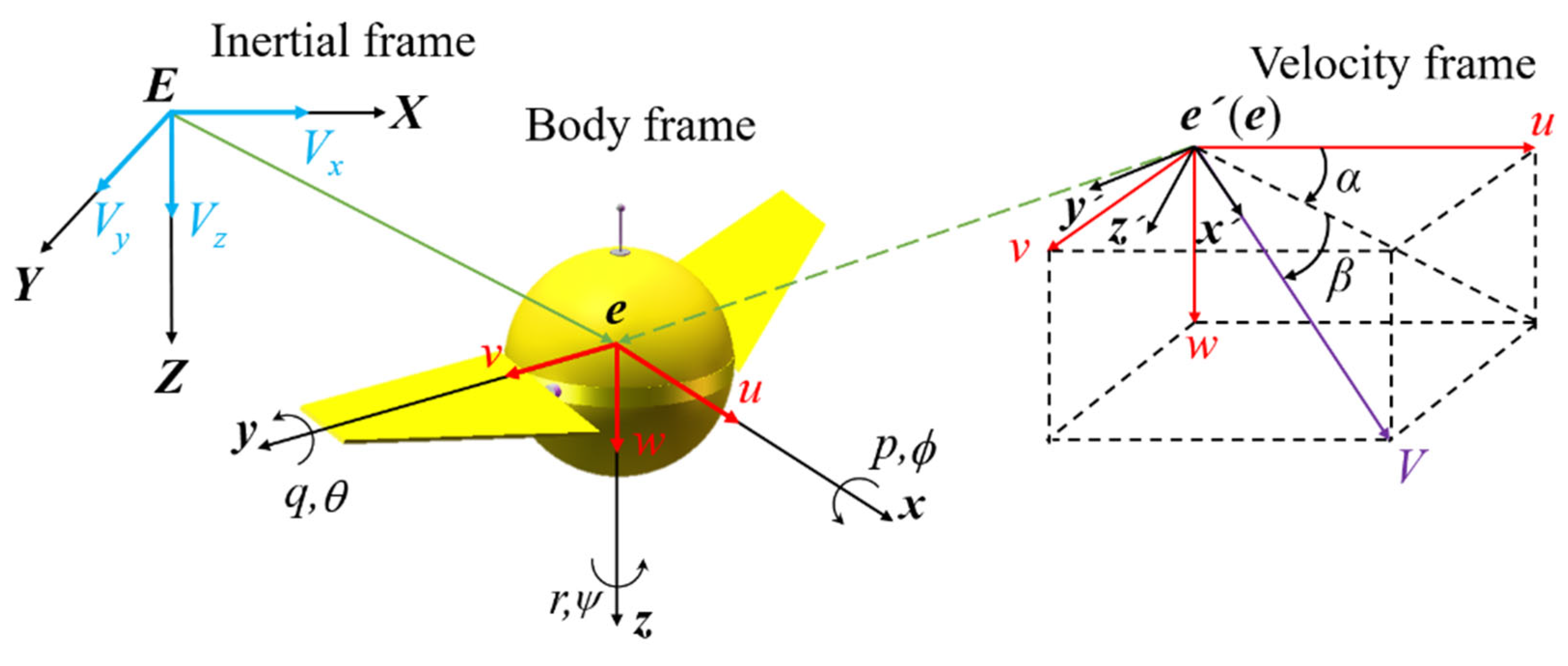
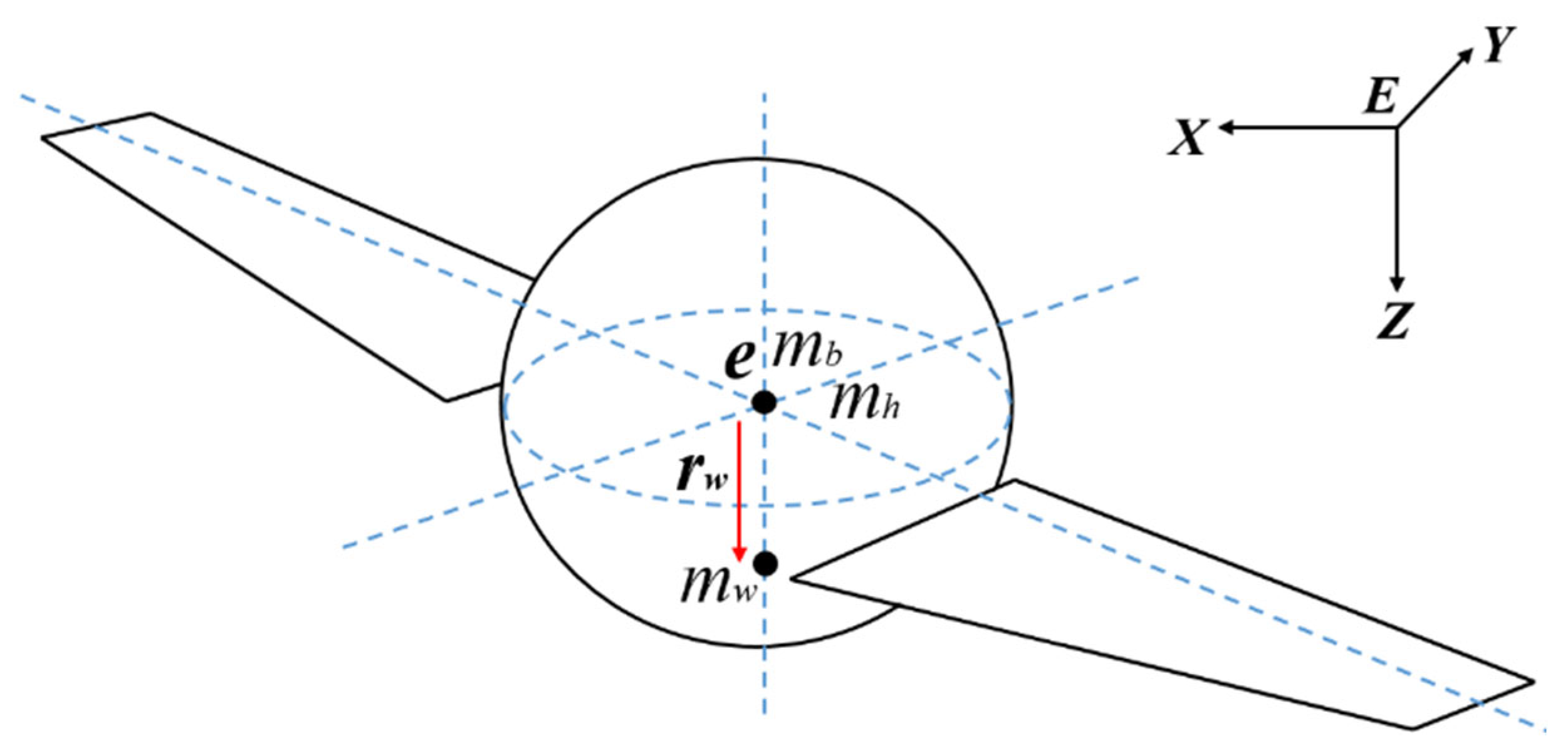
3.2. Multibody Dynamics Model of the Mobile Buoy
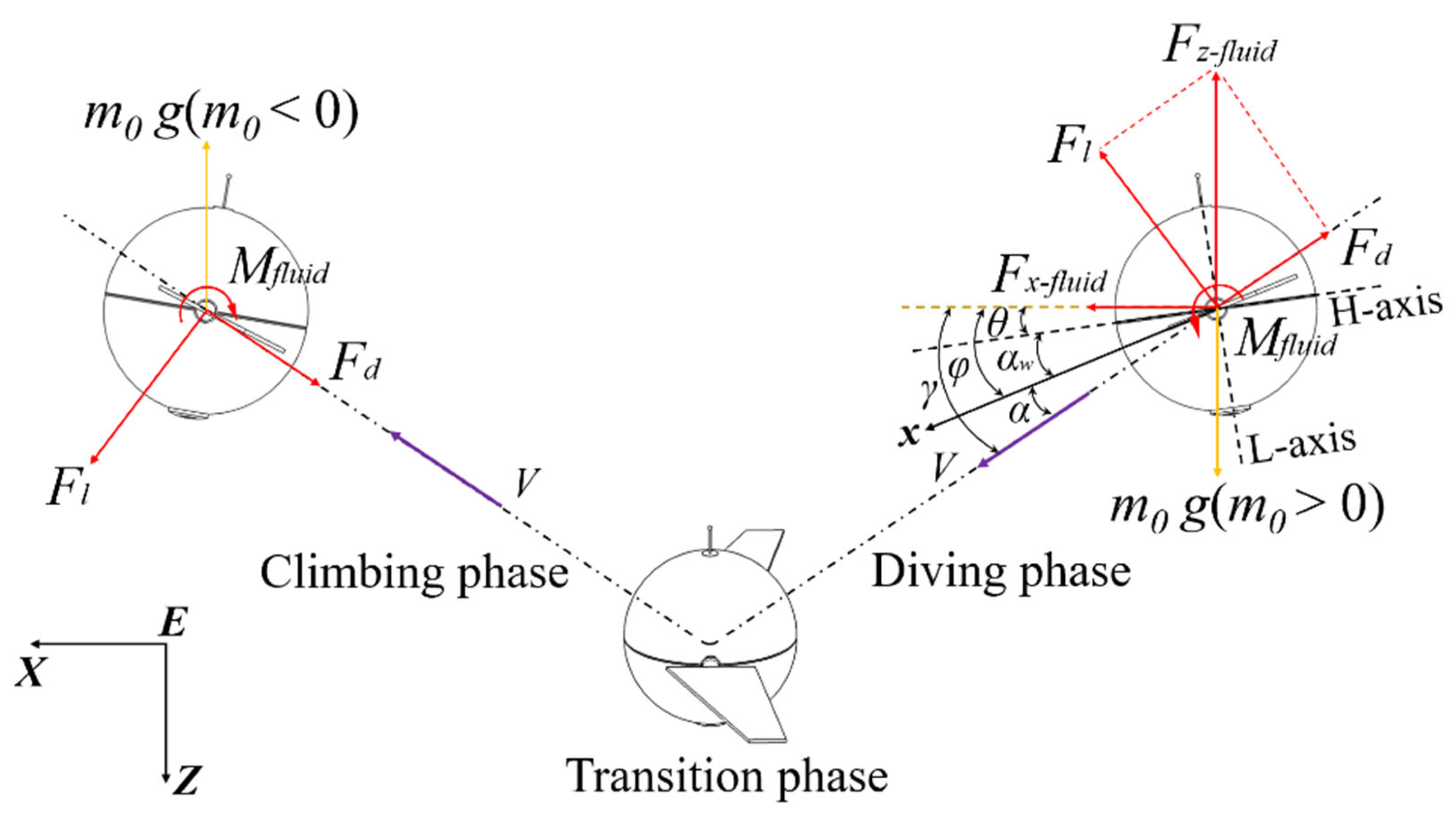
3.3. Hydrodynamics Model of the Mobile Buoy
4. Dynamics Simulation Results
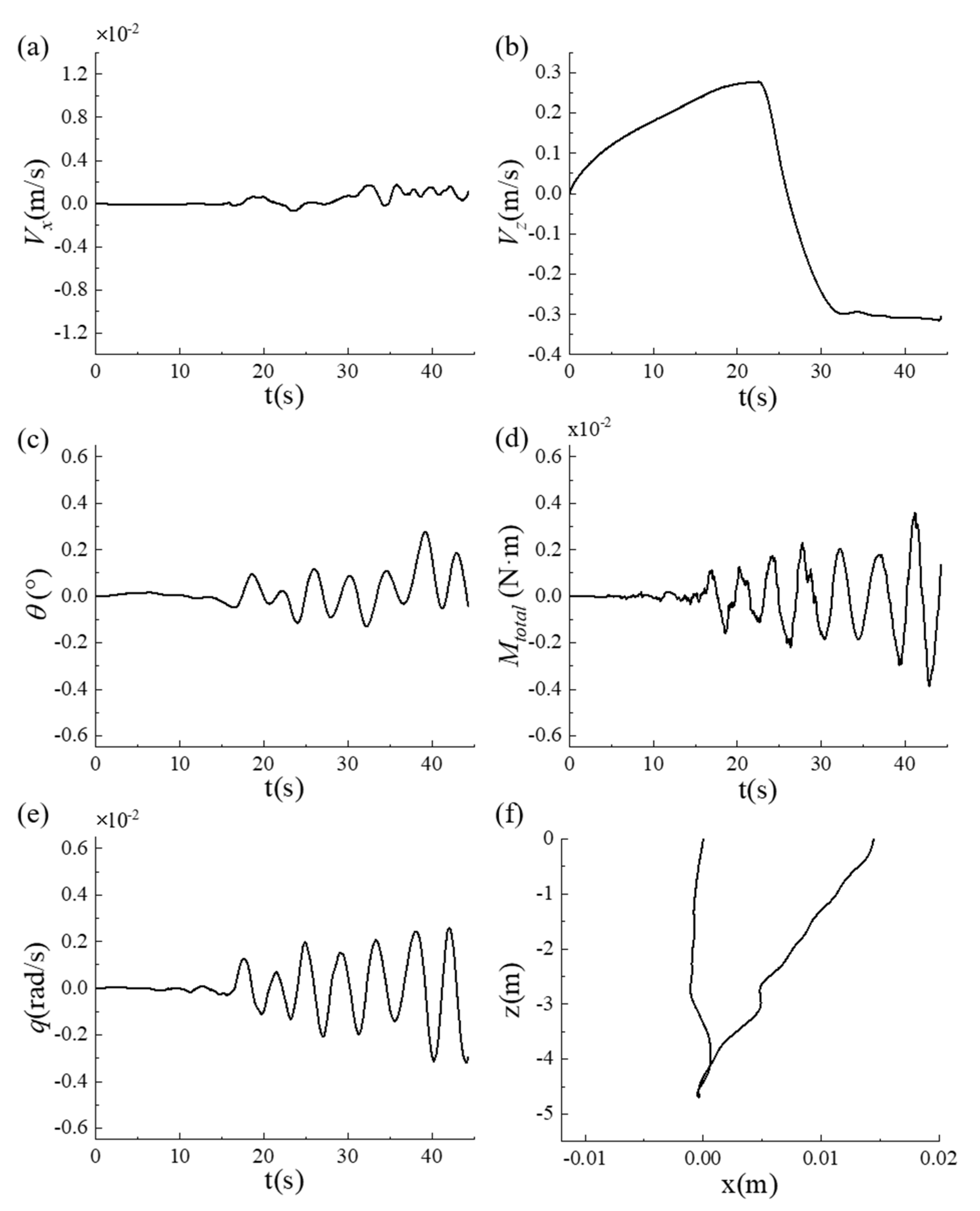
4.1. Dynamic Responses in Argo Mode
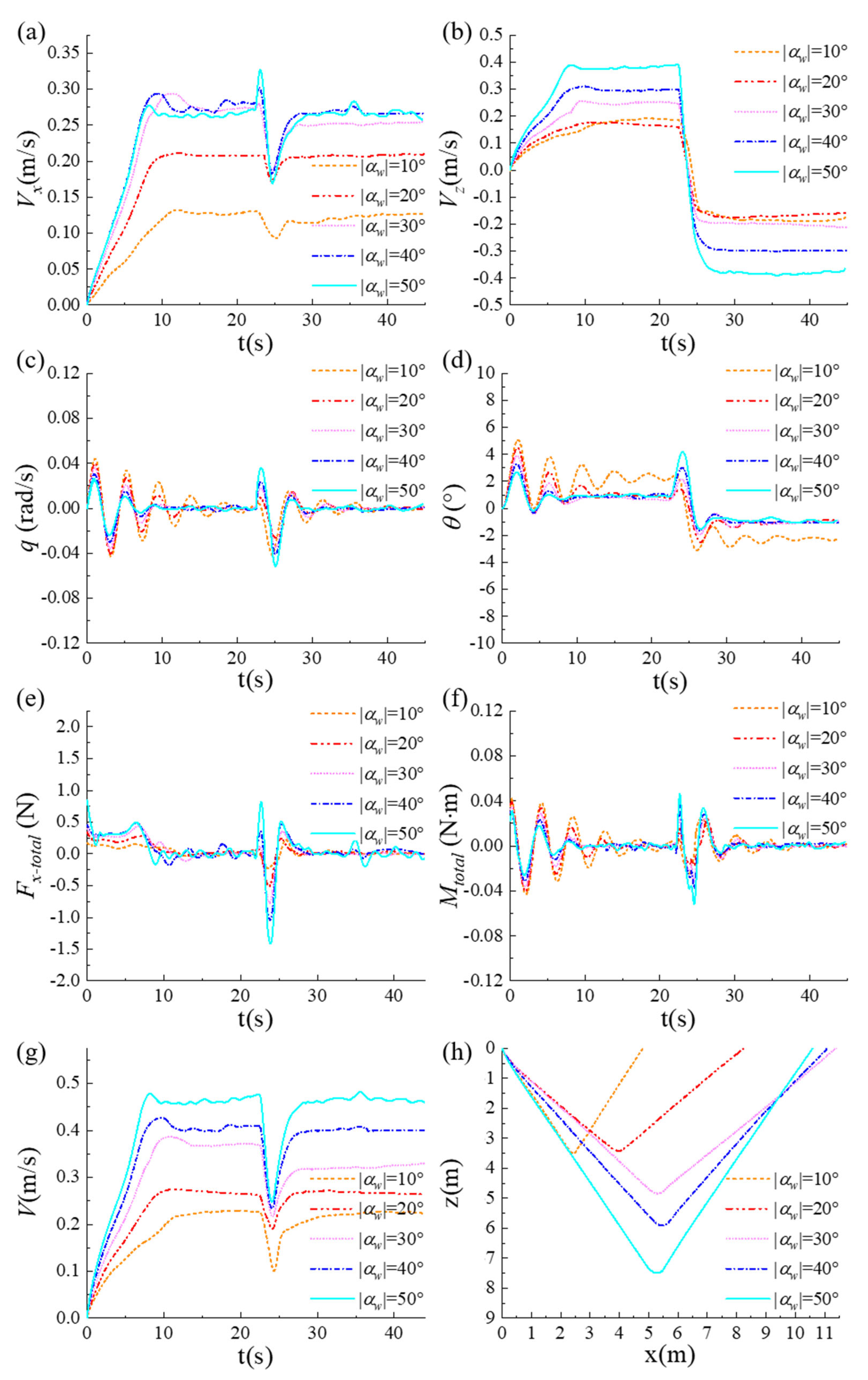
4.2. Dynamic Responses in Glider Mode
5. Experimental Verification
5.1. Experiment Results of Argo Mode
5.2. Experiment Results of Glider Mode
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yuan, S.; Li, Y.; Bao, F.; Xu, H.; Yang, Y.; Yan, Q.; Zhong, S.; Yin, H.; Xu, J.; Huang, Z. Marine environmental monitoring with unmanned vehicle platforms: Present applications and future prospects. Sci. Total Environ. 2023, 858, 159741. [Google Scholar] [CrossRef] [PubMed]
- Verfuss, U.K.; Aniceto, A.S.; Harris, D.V.; Gillespie, D.; Fielding, S.; Jiménez, G.; Johnston, P.; Sinclair, R.R.; Sivertsen, A.; Solbø, S.A. A review of unmanned vehicles for the detection and monitoring of marine fauna. Mar. Pollut. Bull. 2019, 140, 17–29. [Google Scholar] [CrossRef]
- Jones, D.C.; Holt, H.J.; Meijers, A.J.; Shuckburgh, E. Unsupervised clustering of Southern Ocean Argo float temperature profiles. J. Geophys. Res. Ocean. 2019, 124, 390–402. [Google Scholar] [CrossRef]
- Haavisto, N.; Tuomi, L.; Roiha, P.; Siiriä, S.-M.; Alenius, P.; Purokoski, T. Argo floats as a novel part of the monitoring the hydrography of the Bothnian Sea. Front. Mar. Sci. 2018, 5, 324. [Google Scholar] [CrossRef]
- Xue, G.; Liu, Y.; Si, W.; Ji, C.; Guo, F.; Li, Z. Energy recovery and conservation utilizing seawater pressure in the working process of Deep-Argo profiling float. Energy 2020, 195, 116845. [Google Scholar] [CrossRef]
- Cao, J.; Lu, D.; Li, D.; Zeng, Z.; Yao, B.; Lian, L. Smartfloat: A multimodal underwater vehicle combining float and glider capabilities. IEEE Access 2019, 7, 77825–77838. [Google Scholar] [CrossRef]
- Orton, P.; McGillis, W.; Moisan, J.; Higinbotham, J.; Schirtzinger, C. The mobile buoy: An autonomous surface vehicle for integrated ocean-atmosphere studies. In AGU Spring Meeting Abstracts; ADS: Cambridge, MA, USA, 2009; p. OS22A–08. [Google Scholar]
- Zoss, B.M.; Mateo, D.; Kuan, Y.K.; Tokić, G.; Chamanbaz, M.; Goh, L.; Vallegra, F.; Bouffanais, R.; Yue, D.K. Distributed system of autonomous buoys for scalable deployment and monitoring of large waterbodies. Auton. Robots 2018, 42, 1669–1689. [Google Scholar] [CrossRef]
- Senga, H.; Kato, N.; Suzuki, H.; Yoshie, M.; Fujita, I.; Tanaka, T.; Matsuzaki, Y. Development of a new spilled oil tracking autonomous buoy. Mar. Technol. Soc. J. 2011, 45, 43–51. [Google Scholar] [CrossRef]
- Senga, H.; Kato, N.; Suzuki, H.; Akamatsu, T.; Yu, L.; Yoshie, M.; Tanaka, T. Field experiments and new design of a spilled oil tracking autonomous buoy. J. Mar. Sci. Technol. 2014, 19, 90–102. [Google Scholar] [CrossRef]
- Yu, F.; Hu, X.; Dong, S.; Liu, G.; Zhao, Y.; Chen, G. Design of a low-cost oil spill tracking buoy. J. Mar. Sci. Technol. 2018, 23, 188–200. [Google Scholar] [CrossRef]
- Fan, S.; Woolsey, C.A. Dynamics of underwater gliders in currents. Ocean. Eng. 2014, 84, 249–258. [Google Scholar] [CrossRef]
- Wang, S.; Yang, M.; Niu, W.; Wang, Y.; Yang, S.; Zhang, L.; Deng, J. Multidisciplinary design optimization of underwater glider for improving endurance. Struct. Multidiscip. Optim. 2021, 63, 2835–2851. [Google Scholar] [CrossRef]
- Orozco-Muñiz, J.P.; Salgado-Jimenez, T.; Rodriguez-Olivares, N.A. Underwater glider propulsion systems VBS part 1: VBS sizing and glider performance analysis. J. Mar. Sci. Eng. 2020, 8, 919. [Google Scholar] [CrossRef]
- Riser, S.C.; Freeland, H.J.; Roemmich, D.; Wijffels, S.; Troisi, A.; Belbéoch, M.; Gilbert, D.; Xu, J.; Pouliquen, S.; Thresher, A. Fifteen years of ocean observations with the global Argo array. Nat. Clim. Change 2016, 6, 145–153. [Google Scholar] [CrossRef]
- Roemmich, D.; Alford, M.H.; Claustre, H.; Johnson, K.; King, B.; Moum, J.; Oke, P.; Owens, W.B.; Pouliquen, S.; Purkey, S. On the future of Argo: A global, full-depth, multi-disciplinary array. Front. Mar. Sci. 2019, 6, 439. [Google Scholar] [CrossRef]
- Johnson, K.; Coletti, L.; Jannasch, H.; Martz, T.; Swift, D.; Riser, S. Long-term observations of ocean biogeochemistry with nitrate and oxygen sensors in Apex profiling floats. In AGU Fall Meeting Abstracts; ADS: Cambridge, MA, USA, 2008; p. OS31A–1232. [Google Scholar]
- André, X.; Moreau, B.; Le Reste, S. Argos-3 satellite communication system: Implementation on the arvor oceanographic profiling floats. J. Atmos. Ocean. Technol. 2015, 32, 1902–1914. [Google Scholar] [CrossRef][Green Version]
- Sherman, J.; Davis, R.E.; Owens, W.; Valdes, J. The autonomous underwater glider” Spray”. IEEE J. Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef]
- Webb, D.C.; Simonetti, P.J.; Jones, C.P. SLOCUM: An underwater glider propelled by environmental energy. IEEE J. Ocean. Eng. 2001, 26, 447–452. [Google Scholar] [CrossRef]
- Eriksen, C.C.; Osse, T.J.; Light, R.D.; Wen, T.; Lehman, T.W.; Sabin, P.L.; Ballard, J.W.; Chiodi, A.M. Seaglider: A long-range autonomous underwater vehicle for oceanographic research. IEEE J. Ocean. Eng. 2001, 26, 424–436. [Google Scholar] [CrossRef]
- Yang, Y.; Xiao, Y.; Li, T. A survey of autonomous underwater vehicle formation: Performance, formation control, and communication capability. IEEE Commun. Surv. Tutor. 2021, 23, 815–841. [Google Scholar] [CrossRef]
- Ma, X.; Wang, Y.; Li, S.; Niu, W.; Ma, W.; Luo, C.; Yang, S. Formation control of discrete-time nonlinear multi-glider systems for both leader–follower and no-leader scenarios under switching topology: Cases for a fleet consisting of a wave glider and multiple underwater gliders. Ocean. Eng. 2023, 276, 114003. [Google Scholar] [CrossRef]
- Alvarez, A.; Garau, B.; Caiti, A. Combining networks of drifting profiling floats and gliders for adaptive sampling of the Ocean. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 21 May 2007; pp. 157–162. [Google Scholar]
- Cao, J.; Lin, R.; Yao, B.; Liu, C.; Zhang, X.; Lian, L. Modeling, Control and Experiments of a Novel Underwater Vehicle with Dual Operating Modes for Oceanographic Observation. J. Mar. Sci. Eng. 2022, 10, 921. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, J.; Fu, J.; Liu, C.; Wei, Z.; Yu, C.; Zeng, Z.; Yao, B.; Lian, L. Dynamic modeling and motion control of a novel conceptual multimodal for autonomous sampling. Ocean. Eng. 2021, 240, 109917. [Google Scholar] [CrossRef]
- Liu, B.; Yang, Y.; Wang, S.; Liu, Y. A dual-modal unmanned vehicle propelled by marine energy: Design, stability analysis and sea trial. Ocean. Eng. 2022, 247, 110702. [Google Scholar] [CrossRef]
- Yang, M.; Wang, Y.; Zhang, X.; Liang, Y.; Wang, C. Parameterized dynamic modeling and spiral motion pattern analysis for underwater gliders. IEEE J. Ocean. Eng. 2022, 48, 112–126. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.; Wang, Y.; Niu, W.; Yang, S.; Sun, C.; Luo, C. Dynamics Modeling and Analysis of an Underwater Glider with Dual-Eccentric Attitude Regulating Mechanism Using Dual Quaternions. J. Mar. Sci. Eng. 2022, 11, 5. [Google Scholar] [CrossRef]
- Yang, S.; Li, L.; Li, X.; Liang, F.; Zhang, X.; Sun, W. Dynamics Model of Buoy Unpowered Heave Considering Seawater Density. J. Coast. Res. 2020, 99, 439–446. [Google Scholar] [CrossRef]
- Zhu, X.; Yoo, W.S. Dynamic analysis of a floating spherical buoy fastened by mooring cables. Ocean. Eng. 2016, 121, 462–471. [Google Scholar] [CrossRef]
- Qin, D.; Huang, Q.; Pan, G.; Shi, Y.; Li, F.; Han, P. Numerical simulation of hydrodynamic and noise characteristics for a blended-wing-body underwater glider. Ocean. Eng. 2022, 252, 111056. [Google Scholar] [CrossRef]
- Le, T.-L.; Hong, D.-T. Computational fluid dynamics study of the hydrodynamic characteristics of a torpedo-shaped underwater glider. Fluids 2021, 6, 252. [Google Scholar] [CrossRef]
- Wang, H.; Chen, J.; Feng, Z.; Li, Y.; Deng, C.; Chang, Z. Dynamics analysis of underwater glider based on fluid-multibody coupling model. Ocean. Eng. 2023, 278, 114330. [Google Scholar] [CrossRef]
- Grande, D.; Huang, L.; Harris, C.A.; Wu, P.; Thomas, G.; Anderlini, E. Open-source simulation of underwater gliders. In Proceedings of the OCEANS 2021: San Diego–Porto, San Diego, CA, USA, 20–23 September 2021; pp. 1–8. [Google Scholar]
- Liu, T. Evolutionary understanding of airfoil lift. Adv. Aerodyn. 2021, 3, 37. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Mass of mobile buoy mt (kg) | 14.7 |
| Inertia of the buoy with respect to y-axis I (kg·m2) | 2.1 |
| Span of the buoy W (m) | 1.4 |
| Buoy fuselage length L (m) | 0.35 |
| Water depth H (m) | 10 |
| Fluid density ρ (g/cm3) | 1.025 |
| Buoy fuselage diameter d (m) | 0.35 |
| Nonuniformly distributed mass mw (kg) | 3 |
| Net buoyancy mass m0 (kg) during the diving phase | 0.1~0.5 |
| Net buoyancy mass m0 (kg) during the climbing phase | −0.5~−0.1 |
| Displacement of the nonuniform hull-distributed point mass mw with respect to GC rw (m) | 0.14 |
| Variation range of the wing rotation angle αw (°) | −90°~90° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Chen, J.; Feng, Z.; Du, G.; Li, Y.; Tang, C.; Zhang, Y.; He, C.; Chang, Z. Development of a Mobile Buoy with Controllable Wings: Design, Dynamics Analysis and Experiments. J. Mar. Sci. Eng. 2024, 12, 150. https://doi.org/10.3390/jmse12010150
Wang H, Chen J, Feng Z, Du G, Li Y, Tang C, Zhang Y, He C, Chang Z. Development of a Mobile Buoy with Controllable Wings: Design, Dynamics Analysis and Experiments. Journal of Marine Science and Engineering. 2024; 12(1):150. https://doi.org/10.3390/jmse12010150
Chicago/Turabian StyleWang, Haibo, Junsi Chen, Zhanxia Feng, Guangchao Du, Yuze Li, Chao Tang, Yang Zhang, Changhong He, and Zongyu Chang. 2024. "Development of a Mobile Buoy with Controllable Wings: Design, Dynamics Analysis and Experiments" Journal of Marine Science and Engineering 12, no. 1: 150. https://doi.org/10.3390/jmse12010150
APA StyleWang, H., Chen, J., Feng, Z., Du, G., Li, Y., Tang, C., Zhang, Y., He, C., & Chang, Z. (2024). Development of a Mobile Buoy with Controllable Wings: Design, Dynamics Analysis and Experiments. Journal of Marine Science and Engineering, 12(1), 150. https://doi.org/10.3390/jmse12010150







