A Multifractal Cascade Model for Energy Evolution and Dissipation in Ocean Turbulence
Abstract
1. Introduction
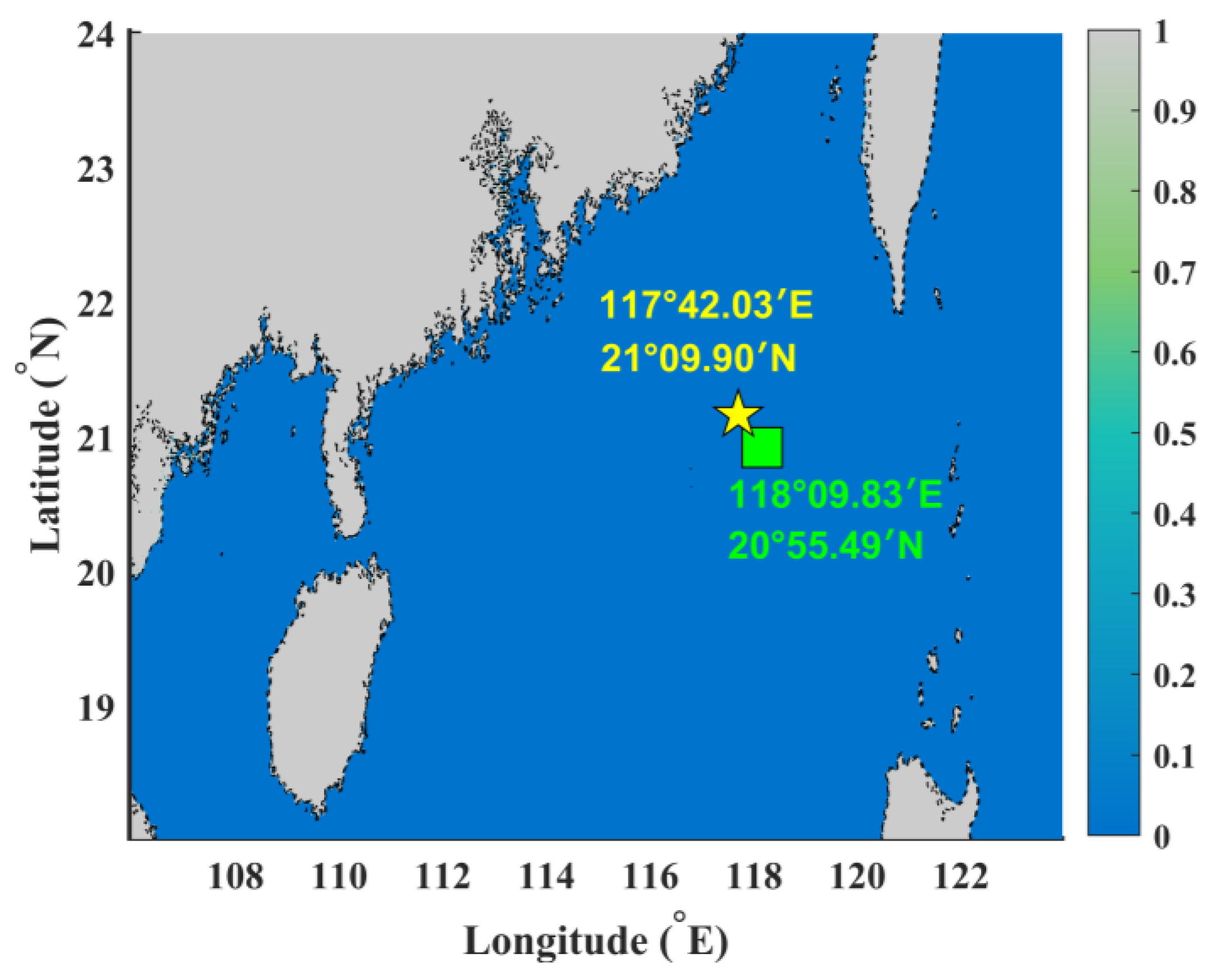
2. Data Collection
2.1. The Horizontal MTMI Dataset
2.2. The Vertical AVRP Dataset
3. Methodology
3.1. Empirical Mode Decomposition
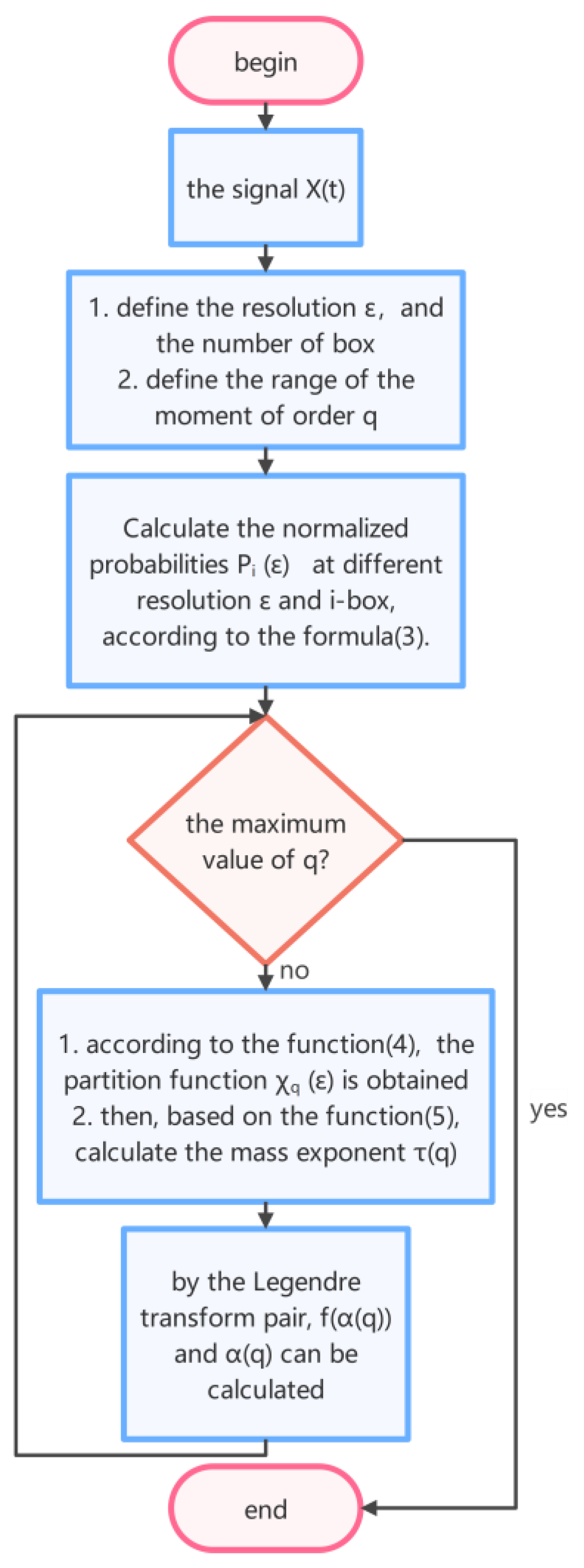
3.2. Multifractal cascade Model
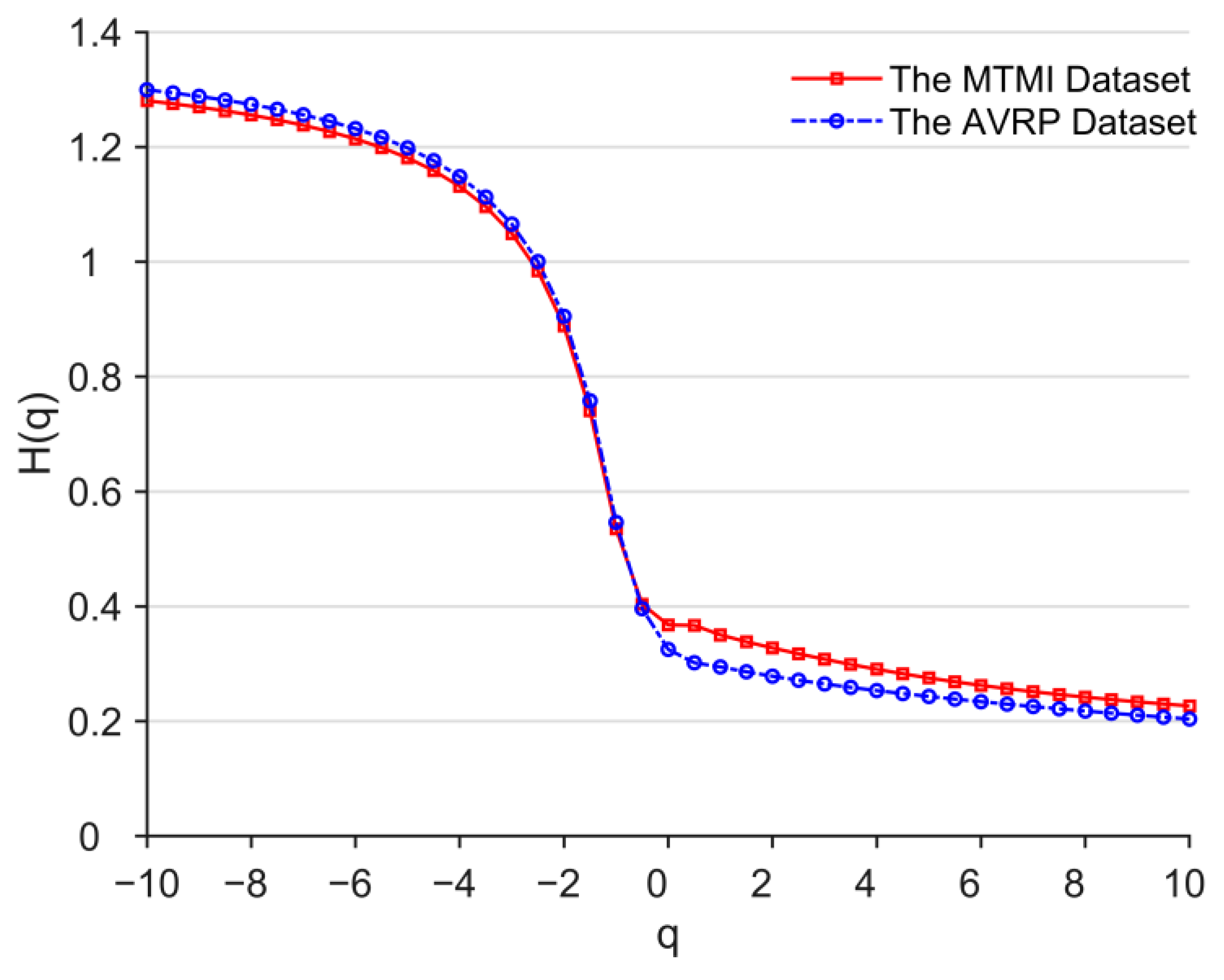
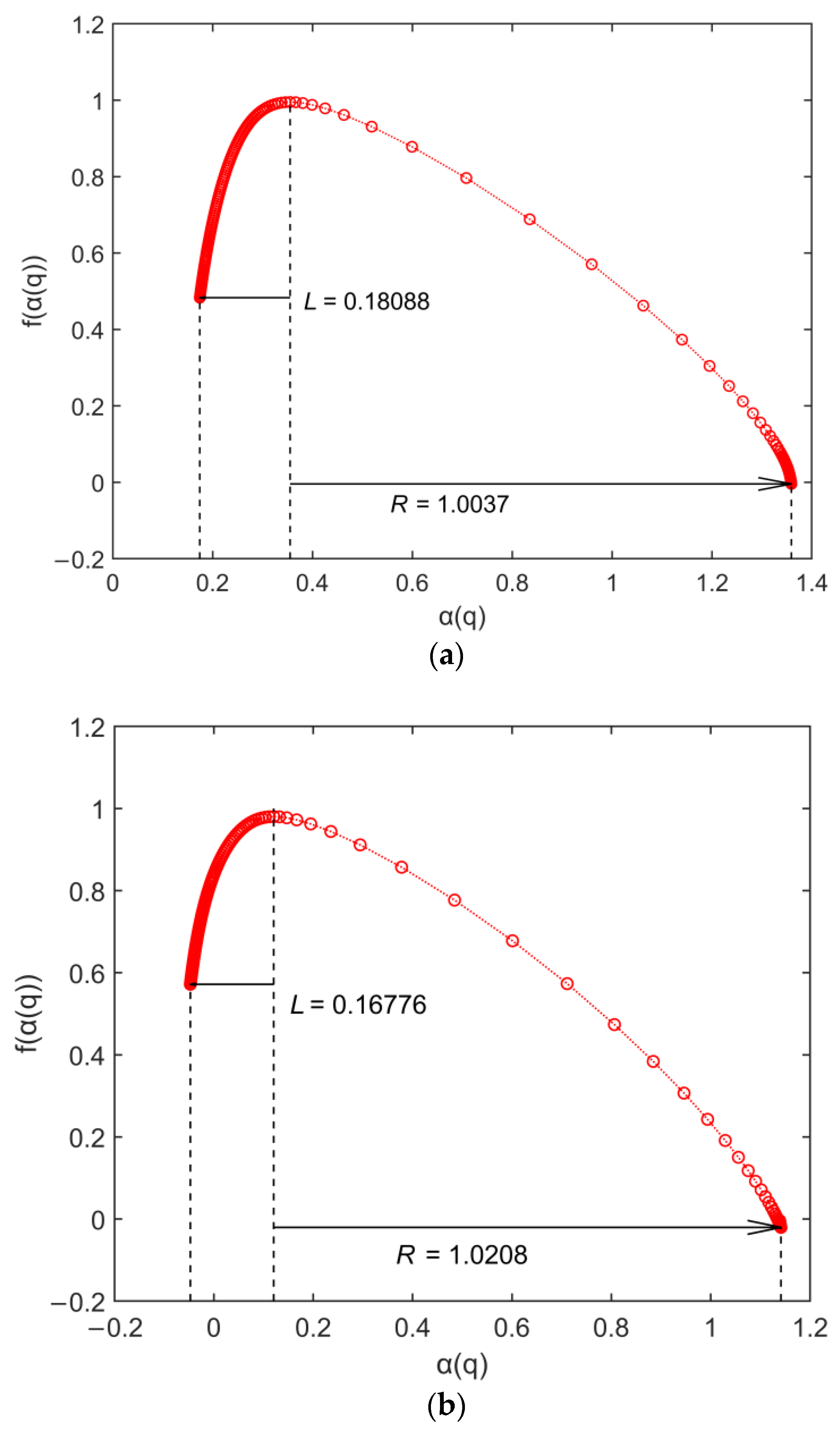
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McKeown, R.; Ostilla-Mónico, R.; Pumir, A.; Brenner, M.P.; Rubinstein, S.M. Turbulence generation through an iterative cascade of the elliptical instability. Sci. Adv. 2020, 6, eaaz2717. [Google Scholar] [CrossRef] [PubMed]
- Perri, S.; Carbone, V.; Vecchio, A.; Bruno, R.; Korth, H.; Zurbuchen, T.; Sorriso-Valvo, L. Phase-synchronization, energy cascade, and intermittency in solar-wind turbulence. Phys. Rev. Lett. 2012, 109, 245004. [Google Scholar] [CrossRef]
- Sorriso-Valvo, L.; Carbone, F.; Leonardis, E.; Chen, C.H.; Šafránková, J.; Němeček, Z. Multifractal analysis of high resolution solar wind proton density measurements. Adv. Space Res. 2017, 59, 1642–1651. [Google Scholar] [CrossRef]
- Benzi, R.; Biferale, L. Fully developed turbulence and the multifractal conjecture. J. Stat. Phys. 2009, 135, 977–990. [Google Scholar] [CrossRef][Green Version]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Saito, Y. Log-gamma distribution model of intermittency in turbulence. J. Phys. Soc. Jpn. 1992, 61, 403–406. [Google Scholar] [CrossRef]
- Schmitt, F.; La Vallee, D.; Schertzer, D.; Lovejoy, S. Empirical determination of universal multifractal exponents in turbulent velocity fields. Phys. Rev. Lett. 1992, 68, 305. [Google Scholar] [CrossRef]
- She, Z.-S.; Leveque, E. Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 1994, 72, 336. [Google Scholar] [CrossRef]
- Xu, C.-X.; Li, L.; Cui, G.-X.; Zhang, Z.-S. Multi-scale analysis of near-wall turbulence intermittency. J. Turbul. 2006, 7, N25. [Google Scholar] [CrossRef]
- Zhdankin, V.; Uzdensky, D.A.; Boldyrev, S. Temporal intermittency of energy dissipation in magnetohydrodynamic turbulence. Phys. Rev. Lett. 2015, 114, 065002. [Google Scholar] [CrossRef]
- Vela-Martín, A. The energy cascade as the origin of intense events in small-scale turbulence. J. Fluid Mech. 2022, 937, A13. [Google Scholar] [CrossRef]
- Foucher, F.; Ravier, P. Determination of turbulence properties by using empirical mode decomposition on periodic and random perturbed flows. Exp. Fluids 2010, 49, 379–390. [Google Scholar] [CrossRef]
- Breaker, L.C.; Carroll, D. A Closer Look at Power-Law Scaling Applied to Sea Surface Temperature from Scripps Pier Using Empirical Mode Decomposition. J. Atmos. Ocean. Technol. 2021, 38, 777–787. [Google Scholar] [CrossRef]
- Isern-Fontanet, J.; Turiel, A. On the connection between intermittency and dissipation in ocean turbulence: A multifractal approach. J. Phys. Oceanogr. 2021, 51, 2639–2653. [Google Scholar] [CrossRef]
- Luan, X.; Liu, X.; Yang, H.; Wang, S.; Hou, G.; Song, D. Characteristics of microstructure turbulence measurements with a moored instrument in the South China Sea. Mar. Technol. Soc. J. 2016, 50, 54–62. [Google Scholar] [CrossRef]
- Liu, X.; Luan, X.; Daniel Deng, Z.; Song, D.; Zang, S.; Yang, H.; Xin, J.; Chen, X. Autonomous ocean turbulence measurements from a moored upwardly rising profiler based on a buoyancy-driven mechanism. Mar. Technol. Soc. J. 2017, 51, 12–22. [Google Scholar] [CrossRef]
- Liu, X.; Song, D.; Yang, H.; Wang, X.; Nie, Y. An Integrated Spatio-Temporal Features Analysis Approach for Ocean Turbulence Using an Autonomous Vertical Profiler. Appl. Sci. 2021, 11, 9455. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ismail, D.K.B.; Lazure, P.; Puillat, I. Advanced spectral analysis and cross correlation based on the empirical mode decomposition: Application to the environmental time series. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1968–1972. [Google Scholar] [CrossRef]
- Pan, H.; Guo, Z.; Wang, Y.; Lv, X. Application of the EMD method to river tides. J. Atmos. Ocean. Technol. 2018, 35, 809–819. [Google Scholar] [CrossRef]
- Chen, W.; Ma, X.; Ma, Q.; Wen, J. Denoising method of the Φ-OTDR system based on EMD-PCC. IEEE Sens. J. 2020, 21, 12113–12118. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Lozovatsky, I.; Roget, E.; Planella, J.; Fernando, H.J.S.; Liu, Z. Intermittency of near-bottom turbulence in tidal flow on a shallow shelf. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Skákala, J.; Smyth, T.J. Complex coastal oceanographic fields can be described by universal multifractals. J. Geophys. Res. Ocean. 2015, 120, 6253–6265. [Google Scholar] [CrossRef]
- Cabrera-Brito, L.; Rodriguez, G.; García-Weil, L.; Pacheco, M.; Perez, E.; Waniek, J.J. Fractal analysis of deep ocean current speed time series. J. Atmos. Ocean. Technol. 2017, 34, 817–827. [Google Scholar] [CrossRef]
- De Souza, J.; Rostirolla, S.P. A fast MATLAB program to estimate the multifractal spectrum of multidimensional data: Application to fractures. Comput. Geosci. 2011, 37, 241–249. [Google Scholar] [CrossRef]
- So, G.-B.; So, H.-R.; Jin, G.-G. Enhancement of the box-counting algorithm for fractal dimension estimation. Pattern Recognit. Lett. 2017, 98, 53–58. [Google Scholar] [CrossRef]
- Salat, H.; Murcio, R.; Arcaute, E. Multifractal methodology. Phys. A Stat. Mech. Its Appl. 2017, 473, 467–487. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141. [Google Scholar] [CrossRef]


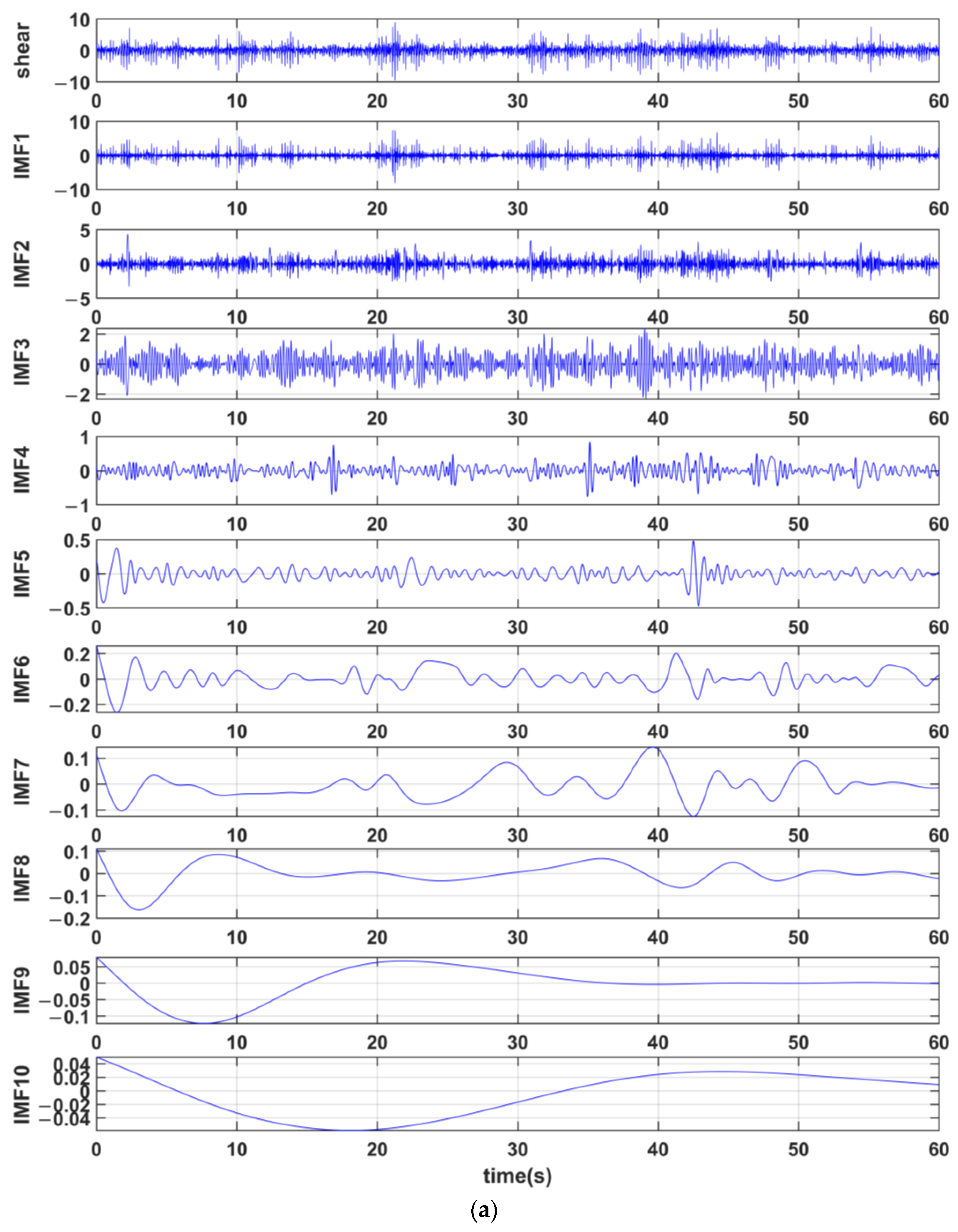
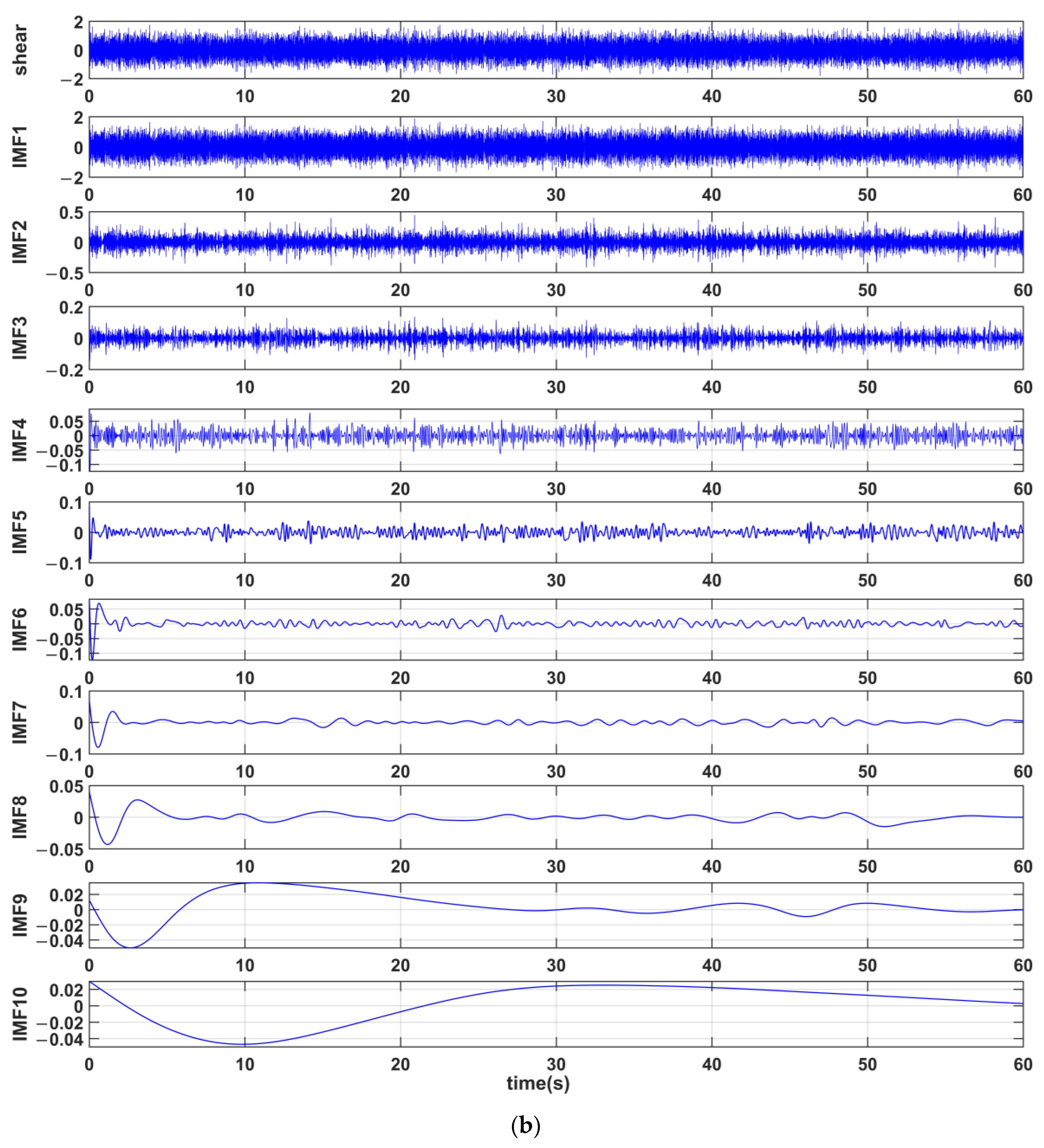

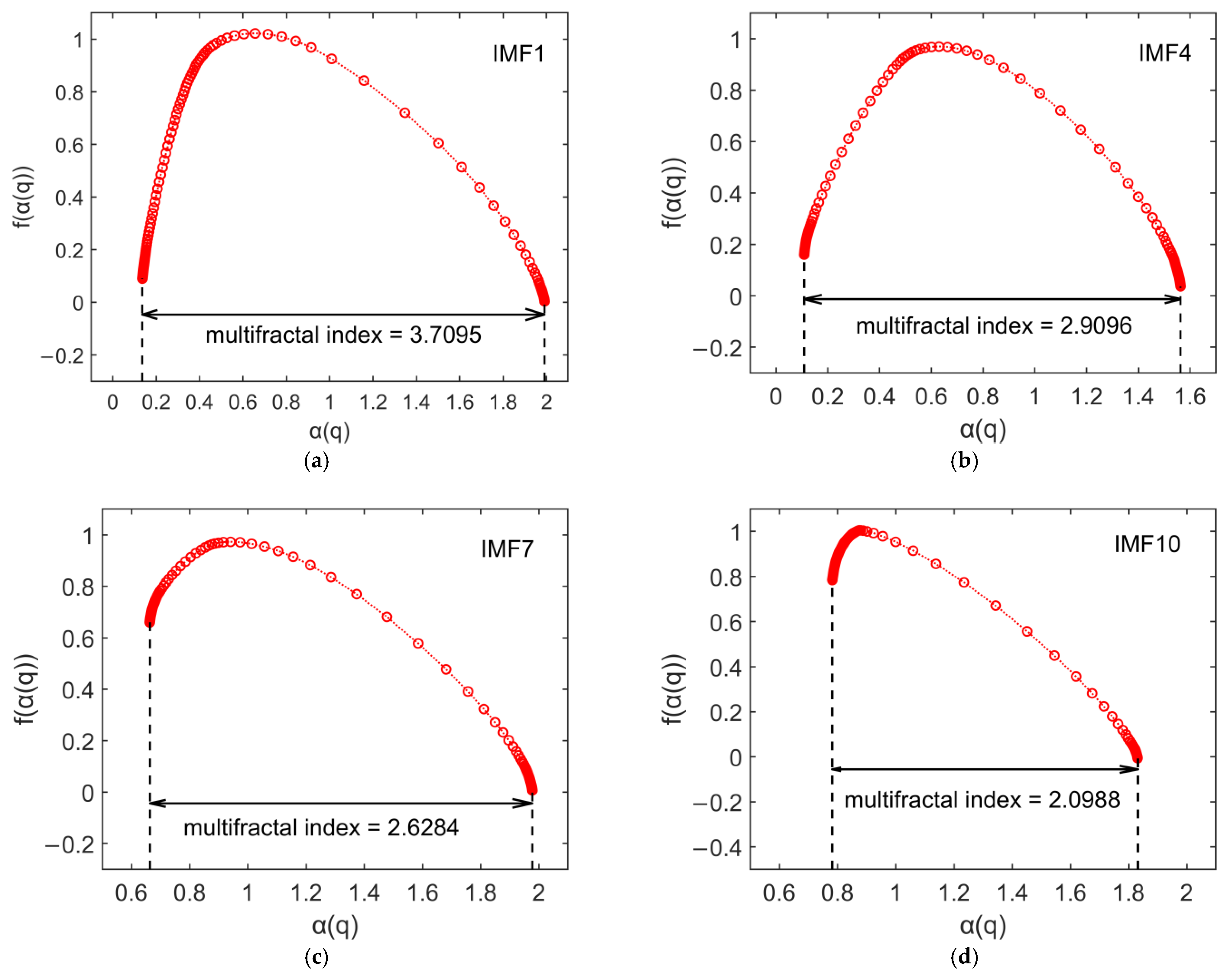

| IMFs | MTMI Dataset | AVRP Dataset |
|---|---|---|
| IMF1 | 3.0103 | 3.7095 |
| IMF2 | 2.5663 | 3.2598 |
| IMF3 | 2.6351 | 3.2339 |
| IMF4 | 2.5427 | 2.9096 |
| IMF5 | 2.4040 | 3.0028 |
| IMF6 | 2.2894 | 2.5732 |
| IMF7 | 2.4028 | 2.6284 |
| IMF8 | 2.3342 | 2.6646 |
| IMF9 | 2.3028 | 2.3724 |
| IMF10 | 1.9056 | 2.0988 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, Y.; Song, D.; Yang, H.; Li, X. A Multifractal Cascade Model for Energy Evolution and Dissipation in Ocean Turbulence. J. Mar. Sci. Eng. 2023, 11, 1768. https://doi.org/10.3390/jmse11091768
Liu X, Zhang Y, Song D, Yang H, Li X. A Multifractal Cascade Model for Energy Evolution and Dissipation in Ocean Turbulence. Journal of Marine Science and Engineering. 2023; 11(9):1768. https://doi.org/10.3390/jmse11091768
Chicago/Turabian StyleLiu, Xiuyan, Yufei Zhang, Dalei Song, Hua Yang, and Xinyu Li. 2023. "A Multifractal Cascade Model for Energy Evolution and Dissipation in Ocean Turbulence" Journal of Marine Science and Engineering 11, no. 9: 1768. https://doi.org/10.3390/jmse11091768
APA StyleLiu, X., Zhang, Y., Song, D., Yang, H., & Li, X. (2023). A Multifractal Cascade Model for Energy Evolution and Dissipation in Ocean Turbulence. Journal of Marine Science and Engineering, 11(9), 1768. https://doi.org/10.3390/jmse11091768





