Underwater Geomagnetic Localization Based on Adaptive Fission Particle-Matching Technology
Abstract
1. Introduction
- Particle-matching technology is employed to realize underwater geomagnetic localization.
- An adaptive fission particle-filtering algorithm is proposed to solve the problem of particle degeneration and particle impoverishment. Compared with advanced intelligent particle-filtering methods, our method achieves better localization accuracy.
- The proposed method was tested in a marine environment, and the results show that our proposed geomagnetic localization method can effectively achieve underwater navigation error correction.
2. Principle of Geomagnetic Matching Localization
3. Problems and Methods
3.1. Particle Filter
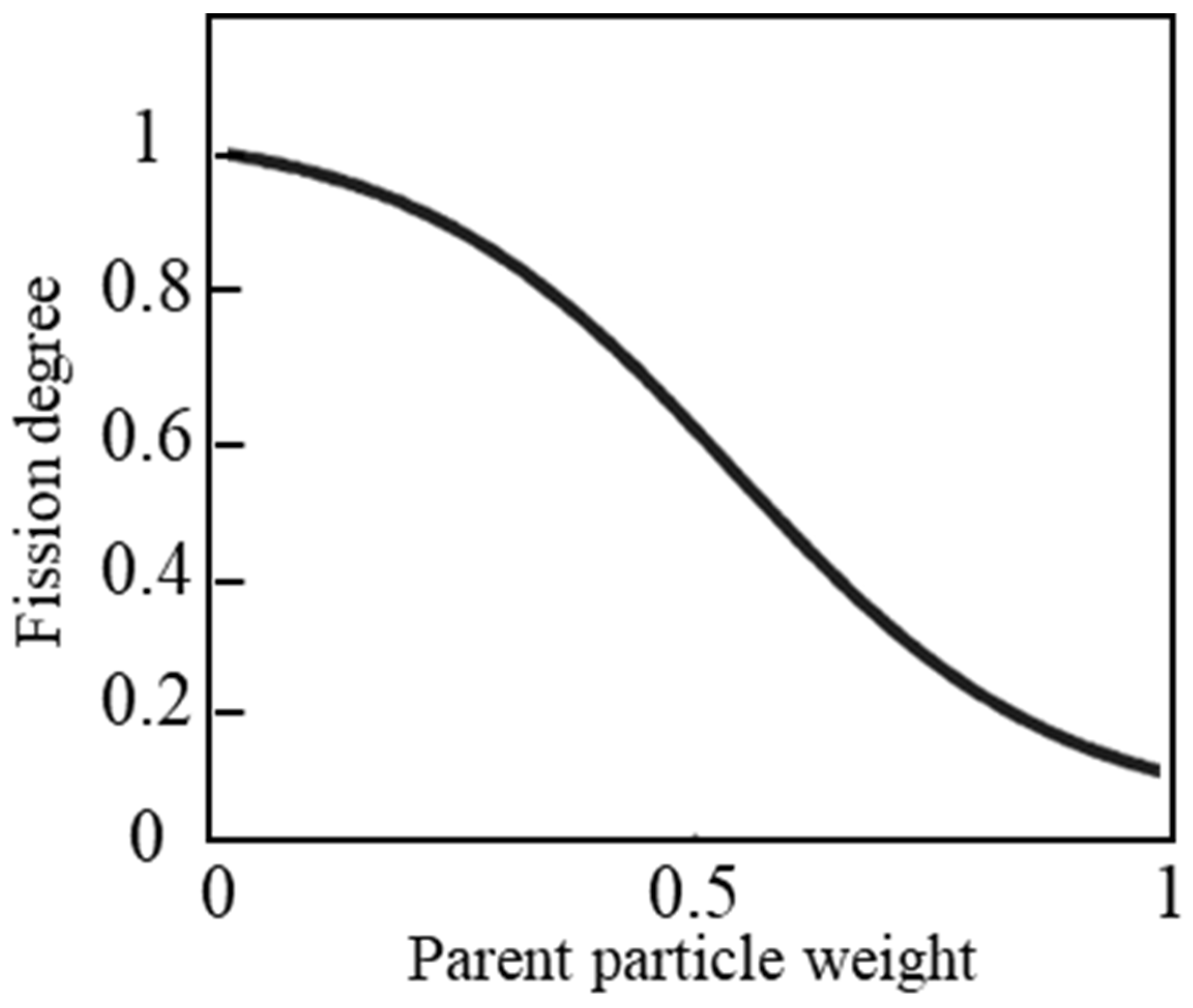
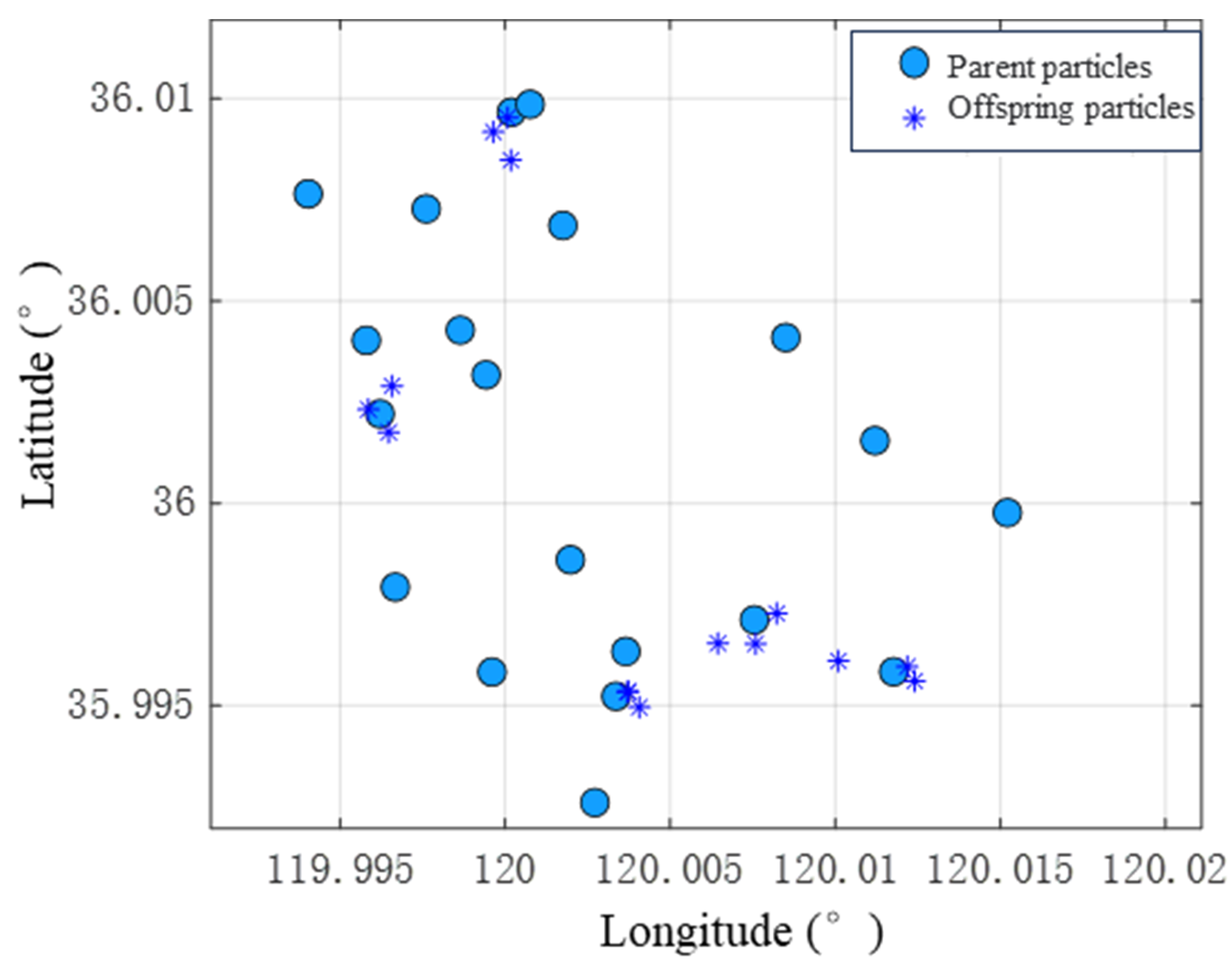
3.2. Geomagnetic Localization with Adaptive Particle Fission
| Algorithm 1: The adaptive fission particle-filtering geomagnetic matching localization |
|
|
|
|
|
|
|
4. Experiments
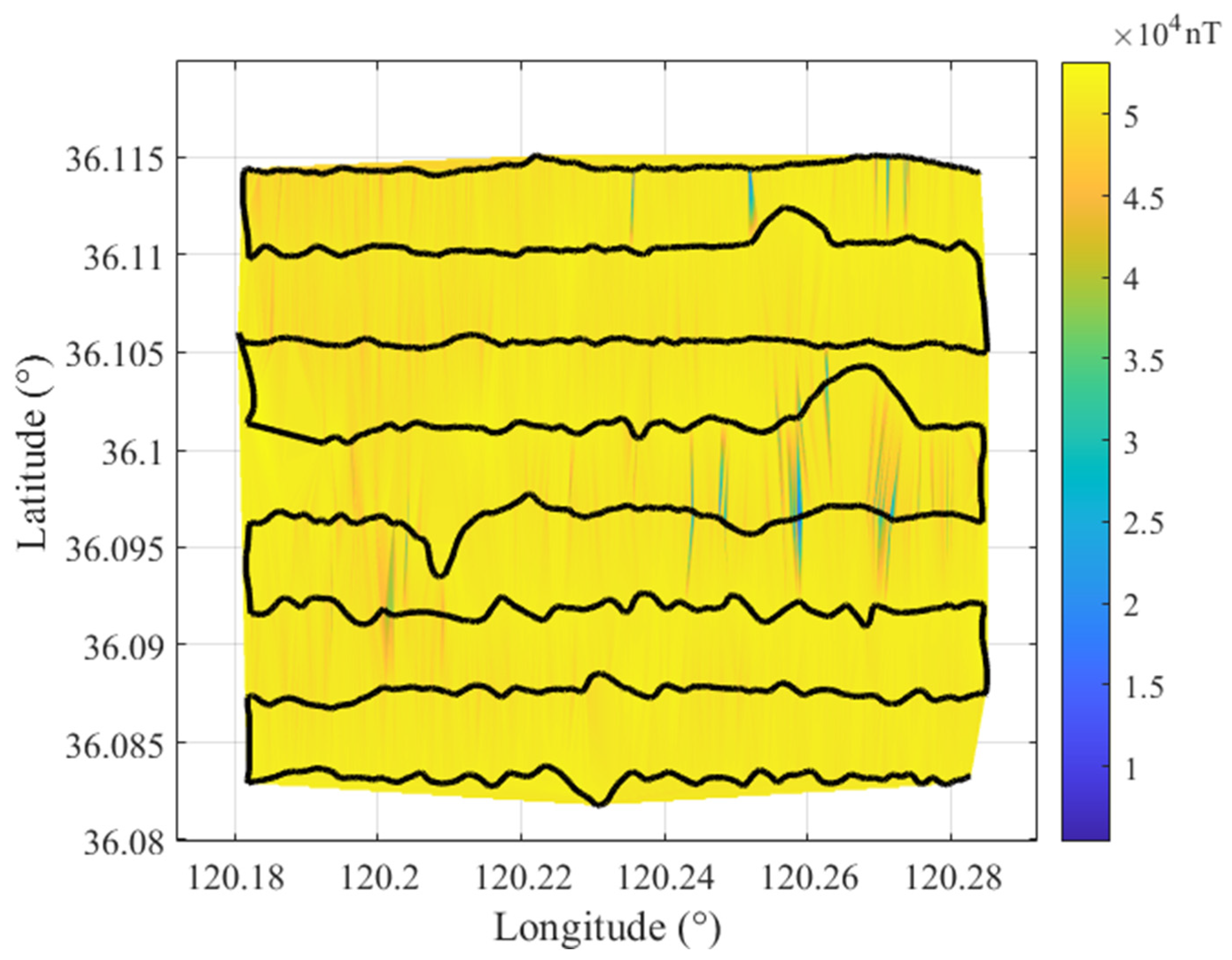
4.1. Experimental Setup
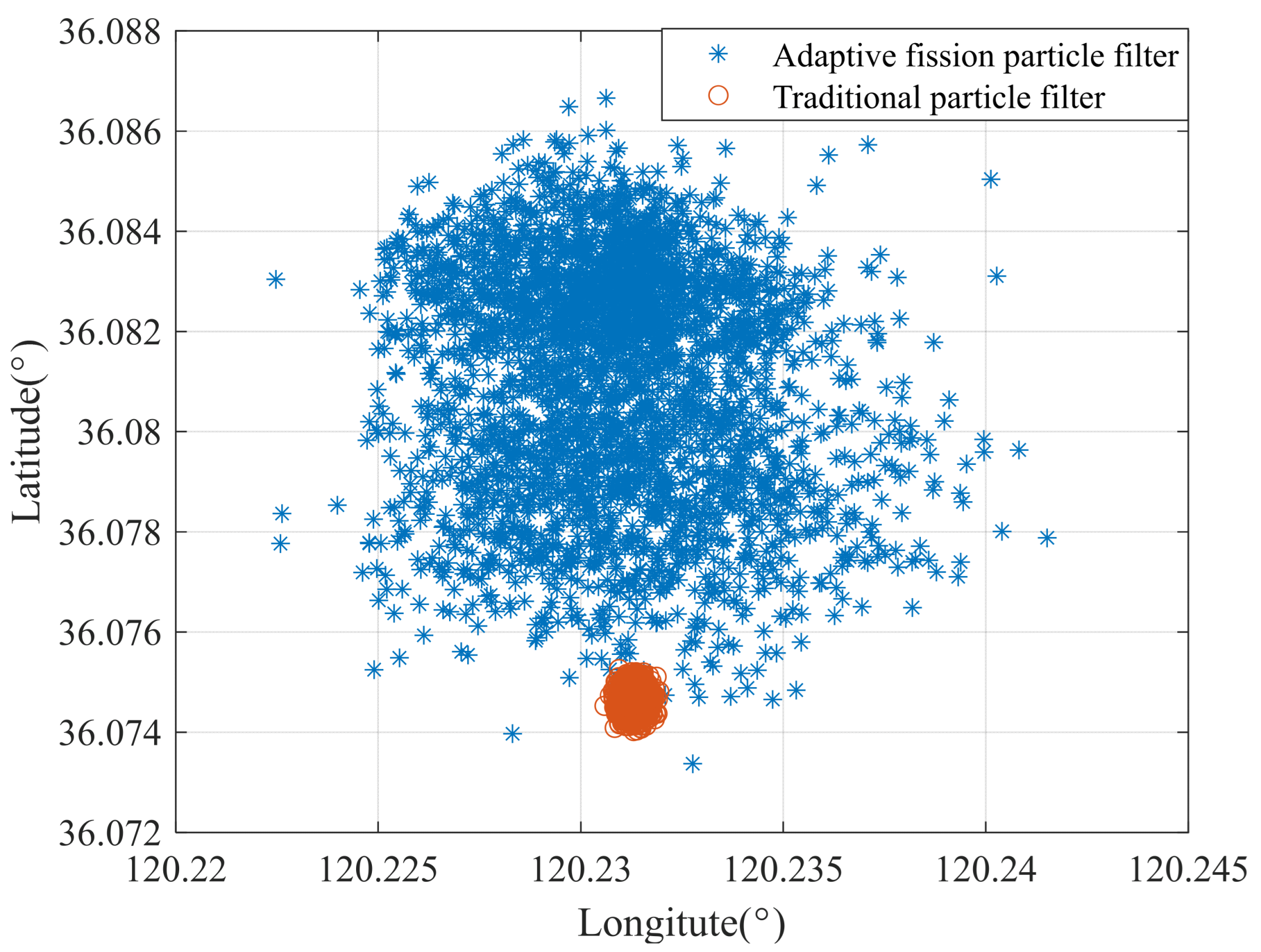
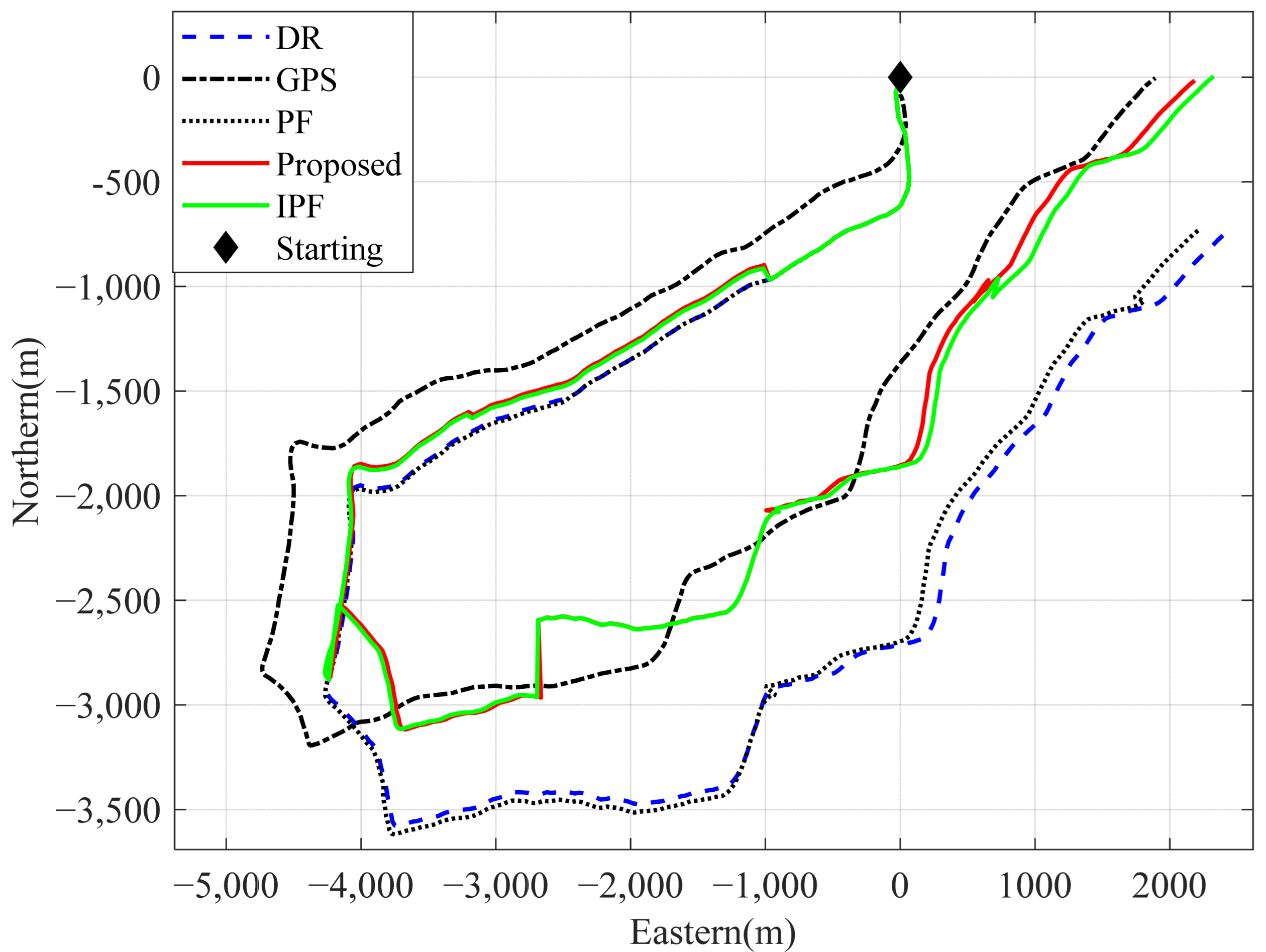
4.2. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, T.; Ding, S.; Li, Y.; Fan, J. A review of terrain aided navigation for underwater vehicles. OcEng 2023, 281, 114779–114795. [Google Scholar] [CrossRef]
- Zhou, J.; Pang, L.; Zhang, D.; Zhang, W. Underwater Image Enhancement Method via Multi-Interval Subhistogram Perspective Equalization. IJOE 2023, 48, 474–488. [Google Scholar] [CrossRef]
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and Localization: A Review. IJOE 2014, 39, 131–149. [Google Scholar] [CrossRef]
- Mu, X.; He, B.; Wu, S.; Zhang, X.; Song, Y.; Yan, T. A practical INS/GPS/DVL/PS integrated navigation algorithm and its application on Autonomous Underwater Vehicle. Appl. Ocean Res. 2021, 106, 102441. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, J.; Zhang, W.; Zifan, L. Multi-view underwater image enhancement method via embedded fusion mechanism. Eng. Appl. Artif. Intell. 2023, 121, 105946. [Google Scholar] [CrossRef]
- Maurelli, F.; Krupiński, S.; Xiang, X.; Petillot, Y. AUV localisation: A review of passive and active techniques. Int. J. Intell. Robot. Appl. 2021, 6, 246–269. [Google Scholar] [CrossRef]
- Minligareev, V.T.; Sazonova, T.V.; Arutyunyan, D.A.; Tregubov, V.V.; Khotenko, Y.N. Geophysical Support of Advanced Autonomous Magnetometric Navigation Systems. Gyroscopy Navig. 2020, 11, 350–356. [Google Scholar] [CrossRef]
- Xie, W.; Li, Q.; Huang, L.; Qu, Z.; Wang, Z. A Robust Geomagnetic Matching Algorithm Based on L1 Norm. In Proceedings of the 2018 Eighth International Conference on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Harbin, China, 19–21 July 2018; pp. 1209–1214. [Google Scholar]
- Li, H.; Liu, M.Y.; Liu, K. Bio-inspired geomagnetic navigation method for autonomous underwater vehicle. J. Syst. Eng. Elec. 2017, 28, 1203–1209. [Google Scholar] [CrossRef][Green Version]
- Bhat, P.G.; Subudhi, B.N.; Veerakumar, T.; Laxmi, V.; Gaur, M.S. Multi-Feature Fusion in Particle Filter Framework for Visual Tracking. IEEE Sens. J. 2020, 20, 2405–2415. [Google Scholar] [CrossRef]
- Karshakov, E.V.; Pavlov, B.V.; Tkhorenko, M.Y.; Papusha, I.A. Promising Map-Aided Aircraft Navigation Systems. Gyroscopy Navig. 2021, 12, 38–49. [Google Scholar] [CrossRef]
- Wang, A.; Ou, X. PDR/geomagnetic fingerprint indoor positioning method based on particle filter. Bull. Surv. Mapp. 2021, 1, 24–28. [Google Scholar]
- Chen, Z.; Zhang, Q.; Pan, M.C.; Chen, D.X.; Wan, C.B.; Wu, F.H.; Liu, Y. A New Geomagnetic Matching Navigation Method Based on Multidimensional Vector Elements of Earth’s Magnetic Field. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1289–1293. [Google Scholar] [CrossRef]
- Viset, F.; Helmons, R.; Kok, M. An Extended Kalman Filter for Magnetic Field SLAM Using Gaussian Process Regression. Sensors 2022, 22, 2833–2852. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Shen, T.; Li, Z. Segmented Matching Method of Multi-Geophysics Field SLAM Data Based on LSTM. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 147–151. [Google Scholar]
- Hong, L. Research on the Geomagnetic Bio-Inspired Navigation for AUV Based on Optimization Searching Strategy; Northwestern Polytechnical University: Xi’an, China, 2018. [Google Scholar]
- Wu, Z.; Hu, X.; Wu, M.; Mu, H.; Cao, J.; Zhang, K.; Tuo, Z. An experimental evaluation of autonomous underwater vehicle localization on geomagnetic map. Appl. Phys. Lett. 2013, 103, 104102. [Google Scholar] [CrossRef]
- Li, X.; Cheng, D.; Zhou, Z. A matching Algorithm Based on the Gradient of the Total Geomagnetic. Chin. J. Sens. Actuators 2018, 30, 1869–1875. [Google Scholar]
- Zhang, Q.; Li, Y.; Ma, T.; Cong, Z.; Zhang, W. Bathymetric Particle Filter SLAM With Graph-Based Trajectory Update Method. IEEE Access 2021, 9, 85464–85475. [Google Scholar] [CrossRef]
- Stepanov, O.A.; Toropov, B. Nonlinear filtering for map-aided navigation. Part 1. An overview of algorithms. Gyroscopy Navig. 2015, 6, 324–337. [Google Scholar] [CrossRef]
- Kuptametee, C.; Aunsri, N. A review of resampling techniques in particle filtering framework. Measurement 2022, 193, 110836. [Google Scholar] [CrossRef]
- Quintas, J.a.; Cruz, J.; Pascoal, A.; Teixeira, F.C. A Comparison of Nonlinear Filters for Underwater Geomagnetic Navigation. In Proceedings of the 2020 IEEE/OES Autonomous Underwater Vehicles Symposium (AUV), St. Johns, NL, Canada, 30 September–2 October 2020. [Google Scholar]
- Solin, A.; Särkkä, S.; Kannala, J.; Rahtu, E. Terrain navigation in the magnetic landscape: Particle filtering for indoor positioning. In Proceedings of the 2016 European Navigation Conference (ENC), Helsinki, Finland, 30 May–2 June 2016. [Google Scholar]
- Zhou, J.; Yang, T.; Zhang, W. Underwater vision enhancement technologies: A comprehensive review, challenges, and recent trends. Appl. Intell. 2022, 53, 3594–3621. [Google Scholar] [CrossRef]
- Lu, L.; Wei, D.; Ji, X.; Yuan, H. Review of Geomagnetic Positioning Method. Navig. Position Timing 2022, 9, 118–130. [Google Scholar]
- Zhang, Q.; Li, Y.; Ma, T.; Cong, Z.; Zhang, W. Bathymetric Particle Filter SLAM Based on Mean Trajectory Map Representation. IEEE Access 2021, 9, 71725–71736. [Google Scholar] [CrossRef]
- Doucet, A.; Godsill, S.; Andrieu, C. On Sequential Monte Carlo Sampling Methods for Bayesian filtering. Stat. Comput. 2000, 10, 197–208. [Google Scholar] [CrossRef]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2002, 50, 174–188. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X. Intelligent Particle Filter and Its Application on Fault Detection of Nonlinear System. IEEE Trans. Ind. Electron. 2015, 62, 3852–3861. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Y.; Xu, S.; Cao, H.; Si, M. Indoor Positioning Integrating PDR/Geomagnetic Positioning Based on the Genetic-Particle Filter. Appl. Sci. 2020, 10, 668. [Google Scholar] [CrossRef]
- Xue, H.; Hongbo, L.; Yue, L.; Haitao, M.; Xian, Z. Adaptive Fission Particle Filter for Seismic Random Noise Attenuation. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1918–1922. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Shen, T.; Li, Y.; Zhang, W. Bionic Magnetic Compass Algorithm Based on Radical Pair Theory. IEEE Sens. J. 2022, 22, 23812–23820. [Google Scholar] [CrossRef]
- Chulliat, A.; Brown, W.; Alken, P.; Beggan, C.; Nair, M.; Cox, G.; Woods, A.; Macmillan, S.; Meyer, B.; Paniccia, M. The US/UK World Magnetic Model for 2020–2025: Technical Report; NOAA: Silver Spring, MD, USA, 2020. [Google Scholar]
- Available online: http://www.sepc.ac.cn/cosmicRays1.php (accessed on 1 January 2023).
- Asraf, O.; Shama, F.; Klein, I. PDRNet: A Deep-Learning Pedestrian Dead Reckoning Framework. IEEE Sens. J. 2022, 22, 4932–4939. [Google Scholar] [CrossRef]





| Magnetometer | Inertial Measurement Unit (IMU) | Integrated Navigation | |||
|---|---|---|---|---|---|
| Accuracy/axis | 0.5% Reading ±0.1% FS | Acceleration zero-bias stability | ≤0.1 mg | Heading accuracy | 0.1° |
| Range | ±100 μT | Acceleration range | ±5 g | Attitude accuracy | 0.1° (1) |
| Orthogonal error | <0.1° | Gyroscope zero-bias stability | 10°/h | Position accuracy | ≤1.2 m |
| Resolution | 0.1 nT | Gyroscope range | ±500°/s | Velocity accuracy | 0.02 m/s |
| Rate | 10 Hz | Rate | 100 Hz | Rate | 10 Hz |
| Traditional Particle Filter | Intelligent Particle Filter | Proposed Method | ||||
|---|---|---|---|---|---|---|
| Test 1 | Test 2 | Test 1 | Test 2 | Test 1 | Test 2 | |
| RMSE | 804.64 | 631.75 | 819.42 | 501.50 | 767.18 | 482.40 |
| Mean positioning error | 674.06 | 582.18 | 685.08 | 468.61 | 647.99 | 444.89 |
| Error at the end | 138.08 | 794.93 | 119.02 | 433.23 | 43.68 | 292.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Li, Z.; Yang, W.; Shen, T.; Liang, D.; He, Q. Underwater Geomagnetic Localization Based on Adaptive Fission Particle-Matching Technology. J. Mar. Sci. Eng. 2023, 11, 1739. https://doi.org/10.3390/jmse11091739
Yu H, Li Z, Yang W, Shen T, Liang D, He Q. Underwater Geomagnetic Localization Based on Adaptive Fission Particle-Matching Technology. Journal of Marine Science and Engineering. 2023; 11(9):1739. https://doi.org/10.3390/jmse11091739
Chicago/Turabian StyleYu, Huapeng, Ziyuan Li, Wentie Yang, Tongsheng Shen, Dalei Liang, and Qinyuan He. 2023. "Underwater Geomagnetic Localization Based on Adaptive Fission Particle-Matching Technology" Journal of Marine Science and Engineering 11, no. 9: 1739. https://doi.org/10.3390/jmse11091739
APA StyleYu, H., Li, Z., Yang, W., Shen, T., Liang, D., & He, Q. (2023). Underwater Geomagnetic Localization Based on Adaptive Fission Particle-Matching Technology. Journal of Marine Science and Engineering, 11(9), 1739. https://doi.org/10.3390/jmse11091739









